:THE COSMOLOGICAL OTOC: Formulating New Cosmological Micro-Canonical Correlation Functions for Random Chaotic Fluctuations in Out-Of-Equilibrium Quantum Statistical Field Theory
Abstract
| Contents | ||||
| 1 | Introduction | 4 | ||
| 2 | Formulation of OTOC in Cosmology | 18 | ||
| 2.1 | General Remarks on OTOC……………………………………………………………………………………………… | 18 | ||
| 2.2 | Eigenstate Representation of OTOC in Quantum Statistical Mechanics…………………………………………… | 20 | ||
| 2.3 | Constructing OTOC in Cosmology……………………………………………………………………………………… | 23 | ||
| 2.3.1 | For Massless Scalar Field……………………………………………………………………………………… | 29 | ||
| 2.3.2 | For Partially Massless Scalar Field……………………………………………………………………………… | 33 | ||
| 2.3.3 | For Massive Scalar Field……………………………………………………………………………………… | 34 | ||
| 3 | Quantum Micro-Canonical OTO Amplitudes and OTOC in Cosmology | 36 | ||
| 3.1 | Computational Strategy……………………………………………………………………………………………… | 37 | ||
| 3.2 | Classical Mode Functions in Cosmology……………………………………………………………………………… | 38 | ||
| 3.3 | Quantum Mode Function in Cosmology……………………………………………………………………………… | 41 | ||
| 3.4 | Canonical Quantization of Cosmological Hamiltonian: Classical to Quantum Map……… | 43 | ||
| 3.5 | Cosmological Two-Point and Four-Point “In-In" OTO Micro-Canonical Amplitudes……… | 44 | ||
| 3.5.1 | OTOC Meets Cosmology……………………………………………………………………………………… | 44 | ||
| 3.5.2 | Fourier Space Representation of the Commutator Bracket: Application to Two-Point OTOC……… | 46 | ||
| 3.5.3 | Fourier Space Representation of Square of the Commutator Bracket Application to Four-PointOTOC……………………………………………………………………………………………… | 48 | ||
| 3.6 | Cosmological Thermal Partition Function: Quantum Version……………………………………………………… | 52 | ||
| 3.6.1 | Quantum Vacuum State in Cosmology……………………………………………………………………… | 52 | ||
| 3.6.2 | Quantum Partition Function in Terms of Rescaled Field Variable……………………………………… | 52 | ||
| 3.6.3 | Quantum Partition Function in Terms of Curvature Perturbation Field Variable……………………………………… | 53 | ||
| 3.7 | Trace of Two-Point “In-In" OTO Amplitude for Cosmology……………………………………………………………………… | 54 | ||
| 3.8 | OTOC from Regularised Two-Point “In-In" OTO Micro-Canonical Amplitude: Rescaled Field Version……………………………………………………………………………………… | 55 | ||
| 3.9 | OTOC from Regularised Four-Point “In-In" OTO Micro-Canonical Amplitude: Curvature Perturbation Field Version……………………………………………………………………………………………………………… | 56 | ||
| 3.10 | Trace of Four-Point “In-In" OTO Amplitude for Cosmology……………………………………………………………… | 58 | ||
| 3.11 | OTOC from Regularised Four-Point “In-In" OTO Micro-Canonical Amplitude: Rescaled Field Version……………………………………………………………… | 60 | ||
| 3.11.1 | Without Normalization……………………………………………………………… | 60 | ||
| 3.11.2 | With Normalization……………………………………………………………… | 64 | ||
| 3.12 | OTOC from Regularised Four-Point “In-In" OTO Micro-Canonical Amplitude: Curvature Perturbation Field Version……………… | 64 | ||
| 3.12.1 | Without Normalization…………………………………………………………………………… | 64 | ||
| 3.12.2 | With Normalization…………………………………………………………………………… | 64 | ||
| 4 | Numerical ResultsI: Interpretation of Two-Point Micro-Canonical OTOC in Cosmology | 65 | ||
| 5 | Numerical ResultsII: Interpretation of Four-Point Micro-Canonical OTOC in Cosmology | 73 | ||
| 6 | Lyapunov Spectrum and Quantum Chaos in Cosmology | 86 | ||
| 7 | Numerical ResultsIII: Interpretation of Cosmological Lyapunov Spectrum | 89 | ||
| 8 | Classical Limit of Micro-Canonical OTO Amplitudes and Related OTOC in Cosmology | 93 | ||
| 8.1 | Computational Strategy……………………………………………………………………………… | 93 | ||
| 8.2 | Classical Limit of Cosmological Two-Point “In-In" OTO Micro-Canonical Amplitudes……………… | 94 | ||
| 8.3 | Classical Limit of Cosmological Four-Point “In-In" OTO Micro-Canonical Amplitudes……………… | 95 | ||
| 8.4 | Cosmological Micro-Canonical Partition Function: Classical Version……………………………………………… | 98 | ||
| 8.4.1 | Classical Micro-Canonical Partition Function in Terms of Rescaled Field Variable | 98 | ||
| 8.4.2 | Classical Micro-Canonical Partition Function in Terms of Curvature Perturbation Field Variable…………………………………… | 99 | ||
| 8.5 | Classical Limit of Cosmological Two-Point Micro-Canonical OTOC: Rescaled Field Version | 99 | ||
| 8.6 | Classical Limit of Cosmological Two-Point Micro-Canonical OTOC: Curvature Perturbation Field Version………………………………… | 101 | ||
| 8.7 | Classical Limit of Cosmological Four-Point Micro-Canonical OTOC: Rescaled Field Version……………………………………… | 101 | ||
| 8.7.1 | Without Normalization……………………………………………………………………………… | 101 | ||
| 8.7.2 | With Normalization……………………………………………………………………………… | 103 | ||
| 8.8 | Classical Limit of Cosmological Four-Point Micro-Canonical OTOC: Curvature Perturbation Field Version……………………………………… | 104 | ||
| 8.8.1 | Without Normalization……………………………………………………………………… | 104 | ||
| 8.8.2 | With Normalization……………………………………………………………………………… | 104 | ||
| 9 | Summary and Outlook | 105 | ||
| A | Asymptotic Behaviour of the Cosmological Mode Functions | 108 | ||
| B | WKB Solution of the Cosmological Mode Functions for Time Dependent Protocols | 115 | ||
| C | Quantum Two-Point OTO Micro-Canonical Amplitudes for Cosmology | 116 | ||
| C.1 | Definition of Micro-Canonical OTO Amplitude ……………………………… | 116 | ||
| C.2 | Definition of Micro-Canonical OTO Amplitude ……………………………… | 117 | ||
| D | Quantum Four-Point OTO Micro-Canonical Amplitudes for Cosmology | 117 | ||
| D.1 | Definition of Micro-Canonical OTO Amplitude ……………………… | 117 | ||
| D.2 | Definition of Micro-Canonical OTO Amplitude ……………………… | 118 | ||
| D.3 | Definition of Micro-Canonical OTO Amplitude ……………………… | 119 | ||
| D.4 | Definition of Micro-Canonical OTO Amplitude ……………………… | 120 | ||
| E | Computation of Classical Limit of Four-Point “In-In” OTO Micro-Canonical Amplitudes for Cosmology | 121 | ||
| F | Computation of Quantum Micro-Canonical Partition Function in Cosmology | 124 | ||
| F.1 | Quantum Micro-Canonical Partition Function in Terms of Rescaled Field Variable……… | 124 | ||
| F.2 | Quantum Micro-Canonical Partition Function in Terms of Curvature Perturbation Field Variable……………………………………… | 125 | ||
| G | Computation of Classical Micro-Canonical Partition Function in Cosmology | 126 | ||
| G.1 | Classical Micro-Canonical Partition Function in Terms of Rescaled Field Variable……… | 126 | ||
| G.2 | Classical Micro-Canonical Partition Function in Terms of Curvature Perturbation Field Variable………………………………………… | 127 | ||
| H | Computation of the Trace of the Two-Point Amplitude in Micro-Canonical OTOC | 128 | ||
| I | Computation of the Trace of the Four-Point Amplitude in Micro-Canonical OTOC | 130 | ||
| J | Time Dependent Two-Point Amplitude in Micro-Canonical OTOC | 135 | ||
| K | Time Dependent Four-Point Amplitudes in Micro-Canonical OTOC | 137 | ||
| K.1 | Computation of ……………………………………………………………………………………………… | 137 | ||
| K.2 | Computation of ……………………………………………………………………………………………… | 151 | ||
| K.3 | Computation of ……………………………………………………………………………………………… | 151 | ||
| K.4 | Computation of ……………………………………………………………………………………………… | 151 | ||
| K.5 | Computation of ……………………………………………………………………………………………… | 152 | ||
| K.6 | Computation of ……………………………………………………………………………………………… | 152 | ||
| K.7 | Computation of ……………………………………………………………………………………………… | 152 | ||
| K.8 | Computation of ……………………………………………………………………………………………… | 153 | ||
| K.9 | Computation of ……………………………………………………………………………………………… | 153 | ||
| L | Computation of the Normalization Factor in Four-Point Micro-Canonical OTOCC | 153 | ||
| L.1 | Normalization Factor of Four-Point Micro-Canonical OTOC Computed from Rescaled Field Variable……………………………………………………………………………………………………… | 153 | ||
| L.2 | Normalization Factor of Four-Point Micro-Canonical OTOC Computed from Curvature Perturbation Field Variable……………………………………………………………………………………… | 156 | ||
| M | Computation of the Normalization Factor in Classical Limit of Four-Point Micro-Canonical OTOC | 157 | ||
| M.1 | Normalization Factor of the Classical Version of Four-Point Micro-Canonical OTOC Computed from Rescaled Field Variable………… | 157 | ||
| M.2 | Normalization Factor of the Classical Version of Four-Point Micro-Canonical OTOC Computed from Curvature Perturbation Field Variable…………… | 158 | ||
| N | Thermal Trace Operation in Terms ofWave Function of the Universe in Cosmology | 159 | ||
| References | 160 | |||
1. Introduction
- Possibility I:The first possibility pointing towards the future observational aspects which can be probed by different ongoing and upcoming experiments to verify various theoretical features of primordial Cosmology. The most significant quantity which is possible to understand the underlying quantum field theory origin of the primordial physics is the tensor-to-scalar ratio. Detection of this with high statistical accuracy will provide us with the information regarding the generation of primordial gravitational waves, which will further confirm the exact origin of the primordial quantum mechanical fluctuations by exactly estimating the scale of inflation. Not only discriminating different frameworks of inflationary paradigm, but also the existence of alternatives to inflationary frameworks, i.e., bouncing cosmology [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90], cyclic cosmology [91,92,93,94,95,96], ekpyrotic scenario [97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112], etc., can also be verified by the confirmation of the primordial gravity waves. The next important quantity within the framework of primordial Cosmology is the study the existence of non-Gaussian features in the quantum mechanical fluctuations and the probability distribution profile of its related correlation functions. For this purpose, the study of bispectrum and trispectrum, which are basically representing the momentum-dependent amplitude of the three-point and four-point correlation function are very important. In the near future, through the upcoming cosmological missions, if it is possible to detect these non-Gaussian amplitudes with high statistical accuracy then more stringent constraints on the primordial physics are put. This is because of the fact that the probability distribution of such quantum fluctuations in the primordial universe is almost following Gaussian profile and a small but significant deviation from such Gaussianity will be extremely helpful to discriminate amongst various possible theoretical models of inflation which can be able to generate a significant amount of non-Gaussian amplitude in the context of three-point and four-point correlation functions. We are very hopeful for the detection of these important observables in near-future cosmological experiments. For this purpose, one needs to upgrade the present experimental tools and techniques or have to wait for upcoming future advanced experiments, which can able to measure these mentioned observables with high statistical accuracy. Now, we all know that for a single field inflationary paradigm the amplitude of the three point function is directly related to scalar spectral index, given by [38] (in ref. [38], the author have considered an additional contribution which is given by the following expression:where is the spectral index of the tensor power spectrum which is appearing from the perturbation of the primordial gravitational waves and not yet observed through CMB observations. On the other hand the scale-dependent factor, , is basically capturing some information regarding the bispectrum and the numerical value of this factor will lie within the window, . Since from inflationary paradigm and the contribution from the factor is very small, then one can easily neglect this terms from the full expression for the non-Gaussian amplitude of the three point scalar fluctuations. In the future, if we can able to detect the primordial gravitational waves at CMB B-modes and from that can able to extract the individual contribution of the tensor perturbation then adding the contribution of such terms will be more relevant in the present context of discussion):which in this literature is treated as a very strong theoretical probe, commonly known as Maldacena’s consistency relation. Now just from theoretical understanding of inflationary paradigm from this relation the expectation is that the amplitude of the three point non-Gaussian amplitude has to be very small for single filed slow-roll inflation. To detect this very small value, very high precision from observation is required. On the other hand, if the cosmological power spectrum have any additional characteristic features, like the running and running of spectral index then theoretically using the mentioned consistency relationship one can translate the statement in terms of the running or the certain scale dependence of the amplitude of the three point function. This fact can be expressed by the two new derived consistency conditions, which are given by,which further allows us to write a generic expansion for a scale-dependent three point non-Gaussian amplitude as:where the scale-dependent index is defined as:Here, it is important to note that is the momentum scale on which the CMB observation is performed and is computed in terms of scalar spectral index using the previously mentioned Maldacena’s consistency relation. All these three relations can be further written in terms of the slow-roll parameters, which can be constructed from the field derivative of the inflationary potentials or the time derivative from the Hubble parameter. Now as we have mentioned, if we can verify this relation through cosmological observation with high statistical accuracy, then not only the appearance of non-Gaussian fluctuations in the primordial cosmological perturbation can be immediately tested, but also the appearance of the scale dependence of primordial power spectrum through the running and running of the scalar spectral index can also be verified by considering the above mentioned consistency relations.
- Possibility II:The second possibility is pointing towards the probing of new physical concepts by incorporating additional but significant features within the framework of early universe Cosmology. Until now all of the features are studied by considering the fact that the quantum fluctuations appearing in the primordial universe is at thermal equilibrium. However, if the quantum mechanical systems which we use to study to describe the early universe Cosmology are not in thermal equilibrium then quantifying the quantum correlation functions within the framework of finite temperature out-of-equilibrium quantum field theory of Cosmology is extremely difficult to compute and until now in the literature of Cosmology no such framework is available using which one can pursue this specific computation. On the other hand, anybody can ask us here why at all computation and quantification of all such quantum mechanical correlation function for the primordial Cosmology describing an out-of-equilibrium is important at all and if these ideas can be provided theoretically then in which stages of the evolutionary scale of our universe this can be really implemented? The answer is very simple and it is already hidden there in the study of the early universe Cosmology. In the following we now explicitly mention about these phenomena where this methodology can be applicable:
- Stochasticity and particle production during inflation:During the epoch of inflation [40,49,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142], we describe the physics of inflationary paradigms with scalar field which have a negligible mass compared to the Hubble scale, which is treated as the reference characteristic scale of early universe Cosmology. However, during inflation many particle produces in a stochastic manner which have masses either of the order of Hubble scale or have mass very heavier than the Hubble scale. These particles are commonly known as partially massless or heavy scalar fields whose origin can be explained from the randomness appearing in the quantum mechanical stochastic fluctuation appearing in the early universe where various unknown out-of-equilibrium features play significant role. However, it is extremely difficult to quantify or describing this phenomenon correctly at the out-of-equilibrium regime of quantum field theory which consistently describe a quantum mechanical theory of primordial Cosmology. Additionally it is important to note that during the stochastic particle production during inflation due to the presence of randomness noise plays significant role to describe the quantum mechanical phenomenon during this particular epoch in the cosmological evolutionary time scale. However, we have a very small understanding regarding the time-dependent random noise within the framework of out-of-equilibrium quantum field theory until now. Only in some specific situations if we provide some additional constraints on the two-point and the one-point correlation of the time-dependent noise, which have the Gaussian probability distribution profile one can deal with noise. However, such analysis within the framework of quantum field theory is not exactly correct which in turn could not able to gives us the correct predictions from the quantum theory of early universe. One the other hand, we really do not know about the nature of the time-dependent noise which we are studying in the present context. This means we do not know that whether the time-dependent noise have Gaussian or non-Gaussian probability distribution profile, which information can be directly understandable if we really know the exact computation of N-point correlation functions of time-dependent noise in cosmology. A lot of attempts have been made within the framework of quantum-field theory to study the quantum mechanical features and the related N-point correlation functions to study the exact nature, behaviour and magnitude of the noise. However, apart from its rigor, not much is known about the detailed quantum filed theory structure from which one can reliably compute such correlation functions as quantum mechanics. Here lies one of the prime motivations to write this paper. Our expectation from the presented computation of this paper is that the cosmological version of OTOC is defined in a specific quantum mechanical vacuum state, which actually describes the initial condition in early universe Cosmology, which describes the randomness and stochastic features of quantum mechanical fluctuations in the out-of-equilibrium regime in a perfectly correct fashion. This is just not an arbitrary claim, but also one can appear at such conclusion by considering the basic understandings of the background physical phenomenon which describes the particle production mechanism during the epoch of inflation. Throughout our paper, we have explicitly established the framework for the first time in the Cosmology literature using which one can explicitly perform the computation of the cosmological correlation functions of the random quantum mechanical fluctuations in the out-of-equilibrium regime of quantum field theory. Instead of studying the quantum correlations with the time ordered or the anti-time ordered physics, in the present context cosmological OTOC functions are playing significant role to describe the underlying hidden features of out-of-equilibrium physics to describe the stochastic randomness during the particle production mechanism during inflation (here it is important to note that the Random Matrix Theory is an another alternative framework using which one can compute these quantum mechanical cosmological correlation functions within the framework of out-of-equilibrium quantum field theory [143,144]).
- Reheating / Warm Inflation:Reheating is an epoch in the evolutionary time scale of our universe which appears just after inflation. During inflation the inflaton field started slowly rolling through the valley of the inflationary potential under consideration and it is expected that after a certain time the inflaton field will reach the stable minimum of the potential and the inflationary mechanism just stops there. However, is the the end of the story? Obviously it is not the end. Once the inflation ends, the inflation field started oscillating around the stable minimum of the potential and started interacting with the valley of the potential as well as some other field, which we identify as the reheaton, the field who is mostly responsible for reheating (it is important to note that in the Cosmology literature there exists a few models of inflation where reheating is not required and without having any reheating phase in those models one can able to describe the genesis of the dark matter candidate theoretically. However, these models are very small in number and the construction of these models relies on various underlying assumptions, which may not be completely correct as far as the technical rigour of the quantum field theory for Cosmology is concerned. So for our discussion we stick to the general models of inflations which are developed from more reliable version of UV complete theories at very high energy scale and these models has to have the reheating phenomenon in the evolutionary cosmological time scale of our universe). As a consequence of such interactions enormous amount of heat is generated and the quantum mechanical system that we are studying immediately goes to its out-of-equilibrium phase. From the previous understanding of the subject it was extremely difficult to determine the quantum effects in terms of studying the quantum correlations in this out-of-equilibrium phase. However, it is expected from our basic understanding of quantum statistical mechanics that if we wait for long cosmological time scale then the system reaches the equilibrium where it is possible to associate an equilibrium reheating temperature associated with the system. After reaching equilibrium the reheaton field started decaying to some new particle contents which are responsible to describe the genesis of dark matter in the early universe Cosmology. That means without explaining the detailed quantum aspects throughout the total cosmological time scale in detail it is impossible to study the genesis of the dark matter contents of our universe and this actually motivates us to study this hidden unexplored phenomenon in this paper. Until now we have very less description available regarding the quantum mechanical aspects during the epoch of reheating. Only the quadratic and quartic inflationary models are studied phenomenologically in this context and it is until unknown how to quantify and estimate the quantum mechanical correlations and study the detailed quantum field theory aspects of reheating. On the other hand, as we have already mentioned, it is extremely important to determine the quantum mechanical correlations during this epoch to study the genesis of the dark matter contents where the principles of out-of-equilibrium quantum field theory will play significant role. However, until now there are no such significant inputs available from the theory side which can be able to provide us the relevant tools and techniques to compute such quantum mechanical correlation function and study various other quantum field theory aspects related to reheating at out-of-equilibrium. In this paper, we have established a detailed quantum field theory framework at the out-of-equilibrium phase which helps us to quantify the extremely relevant quantum mechanical correlation functions in terms of OTOCs. The methodology presented in this paper not only helps us to quantify the correlation at the out-of-equilibrium phase, but also provides us a detailed understanding about the equilibrium behaviour of the correlation functions at a large time limit in the cosmological time scale. Additionally, this detailed study through the cosmological generalization of OTOCs helps us to determine a lower bound on the reheating temperature in a completely model independent way. From the previously available understanding of the subject it was possible to give an estimate of the reheating temperature in a completely model-dependent way after knowing about the relativistic degrees of freedom which are participating during the epoch of reheating. However, apart from having a model-dependent expression, that expression actually relies on the scale of inflation completely, which is not known from the observation side until now; only an upper bound on the scale of inflation in terms of the tensor-to-scalar ratio is known from the observational probes. So the previously described method of determining the reheating temperature is not very reliable and only helps us to know about the upper bound on the reheating temperature in a completely model-dependent way. On the other hand, the present study helps us to determine the exact time-dependent behaviour of the reheating temperature and additionally provides a lower bound of reheating temperature which we have derived in a completely model independent way. As we proceed through the subject material of the paper, one can have a clear understanding about each of our big claim which we have explicitly established with detailed analysis. Apart from this, one can consider another well known framework, which is described by the warm inflationary paradigm [145,146], where the radiation appears due to the stochastic particle production concurrently with inflationary expansion in the early universe evolutionary time scale. Sometimes this framework can be treated as the finite temperature generalization of usual well known zero temperature inflationary paradigm, which is mostly studied in cosmology literature. The presence of the effect of radiation during the epoch of inflation implies that there is a possibility exists on which the epoch of inflation could smoothly end directly into a radiation-dominated epoch, particularly without having a separate reheating epoch. This is one of the early universe phenomena apart from reheating where the effect of out-of-equilibrium physics is significantly dominating and the detailed quantum field theoretic phenomena have not been studied yet in detail. Until now, from the previous work, it is very clear that this phenomenon is very model-dependent and only a few models have studied this possibility. This is because of the fact that handling the out-of-equilibrium dynamics in the quantum regime is extremely complicated. However, we are again very hopeful that, similar to reheating, OTOC at finite temperature studied in this paper is able to describe the quantum correlation functions for the warm inflationary scenario, which is able to describe the out-of-equilibrium dynamical phenomenon in the quantum regime in a very elegant and model-independent way. Though it is true that our computation performed in this paper will be applicable to the warm inflationary scenario, we will restricted our analysis here to describe only the quantum effects during the epoch of reheating particularly in the very early time scale of evolutionary scale of our universe where the contribution of the out-of-equilibrium physics play pivotal role to control the dynamics.
- Stochastic inflation:Stochastic inflationary [147,148,149,150] paradigm is a very important aspect of the early universe Cosmology whose technical construction is completely different from the usual inflationary paradigm. To have inflation from a model which is derived from some UV complete high energy quantum field theories we do not need any additional source, time-dependent scalar inflaton field slowly rolls down through an inflationary potential and participate in the quantum field theory using which one can explicitly compute the N-point correlation functions within the framework of early universe Cosmology. However, in the framework of stochastic inflationary paradigm a time-dependent stochastic random source function play significant role to study the background construction of the quantum field theory. More precisely, here we have two fields, the inflaton and a stochastic random time-dependent noise field, where both of them are participating to carry forward a correct quantum field theory construction of inflationary paradigm within the framework of early universe Cosmology. To construct a correct and consistent version of these type of quantum field theories one needs to start with a theory where the time-dependent inflaton and the stochastic random time-dependent field coupled to each other. In most of the previous literature, during the construction of these type of quantum field theories the correlation between the time-dependent noise using which one can compute the N-point correlation function using the time-dependent inflation to study the role of quantum mechanical fluctuations in the early universe Cosmology. In this theoretical construction, the correlation between the noise acts as a source of the correlation between the inflaton. However, cannot say concretely about the exact behaviour of the noise at the starting point of the computation. Most of the computation until now have performed in this literature by assuming the underlying Gaussian behaviour of the probability distribution of the time-dependent stochastic noise function. As a consequence of this assumption one can now expect that the one-point function and any odd point correlation function of the time-dependent stochastic noise vanish trivially. On the other hand the two-point function has to de proportional to a time translationally invariant Dirac Delta function and the proportionality constant actually determine the amplitude of two-point correlation function, which we identify as the power spectrum of the time-dependent stochastic noise in the context of early universe Cosmology. One can also compute any other higher point even correlation functions from this construction, where one can explicitly show that the connected part of these correlations are factorizable in terms of the two-point function or the Green’s function of the theory which we are considering to describe the background quantum field theory of early universe Cosmology. If we believe that the initial assumption regarding having a Gaussian probability distribution of time-dependent stochastic noise is perfectly correct then everything we have mentioned above are the automatic consequence of that and using these information one can determine the N-point correlation function from the inflaton field consistently. Here the type of the noise we have pointed which follow the Gaussian probability distribution is commonly known as the white noise within the framework of quantum field theory. However, unfortunately we really do not have any idea if the assumption that we have taken at the starting point is correct at all or not when one can think of any arbitrary stochastic randomness within the framework of quantum field theory. This allows to think about considering non-Gaussian noise, which commonly identified as the coloured noise in the present context. However, if we have some time-dependent stochastic coloured non-Gaussian noise then it is extremely complicated to determine the quantum correlations between the noise and hence the N-point quantum correlation for inflaton field which is sourced by the coloured noise time-dependent profile. Furthermore, it is expected that the random quantum fluctuations in the stochastic noise is the prime source for which the background equilibrium quantum filed theory set up goes to its out-of equilibrium phase, where we have very less information regarding the cosmological correlation functions within the framework of quantum field theory of early universe Cosmology. This actually motivates us to think about some alternative construction of computing the N-point quantum correlation functions due to the presence of coloured time-dependent noise profile and in this paper by constructing the cosmological version of OTOC we have tried to address this crucial issue in an alternative way within the framework of out-of-equilibrium quantum field theory.
- Quantum quench in Cosmology:The study of quantum mechanical quench in the presence of time-dependent random coupling and its consequences in quantum correlation functions in Cosmology is a very important topic of study in the context of theoretical physics. Until now, this has not been very well understood and studied in the context of Cosmology. In the earlier literature for various statistical mechanical and condensed matter systems quantum quench has been studied rigorously, but its extension in the framework of early universe Cosmology will provide us the understanding of the thermalization phenomenon and the details of the achieving thermal equilibrium from an out-of-equilibrium phase in the presence of a random time-dependent coupling parameter. One can start with various possibilities here where in each case, theories are minimally coupled with classical FLRW conformally flat cosmological metric in a minimal fashion. The first and the simplest possibility appears in free scalar field theory where we consider a time-dependent mass, which is a random coupling parameter within the framework of quench. The second possibility appears within the framework of an interacting quantum field theory where one can consider a situation where two scalar fields with constant mass are interacting with each other in presence of a random time-dependent coupling parameter. If we treat the interaction term between the two scalar fields as quadratic, then constructing the effective theories of each scalar field becomes simpler after performing the path integration over the other unwanted scalar field for the description. In the quantum description, sometimes this is identified to be the partial trace operation when we are describing everything in terms of density matrix and similar approach have been followed in the context of quantum field theories driven by an open quantum system, where the system is non-adiabatically interacting with the environment. One can further generalize this idea for N number of scalar fields which are placed at the thermal bath and interacting with a system which is described by a singe scalar field. In terms of the interaction here one can consider the quadratic or any other non linear interactions. This description can be identified as the quantum field theory generalization of the well known Feynman–Vernon model of influence functional theories or the Caldeira Leggett model which describes the quantum dissipation phenomenon in the Quantum Brownian motion picture within the framework of early universe Cosmology. Considering these mentioned frameworks, one can explicitly compute the OTOCs using the methodology presented in this paper to study the quantum mechanical N-point out-of-time ordered correlation functions in presence of a quantum mechanical quench within the framework of out-of-equilibrium version [151,152,153,154] of open quantum field theory of Cosmology [155,156,157,158].
- Highlight I:The methodology presented in this paper helps us to quantify the quantum mechanical correlation functions within the framework of Cosmology in the presence of random quantum fluctuations. In this connection, we have computed the expressions for the two-point and four-point cosmological OTOC in the quantum regime which will provide the behaviour of the correlation functions in the out-of-equilibrium regime of the quantum field theory of early universe Cosmology.
- Highlight II:We have additionally studied the classical limiting version of the two-point and four-point cosmological OTOCs which will provide the decaying large time behaviour of the correlation function, which perfectly matches with the expectations from the chaotic phenomenon in the classical regime of the field theory.
- Highlight III:The large time limiting behaviour of the four-point OTOC helps us to comment on the equilibrium behaviour of the quantum correlations and to determine the lower bound of the equilibrium temperature. Using this concept, one can further determine the lower bound on the reheating temperature within the framework of early universe Cosmology.
- Highlight IV:We have also studied the quantum Lyapunov spectrum for Cosmology and computed the associated quantum Lyapunov exponent to have a consistent chaotic description in the quantum regime from the four-point cosmological OTOC derived in this paper.
- Highlight V:We have explicitly proved from our detailed computation that the results obtained from the normalized version of the four-point cosmological OTOC is completely independent of the choice of the time-dependent perturbation variable as appearing in the specific scheme of the cosmological perturbation theory.
- In Section 2, we discuss how one can formulate the OTOC in the context of Cosmology and what exact quantity we have to compute for this study.
- In Section 3, we discuss about the detailed computation of quantum micro-canonical two-point and four-point OTO amplitudes and the related OTOC in Cosmology.
- In Section 8, we discuss about classical limit of micro-canonical two-point and four-point OTO amplitudes and the related OTOC in Cosmology.
2. Formulation of OTOC in Cosmology
2.1. General Remarks on OTOC
2.2. Eigenstate Representation of OTOC in Quantum Statistical Mechanics
2.3. Constructing OTOC in Cosmology
- We are dealing with commutative version of the quantum field theory, i.e., all the field momenta and the fields are commutative amongst themselves. Things will change when one deals with the non commutative version of the quantum field theory which means in that in that case all the field momenta and the fields are non-commutative amongst themselves. Usually in both of the versions of quantum field theories we mostly consider the equal time commutation relations at different space points (ETCR) and the unequal time commutation relations (UETCR). In the Fourier transformed versions which can be translated as computing commutation relations at different momenta with same time for ETCR and with different time for UETCR. However, if we look into the specific mathematical structure of OTOC, then we see that the commutators are either ETCR or UETCR with fixed momentum or position.
- If we get divergence to compute OTOC, then like the previous cases we deform the contour of integration in Schwinger–Keldyshpath integral formalism by introducing one or more regulators in the theory. In the technical ground, introducing the regulator cut-off means one needs to deform the Schwinger–Keldyshpath integral contour at finite temperature by introducing a single or more than one parameter. Consequently, in that context we will get a finite regulated result. On the other hand, in the context of non-commutative version of the quantum field theory it is expected that the form OTOC (the mathematical definition of OTOC is provided in the next subsections explicitly for massless, partially massless and massive scalar field theories) we get non vanishing physically relevant answers. During the computation of the OTOC if we get some divergences then like previous case here we also deform the contour of integration by introducing a cut-off to get finite results.
- The explicit time-dependence of the OTOC is very important in the present context, particularly the study the physics of out-of-equilibrium. If the second term of the OTOC grows exponentially with time then one can quantify quantum chaos from the present computation and check whether the final result saturated the chaos bound on the Lyapunov exponent or not. On the other hand, if instead of getting an exponentially growing time-dependent behaviour if we get some other non-trivial characteristic behaviour as a function of time that is also very important to study in the present context to study the out-of-equilibrium behaviour of quantum mechanical systems considered in the framework of Cosmology. Particularly in Cosmology, studying the non trivial time-dependent behaviour of the OTOC for stochastic particle production during inflation, reheating are very useful to extract physical information from the quantum mechanical systems studied. Since we are trying to compute the OTOC for quantum field theory, it is expected to get some interesting physical outcomes from the correlation functions. However, it is also expected from the studies of the OTOC that at very large time limit the correlation functions reach thermal equilibrium and saturates to a finite value. This may not indicate the saturation of the quantum chaos, but this will also play significant role to study the time-dependent behaviour of OTOC. In this context, one can use this information as a limiting boundary condition of OTOC. Apart from that the early time behaviour of OTOC is also good to know. The early time behaviour is physically important as it gives the idea about the initial condition on the time-dependent behaviour of the OTOC. Initial condition OTOC actually fixes from which point in the time scale the quantum system goes to out-of-equilibrium. This information in the context of Cosmology is very useful because it will give a physical picture about a particular out-of-equilibrium phenomenon in which we are interested.
- In this computation, we are considering massless (), partially massless () and massive () scalar field for the computation of OTOC in the context of Cosmology. In the context of Cosmology, the fundamental characteristic scale is described by Hubble scale, i.e., H. Now compared to this characteristic scale we define massless, partially massless and massive scalar field in the de Sitter gravitational background. In the context of massive scalar field theory one usually consider various time-dependent protocols to describe the stochastic particle production phenomenon during inflation and reheating process in the context of primordial Cosmology. For a few types of time-dependent protocols one can exactly analytically solve the field equations for the scalar field, which are commonly used in the study of quantum quench. In general exact solution of the field equation is very difficult so solve and for this purpose one use the WKB approximation method to find out the analytical solution of the scalar field. These solutions are extremely important to study in de Sitter cosmological background as it provide the key ingredient to compute the previously mentioned OTOC in the present context. In the context of stochastic particle production one consider Dirac Delta type of scatterer as a time-dependent protocol, which is nothing but the white noise in the present context. In some cases, one also considers coloured noise time-dependent protocol. In the quantum description, the white noise is identified to be non-Markovian and coloured noise is considered as Markovian at the level of correlation function (quantum analogue: at the level of quantum correlation function for the white and coloured noise are described by the following correlation functions:where and are the amplitude for the white and coloured noise respectively as a function of conformal time. Here represents a localised white noise function at time scale. On the other hand, the coloured noise is represented by the general time-dependent Kernel which is not at all localised at time scale) (classical analogue: at the classical level Delta type of scatterer mimics the role of white noise appearing in the quantum regime. On the other hand, other non trivial time-dependent functions mimics the role of coloured noise at the quantum level. For N number of scatterers at the classical level one can then write:where and are the amplitudes respectively as a function of conformal time. Here represents a localised function at the point of j-th scatterer time scale. On the other hand, the coloured noise is represented by the general time-dependent Kernel which is not at all localised at time scale. However, any reliable physically significant time-dependent protocols are allowed in this context to extract the unknown physical information from the OTOC computation).
2.3.1. For Massless Scalar Field
2.3.2. For Partially Massless Scalar Field
2.3.3. For Massive Scalar Field
3. Quantum Micro-Canonical OTO Amplitudes and OTOC in Cosmology
3.1. Computational Strategy
- At first, we need find out the analytic solution of the equation of motion of the scalar field in the corresponding FLRW flat spatial background.
- From the above mentioned solution we need to find out the canonically conjugated field momentum and using that we need to compute the square of the quantum mechanical commutator bracket. It is proved during performing this operation we need to quantize the field content in terms of the creation and annihilation operators.
- From the above mentioned result we need to further compute the thermal average value of the square of the commutator bracket of the field and its canonically conjugate momenta, which physically represents the four-point out-of-time ordered correlation function.
- Next, we need to compute the partition function the quantum system under consideration by computing the thermal Boltzmann factor and the trace of the corresponding thermal Boltzmann factor. To serve this purpose we need to also compute the expression for the Hamiltonian from the quantum mechanical system under consideration.
- Furthermore, we need to compute the thermal two point out-of-time ordered correlation functions from the field content and the corresponding canonically conjugate momentum. This will help us to find out the expression for the normalised OTOC which is defined in the earlier sections explicitly.
- Furthermore, instead of computing these description in the coordinate space one can do a similar computation of OTOC in Fourier space as well. For this purpose one needs to compute all of the required operators in the Fourier transformed space. Sometimes doing the computation in Fourier transformed space is simpler than the computation in coordinate space. Most importantly, doing the computation in Fourier space is really very helpful in the context of Cosmology. The primary reason is that doing the computation in momentum space (which is the Fourier transformed version of the coordinate space) in the context of Cosmology is more technically interesting. Actually, in momentum space most of the quantum correlation functions in the context of Cosmology preserves the conformal symmetry under conformal transformations. In quasi de Sitter space, this conformal symmetry is slightly broken in Fourier space by the amount of slow-roll parameters, which we have taken into account in our computations.
- In the present context it is better to perform the whole computation in a preferred choice of gauge, which is commonly performed in the context of Cosmological Perturbation Theory. Following the same strategy here we work on gauge, which makes the computation of OTOC simpler than doing the computation doing without the choice of a preferred gauge.
- It is important to mention here that doing the computation of OTOC for N interacting scalar field analytically are extremely complicated. On the other hand, doing the computation with N non-interacting multi scalar field is also not very simple. For this reason we try in this paper to restrict ourself to the non-interacting single field and N field case. For the single field case we also provide the computation of OTOC in the previously mentioned preferred gauge choice.
- Last but not least, doing the computation of OTOC in any arbitrary dimensions is not at all possible analytically. So we have to restrict our computation in this article in spatial dimension which is compatible with our spatially flat dimensional space time in FLRW cosmological background.
3.2. Classical Mode Functions in Cosmology
3.3. Quantum Mode Function in Cosmology
- In the de Sitter case with FLRW background is a slowly varying conformal time-dependent function in general, which physically represents a very slight deviation from the de Sitter solution, where the Hubble parameter is dominated by Cosmological Constant in Planckian units. It is observed from the computation and that both of the parameters capture the effect of such deviation and for this reason sometimes one refers this as the quasi de Sitter space-time.
- Another important fact is that since we strictly do not know the explicit conformal tie dependence of the reheating equation of state , we have assumed that the time-dependence is very slow and for this purpose, this crucial parameter exactly behaves like a constant with the restriction that . This fact is extremely important to mention as it fixes the form of the scale factor , parameter (the slow-roll parameter is commonly used in the context of quasi de Sitter inflationary phase where the scale factor can be expressed as . During inflation and at the end of inflationary phase , which is very useful to determine the corresponding field value at the end of inflation. So during stochastic particle production during the inflationary phase, we will respect these constraints on the slow-roll parameter . On the other hand, since reheating happened after inflation then it is expected that the magnitude of the parameter during reheating, where the scale factor can be expressed as . This statement can be justified very easily in the context during the epoch of reheating. From the previously derived expression for the parameter in the context of reheating we have found that , where the equation of state parameter . This directly implies that during the epoch of reheating the parameter will lie within the window, (alternatively one can say that the Hubble velocity is lying within the window in the Planckian units), which is obviously a very strong and specific information we get from the from the present computation) and the Mukhanov–Sasaki variable in terms of conformal time as well as the equation of state parameter in the present context.
3.4. Canonical Quantization of Cosmological Hamiltonian: Classical to Quantum Map
3.5. Cosmological Two-Point and Four-Point “In-In" OTO Micro-Canonical Amplitudes
3.5.1. OTOC Meets Cosmology
- Information I:First of all, one need the quantum operators corresponding to the rescaled field and its canonically conjugate momenta, which is actually written in terms of the classical solution obtained from the mode equation and the creation and annihilation operators. Actually, in the context of Cosmology one can write down the Hamiltonian of the system in terms of an Harmonic oscillator with conformal time-dependent frequency in a Fourier space and after constructing this Hamiltonian one needs to integrate over all possible momenta. Using this prescription and using the canonical quantization procedure one can easily quantize the system Hamiltonian in the framework of Cosmology.
- Information II:Next, one needs to compute the expression for the expression for the square of the commutator bracket in the background of FLRW space-time in curved space quantum field theory in coordinate space. This is the prime component which will fix the final expression for OTOC in the framework of Cosmology. We will explicitly show that this contribution can be written in terms of four parts where each of the parts in Fourier transformed space mimics the role of some kind of scattering amplitudes after taking its trace, which are functions of four momenta and two time scales as appearing in the definition of OTOC. Precisely these four momenta are coming due to the fact that in each contribution, we are dealing with four quantum operators. Now if we are careful about the technicality then we have to say these four-point scattering amplitudes are basically the four-point time-dependent correlation functions in the framework of Cosmology as during performing the trace operation we have to use the same quantum vacuum state, which means that the initial and final state both are the same, and identified as the “in” state. So it is basically an in-in amplitude rather than an usual “in-out” amplitude. The usual “in-out” amplitude can be usually computed using the idea of S matrix, which is a Schwinger Dyson series in the context of quantum field theory and this is an unitary matrix in the context of a closed system in our Universe when the system under consideration is not exchanging any information with the surroundings. On the other hand, in the Cosmological set-up we deal with “in-in” amplitudes which can be computed using the well known Schwinger–Keldyshformalism. Instead of calling this quantity which we want to evaluate as “in-in” amplitude we call these contributions “in-in” quantum correlation functions in the framework of Cosmology.
- Information III:Furthermore, we have to fix the definition of trace in the context of quantum field theory in a classical gravitational background, specifically in the context of FLRW Cosmology. To serve this purpose, we need to first use a standard definition of the quantum wave function of our Universe. For this purpose, the most common choice is to use the definition of standard Bunch–Davies vacuum state, which is basically a thermal ground state in the framework of Cosmology. Sometimes this vacuum is identified to be the Hartle–Hawking or Cherenkov vacuum state in quantum field theory theory of curved space-time with Cosmological background. Apart from that, another useful vacuum is the vacuum, which is mostly used in the context of interacting quantum field theory in curved space-time with cosmological background. Here in the construction of the vacuum it appears as a one real parameter family which can take any continuous value starting from the zero value. The zero value is a special case of the vacuum which is basically the well known Bunch–Davies quantum vacuum ground state. One the other hand, for the other values of one can construct infinite number of states which can be considered as some excited states which can be expressed in terms of the known Bunch–Davies vacuum state using the Bogoliubov transformation.
- Information IV:Using the above mentioned vacuum or the Bunch–Davies quantum vacuum one can further compute the numerator of OTOC, which is the trace of the square of the commutator bracket of the rescaled field variable and its canonically conjugate momenta along with the thermal Botzmann factor in which the system Hamiltonian is appearing explicitly. Furthermore, one can compute the denominator of the OTOC which represents the expression for the trace of the only thermal Boltzmann factor, which is physically identified to be the thermal partition function in the Cosmological framework. Then putting a negative sign in front of the computed object, one can derive the expression for the OTOC in un normalized form. This overall negative sign is very important as it makes the un normalized OTOC positive and growing with the combined time scale in which both of the above mentioned quantum extended operators are defined. In this computation, the thermal partition function and the trace of the commutator bracket square at finite temperature are evaluated using semi classical approximation, which means that we treat the fluctuation of scalar modes appearing from cosmological perturbation theory in the primordial universe. Precisely the perturbation in the metric in the FLRW background can be written in terms of scalar, vector and tensor modes in Fourier transformed space. This is commonly known as the SVT decomposition in Cosmology. In this computation, we have restricted our attention to scalar modes which can promoted to be a quantum operator during the computation of OTOC. It is obvious that the canonically conjugate momenta computed from the scalar modes can also be promoted to be a quantum mechanical operator. However, if we look into this problem very carefully, then we observe that the origin of the quantum fluctuations from the scalar modes are coming from metric perturbation in the FLRW background, which we actually treat purely classically. For this reason we will do a semi-classical (not purely quantum or classical) computation for the computation of OTOC in the framework of primordial cosmology.
- Information V:Last but not least, we have to fix the normalization of OTOC. This can be perfectly done using the previously mentioned thermal trace operation in presence of vacua or Bunch–Davies quantum vacuum state in the context of Cosmology. After normalization we can able to construct a dimensionless cosmological four-point “in-in" amplitude or quantum OTOC. We have computed the normalization factor in the Appendix A, Appendix B, Appendix C, Appendix D, Appendix E, Appendix F, Appendix G, Appendix H, Appendix I, Appendix J, Appendix K, Appendix L and Appendix M in detail. Please look into the technical details in the Appendix C, Appendix D and Appendix M.2 respectively.
3.5.2. Fourier Space Representation of the Commutator Bracket: Application to Two-Point OTOC
3.5.3. Fourier Space Representation of Square of the Commutator Bracket Application to Four-Point OTOC
3.6. Cosmological Thermal Partition Function: Quantum Version
3.6.1. Quantum Vacuum State in Cosmology
3.6.2. Quantum Partition Function in Terms of Rescaled Field Variable
3.6.3. Quantum Partition Function in Terms of Curvature Perturbation Field Variable
3.7. Trace of Two-Point “In-In" OTO Amplitude for Cosmology
3.8. OTOC from Regularised Two-Point “In-In" OTO Micro-Canonical Amplitude: Rescaled Field Version
3.9. OTOC from Regularised Four-Point “In-In" OTO Micro-Canonical Amplitude: Curvature Perturbation Field Version
- First, we have explicitly shown that the definition of the two-point OTOC is completely coordinate-independent and just only depend on the time scale on which the operators in cosmological perturbation theory are time scale separated. Even if we start defining the operators in a specific space point at different times, in the final result all such information is integrated out and we get completely a time-dependent two-point OTOC.
- Next, it is important to note that for , which implies , the two-point OTOC trivially vanishes. However, for partially massless and heavy scalar fields, two-point OTOC becomes non-trivial and carries significant information of the theory.
- We also have found that the final obtained result of the two-point OTOC is -independent even though we start with a thermal micro-canonical statistical ensemble during definition the two-point OTOC in the trace formula.
- Furthermore, we observe that if we fix , that means if both the quantum operators representing the cosmological fluctuations are defined at the same time then two-point OTOC explicitly gives diverging contribution in the quantum regime. This is perfectly consistent with the definition of any general OTOC and also supports all the physical requirements to construct the foundational set-up to compute OTOC.
- If we perform an explicit computation, then it is possible to show that in our set-up the one-point functions in the context of Cosmology are given by the following expressions:The similar statement is also valid if we define the one-point functions for Cosmology in terms of the curvature perturbation field variable and its canonically conjugate momentum. This result implies that there is no point of performing normalization of the obtained two-point OTOC for Cosmology with respect to the above mentioned one-point functions. So technically, it is sufficient enough to compute the two-point OTOC without normalization in the context of Cosmology.
- Another important point we have to mention is that not only the one point function but also the three point functions in the present context is trivially zero which can be explicitly proved by making use of the well known Kubo–Martin–Schwinger condition in terms of time translational symmetry of the thermal correlation functions computed for Cosmology. These possibilities are explicitly mentioned below:which in principle can be further generalized to any odd N point thermal correlation function for micro-canonical ensemble within the framework of Cosmology.
3.10. Trace of Four-Point “In-In" OTO Amplitude for Cosmology
3.11. OTOC from Regularised Four-Point “In-In" OTO Micro-Canonical Amplitude: Rescaled Field Version
3.11.1. Without Normalization
3.11.2. With Normalization
3.12. OTOC from Regularised Four-Point “In-In" OTO Micro-Canonical Amplitude: Curvature Perturbation Field Version
3.12.1. Without Normalization
3.12.2. With Normalization
4. Numerical Results I: Interpretation of Two-Point Micro-Canonical OTOC in Cosmology
- In Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, conformal time-dependent behaviour of the two-point function with respect to the two time scale of the Cosmology are explicitly shown. From these plots it is clearly observed that with respect both the time scales the two-point function show random fluctuating behaviour. The amplitude of the fluctuation is small for the result obtained from the Bunch–Davies vacuum state and very large for the general vacuum state.
- For both the cases it is observed that we get the significant feature in the time-dependent two-point function for partially massless or heavy scalar field those who have the imaginary value of the mass parameter . This behaviour of the two-point spectrum is explicitly depicted in Figure 10. From this plot, one can clearly see that for the result obtained using Bunch–Davies initial condition the two-point spectra significantly decay very fast with respect to the magnitude of the mass parameter . This implies that for very heavy or partially massless scalar fields if we increase the mass parameter value then the mentioned two-point correlation between the cosmological perturbation variable and its canonically conjugate momenta decrease very fast in a fixed time scale. On the other hand, if we change the quantum initial condition by changing the initial vacuum state by introducing vacua then it can be clearly observed from the plot that if increase the value of the vacuum parameter gradually then we get significant change compared to the feature observed for the Bunch–Davies vacuum state. We have explicitly shown the behaviour of the two-point spectrum for and , where it is clearly observed that the correlation decays very slowly with the increase in the magnitude of the mass parameter value and for very large value of it will saturate to a non-zero large amplitude for a fixed time time scale. There is as such no significant change we have observed from the plots that we have drawn for and cases, except for an amplitude shift for the large values of the mass parameter. For very small values of the mass parameter all the different profiles obtained for zero value and non-zero values of the vacuum parameter start approaching to meet together and at the amplitude of the two-point correlation of the out-of-time ordered spectrum in Cosmology shoots up with a very large amplitude.
- Furthermore, we have observed from the plots that the random fluctuations with respect to the conformal time scale show small but decaying time-dependent behaviour up to a very late time scale as far as the amplitude of the spectra are concerned. After crossing that late time region the amplitude start increasing and reaches a very large value which we have not shown explicitly in these plots. After reaching this maximum value it will again start decaying very fast up to the present day epoch. This large peak value of the spectrum is obtained at the scale when the two time scales of the theory becomes same and the two operators of cosmological perturbation theory taken to be exactly same. Physically this information is very important for our study in this paper, as it pointing towards the fact that at this particular time scale we are actually getting zero information from the out-of-time ordered physics in the present context. So at very early time scale of the universe and after crossing the peak we will get the information regarding the out-of-time ordered physics from the present cosmological set up.
- Last but not least, in the second plot of Figure 10, we have explicitly depicted the behaviour of the two-point spectrum of the out-of-time ordered aspect of Cosmology with respect to the vacuum parameter . Here we get a very interesting symmetric feature for the positive and negative values of the vacuum parameter around . As we increase the value of along the positive axis, then the two-point function increase very fast with large amplitude. Similar symmetric behaviour is also observed for side as well. As we approach towards , we see that the amplitude of the two-point out-of-time ordered spectrum for the fixed values of the time parameters of the theory asymptotically approaches to the zero value from both and side.
5. Numerical Results II: Interpretation of Four-Point Micro-Canonical OTOC in Cosmology
- Before normalisation, OTOC computed from both the sides are not same and connected via a time-dependent Mukhanov–Sasaki variable-dependent factor .
- After normalisation, OTOC computed from both the sides are exactly same and this is really good that after normalisation we do not need to think about the explicit origin or any preferred cosmological perturbation variable.
- In our computed OTOC in the context of Cosmology two time scales are involved which are associated with the two operators, rescaled field variable and its canonically conjugate momenta. During the study of the behaviour of the OTOC we have actually have fixed one time scale and have studied the time-dependent dynamical behaviour of OTOC with respect to the other time scale, which have not fixed. We have found that the behaviour with respect to both and , using both Bunch–Davies and vacua as quantum vacuum state. See Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 to know about the detailed conformal time-dependent feature of the cosmological normalised OTOC. One crucial thing we have to mention here that since we are dealing with conformal time, it varies from, (Big Bang) to 0 (present day universe), which will be very useful to understand the physical outcomes of these plots. For this reason we get completely opposite behaviour of the cosmological OTOC compared to the usual quantum mechanical systems. In quantum mechanical random system we actually deal with the usual time scale, which various from 0 to ∞. Here 0 corresponds to the initial condition on the system when the quantum mechanical system goes to the out-of-equilibrium state and it is expected from our basic understanding of statistical mechanics that if we wait for a very longer time scale then the OTOC will saturates to a specific value where the system actually achieve equilibrium, where one can associate an equilibrium temperature with the quantum system under consideration. Just using the concept of retarded quantum correlators, explaining these features is extremely difficult and at the end computation probing those results in experiments is also a very complicated job. OTOC plays here a significant role to probe such quantum correlations experimentally in a very simple fashion. In the cosmological set up, things are not same though we study the quantum correlations at the out-of-equilibrium case here also. The prime reason for the difference between the study of both types of OTOC is lying in the time scale. In usual quantum mechanical systems, we are actually interested in the growth of the correlation function and if it is an exponential growth then we identify this feature as the signature of quantum chaos. On the other hand, in the cosmological set up we expect the randomness or stochasticity will decrease with respect to the conformal time scale and such decrease is following an exponential decay with respect to the conformal time scale then this is the signature of quantum chaos in the context of primordial universe. In the cosmological set up at far past the quantum fluctuations appearing during the epoch of reheating or during the stochastic particle production during inflation goes to the out-of-equilibrium state and like usual quantum systems, it is expected that if we wait for a longer conformal time scale then at a later time it will achieve equilibrium, with which similarly one can associate an equilibrium temperature. For this equilibrium case in the context of Cosmology the OTOC if saturates to a constant value then one can identify this phenomenon as quantum mechanical chaos. We will discuss about this particular feature in detail in the next section of this paper. In the next point, we will discuss about the features obtained from the numerical studies of the quantum OTOC we have studied from the primordial cosmology set up. We are very positive that this discuss will explore various underlying features of primordial universe when a cosmological system goes out-of-equilibrium.
- If we fix the time scale, and study the behaviour of OTOC with respect to the scale then we found that as we approach from very early universe to the late time scale the normalised OTOC in the context of cosmology shows random decreasing behaviour. This behaviour is quite consistent with the usual expectation. It is observed that in the very early universe , near to the Big Bang all such random fluctuations are appearing with large amplitude and very significant to describe the time-dependent behaviour of the quantum correlation function during stochastic particle production during inflation and during the epoch of reheating, when the finite temperature out-of-equilibrium physics play significant role. If we wait for a longer time, specifically at the late time scale it is observed from the Figure 11, Figure 12, Figure 13 and Figure 14 that the quantum correlation OTOC decrease very fast and we get very small amplitude for the random or stochastic quantum mechanical fluctuations. Now if we closely look all of these mentioned plots then we see that we decreasing behaviour of OTOC in these cases would not follow any exponential decaying behaviour. So we cannot identify the decreasing behaviour of this OTOC computed from the primordial cosmological set-up with the concept of quantum mechanical chaos. Though it is clear from the plots that the random fluctuations originating from the out-of-equilibrium physics dominates in far past and becomes very very small at the late time universe.
- If we fix the time scale, and study the behaviour of OTOC with respect to the scale then we found that as we approach from very early universe to the late time scale the normalised OTOC in the context of cosmology shows random decreasing on top of it with an exponentially decaying behaviour. This behaviour is quite consistent with the usual expectation of quantum mechanical chaos along with stochastic randomness. It is observed that in very early universe , near to the Big Bang, all such random fluctuations are appearing with large amplitude and very significant to describe the time-dependent behaviour of the OTOC during stochastic particle production during inflation and during the epoch of reheating like the previous case. If we wait for a longer time, specifically at the late time scale it is observed from the Figure 16, Figure 17, Figure 18 and Figure 19, shows that OTOC decreases very fast with an exponentially decaying amplitude for the random or stochastic fluctuations. Now if we closely look all of these mentioned plots then we see that the behaviour of OTOC in these cases would exactly follow the exponential decaying time-dependent behaviour. So we identify the such behaviour of this OTOC computed from the primordial cosmological set-up with the concept of quantum chaos. It is clear from the plots that the quantum chaos, which is a very specific kind of random fluctuations originating in far past and becomes small at the late time scale.
- Additionally we have observed that we can get the expected behaviour from the OTOC with respect to both the time scales when the mass parameter, can be analytically continued to . So the massless de Sitter case, which is is clearly discarded here. Consequently, we left with the following possibilities:
- The Partially massless de Sitter case is one of the possibilities, where we can estimate the following parameter from the present understanding:which immediately implies the following bound on the mass parameter:This is a very great fact because we have studied the plots for the following values of the mass parameter:
- Furthermore, we have to mention that since a lot of complex gamma function is appearing and mass parameter is , during the numerical analysis we have taken the absolute value of OTOC during numerical computation. Consequently, the final expression for the cosmological OTOC can be re-expressed for vacua as:Here in the factors appearing with we have replaced with .
- The Massive de Sitter case is one of the possibilities, where we can estimate the following parameter from the present understanding:Since we have studied the case for , we get the following bound on the mass of the heavy field, which is given by the following expression:
- The Reheating case is the last possibility, where we can estimate the following parameter from the present understanding:
- After fixing both the time scales at far past, the behaviour of OTOC with respect to the mass parameter is depicted in the Figure 15 for Bunch–Davies and vacua as quantum mechanical vacuum state. This plot explicitly shows that if we increase the value of mass parameter then OTOC amplitude increases like an exponential growth. This behaviour is consistent with constraints obtained for the partially massless scalar, massive scalar and reheating phenomenon mentioned in the previous point.
- After fixing both the time scales at far past and fix , the behaviour of OTOC with respect to the vacuum parameter is depicted in the Figure 15. This plot explicitly shows that if we increase the value of mass parameter then OTOC amplitude fluctuates like a random stochastic signal.
- All the momentum-dependent integrals appearing in cosmological OTOC is divergent at ∞, for which we have introduced an UV regulator at a finite but at large value. This makes the final result of OTOC convergent and finite.
- Furthermore, we define a relative change in normalized OTOC where the relativeness is defined with respect to the definition of quantum mechanical vacuum state in the definition of normalized OTOC, given by:In Figure 20 and Figure 21, we have explicitly shown the behaviour of the relative change in normalized OTOC with respect to the two time scales appearing in the computation of OTOC. Here once we see the behaviour of OTOC with respect to one time scale, we keep the other time scale fixed for the computation and numerical estimation of the relative change in the normalized OTOC. Here the relative change we have studies for with respect to for all previously allowed values of the mass parameter. This is a very important parameter where one can explicitly see the role of mass parameter and vacuum parameter together. Furthermore, from this relative change one can also study about the fact that in which time scale the stochastic randomness appearing in the quantum fluctuation appearing in cosmological OTOC is large or small. The detailed features obtained from these plots show that the relative change in cosmological OTOC will not change much starting from Big Bang to the present epoch, apart from the irregular random fluctuations. However, the explicit time-dependence of OTOC obtained from Bunch–Davies and vacua is consistent with the expectation from the cosmological set up studied here.
- Furthermore, we have to mention here that the computed cosmological OTOC is any specific coordinate independent. If we go through the computation then we see that even we have started defining the cosmological OTOC in coordinate space, after taking Fourier transformation and applying the momentum conservation appearing in terms of Dirac Delta functions, the exponential factor which captures both momenta and coordinate will be unity. Finally, we get a momentum integrated cut-off regulated result which only depend on the two dynamical conformal time scale in which we have defined the rescaled perturbation variable and its canonically conjugate momenta. So this implies that the final expression of cosmological OTOC is only conformal time-dependent, not depend on any specific choice of coordinate. This is quite impressive outcome and physically consistent with the mathematical framework of cosmological perturbation theory in the early universe. In general, when one define the quantum operators in a specific time and in a specific coordinate system then it always appears in the final result and captures the effect of inhomogeneity in the space-time coordinate. In the context of Cosmology we have found that the final result of OTOC captures the effect of inhomogeneity as we have defined the two quantum cosmological operators in different time scales at the starting point of the definition of OTOC. This have been done in such a way because in cosmology we are actually interested in the time evolution of the quantum cosmological operators which are separated in time scale, which is one of the crucial constraint in the definition of any general OTOC. However, such OTOC in cosmology do not capture the effects of inhomogeneity at all.
- The final result of cosmological OTOC is not explicitly dependent of the factor which is appearing in the expression for thermal partition function which we have computed in the context of Cosmology. This implies that the final result is also independent of the thermal partition function computed for Cosmology. This is quite consistent with the basic understanding of out-of-equilibrium aspects of quantum statistical mechanics. Because when a system goes to out-of-equilibrium one cannot associate a temperature with that system as the concept of temperature is always appearing from thermodynamic equilibrium. One can only associate a temperature with the system if we wait for very longer time scale and wait for saturation of OTOC at a finite value. If such feature appears in OTOC then in that specific context this saturation is actually correspond to the thermodynamic equilibrium in which one can define an equilibrium temperature. The similar phenomenon we can actually observed in the context of cosmological OTOC as well where we explicitly found that if we wait for very late time scale during the evolution of our universe in conformal time scale then the OTOC exponentially decays with time and saturates to a finite value at late time scales. We can actually find the specific time scale in terms of conformal time coordinate and associate the concept of quantum chaos, where we can give a measure of quantum Lyapunov exponent from the present framework. In the next section, we will show that even there is no explicit dependence in the calculation of cosmological OTOC, such dependencies will appear once we connect the present concept with quantum chaos through quantum Lyapunov exponent and the well known MSS bound on it, i.e., .
6. Lyapunov Spectrum and Quantum Chaos in Cosmology
7. Numerical Results III: Interpretation of Cosmological Lyapunov Spectrum
- First of all, in the cosmological OTOC when we have considered as the dynamical variable and have fixed the other time scale then for very late time of the cosmological evolution of our universe we have found an exponentially decaying behaviour with respect to the dynamical time scale under consideration. One can identify this phenomenon with the quantum chaos, which is actually estimated by the decay coefficient appearing in the exponential factor. This coefficient is known as the Lyapunov exponent at late time scale. When the cosmological OTOC have started saturating to a fixed non vanishing value at that point we fix the dynamical time scale and from the OTOC using the exponential decaying behaviour one can explicitly compute the expression for the Lyapunov exponent at fixed late time scale. However, if anyone is interested to find out the whole conformal time-dependent Lyapunov spectrum that can also be found using the cosmological OTOC computed in the previous section of this paper. We have explicitly computed this expression in this section for completeness.
- Additionally, it is important to note that since we have used two different cosmological perturbation variable for our present computation, we get two equivalent but not exactly same expression for the Lyapunov spectrum. If we compute the Lyapunov spectrum for the rescaled perturbation variable f then we see that in the mass parameter all the information regarding the background cosmological frameworks, like, partially massless or heavy particle production during the epoch of inflation or the phenomenon of reheating are encoded. We do not need to think about all of these phenomena separately. On the other hand, if we do the computation in terms of curvature perturbation variable then we found that the the information regarding the background cosmological frameworks, as mentioned above we have to think separately. This is because in this framework, we have some additional contribution which is actually appearing from the definition of Mukhanov–Sasaki variable which contain the scale factor of the cosmological expansion of de Sitter phase or reheating phase and the very small contribution comping from slow-roll factor, which is basically taking care of the small deviation from exact evolution in de Sitter space or during reheating and interpreted as conformal symmetry breaking parameter. Now if we neglect such small contribution then one can separately compute the expression for the Lyapunov spectrum from the variable .
- Furthermore, we have also have estimated the relative difference between the Lyapunov spectra computed from two different prescriptions. This difference is different for the stochastic particle production during inflation and reheating epoch respectively.
- In our computed Lyapunov spectrum in the context of Cosmology two time scales are involved which are associated with the two operators, rescaled field variable and its canonically conjugate momenta. We have found that the behaviour with respect to , using both Bunch–Davies and vacua as quantum vacuum state. See Figure 22, Figure 23 and Figure 24 to know about the detailed conformal time-dependent feature of the cosmological Lyapunov spectrum. In the cosmological set up we expect the Lyapunov spectrum will decrease with respect to the conformal time scale and such decrease is following an exponential decay with respect to the conformal time scale then this carries the signature of quantum chaos in the context of primordial universe.
- Here we fix the time scale, and study the behaviour of Lyapunov spectrum with respect to the scale and we found that as we approach from very early universe to the late time scale the Lyapunov spectrum in the context of cosmology shows random decreasing on top of it with an exponentially decaying behaviour. This behaviour is quite consistent with the usual expectation of quantum mechanical chaos along with stochastic randomness. It is observed that in very early universe , near to the Big Bang all such random fluctuations are appearing with large amplitude and very significant to describe the time-dependent behaviour of the Lyapunov spectrum during stochastic particle production during inflation and during the epoch of reheating like the previous case. If we wait for longer time, specifically at the late time scale it is observed from the Figure 22, Figure 23 and Figure 24, that Lyapunov spectrum decrease very fast with an exponentially decaying amplitude for the random or stochastic fluctuations.
- We have also observed that we can get the expected behaviour from the Lyapunov spectrum with respect to both the time scales when the mass parameter, can be analytically continued to .
- Another important point we have to mention that since the Lyapunov spectrum is computed from the cosmological OTOC in which the information of the initial quantum mechanical vacuum states are encoded, the final expressions for the Lyapunov spectrum computed for the vacua and Bunch–Davies vacua are different. This non-unique result appears due to the fact that in curved space-time definition of quantum mechanical vacuum state is unique.
- Last but not least, using the saturation bound on Lyapunov exponent obtained from MSS bound we have finally estimated the bound on the equilibrium temperature of our universe at late time scale. Basically this equilibrium temperature corresponds to the starting point of saturation of the Lyapunov spectrum at the late time scale .
8. Classical Limit of Micro-Canonical OTO Amplitudes and Related OTOC in Cosmology
8.1. Computational Strategy
- First of all, we have to take the quantum to classical map of all the operators that we have used to compute the expression for cosmological four-point OTOC in this paper. We have already demonstrated clearly in the previous sections that during the computation of cosmological OTOC all the operators that we have considered considered by making use of canonical quantization of these operators. This means that we have written the quantum version of the modes in Fourier space in terms of creation and annihilation operators just like quantum harmonic oscillators and these creation and annihilation operators actually creates or destroy the quantum mechanical vacuum state, which we have taken as the usual well known Bunch–Davies vacuum or the more general vacua. Now during taking the classical limit of this formulation we all know that there is no concept of vacuum as such exists. As a result there is nothing called creation and annihilation of vacuum state in the context of classical limit of quantum fluctuation of cosmological perturbation theory. This further implies that writing down the quantum to classical map becomes very simple. For this purpose we just have to consider the classical mode function and its canonically conjugate momentum that we have derived already in the earlier section of this paper.
- Next, instead of using commutator bracket square in the classical limit we have to use the Poisson Bracket of the classical variables which are appearing as an outcome of cosmological perturbation theory.
- Furthermore, we have to fix the definition and the representation of the trace in the classical limit. Since we do not have any complete set of basis and any vacuum state in the classical limit we have to be very careful to define the trace operation. Again this can be easily done by making use the basic concepts of classical statistical mechanics. In the classical limit the usual definition of quantum mechanical trace will be replaced by phase space volume, which is basically playing the role of path integral measure, in the classical field theory of scalar field in FLRW cosmological background. We set, in natural units, which implies and this is the origin of the factor which appearing in the denominator of the phase space volume or in the path integral measure. Furthermore, it is important to note that only one power of is appearing since we are dealing with a one dimensional parametric oscillator problem with conformal time time-dependent frequency where the phase space is constructed out of two canonically conjugate variables, the cosmological perturbation variable and iyts conjugate momentum, which are derived from the classical field theory of the scalar fields in conformally and spatially flat FLRW background. As a consequence the phase space trajectory is lying in a two dimensional plane. If we deal with N number of classical scalar fields in that case in the denominator factor will appear and in the large N thermodynamic limit we will get physically consistent result in the purely classical limit of quantum version of Cosmology. Additionally, it important to note that during this computation we have to take care of an additional thermal Boltzmann factor as we are doing the computation for the finite temperature extended version of the classical scalar field theory.
- Next, by following the same procedure mentioned above we compute the expression for the classical thermal partition function for Cosmology, which perfectly matches with the the quantum mechanical thermal partition function for Cosmology.
- Finally, we compute the expression for the normalisation factor of the classical version of the cosmological four-point OTOC using the above mentioned phase space formalism. This will help us to write down the normalised version of cosmological four-point OTOC in the classical limit.
8.2. Classical Limit of Cosmological Two-Point “In-In" OTO Micro-Canonical Amplitudes
8.3. Classical Limit of Cosmological Four-Point “In-In" OTO Micro-Canonical Amplitudes
- For coloured noise two point classical correlation function is time translation invariant.
- For this random coloured noise, at the classical level we have:where is the conformal time-dependent coloured noise. Here we have assumed that the time-dependent kernel is in general have some non-Gaussian probability distribution profile. In the computation, is the Green’s function which is appearing from the two point classical correlation from the coloured noise defined at two different time scales. In Cosmology, this conformal time-dependent function sometimes identified to be the power spectrum as well and for coloured noise it is expected to be non-Gaussian from the above mentioned properties. Furthermore, is the amplitude of the spectrum of any point classical correlations. Here all point amplitudes are non-zero for non-Gaussian coloured noise contributions, which are sourced from random, chaotic and stochastic fluctuations in the classical limit in cosmological paradigm.
- For white noise two point classical correlation function is time translation invariant, which is exactly same as the coloured noise case.
- For this random white noise, at the classical level we have:where is the conformal time-dependent white noise. Here we have assumed that the time-dependent kernel is in general have some Gaussian probability distribution profile. Furthermore, and are the amplitude of the spectrum of any and even point classical correlations. Due to the Gaussian probability distribution profile all the odd point classical correlation of white noise exactly vanish trivially. Consequently, all even point amplitudes are non-zero and all odd point amplitudes become zero for Gaussian white noise contributions, which are again sourced from random, chaotic and stochastic fluctuations in the classical limit in cosmological paradigm.
- In the obtained result, we have introduced a conformal time-dependent noise kernel phenomenologically to describe the randomness and chaoticity of the fluctuations at the classical limit.
- Furthermore, we have included an exponentially conformal time-dependent decay term as we are interested in to explain the classical limit of the quantum chaotic behaviour that we have obtained in the context of cosmological four-point OTOC at late time scale of our universe. To get a similar behaviour we have included this decaying feature in the classical version of the four-point OTO micro-canonical amplitude. In usual literature this is appearing as an exponential time-dependent growth factor. However, since we are dealing with conformal time scale in the context of Cosmology, , we write it as, for the simplicity. So this negative sign in the conformal time scale is responsible for the decaying feature of the classical limit of the four-point cosmological OTOC, instead of having an exponential growth.
- If we compare the obtained result in the classical limit with the quantum version of the four-point “in-in” OTO micro-canonical amplitude then we can see that for both the cases we get twelve contributions, but amplitudes in classical limit for all of these contributions are same. On the other hand, in the quantum version of the amplitude we have different individual contributions for these mentioned twelve terms. Additionally, we can observe another similarity in these two results are that for both the cases momentum conservation is applied through the momentum-dependent three dimensional Dirac Delta functions.
8.4. Cosmological Micro-Canonical Partition Function: Classical Version
8.4.1. Classical Micro-Canonical Partition Function in Terms of Rescaled Field Variable
8.4.2. Classical Micro-Canonical Partition Function in Terms of Curvature Perturbation Field Variable
8.5. Classical Limit of Cosmological Two-Point Micro-Canonical OTOC: Rescaled Field Version
8.6. Classical Limit of Cosmological Two-Point Micro-Canonical OTOC: Curvature Perturbation Field Version
8.7. Classical Limit of Cosmological Four-Point Micro-Canonical OTOC: Rescaled Field Version
8.7.1. Without Normalization
8.7.2. With Normalization
8.8. Classical Limit of Cosmological Four-Point Micro-Canonical OTOC: Curvature Perturbation Field Version
8.8.1. Without Normalization
8.8.2. With Normalization
9. Summary and Outlook
- First of all in this paper we have provided a detailed formalism using which it is possible now to compute the expression for OTOC in the context of Cosmology. OTOC is a very strong probe to study the quantum correlation in presence of randomness and chaoticity. It was used in a different context to Cosmology. As we all know, finding quantum correlation functions in the early universe in presence of such randomness or chaoticity was a long standing problem which nobody has addressed yet properly. We believe our computation and findings from the cosmological OTOC in this paper will surely be helpful to understand the quantum field theory of various unexplored random cosmological events, i.e., stochastic particle production during inflation, reheating, etc. Since we did the computation for the first time from a very simple understandable cosmological perturbation theory, we believe that these results will also be used to study some other random cosmological events appear in the evolutionary time scale of our universe.
- We have presented the computation of cosmological OTOC by making use of the well know Bunch–Davies and vacua as a choice of initial quantum vacuum state. So it is expected that the final results of cosmological OTOC may show similar feature, but with different amplitude and in different scale. This statement we have verified explicitly by numerically studying the obtained solutions of the cosmological OTOC using both the definition of quantum mechanical vacuum state.
- It is a very well known fact that in general, prescription OTOCs are usually defined with two quantum operators which are separated by time scale. Following the same prescription in Cosmology, we have also defined two quantum operators which are the cosmological perturbation variable describing the quantum fluctuation from scalar modes and its associated canonically conjugate momentum, which are defined in two different time scales in the evolution of our universe. During the computation of cosmological OTOC, the final result for this reason depends on these two time scales. Now, to study the cosmological consequences of the OTOC we fix one of the time scales between the two and study the dynamical feature with respect to the other time variable which we have not fixed. We have found that both of the features of cosmological OTOC with respect to the two different time scales describe the randomness in the quantum correlation function at out-of-equilibrium. On top of that we have additionally found that particularly once we fix the first time scale and study the time evolution behaviour, the cosmological OTOC shows exponentially decaying behaviour, which supports the phenomenon of quantum chaos in the cosmological paradigm as well. In the usual scenario, one gets exponential growth with respect to the time scale in OTOC. However, to remind everyone, it is important to note that instead of dealing actual time scale which is varying from in the present context we are dealing with the conformal time scale which is varying from , which is the most commonly used time scale in the context of Cosmology. Because of this reason, instead of exponentially increasing behaviour we have observed exponentially decreasing behaviour. This behaviour is perfectly consistent with the expectation from the time evolution of the quantum mechanical correlations for the system when it goes to the out-of-equilibrium state.
- Additionally, from the present formalism we have derived the expression for the quantum Lyapunov spectrum as well the lower bound on the equilibrium temperature for Cosmology. At the very early epoch of the evolution of our universe, the quantum fluctuations go to the out-of-equilibrium state for which one cannot associate the concept of temperature, as it is only interpreted when a system under study reaches to equilibrium state. We have derived the expression for cosmological OTOC which is very helpful to understand the quantum mechanical correlation function at out-of-equilibrium state. Now from the exponential decay of this cosmological OTOC one can easily estimate the lower bound on the equilibrium temperature associated with our universe. This can be done in a very simple way. For this purpose we need to identify the exact time scale at which the cosmological OTOC after decaying with respect to the conformal time scale starts to saturate to a non vanishing small value. From this time-scale, one can further explicitly derive and give an estimate of the temperature of the system when cosmological OTOC saturates to an equilibrium value. After getting an estimate of this lower bound of equilibrium temperature one can give a physical interpretation of this temperature in the cosmological paradigm. One can associate the obtained lower bound on the equilibrium temperature with the temperature of de Sitter space for the stochastic particle production during inflation and with the reheating temperature. Usually, in the cosmology literature, one actually compute the expression for the reheating temperature by making use of information from quantum statistical mechanics. Using the approximate energy scale for inflation and by making use the information regarding the number of relativistic degrees of freedom one computes a bound on the reheating temperature in the framework of primordial cosmology. Since earlier we do not have any information regarding time-dependent behaviour of the cosmological OTOC one does not have any option to compute reheating temperature from the quantum field theory side. So the derived bound on the reheating temperature can be treated as a model-independent bound, which is better than the previously known model-dependent bound to reheating temperature.
- Furthermore, we have found that the cosmological OTOC at finite temperature is dependent on two time scale and independent of any preferred choice of the coordinate system and the parameter . In short, the derived expression for the cosmological OTOC is homogeneous in nature with respect to the space coordinate, or its Fourier transformed momentum coordinate. Furthermore, the final result obtained for the cosmological OTOC is independent of the partition function which we have computed for Cosmology. This feature is exactly similar to the OTOC computed from simple harmonic oscillator with time-independent frequency. Basically, one can map the stochastic particle production problem during inflation or solving the reheating problem to a parametric oscillator problem whose frequency is function of the magnitude of the momentum in the Fourier transformed space and conformal time scale, where the time is actually associated with the evolution scale of our universe.
- By doing the numerical estimations and during the study of detailed time-dependent behaviour of the cosmological OTOC we have found that our analysis can give physically consistent results only for partially massless or massive scalar particle production during inflation and during reheating epoch.
- We have also studied the classical limit of the two-point and four-point OTOC to check the consistency with the late time behaviour which supports the exponential decay of the quantum correlators in the classical regime.
- Finally, we have explicitly proved that the definition of cosmological OTOC is completely independent of the choice of preferred perturbation variable in a specific scheme of cosmological perturbation theory. On the other hand, we have also found that this statement does not hold good for the un-normalized cosmological OTOC. We have demonstrated that both the results are related through some factor which is basically a function of conformal time-dependent Mukhanov–Sasaki variables.
- In this, we have restricted our analysis only for cosmological spatially flat FLRW space-time, which is more observationally relevant. We are very hopeful that our obtained result in this paper can be probed by various cosmological future missions and if the amplitudes of the cosmological OTOC can able to be measured with significant statistical accuracy then the obtained result for cosmological OTOC can be treated as a standard benchmark using which one can study various unexplored features of early universe cosmology in the presence of random quantum fluctuations in out-of-equilibrium state. To know about the cosmological consequences of our derived result one can further extend the present methodology for computing OTOC for open and flat FLRW space time as well. This study will give a better understanding to know about the explicit role of spatial curvature in cosmological FLRW space-time to explore the out-of-equilibrium features. Not only this, using the present methodology of computing cosmological OTOC one can further extend any arbitrary spatial dimensions, which will give a clear picture that if one varies the space at very lower or higher dimensions how the cosmological OTOC behaves with the time scale. No one has explored such possibilities yet, so it will be good to study these mentioned aspects in detail.
- The present methodology of computing the cosmological OTOC is not only restricted to describe stochastic particle production during inflation and during the reheating epoch, but also one can extend this tool to compute the quantum mechanical OTOC in presence of non singular bounce. It may happen that during the non singular bouncing phenomenon, somehow stochasticity or some random quantum mechanical fluctuations appear and since now it is known how to quantify and compute the quantum correlation functions at out-of-equilibrium state, one can carry forward the similar calculation in this context as well.
- Another important aspect one can study is the role of quantum entanglement [159,160,161,162,163,164,165,166] in cosmological OTOC at out-of-equilibrium. Quantum correlation functions in presence of entanglement was studied at equilibrium in various earlier works. It is good to apply the present methodology to know about cosmological OTOC in the presence of quantum entanglement in the early universe. Specifically if one can study the cosmological OTOC in Bell’s inequality violating set-up then one can actually study the effect of long range sustainable small amplitude cosmological correlation at out-of-equilibrium.
Funding
Acknowledgments
Appendix A. Asymptotic Behaviour of the Cosmological Mode Functions
Appendix B. WKB Solution of the Cosmological Mode Functions for Time Dependent Protocols
Appendix C. Quantum Two-Point OTO Micro-Canonical Amplitudes for Cosmology
Appendix C.1. Definition of Micro-Canonical OTO Amplitude
Appendix C.2. Definition of Micro-Canonical OTO Amplitude
Appendix D. Quantum Four-Point OTO Micro-Canonical Amplitudes for Cosmology
Appendix D.1. Definition of Micro-Canonical OTO Amplitude
Appendix D.2. Definition of Micro-Canonical OTO Amplitude
Appendix D.3. Definition of Micro-Canonical OTO Amplitude
Appendix D.4. Definition of Micro-Canonical OTO Amplitude
Appendix E. Computation of Classical Limit of Four-Point “In-In” OTO Micro-Canonical Amplitudes for Cosmology
- The time-dependent part as such very complicated as it contain the information regarding classical statistical version of random chaotic stochastic quantum fluctuations in the primordial universe. In the present context it is hypothesized by a random function which incorporates the two conformal time scales.
- Furthermore, it is important to not that is a homogeneous and isotropic function, which captures the dynamical effect of the classical spatially flat FLRW geometrical background. For this reason the random function, is completely i and j momentum index independent.
- Moreover, the interesting to point here that one can explicitly separately write down the contribution of the inhomogeneity and time dynamics in Fourier space after computing the classical Poisson bracket in this context.
- Finally, the appearance of the three dimensional Dirac Delta function confirms the momentum conservation in the Fourier space in the classical two point OTO micro-canonical amplitude in Cosmology.
Appendix F. Computation of Quantum Micro-Canonical Partition Function in Cosmology
Appendix F.1. Quantum Micro-Canonical Partition Function in Terms of Rescaled Field Variable
Appendix F.2. Quantum Micro-Canonical Partition Function in Terms of Curvature Perturbation Field Variable
Appendix G. Computation of Classical Micro-Canonical Partition Function in Cosmology
Appendix G.1. Classical Micro-Canonical Partition Function in Terms of Rescaled Field Variable
Appendix G.2. Classical Micro-Canonical Partition Function in Terms of Curvature Perturbation Field Variable
Appendix H. Computation of the Trace of the Two-Point Amplitude in Micro-Canonical OTOC
Appendix I. Computation of the Trace of the Four-Point Amplitude in Micro-Canonical OTOC
Appendix J. Time Dependent Two-Point Amplitude in Micro-Canonical OTOC
Appendix K. Time Dependent Four-Point Amplitudes in Micro-Canonical OTOC
Appendix K.1. Computation of
Appendix K.2. Computation of
Appendix K.3. Computation of
Appendix K.4. Computation of
Appendix K.5. Computation of
Appendix K.6. Computation of
Appendix K.7. Computation of
Appendix K.8. Computation of
Appendix K.9. Computation of
Appendix L. Computation of the Normalization Factor in Four-Point Micro-Canonical OTOC
Appendix L.1. Normalization Factor of Four-Point Micro-Canonical OTOC Computed from Rescaled Field Variable
Appendix L.2. Normalization Factor of Four-Point Micro-Canonical OTOC Computed from Curvature Perturbation Field Variable
Appendix M. Computation of the Normalization Factor in Classical Limit of Four-Point Micro-Canonical OTOC
Appendix M.1. Normalization Factor of the Classical Version of Four-Point Micro-Canonical OTOC Computed from Rescaled Field Variable
Appendix M.2. Normalization Factor of the Classical Version of Four-Point Micro-Canonical OTOC Computed from Curvature Perturbation Field Variable
Appendix N. Thermal Trace Operation in Terms of Wave Function of the Universe in Cosmology
References
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 2016, 106. [Google Scholar]
- Hashimoto, K.; Murata, K.; Yoshii, R. Out-of-time-order correlators in quantum mechanics. J. High Energy Phys. 2017, 2017, 138. [Google Scholar]
- Chakrabarty, B.; Chaudhuri, S.; Loganayagam, R. Out of Time Ordered Quantum Dissipation. J. High Energy Phys. 2019, 2019, 102. [Google Scholar]
- Chaudhuri, S.; Chowdhury, C.; Loganayagam, R. Spectral Representation of Thermal OTO Correlators. J. High Energy Phys. 2019, 2019, 18. [Google Scholar]
- Chaudhuri, S.; Loganayagam, R. Probing Out-of-Time-Order Correlators. J. High Energy Phys. 2019, 2019, 6. [Google Scholar]
- Haehl, F.M.; Loganayagam, R.; Narayan, P.; Nizami, A.A.; Rangamani, M. Thermal out-of-time-order correlators, KMS relations, and spectral functions. J. High Energy Phys. 2017, 2017, 154. [Google Scholar]
- Akutagawa, T.; Hashimoto, K.; Sasaki, T.; Watanabe, R. Out-of-time-order correlator in coupled harmonic oscillators. arXiv 2004, arXiv:2004.04381. [Google Scholar]
- Bhagat, K.Y.; Bose, B.; Choudhury, S.; Chowdhury, S.; Das, R.N.; Dastider, S.G.; Gupta, N.; Maji, A.; Pasquino, G.D.; Paul, S. The Generalized OTOC from Supersymmetric Quantum Mechanics: Study of Random Fluctuations from Eigenstate Representation of Correlation Functions. arXiv, 2020; arXiv:2008.03280. [Google Scholar]
- Romero-Bermúdez, A.; Schalm, K.; Scopelliti, V. Regularization dependence of the OTOC. Which Lyapunov spectrum is the physical one? J. High Energy Phys. 2019, 2019, 107. [Google Scholar]
- Larkin, A.L.; Ovchinnikov, Y.N. Quasiclassical method in the theory of superconductivity. Sov. Phys. JETP 1969, 28, 1200–1205. [Google Scholar]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113. [Google Scholar]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rep. 2000, 323, 183. [Google Scholar]
- Shenker, S.H.; Stanford, D. Black holes and the butterfly effect. J. High Energy Phys. 2014, 2014, 67. [Google Scholar]
- Roberts, D.A.; Stanford, D.; Susskind, L. Localized shocks. J. High Energy Phys. 2015, 2015, 51. [Google Scholar]
- Stanford, D.; Susskind, L. Complexity and Shock Wave Geometries. Phys. Rev. D 2014, 90, 126007. [Google Scholar]
- Shenker, S.H.; Stanford, D. Multiple Shocks. J. High Energy Phys. 2014, 2014, 46. [Google Scholar]
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black Holes and Random Matrices. J. High Energy Phys. 2017, 2017, 118, Erratum: J. High Energy Phys. 2018, 2018, 2. [Google Scholar]
- Klebanov, I.R.; Tarnopolsky, G. Uncolored random tensors, melon diagrams, and the Sachdev–Ye–Kitaev models. Phys. Rev. D 2017, 95, 046004. [Google Scholar]
- Maldacena, J.; Stanford, D. Remarks on the Sachdev–Ye–Kitaev model. Phys. Rev. D 2016, 94, 106002. [Google Scholar]
- Choudhury, S.; Dey, A.; Halder, I.; Janagal, L.; Minwalla, S.; Poojary, R. Notes on melonic O(N)q−1 tensor models. J. High Energy Phys. 2018, 2018, 94. [Google Scholar]
- Klebanov, I.R.; Popov, F.; Tarnopolsky, G. TASI Lectures on Large N Tensor Models. arXiv 2018, arXiv:1808.09434. [Google Scholar]
- Bulycheva, K.; Klebanov, I.R.; Milekhin, A.; Tarnopolsky, G. Spectra of Operators in Large N Tensor Models. Phys. Rev. D 2018, 97, 026016. [Google Scholar]
- Kim, J.; Klebanov, I.R.; Tarnopolsky, G.; Zhao, W. Symmetry Breaking in Coupled SYK or Tensor Models. Phys. Rev. X 2019, 9, 021043. [Google Scholar]
- Gurau, R. Notes on Tensor Models and Tensor Field Theories. arXiv 2019, arXiv:1907.03531. [Google Scholar]
- Gurau, R. The 1/N expansion of tensor models with two symmetric tensors. Commun. Math. Phys. 2018, 360, 985–1007. [Google Scholar]
- Benedetti, D.; Gurau, R. Symmetry breaking in tensor models. Phys. Rev. D 2015, 92, 104041. [Google Scholar]
- Gurau, R. A review of the large N limit of tensor models. arXiv 2013, arXiv:1209.4295. [Google Scholar]
- Gurau, R. A review of the 1/N expansion in random tensor models. arXiv 2014, arXiv:1209.3252. [Google Scholar]
- Fu, W.; Gaiotto, D.; Maldacena, J.; Sachdev, S. Supersymmetric Sachdev–Ye–Kitaev models. Phys. Rev. D 2017, 95, 026009, Addendum: Phys. Rev. D 2017, 95, 069904. [Google Scholar]
- Witten, E. An SYK-Like Model Without Disorder. J. Phys. A 2019, 52, 474002. [Google Scholar]
- Li, T.; Liu, J.; Xin, Y.; Zhou, Y. Supersymmetric SYK model and random matrix theory. J. High Energy Phys. 2017, 2017, 111. [Google Scholar]
- Turiaci, G.; Verlinde, H. Towards a 2d QFT Analog of the SYK Model. J. High Energy Phys. 2017, 2017, 167. [Google Scholar]
- Rosenhaus, V. An introduction to the SYK model. J. Phys. A 2019, 52, 323001. [Google Scholar]
- Gross, D.J.; Rosenhaus, V. All point correlation functions in SYK. J. High Energy Phys. 2017, 2017, 148. [Google Scholar]
- Gross, D.J.; Rosenhaus, V. A line of CFTs: from generalized free fields to SYK. J. High Energy Phys. 2017, 2017, 86. [Google Scholar]
- Gross, D.J.; Rosenhaus, V. The Bulk Dual of SYK: Cubic Couplings. J. High Energy Phys. 1705, 2017, 92. [Google Scholar]
- Polchinski, J.; Rosenhaus, V. The Spectrum in the Sachdev–Ye–Kitaev Model. J. High Energy Phys. 2016, 2016, 1. [Google Scholar]
- Maldacena, J.M. Non-Gaussian features of primordial fluctuations in single field inflationary models. J. High Energy Phys. 2003, 2003, 13. [Google Scholar]
- Maldacena, J.M.; Pimentel, G.L. On graviton non-Gaussianities during inflation. J. High Energy Phys. 2011, 2011, 45. [Google Scholar]
- Choudhury, S.; Pal, S. Primordial non-Gaussian features from DBI Galileon inflation. Eur. Phys. J. C 2015, 75, 241. [Google Scholar]
- Choudhury, S. Constraining N = 1 supergravity inflation with non-minimal Kaehler operators using δN formalism. J. High Energy Phys. 2014, 2014, 105. [Google Scholar]
- Choudhury, S. COSMOS-e′- soft Higgsotic attractors. Eur. Phys. J. C 2017, 77, 469. [Google Scholar]
- Green, D.; Lewandowski, M.; Senatore, L.; Silverstein, E.; Zaldarriaga, M. Anomalous Dimensions and Non-Gaussianity. J. High Energy Phys. 2013, 2013, 171. [Google Scholar]
- Behbahani, S.R.; Dymarsky, A.; Mirbabayi, M.; Senatore, L. (Small) Resonant non-Gaussianities: Signatures of a Discrete Shift Symmetry in the Effective Field Theory of Inflation. J. Cosmol. Astropart. Phys. 2012, 12, 36. [Google Scholar]
- Senatore, L.; Smith, K.M.; Zaldarriaga, M. Non-Gaussianities in Single Field Inflation and their Optimal Limits from the WMAP 5-year Data. J. Cosmol. Astropart. Phys. 2010, 1, 28. [Google Scholar]
- Senatore, L.; Tassev, S.; Zaldarriaga, M. Non-Gaussianities from Perturbing Recombination. J. Cosmol. Astropart. Phys. 2009, 9, 038. [Google Scholar]
- Creminelli, P.; Senatore, L.; Zaldarriaga, M. Estimators for local non-Gaussianities. J. Cosmol. Astropart. Phys. 2007, 3, 19. [Google Scholar]
- Lehners, J.L.; Steinhardt, P.J. Non-Gaussianity Generated by the Entropic Mechanism in Bouncing Cosmologies Made Simple. Phys. Rev. D 2009, 80, 103520. [Google Scholar]
- Baumann, D. TASI lectures on inflation. arXiv 2009, arXiv:0907.5424. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration], Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Anabalón, A.; Bramberger, S.F.; Lehners, J.L. Kerr-NUT-de Sitter as an Inhomogeneous Non-Singular Bouncing Cosmology. J. High Energy Phys. 2019, 2019, 96. [Google Scholar]
- Bramberger, S.F.; Lehners, J.L. Nonsingular bounces catalyzed by dark energy. Phys. Rev. D 2019, 99, 123523. [Google Scholar]
- Fertig, A.; Lehners, J.L.; Mallwitz, E.; Wilson-Ewing, E. Converting entropy to curvature perturbations after a cosmic bounce. J. Cosmol. Astropart. Phys. 2016, 2016, 005. [Google Scholar]
- Koehn, M.; Lehners, J.L.; Ovrut, B. Nonsingular bouncing cosmology: Consistency of the effective description. Phys. Rev. D 2016, 93, 103501. [Google Scholar]
- Lehners, J.L.; Wilson-Ewing, E. Running of the scalar spectral index in bouncing cosmologies. J. Cosmol. Astropart. Phys. 2016, 2016, 038. [Google Scholar]
- Fertig, A.; Lehners, J.L.; Mallwitz, E. Conflation: A new type of accelerated expansion. J. Cosmol. Astropart. Phys. 2016, 2016, 073. [Google Scholar]
- Battarra, L.; Koehn, M.; Lehners, J.L.; Ovrut, B.A. Cosmological Perturbations Through a Non-Singular Ghost-Condensate/Galileon Bounce. J. Cosmol. Astropart. Phys. 2014, 2014, 007. [Google Scholar]
- Koehn, M.; Lehners, J.L.; Ovrut, B.A. Cosmological super-bounce. Phys. Rev. D 2014, 90, 025005. [Google Scholar]
- Lehners, J.L. Diversity in the Phoenix Universe. Phys. Rev. D 2011, 84, 103518. [Google Scholar]
- Cook, W.G.; Glushchenko, I.A.; Ijjas, A.; Pretorius, F.; Steinhardt, P.J. Supersmoothing through Slow Contraction. Phys. Lett. B 2020, 808, 135690. [Google Scholar]
- Ijjas, A.; Steinhardt, P.J. Implications of Planck2015 for inflationary, ekpyrotic and anamorphic bouncing cosmologies. Class. Quant. Grav. 2016, 33, 044001. [Google Scholar]
- Bars, I.; Chen, S.H.; Steinhardt, P.J.; Turok, N. Complete Set of Homogeneous Isotropic Analytic Solutions in Scalar-Tensor Cosmology with Radiation and Curvature. Phys. Rev. D 2012, 86, 083542. [Google Scholar]
- Bars, I.; Chen, S.H.; Steinhardt, P.J.; Turok, N. Antigravity and the Big Crunch/Big Bang Transition. Phys. Lett. B 2012, 715, 278. [Google Scholar]
- Xue, B.; Steinhardt, P.J. Evolution of curvature and anisotropy near a nonsingular bounce. Phys. Rev. D 2011, 84, 083520. [Google Scholar]
- Alexander, S.; Biswas, T.; Brandenberger, R.H. On the Transfer of Adiabatic Fluctuations through a Nonsingular Cosmological Bounce. arXiv 2007, arXiv:0707.4679. [Google Scholar]
- Cai, Y.F.; Qiu, T.; Brandenberger, R.; Piao, Y.S.; Zhang, X. On Perturbations of Quintom Bounce. J. Cosmol. Astropart. Phys. 2008, 2008, 013. [Google Scholar]
- Brandenberger, R. Alternatives to cosmological inflation. Phys. Today 2008, 61N3, 44. [Google Scholar]
- Cai, Y.F.; Qiu, T.t.; Brandenberger, R.; Zhang, X.M. A Nonsingular Cosmology with a Scale-Invariant Spectrum of Cosmological Perturbations from Lee-Wick Theory. Phys. Rev. D 2009, 80, 023511. [Google Scholar]
- Brandenberger, R.; Zhang, X.M. The Trans-Planckian Problem for Inflationary Cosmology Revisited. arXiv 2009, arXiv:0903.2065. [Google Scholar]
- Gao, X.; Wang, Y.; Xue, W.; Brandenberger, R. Fluctuations in a Horava-Lifshitz Bouncing Cosmology. J. Cosmol. Astropart. Phys. 2010, 2010, 020. [Google Scholar]
- Brandenberger, R.H. Cosmology of the Very Early Universe. AIP Conf. Proc. 2010, 1268, 3–70. [Google Scholar] [CrossRef]
- Karouby, J.; Brandenberger, R. A Radiation Bounce from the Lee-Wick Construction? Phys. Rev. D 2010, 82, 063532. [Google Scholar]
- Cai, Y.F.; Brandenberger, R.; Zhang, X. The Matter Bounce Curvaton Scenario. J. Cosmol. Astropart. Phys. 2011, 2011, 003. [Google Scholar]
- Cai, Y.F.; Easson, D.A.; Brandenberger, R. Towards a Nonsingular Bouncing Cosmology. J. Cosmol. Astropart. Phys. 2012, 2012, 020. [Google Scholar]
- Brandenberger, R.H. The Matter Bounce Alternative to Inflationary Cosmology. arXiv 2012, arXiv:1206.4196. [Google Scholar]
- Cai, Y.F.; Brandenberger, R.; Peter, P. Anisotropy in a Nonsingular Bounce. Class. Quantum Gravity 2013, 30, 075019. [Google Scholar]
- Brandenberger, R.H.; Kounnas, C.; Partouche, H.; Patil, S.P.; Toumbas, N. Cosmological Perturbations Across an S-brane. J. Cosmol. Astropart. Phys. 2014, 2014, 015. [Google Scholar]
- Li, C.; Brandenberger, R.H.; Cheung, Y.K.E. Big-Bounce Genesis. Phys. Rev. D 2014, 90, 123535. [Google Scholar]
- Brandenberger, R.H.; Ferreira, E.G.M.; Morrison, I.A.; Cai, Y.F.; Das, S.R.; Wang, Y. Fluctuations in a cosmology with a spacelike singularity and their gauge theory dual description. Phys. Rev. D 2016, 94, 08350. [Google Scholar]
- Ferreira, E.G.M.; Brandenberger, R. Holographic Curvature Perturbations in a Cosmology with a Space-Like Singularity. J. Cosmol. Astropart. Phys. 2016, 2016, 030. [Google Scholar]
- Hipolito-Ricaldi, W.S.; Brandenberger, R.; Ferreira, E.G.M.; Graef, L.L. Particle Production in Ekpyrotic Scenarios. J. Cosmol. Astropart. Phys. 2016, 2016, 024. [Google Scholar]
- Brandenberger, R.; Liang, Q.; Ramos, R.O.; Zhou, S. Fluctuations through a Vibrating Bounce. Phys. Rev. D 2018, 97, 043504. [Google Scholar]
- Lin, C.; Quintin, J.; Brandenberger, R.H. Massive gravity and the suppression of anisotropies and gravitational waves in a matter-dominated contracting universe. J. Cosmol. Astropart. Phys. 2018, 2018, 011. [Google Scholar]
- Quintin, J. Topics in Pre-Big Bang Cosmology. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2019. [Google Scholar]
- Quintin, J.; Yoshida, D. Cuscuton gravity as a classically stable limiting curvature theory. J. Cosmol. Astropart. Phys. 2020, 2020, 016. [Google Scholar]
- Li, Y.B.; Quintin, J.; Wang, D.G.; Cai, Y.F. Matter bounce cosmology with a generalized single field: non-Gaussianity and an extended no-go theorem. J. Cosmol. Astropart. Phys. 2017, 2017, 031. [Google Scholar]
- Quintin, J.; Brandenberger, R.H. Black hole formation in a contracting universe. J. Cosmol. Astropart. Phys. 2016, 2016, 029. [Google Scholar]
- Quintin, J.; Sherkatghanad, Z.; Cai, Y.F.; Brandenberger, R.H. Evolution of cosmological perturbations and the production of non-Gaussianities through a nonsingular bounce: Indications for a no-go theorem in single field matter bounce cosmologies. Phys. Rev. D 2015, 92, 063532. [Google Scholar]
- Quintin, J.; Cai, Y.F.; Brandenberger, R.H. Matter creation in a nonsingular bouncing cosmology. Phys. Rev. D 2014, 90, 063507. [Google Scholar]
- Cai, Y.F.; Quintin, J.; Saridakis, E.N.; Wilson-Ewing, E. Nonsingular bouncing cosmologies in light of BICEP2. J. Cosmol. Astropart. Phys. 2014, 2014, 033. [Google Scholar]
- Erickson, J.K.; Gratton, S.; Steinhardt, P.J.; Turok, N. Cosmic perturbations through the cyclic ages. Phys. Rev. D 2007, 75, 123507. [Google Scholar]
- Boyle, L.A.; Steinhardt, P.J.; Turok, N. The Cosmic gravitational wave background in a cyclic universe. Phys. Rev. D 2004, 69, 127302. [Google Scholar]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar]
- Turok, N.; Seinhardt, P.J. Beyond inflation: A Cyclic universe scenario. Phys. Scr. T 2005, 117, 76. [Google Scholar]
- Steinhardt, P.J.; Turok, N. Is vacuum decay significant in ekpyrotic and cyclic models? Phys. Rev. D 2002, 66, 101302. [Google Scholar]
- Khoury, J.; Steinhardt, P.J.; Turok, N. Inflation versus cyclic predictions for spectral tilt. Phys. Rev. Lett. 2003, 91, 161301. [Google Scholar]
- Bramberger, S.F.; Hertog, T.; Lehners, J.L.; Vreys, Y. Quantum Transitions Through Cosmological Singularities. J. Cosmol. Astropart. Phys. 2017, 2017, 007. [Google Scholar]
- Lehners, J.L. New Ekpyrotic Quantum Cosmology. Phys. Lett. B 2015, 750, 242. [Google Scholar]
- Lehners, J.L. Classical Inflationary and Ekpyrotic Universes in the No-Boundary Wavefunction. Phys. Rev. D 2015, 91, 083525. [Google Scholar]
- Battarra, L.; Lehners, J.L. On the Creation of the Universe via Ekpyrotic Instantons. Phys. Lett. B 2015, 742, 167. [Google Scholar]
- Fertig, A.; Lehners, J.L.; Mallwitz, E. Ekpyrotic Perturbations With Small Non-Gaussian Corrections. Phys. Rev. D 2014, 89, 103537. [Google Scholar]
- Battarra, L.; Lehners, J.L. Quantum-to-classical transition for ekpyrotic perturbations. Phys. Rev. D 2014, 89, 063516. [Google Scholar]
- Khoury, J.; Lehners, J.L.; Ovrut, B.A. Supersymmetric Galileons. Phys. Rev. D 2011, 84, 043521. [Google Scholar]
- Lehners, J.L.; Steinhardt, P.J. Dynamical Selection of the Primordial Density Fluctuation Amplitude. Phys. Rev. Lett. 2011, 106, 081301. [Google Scholar]
- Ijjas, A.; Steinhardt, P.J. The anamorphic universe. J. Cosmol. Astropart. Phys. 2015, 2015, 001. [Google Scholar]
- Levy, A.M.; Ijjas, A.; Steinhardt, P.J. Scale-invariant perturbations in ekpyrotic cosmologies without fine-tuning of initial conditions. Phys. Rev. D 2015, 92, 063524. [Google Scholar]
- Ijjas, A.; Lehners, J.L.; Steinhardt, P.J. General mechanism for producing scale-invariant perturbations and small non-Gaussianity in ekpyrotic models. Phys. Rev. D 2014, 89, 123520. [Google Scholar]
- Khoury, J.; Steinhardt, P.J. Adiabatic Ekpyrosis: Scale-Invariant Curvature Perturbations from a Single Scalar Field in a Contracting Universe. Phys. Rev. Lett. 2010, 104, 091301. [Google Scholar]
- Gratton, S.; Khoury, J.; Steinhardt, P.J.; Turok, N. Conditions for generating scale-invariant density perturbations. Phys. Rev. D 2004, 69, 103505. [Google Scholar]
- Turok, N. The ekpyrotic universe and its cyclic extension, in The future of theoretical physics and cosmology: Celebrating Stephen Hawking’s 60th birthday. In Proceedings of the Workshop on Conference on the Future of Theoretical Physics and Cosmology in Honor of Steven Hawking’s 60th Birthday, Cambridge, UK, 7–10 January 2002. [Google Scholar]
- Brandenberger, R.; Dasgupta, K.; Wang, Z. Reheating after S-Brane Ekpyrosis. arXiv 2020, arXiv:2007.01203. [Google Scholar]
- Brandenberger, R.; Wang, Z. Ekpyrotic cosmology with a zero-shear S-brane. Phys. Rev. D 2020, 102, 023516. [Google Scholar]
- Deshamukhya, A.; Panda, S. Warm tachyonic inflation in warped background. Int. J. Mod. Phys. D 2009, 18, 2093–2106. [Google Scholar]
- Ali, A.; Chingangbam, R.; Panda, S.; Sami, M. Prospects of inflation with perturbed throat geometry. Phys. Lett. B 2009, 674, 131–136. [Google Scholar]
- Panda, S.; Sami, M.; Tsujikawa, S. Prospects of inflation in delicate D-brane cosmology. Phys. Rev. D 2007, 76, 103512. [Google Scholar]
- Panda, S.; Sami, M.; Tsujikawa, S.; Ward, J. Inflation from D3-brane motion in the background of D5-branes. Phys. Rev. D 2006, 73, 083512. [Google Scholar]
- Choudhury, D.; Ghoshal, D.; Jatkar, D.P.; Panda, S. Hybrid inflation and brane - anti-brane system. J. Cosmol. Astropart. Phys. 2003, 2003, 009. [Google Scholar] [CrossRef][Green Version]
- Mazumdar, A.; Panda, S.; Perez-Lorenzana, A. Assisted inflation via tachyon condensation. Nucl. Phys. B 2001, 614, 101–116. [Google Scholar]
- Choudhury, S. Reconstructing inflationary paradigm within Effective Field Theory framework. Phys. Dark Univ. 2016, 11, 16–48. [Google Scholar]
- Choudhury, S.; Mazumdar, A. Reconstructing inflationary potential from BICEP2 and running of tensor modes. arXiv 2014, arXiv:1403.5549. [Google Scholar]
- Choudhury, S.; Mazumdar, A. An accurate bound on tensor-to-scalar ratio and the scale of inflation. Nucl. Phys. B 2014, 882, 386–396. [Google Scholar]
- Choudhury, S.; Pal, S. Brane inflation: A field theory approach in background supergravity. J. Phys. Conf. Ser. 2012, 405, 012009. [Google Scholar]
- Choudhury, S.; Pal, S. DBI Galileon inflation in background SUGRA. Nucl. Phys. B 2013, 874, 85–114. [Google Scholar]
- Choudhury, S.; Pal, S. Fourth level MSSM inflation from new flat directions. J. Cosmol. Astropart. Phys. 2012, 2012, 018. [Google Scholar]
- Choudhury, S.; Pal, S. Reheating and leptogenesis in a SUGRA inspired brane inflation. Nucl. Phys. B 2012, 857, 85–100. [Google Scholar]
- Choudhury, S.; Pal, S. Brane inflation in background supergravity. Phys. Rev. D 2012, 85, 043529. [Google Scholar]
- Baumann, D.; McAllister, L. Inflation and String Theory. arXiv 2015, arXiv:1404.2601. [Google Scholar]
- Baumann, D.; Green, D.; Porto, R.A. B-modes and the Nature of Inflation. J. Cosmol. Astropart. Phys. 2015, 2015, 016. [Google Scholar]
- Baumann, D.; Green, D.; Lee, H.; Porto, R.A. Signs of Analyticity in Single-Field Inflation. Phys. Rev. D 2016, 93, 023523. [Google Scholar]
- Baumann, D.; Lee, H.; Pimentel, G.L. High-Scale Inflation and the Tensor Tilt. J. High Energy Phys. 2016, 2016, 101. [Google Scholar]
- Finelli, F.; Bucher, M.; Achúcarro, A.; Ballardini, M.; Bartolo, N.; Baumann, D.; Clesse, S.; Errard, J.; Handley, W.; Hindmarsh, M.; et al. Exploring cosmic origins with CORE: Inflation. J. Cosmol. Astropart. Phys. 2018, 2018, 016. [Google Scholar]
- Baumann, D.; Goon, G.; Lee, H.; Pimentel, G.L. Partially Massless Fields During Inflation. J. High Energy Phys. 2018, 2018, 140. [Google Scholar]
- Assassi, V.; Baumann, D.; Green, D. Symmetries and Loops in Inflation. J. High Energy Phys. 2013, 2013, 151. [Google Scholar]
- Assassi, V.; Baumann, D.; Green, D. On Soft Limits of Inflationary Correlation Functions. J. Cosmol. Astropart. Phys. 2012, 2012, 047. [Google Scholar]
- Baumann, D.; Green, D. Inflating with Baryons. J. High Energy Phys. 2011, 2011, 071. [Google Scholar]
- Baumann, D.; Green, D. Desensitizing Inflation from the Planck Scale. J. High Energy Phys. 2010, 2010, 57. [Google Scholar] [CrossRef]
- Lemoine, M.; Martin, J.; Peter, P. Inflationary Cosmology; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 738. [Google Scholar]
- Martin, J.; Yokoyama, J. Generation of Large-Scale Magnetic Fields in Single-Field Inflation. J. Cosmol. Astropart. Phys. 2008, 2008, 025. [Google Scholar]
- Lorenz, L.; Martin, J.; Ringeval, C. Brane inflation and the WMAP data: A Bayesian analysis. J. Cosmol. Astropart. Phys. 2008, 2008, 001. [Google Scholar]
- Martin, J. Inflationary perturbations: The Cosmological Schwinger effect. In Inflationary Cosmology; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 738, pp. 193–241. [Google Scholar]
- Martin, J. Inflation: Where do we stand? Int. J. Mod. Phys. A 2005, 20, 4676–4682. [Google Scholar]
- Martin, J. Inflation and precision cosmology. Braz. J. Phys. 2004, 34, 1307–1321. [Google Scholar] [CrossRef]
- Choudhury, S.; Mukherjee, A.; Chauhan, P.; Bhattacherjee, S. Quantum Out-of-Equilibrium Cosmology. Eur. Phys. J. C 2019, 79, 320. [Google Scholar]
- Choudhury, S.; Mukherjee, A. Quantum randomness in the Sky. Eur. Phys. J. C 2019, 79, 554. [Google Scholar]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar]
- Berera, A. The Warm inflation early universe. Contemp. Phys. 2006, 47, 33–49. [Google Scholar]
- Vennin, V.; Starobinsky, A.A. Correlation Functions in Stochastic Inflation. Eur. Phys. J. C 2015, 75, 413. [Google Scholar]
- Noorbala, M.; Vennin, V.; Assadullahi, H.; Firouzjahi, H.; Wands, D. Tunneling in Stochastic Inflation. J. Cosmol. Astropart. Phys. 2018, 2018, 032. [Google Scholar]
- Grain, J.; Vennin, V. Stochastic inflation in phase space: Is slow roll a stochastic attractor? J. Cosmol. Astropart. Phys. 2017, 2017, 045. [Google Scholar]
- Vennin, V.; Assadullahi, H.; Firouzjahi, H.; Noorbala, M.; Wands, D. Critical Number of Fields in Stochastic Inflation. Phys. Rev. Lett. 2017, 118, 031301. [Google Scholar]
- Weiss, U. Quantum Dissipative Systems; World Scientific: Singapore, 2012; Volume 13. [Google Scholar]
- Calzetta, E.; Hu, B. Nonequilibrium Quantum Field Theory (Cambridge Monographs on Mathematical Physics); Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Rammer, J. Quantum Field Theory of Non-Equilibrium States; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kamenev, A. Field Theory of Non-Equilibrium Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Banerjee, S. Open Quantum Systems: Dynamics of Nonclassical Evolution; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Bohra, H.; Choudhury, S.; Chauhan, P.; Mukherjee, A.; Narayan, P.; Panda, S.; Swain, A. Relating the curvature of de Sitter Universe to Open Quantum Lamb Shift Spectroscopy. arXiv 2019, arXiv:1905.07403. [Google Scholar]
- Akhtar, S.; Choudhury, S.; Chowdhury, S.; Goswami, D.; Panda, S.; Swain, A. Open Quantum Entanglement: A study of two atomic system in static patch of de Sitter space. Eur. Phys. J. C 2020, 80, 748. [Google Scholar]
- Banerjee, S.; Choudhury, S.; Chowdhury, S.; Das, R.N.; Gupta, N.; Panda, S.; Swain, A. Indirect detection of Cosmological Constant from large N entangled open quantum system. arXiv 2020, arXiv:2004.13058. [Google Scholar]
- Choudhury, S.; Panda, S. Spectrum of cosmological correlation from vacuum fluctuation of Stringy Axion in entangled de Sitter space. Eur. Phys. J. C 2020, 80, 67. [Google Scholar]
- Choudhury, S.; Panda, S. Quantum entanglement in de Sitter space from stringy axion: An analysis using α vacua. Nucl. Phys. B 2019, 943, 114606. [Google Scholar]
- Choudhury, S.; Panda, S. Entangled de Sitter from stringy axionic Bell pair I: an analysis using Bunch–Davies vacuum. Eur. Phys. J. C 2018, 78, 52. [Google Scholar]
- Choudhury, S.; Panda, S.; Singh, R. Bell violation in the Sky. Eur. Phys. J. C 2017, 77, 60. [Google Scholar]
- Choudhury, S.; Panda, S.; Singh, R. Bell violation in primordial cosmology. Universe 2017, 3, 13. [Google Scholar]
- Maldacena, J. A model with cosmological Bell inequalities. Fortsch. Phys. 2016, 64, 10–23. [Google Scholar]
- Maldacena, J.; Pimentel, G.L. Entanglement entropy in de Sitter space. J. High Energy Phys. 2013, 2013, 38. [Google Scholar]
- Kanno, S.; Murugan, J.; Shock, J.P.; Soda, J. Entanglement entropy of α-vacua in de Sitter space. J. High Energy Phys. 2014, 2014, 72. [Google Scholar]

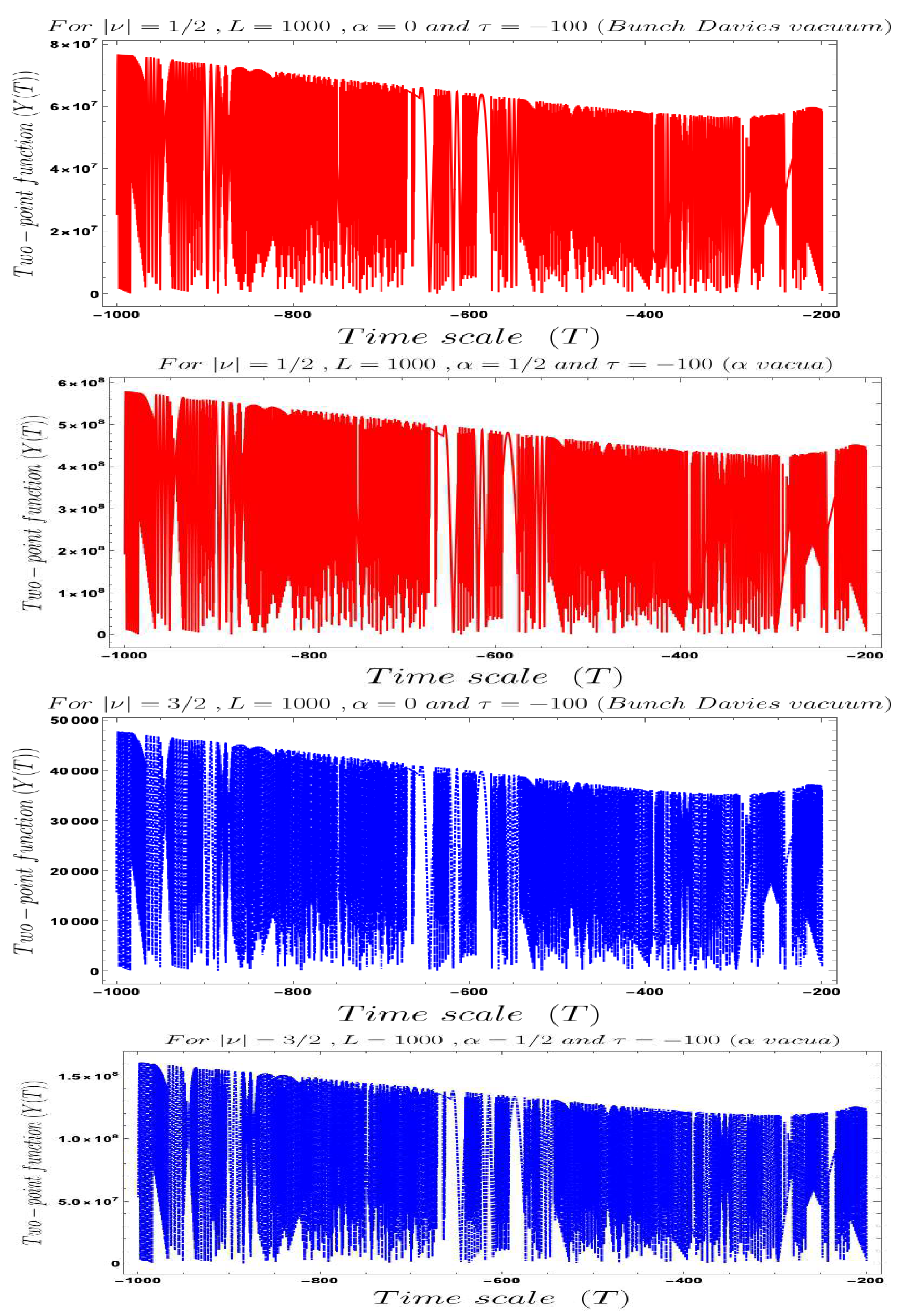

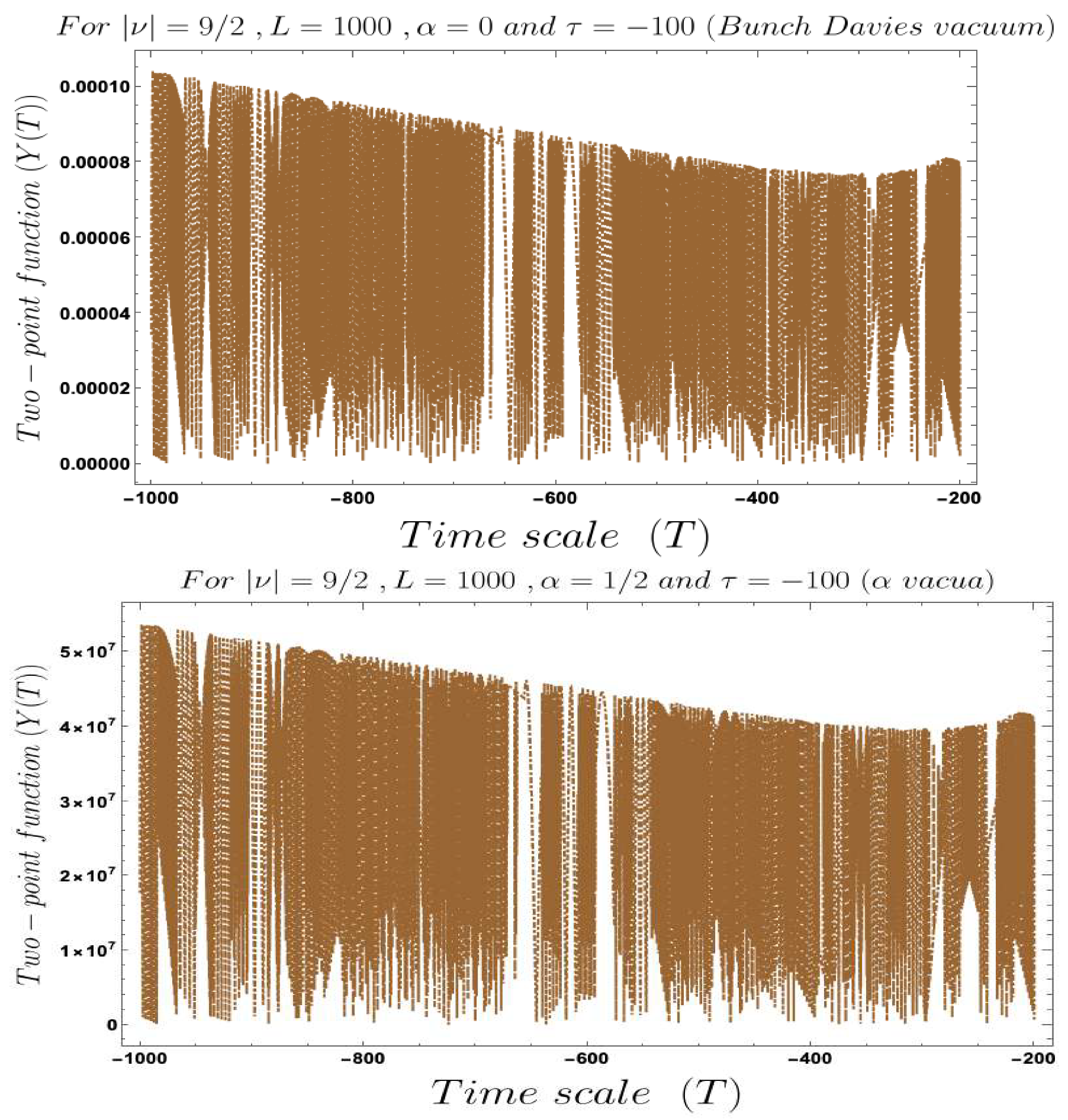
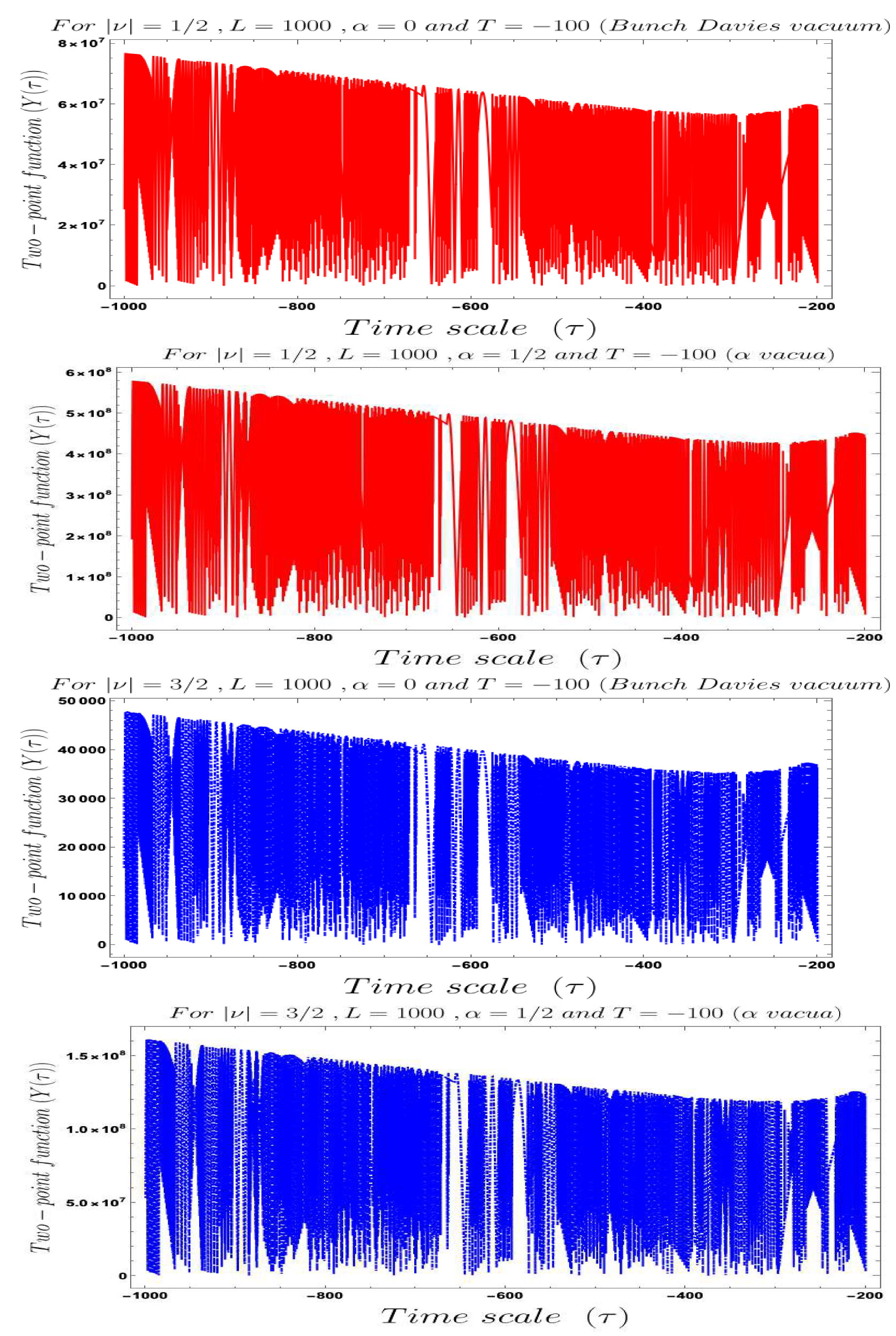
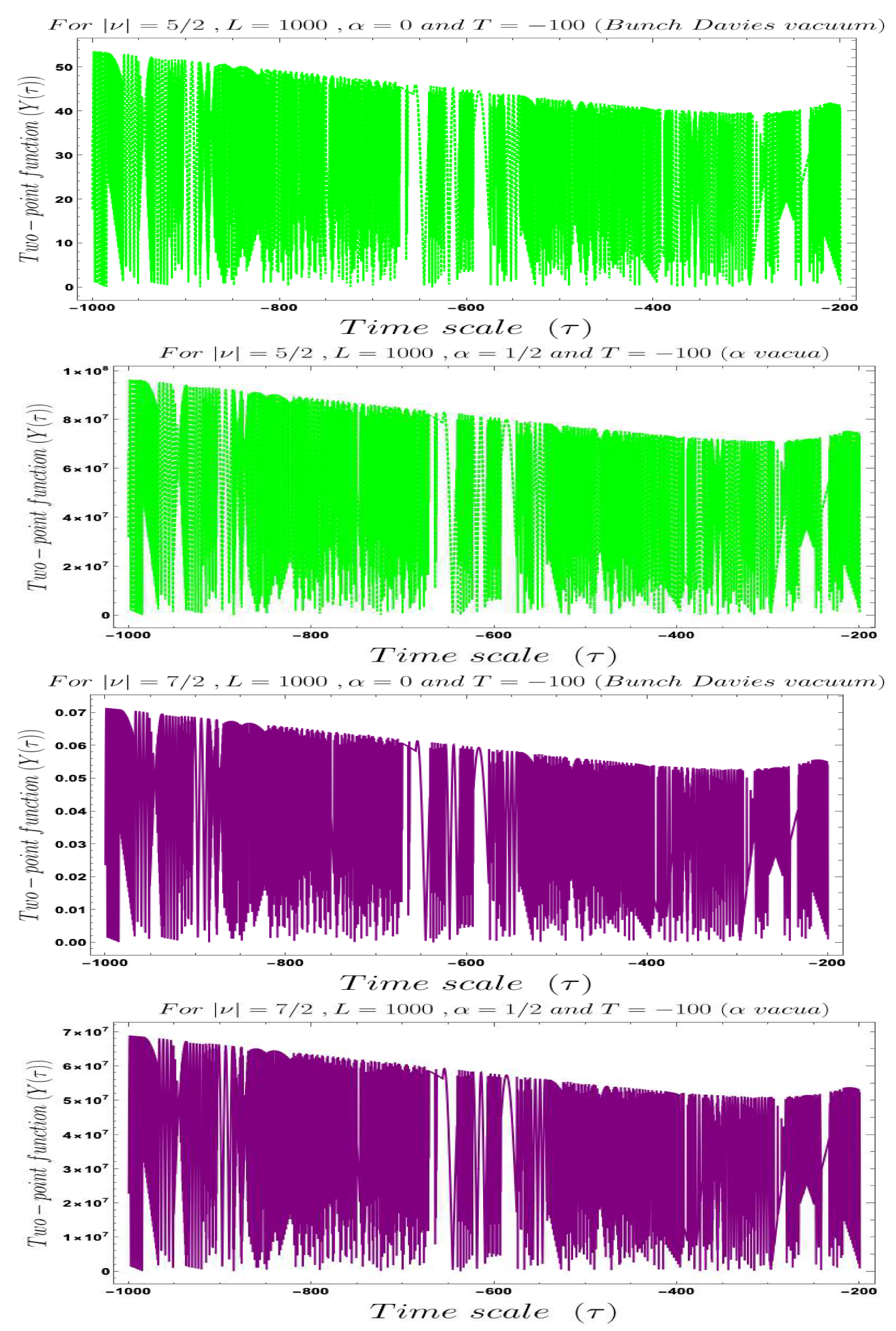
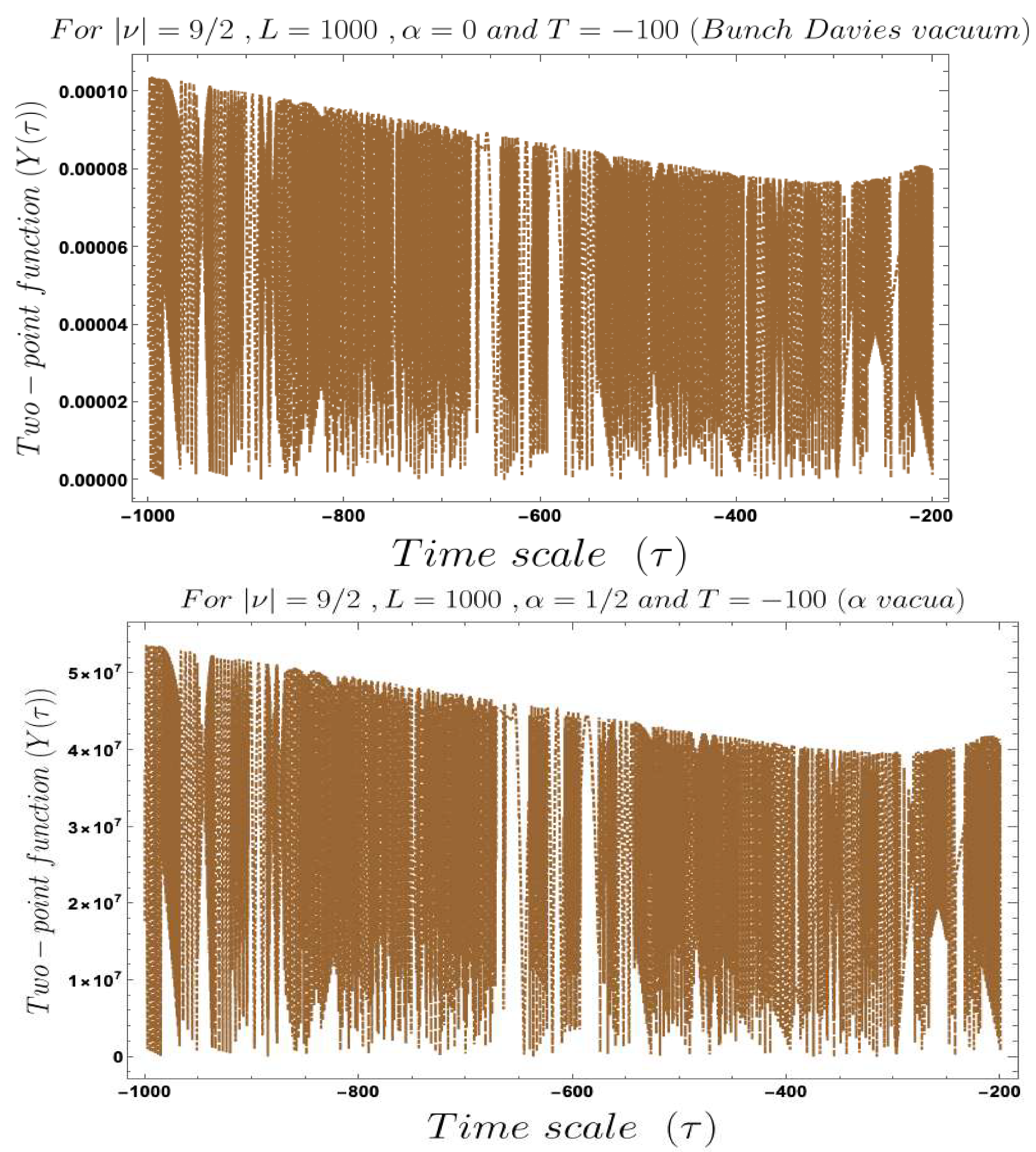
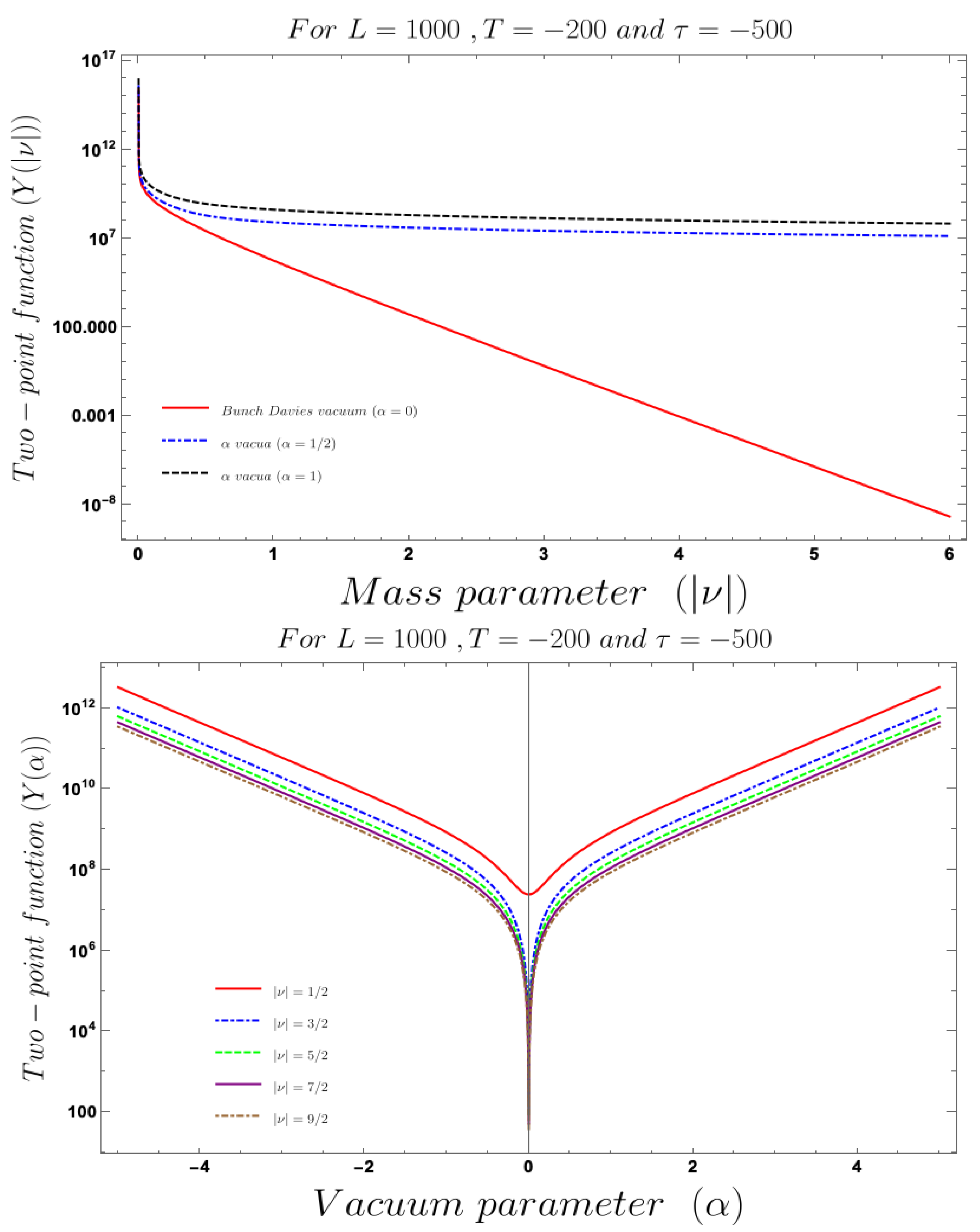
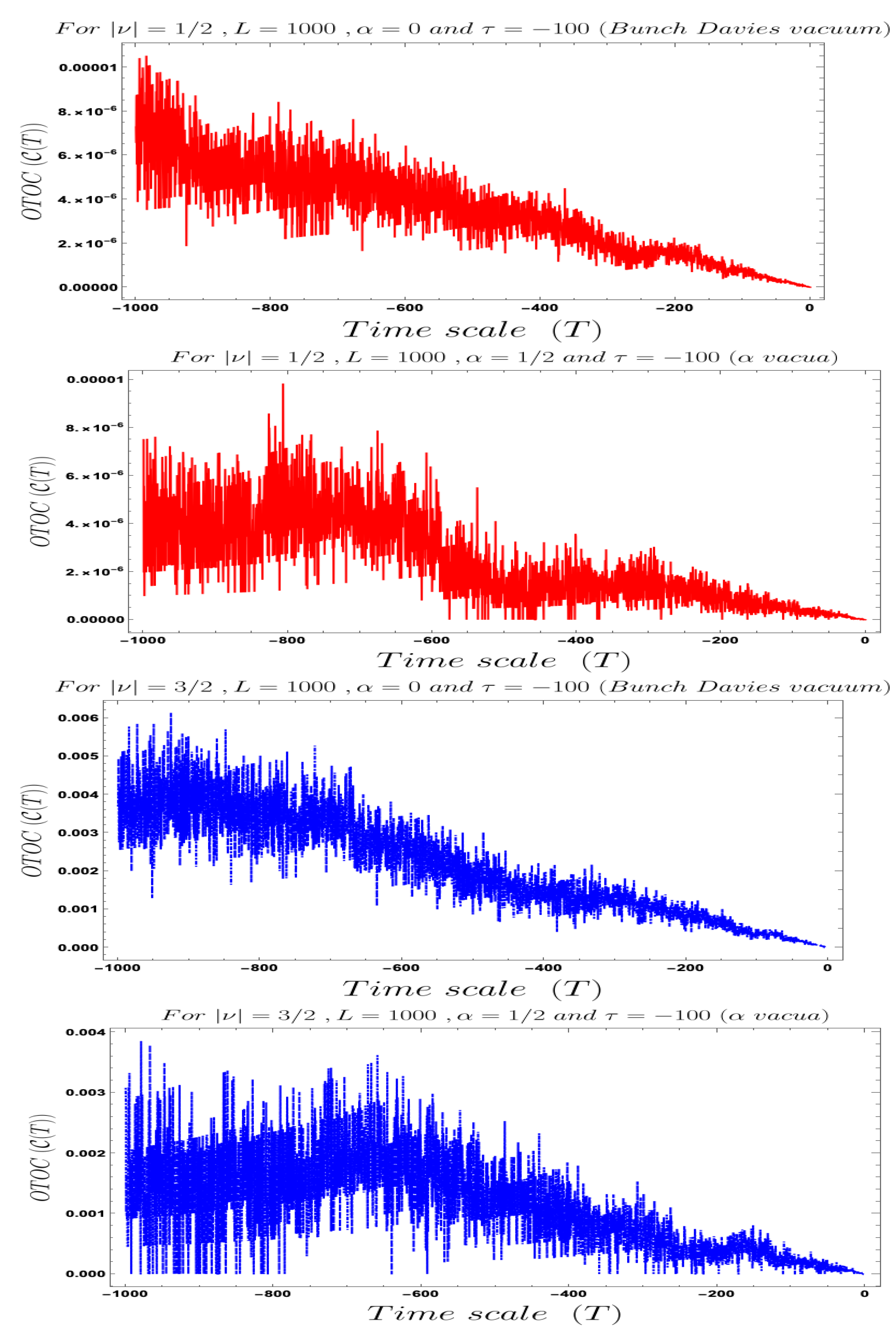
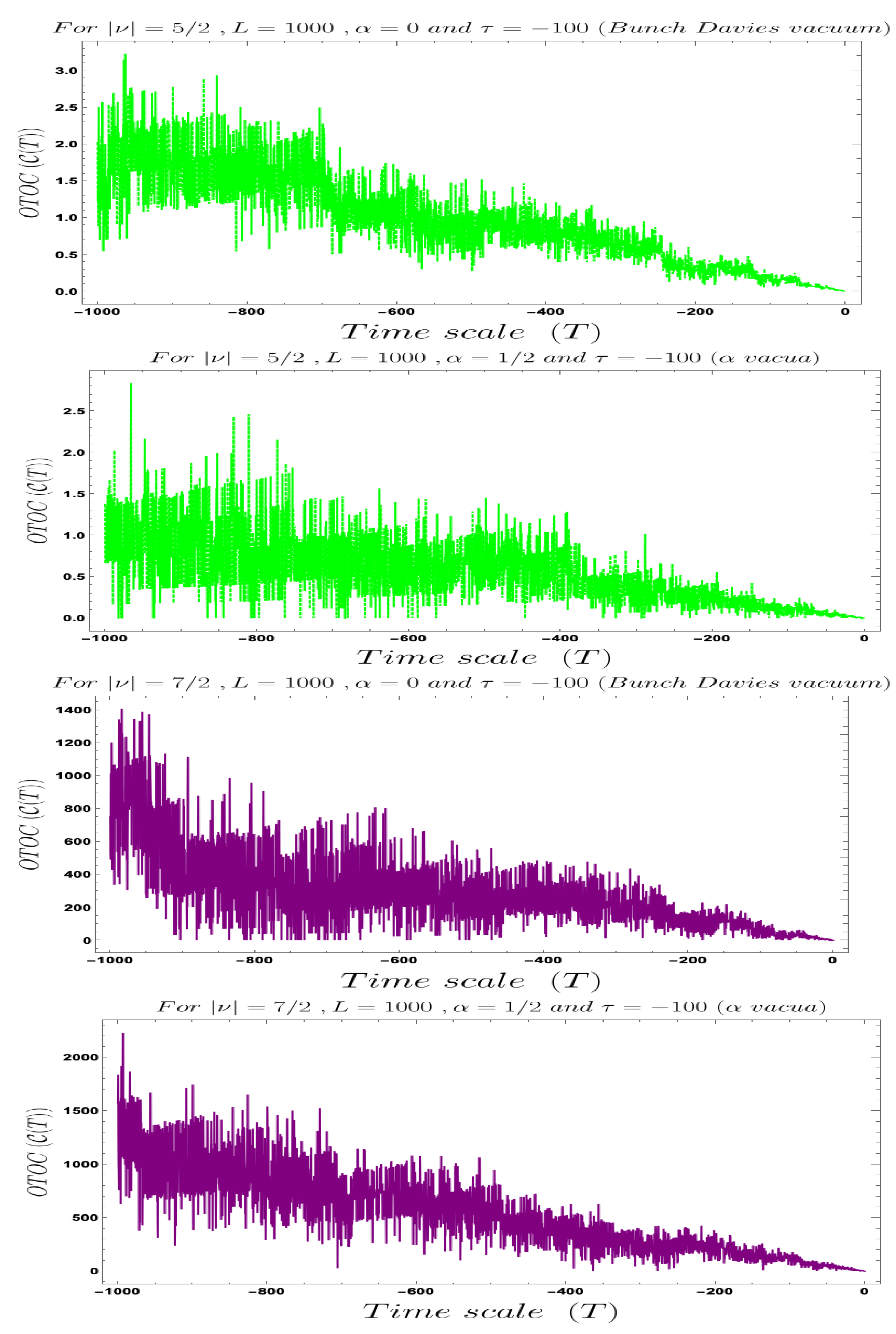
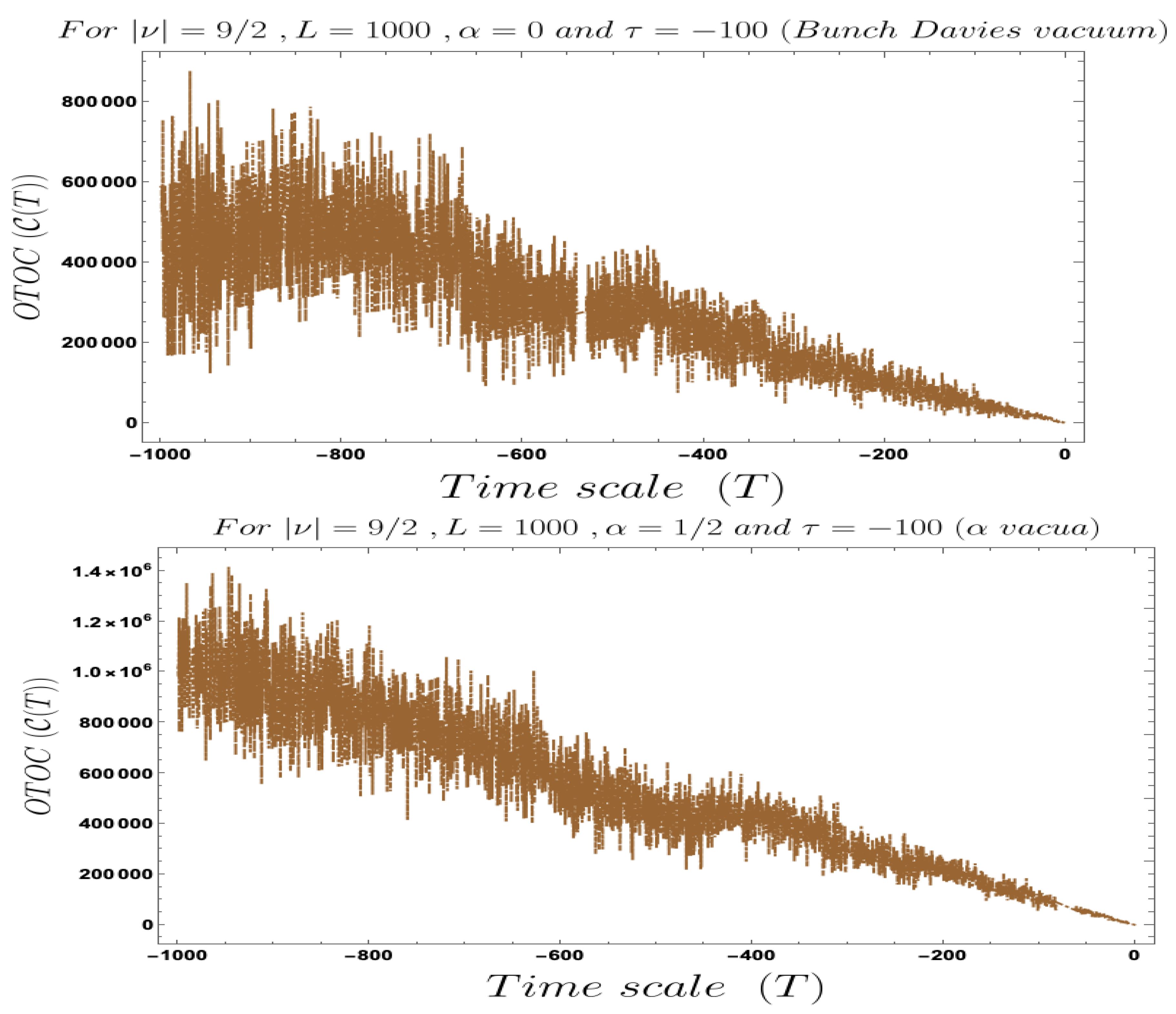
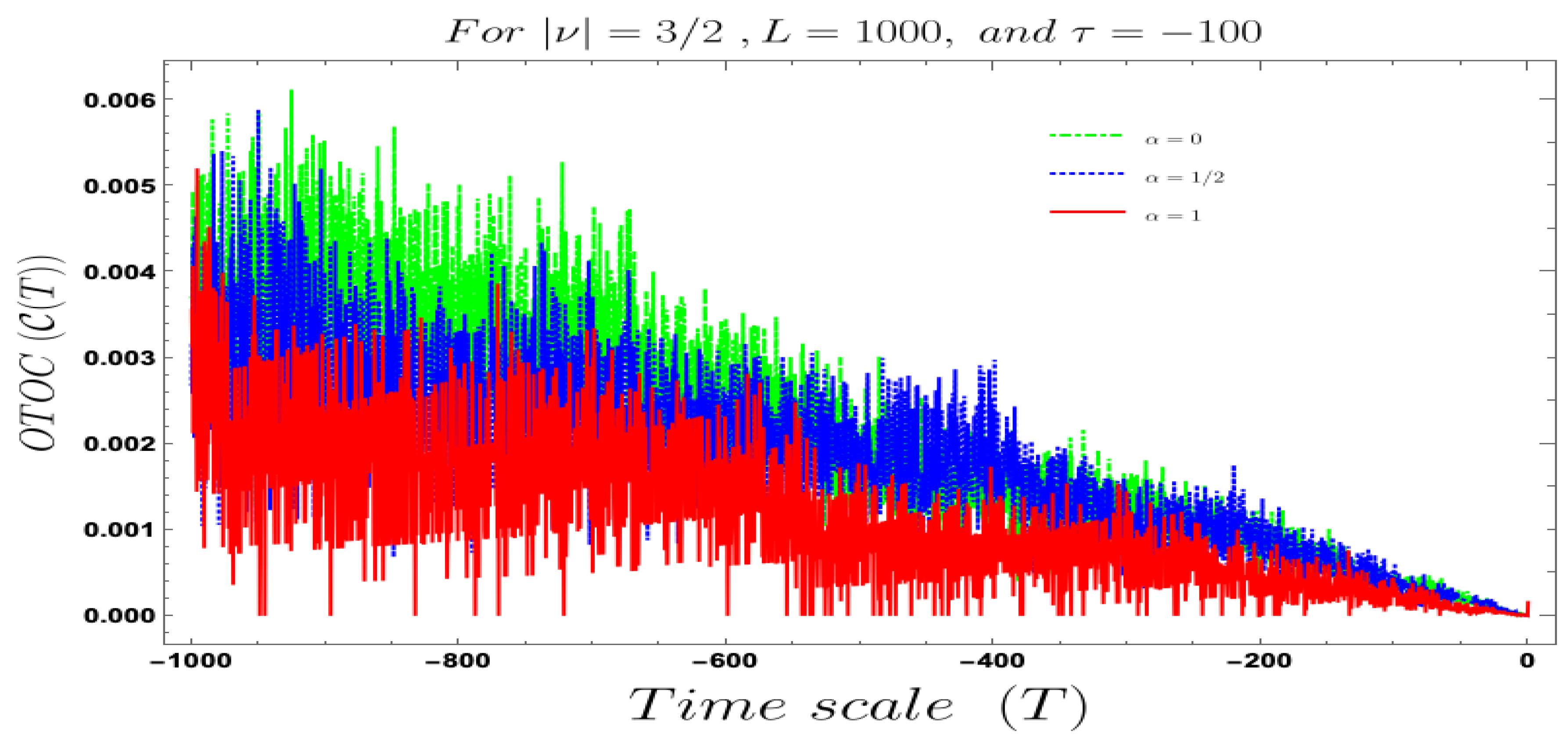
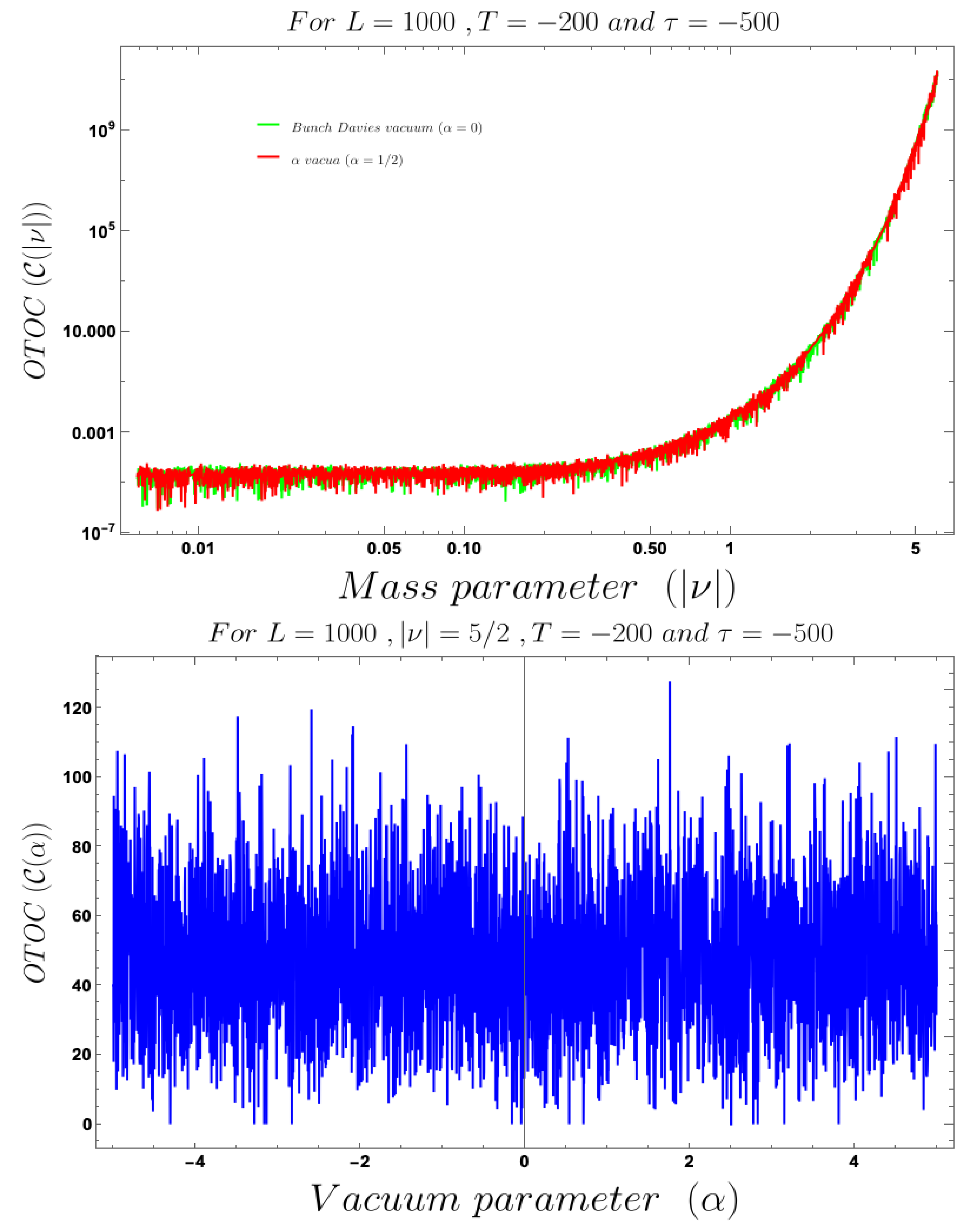
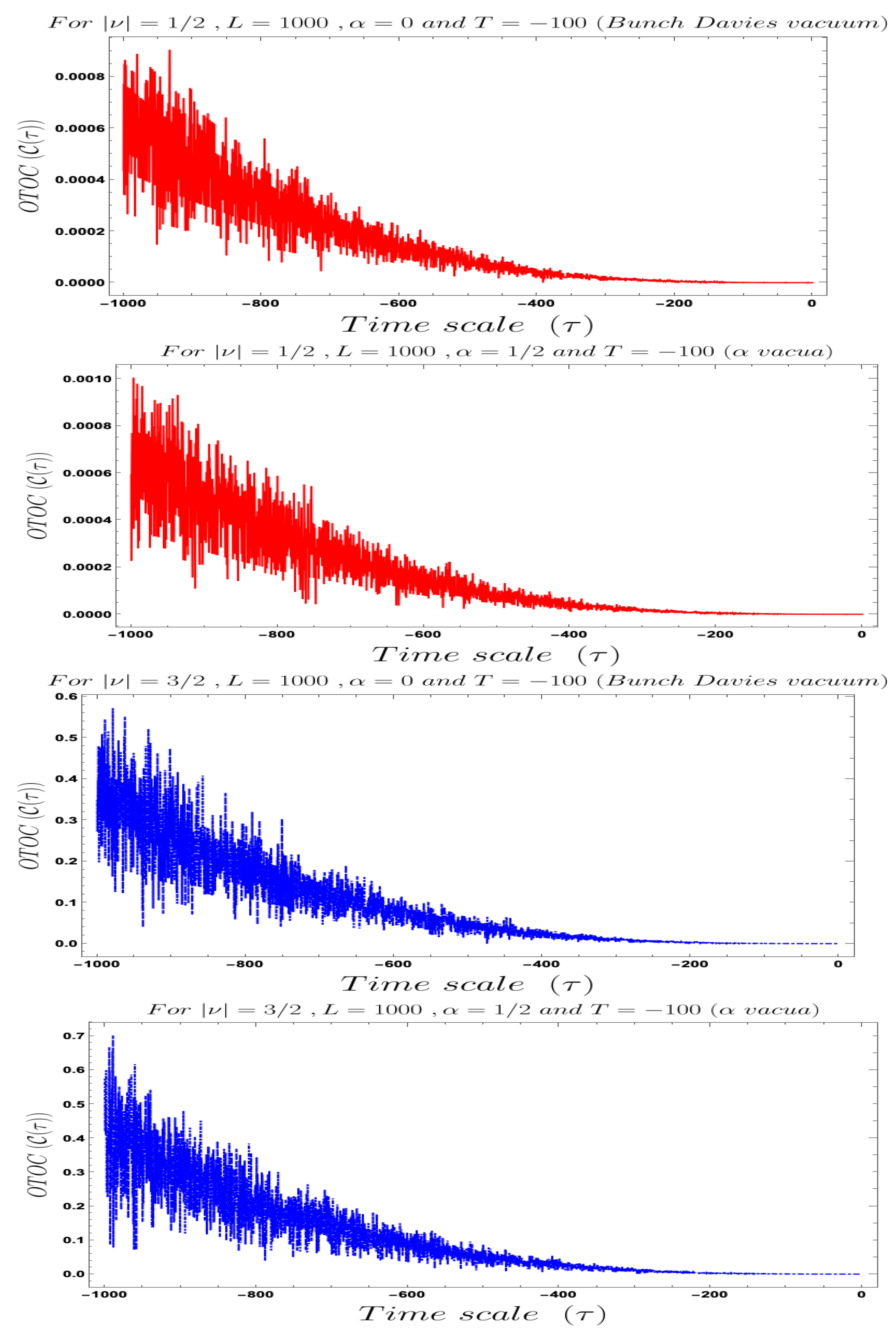
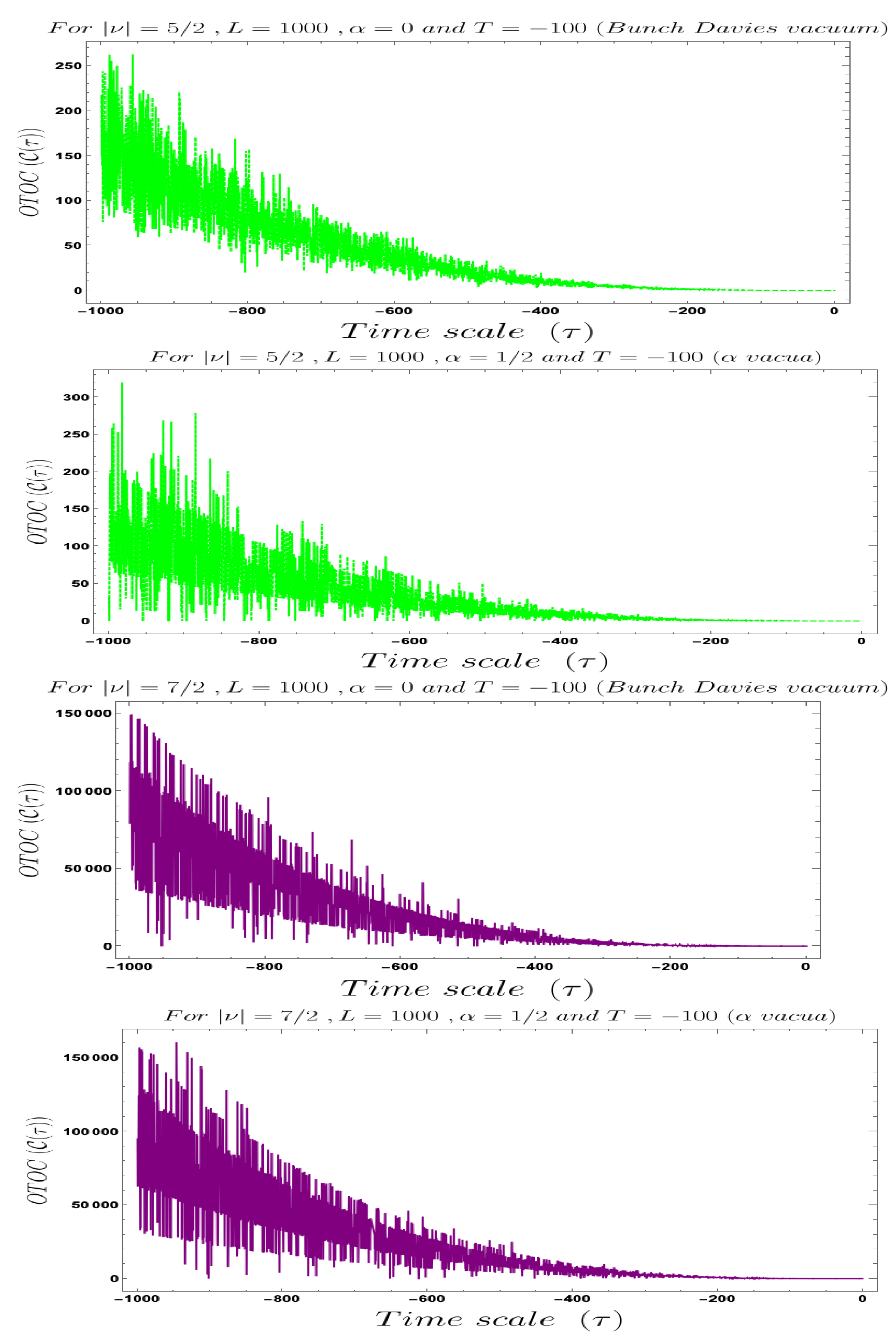
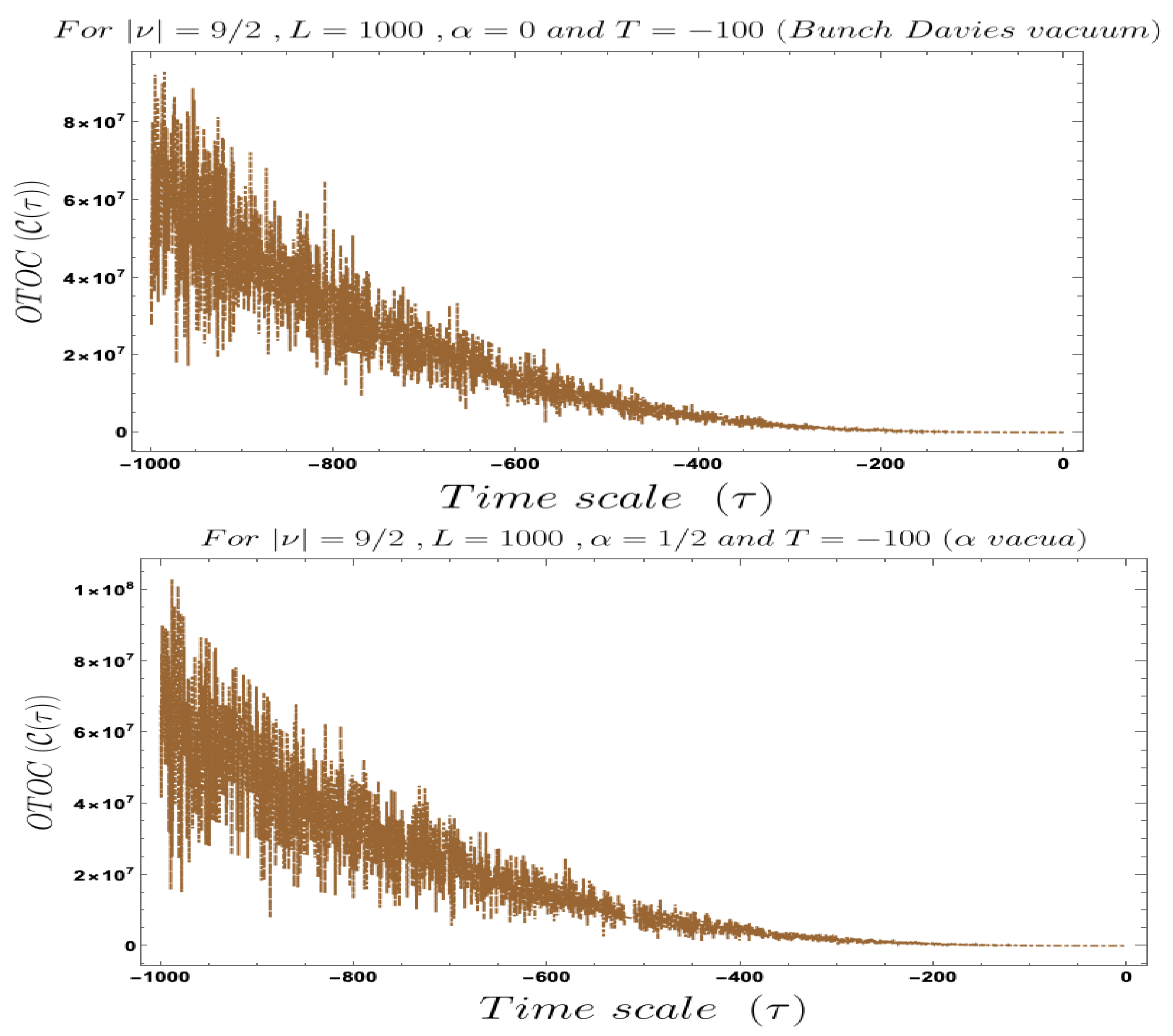

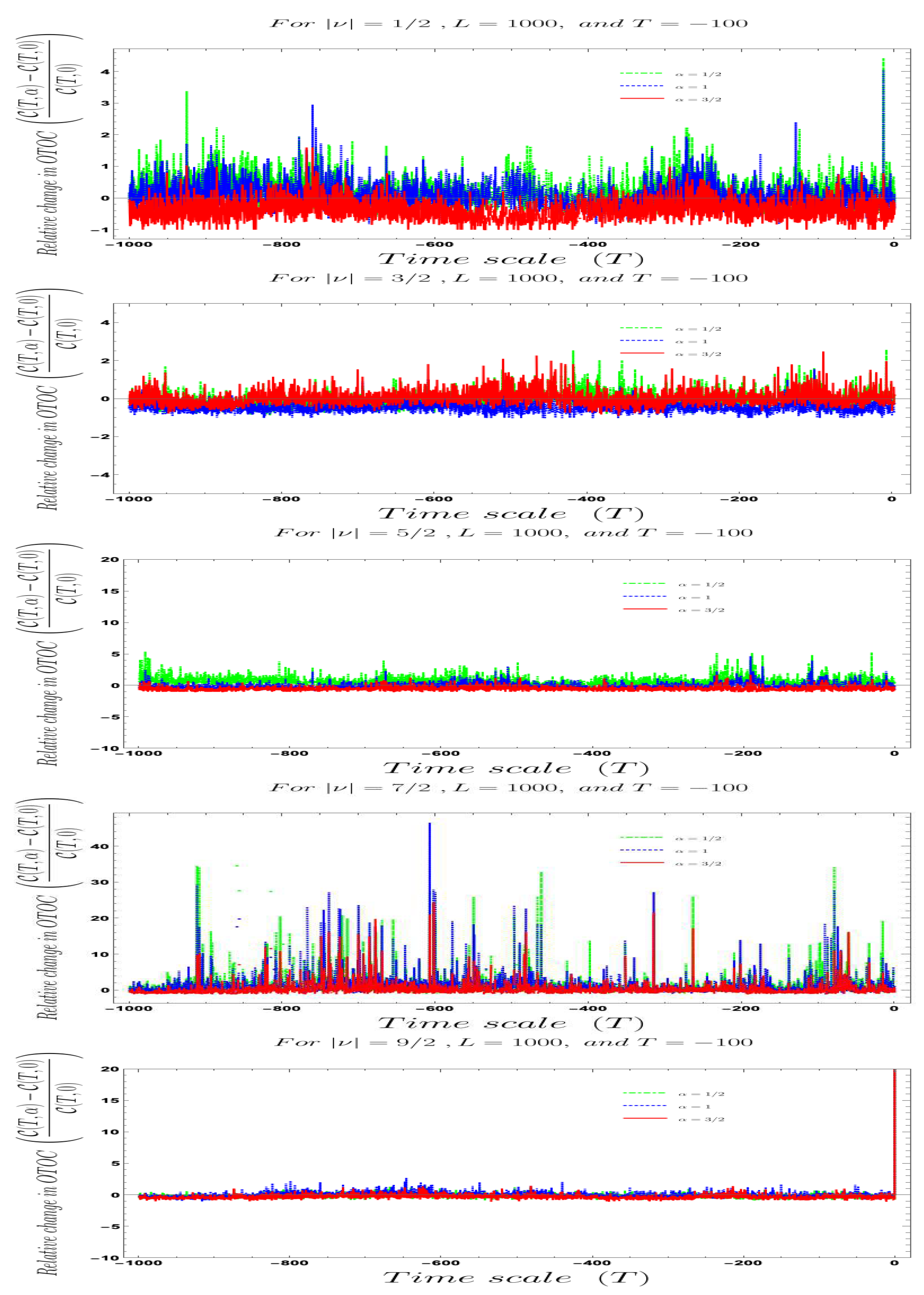
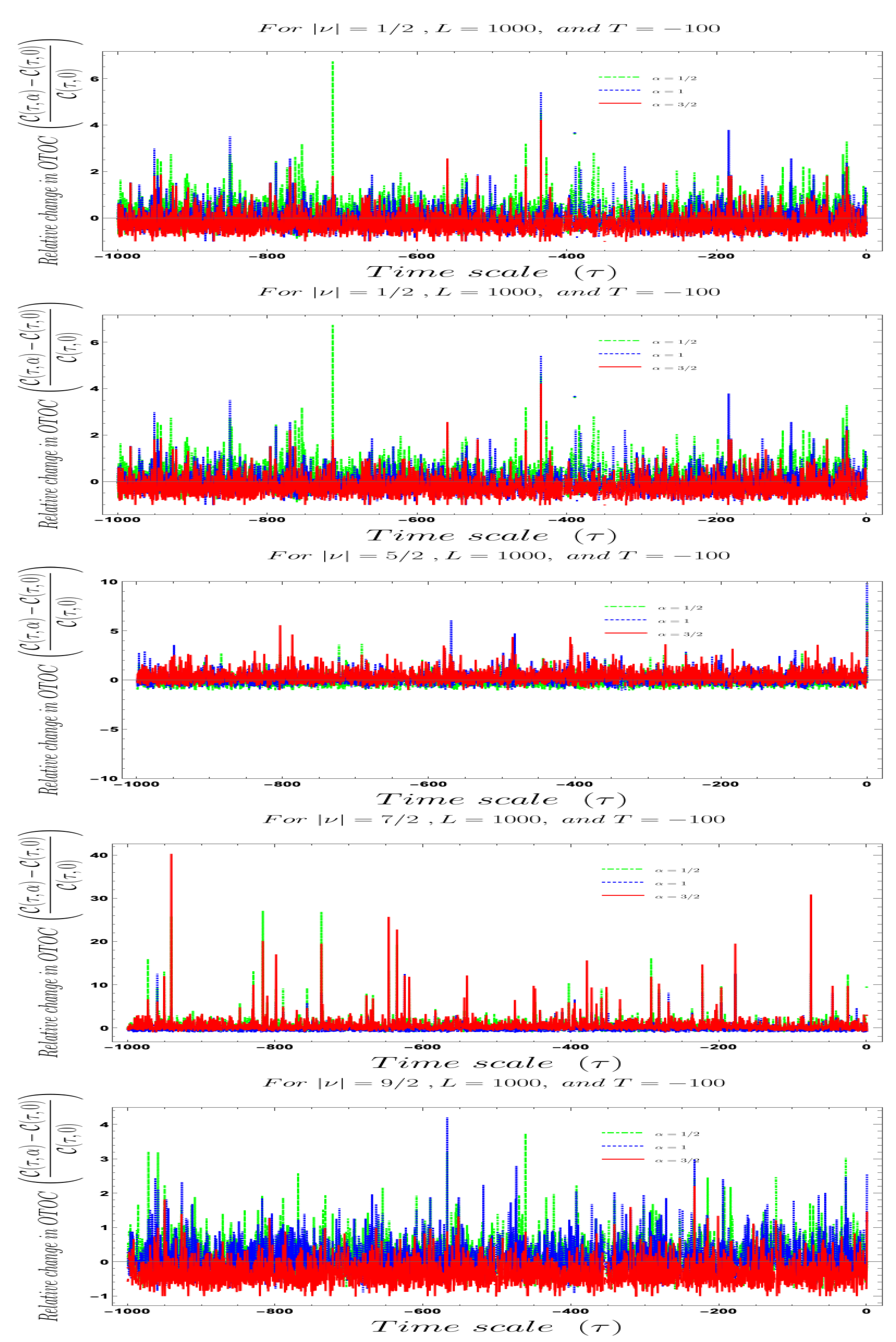
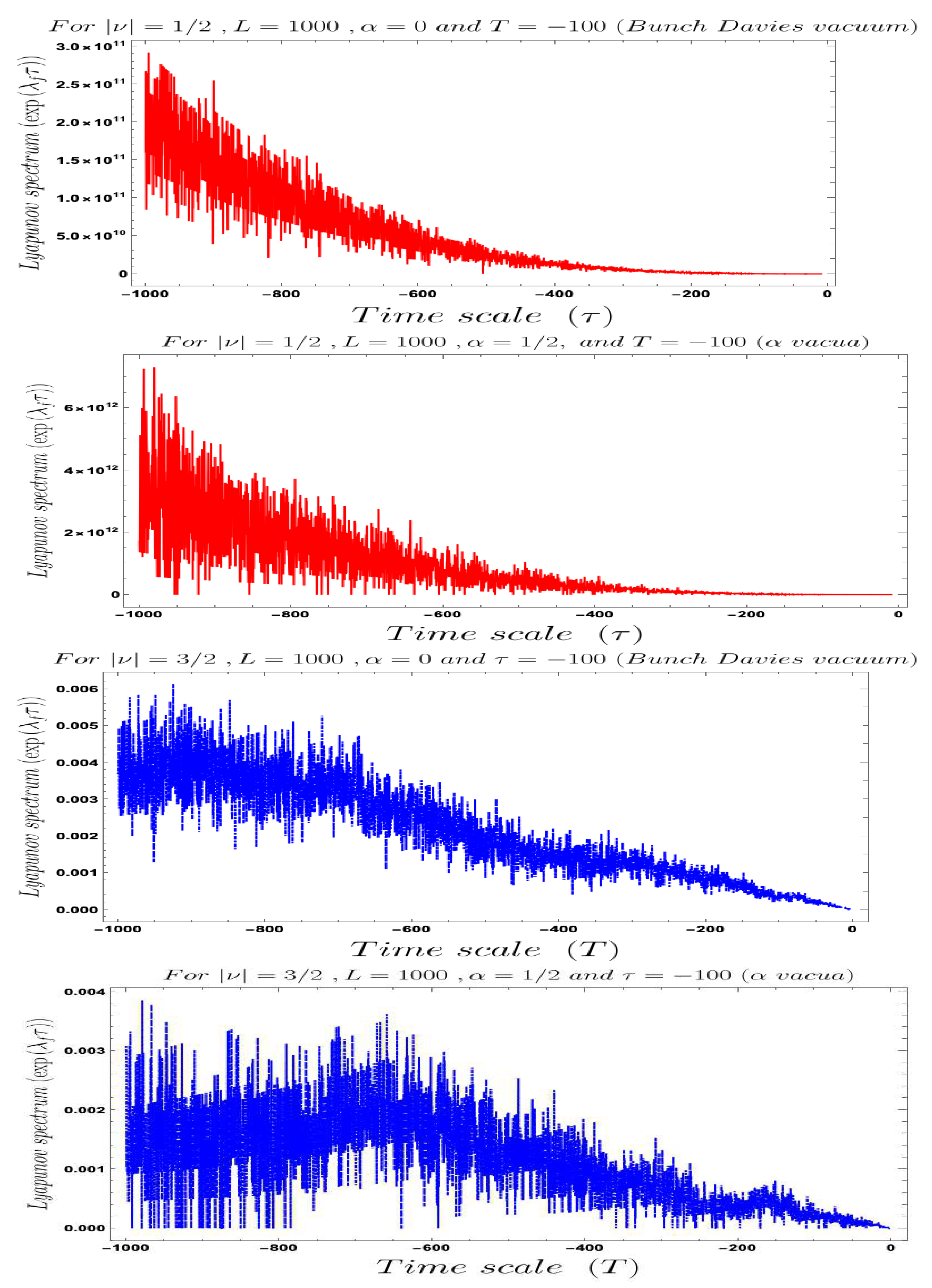
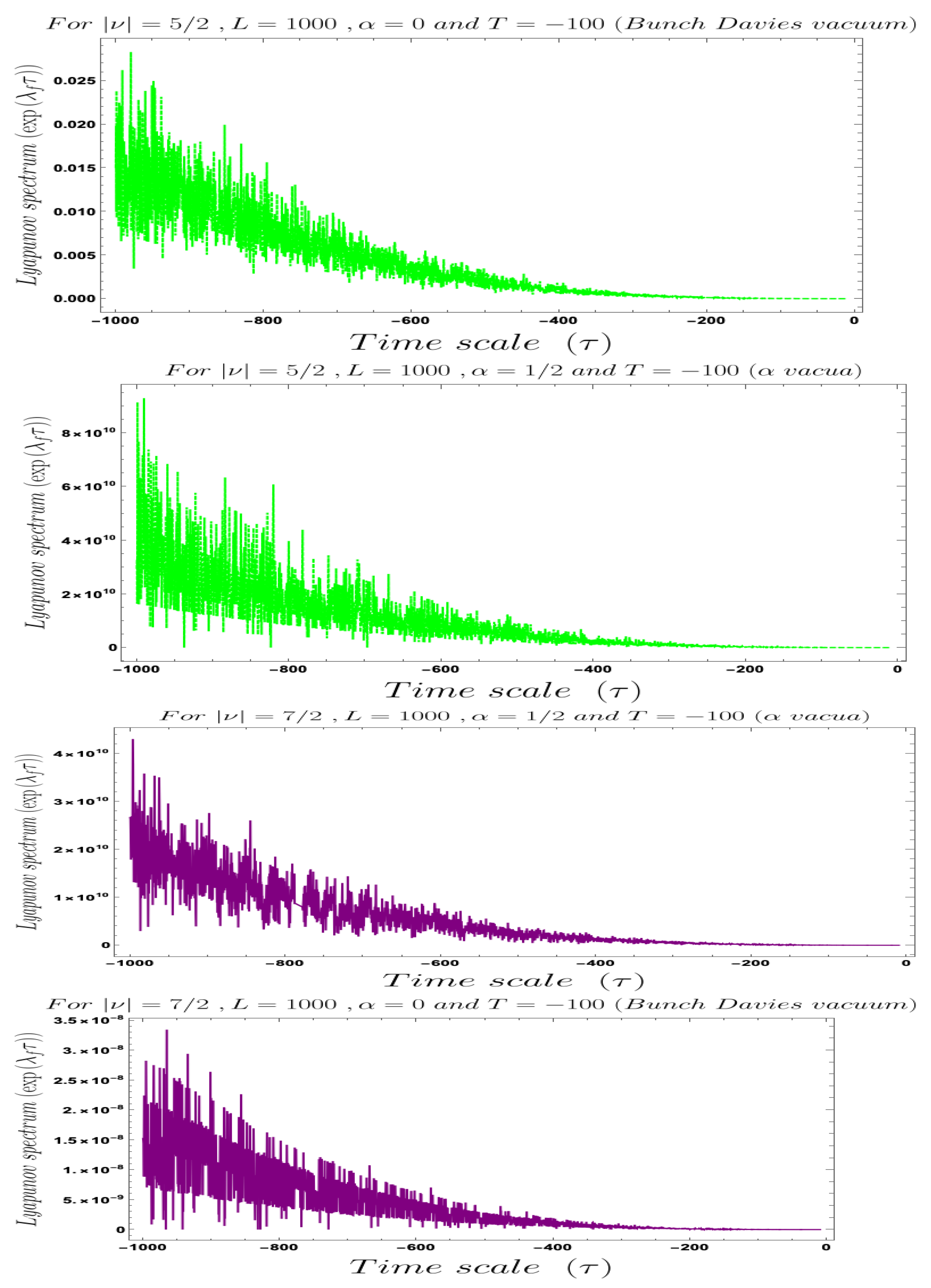
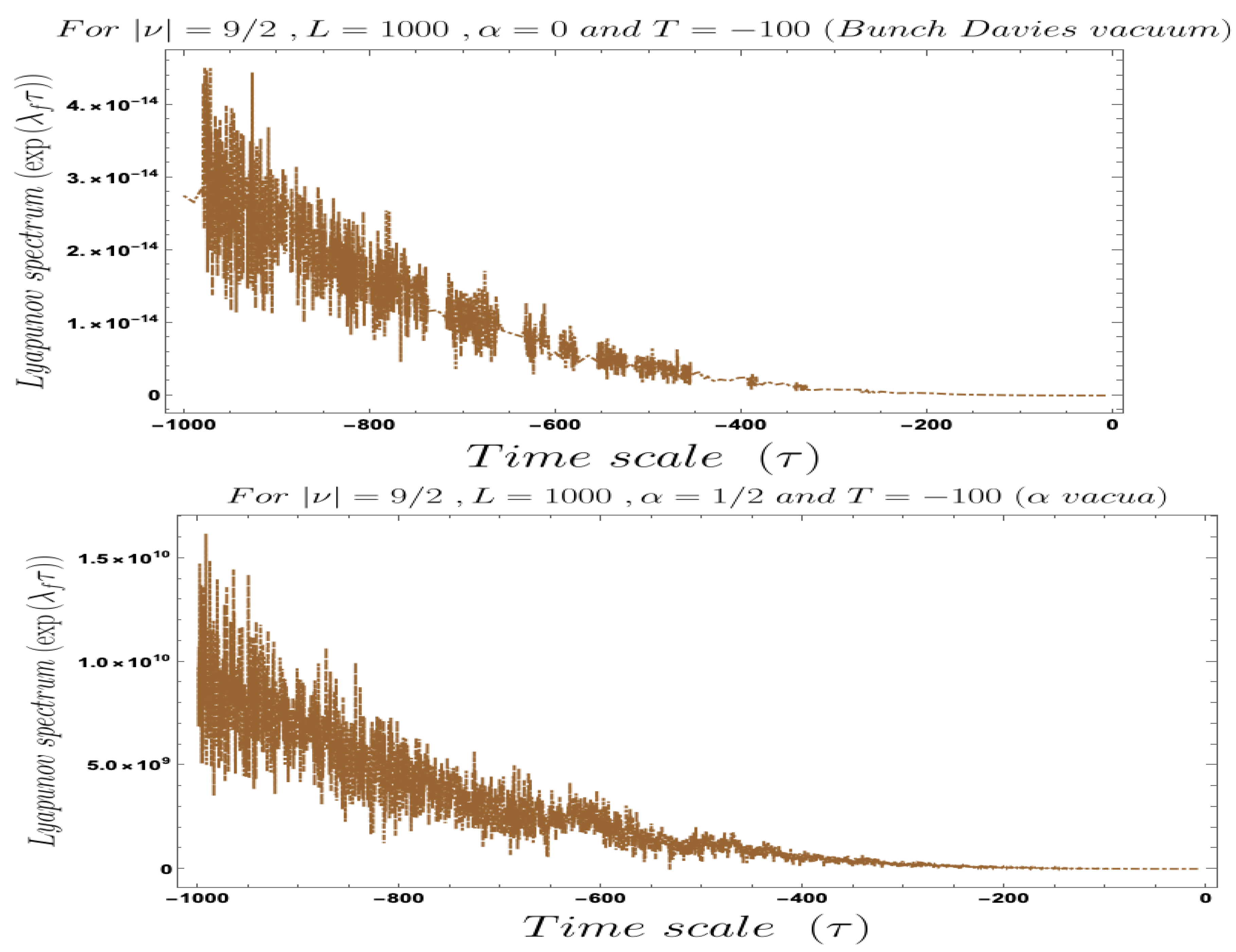
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhury, S. :THE COSMOLOGICAL OTOC: Formulating New Cosmological Micro-Canonical Correlation Functions for Random Chaotic Fluctuations in Out-Of-Equilibrium Quantum Statistical Field Theory. Symmetry 2020, 12, 1527. https://doi.org/10.3390/sym12091527
Choudhury S. :THE COSMOLOGICAL OTOC: Formulating New Cosmological Micro-Canonical Correlation Functions for Random Chaotic Fluctuations in Out-Of-Equilibrium Quantum Statistical Field Theory. Symmetry. 2020; 12(9):1527. https://doi.org/10.3390/sym12091527
Chicago/Turabian StyleChoudhury, Sayantan. 2020. ":THE COSMOLOGICAL OTOC: Formulating New Cosmological Micro-Canonical Correlation Functions for Random Chaotic Fluctuations in Out-Of-Equilibrium Quantum Statistical Field Theory" Symmetry 12, no. 9: 1527. https://doi.org/10.3390/sym12091527
APA StyleChoudhury, S. (2020). :THE COSMOLOGICAL OTOC: Formulating New Cosmological Micro-Canonical Correlation Functions for Random Chaotic Fluctuations in Out-Of-Equilibrium Quantum Statistical Field Theory. Symmetry, 12(9), 1527. https://doi.org/10.3390/sym12091527




