Glimpses on the Micro Black Hole Planck Phase

Abstract

Mass thresholds, lifetimes, entropy and heat capacity for micro black holes close to their late Schwarzschild phase are computed using two different generalized uncertainty principles, in the framework of models with extra spatial dimensions. Emissions of both photons and gravitons (in the bulk) are taken into account. Results are discussed and compared.

1. Introduction

The appearance, some years ago, of scenarî contemplating the existence of extra space-like dimensions has had many different and deep impacts on the fundamental physics.

One of the most astonishing consequences of such framework seems to be the lowering of the Planck scale to the TeV region, predicted by both the large extra dimensions models [1,2], and by models with warped extra-dimensional geometries [3,4]. The explicit dependence of $M_{Planck}$ on the number of extra spatial dimensions varies from a formulation to another, but all the formulations exhibit a value of $M_P$ which, at least for some number of extra dimensions n, lies at the few TeV scale. This has had, as an immediate consequence, the possibility to bring down to laboratory scale the “most wanted” Holy Graal of modern theoretical physics, namely the Quantum Gravity regime. The unreachable threshold of ${10}^{19}$ GeV (Planck energy in four dimensions) is reduced, in these frameworks, to energies that can be vastly probed by the CERN collider machines, LHC and the next generation. Although not produced so far, it still remains open the possibility to observe some of these objects in the next runnings of LHC at full regime (14 TeV), or perhaps in the next generation machines.

Much work has been devoted to the understanding of the behavior of these genuinely non perturbative quantum gravity objects, from the seminal papers of [5,6,7,8,9,10] to the more recent analysis of the many possible signatures, which could reveal these objects in the LHC (or similar) runnings. See [11,12,13,14,15] for a (very) incomplete list of papers and further references.

The usual classification of the phases of the life of a micro black hole (produced in a high energy collision) states that the decay of an excited spinning black hole proceeds through several stages. There is a balding phase, where the hole loses “hair” via the emission of classical gravitational and gauge radiation. Gauge charges inherited from the initial colliding particles are being lost in this phase. After, there is a brief rotating phase (spindown phase) in which the black hole loses angular momentum and energy, via super-radiance and semiclassical Hawking radiation, until it settles down to a longer Schwarzschild phase. Here, the black hole evaporates by losing mass/energy through the Hawking effect. According to the semiclassical approximation, the hole should then shrink to zero, in a sort of final explosive state. At the very end point, the hole should reach (according to the semiclassical picture) an infinite temperature and an infinite emission rate. Of course, it is widely believed that this semiclassical approximation breaks down somewhere (well) before the Planck mass is reached.

While the first phases of the black hole life are intensely studied, and quite well understood, with the tools of QFT on curved space-time, the final part of the Schwarzschild phase, namely the so called Planck phase, is still by far the most puzzling sector of the problem. We do not know much about this phase, mainly because we do not have a complete theory of quantum gravity at our disposal [16]. However, some light on the close proximity of the Planck phase (or, at least, on the last part of the Schwarzschild semiclassical phase) seems to have been shred by several authors [17,18,19,20,21,22]. They all use, as a good approximation of the final full quantum gravity theory, calculations based on generalized uncertainty principle(s) (GUP), i.e., deformed commutators, in order to compute the relevant quantities of the phenomenon, namely temperature, mass thresholds, black hole lifetimes. As we shall see, a striking consequence of the GUP formalism is a direct prediction of the stopping of the evaporation and the consequent existence of remnants.

The main novelty of this paper in respect to the current literature is that the Hawking evaporation process for (micro) black hole is dealt with two different GUPs, which remarkably yield different predictions (about mass thresholds, lifetimes, entropy and heat capacity for micro black holes close to their late Schwarzschild phase) in the framework of extra dimensions. However, in four dimensions the two GUPs have the same form, and their predictions coincide with those already well established in the GUP literature.

The present paper, which moves along the research lines just above-mentioned, is organized as follows: in Section 2 we introduce the two generalized uncertainty principles we are dealing with; in Section 3 and Appendix A we prove the translation and rotation invariance of such GUPs; Section 4 and Section 5 are dedicated to the mass–temperature relation inferred by the GUPs and to the mass thresholds; in Section 6 and Section 7 we set up an emission rate equation, and use it to compute properties of the micro black hole lifetime; Section 8 deals with the end point behavior of the emission rate; in Section 9 we compute with the GUPs the entropy and the heat capacity of the micro black holes, and discuss the important end point properties of the heat capacity. Section 10 is dedicated to the conclusions.

Throughout the paper, in $4+n$ dimensions, the Planck length is defined as ${\ell }_{4n}^{2+n}=G_{4n}ħ/c^3$, the Planck energy as ${\mathcal{E}}_{4n}{\ell }_{4n}=ħc/2$, the Planck mass as $M_{4n}={\mathcal{E}}_{4n}/c^2$. The value of the $4+n$ dimensional Newton constant $G_{4n}$, and its link with the four dimensional $G_N$, is in general model dependent (see, e.g., [10] for the ADD and RS model). A specific example will be discussed in Section 5.

2. Gups

Having in mind a high energy collision, we know that the Heisenberg principle $\Delta p\Delta x\ge ħ/2$ can be casted in the form $\Delta E\Delta x\ge ħc/2$ (since $\Delta E\simeq c\Delta p$). It is worth noting that Heisenberg commutators in QFT are Lorentz invariant statements, which means that they are valid, in principle, at any energy scale. Actually, the main reason of why larger and larger energies are required to explore smaller and smaller details is that the size of the smallest detail theoretically detectable with a beam of energy E is $\delta x=ħc/(2E)$. An equivalent argument comes from considering the resolving power of a “microscope”: the smallest resolvable detail goes roughly as the wavelength of the employed photons, and therefore $\delta x\simeq \lambda =\frac{c}{\nu }=\frac{hc}{ϵ}$.

The research on viable generalizations of the Heisenberg uncertainty principle traces back to many decades (see for early approaches [23,24], etc. See for a review [25] and for more recent approaches [26,27]). In the last 30 years, there have been important studies in string theory [28,29,30,31] suggesting that, in Gedanken experiments about high energy scattering with high momentum transfer, the uncertainty relation should be written as

$$\begin{array}{c}\hfill \delta x\gtrsim \frac{ħ}{2p}+2\beta {\ell }_{4n}^2\frac{p}{ħ},\end{array}$$

(1)

where ${\ell }_{4n}$ is the $4+n$ dimensional Planck length and $\beta {\ell }_{4n}^2\sim {\lambda }_s^2$ (${\lambda }_s$ is the characteristic string length). Since in our high energy scattering $E\simeq cp$, the stringy GUP can be also written as

$$\begin{array}{c}\hfill \delta x\gtrsim \frac{ħc}{2E}+2\beta {\ell }_{4n}^2\frac{E}{ħc},\end{array}$$

(2)

where E is the energy of the colliding beams.

If however we take into account the possibility of a formation of micro black holes in the scattering, with a gravitational radius of $R_S\sim {(E)}^{1/(n+1)}$, then we easily see that in $4+n$ dimensions (and $n\ge 1$) the stringy principle seems to forbid the very observation of the micro hole itself. In fact, at high energy the error predicted by the stringy GUP goes like $\delta x\sim E$, while the size of the hole goes like $R_S\sim {(E)}^{1/(n+1)}$. For E enough large and $n\ge 1$, we always would have $E>{(E)}^{1/(n+1)}$, thereby losing the possibility of observing micro black holes just when they become more massive. Also to avoid this state of affairs, and on the ground of Gedanken experiments involving the formation of micro black holes, it has been proposed [27,32] a modification of the uncertainty principle that in $4+n$ dimensions reads

$$\begin{array}{c}\hfill \delta x\gtrsim \left\{\begin{array}{c}\frac{ħc}{2E}\mathrm{for}E<{\mathcal{E}}_{4n}\hfill \\ \\ \beta R_{4n}(E)\mathrm{for}E\ge {\mathcal{E}}_{4n},\hfill \end{array}\right.\end{array}$$

(3)

where $R_{4n}$ is the $4+n$ dimensional Schwarzschild radius associated with the energy E (see [33])

$$\begin{array}{c}\hfill R_{4n}={\left[\frac{16\pi G_{4n}E}{(N-1){\mathsf{\Omega }}_{N-1}{c}^4}\right]}^{\frac{1}{N-2}}={\ell }_{4n}{\left({\omega }_n\frac{E}{{\mathcal{E}}_{4n}}\right)}^{\frac{1}{N-2}}\end{array}$$

(4)

and $N=3+n$ is the number of space-like dimensions, ${\omega }_n=8\pi /((N-1){\mathsf{\Omega }}_{N-1})$, ${\mathsf{\Omega }}_{N-1}=2{\pi }^{N/2}/\mathsf{\Gamma }(N/2)=\mathrm{area}\mathrm{of}\mathrm{the}\mathrm{unit}{\mathrm{S}}^{\mathrm{N}-1}\mathrm{sphere}$. Combining linearly the above inequalities we get

$$\begin{array}{c}\hfill \delta x\gtrsim \frac{ħc}{2E}+\beta R_{4n}(E).\end{array}$$

(5)

Thus, the GUP originating from micro black hole Gedanken experiments (MBH GUP) can be written as

$$\begin{array}{c}\hfill \delta x\gtrsim \frac{ħc}{2E}+\beta {\ell }_{4n}{\left({\omega }_n\frac{E}{{\mathcal{E}}_{4n}}\right)}^{\frac{1}{N-2}}.\end{array}$$

(6)

Using again the relation ${\mathcal{E}}_{4n}{\ell }_{4n}=ħc/2$ the stringy inspired GUP (ST GUP, Equation (2)) can be written in $4+n$ dimensions as

$$\begin{array}{c}\hfill \delta x\gtrsim \frac{ħc}{2E}+\beta {\ell }_{4n}\frac{E}{{\mathcal{E}}_{4n}}.\end{array}$$

(7)

where $\beta$ is the deformation parameter, generally believed of $O(1)$. Remarkably, in four dimensions ($N=3$, $n=0$) the two principles coincide. The deformation parameter $\beta$, supposed independent from the dimensions N, can be therefore chosen as the same for both principles. A recent, explicit calculation performed in Reference [34] has confirmed that $\beta \sim O(1),O(10)$. On the formation of (micro) black holes by particle collisions is also useful in Reference [35].

A comparison between the two principles yields

$$\begin{array}{c}\hfill \beta {\ell }_{4n}\frac{E}{{\mathcal{E}}_{4n}}>\beta {\ell }_{4n}{\left({\omega }_n\frac{E}{{\mathcal{E}}_{4n}}\right)}^{\frac{1}{N-2}}⟺E>{({\omega }_n)}^{\frac{1}{n}}{\mathcal{E}}_{4n}\end{array}$$

(8)

The last condition is easily met when $N=3,4,\dots ,9$, in all the planned LHC collision experiments, since $0.35<{({\omega }_n)}^{\frac{1}{n}}<0.55$, and ${\mathcal{E}}_{4n}$ is believed to be of the order of few TeV (if extra dimensions are really there). As we mentioned, the above inequality means that $\delta x_{ST}>\delta x_{MBH}$, so that at very high energies stringy GUP seems to produce an error, $\delta x_{ST}$, larger then the size of the micro black hole itself. In other words the stringy GUP does not seem to allow, in principle, for the observation of (massive) micro black hole (error larger than the geometric size of the hole). This could be an indication supporting the MBH GUP (6) in respect to ST GUP (7).

3. Translation and Rotation Invariance of the Gups

In this section we shall prove that the GUPs previously introduced do respect the constraints posed by requiring the conventional translation and rotation invariance of the commutation relations. First, we show what these kinematic constraints imply about the structure, in n dimensions, of the $[x,p]$ commutations relations. In this, we follow closely Reference [36,37]. As a general ansatz for the $x,p$ commutation relation in n dimensions we take

$$\begin{array}{c}\hfill [x_i,p_j]=iħ{\mathsf{\Xi }}_{ij}(p),\end{array}$$

(9)

where the symbol ${\mathsf{\Xi }}_{ij}(p)$ is an element of an $n\times n$ matrix, which in general depends on p and differs significantly from ${\delta }_{ij}$ only for large momenta. We assume also $[p_i,p_j]=0$ and we compute the remaining commutation relation through the Jacobi identities, obtaining

$$\begin{array}{c}\hfill [x_i,x_j]=iħ\{x_a,{\mathsf{\Xi }}_{ar}^{-1}{\mathsf{\Xi }}_{s[i}{\mathsf{\Xi }}_{j]r,s}\}\end{array}$$

(10)

where $\left\{\right\}$ are the anti-commutators and $Q{,}_s:=\partial Q/\partial s$. The commutation relations (9) are translation invariant (they are preserved under the transformations $x_i\to x_i+d_i,p_i\to p_i$). However, the commutation relations (10) are not invariant under translation, unless we require ${\mathsf{\Xi }}_{ij}(p)$ to be such that it yields $[x_i,x_j]=0$. Thus, in order to implement translation invariance, ${\mathsf{\Xi }}_{ij}$ must satisfy the necessary and sufficient condition (read off from the (10))

$$\begin{array}{c}\hfill {\mathsf{\Xi }}_{ia}{\partial }_{p_i}{\mathsf{\Xi }}_{bc}={\mathsf{\Xi }}_{ib}{\partial }_{p_i}{\mathsf{\Xi }}_{ac}\end{array}$$

(11)

where sum over i is understood. The rotation invariance can be implemented by requiring ${\mathsf{\Xi }}_{ij}$ to have the form

$$\begin{array}{c}\hfill {\mathsf{\Xi }}_{ij}(p)=f(p^2){\delta }_{ij}+g(p^2)p_i{p}_j.\end{array}$$

(12)

Together, conditions (11) and (12) imply that f and g must satisfy the differential equation

$$\begin{array}{c}\hfill 2f^{\prime }f+(2f^{\prime }{p}^2-f)g=0\end{array}$$

(13)

where $f^{\prime }(p^2)=df/d(p^2)$. Under these conditions commutation relations do obey translation and rotation invariance.

Considering, for the sake of simplicity, the mono-dimensional case $i=j$, we write for the main commutator

$$\begin{array}{c}\hfill [x,p]=iħ(f(p^2)+g(p^2)p^2).\end{array}$$

(14)

The usual Heisenberg commutator is recovered by choosing, for example, $f(p^2)=1$. Then Equation (13) implies $g(p^2)=0$ and $[x,p]=iħ$. The stringy inspired commutator is obtained, to the first order in $\beta$, by choosing $g(p^2)=\beta$ (see [37]). Then, in fact, solving (13) we find

$$\begin{array}{c}\hfill f(p^2)=\frac{\beta p^2}{\sqrt{1+2\beta p^2}-1}\simeq 1+\frac{\beta }{2}{p}^2+O({(\beta p^2)}^2)\end{array}$$

(15)

and, to the first order in $\beta$ (or, equivalently, for small p) we have

$$\begin{array}{c}\hfill [x,p]=iħ\left(1+\frac{3}{2}\beta p^2+O({\beta }^2)\right).\end{array}$$

(16)

The MBH GUP (6) can be written in terms of momentum transferred as

$$\begin{array}{c}\hfill p\delta x\gtrsim \frac{ħ}{2}\left(1+\gamma p^{\frac{n+2}{n+1}}\right)\end{array}$$

(17)

where

$$\begin{array}{c}\hfill \gamma =\beta {({\omega }_n)}^{\frac{1}{n+1}}{\left(\frac{2{\ell }_{4n}}{ħ}\right)}^{\frac{n+2}{n+1}}\end{array}$$

(18)

and this in terms of commutators becomes

$$\begin{array}{c}\hfill [x,p]=iħ\left(1+\gamma p^{\frac{n+2}{n+1}}\right).\end{array}$$

(19)

To show that MBH GUP is translation and rotation invariant we must show that the commutator (19) is of the same form of commutator (14) (when $p\to 0$), with f and g satisfying (13) (in particular we would like to have $f(p^2)\to 1$ for $p\to 0$). However, the previous strategy, namely to fix a priori a given form for $g(p^2)$ and then to compute $f(p^2)$ by solving (13) (as we did for HUP, $g(p^2)=0$, and for stringy GUP, $g(p^2)=\beta$), in this case does not work. Even if one puts $p^{2}g(p^2)=\gamma p^{(n+2)/(n+1)}$, Equation (13) becomes however rather complicated (it is a Abel equation of 2nd kind), and we can hardly hope it gives $f(p^2)\to 1$ for $p\to 0$. Moreover, an explicit solution could not be so useful, since we are mainly interested in an asymptotic behavior. Therefore we ask the following general properties to be satisfied by the functions f and g

$$\begin{array}{c}\hfill \left\{\begin{array}{c}[f(p^2)+g(p^2)p^2]\to [1+\gamma p^{\frac{n+2}{n+1}}]\mathrm{for}p\to 0\hfill \\ \\ 2f^{\prime }f+(2f^{\prime }{p}^2-f)g=0,\hfill \end{array}\right.\end{array}$$

(20)

We shall look if there actually exist f and g such that the above two properties can be simultaneously satisfied. In this way the rotational and translational invariance of GUP (6) will result proved. In Appendix A such solutions are proved to exist, provided we allow g to develop poles (of course, the function f and the whole function $f+g{p}^2$ remain perfectly finite).

4. From the Uncertainty Principle to the Mass–Temperature Relation

Naturally, the modification of the uncertainty relation, i.e., of the basic commutators, has deep consequences on the quantum mechanics, and on the quantum field theory, built upon it. The general implementation of such commutation rules as regards the Hilbert space representation, ultraviolet regularization, or modified dispersion relations has been discussed in a vast literature (see for an incomplete list References [38,39,40,41,42,43]). In the present section, we want to focus on the use of (generalized) uncertainty relations to compute the basic feature of the Hawking effect, namely the formula linking the temperature of the black hole to its mass M. The seminal results of Hawking and Unruh [44,45] are rigorously computed using QFT, based on the Heisenberg uncertainty principle, on curved space-time. However, it has been shown [17,46,47,48,49] that the full calculation of QFT in curved space-time (with standard commutators for the ordinary uncertainty principle, or with deformed commutators for the GUP) can be safely replaced by a computation employing only the (generalized) uncertainty relation and some basic physical considerations, in order to obtain the mass–temperature formula.

For example, in the case of the standard Hawking effect, we can consider a quantum of Hawking radiation (a photon) just outside the event horizon of a Schwarzschild black hole of a given mass M. Then, the uncertainty in the position of such quantum will be $\Delta x\simeq 2R_S=4GM/c^2$. The correspondent uncertainty $\Delta E$ in the energy of the emitted quantum is identified with the thermal energy of the quantum itself. For photons, the link between temperature and average thermal energy of photons is $\Delta E\simeq 3k_{B}T$. Therefore, the Heisenberg relation $\Delta x\Delta E\simeq ħc/2$ implies

$$\begin{array}{c}\hfill \frac{4GM}{c^2}3k_{B}T\simeq \frac{ħc}{2}\Rightarrow T=\frac{ħc^3}{24G{k}_{B}M}.\end{array}$$

(21)

Note that the exact Quantum Field Theoretic coefficient is $8\pi$($\simeq 24$), computed by Hawking in Reference [44] on the basis of the standard Heisenberg uncertainty principle (HUP). In that case, the evaporation is predicted to continue until the mass of the black hole reaches zero, $M=0$, and the final temperature becomes presumably infinite. On the contrary, a similar computation in Reference [17], based on the GUP in four dimensions, namely on

$$\begin{array}{c}\hfill \Delta x\Delta E\simeq \frac{ħc}{2}\left[1+\beta {\left(\frac{\Delta E}{E_p}\right)}^2\right],\end{array}$$

(22)

with similar identifications as the above, $\Delta x\simeq 2R_S=4GM/c^2$ and $\Delta E\simeq \pi k_{B}T$, has brought to a modification of the Hawking formula for high temperatures,

$$\begin{array}{c}\hfill M\simeq \frac{ħc^3}{8\pi G{k}_{B}T}+\beta \frac{\pi k_{B}T}{2c^2}\end{array}$$

(23)

from which the remarkable prediction of black hole remnants of finite positive mass as the final stage of the Hawking evaporation has been obtained. In fact, it is already clear from Equation (23) that the mass M cannot drop below $M_{min}=m_p\sqrt{\beta }$ during the evaporation process.

As we will see, the predictions of the GUPs described in the present paper agree perfectly, in four dimensions, with those of Reference [17], and in particular with Equation (23).

Let us now consider, in $4+n$ dimensions, the two GUPs Equations (7) and (6) described in the Section 2. Suppose that, in a brane world scenario (ADD model or RS model) a micro black hole with initial mass M has been formed. Then, following the previous argument, let us consider a quantum of Hawking radiation (photon or graviton) just outside the event horizon (for simplicity, we suppose the black hole already in the Schwarzschild phase). The uncertainty in the position of this quantum is $\delta x\simeq 2R_{4n}=2{\ell }_{4n}{({\omega }_{n}m)}^{\frac{1}{n+1}}$, where $m=M/M_{4n}$. The correspondent uncertainty in energy of this quantum is identified with its thermal energy E, and it is linked with the mass of the hole through the inequalities (7) or (6), now saturated. Reminding the relation ${\mathcal{E}}_{4n}{\ell }_{4n}=ħc/2$, from the GUPs formulae we can write

$$\begin{array}{ccc}\hfill 2{({\omega }_{n}m)}^{\frac{1}{n+1}}& =& \frac{{\mathcal{E}}_{4n}}{E}+\beta \frac{E}{{\mathcal{E}}_{4n}}(\mathrm{ST})\hfill \\ \hfill 2{({\omega }_{n}m)}^{\frac{1}{n+1}}& =& \frac{{\mathcal{E}}_{4n}}{E}+\beta {\left({\omega }_n\frac{E}{{\mathcal{E}}_{4n}}\right)}^{\frac{1}{n+1}}(\mathrm{MBH}).\hfill \end{array}$$

(24)

Now, it is of fundamental importance to note that relations like the previous two can allow, in principle, for arbitrary connections between energy E and temperature T, without any affection of the formulae for the minimum masses predicted by the relations themselves. In Appendix B we show that the expression of the minimum mass predicted by Equation (24) is independent from the analytic structure of the relation $E(T)$.

This freedom in the choice of $E(T)$ can be used to implement the correct semiclassical limit, in $4+n$ dimensions, in relations like (24). Supposing still true a linear relation between E and T, $E=\alpha (n)T$, the correct form of $E(T)$ in $4+n$ dimensions can be inferred by imposing a matching with the Hawking semiclassical limit. In the limit $\beta \to 0$ we have, from (24),

$$\begin{array}{ccc}& & 2{({\omega }_{n}m)}^{\frac{1}{n+1}}=\frac{{\mathcal{E}}_{4n}}{\alpha (n)T}\Rightarrow \hfill \\ & & T=\frac{{\mathcal{E}}_{4n}}{2\alpha (n){({\omega }_{n}m)}^{\frac{1}{n+1}}}=\frac{ħc}{4\alpha (n)R_{4n}}\hfill \end{array}$$

(25)

and the matching with the correct Hawking semiclassical formula, in $4+n$ dimensions,

$$\begin{array}{c}\hfill T=\frac{(n+1)ħc}{4\pi k_B{R}_{4n}},\end{array}$$

(26)

can be obtained by setting

$$\begin{array}{c}\hfill \alpha (n)=\frac{\pi k_B}{n+1}.\end{array}$$

(27)

Therefore $E(T)=\alpha (n)T=\pi k_{B}T/(n+1)$. Introducing the Planck temperature $T_{4n}$ defined by ${\mathcal{E}}_{4n}=\frac{1}{2}{k}_B{T}_{4n}$, and using Planck units for the temperature itself $\mathsf{\Theta }=T/T_{4n}$, we can write from the (24) the mass–temperature relations as

$$\begin{array}{ccc}\hfill & & 2{({\omega }_{n}m)}^{\frac{1}{n+1}}=\frac{(n+1)}{2\pi \mathsf{\Theta }}+\beta \frac{2\pi \mathsf{\Theta }}{(n+1)}(\mathrm{ST})\hfill \\ \hfill \\ & & 2{({\omega }_{n}m)}^{\frac{1}{n+1}}=\frac{n+1}{2\pi \mathsf{\Theta }}+\beta {\left(\frac{2\pi {\omega }_n\mathsf{\Theta }}{n+1}\right)}^{\frac{1}{n+1}}(\mathrm{MBH})\hfill \end{array}$$

(28)

A possible source of ambiguity in relations like (28) is the relation between the uncertainty in the position of the Hawking quantum, $\delta x$, and the geometric size of the hole, $R_{4n}$. However, if we consider as valid a linear relation even with a free parameter $\mu$, like $\delta x=2\mathsf{\mu }{R}_{4n}$, we then see that the Hawking limit can be recovered only by writing

$$\begin{array}{c}\hfill 2\mathsf{\mu }{({\omega }_{n}m)}^{\frac{1}{n+1}}=\mathsf{\mu }\frac{n+1}{2\pi \mathsf{\Theta }}\end{array}$$

(29)

and this, in the final mass–temperature relation, means

$$\begin{array}{c}\hfill 2\mathsf{\mu }{({\omega }_{n}m)}^{\frac{1}{n+1}}=\mathsf{\mu }\frac{n+1}{2\pi \mathsf{\Theta }}+\beta \frac{2\pi \mathsf{\Theta }}{n+1}\end{array}$$

(30)

which is always equivalent to a re-scaling of the unknown deformation parameter $\beta$

$$\begin{array}{c}\hfill 2{({\omega }_{n}m)}^{\frac{1}{n+1}}=\frac{n+1}{2\pi \mathsf{\Theta }}+\left(\frac{\beta }{\mu }\right)\frac{2\pi \mathsf{\Theta }}{n+1};{\beta }^{\prime }=\frac{\beta }{\mu }\end{array}$$

(31)

Analogous considerations hold for the MBH GUP.

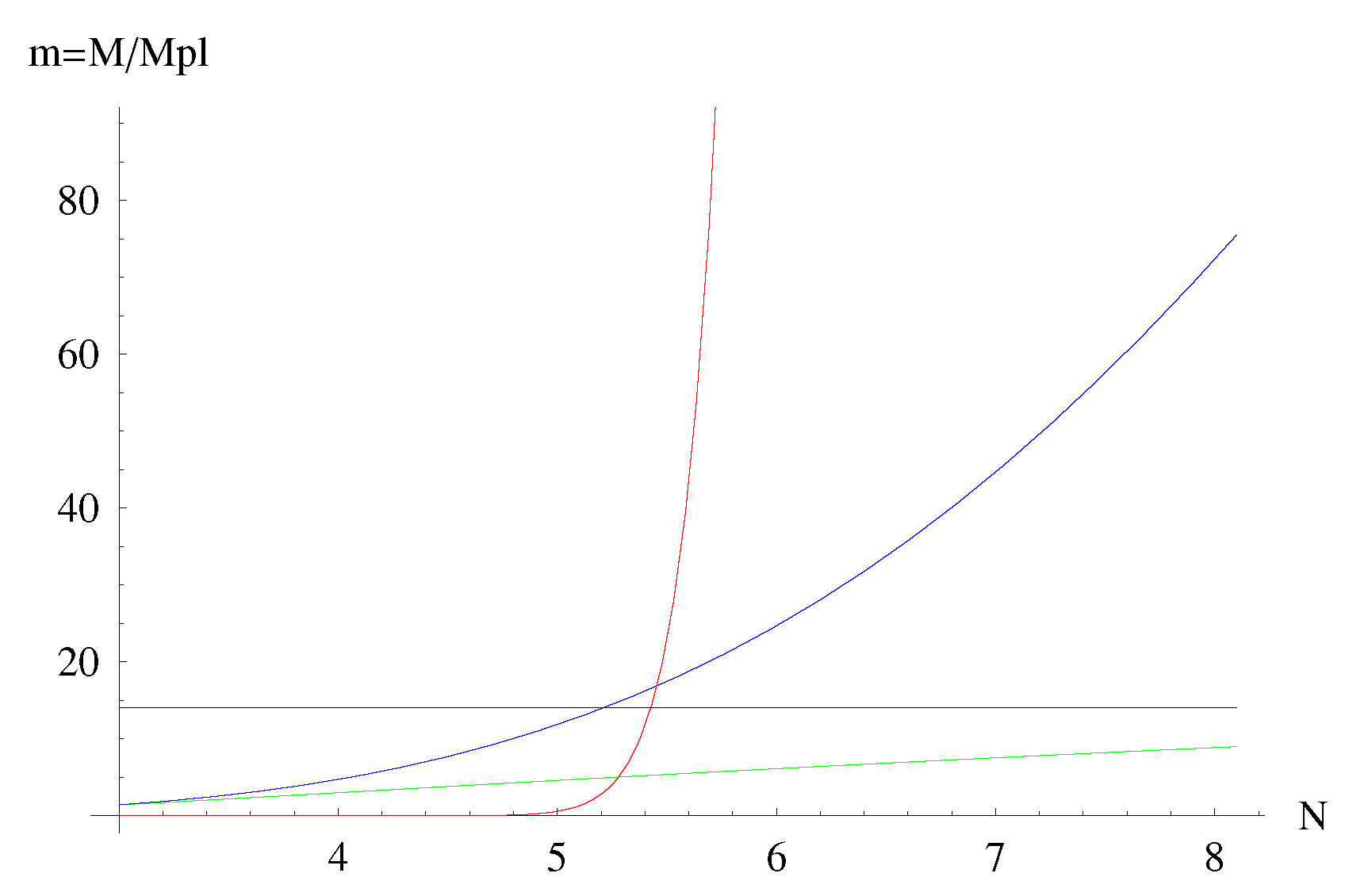
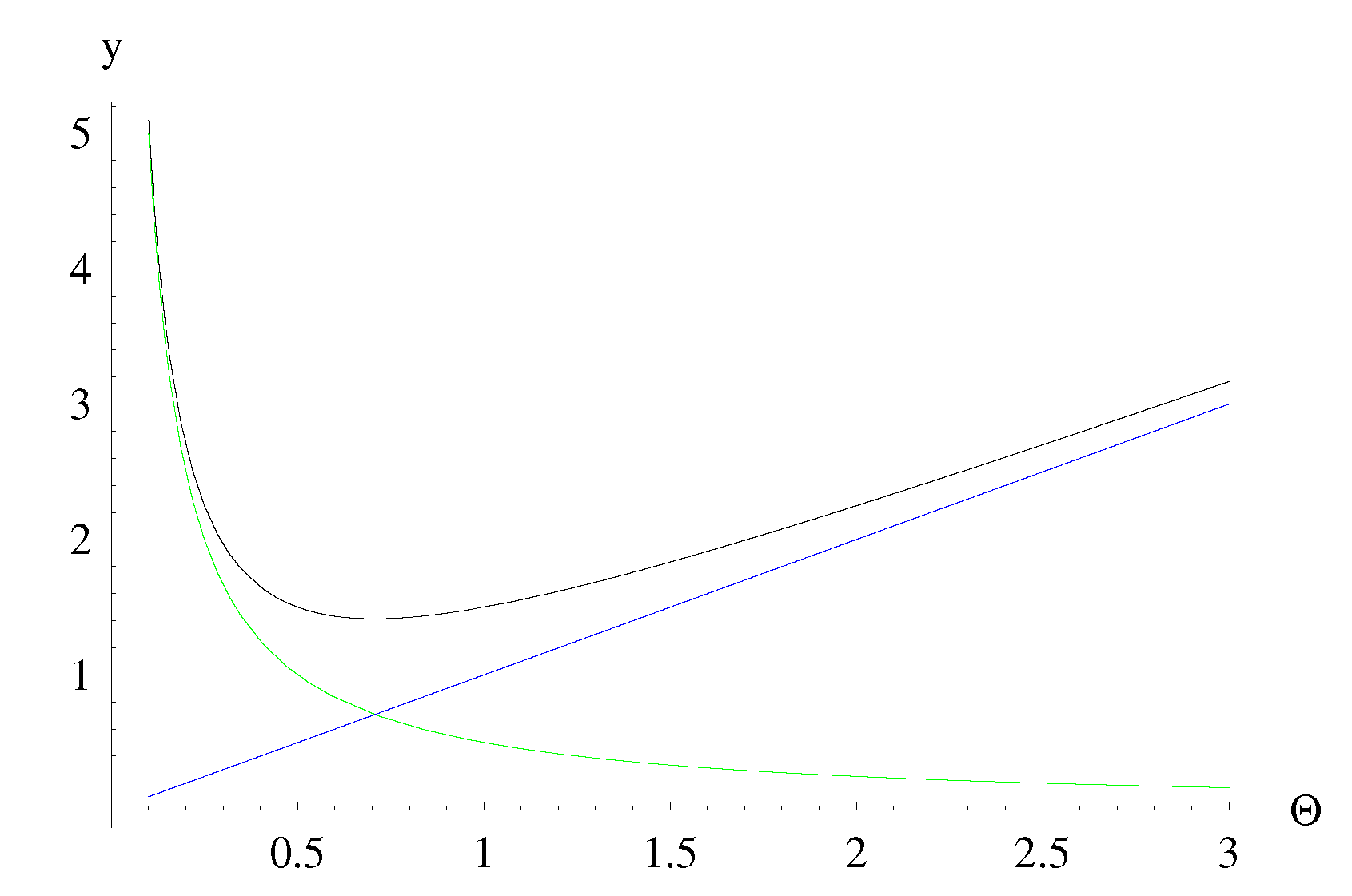
5. Minimum Masses, Maximum Temperatures

The standard Hawking formula predicts a complete evaporation of a black hole, from an initial mass M down to zero mass. As we have seen this is a direct consequence of the Heisenberg principle. In the language of the mass–temperature formula we have

$$\begin{array}{c}\hfill 2{({\omega }_{n}m)}^{\frac{1}{n+1}}=\frac{n+1}{2\pi \mathsf{\Theta }}\end{array}$$

(32)

and the temperature should become infinite at the very end of the process. Of course, as said in the introduction, corrections are expected from quantum gravity processes in the final phases of the evaporation. The GUPs seem to provide such corrections in a straightforward way. In fact, the mass–temperature Formulae (28) described in previous sections provide immediately a minimum mass for the evaporating black hole and a maximum temperature. Precisely we have for the stringy GUP (reminding $N=n+3$, number of space-like dimensions)

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_{MAX}^{ST}=\frac{N-2}{2\pi \sqrt{\beta }}\end{array}$$

(33a)

$$\begin{array}{c}\hfill m_{MIN}^{ST}=\frac{{\beta }^{\frac{1}{2}(N-2)}}{{\omega }_n}\end{array}$$

(33b)

while for the MBH GUP we have

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_{MAX}^{MBH}=\left(\frac{N-2}{2\pi }\right){\left[\frac{N-2}{\beta {({\omega }_n)}^{\frac{1}{N-2}}}\right]}^{\frac{N-2}{N-1}}\end{array}$$

(34a)

$$\begin{array}{c}\hfill m_{MIN}^{MBH}={\left[\frac{N-1}{2{(N-2)}^{\frac{N-2}{N-1}}}\right]}^{N-2}{({\omega }_n)}^{-\frac{1}{N-1}}{\beta }^{\frac{{(N-2)}^2}{N-1}}\end{array}$$

(34b)

Note that, as expected, ${\mathsf{\Theta }}_{MAX}\to \infty$ and $m_{MIN}\to 0$ in the Hawking limit $\beta \to 0$. Therefore the use of the GUP eliminates the problem of an infinite temperature (clearly un-physical) at the end of the evaporation [17,18,48] (it is interesting to note that analogous results have been obtained in a completely different framework, via non commutative geometry inspired black holes; see [50,51] and references therein). In Section 8 we shall show that also the emission rate (erg/sec) is kept finite by the GUP mass–temperature formulae, in contrast with an infinite output predicted by the Hawking formula (which is based on the Heisenberg uncertainty principle).

As it is clear from the mass–temperature diagrams (see Figure 1), black hole temperature is undefined for $m<m_{MIN}$. Black holes with mass less than $m_{MIN}$ do not exist, since their horizon radius would fall below the minimum allowed length. The mass–temperature relations derived from the GUPs, hence, predict the existence of mass thresholds for the creation of micro black holes. A head-on collision of partons with a center-of-mass energy below $m_{MIN}$ (in Planck units) will not result in production of black holes (at least black holes as we define them today). It is interesting to compare the two diagrams of $m_{MIN}^{ST}$ and $m_{MIN}^{MBH}$ as functions of the number N of space-like dimensions.

In Figure 2 these functions are plotted for $\beta =2$. On the y-axis we have the mass $m=M/M_{Pl}$ in Planck units. If we assume that $M_{Pl}\simeq O(1)\mathrm{TeV}$ for $4\le N\le 9$, as it is customary in many brane world models, then the diagram should be considered for $N\ge 4$ only. (In fact, it is well known that for $N=3$ we have $M_{Pl}\simeq {10}^{16}\mathrm{TeV}$, so surely LHC would not create any black hole if the space-time dimensions are only 4). If $M_{Pl}\simeq O(1)\mathrm{TeV}$, then the horizontal red line represents the energy limit of LHC. We see that we have $m_{MIN}^{MBH}<m_{MIN}^{ST}$ for $N\ge 4$. In $N=4$ or $N=5$ both GUPs allow for the formation of black holes below the LHC threshold, since $m_{MIN}<14$. On the contrary, already for $N=6$, and larger, only $m_{MIN}^{MBH}$ lies below the LHC energy limit, while the stringy GUP predicts a $m_{MIN}^{ST}$ well above the energy reachable by LHC. Therefore, productions of micro black holes in a scenario with $N\ge 6$ ($n\ge 3$ extra dimensions) should be considered, if accompanied with remnants, an evidence in favor of the MBH GUP.

However, it is also true that for $0<\beta \lesssim 1.11$ both diagrams lie below the limit of 14 TeV (for $4\le N\le 9$) so production of micro black holes is in principle allowed by both GUPs for such values of $\beta$, although it is much more enhanced by MBH GUP.

As we know, the dependence of $M_{4n}$ from the dimensionality N is different for different extra dimensions scenarios. For example, in the ADD model [1] the extra dimensions have a finite size L. The link between $G_{4n}$ and the usual Newton constant $G_N$ is $G_{4n}\simeq G_N{L}^{N-3}$ ($N=$ number of space-like dimensions). Therefore the relation among ${\mathcal{E}}_{4n}$, the 4-dimensional Planck energy ${\mathcal{E}}_{Pl}$, and length ${\ell }_{Pl}$, is

$$\begin{array}{c}\hfill {\mathcal{E}}_{4n}={\left(\frac{{\ell }_{Pl}}{L}\right)}^{\frac{N-3}{N-1}}{\mathcal{E}}_{Pl}.\end{array}$$

(35)

Considering “large” extra dimensions of size $L=1\mathsf{\mu }$m $={10}^{-4}$ cm (and ${\ell }_{Pl}=1.6\times {10}^{-33}$ cm, ${\mathcal{E}}_{Pl}=6.13\times {10}^{15}$ TeV), we have that in this model the Planck energy unit scales with the number N of dimensions like

$$\begin{array}{c}\hfill {\mathcal{E}}_{4n}={(1.6\times {10}^{-29})}^{\frac{N-3}{N-1}}(6.13\times {10}^{15})\mathrm{TeV}\end{array}$$

(36)

Figure 3 displays a diagram with the “limit-line” of 14 TeV plotted in red in terms of Planck mass units. The energies reachable by LHC lie below the red curve. We see that in this particular ADD model there is no hope to detect black holes for $N=4,5$, while for $N\ge 6$ they should be detectable in any case, and they are allowed by both GUPs, in that energy region.

However, the most striking prediction made by the GUPs mass–temperature relations (both versions) is, without doubt, the existence of “remnants”, i.e., of a final product of finite mass of the Hawking evaporation. We shall show in Section 8 and Section 9 that Hawking evaporation should stop once the black hole mass reaches $m_{MIN}$. The specific heat vanishes at the end point, so that the black hole cannot exchange heat with a surrounding environment, and the final object, a remnant, should be inert from the thermodynamical point of view. Remnants from primordial black holes have been proposed as a dark matter candidate [52], and they are also predicted by some models of quantum black holes [53,54]. An obvious signature for revealing remnants at the LHC collider would be the detection of a missing energy of the order of the minimal mass of the black hole (plus missing energy due to invisible decay products). Moreover, we see that both versions of GUP (stringy GUP and MBH GUP) require the existence of remnants. A detection of micro black holes, together with a non detection of remnants, would imply $\beta =0$ (within experimental errors, of course). This would be a very strong assertion on the validity of the usual (classical) Heisenberg principle down to any scale, and therefore a very deep insight on the ultimate nature of the space time microstructure.

6. Emission Rate Equation

In this section we describe the evaporation process of the micro black hole. As it is well known, in the minimal scenario of the braneworld models only gravity propagates also in the $4+n$ dimensional bulk, whereas the Standard Model bosonic or fermionic fields are confined on a four dimensional brane. In the present model we take into account two species of particles, photons and gravitons. This is because of several reasons: first, we wish to investigate typical examples of the two different geometries of emission; second, some recent works [55,56,57,58,59] seem to show that the emission of gravitons in the bulk may not be a negligible part of the total black hole emission, as previously believed [9]; third, for sake of simplicity, we consider only photons as emitted on the brane, in order to keep the model clear. Nevertheless, other kinds of gauge or fermionic fields can be added in a straightforward way.

Before writing down the emission rate equation, we review some delicate issues about greybody factors, emitted energy, and the Stefan–Boltzamann constant, in 4 and $4+n$ dimensions.

In 4 dimensions, the number of photons (or gravitons) with frequency within $\omega$ and $\omega +d\omega$, in a volume V, is given by

$$\begin{array}{c}\hfill d{n}_{\gamma /g}=\frac{V{\omega }^2}{{\pi }^2{c}^3}\frac{{\mathsf{\Gamma }}_{\gamma /g}(\omega )}{e^{ħ\omega /k_{B}T}-1}d\omega .\end{array}$$

(37)

Along the main investigation of this paper, in order to keep the procedure simple and clear, we neglect the squeezing of the fundamental cell in momentum space due to the presence of a GUP, i.e., of a minimal length (about this, see References [22,36,37,60]). In Appendix C, in fact, we show that the squeezing results in higher order corrections in $\beta$ to the Formulas (41) and (44). The global luminosity (49) generically decreases, and thus the micro black hole lifetime $\tau$ results to be extended in respect to the lifetime computed without the squeezing correction function. However, mass thresholds are not at all affected by this squeezing in momentum space.

In the case of a perfect black body (perfect emitter) we have for the greybody factor ${\mathsf{\Gamma }}_{\gamma /g}(\omega )=1$ for any $\omega$. The dependence of $\mathsf{\Gamma }(\omega )$ from the frequency $\omega$ is in general very complicated. It has been studied in many papers (for four dimensional black holes see [61], for emission of gravitons in $4+n$ dimensions see [55,56,57,58,59]), it is in some cases partially unknown, and in many cases can be computed only numerically. In the present model, we neglect the dependence of the $\mathsf{\Gamma }s$ from the frequency, and therefore we consider a value ${\mathsf{\Gamma }}_{\gamma /g}:=\langle {\mathsf{\Gamma }}_{\gamma /g}(\omega )\rangle$ averaged on all the frequencies. Thus, for the number of photons (or gravitons) in the interval ($\omega$, $\omega +d\omega$) in a volume V we write (in four dimensions)

$$\begin{array}{c}\hfill d{n}_{\gamma /g}=\frac{V{\omega }^2}{{\pi }^2{c}^3}\frac{{\mathsf{\Gamma }}_{\gamma /g}}{e^{ħ\omega /k_{B}T}-1}d\omega .\end{array}$$

(38)

Obviously in a real black body (not the ideal one) will be ${\mathsf{\Gamma }}_g\ll {\mathsf{\Gamma }}_{\gamma }<1$.

The total energy of photons (gravitons) contained in a volume V in four dimensions is then

$$\begin{array}{c}\hfill E_{\mathrm{TOT}}^{\gamma /g}(V)={\int }_0^{\infty }ħ\omega d{n}_{\gamma /g}=\frac{V{\mathsf{\Gamma }}_{\gamma /g}}{{\pi }^2{c}^3{ħ}^3}{(k_{B}T)}^4\mathsf{\Gamma }(4)\zeta (4)\\ \hfill \end{array}$$

(39)

where we used

$$\begin{array}{c}\hfill {\int }_0^{\infty }\frac{x^N}{e^x-1}dx=\mathsf{\Gamma }(N+1)\zeta (N+1)\end{array}$$

($\mathsf{\Gamma }(x)=$ Euler Gamma function; $\zeta (x)=$ Riemann zeta function; in particular $\mathsf{\Gamma }(4)\zeta (4)={\pi }^4/15$). Defining the Stefan–Boltzmann constant in four dimensions as

$$\begin{array}{c}\hfill {\sigma }_3=\frac{c}{3}\frac{\mathsf{\Gamma }(4)\zeta (4)}{{\pi }^2{c}^3{ħ}^3}{k}_B^4\end{array}$$

(40)

this energy can be written

$$\begin{array}{c}\hfill E_{\mathrm{TOT}}^{\gamma /g}(V)={\mathsf{\Gamma }}_{\gamma /g}\frac{3{\sigma }_3}{c}V{T}^4.\end{array}$$

(41)

In $4+n$ dimensions, only gravitons propagate in the bulk, and, taking into account their helicity, we write for the number of gravitons in a volume V and with frequency in the range $\omega$, $\omega +d\omega$

$$\begin{array}{c}\hfill d{n}_g=\frac{(N+1)(N-2)}{2}·\frac{V{\mathsf{\Omega }}_{N-1}{\omega }^{N-1}}{{(2\pi c)}^N}\times \\ \hfill \times \frac{{\mathsf{\Gamma }}_g}{e^{ħ\omega /k_{B}T}-1}d\omega \end{array}$$

(42)

where N is the number of space-like dimensions.

The total energy of gravitons contained in a volume V is then

$$\begin{array}{ccc}& & E_{\mathrm{TOT}}^g(V)={\int }_0^{\infty }ħ\omega d{n}_g=\frac{(N+1)(N-2)}{2}\times \hfill \\ & & \times \frac{V{\mathsf{\Gamma }}_g{\mathsf{\Omega }}_{N-1}ħ\mathsf{\Gamma }(N+1)\zeta (N+1)}{{(2\pi c)}^N}{\left(\frac{k_{B}T}{ħ}\right)}^{N+1}\hfill \end{array}$$

(43)

which can be written as

$$\begin{array}{c}\hfill E_{\mathrm{TOT}}^g(V)={\mathsf{\Gamma }}_g\frac{N{\sigma }_N}{c}V{T}^{N+1}\end{array}$$

(44)

where

$$\begin{array}{ccc}\hfill {\sigma }_N& =& \frac{c}{N}\frac{(N+1)(N-2)}{2}\frac{{\mathsf{\Omega }}_{N-1}{k}_B^{N+1}}{{(2\pi c)}^N{ħ}^N}\times \hfill \\ & \times & \mathsf{\Gamma }(N+1)\zeta (N+1)\hfill \end{array}$$

(45)

is the Stefan–Boltzmann constant in N space-like dimensions ($4+n$ dimensions).

The total energy $dE$ radiated from the black hole in a time $dt$, measured by the far observer, can be written (for photons and gravitons)

$$\begin{array}{c}\hfill dE={\mathsf{\Gamma }}_{\gamma }\frac{3{\sigma }_3}{c}{\mathcal{V}}_3{T}^4+{\mathsf{\Gamma }}_g\frac{N{\sigma }_N}{c}{\mathcal{V}}_N{T}^{N+1}\end{array}$$

(46)

where ${\mathcal{V}}_3$ is the effective volume occupied by photons

$$\begin{array}{c}\hfill {\mathcal{V}}_3={\mathsf{\Omega }}_2{R}_{4n}^{2}cdt\end{array}$$

(47)

and ${\mathcal{V}}_N$ is the effective volume occupied by gravitons

$$\begin{array}{c}\hfill {\mathcal{V}}_N={\mathsf{\Omega }}_{N-1}{R}_{4n}^{N-1}cdt.\end{array}$$

(48)

Note that the Schwarzschild radius considered is always $R_{4n}$, i.e., the radius of the $4+n$ dimensional black hole. This because we are dealing with micro black holes small enough than $R_{4n}<L$, where L is the typical size of the extra dimensions (in the ADD model), or the effective size of the confinement of the zero mode of the gravitational field (in the RS model). Thus, finally, the differential equation of the emission rate is [5,7,8,9,59]

$$\begin{array}{ccc}\hfill -\frac{dE}{dt}& =& 3{\mathsf{\Gamma }}_{\gamma }{\sigma }_3{\mathsf{\Omega }}_2{R}_{4n}^2{T}^4\hfill \\ & +& N{\mathsf{\Gamma }}_g{\sigma }_N{\mathsf{\Omega }}_{N-1}{R}_{4n}^{N-1}{T}^{N+1}.\hfill \end{array}$$

(49)

where the minus sign indicates the loss of mass/energy. With the explicit definitions of ${\sigma }_3$, ${\sigma }_N$, $R_{4n}$, and with the Planck variables $m=M/M_{4n}=E/{\mathcal{E}}_{4n}$, $\mathsf{\Theta }=T/T_{4n}$, $\tau =t/t_{4n}$ (where ${\mathcal{E}}_{4n}=\frac{1}{2}{k}_B{T}_{4n}$ and $t_{4n}={\ell }_{4n}/c$), we can rewrite the emission rate equation as

$$\begin{array}{ccc}\hfill -\frac{dm}{d\tau }& =& \frac{2}{{\pi }^2}{\mathsf{\Gamma }}_{\gamma }{\mathsf{\Omega }}_2\mathsf{\Gamma }(4)\zeta (4){({\omega }_{n}m)}^{\frac{2}{N-2}}{\mathsf{\Theta }}^4\hfill \\ & +& \frac{(N+1)(N-2)}{{(2\pi )}^N}{\mathsf{\Gamma }}_g{\mathsf{\Omega }}_{N-1}^2\times \hfill \\ & \times & \mathsf{\Gamma }(N+1)\zeta (N+1){({\omega }_{n}m)}^{\frac{N-1}{N-2}}{\mathsf{\Theta }}^{N+1}\hfill \end{array}$$

(50)

This form will be useful in the following steps.

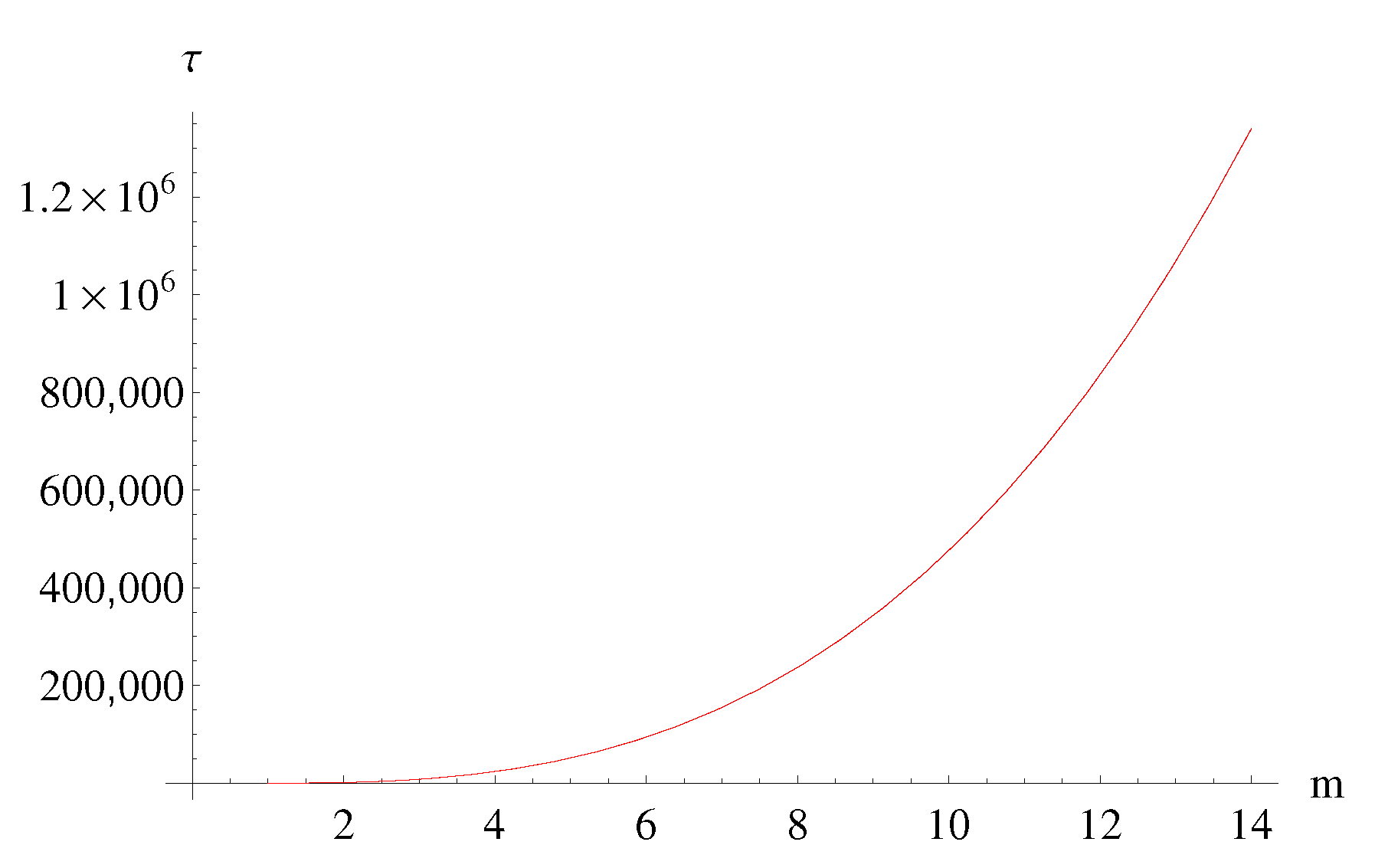
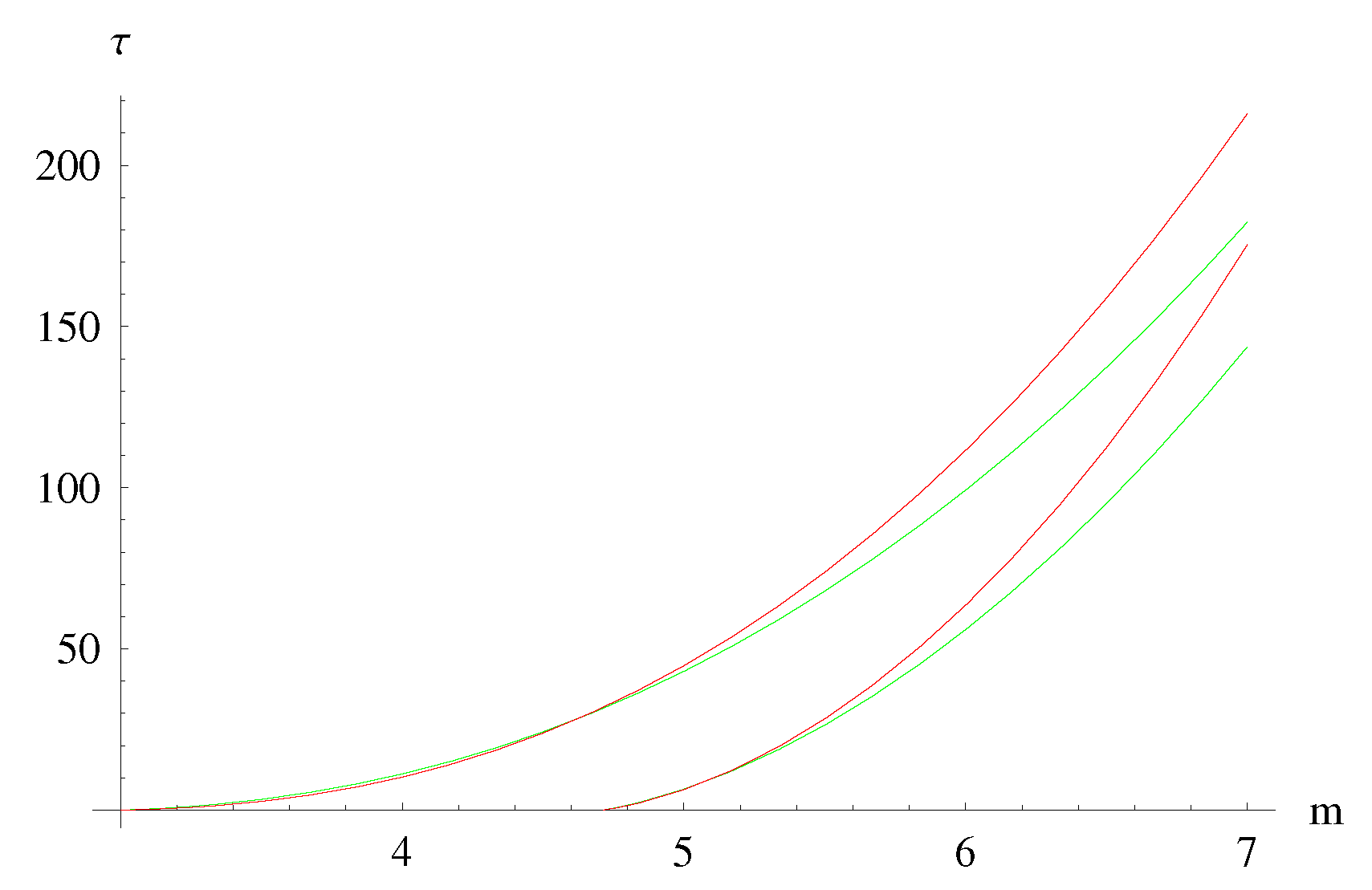
7. Micro Black Hole Lifetime

In this section we study the emission rate equation in order to compute the micro black hole lifetime. As a result, we shall display and comment various diagrams, in particular for the limiting cases ${\mathsf{\Gamma }}_{\gamma }\gg {\mathsf{\Gamma }}_g$, ${\mathsf{\Gamma }}_{\gamma }\ll {\mathsf{\Gamma }}_g$.

Equation (50) can be put in a simpler form by multiplying it by ${\omega }_n$ and defining

$$\begin{array}{c}\hfill y={({\omega }_{n}m)}^{\frac{1}{N-2}}.\end{array}$$

(51)

Then we have

$$\begin{array}{c}\hfill \frac{d({\omega }_{n}m)}{d\tau }=(N-2)y^{N-3}\frac{dy}{d\tau }\end{array}$$

(52)

and Equation (50) becomes

$$\begin{array}{ccc}\hfill & -& \frac{dy}{d\tau }=2{\mathsf{\Gamma }}_{\gamma }{\mathsf{\Omega }}_2\frac{\mathsf{\Gamma }(4)\zeta (4){\omega }_n}{{\pi }^2(N-2)}{y}^{5-N}{\mathsf{\Theta }}^4\hfill \\ & +& (N+1)\frac{{\mathsf{\Gamma }}_g{\omega }_n{\mathsf{\Omega }}_{N-1}^2\mathsf{\Gamma }(N+1)\zeta (N+1)}{{(2\pi )}^N}{y}^2{\mathsf{\Theta }}^{N+1}.\hfill \end{array}$$

(53)

Let us now examine separately the cases of the two different GUPs.

(a) Stringy GUP: With the position (51), the stringy GUP can be written

$$\begin{array}{c}\hfill 2y=\frac{1}{\lambda \mathsf{\Theta }}+\beta \lambda \mathsf{\Theta }=\frac{1}{\overline{\mathsf{\Theta }}}+\beta \overline{\mathsf{\Theta }}\end{array}$$

(54)

where $\lambda =2\pi /(N-2)$ and $\overline{\mathsf{\Theta }}=\lambda \mathsf{\Theta }$. Then (53) becomes

$$\begin{array}{c}\hfill -\frac{d(2y)}{d\tau }={\mathsf{\Gamma }}_{\gamma }{G}_n{(2y)}^{5-N}{\overline{\mathsf{\Theta }}}^4+{\mathsf{\Gamma }}_g{H}_n{(2y)}^2{\overline{\mathsf{\Theta }}}^{N+1}\end{array}$$

(55)

with

$$\begin{array}{c}\hfill G_n=\frac{2^{N-3}{\omega }_n{\mathsf{\Omega }}_2\mathsf{\Gamma }(4)\zeta (4)}{{\pi }^2(N-2){\lambda }^4}\end{array}$$

(56)

and

$$\begin{array}{c}\hfill H_n=(N+1)\frac{{\omega }_n{\mathsf{\Omega }}_{N-1}^2\mathsf{\Gamma }(N+1)\zeta (N+1)}{2{(2\pi )}^N{\lambda }^{N+1}}.\end{array}$$

(57)

So we have a system of differential-algebraic equations

$$\begin{array}{c}\hfill \left\{\begin{array}{c}-\frac{d(2y)}{d\tau }={\mathsf{\Gamma }}_{\gamma }{G}_n{(2y)}^{5-N}{\overline{\mathsf{\Theta }}}^4+{\mathsf{\Gamma }}_g{H}_n{(2y)}^2{\overline{\mathsf{\Theta }}}^{N+1}\hfill \\ \\ 2y=\frac{1}{\overline{\mathsf{\Theta }}}+\beta \overline{\mathsf{\Theta }}.\hfill \end{array}\right.\end{array}$$

(58)

This is easily reduced to a separable equation, in fact

$$\begin{array}{c}\hfill {\mathcal{G}}_N(\overline{\mathsf{\Theta }})d\overline{\mathsf{\Theta }}=d\tau \end{array}$$

(59)

where

$$\begin{array}{c}\hfill {\mathcal{G}}_N(\overline{\mathsf{\Theta }})=\frac{(1-\beta {\overline{\mathsf{\Theta }}}^2)}{[{\mathsf{\Gamma }}_{\gamma }{G}_n{(\beta {\overline{\mathsf{\Theta }}}^2+1)}^{3-N}+{\mathsf{\Gamma }}_g{H}_n]{(\beta {\overline{\mathsf{\Theta }}}^2+1)}^2{\overline{\mathsf{\Theta }}}^{N+1}}.\end{array}$$

Suppose at time $\tau =0$ a micro black hole is created with an initial mass $m_0$ and a (low) temperature ${\overline{\mathsf{\Theta }}}_0$. At time $\tau$ the temperature has become $\overline{\mathsf{\Theta }}(\tau )$, with $\overline{\mathsf{\Theta }}(0)={\overline{\mathsf{\Theta }}}_0$. Then

$$\begin{array}{c}\hfill \tau ={\int }_0^{\tau }d\tau ={\int }_{{\overline{\mathsf{\Theta }}}_0}^{\overline{\mathsf{\Theta }}(\tau )}{\mathcal{G}}_N(\overline{\mathsf{\Theta }})d\overline{\mathsf{\Theta }}.\end{array}$$

(60)

By inverting this relation for $\overline{\mathsf{\Theta }}$ one would get $\overline{\mathsf{\Theta }}=f(\tau ,{\overline{\mathsf{\Theta }}}_0)$, that is the temperature $\overline{\mathsf{\Theta }}$ as a function of time $\tau$ and of the initial temperature ${\overline{\mathsf{\Theta }}}_0$. We are interested in the lifetime of the black hole. $\overline{\mathsf{\Theta }}(\tau )$ grows with $\tau$ until a certain value ${\overline{\mathsf{\Theta }}}_{MAX}$, when the emission, as we shall see in Section 9, stops. That value of $\tau$ will be the lifetime ${\tau }_{bh}$ of the black hole. So

$$\begin{array}{c}\hfill {\tau }_{bh}^{ST}={\int }_{{\overline{\mathsf{\Theta }}}_0}^{{\overline{\mathsf{\Theta }}}_{MAX}}{\mathcal{G}}_N(\overline{\mathsf{\Theta }})d\overline{\mathsf{\Theta }}.\end{array}$$

(61)

It is easy to compute ${\overline{\mathsf{\Theta }}}_{MAX}$ from Equation (54):

$$\begin{array}{c}\hfill {\overline{\mathsf{\Theta }}}_{MAX}=\lambda {\mathsf{\Theta }}_{MAX}=\frac{1}{\sqrt{\beta }}\end{array}$$

(62)

which implies

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_{MAX}=\frac{N-2}{2\pi \sqrt{\beta }}\end{array}$$

(63)

in agreement with Equation (33).

In order to obtain ${\overline{\mathsf{\Theta }}}_0$ as a function of the initial mass $m_0$, as it is customary to do, we have to invert the relation

$$\begin{array}{c}\hfill 2{({\omega }_n{m}_0)}^{\frac{1}{N-2}}=\frac{1}{\overline{\mathsf{\Theta }}}+\beta \overline{\mathsf{\Theta }}\end{array}$$

(64)

that is

$$\begin{array}{c}\hfill \beta {\overline{\mathsf{\Theta }}}^2-2{({\omega }_n{m}_0)}^{\frac{1}{N-2}}\overline{\mathsf{\Theta }}+1=0.\end{array}$$

(65)

This can be done exactly (2nd degree equation). We choose the smallest positive solution (a simple glance to the diagram in Figure 4 shows that such a solution always exists when $y>y_{MIN}$), which means the solution of minimal temperature

$$\begin{array}{c}\hfill {\overline{\mathsf{\Theta }}}_0(m_0)=\frac{1}{\beta }\left[{({\omega }_n{m}_0)}^{\frac{1}{N-2}}-{\left({({\omega }_n{m}_0)}^{\frac{2}{N-2}}-\beta \right)}^{\frac{1}{2}}\right].\end{array}$$

(66)

Then we finally write for the lifetime of a micro black hole

$$\begin{array}{c}\hfill {\tau }_{bh}^{ST}={\int }_{{\overline{\mathsf{\Theta }}}_0(m_0)}^{{\overline{\mathsf{\Theta }}}_{MAX}}{\mathcal{G}}_N(\overline{\mathsf{\Theta }})d\overline{\mathsf{\Theta }}.\end{array}$$

(67)

In the following, we shall use numerical integration in order to produce some plots of the function ${\tau }_{bh}^{ST}(m_0;N,{\mathsf{\Gamma }}_{\gamma },{\mathsf{\Gamma }}_g,\beta )$ for several values of the parameters ${\mathsf{\Gamma }}_{\gamma }$, ${\mathsf{\Gamma }}_g$.

(b) MBH GUP: Here we proceed in an analogous way. Again with the position (51) the MBH GUP can be written

$$\begin{array}{c}\hfill 2y=\frac{1}{\lambda \mathsf{\Theta }}+\beta {({\omega }_n\lambda \mathsf{\Theta })}^{\frac{1}{N-2}}\end{array}$$

(68)

where $\lambda =2\pi /(N-2)$. Defining $\mathsf{\Lambda }:={({\omega }_n\lambda \mathsf{\Theta })}^{\frac{1}{N-2}}$, which means $\mathsf{\Theta }={\mathsf{\Lambda }}^{N-2}/(\lambda {\omega }_n)$, then Equation (68) becomes

$$\begin{array}{c}\hfill 2y=\frac{{\omega }_n}{{\mathsf{\Lambda }}^{N-2}}+\beta \mathsf{\Lambda }.\end{array}$$

(69)

Equation (53) by virtue of $\mathsf{\Theta }={\mathsf{\Lambda }}^{N-2}/(\lambda {\omega }_n)$ can be written

$$\begin{array}{ccc}\hfill -\frac{d(2y)}{d\tau }& =& {\mathsf{\Gamma }}_{\gamma }{\tilde{G}}_n{(2y)}^{5-N}{\mathsf{\Lambda }}^{4(N-2)}\hfill \\ & +& {\mathsf{\Gamma }}_g{\tilde{H}}_n{(2y)}^2{\mathsf{\Lambda }}^{(N-2)(N+1)}\hfill \end{array}$$

(70)

where now

$$\begin{array}{c}\hfill {\tilde{G}}_n=\frac{2^{N-3}{\mathsf{\Omega }}_2\mathsf{\Gamma }(4)\zeta (4)}{{\pi }^2(N-2){\lambda }^4{\omega }_n^3}\end{array}$$

(71)

and

$$\begin{array}{c}\hfill {\tilde{H}}_n=(N+1)\frac{{\mathsf{\Omega }}_{N-1}^2\mathsf{\Gamma }(N+1)\zeta (N+1)}{2{(2\pi )}^N{\lambda }^{N+1}{\omega }_n^N}.\end{array}$$

(72)

Thus we have the system

$$\begin{array}{c}\hfill \left\{\begin{array}{c}-\frac{d(2y)}{d\tau }={\mathsf{\Gamma }}_{\gamma }{\tilde{G}}_n{(2y)}^{5-N}{\mathsf{\Lambda }}^{4(N-2)}\hfill \\ \\ +{\mathsf{\Gamma }}_g{\tilde{H}}_n{(2y)}^2{\mathsf{\Lambda }}^{(N-2)(N+1)}\hfill \\ \\ 2y=\frac{{\omega }_n}{{\mathsf{\Lambda }}^{N-2}}+\beta \mathsf{\Lambda }.\hfill \end{array}\right.\end{array}$$

(73)

Again, this can be reduced to a separable equation

$$\begin{array}{c}\hfill {\mathcal{F}}_N(\mathsf{\Lambda })d\mathsf{\Lambda }=d\tau \end{array}$$

(74)

where

$$\begin{array}{ccc}& & {\mathcal{F}}_N(\mathsf{\Lambda })=\hfill \\ & & \frac{((N-2){\omega }_n-\beta {\mathsf{\Lambda }}^{N-1})}{[{\mathsf{\Gamma }}_{\gamma }{\tilde{G}}_n{(\beta {\mathsf{\Lambda }}^{N-1}+{\omega }_n)}^{3-N}+{\mathsf{\Gamma }}_g{\tilde{H}}_n]{(\beta {\mathsf{\Lambda }}^{N-1}+{\omega }_n)}^2{\mathsf{\Lambda }}^{{(N-1)}^2}}.\hfill \end{array}$$

We can now repeat the steps of the previous section (reminding that the change of variable $\lambda {\omega }_n\mathsf{\Theta }={\mathsf{\Lambda }}^{N-2}$ is a monotonic one). At time $\tau =0$ a micro black hole with mass $m_0$ and temperature ${\mathsf{\Theta }}_0$ (${\mathsf{\Lambda }}_0^{N-2}=\lambda {\omega }_n{\mathsf{\Theta }}_0$) is created. At time $\tau$, the temperature has grown to $\mathsf{\Theta }(\tau )$, with ${\mathsf{\Lambda }}^{N-2}(\tau )=\lambda {\omega }_n\mathsf{\Theta }(\tau )$ and $\mathsf{\Theta }(0)={\mathsf{\Theta }}_0$, $\mathsf{\Lambda }(0)={\mathsf{\Lambda }}_0$. Then

$$\begin{array}{c}\hfill \tau ={\int }_{{\mathsf{\Lambda }}_0}^{\mathsf{\Lambda }(\tau )}{\mathcal{F}}_N(\mathsf{\Lambda })d\mathsf{\Lambda }.\end{array}$$

(75)

When $\mathsf{\Theta }(\tau )$ reaches ${\mathsf{\Theta }}_{MAX}$ (and $\mathsf{\Lambda }(\tau )$ goes to ${\mathsf{\Lambda }}_{MAX}$, respectively), then the emission stops. ${\mathsf{\Lambda }}_{MAX}$ can be computed as usual from (69) and we get

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_{MAX}={\left[\frac{(N-2){\omega }_n}{\beta }\right]}^{\frac{1}{N-1}},\end{array}$$

(76)

in agreement with (34). ${\mathsf{\Lambda }}_0$ as a function of the initial mass $m_0$ can be obtained as the smallest positive root of the equation (numerical solution)

$$\begin{array}{c}\hfill \beta {\mathsf{\Lambda }}_0^{N-1}-2{({\omega }_n{m}_0)}^{\frac{1}{N-2}}{\mathsf{\Lambda }}_0^{N-2}+{\omega }_n=0.\end{array}$$

(77)

Again, a simple glance to the plot of Equation (69) assures us that such a solution always exists, provided that $y>y_{MIN}$.

So, finally we can write for the lifetime of the micro black hole computed with the MBH GUP

$$\begin{array}{c}\hfill {\tau }_{bh}^{MBH}={\int }_{{\mathsf{\Lambda }}_0(m_0)}^{{\mathsf{\Lambda }}_{MAX}}{\mathcal{F}}_N(\mathsf{\Lambda })d\mathsf{\Lambda }.\end{array}$$

(78)

We can use numerical integration to produce some plots of the functions ${\tau }_{bh}^{ST}(m_0;N,{\mathsf{\Gamma }}_{\gamma },{\mathsf{\Gamma }}_g,\beta )$, ${\tau }_{bh}^{MBH}(m_0;N,{\mathsf{\Gamma }}_{\gamma },{\mathsf{\Gamma }}_g,\beta )$ for several value of the parameters ${\mathsf{\Gamma }}_{\gamma }$, ${\mathsf{\Gamma }}_g$.

For example, for $N=3$ (the usual space-time), we see that the two GUPs, stringy and MBH, coincide, and so do the two parts of the emission rate equation (photons and gravitons are both emitted on the brane, since there is not anything else outside). Also the mass threshold formulae of the two GUPs go to coincide. Hence, we have one single diagram for the functions ${\tau }_{bh}^{ST}(m_0;3,{\mathsf{\Gamma }}_{\gamma },{\mathsf{\Gamma }}_g,2)$, ${\tau }_{bh}^{MBH}(m_0;3,{\mathsf{\Gamma }}_{\gamma },{\mathsf{\Gamma }}_g,2)$, as we see in Figure 5.

Of course, Figure 5 is purely academical, since we know that for $N=3$ space-like dimensions, the Planck mass is about ${10}^{19}$ GeV, completely out of the energy range of LHC.

Instead, Figure 6 could be interesting, where ${\tau }_{bh}^{ST}$ and ${\tau }_{bh}^{MBH}$ are plotted for $N=4$. In green, we represent the emission (on the brane) of photons only (${\mathsf{\Gamma }}_{\gamma }=1,{\mathsf{\Gamma }}_g=0$); in red, the emission (bulk and brane) of gravitons only (${\mathsf{\Gamma }}_{\gamma }=0,{\mathsf{\Gamma }}_g=1$).

The upper diagram is obtained by the MBH GUP, the lower diagram represents the stringy GUP. We note that the final mass predicted by the MBH GUP is lower than the final mass predicted by the stringy GUP, as we already know from Formulae (33) and (34) and from Figure 2.

In Figure 7 we plot the diagrams describing the situation at $N=5$ (i.e., $n=2$ extra dimensions). The gap between the two mass’ thresholds, predicted by the two different GUPs, has been further increased. Note the switching between the photons and the gravitons emission lines (green and red) in respect to the $N=4$ diagrams.

Finally, it is interesting to have a look to diagrams (Figure 8) representing the Hawking limit $\beta \to 0$. In such a limit the minimum masses go to zero, and obviously the two GUPs are going to coincide in between them, and with the usual Heisenberg uncertainty principle.

8. Emission Rate Equation at the End Point

In this section we show that the GUPs are able to keep finite the output rate of the black hole, also at the end of the emission process. This, we shall see, is a completely different prediction from the one made by the standard Hawking effect, which is in fact based on the usual Heisenberg principle.

Before going any further, it is useful to expand the temperature $\mathsf{\Theta }$ in series of the deformation parameter $\beta$. In the case of the MBH GUP, since it is not possible to obtain an explicit form of $\mathsf{\Theta }(m)$, we shall use the implicit function theorem. The ST GUP case can be treated as well with the implicit theorem, even if here $\mathsf{\Theta }(m)$ can also be obtained, obviously, in an explicit form.

(a) Stringy GUP: Rewriting the first of Equation (28) with the variables $y={({\omega }_{n}m)}^{1/(n+1)}$ and $\overline{\mathsf{\Theta }}=2\pi \mathsf{\Theta }/(n+1)$, we have Equation (54)

$$\begin{array}{c}\hfill 2y=\frac{1}{\overline{\mathsf{\Theta }}}+\beta \overline{\mathsf{\Theta }}\end{array}$$

(79)

The function $\overline{\mathsf{\Theta }}=\overline{\mathsf{\Theta }}(y,\beta )$ is implicitly defined by the equation

$$\begin{array}{c}\hfill f(y,\overline{\mathsf{\Theta }},\beta )=\beta {\overline{\mathsf{\Theta }}}^2-2y\overline{\mathsf{\Theta }}+1=0\end{array}$$

(80)

We are interested in $\overline{\mathsf{\Theta }}$ as a function of $\beta$, therefore we consider y to be constant. Then

$$\begin{array}{c}\hfill df=0⟹\frac{d\overline{\mathsf{\Theta }}}{d\beta }=-\frac{\partial f/\partial \beta }{\partial f/\partial \overline{\mathsf{\Theta }}}\end{array}$$

(81)

and for the MacLaurin series of $\overline{\mathsf{\Theta }}$ we get

$$\begin{array}{c}\hfill \overline{\mathsf{\Theta }}(y,\beta )=\overline{\mathsf{\Theta }}(y,0)+\frac{d\overline{\mathsf{\Theta }}}{d\beta }(y,0)·\beta +O({\beta }^2)\end{array}$$

(82)

with

$$\begin{array}{c}\hfill \overline{\mathsf{\Theta }}(y,0)=\frac{1}{2y};\frac{d\overline{\mathsf{\Theta }}}{d\beta }(y,0)=\frac{1}{8y^3}\end{array}$$

(83)

So finally

$$\begin{array}{c}\hfill \overline{\mathsf{\Theta }}(y,\beta )=\frac{1}{2y}+\frac{\beta }{8y^3}+O({\beta }^2)\end{array}$$

(84)

Writing this in terms of the standard Hawking temperature ${\overline{\mathsf{\Theta }}}_H=\frac{1}{2y}$ we have

$$\begin{array}{c}\hfill \overline{\mathsf{\Theta }}={\overline{\mathsf{\Theta }}}_H(1+\beta {\overline{\mathsf{\Theta }}}_H^2+O({\beta }^2))\end{array}$$

(85)

Using instead the usual variables $(m,\mathsf{\Theta })$ the expansion becomes

$$\begin{array}{c}\hfill \mathsf{\Theta }=\frac{n+1}{4\pi {({\omega }_{n}m)}^{\frac{1}{n+1}}}\left(1+\frac{\beta }{4{({\omega }_{n}m)}^{\frac{2}{n+1}}}+\dots \right).\end{array}$$

(86)

(b) MBH GUP: The MBH GUP in $4+n$ dimensions, in the $(m,\mathsf{\Theta })$ variables, is given by the second of Equation (28). Here we should use the implicit function method to obtain an expansion in $\beta$ of $\mathsf{\Theta }(m,\beta )$. Using the variables $y={({\omega }_{n}m)}^{1/(n+1)}$ and ${\mathsf{\Lambda }}^{n+1}=2\pi {\omega }_n\mathsf{\Theta }/(n+1)$, the MBH GUP reads

$$\begin{array}{c}\hfill 2y=\frac{{\omega }_n}{{\mathsf{\Lambda }}^{n+1}}+\beta \mathsf{\Lambda }\end{array}$$

(87)

The function $\mathsf{\Lambda }=\mathsf{\Lambda }(y,\beta )$ is implicitly defined by the equation

$$\begin{array}{c}\hfill f(y,\mathsf{\Lambda },\beta )=\beta {\mathsf{\Lambda }}^{n+2}-2y{\mathsf{\Lambda }}^{n+1}+{\omega }_n=0\end{array}$$

(88)

For MacLaurin at first order in $\beta$ we have

$$\begin{array}{c}\hfill \mathsf{\Lambda }(y,\beta )={\left(\frac{{\omega }_n}{2y}\right)}^{\frac{1}{n+1}}+\frac{\beta }{2(n+1)y}{\left(\frac{{\omega }_n}{2y}\right)}^{\frac{2}{n+1}}+\dots \end{array}$$

(89)

Going back to the $(y,\mathsf{\Theta })$ variables, we have

$$\begin{array}{c}\hfill {\mathsf{\Theta }}^{MBH}=\frac{n+1}{4\pi y}\left[1+\frac{\beta }{2y}{\left(\frac{{\omega }_n}{2y}\right)}^{\frac{1}{n+1}}+\dots \right]\end{array}$$

(90)

while for the ST GUP in the same variables we had

$$\begin{array}{c}\hfill {\mathsf{\Theta }}^{ST}=\frac{n+1}{4\pi y}\left[1+\frac{\beta }{4y^2}+\dots \right]\end{array}$$

(91)

The results just obtained will be used later to construct an expansion in $\beta$ of the lifetime $\tau$.

Let us now discuss some limit properties of the emission rate equation.

Starting from Equation (50) and introducing as usual the variable y we arrive to Equation (53), that can be written as

$$\begin{array}{c}\hfill -\frac{dy}{d\tau }=A{y}^{2-n}{\mathsf{\Theta }}^4+B{y}^2{\mathsf{\Theta }}^{n+4}\end{array}$$

(92)

with

$$\begin{array}{c}\hfill A=2{\mathsf{\Gamma }}_{\gamma }{\mathsf{\Omega }}_2\frac{\mathsf{\Gamma }(4)\zeta (4){\omega }_n}{{\pi }^2(n+1)}\end{array}$$

(93)

$$\begin{array}{c}\hfill B=(n+4)\frac{{\mathsf{\Gamma }}_g{\omega }_n{\mathsf{\Omega }}_{n+2}^2\mathsf{\Gamma }(n+4)\zeta (n+4)}{{(2\pi )}^{n+3}}.\end{array}$$

(94)

In the limit $\beta \to 0$ the Hawking temperature can be recovered

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_H=\frac{n+1}{4\pi y}\end{array}$$

(95)

and the standard Hawking emission rate (in $4+n$ dimensions) reads

$$\begin{array}{ccc}\hfill -{\left.\frac{dy}{d\tau }\right)}_H& =& A{y}^{2-n}{\mathsf{\Theta }}_H^4+B{y}^2{\mathsf{\Theta }}_H^{n+4}\hfill \\ & =& (\tilde{A}+\tilde{B})\frac{1}{y^{n+2}}\hfill \end{array}$$

(96)

where

$$\begin{array}{c}\hfill \tilde{A}:=A{\left(\frac{n+1}{4\pi }\right)}^4;\tilde{B}:=B{\left(\frac{n+1}{4\pi }\right)}^{n+4}.\end{array}$$

(97)

We see now clearly that, in the case of the standard Hawking emission rate, we have an infinite spike at the end of the evaporation process. In fact, when $m\to 0$, then $y\to 0$, ${\mathsf{\Theta }}_H\to \infty$, and $-{\left.\frac{dy}{d\tau }\right)}_H\to \infty$.

On the other hand, since the emission rate $\frac{dm}{d\tau }$ (or $\frac{dy}{d\tau }$) has to be a real number, we must require that the function $\mathsf{\Theta }=\mathsf{\Theta }(y,\beta )$ (implicitly defined by the GUPs relations) is a real number.

A simple glance to the plots of the functions $(y,\mathsf{\Theta })$, for the ST and MBH GUPs, shows that $\mathsf{\Theta }$ can be real if and only if $y>y_{MIN}$. In the case of ST GUP we have (from Equation (54)) $y_{MIN}^{ST}=\sqrt{\beta }$, while for the MBH GUP (from Equation (69)) we get

$$\begin{array}{c}\hfill y_{MIN}^{MBH}=\frac{(n+2){\omega }_n}{2}{\left(\frac{\beta }{(n+1){\omega }_n}\right)}^{\frac{n+1}{n+2}}\end{array}$$

(98)

Therefore, the request $\frac{dm}{d\tau }\in \mathbb{R}$ implies $y\ge y_{MIN}$, that is $m\ge m_{MIN}$. If now we compute the emission rate at the end point, when $m\to m_{MIN}$ (or $y\to y_{MIN}$) and $\mathsf{\Theta }\to {\mathsf{\Theta }}_{MAX}$, we get, respectively,

$$\begin{array}{c}\hfill -{\left.\frac{dy}{d\tau }\right)}_{ST}=(\tilde{A}+\tilde{B})\frac{1}{{\beta }^{1+\frac{n}{2}}}\end{array}$$

(99)

$$\begin{array}{c}\hfill -{\left.\frac{dy}{d\tau }\right)}_{MBH}=(\tilde{E}+\tilde{F})\frac{1}{{\beta }^{1+n}}\end{array}$$

(100)

where $\tilde{A},\tilde{B},\tilde{E},\tilde{F}$ are unimportant numerical factors. Since $\beta >0$, in both cases we see that the emission rate turns out to be finite at the end point of the evaporation. While the final stage of the standard Hawking process is catastrophic (the black hole reaches in a finite time a stage with zero rest mass, infinite emission rate, and infinite temperature), the GUP (both versions) keeps all these quantities finite at the end of the evaporation. The modified results appear to be more physically reasonable than the standard ones.

Expansion of lifetime $\tau$ in powers of $\beta$: We conclude the section presenting an expansion in series of $\beta$ of the emission rate equation, and the consequent expansion of the lifetime $\tau$ of black holes. We use the variables $(y,\mathsf{\Theta })$. From the Equations (90) and (91) for ${\mathsf{\Theta }}^{MBH}$ and ${\mathsf{\Theta }}^{ST}$, and from Equation (92) we can write, for the ST GUP

$$\begin{array}{c}\hfill {\left.-\frac{dy}{d\tau }\right)}_{ST}=A{y}^{2-n}{\mathsf{\Theta }}^4+B{y}^2{\mathsf{\Theta }}^{n+4}\\ \hfill =(\tilde{A}+\tilde{B})\frac{1}{y^{n+2}}\left(1+\beta \frac{\tilde{C}}{y^2}+\dots \right)\end{array}$$

(101)

where $\tilde{A}$, $\tilde{B}$ are defined as in (97) and $\tilde{C}=(1+\frac{\tilde{B}}{\tilde{A}+\tilde{B}}·\frac{n}{4})$.

For the MBH GUP we have, to the first order in $\beta$

$$\begin{array}{ccc}& & {\left.-\frac{dy}{d\tau }\right)}_{MBH}=\hfill \\ & =& (\tilde{A}+\tilde{B})\frac{1}{y^{n+2}}\left(1+\frac{2\beta \tilde{C}}{y}{\left(\frac{{\omega }_n}{2y}\right)}^{\frac{1}{n+1}}+\dots \right)\hfill \end{array}$$

(102)

with $\tilde{A}$, $\tilde{B}$, $\tilde{C}$ defined as before.

We are now enabled to develop the lifetime $\tau$ of the black hole in series of $\beta$. Essentially, we integrate the expressions just found above for the emission rate equation (an expansion in $\beta$ of the exact formulas (67) and (78) for $\tau$ is in principle possible, but much more cumbersome than the method followed here.).

For the ST GUP, from (101) we have

$$\begin{array}{c}\hfill -d\tau =\frac{y^{n+2}}{\tilde{A}+\tilde{B}}\left(1-\beta \frac{\tilde{C}}{y^2}+\dots \right)dy\end{array}$$

(103)

Taking the integral of the LHS between 0 and $\tau$, and of the RHS between the initial mass m and the final mass $m_{MIN}$ (i.e., between y and $y_{MIN}=\sqrt{\beta }$), we have finally

$$\begin{array}{ccc}\hfill \tau & =& \frac{y^{n+3}}{(n+3)(\tilde{A}+\tilde{B})}-\beta \frac{\tilde{C}{y}^{n+1}}{(n+1)(\tilde{A}+\tilde{B})}+\dots \hfill \\ & =& \frac{{({\omega }_{n}m)}^{\frac{n+3}{n+1}}}{(n+3)(\tilde{A}+\tilde{B})}-\beta \frac{\tilde{C}({\omega }_{n}m)}{(n+1)(\tilde{A}+\tilde{B})}+\dots \hfill \end{array}$$

(104)

The trend of $\tau$ with m coincides with those found in Reference [18].

For the MBH GUP, proceeding in an analogous way from Equation (102), we find

$$\begin{array}{ccc}\hfill \tau & =& \frac{y^{n+3}}{(n+3)(\tilde{A}+\tilde{B})}\hfill \\ & -& 2\beta \left(\frac{\tilde{C}{({\omega }_n/2)}^{\frac{1}{n+1}}}{\tilde{A}+\tilde{B}}\right)\frac{(n+1)}{[{(n+1)}^2+n]}{y}^{\frac{{(n+1)}^2+n}{(n+1)}}+\dots \hfill \\ & =& \frac{{({\omega }_{n}m)}^{\frac{n+3}{n+1}}}{(n+3)(\tilde{A}+\tilde{B})}\hfill \\ & -& 2\beta \left(\frac{\tilde{C}{({\omega }_n/2)}^{\frac{1}{n+1}}}{\tilde{A}+\tilde{B}}\right)\frac{(n+1)}{[{(n+1)}^2+n]}{({\omega }_{n}m)}^{1+\frac{n}{{(n+1)}^2}}+\dots \hfill \end{array}$$

(105)

Once again we note that the zero order term ($\beta =0$) is the Hawking term (in $4+n$ dimensions) and coincides with that computed with ST GUP.

9. Entropy and Heat Capacity

In this section we compute the exact formulae for the thermodynamical entropy and for the heat capacity of a (micro) black hole, using the two versions of the GUP previously introduced. For the sake of completeness, we shall give also an expansion in $\beta$ of the entropy S.

9.1. Entropy

From the first law of black hole thermodynamics [62] we know that the differential of the thermodynamical entropy of a Schwarzschild black hole reads

$$\begin{array}{c}\hfill dS=\frac{dE}{T_H}\end{array}$$

(106)

where $dE$ is the quantity of energy swallowed by a black hole with Hawking temperature $T_H$. Rewriting Equation (106) with the a-dimensional variables $(m,\mathsf{\Theta })$ we get

$$\begin{array}{c}\hfill dS=\frac{1}{2}{k}_B\frac{dm}{\mathsf{\Theta }}.\end{array}$$

(107)

Considering that $(m,\mathsf{\Theta })$ are linked by the GUP relation, we can in principle write $\mathsf{\Theta }=\mathsf{\Theta }(m)$, and then obtain S as a function of m (mass of the micro hole), $S=S(m)$. This procedure is easily applicable to the ST GUP, since $\mathsf{\Theta }(m)$ can be found explicitly. However, this is not the case for the MBH GUP: the function $\mathsf{\Theta }(m)$ is determined only implicitly. Therefore, it is useful to express $m=m(\mathsf{\Theta })$ and then to arrive at S as a function of $\mathsf{\Theta }$, $S=S(\mathsf{\Theta })$. The integrals obtained in this way are also more easily doable than those computed via the “$\mathsf{\Theta }(m)$” method.

Let us study the two cases separately, as usual.

(a) Stringy GUP: Referring to formula (79) and using the variables $(y,\overline{\mathsf{\Theta }})$ we have

$$\begin{array}{ccc}\hfill dS& =& \frac{1}{2}{k}_B\frac{dm}{\mathsf{\Theta }}=\frac{\pi k_B}{{\omega }_n}\frac{y^{n}dy}{\overline{\mathsf{\Theta }}}\hfill \\ & =& \frac{\pi k_B}{2^{n+1}{\omega }_n}\frac{{(1+\beta {\overline{\mathsf{\Theta }}}^2)}^n(\beta {\overline{\mathsf{\Theta }}}^2-1)}{{\overline{\mathsf{\Theta }}}^{n+3}}d\overline{\mathsf{\Theta }}\hfill \end{array}$$

(108)

By integrating $dS$ we obtain $S=S(\overline{\mathsf{\Theta }})$. We write the additive constant in S so that $S=0$ when $\mathsf{\Theta }\to {\mathsf{\Theta }}_{MAX}^{ST}=\frac{n+1}{2\pi \sqrt{\beta }}$ (i.e., $\overline{\mathsf{\Theta }}\to {\overline{\mathsf{\Theta }}}_{MAX}=\frac{1}{\sqrt{\beta }}$). This is equivalent to what is usually done with the standard Hawking effect, where one fixes the additive constant $=0$ for $m=0$ (the minimum mass attainable in the standard Hawking effect is $m=0$). Finally we can write

$$\begin{array}{c}\hfill S=\frac{\pi k_B}{2^{n+1}{\omega }_n}{\int }_{{\overline{\mathsf{\Theta }}}_0(m_0)}^{{\overline{\mathsf{\Theta }}}_{MAX}}\frac{{(1+\beta {\overline{\mathsf{\Theta }}}^2)}^n(1-\beta {\overline{\mathsf{\Theta }}}^2)}{{\overline{\mathsf{\Theta }}}^{n+3}}d\overline{\mathsf{\Theta }}\end{array}$$

(109)

where ${\overline{\mathsf{\Theta }}}_0$ is the initial temperature. ${\overline{\mathsf{\Theta }}}_0$ is fixed by the initial mass $m_0$ and can be expressed as a function of the initial mass $m_0$ by taking the smallest positive solution of the equation

$$\begin{array}{c}\hfill \beta {\overline{\mathsf{\Theta }}}_0^2-2{({\omega }_n{m}_0)}^{\frac{1}{n+1}}{\overline{\mathsf{\Theta }}}_0+1=0.\end{array}$$

(110)

The integral (109) can be easily solved analytically. For example in four dimensions we have ($n=0$)

$$\begin{array}{c}\hfill dS=\frac{k_B}{4}\left(-\frac{1}{2\pi {\mathsf{\Theta }}^3}+\frac{2\pi \beta }{\mathsf{\Theta }}\right)d\mathsf{\Theta }\end{array}$$

(111)

and

$$\begin{array}{c}\hfill S(\mathsf{\Theta })=\frac{k_B}{16\pi }\left(\frac{1}{{\mathsf{\Theta }}^2}-\frac{1}{{\mathsf{\Theta }}_{MAX}^2}+8{\pi }^2\beta log\frac{\mathsf{\Theta }}{{\mathsf{\Theta }}_{MAX}}\right)\end{array}$$

(112)

Note that $S\to 0^{+}$ for $\mathsf{\Theta }\to {\mathsf{\Theta }}_{MAX}^{-}$.

(b) MBH GUP: Referring to formula (87) and using the variables $(y,\mathsf{\Lambda })$ we have

$$\begin{array}{ccc}\hfill dS& =& \frac{1}{2}{k}_B\frac{dm}{\mathsf{\Theta }}=\pi k_B\frac{y^n}{{\mathsf{\Lambda }}^{n+1}}dy\hfill \\ & =& \frac{\pi k_B}{2^{n+1}}\frac{{(\beta {\mathsf{\Lambda }}^{n+2}+{\omega }_n)}^n(\beta {\mathsf{\Lambda }}^{n+2}-(n+1){\omega }_n)}{{\mathsf{\Lambda }}^{(n+2)(n+1)+1}}d\mathsf{\Lambda }\hfill \end{array}$$

(113)

Integrating and choosing the additive constant so that $S\to 0$ when $\mathsf{\Theta }\to {\mathsf{\Theta }}_{MAX}$ (i.e., $\mathsf{\Lambda }\to {\mathsf{\Lambda }}_{MAX}={((n+1){\omega }_n/\beta )}^{1/(n+2)}$) we have, finally,

$$\begin{array}{ccc}\hfill & & S=\hfill \\ & & \frac{\pi k_B}{2^{n+1}}{\int }_{{\mathsf{\Lambda }}_0(m_0)}^{{\mathsf{\Lambda }}_{MAX}}\frac{{({\omega }_n+\beta {\mathsf{\Lambda }}^{n+2})}^n((n+1){\omega }_n-\beta {\mathsf{\Lambda }}^{n+2})}{{\mathsf{\Lambda }}^{(n+2)(n+1)+1}}d\mathsf{\Lambda }\hfill \end{array}$$

(114)

where, as usual, ${\mathsf{\Lambda }}_0$ is linked to the initial (low) temperature by ${\mathsf{\Lambda }}^{n+1}=2\pi {\omega }_n{\mathsf{\Theta }}_0/(n+1)$ and can be expressed, if required, as function of the initial mass $m_0$ by taking the smallest positive solution of the equation

$$\begin{array}{c}\hfill \beta {\mathsf{\Lambda }}_0^{n+2}-2{({\omega }_n{m}_0)}^{\frac{1}{n+1}}{\mathsf{\Lambda }}_0^{n+1}+{\omega }_n=0\end{array}$$

(115)

The integral (114) is analytically feasible, even if tedious. Of course, if we compute Equation (114) for $n=0$ (when the two GUPs coincide) we re-obtain Equation (112).

Expansion of S in $\beta$. From a physical point of view we are interested also in the series in $\beta$ of the entropy S. Following a method already used for the series of lifetime $\tau$, we expand the differential form $dS$ and then we integrate it.

In the case of ST GUP we have

$$\begin{array}{ccc}\hfill dS& =& \frac{\pi k_B}{{\omega }_n}\frac{y^{n}dy}{\overline{\mathsf{\Theta }}}\hfill \\ & =& \frac{2\pi k_B}{{\omega }_n}\left(y^{n+1}-\frac{\beta }{4}{y}^{n-1}+O({\beta }^2)\right)dy\hfill \end{array}$$

(116)

where variables $(y,\overline{\mathsf{\Theta }})$ have been used, as well as formula (84). Adopting the usual normalization condition, that is $S=0$ for $m=m_{MIN}$ (i.e., for $y=y_{MIN}=\sqrt{\beta }$) and integrating we have

$$\begin{array}{c}\hfill S=\frac{2\pi k_B}{{\omega }_n}{\int }_{y_{MIN}}^y\left(y^{n+1}-\frac{\beta }{4}{y}^{n-1}+O({\beta }^2)\right)dy\end{array}$$

(117)

• for $n>0$

  $$\begin{array}{c}\hfill S=\frac{2\pi k_B}{{\omega }_n}\left(\frac{y^{n+2}}{n+2}-\frac{\beta }{4n}{y}^n+O({\beta }^{1+\frac{n}{2}})\right)\end{array}$$

  (118)
• for $n=0$

  $$\begin{array}{ccc}\hfill S& =& 2\pi k_B{\int }_{y_{MIN}}^y\left(y-\frac{\beta }{4}{y}^{-1}+O({\beta }^2)\alpha y^{-3}\right)dy\hfill \\ & =& 2\pi k_B{\left[\frac{y^2}{2}-\frac{\beta }{4}logy+O({\beta }^2)\frac{\alpha }{2y^2}\right]}_{\sqrt{\beta }}^y\hfill \\ & =& 2\pi k_B\left[\frac{y^2}{2}-\frac{\beta }{4}\left(logy+2+K\right)+\frac{\beta }{8}log\beta +O({\beta }^2)\right]\hfill \end{array}$$

  (119)

where K is a numerical factor which includes all the contributions from terms of the form $O({\beta }^{p+1})y^{-2p}$, $p=1,2,3,\dots$ computed in $y=\sqrt{\beta }$. We see that the standard Bekenstein–Hawking entropy in $4+n$ dimensions is recovered in the limit $\beta \to 0$. In particular, for $n=0$ we have $S\propto m^2\sim A$, area of the black hole horizon. Furthermore, we see that the leading correction to the standard BH entropy induced by the GUPs is always negative: this means that the GUP-corrected entropy is smaller than the semiclassical Bekenstein–Hawking entropy.

In the case MBH GUP, using the variables $(y,\mathsf{\Lambda })$ and referring to Formula (89), we can write

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}^{n+1}(y,\beta )=\frac{{\omega }_n}{2y}\left(1+\frac{\beta }{2y}{\left(\frac{{\omega }_n}{2y}\right)}^{\frac{1}{n+1}}+\dots \right)\end{array}$$

(120)

Therefore

$$\begin{array}{ccc}\hfill dS& =& \pi k_B\frac{y^n}{{\mathsf{\Lambda }}^{n+1}}dy\hfill \\ & =& \frac{2\pi k_B}{{\omega }_n}\left(y^{n+1}-\frac{\beta }{2}{\left(\frac{{\omega }_n}{2}\right)}^{\frac{1}{n+1}}{y}^{n-\frac{1}{n+1}}+\dots \right)dy\hfill \end{array}$$

(121)

With the usual normalization condition ($S=0$ for $m=m_{MIN}$), we integrate from

$$\begin{array}{c}\hfill y_{MIN}=\frac{(n+2){\omega }_n}{2}{\left(\frac{\beta }{(n+1){\omega }_n}\right)}^{\frac{n+1}{n+2}}\end{array}$$

to a generic y, and obtain

$$\begin{array}{ccc}\hfill S& =& \frac{2\pi k_B}{{\omega }_n}\times \hfill \\ & \times & {\int }_{y_{MIN}}^y\left(y^{n+1}-\frac{\beta }{2}{\left(\frac{{\omega }_n}{2}\right)}^{\frac{1}{n+1}}{y}^{n-\frac{1}{n+1}}+\dots \right)dy\hfill \end{array}$$

(122)

• for $n>0$

  $$\begin{array}{ccc}& S& =\frac{2\pi k_B}{{\omega }_n}\times \hfill \\ & \times & \left(\frac{y^{n+2}}{n+2}-\frac{\beta }{2}{\left(\frac{{\omega }_n}{2}\right)}^{\frac{1}{n+1}}\left(\frac{n+1}{n(n+2)}\right)y^{\frac{n(n+2)}{n+1}}+\dots \right)\hfill \end{array}$$

  (123)
• for $n=0$

Here the results are exactly the same as for the ST GUP, formula (119), and this is obvious, since for $n=0$ the two GUPs, ST and MBH, go to coincide. Again, we note that the zero order, $\beta =0$, coincides with the usual Hawking entropy in $4+n$ dimensions and with the value just previously obtained for the ST GUP.

9.2. Heat Capacity

In this section we compute the heat capacity of the (micro) black hole using the GUPs. This quantity will give us important insights on the final stage of the evaporation process (in particular, on the remnant state).

The heat capacity C of a body is defined via the relation

$$\begin{array}{c}\hfill dE=CdT\end{array}$$

(124)

meaning that the transfer to a body of an energy $dE$ produces a variation $dT$ in the temperature of the body itself. Usually $dT>0$, for usual bodies, and therefore $C>0$. As we know, this is not the case for the black holes. Expressing the heat capacity via the variables $(m,\mathsf{\Theta })$ we get

$$\begin{array}{c}\hfill C=\frac{dE}{dT}=\frac{1}{2}{k}_B\frac{dm}{d\mathsf{\Theta }}\end{array}$$

(125)

So, for the ST GUP, using the variables $(y,\overline{\mathsf{\Theta }})$ we can write

$$\begin{array}{c}\hfill C=\frac{\pi k_B}{2^{n+1}{\omega }_n}\frac{{(1+\beta {\overline{\mathsf{\Theta }}}^2)}^n(\beta {\overline{\mathsf{\Theta }}}^2-1)}{{\overline{\mathsf{\Theta }}}^{n+2}}\end{array}$$

(126)

Since in general $0<\overline{\mathsf{\Theta }}<{\overline{\mathsf{\Theta }}}_{MAX}=\frac{1}{\sqrt{\beta }}$, from the above relation results $C<0$. Note also that

• If $\beta =0$, then $C<0$ for any $\mathsf{\Theta }$. Black holes are bodies with negative specific heat.
• If $\beta =0$, then C approaches 0 ($C\to 0^{-}$) only when $\overline{\mathsf{\Theta }}\to +\infty$.
• If $\beta >0$, then we have $C=0$ for $\overline{\mathsf{\Theta }}={\overline{\mathsf{\Theta }}}_{MAX}=\frac{1}{\sqrt{\beta }}$, i.e. $\mathsf{\Theta }=(n+1)/(2\pi \sqrt{\beta })$.

This means that if $\beta >0$ the specific heat vanishes at the end point of the evaporation process in a finite time, so that the black hole at the end of its evolution cannot exchange energy with the surrounding space. In other words, the black hole stops to interact thermodynamically with the environment. The final stage of the Hawking evaporation according to the GUP scenario contains a Planck-size remnant with a maximal temperature $\mathsf{\Theta }={\mathsf{\Theta }}_{MAX}$.

In particular, for $\beta =0$, we have, reintroducing the mass m,

$$\begin{array}{c}\hfill C=-\frac{2\pi k_B}{{\omega }_n}{({\omega }_{n}m)}^{\frac{n+2}{n+1}}\end{array}$$

(127)

For the MBH GUP we use the variables $(y,\mathsf{\Lambda })$ and we have

$$\begin{array}{ccc}\hfill C& =& \frac{\pi k_B}{n+1}\frac{y^n}{{\mathsf{\Lambda }}^n}\frac{dy}{d\mathsf{\Lambda }}\hfill \\ & =& \frac{\pi k_B}{2^{n+1}(n+1)}\frac{1}{{\mathsf{\Lambda }}^n}{\left(\frac{{\omega }_n}{{\mathsf{\Lambda }}^{n+1}}+\beta \mathsf{\Lambda }\right)}^n\left(\beta -\frac{(n+1){\omega }_n}{{\mathsf{\Lambda }}^{n+2}}\right)\hfill \end{array}$$

(128)

If $\beta >0$ then $C=0$ when $\mathsf{\Lambda }={\mathsf{\Lambda }}_{MAX}={\left[\frac{(n+1){\omega }_n}{\beta }\right]}^{\frac{1}{n+2}}$, which means, again, that the heat capacity vanishes at the end point and the black hole is then thermodynamically inert. When $\beta =0$ it is easy to verify that the above C coincides with the one computed in the previous paragraph, namely the case of standard Hawking effect in $4+n$ dimensions.

10. Conclusions and Outlooks

In this paper we have examined the consequences that a deformed uncertainty principle has upon relevant properties (mass threshold, lifetime, entropy, heat capacity) of micro black holes, which could be produced in the colliders successor of LHC in the (next) future (or could have been produced in the early universe), in the framework of models with extra spatial dimensions.

We have considered two possible deformations of the usual Heisenberg principle: one coming from scattering Gedanken experiments in string theory (shortly named ST GUP), the other coming from Gedanken experiments involving the formations of micro black holes (named MBH GUP). A comparison of the basic predictions of the two principles at high energies seems to favor the MBH GUP predictions, as those having a greater chance to be experimentally detected in colliders like LHC (see for example Section 5 and Figure 2). However, throughout the paper we have computed, and compared, the consequences of both principles, using the same formalism, so that ultimately the possible actual experiments could be the last judge of the predictions made by the two principles. In respect to the previous literature on the subject, we have considered also a non negligible emission of gravitons in the $4+n$ dimensional bulk. In addition, the MBH GUP is a novel approach, since it has not been treated in precedent literature about micro black holes in extra dimensions.

The main conclusions of the paper can be summarized as follows:

• Both principles predict remnants of finite rest mass as the end product of Hawking evaporation of black holes.
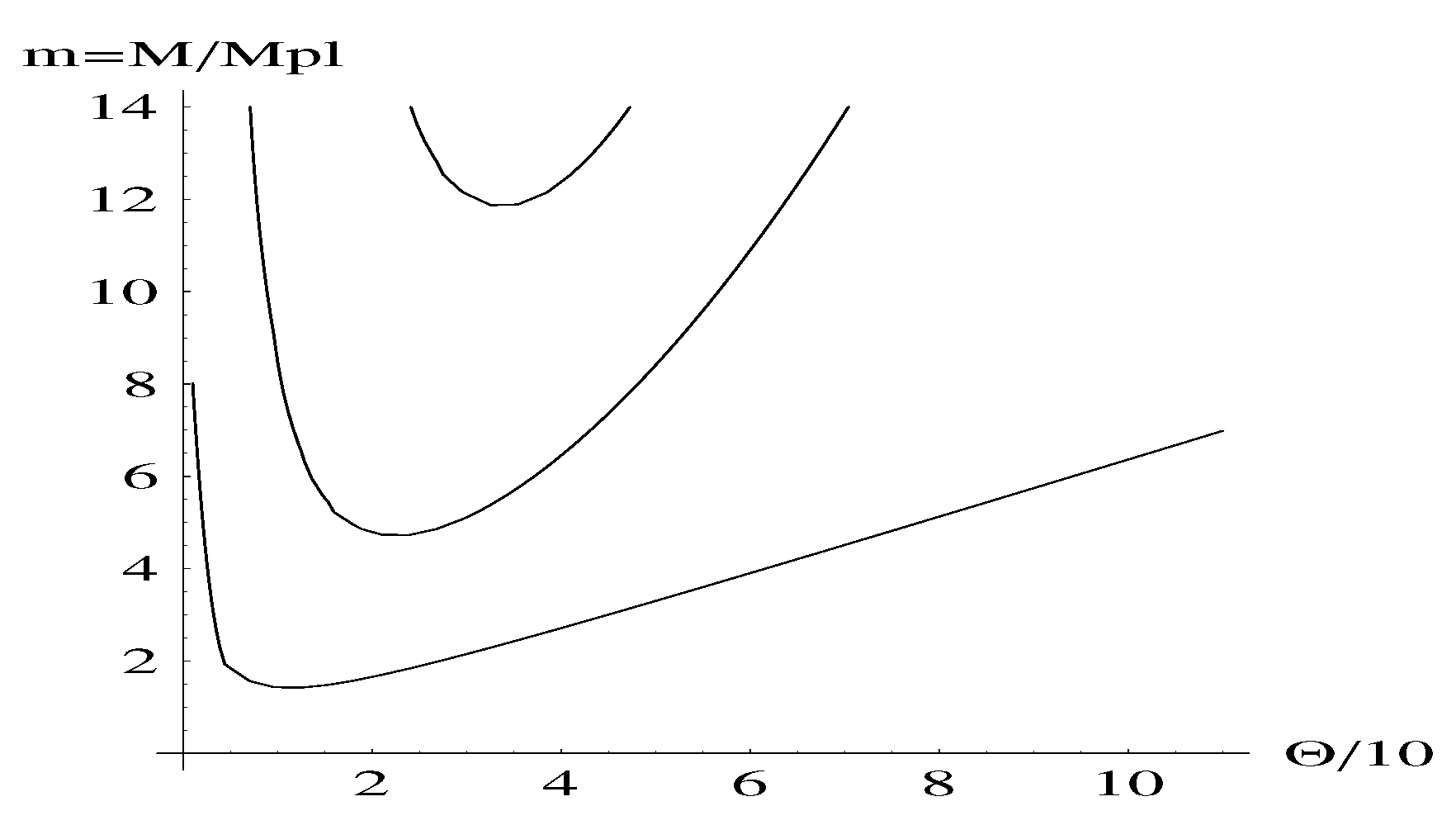
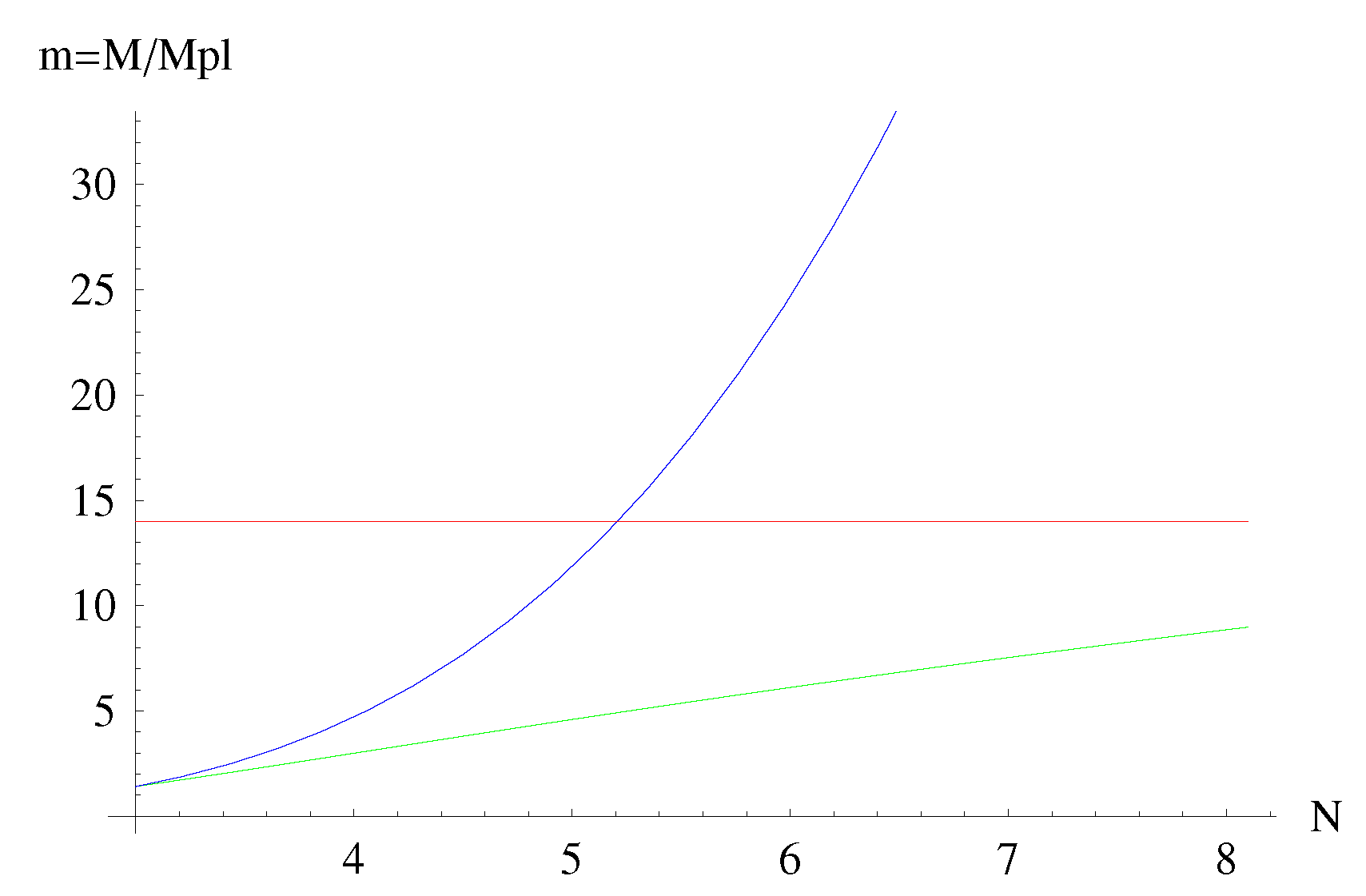
• For deformation parameter $\beta \simeq 1.5$ or greater the mass thresholds predicted by MBH GUP are remarkably lower than those of ST GUP, meaning that the production of a micro black hole is largely enhanced by the MBH GUP. In particular, micro black holes should have been detectable in any number of extra dimensions, at the designed energy for LHC-like machines, or larger.
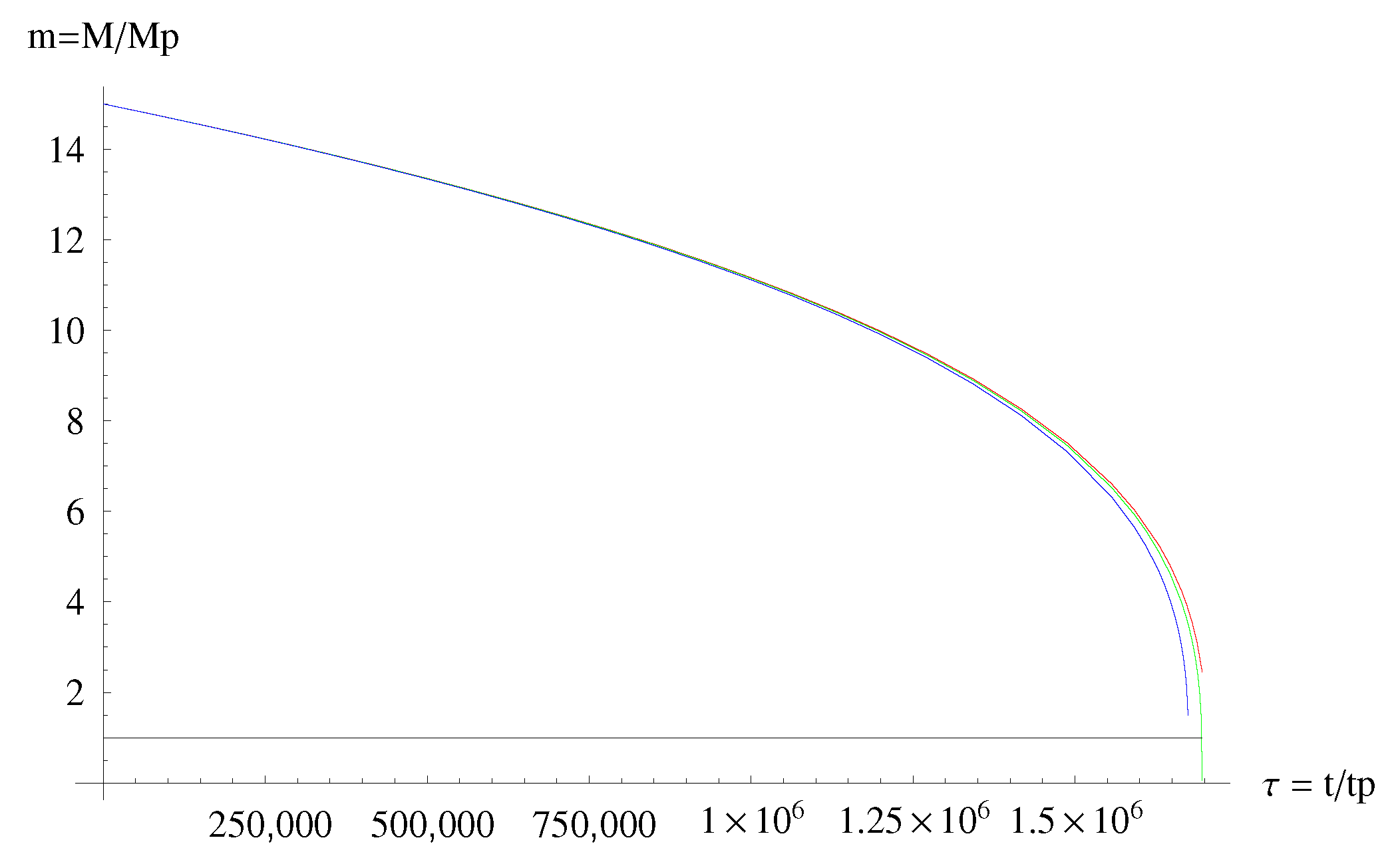
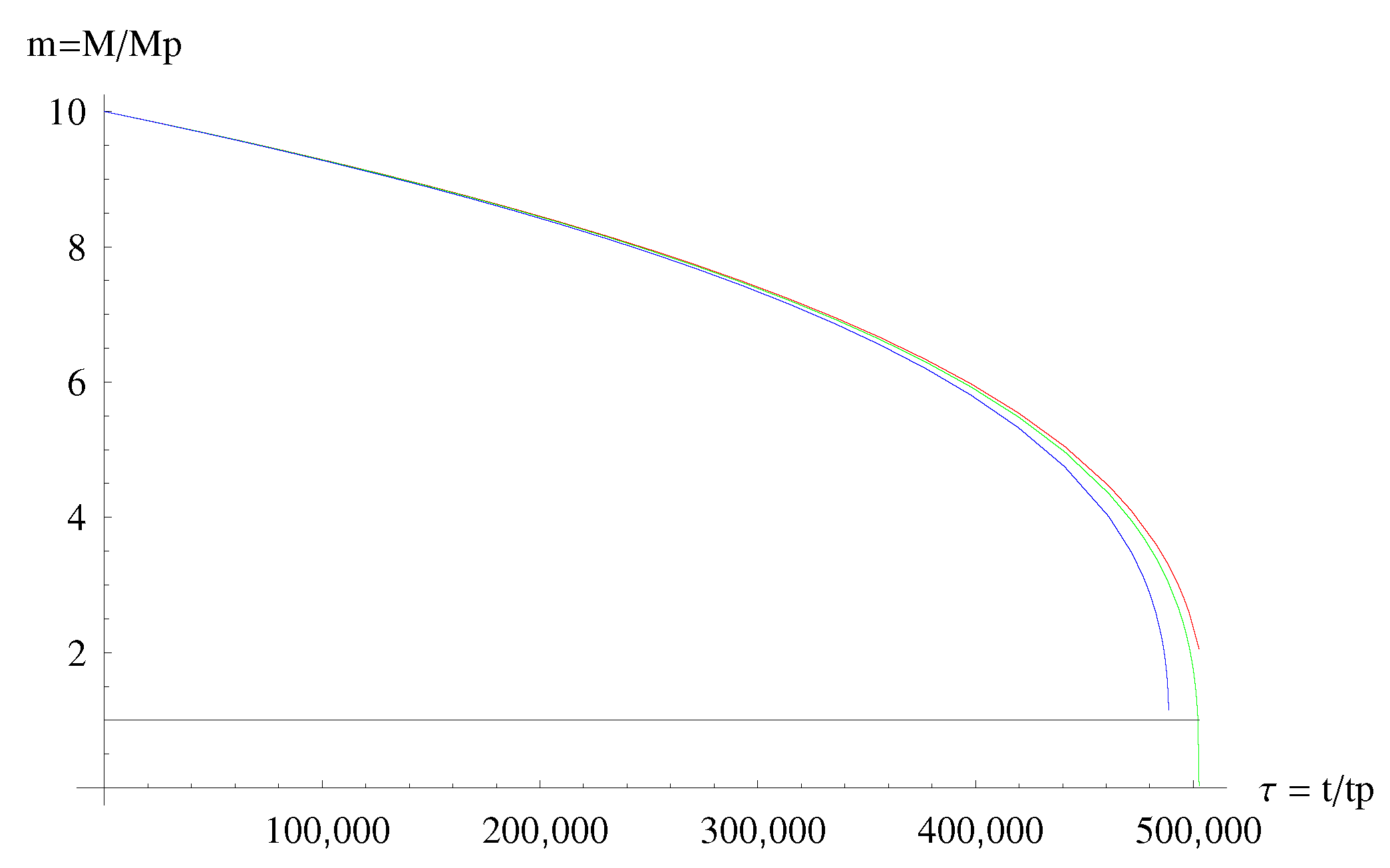
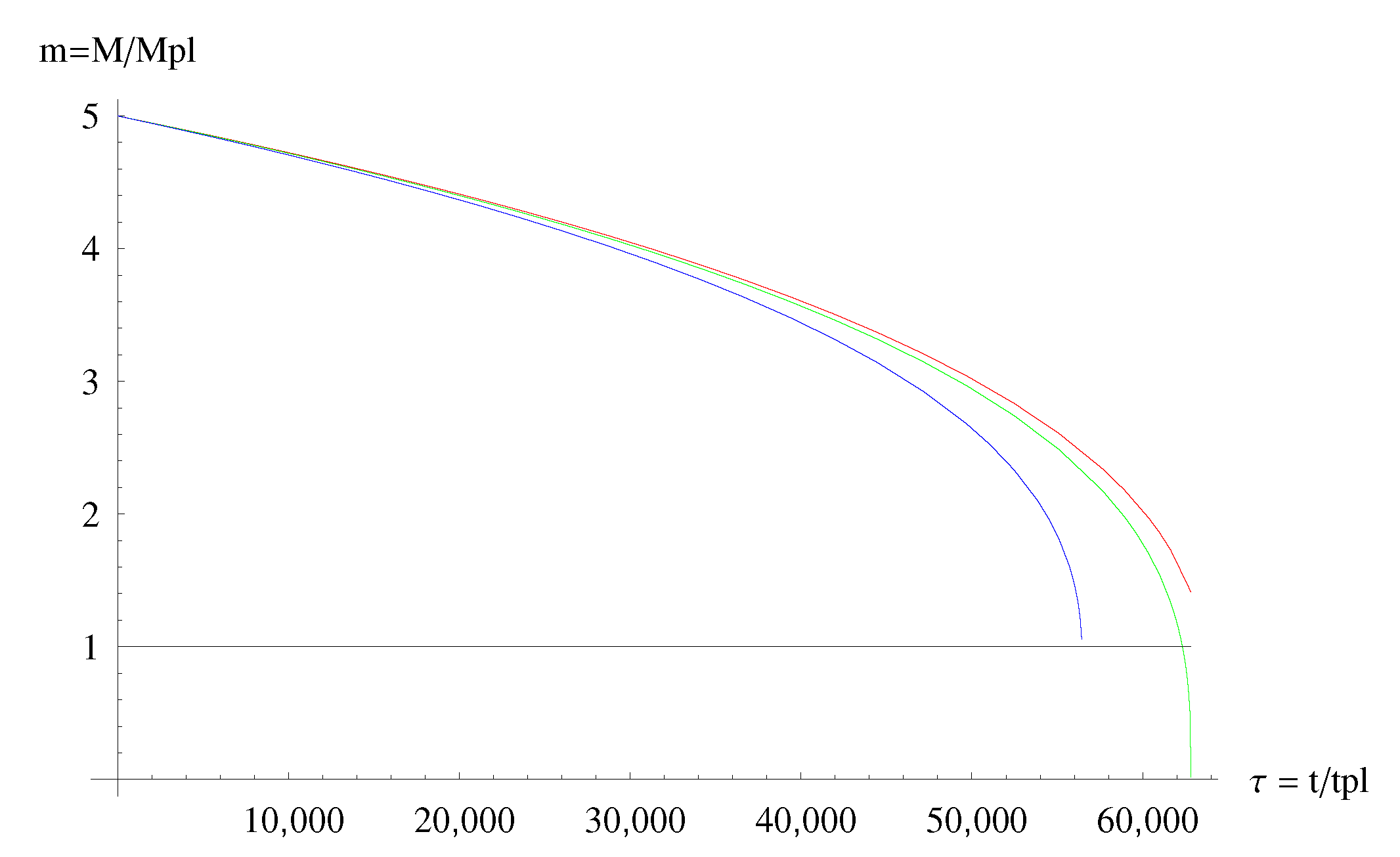
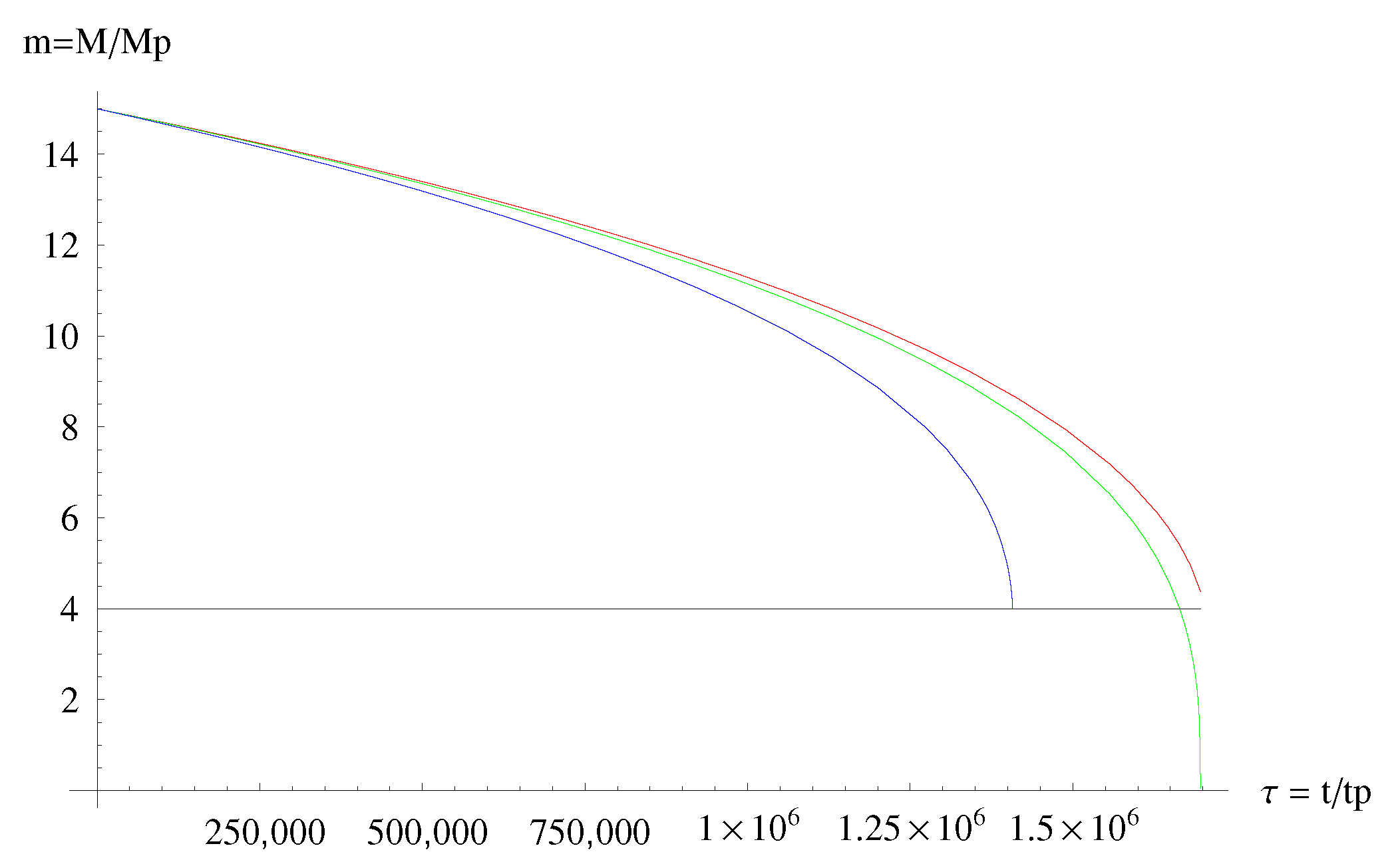
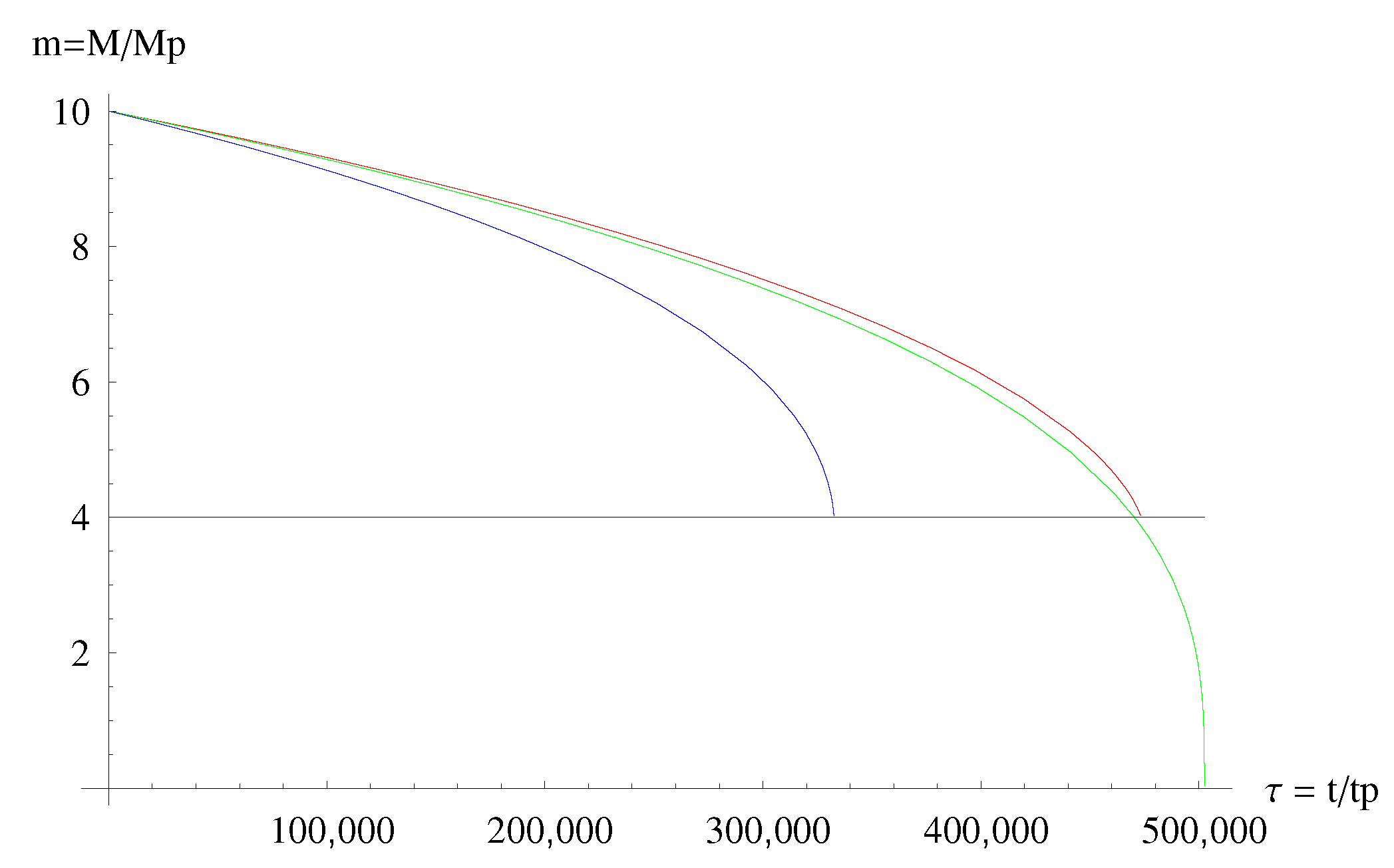
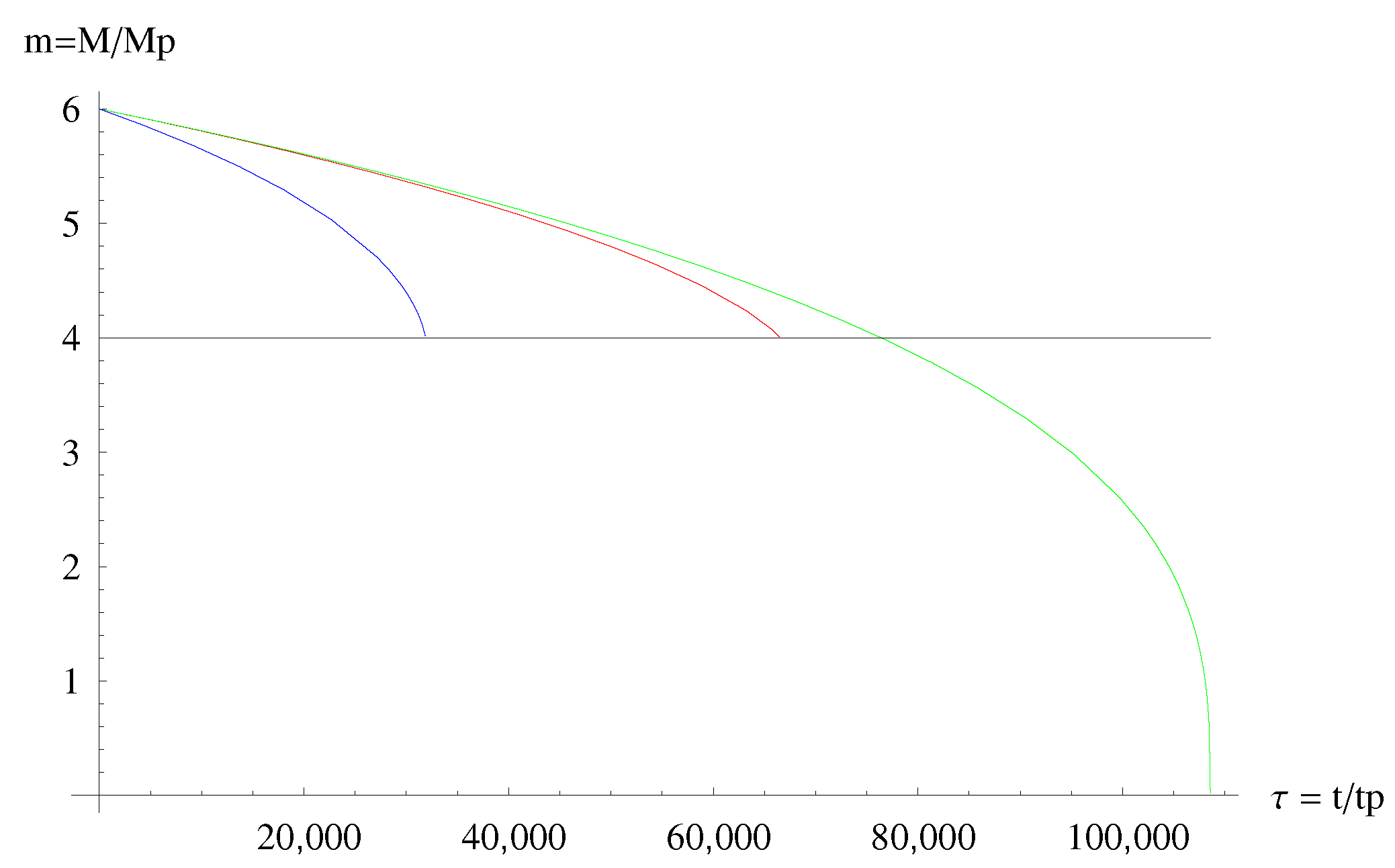
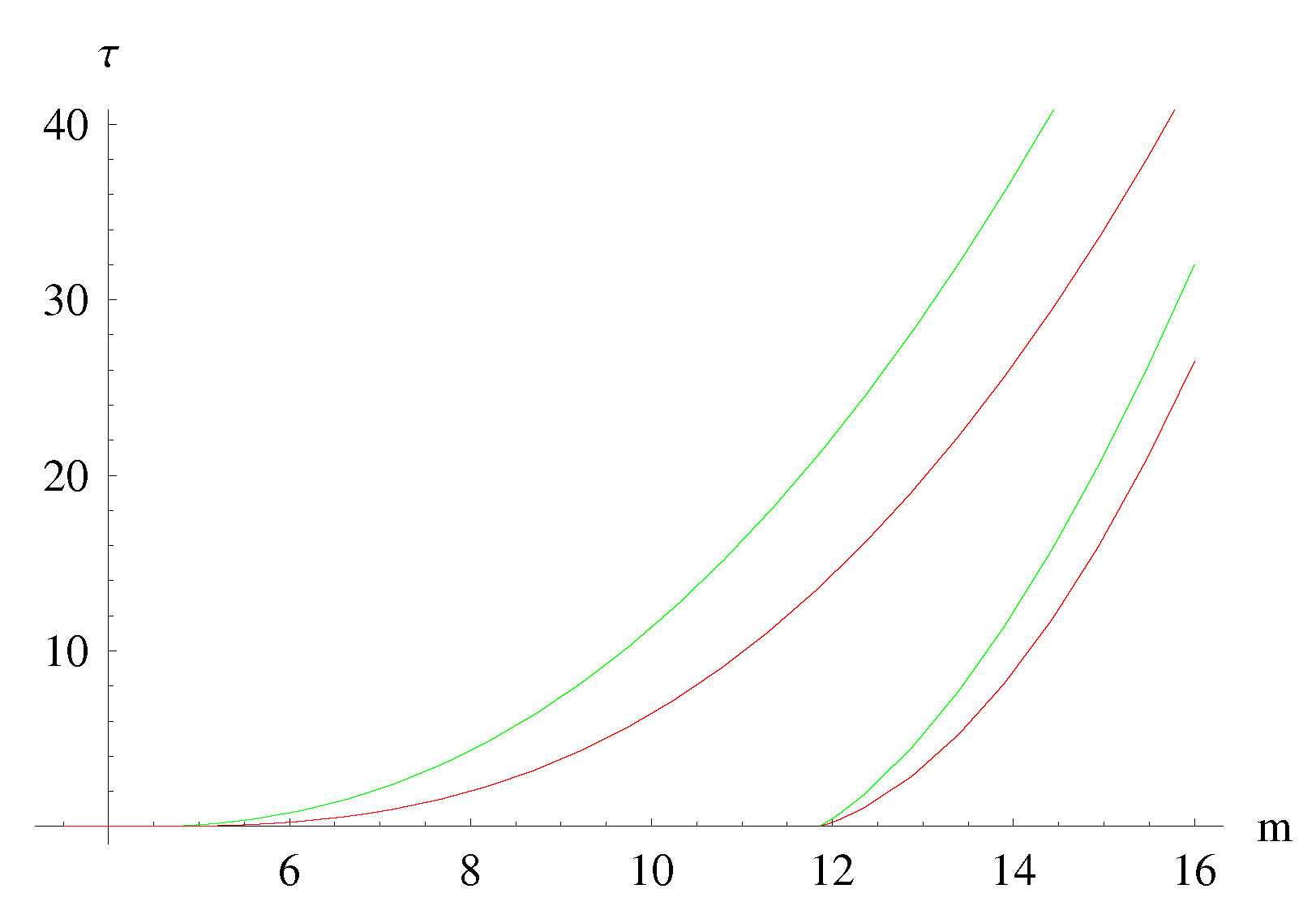
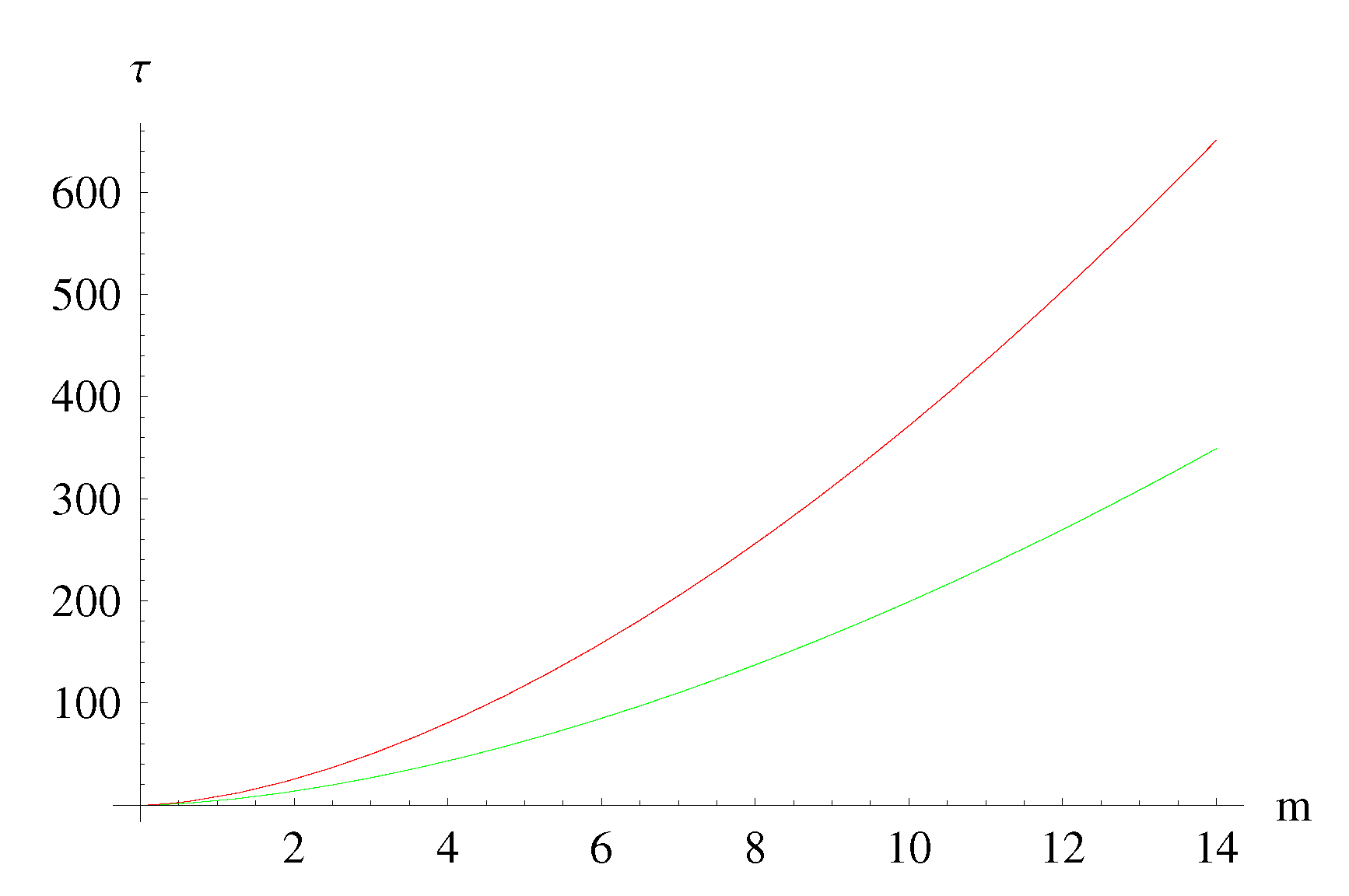
• The micro black hole lifetimes predicted by MBH GUP are in general always longer that those predicted by the ST GUP (and the difference is particularly noticeable for $N=5,6,\dots$ spatial dimensions). However the lifetimes predicted by both GUPs are, roughly, one order of magnitude shorter than those predicted by the standard Hawking evaporation (based on the standard Heisenberg principle) (see Figure 7 and Figure 8).
• The GUP-corrected entropy, for both GUPs, is lower than the standard Hawking entropy. In fact, as we see in Equations (118), (119) and (124), the leading corrective terms in $\beta$ have negative signs. The reason for this diminished entropy, in respect to the standard entropy (which is computed on the basis of the Heisenberg principle), can be traced back to the squeezing of the volume of the elementary cells in phase space, due to the new measure introduced by the GUPs (on this, see also Appendix C).
• The heat capacity predicted by both GUPs drops to zero in a finite time, at a finite temperature, meaning that the evaporation stops, and the black hole in its final stage cannot exchange energy with the surrounding space. It ceases then to interact thermodynamically with the environment. In the present framework, this is a strong indication for the existence of a final evaporation product of finite rest mass, denoted as remnant. We can expect therefore that for this remnant, which interacts with the environment only gravitationally, through its mass, the very concept of temperature becomes meaningless, being it an object with zero heat capacity, comparable for example with an elementary particle.