Learning Multimodal Representations by Symmetrically Transferring Local Structures

Abstract

Multimodal representations play an important role in multimodal learning tasks, including cross-modal retrieval and intra-modal clustering. However, existing multimodal representation learning approaches focus on building one common space by aligning different modalities and ignore the complementary information across the modalities, such as the intra-modal local structures. In other words, they only focus on the object-level alignment and ignore structure-level alignment. To tackle the problem, we propose a novel symmetric multimodal representation learning framework by transferring local structures across different modalities, namely MTLS. A customized soft metric learning strategy and an iterative parameter learning process are designed to symmetrically transfer local structures and enhance the cluster structures in intra-modal representations. The bidirectional retrieval loss based on multi-layer neural networks is utilized to align two modalities. MTLS is instantiated with image and text data and shows its superior performance on image-text retrieval and image clustering. MTLS outperforms the state-of-the-art multimodal learning methods by up to 32% in terms of R@1 on text-image retrieval and 16.4% in terms of AMI onclustering.

1. Introduction

Multimodal data, such as image-text and speech-video, commonly exists in the real-world and is critical for applications, such as image captioning [1,2], visual question answering [3,4], and audio-visual speech recognition [5]. Multimodal representation learning aims to embed data with multimodal information into a vector space so that they can be compared directly and learn complementary information from other modalities. Learning multimodal representations is a fundamental task in multimodal learning since an informative and complementary representation can largely facilitate the following learning tasks [6,7,8,9].

However, unifying heterogeneous modalities and acquiring complementary knowledge from multiple modalities in multimodal representations is still a challenging task. Most existing multimodal representation learning approaches aim to project the multimodal data into a common space by aligning different modalities with similarity constraints. However, these methods only focus on the object-level alignment, which means they try to align two corresponding objects in different modalities. Further, these methods cannot effectively capture the complementary intra-modal local structures across modalities. Object-level alignment is crucial to the modality, aligning especially for cross-modal retrieval tasks. Furthermore, the structure-level alignment can enhance the local structure in one modality through learning from the other modality, which is beneficial for the classification and clustering. Neural networks, such as autoencoders, are common tools to learn joint multimodal representations that fuse unimodal representations and are trained to perform a particular task [5,10]. In most multimodal learning tasks, such as cross-modal retrieval and translation, coordinated representations which aligning different modalities are more practical than joint representation. Most coordinated multimodal representation learning methods align two modalities with similarity models. DeViSE [11] and Visual Semantic Embedding (VSE) [12] are typical multimodal learning models, both of which use similar inner product and rank loss function to align image and text data. Two-branch neural networks (TBNN) [13] build an embedding network and similarity network with bidirectional ranking constraints and neighborhood-preserving constraints within each modality. Although TBNN tries to preserve the intra-modal structure to facilitate matching within the same modality, it cannot learn from the other modality.

In this work, we propose to learn multimodal representations by symmetrically transferring local structures across two modalities (MTLS for short) which not only considers the object-level alignment but also involves the structure-level alignment by local structure transferring objectives. The multimodal representation learning in one modality is instructed by the other modality and vice versa. Specifically, the local structure in one modality is used to enhance that in the other modality to build complementary multimodal representations. As illustrated in Figure 1, comparing with the original unimodal representation (i.e., before MTLS), the multimodal representations (i.e., after MTLS) not only align data instances from two modalities but also transfer local cluster structures from each other. The learned multimodal representations have clearer cluster structures within each modality, which are obviously much more friendly to the following multimodal retrieval and intra-modal learning tasks, such as clustering or classification. Overall, the contributions of this work include:

• A novel symmetric multimodal representation learning framework MTLS is proposed to learn complementary information from the other modality and has the potential to be instantiated into various modalities.
• MTLS builds a soft metric learning strategy to transfer local structures across modalities and enhances the intra-modal cluster structure through infinite-margin loss.
• MTLS is constrained by bidirectional retrieval loss to achieve modality aligning and trained by a customized iterative parameter updating process.

MTLS is instantiated with image-text data, and the learned multimodal representations are evaluated by cross-modal retrieval tasks and image clustering. The proposed MTLS shows its competitive performance compared with the state-of-the-art methods on two standard datasets for both image-to-text and text-to-image retrieval in terms of recall. Moreover, the superior image clustering performance and the visualization results also demonstrate that the local structures are successfully transferred across modalities and complement the original image representations.

2. Related Work

Following the categories in [7], we summarize the multimodal representations in terms of joint representations and coordinated representations. Since various unimodal data, such as text, image, and audio, can be represented by neural networks [6], they have become common tools to build a joint representation space for multimodal data [3,14,15,16]. To overcome the problem of limited labeled data in neural network training, autoencoders and stacked denoising autoencoders are usually used to be trained on unlabeled data [5,10]. The joint representations are usually trained for some specific learning tasks, such as classification [17], and the unimodal representations cannot absorb the complementary information from other modalities, which cannot benefit the intra-modal learning tasks.

Alternatively, unimodal representations could be coordinated through some constraints, such as similarity or ordering. Besides the simple linear map from image and text features in WSABIE [18], neural networks have become a popular way to coordinate multimodal data [13,19]. The most straightforward way is to match the data instances from two modalities and transform this problem into a binary classification problem. For example, the methods [20,21,22,23] predict match or mismatch (i.e., “+1” and “−1”) for an image-text pair input by optimizing a logistic regression loss. Both DeViSE [11] and VSE [12] use pre-trained image and word embeddings to construct similarity ranking functions for modality coordination. Following this idea, Order-Embeddings (Order) [24] coordinates two modalities and optimizes a partial order over the embedding spaces. The work in [13] builds embedding network and similarity network to learn the correspondence between image and text data for phrase localization and image-sentence search by emphasizing the neighborhood-preserving. Multimodal Tensor Fusion Network (MTFN) [19] learns an accurate image-text similarity function with rank-based tensor fusion rather than seeking a common embedding space for each image-text instance which omits the complementary information from multimodal data. The canonical correlation analysis (CCA) based models, such as Kernel CCA [25], Deep CCA [26], and Fisher Vectors derived from Gaussian mixture model [27] are also widely used for cross-modal retrieval [28]. However, these methods only capture the common information between modalities and cannot acquire complementary information from other modalities. Instead of learning general multimodal representations of whole image or text, some multimodal learning methods aim to a latent region-word correspondence through correlating shared semantics comprised of regions and words. For example, both Stacked Cross Attention (SCAN) [29] and Bidirectional Focal Attention Network (BFAN) [30] utilize attention mechanism to align the fragments in image and text to facilitate the across-modal retrieval while they cannot enhance the knowledge in one modality. GCH [31] and EGDH [32] utilize the high level semantic to guide the encoding process. DLA-CMR [33] considers complex statistical properties of multimodal data. It utilizes dictionary learning as a feature re-constructor to reconstruct discriminative features, while adversarial learning mines the statistical characteristics for each modality. BW [34] proposes cross-modality bridging dictionary to solve the image understanding, which characterizes the probability distribution of semantic categories for the visual appearances. UDCH-VLR [35] directly learns discriminative discrete hash codes under the unsupervised learning paradigm. Furthermore, it learns unified hash codes via collaborative matrix factorization on the deep multimodal representations to preserve the multimodal shared semantics. However, these previous works did not consider the structure-level alignment across modalities, which we think is crucial for understanding data.

Our work transfers local cluster structure with newly proposed soft metric learning and iterative learning process, none of which has been explored in any other multimodal learning work to the best of our knowledge.

3. Multimodal Representations with Local Structure Transferring

The framework of MTLS is demonstrated in Figure 2, which learns multimodal representations by coordinating two unimodal representations from modality A and modality B through two local structure transferring losses, i.e., ${\mathcal{L}}_{lst}^A$ and ${\mathcal{L}}_{lst}^B$, and modality aligning loss, i.e., ${\mathcal{L}}_{ma}$. The multimodal representations are derived from multimodal encoders, i.e., $f^A$ and $f^A$, and unimodal encoders, i.e., $f_{uni}^A$ and $f_{uni}^B$, which can be pre-trained and fine-tuned with following losses. Both local structure transferring and modality aligning are based on the triplets consist of one target object and two comparative objects from each modality, i.e., $\langle {\mathbf{h}}^A,{\mathbf{h}}_i^A,{\mathbf{h}}_j^A\rangle$ and $\langle {\mathbf{h}}^B,{\mathbf{h}}_i^B,{\mathbf{h}}_j^B\rangle$. The distance metric orders, i.e., ${\delta }^A$ and ${\delta }^B$, generated by one modality, are transferred to the other modality and are used to instruct the metric learning in that modality. Then a customized parameter updating process is designed to train the compound loss in turn, i.e., ${\mathcal{L}}_{lst}^A+{\mathcal{L}}_{ma}$ and ${\mathcal{L}}_{lst}^B+{\mathcal{L}}_{ma}$. In the following, we will introduce the representation encoding, local structure transferring, and modality aligning processes. Then the detailed learning algorithm will be introduced.

First, we formalize the multimodal representation learning problem. Let ${\mathcal{X}}^A$ and ${\mathcal{X}}^B$ denote the datasets in modality A and modality B, respectively. ${\mathbf{H}}_{uni}^A$ and ${\mathbf{H}}_{uni}^B$ are the unimodal representation spaces. ${\mathbf{H}}^A$ and ${\mathbf{H}}^B$ are the multimodal representation spaces, where the representations from modality A and modality B can be compared directly. Let $\mathbf{h}\in \mathbf{H}$ denotes the specific representation of one data object in the multimodal representation space. The dimension of $\mathbf{h}$ is denoted as l. Given a target object $\mathbf{h}$ and two comparative objects ${\mathbf{h}}_i$ and ${\mathbf{h}}_j$, we denote them as a triplet $\langle \mathbf{h},{\mathbf{h}}_i,{\mathbf{h}}_j\rangle$.

3.1. Representation Encoding

The multimodal representations are based on the unimodal representations, which are derived from unimodal encoders. Initially, the data objects in modality A are encoded into unimodal representations, which aim to capture the intra-modal information as shown in Equation (1). Similarly, the data objects in modality B are encoded into their unimodal representation space as shown in Equation (2).

$$f_{uni}^A({\mathcal{X}}^A;{\mathbf{\theta }}^A):{\mathcal{X}}^A\mapsto {\mathbf{H}}_{uni}^A$$

(1)

$$f_{uni}^B({\mathcal{X}}^B;{\mathbf{\theta }}^B):{\mathcal{X}}^B\mapsto {\mathbf{H}}_{uni}^B$$

(2)

where $f_{uni}^A$ and $f_{uni}^B$ denote the unimodal encoders of modality A and modality B. They project the data from heterogeneous modalities into low dimensional vector spaces ${\mathbf{H}}_{uni}^A$ and ${\mathbf{H}}_{uni}^B$ independently. ${\mathbf{\theta }}^A$ and ${\mathbf{\theta }}^B$ are the parameters in unimodal encoders of modality A and modality B, respectively. The unimodal encoders can be implemented with pre-trained neural networks, such as VGG [36] or ResNet [37] for images, and LSTM or GRU [38] for texts, or Fisher Vectors [27].

Although both ${\mathbf{H}}_{uni}^A$ and ${\mathbf{H}}_{uni}^B$ are continuous vector spaces, the unimodal representations from different spaces cannot be compared directly. To learn the complementary information in the other modality and align two modalities, we build multimodal representation spaces, which are shown as follows:

$$f^A({\mathbf{H}}_{uni}^A,{\mathbf{\psi }}^A):{\mathbf{H}}_{uni}^A\mapsto {\mathbf{H}}^A$$

(3)

$$f^B({\mathbf{H}}_{uni}^B,{\mathbf{\psi }}^B):{\mathbf{H}}_{uni}^A\mapsto {\mathbf{H}}^B$$

(4)

where $f^A$ and $f^B$ are the multimodal encoders which project the unimodal representation spaces into comparable multimodal representation spaces ${\mathbf{H}}^A$ and ${\mathbf{H}}^B$, respectively. ${\mathbf{\psi }}^A$ and ${\mathbf{\psi }}^B$ are the parameter sets in $f^A$ and $f^B$, respectively. The multimodal encoders are constructed based on the unimodal encoders which can be implemented by neural networks or mixture models.

During the learning of multimodal representations, we search a collection of parameters $\{{\mathbf{\theta }}^A,{\mathbf{\theta }}^B,{\mathbf{\psi }}^A,{\mathbf{\psi }}^B\}$ to generate multimodal representations for the given data when optimizing the following objectives, i.e., local structure transferring and modality aligning.

3.2. Local Structure Transferring

To capture complementary information from two modalities, we design two learning objectives, i.e., ${\mathcal{L}}_{lst}^A$ and ${\mathcal{L}}_{lst}^B$, to symmetrically transfer local structures across modalities based on metric learning. In detail, the order of distance relationships for a triplet in modality A is used to instruct the metric learning of the corresponding triplet in modality B, and vise versa.

Given a triplet of objects in modality A including a target object and two comparative objects, i.e., $\langle {\mathbf{h}}^A,{\mathbf{h}}_i^A,{\mathbf{h}}_j^A\rangle$, we define the distance metric $D_i^A$ and $D_j^A$ as follows:

$$D_i^A({\mathbf{h}}^A,{\mathbf{h}}_i^A)=({\mathbf{h}}^A-{\mathbf{h}}_i^A){\mathbf{W}}^A{({\mathbf{h}}^A-{\mathbf{h}}_i^A)}^{\mathrm{T}}$$

(5)

$$D_j^A({\mathbf{h}}^A,{\mathbf{h}}_j^A)=({\mathbf{h}}^A-{\mathbf{h}}_j^A){\mathbf{W}}^A{({\mathbf{h}}^A-{\mathbf{h}}_j^A)}^{\mathrm{T}}$$

(6)

where ${\mathbf{W}}^A\in {\mathbb{R}}^{l\times l}$ is a symmetric positive semi-definite matrix which can be decomposed as ${\mathbf{W}}^A={\mathbf{M}}_1{\mathbf{M}}_1^{\mathrm{T}}$.

Similarly, the distance metric $D_i^B$ and $D_j^B$ in term of the triplet $\langle {\mathbf{h}}^B,{\mathbf{h}}_i^B,{\mathbf{h}}_j^B\rangle$ from modality B are defined as follows:

$$D({\mathbf{h}}^B,{\mathbf{h}}_i^B)=({\mathbf{h}}^B-{\mathbf{h}}_i^B){\mathbf{W}}^B{({\mathbf{h}}^B-{\mathbf{h}}_i^B)}^{\mathrm{T}}$$

(7)

$$D({\mathbf{h}}^B,{\mathbf{h}}_j^B)=({\mathbf{h}}^B-{\mathbf{h}}_j^B){\mathbf{W}}^B{({\mathbf{h}}^B-{\mathbf{h}}_j^B)}^{\mathrm{T}}$$

(8)

where ${\mathbf{W}}^B\in {\mathbb{R}}^{l\times l}$ is also a symmetric positive semi-definite matrix.

In traditional metric learning methods [39], the order of metric pairs $D(\mathbf{h},{\mathbf{h}}_i)$ and $D(\mathbf{h},{\mathbf{h}}_j)$ are needed. However, we do not have class labels to define this order in an unsupervised way. A natural solution is to use the distance order of a triplet in one modality to instruct the metric learning in the other modality. Specifically, we can define a binary function ${\delta }^A$ for modality A according to the representations of modality B [40]:

$${\delta }^A({\mathbf{h}}_i,{\mathbf{h}}_j)=\left\{\begin{array}{c}1,\mathrm{if}d({\mathbf{h}}^B,{\mathbf{h}}_i^B)>d({\mathbf{h}}^B,{\mathbf{h}}_j^B)\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(9)

where d is a local distance function, e.g., Euclidean distance, cosine dissimilarity.

However, the above design may lead to the oscillations in parameter optimizing process when the local distance order from modality A is inconsistent with that from modality B. Considering this problem, we design a soft metric learning strategy which takes both local distance order from modality B and modality A into account:

$$\delta ({\mathbf{h}}_i,{\mathbf{h}}_j)=\left\{\begin{array}{c}1,\mathrm{if}{d}_i^A>d_j^A\cap d_i^B>d_j^B\hfill \\ 0,\mathrm{if}{d}_i^A<d_j^A\cap d_i^B<d_j^B\hfill \\ \sigma \left(\right|d_i^A-d_j^A|-|d_i^B-d_j^B\left|\right),\hfill \\ \mathrm{if}{d}_i^A>d_j^A\cap d_i^B<d_j^B\hfill \\ \sigma \left(\right|d_i^B-d_j^B|-|d_i^A-d_j^A\left|\right),\hfill \\ \mathrm{if}{d}_i^A<d_j^A\cap d_i^B>d_j^B\hfill \end{array}\right.$$

(10)

where $\sigma \left(x\right)=\frac{1}{1+e^{-x}}$ is sigmoid function, $d_i^A$ and $d_i^B$ are the simplified notations of $d({\mathbf{h}}^A,{\mathbf{h}}_i^A)$ and $d({\mathbf{h}}^B,{\mathbf{h}}_i^B)$, respectively. Here we choose $d(\mathbf{h},{\mathbf{h}}_i)={\parallel \mathbf{h}-{\mathbf{h}}_i\parallel }_2$. In this way, the metric label follows the probability of difference between local distance pairs from two modalities when the distance order from two modalities are inconsistent.

Then the log probability of $D_i^A>D_j^A$ conditional on $\delta$ is defined as follows:

$$\begin{array}{c}\hfill logP(D_i^A>D_j^A|\delta )=\delta ({\mathbf{h}}_i,{\mathbf{h}}_j)log\sigma (D_i^A-D_j^A)\\ \hfill +(1-\delta ({\mathbf{h}}_i,{\mathbf{h}}_j))log(1-\sigma (D_i^A-D_j^A)).\end{array}$$

(11)

Similarly, the log probability of $D_i^B>D_j^B$ conditional on $\delta$ is:

$$\begin{array}{c}\hfill logP(D_i^B>D_j^B|\delta )=\delta ({\mathbf{h}}_i,{\mathbf{h}}_j)log\sigma (D_i^B-D_j^B)\\ \hfill +(1-\delta ({\mathbf{h}}_i,{\mathbf{h}}_j))log(1-\sigma (D_i^B-D_j^B)).\end{array}$$

(12)

Accordingly, the loss function of transferring local structures of modality B to A could be written as:

$${\mathcal{L}}_{lst}^A=-\sum _{\langle {\mathbf{h}}^A,{\mathbf{h}}_i^A,{\mathbf{h}}_j^A\rangle }logP(D_i^A>D_j^A|\delta ).$$

(13)

Correspondingly, the loss function of transferring local structures of modality A to B is:

$${\mathcal{L}}_{lst}^B=-\sum _{\langle {\mathbf{h}}^B,{\mathbf{h}}_i^B,{\mathbf{h}}_j^B\rangle }logP(D_i^B>D_j^B|\delta ).$$

(14)

Specially, when $\delta ({\mathbf{h}}_i,{\mathbf{h}}_j)=1$, we have the following log loss:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{lst}^A& =-logP(D_i^A>D_j^A)=-log\sigma (D_i^A-D_j^A)\hfill \\ \hfill & =log(1+e^{(D_i^A-D_j^A)}).\hfill \end{array}$$

(15)

This form and the form when $\delta ({\mathbf{h}}_i,{\mathbf{h}}_j)=0$ are the common variation of hinge loss, which could be seen as a “soft” version of the hinge loss with an infinite margin [41]. With this loss, the local structure in one modality will be amplified through the other modality, which leads to the circumstance in Figure 1. Hence, ${\mathcal{L}}_{lst}^A$ in modality A and ${\mathcal{L}}_{lst}^B$ in modality B complement the learning of local structures in each other and enhance the intra-modal cluster structure as well.

3.3. Modality Aligning

To align two modalities, we build a similarity ranking model based on the comparative triplet across modalities, i.e., $\langle {\mathbf{h}}^A,{\mathbf{h}}^B,{\mathbf{h}}_{-}^B\rangle$. Given the a target object ${\mathbf{h}}^A$ in modality A, the corresponding object in modality B is ${\mathbf{h}}^B$, and vise versa. Hence, $\langle {\mathbf{h}}^A,{\mathbf{h}}^B\rangle$ could be treated as the positive pair and $\langle {\mathbf{h}}^A,{\mathbf{h}}_{-}^B\rangle$ as the negative pair. We define a similarity function $s({\mathbf{h}}^A,{\mathbf{h}}^B)$ which should give higher similarity score to the positive pair than the negative pair. Then the bidirectional triplet ranking loss for modality aligning is defined as follows:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{ma}({\mathbf{h}}^A,{\mathbf{h}}^B)& =\sum _{{\mathbf{h}}_{-}^B}max(0,[m-s({\mathbf{h}}^A,{\mathbf{h}}^B)+s({\mathbf{h}}^A,{\mathbf{h}}_{-}^B)])\hfill \\ \hfill & +\sum _{{\mathbf{h}}_{-}^A}max(0,[m-s({\mathbf{h}}^A,{\mathbf{h}}^B)+s({\mathbf{h}}_{-}^A,{\mathbf{h}}^B)]),\hfill \\ \hfill & {\mathbf{h}}_{-}^B\in {\mathcal{H}}_{-}^B,{\mathbf{h}}_{-}^A\in {\mathcal{H}}_{-}^A\end{array}$$

(16)

where m is the enforced margin hyper parameter. ${\mathbf{h}}_{-}^B$ is the negative representation in terms of ${\mathbf{h}}^A$, and ${\mathcal{H}}_{-}^B$ is the negative set. The similarity score is defined as follows:

$$s=\sigma \left(\mathbf{W}({\mathbf{h}}^A\odot {\mathbf{h}}^B)\right),$$

(17)

where ⊙ is the element-wise product, and $\mathbf{W}\in {\mathbb{R}}^{1\times l}$. Compared with directly calculating the inner product, the defined similarity score s captures more comprehensive interactions between ${\mathbf{h}}^A$ and ${\mathbf{h}}^B$ since it can be trained through the whole neural networks. This loss function constrains the local structure transferring process and keeps the matching relationships across modalities.

Intuitively, the negative set consists of all the non-target data in terms of one target object. However, among all the non-target data, the negative objects closest to the target determine the success or failure of retrieval. Thus we use the hard negative sampling strategy to construct the negative set which is also proved to be effective in previous works [42,43,44]. Specifically, given a target object ${\mathbf{h}}^A$ in modality A, negative set ${\mathcal{H}}_{-}^B$ consists of the top K ($K\ge 1$) similar objects ${\mathbf{h}}_{-}^B$ from modality B according to the similarity scores, i.e., $s({\mathbf{h}}^A,{\mathbf{h}}_{-}^B)$. Similarly, we build the negative set ${\mathcal{H}}_{-}^A$ for the target object ${\mathbf{h}}^B$ in modality B.

3.4. Learning Algorithm

To learn the multimodal representations, we design an iterative training strategy and construct the training loss as follows:

$$\left\{\begin{array}{c}{\mathcal{L}}^A({\mathcal{X}}^A,{\mathcal{X}}^B;{\Theta }^A)={\mathcal{L}}_{lst}^A+{\mathcal{L}}_{ma}\hfill \\ {\mathcal{L}}^B({\mathcal{X}}^A,{\mathcal{X}}^B;{\Theta }^B)={\mathcal{L}}_{lst}^B+{\mathcal{L}}_{ma}\hfill \end{array}\right.$$

(18)

where ${\Theta }^A=\left\{{\mathbf{W}}^A\right\}\cup \Theta$ and ${\Theta }^B=\left\{{\mathbf{W}}^B\right\}\cup \Theta$ are the parameter sets, and $\Theta =\{\mathbf{W},{\mathbf{\theta }}^A,{\mathbf{\theta }}^B,{\mathbf{\psi }}^A,{\mathbf{\psi }}^B\}$. ${\mathcal{L}}^A$ is the modality aligning constrained local structure transferring loss function for modality A with the instruction from modality B. When minimizing ${\mathcal{L}}^A$, the parameter ${\mathbf{W}}^B$ is fixed, and ${\mathbf{W}}^A$ and parameters in $\Theta$ are updated. Similarly, ${\mathcal{L}}^B$ transfers local structure from modality A to modality B. In this iterative way, the local structure information can be transferred and enhanced during the training process. The complete learning process of MTLS is briefly demonstrated in Algorithm 1, where $\Gamma$ is a function to assign the adaptive learning rate in the parameter optimizing process, e.g., AdaGrad, Adam [45].

Triplet Sampling. To compute the local structure transferring loss, i.e., ${\mathcal{L}}_{lst}^A$ and ${\mathcal{L}}_{lst}^B$, we need to sample intra-modal triplets $\langle {\mathbf{h}}^A,{\mathbf{h}}_i^A,{\mathbf{h}}_j^A\rangle$ and $\langle {\mathbf{h}}^B,{\mathbf{h}}_i^B,{\mathbf{h}}_j^B\rangle$. Furthermore, according to Section 3.3, we need to sample comparative cross-modal triplets $\langle {\mathbf{h}}^A,{\mathbf{h}}^B,{\mathbf{h}}_{-}^B\rangle$ and $\langle {\mathbf{h}}^A,{\mathbf{h}}_{-}^A,{\mathbf{h}}^B\rangle$. To unify these two triplet samplings, we apply the hard negative sampling strategy to the intra-modal triplet sampling. In detail, given a positive pair $\langle {\mathbf{h}}^A,{\mathbf{h}}^B\rangle$, we set $K=1$, which means we choose the most violating negative match as ${\mathbf{h}}_{i-}^B$ and ${\mathbf{h}}_{j-}^A$. Further, we could easily get the corresponding objects in the other modality. As a result, we get the triplet for ${\mathcal{L}}_{lst}^A$ and ${\mathcal{L}}_{lst}^B$, i.e., $\langle {\mathbf{h}}^A,{\mathbf{h}}_{i-}^A,{\mathbf{h}}_{j-}^A\rangle$ and $\langle {\mathbf{h}}^B,{\mathbf{h}}_{i-}^B,{\mathbf{h}}_{j-}^B\rangle$.

Algorithm 1 The learning process of MTLS

1: Let $\Theta =\{\mathbf{W},{\mathbf{\theta }}^A,{\mathbf{\psi }}^A,{\mathbf{\theta }}^B,{\mathbf{\psi }}^B\}$ Input:  ${\mathcal{X}}^A$, ${\mathcal{X}}^B$, $N_b$: batchSize, $MaxIter$: maximum iterations, $perIter$: number of epochs in one modality. Output:  $\Theta ,{\mathbf{W}}^A,{\mathbf{W}}^B-\mathrm{the}\mathrm{modal}\mathrm{parameters}$ 2: Initialize $\Theta ,{\mathbf{W}}^A,{\mathbf{W}}^B$ 3: for$iteration=1$ to $MaxIter$ do 4:  for $u=1$ to $perIter$ do 5:    Freezing the parameter ${\mathbf{W}}^B$ 6:    for $q=1$ to # training batches do 7:   ${\mathcal{B}}^A,{\mathcal{B}}^B\leftarrow getMinibatch\left(\right)$ 8:   ${\mathbf{H}}_{uni}^A\leftarrow f({\mathcal{B}}^A,{\mathbf{\theta }}^A)$, ${\mathbf{H}}_{uni}^B\leftarrow f({\mathcal{B}}^B,{\mathbf{\theta }}^B)$ 9:   ${\mathbf{H}}^A\leftarrow f({\mathbf{H}}_{uni}^A,{\mathbf{\psi }}^A)$, ${\mathbf{H}}^B\leftarrow f({\mathbf{H}}_{uni}^B,{\mathbf{\psi }}^B)$ 10:   Sampling: ${\{\langle {\mathbf{h}}^A,{\mathbf{h}}_{i-}^A,{\mathbf{h}}_{j-}^A\rangle ,\langle {\mathbf{h}}^B,{\mathbf{h}}_{i-}^B,{\mathbf{h}}_{j-}^B\rangle \}}^{N_b}$ 11:   Calculate $\delta$ (cf. Equation (10)) 12:   ${\mathcal{L}}^A\leftarrow {\mathcal{L}}_{lst}^A+{\mathcal{L}}_{ma}$ 13:   $\Theta \leftarrow \Theta -\Gamma \left({\nabla }_{\Theta }{\mathcal{L}}^A\right)$ 14:   ${\mathbf{W}}^A\leftarrow {\mathbf{W}}^A-\Gamma \left({\nabla }_{{\mathbf{W}}^A}{\mathcal{L}}^A\right)$ 15:    end for 16:  end for 17:  for $v=1$ to $perIter$ do 18:    Freezing the parameters $\{{\mathbf{\theta }}^A,{\mathbf{\psi }}^A\}$ in ${\Theta }^A$ 19:    for $q=1$ to # training batches do 20:   ${\mathcal{B}}^A,{\mathcal{B}}^B\leftarrow getMinibatch\left(\right)$ 21:   ${\mathbf{H}}_{uni}^A\leftarrow f({\mathcal{B}}^A,{\mathbf{\theta }}^A)$, ${\mathbf{H}}_{uni}^B\leftarrow f({\mathcal{B}}^B,{\mathbf{\theta }}^B)$ 22:   ${\mathbf{H}}^A\leftarrow f({\mathbf{H}}_{uni}^A,{\mathbf{\psi }}^A)$, ${\mathbf{H}}^B\leftarrow f({\mathbf{H}}_{uni}^B,{\mathbf{\psi }}^B)$ 23:   Sampling: ${\{\langle {\mathbf{h}}^A,{\mathbf{h}}_{i-}^A,{\mathbf{h}}_{j-}^A\rangle ,\langle {\mathbf{h}}^B,{\mathbf{h}}_{i-}^B,{\mathbf{h}}_{j-}^B\rangle \}}^{N_b}$ 24:   Calculate $\delta$ (cf. Equation (10)) 25:   ${\mathcal{L}}^B\leftarrow {\mathcal{L}}_{lst}^B+{\mathcal{L}}_{ma}$ 26:   $\Theta \leftarrow \Theta -\Gamma \left({\nabla }_{\Theta }{\mathcal{L}}^B\right)$ 27:   ${\mathbf{W}}^B\leftarrow {\mathbf{W}}^B-\Gamma \left({\nabla }_{{\mathbf{W}}^B}{\mathcal{L}}^B\right)$ 28:    end for 29:  end for 30: end for 31: The gradient-based optimization is based on Adam [45].

4. Experiments

In this section, we apply MTLS to image-text data. Further, we evaluate MTLS with the cross-modal retrieval (i.e., image-to-text and text-to-image retrieval) and the image clustering. Moreover, we visualize the image representations generated by different multimodal representation learning methods and analyze the results.

4.1. Implementation Details

In the initial step, given an original $256\times 256$ image, we use its center crop of size $224\times 224$. We utilize the ResNet152 [37] as $f_{uni}^A$, which is pre-trained on ImageNet, and we extract image features from the penultimate fully connected layer, which is 2048-dimension. For the text unimodal embedding, we implement GRU as $f_{uni}^B$ to encode the text based on the word embedding in [12]. We set the dimension of unimodal text representations to 1024. In addition, we set the dimension of word embedding to 300.

The dimension of multimodal representation space is set to 1024. The projection function $f^A$ and $f^B$ are defined as tanh projection functions, which are implemented as a full-connected layer with tanh activation. Hence, ${\mathbf{\psi }}^{\mathbf{A}}$ and ${\mathbf{\psi }}^{\mathbf{B}}$ are $2048\times 1024$ and $1024\times 1024$ matrices, respectively. In the local structure transferring process, both ${\mathbf{W}}^A$ and ${\mathbf{W}}^B$ are $1024\times 1024$ matrices.

In the training phase, we set the max iteration $maxIter$ to 7, and set the number of epochs in one modality $perIter$ to 10. We use a mini-batch size of 128 in all experiments. For the modality aligning loss ${\mathcal{L}}_{ma}$, we set the margin m to 0.2 for all experiments. Moreover, we use Adam optimizer [45]. For the comparison methods, the parameter configurations are used as default in original papers.

4.2. Experimental Setup

Dataset. We select two widely used datasets, Flickr30k dataset [46] and Microsoft COCO dataset (MSCOCO) [47] in our experiments. Flickr30k dataset contains 31,000 images collected from the Flickr website. Each image comes with five captions. We use the split setting as [29], which contains 28,000 images for training, 1000 images for validation, and 1000 images for the test. Further, we use the splits of [48] for MSCOCO in the cross-modal retrieval task. This split consists of 113,283 images in the training set, and 5000 images in both validation and test sets. Similarly, each image is annotated by 5 sentences. Furthermore, each image in MSCOCO is associated with a class label. For the cross-modal retrieval experiments, we use the two datasets above. As to the image clustering and visualization tasks, we collect two subsets of images from MSCOCO.

Comparison Methods. For cross-modal retrieval, we compare our method with the baseline Gaussian-Laplacian mixture models and state-of-the-art neural network models:

• Mean Vector (MV) [27]: it adopts the mean vector of word2vec embeddings as the caption embeddings.
• CCA (CCA${}_G$) [27]: it adopts the fisher vectors with the fusion of Gaussian Mixture Model (GMM) and HGLMM.
• VSE [12]: it uses inner product and ranking loss to align image and text.
• VSE++ [44]: it updates VSE with hard negative sampling.
• Order-embeddings (Order) [24]: it optimizes the partial order of image-text pair.
• Embedding network in two-branch neural networks (TBNN) [13]: it emphasis intra-modal structure in the aligning process.
• Stacked cross attention networks (SCAN) [29]: it learns attention weights of image regions or text words for inferring image-text similarity.
• Bidirectional Focal Attention Network (BFAN) [30]: it reassigns attention to relevant image regions instead of all the regions based on inter-modality relation and intra-modality relation.
• Multimodal Tensor Fusion Network (MTFN) [19]: it explicitly learns the image-text similarity function with rank-based tensor fusion.

In our proposed MTLS and above comparison methods, we use ResNet152 [37] which are pre-trained on ImageNet as the original image embeddings and the caption embeddings follows the settings in original papers.

4.3. Cross-Modal Retrieval

In the evaluation phase, following the settings in [13], we adopt a test set of 1000 images and 5000 corresponding captions for both the Flickr30k dataset and MSCOCO datasets. We use the images to retrieve captions (i.e., image-to-text retrieval) and captions to retrieve images (i.e., text-to-image retrieval). As to the performance measurement, we report Recall@K (K = 1,5,10), which corresponds to the percentage of test queries for which the correct response is among the top K results [49].

Due to the performance improvement brought by the re-ranking method in [19,50], we conduct re-ranking to refine the retrieval results. Specifically, we consider the interactions between the bi-directional retrieval and take the image-to-text retrieval as an example. Given a query image I, we could get the corresponding text set according to the similarity. The top k texts could be seen as k-reciprocal candidate texts. Moreover, we use these texts to search corresponding image sets, respectively. The rank of query image I in these sets could be sorted to replace the rank of these texts in the corresponding text set for query image I. Furthermore, the same for text-image retrieval.

The cross-modal retrieval results on Flickr30k and MSCOCO datasets, including image-to-text retrieval and text-to-image retrieval, are demonstrated in

Table 1. The result of cross-modal retrieval on Flickr30k dataset and MSCOCO dataset. The best results are marked in bold font.

	Flickr30k Dataset								MSCOCO Dataset
Method	Image-To-Text				Text-To-Image				Image-To-Text				Text-To-Image
	R@1	R@5	R@10	mR	R@1	R@5	R@10	mR	R@1	R@5	R@10	mR	R@1	R@5	R@10	mR
MV [27]	24.8	52.5	64.3	47.2	20.5	46.3	59.3	42.0	33.2	61.8	75.1	56.7	24.2	56.4	72.4	51.0
CCA${}_H$ [27]	34.4	61.0	72.3	55.9	24.4	52.1	65.6	47.3	37.7	66.6	79.1	61.1	24.9	58.8	76.5	53.4
CCA${}_G$ [27]	35.0	62.0	73.3	56.7	25.0	52.7	66.0	47.9	39.4	67.9	80.9	62.7	25.1	59.8	76.6	53.8
VSE [12]	42.1	73.2	84.0	66.4	31.8	62.6	74.1	56.1	56.0	85.8	93.5	78.4	43.7	79.4	89.7	70.9
VSE++ [44]	52.9	80.5	87.2	73.5	39.6	70.1	79.5	63.1	64.6	90.0	95.7	83.4	52.0	84.3	92.0	76.1
Order [24]	52.0	80.5	89.5	74.0	37.8	67.6	77.7	61.0	48.5	80.9	90.3	73.2	39.6	75.3	86.7	67.2
TBNN [13]	43.2	71.6	79.8	64.8	31.7	61.3	72.4	55.1	54.9	84.0	92.2	77.0	43.3	76.4	87.5	59.8
SCAN [29]	67.9	89.0	94.4	83.7	43.9	74.2	82.8	66.9	72.7	94.8	98.4	88.6	58.8	88.4	94.8	80.6
BFAN [30]	68.1	91.4	-	79.7	59.4	88.4	-	73.9	74.9	95.2	-	85.0	59.4	88.4	-	73.9
MTFN [19]	65.3	88.3	93.3	82.3	52.0	80.1	86.1	72.7	74.3	94.9	97.9	89.0	60.1	89.1	95.0	81.4
MTLS	67.5	89.7	94.6	84.0	68.8	87.7	89.6	82.1	76.4	96.5	98.5	90.5	79.4	97.0	98.1	91.5

. Some retrieval examples obtained by our method and the other two typical methods are shown in Figure 3 and Figure 4. According to the results, we have the following observations:

• All the similarity-based neural network models, i.e., VSE, VSE++, Order, TBNN, SCAN, MTFN, BFAN, and our proposed MTLS perform better than the baseline models on both datasets, i.e., MV, CCA${}_H$, and CCA${}_G$, which indicates the representation ability of neural networks and the advantages of ranking loss.
• On Flickr30k dataset, our proposed MTLS achieves competitive results with state-of-the-art BFAN, which is more complex than our method since it considers the image regions and corresponding text words. Moreover, the BFAN is specially designed for image-text matching while our MTLS learns general multimodal representations for several tasks.
• On MSCOCO dataset, our method MTLS significantly outperforms other state-of-the-art methods. Especially for text-to-image retrieval task, MTLS achieves 81.7%, 52.7%, 100%, 83.0%, 35%, 32%, 33% improvements over the comparison methods VSE, VSE++, Order, TBNN, SCAN, MTFN and BFAN respectively in terms of R@1. This is because text-to-image retrieval is more challenging than image-to-text retrieval since one image is corresponding to five captions and MTLS captures complementary information in both text and image representations.
• According to the examples in Figure 3 and Figure 4, among the top five captions retrieved by our method MTLS four captions are the ground-truth ones and MTLS can find the most matching images from a bunch of ambiguous images according to the query text. Because in MTLS the local structures are not only enhanced within modality but also transferred between modalities, it is easier to retrieve the most relevant images or captions.

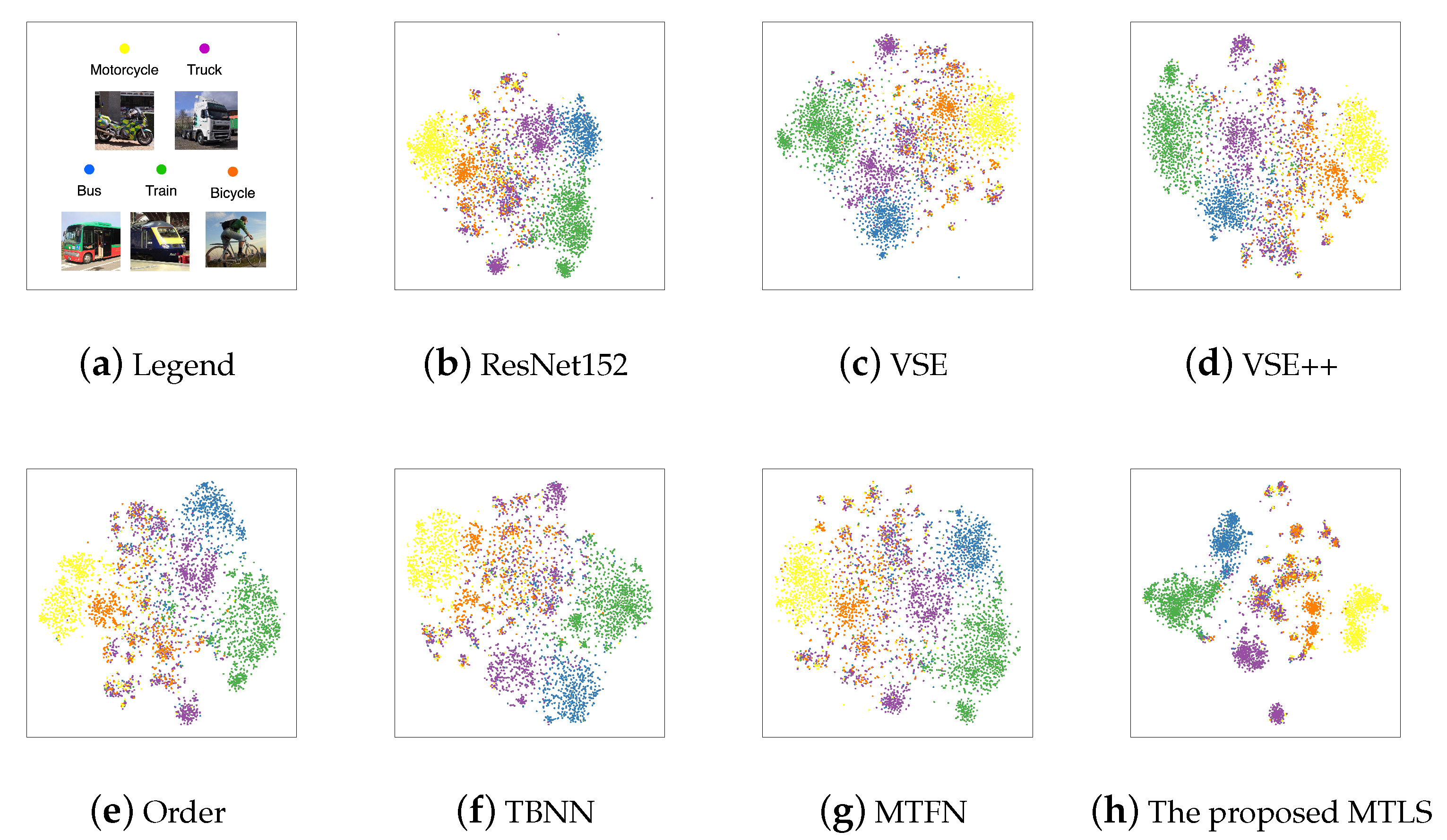
4.4. Image Clustering

To demonstrate the complementary information acquired by multimodal representation learning, we use the trained representations to do intra-modal clustering. Since only class labels of images in MSCOCO dataset are available, we construct two subsets of Vehicle category and Animal category respectively in MSCOCO dataset.

• Vehicle Dataset: it contains five subcategories images, i.e., bus, train, truck, bicycle, and motorcycle, which contains 4983 images in total. The representative image in each category is shown in Figure 5a.
• Animal Dataset: it contains seven subcategories images, i.e., horse, sheep, cow, elephant, bear, zebra, and giraffe, which contains 4737 images in total.

Because there is no intra-modal representation learned in the baseline models, i.e., MV, CCA${}_H$, and CCA${}_H$ and the attention based models, i.e., SCAN and BFAN, need multiple regions of each image, we only demonstrate the clustering results of Original image embeddings (i.e., Resnet152) and the image representations learned by VSE, VSE++, Order, TBNN, MTFN and our MTLS. The images and their corresponding captions in Vehicle Dataset and Animal Dataset are used to train the models. Moreover, the learned image representations are fed into k-means clustering and the number of clusters are set to the number of subcategories in each dataset. Since the initial cluster centers are random among the data points, we run k-means clustering 10 times to make the result stable. Fowlkes–Mallows scores (FMS) [51] and Adjusted Mutual Information (AMI) [52] are adopted as the metrics to measure the clustering performance.

As the

Table 2. The k-means clustering result of multimodal image representations generated by different methods on Vehicle Dataset and Animal Dataset. The best results are marked in bold font.

	Vehicle Dataset			Animal Dataset
Method	FMS	AMI	INC	FMS	AMI	INC
Resnet152 [37]	52.5	45.5	31.3	63.4	58.4	10.7
VSE [12]	50.3	42.7	40.1	60.6	55.2	16.4
VSE++ [44]	52.8	45.5	31.5	61.9	56.1	14.3
Order [24]	58.7	53.5	11.6	59.3	52.7	23.1
TBNN [13]	52.8	48.0	24.7	55.2	51.0	28.0
MTFN [19]	55.1	51.4	16.4	63.3	56.5	14.3
MTLS	64.0	59.8	-	68.0	64.6	-

shows, MTLS achieves 31.3%, 40.1%, 31.5%, 11.6%, 24.7% and 16.4% improvements (INC) over ResNet152, VSE, VSE++, Order, TBNN and MTFN respectively in terms of AMI. In terms of FMS, MTLS also outperforms all comparison methods. Among all the comparison methods, Order embedding achieves better clustering performance than other comparison methods while it do not perform well in cross-modal retrieval task. Although MTFN achieves good performance on cross-modal retrieval task, it underperforms the Resnet152 image embeddings according to the clustering results. This indicates that aligning two modalities and absorbing complementary information to enhance the information in intra-modal representations at the same time is not a trivial task. However, our proposed MTLS achieves the state-of-the-art performance on both cross-modal retrieval and image clustering tasks which shows the effectiveness of the symmetrically local structure transferring. Due to the soft metric learning across image and text modalities, the complementary local structure information from the captions is transferred to images which leads to clearer cluster margins and better clustering results.

4.5. Visualization

For a better understanding of local structure transferring, we visualize the image representations in the Vehicle dataset which are generated by ResNet152, VSE, VSE++, Order, TBNN, MTFN, and MTLS. The t-SNE visualization results are demonstrated in Figure 5, and the legend of visualization is in Figure 5a.

As shown in Figure 5b, a large portion of images from different subcategories are hard to distinguish when images are represented by ResNet152 embeddings since the visual features of different type of vehicles are quite similar. The boundaries between different subcategories represented by our MTLS in Figure 5h is much clearer than that represented by other multimodal representation learning methods. These visualization results also demonstrate the reason for the good clustering performance of MTLS.

5. Conclusions and Future Work

In this paper, we propose a novel multimodal representation learning framework, MTLS, which symmetrically transfers local structure across modalities by a customized soft metric learning strategy and an iterative parameter learning process. We apply the MTLS in image-text data and evaluate it on two benchmark datasets, on which MTLS achieves state-of-the-art performance on both the cross-modal retrieval and image clustering tasks. MTLS outperforms state-of-the-art multimodal learning methods by up to 32% in terms of R@1 on text-image retrieval and 16.4% in terms of AMI on clustering. And the real case demonstration and visualization results also demonstrate the representation learning ability of MTLS.

There are several extensions of MTLS. First, MTLS can be instantiated with more complex representation encoding modules to handle other modalities besides image and text data. Second, MTLS can be extended for some specific multimodal learning tasks, such as zero-shot learning, cross-modal translation and generation. Third, MTLS has the potential to address multiple modality (more than two modalities) representation learning problems.