Exact Solution for Relativistic Trajectories Using Modal Transseries

Abstract

In this article, we design a novel method for finding the exact solution of the geodesic equation in Schwarzschild spacetime, which represents the trajectories of the particles. This is a fundamental problem in astrophysics and astrodynamics if we want to incorporate relativistic effects in high precision calculations. Here, we show that exact analytical expressions can be given, in terms of modal transseries for the spiral orbits as they approach the limit cycles given by the two circular orbits that appear for each angular momentum value. The solution is expressed in terms of transseries generated by transmonomials of the form $e^{-n\theta }$, $n=1$, 2, …, where $\theta$ is the angle measured in the orbital plane. Examples are presented that verify the effect of the solutions.

1. Introduction

General Relativity is one of the most fundamental and successful theories of physics [1]. It predicts both the large-scale expansion of the Universe [2], the behavior of small gyroscopes in orbit around the Earth [3], the so-called de Sitter and Lense–Thirring precessions, and the propagation of gravitational waves from distant black hole sources, among many other phenomena [4]. However, the field and motion equations of the theory are nonlinear, and many of these areas require the implementation of numerical methods to yield results capable of being tested by experiments and observations [5].

This is a handicap not only of General Relativity, but also of many physical theories whose equations are also nonlinear: Navier–Stokes equations in hydrodynamics [6], Yang–Mills equations in quantum field theory [7], or the Korteweg–de Vries equation for shallow waves [8], only to name a few. In mathematical finance, we have, for example, the Black–Scholes equation [9], or the Fitzhugh–Nagumo model for neurons in biology [10,11]. Therefore, it needs no further discussion to realize that nonlinear differential equations are an indispensable tool in our knowledge of the world. Numerical methods are not always reliable, especially when we are interested in the asymptotic behavior of the solutions, we are looking for very accurate predictions, or we are simply interested in the classification of the different behavior predicted by the equations or the existence and uniqueness of solutions under certain conditions. These are situations in which an analytical solution certainly has an advantage.

The interest in analytical and semi-analytical methods has increased in the last few decades with the development of the $\delta$-expansion and Adomian’s decomposition methods, as well as the homotopy method, which includes the other as particular cases [12]. The homotopy method is based on a continuous mapping of the solution to a function $\Phi (t;q)$ depending on an embedding parameter, q, ranging from zero to one in such a way that for $q=1$, we get the solution of the nonlinear problem. The nonlinear equation is then mapped into a family of equations involving a linear operator, i.e., a set of deformation equations that correspond to the original equation for $q=1$. However, the solution series involve derivatives of the auxiliary function $\Phi (t;q)$ that may become very complicated, and resorting to Padé’s approximants is usual for many problems to accelerate convergence.

In the domain of linear differential equations, a special role is played by Fourier series and Laurent series for which a general theory slowly emerged in the works of Taylor, Fourier, Cauchy, and Laurent in the XVIIIth and XIXth Centuries, and it allowed the development of an analytical approach for many equations appearing in the sciences, which now carry the name of the mathematicians that investigated them: the Bessel, Legendre, Laguerre, Hermite, or Mathieu equations [13,14].

In recent times, a generalization of the theory of Laurent series has been formalized by several authors following a work that dates back to Levi–Civita and Hahn more than a century ago and that was extended later by the model theorists Dahn and Göring [15] in connection with Tarski’s exponential function problem and by Écalle in his proof of the Dulac conjecture on plane analytic vector fields [16]. More recent reviews were given by Edgar [17] and in books by van der Hoeven [18] and Aschenbrenner et al. [19]. These authors approached the topic from the point of view of model theory, and they proved model completeness among many other results.

In this paper, we will not need all this machinery, but only a subfield of the field of transseries known as modal transseries. This can be defined as a trascendental extension of the field of reals, $\mathbb{R}\left[f\right(x\left)\right]$, where $f\left(x\right)$ is a continuous and differentiable function [20]. This structure has proven very useful in the solution of nonlinear differential equations with polynomial nonlinearities (appearing as powers of the function and/or its derivatives). These techniques are in the spirit of traditional analysis of linear differential equations, and they provide solutions in closed analytical form with a series of coefficients that can be obtained by recurrence. For example, by using the modal transseries method, we solved the SIRmodel of epidemiology [21,22], the Michaelis–Menten equation for enzyme kinetics [23], the Lorenz system in the laminar regime [24], and Einstein’s field equations for planar gravitational waves [4].

These efforts, unsystematic to the present day, show a path towards a general technique for finding analytical solutions of nonlinear differential and integral equations with polynomial nonlinearities. The adequate context for them is the real analysis of transseries, and in Appendix A, we give some formal definitions that could help in the formalization of the modal series method.

In particular, in this paper, we will discuss the orbital equation for a particle in Schwarzschild spacetime, and it will be shown that $e^{-\theta }$ is a resolvent generator (see Appendix A) for it, providing a method for an analytical discussion of spiral orbits that, up to now, have only been studied numerically [25,26].

There are techniques to tackle this classic problem. For example, Friedman and Steiner [27] used perturbation methods to analyze the precession of Mercury’s perihelion at a high order of correction. Exact solutions are also available using Jacobi’s elliptical functions [28]. However, we consider that this problem is ideal for testing the modal series method, which has also been fruitful in other areas of research since it is computationally very simple to program.

Spiral orbits are a special solution of the orbital equation in general relativity not found in Newtonian mechanics. A curious anecdote is the letter written by Isaac Newton and addressed to Robert Hooke in which a drawing of a spiral orbit followed by a projectile towards the center of the Earth appears. Later on, Hooke bitterly critiqued Newton on this subject spurred by his unbounded claiming of his priority in the discovery of Universal Gravitation.

Newton replied that the spiral has only been a “negligent stroke whit his pen”. Surprisingly, spiral orbits recuperated in the General Theory of Gravitation, which superseded Newton’s Theory of Gravity as action at a distance.

In contrast with the amplitudes of Newtonian orbits in the two-body problem, solutions for the orbits in General Relativity are often treated numerically or implicitly.

Einstein’s equations can also be solved on a computer using sophisticated numerical methods. Given sufficient computer power, such solutions can be more accurate than post-Newtonian solutions. However, such calculations are demanding because the equations must generally be solved in a four-dimensional space. Nevertheless, beginning in the late 1990s, it became possible to solve difficult problems such as the merger of two black holes, which is a very difficult version of the Kepler problem in general relativity.

This paper is organized as follows. In Section 2, we present the equation of study. Section 3 is devoted to the proposed methodology and its numerical analysis. In Section 4, scattering and bound precessing orbits are presented. In Section 5, the simulation results and applications are shown, and the last section is devoted to the discussions. Finally, some formal definitions are given in Appendix A.

2. Equation of the Orbit

In this paper, we are interested in studying the exact solutions of the nonlinear differential equation for the orbit of a test particle in Schwarzschild spacetime. For the sake of clarity, the ordinary differential equation is presented in the following form,

$$\ddot{u}\left(\theta \right)+u\left(\theta \right)=\beta +\alpha u^2\left(\theta \right),$$

(1)

where ${\displaystyle u=\frac{1}{r}}$ and r is the inverse of the radial coordinate towards the center of the large body. The derivative is with respect to the angle $\theta$, $\beta =\frac{M}{h^2}$ (h being the angular momentum, M the black hole mass in terms of distance), and $\alpha =3M$. Both M and h are normalized to have units of length; see [29]. Multiplying both sides of the equation by Schwarzschild’s radius $r_S=2GM/c^2$ and redefining $u=r_S/r$, we obtain an equation for an adimensional variable with adimensional parameters.

3. Proposed Methodology

Following a technique proposed in [21,22], we consider a series solution of the form:

$${\displaystyle u\left(\theta \right)=\sum _{n=0}^{\infty }{u}_n{e}^{-nw\theta },}$$

(2)

where w and the coefficients $u_n$ will be determined after.

Therefore, the second order derivative in (2) is then given by:

$${\displaystyle \ddot{u}\left(\theta \right)=\sum _{n=0}^{\infty }{u}_n{\left(nw\right)}^2{e}^{-nw\theta }.}$$

(3)

Now, on the other hand, the expression $u^2\left(\theta \right)$ can be rearranged as a Cauchy product, i.e., the discrete convolution of the two is:

$$\begin{array}{cc}\hfill u^2\left(\theta \right)=& {\displaystyle \sum _{k=0}^{\infty }{u}_k{e}^{-kw\theta }\sum _{j=0}^{\infty }{u}_j{e}^{-jw\theta }=\sum _{n=0}^{\infty }\left(\sum _{k=0}^n{u}_k{u}_{n-k}\right)e^{-nw\theta }.}\hfill \end{array}$$

(4)

By direct substitution of (2), (3), and (4) into Equation (1), we obtain the following expression:

$$\begin{array}{c}\hfill {\displaystyle \sum _{n=0}^{\infty }\left(u_n{\left(nw\right)}^2+u_n-\sum _{k=0}^n{u}_k{u}_{n-k}\right)e^{-nw\theta }=\beta .}\end{array}$$

(5)

In the expression (5), we impose the condition that:

$$u_0-\alpha u_0^2=\beta ,$$

(6)

and that

$${\displaystyle \sum _{n=1}^{\infty }\left(u_n{\left(nw\right)}^2+u_n-\sum _{k=0}^n{u}_k{u}_{n-k}\right)e^{-nw\theta }=0.}$$

(7)

Therefore, from (6), $u_0$ is given by:

$$u_0=\frac{1\pm \sqrt{1-4\alpha \beta }}{2\alpha }.$$

(8)

We know that $u_0$ is real if $4\alpha \beta >1$. Then, $12M^2>h^2.$ Thus, there are two possible circular orbits, for each angular momentum $h>2\sqrt{3}$ m. Now, for $h=2\sqrt{3}$ m, i.e., $4\alpha \beta =1$, we find the smallest possible circular orbit; that is,

$$u_0=\frac{1}{2\alpha },\mathrm{s}\mathrm{o} r=6M.$$

On the other hand, from (7) and using the technique proposed in [23], we have that:

$$u_n{\left(nw\right)}^2+u_n-\sum _{k=0}^n{u}_k{u}_{n-k}=0.$$

(9)

Thus, for $n=1$:

$$u_1{w}^2+u_1=2\alpha u_1{u}_0.$$

(10)

If we choose $u_1\ne 0$, then it follows that $w=\sqrt{2\alpha u_0-1}$. For the minus sign in Equation (2), we have that:

$$w={(1-4\alpha \beta )}^{\frac{1}{4}}.$$

(11)

Thus, for $n=2,3,4,\dots$, from (9), it follows that:

$${\displaystyle u_n=\frac{\alpha }{w^2}\frac{{\displaystyle \sum _{k=1}^{n-1}{u}_k{u}_{n-k}}}{n^2-1}.}$$

(12)

3.1. Analysis of Convergence

In this subsection, we analyze the convergence of series given by (2), where the coefficients $u_n$ are calculated by (12).

We put ${\mathcal{U}}_1=\left|u_1\right|$ and ${\mathcal{U}}_k=\left|u_k\right|$ for $k\ge 2$. Therefore, we obtain the following expression to (12):

$${\mathcal{U}}_k=\frac{\alpha }{w^2(k^2-1)}\sum _{j=1}^{k-1}{\mathcal{U}}_j{\mathcal{U}}_{k-j}k\ge 2.$$

(13)

Thus, one gets the recurrence relation:

For $k=2$ in (13),

$${\mathcal{U}}_2=\frac{\alpha }{w^2(2^2-1)}\sum _{j=1}^1{\mathcal{U}}_j{\mathcal{U}}_{2-j}=\frac{\alpha {\mathcal{U}}_1{\mathcal{U}}_1}{3w^2}.$$

Therefore,

$$\frac{{\mathcal{U}}_2}{{\mathcal{U}}_1}=\frac{1}{3}\frac{\alpha {\mathcal{U}}_1}{w^2}=\frac{(1+1)}{6}\frac{\alpha {\mathcal{U}}_1}{w^2}.$$

(14)

Now, for $k=3$ in (13),

$${\mathcal{U}}_3=\frac{\alpha }{w^2(3^2-1)}\sum _{j=1}^2{\mathcal{U}}_j{\mathcal{U}}_{3-j}=\frac{2\alpha {\mathcal{U}}_1{\mathcal{U}}_2}{8w^2}.$$

Thus,

$$\begin{array}{cc}\hfill \frac{{\mathcal{U}}_3}{{\mathcal{U}}_2}& {\displaystyle =\frac{\frac{2\alpha {\mathcal{U}}_1{\mathcal{U}}_2}{8w^2}}{\frac{\alpha {\mathcal{U}}_1{\mathcal{U}}_1}{3w^2}}=\frac{6{\mathcal{U}}_2}{8{\mathcal{U}}_1}=\frac{\frac{6\alpha {\mathcal{U}}_1{\mathcal{U}}_1}{3w^2}}{8{\mathcal{U}}_1}=\frac{1}{4}\frac{\alpha {\mathcal{U}}_1}{w^2}=\frac{(1+2)}{6\ast 2}\frac{\alpha {\mathcal{U}}_1}{w^2}.}\hfill \end{array}$$

(15)

We can continue, and finally, it follows that:

$$\frac{{\mathcal{U}}_{k+1}}{{\mathcal{U}}_k}=\frac{1}{6}\left(1+\frac{1}{k}\right)\frac{\alpha {\mathcal{U}}_1}{w^2}.$$

(16)

Let $C={\displaystyle \frac{\alpha {\mathcal{U}}_1}{w^2}}$, and we put Equation (16) as:

$$\begin{array}{c}\hfill {\mathcal{U}}_{k+1}={\mathcal{U}}_k\left(1+{\displaystyle \frac{1}{k}}\right){\displaystyle \frac{C}{6}},\end{array}$$

(17)

the iterating (17), we have that:

$$\begin{array}{c}\hfill {\mathcal{U}}_{k+1}={\mathcal{U}}_2\prod _{j=0}^{k-1}\left(1+{\displaystyle \frac{1}{k-j}}\right){\left({\displaystyle \frac{C}{6}}\right)}^k.\end{array}$$

(18)

Thus, using the method of mathematical induction, one gets that:

$$\begin{array}{cc}\hfill {\mathcal{U}}_{k+2}& ={\mathcal{U}}_2\prod _{j=0}^k\left(1+{\displaystyle \frac{1}{k+1-j}}\right){\left({\displaystyle \frac{C}{6}}\right)}^{k+1}={\mathcal{U}}_{k+1}\left(1+{\displaystyle \frac{1}{k+1}}\right){\displaystyle \frac{C}{6}},\hfill \end{array}$$

i.e.,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\mathcal{U}}_{k+2}}{{\mathcal{U}}_{k+1}}}=\left(1+{\displaystyle \frac{1}{k+1}}\right){\displaystyle \frac{\alpha {\mathcal{U}}_1}{w^2}}{\displaystyle \frac{1}{6}}.\end{array}$$

(19)

If we choose ${\mathcal{U}}_1=\left|u_1\right|\le \frac{3w^2}{\alpha }$, then ${\mathcal{U}}_k$ is a monotone decreasing sequence, and the series ${\displaystyle \sum _{k=1}^{\infty }}{(-1)}^k{\mathcal{U}}_k$ converges absolutely. The above analysis allows us to state the following theorem:

Theorem 1.

If ${\mathcal{U}}_1=\left|u_1\right|\le \frac{3w^2}{\alpha }$, and ${\mathcal{U}}_k=\left|u_k\right|$ for $k\ge 2$, then the series ${\displaystyle \sum _{k=1}^{\infty }}{(-1)}^k{\mathcal{U}}_k$ converges absolutely.

4. Scattering and Bound Precessing Orbits

It is clear that the series in Equation (2) corresponds to a spiral orbit. Obviously, a series of exponentials cannot describe other kinds of orbits to be found around a star or black hole [26]. However, we can look for another resolvent generator in consonance with Definition A3. Sine powers can also play this role, and consequently, we propose another family of solutions in the form:

$${\displaystyle u\left(\theta \right)=\sum _{n=0}^{\infty }{u}_n{sin}^n\left(w\theta \right).}$$

(20)

We will show that this series encompasses two different families of orbits: (i) the unbounded scattering orbits and (ii) the bounded precessing orbits.

4.1. Scattering Orbits

In this kind of orbit, the particle comes from infinity and goes to infinity. As u is the reciprocal of the distance to the mass center, we should choose $u_0=0$. For $\theta =0$ and $\theta =\pi /w$, we have then that $u\left(0\right)=u(\pi /w)=0$, and the orbit is unbounded. Another physical condition comes from the fact that the incoming and outgoing radial velocities must be finite (indeed, they should be strictly smaller than the speed of light), and so:

$${\displaystyle \underset{\theta \to 0}{lim}\dot{u}\left(\theta \right)=\underset{\theta \to 0}{lim}\frac{\dot{r}\left(\theta \right)}{r^2\left(\theta \right)}=0,}$$

(21)

because $\underset{\theta \to 0}{lim}r\left(\theta \right)=\infty$. This implies that $u_1=0$. By substitution of Equation (21) into the equation of the orbit in (1), we also find that:

$${\displaystyle u_2=\frac{\beta }{w^2},u_3=0,}$$

(22)

and the recurrence relation:

$${\displaystyle u_{n+2}=\frac{{\displaystyle u_n\left(n^2{w}^2-1\right)+\alpha \sum _{k=0}^n{u}_k{u}_{n-k}}}{(n+2)(n+1)w^2},}$$

(23)

for $n\ge 2$. In this case, the parameter w can be chosen freely, and it determines the number of loops the particle performs around the black hole before escaping again to infinity. An example of an orbit of this kind will be given in Section 5.

4.2. Bounded Precessing Orbits

By using the same series as given in Equation (21), but taking the following conditions on the coefficients: $u_2=u_3=0$, $u_1\ne 0$, we obtain a bounded orbit. This is the consequence of a nonzero $u_0$ value obtained as the solution of:

$$2u_2{w}^2=\beta +\alpha u_0^2-u_0=0.$$

(24)

The physical solution corresponding to a precessing orbit at a large distance from the black hole will be obtained by taking the minus sign in Equation (8):

$$u_0=\frac{1-\sqrt{1-4\alpha \beta }}{2\alpha },$$

(25)

The first recurrence for the coefficients with an odd index is:

$$6w^2{u}_3=u_1\left(w^2-1+2\alpha u_0\right)=0,$$

(26)

and this gives us the value of the frequency w:

$$w=\sqrt{1-2\alpha u_0}={(1-4\alpha \beta )}^{1/4}.$$

(27)

The coefficients $u_n$, $n=4$, 5, … are then found by using the general recurrence relation in Equation (23).

A special case corresponds to $\alpha =0$, i.e., to Newtonian mechanics. In this particular case, we obtain $u_0=\beta$, $\omega =1$, $u_n=0$ for $n\ge 2$, and $u_1$ is a free parameter. In celestial mechanics, we usually define $u_1=ϵ\beta$, yielding:

$$u\left(\theta \right)=\beta \left(1+ϵsin\theta \right).$$

(28)

This is the equation for a Keplerian elliptic orbit, $ϵ$ being the orbital eccentricity.

4.3. Raabe–Duhamel’s Convergence Test

In this case, the study of convergence is more complicated than for the exponential series as discussed in Section 3.1. A general expression for the series coefficients cannot be obtained, but we can check numerically that ${lim}_{n\to \infty }{u}_{n+2}/u_n=1$; consequently, we cannot prove convergence by Cauchy’s test.

Some insight is provided by the particular series given by Equation (23) with $\alpha =0$:

$${\displaystyle u_{n+2}=u_n\frac{n^2{\omega }^2-1}{(n+2)(n+1){\omega }^2}.}$$

(29)

Therefore, we have two independent series for the odd and even subscripts, and each of them can be proven to be convergent for any real value of $\omega$. Firstly, if $\sqrt{1/\omega }$ is an integer, the number of nonzero terms defined by Equation (29) is finite. For other values of $\omega$, we can write:

$${\displaystyle \underset{n\to \infty }{lim}\frac{n}{2}\left(\left|{\displaystyle \frac{u_n}{u_{n+2}}}\right|-1\right)=\frac{3}{2}>1,}$$

(30)

and we conclude that the series is convergent by Raabe–Duhamel’s test [27]. From Equation (30), we also have: $u_n/u_{n+2}=1+3/n+\mathcal{O}\left(n^{-2}\right)$. By assuming that this expression can be generalized for the general case with $\alpha \ne 0$, we can prove convergence for small values of $\alpha$.

Theorem 2.

The series defined by the recurrence relation in Equation (23) for $u_1=0$, $u_0\ne 0$ converges absolutely if $u_n/u_{n+2}=1+f\left(\alpha \right)/n+\mathcal{O}\left(n^{-2}\right)$ for $n\gg 1$, $f\left(\alpha \right)$ being a positive real value that depends on α and $\alpha |u_0{u}_2|e^{f\left(\alpha \right)/2}<4\omega$.

Proof. 

The idea is to find a bound for the Cauchy product:

$${\displaystyle {\mathcal{C}}_n=\sum _{k=0}^n{u}_k{u}_{n-k},}$$

(31)

which for n even can be written as:

$${\mathcal{C}}_n=2u_0{u}_n+2u_2{u}_{n-2}+\dots +u_{n/2}{u}_{n/2},$$

(32)

and a similar expression for n odd with $u_{(n-1)/2}\ne 0$, $u_{(n+1)/2}$ for the last term. We will assume n to be even (the proof runs in parallel for n odd). We propose the hypothesis that $u_n$ is a decreasing series, and consequently:

$$\begin{array}{cc}\hfill {\mathcal{C}}_n& =u_0{u}_n\left(1+u_2\left({\displaystyle 1+\frac{f\left(\alpha \right)}{n}}\right)+u_4\left({\displaystyle 1+\frac{f\left(\alpha \right)}{n}}\right)\left({\displaystyle 1+\frac{f\left(\alpha \right)}{n-2}}\right)+\cdots \right).\hfill \end{array}$$

(33)

By the triangular inequality, we constrain the absolute value of ${\mathcal{C}}_n$ as follows:

$$\begin{array}{ccc}\hfill |{\mathcal{C}}_n|& \le & |u_0{u}_n|\left({\displaystyle 1+\sum _{k=1}^{[n/4]}\left|u_{2k}\right|{\left({\displaystyle 1+\frac{2f\left(\alpha \right)}{n}}\right)}^k}\right)\hfill \\ \hfill & \le & |u_0{u}_n|\left[{\displaystyle \frac{n}{4}}\right]\left|u_2\right|{\left({\displaystyle 1+\frac{2f\left(\alpha \right)}{n}}\right)}^{[n/4]}+K,\hfill \end{array}$$

where K is a constant and $\left[\right]$ denotes the integer part. Now, from Equation (23), we have:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{u_n}{u_{n+2}}-1}& =& {\displaystyle \frac{3}{n}-\frac{\alpha }{n^2{\omega }^2-1}\frac{{\mathcal{C}}_n}{u_{n+2}}+\mathcal{O}\left(n^{-2}\right)}\hfill \\ \hfill & \ge & {\displaystyle \frac{3}{n}-\frac{\alpha \omega |u_0{u}_2|e^{f\left(\alpha \right)/2}}{4n}+\mathcal{O}\left(n^{-2}\right),}\hfill \end{array}$$

where we used the bound in Equation (34) and the assumption that all $u_n$, $n=0$, 1, … have the same sign. Consequently, Raabe–Duhamel’s test implies convergence for any value of $\alpha$ sufficiently small to verify:

$$\alpha e^{f\left(\alpha \right)/2}\left|u_0{u}_2\right|<4\omega .$$

(34)

This gives us a very stringent condition for convergence, and in practice, it is found numerically that values of $\alpha$ larger than those provided by Equation (34) also provide convergent solutions. ☐

5. Simulation Results and Applications

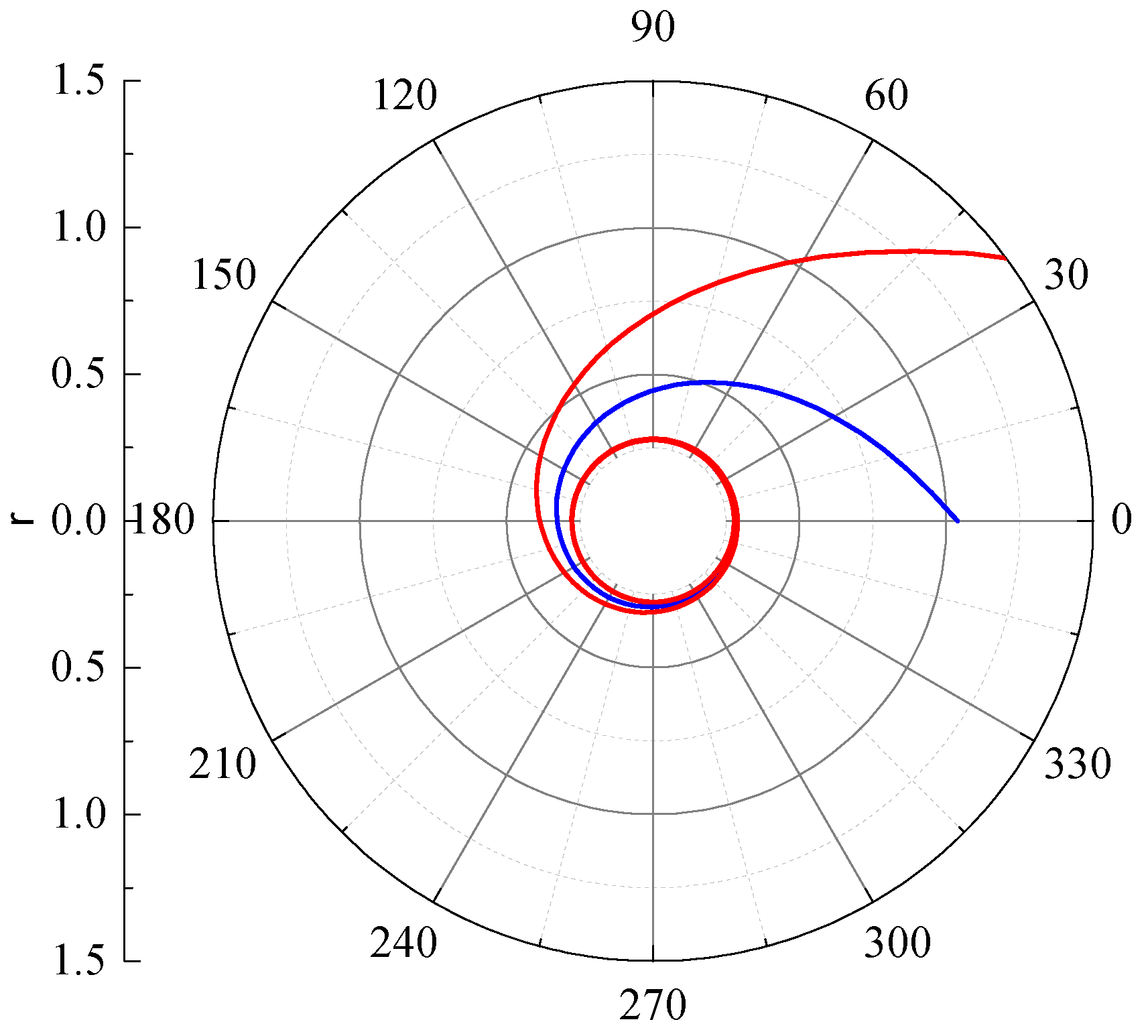
In this section, we will discuss some examples for orbits calculated with the modal series obtained in this paper. We will show that modal series have an advantage over other numerical methods for calculating high precision trajectories in the two-body problem for General Relativity. In Figure 1, we show two examples of spiral orbits calculated by summing 1000 terms in Equation (2). Both cases correspond to $\alpha =1/5$ and $\beta =1$, so the radius for the inner unstable circular orbit is given by:

$${\displaystyle r_{in}=\frac{2\alpha }{1-\sqrt{1-4\alpha \beta }}=\frac{2}{5+\sqrt{5}}\simeq 0.276393.}$$

(35)

We studied two spiral orbits by choosing different values of $u_1$ and taking $u_0=1/r_{in}$. For $u_1=-5$, the inner orbit in Figure 1 is found. This orbit starts for $\theta =0$ at a distance $r\simeq 1.03686$ from the center of the massive body. Similarly, for $u_1=-10$, the outer trajectory plotted in the polar graph starts at $r\simeq 2.98215$ for $\theta =0$ (this point is outside the plot of Figure 1). The convergence of the series in Equation (2) is very fast for both cases, and the coefficient $u_{1000}$ is of order ${10}^{-124}$ for the second case and even smaller for the first case.

This means that a very accurate calculation of the spiral orbit is possible with a relatively small number of coefficients and that precision will be limited by the accuracy of the physical parameters of the system of interest and finite arithmetic instead of the truncation of the series.

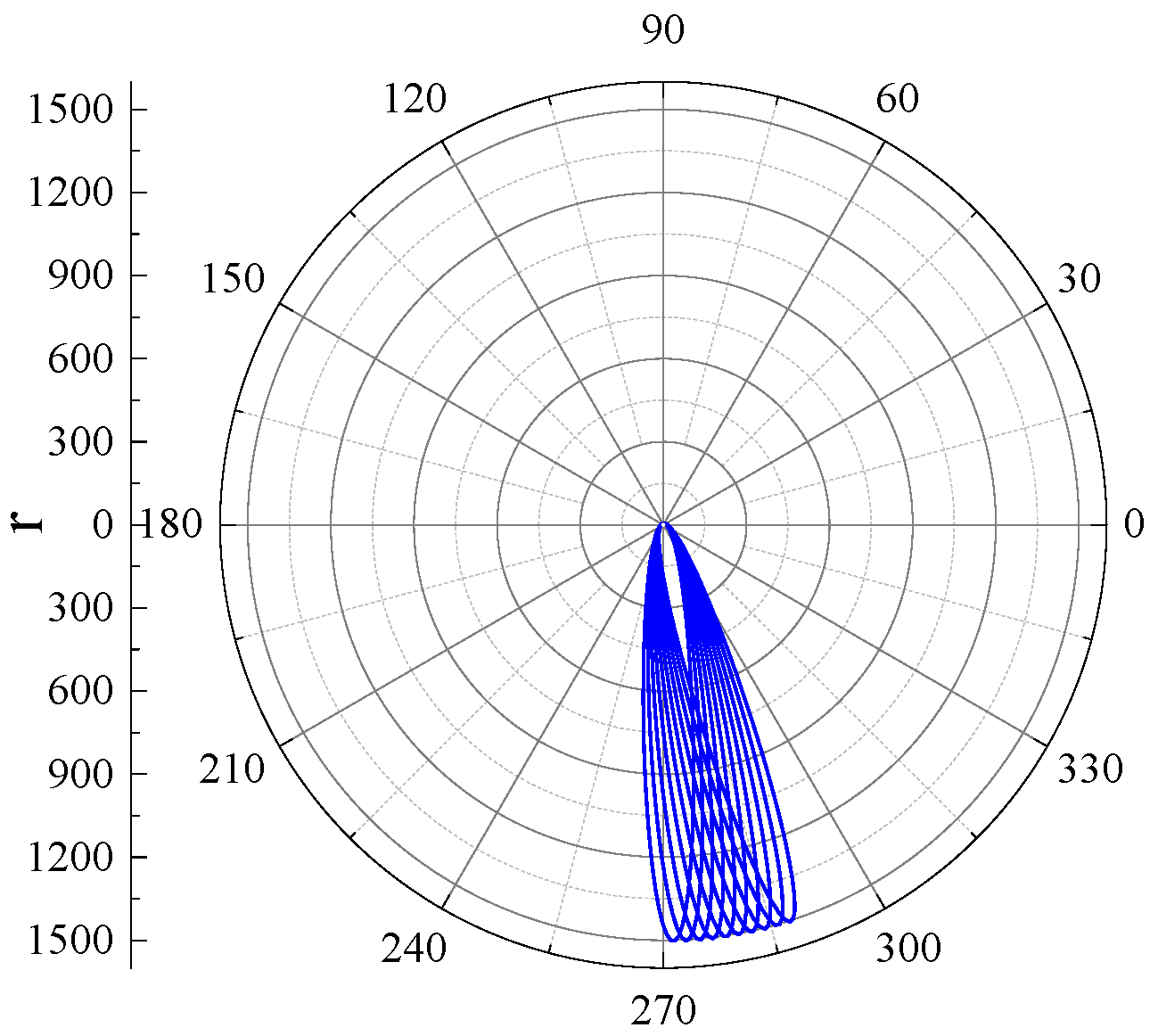
Scattering orbits were studied in Section 4.1. They correspond to a particle with sufficient energy to be unbound from the central body, so it may come from a large distance, perform a flyby with one or several loops around the main body, and escape again to infinity. In classical Newtonian physics, only hyperbolic and parabolic orbits are found, but General Relativity shows a richer casuistry.

As an example, we chose the parameters $\beta =1/100$, $\alpha =1/5$, $w=2/5$, $u_0=u_1=0$, and $u_2=\beta /\left(2w^2\right)=1/32$ as fixed by Equation (22). The resulting one-loop orbit is shown in Figure 2. The reason that the orbit exhibits a single loop is a consequence of the chosen value of w: Notice that for $\theta =0$, we have $u=0$ (see Equation (20)), and this means that the particle comes from infinity. The same value is found again for $\theta =\pi /w=5\pi /2=2\pi +\pi /2$. Therefore, the particle escapes at a right angle from the initial direction after performing a loop around the black hole.

Convergence is not so fast for scattering orbits as in the case of spiral ones because the coefficients’ ratio tends to unity for large n. We have that $u_{1000}\simeq -4.4386\times {10}^{-7}$, and double precision is not achieved with this number of terms. Anyway, uncertainty in the masses of the bodies or their distances is indeed a most important limiting factor for increasing the accuracy of astronomical observations.

Finally, we considered a bounded precessing orbit for $\alpha =0.05$, $\beta =0.1$, $u_1=0.1$, $u_0\simeq =0.100505$, and $w\simeq 0.994962$. The values of w and $u_0$ are fixed by Equations (11) and (25), respectively. Remember that $u_2=u_3=0$ in this case, and the rest of the coefficients are obtained by the recurrence relation in Equation (23). The result is a precessing elliptic orbit with an advance of the perihelion per revolution given by:

$$\delta \theta =2\pi \left({\displaystyle \frac{1}{w}-1}\right),$$

(36)

corresponding to $1.82284$ degrees in the case of Figure 3.

The anomalous advance of the perihelion of Mercury was already known by astronomers since the XIXth Century [28], and this was the first prediction of General Relativity that convinced Einstein himself of its validity.

The result obtained from approximate perturbation methods gives the well-known formula:

$${\displaystyle \delta \theta =\frac{6\pi GM}{c^{2}a(1-e^2)},}$$

(37)

where the gravitational constant, G, and the speed of light, c, have been explicitly restored and we have taken into account that $\beta =M/h^2=1/\left(a(1-e^2)\right)$ is the reciprocal of the semi-latus rectum [29]. The accepted values for the parameters in Equation (37) for Mercury’s orbit [30] are $G=6.67408\left(31\right)\times {10}^{-11}{\mathrm{m}}^3 \mathrm{k}{\mathrm{g}}^{-1}{\mathrm{s}}^{-2}$, $c=299792458 \mathrm{m} {\mathrm{s}}^{-1}$, $a=0.38709893$ AU (astronomical unit), $e=0.20563069$, and $M=1.98850\left(25\right)\times {10}^{30} \mathrm{kg}$ for the mass of the Sun and $T=0.240846$ for the period of revolution of Mercury around the Sun. The astronomical unit is a scale of distance used in the Solar system given by $\mathrm{AU}=$ 149,597,870,700 m. By using these values, we find $\delta \theta =42.98117474$ arcsec per century. However, according to Equation (37), the exact expression for the perihelion advance is:

$$\delta \theta =2\pi \left[{\left({\displaystyle 1-\frac{12GM}{c^{2}a(1-e^2)}}\right)}^{-1/4}-1\right],$$

(38)

yielding the value of $42.98118333$ arcsec per century. This corresponds to $0.00858$ milliarcseconds per century more than the prediction of the approximate formula usually given in textbooks [28].

We should notice that, by using elliptic functions, Saca obtained an improved formula for the perihelion advance, which leads to similar results to ours [31], but his approach is more cumbersome.

6. Conclusions

Nonlinear differential equations have been known and used for a long time. Perhaps the canonical example is that of the three-body problem in celestial mechanics necessary to explain the motion of the Moon under the mutual influence of the Earth and the Sun. With this idea in mind, Euler developed his famous numerical method widely used since [32]. The difficulties in solving these equations have promoted the preponderance of numerical methods throughout the history of the subject. Particular analytical solutions have been found for some problems, but they are restricted to special cases or convergence is very slow. In the case of the three-body and N-body problems, the series solutions by Sundman [33] and Wang [34] provide almost a complete analytical treatment of these problems, but their practical application is very limited because we will need to add millions of terms to obtain predictions even for short periods of time. These series are given in powers of $t^{2/3}$, and they are an example of transseries.

However, solutions in terms of transseries can be useful in many problems of interest for physics or engineering, and moreover, they can be studied systematically. In this paper, we provided such solutions for the orbits in a Schwarzschild spacetime. These solutions are found in terms of powers of exponential or sine functions showing that different functions can be used as a basis to solve the same problem depending on the initial conditions. The existence of a resolvent generator as defined in (A2) gives the chance to find a modal transseries solution, but we have shown that several series can be found for the same equation and can describe different classes of trajectories. Another advantage of transseries over traditional numerical or approximate methods is the calculation of an exact expression for the advance of the perihelion in bounded trajectories as given in Equation (38). This expression is usually approximated by Equation (37), but this yields the wrong predictions for very massive objects such as neutron star binaries or black holes.

Apart from the problems discussed at the Introduction, we also successfully applied the modal transseries method to another problem in General Relativity: gravitational waves [4], for which explicit solutions corresponding to plane waves are given. This proves the fecundity of the transseries approach to nonlinear differential equations.

We hope that these works stimulate the research in modal transseries solutions for nonlinear differential equations of interest in physics, chemistry, or engineering by providing an alternative to traditional numerical methods in finite differences, which can be used to back the numerical computations or to provide accurate results and a deeper analytical understanding of the solutions and behavior of these systems.