Abstract
The selection of sustainable supplier is an extremely important for sustainable supply chain management (SSCM). The assessment process of sustainable supplier selection is a complicated task for decision experts due to involvement of several qualitative and quantitative criteria. As the uncertainty is commonly occurred in sustainable supplier selection problem and hesitant fuzzy set (HFS), an improvement of Fuzzy Set (FS), has been proved as one of the efficient and superior ways to express the uncertain information arisen in practical problems. The present study proposes a novel framework based on COPRAS (Complex Proportional Assessment) method and SWARA (Step-wise Weight Assessment Ratio Analysis) approach to evaluate and select the desirable sustainable supplier within the HFSs context. In the proposed method, an extended SWARA method is employed for determining the criteria weights based on experts’ preferences. Next, to illustrate the efficiency and practicability of the proposed methodology, an empirical case study of sustainable supplier selection problem is taken under Hesitant Fuzzy (HF) environment. Further, sensitivity analysis is performed to check the stability of the presented methodology. At last, a comparison with existing methods is conducted to verify the strength of the obtained result. The final outcomes confirm that the developed framework is more consistent and powerful than other existing approaches.
1. Introduction
With the increasing public concern over the environment and strict government policies, lean and green thinking has emerged as an attractive scheme to increase the profitability for businesses and to improve the environmental protection [1,2]. Sustainable Supply Chain Management (SSCM) is a broader idea which aims to enhance the company’s social, economic, and environmental objectives and eliminate the waste of resources [3,4,5]. Nowadays, several companies have distinguished the need to execute sustainable development goals [6,7,8]. In order to meet the sustainability policies, the selection of most Sustainable Supplier (SS) is one of the important and critical decisions for companies [9,10]. In the recent past, numerous articles have been presented to evaluate the SS options and also tried to help organizations for improving their sustainable performances [11,12].
Sustainable supplier selection (SSS) is a significant operational activity of SSCM. The performance of suppliers not only influences the producers’ performance but also influences the performance of downstream enterprises [13]. Therefore, SSS is a key factor for enterprises seeking to achieve sustainable development. Compared with the traditional supplier selection process, SSS should not only consider a supplier’s economic performance, such as product quality, price, transportation, after-sales service, and production management, but also consider their environmental protection, energy-saving performance and social responsibility [1].
In recent times, hesitant fuzzy set (HFS) [14,15] is an effective means to model the uncertain information arisen in practical complicated Multi-Criteria Decision Making (MCDM) problems. Consequently, numerous theories and methodologies have been developed under the HFSs environment. Due to its unique advantages, the present study focuses on the context of HFSs. In this study, a new integrated MCDM framework is developed to handle the SSS process in which the preference information is given in the form of Hesitant Fuzzy Number (HFN). In the literature, there are numerous articles which are employed the HFSs in many application areas, though some of them have utilized the HFS based methodologies in the SSS process. Nonetheless, there has been no work regarding the developed framework in the context of choosing an ideal SS option.
The evaluation and selection of desirable SS option often involves several qualitative and quantitative criteria; therefore, this process can be considered as MCDM problem. In the MCDM process, the computation of attribute weights and the determination of preference ordering of the options are significant concerns for the experts. In the available studies, two kinds of criterion weights are discussed, which are objective and subjective weights [16]. The objective weights are evaluated from the decision-matrices and are obtained based on the information given by the decision experts (DEs) [17]. While the subjective criteria weights inform the subjective opinions of DEs regarding the relative significance of criteria [18]. In 2010, Kersuliene et al. [19] initiated an innovative approach for evaluating the subjective criteria weights and named as SWARA (Step-wise Weight Assessment Ratio Analysis). In the SWARA method, the relative significance and the initial prioritization of the options for each criterion are decided by the opinion of the DEs and then, the relative weight of each criterion is estimated. As compared to the Analytic Hierarchy Process (AHP), the SWARA approach does not require a pairwise comparison and has a higher degree of consistency, less computational complexity, and easy procedures [20].
Moreover, the Complex Proportional Assessment (COPRAS) [21] approach is one of the realistic and well-organized approaches to rank the options in MCDM problems. The COPRAS approach has some advantages, which as (i) it is a flexible and valuable tool to tackle the practical MCDM problems. (ii) It assumes both the characteristics, that is, cost and benefit types of criteria. (iii) In addition, it depicts the ratio to the worst and the best results concurrently [22]. Several authors have extended the COPRAS approach in different uncertain environments. Recently, Mishra et al. [23] studied a Shapley function based COPRAS methodology for evaluating service quality of vehicle insurance companies under the HFSs environment. However, if the numbers of criteria are large, then the Shapley function based COPRAS method has a difficult computational procedure. Therefore, there is a need to modify the COPRAS method for solving the MCDM problems with a large number of criteria.
Moreover, these two approaches, that is, SWARA and COPRAS, have their own benefits in the determination of subjective weights of the criteria and preference ordering of the options, respectively. Although, few past studies have used the combined SWARA-COPRAS methodology in different domains, but no one has proposed an integrated method by combining SWARA and COPRAS approaches within the HFSs environment. To the best of our knowledge, this study firstly develops an integrated hesitant fuzzy-SWARA-COPRAS (HF-SWARA-COPRAS) methodology for the evaluation and selection of SS options from a sustainability perspective. This method can be employed to several decision-making problems such as COVID-19 medication selection, medical waste treatment technology selection, third-party reverse logistics providers and so forth. The innovations of this research are given as
- ▪
- A novel HF-SWARA-COPRAS method is introduced.
- ▪
- The criteria weights are evaluated by the SWARA method.
- ▪
- To illustrate the feasibility and usefulness of the HF-SWARA-COPRAS method, an empirical case study of SSS problem is discussed under HFSs environment.
- ▪
- Sensitivity analysis and comparative study are discussed to confirm the stability and validity of the developed methodology.
The remaining study is prepared in the following way—Section 2 describes the literature reviews of related works. Section 3 presents the basic concepts of HFSs and proposes a new HF-SWARA-COPRAS approach. Section 4 presents an application related to SSS problem that reveals the feasibility and usefulness of the HF-SWARA-COPRAS approach. In addition, sensitivity and comparative analyses are discussed in this section. At last, Section 5 discusses the conclusion and recommendation for further study.
2. Literature Review
This section presents the literature of the present study.
2.1. Hesitant Fuzzy Sets
Hesitant fuzzy set (HFS), originated by Torra [14] and Torra & Narukawa [15], is recognized as one of the flexible and eminent tools to tackle the vagueness occurred in people’s life. It is characterized by a membership function and represented by a set of possible values. Existing studies on HFSs concluded that the HFSs have a strong association with the Fuzzy Sets (FSs) [24] and their extensions viz. Type-2 Fuzzy Sets (T2FSs) [25], Fuzzy Multi-Sets (FMSs) [26], Intuitionistic Fuzzy Sets (IFSs) [27]. In addition, Torra [14] presented the envelope of HFS, which can convert HFSs into IFSs. As an extension of FS, numerous studies have been utilized the notion of HFS to portray the uncertain information. Xia and Xu [28] studied some aggregation operators for HFSs and also conferred the correlations among them. Then, Xu and Xia [29] proposed entropy, cross-entropy, and similarity measures under the HFSs environment. Liao et al. [30] initiated the new correlation measures for HFSs. He et al. [31] suggested the Hesitant Fuzzy (HF) power Bonferroni mean operators with their desirable properties. Qin et al. [32] recommended a variety of HF-aggregation operators based on Frank t-norms. Liao and Xu [33] presented a satisfaction degree-based innovative technique and applied to solve MCDM problems under the HFS environment. Peng et al. [34] studied two MCDM problems-based on prospect doctrine for HFSs. Zhao et al. [35] recommended two categories of MCDM methods with HF-information based on minimum discriminations between objective and subjective preferences. Faizi et al. [36] extended the Characteristic Objects Method (COMET) method within the HFSs environment. In addition, they discussed the theoretical foundations and principles of the proposed method. Mishra et al. [23] proposed a Shapley function-based HF-COPRAS approach for handling the correlative MCDM problems for HFSs. Xu and Zhang [37] presented an outline of implementations of group decision making from three different aspects for HFSs. Mishra et al. [38] suggested an integrated HF-Weighted Aggregated Sum Product Assessment (WASPAS) method to choose an ideal green supplier for HFSs. Recently, several other studies have been presented under the HFSs context [39,40,41].
2.2. Step-Wise Weight Assessment Ratio Analysis (SWARA)
Kersuliene et al. [19] studied a novel SWARA method for the computation of subjective criteria weights in the process of MCDM. The SWARA method has lesser mathematical difficulty as compared to AHP. Just a while ago, this approach has extensively been employed in several real-life decision-making problems. Dehnavi et al. [42] studied a hybrid technique by combining the Geographic Information System (GIS), Adaptive Network-Based Fuzzy Inference System (ANFIS) and SWARA methods and applied to assess the landslide susceptible regions. Karabasevic et al. [43] designed a new Additive Ratio ASsessment (ARAS) and SWARA based model for personnel selection problem within FS context. Nakhaei et al. [44] established a hybrid methodology by utilizing the Simple Multi-Attribute Ranking Technique (SMART) and SWARA approaches to assess the vulnerability of buildings against explosion. Shukla et al. [45] introduced a hybrid technique by employing SWARA and Preference Ranking Organization Method For Enrichment Evaluation (PROMETHEE) approaches and then utilized for the evaluation of an Enterprise Resource Planning (ERP) system. Isık and Adalı [46] designed a methodology by using Operational Competitiveness Rating Analysis (OCRA) and SWARA methods and then utilized to assess and rank the hotels. Mavi et al. [47] developed a fuzzy SWARA-Multi-Objective Optimization Method by Ratio Analysis (MOORA) approach for the evaluation of MCDM problems. Panahi et al. [48] recommended a combined SWARA and GIS-based approach for the determination of copper prospects. Stanujkic et al. [49] introduced a new framework by combining ARAS and SWARA approaches. Their findings proved the flexibility and effectiveness of the developed approach. Karabaševic et al. [50] designed a methodology based on the combination of Delphi and adapted SWARA techniques. Urosevic et al. [51] designed SWARA and WASPAS based approach for the selection of personnel in the tourism business. Jamali et al. [52] discussed the SWARA, SWOT (Strengths, Weaknesses, Opportunities, Threats) and Strategic Position and Action Evaluation (SPACE) methods and then analyzed the Lean, Agile, Resilient, and Green (LARG) supply chain management competitive strategies in Iranian cement companies. Juodagalviene et al. [53] recommended a combined methodology based on Evaluation Based on Distance from Average Solution (EDAS) and SWARA approaches for evaluating the house’s plan shape. Tayyar and Durmu [54] presented a comparative study of range variability between the criteria for Max100, SWARA, and Pairwise Comparison. Ghorabaee et al. [55] developed an integrated method by employing SWARA, CRiteria Importance Through Intercriteria Correlation (CRITIC), and EDAS approaches to assess the construction equipment from sustainable perspectives. Dahooie et al. [56] designed a model based on SWARA and grey ARAS approaches for selecting a suitable information technology expert. Rani et al. [57] designed a hybrid methodology by combining SWARA and VIKOR (VlseKriterijumska Optimizcija I Kaompromisno Resenje in Serbian) methods to evaluate and choose ideal solar panel within Pythagorean Fuzzy Sets (PFSs) context. Rani and Mishra [58] proposed a single-valued neutrosophic fuzzy MCDM framework based on SWARA and VIKOR methods. Mishra et al. [59] introduced a combined methodology based on SWARA, and COPRAS approaches for assessing bioenergy production processes. However, no one has combined the SWARA and COPRAS methods within the HFSs context.
2.3. Complex Proportional Assessment (COPRAS) Approach
The goal of the MCDM method is to obtain the most desirable alternative among a set of options over a set of multiple quantitative and qualitative criteria. Based on compromise programming, Zavadskas et al. [21] originated the idea of the COPRAS approach. This method provides an efficient and reasonable evaluation process that tries to rank the options portrayed in terms of both aspects, that is, benefit and cost types of criteria. In the recent past, various extensions of the COPRAS approach have been introduced under diverse uncertain environments. For example, Yazdani et al. [60] pioneered the fuzzy COPRAS method for evaluating risk analysis of critical infrastructures. Fouladgar et al. [61] studied a fuzzy model by employing COPRAS and AHP methods. Antucheviciene et al. [62] proposed the COPRAS-F framework to evaluate the building’s redevelopment. Das et al. [63] suggested a fuzzy model based on the combination of COPRAS and AHP methods for assessing the performance of the Indian Institute of Technology. Tavana et al. [64] recommended the COPRAS based methodology for choosing the optimal social media platform. Aghdaie et al. [65] studied an innovative integrated framework by employing fuzzy AHP and COPRAS-G for evaluating the market segments. Hajiagha et al. [66] firstly developed an interval-valued intuitionistic fuzzy (IVIF) based COPRAS technique. Ghorabaee et al. [67] studied the IT2F-COPRAS model to select and evaluate the suppliers. Zavadskas et al. [68] introduced IVIF-MULTIMOORA (Multi-Objective Optimization on the basis of Ratio Analysis Plus Full Multiplicative Form) for MCDM problems and then compared their results with the COPRAS method. Akhavan et al. [69] designed an integrated COPRAS based model for evaluating suitable strategic alliance partners. Bekar et al. [70] developed a hybrid model based on grey relations, COPRAS and FS theory for evaluating the performance measures. Garg [71] designed the COPRAS based framework to evaluate the desirable e-learning website. Wang et al. [72] implemented a soft set based COPRAS technique to estimate the risk model for failure mode and effect analysis. Mahdiraji et al. [73] identified, ordered, and assessed the ecological sustainability factors of sustainable architecture through triangular fuzzy COPRAS and Best Worst Method (BWM) approaches. Kurtulmuşoğlu et al. [74] ranked the service feature critical to evaluate the airline industry by employing the fuzzy COPRAS method. Barak and Dahooei [75] suggested a hybrid fuzzy method by combining COPRAS and Data Envelopment Analysis (DEA) techniques and applied to assess the airlines. Mishra et al. [23] evaluated and ranked the service quality options based on the HF-Shapley COPRAS method. Krishankumar et al. [76] presented a new extension to COPRAS under a double hierarchy context for selecting an apt green supplier for a dairy company. Garg and Nancy [77] developed Possibility Linguistic Single-Valued Neutrosophic Set (PLSVNS)-COPRAS for IT outsourcing selection. Hajek and Froelich [78] pioneered IVIF- Cognitive Maps (CM)- Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) model by integrating TOPSIS and IVIF-cognitive maps and utilized to find the ideal supplier. Sivagami et al. [79] studied a modified COPRAS method under Probabilistic Linguistic Term Sets (PLTSs) environment and applied to evaluate cloud vendor prioritization. Mishra et al. [80] suggested an integrated IVIF-COPRAS framework for evaluating the hazardous waste recycling facility options. Kumari and Mishra [81] studied the intuitionistic fuzzy-based COPRAS model for evaluating and selecting an ideal green supplier. Rani et al. [22] proposed the Pythagorean fuzzy (PF)-COPRAS method to assess and choose desirable pharmacological therapy for type 2 diabetes patients. However, there is no work regarding the combined SWARA-COPRAS method under the HFSs environment.
2.4. Sustainable Supplier Selection (SSS)
In SSCM, the evaluation and selection of an ideal supplier is one of the most significant processes for enterprises. Various qualitative and quantitative criteria are involved in the assessment of SSS; consequently, the assessment of the SSS process can be regarded as an MCDM problem. Recently, numerous researches have been performed in the context of SSS problem. For instance, Kannan et al. [82] designed TOPSIS framework to choose the ideal supplier for an electronics enterprise. Ghorabaee et al. [67] evaluated the best material supplier by using COPRAS method. You et al. [83] studied the multi-criteria assessment of SSs based on IT2L-VIKOR technique. Quan et al. [3] designed a hybrid method for the assessment of SSS problem. Further, Xu et al. [84] evaluated the green supplier selection problem by employing an extended Multi-Attributive Border Approximation area Comparison (MABAC) approach. Meksavang et al. [4] suggested a modified VIKOR technique to assess the SSS problem under Picture Fuzzy Sets (PFSs) context. Liu et al. [85] studied a combined BWM-Advanced Quantitative Methods (AQM) methodology for the selection of an ideal green supplier. Liu et al. [86] recommended a hybrid technique to evaluate bike-share suppliers. Later, Lu et al. [87] designed a hybrid methodology to choose the appropriate SS in a straw biomass power plant context. Memari et al. [88] suggested the Intuitionistic Fuzzy-TOPSIS (IF-TOPSIS) framework for the evaluation of the SSS problem. Mishra et al. [38] designed a combined structure with the combination of information measures and the WASPAS method under the HFSs context and then applied to evaluate the green supplier selection problem. Stevic et al. [2] recommended a Measurement Alternatives and Ranking according to the COmpromise Solution (MARCOS) method to select the optimum SS in the healthcare industry. Peng et al. [89] suggested a hybrid technique by integrating picture fuzzy exponential entropy measure and the VIKOR approach and utilized to handle the SSS problem. You et al. [90] studied a new SSS and order allocation (SSS & OA) model to evaluate and choose the ideal SS and determine the optimal order sizes among them.
On the basis of the above studies, we can see that the theory of HFS, which allows the membership to have a set of possible values, is one of the remarkable and valuable tools to handle the real-life applications with anonymity. In view of that, numerous existing studies have focused their concentration on the development of HFS theory and its applications from different points of view. Consequently, the proposed work focuses on the HFSs environment. In recent times, the evaluation and selection of SS options consist of several qualitative and quantitative criteria; therefore, there is a need to develop a suitable tool to handle the SSS problem with uncertainty from sustainable perspectives. To tackle this issue, in this study, we have proposed a hybrid HF-SWARA-COPRAS method that can effectively handle the inherent uncertainty and the hesitancy in DE’s opinions. In this method, the subjective weights decided by the SWARA method are more reasonable for the decision-making process. And, the COPRAS approach provides a simple computation procedure with precise and effective outcomes for SSS problem with HF information.
3. Proposed Methodology
This section discusses preliminaries and proposed framework under HFSs for the SSS problem.
3.1. Prerequisites
Here, we confer various outlets of HFSs and information measures.
Definition 1
[14,15]. Given a discourse set Y. A HFS R on Y is defined by the function implemented to Y, which maps a finite subset of is denoted by
wherein denotes a set of various values in illustrating the feasible membership degrees of an object to R. For ease of simplicity, is defined as a hesitant fuzzy element (HFE) satisfying
Definition 2
[14,28]. Assume that then the fundamental laws on HFEs are discussed as below:
Definition 3.
In HFS, the score function of the elementis presented by:
Here, denotes the number of objects inFor any HFEsandifthenifthen.
In various cases, the above-discussed comparison law does not hold good. To handle this concern, Liao et al. [39] initiated a concept of variance to compare the HFEs. For an HFEthe variance function of the elementis given by
On the basis ofandthe following systematic procedures are derived:
Definition 4
[28,39]. Consider a set of HFEs then the Hesitant Fuzzy Weighted Average (HFWA) and geometric (HFWG) operators are mappings such that
Definition 5.
Letthen, an entropy measure defined by Mishra et al. [23], is given as
3.2. Hesitant Fuzzy SWARA-COPRAS Method
This section develops a novel decision-making framework, named as HF-SWARA-COPRAS method, to solve the MCDM problems under the HFSs environment. This method develops based on the SWARA approach and COPRAS method with HFSs. The computation process of the proposed method is discussed as in the following steps:
Step I: Originate the option and criteria.
A group of DEs determines the sets of ‘m’ alternatives and ‘n’ criteria respectively. Assume that be the hesitant fuzzy decision matrix presented by kth DE, wherein means the assessment of an option concerning a criterion in terms of HFNs for kth DE.
Step II: Compute the crisp DEs’ weights.
The formula for the determination of kth DE’s weight is as follows:
Clearly, and .
Step III: Calculate the aggregated hesitant fuzzy decision (AHF-D) matrix.
In the process of MCDM, aggregation of individual decision matrices is an important concern. To aggregate the matrices, the HFWA operator is applied and then be the required AHF-D matrix in which
Step IV: Determine the criteria weights by the SWARA method.
Ranking the criteria is the first step of the SWARA method and compares pairwise direct highest to lowest-ranking criterion. Subsequently, a relative coefficient should be calculated. Next, the weight which is required for dealing with MCDM problems should be evaluated. In the following, the steps of the criteria weight’s evaluation using SWARA are presented:
Step IV-A: Compute the score values. Score values of HFNs are calculated based on Equation (2).
Step IV-B: Sorting criteria based on DE’s opinions. According to DE’s choice, the most significant criterion is ranked first, and less significant are in the next ranks.
Step IV-C: Estimate the degree of comparative significance (sj). The relative significance of each criterion is estimated in relation to preceding criteria.
Step IV-D: Calculate the comparative coefficient (kj) by using
Step IV-E: Compute the recalculated weight (pj) by using
Step IV-F: Determine the final weight of each criterion with the use of the following formula:
Step V: Add the values of criteria for benefit and cost.
In the developed framework, each option is described with its addition of maximizing benefit type criteria and minimizing cost type criteria . In these conditions, the procedures for the computation of and are given as
Assume that be the beneficial type of criteria. Now, the maximum index value in terms of HFNs for each option is presented as
Assume that be the non-beneficial type of criteria. Next, the minimum index value in terms of HFNs for each option is presented as
Here, ‘l’ defines the number of beneficial type criteria, and ‘n’ defines the total number of criteria.
Step VI: Estimate the relative weight.
The formula for the computation of the relative weight of each option is
Equation (14) can also be demonstrated as below:
Here, and denote the score degrees of and respectively. In addition, the parameter indicates the strategy value of the DE in a unit interval. The physical analysis of strategic value is that when the DE presents pessimistic nature and therefore, high value is associated with weight to the non-beneficial type criteria. Alternatively, when the DE shows optimistic nature and so, high value is associated as the weight to the beneficial type criteria. Also, when the DE shows neutral behavior and then the same importance degree is associated with both beneficial and non-beneficial type criteria.
Step VII: Compute the priority order.
The priority order of options is exemplified as
The option with maximum relative weight is ranked first, and hence, it is an ideal choice.
Step VIII: Determine the degree of utility.
The degree of utility is calculated with the use of formula
Step IX: End.
4. An Empirical Study: Sustainable Supplier Selection (SSS)
In this section, an empirical case study of SSS for a trading firm ABC in India is considered to express the usefulness and practicability of the developed HF-SWARA-COPRAS technique. In the process of the present methodology, the company formed a team in which there are three DEs who are responsible for SSS. The team comprises a strategic sourcing manager (B1), a production manager (B2), and a quality control manager (B3). This team initiates its work with the expectation and description of the assessment criteria. In accordance with the previous operation reviews, the five main suppliers (G1, G2, G3, G4, and G5) options are preferred with respect to the various criteria after an initial screening. As the selected supplier options and criteria have different advantages in communal performance, given in Table 1. For this reason, the most favorable supplier cannot be chosen and needs validating during an adequate and logical inspection. Next, the procedure for the execution of the developed HF-SWARA-COPRAS approach is discussed as follows:

Table 1.
Details of the criteria for sustainable supplier selection (SSS) problem.
Table 2 and Table 3 present the Linguistic Values (LVs) and their corresponding HFNs for the rating of the relative importance of criteria and options in terms of the SSS problem, respectively. Due to a lack of information, time limitation, and qualitative nature of preferred criteria, it is effortless for the DEs to express their judgments based on LVs [38].

Table 2.
Ratings for the significance of criteria and DEs (decision experts).

Table 3.
Linguistic variables for the importance of criteria and options.
Let us consider the weights of DEs in the forms of LVs and are given as {H, VH, M}. Therefore, by using Table 2, Equations (6), and (7), the crisp weights of DEs are obtained as {0.3432, 0.3486, 0.3082}. The HF-decision opinions expressed by the DEs are given in Table 4.

Table 4.
Hesitant fuzzy information was given by DEs for SSS.
The judgment provided by three DEs has been aggregated utilizing Equation (8) and Table 4 and then creates the AHF-D matrix taking into effect the importance of individual DE and are provided in Table 5.

Table 5.
Aggregated hesitant fuzzy decision (AHF-D) matrix for SSS problem.
For the SWARA procedure, the opinions of the experts are a significant part of the assessment of criteria weights. The DE gives the preferences of every criterion on the basis of their information and practices (see Table 6). In Table 7, the criterion with the highest significance degree is ranked first, and less significant criteria are at the next levels. Now, with the use of Equations (9)–(11) and Table 7, the final criteria weights are as follows:

Table 6.
Linguistic values for criteria performances of SSS.

Table 7.
Results obtained by SWARA (Step-wise Weight Assessment Ratio Analysis) method for SSS.
Using Equations (12)–(17), the calculated values of and of the options concerning the criteria are given in Table 8.

Table 8.
The obtained outcomes by the HF-SWARA-COPRAS framework.
Based on Table 8, the preference ordering of the supplier options is and thus, is the best SS choice.
4.1. Sensitivity Analysis
In the present study, we discuss a sensitivity investigation according to the different values of the parameter . To do this, various values of are taken for investigation, and the varying values of can aid us to assess the sensitivity of the COPRAS approach. The ranking orders of the options with respect to diverse parameter values are depicted in Table 9 and Figure 1. We can see that in all the sets given in Table 9, the option G3 has the highest rank, when to 0.2, while G2 has the highest rank when to 1.0. Further, the option G5 has the worst rank when to 0.7, whereas G1 has the worst rank when to 1.0. Accordingly, it can be noticed that the HF-SWARA-COPRAS approach has better stability for the diverse values of the parameter . Furthermore, the subjective weights evaluated by the SWARA technique preserve to enhance the sensitivity of the proposed framework. As per the above discussion, we realize that the use of different values of parameter will increase the stability of the introduced framework.

Table 9.
Diverse values of compromise solution w. r. t. .
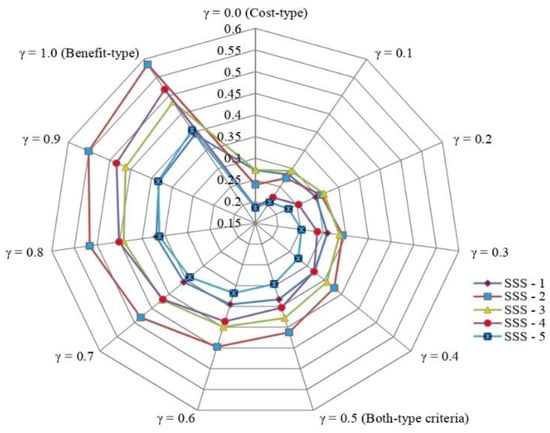
Figure 1.
Representation of utility degree of SSS option over different parameter γ value.
4.2. Comparison with Existing Methods
Here, a comparative analysis is discussed to validate the robustness of the developed HF-SWARA-COPRAS method. For this, a comparison is made between the developed approach and some existing methods given by Liu et al. [85] and You et al. [90]. From BWM and AQM [85], the final ranking order of the supplier options is and the most suitable SS option is SSS-2 (G2). On the similar line, from SSS &OA [90] method, the final preference order of the SS option is and hence, the most suitable SS option is SSS-2 (G2). Hence, we observe that the optimal SS option, that is, SSS-2(G2) is same with all the proposed and existing approaches, while the preference order outcomes slightly vary with different methods.
It is clear from Figure 2 that the proposed approach is more consistent with the existing approaches. To compare the proposed method, we consider the approaches viz., Liu et al. [85] and You et al. [90]. The Spearman correlation values of proposed method (HF-SWARA-COPRAS, γ = 0.5), BWM-AQM, SSS & OA model, HF-SWARA-COPRAS (Cost-type, γ = 0.0) measure and HF-SWARA-COPRAS (Benefit-type, γ = 1.0) measure with HF-SWARA-COPRAS (γ = 0.5) measure solution are given by (1.00, 0.70, 0.70, 0.80, 0.50).
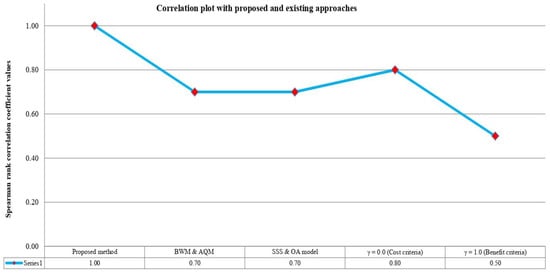
Figure 2.
Correlation plot of various measures of the proposed approach with existing approaches.
As compared to the above-discussed methods, the HF-SWARA-COPRAS method is more robust and thus has wider applicability. The key benefits of HF-SWARA-COPRAS method are the following:
- The HFS can reflect the DE’s hesitancy more objectively than other classical extensions of FS. Therefore, the use of the developed HF-SWARA-COPRAS approach gives a more flexible way to express the uncertainty in the selection of SS.
- The SWARA method is employed to evaluate the criteria weights in the evaluation of the SSS process, which makes the introduced HF-SWARA-COPRAS method more reliable, efficient and sensible tool.
- The proposed HF-SWARA-COPRAS can process the information in a more useful and suitable way and from different perspectives, such as benefit-type and cost-type criteria.
4.3. Discussion and Implications
Notwithstanding the growing volume of studies on SSS in the latest years, but still need slight research work on supplier sustainability in trade organizations. Consistently, the process of assessing and select SSs is inadequate and needs enlightening. Therefore, this study gives a theoretic supplement for SSS. Afterward, broad studies and discussions with different experts in the organization, according to the TBL and stakeholder doctrines, a procedure comprising economic, environmental, and social factors have been developed. Later on, we assume 8 major criteria from the economic, environmental, and social aspects. Predominantly, we need SSs to offer evidence of their social accountability satisfaction to internal and external participants. Out of these 8 criteria, Health and safety (F8) achieves the highest weight (0.1429) and industry reputation (f7) (0.1359) is attained in second rank, followed by pollution (f6) (0.1312), cost (f2) (0.1264), quality (f1) (0.1204), eco-design (f4) (0.1203), sustainable materials (f5) (0.1130) and production capacity (f3) (0.1099). This weight assessment is instinctively formulated, as we applied to consider that the economic aspect should be the leading factor, even amongst SSs. Several DEs in the case rely on the sustainability of SSSs should initially be revealed in their corporate ethics [95]. Though, criteria containing cost, quality, production capacity, and eco-design are usually supposed to be leading significances in the conventional SSs [11]. It is significant to remark that health and safety, as transparent and assessable indicators of social duty, are observed as the significant factors within eight considered criteria [96]. Nonetheless, the procedure that we have developed for SSS, cannot be static to be more applicable and robust and essential to be dynamic adjusted based on the variations in the real-life circumstances and demand of business organizations.
With the implementation of the HF-SWARA COPRAS approach, the SWARA model is utilized for determining the criteria weights, which lessens the calculation procedure essential to achieve the outcomes [57,58,59]. The COPRAS approach is implemented to obtain the optimal SSs and explore gaps in the preferred level of sustainable presentation for each supplier. By showing the sensitivity analysis, G2 (0.412) is the optimal SS in most cases, which spectacles the strength of the introduced framework. Further, to validate the applicability of the introduced framework, we implement the BWM-AQM model, SSS & OA model to compute a SS option-based on the above-mentioned problem. Afterward, we obtained a similar outcome by existing models, although the robustness of the BWM-AQM model, SSS & OA model were weaker than the proposed method. In contrast, the HF-SWARA-COPRAS framework displayed higher robustness when the criteria weights shifted, which facilitated the DEs to offer decision-making orientations to a certain amount. This outcome delivers accurate indication for the comparison of Liu et al. [85] and You et al. [90].
5. Conclusions
Due to the growing economy, urbanization, competition among enterprises intensifying and increasing concern about social responsibility, the selection of SS is an important decision in sustainable development. This study presents a novel integrated framework based on the HF-entropy measure, SWARA approach, and COPRAS method to handle the SSS problems. In the proposed framework, HF-entropy measure has been used to compute the DEs weights. The SWARA approach has been applied to elicit the preferences of a set of DEs under uncertainty and then, an aggregated subjective weight has been provided for each criterion in terms of HFNs. Next, the COPRAS approach has been applied to evaluate the ranking order of SS options. To validate the results, the sensitivity and comparative studies have been discussed, which also verifies the reasonability of the HF-SWARA-COPRAS method. Thus the final results confirm that the developed method is more useful and feasible than other approaches. The drawback of this research is that the number of DEs involved was small, and the interrelationships between the criteria were not taken into consideration; this may limit the application scope of the proposed framework to some extent. Therefore, further research will need to be conducted in the future, such as considering a larger number of DMs as well as the inter and intra relationships between the SS’s criteria.
Author Contributions
P.R., A.R.M. and R.K. prepared the initial idea for sustainable supplier evaluation and developed a prototype model. K.S.R. and K.B. provided suggestions related to the literature review and gave insightful thoughts on the implementation. P.R. and A.R.M. implemented the prototype into a workable model, which was validated by R.K. using different data patterns, and fine-tuning was performed on the workable model. Verification of the result was done by A.M., and F.C. and idea pertaining to comparative study and representation of the results were provided by A.M., and F.C. Initial draft of the paper was prepared by P.R., A.R.M., and R.K., which was finely drafted by F.C. and A.M. K.B. and K.S.R. made language edit to the article and provided suggestions related to the representation of tables and figures. Final, master edit was done by A.M. and F.C. before submission of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.; Jin, L.; Zhu, F. A multi-criteria group decision making model for green supplier selection under the ordered weighted hesitant fuzzy environment. Symmetry 2019, 11, 17. [Google Scholar] [CrossRef]
- Stevic, Ž.; Pamucar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to Compromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Quan, M.; Wang, Z.; Liu, H.; Shi, H. A hybrid MCDM approach for large group green supplier selection with uncertain linguistic information. IEEE Access 2018, 6, 50372–50383. [Google Scholar] [CrossRef]
- Meksavang, P.; Shi, H.; Lin, S.M.; Liu, H.C. An extended picture fuzzy VIKOR approach for sustainable supplier management and its application in the beef industry. Symmetry 2019, 11, 468. [Google Scholar] [CrossRef]
- Carter, C.R.; Easton, L.P. Sustainable supply chain management: Evolution and future directions. Int. J. Phys. Distrib. Logist. Manag. 2011, 41, 46–62. [Google Scholar] [CrossRef]
- Lo, H.W.; Liou, J.J.H.; Wang, H.S.; Tsai, Y.S. An integrated model for solving problems in green supplier selection and order allocation. J. Clean. Prod. 2018, 190, 339–352. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.W.; Qin, J.D. An integrated ANP-VIKOR methodology for sustainable supplier selection with interval type-2 fuzzy sets. Granul. Comput. 2018, 3, 193–208. [Google Scholar] [CrossRef]
- Wang, J.; Gao, H.; Wei, G.; Wei, Y. Methods for multiple-attribute group decision making with q-rung interval-valued orthopair fuzzy information and their applications to the selection of green suppliers. Symmetry 2019, 11, 56. [Google Scholar] [CrossRef]
- Wang, K.Q.; Liu, H.C.; Liu, L.; Huang, J. Green supplier evaluation and selection using cloud model theory and the QUALIFLEX method. Sustainability 2017, 9, 688. [Google Scholar] [CrossRef]
- Shi, H.; Quan, M.Y.; Liu, H.C.; Duan, C.Y. A novel integrated approach for green supplier selection with interval-valued intuitionistic uncertain linguistic information: A case study in the agri-food industry. Sustainability 2018, 10, 733. [Google Scholar] [CrossRef]
- Govindan, K.; Sivakumar, R. Green supplier selection and order allocation in a low-carbon paper industry: Integrated multi-criteria heterogeneous decision-making and multi-objective linear programming approaches. Ann. Oper. Res. 2016, 238, 243–276. [Google Scholar] [CrossRef]
- Duan, C.Y.; Liu, H.C.; Zhang, L.J.; Shi, H. An extended alternative queuing method with linguistic Z-numbers and its application for green supplier selection and order allocation. Int. J. Fuzzy Syst. 2019, 21, 2510–2523. [Google Scholar] [CrossRef]
- Mou, N.Y.; Chang, J.P.; Chen, Z.S. Sustainable supplier selection based on Pd-HFLTS and group decision-making theory. Comput. Integr. Manuf. Syst. 2018, 24, 1261–1278. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the 18th IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009. [Google Scholar]
- Liu, J.; Liu, P.; Liu, S.F.; Zhou, X.Z.; Zhang, T. A study of decision process in MCDM problems with large number of criteria. Int. Trans. Oper. Res. 2015, 22, 237–264. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The CRITIC method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Goldstein, W.M. Judgments of relative importance in decision making: Global vs local interpretations of subjective weight. Organ. Behav. Hum. Decis. Process. 1990, 47, 313–336. [Google Scholar] [CrossRef]
- Kersuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Wen, Z.; Liao, H.; Ren, R.; Bai, C.; Zavadskas, E.K.; Antucheviciene, J.; Al-Barakati, A. Cold chain logistics management of medicine with an integrated multi-criteria decision-making method. Int. J. Environ. Res. Public Health 2019, 16, 4843. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Sarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Rani, P.; Mishra, A.R.; Mardani, A. An extended Pythagorean fuzzy complex proportional assessment approach with new entropy and score function: Application in pharmacological therapy selection for type 2 diabetes. Appl. Soft Comput. 2020. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Pardasani, K.R. Multiple-criteria decision-making for service quality selection based on Shapley COPRAS method under hesitant fuzzy sets. Granul. Comput. 2019, 4, 435–449. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning Part I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Yager, R.R. On the theory of bags. Int. J. Gen. Syst. 1986, 13, 23–37. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Xu, Z.S.; Xia, M. Hesitant fuzzy entropy and cross-entropy and their use in multiattribute decision-making. Int. J. Intell. Syst. 2012, 27, 799–822. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.S.; Zeng, X.J. Novel correlation coefficients between hesitant fuzzy sets and their application in decision making. Knowl.-Based Syst. 2015, 82, 115–127. [Google Scholar] [CrossRef]
- He, Y.; He, Z.; Wang, G.; Chen, H. Hesitant Fuzzy Power Bonferroni Means and Their Application to Multiple Attribute Decision Making. IEEE Trans. Fuzzy Syst. 2015, 23, 1655–1668. [Google Scholar] [CrossRef]
- Qin, J.; Liu, X.; Pedrycz, W. Frank aggregation operators and their application to hesitant fuzzy multiple attribute decision making. Appl. Soft Comput. 2016, 41, 428–452. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.S. Satisfaction degree based interactive decision making under hesitant fuzzy environment with incomplete weights. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2014, 22, 553–572. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H. Novel multi-criteria decision-making approaches based on hesitant fuzzy sets and prospect theory. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 1–23. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, Z.S.; Wang, H.; Liu, S. Hesitant fuzzy multi-attribute decision-making based on the minimum deviation method. Soft Comput. 2017, 21, 3439–3459. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, T.; Salabun, W.; Zafar, S.; Watrobski, J. Decision making with uncertainty using hesitant fuzzy sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar] [CrossRef]
- Xu, Z.S.; Cheng, S. An overview on the applications of the hesitant fuzzy sets in group decision-making: Theory, support and methods. Front. Eng. Manag. 2019, 6, 163–182. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Pardasani, K.R.; Mardani, A. A novel hesitant fuzzy WASPAS method for assessment of green supplier problem based on exponential information measures. J. Clean Prod. 2019. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S.; Xia, M.M. Multiplicative consistency of hesitant fuzzy preference relation and its application in group decision making. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 47–76. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran, K.S.; Murthy, K.K.; Saeid, A.B. A scientific decision-making framework for supplier outsourcing using hesitant fuzzy information. Soft Comput. 2018, 22, 7445–7461. [Google Scholar] [CrossRef]
- Wang, F. Aggregation Similarity Measure Based on Hesitant Fuzzy Closeness Degree and Its Application to Clustering Analysis. J. Syst. Sci. Inf. 2019, 7, 70–89. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Morshed Varzandeh, M.H. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. CATENA 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Karabasevic, D.; Zavadskas, E.K.; Turskis, Z.; Stanujkic, D. The framework for the selection of personnel based on the SWARA and ARAS methods under uncertainties. Informatica 2016, 27, 49–65. [Google Scholar] [CrossRef]
- Nakhaei, J.; Bitarafan, M.; LaleArefi, S.; Kaplinski, O. Model for rapid assessment of vulnerability of office buildings to blast using SWARA and SMART methods (a case study of swiss re tower). J. Civ. Eng. Manag. 2016, 22, 831–843. [Google Scholar] [CrossRef]
- Shukla, S.; Mishra, P.; Jain, R.; Yadav, H. An integrated decision making approach for ERP system selection using SWARA and PROMETHEE method. Int. J. Intell. Enterp. 2016, 3, 120–147. [Google Scholar] [CrossRef]
- Isık, A.T.; Adalı, E.A. A new integrated decision making approach based on SWARA and OCRA methods for the hotel selection problem. Int. J. Adv. Oper. Manag. 2016, 8, 140–151. [Google Scholar]
- Mavi, R.K.; Goh, M.; Zarbakhshnia, N. Sustainable third-party reverse logistic provider selection with fuzzy SWARA and fuzzy MOORA in plastic industry. Int. J. Adv. Manuf. Technol. 2017, 91, 2401–2418. [Google Scholar] [CrossRef]
- Panahi, S.; Khakzad, A.; Afzal, P. Application of stepwise weight assessment ratio analysis (SWARA) forcopperprospectivity mapping in the Anarak region, central Iran. Arab. J. Geosci. 2017, 10, 484. [Google Scholar] [CrossRef]
- Stanujkic, D.; Zavadskas, E.K.; Karabasevic, D.; Turskis, Z.; Kersuliene, V. New group decision-making ARCAS approach based on the integration of the SWARA and the ARAS methods adapted for negotiations. J. Bus. Econ. Manag. 2017, 18, 599–618. [Google Scholar] [CrossRef]
- Karabaševic, D.; Stanujkic, D.; Urosevic, S.; Popovic, G.; Maksimovic, M. An approach to criteria weights determination by integrating the Delphi and the adapted SWARA methods. Manag. J. Theory Pract. Manag. 2017, 22, 15–25. [Google Scholar] [CrossRef]
- Urosevic, S.; Karabasevic, D.; Stanujkic, D.; Maksimovic, M. An approach to personnel selection in the tourism industry based on the SWARA and the WASPAS methods. Econ. Comput. Econ. Cybern. Stud. Res. 2017, 51, 75–88. [Google Scholar]
- Jamali, G.; Asl, E.K.; Hashemkhani Zolfani, S.; Saparauskas, J. Analysing larg supply chain management competitive strategies in Iranian cement industries. E+M Ekon. Manag. 2017, 20, 70–83. [Google Scholar] [CrossRef]
- Juodagalviene, B.; Turskis, Z.; Šaparauskas, J.; Endriukaityte, A. Integrated multi-criteria evaluation of house’s plan shape based on the EDAS and SWARA methods. Eng. Struct. Technol. 2017, 9, 117–125. [Google Scholar] [CrossRef]
- Tayyar, N.; Durmu, M. Comparison of Max100, SWARA and pairwise weight elicitation methods. Int. J. Eng. Res. Appl. 2017, 7, 67–78. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. A new hybrid fuzzy MCDM approach for evaluation of construction equipment with sustainability considerations. Arch. Civ. Mech. Eng. 2018, 18, 32–49. [Google Scholar] [CrossRef]
- Dahooie, J.H.; Abadi, E.B.J.; Vanaki, A.S.; Firoozfar, H.R. Competency-based IT personnel selection using a hybrid SWARA and ARAS-G methodology. Hum. Factors Ergon. Manuf. Serv. Ind. 2018, 28, 5–16. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Mardani, A.; Cavallaro, F.; Streimikiene, D.; Khan, S.A.R. Pythagorean fuzzy SWARA–VIKOR framework for performance evaluation of solar panel selection. Sustainability 2020, 12, 4278. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Single-valued neutrosophic SWARA-VIKOR framework for performance assessment of eco-industrial thermal power plants. ICSES Trans. Neural Fuzzy Comput. 2020, 3, 1–9. [Google Scholar]
- Mishra, A.R.; Rani, P.; Pandey, K.; Mardani, A.; Streimikis, J.; Streimikiene, D.; Alrasheedi, M. Novel multi-criteria intuitionistic fuzzy SWARA–COPRAS approach for sustainability evaluation of the bioenergy production process. Sustainability 2020, 12, 4155. [Google Scholar] [CrossRef]
- Yazdani, M.; Alidoosti, A.; Zavadskas, E.K. Risk Analysis of Critical Infrastructures Using Fuzzy COPRAS. Econ. Res. 2011, 24, 27–40. [Google Scholar] [CrossRef]
- Fouladgar, M.M.; Yazdani-Chamzini, A.; Lashgari, A.; Zavadskas, E.K.; Turskis, Z. Maintenance strategy selection using AHP and COPRAS under fuzzy environment. Int. J. Strateg. Prop. Manag. 2012, 16, 85–104. [Google Scholar] [CrossRef]
- Antucheviciene, J.; Zavadskas, E.K.; Zakarevicius, A. Ranking redevelopment decisions of derelict buildings and analysis of ranking results. Econ. Comput. Econ. Cybern. Stud. Res. 2012, 46, 37–62. [Google Scholar]
- Das, M.C.; Sarkar, B.; Ray, S. A framework to measure relative performance of Indian technical institutions using integrated fuzzy AHP and COPRAS methodology. Socio-Econ. Plan. Sci. 2012, 46, 230–241. [Google Scholar] [CrossRef]
- Tavana, M.; Momeni, E.; Rezaeiniya, N.; Mirhedayatian, S.M.; Rezaeiniya, H. A novel hybrid social media platform selection model using fuzzy ANP and COPRAS-G. Exp. Syst. Appl. 2013, 40, 5694–5702. [Google Scholar] [CrossRef]
- Aghdaie, M.H.; Zolfani, S.H.; Zavadskas, E.K. Market segment evaluation and selection based on application of fuzzy AHP and COPRAS-G methods. J. Bus. Econ. Manag. 2013, 14, 213–233. [Google Scholar] [CrossRef]
- Hajiagha, S.H.R.; Hashemi, S.S.; Zavadskas, E.K. A complex proportional assessment method for group decision making in an interval-valued intuitionistic fuzzy environment. Technol. Econ. Dev. Econ. 2013, 19, 22–37. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Salehi Sadaghiani, J.; HassaniGoodarzi, G. Multiple criteria group decision-making for supplier selection based on COPRAS method with interval type-2 fuzzy sets. Int. J. Adv. Manuf. Technol. 2014, 75, 1115–1130. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Hajiagha, S.H.R.; Hashemi, S.S. The interval-valued intuitionistic fuzzy MULTIMOORA method for group decision making in engineering. Math. Probl. Eng. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Akhavan, P.; Barak, S.; Maghsoudlou, H.; Antucheviciene, J. FQSPM-SWOT for strategic alliance planning and partner selection; case study in a holding car manufacturer company. Technol. Econ. Dev. Econ. 2015, 21, 165–185. [Google Scholar] [CrossRef]
- Bekar, E.T.; Cakmakci, M.; Kahraman, C. Fuzzy COPRAS method for performance measurement in total productive maintenance: A comparative analysis. J. Bus. Econ. Manag. 2016, 17, 663–684. [Google Scholar] [CrossRef]
- Garg, R. Optimal selection of E-learning websites using multi-attribute decision-making approaches. J. Multi-Crit. Decis. Anal. 2017, 24, 187–196. [Google Scholar] [CrossRef]
- Wang, Z.-L.; You, J.-X.; Liu, H.-C.; Wu, S.-M. Failure Mode and Effect Analysis using Soft Set Theory and COPRAS Method. Int. J. Comput. Intell. Syst. 2017, 10, 1002–1015. [Google Scholar] [CrossRef]
- Mahdiraji, H.A.; Arzaghi, S.; Stauskis, G.; Zavadskas, E.K. A hybrid fuzzy BWM-COPRAS method for analyzing key factors of sustainable architecture. Sustainability 2018, 10, 1626. [Google Scholar] [CrossRef]
- Kurtulmuşoğlu, F.B.; Can, G.F.; Pakdil, F.; Tolon, M. Does gender matter? Considering gender of service in the airline industry. J. Air Transp. Manag. 2018, 70, 73–82. [Google Scholar] [CrossRef]
- Barak, S.; Dahooei, J.H. A novel hybrid fuzzy DEA-Fuzzy MADM method for airlines safety evaluation. J. Air Transp. Manag. 2018, 73, 134–149. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran KSSneha SVShyam, S.; Kar, S.; Garg, H. Multi-attribute group decision-making using double hierarchy hesitant fuzzy linguistic preference information. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Garg, H.; Nancy. Algorithms for possibility linguistic single-valued neutrosophic decision-making based on COPRAS and aggregation operators with new information measures. Measurement 2019, 138, 278–290. [Google Scholar] [CrossRef]
- Hajek, P.; Froelich, W. Integrating TOPSIS with interval-valued intuitionistic fuzzy cognitive maps for effective group decision making. Inf. Sci. 2019, 485, 394–412. [Google Scholar] [CrossRef]
- Sivagami, R.; Ravichandran, K.S.; Krishankumar, R.; Sangeetha, V.; Kar, S.; Gao, X.-Z.; Pamucar, D. A Scientific Decision Framework for Cloud Vendor Prioritization under Probabilistic Linguistic Term Set Context with Unknown/Partial Weight Information. Symmetry 2019, 11, 682. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Mardani, A.; Pardasani, K.R.; Govindan, K.; Alrasheedi, M. Healthcare evaluation in hazardous waste recycling using novel interval-valued intuitionistic fuzzy information based on complex proportional assessment method. Comput. Ind. Eng. 2020, 139, 106140. [Google Scholar] [CrossRef]
- Kumari, R.; Mishra, A.R. Multi-criteria COPRAS method based on parametric measures for intuitionistic fuzzy sets: Application of green supplier selection. Iran. J. Sci Technol. Trans. Electr. Eng. 2020. [Google Scholar] [CrossRef]
- Kannan, D.; Lopes de Sousa Jabbour, A.B.; Jabbour, C.J.C. Selecting green suppliers based on GSCM practices: Using fuzzy TOPSIS applied to a Brazilian electronics company. Eur. J. Oper. Res. 2014, 233, 432–447. [Google Scholar] [CrossRef]
- You, X.Y.; You, J.X.; Liu, H.C.; Zhen, L. Group multi-criteria supplier selection using an extended VIKOR method with interval 2-tuple linguistic information. Exp. Syst. Appl. 2015, 42, 1906–1916. [Google Scholar] [CrossRef]
- Xu, X.G.; Shi, H.; Zhang, L.J.; Liu, H.C. Green supplier evaluation and selection with an extended MABAC method under the heterogeneous information environment. Sustainability 2019, 11, 6616. [Google Scholar] [CrossRef]
- Liu, H.C.; Quan, M.Y.; Li, Z.; Wang, Z.L. A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment. Inf. Sci. 2019, 486, 254–270. [Google Scholar] [CrossRef]
- Liu, P.; Gao, H.; Ma, J. Novel green supplier selection method by combining quality function deployment with partitioned Bonferroni mean operator in interval type-2 fuzzy environment. Inf. Sci. 2019, 490, 292–316. [Google Scholar] [CrossRef]
- Lu, Z.; Sun, X.; Wang, Y.; Xu, C. Green supplier selection in straw biomass industry based on cloud model and possibility degree. J. Clean. Prod. 2019, 209, 995–1005. [Google Scholar] [CrossRef]
- Memari, A.; Dargi, A.; Jokar, M.R.A.; Ahmad, R.; Rahim, A.R.A. Sustainable supplier selection: A multi-criteria intuitionistic fuzzy TOPSIS method. J. Manuf. Syst. 2019, 50, 9–24. [Google Scholar] [CrossRef]
- Peng, J.J.; Tian, C.; Zhang, W.Y.; Zhang, S.; Wang, J.Q. An integrated multi-criteria decision-making framework for sustainable supplier selection under picture fuzzy environment. Technol. Econ. Dev. Econ. 2020. [Google Scholar] [CrossRef]
- You, S.Y.; Zhang, L.J.; Xu, X.G.; Liu, H.C. A new integrated multi-criteria decision making and multi-objective programming model for sustainable supplier selection and order allocation. Symmetry 2020, 12, 302. [Google Scholar] [CrossRef]
- Hassini, E.; Surti, C.; Searcy, C. A literature review and a case study of sustainable supply chains with a focus on metrics. Int. Prod. Econ. 2012, 140, 69–82. [Google Scholar] [CrossRef]
- Osiro, L.; Lima-Junior, F.R.; Carpinetti, L.C.R. A group decision model based on quality function deployment and hesitant fuzzy for selecting supply chain sustainability metrics. J. Clean. Prod. 2018, 183, 964–978. [Google Scholar] [CrossRef]
- Sarkis, J.; Dhavale, D.G. Supplier selection for sustainable operations: A triple-bottom-line approach using a Bayesian framework. Int. J. Prod. Econ. 2015, 166, 177–191. [Google Scholar] [CrossRef]
- Awasthi, A.; Govindan, K.; Gold, S. Multi-tier sustainable global supplier selection using a fuzzy AHP-VIKOR based approach. Int. J. Prod. Econ. 2018, 195, 106–117. [Google Scholar] [CrossRef]
- Zimmer, K.; Froehling, M.; Schultmann, F. Sustainable supplier management—A review of models supporting sustainable supplier selection, monitoring and development. Int. J. Prod. Res. 2016, 54, 1412–1442. [Google Scholar] [CrossRef]
- Amindoust, A.; Ahmed, S.; Saghafinia, A.; Bahreininejad, A. Sustainable supplier selection: A ranking model based on fuzzy inference system. Appl. Soft Comput. 2012, 12, 1668–1677. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).