An Extended Object-Oriented Petri Net Model for Vulnerability Evaluation of Communication-Based Train Control System
Abstract
1. Introduction
2. Vulnerability Modeling Framework with EOOPN
2.1. Formal Specification of EOOPN
- is a finite places set of , and it is divided into three types: state place, input place and output place;
- is a finite transitions set of ;
- is a finite input information places set of ;
- is a finite output information places set of ;
- is the input map from place to transition , . It is a colored arc from ;
- is the output map from transition to place , where . It is a colored arc from ;
- is the color set for state places of ;
- is the color set for input places of ;
- is the color set for output places of ;
- is the color set for active transitions of ;
- is the network relevance degree. It is connection relationship among subnet and other subnets;
- is the attack severity when place of is attacked.
2.2. Vulnerability Computing Framework
2.2.1. Vulnerability Attack Path Searching Algorithm
- 1)
- Obtain input matrix and output matrix of the model from the Petri net structure, and make the counting variable and paths ;
- 2)
- Search for the columns corresponding to the transition in the output matrix . If exists, go to step 3. Else , Loop ;
- 3)
- Search for the rows corresponding to the input matrix in which the place is located. If , go to next step. Otherwise , go to step 3;
- 4)
- Judge the structural relationship between the transition and , if , then , all nodes in the system end traversal and exit the program. Else , go to step 2;
2.2.2. Attack Rules of Vulnerability Influencing Factors
2.2.3. System Vulnerability Calculation
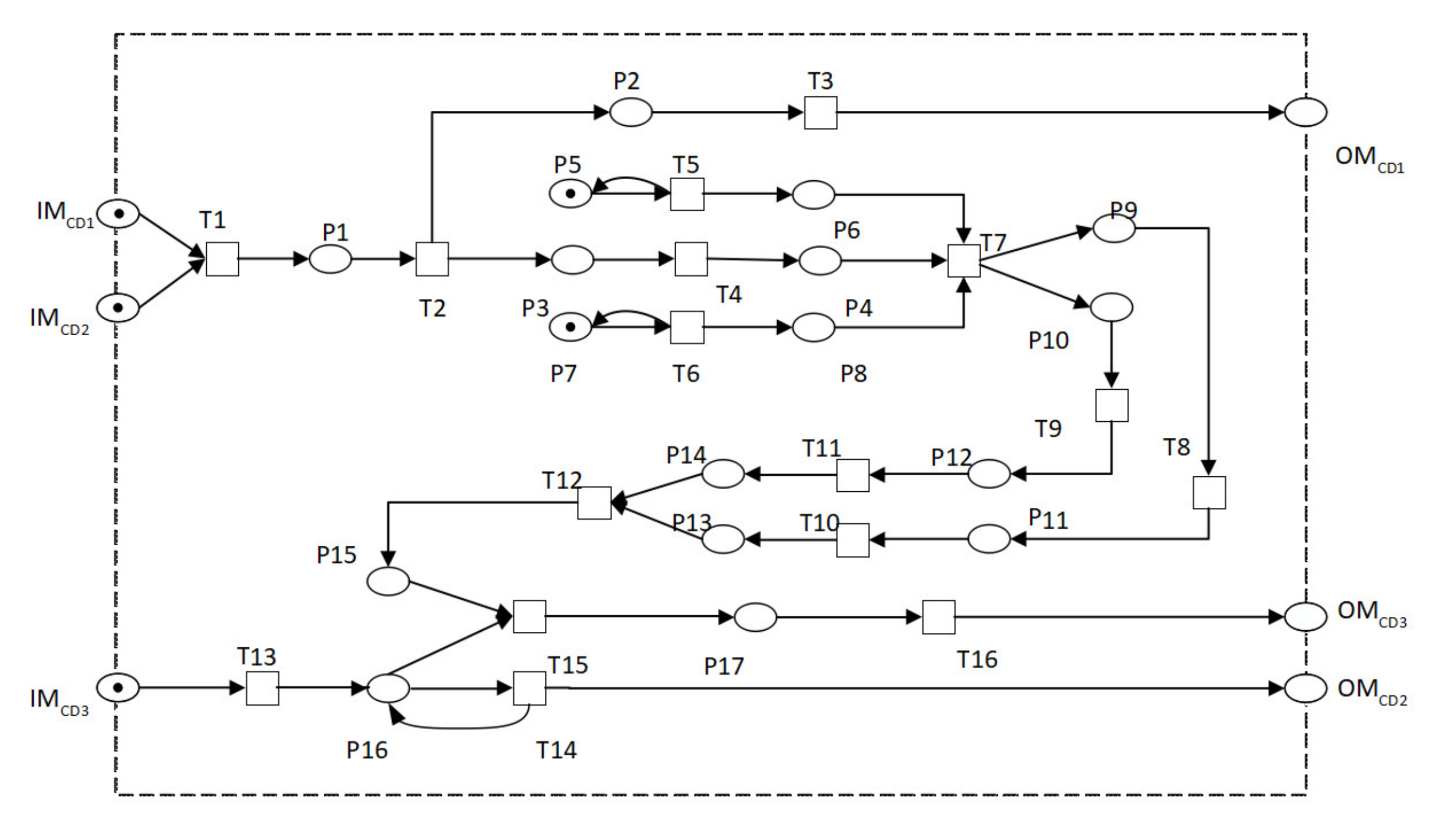
3. CBTCs Modeling Based on EOOPN
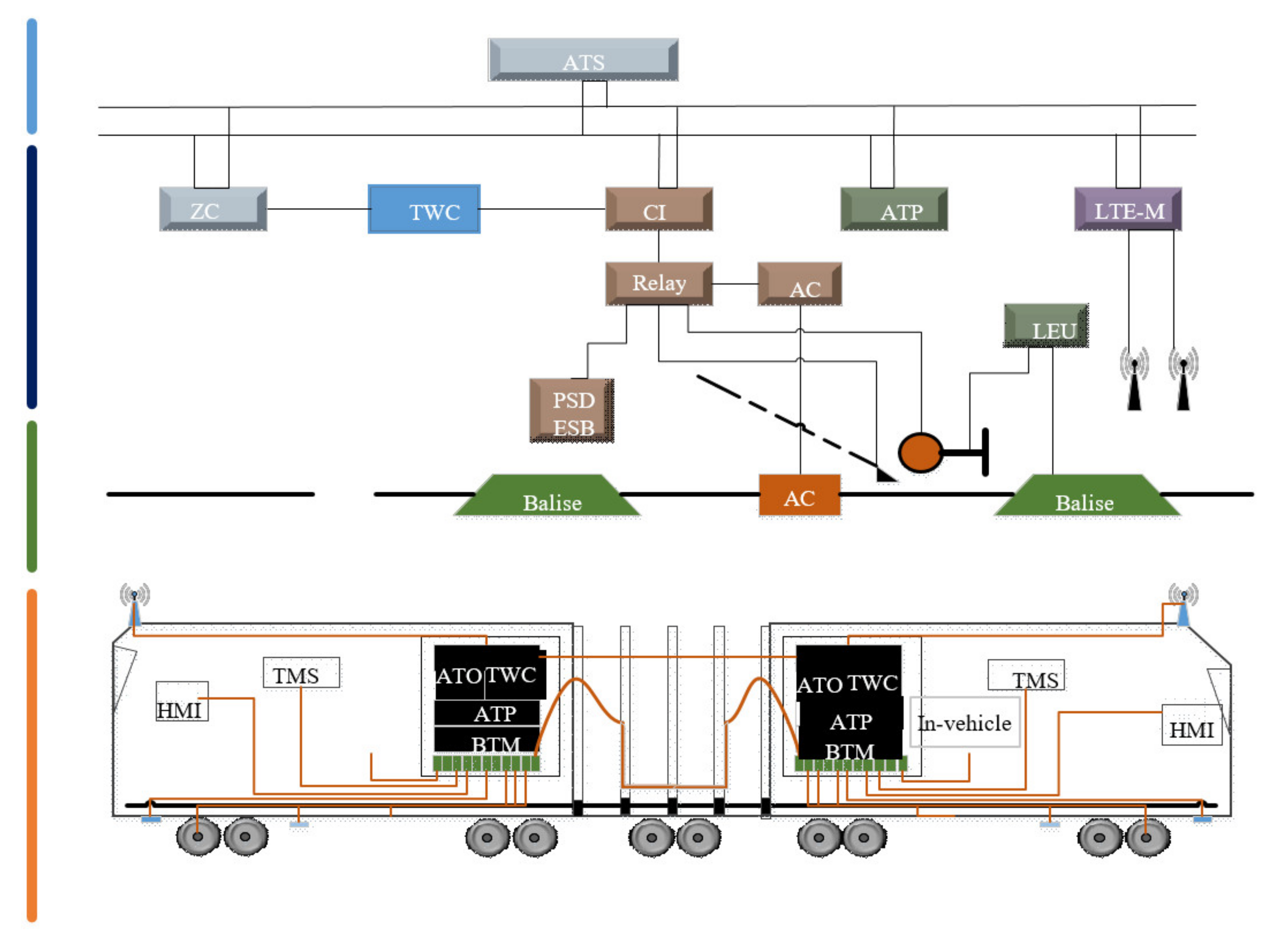
3.1. Architecture of CBTCs
- (1)
- Control center system communicates with in-vehicle system. The control center ATS displays the train number, online running position, running direction and other information on the large screen through two-way communication with the train. The train receives the temporary shunting command from the control center ATS for schedule adjustments.
- (2)
- Control center system communicates with depot system. The control center sends the completed train operation map and operation plan to the depot ATS extension. The depot system dispatches according to the train operation plan and sends the train identification number to the control center through the depot ATS extension. The control center sends the temporary adjustment commands, train shunting arrangement and return commands to the ATS extension of the depot. Then, the depot equipment executes the operation and the procedure are monitored by the control center.
- (3)
- Control center system communicates with trackside system. The control center system communicates with the ATS extension of the station to provide information, such as train schedule, route control commands, real-time train position, train identification number and equipment status. The trackside system transfers equipment operating status information to the control center.
- (4)
- Depot system communicates with in-vehicle system. The depot system realizes the driving mode management for train access sections through communication with the in-vehicle equipment. It also administers train entering and shunting within the depot.
- (5)
- In-vehicle system communicates with trackside system. The data communication between the in-vehicle equipment and the trackside equipment is the key to the normal operation of the train. The two-way communication between the vehicle and the trackside is used to detect the train position, calculate the train movement authorization and link the safety equipment. It remotely controls the train and the screen door, and route management.
3.2. CBTCs Modeling Based on EOOPN
- (1)
- CBTCs system level model
- (2)
- Control center system subnet model
- (3)
- Trackside system subnet model
- (4)
- In-vehicle system subnet model
- (5)
- Depot system subnet model
4. Vulnerability Analysis Based on EOOPN for CBTCs
4.1. Case of Attack Paths Search
4.2. Vulnerability Quantitative Evaluation Cases of CBTCs Based on EOOPN
- (1)
- Calculation of network correlation
- (2)
- Calculation of attack severity degree of vulnerable nodes
- (3)
- Determine the attack path
- (4)
- Network efficiency loss calculation
- 1)
- Assuming that the interlocked host is attacked and fails, the successive failure are in and the network loss rate is obtained:
- 2)
- Assuming that the in-vehicle computer is attacked and fails, the successive failures are in , and the network efficiency loss rate is obtained:
- (5)
- Node vulnerability calculation
4.3. Discussions
- 1)
- Vulnerability contains a series of concepts such as risk, sensitivity, adaptability and resilience. It not only considers the influence of internal conditions of the system, but also includes the characteristics of the interaction between the system and the external environment. Therefore, when calculating the attack threat degree of vulnerability influencing factors, not only is the threat degree of a single vulnerability factor, but also the correlation degree of the object subnet where the vulnerability factor is located in the entire system should be considered.
- 2)
- Vulnerability is the degree of damage or threats from adverse effects. It is the loss of functions to system components under the influence of external factors. Selecting a certain high-vulnerability device as the object, the proposed vulnerability method is used to conduct an in-depth analysis and grasp the vulnerability of the internal components of the device, so it will support the designers from the perspective of intrinsic safety.
- 3)
- Vulnerability is the ability to withstand external disturbances. It is the system’s ability responding to external disturbance factors, including resistance and recovery. The process of vulnerability factors to the entire system is the dynamic process of change. The attack rule of the vulnerability factor is the successive failure path of change. According to the attack path search algorithm of influencing factors, the disturbance path of a certain vulnerability factor to the system can be determined.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Crawford, E.; Kift, R.L. Keeping track of railway safety and the mechanisms for risk. Saf. Sci. 2018, 110, 195–205. [Google Scholar] [CrossRef]
- Gol’Dshtein, V.; Koganov, G.A.; Surdutovich, G.I. Vulnerability and hierarchy of complex networks. arXiv 2004, arXiv:cond-mat/0409298. [Google Scholar]
- Haimes, Y.Y. On the definition of vulnerabilities in measuring risks to infrastructures. Risk Anal. 2006, 26, 293–296. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, M. Review on modeling and simulatio of interdependent critical infrastructure systems. Reliab. Eng. Syst. Saf. 2014, 121, 43–60. [Google Scholar] [CrossRef]
- Chazelle, B.; Lambert, L.; Capoccioni, C.P. Railway vulnerability in case of extremes floods. Knowledge and risk management. Houille Blanche 2014, 2, 48–54. [Google Scholar] [CrossRef]
- Arsuaga, I.; Toledo, N.; Lopez, I.; Aguado, M. A framework for vulnerability detection in european train control railway communications. Secur. Commun. Netw. 2018, 2018, 5634181. [Google Scholar] [CrossRef]
- Xing, Y.; Lu, J.; Chen, S.; Dissanayake, S. Vulnerability analysis of urban rail transit based on complex network theory: A case study of Shanghai Metro. Public Transp. 2017, 9, 501–525. [Google Scholar] [CrossRef]
- Wu, J.; Deng, H.-Z.; Tan, Y.-J.; Li, Y.; Zhu, D.-Z. Attack vulnerability of complex networks based on local information. Mod. Phys. Lett. B 2007, 21, 1007–1014. [Google Scholar] [CrossRef]
- Ouyang, M.; Pan, Z.; Hong, L.; He, Y. Vulnerability analysis of complementary transportation systems with applications to railway and airline systems in China. Reliab. Eng. Syst. Saf. 2015, 142, 248–257. [Google Scholar] [CrossRef]
- Eduardo, L.D.; Licínio, D.P.; Walter, P.J. Indicators of reliability and vulnerability: Similarities and differences in ranking links of a complex road system. Transp. Res. Part A Policy Pract. 2016, 88, 195–208. [Google Scholar]
- Rodríguez-Núñez, E.; Palomares, J.C.G. Measuring the vulnerability of public transport networks. J. Transp. Geogr. 2014, 35, 50–63. [Google Scholar] [CrossRef]
- Balijepalli, C.; Oppong, O. Measuring vulnerability of road network considering the extent of serviceability of critical road links in urban areas. J. Transp. Geogr. 2014, 39, 145–155. [Google Scholar] [CrossRef]
- Demirel, H.; Kompil, M.; Nemry, F. A framework to analyze the vulnerability of European road networks due to Sea-Level Rise (SLR) and sea storm surges. Transp. Res. Part A Policy Pract. 2015, 81, 62–76. [Google Scholar] [CrossRef]
- Jenelius, E.; Petersen, T.; Mattsson, L.-G. Importance and exposure in road network vulnerability analysis. Transp. Res. Part A Policy Pract. 2006, 40, 537–560. [Google Scholar] [CrossRef]
- Zenil, H.; Delahaye, J.-P.; Gaucherel, C. Image characterization and classification by physical complexity. Complexity 2011, 17, 26–42. [Google Scholar] [CrossRef]
- Zio, E. Challenges in the vulnerability and risk analysis of critical infrastructures. Reliab. Eng. Syst. Saf. 2016, 152, 137–150. [Google Scholar] [CrossRef]
- Berdica, K. An introduction to road vulnerability: What has been done, is done and should be done. Transp. Policy 2002, 9, 117–127. [Google Scholar] [CrossRef]
- Liu, X.; Sun, L.; Sun, Q. Cloud matter-element comprehensive evaluation on vulnerability of urban road traffic network. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2019, 38, 6–11. [Google Scholar]
- Jenelius, E.; Mattsson, L.G. Developing a Methodology for Road Network Vulnerability Analysis; Royal Institute of Technology: Stockholm, Sweden, 2006. [Google Scholar]
- Minciardi, R.; Sacile, R.; Taramasso, A.; Trasforini, E.; Traverso, S. Modeling the vulnerability of complex territorial systems: An application to hydrological risk. Environ. Model. Softw. 2006, 21, 949–960. [Google Scholar] [CrossRef]
- Myung, Y.-S.; Kim, H.-J. A cutting plane algorithm for computing k-edge survivability of a network. Eur. J. Oper. Res. 2004, 156, 579–589. [Google Scholar] [CrossRef]
- Feng, C.; Zhu, Q.; Yu, B.; Zhang, Y. Complexity and vulnerability of high-speed rail network in China. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 10034–10039. [Google Scholar]
- Khanmohamadi, M.; Bagheri, M.; Khademi, N.; GhannadPour, S.F. A security vulnerability analysis model for dangerous goods transportation by rail—Case study: Chlorine transportation in Texas-Illinois. Saf. Sci. 2018, 110, 230–241. [Google Scholar] [CrossRef]
- Nielsen, M.; Plotkin, G.; Winskel, G. Petri nets, event structures and domains, part I. Theor. Comput. Sci. 1981, 13, 85–108. [Google Scholar] [CrossRef]
- Best, E.; Devillers, R.; Koutny, M. Petri Net Algebra; Springer: Berlin, Germany, 2001. [Google Scholar]
- Blätke, M.A.; Heiner, M.; Marwan, W. Tutorial: Petri Nets in Systems Biology; Otto-von-Guericke University: Magdeburg, Germany, 2011. [Google Scholar]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Malakar, B.; Roy, B. Railway fail-safe signalization and interlocking design based on automation Petri Net. In Proceedings of the International Conference on Information Communication and Embedded Systems (ICICES2014), Chennai, India, 27–28 February 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Shen, J.J.; Feng, D.Q. Vulnerability analysis of clock synchronization protocol using stochastic Petri Net. In Proceedings of the 2014 IEEE International Conference on High Performance Computing and Communications, Paris, France, 20–22 August 2014; pp. 615–620. [Google Scholar]
- Berthomieu, B.; Ribet, P.O.; Vernadat, F. The tool TINA—Construction of abstract state spaces for petri nets and time petri nets. Int. J. Prod. Res. 2004, 14–16. [Google Scholar] [CrossRef]
- Giglio, D.; Sacco, N. A Petri net model for analysis, optimisation, and control of railway networks and train schedules. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 2442–2449. [Google Scholar] [CrossRef]
- Wu, D.; Schnieder, E. Scenario-based modeling of the on-board of a satellite-based train control system with colored petri nets. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3045–3061. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Z.; Liu, Z. A novel matrix approach for the stability and stabilization analysis of colored Petri nets. Sci. China Inf. Sci. 2019, 62, 98–111. [Google Scholar] [CrossRef]
- Boudi, Z.; Koursi, E.; Collard-Dutilleul, M.E.; Khaddour, M. High Level Petri Net Modeling For Railway Safety Critical Scenarios. In Proceedings of the 10th FORMS-FORMAT Symposium on Formal Methods for Automation and Safety in Railway and Automotive Systems, Braunschweig, Germany, 30 September–2 October 2014; pp. 65–75. [Google Scholar]
- Hua, Y.Z.; Li, C.Y. A novel object-oriented petri nets and its applications. Mech. Sci. Technol. 2005, 24, 8–11. [Google Scholar]
- Wu, J.; Yuan, J.; Gao, W. Analysis of fractional factor system for data transmission in SDN. Appl. Math. Nonlinear Sci. 2019, 4, 191–196. [Google Scholar] [CrossRef]
- Li, T.; Yang, W. Solution to chance constrained programming problem in swap trailer transport organisation based on improved simulated annealing algorithm. Appl. Math. Nonlinear Sci. 2020, 5, 47–54. [Google Scholar] [CrossRef]

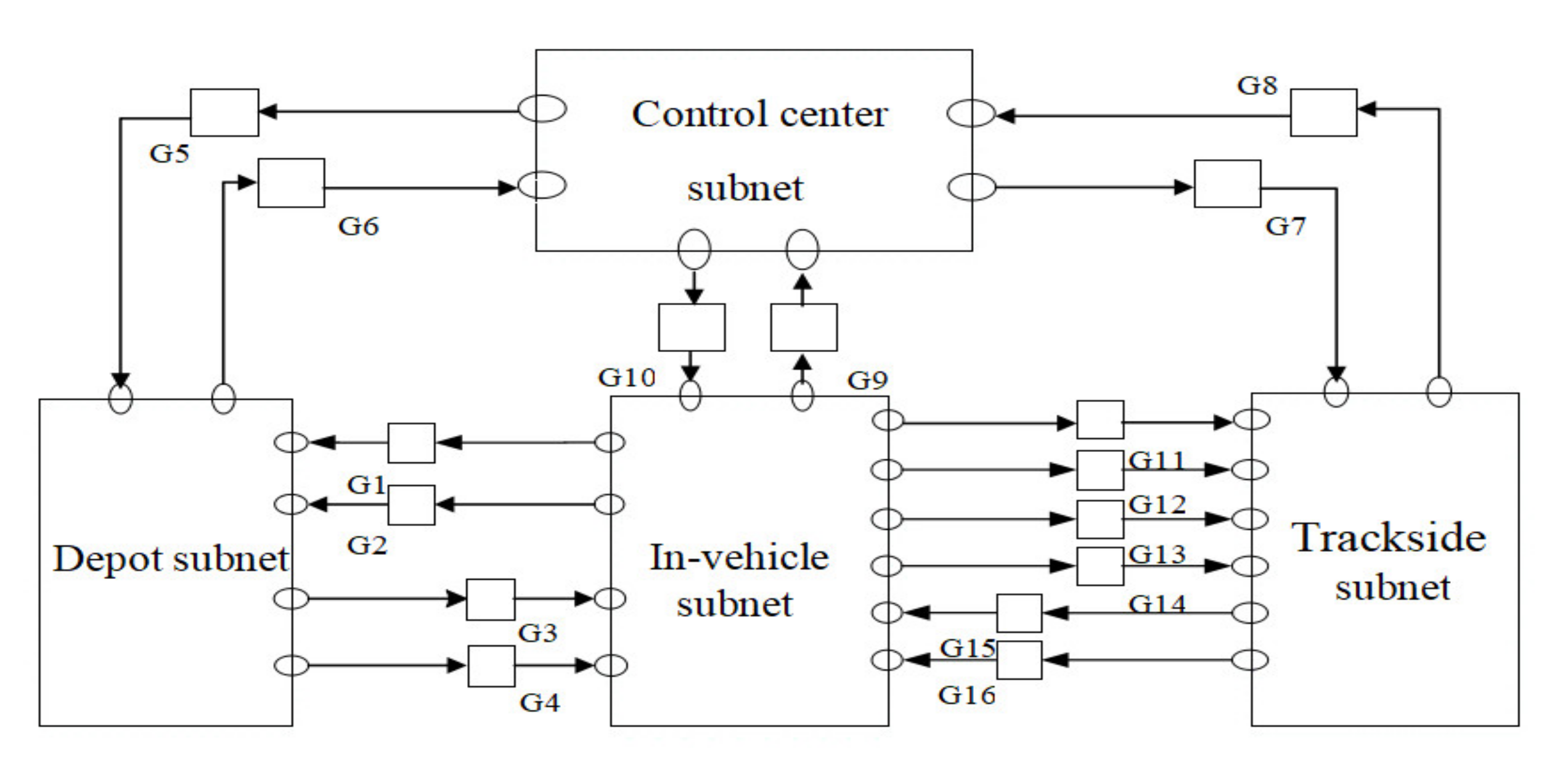
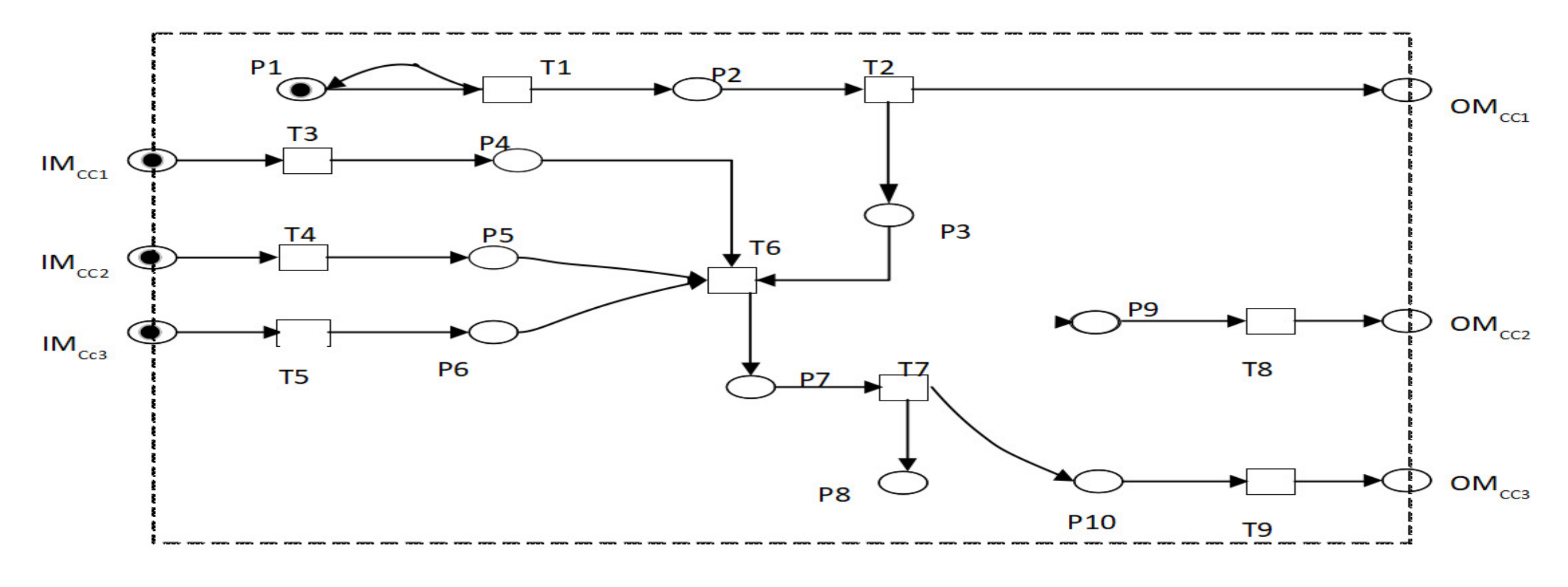

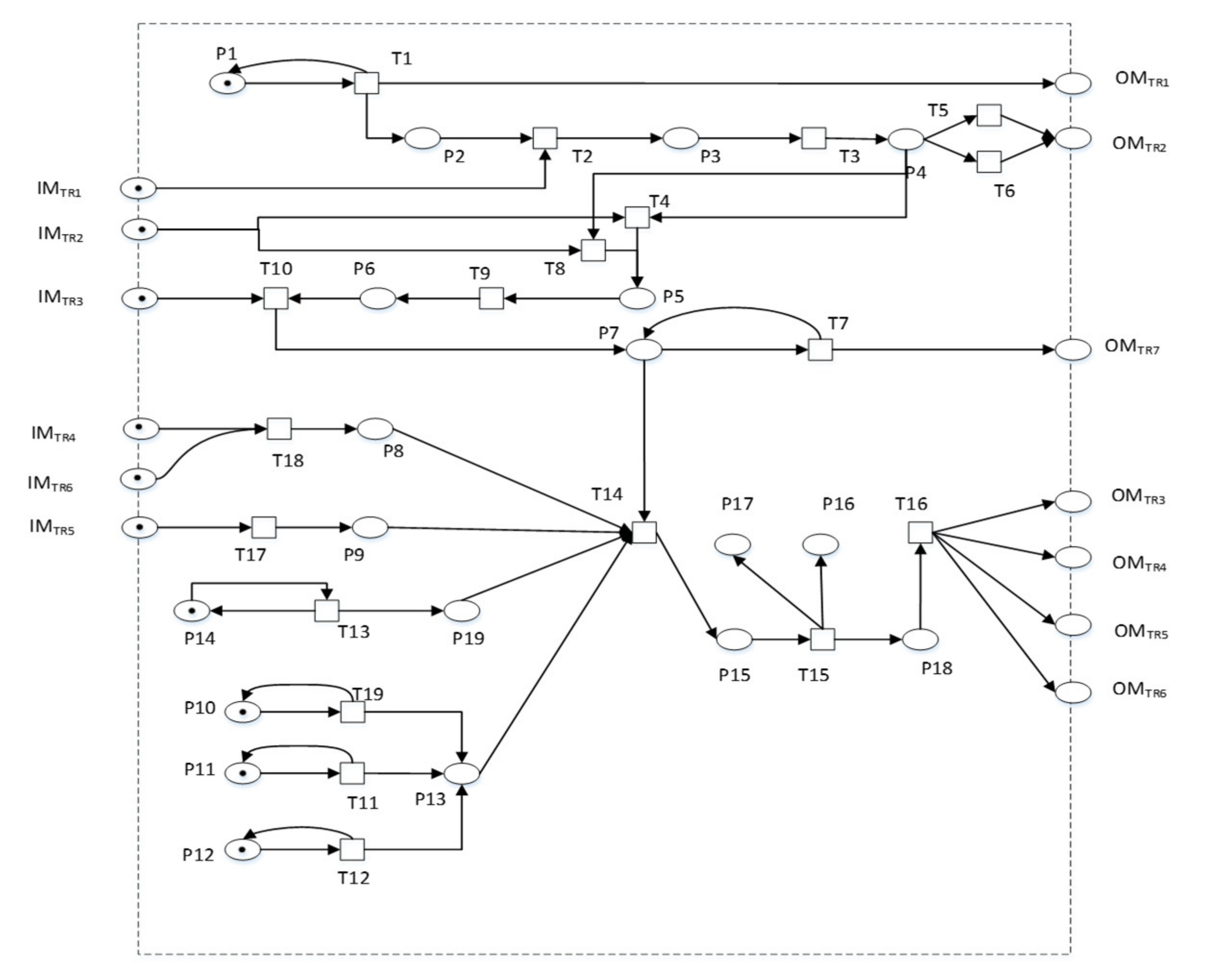

| Transition | Implication | Transition | Implication |
|---|---|---|---|
| G1 | Train departure request | G9 | Train operation status information |
| G2 | Train departure authorization | G10 | Train adjustment command |
| G3 | Beacon antenna pulse information | G11 | Train operation status information |
| G4 | Line information | G12 | Door status information |
| G5 | Train schedule | G13 | PSD linkage command |
| G6 | Device status information | G14 | Beacon antenna pulse information |
| G7 | Route control command | G15 | Line information |
| G8 | Device status information | G16 | Mobile authorization |
| Failure Transition | Successive Failure Transitions | Failure Transition | Successive Failure Transitions | Failure Transition | Successive Failure Transitions |
|---|---|---|---|---|---|
| T1 | T2, T3, T4, T5, T7, T10, T23 | T12 | -- | T23 | -- |
| T2 | T3, T4, T5, T7, T10, T23 | T13 | T15, T16, T22, T23 | T24 | T26, T27, T29 |
| T3 | T4, T5, T7, T10, T23 | T14 | T22, T23 | T25 | -- |
| T4 | T5, T7, T10, T23 | T15 | T16, T22, T23 | T26 | -- |
| T5 | T7, T10, T23 | T16 | T22, T23 | T27 | T29 |
| T6 | T21, T22, T23 | T17 | T15, T16, T22, T23 | T28 | T27, T29 |
| T7 | T10, T23 | T18 | T15, T16, T22, T23 | T29 | -- |
| T8 | T9, T7, T10 | T19 | T15, T16, T22, T23 | T30 | T12 |
| T9 | T8, T7, T10 | T20 | T15, T16, T22, T23 | T31 | T11, T12 |
| T10 | -- | T21 | T22, T23 | ||
| T11 | T12 | T22 | T23 |
| NO. | Vulnerability Factor | Threat Degree T |
|---|---|---|
| 1 | Interlocking host | 0.0565 |
| 2 | Tuning unit | 0.0484 |
| 3 | TCOM | 0.0484 |
| 4 | Sending module | 0.0484 |
| 5 | Receiving module | 0.0484 |
| 6 | Axial head | 0.0484 |
| 7 | Code generator | 0.0484 |
| 8 | HMI workstation | 0.0484 |
| 9 | HMI | 0.0484 |
| 10 | Axis card | 0.0484 |
| 11 | Console | 0.0484 |
| 12 | Monitoring computer | 0.0484 |
| 13 | ZC host | 0.0403 |
| 14 | Conversion force | 0.0323 |
| 15 | Representation loop | 0.0323 |
| 16 | Relay | 0.0323 |
| 17 | Switch control circuit | 0.0160 |
| 18 | Switch machine | 0.0081 |
| 19 | Drive loop | 0.0081 |
| 20 | Connecting rod | 0.0081 |
| 21 | Signal control circuit | 0.0081 |
| NO. | Vulnerability Factor | Threat Degree T |
|---|---|---|
| 1 | In-vehicle computer | 0.1167 |
| 2 | Antenna | 0.0441 |
| 3 | HMI | 0.0221 |
| 4 | Button | 0.0221 |
| 5 | Speed measuring motor | 0.0221 |
| 6 | Coded odometer | 0.0221 |
| 7 | Wireless loss | 0.0726 |
| 8 | Doppler radar | 0.0221 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, Y.; Wang, L.; Cai, G. An Extended Object-Oriented Petri Net Model for Vulnerability Evaluation of Communication-Based Train Control System. Symmetry 2020, 12, 1474. https://doi.org/10.3390/sym12091474
Zhang Y, Wang Y, Wang L, Cai G. An Extended Object-Oriented Petri Net Model for Vulnerability Evaluation of Communication-Based Train Control System. Symmetry. 2020; 12(9):1474. https://doi.org/10.3390/sym12091474
Chicago/Turabian StyleZhang, Ye, Yatao Wang, Lin Wang, and Guoqiang Cai. 2020. "An Extended Object-Oriented Petri Net Model for Vulnerability Evaluation of Communication-Based Train Control System" Symmetry 12, no. 9: 1474. https://doi.org/10.3390/sym12091474
APA StyleZhang, Y., Wang, Y., Wang, L., & Cai, G. (2020). An Extended Object-Oriented Petri Net Model for Vulnerability Evaluation of Communication-Based Train Control System. Symmetry, 12(9), 1474. https://doi.org/10.3390/sym12091474





