Numerical Solutions of Unsteady Boundary Layer Flow with a Time-Space Fractional Constitutive Relationship
Abstract
1. Introduction
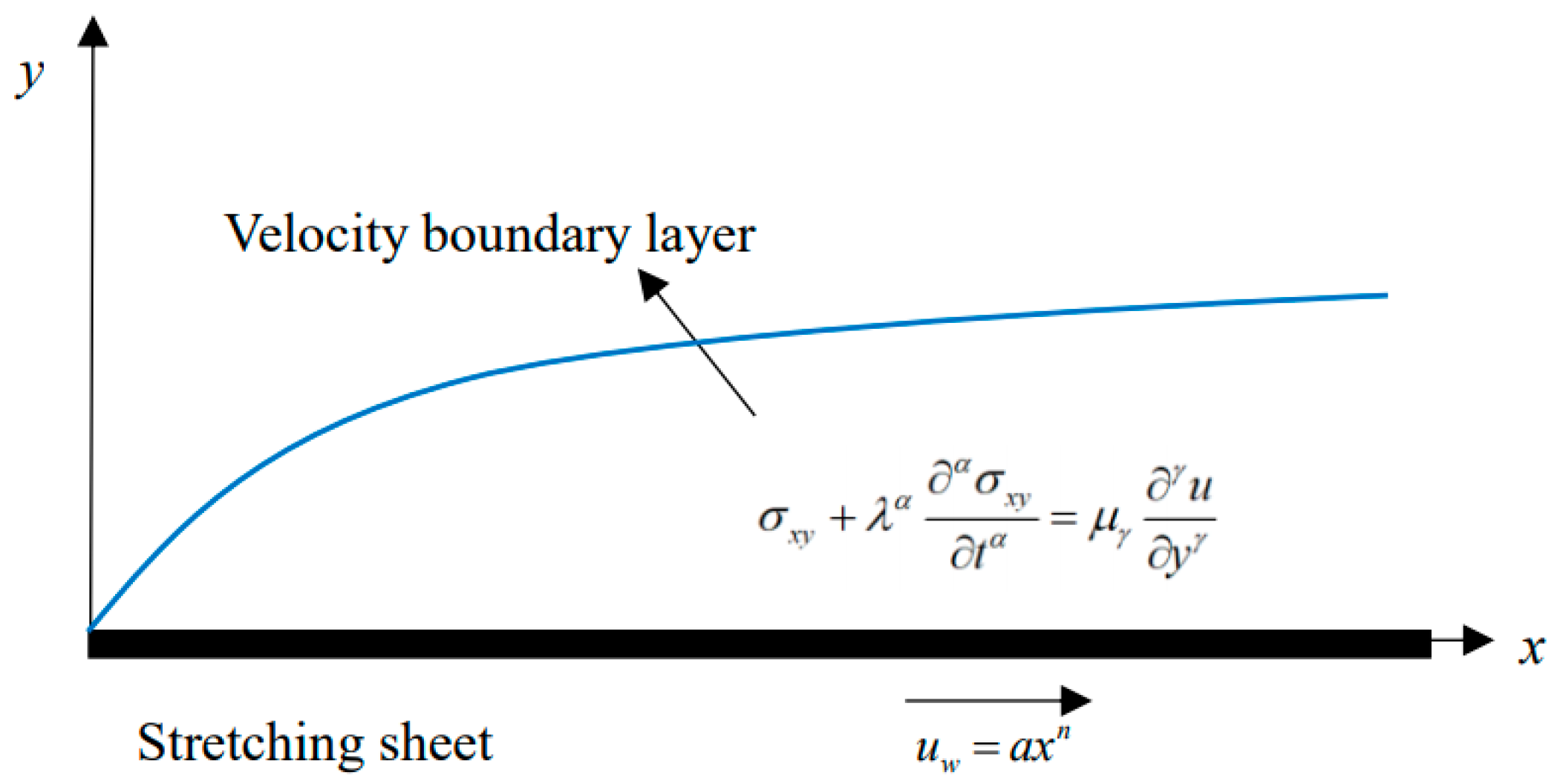
2. Governing Equations
3. The Numerical Technique
3.1. Discretization Method
3.2. Solvability of the Implicit Difference Scheme
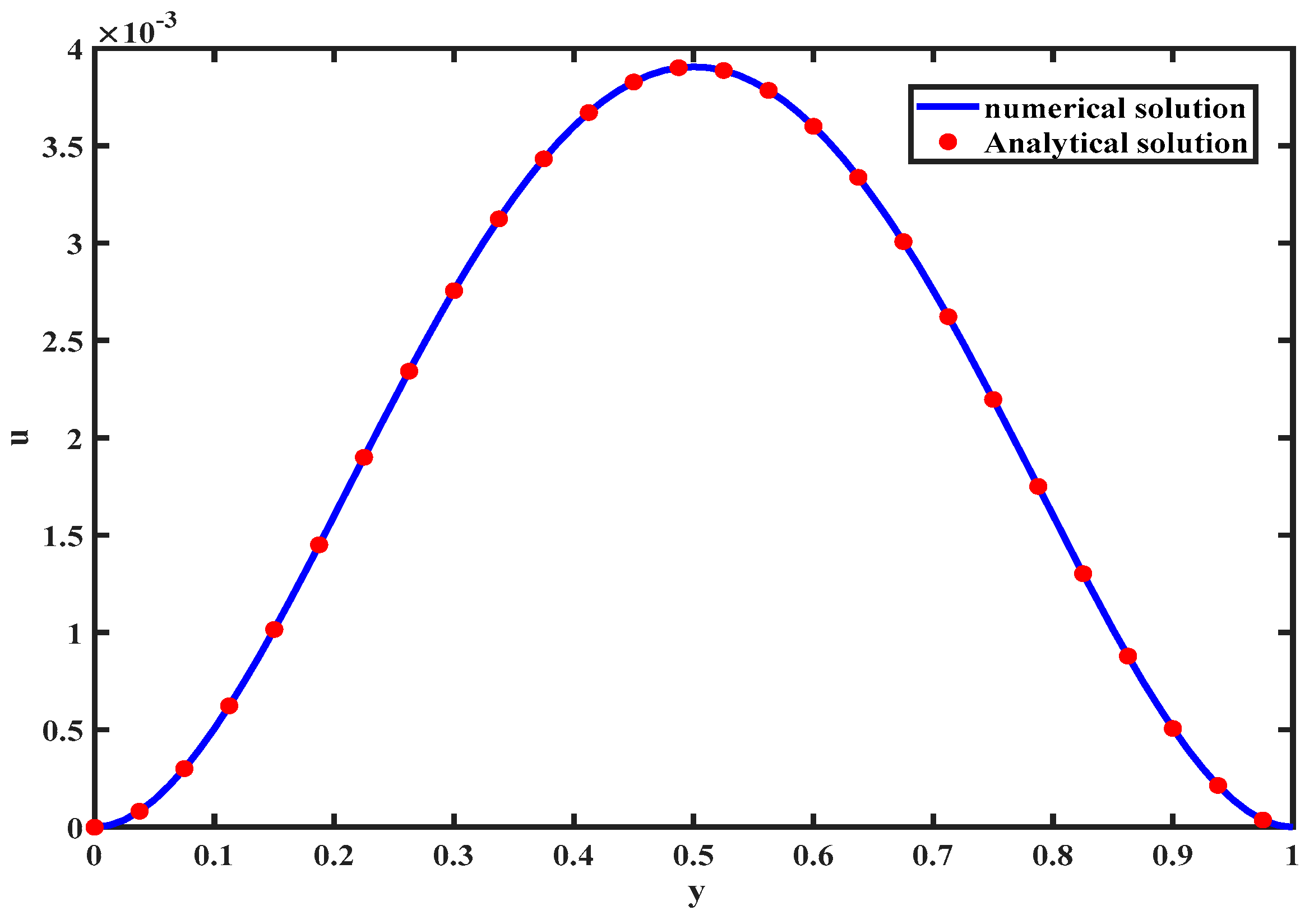
4. Validation of the Numerical Discretization Method
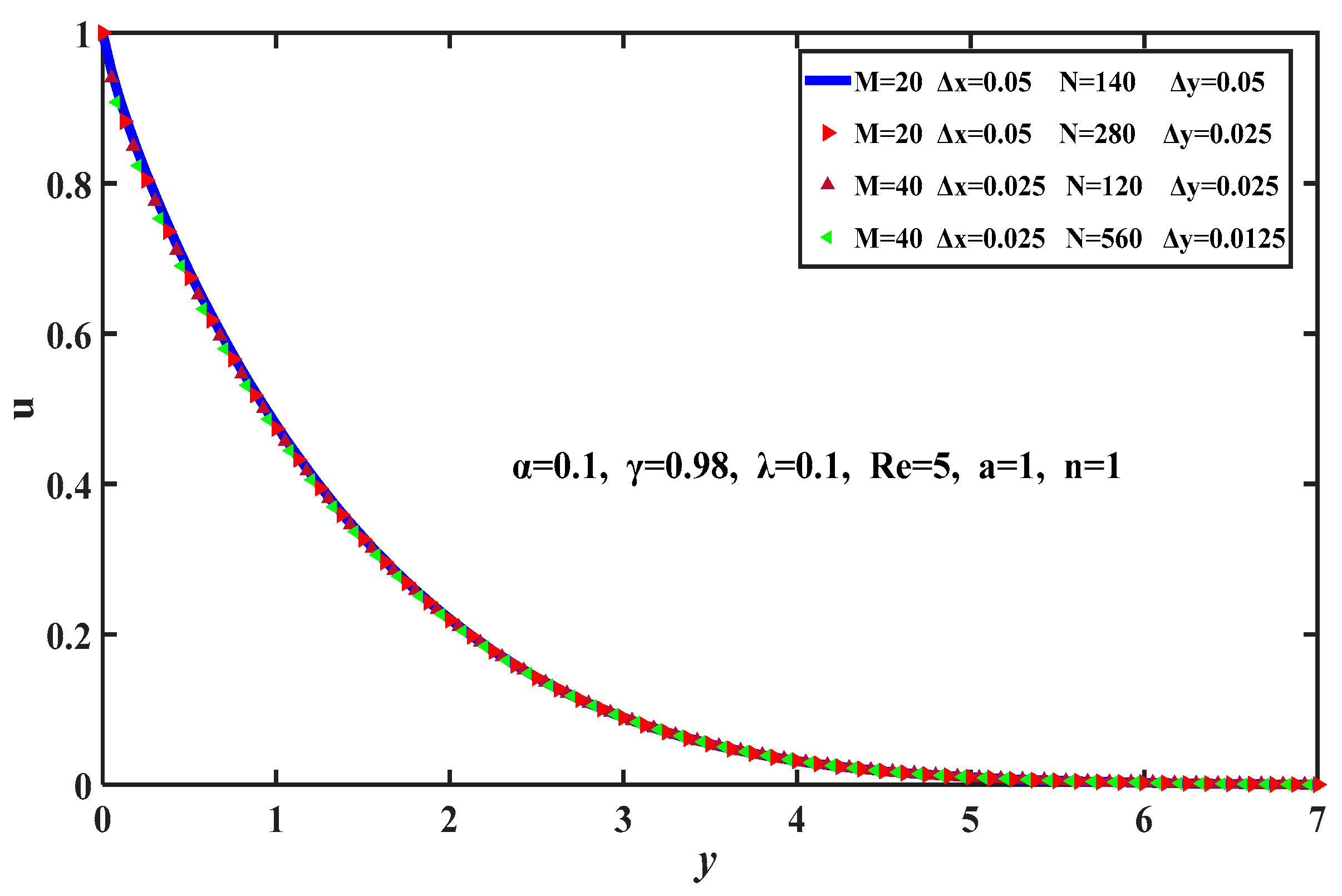
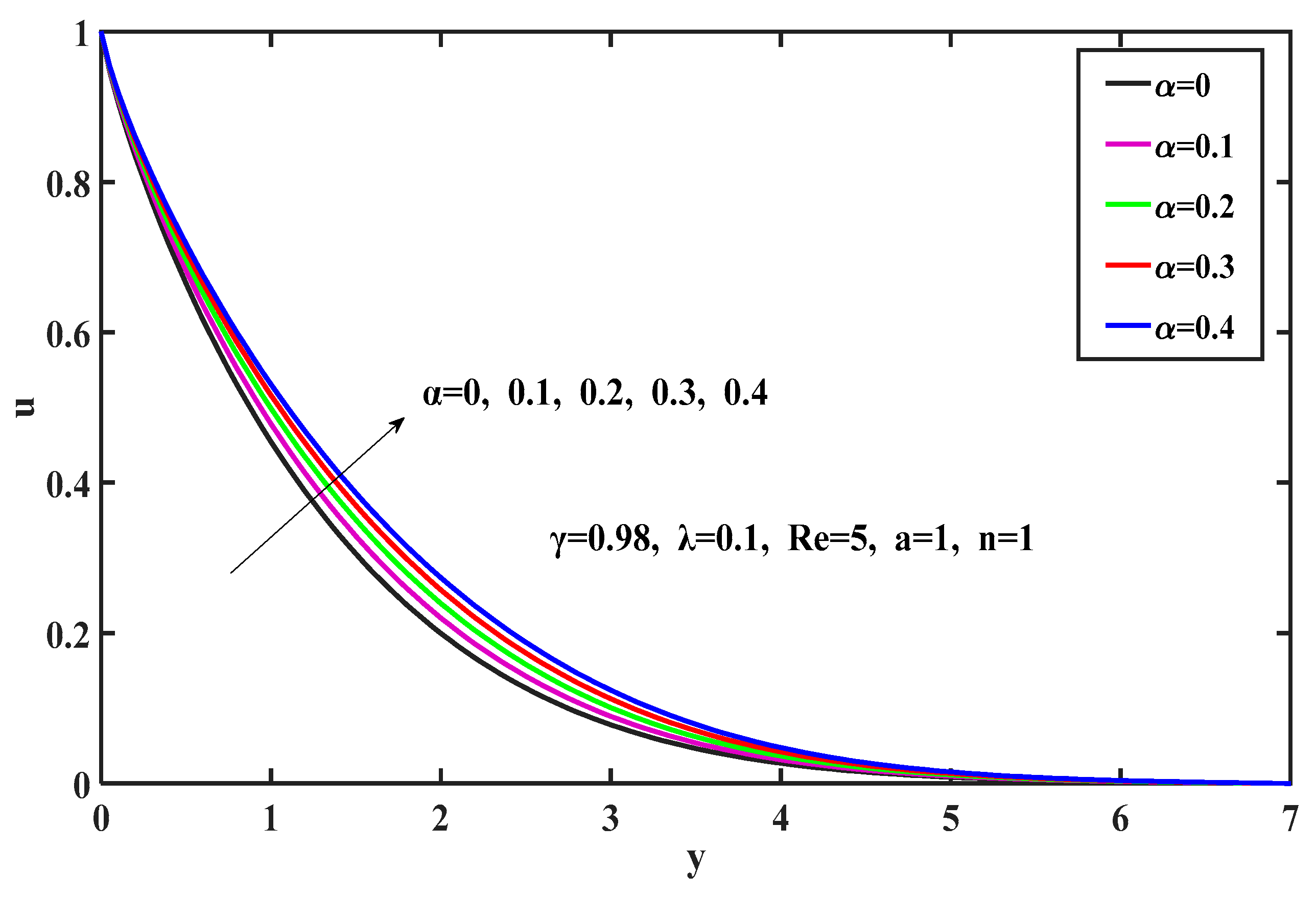
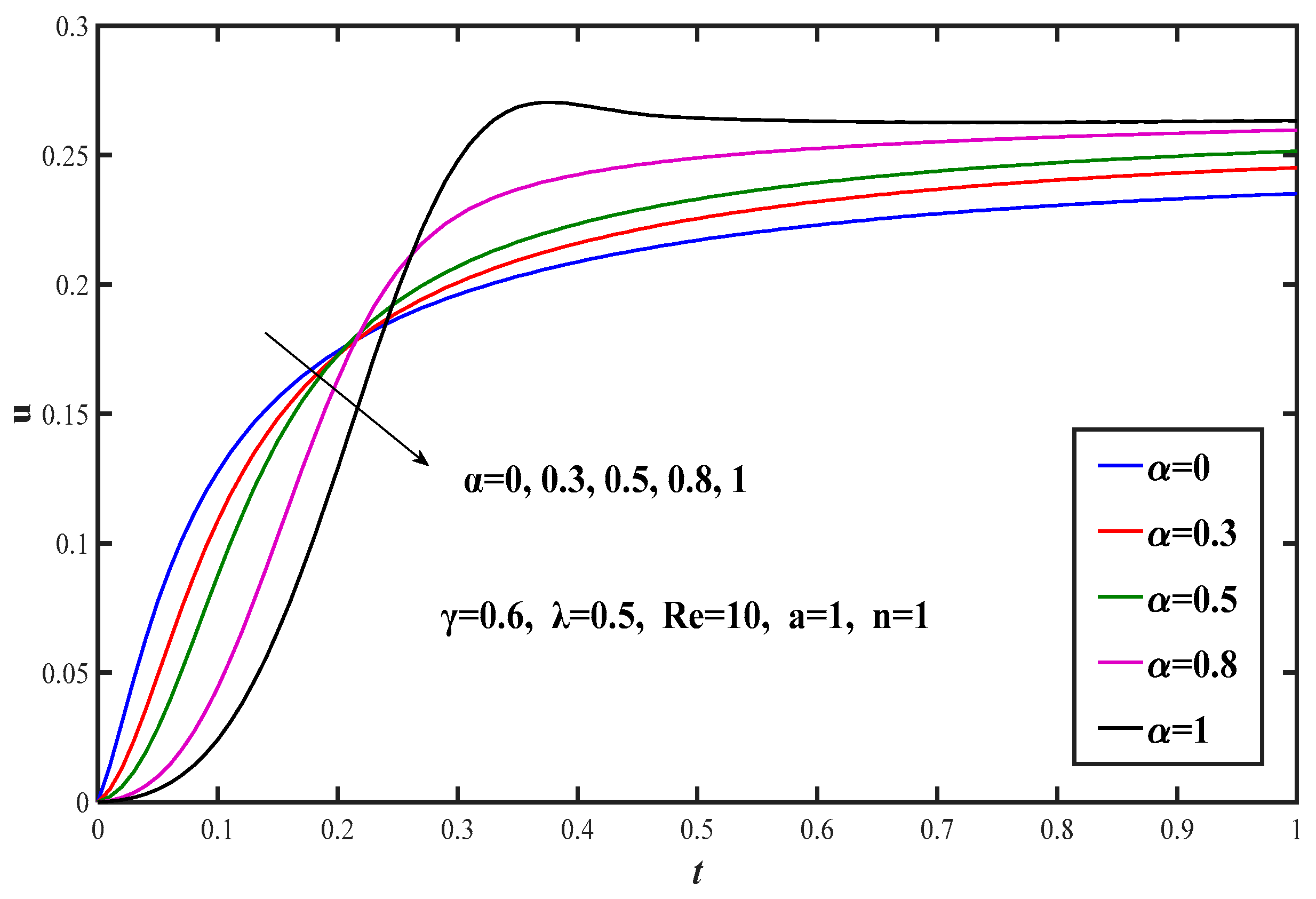
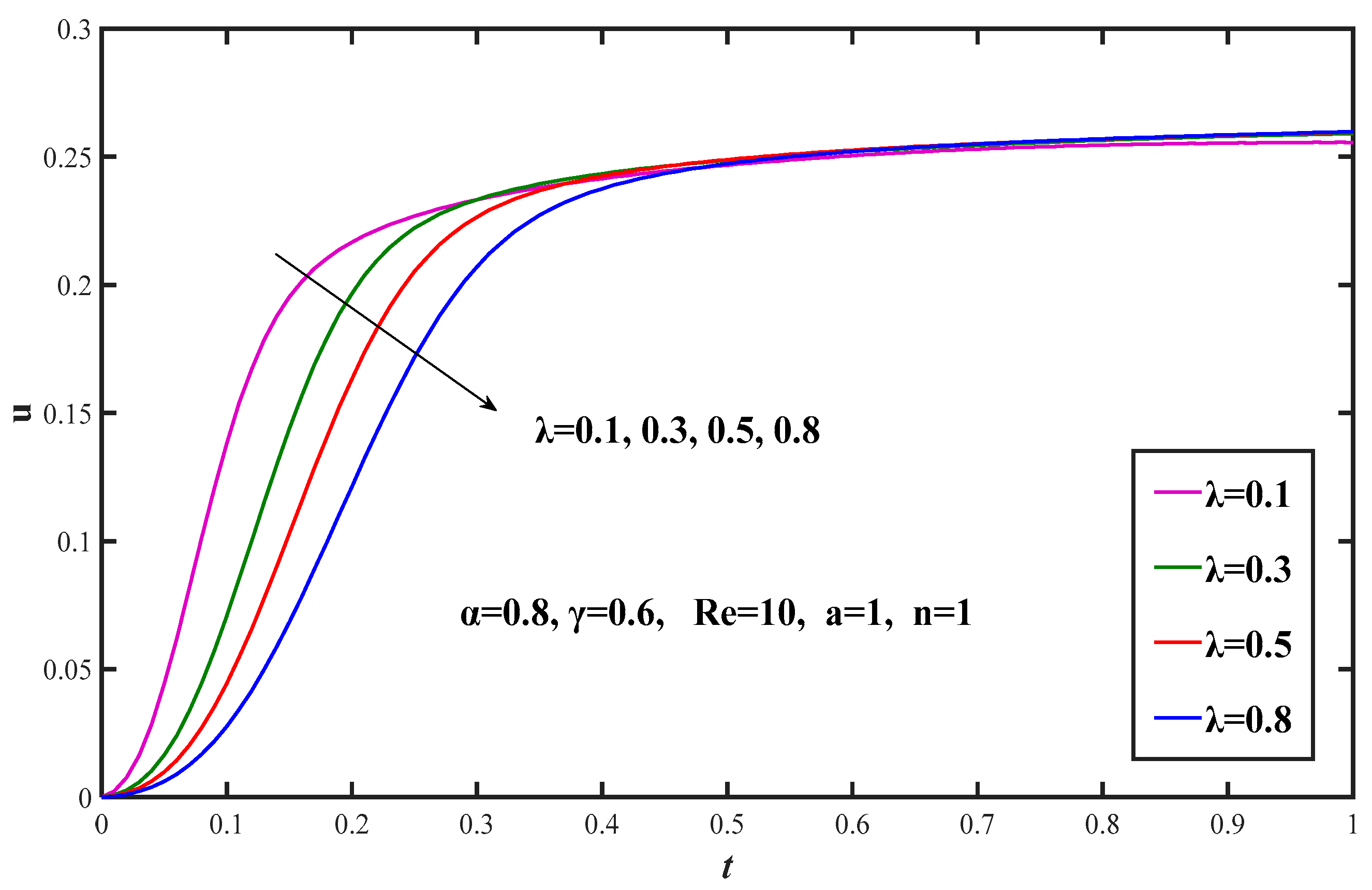
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Term | Definition |
| velocity component in the x-direction | |
| velocity component along -direction | |
| constant parameter | |
| stretching index | |
| shear stress | |
| density of fluid | |
| stress fractional parameter | |
| space fractional parameter | |
| relaxation parameter | |
| Reynolds number | |
| fractional dynamic viscosity |
References
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Caputo, M. Vibrations on an infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 1974, 56, 897–904. [Google Scholar] [CrossRef]
- Friedrich, C. Relaxation and retardation functions of the Maxwell model with fractional derivatives. Rheol. Acta 1991, 30, 151–158. [Google Scholar] [CrossRef]
- Makris, N.; Dargusf, D.F.; Constantinou, M.C. Dynamic analysis of generalized viscoelastic fluids. J. Eng. Mech. 1993, 119, 1663–1679. [Google Scholar] [CrossRef]
- Palade, L.I.; Verney, V.; Attane, P. A modified fractional model to describe the entire viscoelastic behavior of polybutadienes from flow to glassy regime. Rheol. Acta 1996, 35, 265–279. [Google Scholar] [CrossRef]
- Li, J.; Jiang, T.Q. The Research on Viscoelastic Constitutive Relationship Model with Fractional Derivative Operator; South China Technological University Press: Guangzhou, China, 1993. [Google Scholar]
- Song, D.Y.; Jiang, T.Q. Study on the constitutive equation with fractional derivative for the viscoelastic fluids—Modified Jeffreys model and its application. Rheol. Acta 1998, 27, 512–517. [Google Scholar] [CrossRef]
- Song, D.Y. Study of theological characterization of fenugreek gum with modified Maxwell. J. Chem. Eng. 2000, 8, 85–88. [Google Scholar]
- Tan, W.C.; Xu, M.Y. Plane surface suddenly set in motion in a viscoelastic fluid with fractional Maxwell model. Acta Mech. Sin. 2002, 18, 342–349. [Google Scholar]
- Tan, W.C.; Pan, W.X.; Xu, M.Y. A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates. Int. J. Nonlinear Mech. 2003, 38, 645–650. [Google Scholar]
- Zhu, K.Q.; Lu, Y.J.; Shen, P.P.; Wang, J.L. A study of start-up pipe flow of Maxwell fluid. Acta Mech. Sin. 2003, 35, 218–233. [Google Scholar]
- Tripathi, D.; Pandey, S.K.; Das, S. Peristaltic flow of viscoelastic fluid with fractional Maxwell model through a channel. Appl. Math. Comput. 2010, 215, 3645–3654. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C. Flow of a viscoelastic fluid with the fractional Maxwell model between two side walls perpendicular to a plate. Appl. Math. Comput. 2008, 200, 459–464. [Google Scholar] [CrossRef]
- Bekir, A.; Kaplan, M. Exponential rational function method for solving nonlinear equations arising in various physical models. Chin. J. Phys. 2016, 54, 365–370. [Google Scholar] [CrossRef]
- Uchalkin, V.V. Fractional Derivatives for Physicists and Engineers, Backgraound and Theory; Springer: Berlin, Germany, 2013; Volume 2. [Google Scholar]
- Zhao, J.H.; Zheng, L.C.; Zhang, X.X.; Liu, F.W. Unsteady natural convection boundary layer heat transfer of fractional Maxwell viscoelastic fluid over a vertical plate. Int. J. Heat Mass Transf. 2016, 97, 760–766. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhang, Y.; Wei, S.; Zhu, J.T.; Chen, W. A space fractional constitutive equation model for non-Newtonian fluid flow. Commun. Nonlinear Sci. Numer. Simulat. 2018, 62, 409–417. [Google Scholar] [CrossRef]
- Helin, T.; Lassas, M.; Ylianen, L.; Zhang, Z.D. Inverse problems for heat equation and space–time fractional diffusion equation with one measurement. J. Diff. Equ. 2020, 269, 7498–7528. [Google Scholar] [CrossRef]
- Lopushansky, A.; Lopushansky, O.; Sharyn, S. Nonlinear inverse problem of control diffusivity parameter determination for a space-time fractional diffusion equation. App. Math. Comput. 2020, 391, 125589. [Google Scholar] [CrossRef]
- Li, L.; Lin, R.M.; Ng, T.G. A fractional nonlocal time-space viscoelasticity theory and its applications in structural dynamics. Appl. Math. Model. 2020, 84, 116–136. [Google Scholar] [CrossRef]
- Chen, S.; Zheng, L.; Shen, B.; Chen, X. Time–space dependent fractional boundary layer flow of Maxwell fluid over an unsteady stretching surface. Theor. Appl. Mech. Lett. 2015, 5, 262–266. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.; Liu, F.; Zhang, X. Heat conduction with fractional cattaneo-christov upper-convective derivative flux model. Int. J. Therm. Sci. 2017, 112, 421–426. [Google Scholar] [CrossRef]
- Povstenko, Y. Thermoelasticity based on space-time-fractional heat conduction equation. Solid Mech. Appl. 2015, 219, 171–190. [Google Scholar]
- Atanacković, T.; Sanja, K.; Ljubica, O.; Dušan, Z. The cattaneo type space-time fractional heat conduction equation. Contin. Mech. Thermodyn. 2012, 24, 293–311. [Google Scholar] [CrossRef]
- Chen, X.; Ye, Y.; Zhang, X.; Zheng, L. Lie-group similarity solution and analysis for fractional viscoelastic MHD fluid over a stretching sheet. Comput. Math. Appl. 2018, 75, 3002–3011. [Google Scholar] [CrossRef]
- Jannelli, A.; Ruggieri, M.; Speciale, M.P. Analytical and numerical solutions of time and space fractional advection–diffusion–reaction equation. Commun. Nonlinear Sci. Numer. Simulat. 2019, 70, 89–101. [Google Scholar] [CrossRef]
- Pan, M.Y.; Zheng, L.C.; Liu, F.W.; Zhang, X.X. Lie group analysis and similarity solution for fractional Blasius flow. Commun. Nonlinear Sci. Numer. Simulat. 2016, 37, 90–101. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Liu, F.; Bai, Y. Analytical and numerical solutions of the unsteady 2D flow of MHD fractional Maxwell fluid induced by variable pressure gradient. Comput. Math. Appl. 2018, 75, 965–980. [Google Scholar] [CrossRef]
- Yang, D.; Zhu, K. Start-up flow of a viscoelastic fluid in a pipe with a fractional Maxwell’s model. Comput. Math. Appl. 2010, 60, 2231–2238. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Davarpanah, A.; Zarei, M.; Valizadeh, K.; Mirshekari, B. CFD design and simulation of ethylene dichloride (EDC) thermal cracking reactor. Energy Sources Part A 2019, 41, 1573–1587. [Google Scholar] [CrossRef]
- Valizadeh, K.; Farahbakhsh, S.; Bateni, A.; Zargarian, A.; Davarpanah, A.; Alizadeh, A.; Zarei, M. A parametric study to simulate the non-Newtonian turbulent flow in spiral tubes. Wiley Online Libr. 2020, 8, 134–149. [Google Scholar] [CrossRef]
- Li, B.; Liu, F.W. Boundary layer flows of viscoelastic fluids over a nonuniform permeable surface. Comput. Math. Appl. 2020, 79, 2376–2387. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
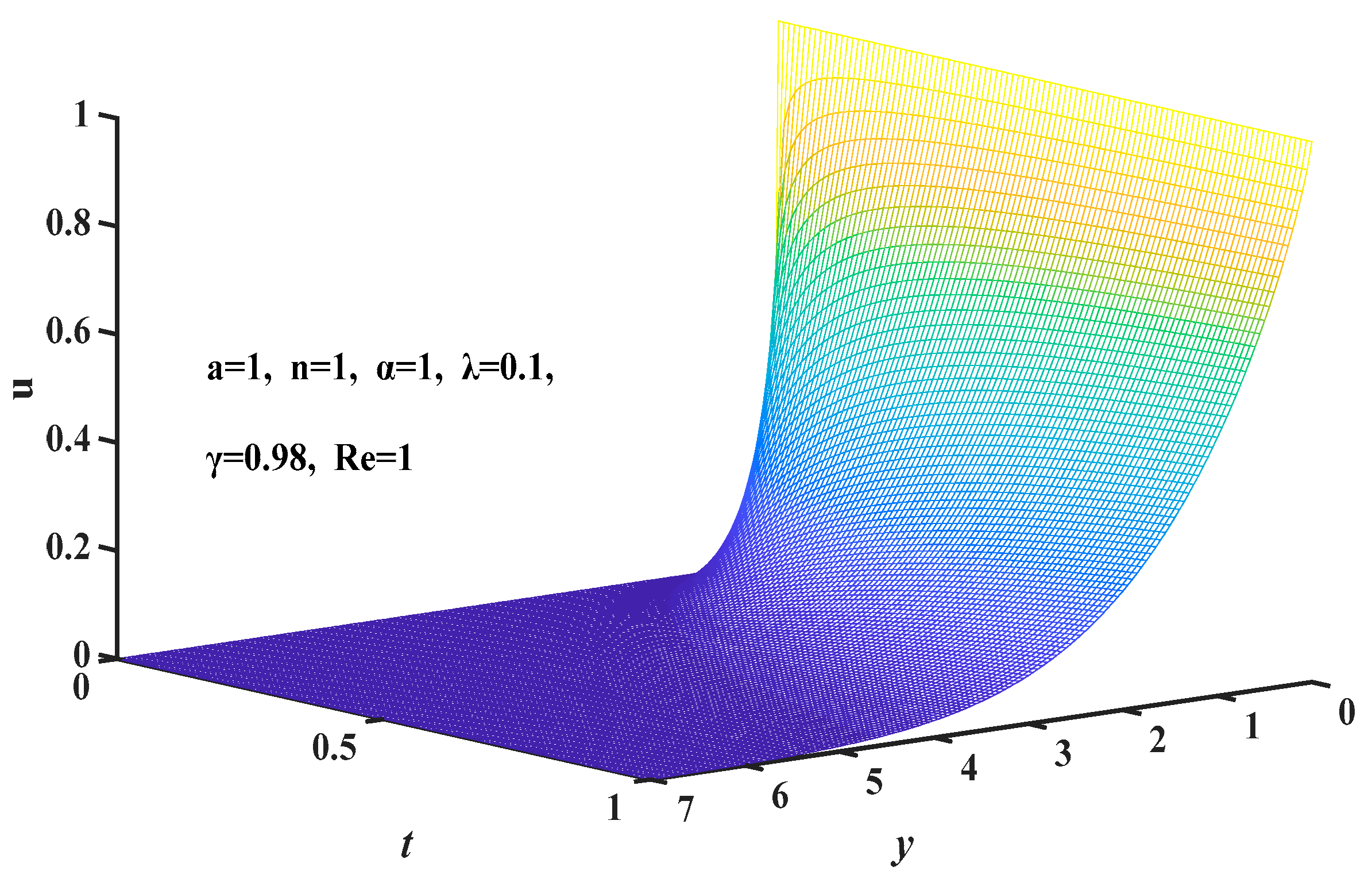

| Error | Order | Error | Order | |
| 1/8 | 3.9055e-05 | - | 8.4866e-05 | - |
| 1/16 | 1.9529e-05 | 0.9989 | 4.2644e-05 | 0.9282 |
| 1/32 | 9.7050e-06 | 1.0088 | 2.1337e-05 | 0.9901 |
| 1/64 | 4.8460e-06 | 1.0019 | 1.0655e-05 | 1.0018 |
| Error | Order | Error | Order | |
| 1/8 | 4.0576e-05 | - | 8.9865e-05 | - |
| 1/16 | 2.0305e-05 | 0.9988 | 4.4954e-05 | 0.9993 |
| 1/32 | 1.0087e-05 | 1.0093 | 2.2335e-05 | 1.0092 |
| 1/64 | 5.0183e-06 | 1.0071 | 1.1127e-05 | 1.0052 |
| Error | Order | Error | Order | |
| 1/8 | 5.7726e-05 | - | 1.3641e-04 | - |
| 1/16 | 2.6869e-05 | 1.1033 | 6.3664e-05 | 1.0993 |
| 1/32 | 1.2973e-05 | 1.0504 | 3.0797e-05 | 1.0477 |
| 1/64 | 6.3905e-06 | 1.0215 | 1.5257e-05 | 1.0133 |
| Error | Order | Error | Order | |
| 1/8 | 5.6212e-05 | - | 1.3151e-04 | - |
| 1/16 | 2.6040e-05 | 1.1101 | 6.1069e-05 | 1.1067 |
| 1/32 | 1.2539e-05 | 1.0543 | 2.9888e-05 | 1.0309 |
| 1/64 | 6.1704e-06 | 1.0230 | 1.4809e-05 | 1.0131 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Chen, X.; Meng, Y.; Zhang, X.; Mi, S. Numerical Solutions of Unsteady Boundary Layer Flow with a Time-Space Fractional Constitutive Relationship. Symmetry 2020, 12, 1446. https://doi.org/10.3390/sym12091446
Yang W, Chen X, Meng Y, Zhang X, Mi S. Numerical Solutions of Unsteady Boundary Layer Flow with a Time-Space Fractional Constitutive Relationship. Symmetry. 2020; 12(9):1446. https://doi.org/10.3390/sym12091446
Chicago/Turabian StyleYang, Weidong, Xuehui Chen, Yuan Meng, Xinru Zhang, and Shiyun Mi. 2020. "Numerical Solutions of Unsteady Boundary Layer Flow with a Time-Space Fractional Constitutive Relationship" Symmetry 12, no. 9: 1446. https://doi.org/10.3390/sym12091446
APA StyleYang, W., Chen, X., Meng, Y., Zhang, X., & Mi, S. (2020). Numerical Solutions of Unsteady Boundary Layer Flow with a Time-Space Fractional Constitutive Relationship. Symmetry, 12(9), 1446. https://doi.org/10.3390/sym12091446






