Nonstandard Finite Difference Schemes for the Study of the Dynamics of the Babesiosis Disease
Abstract
1. Introduction
2. Mathematical Model
- (i)
- System (2) has the disease-free equilibrium point for all values of the parameters in this system, whereas, only if , there is a (unique) endemic equilibrium point in the interior of given by
- (ii)
- If , then the disease-free point is globally asymptotically stable; otherwise, the disease-free point is unstable.
- (iii)
- If , then the endemic point is shown to be locally asymptotically stable by numerical simulations.
3. Nonstandard Finite Difference Schemes for System (2)
- (i)
- If, then the disease-free equilibrium pointis globally asymptotically stable.
- (ii)
- If, then the disease-free equilibrium pointis unstable.
- (i)
- We will use an extension for the discrete case (see in [28], Theorem 3.3) of the Lyapunov stability theorem [29] to prove this part. For this purpose, consider a function defined byClearly, V is continuous, for all , and .From (6), we havewhich implies that for all .Let be the largest positively invariant set contained inThen, by using (9) we have thatConsequently, it is easy to verify that is -globally asymptotically stable if .
- (ii)
- Computing the Jacobian matrix of system (6) evaluated at the disease free point, one obtainsConsequently, the eigenvalues of are and , where are the eigenvalues ofWe haveThus, if , then . By Theorem 1.3.7 in [30] and Theorem 2.10 in [31], we can conclude that if then the disease-free equilibrium point is unstable.Thus, the theorem is proved. □
- Part (i) of Theorem 2 is only appropriate when is a positively invariant set of (6).
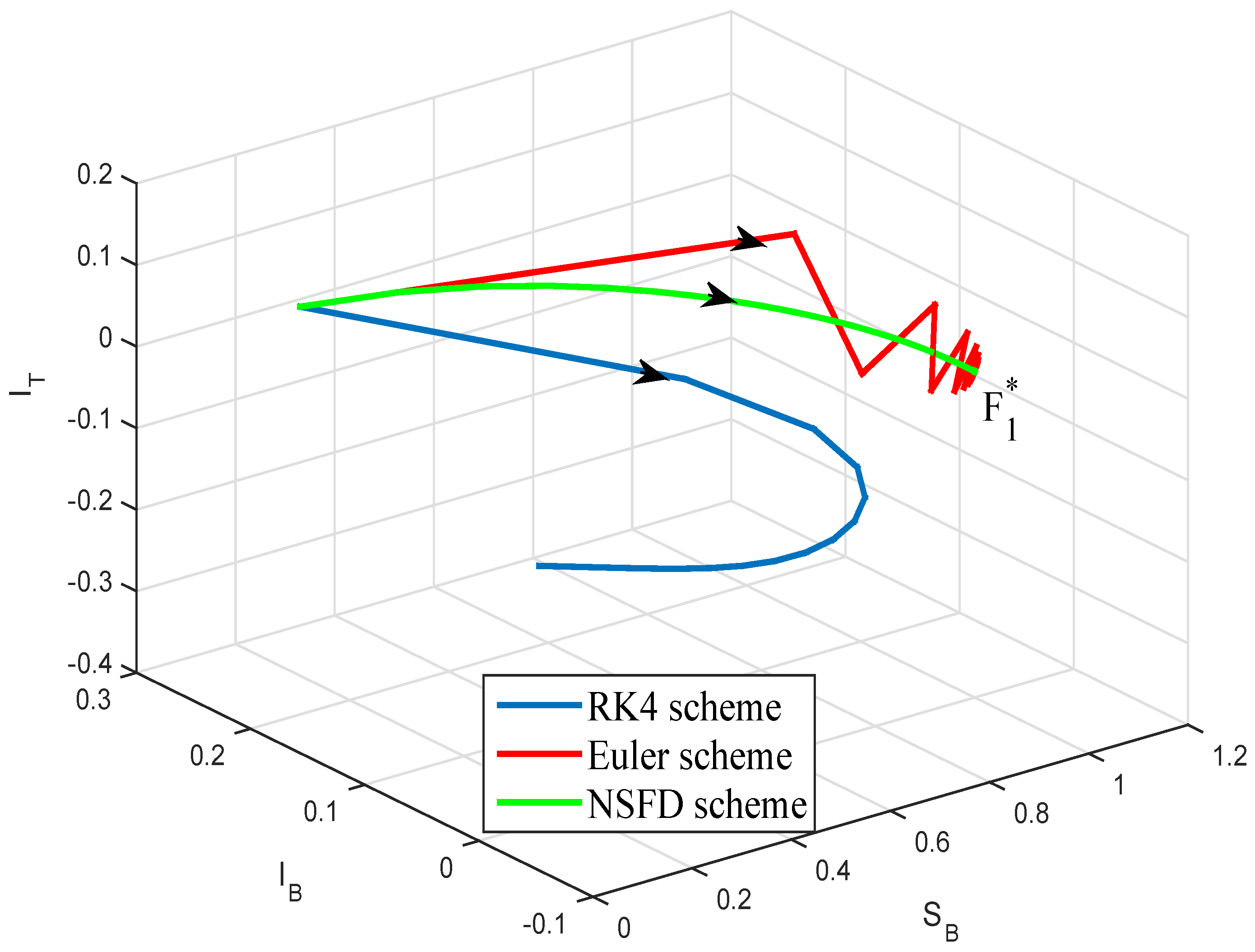
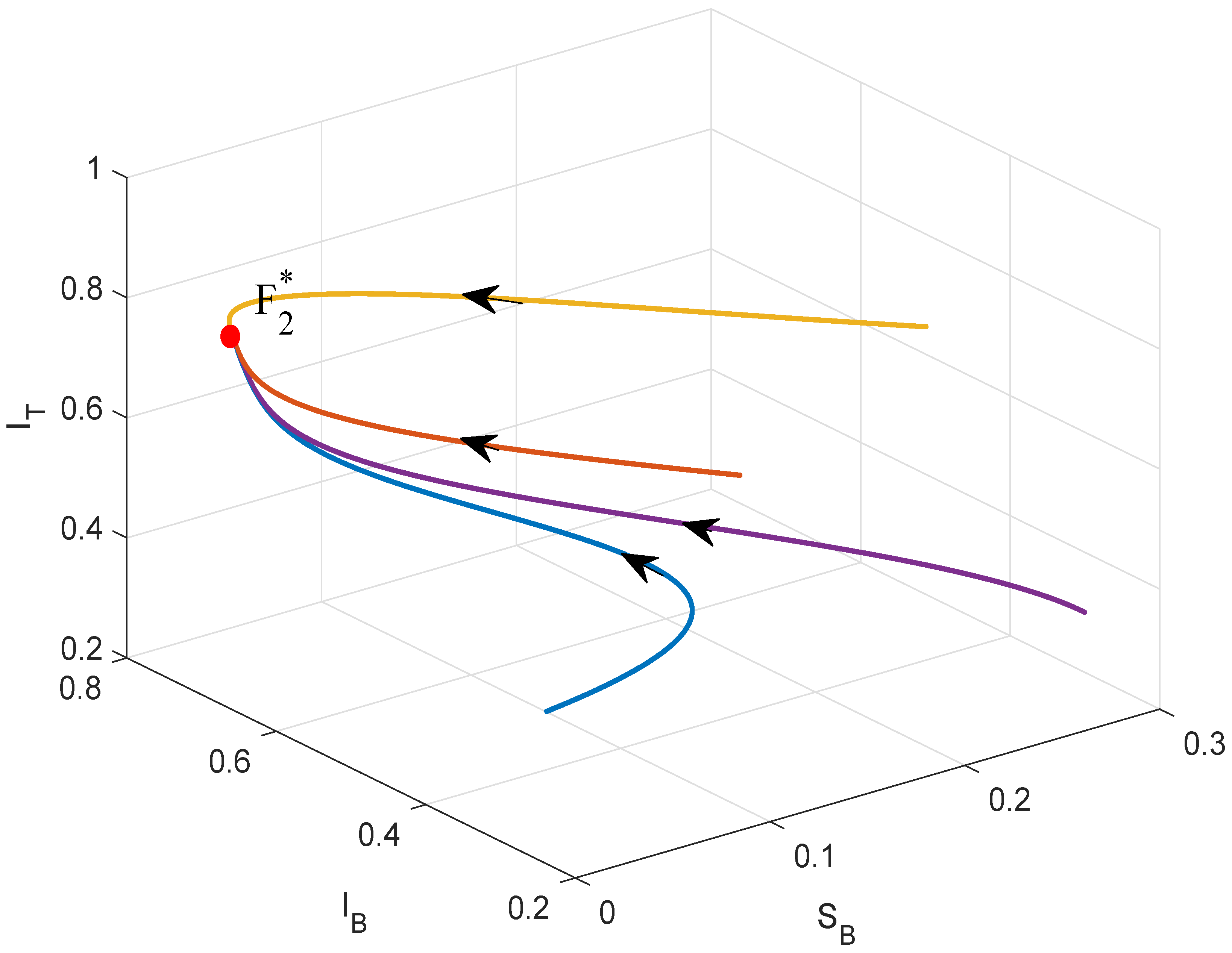
4. Numerical Simulations
5. Conclusions
Supplementary materials
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Solorio-Rivera, J.L.; Rodriguez-Vivas, R.I. Epidemiology of bovine babesiosis. I. Epidemiological Components. Rev. Biomed. 1997, 8, 37–47. [Google Scholar]
- Solorio-Rivera, J.L.; Rodriguez-Vivas, R.I. Epidemiology of the babesiosis bovis. II. Epidemiologic indicators and elements for the design of strategies of control. Rev. Biomed. 1997, 8, 95–105. [Google Scholar]
- Aranda, D.F.; Trejos, D.Y.; Valverde, J.C.; Villanueva, R.-J. A mathematical model for Babesiosis disease in bovine and tick populations. Math. Methods Appl. Sci. 2011, 35, 249–256. [Google Scholar] [CrossRef]
- Bouzid, L.; Belhamiti, O. Effect of seasonal changes on predictive model of bovine babesiosis transmission. Int. J. Model. Simul. Sci. Comput. 2017, 8, 1750030. [Google Scholar] [CrossRef]
- Carvalho dos Santos, J.P.; Cardoso, L.C.; Monteiro, E.; Lemes, N.H.T. A Fractional-Order Epidemic Model for Bovine Babesiosis Disease and Tick Populations. Abstr. Appl. Anal. 2015, 2015, 729894. [Google Scholar] [CrossRef]
- Friedman, A.; Yakubu, A.-A. A Bovine Babesiosis Model with Dispersion. Bull. Math. Boil. 2013, 76, 98–135. [Google Scholar] [CrossRef]
- Pourbashash, H. Global Analysis of the Babesiosis Disease in Bovine and Tick Populations Model and Numerical Simulation with Multistage Modified Sinc Method. Iran. J. Sci. Technol. Trans. A Sci. 2018, 42, 39–46. [Google Scholar] [CrossRef]
- Saad-Roy, M.C.; Shuai, Z.; Van den Driessche, P. Driessche, Models of bovine Babesiosis including juvenile cattle. Bull. Math. Biol. 2015, 77, 514–547. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; Rehan, K.; Mushtaq, M. Fractional-order scheme for bovine babesiosis disease and tick populations. Adv. Differ. Equ. 2017, 2017, 4. [Google Scholar] [CrossRef]
- Aranda, D.F.; Trejos-Angel, D.Y.; Valverde, J.C. A discrete epidemic model for bovine Babesiosis disease and tick populations. Open Phys. 2017, 15, 360–369. [Google Scholar] [CrossRef]
- Mickens, R.E. Applications of Nonstandard Finite Difference Schemes; World Scientific: Singapore, 2000. [Google Scholar]
- Adekanye, O.; Washington, T. Nonstandard finite difference scheme for a Tacoma Narrows Bridge model. Appl. Math. Model. 2018, 62, 223–236. [Google Scholar] [CrossRef]
- Dimitrov, D.T.; Kojouharov, H.V. Stability-Preserving Finite-Difference Methods For General Multi-Dimensional Autonomous Dynamical Systems. Int. J. Numer. Anal. Model 2007, 4, 280–290. [Google Scholar]
- Dimitrov, D.T.; Kojouharov, H.V. Nonstandard finite-difference schemes for general two-dimensional autonomous dynamical systems. Appl. Math. Lett. 2005, 18, 769–774. [Google Scholar] [CrossRef]
- Dimitrov, D.T.; Kojouharov, H.V. Positive and elementary stable nonstandard numerical methods with applications to predator–prey models. J. Comput. Appl. Math. 2006, 189, 98–108. [Google Scholar] [CrossRef]
- Dimitrov, D.T.; Kojouharov, H.V. Nonstandard finite-difference methods for predator–prey models with general functional response. Math. Comput. Simul. 2008, 78, 1–11. [Google Scholar] [CrossRef]
- Gurski, K.F. A simple construction of nonstandard finite-difference schemes for small nonlinear systems applied to SIR models. Comput. Math. Appl. 2013, 66, 2165–2177. [Google Scholar] [CrossRef]
- Korpusik, A. A nonstandard finite difference scheme for a basic model of cellular immune response to viral infection. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 369–384. [Google Scholar] [CrossRef]
- Roeger, L.-I.W.; Gelca, R. Dynamically Consistent Discrete-Time Lotka-Volterra Competition Models. In Proceedings of the 7th AIMS International Conference, Arlington, TX, USA, 18–21 May 2009; pp. 650–658. [Google Scholar]
- Wood, D.; Kojouharov, H.V. A class of nonstandard numerical methods for autonomous dynamical systems. Appl. Math. Lett. 2015, 50, 78–82. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Dynamically consistent discrete metapopulation model. J. Differ. Equ. Appl. 2016, 22, 1325–1349. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Lyapunov direct method for investigating stability of nonstandard finite difference schemes for metapopulation models. J. Differ. Equ. Appl. 2017, 24, 32–47. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Complete Global Stability of a Metapopulation Model and Its Dynamically Consistent Discrete Models. Qual. Theory Dyn. Syst. 2018, 18, 461–475. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Nonstandard finite difference schemes for a general predator–prey system. J. Comput. Sci. 2019, 36, 101015. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Positivity and global stability preserving NSFD schemes for a mixing propagation model of computer viruses. J. Comput. Appl. Math. 2020, 374, 112753. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Positive and elementary stable explicit nonstandard Runge-Kutta methods for a class of autonomous dynamical systems. Int. J. Comput. Math. 2019. [Google Scholar] [CrossRef]
- Hoang, M.T.; Nagy, A.M. Uniform asymptotic stability of a Logistic model with feedback control of fractional order and nonstandard finite difference schemes. Chaos Solitons Fractals 2019, 123, 24–34. [Google Scholar] [CrossRef]
- Iggidr, A.; Bensoubaya, M. New Results on the Stability of Discrete-Time Systems and Applications to Control Problems. J. Math. Anal. Appl. 1998, 219, 392–414. [Google Scholar] [CrossRef]
- LaSalle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Stuart, A.M.; Humphries, A.R. Dynamical Systems and Numerical Analysis, Cambridge Monographs on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Allen, L.J.S. An Introduction to Mathematical Biology; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, Q.A.; Hoang, M.T.; Trejos, D.Y.; Valverde, J.C. Nonstandard Finite Difference Schemes for the Study of the Dynamics of the Babesiosis Disease. Symmetry 2020, 12, 1447. https://doi.org/10.3390/sym12091447
Dang QA, Hoang MT, Trejos DY, Valverde JC. Nonstandard Finite Difference Schemes for the Study of the Dynamics of the Babesiosis Disease. Symmetry. 2020; 12(9):1447. https://doi.org/10.3390/sym12091447
Chicago/Turabian StyleDang, Quang A., Manh T. Hoang, Deccy Y. Trejos, and Jose C. Valverde. 2020. "Nonstandard Finite Difference Schemes for the Study of the Dynamics of the Babesiosis Disease" Symmetry 12, no. 9: 1447. https://doi.org/10.3390/sym12091447
APA StyleDang, Q. A., Hoang, M. T., Trejos, D. Y., & Valverde, J. C. (2020). Nonstandard Finite Difference Schemes for the Study of the Dynamics of the Babesiosis Disease. Symmetry, 12(9), 1447. https://doi.org/10.3390/sym12091447




