A Collocation Method Using Radial Polynomials for Solving Partial Differential Equations
Abstract
1. Introduction
2. Formulation of the Radial Polynomials
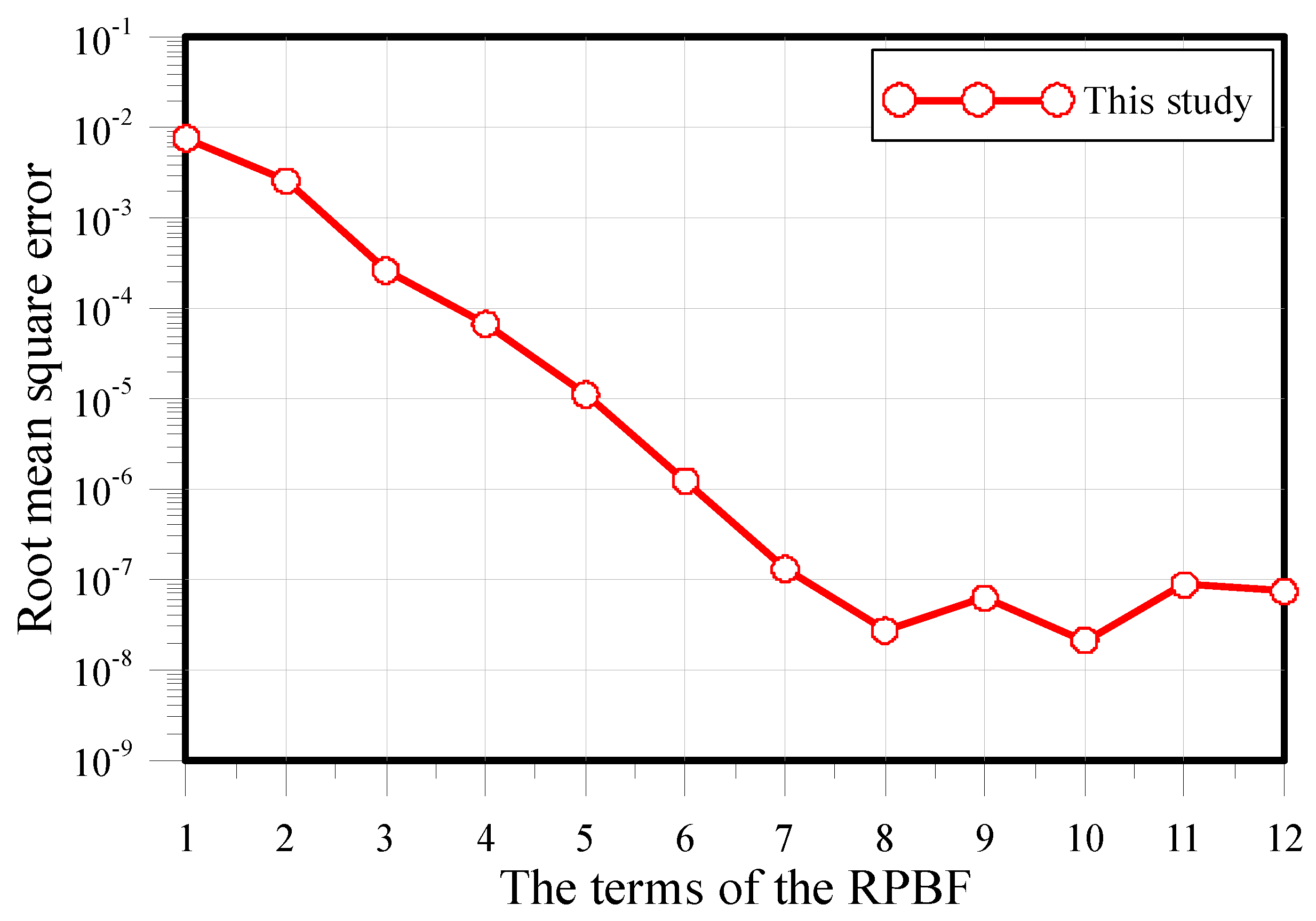
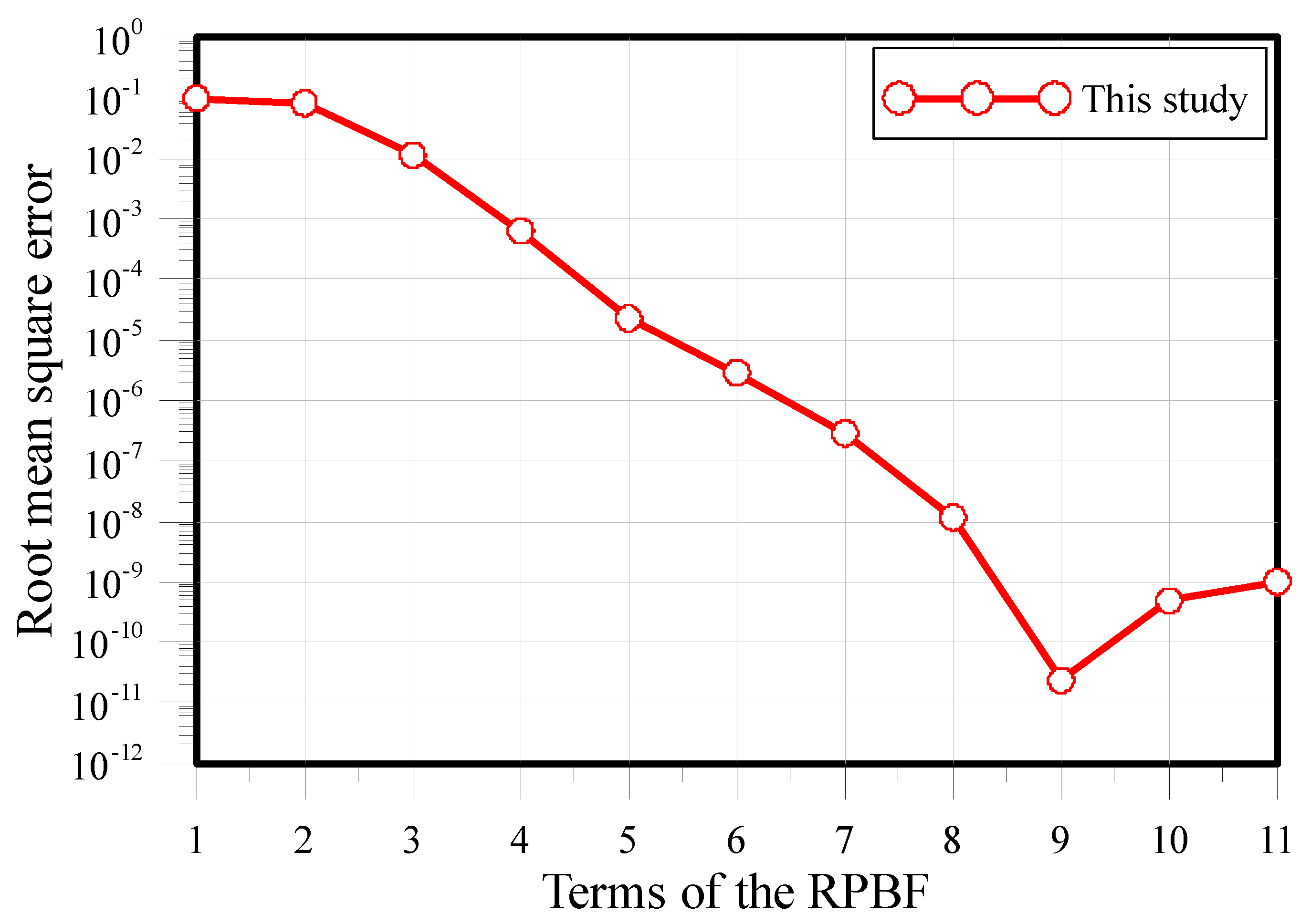
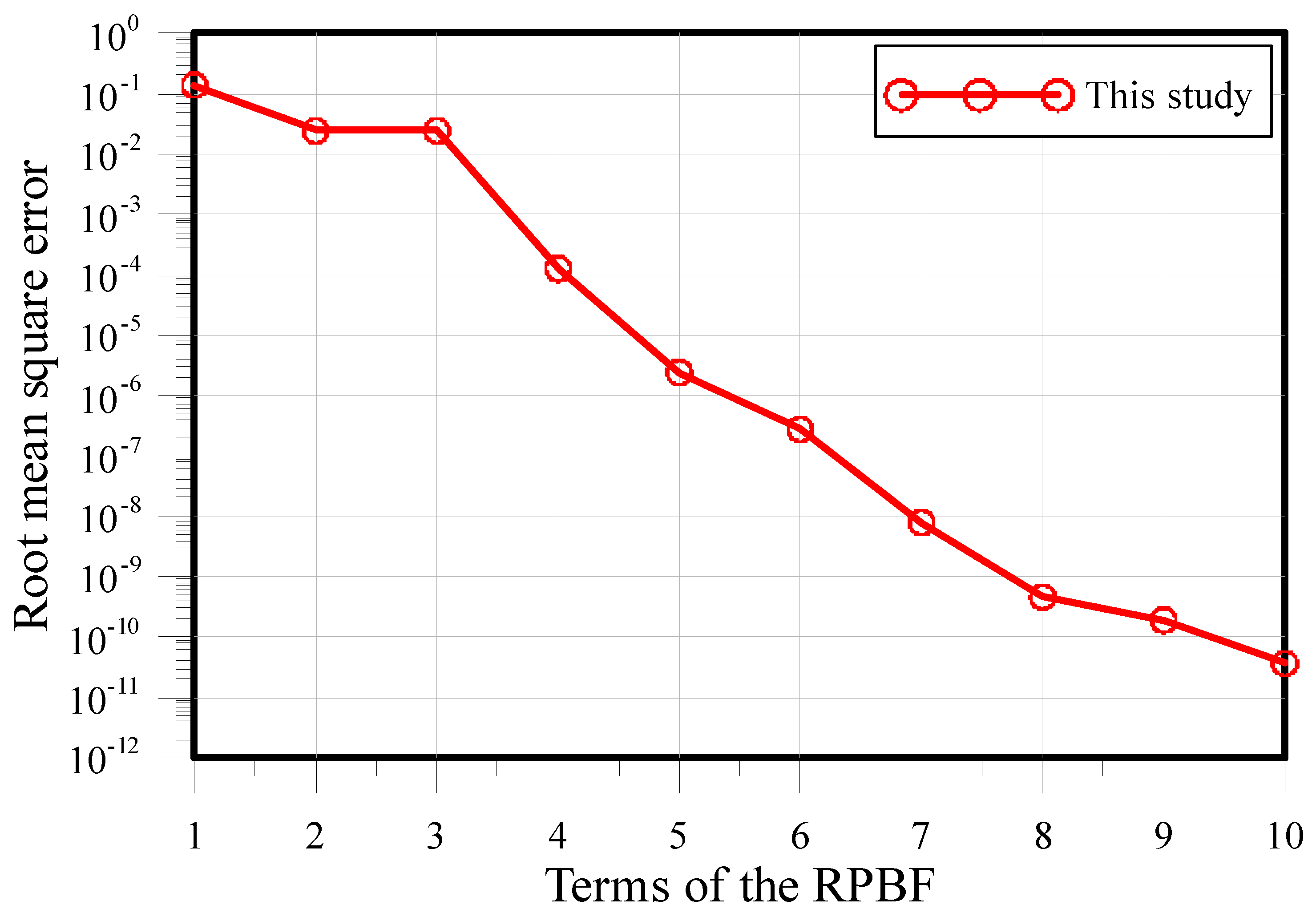
3. Accuracy and Convergence Analysis
4. Numerical Examples
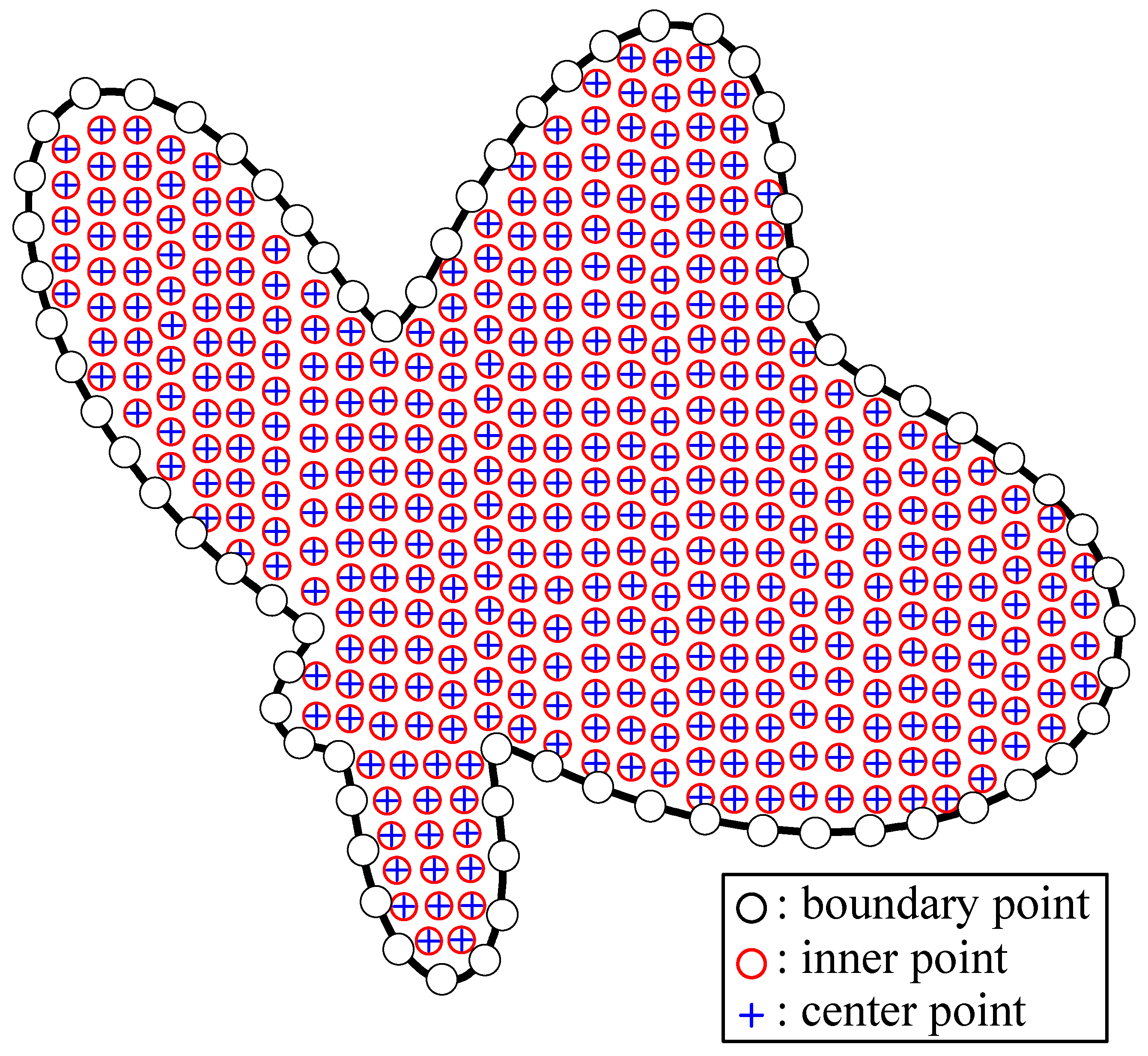
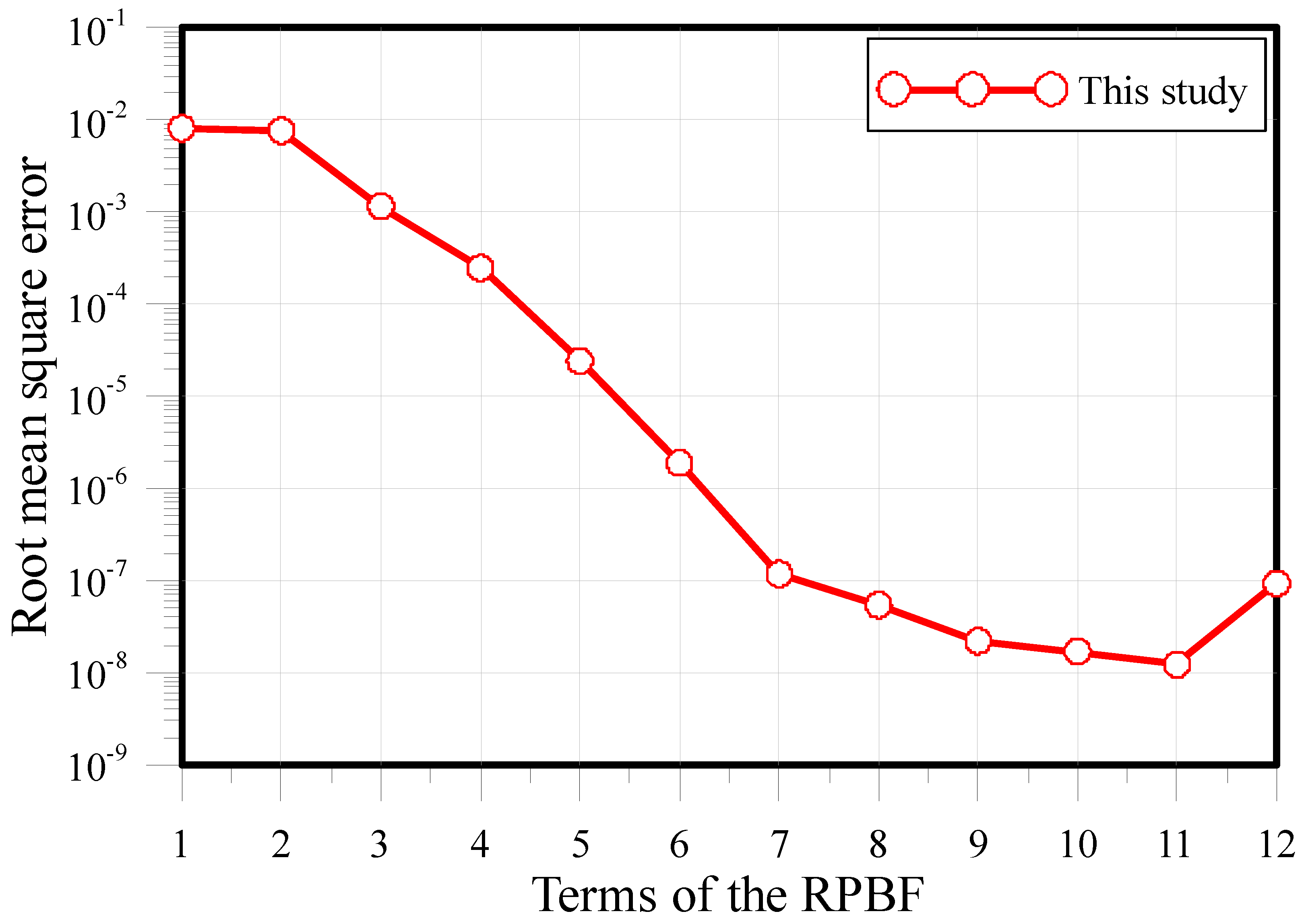
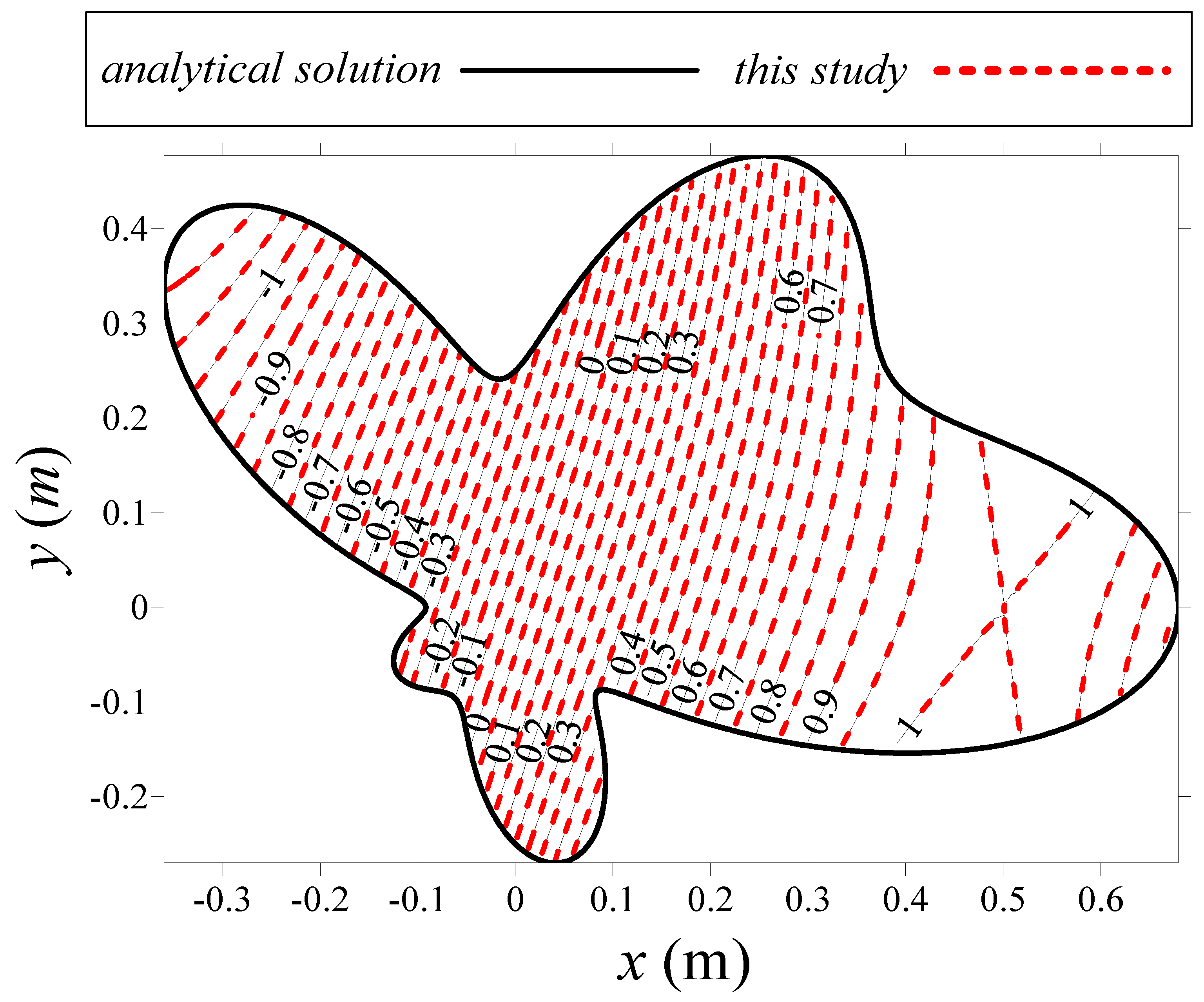
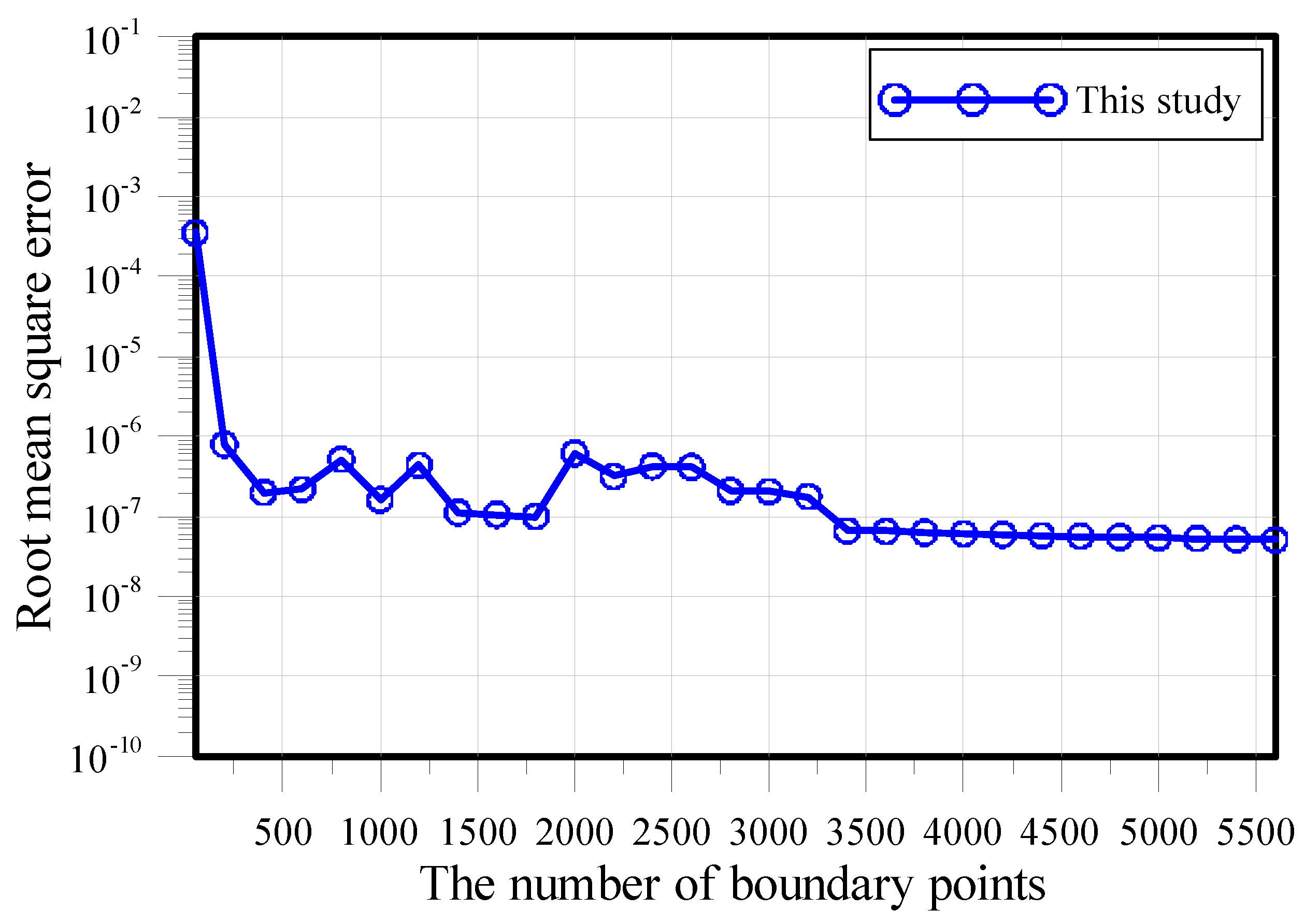
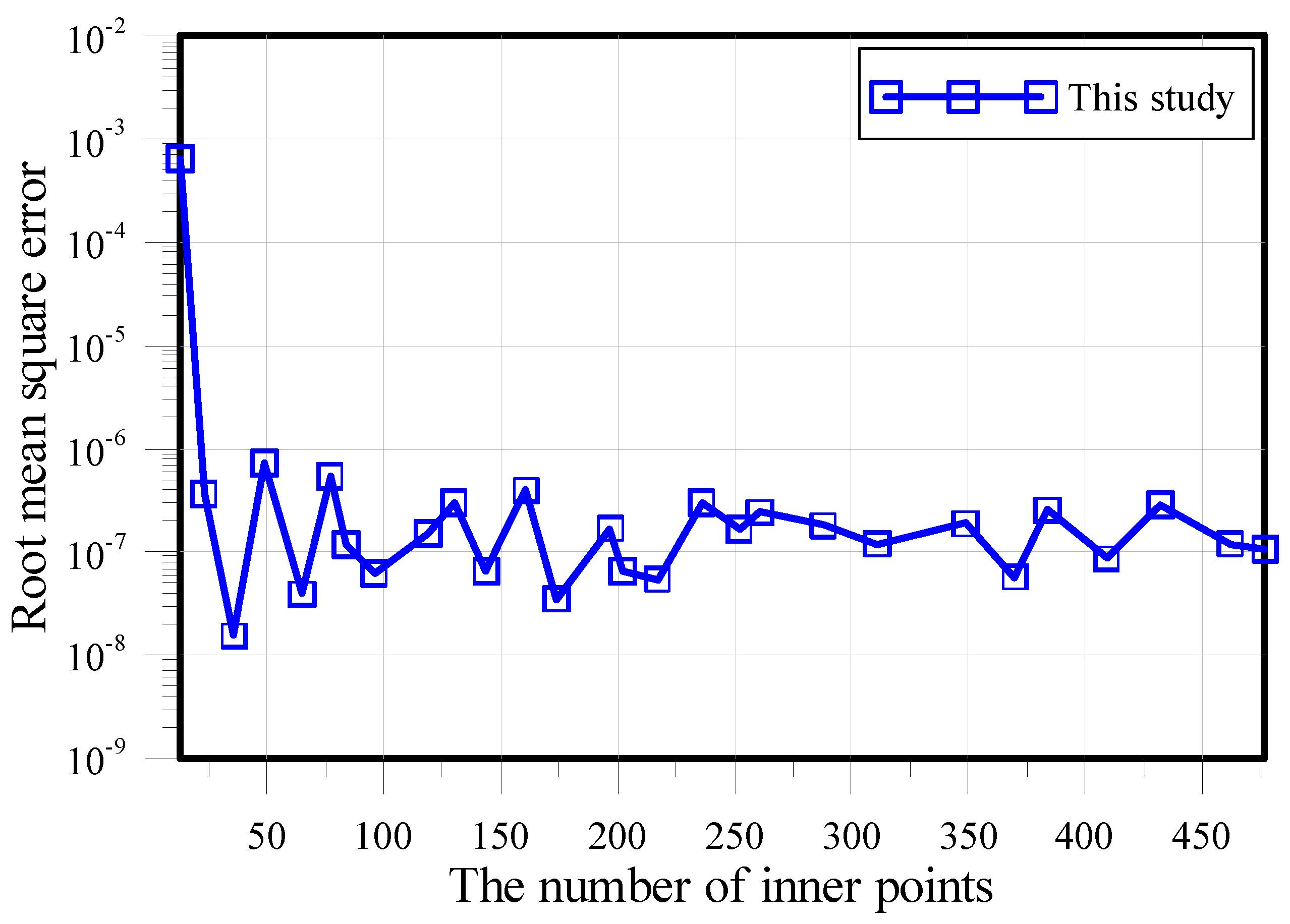
4.1. A Two-Dimensional Ameoba-Shaped Problem
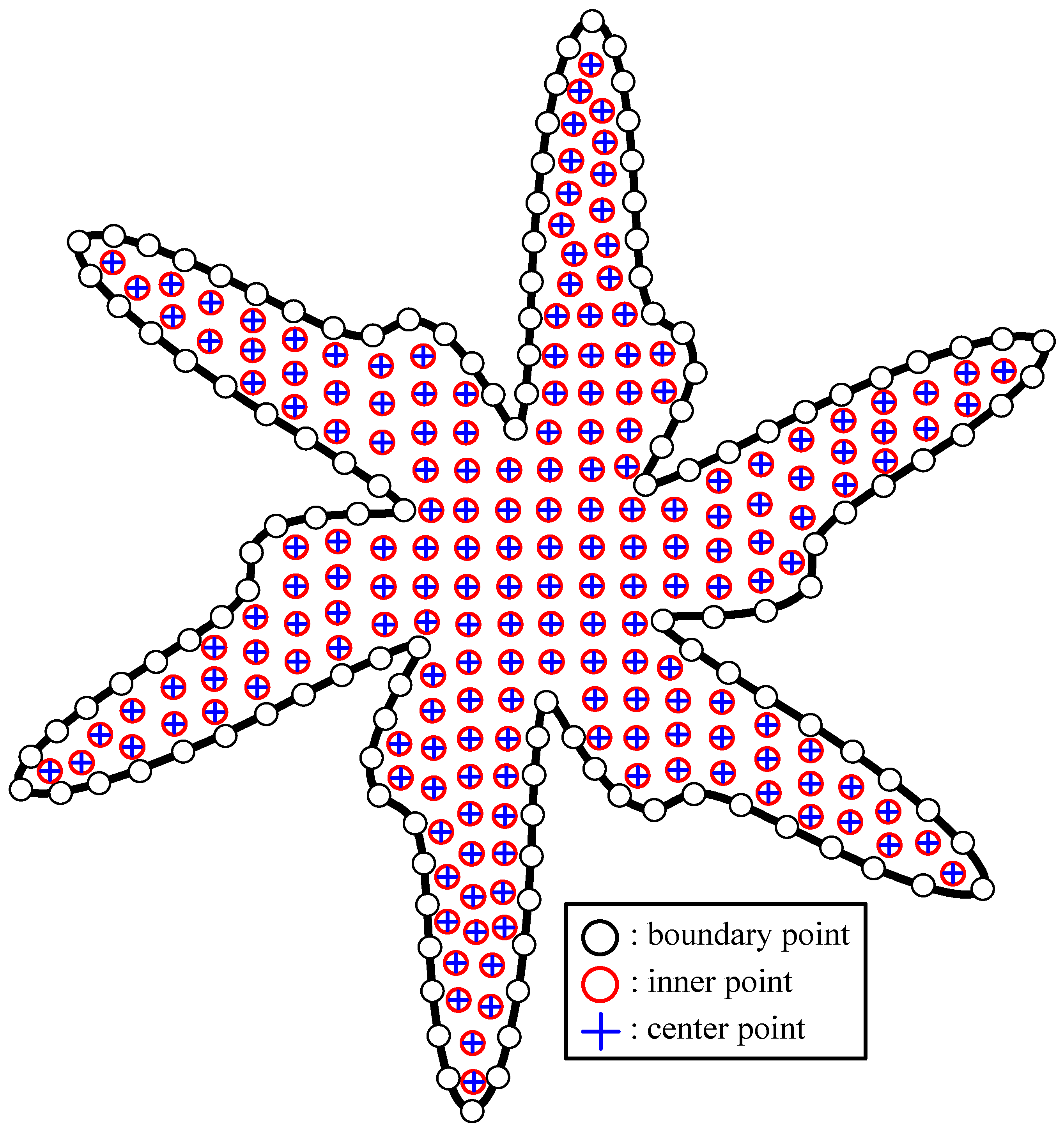
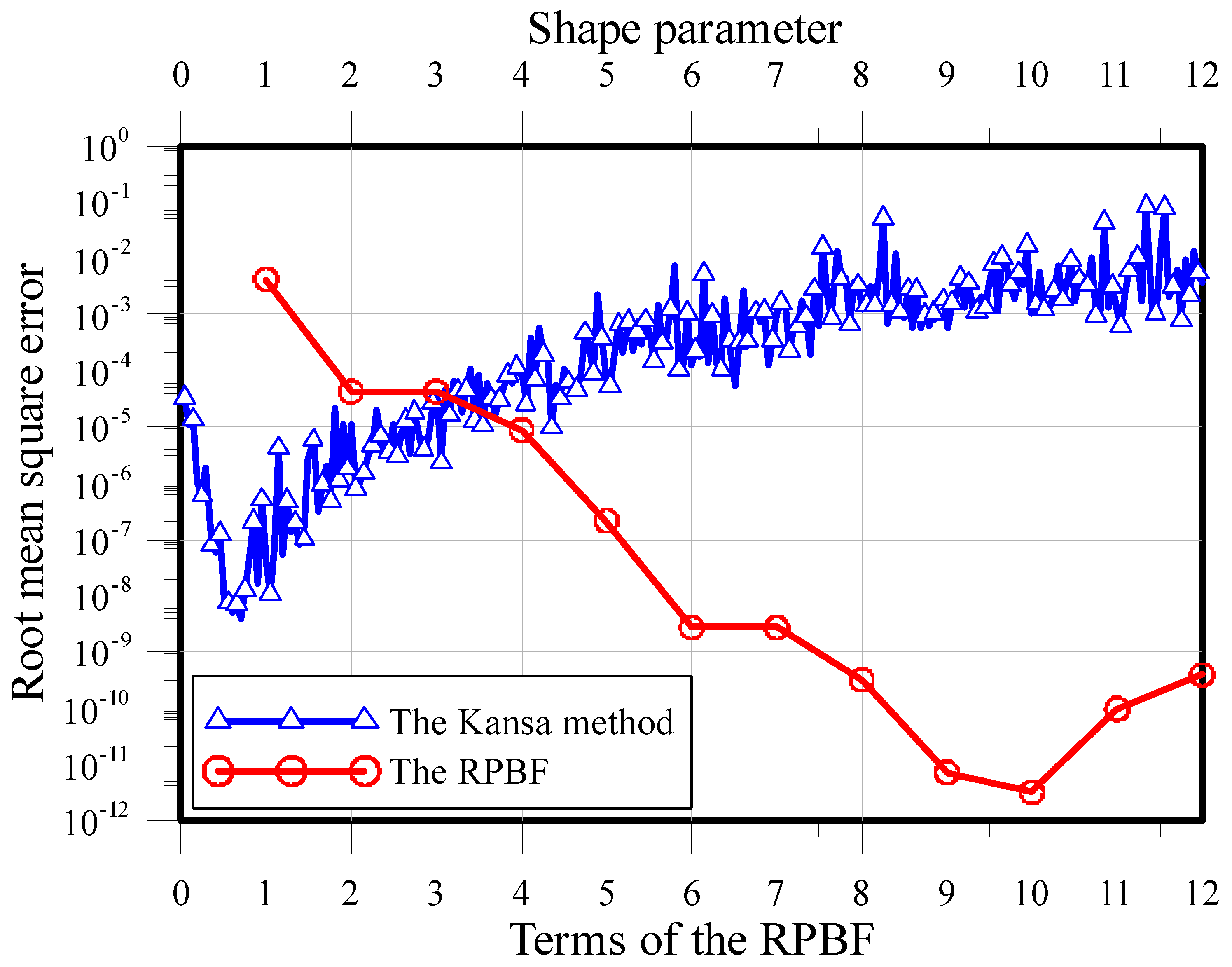
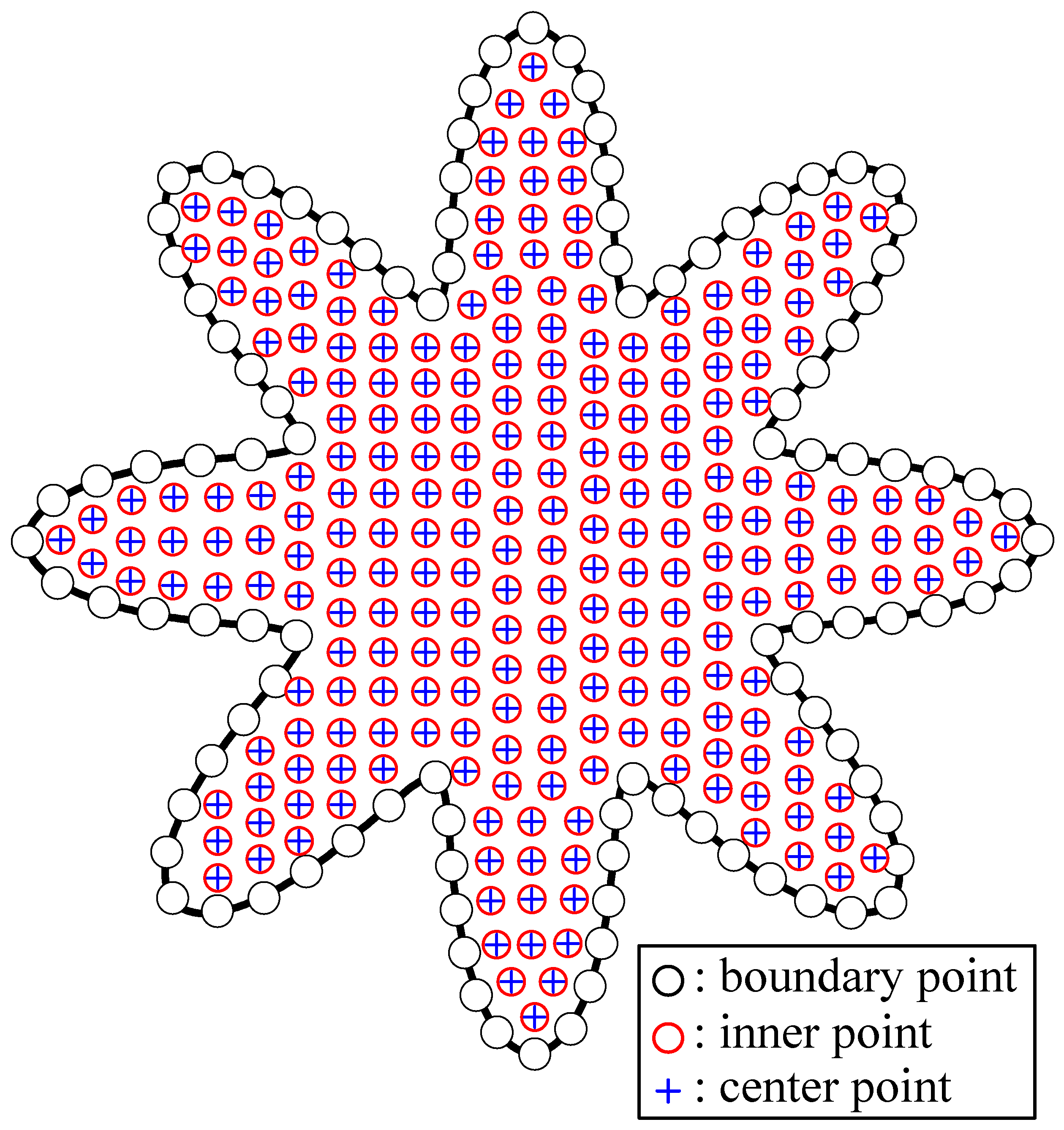
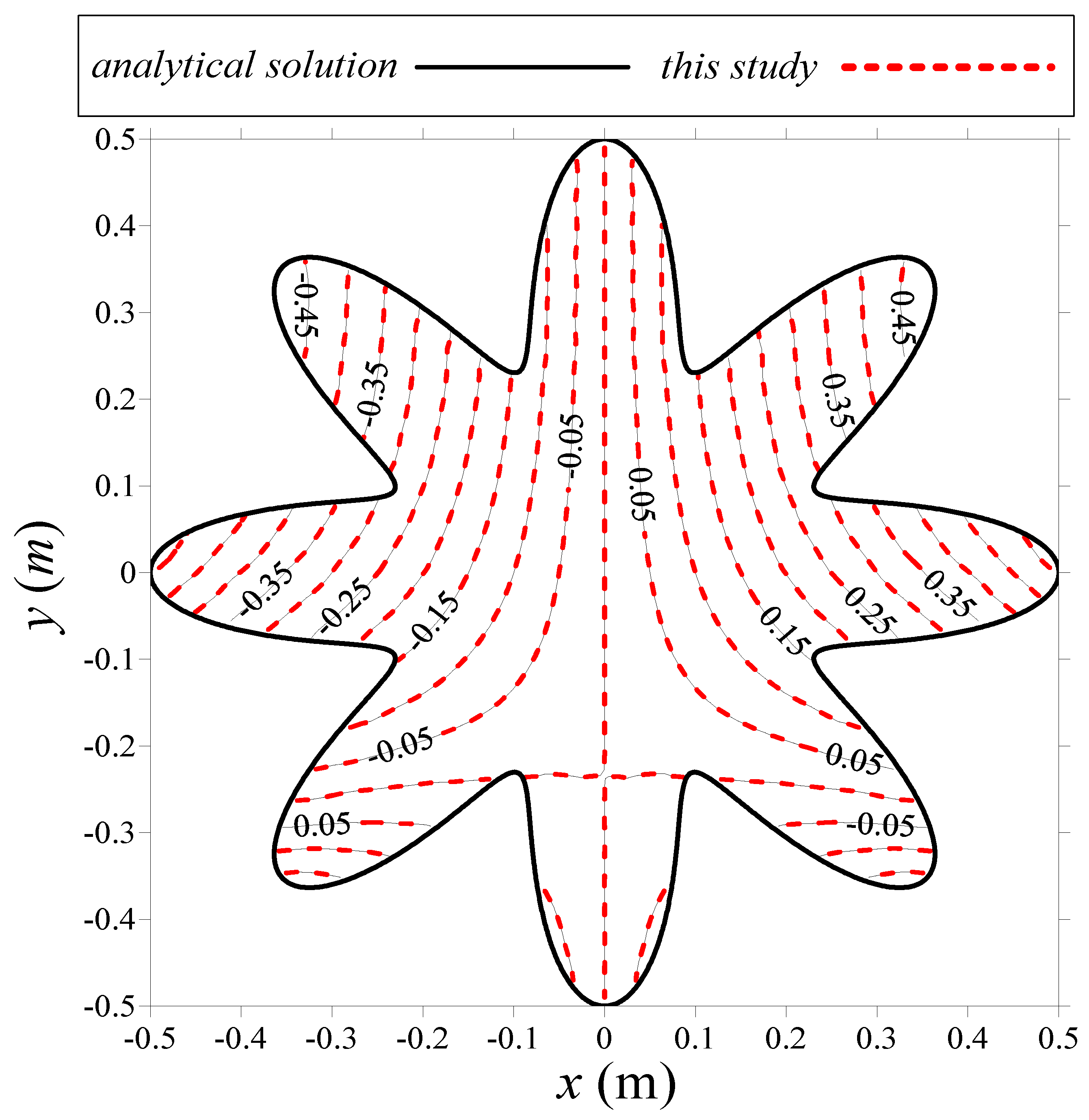
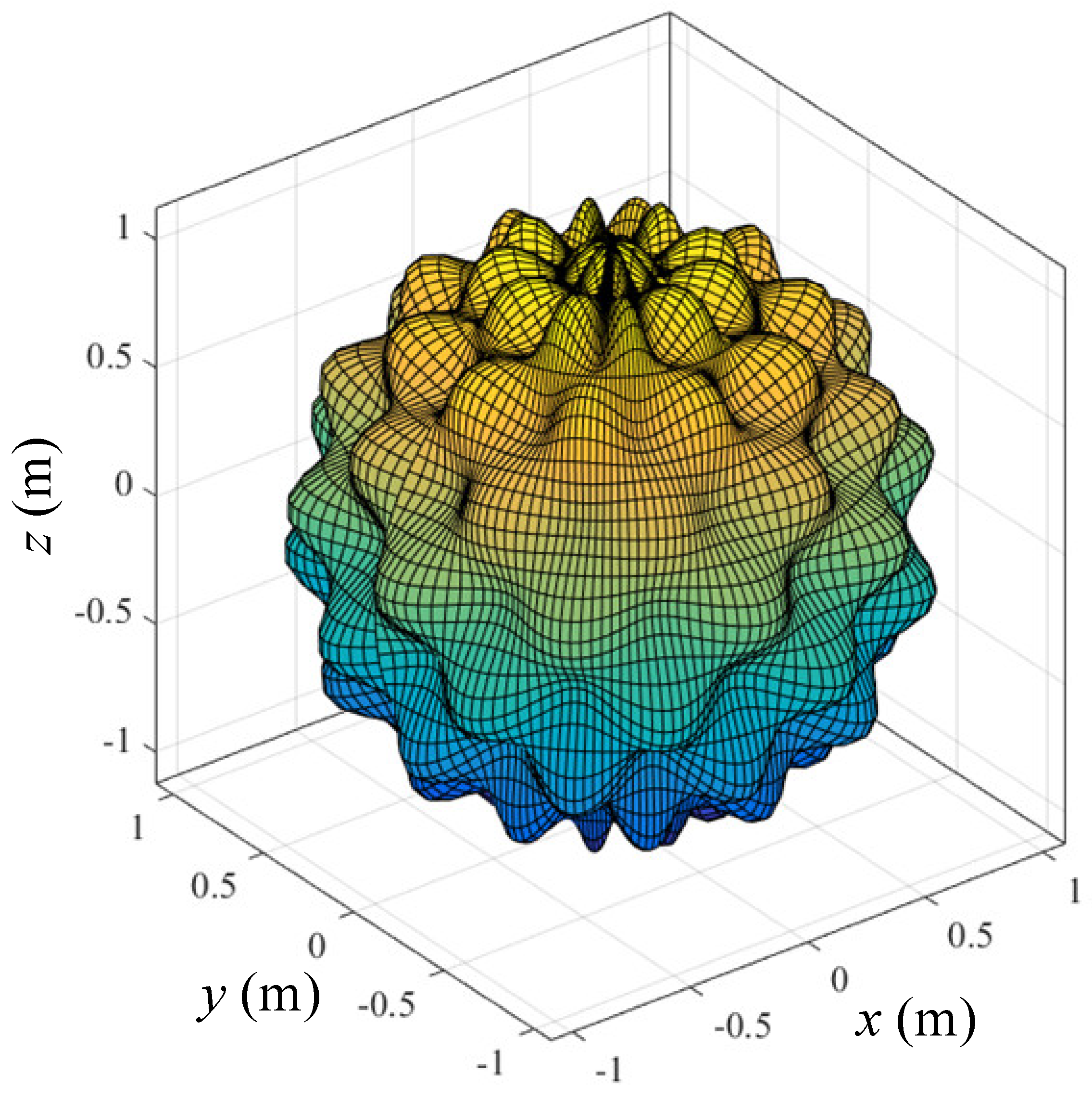
4.2. A Two-Dimensional Star-Shaped Problem
4.3. A Three-Dimensional Modified Helmholtz Problem
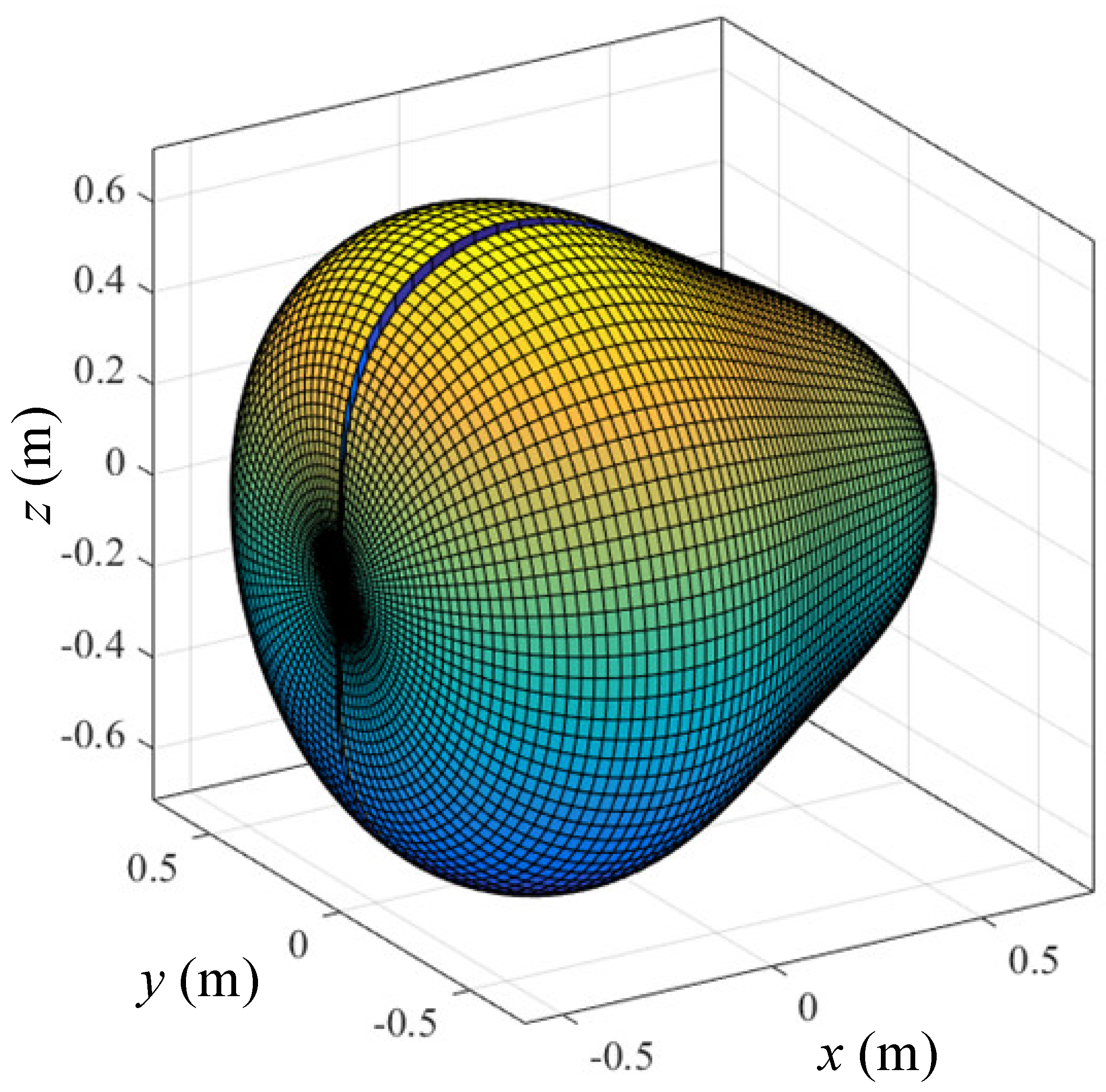
4.4. A Three-Dimensional Poisson Problem
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yao, G.; Tsai, C.H.; Chen, W. The comparison of three meshless methods using radial basis functions for solving fourth-order partial differential equations. Eng. Anal. Bound. Elem. 2010, 34, 625–631. [Google Scholar] [CrossRef]
- Uddin, M.; Haq, S. RBFs approximation method for time fractional partial differential equations. Commun. Nonlinear Sci. 2011, 16, 4208–4214. [Google Scholar] [CrossRef]
- Yao, G.; Chen, C.S.; Zheng, H. A modified method of approximate particular solutions for solving linear and nonlinear PDEs. Numer. Meth. Part. Differ. Equ. 2017, 33, 1839–1858. [Google Scholar] [CrossRef]
- Alipanah, A.; Esmaeili, S. Numerical solution of the two-dimensional Fredholm integral equations using Gaussian radial basis function. J. Comput. Appl. Math. 2011, 235, 5342–5347. [Google Scholar] [CrossRef]
- Lamichhane, A.R.; Chen, C.S. The closed-form particular solutions for Laplace and biharmonic operators using a Gaussian function. Appl. Math. Lett. 2015, 46, 50–56. [Google Scholar] [CrossRef]
- Karimi, N.; Kazem, S.; Ahmadian, D.; Adibi, H.; Ballestra, L.V. On a generalized Gaussian radial basis function: Analysis and applications. Eng. Anal. Bound. Elem. 2020, 112, 46–57. [Google Scholar] [CrossRef]
- Reutskiy, S.Y. Meshless radial basis function method for 2D steady-state heat conduction problems in anisotropic and inhomogeneous media. Eng. Anal. Bound. Elem. 2016, 66, 1–11. [Google Scholar] [CrossRef]
- Sarra, S.A. Integrated multiquadric radial basis function approximation methods. Comput. Math. Appl. 2006, 51, 1283–1296. [Google Scholar] [CrossRef]
- Soleymani, F.; Barfeie, M.; Haghani, F.K. Inverse multi-quadric RBF for computing the weights of FD method: Application to American options. Commun. Nonlinear Sci. 2018, 64, 74–88. [Google Scholar] [CrossRef]
- Sivaram, S.A.; Vinoy, K.J. Inverse multiquadric radial basis functions in eigenvalue analysis of a circular waveguide using radial point interpolation method. IEEE Microw. Wirel. Co. 2020, 30, 537–540. [Google Scholar] [CrossRef]
- Kamath, A.; Manzhos, S. Inverse Multiquadratic Functions as the Basis for the Rectangular Collocation Method to Solve the Vibrational Schrödinger Equation. Mathematics 2018, 6, 253. [Google Scholar] [CrossRef]
- Kansa, E.J.; Hon, Y.C. Circumventing the ill-conditioning problem with multiquadric radial basis functions: Applications to elliptic partial differential equations. Comput. Math. Appl. 2000, 39, 123–137. [Google Scholar] [CrossRef]
- Hashemi, M.R.; Hatam, F. Unsteady seepage analysis using local radial basis function-based differential quadrature method. Appl. Math. Model. 2011, 35, 4934–4950. [Google Scholar] [CrossRef]
- Xie, H.; Li, D. A meshless method for Burgers’ equation using MQ-RBF and high-order temporal approximation. Appl. Math. Model. 2013, 37, 9215–9222. [Google Scholar]
- Zheng, H.; Yao, G.; Kuo, L.H.; Li, X.X. On the Selection of a Good Shape Parameter of the Localized Method of Approximated Particular Solutions. Adv. Appl. Math. Mech. 2018, 10, 896–911. [Google Scholar] [CrossRef]
- Rippa, S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv. Comput. Math. 1999, 11, 193–210. [Google Scholar] [CrossRef]
- Cavoretto, R.; De Rossi, A.; Mukhametzhanov, M.S.; Sergeyev, Y.D. On the search of the shape parameter in radial basis functions using univariate global optimization methods. J. Glob. Optim. 2019, 2019, 1–23. [Google Scholar] [CrossRef]
| RMSE | Condition Number | |||||
|---|---|---|---|---|---|---|
| This Study | The Kansa Method (Optimal Shape Parameter) | This Study | The Kansa Method | |||
| 736 | 92 | 92 | ||||
| 1208 | 151 | 151 | ||||
| 1792 | 224 | 224 | ||||
| 2480 | 310 | 310 | ||||
| 3240 | 405 | 405 | ||||
| 4115 | 514 | 514 | ||||
| RMSE | ||||
|---|---|---|---|---|
| This Study | The Kansa Method (Optimal Shape Parameter) | |||
| 1050 | 300 | 300 | ||
| 1400 | 400 | 400 | ||
| 1750 | 500 | 500 | ||
| 2100 | 600 | 600 | ||
| 2450 | 700 | 700 | ||
| 2800 | 800 | 800 | ||
| RMSE | ||||
|---|---|---|---|---|
| This Study | The Kansa Method (Optimal Shape Parameter) | |||
| 6724 | 700 | 700 | ||
| 7569 | 800 | 800 | ||
| 8100 | 900 | 900 | ||
| 9025 | 1000 | 1000 | ||
| 10,000 | 1100 | 1100 | ||
| RMSE | |||
|---|---|---|---|
| This Study | |||
| 5706 | 630 | 630 | |
| 7357 | 756 | 756 | |
| 9208 | 882 | 882 | |
| 11,259 | 1008 | 1008 | |
| 13,510 | 1134 | 1134 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Xiao, J.-E. A Collocation Method Using Radial Polynomials for Solving Partial Differential Equations. Symmetry 2020, 12, 1419. https://doi.org/10.3390/sym12091419
Ku C-Y, Xiao J-E. A Collocation Method Using Radial Polynomials for Solving Partial Differential Equations. Symmetry. 2020; 12(9):1419. https://doi.org/10.3390/sym12091419
Chicago/Turabian StyleKu, Cheng-Yu, and Jing-En Xiao. 2020. "A Collocation Method Using Radial Polynomials for Solving Partial Differential Equations" Symmetry 12, no. 9: 1419. https://doi.org/10.3390/sym12091419
APA StyleKu, C.-Y., & Xiao, J.-E. (2020). A Collocation Method Using Radial Polynomials for Solving Partial Differential Equations. Symmetry, 12(9), 1419. https://doi.org/10.3390/sym12091419






