WebShell Attack Detection Based on a Deep Super Learner

Abstract

WebShell is a common network backdoor attack that is characterized by high concealment and great harm. However, conventional WebShell detection methods can no longer cope with complex and flexible variations of WebShell attacks. Therefore, this paper proposes a deep super learner for attack detection. First, the collected data are deduplicated to prevent the influence of duplicate data on the result. Second, to detect the results of the algorithm, static and dynamic feature are taken as the feature of the algorithm to construct a comprehensive feature set. We then use the Word2Vec algorithm to vectorize the features. During this period, to prevent the outbreak of the number of features, we use a genetic algorithm to extract the validity of the feature dimension. Finally, we use a deep super learner to detect WebShell. The experimental results show that this algorithm can effectively detect WebShell, and its accuracy and recall are greatly improved.

1. Introduction

With the development of Internet technology, web-based applications have been assimilated into all aspects of our lives. With the rapid growth of the number of website visitors, websites also store large amounts of our personal information; thus, the issue of how to protect this private information has become the primary task of website maintenance staff. According to the “Overview of China’s Internet Network Security Situation in 2019” released by the National Internet Emergency Center [1], in 2019, CNCERT monitors found that approximately 45,000 IP addresses inside and outside China implanted backdoors into approximately 85,000 websites in China and that the number of websites with backdoors implanted in China has increased by more than 2.59 times compared to the number found in 2018. As the number of backdoors implanted in websites increases year by year, the issue of how to detect backdoors in websites is critical for data security. Malicious WebShell files can function as website backdoors, so the detection of WebShell files on websites is also very important.

WebShell is an executable program language written with web scripts such as ASP, PHP, and JSP. It is always referred to as a web backdoor because users can upload malicious files to a web page and obtain database information by executing OS commands to view the database. As PHP is the preferred language for website development, it is also very important to study the detection method of PHP-type WebShell.

Webshell attack can be divided into two categories, “large Trojan” file for attack and “micro Trojan” file for attack. “micro Trojan” file code is small, usually a few lines to dozens of lines, its main function is used to assist“ large Trojan”file upload, execution script command. Compared with “micro Trojan” file size is much larger, “large Trojan” file size even more than 1 MB, its functions are complex, including the execution of command line procedures, database operations, etc. In addition, “large Trojan” to complete its function can also cooperate with other offensive files to operate jointly, to achieve the purpose of attack.

2. Related Work

At present, WebShell detection methods based on the PHP language can be divided into two types: static feature detection based on .php files and dynamic feature detection based on the execution process of .php files.

Detection based on the static feature of .php files finds WebShell by matching specified scripts with special function names and strings, file modification time, file execution permissions, and so on. This method can find only the existing WebShell and thus has certain limitations for the new WebShell. Session-Based Webshell Detection Using Machine Learning in Web Logs [2] extracts the features directly from the original files of the Web logs and proposes a statistical method based on time interval to identify the features. The long short-term memory and hidden Markov model were used to construct the framework and detect it. Webshell detection techniques in web applications [3] proposed a novel method based on an optimal threshold to identify files containing malicious code in web applications. The detection system finds all the files in classifiers target folder and provides suspicious files to the administrator for inspection.

Detection based on the dynamic feature of .php file execution determines whether the file is a malicious WebShell file through the degree of abnormal opcodes invoked by WebShell runtime. First, the system must acquire the existing WebShell files and the opcode sequence feature of these files. Every time a new WebShell appears, this feature library must be updated. If the feature database is not regularly updated, the alarm failure rate will be high. Webshell Detection Based on Random Forest-Gradient Boosting Decision Tree Algorithm [4] extracts static features from .php source files and uses the TF-IDF vector and hash vector to extract dynamic features under the opcode. The two features are unified as WebShell features. Finally, classification is carried out by combining the random forest classifier and gbdt classifier. In Research on Webshell Detection Method Based on Machine Learning [5], it is proposed to use opcode to extract the dynamic features of Webshell files, and then use TF-IDF for feature vectorization; secondly, use XGBoost, Multilayer Perceptron, RandomForestClassifier, and NaiveBeyesians for comparison; finally, select XGBoost as the optimal detection model through comparison. In Detecting Webshell Based on Random Forest with FastText [6], a PHP opcode sequence and static feature were first used, the dynamic features were vectorized using FastText, the two features were fused, and the random forest was used for model training and prediction. In Toward a Deep Learning Approach for Detecting PHP Webshell [7], Yara rule technology is used to convert the PHP source code into opcodes to determine whether a file is malicious code.

To summarize, detection based on static features and dynamic features exhibit certain advantages, but both have certain limitations. WebShell detection mainly presents the following three difficulties:

(1)

Extremely unbalanced datasets,

(2)

Irrelevant or redundant features, and 

(3)

Certain limitations in the detection algorithm.

3. Webshell Attack Detection Based on a Deep Super Learner

3.1. System Architecture

This article uses a deep super learner with the structure shown in Figure 1. The research can be divided into three modules: data preprocessing, feature selection, model building and prediction.

3.2. Opcode

Opcode refers to the portion of instructions or fields specified in a computer program to perform an operation, and the opcode generated by PHP refers to the sequence of bytecodes that can be recognized by the Zend engine virtual machine. This is similar to a bytecode file in Java, or a bytecode object in Python, pycodeObject. Essentially, the opcode bytecode tells the machine what to do and what it is doing. Therefore, we can determine whether this file belongs to a malicious WebShell file through the opcode generated during the execution of the malicious WebShell file uploaded by the user.

In the Zend engine, the opcode bytecode file can be obtained through the Vulcan Logic Dump (VLD) tool. An example listed below is a typical malicious WebShell file parsed by the Zend engine:

<?php @eval($_POST[’password’]);?>

We use the VLD tool to run the above malicious WebShell file, and the opcode is shown in

Table 1. Opcode compiled files.

#	OPCODE
1	BEGIN_SILENCE
2	FETCH_R
3	FETCH_DIM_R
4	INCLUDE_OR_EVAL
5	END_SILENCE
6	RETURN

.

3.3. Static Feature Extraction

3.3.1. Static Character of the String Length Variance

Variance is a measure of dispersion in probability theory and statistical variance used to measure a random variable or a set of data. WebShell files are encrypted to avoid detection tools. Extremely long words and strings generated by encryption algorithms, in which abnormal characters are exhibited or the string length is longer than normal file strings, ultimately lead to greater string length variance of the files and therefore can be used as features for detecting malicious WebShell files.

3.3.2. Static Character of the Index of Coincidence

Index of Coincidence (IC) is a mathematical index. Let y be a ciphertext of length n—that is, y = y1y2y3… yi… yn—where yi is ciphertext and the index of coincidence is the probability of picking two identical letters at random. The encrypted WebShell file is similar to the random file, and the encryption algorithm increases the randomness of the characters in the encrypted WebShell file; ultimately, the file IC is small. Therefore, it can be used as a feature to detect malicious WebShell files.

3.3.3. Static Character of Information Entropy

Information entropy is a measure of the degree of systematization. The more chaotic a system is, the higher its information entropy. The encrypted WebShell file contains many random strings for the purpose of obfuscation. These files produce a significant amount of ASCII code, increasing the entropy of the file. In contrast, the ASCII code of normal files is between 1 and 255 (excluding the ASCII space of 127), which is relatively fixed. Therefore, information entropy can be used as a feature for detecting malicious WebShell files. The calculation formula of information entropy is as follows:

$$H\left(x\right)=-\sum _{n=1}^{255}{p}_{n}lo{g}_2{p}_n(n\ne 127)$$

(1)

where n is ASCII code and the judgment of ASCII (space) with an ASCII value of 127 is meaningless, so $p_n$ represents the occurrence probability of the current character relative to the total character.

3.3.4. Static Character of the File Compression Ratio

The compression ratio is the ratio of the original file size to the compressed file size. Low-frequency characters correspond to long code, and high-frequency characters correspond to short code, which can effectively balance the length of the original string. Encrypted WebShell files have a more balanced distribution of specific characters. Therefore, compression ratio can be used as a feature to detect malicious WebShell files. The compression ratio formula is as follows:

$$Compressionratio=\frac{Originalfilesize}{Compressedfilesize}$$

(2)

3.3.5. Static Character of Eigencode Matching

In malicious WebShell files, special variables or expressions are often used, such as eval, base64_decode and other functions. We match these special feature codes one by one to each test file, and the matching result is a feature of detecting malicious WebShell files.

3.4. Feature Vectorization

Word2vec is a feature vectorization tool that Google opened open in 2013, which is a deep learning model [8,9]. By training word vectors, Word2Vec can use low-latitude features to represent complex words, which can well reduce the feature dimension disaster caused by the traditional way to represent word vectors, thus reducing the time and space complexity of later algorithms. There are two implementations, CBOW and Skip-Gramm. CBOW predicts the target words by the context, and its model structure is shown on the left of in Figure 2. Skip-gramm predicts context through the target words, and its model structure is shown on the right of Figure 2. For a Word2vec implementation of words, in a good word vector, the relationship between the similarity of words can be expressed as a function of the distance between the words.

Word2Vec is one of the most popular fields in NLP [10,11,12]. In Research on the Construction of Sentiment Dictionary Based on Word2vec [13], SO-PMI algorithm was used to judge the emotional state of the words not recorded in the dictionary, and word2Vec algorithm was used to correct them. Finally, the corrected words were added to the dictionary to complete the reconstruction of the dictionary. In Using Word2Vec to Process Big Text Data [14], the Word2Vec algorithm is first used to train the data model and obtain the word similarity, similar words are clustered together, and the generated cluster is used to adapt to the new data dimension to reduce the data dimension. A Study on Sentiment Computing and Classification of Sina Weibo with Word2vec [15] proposed a semantic orientation pointwise similarity distance (SO-SD) model, built an emotional dictionary using the Word2Vec tool, and then used the emotion dictionary to determine the emotional tendency of the microblog information.

3.5. Feature Selection

Feature selection is one of the most commonly used and important techniques in data preprocessing and has become an indispensable component of machine learning processes [16]. Feature selection is a way to select some of the most effective features from the original features. In this paper, it is the feature that can distinguish malicious files from non-malicious files. It is also a means to improve the efficiency of the algorithm on the basis of ensuring the evaluation index. Feature selection based on a genetic algorithm is a wrapper method. The basic execution process is as follows.

(1)

Determine the search space: All feature sets after Word2Vec feature vectorization.

(2)

Chromosome encoding: A binary encoding method is adopted. Each feature is represented by encoding “0” or “1”, where “0” indicates that the feature is not selected and “1” indicates that the feature is selected.

(3)

Generation of initial population: N initial individuals are randomly generated to form the initial population, and each individual consists of 0 and 1, which represents whether or not this feature is selected.

(4)

Fitness function: Fitness function can calculate the pros and cons of an individual. In feature selection, the fitness function mainly judges the ability of features to distinguish malicious and nonmalicious WebShell files.

(5)

There are three important steps in a genetic algorithm: selection, crossover and mutation. Generally, “roulette” is used as the selection method to randomly select m individuals with the highest fitness, which are the sub-feature sets that can well distinguish malicious and non-malicious samples and are unconditionally copied to the next total group. N-m individuals are selected by crossover and mutation operators to restore the original N individuals. Crossover probability and mutation probability are parameters and must be adjusted. If the crossover probability is too high, the individual structure with high fitness will be destroyed quickly. If it is too small, the search stops. If the mutation probability is too high, the genetic algorithm will become a random search. If the probability is too small, no new individuals will be created.

(6)

If the self-set reproduction algebra is exceeded, the best individual is returned and used as the basis for feature selection, and the algorithm will end. Otherwise, the process returns to (5) to continue the reproduction of the next generation.

The flowchart of the genetic algorithm is shown in Figure 3.

3.6. Data Sampling Based on the Smote Algorithm

The SMOTE algorithm [17] is a method for managing unbalanced datasets put forward by Chawla et al. in 2002. In the real world, datasets are mainly composed of “normal” samples, with only a small fraction of “abnormal” examples, so the SMOTE algorithm treats the minority “anomalies” by using the method of linear interpolation between the two minority class sample syntheses of new samples, thus effectively relieving the unbalanced data and the effects on the classifier [18,19,20,21]. The proportion of malicious WebShell samples to nonmalicious samples in the datasets in this study is approximately 10:1. This causes data imbalance. Therefore, this study uses the SMOTE algorithm to oversample the datasets to reduce the impact of data imbalance on the classifier.

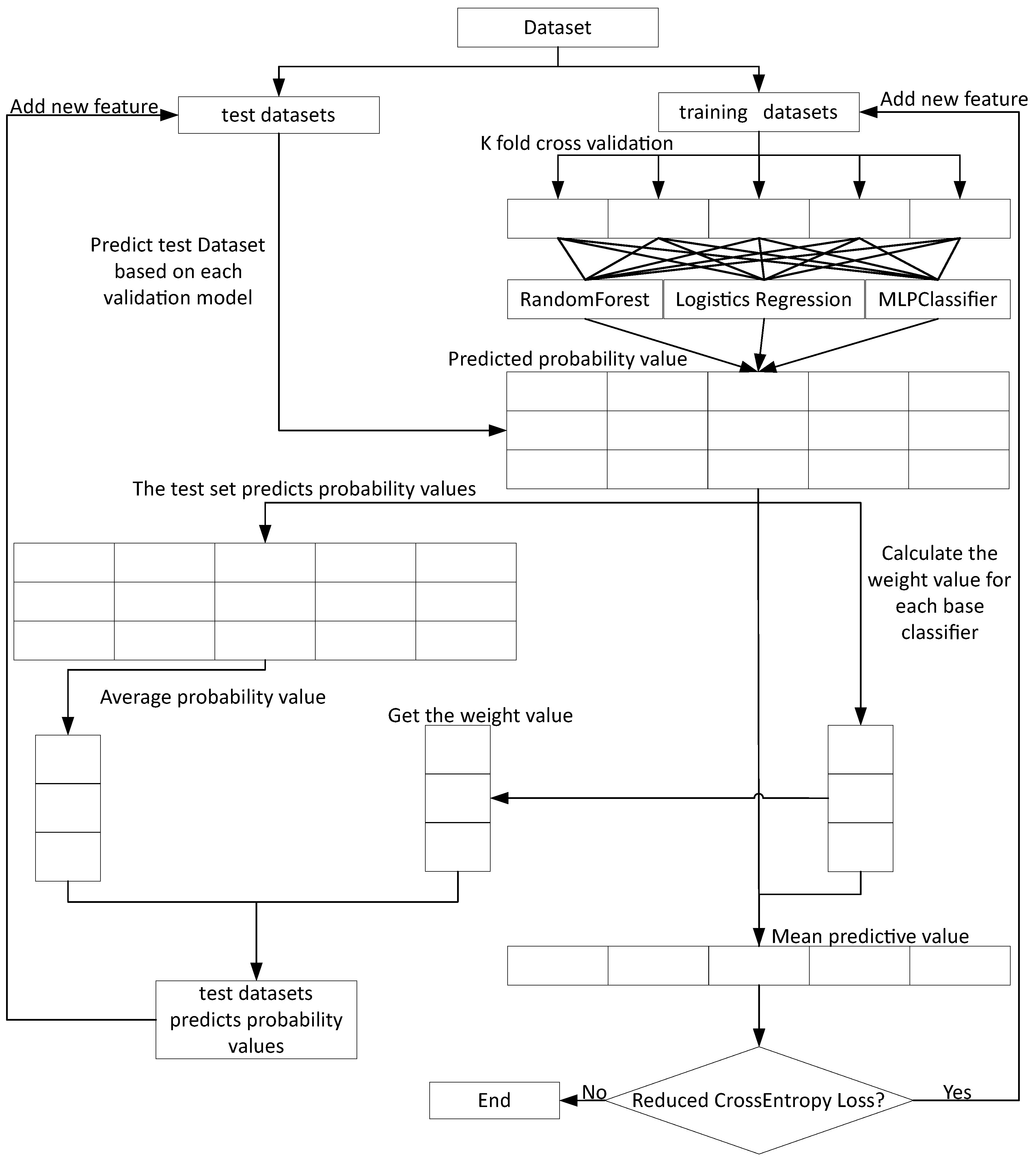
3.7. Deep Super Learner

Through the Data preprocessing operations of opcode dynamic feature extraction, static feature extraction, feature vectorization, feature selection and data sampling, the best feature set can be obtained to ensure that the deep integrated learning algorithm can give full play to the best detection effect.

Traditional machine learning algorithms are relatively simple and have strong interpretable, but their accuracy is often not as high as that of deep neural networks (DNN). The DNN output accuracy is often relatively high, and has a good application scenario in many aspects [22,23,24]. However, DNN is poor in interpretation and the algorithm implementation is complex. Therefore, Deep Super Learner: A Deep Ensemble for Classification Problems [25] proposed a deep super learner to enable the advantages of fusion between the two, and this algorithm was applied to detect WebShell files in this study. Among them, LogisticRegression, MLPClassifier and RandomForestClassifier are used as the base classifier in the deep super learner. They can compensate for each other’s disadvantages. The advantages and disadvantages between the base classifier are shown in

Table 2. The advantages and disadvantages of the base classifier.

Base Classifier	Advantages	Disadvantages
LogisticRegression	Clear model, strong interpretability, simple implementation, high efficiency [26,27].	Easy to underfit; if the feature space is too large, the performance will be reduced; cannot handle feature dependent situations [28].
MLPClassifier	Can learn nonlinear models [29,30].	Slow learning speed, easy to fall into local extrema, learning may not be sufficient [31].
RandomForestClassifier	High latitude data processing, rapid training speed, easy parallel processing [32,33].	Models are not easy to interpret and can have bad consequences for small datasets [34].

. The specific implementation of model training for deep super learner is shown in Algorithm 1, the specific implementation of model test is shown in Algorithm 2, and the overall flowchart is shown in Figure 4.

Algorithm 1 Model training.

Input: Training datasets: $X\_data,Y\_data$; List of base classifiers: $Bas{e}_s$; K-fold cross-validation: K; Maximum iteration number: $MaxIterations$.

Output: K-fold cross-validated base classifiers model: $fitted\_classifiers\_per\_fold$, base classifiers temporary weight value: $weights\_per\_iteration$.

1: $fitted\_classifiers\_per\_fold$ = [] 2: $weights\_per\_iteration$ = [] 3: for$t1=1,2,\dots ,MaxIterations$do 4:     K-fold cross-validation in $X\_data$, $Y\_data$ to obtain training datasets and validation datasets; 5:     for $t2=1,2,\dots ,K$ do 6:         for classifier $Bas{e}_i$ is extracted from base classifier list $Bas{e}_s$ in turn do 7:            The K-fold model is trained in $Bas{e}_i$; 8:            add $Bas{e}_i$ to $fitted\_classifiers\_per\_fold$; 9:            under the model $Bas{e}_i$, obtain the predicted probability value of the verification data at this time; 10:         end for 11:     end for 12:     the weight value of $Bas{e}_i$ is calculated using predicted probability value of the verification data and $Y\_data$; 13:     add the weight value of $Bas{e}_i$ to $weights\_per\_iteration$; 14:     predicted probability value and weight value of $Bas{e}_i$ are used to calculate the average predicted probability value of each sample; 15:     loss minimization is calculated using average predicted probability value and $Y\_data$; 16:     if the loss is smaller now than it was last time then 17:         Add the average predicted probability value to $X\_data$ as a new feature; 18:     else 19:         break 20:     end if 21: end for 22: return$fitted\_classifiers\_per\_fold,weights\_per\_iteration$.

Algorithm 2 Model test.

Input: Test datasets: $X\_test$, $Y\_test$; base classifiers model:$fitted\_classifiers\_per\_fold$; K-fold cross-validation: K; base classifiers weight parameter: $weights\_per\_iteration$.

Output: The average predicted probability value of the test sets sample.

1: for weights value w is extracted from $weights\_per\_iteration$ in turn do 2:     K-fold cross-validation in $X\_test$, $Y\_test$ to obtain training datasets and validation datasets; 3:     for model m is extracted from $fitted\_classifiers\_per\_fold$ in turn do 4:         for $t3=1,2,\dots ,K$ do 5:            model m training and prediction based on k-fold cross validation; 6:         end for 7:         In the base classifier model m on the testsets to calculate the average predicted probability value; 8:     end for 9:     average predicted probability value and weights value w are used to calculate the average prediction probability value avg_probs of each sample in the test sets; 10:     Take avg_probs as a new feature of X_data; 11: end for 12: return avg_probs

The SLSQP Algorithm was used to calculate the algorithm weight value in the 12th line of Algorithm 1 model training. SLSQP (Sequential Least Squares Programming), which was proposed and written by Kraft in 1988 [35], can be used to solve nonlinear programming problems that minimize scalar functions:

$$\underset{x\in R^n}{min}F\left(x\right)$$

(3)

when constrained by equality and inequality:

$$g_j\left(x\right)=0,j=1,\dots ,m_e$$

(4)

$$g_j\left(x\right)\ge 0,j=m_e+1,\dots ,m$$

(5)

The upper and lower limits of the variable are

$$l_i\le xi\le u_i,i=1,\dots ,n$$

(6)

where m represents the number of equality and inequality constraints, m${}_e$ represents the number of equality constraints, l${}_i$ is the lower limit of variable x${}_i$, u${}_i$ is the upper limit of variable x${}_i$, and n is the sample size.

The SLSQP algorithm is integrated in PyOpt and SciPy. Pyopt is a python-based nonlinear constraint optimization package used to solve the optimal solution under nonlinear constraints. SciPy, a Python-based optimization package, also integrates the algorithm. In this study, however, we will use only SLSQP in SciPy.

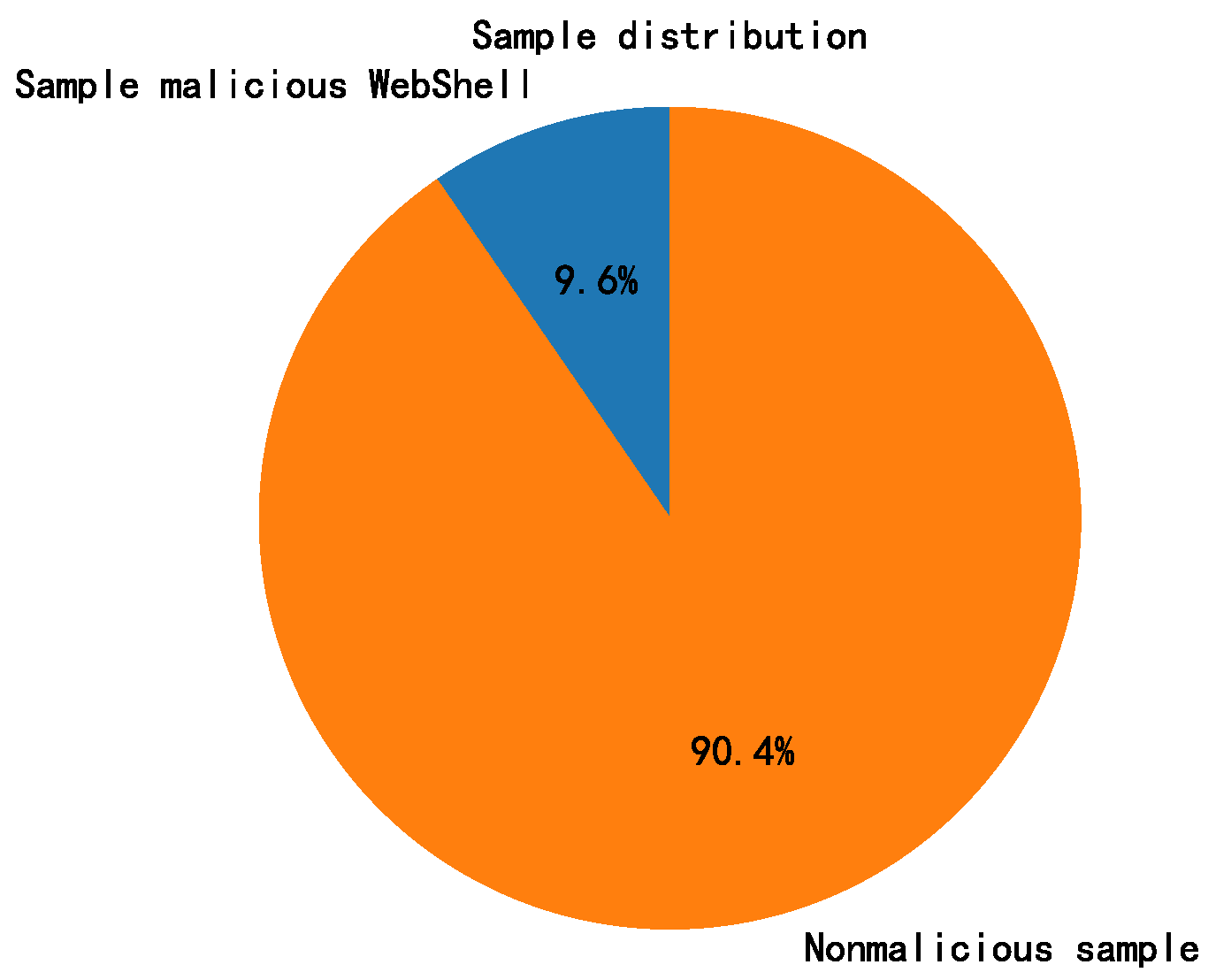
Since this study focuses on the dichotomy of WebShell samples, y can only be 0 or 1. The model predicts that the probability of a sample labeled 1 is:

$$\widehat{y}=P(y=1|x)$$

(7)

The probability that the sample label is 0 is:

$$1-\widehat{y}=P(y=0|x)$$

(8)

Using maximum likelihood estimation is:

$$P\left(y\right|x)={\widehat{y}}^y\ast {(1-\widehat{y})}^{1-y}$$

(9)

The above equation is the probability that the model predicts that it belongs to the sample label y. Since y is the correct result given in the data set, the larger the above equation is, the better. In the formula above, we use the log transformation to get the following result:

$$log\left(P\left(y\right|x)\right)=log({\widehat{y}}^y\ast {(1-\widehat{y})}^{1-y})=y\ast log\widehat{y}+(1-y)\ast log(1-\widehat{y})$$

(10)

Generally, the smaller the loss function is, the better. Therefore, by adding a negative sign to the above formula, the following formula can be obtained, namely the crossentropy loss in line 15 of Algorithm 1 model training.

$$L=-[y\ast log\widehat{y}+(1-y)\ast log(1-\widehat{y})]$$

(11)

where y is the true category of the input instance x and $\widehat{y}$ is the probability that the input instance x belongs to the malicious WebShell category.

3.8. Research Features

In this study, static feature detection and dynamic feature detection are combined to extract as much feature data as possible. Next, Word2Vec is used for feature vectorization. A genetic algorithm is used for feature dimension reduction. Finally, the deep super learner is used to improve the recognition rate of WebShell detection. The main contributions of this paper are as follows:

(1)

Using SMOTE effectively solves the misjudgment result caused by the imbalance of the datasets;

(2)

Using a genetic algorithm effectively solves irrelevant or redundant features;

(3)

Using the deep super learner effectively solves the limitations of a single algorithm, so that the algorithm can achieve the best expected results.

4. Experiment

4.1. Experimental Conditions

The experimental environment in this study is based on the Ubuntu 64-bit operating system, and the processor is an Intel Xeon CPU E5-2650 [email protected] GHz. Based on the Python language implementation, the Python version is 3.5.1.

4.2. Experimental Data

Since this paper is only an exploration and study of WebShell samples of the .php type, this study first downloads all WebShell samples from Github, categorizes the malicious WebShell, extracts files with the suffix .php, and finally acquires the required samples. There are 571 WebShell samples in total. The nonmalicious PHP files mainly come from common PHP development frameworks, including phpCMS, Yii2, WordPress, oa, and Fenxiangyo. The collected data are extracted only from files with the suffix .php and processed again, and 5,379 nonmalicious samples are ultimately obtained. The datasets distribution is shown in Figure 5 and

Table 3. Dataset distribution.

Sample	Project Name	URL
Nonmalicious sample	phpCMS	https://github.com/johnshen/phpcms
	yii2	https://github.com/yiisoft/yii2
	WordPress	https://github.com/WordPress
	oa	https://github.com/rainrocka/xinhu
	Fenxiangyo	https://github.com/learnstartup/4tweb
Sample malicious WebShell		https://github.com/JohnTroony/php-WebShells
		https://github.com/tanjiti/WebShellSample
		https://github.com/tennc/WebShell

.

4.3. Evaluation Standard

The WebShell detection method based on a deep super learner is evaluated in terms of accuracy, recall, and specificity. The confusion matrix of model evaluation is shown in

Table 4. Confusion matrix.

Reality	Prediction
	Positive	Negative
Positive	TP	FN
Negative	FP	TN

below, where “Positive” represents the WebShell sample and “Negative” represents the nonmalicious sample.

(1)

If an instance is a WebShell sample and is predicted to be a WebShell sample, it is a true positive (TP).

(2)

If an instance is a nonmalicious sample and is predicted to be a nonmalicious sample, it is a true negative (TN).

(3)

If an instance is a nonmalicious sample but is predicted to be a WebShell sample, it is a false positive (FP).

(4)

If an instance is a WebShell sample but is predicted to be a nonmalicious sample, it is a false negative (FN).

$$Recall=\frac{TP}{TP+FN}$$

(12)

Equation (12) indicates the proportion of model prediction pairs among all results whose true values are WebShell samples and reflects the classifier’s recognition ability of positive examples (WebShell sample).

$$Accuracy=\frac{TP+TN}{TP+FN+FP+TN}$$

(13)

Formula (13) indicates the proportion of correct samples in the model prediction.

$$Specificity=\frac{TN}{TN+FP}$$

(14)

Formula (14) indicates the proportion of a nonmalicious sample correctly predicted by the model, and the ability of the classifier to recognize a normal PHP file.

4.4. Algorithm Parameter Selection

4.4.1. Feature Vectorization

Based on the feature vectorization of Word2Vec, K is a very important parameter: it is the choice of the K value in the k-dimensional vector mapped to each word. Too many or too few feature dimensions will influence the experimental results to some extent. Too many feature dimensions will result in feature redundancy, which will greatly increase the spatial complexity of subsequent experiments and ultimately affect algorithm efficiency. Meanwhile, redundant features will have an adverse effect on algorithm detection. Too few feature dimensions will greatly reduce the ability of the algorithm to distinguish black and white lists. Therefore, this study tested this parameter with respect to integer values from 100 to 10,100. The experimental results are shown in

Table 5. The influence of different K values on accuracy, recall and specificity.

K	Accuracy	Recall	Specificity
100	0.98741611	0.94871795	0.99162791
1100	0.98571429	0.94017094	0.99068034
2100	0.98403361	0.94871795	0.98788444
3100	0.98739496	0.94017094	0.99254427
4100	0.98655462	0.94871795	0.99068034
5100	0.98658843	0.94017094	0.99163569
6100	0.98739496	0.94871795	0.99161230
7100	0.98907563	0.95726496	0.99254427
8100	0.98487395	0.94871795	0.98881640
9100	0.98823529	0.95726496	0.99161230
10100	0.98655462	0.95726496	0.98974837

and Figure 6. It can be observed that the three detection indexes of K values from 100 to 7100—namely accuracy, recall, and specificity—do not change very much, but when the feature dimension(K) is kept at 7100, the accuracy and recall reach the highest values. The specificity is not at the highest value in this case but tends to remain at the maximum value. Therefore, the feature vectorization parameter K in Word2Vec is set to 7100.

4.4.2. Deep Super Learner

Deep super learner is the more important parameter for the training datasets of cross-validation K_flod values because each time, the cross-validation will first affect the weight value of learning, thereby affecting the algorithm of crossentropy loss value calculation, and then the learning of crossentropy loss value calculation, ultimately affecting the depth of integration testing efficiency of the algorithm. Therefore, this study tests the parameters from 3-fold cross-validation to 10-fold cross-validation. The test results are shown in

Table 6. The influence of different K_flod values on accuracy, recall and specificity.

K_Fold	Accuracy	Recall	Specificity
3_fold	0.98067227	0.94871795	0.98415657
4_fold	0.98403361	0.95726496	0.98695247
5_fold	0.98655462	0.95726496	0.98974837
6_fold	0.98571429	0.95726496	0.9888164
7_fold	0.98907563	0.95726496	0.99254427
8_fold	0.98571429	0.95726496	0.9888164
9_fold	0.98151261	0.95726496	0.98415657
10_fold	0.98655462	0.95726496	0.98974837

and Figure 7 below. It can be determined from the figure that the recall has not changed from 4-fold cross-validation, that accuracy and special effects in the 3-fold cross-validation to 7-fold cross-validation increase, and that these values peak for 7-fold cross-validation; the values of the cross-validation test indicators exhibit fluctuations, but the peak is exhibited for 7-fold cross-validation. Therefore, the K_flod value of the deep super learner is set as 7-fold cross validation in this study.

4.5. Comparison with Other Algorithms

LogisticRegression, MLPClassifier and RandomForestClassifier are used as the basic learners in the deep super learner. To enable the deep super learner to produce better results, this study uses a Bayesian optimization-based Python module called Hyperopt. Using Bayesian optimization for tuning parameters allows us to obtain the best parameters of the base classifier. In logistic regression, the regularization selection parameter “penalty” is “L1”; in the MLPClassifier, the regularization parameter “alpha” is “0.369841375226992”, the number of neurons of each layer “hidden_layer_sizes” is (5,5), the activation function parameter “activation” is “logistic” and the solver parameter of weight optimization is “lbfgs”; in the RandomForestClassifier, the number parameter “n_estimators” in the random forest is “47”, the maximum depth parameter “max_depth” of the tree is “18”, the sample set segmentation policy parameter “criterion” is “gini”, the number of randomly selected features per decision tree “max_features” is “3”, and the minimum number of separable samples “min_samples_split” is “2”.

To verify the performance of the algorithm, this paper presents a one-to-one comparison of the single algorithm and common ensemble algorithm. The preliminary work of all the following algorithms is fully consistent with the preliminary work data of the deep super learner used in this study. This study compares the accuracy, recall, specificity and test time. The experimental results are shown in

Table 7. Contrast experiment.

Grand Classification	Fine Classification	Specific Algorithm	Accuracy	Recall	Specificity	Test Time (s)
Single algorithm		Logistics Regression	0.94874	0.59829	0.98695	0.07679
Ensembles algorithm	Boost	Adaboost	0.98067	0.91453	0.98788	2.47327
		Xgboost	0.97479	0.88034	0.98509	0.62096
		LightGBM	0.98655	0.91453	0.99441	8.43800
	Bagging	Random Forest	0.98655	0.91453	0.99441	0.09772
	Stacking		0.98571	0.93162	0.99161	0.35306
Deep Super Learner			0.98908	0.95727	0.99254	2.89614

. It can be determined that the algorithm presented in this paper requires a longer duration than other algorithms in terms of time efficiency, but the deep super learner can collect the advantages of the algorithm and combine them together to give full play to the advantages of each base classifier, so the three evaluation indexes—accuracy, recall and specificity—achieve good results.

5. Conclusions

This paper conducts an in-depth analysis of the existing problems of malicious WebShell detection. The feature library of malicious WebShell files is not perfect; the existing features cannot effectively distinguish malicious samples from nonmalicious samples, and the detection algorithm cannot produce good results. Thus, this study uses dynamic and static feature for the combination of diverse feature of the data and then uses a genetic algorithm to filter feature to maintain the accuracy and recall, produce effects of roughly the same conditions, and greatly reduce the feature dimensions to reduce the time and space complexity. The deep super learner is then applied to the detection algorithm. The experimental results show that even though the algorithm presented in this paper has certain limitations in time, it exhibits a better WebShell detection effect than other algorithms. Future research can focus on improving the time efficiency of the deep super learner and improving the practical application ability of the algorithm.