Design of a Predictive Model of Rock Breakage by Blasting Using Artificial Neural Networks
Abstract
1. Introduction
2. Theoretical Frame
- Controllable variables: Explosives, Geometric blasting design and Startup sequences.
- Uncontrollable variables: Geological and Geomechanical characteristics of the rock mass.
2.1. Kuz–Ram Equation
- = Percentage of passing fragments less than 50%.A = Rock factor.= Explosive mass per drill.E = Relative weight Strength of explosive= Volume per kg of explosive.
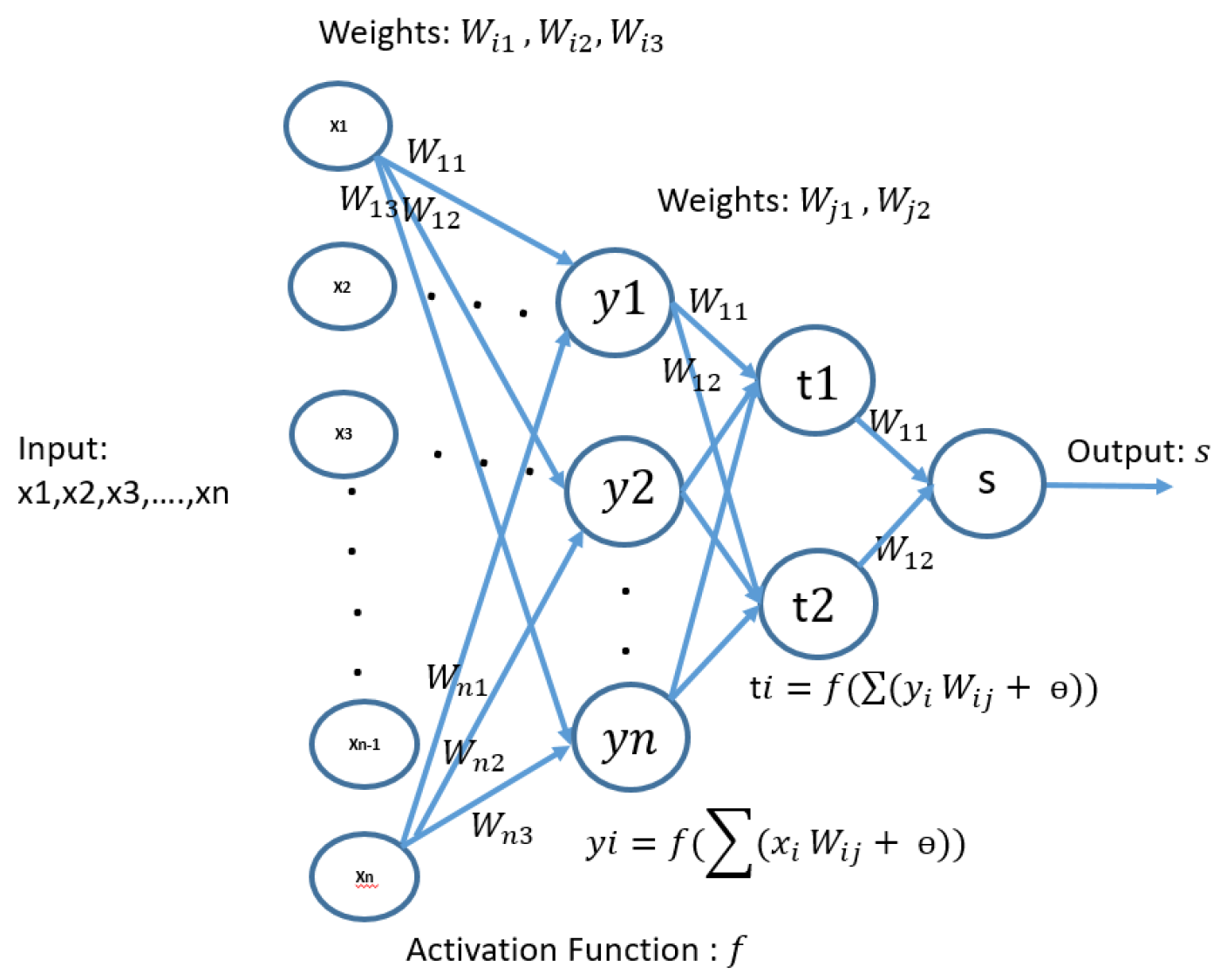
2.2. Use of the Artificial Neural Network (Ann)
2.3. Design of a Feedforward Neural Network (Fnn) for the Case Study
2.3.1. Number of Layers
2.3.2. Number of Neurons in Each Layer
2.3.3. Initialization of Weight
2.3.4. Activation Function of Each Layer
- f: Sigmoid functionx: variable
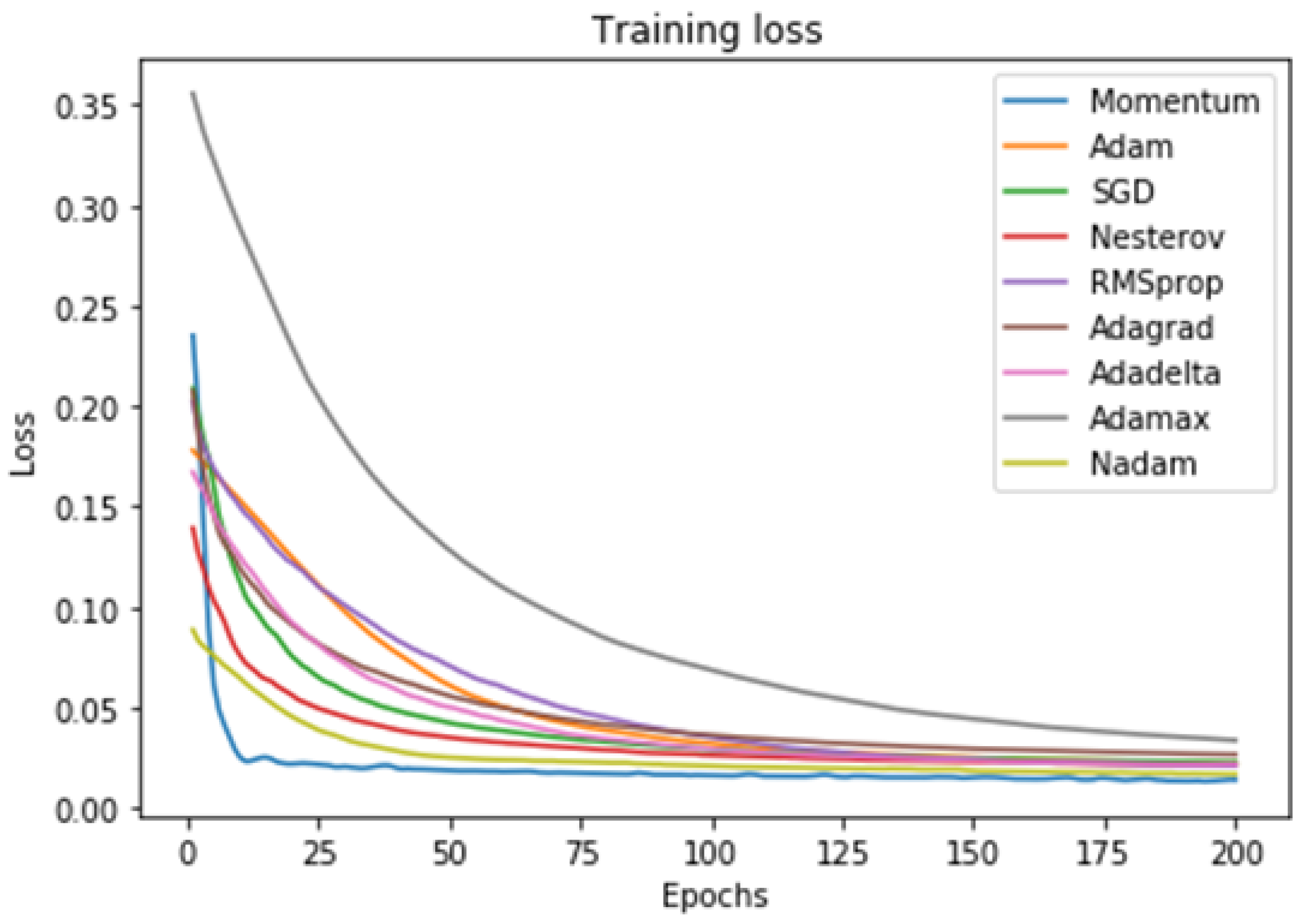
2.3.5. Training Algorithm
- : Weights: Coefficient of friction: Learning rate: Gradient of the function f
2.4. Multiple Linear Regression (Mlr)
- : is the ordinate in the origin, namely is the value of the dependent variable Y when all the predictors are zero.: is the average effect that the increase in one unit of the predictor variable has on the dependent variable Y, holding all else constant. This are known as partial regression coefficients.: is the residual or error, namely the difference between the observed value and the one estimated by the model.
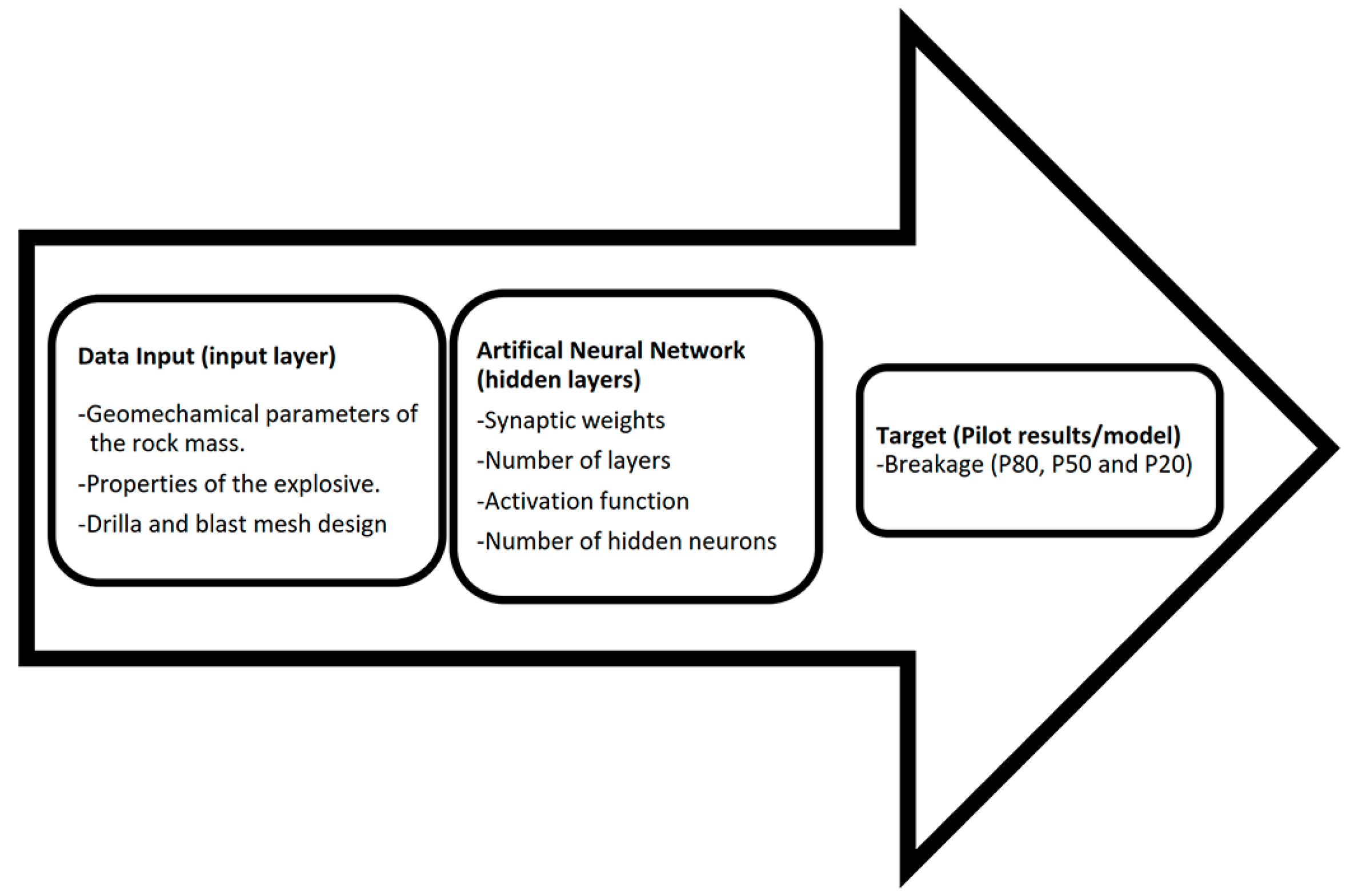
3. Methodology for the Design of the Ann Computer Model
4. Collection of Field Data
5. Design and Experimentation of ANN
- n: number of input parameters = 8K: used dataset number = 47N: number of hidden neurons to be determinedResulting N > 8. Therefore: 9 ≤ N ≤ 17.
6. Experimental Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
References
- Oraee, K.; Asi, B. Prediction of Rock Fragmentation in Open Pit Mines, using Neural Network Analysis. In Proceedings of the Fifteenth International Symposium on Mine Planning and Equipment Selection (MPES 2006), Torino, Italy, 19–22 September 2006. [Google Scholar]
- Kulatilake, P.; Qiong, W.; Hudaverdi, T.; Kuzu, C. Mean particle size prediction in rock blast fragmentation using neural networks. Eng. Geol. 2010, 114, 298–311. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, J.; Wu, B.B.; Huang, D.; Wei, W. Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction. Trans. Nonferr. Met. Soc. China 2012, 22, 432–441. [Google Scholar] [CrossRef]
- Gao, H.; Fu, Z.L. Forecast of Blasting Fragmentation Distribution Based on BP Neural Network. Adv. Mater. Res. Trans. Tech. Publ. 2013, 619, 3–8. [Google Scholar] [CrossRef]
- Sayadi, A.; Monjezi, M.; Talebi, N.; Khandelwal, M. A comparative study on the application of various artificial neural networks to simultaneous prediction of rock fragmentation and backbreak. J. Rock Mech. Geotech. Eng. 2013, 5, 318–324. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Armaghani, D.J.; Hajihassani, M.; Faizi, K.; Marto, A. A simulation approach to predict blasting-induced flyrock and size of thrown rocks. Electron. J. Geotech. Eng. 2013, 18, 365–374. [Google Scholar]
- Saadat, M.; Khandelwal, M.; Monjezi, M. An ANN-based approach to predict blast-induced ground vibration of Gol-E-Gohar iron ore mine, Iran. J. Rock Mech. Geotech. Eng. 2014, 6, 67–76. [Google Scholar] [CrossRef]
- Marto, A.; Hajihassani, M.; Jahed Armaghani, D.; Tonnizam Mohamad, E.; Makhtar, A.M. A novel approach for blast-induced flyrock prediction based on imperialist competitive algorithm and artificial neural network. Sci. World J. 2014, 2014, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Enayatollahi, I.; Bazzazi, A.A.; Asadi, A. Comparison between neural networks and multiple regression analysis to predict rock fragmentation in open-pit mines. Rock Mech. Rock Eng. 2014, 47, 799–807. [Google Scholar] [CrossRef]
- Dhekne, P.; Pradhan, M.; Jade, R. Artificial Intelligence and Prediction of Rock Fragmentation. In Mine Planning and Equipment Selection; Springer: Berlin/Heidelberg, Germany, 2014; pp. 891–898. [Google Scholar]
- Tiile, R.N. Artificial Neural Network Approach to Predict Blast-Induced Ground Vibration, Airblast and Rock Fragmentation. Master’s Thesis, Missouri University of Science and Technology, Rolla, MI, USA, 2016. Available online: https://scholarsmine.mst.edu/masters_theses/7571/ (accessed on 13 June 2020).
- Taheri, K.; Hasanipanah, M.; Golzar, S.B.; Majid, M.Z.A. A hybrid artificial bee colony algorithm-artificial neural network for forecasting the blast-produced ground vibration. Eng. Comput. 2017, 33, 689–700. [Google Scholar] [CrossRef]
- Castillo-Martinez, A.; Ramon Almagro, J.; Gutierrez-Escolar, A.; Del Corte, A.; Castillo-Sequera, J.L.; Gómez-Pulido, J.M.; Gutiérrez-Martínez, J.M. Particle Swarm Optimization for Outdoor Lighting Design. Energies 2017, 10, 141. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Dhekne, P.; Pradhan, M.; Jade, K.; Mishra, R. Boulder prediction in rock blasting using artificial neural network. ARPN J. Eng. Appl. Sci. 2017, 12, 47–61. [Google Scholar]
- Murlidhar, B.R.; Armaghani, D.J.; Mohamad, E.T.; Changthan, S. Rock fragmentation prediction through a new hybrid model based on Imperial competitive algorithm and neural network. Smart Constr. Res. 2018, 2, 1–12. [Google Scholar]
- Asl, P.F.; Monjezi, M.; Hamidi, J.K.; Armaghani, D.J. Optimization of flyrock and rock fragmentation in the Tajareh limestone mine using metaheuristics method of firefly algorithm. Eng. Comput. 2018, 34, 241–251. [Google Scholar] [CrossRef]
- Das, A.; Sinha, S.; Ganguly, S. Development of a blast-induced vibration prediction model using an artificial neural network. J. S. Afr. Inst. Min. Metall. 2019, 119, 187–200. [Google Scholar] [CrossRef]
- Lawal, A.I.; Idris, M.A. An artificial neural network-based mathematical model for the prediction of blast-induced ground vibrations. Int. J. Environ. Stud. 2020, 77, 318–334. [Google Scholar] [CrossRef]
- Dinis da Gama, C.; Lopez Jimeno, C. Rock fragmentation control for blasting cost minimization and environmental impact abatement. In Proceedings of the International Symposium on Rock Fragmentation by Blasting, Vienna, Austria, 5–8 July 1993; pp. 273–280. [Google Scholar]
- Kanchibotla, S.S. Optimum blasting? Is it minimum cost per broken rock or maximum value per broken rock? Fragblast 2003, 7, 35–48. [Google Scholar] [CrossRef]
- Minimizing Quarrying Costs by Correct Shotrock Fragmentation and In-Pit Crushing. Available online: https://www.911metallurgist.com/blog/wp-content/uploads/2016/01/Minimizing-Reducing-Crusher-Operating-costs.pdf (accessed on 13 June 2020).
- Cunningham, C. The Kuz-Ram Model for production of fragmentation from blasting. In Proceedings of the Symposium on Rock Fragmentation by Blasting, Lulea, Sweden, 23–26 August 1983. [Google Scholar]
- Cunningham, C. Fragmentation estimations and the Kuz-Ram model-four years on. In Proceedings of the 2nd International Symposium on Rock Fragmentation by Blasting, Keystone, CO, USA, 23–26 August 1987; pp. 475–487. [Google Scholar]
- Kuznetsov, V. The mean diameter of the fragments formed by blasting rock. Sov. Min. 1973, 9, 144–148. [Google Scholar] [CrossRef]
- Rosin, P.; Rammler, E. The laws of governing the fineness of powdered coal. J. Inst. Fuel 1933, 7, 29–36. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- McDonald, J. Handbook of Biological Statistics, 3rd ed.; Sparky House Publishing: Baltimore, MD, USA, 2014. [Google Scholar]
- Silva, J.; Amaya, J.; Basso, F. Development of a predictive model of fragmentation using drilling and blasting data in open pit mining. J. S. Afr. Inst. Min. Metall. 2017, 117, 1089–1094. [Google Scholar] [CrossRef][Green Version]
- Hunter, G.; McDermott, C.; Miles, N.; Singh, A.; Scoble, M. A review of image analysis techniques for measuring blast fragmentation. Min. Sci. Technol. 1990, 11, 19–36. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Garces-Jimenez, A.; Castillo-Sequera, J.L.; Del Corte-Valiente, A.; Gómez-Pulido, J.M.; González-Seco, E.P.D. Analysis of artificial neural network architectures for modeling smart lighting systems for energy savings. IEEE Access 2019, 7, 119881–119891. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Counterpropagation networks. Appl. Opt. 1987, 26, 4979–4984. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A.N. On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition. Dokl. Akad. Nauk. Russ. Acad. Sci. 1957, 114, 953–956. [Google Scholar]
- Ge, Z.; Sun, Z. Neural Network Theory and MATLAB R2007 Application; Publishing House of Electronics Industry: Beijing, China, 2007; pp. 108–122. [Google Scholar]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]



| B(m) | S(m) | GU | Mineral Density (t/m3) | Diameter (Inches) | Bench (m) | Overdrilling (m) | Stemming (m) | D.Expl (ton/m3) | Kg.Expl | Powder Factor (kg/ton) | P80 | P50 | P20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9.3 | 10.7 | 4 | 2.45 | 10.625 | 15 | 2 | 6.5 | 1.3 | 709 | 194 | 83.4 | 47.2 | 12.3 |
| 9.3 | 10.7 | 4 | 2.45 | 10.625 | 15 | 2 | 6.5 | 1.3 | 709 | 194 | 91.8 | 51 | 12.81 |
| 9.3 | 10.7 | 3 | 2.35 | 10.625 | 15 | 2 | 6.5 | 1.3 | 709 | 202 | 86.3 | 47.9 | 9.34 |
| 9.3 | 10.7 | 3 | 2.35 | 10.625 | 15 | 2 | 6.5 | 1.3 | 709 | 202 | 88.3 | 47.9 | 9.76 |
| 9.3 | 10.7 | 4 | 2.45 | 10.625 | 15 | 2 | 6.5 | 1.3 | 709 | 194 | 80.5 | 44.3 | 7.9 |
| 8 | 8 | 5 | 2.48 | 10.625 | 14 | 0 | 7 | 1.2 | 436 | 196 | 74.1 | 39.9 | 4.21 |
| 8.8 | 10.2 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 225 | 70.3 | 38.6 | 7.61 |
| 8.8 | 10.2 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 225 | 75.6 | 40.7 | 8.04 |
| 9 | 12 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 187 | 63.4 | 37.8 | 6.7 |
| 9 | 12 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 187 | 80.6 | 45.6 | 8.28 |
| 9 | 12 | 3 | 2.35 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 195 | 94.4 | 51.6 | 14.08 |
| 9 | 12 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 187 | 76.6 | 45.7 | 11.89 |
| 9 | 12 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 187 | 86 | 51 | 13.42 |
| 9 | 12 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 187 | 82.3 | 47.8 | 11.5 |
| 9 | 12 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 187 | 66.2 | 39.5 | 8.35 |
| 9 | 12 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 187 | 87.3 | 49.1 | 7.8 |
| 9 | 12 | 3 | 2.35 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 195 | 71.6 | 42.2 | 5.97 |
| 9 | 12 | 3 | 2.35 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 195 | 72.3 | 41.5 | 4.74 |
| 10 | 13 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 155 | 61.9 | 37.4 | 7.07 |
| 10 | 13 | 3 | 2.35 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 162 | 60.9 | 36.8 | 6.54 |
| 10 | 13 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 155 | 69.5 | 40.3 | 5.66 |
| 10 | 13 | 4 | 2.45 | 10.625 | 15 | 2 | 6 | 1.3 | 743 | 155 | 84 | 48.1 | 8.19 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 260.5 | 135.9 | 43.6 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 225.9 | 119.8 | 37.3 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 237.6 | 131.6 | 42.3 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 222.9 | 118.1 | 36.8 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 232.1 | 128.8 | 41.3 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 216.2 | 119 | 37.8 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 236.3 | 121.3 | 38.5 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 161 | 85.1 | 24.8 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 218.8 | 127.6 | 40.8 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 218.5 | 119.5 | 37.5 |
| 7 | 8 | 5 | 2.48 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 318 | 184.4 | 99.8 | 30.3 |
| 7 | 8 | 6 | 2.57 | 10.625 | 15 | 2 | 7.5 | 1.22 | 663 | 307 | 180 | 103.2 | 31.6 |
| 8.8 | 10.2 | 5 | 2.48 | 10.625 | 15 | 2 | 6 | 1.22 | 768 | 230 | 276.6 | 152.6 | 54.6 |
| 8.8 | 10.2 | 6 | 2.57 | 10.625 | 15 | 2 | 6 | 1.22 | 768 | 222 | 234.2 | 122.9 | 42.8 |
| 8.8 | 10.2 | 6 | 2.57 | 10.625 | 15 | 2 | 6 | 1.22 | 768 | 222 | 178.2 | 85.2 | 26.1 |
| 6 | 7 | 6 | 2.57 | 10.625 | 15 | 2 | 6 | 1.22 | 719 | 444 | 194.8 | 102.7 | 24.1 |
| 6 | 7 | 5 | 2.48 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 460 | 140.3 | 79.8 | 21.2 |
| 6 | 7 | 5 | 2.48 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 460 | 272.9 | 141.7 | 24.1 |
| 6 | 7 | 5 | 2.48 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 460 | 192.1 | 91.8 | 24.7 |
| 6 | 7 | 6 | 2.47 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 444 | 314.7 | 179.3 | 62.4 |
| 6 | 7 | 6 | 2.57 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 444 | 348 | 199 | 60.3 |
| 6 | 7 | 6 | 2.57 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 444 | 322.1 | 179.2 | 51.6 |
| 6 | 7 | 6 | 2.57 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 444 | 220.9 | 108.7 | 31.4 |
| 6 | 7 | 6 | 2.57 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 444 | 288.8 | 152.1 | 36.1 |
| 6 | 7 | 6 | 2.57 | 10.625 | 15 | 2 | 6.7 | 1.22 | 719 | 444 | 241.2 | 127.6 | 38.5 |
| Mean Squared Error by Number of Simulations | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Hidden Neurons | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Average |
| 10 | 0.013934 | 0.010181 | 0.010772 | 0.011604 | 0.013516 | 0.010188 | 0.009633 | 0.014887 | 0.011839 |
| 11 | 0.014779 | 0.010263 | 0.00894 | 0.0091 | 0.009728 | 0.010336 | 0.011956 | 0.0098 | 0.010613 |
| 12 | 0.011681 | 0.009246 | 0.009824 | 0.012855 | 0.010517 | 0.011888 | 0.008056 | 0.010981 | 0.010631 |
| 13 | 0.012474 | 0.011985 | 0.008593 | 0.008027 | 0.008891 | 0.008518 | 0.00879 | 0.00918 | 0.009557 |
| 14 | 0.009478 | 0.00777 | 0.012028 | 0.008874 | 0.012441 | 0.010617 | 0.010151 | 0.01007 | 0.010179 |
| 15 | 0.007212 | 0.008788 | 0.009467 | 0.012912 | 0.011154 | 0.00952 | 0.011585 | 0.010223 | 0.010108 |
| Training | Testing | |||||
|---|---|---|---|---|---|---|
| Statistical parameters | ||||||
| (Real) | (ANN) | (MLR) | (Real) | (ANN) | (MLR) | |
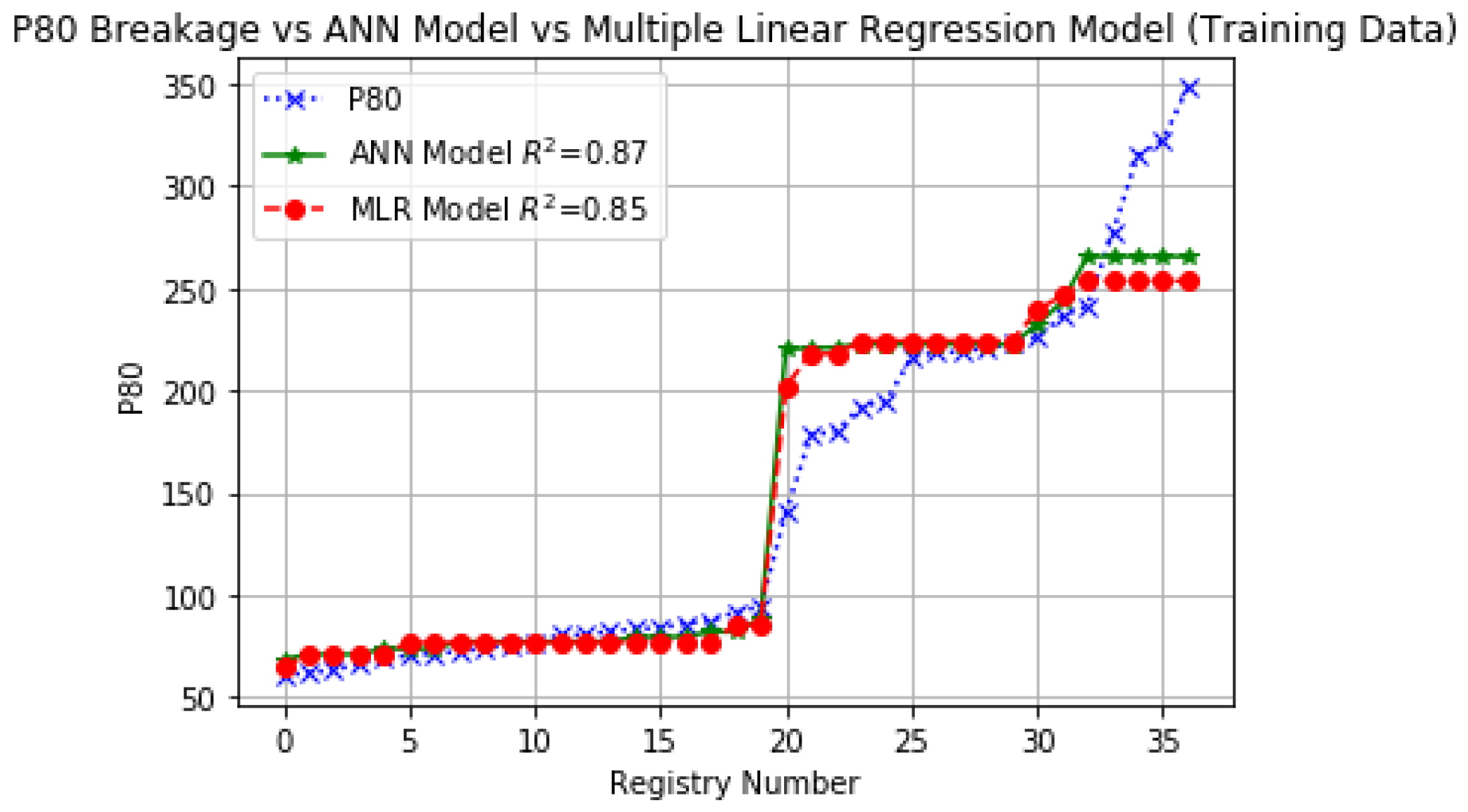
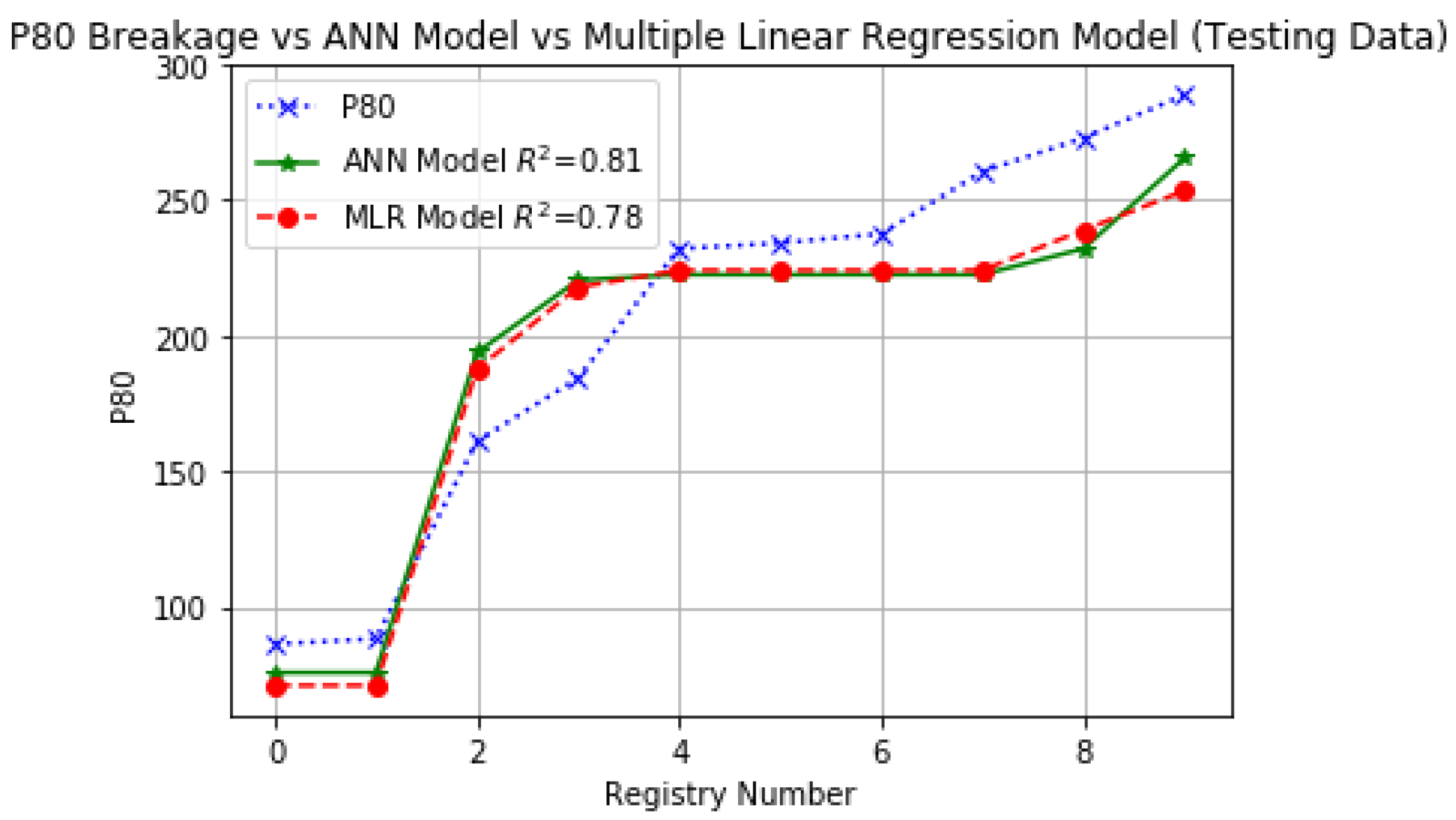
| Correlation coefficient | 0.87 | 0.85 | 0.81 | 0.78 | ||
| Mean (mm) | 148.1 | 150.2 | 148.11 | 204.61 | 195.36 | 193.65 |
| Standard deviation | 85.82 | 80.8 | 78.98 | 68.86 | 61.99 | 63.27 |
| Coefficient of variation | 0.58 | 0.54 | 0.53 | 0.33 | 0.32 | 0.32 |
| Training | Testing | |||||
|---|---|---|---|---|---|---|
| Statistical parameters | ||||||
| (Real) | (ANN) | (MLR) | (Real) | (ANN) | (MLR) | |
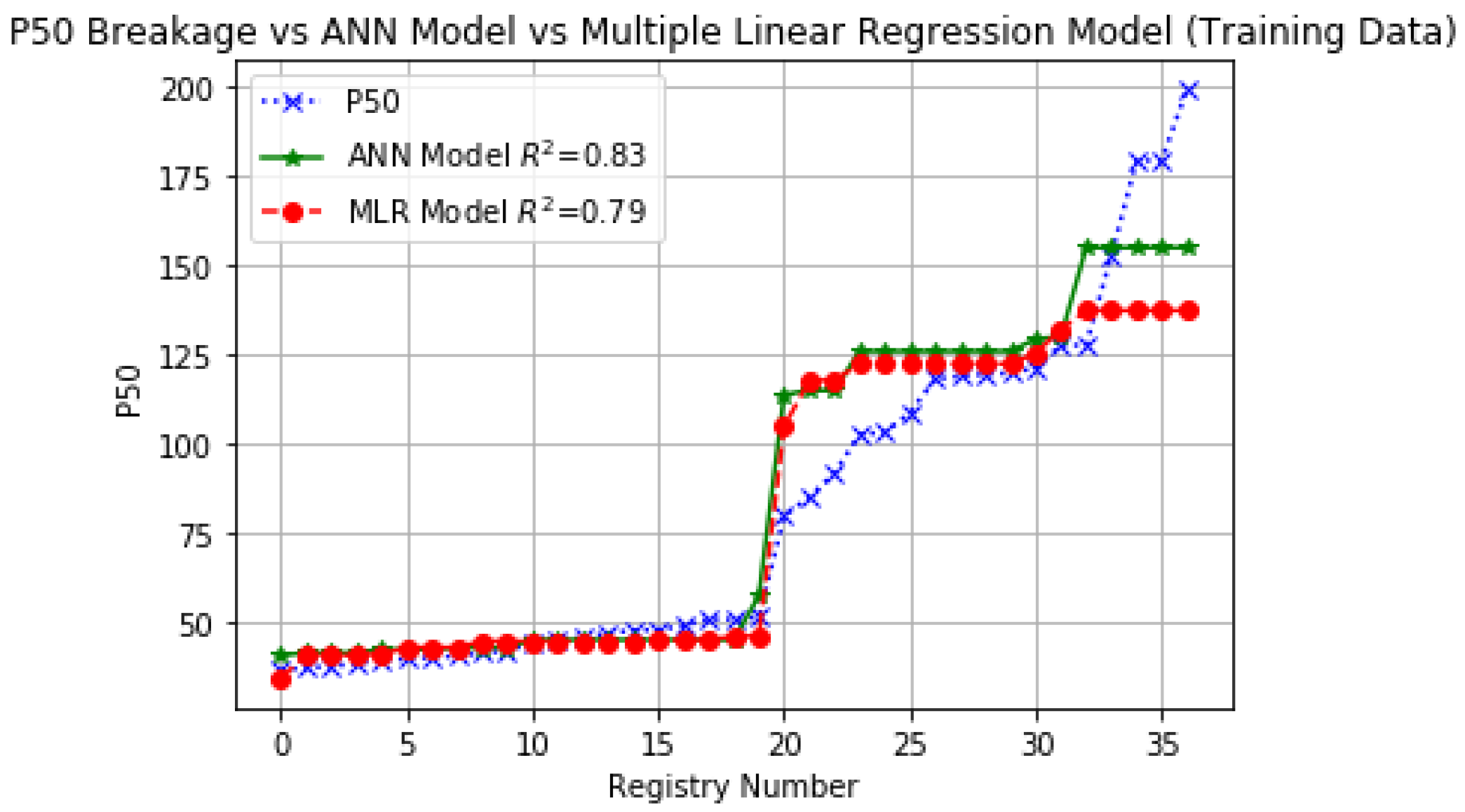
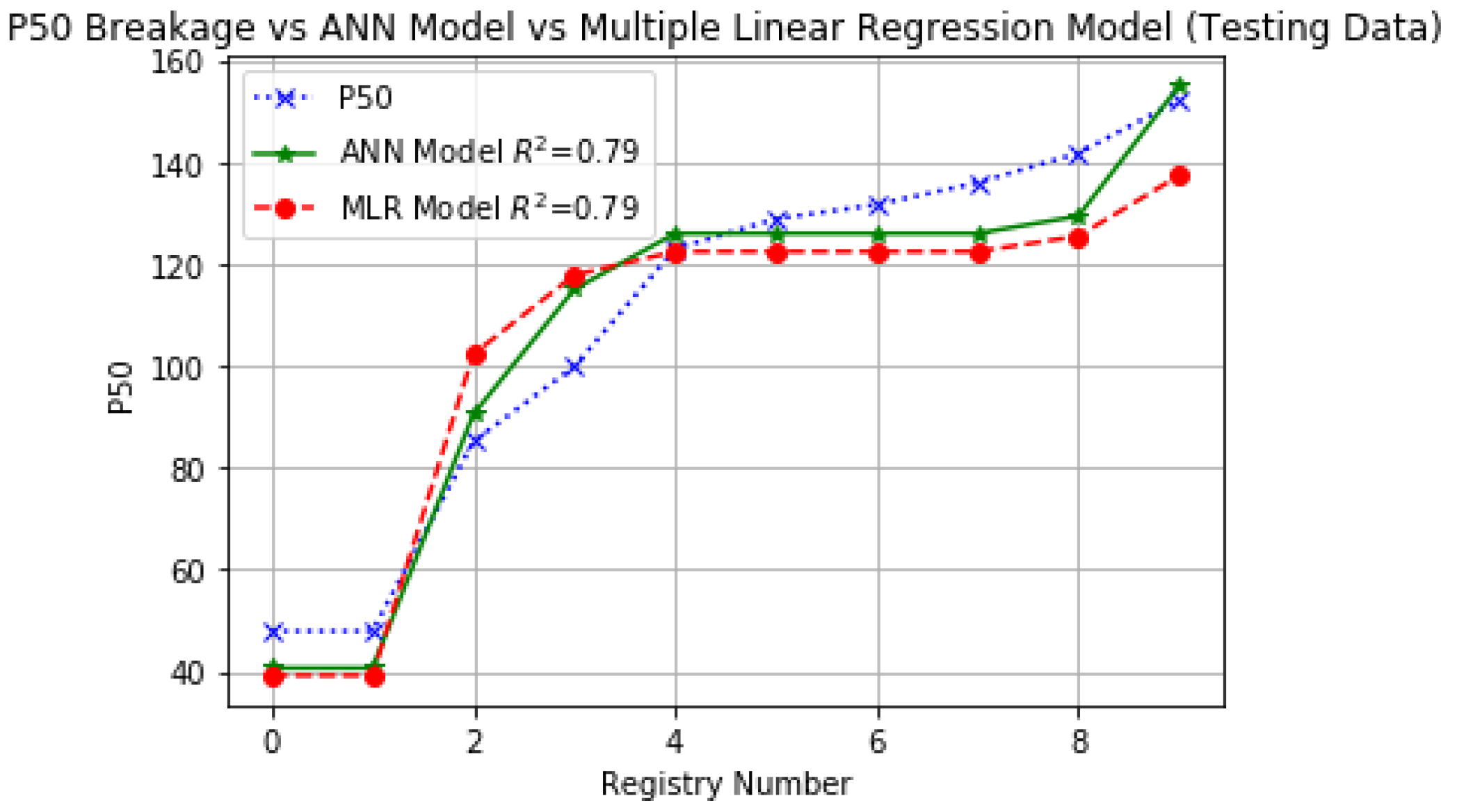
| Correlation coefficient | 0.83 | 0.79 | 0.79 | 0.79 | ||
| Mean (mm) | 81.36 | 85.03 | 81.36 | 109.37 | 107.47 | 105.06 |
| Standard deviation | 46.53 | 45.34 | 41.59 | 35.87 | 36.56 | 33.91 |
| Coefficient of variation | 0.57 | 0.53 | 0.51 | 0.32 | 0.34 | 0.32 |
| Training | Testing | |||||
|---|---|---|---|---|---|---|
| Statistical parameters | ||||||
| (Real) | (ANN) | (MLR) | (Real) | (ANN) | (MLR) | |
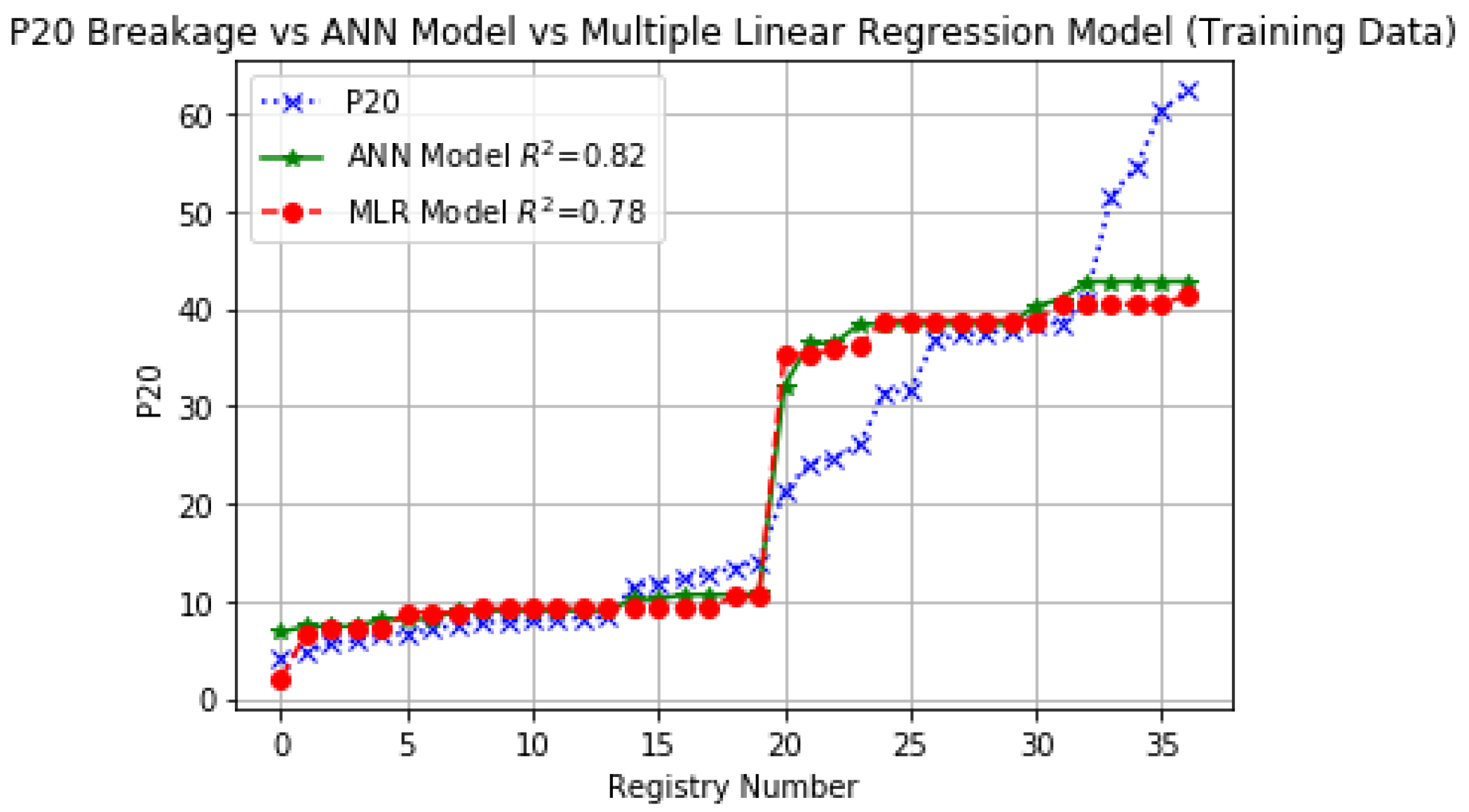
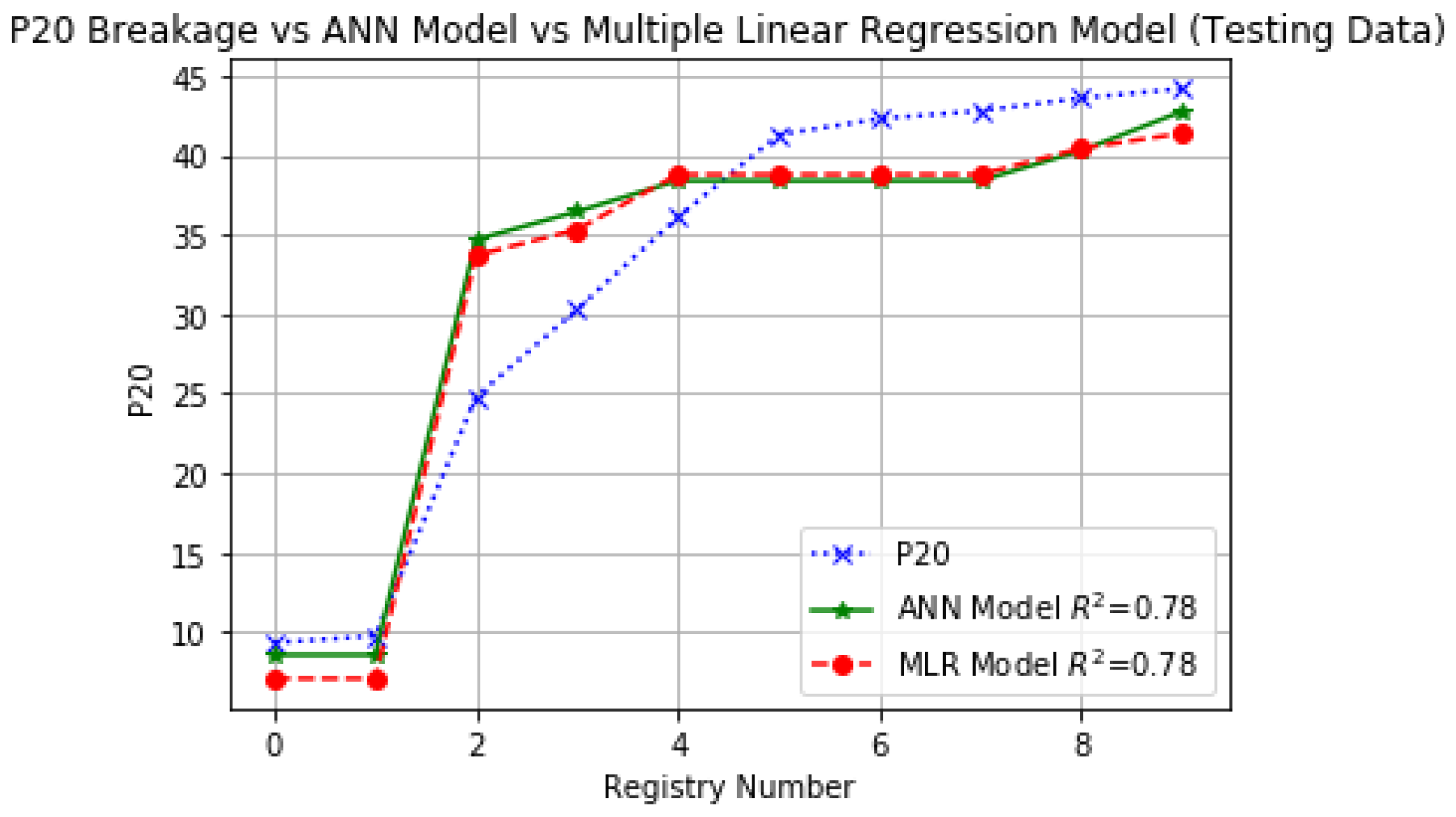
| Correlation coefficient | 0.82 | 0.78 | 0.78 | 0.78 | ||
| Mean (mm) | 22.38 | 22.93 | 22.38 | 32.45 | 32.49 | 32.01 |
| Standard deviation | 17.09 | 15.27 | 15.15 | 12.92 | 12.13 | 12.65 |
| Coefficient of variation | 0.76 | 0.66 | 0.67 | 0.39 | 0.37 | 0.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosales-Huamani, J.A.; Perez-Alvarado, R.S.; Rojas-Villanueva, U.; Castillo-Sequera, J.L. Design of a Predictive Model of Rock Breakage by Blasting Using Artificial Neural Networks. Symmetry 2020, 12, 1405. https://doi.org/10.3390/sym12091405
Rosales-Huamani JA, Perez-Alvarado RS, Rojas-Villanueva U, Castillo-Sequera JL. Design of a Predictive Model of Rock Breakage by Blasting Using Artificial Neural Networks. Symmetry. 2020; 12(9):1405. https://doi.org/10.3390/sym12091405
Chicago/Turabian StyleRosales-Huamani, Jimmy Aurelio, Roberth Saenz Perez-Alvarado, Uwe Rojas-Villanueva, and Jose Luis Castillo-Sequera. 2020. "Design of a Predictive Model of Rock Breakage by Blasting Using Artificial Neural Networks" Symmetry 12, no. 9: 1405. https://doi.org/10.3390/sym12091405
APA StyleRosales-Huamani, J. A., Perez-Alvarado, R. S., Rojas-Villanueva, U., & Castillo-Sequera, J. L. (2020). Design of a Predictive Model of Rock Breakage by Blasting Using Artificial Neural Networks. Symmetry, 12(9), 1405. https://doi.org/10.3390/sym12091405








