Abstract
Intelligent surveillance systems enable secured visibility features in the smart city era. One of the major models for pre-processing in intelligent surveillance systems is known as saliency detection, which provides facilities for multiple tasks such as object detection, object segmentation, video coding, image re-targeting, image-quality assessment, and image compression. Traditional models focus on improving detection accuracy at the cost of high complexity. However, these models are computationally expensive for real-world systems. To cope with this issue, we propose a fast-motion saliency method for surveillance systems under various background conditions. Our method is derived from streaming dynamic mode decomposition (s-DMD), which is a powerful tool in data science. First, DMD computes a set of modes in a streaming manner to derive spatial–temporal features, and a raw saliency map is generated from the sparse reconstruction process. Second, the final saliency map is refined using a difference-of-Gaussians filter in the frequency domain. The effectiveness of the proposed method is validated on a standard benchmark dataset. The experimental results show that the proposed method achieves competitive accuracy with lower complexity than state-of-the-art methods, which satisfies requirements in real-time applications.
1. Introduction
Nowadays, intelligent surveillance systems are gaining attention due to the demand for safety and security in critical infrastructures, such as military surveillance, home security, public transportation, etc. In these systems, video information acquired from sensors in devices is analyzed to assist in speeding up computer vision tasks like object tracking and vehicle detection. Therefore, the pre-processing method becomes an essential step that requires fast computation and high accuracy. One of the well-known pre-processing techniques is saliency detection. There are many studies on saliency detection from different aspects, such as object detection [1], object segmentation [2], video coding [3], image re-targeting [4], image quality assessment [5], and image compression [6]. The concept of saliency was inspired by neuroscience theory in which the human eye tends to focus on particular regions of the scene that stand out from their neighbors. The terms visual saliency or image saliency were first introduced in Itti et al. [7]. In these terms, the saliency model provides a mechanism to highlight the significant objects or regions that are most representative of a scene, while disposing of insignificant information retrieved from the surroundings. A saliency map is a grayscale image in which each pixel is mapped with an intensity value representing how much it differs from its surroundings. Preliminary research on visual saliency focused on still images. Various works have been proposed, and have achieved good performance, such as the graph-based model [8], the Bayesian-based model [9], the super-pixel–based model [10], histogram-based contrast [11], the frequency-based model [12], the patch-based local–global mixture approach [13], low-rank matrix recovery [14], context-awareness [15], and spectral residuals [16]. These approaches are divided into two categories: local-based approaches and global-based approaches. The first category employs low-level cues from small regions to obtain the saliency map. Itti et al. [7] decomposed images into a set of multi-scale features, and the saliency map was obtained through center-surround contrast in different scales. Harel and Perona [8] introduced graph models to compute the saliency map based on Itti et al. [7]. Zhang et al. [9] integrated the advantages of the Bayesian framework and local self-information to improve performance. Jiang et al. [10] introduced a super-pixel–based method by formulating saliency detection via the Markov chain framework. In the second category, global feature–based approaches were introduced [11,12,13,14,15,16]. Cheng et al. [11] used color statistics to compute a regional color histogram, and then measured its color contrast with other regions as a saliency value. Achanta et al. [12] analyzed the efficiency of color and luminance features in the frequency domain. Yeh et al. [13] incorporated patch-based local saliency with background/foreground seed likelihood in order to generate the saliency map. In [14], Shen formulated an image saliency problem as low-rank sparse decomposition in the feature space, and then, the salient region was indicated by the sparse matrix. Goferman et al. [15] measured the distinctiveness of every pixel by considering its appearance with the most similar surrounding patch. Although they achieved successful performance, using a multi-scale framework or image segmentation only added more complexity to their models.
Despite these image saliency models, saliency for videos is more complicated because they contain more information than still images. Video saliency considers not only spatial information within a frame but also the temporal information between consecutive frames. In a surveillance system, temporal information such as motion cues or flicker gains a lot of attention from viewers. For example, a specific region considered important in a still image becomes less important in a video when objects move across the scene. Notably, in surveillance videos, moving objects catch more attention than other regions, so the salient regions can be people walking or cars moving. As a result, when applied to videos, traditional image saliency becomes less useful for highlighting these regions. Therefore, temporal information has been exploited in saliency models to make use of existing image saliency for videos [17,18,19,20,21,22,23,24,25,26]. Although these methods are robust and versatile, they demand high computational costs with complex models not fast enough to use as a pre-processing algorithm in surveillance systems.
To cope with these issues, we introduce a fast-motion saliency method for surveillance videos. When compared with existing approaches, the proposed method is more practical in real-time applications, because feature extraction is an important and time-consuming step in saliency models. Our proposed method rapidly extracts spatial–temporal features from streaming data. The spatial and temporal information is represented by eigenvectors and eigenvalues of equation-free systems. This process is updated incrementally when a new frame is available, which allows our method to run in a streaming manner. The main contributions are summarized as follows.
- We introduce a new approach to generating motion saliency for surveillance systems, which is fast and memory-efficient for applications with streaming data.
- The spatial–temporal features from video are generated from a sparse reconstruction process using streaming dynamic mode decomposition (s-DMD).
- We compute a motion saliency map from the refinement process using a difference-of-Gaussians (DoG) filter in the frequency domain.
The remainder of the paper is organized as follows. Section 2 reviews the existing saliency detection methods. Section 3 introduces the background to dynamic mode decomposition. We describe the algorithms of the proposed methodology in Section 4. Experiment results are discussed in Section 5, and the conclusion is given in Section 6.
2. Related Works
There have been numerous studies into video saliency detection over the past two decades. Based on the applications, we classify these methods into the fusion strategy approach [17,18,19,20,21,22,23] and the direct-pipeline approach [24,25,26].
In the first category, several works added temporal information into image saliency models. Zhang et al. [17] extended SUN models [9] to videos by introducing a temporal filter, and used a generalized Gaussian distribution to estimate the filter response. Zhong et al. [18] added optical flow to the existing graph-based visual saliency (GBVS) [8]. Besides, Mauthner et al. [19] encoded a color histogram structure, and estimated the local saliency to different scales using foreground and background patches. Wang et al. [20] used geodesic distance to estimate a spatiotemporal saliency map based on motion boundaries, edges, and colors. Yubing et al. [21] generated static saliency based on face detection and low-level features, with motion saliency calculated based on a motion vector analysis of the foreground region, and then both maps were weighted by a Gaussian function. In [22], motion trajectories were learned via sparse coding frameworks, and a sparse reconstruction process was developed to capture regions with high center-surround contrast. Chen et al. [23] defined spatial saliency via color contrast, with motion guide contrast computed to define temporal saliency.
The second category includes various works that generate spatial–temporal saliency directly from the pipeline. Xue et al. [24] used low-rank and sparse decomposition on video slices where sparse components represent the salient region. Bhattacharya et al. [25] obtained spatial features based on video decomposition, and identified salient regions using the sparsest features. Wang et al. [26] considered spatial–temporal consistency over frames by using gradient flow field and energy optimization. All of these methods achieved good results; however, the performance heavily relies on how good the fusion strategy is [23,24], or demands high complexity in the models [25,26,27]. Therefore, these works have to deal with execution time to satisfy the requirements of pre-processing methods in surveillance systems.
To solve the complexity issue, some models have been proposed recently to speed up the calculations. Cui et al. [28] extended spectral residual models [16] onto the temporal domain to achieve computational efficiency. However, the plausibility of spectrum analysis in saliency detection is still not clear. Recently, Alshawi [29] explored the relation between QR factorization and saliency detection owing to the capability of hardware accelerators for matrix factorization in terms of processing speed. These methods were mainly designed for images, and lack motion features when applied to videos. In contrast to the above methods, our proposed model does not require hardware acceleration, is very fast, and is more specifically concerned with motion saliency. In Table 1, we summarize the state-of-the-art video saliency methods. Please see [30,31,32] for details and comparisons of these studies.

Table 1.
Overview of various state of the art video saliency methods.
3. Dynamic Mode Decomposition Background
The fluid mechanics community has been gaining interest in DMD [33,34] as a data-driven method. It approximates a set of dynamic modes that represent non-linear dynamics of the experimental data. Originally, DMD was designed for data collected in regular space–time intervals. Moreover, the DMD framework is described from an equation-free perspective, where the method relies on a sequence of snapshots generated from a dynamic system over time. It uses batch processing that combines dimensionality-reduction techniques and frequency domain techniques.
Let xi be the vector observed from n data points taken at time tj, j = 1, 2, …, m. We have a dynamic system with two matrices, , for m snapshots, as follows:
Assume that a linear mapping, A, connects the data, , to the subsequent data, , and the relation between two matrices is given by the following equation:
DMD determines eigenvectors and eigenvalues of A, which are considered DMD modes and DMD eigenvalues. In case n is large, and solving the best-fit A is computationally expensive, companion matrix S is introduced as follows:
In [29], a robust solution using SVD decomposition is applied to X, so equation (2) can be rewritten as:
where S is obtained as follows:
The full-rank matrix, , is derived via similarity transformation of matrix . It defines the low-dimensional linear model of the system. After computing the eigen-decomposition of , we have:
where columns of are eigenvectors of S, and Λ is a diagonal matrix that contains the corresponding eigenvalues, . The eigen-decomposition of can be related to eigenvalues and eigenvectors of A. Then DMD modes are given by columns of ϕ:
DMD eigenvectors and DMD eigenvalues provide the spatial information and temporal information, respectively, of each mode. This information is able to capture the dynamics of A.
The frequency of DMD modes is computed as follows:
where is the time interval between snapshots. The low rank and sparse components are given by:
The power of DMD was recently analyzed in various domains, such as image and video processing [35,36,37,38,39,40]. Grosek and Kutz [35] considered DMD modes with a frequency near the origin as background, with other modes as foreground, as described in Equation (8). Bi et al. [36] determined video boundaries based on the amplitudes of foreground and background modes. Besides, Sikha and colleagues [37,38] adapted DMD on different color channels for image saliency.
4. The Proposed Methodology
In general, the proposed method includes two main phases: (1) generate a raw saliency map based on sparse reconstruction, and (2) apply a coarse- to fine-motion refinement process. Figure 1 shows the architecture overview of the proposed model. For decomposition, we used s-DMD [40] for fast computation on video. Then, we use a difference-of-Gaussians filter on the frequency domain to refine the map.
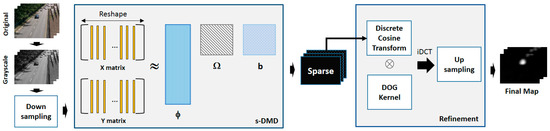
Figure 1.
The architecture overview of the proposed model.
4.1. Motion Saliency Generation Based on s-DMD
Surveillance systems require rapid response and intelligent analysis [39]; therefore, our target is to develop a method to extract features quickly in a relatively reliable way. Although batch-processing DMD described in Section 2 performs well, it requires an entire dataset to be known in advance. Therefore, we used an extended version of DMD called s-DMD for this step. s-DMD can exploit the spatial–temporal coherence structure of the video to extract features in a streaming manner.
In our method, each frame of the video is converted to grayscale and transformed into a column vector of two matrices, , where and For efficient computation, we resize the frame resolution before creating the data matrix. In order to compute from Equation (5), s-DMD reformulates Equation (4) of the original DMD using the Gram–Schmidt process, which helps to update DMD computation incrementally when new frames become available. First, we compute matrix to form the orthonormal basis of , and the DMD operator is given as follows:
is an × matrix defined as
where , is the Moore–Penrose pseudoinverse of , and denotes the rank of and . The DMD eigenvalues and modes of can now be obtained from the much smaller matrix . For every pair of frames, s-DMD updates the computation to generate a set of DMD modes and DMD eigenvalues. When there is a new pair of frames, the number of columns for and rows for increase. Therefore, to compute without storing the previous snapshot, we determine the orthonormal bases of and as . The coming pair of snapshots may very large, so they can be projected onto a low-dimensional space given as: , , and we then define new matrices, and If the size of is larger than the given rank, we apply proper orthogonal decomposition (POD) compression incrementally by introducing new matrix , where rY denotes the rank of and compute leading eigenvalues and eigenvectors of . In order to update operator , we use the identity matrix , and Equation (10) is rewritten as follows:
In our case, rank , is much less than m, which is the number of snapshots in the video, so can be updated incrementally. Moreover, we consider giving more weight to the recent frames by introducing weight parameter p while updating matrices . DMD modes and DMD eigenvalues can be derived from eigenvector and eigenvalues of according to Equation (5) in a streaming manner. The s-DMD mode is computed according to [31]:
The DMD approximation data can be reconstructed as follows:
where is the initial amplitude of each mode, ϕ is a matrix where columns are DMD eigenvectors, , and Ω is a diagonal matrix where the entries are eigenvalues, . Stationary regions are related to DMD modes with frequency ≈ 0, and these modes represent a region that slowly varies in time. Moving regions are selected from the remaining frequencies. Based on this calculation, the approximate sparse components are computed as follows:
According to Equation (13), s-DMD decomposes the video sequence into three matrices: DMD mode matrix ϕ, singular values matrix Λ, and amplitude matrix . The mode matrix represents the relative spatial and temporal information of the scene over time. The singular values matrix is the feature of these regions in the video. The amplitude matrix represents the weighted features of these modes in each frame, or how much these regions have changed in the video. When objects move across the scene, this model captures the energy of temporal modes corresponding to moving regions through the sparse reconstruction process. Therefore, s-DMD can be used to extract the salient region from the video.
4.2. From Coarse to Fine Motion Saliency Map
The sparse components of the video generated in Section 4.1 are subjected to the refinement process. To suppress non-salient pixels falsely detected in the sparse components, the saliency map is subjected to the difference-of-Gaussians filter in the frequency domain. The proposed coarse-to fine-motion process can suppress interference effectively. The DoG filter is known as a feature enhancement that preserves spatial information that lies within the range of frequencies. It is a combination of low-pass filtering and high-pass filtering. Given an image, f, the DoG applied on f is defined as:
where is the Gaussian kernel with standard deviation σ, represents the convolution of the image with the Gaussian kernel, and denotes the input image. In our case, we observe that falsely detected salient pixels are often distributed on low-frequency components of the raw saliency map. Therefore, we apply DoG to the sparse components derived from Section 4.1 to suppress these false detections. Compared to the state-of-the-art methods, such as Itti [7], GBVS [8], and spectral residual (SR) [16], they perform low-pass filtering using very low–frequency contents of the image in the spatial domain. Our method applies the DoG in a different way. First, we apply DoG to the frequency domain using a discrete cosine transform (DCT) in the Fourier transform. Secondly, we only compute the DoG on sparse components of the image. This step is similar to traditional DoG, but considers the information generated by different frequencies in the spectrum of the sparse components. Compared with traditional multi-scale DoG, the result is smoother, more accurate, and more efficient in computation. The Fourier transform of Equation (14) to express the DoG in the frequency domain is as follows:
where F denotes the Fourier transform. We used a DoG with σ1 = 2, σ2 = 10 in the experiments. The proposed DoG removes falsely detected non-salient pixels, and smooths the result. The final saliency map is obtained as:
where denotes the inverse fourier transform of the image. The overall algorithms of the proposed method are summarized in Algorithm 1 and Algorithm 2. The first algorithm is the modified s-DMD for generating DMD modes and DMD eigenvalues. The second algorithm is to generate and refine the saliency map based on the output of the s-DMD module.
| Algorithm 1: s-DMD for motion saliency. |
 |
| Algorithm 2: Generation of motion saliency map |
 |
5. Experiments Results
We evaluate the performance of the proposed method on the standard Change Detection 2014 (CDNet2014s) dataset [41]. The dataset contains different categories in various environments. We select 12 videos from five categories for details analysis. The salient region labeled from the human is used as ground-truth. In the experiments, we keep the resolution of the saliency maps the same as the original solutions of the frames. Video information for evaluation is summarized in Table 2. All of the tests were run using Matlab R2016a. The computer is equipped with 16 GB of memory.

Table 2.
The summarization of videos information in Change Detection 2014 (CDNet2014s) dataset used in performance evaluation.
5.1. Evaluation Metrics
We used various standard performance metrics to evaluate the performance of the algorithms, including precision recall curve (PR curve), mean absolute error (MAE), area under the Receiver Operating Characteristics (ROC) curve (AUC-Borji) [42], structure measure (S-measure) [43], normalized scan path saliency (NSS) [44], and correlation coefficient (CC) [45]. They are defined as follows.
PR curve: A precision value is the ratio of all salient pixels distributed correctly to all pixels in the image. Recall is the fraction of detected salient pixels to all ground truth pixels. The saliency map was converted to binary image S using a fixed threshold, which was used to compare against ground truth, G, to compute the precision and recall. PR curves show how reliable the saliency maps are, and how well they assign a salient score:
MAE: Mean absolute error provides a method to measure the difference between the saliency map and ground truth. MAE was normalized to [0, 1], which is defined as follows:
AUC-Borji: The area under the ROC curve (AUC) [42] measures the area under true positive and false positive rates (ROC curve), and ranges between 0 and 1. A perfect model has an AUC of 1.
S-measure: The structure measure [43] evaluates the structure information that pixel-based metrics (precision, recall) do not consider. The S-measure score is expressed as:
where x and y are vectors of saliency and ground truth values, respectively, , denote mean values, and denotes covariance values.
NSS: Normalized scan path saliency [44] measures the average saliency values at fixation pixels in the normalized saliency map. Given saliency map P and binary fixation map QB, the NSS score is defined as:
CC: The correlation coefficient [45] measures the Euclidean distance between the saliency map and the normalized empirical saliency map. The CC has a large value when two saliency maps have the same magnitude. Given saliency map P and fixation map , the CC score is defined as:
5.2. Comparision Results of Various State-of-the-Art Methods
In our method, we set weighting parameter p to 0.5, the scaling factor parameter to 0.25, and the max_rank parameter to 100 when performing experiments. The quantitative results of the CDNet2014s dataset are reported in Table 3 for detailed analysis. The proposed method showed the best results with the PETS2006 video. For other videos in the baseline category, MAE score decreased significantly. In other challenging categories, which consist of dynamic or interrupted motion, the proposed method showed comparative performance in terms of accuracy and structure measure.

Table 3.
The accuracy performance of the proposed method on CDNet2014s dataset.
To demontrate the efficiency of our proposal, we compared the proposed method with various state of the art methods including image saliency methods (ITTI [7], GBVS [8], SUN [9], saliency by self-resemblance SSR [46], fast and efficient saliency (FES) [47], quaternion-based spectral saliency (QSS) [48], high-dimensional color transform (HDCT) [49], principle component analysis (PCA) [50], region stability saliency (RSS) [51]) and video saliency method ( consistent video saliency (CVS) [26], random walk with restart (RWRS) [27]), the implementation source code were collected from C.Wloka et al. [52] and the project page of the authors. We keep all parameters of the author’s proposal as the default.
Figure 2 provides the performance of the compared algorithms using PR and ROC curves. The green thick dashed lines represents the proposed results. As shown in Figure 2a, our method outperforms others image saliency method in PR curves. The recall values of some image saliency are very small because their saliency maps cannot locate salient points well on salient objects. Moreover, our method achieves high precision rate that says it can detect salient object well. Figure 2b shows that our method attains higher positive rates for low false positive rates. The area under ROC curves also shows that our method performs slightly better compared with other algorithms.
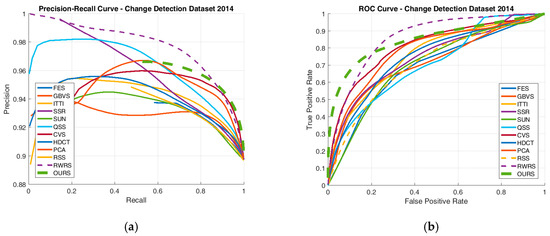
Figure 2.
The comparison of the proposed method on Change Detection 2014 Dataset. (a) Precision and Recall (PR) curve; (b) ROC curve.
Table 4, Table 5, Table 6, Table 7 and Table 8 shows the comparison results of various metrics on CDNet2014s Dataset. The first, second and third-ranked values of the corresponding metrics are highlighted in red, blue and black colors. The obtained results indicate that our method has competitive performance compared with other state-of-the-art algorithms. As shown in Table 4 and Table 5, the MAE and AUC-Borji score of the proposed method is always in top four performance in most of the cases. Although RSS model has lower MAE score in many cases, our method significantly outperforms this model in terms of AUC score. Our method achieves the highest AUC score in four videos of baseline category and has slightly lower MAE score than two complex models (CVS, RWRS) in case of highway and office video. In case the scene is disturbed with complex motions such as dynamic background or bad weather condition, the AUC score of the proposed method decreases slightly but still better than many state-of-the-art models.

Table 4.
Mean absolute error (MAE) comparison of the proposed method on CDNet2014s dataset.

Table 5.
Area under the ROC curve (AUC)-Borji comparison of the proposed method on CDNet2014s dataset.

Table 6.
S-measure comparison of the proposed method on CDNet2014s dataset.

Table 7.
Normalized scan path saliency (NSS) comparison of the proposed method on CDNet2014s dataset.

Table 8.
Correlation coefficient (CC) comparison of the proposed method on CDNet2014s dataset.
In Table 6, we measure structure similarity score (S-measure) of all methods. This metric demonstrate how well each model generates more completed object. Our method preserves global structure quite well in the baseline category; in other categories, our method shows comparative results.
Moreover, we evaluate the performance of the proposed method using NSS and CC metric. NSS metric uses the absolute saliency values in calculation. NSS is quite sensitive to false positive values; therefore, many low false positive values may contribute to low NSS values. CC metric evaluates the similarity of saliency magnitudes at fixation locations. As shown in Table 7 and Table 8, the proposed method achieves best scores in the baseline category and comparative results in another categories compared with other models. This shows that our method achieves relatively reliable accuracy result.
To further demonstrate the effectiveness of the s-DMD core, we compare the computational time for all methods under different resolutions in Table 9. The execution time of twelve algorithms was measured on Matlab 2016a. Although two models CVS and RWRS achieve better accuracy score in some categories, their complex model demands long run time for generating the saliency map. The CVS model requires more than 20 s for computing the optical flow, RWRS requires more than 10 s for the core process. Our method can reach 22 fps in Matlab environment for 320 × 240 px videos. The proposed method is much faster than these complex models, which satisfies the requirement of pre-processing algorithm in surveillance system.

Table 9.
The average time complexity (in seconds) of difference resolutions *.
In Table 10 and Table 11, we show the visual comparison of our method and others image saliency map in which each column shows saliency maps obtained from each method for various categories in each row. Some image saliency methods do not distribute salient points well on the moving object due to the lack of temporal information in their models. SUN does not perform well in detecting salient objects due to the limitation of using local features. FES and QSS cannot preserve the shape of object well. The salient points of RSS mostly distribute on the edge and the saliency map does not completed.

Table 10.
Visual comparison of saliency maps generated of image saliency methods.

Table 11.
Visual comparison of video saliency methods.
In order to validate the competitiveness of our proposal with respect to other models, we provided the statistical test in terms of AUC, NSS, and CC metrics. We use Matlab to perform the t-test at p < 0.05 for 5% significance as in [53]. The results are illustrated in Figure 3, Figure 4 and Figure 5. There are two values “1” and “0” in the table, which indicate the statistical significance of the difference between every pair of compared models. If the mean value of the model in the row is larger than the model in the column, it is represented by “1”; otherwise, it is “0”.
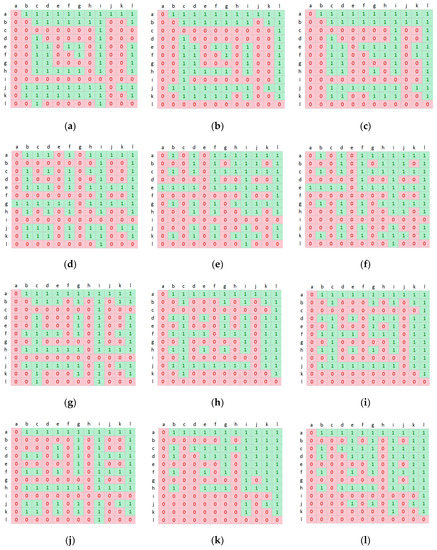
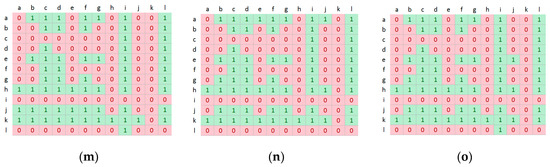
Figure 3.
The results of statistical test over twelve methods. We abbreviate twelve methods from “a” to “h”: a = OURS, b = CVS, c = FES, d = GBVS, e = HDCT, f = IKN, g = PCA, h = QSS, i = RSS, j = RWRS, k = SSR, l = SUN. (a) HIG-AUC. (b) HIG-NSS. (c) HIG-CC. (d) OFF-AUC. (e) OFF-NSS. (f) OFF-CC. (g) PED-AUC. (h) PED-NSS. (i) PED-CC. (j) PET-AUC. (k) PET-NSS. (l) PET-CC. (m) CAN-AUC. (n) CAN-NSS. (o) CAN-CC.
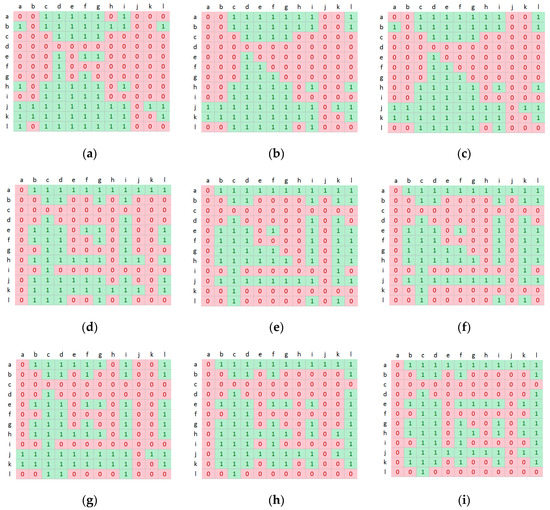
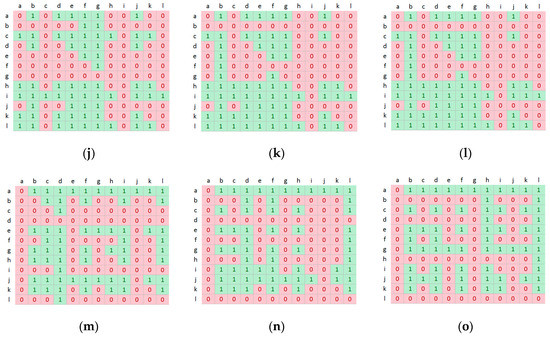
Figure 4.
The results of statistical test over twelve methods. We abbreviate twelve methods from “a” to “h”: a = OURS, b = CVS, c = FES, d = GBVS, e = HDCT, f = IKN, g = PCA, h = QSS, i = RSS, j = RWRS, k = SSR, l = SUN. (a) OVE-AUC. (b) OVE -NSS. (c) OVE -CC. (d) BLI-AUC. (e) BLI-NSS. (f) BLI-CC. (g) SKA-AUC. (h) SKA-NSS. (i) SKA-CC. (j) SID-AUC. (k) SID-NSS. (l) SID-CC. (m) TRA-AUC. (n) TRA-NSS. (o) TRA-CC.
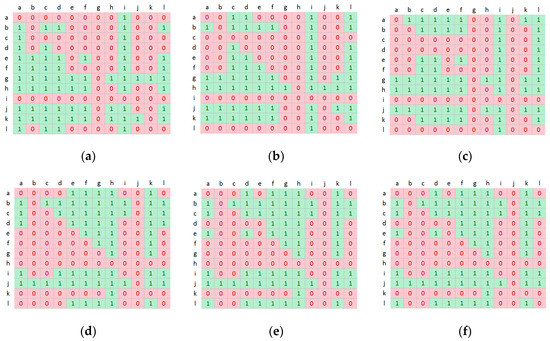
Figure 5.
The results of statistical test over twelve methods. We abbreviate twelve methods from “a” to “h”: a = OURS, b = CVS, c = FES, d = GBVS, e = HDCT, f = IKN, g = PCA, h = QSS, i = RSS, j = RWRS, k = SSR, l = SUN. (a) SOF-AUC. (b) SOF-NSS. (c) SOF-CC. (d) STR-AUC. (e) STR-NSS. (f) STR-CC.
Considering the baseline category, the proposed model is better than other models in terms of AUC, NSS and CC in most cases. Similar results can be observed in the bad weather category for two videos blizzard and skating. In the dynamic background category, our method performs quite well in terms of NSS and CC in two videos canoe and overpass. In the camera jitter category, the proposed method achieves relative performance in the sidewalk video; meanwhile, the proposed method and RWRS perform well in traffic video without significant difference in terms of NSS and CC. In the intermittent object motion category, our method performs better than HDCT, PCA in terms of NSS and CC. From these results, our method is slightly competitive with these advanced models.
5.3. Discussion
From our performance results, we discuss some advantages and disadvantages of our proposal as follows:
First, this paper considers whether matrix decomposition can be used to generate motion saliency effectively in-stream manner, and the results of the experiments have proved our idea. We do not use super-pixels segmentation in pre-processing step or optical flow for generating motion features as other methods. Although ours method does not preserve the shape of the salient object well for all cases as in PCA, CVS or HDCT, the total computational time of our method is 80% faster than such models. According to Table 9, it takes on average 43 ms to process a frame, including about 7 ms for the process of down-sampling/up-sampling, 31 ms for s-DMD computation, and 5 ms for the refinement process. Regarding to time complexity of the s-DMD, the input rank also affects the computational cost of the whole process. Since DMD modes and DMD eigenvalues are required for computing the raw saliency after every iterate, therefore the computational cost is O(nr2) where r is the given rank of matrix (, and n is the number of pixels in a frame. In our case, the rank is much smaller than n, so this model can speed up the performance and especially computational effective and memory-efficient in real-time applications.
Second, the proposed method achieves better results than its competitors in terms of accuracy metrics (MAE, AUC-Borji, NSS and CC) and structure metrics (S-measure) in stationary videos such as baseline, and bad weather categories. In the camera jitter category where videos recorded by vibrational cameras, or when there is interrupted action in the videos like the intermittent object motion category, we achieve top three in the performance. In a challenged category such as dynamic background, which contains moving leaves or dynamic waters, the accuracy performance of our proposal decreases slightly but not far from the top three results. When compared with other complex models for video saliency, our method achieve slight better scores in terms of accuracy metrics in some categories.
Thirdly, we discuss failure cases of the proposed method. When the size of the object is too small compared with the frame size, and multiple moving objects may disturb the accuracy of the algorithm. We can see this in streetlight videos, only moving cars on the bridge are considered as salient regions in the ground truth. However, the proposed method could not distinguish them from other cars moving on the street. It is because we consider the energy of all temporal modes globally without using local features. Moreover, our proposal does not target on preserving of the shape of the salient object in a complex background scene. Therefore, the S-measure of our method is slightly lower than other methods in these categories.
Finally, it is evidence that s-DMD could help to improve motion saliency performance effectively; however, it has limitations to generate good results in some exceptional cases discussed above. In the future, we could distinguish different moving objects in the scene by differentiate their slow and fast modes to get the finer result in different scales of resolutions. This problem requires an effort to incorporate multi-scale s-DMD towards to more comprehensive model.
6. Conclusions
We have introduced a newly fast motion saliency detection algorithm for surveillance systems. Instead of using optical flow for extracting motion features, we directly extract spatial-temporal features from the video in streaming manner. Thanks to the power of streaming dynamic mode decomposition, we compute the spatial-temporal modes via low rank and sparse decomposition fastly. These modes represent the spatial-temporal coherence features of the scene over time. We generate the raw saliency map that represents to motion region from the energy of temporal modes. The refinement process utilized the advantage of the difference of Gaussian on frequency domain to suppress background noise. The computational time across various videos is 80% faster than other complicated models. The quality evaluation and statistical validation tests on different categories in Change Detection Dataset 2014 show that our method can balance the performance in terms of accuracy and time efficiency in different video categories.
Although s-DMD could help to improve motion saliency performance effectively, its limitations are to generate good results in distinguishing multiple salient regions in complex scenes. In future works, considering multi-scale modes with respect to different moving objects, we investigate the ability to use multi-scale resolution features from different DMD modes for streaming data to improve the saliency prediction.
Author Contributions
This paper represents the result of collaborative teamwork. Conceptualization, T.-T.N.; Funding acquisition, E.-N.H.; Software, T.-T.N.; Visualization, T.-T.N.; Writing—original draft, T.-T.N.; Writing—review & editing, T.-T.N., X.-Q.P., V.N., M.-A.H. and E.-N.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Institute for Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No.2019-0-01615, Developed digital signage solution for cloud-based unmanned shop management that provides online video advertising)
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, T.; Yuan, Z.; Sun, J.; Wang, J.; Zheng, N.; Tang, X.; Shum, H.Y. Learning to detect a salient object. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 353367. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, R.; Shen, L.; Xue, Y.; Ngan, K.N.; Zhang, Z. Unsupervised salient object segmentation based on kernel density estimation and two-phase graph cut. IEEE Trans. Multimed. 2012, 14, 1275–1289. [Google Scholar] [CrossRef]
- Hadizadeh, H.; Bajić, I.V. Saliency-aware video compression. IEEE Trans. Image Process. 2014, 23, 19–33. [Google Scholar] [CrossRef] [PubMed]
- Lei, J.; Wu, M.; Zhang, C.; Wu, F.; Ling, N.; Hou, C. Depth preserving stereo image retargeting based on pixel fusion. IEEE Trans. Multimed. 2017, 19, 1442–1453. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, Y.; Li, H. VSI: A visual saliency-induced index for perceptual image quality assessment. IEEE Trans. Image Process. 2014, 23, 4270–4281. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Vasconcelos, N. Image compression using object-based regions of interest. In Proceedings of the 2006 International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; pp. 3097–3100. [Google Scholar]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Harel, C.K.J.; Perona, P. Graph-based visual saliency. In Proceedings of the Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 4–7 December 2006. [Google Scholar]
- Zhang, L.; Tong, M.; Marks, T.; Shan, H.; Cottrell, G. SUN: A Bayesian framework for saliency using natural statistics. J. Vis. 2008, 8, 1–20. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, L.; Lu, H.; Yang, C.; Yang, M.-H. Saliency detection via absorbing Markov chain. In Proceedings of the IEEE International Conference on ComputerVision (2013), Sydney, Australia, 1–8 December 2013; pp. 1665–1672. [Google Scholar]
- Cheng, M.; Zhang, G.; Mitra, N.J.; Huang, X.; Hu, S. Global contrast based salient region detection. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 21–25 June 2011; pp. 409–416. [Google Scholar]
- Achanta, R.; Hemami, S.; Estrada, F. Susstrunk, frequency-tuned salient region detection. In Proceedings of the Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1597–1604. [Google Scholar]
- Yeh, H.-H.; Liu, K.-H.; Chen, C.-S. Salient object detection via local saliency estimation and global homogeneity refinement. Pattern Recognit. 2014, 47, 1740–1750. [Google Scholar] [CrossRef]
- Shen, X.; Wu, Y. A unified approach to salient object detection via low rank matrix recovery. In Proceedings of the Computer Vision and Pattern Recognition (CVPR) 2012, Providence, RI, USA, 16–21 June 2012; pp. 853–860. [Google Scholar]
- Goferman, S.; Zelnik-Manor, L.; Tal, A. Context-aware saliency detection. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2376–2383. [Google Scholar] [CrossRef]
- Hou, X.; Zhang, L. Saliency detection: A spectral residual approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 21–26 July 2007; pp. 1–8. [Google Scholar]
- Zhang, L.; Tong, M.; Cottrell, G. SUNDAy: Saliency using natural statistics for dynamic analysis of scenes. In Proceedings of the 31st Annual Cognitive Science Conference, Amsterdam, The Netherlands, 29 July–1 August 2009. [Google Scholar]
- Zhong, S.-H.; Liu, Y.; Ren, F.; Zhang, J.; Ren, T. Video saliency detection via dynamic consistent spatiotemporal attention modelling. In Proceedings of the National Conference of the American Association for Artificial Intelligence, Washington, DC, USA, 14–18 July 2013; pp. 1063–1069. [Google Scholar]
- Mauthner, T.; Possegger, H.; Waltner, G.; Bischof, H. Encoding based saliency detection for videos and images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2015, Boston, MA, USA, 7–12 June 2015; pp. 2494–2502. [Google Scholar]
- Wang, W.; Shen, J.; Porikli, F. Saliency-aware geodesic video object segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2015, Boston, MA, USA, 7–12 June 2015; pp. 3395–3402. [Google Scholar]
- Yubing, T.; Cheikh, F.A.; Guraya, F.F.E.; Konik, H.; Trémeau, A. A spatiotemporal saliency model for video surveillance. Cogn. Comput. 2011, 3, 241–263. [Google Scholar] [CrossRef]
- Ren, Z.; Gao, S.; Rajan, D.; Chia, L.; Huang, Y. Spatiotemporal saliency detection via sparse representation. In Proceedings of the 2012 IEEE International Conference on Multimedia and Expo Workshops, Melbourne, Australia, 9–13 July 2012; pp. 158–163. [Google Scholar] [CrossRef]
- Chen, C.; Li, S.; Wang, Y.; Qin, H.; Hao, A. Video saliency detection via spatial-temporal fusion and low-rank coherency diffusion. IEEE Trans. Image Process. 2017, 26, 3156–3170. [Google Scholar] [CrossRef]
- Xue, Y.; Guo, X.; Cao, X. Motion saliency detection using low-rank and sparse decomposition. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 1485–1488. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Venkatesh, K.S.; Gupta, S. Visual saliency detection using spatiotemporal decomposition. IEEE Trans. Image Process. 2018, 27, 1665–1675. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Shen, J.; Shao, L. Consistent video saliency using local gradient flow optimization and global refinement. IEEE Trans. Image Process. 2015, 24, 4185–4196. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kim, Y.; Sim, J.-Y.; Kim, C.-S. Spatiotemporal saliency detection for video sequences based on random walk with restart. IEEE Trans. Image Process. 2015, 24, 2552–2564. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Liu, Q.; Zhang, S.; Yang, F.; Metaxas, D.N. Temporal spectral residual for fast salient motion detection. Neurocomputing 2012, 86, 24–32. [Google Scholar] [CrossRef]
- Alshawi, T. Ultra-fast saliency detection using QR factorization. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019; pp. 1911–1915. [Google Scholar] [CrossRef]
- Borji, A.; Cheng, M.; Jiang, H.; Li, J. Salient object detection: A benchmark. IEEE Trans. Image Process. 2015, 24, 5706–5722. [Google Scholar] [CrossRef]
- Cong, R.; Lei, J.; Fu, H.; Cheng, M.; Lin, W.; Huang, Q. Review of visual saliency detection with comprehensive information. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 2941–2959. [Google Scholar] [CrossRef]
- Borji, A.; Itti, L. State-of-the-art in visual attention modeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 185–207. [Google Scholar] [CrossRef]
- Schmid, P.J.; Sesterhenn, J.L. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2008. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014. [Google Scholar] [CrossRef]
- Grosek, J.; Kutz, J.N. Dynamic mode decomposition for real-time background/foreground separation in video. arXiv preprint. 2014, arXiv:1404.7592. [Google Scholar]
- Bi, C.; Yuan, Y.; Zhang, J.; Shi, Y.; Xiang, Y.; Wang, Y.; Zhang, R. Dynamic mode decomposition based video shot detection. IEEE Access 2018, 6, 21397–21407. [Google Scholar] [CrossRef]
- Sikha, O.K.; Kumar, S.S.; Soman, K.P. Salient region detection and object segmentation in color images using dynamic mode decomposition. J. Comput. Sci. 2018, 25, 351–366. [Google Scholar] [CrossRef]
- Sikha, O.K.; Soman, K.P. Multi-resolution dynamic mode decomposition-based salient region detection in noisy images. SIViP 2020, 14, 167–175. [Google Scholar] [CrossRef]
- Yu, C.; Zheng, X.; Zhao, Y.; Liu, G.; Li, N. Review of intelligent video surveillance technology research. In Proceedings of the 2011 International Conference on Electronic and Mechanical Engineering and Information Technology, EMEIT 2011, Harbin, China, 12–14 August 2011; pp. 230–233. [Google Scholar] [CrossRef]
- Hemati, M.S.; Williams, M.O.; Rowley, C.W. Dynamic mode decomposition for large and streaming datasets. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Wang, Y.; Jodoin, P.-M.; Porikli, F.; Konrad, J.; Benezeth, Y.; Ishwar, P. CDnet 2014: An expanded change detection benchmark dataset. In Proceedings of the IEEE Workshop on Change Detection (CDW-2014) at CVPR-2014, Columbus, OH, USA, 23–28 June 2014; pp. 387–394. [Google Scholar]
- Borji, A.; Tavakoli, H.R.; Sihite, D.N.; Itti, L. Analysis of scores, datasets, and models in visual saliency prediction. In Proceedings of the IEEE International Conference on Computer Vision IEEE Computer Society, Sydney, Australia, 1–8 December 2013; pp. 921–928. [Google Scholar]
- Fan, D.-P.; Cheng, M.-M.; Liu, Y.; Li, T.; Borji, A. Structure-measure: A new way to evaluate foreground maps. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4558–4567. [Google Scholar]
- Peters, R.J.; Iyer, A.; Itti, L.; Koch, C. Components of bottom-up gaze allocation in natural images. Vis. Res. 2005, 45, 2397–2416. [Google Scholar] [CrossRef] [PubMed]
- le Meur, O.; le Callet, P.; Barba, D. Predicting visual fixations on video based on low-level visual features. Vis. Res. 2007, 47, 2483–2498. [Google Scholar] [CrossRef]
- Seo, H.J.; Milanfar, P. Non-parametric bottom-up saliency detection by self-resemblance. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, USA, 20–25 June 2009; pp. 45–52. [Google Scholar] [CrossRef]
- Tavakoli, H.R.; Rahtu, E.; Heikkilä, J. Fast and efficient saliency detection using sparse sampling and kernel density estimation. In Proceedings of the 17th Scandinavian conference on Image analysis (SCIA’11), Ystad, Sweden, 23–27 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 666–675. [Google Scholar]
- Schauerte, B.; Stiefelhagen, R. Quaternion-based spectral saliency detection for eye fixation prediction. In Proceedings of the 12th European Conference on Computer Vision—ECCV 2012, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7573, pp. 116–129. [Google Scholar]
- Kim, J.; Han, D.; Tai, Y.; Kim, J. Salient region detection via high-dimensional color transform and local spatial support. IEEE Trans. Image Process. 2016, 25, 9–23. [Google Scholar] [CrossRef]
- Margolin, R.; Tal, A.; Zelnik-Manor, L. What makes a patch distinct? In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1139–1146. [Google Scholar] [CrossRef]
- Lou, J.; Zhu, W.; Wang, H.; Ren, M. Small target detection combining regional stability and saliency in a color image. Multimed. Tools Appl. 2017, 76, 14781–14798. [Google Scholar] [CrossRef]
- Wloka, C.; Kunić, T.; Kotseruba, I.; Fahimi, R.; Frosst, N.; Bruce, N.D.B.; Tsotsos, J.K. SMILER: Saliency model implementation library for experimental research. arXiv 2018, arXiv:1812.08848. [Google Scholar]
- Li, Y.; Mou, X. Saliency detection based on structural dissimilarity induced by image quality assessment model. J. Electron. Imaging 2019, 28, 023025. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).