Formation of Thermal Lesions in Tissue and Its Optimal Control during HIFU Scanning Therapy
Abstract
1. Introduction
2. Theory and Methods
2.1. Description of Acoustic Fields and Temperature Fields
2.2. Parameters for Evaluating the Treatment Effect
2.3. Optimal Control for Formation of Thermal Lesions
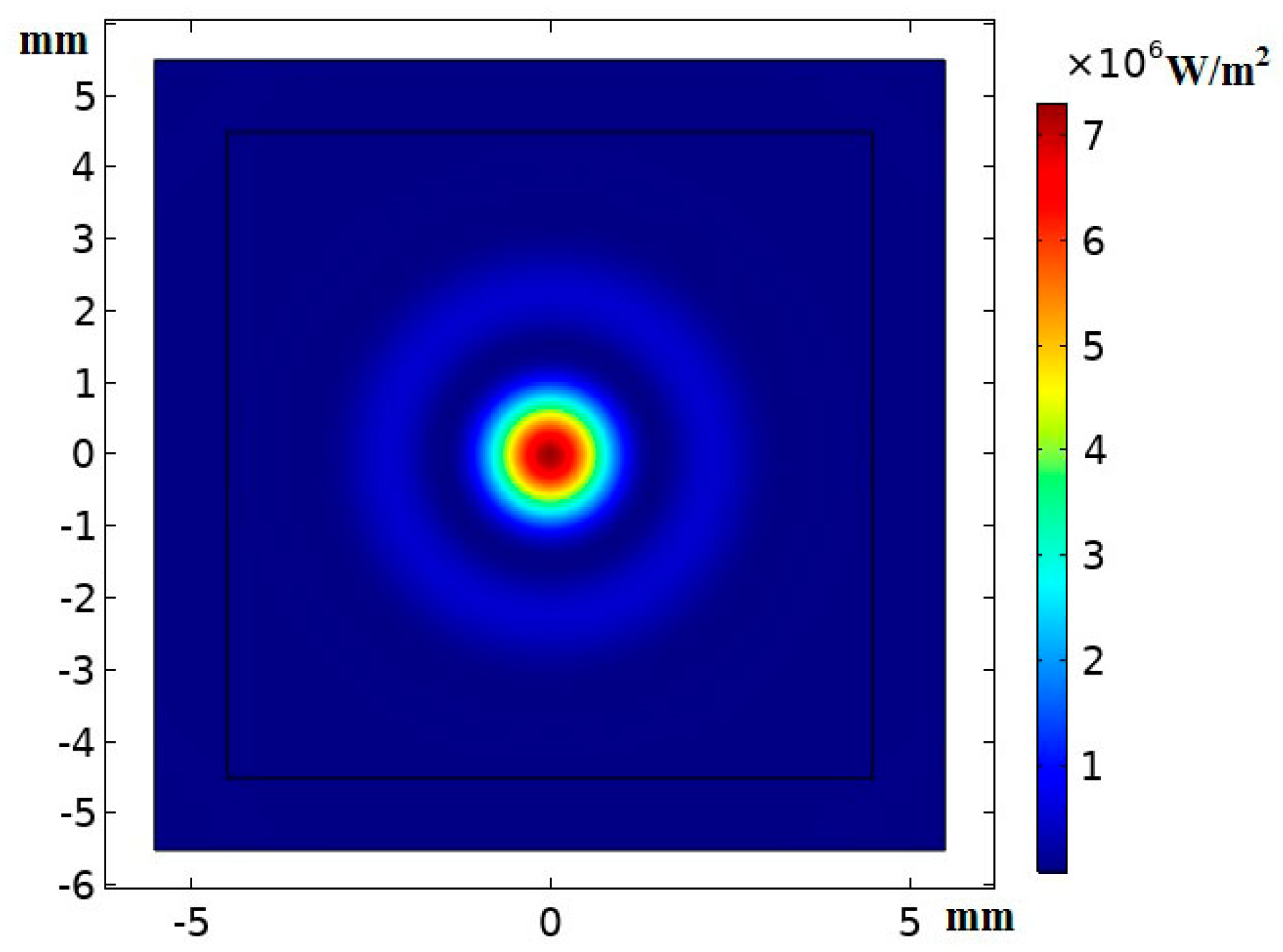
2.4. Simulation Methods and Relevant Conditions
3. Results and Discussion
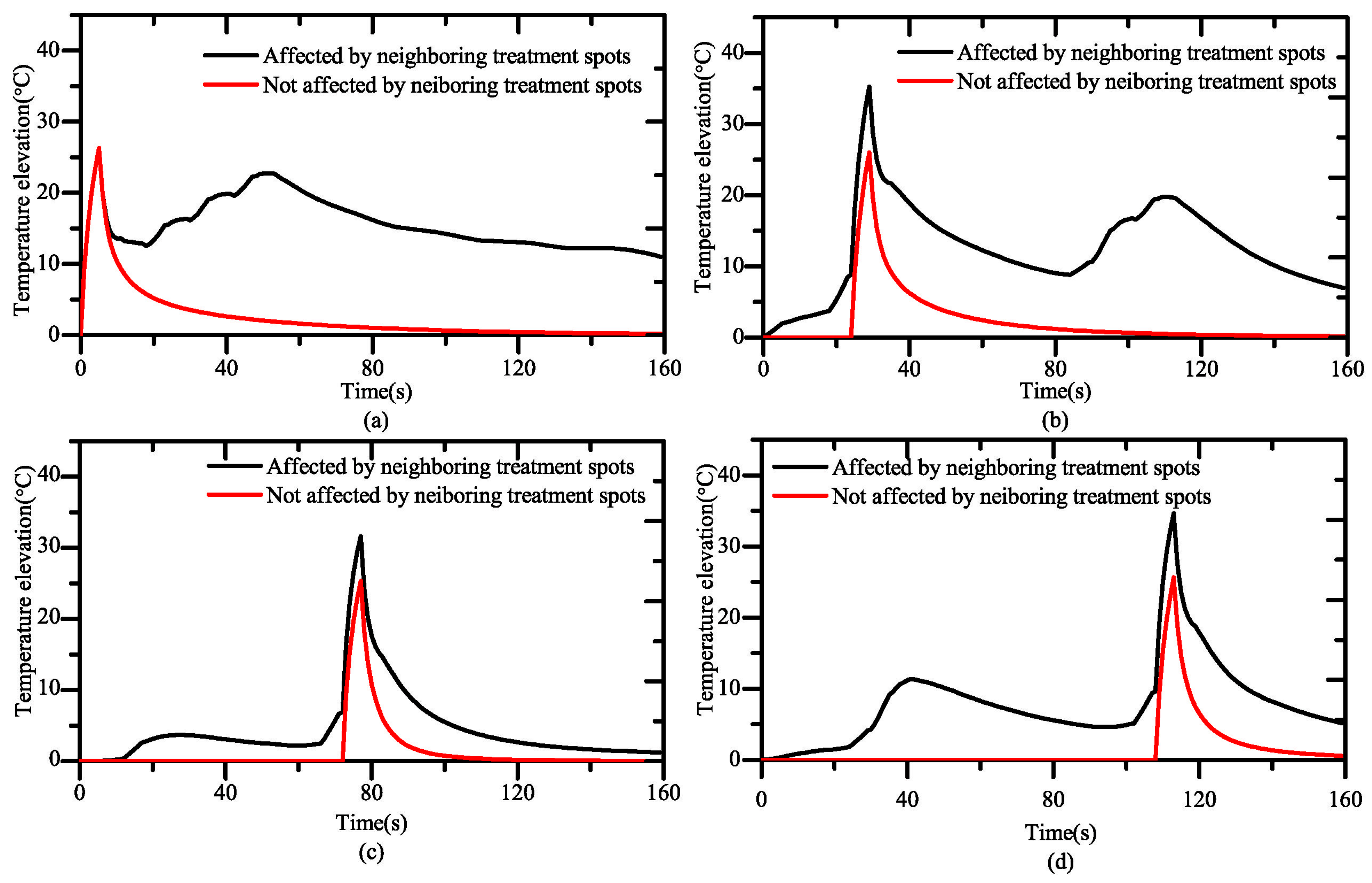
3.1. Influence of Neighboring Treatment Spots on the Temperature Elevation
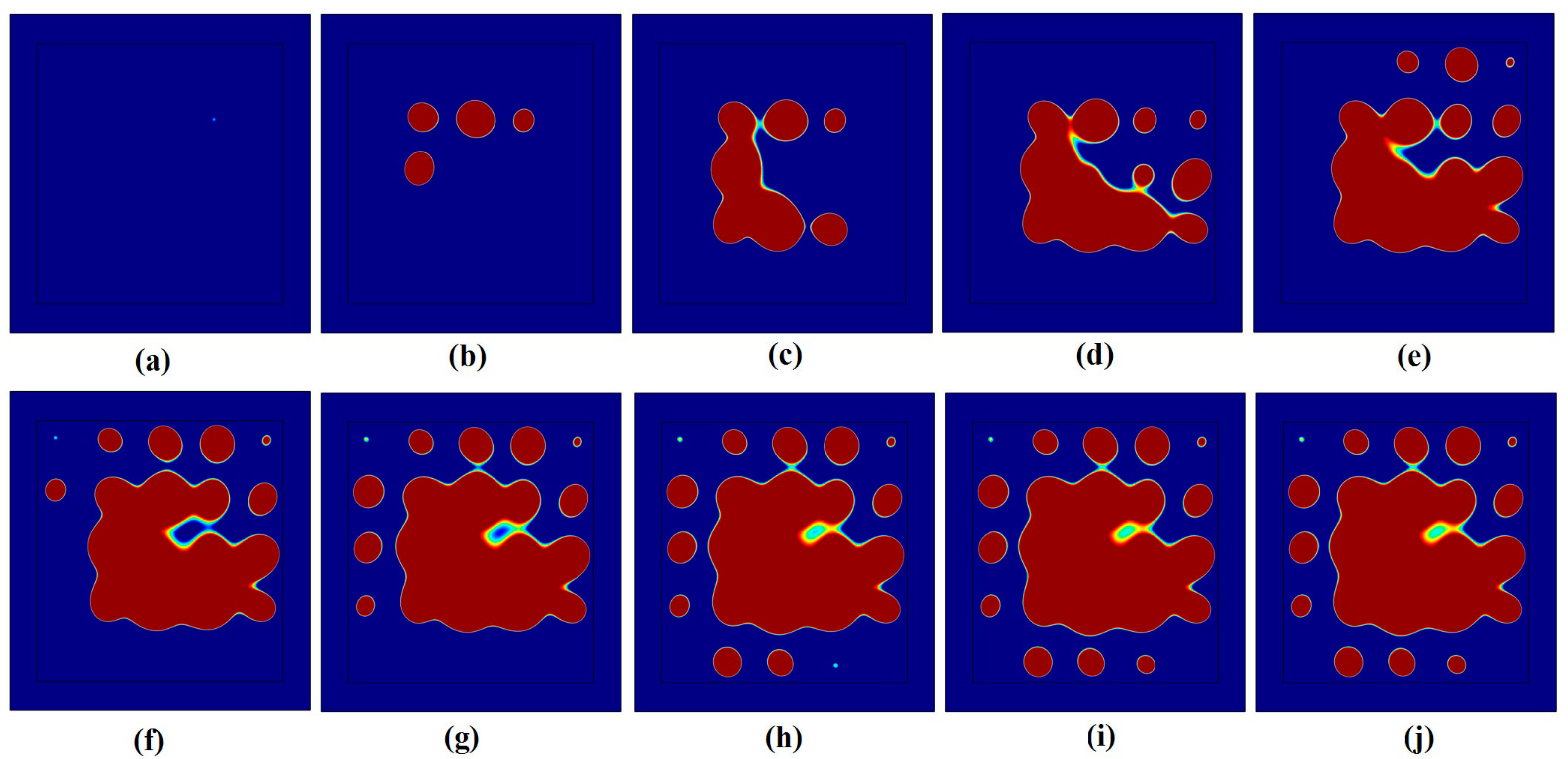
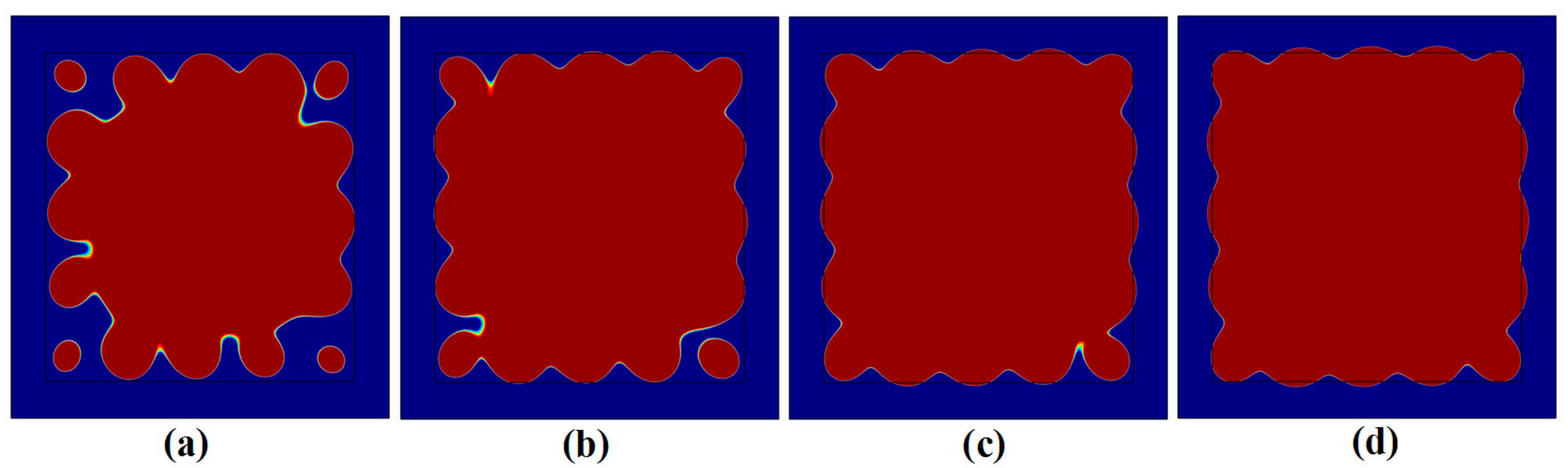
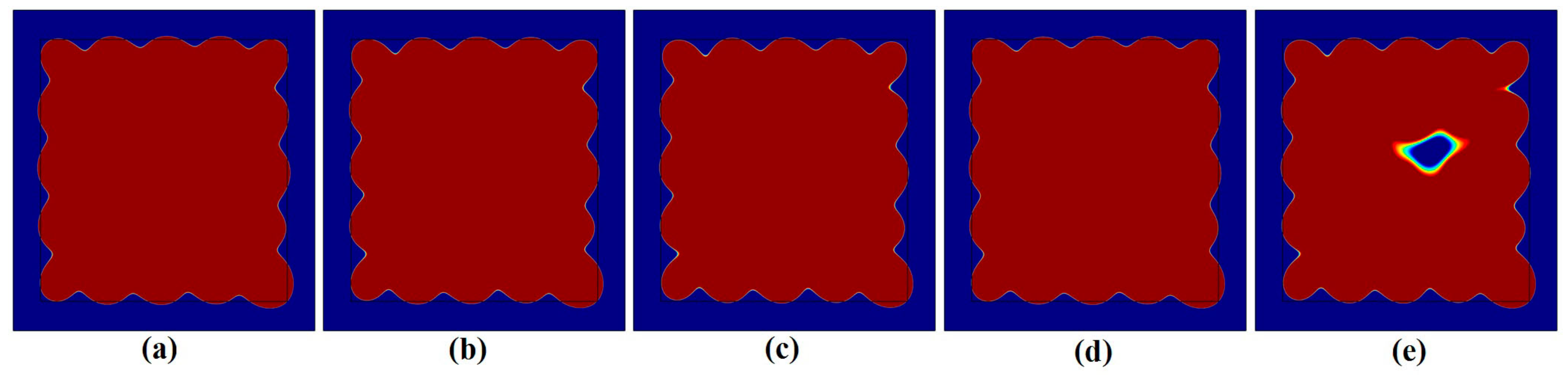
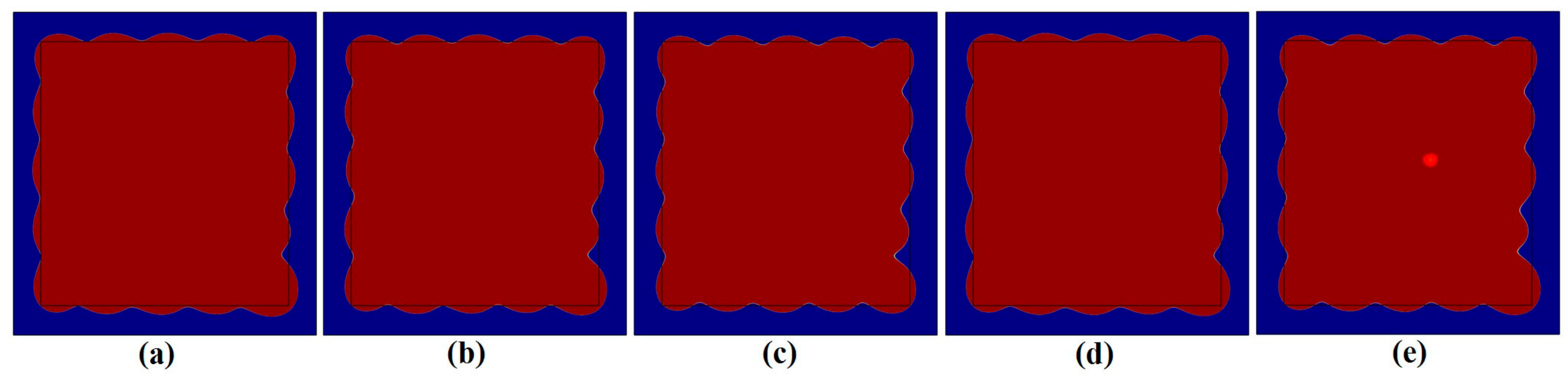
3.2. Influence of Neighboring Treatment Spots on the Formation of Thermal Lesions
3.3. Influence of the Heating Time and Acoustic Intensity on Thermal Lesions
3.4. Optimal Control for the Formation of Thermal Lesions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Illing, R.O.; Kennedy, J.E.; Wu, F.; Ter Haar, G.R.; Protheroe, A.S.; Friend, P.J.; Gleeson, F.V.; Cranston, D.W.; Phillips, R.R.; Middleton, M.R. The safety and feasibility of extracorporeal high-intensity focused ultrasound(HIFU) for the treatment of liver and kidney tumours in a Western population. Brit. J. Cancer 2005, 93, 890–895. [Google Scholar] [CrossRef] [PubMed]
- Leslie, T.; Ritchie, R.; Illing, R.O.; Ter Haar, G.R.; Phillips, R.; Middleton, M.; Bch, B.M.; Wu, F.; Cranstonet, D. High-intensity focused ultrasound treatment of liver tumours: Post-treatment MRI correlates well with intra-operative estimates of treatment volume. Brit. J. Radiol. 2012, 85, 1363–1370. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Chen, W.Z.; Bai, J.; Zou, J.Z.; Wang, Z.L.; Zhu, H.; Wang, Z.B. Tumor vessel destruction resulting from high-intensity focused ultrasound in patients with solid malignancies. Ultrasound Med. Biol. 2002, 28, 535–542. [Google Scholar] [CrossRef]
- Haar, G.T.; Coussios, C. High intensity focused ultrasound: Past, present and future. Int. J. Hyperther. 2007, 23, 85–87. [Google Scholar] [CrossRef]
- Kennedy, J.E. High-intensity focused ultrasound in the treatment of solid tumors. Nat. Rev. Cancer 2005, 5, 321–327. [Google Scholar] [CrossRef]
- Botros, Y.Y.; Ebbini, E.S.; Volakis, J.L. Two-step hybrid virtual array ray (VAR) technique for focusing through the rib cage. IEEE. T. Ultrason. Ferr. 1998, 45, 989–1000. [Google Scholar] [CrossRef]
- White, J.; Clement, G.T.; Hynynen, K. Transcranial ultrasound focus reconstruction with phase and amplitude correction. IEEE. T. Ultrason. Ferr. 2005, 52, 1518–1522. [Google Scholar] [CrossRef]
- Zhou, Y.; Kargl, S.G.; Hwang, J.H. The effect of the scanning pathway in High-Intensity Focused Ultrasound therapy on lesion production. Ultrasound Med. Biol. 2011, 37, 1457–1468. [Google Scholar] [CrossRef]
- Haar, G.T. Ultrasound focal beam surgery. Ultrasound Med. Biol. 1995, 21, 1089–1100. [Google Scholar] [CrossRef]
- Wu, F.; Wang, Z.B.; Chen, W.Z.; Zou, J.Z.; Bai, J.; Zhu, H.; Li, K.Q.; Xie, F.L.; Jin, C.B.; Su, H.B.; et al. Extracorporeal focused ultrasound surgery for treatment of human solid carcinomas: Early Chinese clinical experience. Ultrasound Med. Biol. 2004, 30, 245–260. [Google Scholar] [CrossRef]
- Curiel, L.; Chavrier, F.; Gignoux, B.; Pichardo, S.; Chesnais, S.; Chapelon, J.Y. Experimental evaluation of lesion prediction modelling in the presence of cavitation bubbles: Intended for high-intensity focused ultrasound prostate treatment. Med. Biol. Eng. Comput. 2004, 42, 44–54. [Google Scholar] [CrossRef] [PubMed]
- Damianou, C.; Hynynen, K. Focal spacing and near-field heating during pulsed high temperature ultrasound therapy. Ultrasound Med. Biol. 1993, 19, 777–787. [Google Scholar] [CrossRef]
- Malinen, M.; Huttunen, T.; Hynynen, K.; Kaipio, J.P. Simulation study for thermal dose optimization in ultrasound surgery of the breast. Med. Phys. 2004, 31, 1296–1307. [Google Scholar] [CrossRef] [PubMed]
- Malinen, M.; Huttunen, T.; Kaipio, J.P.; Hynynen, K. Scanning path optimization for ultrasound surgery. Phys. Med. Biol. 2005, 50, 3473–3490. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Shen, G.; Chen, Y. Treatment planning of scanning time and path for phased High-Intensity Focused Ultrasound surgery. In Proceedings of the 2009 IEEE 2nd International Conference on Biomedical Engineering and Informatics, Tianjin, China, 17–19 October 2009. [Google Scholar]
- Arora, D.; Cooley, D.; Perry, T.; Skliar, M.; Roemer, R.B. Direct thermal dose control of constrained focused ultrasound treatments: Phantom and in vivo evaluation. Phys. Med. Biol. 2005, 50, 1919–1935. [Google Scholar] [CrossRef] [PubMed]
- Curra, F.P.; Mourad, P.D.; Khokhlova, V.A.; Cleveland, R.O.; Crum, L.A. Numerical simulations of heating patterns and tissue temperature response due to high-intensity focused ultrasound. IEEE. T. Ultrason. Ferr. 2002, 47, 1077–1089. [Google Scholar] [CrossRef]
- Sonesona, J.E.; Myers, M.R. Thresholds for nonlinear effects in high-intensity focused ultrasound propagation and tissue heating. IEEE. T. Ultrason. Ferr. 2010, 57, 2450–2459. [Google Scholar] [CrossRef]
- Guo, G.P.; Su, H.D.; Ding, H.P.; Ma, Q.Y. Noninvasive temperature monitoring for high intensity focused ultrasound therapy based on electrical impedance tomography. Acta Phys. Sin. 2017, 66, 164301. [Google Scholar]
- Su, H.D.; Guo, G.P.; Ma, Q.Y.; Tu, J.; Zhang, D. Noninvasive treatment efficacy monitoring and dose control for high-intensity focused ultrasound therapy using relative electrical impedance variation. Chin. Phys. B 2017, 26, 054302. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperature in the resting human foearm. J. Appl. Phys. 1948, 1, 93–122. [Google Scholar]
- Palmeri, M.L.; Sharma, A.C.; Bouchard, R.R.; Nightingale, R.W.; Nightingale, K.R. A finite-element method model of soft tissue response to impulsive acoustic radiation force. IEEE. T. Ultrason. Ferr. 2005, 52, 1699–1712. [Google Scholar] [CrossRef]
- Hou, G.Y.; Marquet, F.; Wang, S.; Konofagou, E.E. Multi-parametric monitoring and assessment of high-intensity focused ultrasound (HIFU) boiling by harmonic motion imaging for focused ultrasound (HMIFU): An ex vivo feasibility study. Phys. Med. Biol. 2014, 59, 1121–1145. [Google Scholar] [CrossRef][Green Version]
- Galwey, A.K.; Brown, M.E. Application of the Arrhenius equation to solid state kinetics: Can this be justified? Thermochim. Acta 2002, 386, 91–98. [Google Scholar] [CrossRef]
- Jiang, S.C.; Zhang, X.X. Effects of dynamic changes of tissue properties during laser-induced interstitial thermotherapy (LITT). Laser Med. Sci. 2005, 19, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Shibib, K.S.; Munshid, M.A.; Lateef, H.A. The effect of laser power, blood perfusion, thermal and optical properties of human liver tissue on thermal damage in LITT. Laser Med. Sci. 2017, 32, 2039–2046. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; Dong, H.; Qian, S.Y. Influence of dynamic tissue properties on temperature elevation and lesions during HIFU scanning therapy: Numerical simulation. Chin. Phys. B 2020, 29, 034305. [Google Scholar] [CrossRef]
- Liu, B.; Qian, S.Y.; Hu, W.P. Identification of Denatured Biological Tissues Based on Time-Frequency Entropy and Refined Composite Multi-Scale Weighted Permutation Entropy during HIFU Treatment. Entropy 2019, 21, 666. [Google Scholar] [CrossRef]
- Tan, Q.L.; Zou, X.; Ding, Y.J.; Zhao, X.M.; Qian, S.Y. The Influence of Dynamic Tissue Properties on HIFU Hyperthermia: A Numerical Simulation Study. Appl. Sci. 2018, 8, 1933. [Google Scholar] [CrossRef]

| Materials | Density (kg/m3) | Speed of Sound (m/s) | Attenuation (Np/m/MHz) | Specific Heat (J/(kg.K)) | Thermal Conductivity (W/(m.K)) |
|---|---|---|---|---|---|
| Water | 1000 | 1483 | 0.025 | N/A | N/A |
| Tissue | 1036 | 1551 | 3.5614 | 3560 | 0.5212 |
| Treatment Spots | Neighboring Treated Spots
(mm, s) | Neighboring Untreated Spots (mm, s) |
|---|---|---|
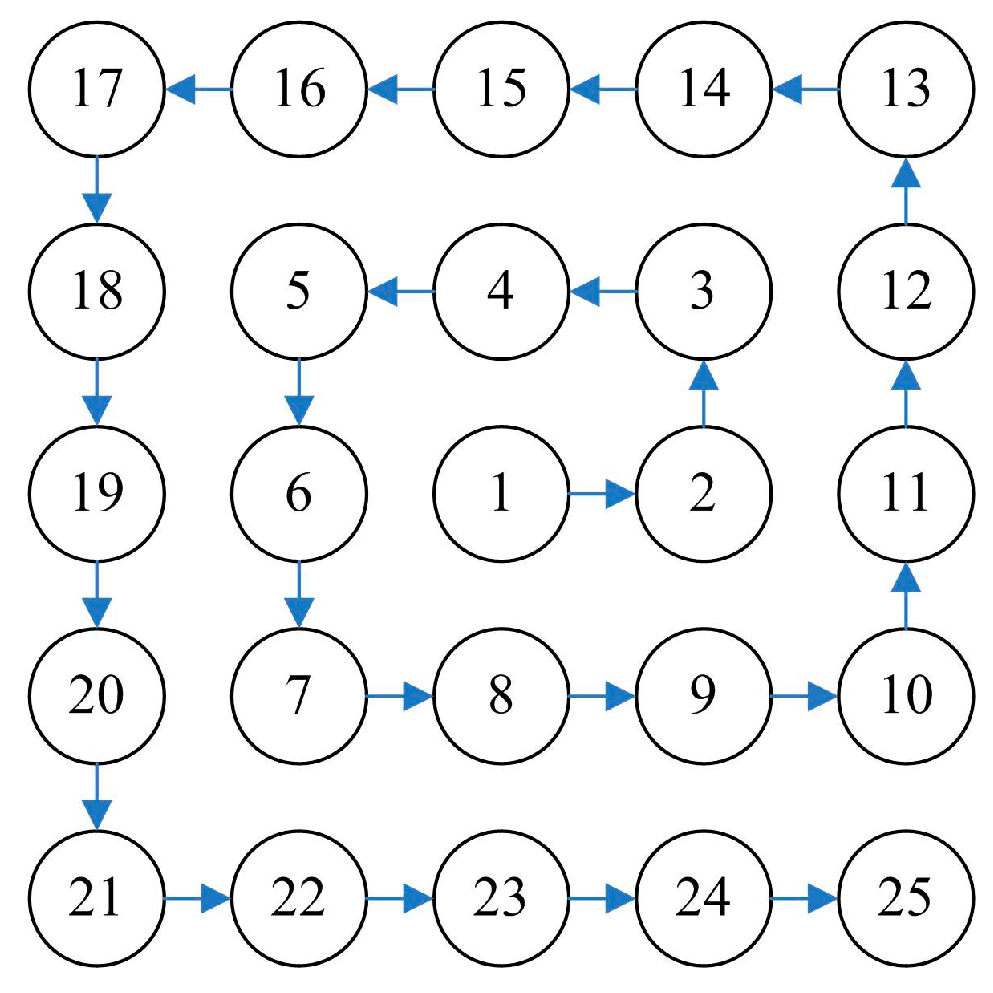
| No.1 | / | No. 2(2,1), No. 3(,7), No. 4(2,13), No. 5(,19), No. 6(2,25), No.7(,31), No. 8(2,37), No. 9(,43) |
| No.5 | No. 4(2,1), No.1(,19) | No. 6(2,1), No.15(,55), No. 16(2,61), No.17(,67), No. 18 (2,73), No.19(,79) |
| No.13 | No.12(2,1), No.3(,55) | No. 14(2,1) |
| No.19 | No.18(2,1), No.6 (2,73), No.5(,79), No.7(,67) | No. 20(2,1) |
| 1.2 | 174 | 37.924 | 12.4869 | 63.822 | 0.0040 | 17.182 |
| 1.4 | 199 | 40.576 | 16.2177 | 73.033 | 0.2360 | 8.2030 |
| 1.6 | 224 | 42.780 | 20.2392 | 77.086 | 0.8760 | 4.7860 |
| 1.8 | 249 | 44.640 | 24.6317 | 78.923 | 1.7140 | 3.7910 |
| 1.2 | 149 | 41.668 | 13.2639 | 72.536 | 0.2050 | 8.6690 |
| 1.4 | 149 | 48.644 | 18.1242 | 79.419 | 2.2623 | 3.8433 |
| 1.6 | 149 | 55.572 | 23.6054 | 80.852 | 5.6758 | 5.8238 |
| 1.8 | 149 | 62.516 | 29.8181 | 80.991 | 9.0998 | 9.1088 |
| 0.7,0.5 | 204 | 38.472 | 13.8263 | 77.872 | 1.2112 | 4.3392 |
| 0.8,0.5 | 194.2 | 37.860 | 11.8358 | 76.641 | 0.7878 | 5.1468 |
| 0.9,0.5 | 188.2 | 37.196 | 11.5362 | 75.838 | 0.6050 | 5.7670 |
| 0.8,0.4 | 205.6 | 38.716 | 13.5256 | 77.946 | 1.1799 | 4.2339 |
| 0.8,0.6 | 187.2 | 36.828 | 20.6404 | 74.996 | 0.7183 | 6.7223 |
| 0.7,0.5 | 149 | 48.3080 | 108.9916 | 80.789 | 6.1953 | 6.4063 |
| 0.8,0.5 | 149 | 45.6080 | 76.4708 | 80.358 | 4.3431 | 4.9851 |
| 0.9,0.5 | 149 | 44.3440 | 62.6392 | 79.797 | 3.2532 | 4.4562 |
| 0.8,0.4 | 149 | 49.1320 | 86.0464 | 80.825 | 6.1612 | 6.3362 |
| 0.8,0.6 | 149 | 43.7040 | 100.1212 | 79.734 | 3.6970 | 4.9630 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, X.; Qian, S.; Tan, Q.; Dong, H. Formation of Thermal Lesions in Tissue and Its Optimal Control during HIFU Scanning Therapy. Symmetry 2020, 12, 1386. https://doi.org/10.3390/sym12091386
Zou X, Qian S, Tan Q, Dong H. Formation of Thermal Lesions in Tissue and Its Optimal Control during HIFU Scanning Therapy. Symmetry. 2020; 12(9):1386. https://doi.org/10.3390/sym12091386
Chicago/Turabian StyleZou, Xiao, Shengyou Qian, Qiaolai Tan, and Hu Dong. 2020. "Formation of Thermal Lesions in Tissue and Its Optimal Control during HIFU Scanning Therapy" Symmetry 12, no. 9: 1386. https://doi.org/10.3390/sym12091386
APA StyleZou, X., Qian, S., Tan, Q., & Dong, H. (2020). Formation of Thermal Lesions in Tissue and Its Optimal Control during HIFU Scanning Therapy. Symmetry, 12(9), 1386. https://doi.org/10.3390/sym12091386





