A Modified Median String Algorithm for Gene Regulatory Motif Classification
Abstract
1. Introduction
2. Background Information
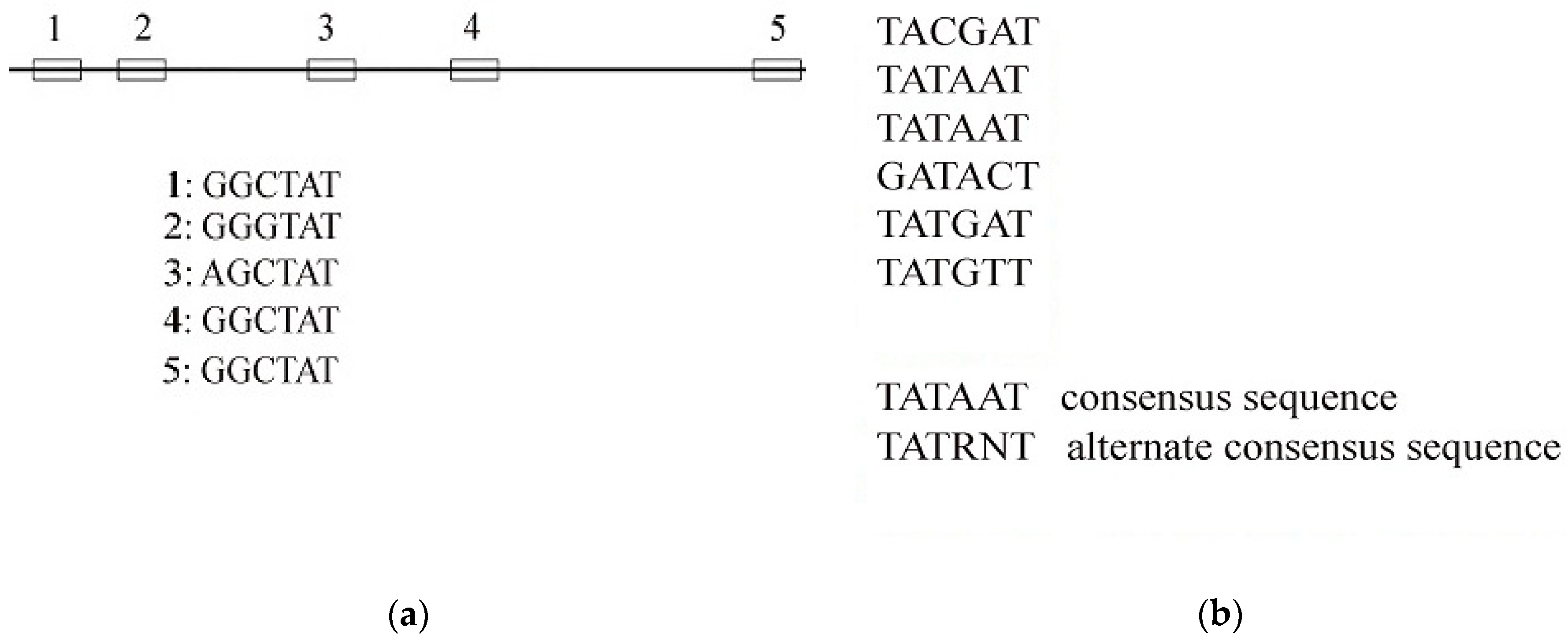
2.1. Median String Algorithm for Consensus Sequence
| Algorithm 1: Median String Search |
| { inputs: DNA,t,n,l output: bestFit_Motif procedure: MedianStringSearch (DNA, t, n, l) bestFit_Motif ← AAA…A bestFit_Score ← ∞ for each l-mer s from AAA…A to TTT…T if TotalFit_Score(s, DNA) < bestFit_Score bestFit_Score ← TotalFit_Score(s, DNA) bestFit_Motif ← s return bestFit_Motif } |
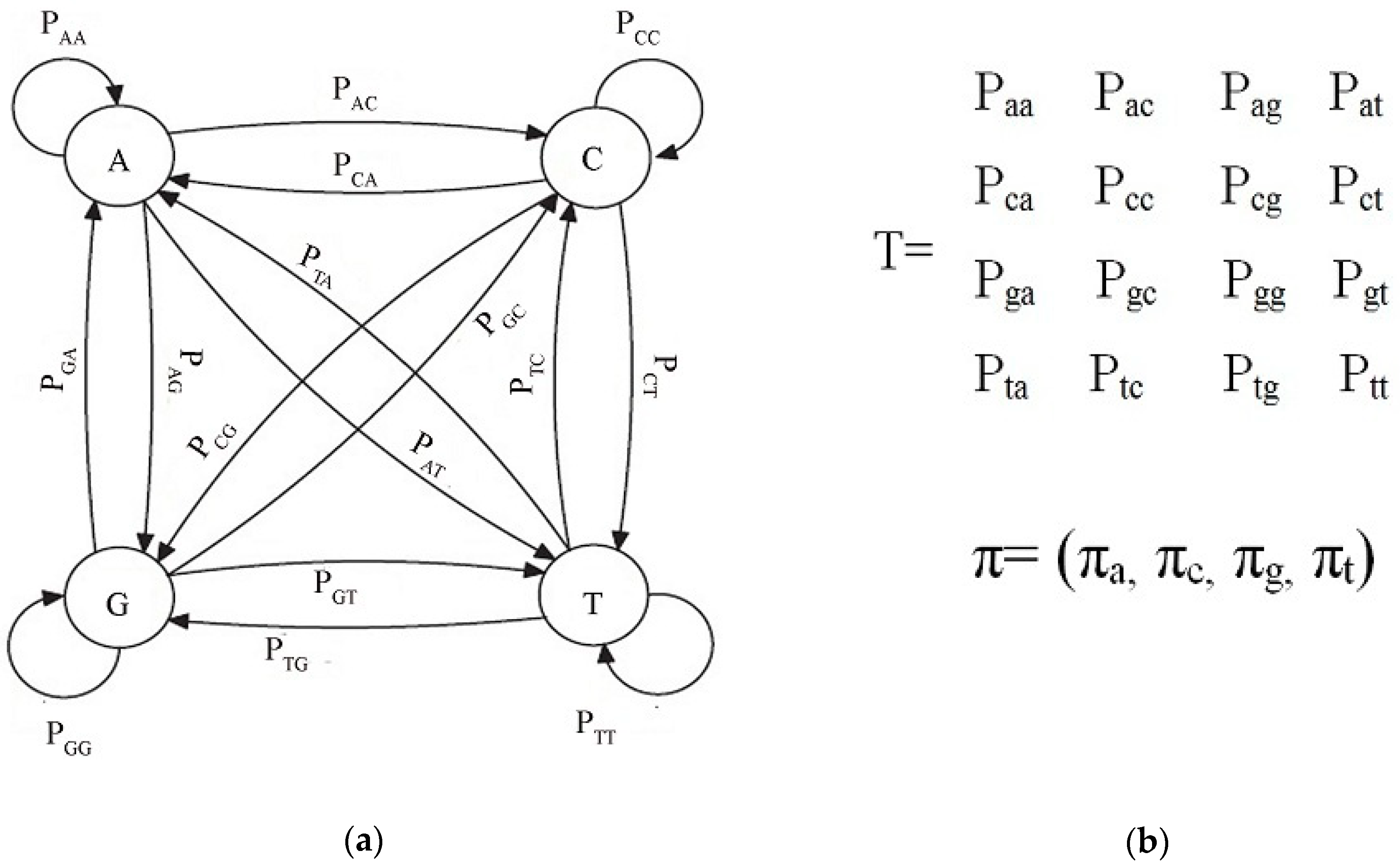
2.2. Markov Chain
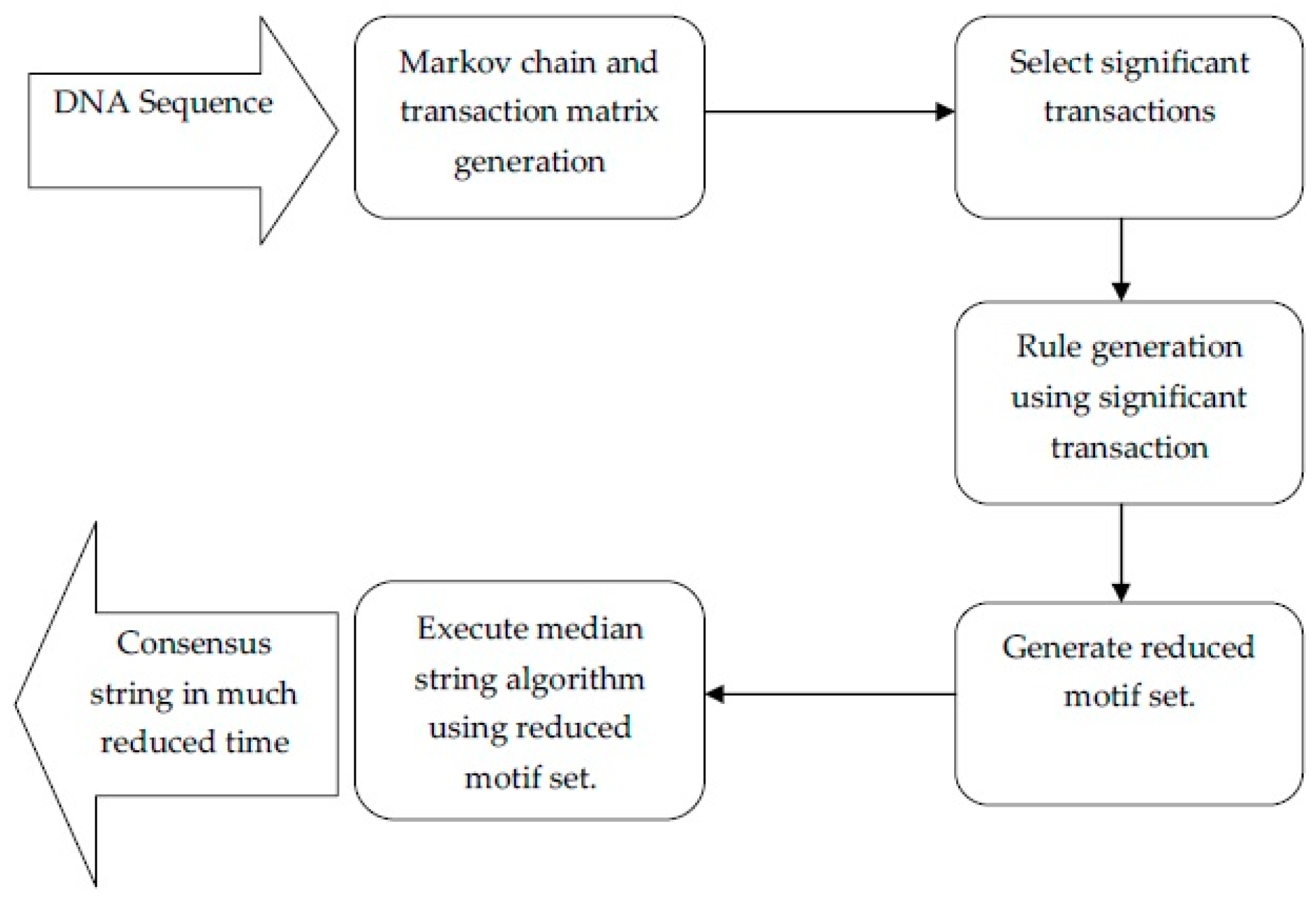
3. Proposed Markov Chain Based Median String Algorithm
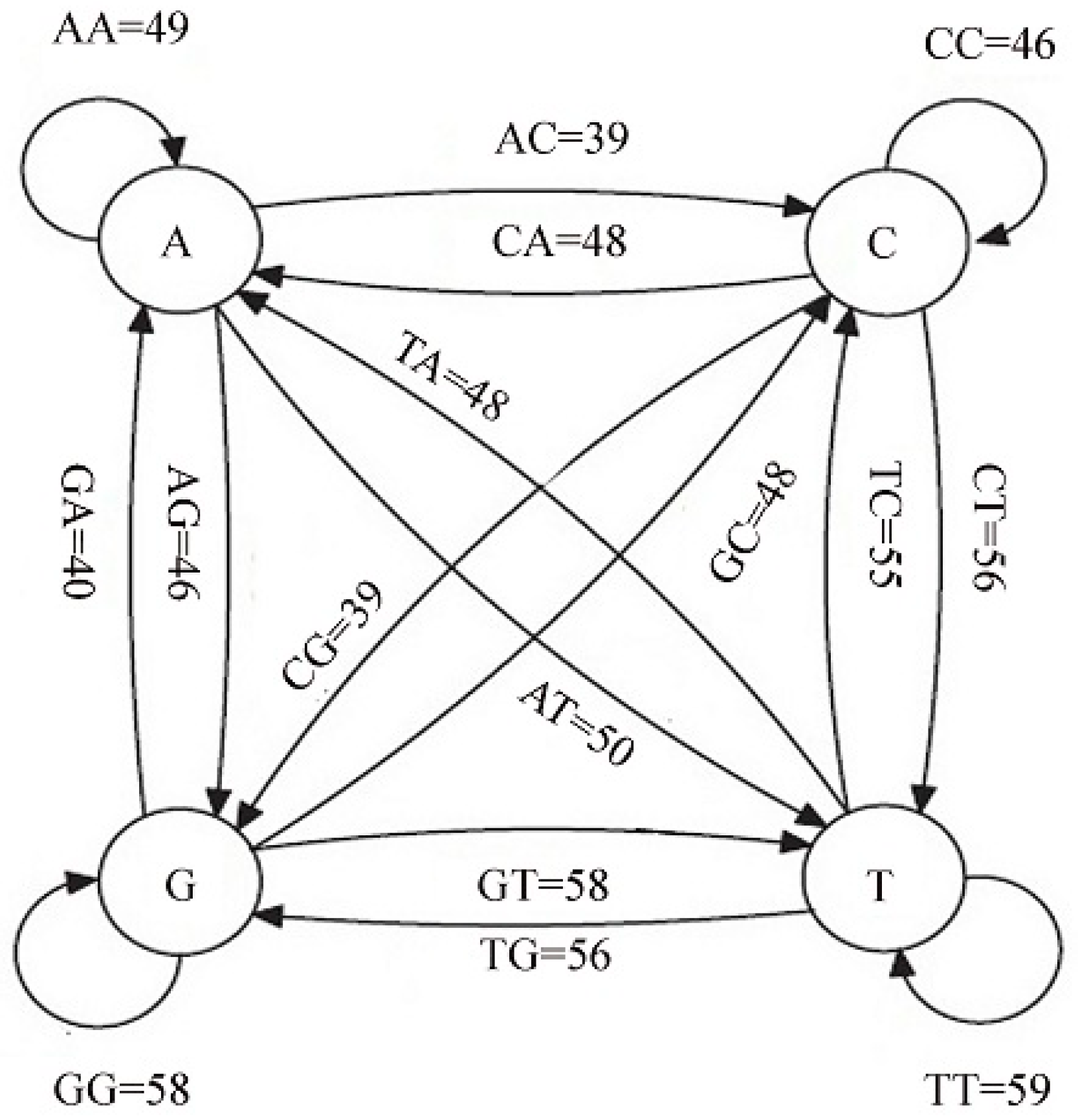
3.1. Markov Chain Generation
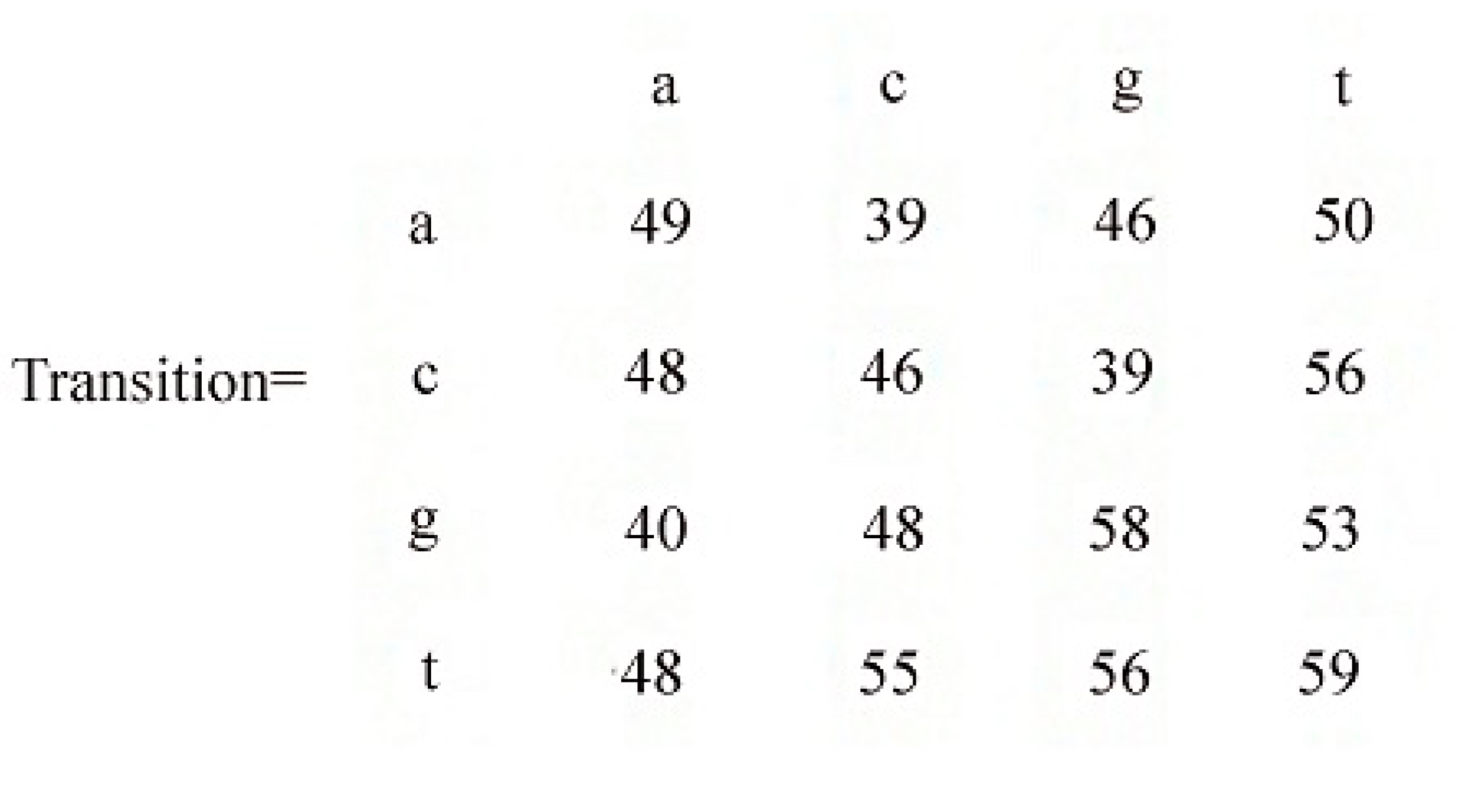
3.2. Transaction Matrix Creation
3.3. Rule Generation
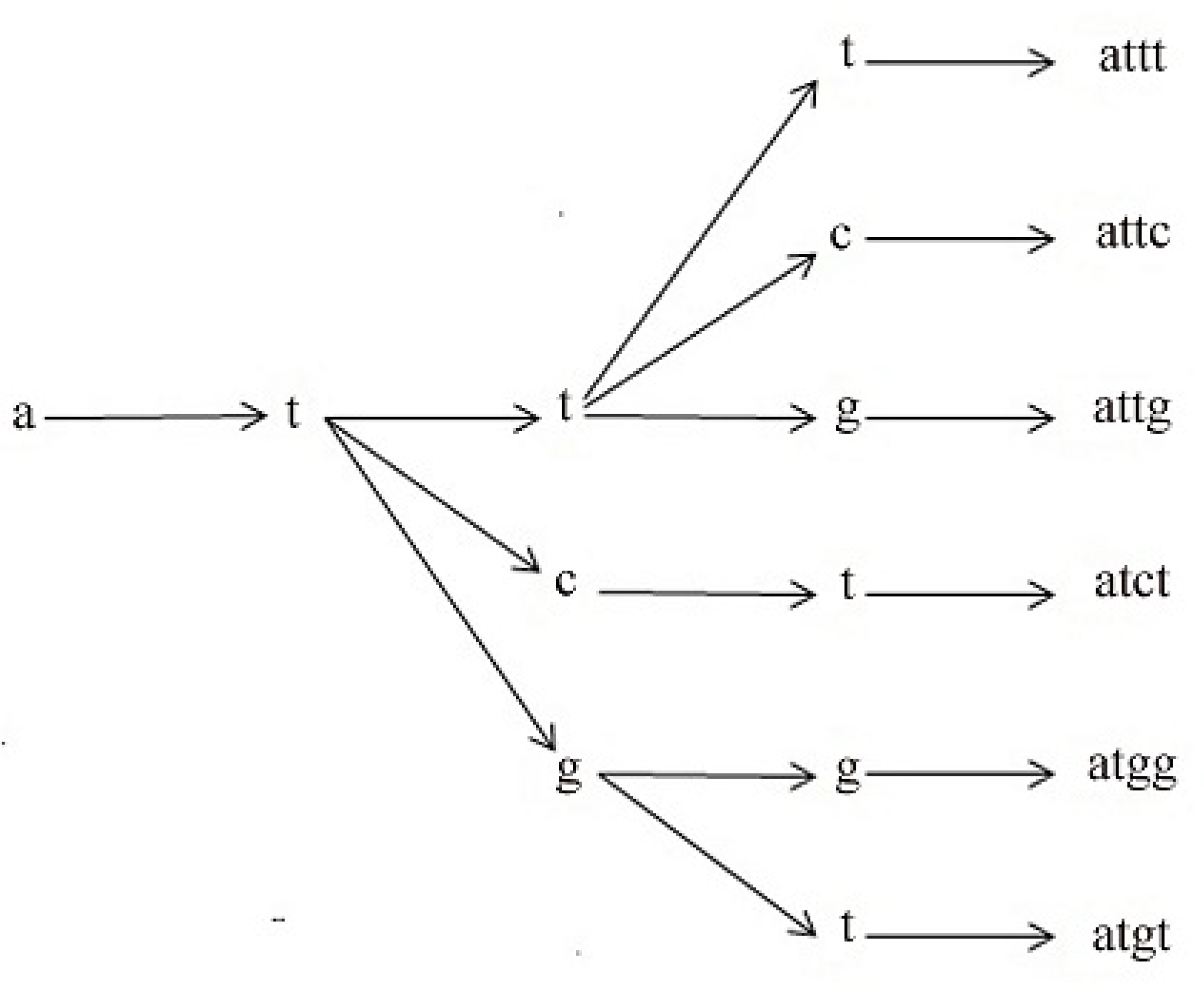
3.4. Reduced l-mer Set Generation
3.5. Proposed Algorithm
| Algorithm 2: Markow chain based median string algorithm(DNA,l) |
| { input:DNA,l Output: consensus sequence Modified_Median_String (DNA,l) { bestFit_Motif ←AAA…A bestFit_Score ←∞ reduced_motif_set = Reduced_Motif_Set_Generator(DNA,l) for each l-mer in reduced_motif_set if TotalFit_Score(s, DNA) < bestFit_Score bestFit_Score←TotalFit_Score(s, DNA) bestFit_Motif ← s return bestFit_Motif } Transaction_Matrix_Generator(DNA) {input:DNA output:Transition_Matrix ngram_dict←new dictionary() i←1 for each sequence in DNA for each character in sequence up to sequence length-1 if character not in ngram_dict.keys() ngram_dict[character]←Null NextCharacter←Sequence[i + 1] ngram_dict[character].append(NextCharacter) ←i + 1 TM←empty matrix for each key in ngram_dict TM ← Counter(ngram_dict(key)) Return TM } Rule_Generator(Transition_Matrix) {input:Transition_Matrix output:rule_list total= ΣTransition_matrixij s ← 0 rule_list ← empty list() for each element in Transition_Matrix in descending order s ← s+ Transition_matrix element if s < total/2 append a rule in rule_list else break return rule_list } Reduced_Motif_Set_Generator(DNA, l) {input:DNA, length of l-mer output:Reduced_Motif_Set TM ← Transition_Matrix_Generator(DNA) rules ← Rule_Generator(TM) S1,tmp,tmp2 ← empty list For each character in {‘a’, ‘c’, ‘g’, ‘t’} if rules.key ==character S1 ← character + rules.value tmp ← S1 for i = 1 to length of l-mer-2 for element in tmp if rules.key ==last character of element tmp2 ← element + rules.value tmp ← tmp2 tmp2 ← null return tmp } |
4. Result and Discussion
- Processor: Intel Core i5 CPU
- Clock rate:2.6 GHz
- HardDisk:1000GB
- RAM:4GB
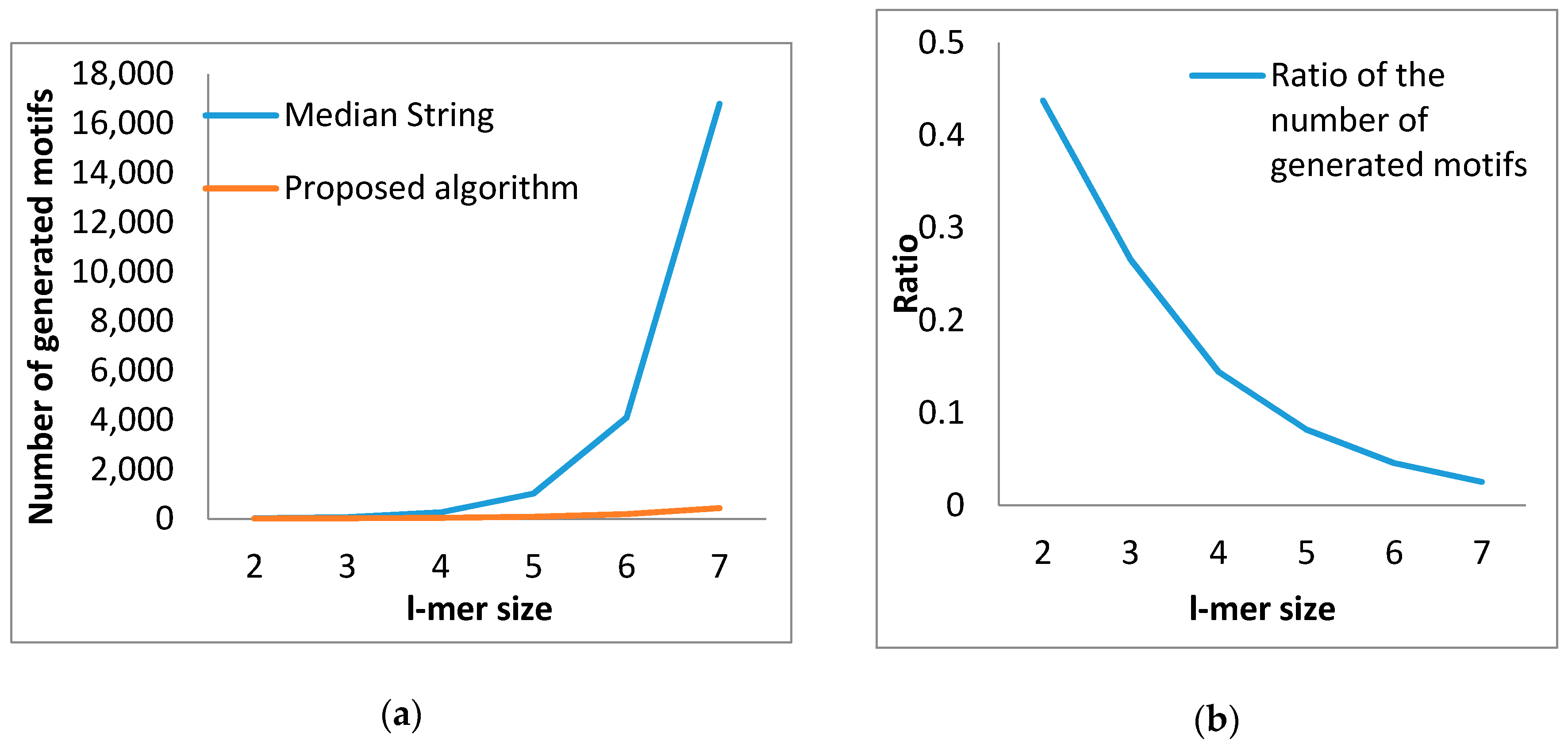
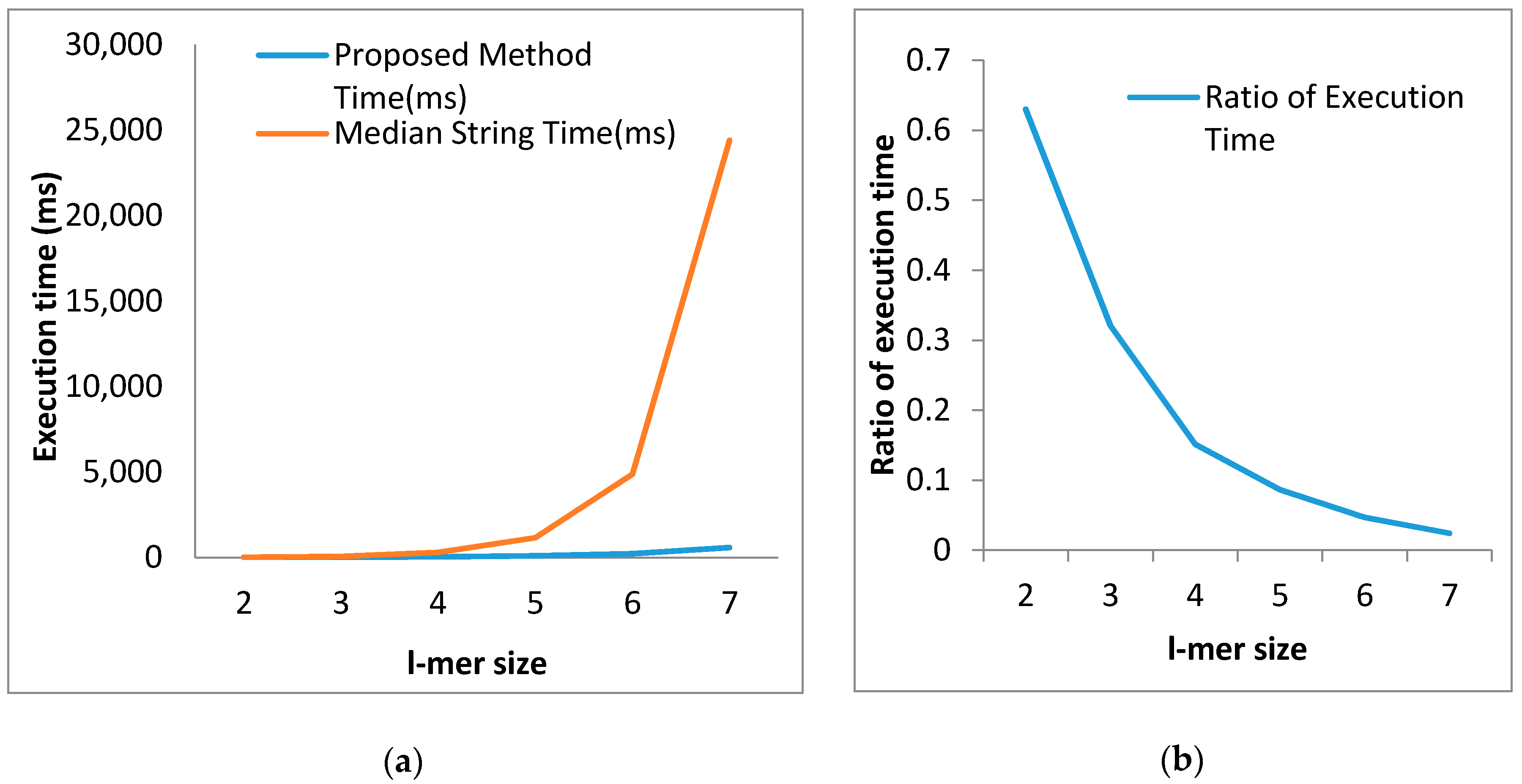
4.1. Comparison with Median String Algorithm
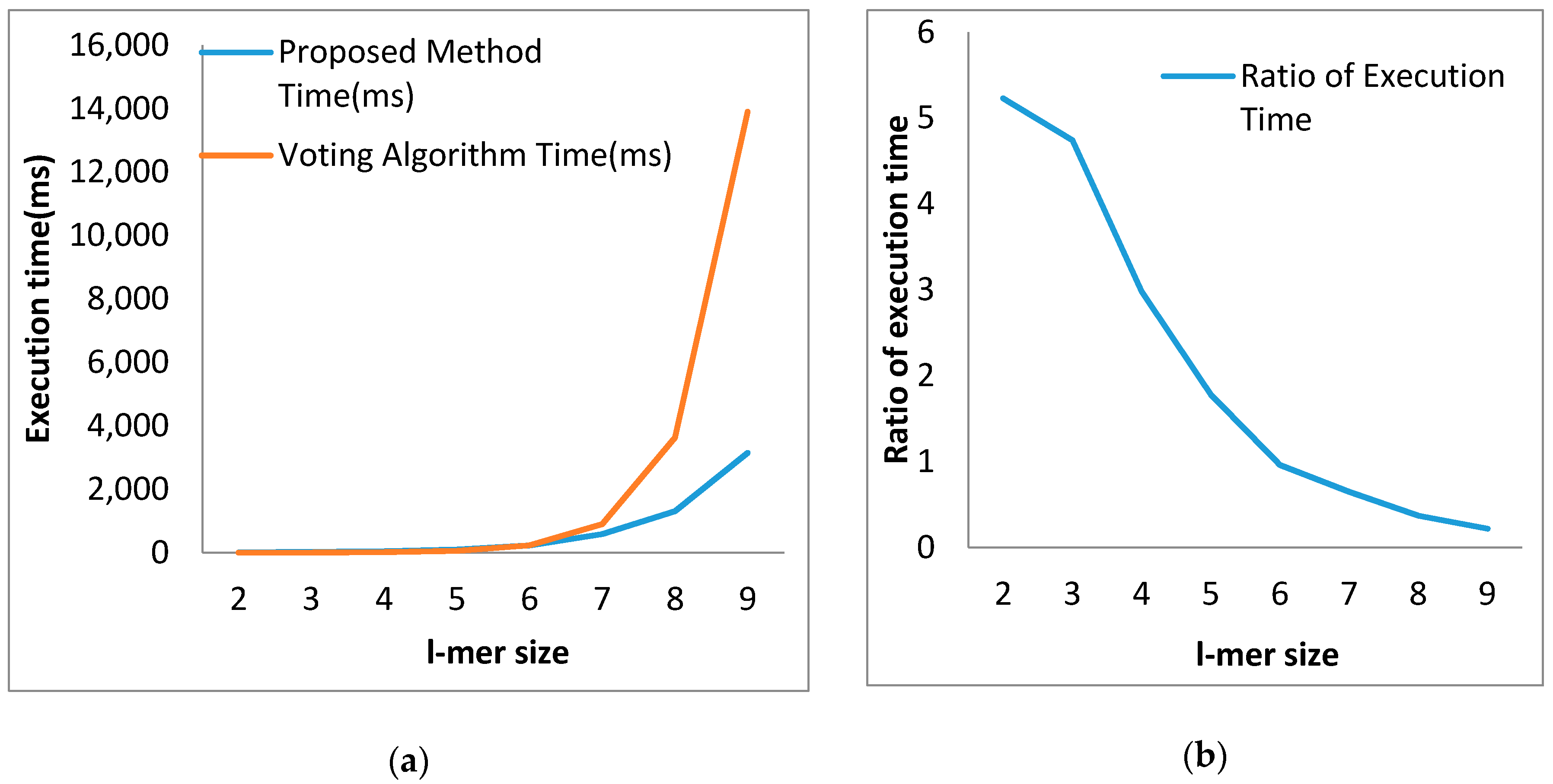
4.2. Comparison with the Voting Algorithm
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Mathematical Proof That the System Will Work
- X = {set of motifs generated by the proposed system},
- W = {set of motifs generated by the rules based on frequencies which are not encircled},
- Z = {set of motifs generated by the rules based on frequencies both encircled and not encircled}.
References
- Kellis, M.; Patterson, N.; Birren, B.; Berger, B.; Lander, E.S. Methods in Comparative Genomics: Genome Correspondence, Gene Identification and Regulatory Motif Discovery. J. Comput. Boil. 2004, 11, 319–355. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.D.; Higgins, D.G.; Gibson, T.J. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994, 22, 4673–4680. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.D. Consensus sequence Zen. Appl. Bioinform. 2002, 1, 111–119. [Google Scholar]
- Lawrence, C.E.; Altschul, S.F.; Boguski, M.S.; Liu, J.S.; Neuwald, A.F.; Wootton, J.C. Detecting subtle sequence signals: A Gibbs sampling strategy for multiple alignment. Science 1993, 262, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Bailey, T.L.; Elkan, C. Fitting a mixture model by expectation maximization to discover motifs in biopolymers. In Proceedings of the International Conference on Intelligent Systems for Molecular Biology, Stanford, CA, USA, 14–17 August 1994; pp. 28–36. [Google Scholar]
- Zhang, Y.; Huo, H.; Yu, Q. A heuristic cluster-based em algorithm for the planted (l, d) problem. J. Bioinform. Comput. Boil. 2013, 11, 1350009. [Google Scholar] [CrossRef] [PubMed]
- Kuksa, P.; Pavlovic, V. Efficient motif finding algorithms for large-alphabet inputs. BMC Bioinform. 2010, 11 (Suppl. S8), S1. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.; Lipman, D. Trees, stars, and multiple sequence alignment. SIAM J. Appl. Math. 1989, 49, 197–209. [Google Scholar] [CrossRef]
- Gramm, J.; Hüffner, F.; Niedermeier, R. Closest strings, primer design, and motif search. In Proceedings of the 6th Annual International Conference on Computational Biology(RECOMB 2002), Washington, DC, USA, 18–21 April 2002; pp. 74–75. [Google Scholar]
- Gramm, J.; Niedermeier, R.; Rossmanith, P. Exact solutions for closest string and related problems. In Proceedings of the 12th International Symposium on Algorithms and Computation, Christchurch, New Zealand, 19–21 December 2001; pp. 441–453. [Google Scholar]
- Karp, R.M. Mapping the genome: Some combinatorial problems arising in molecular biology. In Proceedings of the 25th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 16–18 May 1993; pp. 278–285. [Google Scholar]
- Li, M.; Ma, B.; Wang, L. On the closest string and substring problems. J. ACM 2002, 49, 157–171. [Google Scholar] [CrossRef]
- Mauch, H.; Melzer, M.J.; Hu, J.S. Genetic algorithm approach for the closest string problem. In Proceedings of the 2nd IEEE Computer Society Bioinformatics Conference, Stanford, CA, USA, 11–14 August 2003; pp. 560–561. [Google Scholar]
- Meneses, C.N.; Lu, Z.; Oliveira, C.A.S.; Pardalos, P.M. Optimal Solutions for the Closest-String Problem via Integer Programming. INFORMS J. Comput. 2004, 16, 419–429. [Google Scholar] [CrossRef]
- Nicolas, F.; Rivals, E. Complexities of the centre and median string problems. In Proceedings of the 14th Symposium on Combinatorial Pattern Matching, Michoacan, Mexico, 25–27 June 2003; pp. 315–327. [Google Scholar]
- Gramm, J.; Niedermeier, R.; Rossmanith, P. Fixed-Parameter Algorithms for Closest String and Related Problems. Algorithmica 2003, 37, 25–42. [Google Scholar] [CrossRef]
- Ma, B.; Sun, X. More efficient algorithms for closest string and substring problems. In Proceedings of the 12th Annual International Conference on Research in Computational Molecular Biology, Singapore, 30 March–2 April 2008; pp. 396–409. [Google Scholar]
- Stojanovic, N.; Berman, P.; Gumucio, D.; Hardison, R.; Miller, W. A linear-time algorithm for the 1-mismatch problem. In Proceedings of the 5th International Workshop on Algorithms and Data Structures, NS, Canada, 6–8 August 1997; pp. 126–135. [Google Scholar]
- Ben-Dor, A.; Lancia, G.; Perone, J.; Ravi, R. Banishing bias from consensus sequences. In Proceedings of the 8th Symposium on Combinatorial Pattern Matching, Aarhus, Denmark, 30 June–2 July 1997; pp. 247–261. [Google Scholar]
- Gasieniec, L.; Jansson, J.; Lingas, A. Efficient approximation algorithms for the Hamming center problem. In Proceedings of the 10th ACM-SIAM Symposium on Discrete Algorithms, Baltimore, MD, USA, 17–19 January 1999; pp. 905–906. [Google Scholar]
- Gąsieniec, L.; Jansson, J.; Lingas, A. Approximation algorithms for Hamming clustering problems. J. Discret. Algorithms 2004, 2, 289–301. [Google Scholar] [CrossRef]
- Lanctot, J.K.; Li, M.; Ma, B.; Wang, S.; Zhang, L. Distinguishing string selection problems. Inf. Comput. 2003, 185, 41–55. [Google Scholar] [CrossRef]
- Boucher, C.; Brown, D.; Durocher, S. On the structure of small motif recognition instances. In Proceedings of the 15th Symposium on String Processing and Information Retrieval, Melbourne, Australia, 11–12 November 2008; pp. 269–281. [Google Scholar]
- Sze, S.; Lu, S.; Chen, J. Integrating sample-driven and pattern-driven approaches in motif finding. In Proceedings of the 4th Workshop on Algorithms in Bioinformatics, Bargen, Norway, 17–21 September 2004; pp. 438–449. [Google Scholar]
- Fatma, A.H.; Mai, S.M.; Walid, A.A. Review of different sequence motif finding algorithms. Avicenna J. Med. Biotechnol. 2019, 11, 130–148. [Google Scholar]
- Sun, H.Q.; Low, M.Y.H.; Hsu, W.J.; Tan, C.W.; Rajapakse, J.C. Tree-structured algorithm for long weak motif discovery. Bioinformatics 2011, 27, 2641–2647. [Google Scholar] [CrossRef] [PubMed]
- Jia, C.; Carson, M.B.; Wang, Y.; Lin, Y.; Lu, H. A New Exhaustive Method and Strategy for Finding Motifs in ChIP-Enriched Regions. PLoS ONE 2014, 9, e86044. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bandyopadhyay, S.; Sahni, S.; Rajasekaran, S. PMS6: A fast algorithm for motif discovery. Int. J. Bioinform. Res. Appl. 2014, 10, 369. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S. Improved Exact Enumerative Algorithms for the Planted (l, d)-Motif Search Problem. IEEE/ACM Trans. Comput. Boil. Bioinform. 2014, 11, 361–374. [Google Scholar] [CrossRef] [PubMed][Green Version]

| SID | Sample |
|---|---|
| S1 | tagtggtcttttgagtgtagatctggagggaaagtatttccaccagttcggggtcacccagcagggcagggtgacttaat |
| S2 | cgcgactcggcgctcacagttatcgcacgtttagaccaaaacggagttggatccgaaactggagtttaatcggagtcctt |
| S3 | gttacttgtgagcctggttagacccgaaatataattgttggctgcatagcggagctgacatacgagtaggggaaatgcgt |
| S4 | aacatcaggctttgattaaacaatttaagcacgtaaatccgaattgacctggtgacaatacggaacatgccggctccggg |
| S5 | accaccggataggctggttattaggtccaaaaggtagtatcgtaataatggctcagccatgtcaatgtgcggcattccac |
| S6 | tagattcgaatcgatcgtgtttctccctctggtggttaacgaggggtccgaccttgctcgcatgtgccgaacttgtaccc |
| S7 | gaaatggttcggtgcgatatcaggccgttctcttaacttggcggtgcagatccgaacgtctctggaggggtcgtgcgcta |
| S8 | atgtatactagacattctaacgctcgcttattggcggagaccatttgctccactacaagaggctactggtgtgatccgta |
| S9 | ttcttacacccttctttagatccaaacctgttggcgccatcttcttttcgagtccttgtacctccatttgctctggtgac |
| S10 | ctacctatgtaaaacaacatctactaacgtagtccggtctttcctggtctgccctaacctacaggtcgatccgaaattcg |
| First (l1) | Second (l2) | Count | Rule |
|---|---|---|---|
| t | t | 59 | t→t |
| g | g | 58 | g→g |
| t | g | 56 | t→g |
| c | t | 56 | c→t |
| t | c | 55 | t→c |
| g | t | 53 | g→t |
| a | t | 50 | a→t |
| l-mer Size | Proposed Method | Median String | Ratio of Number of Produced Motifs |
|---|---|---|---|
| 2 | 7 | 16 | 0.4375 |
| 3 | 17 | 64 | 0.2656 |
| 4 | 37 | 256 | 0.1445 |
| 5 | 84 | 1024 | 0.0820 |
| 6 | 188 | 4096 | 0.0458 |
| 7 | 427 | 16,784 | 0.0254 |
| l-mer Size | Proposed Method Time(ms) | Median String Time(ms) | Ratio of Execution Time |
|---|---|---|---|
| 2 | 10.20 | 16.10 | 0.6300 |
| 3 | 21.36 | 66.6 | 0.3207 |
| 4 | 44.84 | 296 | 0.1514 |
| 5 | 100.18 | 1160 | 0.0863 |
| 6 | 228.16 | 4880 | 0.0467 |
| 7 | 587.44 | 24,400 | 0.0240 |
| l-mer Size | Proposed Method Time (ms) | Voting Algorithm Time (ms) | Ratio of Execution Time |
|---|---|---|---|
| 2 | 10.20 | 1.95 | 5.23 |
| 3 | 21.36 | 4.50 | 4.74 |
| 4 | 44.84 | 15.00 | 2.98 |
| 5 | 100.18 | 56.00 | 1.78 |
| 6 | 228.16 | 236.00 | 0.96 |
| 7 | 587.44 | 903.00 | 0.65 |
| 8 | 1310.00 | 3630.00 | 0.37 |
| 9 | 3150.00 | 13,900.00 | 0.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaysar, M.S.; Khan, M.I. A Modified Median String Algorithm for Gene Regulatory Motif Classification. Symmetry 2020, 12, 1363. https://doi.org/10.3390/sym12081363
Kaysar MS, Khan MI. A Modified Median String Algorithm for Gene Regulatory Motif Classification. Symmetry. 2020; 12(8):1363. https://doi.org/10.3390/sym12081363
Chicago/Turabian StyleKaysar, Mohammad Shibli, and Mohammad Ibrahim Khan. 2020. "A Modified Median String Algorithm for Gene Regulatory Motif Classification" Symmetry 12, no. 8: 1363. https://doi.org/10.3390/sym12081363
APA StyleKaysar, M. S., & Khan, M. I. (2020). A Modified Median String Algorithm for Gene Regulatory Motif Classification. Symmetry, 12(8), 1363. https://doi.org/10.3390/sym12081363




