1. Introduction
Opinion dynamics has been an important research topic regarding social network field for a long time, which studies the group behavior of a group of interacting agents (individuals) who hold beliefs or opinions towards given topics, which might be the same as or different to that of the others [
1,
2]. Studies on opinion dynamics have been made from a variety of domains and aspects, e.g., philosophy, sociology, economics, politics, and physics [
3,
4,
5,
6]. In these models, the agents interact with each other and gain information from external sources to reach consensus or seek truth [
7], and it is noted that the agents in a group not only want to achieve a consensus, but also hope the consensus is close to the truth as much as possible in many cases, referred to as ‘correct consensus’ by Zollman [
8].
Agents can learn the truth through different ways, e.g., experiments, books, media, or interaction with other agents. The effect of external information—e.g., social power and mass media, etc.—on opinion dynamics has been studied widely [
9,
10,
11,
12]. Based on the Hegselmann-Krause (HK) model [
13,
14], Douven and Riegler [
15] have shown that introducing the truth, estimated from experimental data, has a dramatic effect on group opinion dynamics: all the agents will converge at the truth sooner or later. This is due to the reason that all the agents can access the truth (experimental data) in their model. However, the ability to gain knowledge about the truth differs among the agents in reality. It is then necessary to study scenarios where different agents have different access to the truth. This has been studied by Fu et al. with respect to heterogeneous bounded confidence [
16].
On the other hand, there are also some agents in the group, called opinion leaders, who are more powerful at influencing others’ opinions [
17,
18,
19]. Opinion leaders may help or hinder the normal agents in finding the truth depending on their own attitudes towards, or access to, the truth due to symmetrical nature.
In most existing models, the opinion leaders opt to be influenced by the expected opinion object (truth) and pass the influence to their followers. For example, in the two-step flow model, the agents are divided into two groups, opinion leaders and their followers, where the followers, unlike the opinion leaders, do not have direct access to the truth or external information. The followers can only indirectly access the external information through their opinion leaders, which was described as a two-step flow process [
20,
21]. It means that the opinion leaders usually hold positive attitudes towards revealing the truth to their followers. However, there are also some situations where the leaders are inclined to hinder the truth from the other agents from the symmetry point of view, which motivates the study in this paper. Changes in scientific paradigms would be an example, where influential scientists have sometimes advocated ideas based on the science of their time and resisted change, but they might turn out to be mistaken. The diffusive and anti-diffusive behavior of agents for kinetic models were studied in [
22], but including opinion leaders was not considered.
We have already analyzed how the opinion dynamics are affected when there are conflicting beliefs in a competing environment [
23] and how the opinion leaders affect opinion dynamics in a bounded confidence model, HK model, under competing environment, by analyzing four characteristics of opinion leaders: reputation, stubbornness, appeal, and extremeness [
24]. As a subsequent work, this paper investigates how the opinion leaders affect (help or hinder) the other agents in seeking the truth in a social group in terms of these four characteristics. Will the opinion leader who takes opposite opinion to the truth always hinder the other agents in finding the truth? Which characteristic will play positive role to the leader on affecting the other agents seeking the truth, and which characteristic will play negative role on this?
The remaining part of this paper is structured as follows. An opinion dynamics model is put forward in
Section 2 for social groups with truth and an opinion leader based on the HK model. In
Section 3, we investigate the effect of opinion leaders on the normal agents when seeking the truth in the proposed model based on computer simulations and discussions.
Section 4 draws some concluding remarks with some suggestions for future research directions.
2. Models and Methods
Two kinds of opinion dynamics models have been studied in the literature: discrete opinion dynamics and continuous opinion dynamics [
5,
6,
25]. In discrete opinion dynamics models, the agents’ opinions take discrete values, and on the other hand, continuous opinion dynamics models treat the agents’ opinions as real variables, often taking values in the unit interval [0, 1]. In both types of models, the agents holding different initial opinions communicate with each other and update their opinions accordingly. As a representative type of continuous opinion dynamics model, the bounded confidence model defines a kind of opinion similarity measurement called the bound of confidence or tolerance, and the agents are only allowed to interact with their neighbors who are within their confidence range, i.e., hold opinions similar to theirs [
8]. As typical bounded confidence models, the HK model and Deffuant–Weisbuch (DW) model have received considerable attention in recent years [
26,
27,
28,
29,
30,
31,
32]. These two models have been widely studied theoretically and experimentally, and it has been shown that there are consensus thresholds in terms of the bound of confidence. A consensus is always achieved in the whole group when the bound of confidence is above the consensus thresholds, while the group will divide into several non-interacting sub-groups where the agents in each sub-group hold the same opinion if the bound of confidence is below the consensus thresholds [
5]. The proposed model in this paper is adapted from the HK model by introducing the truth and opinion leader into the model, and therefore the HK model and the modified model are described correspondingly in the following.
Suppose that there is a complete network with
n vertices, for modeling the social group with
n agents where each agent holds her opinion on a given topic, which takes continuous value in the unit interval [0, 1] in HK model. It means that all the agents in the group are able to interact with the other agents accordingly to update their opinions. The essential aim of opinion dynamics is to study how the agents’ opinions evolve under different environments, to form consensus or divide into several sub-groups holding the same opinion in each sub-group, which reflects the symmetrical nature in physical or social groups. Therefore, the agents’ opinions in HK model are functions of time taking values in the interval [0, 1], and the opinion of the
ith agent at time-step
t is denoted as
xi(
t). On the other hand, for simulation analysis purpose, the opinion functions are sometimes assumed to change over a set of discrete time points based on certain opinion update mechanism. This paper adopts the extended HK model presented in [
13,
14], instead of the original HK model, as the basis for opinion update, which is described in Equation (1).
where
represents the true value of the expected opinion object,
stands for the weight assigned to the
ith agent, which shows the influencing degree of the agent affecting the others’ opinion and might be different for different agents.
is the set of the agents who hold similar opinions as that of the
ith agent at time
t, called its epistemic neighborhoods [
14], with the opinion similarity measured by the bound of confidence
.
is the cardinality of
I(
i,
t), i.e., the number of epistemic neighbors of the
ith agent at time
t.
Douven and Riegler [
15] keep the extremeness of the truth fixed, i.e.,
, and give it complete appeal (i.e., all agents are influenced by the truth). Their results showed that the effect of the truth on influencing the opinions of agents is quite dramatic, i.e., all the agents will reach the truth even if they apply very little weight to the truth. For comparison purposes, we choose the truth
as that in [
15], but consider this from a different angle by lowering the value of appeal of the truth, denoted as
A in the following, so that the agents are influenced by the truth or not depending on whether they are within the appeal range of the truth or not.
The opinion leader, denoted as
L, in a social group might help or hinder the normal agents to reach the truth due to symmetrical nature. Considering that state-of-the-art research mainly focuses on the helping aspect of the leader as pointed in
Section 1, we study mainly how the leader hinders the agents finding the truth from another point of view. We investigate the impact of opinion leaders affecting the normal agents on seeking the truth by considering four characteristics of opinion leaders: reputation, stubbornness, appeal, and extremeness. These four characteristics have been investigated under an environment where there are two competing leaders trying to attract more followers [
24]. The leaders are usually assigned a higher weight than the normal agents, which is known as their reputation [
19] and denoted as
RL for leader
L, while the weights of normal agents are all assumed being 1, much smaller than
RL, in the following discussion. The influencing power of leaders on other agents is called their appeal [
18] and denoted as
AL. The appeal of leaders is reflected by the bounds of confidence of normal agents towards leaders in the following, which is larger than that towards their peers, denoted as
T. On the other hand, the leaders are less, or sometimes not, influenced by the other agents representing their stubbornness [
33,
34], which is reflected by the small bounds of confidence of leaders. Therefore, the stubbornness of opinion leader
L is defined as
SL = 1 −
TL, with
TL being the small bound of confidence of leader
L. The extremeness of opinion leader comes from the competing nature of two opinion leaders [
35,
36], and so the extremeness of the leader is reflected by how close the opinion value of the leader is to the extremes of 0 and 1, because there is only one leader in our model who might be competing with the truth. The opinion value of leader
L is denoted as
xL in the following. We consider in this paper how the group, especially the normal agents, behave as the three characteristics—reputation; appeal and stubbornness; and the opinion of the leader, representing its extremeness—vary. What is the effect on the agents seeking the truth if the reputation, appeal, or stubbornness of the leader increase or decrease in their values? How will the normal agents act if the leader takes different opinion values?
It is worth mentioning that the agents within the appeal range are influenced by the truth, and the agents who are far from the truth are not influenced by it. It is different to the case studied in [
15] where all agents are influenced by the truth, and also different to the two-step flow model where the normal agents have no access to the truth and can only follow what the leaders tell them about it. It is also noticed that Hegselmann and Krause [
37] considered the impact of radical groups and charismatic leaders on opinion dynamics based on the HK model, where the radicals are totally stubborn on holding their opinion and charismatic leaders are more inclined to influence the normal agents that are within their appeal range than other agents, while it has not studied all of the four characteristics in their model. A model similar to the current one is explored in [
38], who compare it with the approach in [
15] and explore results when the percentage of truth seekers is varied. However, [
38] does not investigate how changing the appeal, stubbornness, and extremeness of the opinion leader or conflicting source affects convergence to the truth.
Based on the above analysis, we modify the HK model (1) accordingly to address these questions as
where
rj > 0 and
R > 0 are the weights assigned to agent
j and the truth respectively with
R, also called reputation of leaders, being much larger than
rj, and the function
is the sum of the weights of agents within
and the reputations of truth depending on the value of function
, which is
Since the aim of this paper is to study how opinion leaders affect the other agents on finding the truth, we adopt the proportion of agents who reach the truth as the quantity to investigate this kind of impact of opinion leaders.
3. Simulation Results and Discussions
The simulations are implemented in MATLAB. We would like to first discuss the interpretations of some parameters that are going to be used in the following simulations.
The number of agents in a real-world network could vary from a very low number to a very large number. In order to make the simulation results comparable to that in the literature, the number of agents is set as 100 in our simulations, taking the similar settings in the literature, with one of them being designated the opinion leader whose opinion is specifically valued in the following simulations. In order to verify the rationality of this assumption, we have also experimented the simulations on the group with 500 agents for some situations and the results return no significant difference compared to that on the group with 100 agents.
Initial opinion values of the agents are generated from a uniform random distribution on the unit interval [0, 1], following the similar assumptions in the literature, except that of the opinion leader, which takes some specific values—i.e., 0.25 symmetric to the truth about the centre 0.5 for comparison purposes. We then explore the impact of the four characteristics of opinion leaders, reputation, stubbornness, appeal, and extremeness on the dynamics of the group by varying their values. For extremeness, it is realized by varying the opinion value of leader from 0 to 1 to investigate its impact. It is noted that these assumptions on simplified conditions are mainly to make the impacts of the four characteristics on opinion dynamics clearer.
For repeated runs, it is noted that the simulation results might be different even if the parameter settings are exactly the same, given randomly generated initial opinions. In order to evaluate the effect of the randomness of initial opinions, we have implemented the simulations for 100, 200, and 500 runs with all the parameters taking the same values except for the initial opinions, and found that the results from different runs are actually very similar to each other, with exceptions being less than 10 from 500 runs. Given this, we choose to take the average value over 200 runs for the following simulation analysis.
In order to make the readers better understand how the opinions of agents change over time, we also select some typical time series of opinion update process for this purpose.
Firstly, in
Section 3.1, we show the simulations on group with truth but without opinion leader for comparison purpose, and discuss how the reputation and appeal of the truth affect opinion dynamics. Then, after introducing an opinion leader into the group, the impacts of the reputation, stubbornness, appeal and extremeness of opinion leader on affecting the agents seeking the truth are then analyzed one by one in
Section 3.2.
3.1. Group without Opinion Leader
For comparison purposes, we start with the case where there is no opinion leader but just the truth in the group, and the truth takes fixed value at 0.75 as in the literature. We then vary the reputation and appeal of the truth in the following two subsections respectively to investigate their impacts on the agents seeking the truth.
3.1.1. Impact of the Reputation of Truth
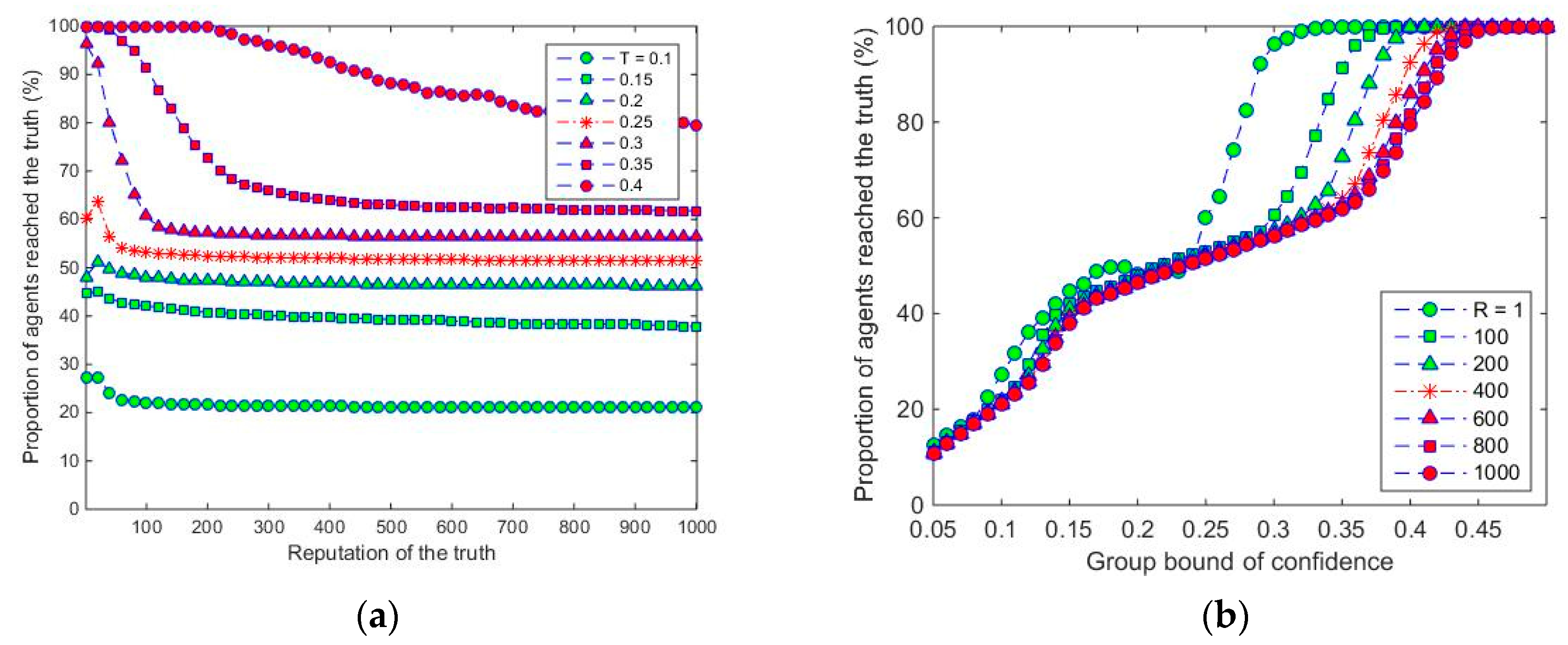
We investigate the average proportion of agents who reach the truth with the group bound of confidence T varying, in steps of 0.01, from 0.05 to 0.5, and the reputation of the truth varying, in steps of 20, from 1 to 1000. We let the appeal of the truth take the same value as the group bound of confidence, i.e., AL = T. The starting value of group bound of confidence T is set to be 0.05 because the agents will be in a great diversity when T is smaller than 0.05, and the impact of truth on the agents will be not so visible.
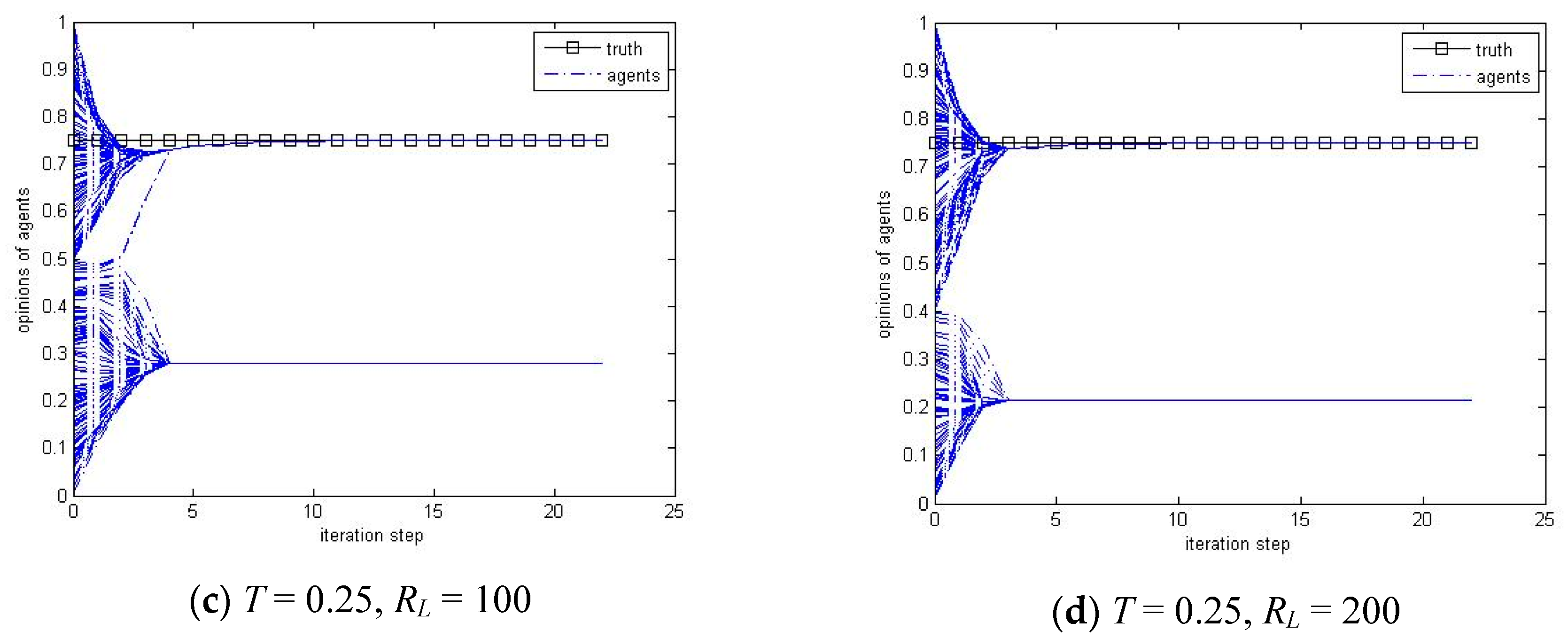
Figure 1 shows that it slightly decreases the proportion of agents reaching the truth by increasing the reputation of truth in the first several steps, i.e., it makes the process for the agents reaching truth become slightly harder. Actually, when the reputation of truth takes small values, most agents, no matter within or outside the confidence range of truth, will be influenced by the truth in the long run, because the agents are communicating with their neighbors. However, when the reputation of truth is sufficiently high—e.g., 100—the agents who are within the confidence range of the truth will reach it much quickly and the other agents that lie outside the confidence range of truth will not be able to communicate with some previous neighbors who ran to the truth from them, and then step away the truth gradually. These findings are similar to results presented in [
38], where a consensus on the truth was found to occur for values of confidence above critical values from about 0.3 to 0.4 depending on the weight/reputation of truth. When the reputation goes still higher, this effect is clearer and the percentage of agents reaching the truth is then stabilized. The stabilized percentages of agents reaching the truth are shown in
Table 1, where it can be seen that more agents will reach the truth when the group bound of confidence takes larger value. It also shows that higher reputation is needed to stabilize the proportion of agents reaching the truth with larger group bound of confidence. Therefore, the reputation of truth is fixed as
R = 50 in the following sections considering that the impact of other parameters might be hidden if there is a much higher reputation.
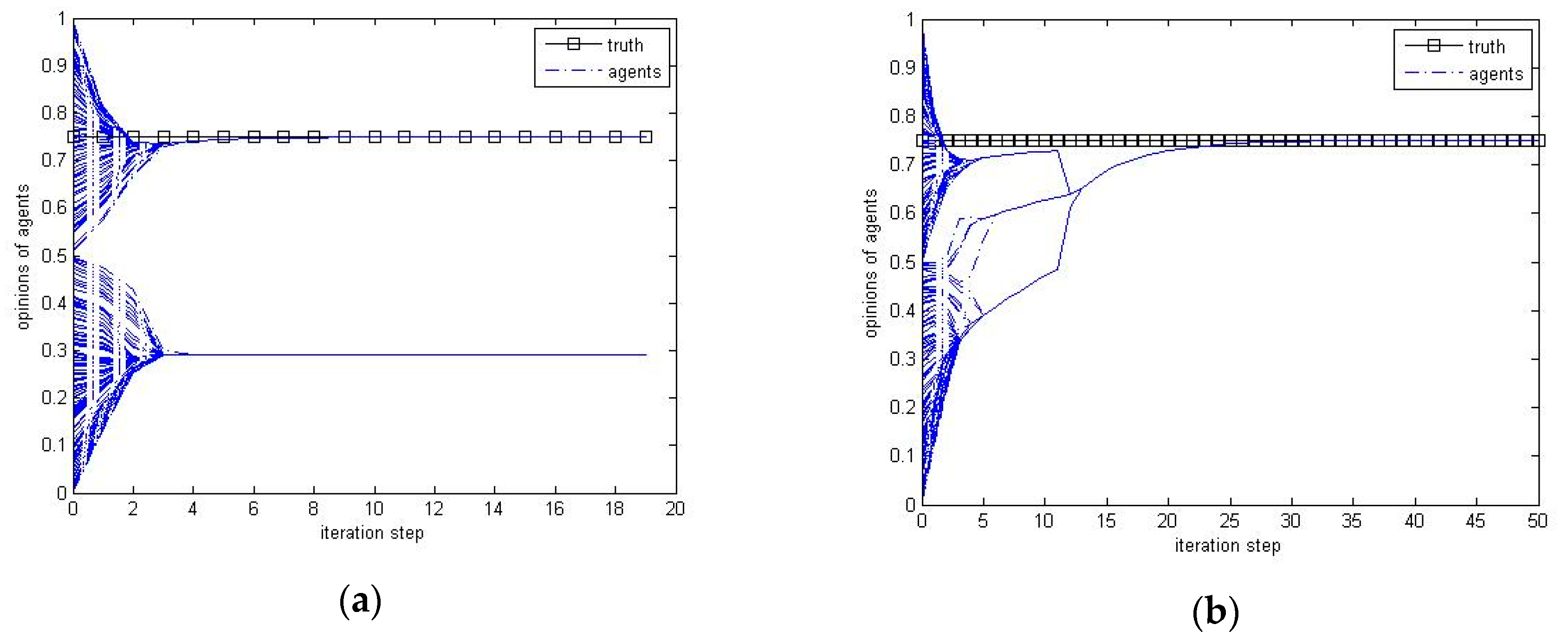
The time-series simulation results as shown in
Figure 2 illustrate the opinion update process will return two different results, one group and two groups, because of the randomness of starting opinions. This phenomenon is the same for most reputation and bound of confidence values, while the probability of all the agents reaching the truth increases when the bound of confidence increases and the reputation decreases as demonstrated in
Figure 1.
3.1.2. Impact of the Appeal of Truth
The impact of appeal of the truth on the opinion dynamics of a group of agents is simulated in this subsection with the results shown in
Figure 3. Similarly, we adopt the average proportion of agents who reach the truth as the quantity to investigate by varying the appeal of truth, in steps of 0.025, from 0.25 to 0.75 (so the truth is able to influence the whole opinion interval) and the group bound of confidence
T, in steps of 0.01, from 0.05 to 0.5. We fix the reputation of truth
R = 50 as discussed in
Section 3.1.1, and choose the starting appeal as 0.25 based on the assumption that the appeal should be normally larger than the group bound of confidence.
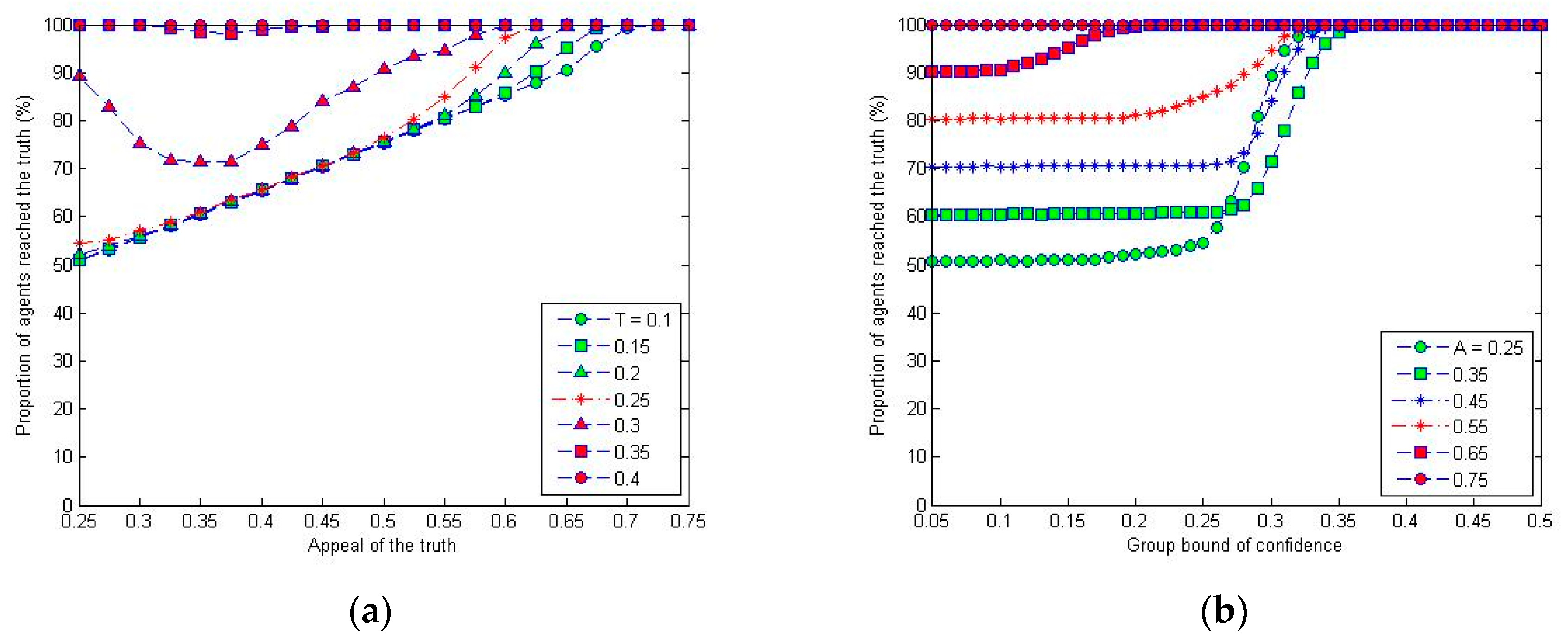
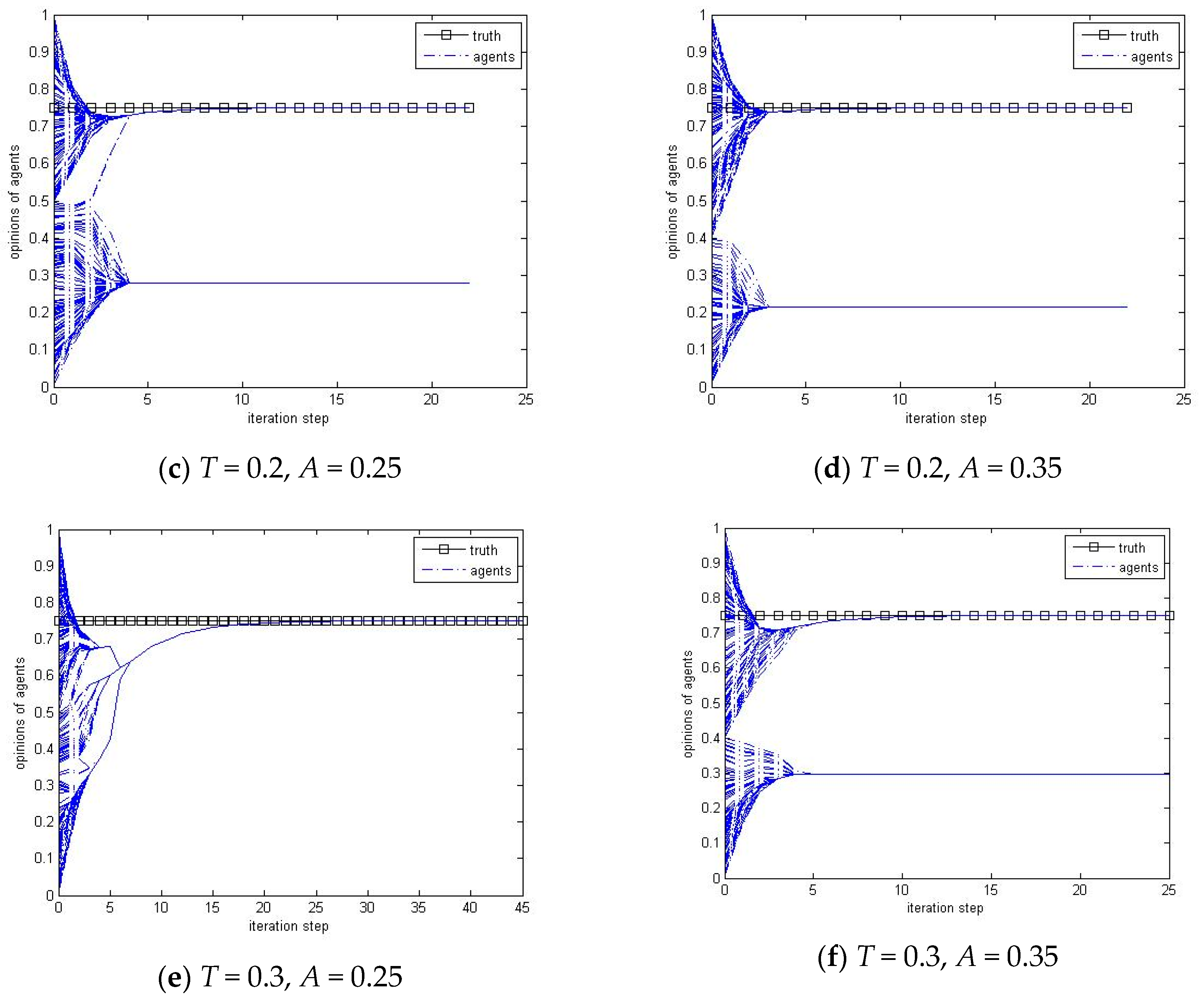
The simulation results in
Figure 3 show that increasing the appeal normally increases the proportion of agents reaching the truth. The truth is able to influence the whole group when its appeal is 0.75, and so all the agents can reach the truth finally, which confirms the findings in [
15]. On the other hand, the proportion of agents reaching the truth decreases firstly and then increases with the increasing of the appeal of truth if the group bound of confidence is near 0.3, although all the agents can reach the truth under some runs when
A = 0.35 and 0.45. This further confirms the findings in [
15] that 0.3 is a threshold for group bound of confidence, and also an unstable point. When the group bound of confidence is close to this value, increasing the appeal slightly from a smaller value makes the agents who are within the appeal range of the truth reach it more quickly, while the other agents that lie outside the appeal range will lose the chance to communicate with the agents that are within the appeal range of the truth quickly, and be influenced by the truth indirectly as a consequence. Of course, if the appeal of truth is sufficiently large—e.g., larger than 0.35—the truth will have a dominating impact on attracting all the agents reaching the truth.
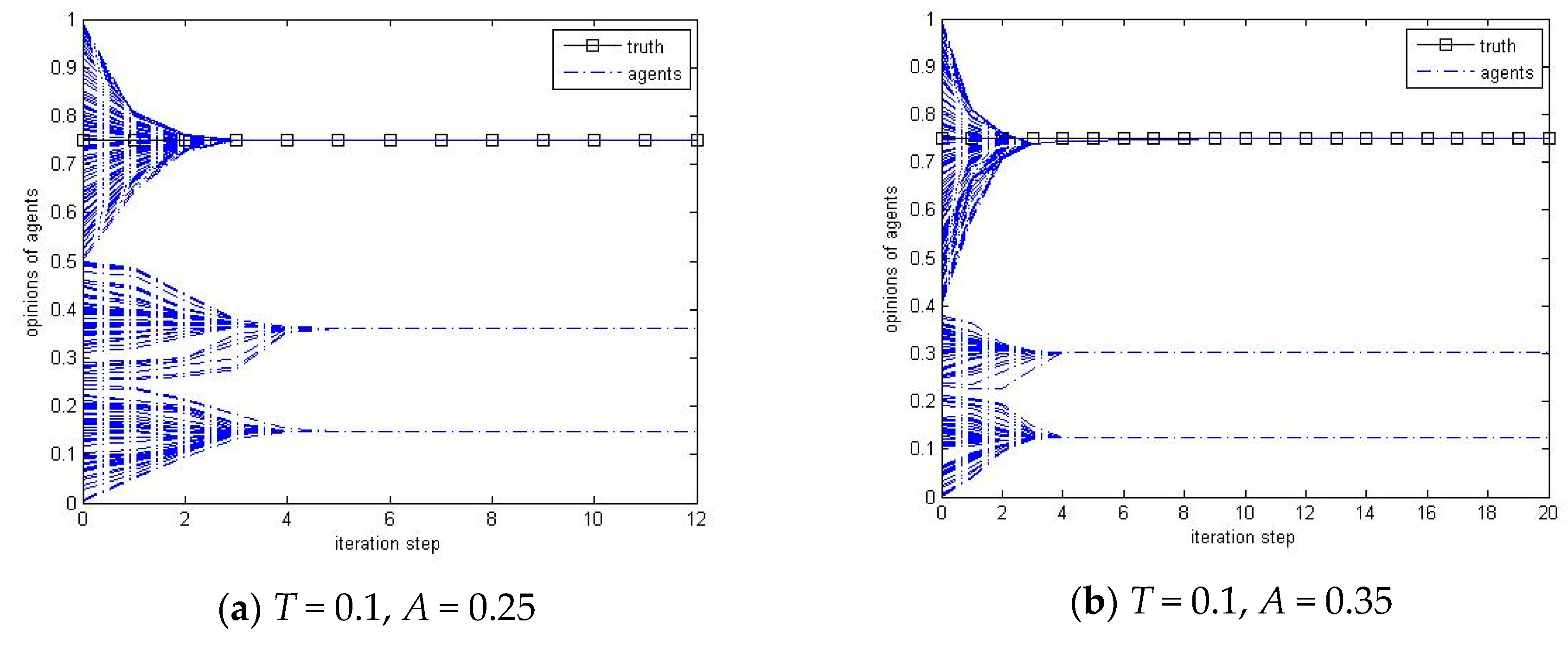
Figure 3b and the time series results in
Figure 4 illustrate that the agents within the appeal range of the truth normally achieve the truth quickly due to its higher reputation when
T is smaller than 0.3 (the consensus threshold if there is no truth) where the agents are more likely to maintain diversity, and the other agents that lie outside the appeal range of the truth will less possibly be influenced by the truth. Therefore, increasing the appeal makes the appeal range wider, and makes more agents achieve the truth consequently. When
T is larger than 0.25, the agents are normally able to achieve the truth, as shown in
Figure 4e, because their larger confidence makes them be able to be influenced by the truth. However, when both
A and
T are between 0.25 and 0.35, increasing the appeal
A will give slightly higher probability to make the agents divide into two groups, as when
T is smaller than 0.25, as shown in
Figure 4f. This is due to the similar reason, as that for the reputation, that the agents who are within the appeal range of the truth reach it more quickly due to its higher reputation, and the other agents that lie outside the appeal range will be less possibly be affected by the truth indirectly by communicating with their neighbors that are within the appeal range of the truth and then form another group by themselves.
If the appeal of the truth is set as 0.5 or larger, the leader (whose opinion is set as 0.25 in the following) will always be influenced by the truth and reach the truth finally, and so the impact of the leader on normal agents cannot be distinguished. It can also be seen from
Figure 1 that reputations higher than 50 make little difference with fixed group bound of confidence when there is no opinion leader. Therefore, we fix the reputation and appeal of the truth in the following sections to
R = 50 and
A = 0.4, and explore how the opinion leader affect the normal agents on finding the truth in terms of the four characteristics.
3.2. Group with Opinion Leader
We then introduce the opinion leader into the group in this section, and then investigate how the leader influences the normal agents on seeking the truth in terms of the four characteristics. As stated previously, we fix the leader’s opinion as xL = 0.25, when exploring the impact of the three characteristics—reputation, stubbornness, and appeal—and vary the leader’s opinion value when investigating the impact of extremeness. It is noted that the value of the leader’s opinion (0.25) is symmetric to the truth value (0.75), about the mid-point 0.5.
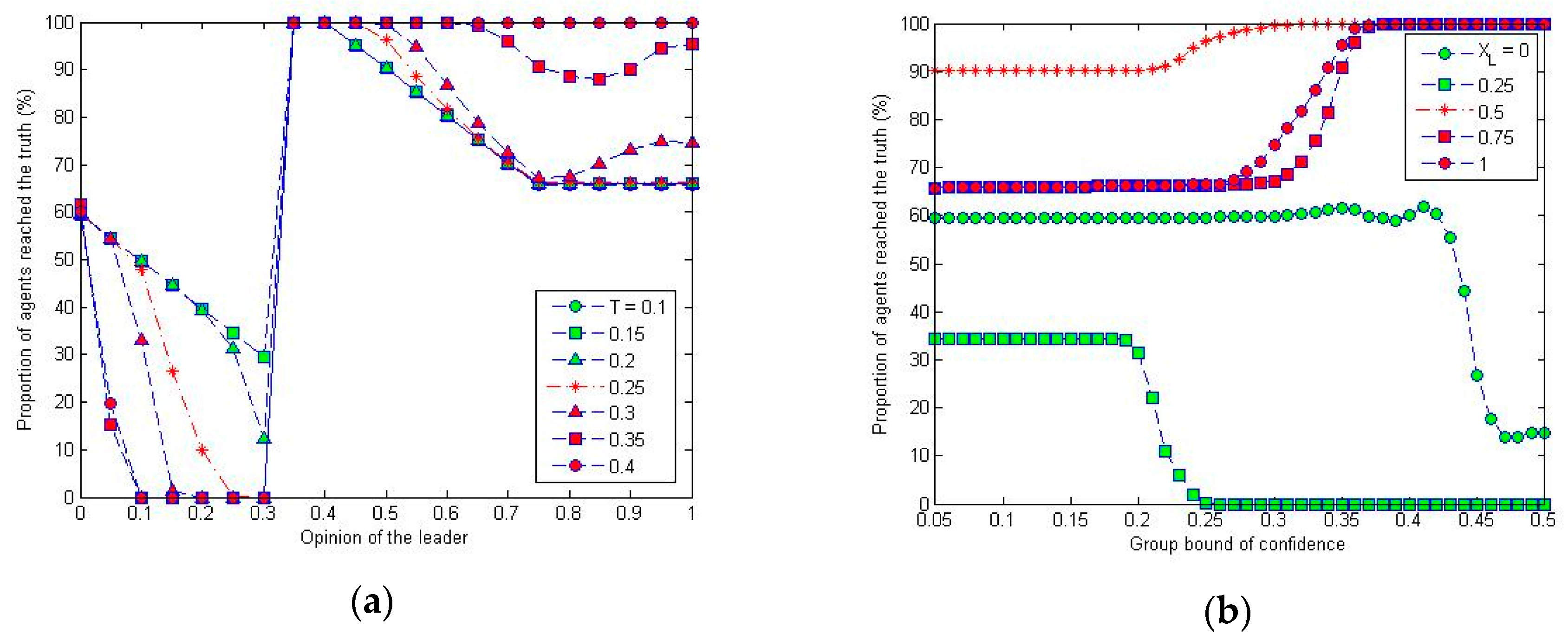
3.2.1. Impact of the Reputation of Leader
We start with exploring the impact of leader’s reputation on the normal agents finding the truth. We set
SL = 1 −
T,
AL =
T, so that the leader only differs from other agents because of reputation, and then we will vary the settings of other characteristics to see their impacts in the following subsections. We then vary the reputation of the leader, in steps of 20, from 1 to 1000 and the group bound of confidence
T, in steps of 0.01, from 0.05 to 0.5.
Figure 5 shows the simulation results on the average proportion of agents reaching the truth.
It is shown in
Figure 5a that the percentage of agents reaching the truth goes up from around 65% to 100% when the leader’s reputation
RL increases from 1 to 50 or 200 depending on the value of
T, and then drops down to some stable value when increasing
RL further. The reason for the percentage increasing is similar to the impact of the truth’s reputation, i.e., higher (but not too high) reputation makes the normal agents that fall outside the confidence range of the leader have less chance of being influenced by the leader, and therefore more chance to be influenced by the truth whose value remains unchanged. At the same time, due to the reason that the leader is not stubborn, it will communicate with the other agents and be affected by the truth indirectly, and change its opinion correspondingly, even becoming the follower of the truth in some cases. When
RL goes still higher, the leader has the ability to attract the normal agents within its confidence range to become its followers sharply, and form its own group that is out of the control of the truth when
T is smaller than the value about 0.45 as shown in
Figure 5b. As a result, the percentage of agents reaching the truth drops down. When
RL is sufficiently high, there will be a trade-off between the impact of the truth and the leader, and the percentage of agents reaching the truth will become stable. The time series plots as shown in
Figure 6 help to illustrate the group opinion dynamics.
Table 2 shows the stabilized percentages of agents reaching the truth. Comparing with the case where there is no opinion leader as shown in
Figure 1 and
Table 1, there is a visible change after introducing the opinion leader. Although the reputation of truth
R = 1000 in
Table 1, but
R = 50 in
Table 2, it is noticed that reputations of truth being higher than 50 make little difference with fixed group bound of confidence when there is no opinion leader as explained at the end of
Section 3.1. Along with the increasing of the group bound of confidence
T, the percentages of agents reaching the truth decreases after introducing the opinion leader instead of increasing when there is no opinion leader. In other words, the opinion leader helps more normal agents to reach the truth when
T is smaller than 0.25, while hindering more agents from the truth when
T is larger than 0.25. When
T is around 0.25 (symmetric to the truth value about 0.5), the impact of the opinion leader on the normal agents is indiscernible, where the investigated percentage is about 50%. The reason comes from the fact that the leader’s initial opinion is symmetrically opposite to the truth, and so it essentially tends to hinder the normal agents from finding the truth. On the other hand, the leader is not completely stubborn, and it can also be influenced by the truth directly or indirectly. When
T is smaller, more agents, including the leader, will be influenced by the truth gradually because the truth is completely stubborn, and then more agents will accept the value of the truth as their opinions. When
T becomes larger, more agents would be influenced by both the truth and the opinion leader, and some agents may change to follow the opinion leader and others may form a group with an opinion different to that of either the truth or the leader. It can be expected that the opinion leader will usually hinder the normal agents in reaching the truth if they are sufficiently stubborn, which will be discussed in the following subsection.
Taking the similar reason as that for the truth, we fix the reputation of the leader RL = 50 in the following subsections when exploring the impact of the other characteristics.
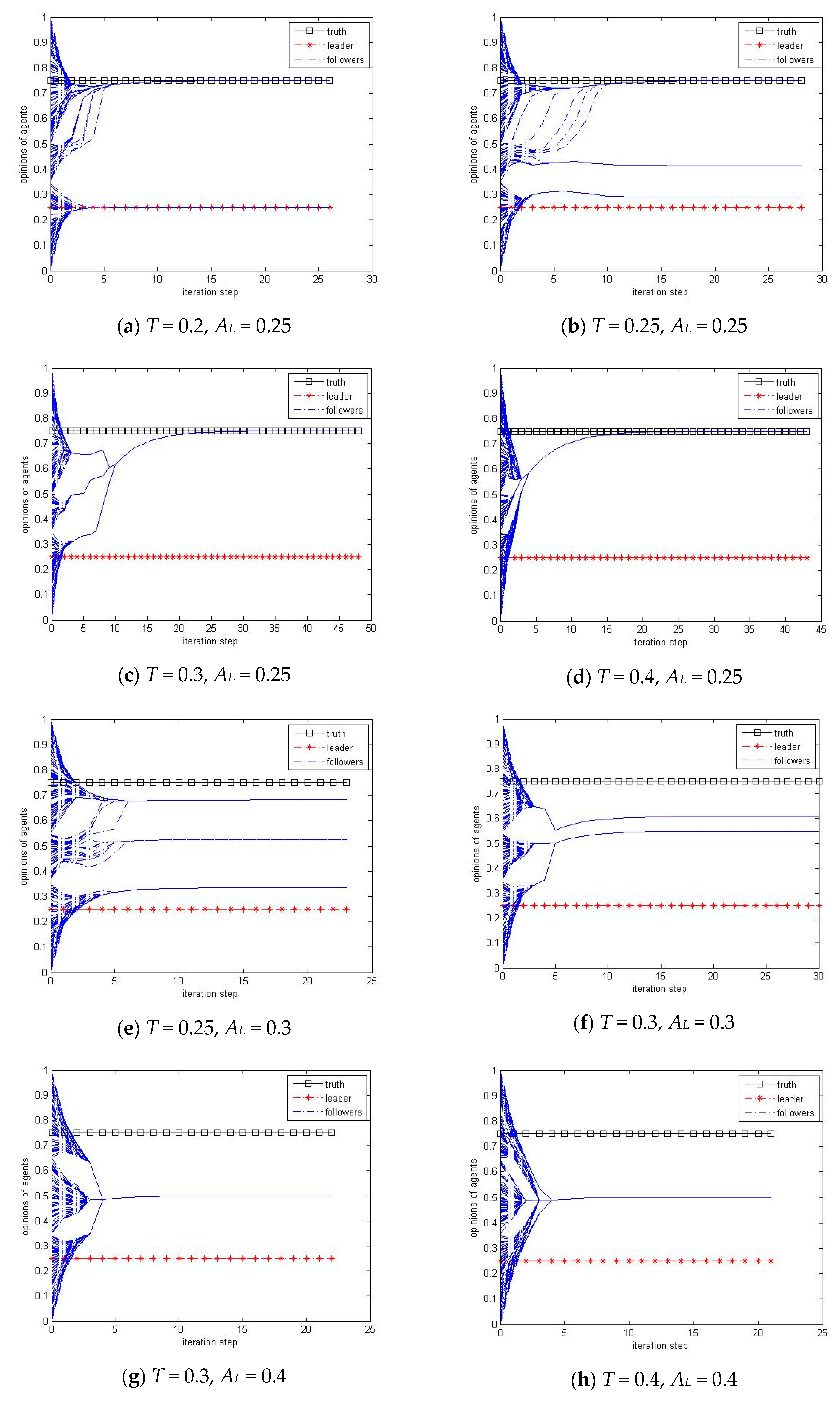
3.2.2. Impact of the Stubbornness of Leader
This subsection investigates the impact of the stubbornness of leader on the normal agents finding the truth, we fix the reputation of leader
RL = 50, and vary its stubbornness
SL, in steps of 0.01, from 0.8 to 1 and the group bound of confidence
T, in steps of 0.01, from 0.05 to 0.5, with its appeal
AL =
T.
Figure 7 shows the simulation results on the average proportion of agents who reached the truth.
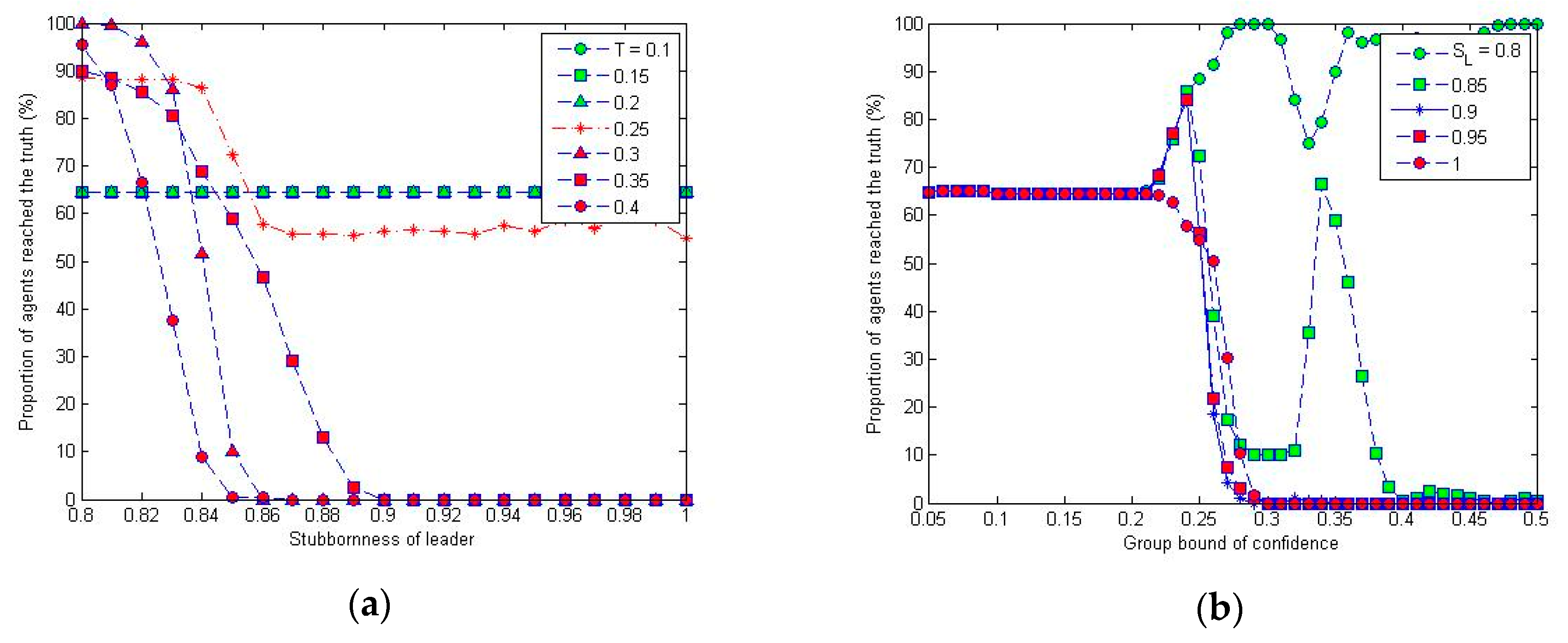
It can be seen from
Figure 7a that stubbornness has no discernible effect when
T is smaller than 0.2, while there is a dramatic change, when
T is larger than 0.3, from the state where all the agents can reach the truth to the state where none of the agents can reach the truth when
SL is around 0.9. The results for high values of stubbornness are consistent with the findings in [
38], where a conflicting source to the truth is assumed to be completely stubborn and it is shown that no agents can converge on the truth for sufficiently high values of confidence.
Figure 7b shows a critical point at about 0.2, before which all stubbornness values (from 0.8 to 1) make the same proportion of agents reach the truth, while thereafter the leader with stubbornness value larger than 0.9 pulls all the other agents away from the truth and that with stubbornness smaller than 0.8 helps the others to reach the truth. However, when
T is between 0.2 and 0.4, the group dynamics are very sensitive, especially when
SL = 0.85 where the percentage of agents reaching the truth fluctuates between 0 and 70% as shown in
Figure 7b. The time series plots on the opinion update process as shown in
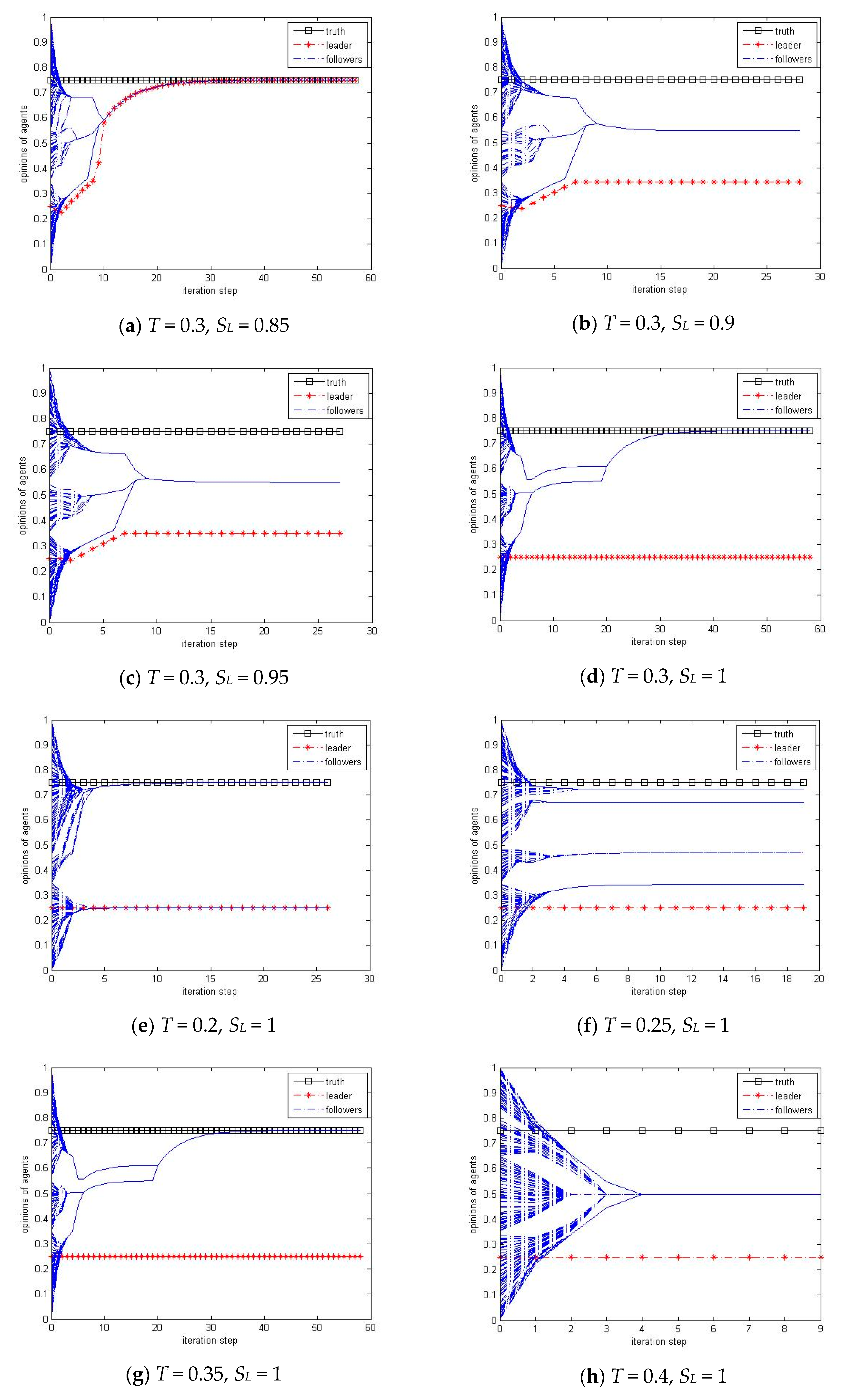
Figure 8 helps to better understand the group opinion dynamics. Note that the group behavior is sensitive when
T is around 0.25, the agents usually divide into more than three groups as shown in
Figure 8f, but sometimes form two groups similar to that in
Figure 8e.
The reason comes from the fact that the stubbornness of the leader relates only to the normal agents. Whenever the opinion leader falls into the confidence range of the truth, he will be influenced by the truth and change his opinion accordingly no matter his stubbornness. Considering that the lower boundary of the confidence range of the truth is 0.35 = 0.75 − 0.4, and so the leader’s opinion will change when the starting value is between 0.35 and 0.5 as will be studied in
Section 3.2.4, and will keep fixed when between 0 and 0.35 if the leader is completely stubborn. Considering the leader’s opinion is 0.25 here, the leader cannot be trapped by the truth and then hinder the truth to the normal agents when he is sufficiently stubborn, e.g., larger than 0.9 for most group bounds of confidence. On the other hand, as shown in
Figure 8a,c, if the leader is not completely stubborn, he could be influenced by the truth indirectly by virtue of the other agents when the group bound of confidence takes larger values.
Given the above analysis, we assume the leader be totally stubborn, i.e., SL = 1, as exploring how the leader influencing the agents seeking the truth in terms of its appeal and opinion value.
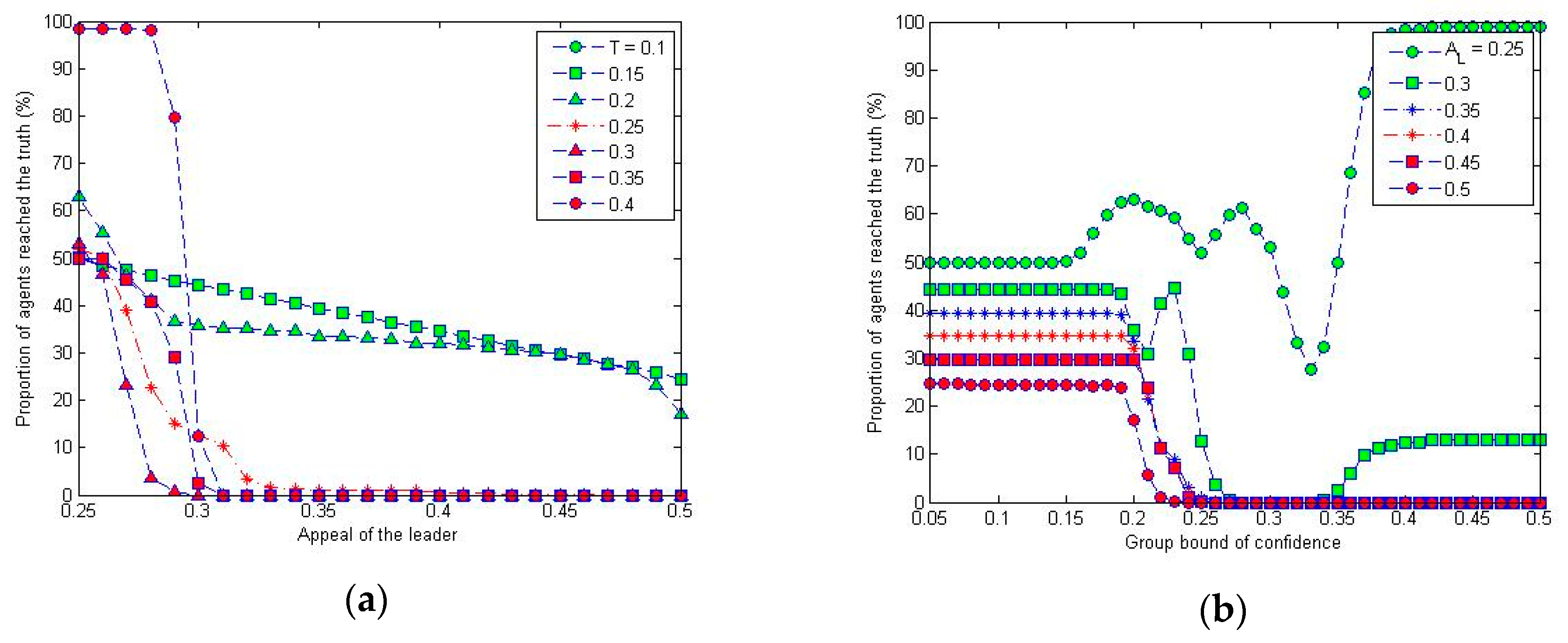
3.2.3. Impact of the Appeal of Leader
This subsection investigates the impact of leader’s appeal on the normal agents finding the truth, we fix the reputation of leader
RL = 50 and its stubbornness
SL = 1, and vary the group bound of confidence
T, in steps of 0.01, from 0.05 to 0.5 and the appeal of the leader on the normal agents
AL, in steps of 0.01, from 0.25 to 0.5.
Figure 9 shows the simulation results on the average proportion of agents who reached the truth.
It is shown in
Figure 9a that the proportion of agents reaching the truth decreases with the increasing of the appeal of leader, and, as shown in
Figure 9b, it also normally decreases if the group bound of confidence
T increases. When
T is larger than 0.3, no agent can reach the truth with
AL also larger than 0.3. We have selected some typical time series plots as shown in
Figure 10 to further illustrate the above results. It can then be concluded that increasing the appeal of the leader whose opinion is opposite to the truth has a straightforward impact, i.e., normally prevents the normal agents from finding the truth. On the other hand, increasing
T also makes the agents who start out close to the truth move away from the truth if there is an opinion leader opposite to the truth. This can be explained as the agents are more likely to be influenced by both the truth and the leader when
T is larger, and will normally converge to an intermediate opinion. Therefore, it means that the opinion of the leader is quite important in affecting the normal agents’ ability to reach the truth. We then vary the opinion of the leader and see how the group behave in the following section, while letting the appeal take the middle value, i.e.,
AL = 0.4 for comparison purposes.
3.2.4. Impact of the Opinion Value of Leader
In order to explore how the leader’s opinion value affect the normal agents finding the truth, we fix the reputation of leader
RL = 50, its stubbornness
SL = 1 and its appeal
AL = 0.4, and vary the group bound of confidence
T, in steps of 0.01, from 0.05 to 0.5 and the leader’s opinion
xL, in steps of 0.05, from 0 to 1.
Figure 11 shows the simulation results on the average proportion of agents who reach the truth.
It is illustrated in
Figure 11 that, generally, the leader with opinion being opposite to the truth (opinion value is less than 0.35 in this simulation) will prevent the normal agents from finding the truth. On the other hand, the leader who has a similar opinion to the truth (opinion value is larger than 0.35 in this simulation) will help the other agents to reach the truth. The critical opinion value, 0.35 here, is determined by the value and appeal of the truth, 0.75 and 0.4 in this simulation. In other words, when the opinion value of leader is within the appeal range of the truth, the leader will help the normal agents to reach the truth. Otherwise, the leader will have the opposite role.
Taking a further look at
Figure 11a, it is noted that when the opinion value of the leader changes from 0 towards 0.35, the critical value, the leader is able to persuade more, until 100%, normal agents stay away from the truth. Actually, the agents will form one or more groups distinct from both the truth and the leader at different opinion values, as illustrated by the time series plots as shown in
Figure 10e,f. After passing the critical opinion value 0.35, all of the normal agents will be able to reach the truth, even those whose initial opinion value is far from the truth. Let us recall that, when there is no opinion leader, those agents will usually reach a consensus different from the truth as shown in
Figure 4d. Therefore, the opinion leader has a good impact on helping the normal agents to reach the truth at this point. However, when the opinion value of the leader goes larger, some agents will escape from the truth. The reason is that both the truth and leader are not able to effectively attract the agents far from them when the leader takes an opinion value close to the truth. Actually, when the leader takes the same opinion value as the truth value, it turns out that there seems to be no visible opinion leader at all for the group. This means that, for better helping the normal agents to reach the truth, the leader should take the opinion value within the appeal range of the truth, but not too close to the truth value. By this, the appeal range of the truth is actually widened by the leader.
Increasing
T also makes the agents who start out close to the truth move away from the truth if there is an opinion leader opposite to the truth as shown in
Figure 11b. This can be explained as the ‘open-minded’ agents are more likely to be influenced by both the truth and the leader when
T is larger and will normally reach a consensus at an intermediate opinion.
4. Conclusions
It has been analyzed in this paper that how the opinion leader affects the other agents in a social group on seeking the truth based on a bounded confidence model by considering its four characteristics: reputation, appeal, stubbornness, and extremeness (opinion value). Whether the leader will help or hinder the normal agents to find the truth normally depends on the compound effect of these four characteristics. It has been shown that, based on the simulations, increasing the reputation of a leader generally makes the percentage of agents reaching the truth goes up, might reach 100%, and then drops down to some stable value when increasing it further. A highly stubborn leader holding an opposite opinion to the truth is usually trying to hinder the other agents from finding the truth if the group bound of confidence is larger than 0.3, when most agents are open to both the truth and the leader directly or indirectly. The impact of the appeal is a bit straightforward that the leader, opposite to the truth, with higher appeal often directing more agents away from the truth. On the other hand, due to the fact that a leader usually has high reputation, high stubbornness, and high appeal (otherwise it is doubtable to be called a leader), helping or preventing the truth finding depends mainly on the opinion value of the leader. Generally, a leader who has close opinion value to the truth helps normal agents find the truth, while a leader with an opposite opinion value to the truth will hinder the normal agents from finding the truth. It is also interesting that, in order to help normal agents to reach the truth, it is better for a leader to take an opinion value within the appeal range of the truth, but not too close to the truth value.
We have investigated the crisp functions reflecting the relationship between the percentages of agents reaching the truth and the four characteristics (or some of them) correspondingly. The group bound of confidence plays an important role on influencing group opinion dynamics, although it seems that this parameter would be out of the control of the opinion leader and out of the scope of this paper, because it reflects the extent of the normal agents being ‘open-minded’ towards their neighbors. If the group bound of confidence is sufficiently large, then all the agents have good access to the truth, opinion leader as well as other agents, and the group will reach consensus more likely. If the group bound of confidence is quite small, which means that the agents are quite stubborn and do not want to learn from others, then the group will keep diversity usually. On the other hand, it has been shown that, based on the simulation results and discussions, there is a trade-off between the four characteristics of the leader and the group bound of confidence, and that relatively small changes in some parameter values can lead to dramatic changes in group behavior, especially at the boundary areas of the characteristics. For example, increasing the group bound of confidence from 0.35 to 0.4 in the group with the opinion leader’s reputation being 200 will make the whole group that were split into several sub-groups to form consensus as shown in
Section 3.2.1. Further study on how the characteristics of the opinion leader and the group bound of confidence work together on affecting the opinion dynamics will be one of our next step research points.
It is also noted that there are some limitations of the research in this paper. The initial opinion values of the agents are generated from a uniform random distribution on the unit interval [0, 1], while the distribution of real opinions might be more complicated, not in such a uniform way. The bounds of confidence might be heterogeneous in real cases, while it is assumed in this paper that all the agents, except for the opinion leader, take the same bound of confidence for simplicity purpose, called the group bound of confidence. The impacts of the four characteristics of the leader on the opinion dynamics are studied separately by assuming that the other characteristics take fixed values when investigating specific characteristic, while the group behavior is actually caused by the compound effects of these characteristics and the group bound of confidence. These assumptions on simplified conditions, following similar assumptions in the literature, are made mainly to make the impacts of the four characteristics easier to understand, and some assumptions—e.g., the randomly generated initial opinion values—are due to the limited resources of simulations. Our future research will try to make the simulation conditions more realistic and focus more on the compound effect of the parameters.