Abstract
A theoretical study of the synchrotron radiation (SR) from electrons in periodic magnetic fields with non-periodic magnetic components is presented. It is applied to several free electron lasers (FELs) accounting for the real characteristics of their electron beams: finite sizes, energy spread, divergence etc. All the losses and off-axis effects are accounted analytically. Exact expressions for the harmonic radiation in multiperiodic magnetic fields with non-periodic components and off-axis effects are given in terms of the generalized Bessel and Airy-type functions. Their analytical forms clearly distinguish all contributions in each polarization of the undulator radiation (UR). The application to FELs is demonstrated with the help of the analytical model for FEL harmonic power evolution, which accounts for all major losses and has been verified with the results of well documented FEL experiments. The analysis of the off-axis effects for the odd and even harmonics is performed for SPRING8 Angstrom Compact free-electron LAser (SACLA) and Pohang Accelerator Laboratory (PAL-XFEL). The modelling describes theoretically the power levels of odd and even harmonics and the spectral line width and shape. The obtained theoretical results agree well with the available data for FEL experiments; where no data exist, we predict and explain the FEL radiation properties. The proposed theoretical approach is applicable to practically any FEL.
1. Introduction
The first theoretical results for the radiation of a charge on a circular orbit were obtained by Lienard in the end of the 19th century. A few years later in 1907 a complete theoretical study was performed by Schott. It was aimed on the description of the atomic spectra, but quantum mechanics was still unknown and this study failed to describe atoms. Instead it perfectly described the spectral and angular distribution of the radiation from electrons in a constant magnetic field. The results did not find application at that time and they were forgotten for almost half a century. The undulator radiation (UR) is a particular case of the synchrotron radiation in periodic magnetic field; it was proposed by Ginsburg [1] and first observed by Motz [2] in the middle of the 20th century. Ginsburg also claimed [1] that coherent radiation could be emitted by electrons in periodic magnetic fields; Ginsburg hypothesized that small groups of electrons, separated by the wavelength of the radiation, would emit coherent radiation. The real story of the synchrotron and undulator radiation began. Since then, the energy E of the electrons in accelerators has been shown to increase, so that now the relativistic factor γ >> 1, ~, where m is the electron mass and c is the speed of light. High demand for coherent radiation in X-ray band pushed towards building X-ray free electron lasers (FELs), which provide coherent radiation pulses in the Roentgen band with a duration of femtoseconds, which allow studies of ultra fast processes on nanoscale. To achieve this, the relativistic beams and undulators must be aligned with micron scale tolerance and the whole installation must be manufactured with highest precision to ensure minimal off-axis deviation of the beam, maximum periodicity of the magnetic field and minimal influence of non-periodic magnetic constituents, which take electrons off their path in undulators and disrupt the coherence of their oscillations. Moreover, the relativistic electron beams must have low energy-spread and emittance, so that there could be efficient electron bunching. The latter occurs due to the interaction of the radiation with the beam; the electrons are grouped in microbunches, separated by the wavelength of the radiation and emit coherent radiation exactly as hypothesized by Ginzburg [1]. Modern FELs can generate gigawatt power in femtosecond pulses in the X-ray band [3,4,5,6,7,8,9,10].
Interest in theoretical studies of the synchrotron radiation in the 21st century is determined in great part by applications to FELs. Modeling of a FEL is usually done by numerical algorithms, which solve complex system of equations for electrons and radiation and describe the evolution of the electron beam and photon pulse. Such programs require computational facilities and qualified personnel for programming, specific for each FEL. While FEL physics is quite clear at the present stage, the particular reasons for the harmonic behavior in specific installations are not clarified by numerical simulations. In what follows we propose the analytical formalism, which is based on the exact solution for the radiation integral in complex multiperiodic magnetic fields with non-periodic constituents. The resulting integral forms of generalized special functions of Bessel- and Airy-types exactly describe the radiation in a given angle from electrons with initial off the axis position in the beam with finite emittance and energy spread. Moreover, the phenomenological model of a single-pass FEL, based on the logistic equation [11], has been redefined in the last decade and turned from a scholastic exercise to a real tool, capable of giving immediate analytical description of the power and bunching evolution in practically any FEL with arbitrary configuration of the undulator fields [12,13,14,15,16,17]. Its analytical formulation is rather simple and can be run by any user on a PC or even scientific calculator.
The novelty consists of a fully analytical description of the UR harmonic generation accounting for the off-axis effects, periodic and non-periodic magnetic field components, found in FEL undulators. The exact analytical results in terms of the generalized Bessel functions describe the effect of the periodic magnetic harmonics and of the angular effects and betatron oscillations in a wide beam; the Airy-type generalized functions describe the exact shape of the spectral line due to the non-periodic components. Coupled with the phenomenological FEL model, whose latest version is given in the Appendix A, we get the analytical description of the harmonic power evolution in FELs. Applications to a number of FEL experiments at SPRING8 Angstrom Compact free-electron LAser (SACLA) and Pohang Accelerator Laboratory X-ray Free electron Laser (PAL-XFEL) are provided and discussed in the context of other facilities, such as at Linac Coherent Light Source (LCLS) etc.
2. Spontaneous UR intensity and Spectrum Distortions
The ideal undulator assumes pure sinusoidal magnetic field along the axis. In the ideal planar undulator only odd harmonics are radiated on the axis. However, the radiation spectrum of real undulators and FELs differs from the ideal: even harmonics appear in FEL experiments [18,19,20,21,22]. This is attributed to the non-ideally harmonic magnetic field and finite beam size. Theoretical estimation for even FEL harmonics in the experiment [21] at Advanced Photon Source’s (APS) Low Energy Undulator Test Line (LEUTL) were based on the work [23]; however, they required the bunching values for the first and second harmonics, which in turn needed numerical simulations or theoretical calculations. Moreover, applying formulae of [21,23] to X-ray experiments, we systematically get harmonic powers ~25 times lower than those measured. To our best knowledge no convincing comprehensive theory has been provided thus far. In what follows we give analytical description of the synchrotron radiation from real electron beams in periodic magnetic fields of FEL undulators accounting for finite beam size and non-periodic magnetic components; the latter deviate electrons off the undulator axis. We demonstrate that this effect may exceed that of the finite size of the electron beam and that of the relevant betatron oscillations on the UR intensity. The UR, accounting for the magnetic field harmonics, has been recently studied, for example, in [24,25]. It was concluded that reasonably strong field harmonics, ○30% of the main periodic field, still mostly influenced the saturation and gain lengths in FELs and had little effect on the FEL harmonic intensities. In what follows we will focus on the effect of weak non-periodic magnetic components , . They are naturally caused by residual magnetic fields in undulators, magnetizing errors of constant magnets, by the field of the Earth, ~0.5 Gauss, and they are weak compared to the undulator field amplitude, H0~1 Tesla. The proposed analytical formalism, however, is not limited to such weak fields Hd/H0~10−4, but allows arbitrary strengths.
As usual in classical electrodynamics, the calculations of the radiation intensity from an electron consist in the computation of the radiation integral:
where the notations are common to SR and UR theories: is the unit-vector from the electron to the observer, is the electron radius-vector, is its velocity and c is the speed of light. For the sake of generality, we consider the radiation from an electron in the two-dimensional bi-harmonic multiperiodic field:
The account for the third field harmonic usually allows good reconstruction of the field for a given radiation pattern [26]. Not limiting ourselves to the third harmonic, the proposed analytical formalism allows field harmonics of arbitrary strength and order. The calculations go along the lines of [27]; the integrand and the exponential of the radiation integral (1) are expanded in series of the small parameter , which naturally arises in the relativistic limit because high-energy electron beams are used in FEL installations. For the two-dimensional field (2) proper formulae are much more cumbersome than in [27], but the approach remains the same: the non-oscillating terms in the exponential in (1) yield the resonances of the UR; their resonant wavelengths are expressed as follows:
where the account for the multiple periods of the undulator is given by , and the angle includes the usual off-axis angle θ and the effective bending angle θH, which describes the effect of the non-periodic magnetic components. The purely periodic terms in the exponential of the radiation integral are collected and form the generalized Bessel-type functions , which naturally arise in the following form:
where:
is the main undulator parameter, θ is the off-axis angle and φ is the azimuthal angle. We assume multiple field harmonics, l, h, p in (2). The additional constant magnetic field components , , can affect the undulator. In relativistic beams the longitudinal constant component can be neglected and the transversal field plays major role. It gives rise to non-periodic components [28,29,30] in the exponential of the radiation integral, such as , etc., where ; similar terms appear for the field harmonics, involving . The effect of the field Hd is accumulated along the undulator length , where N is the total number of periods, and quantified by the normalized bending angle θH:
Physically the constant magnetic field Hd bends the electron trajectory into the effective angle γθH and causes synchrotron radiation from much wider curve, than that of the electron oscillations along the undulator periods. However, its effect in long undulators should not be underestimated, as we will show in what follows. The non-periodic magnetic components in the exponential of the radiation integral compose the following ad-hoc generalized Airy-type function in the integral form:
where is the detuning parameter, describing the deviation of the frequency ω from the UR resonances ,
where for practical evaluations we can use . The special function S can be expressed as the action of the operational differential operators, also employed for the studies of Hermite and Laguerre families of orthogonal polynomials in [31,32,33]. The generalized multivariable Hermite polynomials:
were studied operationally by Srivastava et al. (see, for example, [34,35,36,37]). Exponential differential operators provide the link between S function (9) and function, which describes the shape of the ideal UR spectrum line. The generalization (9) in the non-periodic magnetic field can be given by the following operational relation:
The generalized Airy function S is related to the generalized three-variable Hermite polynomials as follows:
can be expressed as sums of the Hermite polynomials of two variables
are just another form of writing for common Hermite polynomials:
they have the following sum presentation [38]:
Hermite polynomials
possess the generating exponents:
On the undulator axis the second argument of the generalized Airy function S vanishes and simplifies:
The effect of the non-periodic magnetic field is quantified by the induced angle in β; the dependence on the off-axis angle θ is in η. The maximum values and explain why the coefficient 2 is grouped with ∂S/∂vn in (21). Upon computing the radiation integral we get the UR intensity:
where the intensity of the n-th UR harmonic reads as follows:
The generalized Airy function describes the shape of the spectrum line, distorted by the non-periodic magnetic field; the shape of the line for odd UR harmonics is given by function S, of the even harmonics—by . The Bessel coefficients give the amplitudes of proper UR harmonics x- and y-polarizations and are expressed in terms of the generalized Bessel functions (4) as follows:
Formulas (22)–(24) account for the off-axis angle θ and for the non-periodic magnetic field Hd, written in terms of the bending angle θH. For the odd UR harmonics n = 1,3,5,… mainly the Bessel coefficient determines the UR intensity (20). The resonance of the UR has an infrared shift respectively to the ideal value at vn = 0:
Interestingly, the effective angle and the off-axis angle θ can counteract each other’s effect on the radiation. The best compensation occurs for:
It follows from (26) that for . In the simplest case of one-dimensional magnetic field Hd = κH0, for we get the angle , in which the infrared shift of the received radiation is compensated: for ; proper UR resonances are . The examples of the UR lines for the PAL-XFEL [39] undulator with N = 194 periods, k = 1.87, period λu = 2.57 cm, length L = 5 m and the electron energy spread σe = 1.8 × 10−4, is shown in Figure 1a for γθ = 0 and Figure 1b for γθ ≠ 0 in the presence of the non-periodic magnetic component Hd. In Figure 1a, the field Hd causes an infrared shift and broadens the spectrum line, viewed in zero angle γθ = 0. In Figure 1b, note that the same field Hd can improve the shape of the spectrum line viewed in the angle γθ = 0.067. Note in Figure 1b as the initial detuning, caused by the off-axis angle γθ = 0.07, reduces if the undulator is affected by the field Hd = κH0~10−4H0; a further increase of κ broadens the UR line. For the on the axis case, γθ = 0, the effect of Hd is purely detrimental (see Figure 1a).
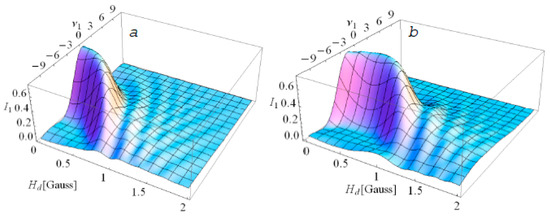
Figure 1.
The PAL-XFEL fundamental UR line shape as the function of the constant magnetic field Hy: (a)—on-the-axis case γθ = 0, (b) off-axis angle γθ = 0.067; the undulator has k = 1.87, period λu = 2.57 cm, length L = 5 m, N = 194 periods.
The effect of the off-axis angles, the constant magnetic field Hd and their interplay are also shown for the fundamental harmonic in Figure 2. In Figure 2a, the symmetric ideal UR line of the fundamental tone is described by the sinc(νn/2) function for γθ = 0, Hd = 0; it shows a red shift, if viewed in the angle γθ ≠ 0; the angles γθ > 0.1 cause a significant shift down from νn = 0 and the intensity slightly decreases.
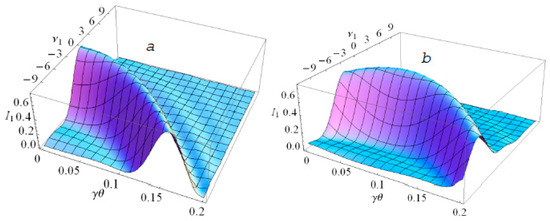
Figure 2.
The PAL-XFEL fundamental UR line shape as the function of the off-axis angle γθ; (a)—no constant magnetic component, κ = 0, (b)—in the presence of the constant magnetic component Hd = 0.5 Gauss; the undulator has k = 1.87, period λu = 2.57 cm, length L = 5 m, N = 194 periods.
The radiation line of the fundamental harmonic n = 1, viewed in the angle γθ ≈ 0.1, is slightly broadened and has red shift in −2π with respect to the resonance νn = 0 (see Figure 2a). In Figure 2b we demonstrate the spectral line of the fundamental tone, broadened and red-shifted in -π by the constant magnetic field H ≈ H0 × 10−4, if viewed on the axis, γθ = 0. In Figure 2b, the spectral line reassumes a more distinct shape with the increase of the off-axis angle γθ from zero to ~0.1. This demonstrates that the non-periodic magnetic component κH0 and the off-axis angle γθ can compensate each other’s effect on the UR. In the presence of the field Hd ≈ 10−4H0, the spectrum line gets narrower and the red shift is smaller for the same angles γθ ≈ 0.1 as shown in Figure 2b.
Our theoretical analysis and (22)–(24) in particular allow the analytical study of even UR harmonics. For the even harmonics the contributions from can be of the same order of magnitude; we distinguish and analyze separately the terms , factorized by S and in (21). Note the value . Upon the comparison of (24) with in (22), (23), we notice that the role of the angle in is formally the same as the role of the off-axis angle θ in , i.e., is involved in the same way as θ is involved in . Moreover, accounting for the factor in (24), we get similar numeric factors in the Bessel coefficients and : vs. . The latter is a typical off-axis term in (22), (23). The angle is induced by the field . In order to have noticeable effect, there must be ⟷0.05–0.1. In a long undulator, this angle can be generated by rather weak magnetic field Hd: for example, the bending angle can have noticeable effect on the FEL performance at LCLS, where the off-axis target deviation was 5 μm. LCLS undulator length, L = 3.4 m, is translated to the field strength H = 0.44 Gauss. The need to screen out such fields was pointed out in [18,19]. Moreover, at the PAL-XFEL the field of the Earth, ~0.5 Gauss, can induce the angle in the 5 m long undulator, and cause even stronger deviation of the electron trajectories.
The contributions to the intensity of the second harmonic of PAL-XFEL undulator is demonstrated in Figure 3, Figure 4 and Figure 5, where we have assumed the off-axis angle γθ = 0.1 and low energy spread σe = 10−4. The contribution to the second harmonic intensity due to the constant field κH0 (24) accounting for the off-axis angle θ is shown in Figure 3. The shape of the spectrum line is given by ∂S/∂vn. The term increases with the increase of the bending field Hd. The interplay with the angles γθ (see Figure 3b) limits the increase of and determines its behavior for the stronger field Hd > 1.5 × 10−4 Gauss. This latter value depends on γθ and on the undulator parameters; for θ = 0, the Bessel coefficient grows further for increasing κH0 (see Figure 3a).
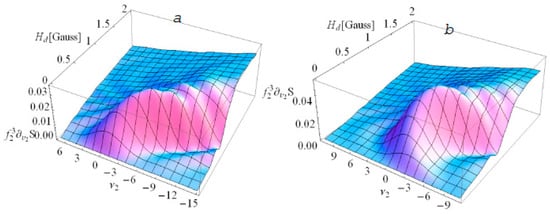
Figure 3.
The contribution of the constant magnetic field term to the UR line of the second UR harmonic, n = 2, of the PAL-XFEL undulator with k = 1.87, period λu = 2.57 cm, length L = 5 m, N = 194 periods: (a)—on the axis case, γθ = 0, (b)—the off-axis angle γθ = 0.067.
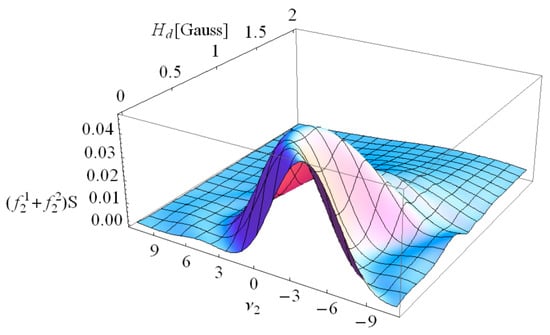
Figure 4.
The contribution of the terms and to the UR line of the second UR harmonic, n = 2, of the PAL-XFEL for the undulator with k = 1.87 period 2.57 cm, length 5 m, N = 194 periods, off-axis angle γθ = 0.067.
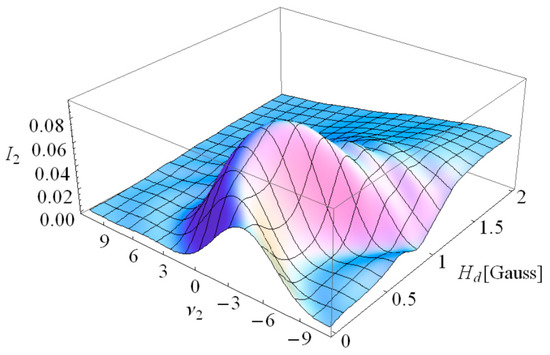
Figure 5.
The total contribution of all terms to the normalized intensity I2 of the harmonic n = 2 accounting for the functions S and , giving the line shape to 2nd UR harmonic of the PAL-XFEL undulator with k = 1.87, period λu = 2.57 cm, length L = 5 m, N = 194 periods for the off-axis angle γθ = 0.067.
The contributions of the terms for the second UR harmonic for γθ = 0.067 are shown in Figure 4; they decrease with the increase of the constant field strength κH0; the associated spectrum line shape is described by the function S. The comprehensive contribution of all terms to the normalized intensity of the second harmonic, I2, is shown in Figure 5; the maximum intensity is at Hd ≈ 0.7 × 10−4 Gauss. The decrease of the UR intensity, caused by γθ~0.067, is compensated by the field Hd ≈ 0.7 × 10−4 Gauss, and at this point, the second harmonic intensity is at its maximum.
The electron energy spread in the beam, σe, is accounted for by the convolution . The effect of the energy spread on the UR harmonics is purely detrimental and it causes symmetric broadening of the spectral lines. In this context it is important to underline that high radiation harmonics are more sensitive to the energy spread and to other loss factors, than the fundamental harmonic. Weak, but detectable at low energy spread, , FEL harmonics can be almost totally suppressed, if the energy spread increases to . The relevant example of SACLA radiation will be considered in what follows.
Eventually, let us evaluate the effect of the betatron oscillations in the finite width of the electron beam, where the electrons enter the undulator off the undulator axis. This topic has been in focus of researchers’ attention since the first accelerators were built in the middle of the 20th century. It is well described in various articles and books (see, for example, [9,40,41,42,43,44]). The field between the arrays of the planar undulator magnets is better approximated by the magnetic components , , which satisfy Maxwell equations in the whole gap between the magnets. The radiation in a two-frequency planar undulator with proper field was considered in [44]; rigorous calculations were explicitly presented there. For the multiharmonic undulator field (2), we follow the approach of [44]; cumbersome calculations do not differ in principle from those in [44]. The transversal oscillations of the electron in the finite sized beam are described by the betatron frequency in its usual form [44]:
where δ = 1 for the common planar undulator, for the bi-harmonic field and for the multiharmonic undulator field (2) we get . The betatron frequency ωβ (27) is much lower than the UR frequency ; their ratio is roughly the inverse of the relativistic factor: This explains the high interest to this topic already in early SR and UR experiments, where relatively low-energy electron beams were used and the contribution of the betatron oscillations was considerable. For the intensity of the UR harmonic n, accounting for the betatron oscillations, we get the following expression:
where are given by (22)–(24), and the Bessel functions:
depend on the arguments:
where y0 is the off-axis position of the electron in the beam and θ is off-axis angle. The summation series over p describe the account for all subharmonics p of the harmonic n. In real devices, finite number q of the subharmonics contribute: ; where q describes the degree of the split of the harmonic n and depends on the beam parameters; it varies strongly from one installation to another. Some examples will be considered in the following section, where we model some FEL experiments. The subharmonics are distant at the betatron frequency ωβ. In the relativistic beams, γ>>1, this split of the UR lines due to the betatron oscillations is small: . The even UR harmonics appear on the undulator axis due to the betatron oscillations [9,40,41,42,43,44]; proper Bessel coefficient expectably differs from that in [44] only in Bessel functions due to different undulator field (2):
where n is the number of the UR harmonic and p is the number of the betatron subharmonic. The physics and the approach with regard to the betatron oscillations remain the same for any undulator. For the bi-harmonic planar undulator , and the result (31) reduces to that in [44] in different notations. For the common planar undulator with single field harmonic , the Bessel functions in (31) reduce to (29), whose arguments are , . Quantitative evaluation of the Bessel coefficients shows that the contribution of the betatron oscillations is usually small: ~10−2, in comparison with other Bessel coefficients: ~0.15–0.8 in (22), (23); usually do not exceed . However, the split of the spectrum lines due to the betatron oscillations can be considerable and it strongly depends on the parameters of the installation and on the beam. Some examples are given in the context of the modeling of FELs in the following section. Beam sizes vary from ~0.2 mm to ~20 μm in modern FELs; beam deviations from the axis are usually small; for example, they are ~5–25 μm on one gain length, Lg = 1.6–3.5 m, in the LCLS FEL experiments [18,19,20]. However, the off-axis deviation of ultrarelativistic electrons in just ~10 μm in one undulator section length, ≅3 m, can cause the effective angle γθ~0.1 and noticeable effects. In what follows we will analyze in detail the harmonic generation in SACLA and PAL-XFELs and compare them with some other user facilities, such as LCLS.
3. Analysis of the Harmonic Generation in Some FEL Experiments
To calculate the harmonics in high gain FELs, we use the above obtained analytical results and the phenomenological FEL model (see the Appendix A). The latter is based on the Pierce parameter ρ [45,46,47,48,49,50], and it significantly develops the first approach in [51,52,53], applied with some modifications in [54,55,56,57,58,59,60]. The present formulation in contrast with [51,52,53] describes all losses separately for each FEL harmonic; it also includes the gradual dual-stage saturation and reproduces the oscillations of the saturated power, differently from that in [54,55,56,57,58,59,60]. Moreover, formulae (4)–(7), (22), (23) above in Section 2 in the limiting cases of the planar 2-frequency undulator correct the misprinted results in [54,55,56,57,58,59,60].
3.1. SACLA FEL Experiment
The SACLA facility first produced coherent radiation with 10 keV photons in 2011 [61]. User operations began in 2012; hard X-ray line BL2 was installed in 2014; soft X-ray line BL1 [62] and the dedicated accelerator SCSS+ were installed in 2014; further upgrades [63] followed, a new BL3 line was installed in 2017 for multiple beamline operation [64] with two-color XFEL and self-seeded XFEL [65]. However, contrary to exhaustive description of user facilities and generic specifications of the range of the parameters, in which SACLA operates, there has been little theoretical analysis of the FEL radiation in the experiments. Moreover, the information available on some instances of the operation of this FEL is incomplete and even controversial. In particular, this regards the electron beam energy spread, which is not stated for the hard X-ray SACLA setup in the papers [64,65,66,67,68] describing the facility. Rather complete data are available only for the undulators for the hard X-rays, commissioned [69] in 2012. As we understand, the facility was upgraded several times since then, but the data for the beam characteristics were not clearly reported. Moreover, for the same year 2012 we find the energy spread 10−4 and betatron value 30 m in [69], while in [61] we find the energy spread (in projection) <10−3 and βx,y = 22 m. One order of magnitude difference in the energy spread together with the change in β from 30 m to 22 m has very strong effect of the FEL radiation: the saturation length can vary from ~20 m to ~60 m, the saturated powers change etc.
Consider first the soft X-ray FEL; it operates with three undulator sections with variable parameter and a total of 777 periods, each λu = 1.8 cm long. The coherent radiation is generated at the fundamental λ~1–12 nm; the details are available in [62]. Despite explicit description, [62] does not contain any data on the power evolution, saturation and gain lengths, although the beam and radiation characteristics are well specified. We have studied the instance of this experiment with the maximum possible value of k = 2.1, the electron energy E = 780 MeV and beta-functions βx = 6 m, βy = 4 m [62]. The current I = 300 A was calculated by the authors of [62] for the bunch charge 0.23 nC and the bunch length τe≈0.7 ps (we get 330 A though). There is a great deal of uncertainty with regard to the values of the energy spread and the emittance; the energy spread per slice is not given, the projected value, σeprojected = 0.6%, is well too high as compared with other installations, such as LCLS [19] etc.; this lack of definite data for experiments also includes the emittance εnx,y: the reported data vary between 0.5–3 mm × mrad [62]. We suppose that most of it is in the projection that is due to transverse centroid shifts along the bunch and the time-sliced values after the injector are well preserved. Reassuming [62], we adopt the data simulation in Table 1, which yields the FEL power evolution, demonstrated in Figure 6.

Table 1.
Some simulation data for SACLA FEL experiment at λ = 12.4 nm at SPRING-8.
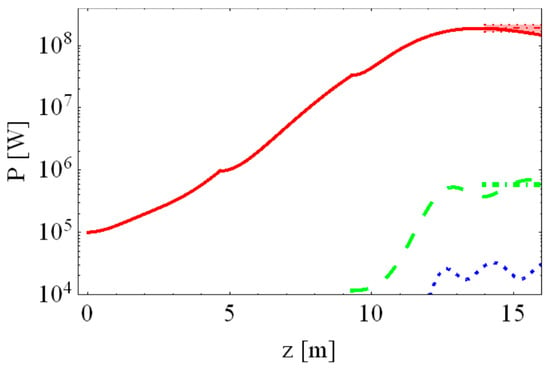
Figure 6.
Evolution of the harmonic power in the SACLA experiment for E = 780 MeV, λ1 = 12.4 nm, σe = 1.6 × 10−3, I0 = 300 A. The harmonics are color coded: n = 1—red solid, n = 3—green dashed, n = 5—blue dotted. The experimental values of the harmonic powers are denoted by the colored dot-dashed lines on the right.
The saturation occurs at the end of the final third undulator section of 4.5 m; we show the simulated FEL harmonic power, the measured energy of the fundamental tone after the third undulator in terms of power and the contribution of the third FEL harmonic, estimated at ~0.3% of the fundamental [62]. We have obtained the simulated value of the saturated fundamental FEL power (red line in Figure 6) P1 ≈ 0.2 GW, coinciding with the value = 0.2 GW, for the measured fundamental energy [62] Eγ ≈ 0.1 mJ ± 13% for the FEL radiation pulse duration = 0.5 ps, emitted from the electron bunch with the root mean square r.m.s. length τe = 0.7 ps. For the third FEL harmonic (see green dashed line in Figure 6) we get ≈0.3% power of the fundamental in agreement with [62]. Note that the second harmonic level is very low. The simulated gain length is Lg ≈ 1 m and the saturated length is Ls ≈ 13 m; other data are collected in Table 1.
The spectrum line contains only few subharmonics with p = −1, 0, +1; their contribution is shown in Figure 7 for off the axis distance.
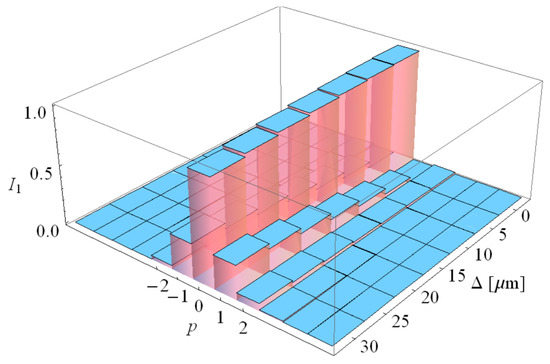
Figure 7.
Split of the fundamental radiation line λ = 12.4 nm for SACLA experiment, as a function of the distance Δ from the electron beam axis.
The main contribution evidently comes from three subharmonics p = [–1, 0, 1]; the respective radiation line width is Δλ/λ~2 × 10−3, comparable with the natural UR line width 1/2N ≈ 2 × 10−3. Theoretical estimation of the relative radiation line bandwidth in SASE FEL after the gain-narrowing in the exponential growth yields similar value ≈ 0.15%, close to the FEL scaling parameter ρ ≈ 0.0016 (see Table 1). Superposition of the randomly distributed over the length of the electron bunch wave trains with the coherence length ~6 μm gives the coherence time ~0.02 ps. The number of the coherence regions in the radiation pulse is therefore ~ 20.
We also modeled SACLA FEL radiation in a hard X-ray band. The results for the recent installation setup [64] are shown in Figure 8 and Figure 9. The electron energy was 10 times higher than in the soft X-ray experiment, and the radiation at the wavelength λ = 0.124 nm was generated. Some data for the simulations of SACLA FEL in hard X-ray region are given in Table 2.
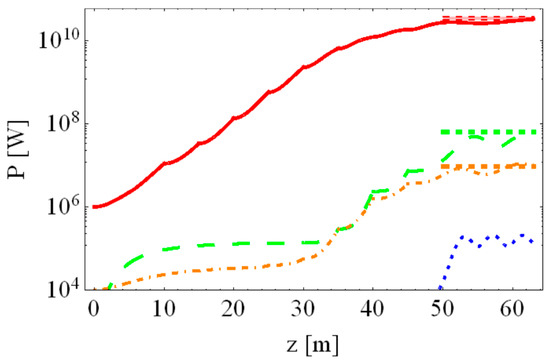
Figure 8.
Evolution of the harmonic power in the SACLA FEL experiment for E = 7800 MeV, λ1 = 0.124 nm, σe = 9.26 × 10−4, I0 = 10 kA. The harmonics are color coded: n = 1—red solid, n = 2—orange dot-dashed, n = 3—green dashed, n = 5—blue dotted. The experimental values of the harmonic powers are denoted by the colored dotted lines on the right.
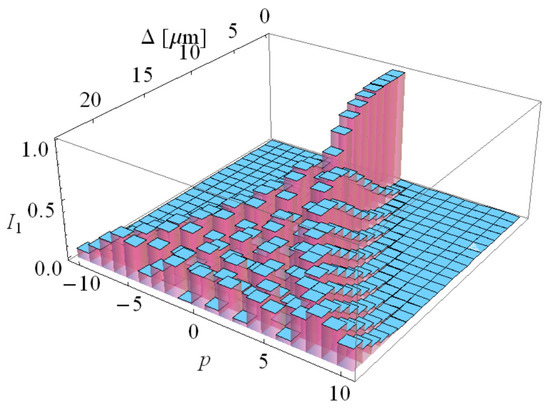
Figure 9.
Split of the fundamental spectrum line λ = 0.124 nm for SACLA BL3 line, as a function ofthe distance Δ from the electron beam axis.

Table 2.
Some simulation data for SACLA FEL experiment at λ = 0.124 nm at SACLA.
Omitting the details of the experiments and installation, which are described in [63,64,65,66,67,68], we note only that the SACLA facility has been continuously upgraded and the data on specific FEL experiments are incomplete (except for the early experiment [61]). For example, the electron beam energy spread for later SACLA setup and hard X-ray experiments is not mentioned in major papers [64,65,66,67,68]; we assumed for the simulation σe = 0.0926%, following [63], where the upgraded RF system of SPRING 8 was described. Considering that the beam was alternatively sourced to BL3 and BL2 undulator lines, and the above spread was reported for E = 6 GeV, we assume that the spread should not increase in the experiment with the energy E = 7.8 GeV on BL3 line and 10 keV photons. Of course, it depends on the spreader, the optics, on whether the dispersion was closed etc., thus, the experimental conditions can be different; however, in the absence of explicitly reported data, we have to assume the first approximation of the only available data from [63,65]. Our simulation results are collected in Table 2; the computed saturated power is compared with that obtained from the measured in this experiment photon energy, Eγ = 0.4–0.5 mJ, reported in [64] (see Figure 2c and Figure 3 in [64]).
With regards to the bunch length τe = 20 fs and charge Q = 0.2 nC, the current I = 10 kA, and other data [64], we get the photon pulse duration τγ≈13 fs, and the saturated powers of the fundamental and third harmonics as shown by the dashed lines after 50 m in Figure 8; they agree with our theoretical simulations. Horizontal dashed green and orange lines in the saturation region in Figure 8 trace the values 0.2% for the third and 0.03% for the second harmonics. Variation of the emittance, ±1 μm, and of energy spread, 0.08–0.1%, influences the gain and the saturation lengths and the third harmonic power; the fundamental power is less sensitive to it.
The radiation spectrum line is split in many subharmonics only at the extremities of the beam (see Figure 9 and Figure 10). The account for the subharmonics p = −5…+5 is sufficient everywhere, but for the maximum angles of electron–photon interaction at the beam edges (see Figure 10). Accounting for the split of the spectrum line in 11 subharmonics, p = −5…+5, we get the total contribution of the latter,, after averaging across the beam for all electron-photon interaction angles, close to unity: 0.97. Accounting for p = −6…+6 or more subharmonics yields even more precise results. The respective spectral width is 0.06–0.1%, the Pierce parameter ρ ≈ 0.07% and the coherence time τc~0.7 fs, which means that less than 20 coherence regions are in τγ ≈ 13 fs photon pulse.
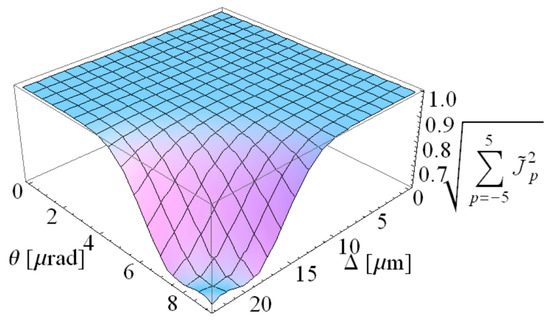
Figure 10.
Total contribution of 11 subharmonics with p = −5…+5, factorizing the Bessel factors fn as a function of the distance Δ from the electron beam axis and electron-photon interaction angle θ.
More data are available for similar experiment [61], conducted earlier at SACLA with the electron energy 7 GeV and the undulator with k = 1.8. The harmonic power evolution was clearly traced along the undulators and the harmonic saturated powers were measured. Omitting the details, we provide in Figure 11 the comparison between our analytical results and the measured data as reported in [61]. The third harmonic content was ~0.3% of the fundamental. The saturation began after 45 m and was obvious after ~50 m (see Figure 3 in [61]). The energy spread and emittance influence the gain and saturation lengths. Genuine simulations in [61] agreed fairly well with the experiment: the discrepancy in the harmonic powers at 25–55 m reached one order of magnitude, dependently on the assumed values for the simulation. We computed the saturation beginning at ~45 m, but the process of the saturation seems very gradual; we get full saturation at 55 m. Our analytical results arguably have an even better match with the experiment than the simulations of the authors in [61] and we reproduced the saturated power oscillations as shown in Figure 11. The third harmonic content also fits the measured range ~0.3% (see Figure 11).
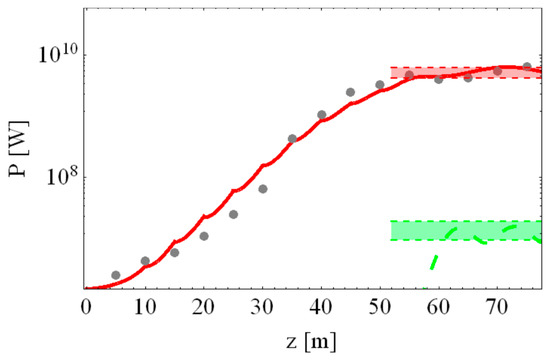
Figure 11.
Evolution of the harmonic power in the SACLA experiment for E = 7 GeV, λ1 = 0.124 nm, σe = 8.7 × 10−4, I0 = 3.5 kA, βx,y = 22 m, εn = 0.6π mm × mrad. The harmonics are color coded: n = 1—red solid, n = 3—green dashed. The experimental values of the harmonic powers are denoted by the dots and by colored areas on the right.
3.2. POHANG FEL X-ray Experiments
FEL experiments for soft and hard X-ray radiation were conducted at PAL-XFEL facility [39]; the fundamental wavelengths at λ = 1.52 nm and λ = 0.144 nm were generated. The experiments were well documented; among other data in [39] the harmonic power evolution was reported. We have analyzed the harmonic generation in both soft and hard X-ray experiments. Some modeling data are collected in Table 3 and Table 4. The results are presented in Figure 12, Figure 13 and Figure 14 and discussed below. The PAL-XFEL resembles in many aspects the LCLS FEL [19]. There is difference in higher energy spread in PAL-XFEL LINAC, also the undulator parameter k = 2 in the PAL-XFEL experiments was lower that k = 3.5 at LCLS; the electron beam had lower energy for the same generated wavelength. The soft X-ray radiation at λ1 = 1.52 nm was produced by the electrons with the energy E = 3 GeV and the energy spread (~five times higher than in LCLS), in the undulators with the total pure length ~40 m; the undulator parameter was k = 2. The hard X-ray radiation at λ1 = 0.144 nm was generated by the electrons with the energy E = 8 GeV (vs. E~13 GeV in LCLS) with the energy spread (~two times higher than in LCLS) in the undulators with the deflection parameter k = 1.87 (vs. k = 3.5 in LCLS) of the total pure length 100 m. The undulator sections were 5 m long.

Table 3.
Some simulation data for PAL-FEL experiment for soft X-rays, λ = 1.52 nm, E = 3 GeV.

Table 4.
Some simulation data for PAL-XFEL experiment for hard X-rays, λ = 0.144 nm, E = 8 GeV.
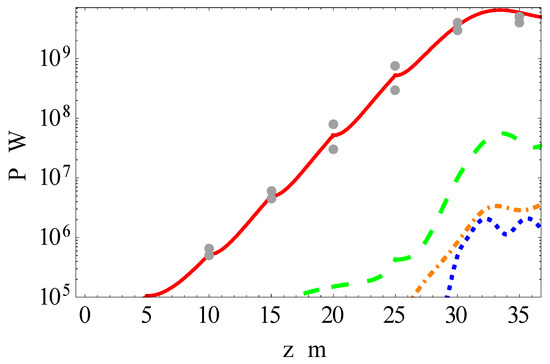
Figure 12.
The harmonic power evolution along the undulators at PAL-XFEL for soft X-rays, λ1 = 1.52 nm. The experimental average values are shown by dots, following the data in [39]. The harmonics are color coded: n = 1—red solid, n = 2—orange dot-dashed, n = 3—green dashed, n = 5—blue dotted.
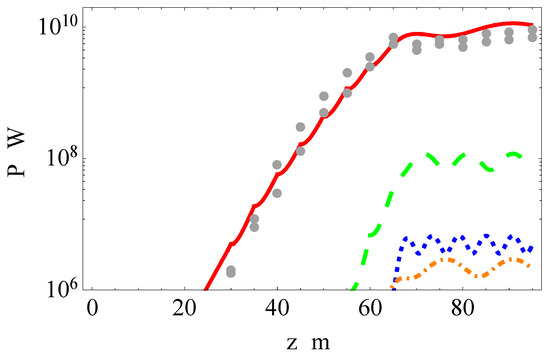
Figure 13.
The harmonic power evolution along the undulators at PAL-XFEL for hard X-rays, λ1 = 0.144 nm. The experimental average values are shown by dots, following the data in [39]. The harmonics are color coded: n = 1—red solid, n = 2—orange dot-dashed, n = 3—green dashed, n = 5—blue dotted.
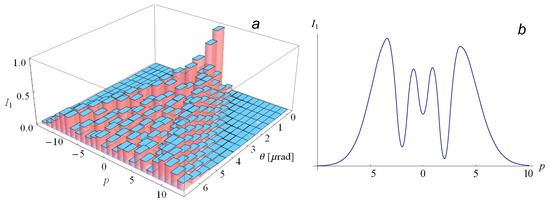
Figure 14.
Split of the fundamental spectrum line λ = 0.144 nm for PAL-XFEL experiment.
The UR in long undulators can be distorted due to non-periodic magnetic fields. The relevant study is presented in the previous section. Using the data from the experimental setup [39], we analytically obtained the evolution of the FEL power for the harmonics, as shown in Figure 12 for soft and Figure 13 for hard X-rays accounting for the beam size, divergences and other data. The results are compared with the measurements of the fundamental harmonic power in [39]. Our analytical modeling gives good match with the experiments (see Figure 12 and Figure 13). The agreement with the experiment for soft X-rays in the exponential growth is even better than that of the authors of [39]. Our analytical results for hard X-ray experiment agree fairly well with the measurements; however, the agreement is marginally better than that of the three-dimensional (3D) numerical simulations in [39]. This evidences the correct analytical account for all underlying physical phenomena.
No data are available for high harmonic generation in PAL-XFEL experiments. For soft X-rays, the energy spread was higher than in LCLS experiments for similar radiation wavelengths: . For the emittance we get pure value ε≅0.94 × 10−10 m to be compared with λ1/4π = 1.2 × 10−10 m. However, for the fifth harmonic we get λ5/4π = 2.5 × 10−11 m and ε≅ λ5/π = 1 × 10−10 m. The third harmonic could appear with the power rate ~0.7% of the fundamental, the second harmonic would have the power rate ~0.05%, as shown in Figure 12 and Figure 13. Our estimation for the third harmonic at PAL-XFEL in soft X-rays, ~0.7%, is roughly a half of that for a similar LCLS experiment, where ~1.3% for λ3 = 0.5 nm [20] with similar radiation parameters. Thus, we can expect some weaker third harmonic at PAL-XFEL due to the smaller value of the undulator parameter k as compared with LCLS; moreover, the detrimental effect of the energy spread is higher for PAL-XFEL, , as compared with that in LCLS, where . The second hard X-ray harmonic at PAL-XFEL is weak; high High harmonics were not registered in the PAL-XFEL experiments.
For hard X-rays the energy spread σe and Pierce parameters ρn are as follows: ,; the relations between σe and ρn are close to those for soft X-ray radiation. Moreover, for hard X-rays the comparison of the pure emittance ε ≅ 3.5 × 10−11 m with λ3/4π = 3.8 × 10−12 m is not favorable for the third harmonic radiation: εx,y ≅ 10 × λ3/(4π). Unsurprisingly, high hard X-rays harmonics were not detected. However, if the energy spread and emittances are improved, then we can expect at the PAL-XFEL high harmonic generation as suggested in Figure 12 and Figure 13. The off-axis deviation of the beam in PAL-XFEL amounted to ~10 μm on one undulator length [39]. This causes the off-axis angle ~2 μrad, comparable with the divergence, ~2 μrad for soft X-rays and ~1 μrad for hard X-rays. In the soft X-ray experiment the deviation of the beam in few undulator segments reached 20 μm on one undulator length [39]; this induces the angle 4 μrad. However, the electron-photon interaction on one gain length must be considered with the angle μrad, far exceeding the beam deviation. The latter angle causes the 2nd FEL harmonic, whose power is estimated ~10−4 of the fundamental (see Figure 12). For the hard X-ray experiment we get much smaller value μrad, and the beam must be kept on the axis more precisely.
The proposed analytical approach allows theoretical study of the spectral line split and width in the PAL-XFEL experiments. Following the developed in Section 2 theory, we compute the split of the soft X-ray spectral line and obtain the main contribution from the subharmonics with p = −4,…,+4; higher subharmonics are negligible. Thus the fundamental tone at λ1 = 1.5 nm is split in ~9 subharmonics. The total width of the line is Δλ~2.3 pm, the relative value is Δλ/λ~1.5 × 10−3. It is small, but it is higher than the respective value in the soft X-ray LCLS experiment, where Δλ/λ~5 × 10−4. For hard X-rays in PAL-XFEL we have to account for more subharmonics: p = −7,…,+7. Nevertheless, the line remains rather narrow even with account for this split; the subharmonics are close to each other because of the electrons are ultrarelativistic. The absolute width of the hard X-ray line is Δλ~0.14 pm and the relative width is Δλ/λ ≈ 1.0 × 10−3. Compared with the respective values in the LCLS experiment, Δλ/λ≈3 × 10−5, the spectrum lines for PAL-XFEL radiation appear wider by ~1–2 orders of magnitude.
The spectral width of the radiation depends on the position of the electrons in the beam. The split of the spectrum line for the hard X-ray radiation from the electrons at the outer extremity of the beam in PAL-XFEL experiment is demonstrated in Figure 14a. Observe that we must account for ~20 subharmonics for the radiation from the edges of the beam, while the theoretical line shape shown in Figure 14b.
We have modeled in a similar way other FEL experiments at other installations; in all the cases the results matched well with the measured data, and the analysis given above worked.
4. Conclusions
We have presented analytical formulation of the harmonic generation in FELs with multiperiodic magnetic fields accounting for the harmonic and constant field components and off-axis effects in undulators. We have obtained exact analytical expressions for the Bessel coefficients in the general case of the multiperiodic elliptic undulator; they account for constant magnetic constituents, finite beam size and off-axis angles, and describe harmonic generation in wide electron beams and in high precision undulators, where fine alignment of narrow beams is required.
The Bessel coefficients for the general elliptic undulator and in its limiting cases of the elliptic and planar undulators with harmonics are provided. The effect of the constant non-periodic magnetic field on the UR line shape is formulated in terms of the generalized Airy function. The corrections for the Bessel coefficients, accounting for the constant magnetic components, off-axis radiation and beam position are given in the analytical integral form of generalized Bessel and Airy functions. The analysis shows that the relevant effects matter for the field-induced and off-axis angles γθ > 0.05. Exact analytical formulae for quantitative calculations of the UR are given in Section 2. Due to the betatron oscillations the UR lines are split in subharmonics; the split is very fine and for relativistic beams the subharmonics are very close to each other: δλ/λ~1/γ<<1. Despite that, it causes noticeable broadening of the spectrum lines. The contribution of the betatron oscillations to the even harmonic generation is one–two orders of magnitude less than that caused by the off-axis and photon-electron interaction angles in real beams.
We have demonstrated theoretical spectrum lines of UR harmonics, their shapes and intensities with the help of the developed theoretical tools. The effect of the non-periodic field and off-axis effects in finite sized beams are clearly distinguished and elucidated in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5.
The obtained rigorous theoretical results are employed for FEL radiation studies with the help of the phenomenological FEL model. We have analyzed the PAL-XFEL experiment at POHANG laboratory [60], where soft and hard X-rays were produced. Our analytical results are in good agreement with the reported values (see Figure 12 and Figure 13). We have modeled possible FEL harmonic behaviors accounting for the beam sizes, divergences, electron-photon interaction angles, energy spread and diffraction; the second harmonic would be very weak, in particular, for hard X-rays. The spectral line in hard X-ray experiment is split in ~15 subharmonics; despite that, we get quite narrow line, Δλ/λ~1.0 × 10−3, Δλ~0.14 pm due to γ~1500 >> 1. However, this is >10 times wider than in the LCLS experiment at the same wavelength, where Δλ/λ ≈ 3 × 10−5. The radiation of high harmonics at PAL-XFEL is limited by a rather high energy spread: for hard X-rays , the Pierce parameters for the n = 1,2,3,5 harmonics are , , , ; for soft X-rays the energy spread is , and the Pierce parameters are , , , . We have demonstrated possible theoretical harmonic radiation at PAL-XFEL; however, due to relatively high energy spread, we can hardly expect radiation of the harmonics higher than the third.
The analysis of the SACLA facility reveals the spectrum and power evolution for the undulator line BL3 with two different designs and k = 1.8 and k = 2.1 with respective electron energies 7 GeV and 7.8 GeV. The modeling for the 7 GeV agrees with the experiment; the modeling for 7.8 GeV gives the prediction of the harmonic evolution in the absence of the measured data. The saturated harmonic powers in all cases agree with those measured. The theoretical spectrum line split is demonstrated for the soft and hard X-rays for the lines BL1 and BL3; the radiation line at 0.124 nm is split is >±5 subharmonic, the spectrum line λ = 12.4 nm at BL1 is split in three subharmonics. The spectrum lines at SACLA are narrower than at PAL-XFEL.
The results, obtained with the help of the developed theoretical formalism for FEL power and spectrum evaluation agree with the experiments in X-ray and other bands. The analytical formulae are relatively simple and the relevant calculations do not require special knowledge and programmer skills; they can be done on any PC. The predictions are accurate and agree with the measurements. This allows the theoretical study of current and planned FEL experiments and estimation of performance, spectrum and harmonic generation in operating and constructed FELs.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to Professor A. Borisov and Leading Researcher A. Lobanov for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Phenomenological Model of Harmonic Power Evolution in High-Gain FELs
The Pierce parameter ρn reads accounting for the diffraction as follows [3,4,5,6,23,45,46,47,48,49,50,51,52,53]:
where n is the harmonic number, [A/m2] is the current density, is the beam section, are the sizes of the beam, are the emittances, are the betatron average values, are the divergences, is the constant of Alfven current [A], (see (3) for ) is the effective undulator parameter, which reduces for the common planar undulator to , is the magnetic field amplitude on the undulator axis, is the Bessel factor for the n-th UR harmonic. The Bessel factors fn in the general case of the two-dimensional field with harmonics (2) are given by (22)–(24) and (31) accounting for the finite beam size effects and constant magnetic components, which cause even harmonics. We assume the fundamental harmonic is not suppressed and it dominates. The saturated n-th harmonic power can be calculated accounting for the loss factors following [53]: , where is the beam power, I0 is the beam current [A], E is the electron energy [eV], ρ1 is the Pierce parameter. The gain length for the n-th harmonic is , where is the undulator period, Φn ηn are the loss factors. For the fundamental tone we denote ; the fundamental tone saturation length is .
The correction factors phenomenologically describe major losses as follows:
The coefficient ζ in (A2) is calculated by the cumbersome formula, involving the betatron parameters (see [24,53]); in matched beam, , and this correction is small. In X-ray FELs, it is even smaller: and often ζ = 1. The beam diffraction lowers the Pierce parameter value ρn; the beam energy spread and the emittances prolong the gain and reduce the saturated powers for harmonics. For stable FEL amplification, weak conditions σe○ρn/2, εx,y○λn/4π should be fulfilled (see, for example, [3,4,5,6,23,45,46,47,48,49,50]); however, failure to satisfy them exactly, especially in X-ray band, does not mean these harmonics will not be radiated at all.
For the harmonic power evolution in the initially unbunched electron beam, we use formula [53]:
where we ad-hoc introduce to describe the saturated FEL power oscillations. The match with FEL experiments appears good, as seen in Figure 11, Figure 12 and Figure 13. In cascaded FELs, the previous cascade feeds the next cascade with the prebunched beam. Even in the case the radiation on the n-th harmonic is suppressed for some reason, the initial power of the n-th UR harmonic can be provided by the bunching, , which is induced by the dominant harmonic and . The fundamental tone induces the bunching [48] where . If the fundamental tone is suppressed, the dominant harmonic induces its sub-harmonics (see [15,16]). The independent harmonic power evolution in the cascade is described by the following formula [53]:
We have revaluated the contribution of the initial shot noise in the self-amplified spontaneous emission (SASE) FEL with respect to all earlier works; fitting with available measurements from many FELs on average yields:
The dominant FEL harmonic (usually the fundamental) generates subharmonics in nonlinear regime: the harmonic powers then grow as the n-th power of the dominant harmonic [23,45,46,47,48,49,50]. The electron-photon interaction at high harmonic wavelengths is more sensitive to losses than that at the fundamental wavelength. Improving the phenomenological description in [12,13,14,15,16] and other earlier works, we now describe gradual harmonic saturation by two terms:
where the bunching is induced by the fundamental harmonic with the initial power P0,1, the n-th harmonic in nonlinear generation begins to saturate at the power level and saturates with oscillations around the power . In an elliptic undulator two polarizations are radiated and the effective Pierce parameter is modified accordingly (see, for example, [16]). The above analytical model of the FEL harmonic power evolution describes independent and induced harmonic contributions, multistage harmonic saturation, power oscillations, all major losses and different sensitivity of the photon-electron interaction at different harmonic wavelengths; it agrees with the available results of FEL experiments in a wide range of conditions and radiated wavelengths.
References
- Ginzburg, V.L. On the radiation of microradiowaves and their absorbtion in the air. Isvestia Akad. Nauk. SSSR (Fizika) 1947, 11, 1651. [Google Scholar]
- Motz, H.; Thon, W.; Whitehurst, R.N.J. Experiments on radiation by fast electron beams. Appl. Phys. 1953, 24, 826. [Google Scholar] [CrossRef]
- McNeil, B.W.J.; Thompson, N.R. X-ray free-electron lasers. Nat. Photonics 2010, 4, 814. [Google Scholar] [CrossRef]
- Pellegrini, C.; Marinelli, A.; Reiche, S. The physics of X-ray free-electron lasers. Rev. Mod. Phys. 2016, 88, 015006. [Google Scholar] [CrossRef]
- Schmüser, P.; Dohlus, M.; Rossbach, J.; Behrens, C. Free-Electron Lasers in the Ultraviolet and X-ray Regime. In Springer Tracts in Modern Physics; Springer: Cham, Switzerland, 2014; Volume 258. [Google Scholar]
- Huang, Z.; Kim, K.J. Review of X-ray free-electron laser theory. Phys. Rev. ST-AB 2007, 10, 034801. [Google Scholar] [CrossRef]
- Margaritondo, G.; Ribic, P.R. A simplified description of X-ray free-electron lasers. J. Synchrotron Rad. 2011, 18, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Margaritondo, G. Synchrotron light: A success story over six decades. Riv. Nuovo Cim. 2017, 40, 411–471. [Google Scholar]
- Bagrov, V.G.; Bisnovaty-Kogan, G.S.; Bordovitsyn, V.A.; Borisov, A.V.; Dorofeev, O.F.; Ya, E.V.; Pivovarov, Y.L.; Shorokhov, O.V.; Zhukovsky, V.C. Synchrotron Radiation Theory and Its Development; Bordovitsyn, V.A., Ed.; Word Scientific: Singapore, 1999; p. 447. [Google Scholar]
- Margaritondo, G. Characteristics and Properties of Synchrotron Radiation. In Synchrotron Radiation; Mobilio, S., Boscherini, F., Meneghini, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Dattoli, G.; Ottaviani, P.L. Semi-analytical models of free electron laser saturation. Opt. Commun. 2002, 204, 283–297. [Google Scholar] [CrossRef]
- Zhukovsky, K.; Kalitenko, A. Phenomenological and numerical analysis of power evolution and bunching in single-pass X-ray FELs. J. Synchrotron Rad. 2019, 26, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Zhukovsky, K.; Kalitenko, A. Analysis of harmonic generation in planar undulators in single-pass free electron lasers. Russ. Phys. J. 2019, 61, 153–160. [Google Scholar]
- Zhukovsky, K.; Kalitenko, A. Phenomenological and numerical analysis of power evolution and bunching in single-pass X-ray FELs. Erratum. J. Synchrotron Rad. 2019, 26, 605–606. [Google Scholar] [CrossRef] [PubMed]
- Zhukovsky, K. Two-frequency undulator in a short SASE FEL for angstrom wavelengths. J. Opt. 2018, 20, 095003. [Google Scholar] [CrossRef]
- Zhukovsky, K. Analysis of harmonic generation in planar and elliptic bi-harmonic undulators and FELs. Results Phys. 2019, 13, 102248. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Analytical Description of Nonlinear Harmonic Generation Close to the Saturation Region in Free Electron Lasers. Mosc. Univ. Phys. Bull. 2019, 74, 480–487. [Google Scholar] [CrossRef]
- Emma, P. First lasing of the LCLS X-ray FEL at 1.5 Å. In Proceedings of the PAC09, Vancouver, BC, Canada, 4–8 May 2009. [Google Scholar]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ratner, D.; Brachmann, A.; Decker, F.J.; Ding, Y.; Dowell, D.; Emma, P.; Frisch, J.; Huang, Z.; Iverson, R.; Krzywinski, J.; et al. Second and third harmonic measurements at the linac coherent light source. Phys. Rev. ST-AB 2011, 14, 060701. [Google Scholar] [CrossRef]
- Biedron, S.G.; Dejusa, R.J.; Huanga, Z.; Miltona, S.V.; Sajaeva, V.; Berga, W.; Borlanda, M.; den Hartoga, P.K.; Erdmanna, M.; Fawleyc, W.M.; et al. Measurements of nonlinear harmonic generation at the Advanced Photon Source’s SASE FEL. Nucl. Instrum. Meth. Phys. Res. 2002, 483, 94–100. [Google Scholar] [CrossRef]
- Milton, S.V.; Gluskin, E.; Arnold, N.D.; Benson, C.; Berg, W.; Biedron, S.G.; Borland, M.; Chae, Y.C.; Dejus, R.J.; den Hartog, P.K.; et al. Exponential Gain and Saturation of a Self-AmpliÞed Spontaneous Emission Free-Electron Laser. Science 2011, 292, 2037–2041. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Nonlinear Harmonic Generation of Coherent Amplification and Self-Amplified Spontaneous Emission. Nucl. Instr. Meth. 2001, 475, 112. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Effect of the 3rd undulator field harmonic on spontaneous and stimulated undulator radiation. J. Synchrotron Rad. 2019, 26, 1481–1488. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Generation of UR Harmonics in Undulators with Multiperiodic Fields. Russ. Phys. J. 2019, 62, 1043–1053. [Google Scholar] [CrossRef]
- Alexeev, V.I.; Bessonov, E.G. On some methods of generating circularly polarized hard undulator radiation. Nucl. Instr. Meth. 1991, 308, 140. [Google Scholar]
- Dattoli, G.; Mikhailin, V.V.; Ottaviani, P.L.; Zhukovsky, K. Two-frequency undulator and harmonic generation by an ultrarelativistic electron. J. Appl. Phys. 2006, 100, 084507. [Google Scholar] [CrossRef]
- Zhukovsky, K. Analytical account for a planar undulator performance in a constant magnetic field. J. Electromagn. Waves Appl. 2014, 28, 1869–1887. [Google Scholar] [CrossRef]
- Dattoli, G.; Mikhailin, V.V.; Zhukovsky, K. Undulator radiation in a periodic magnetic field with a constant component. J. Appl. Phys. 2008, 104, 124507-1–124507-8. [Google Scholar] [CrossRef]
- Dattoli, G.; Mikhailin, V.V.; Zhukovsky, K.V. Influence of a constant magnetic field on the radiation of a planar undulator. Mosc. Univ. Phys. Bull. 2009, 64, 507–512. [Google Scholar] [CrossRef]
- Zhukovsky, K.; Srivastava, H. Operational solution of non-integer ordinary and evolution-type partial differential equations. Axioms 2016, 5, 29. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Solving evolutionary-type differential equations and physical problems using the operator method. Theor. Math. Phys. 2017, 190, 52–68. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Operational solution for some types of second order differential equations and for relevant physical problems. J. Math. Anal. Appl. 2017, 446, 628–647. [Google Scholar] [CrossRef]
- Dattoli, G.; Srivastava, H.M.; Zhukovsky, K.V. Orthogonality properties of the Hermite and related polynomials. J. Comput. Appl. Math. 2005, 182, 165–172. [Google Scholar] [CrossRef]
- Dattoli, G.; Srivastava, H.M.; Zhukovsky, K. Operational Methods and Differential Equations with Applications to Initial-Value problems. Appl. Math. Comput. 2007, 184, 979–1001. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. The operational solution of fractional-order differential equations, as well as Black-Scholes and heat-conduction equations. Mosc. Univ. Phys. Bull. 2016, 71, 237–244. [Google Scholar] [CrossRef]
- Zhukovsky, K. Operational Approach and Solutions of Hyperbolic Heat Conduction Equations. Axioms 2016, 5, 28. [Google Scholar] [CrossRef]
- Gould, H.W.; Hopper, A.T. Operational formulas connected with two generalizations of Hermite polynomials. Duke Math. J. 1962, 29, 51–63. [Google Scholar] [CrossRef]
- Kang, H.-S.; Chang-Ki, M.; Hoon, H.; Changbum, K.; Haeryong, Y.; Gyujin, K.; Inhyuk, N.; Soung, Y.B.; Hyo-Jin, C.; Geonyeong, M.; et al. Hard X-ray free-electron laser with femtosecondscale timing jitter. Nat. Photonics 2017, 11, 708–713. [Google Scholar] [CrossRef]
- Alferov, D.F.; Bashmakov Yu, A.; Bessonov, E.G. Undulator radiation. Sov. Phys. Tech. Phys. 1974, 18, 1336. [Google Scholar]
- Alferov, D.F.; Bashmakov, U.A.; Cherenkov, P.A. Radiation from relativistic electrons in a magnetic undulator. Usp. Fis. Nauk. 1989, 32, 200. [Google Scholar]
- Vinokurov, N.A.; Levichev, E.B. Undulators and wigglers for the production of radiation and other applications. Phys. Usp. 2015, 58, 917–939. [Google Scholar] [CrossRef]
- Dattoli, G.; Renieri, A.; Torre, A. Lectures on the Free Electron Laser Theory and Related Topics; World Scientific: Singapo, 1993. [Google Scholar]
- Prakash, B.; Huse, V.; Gehlot, M.; Mishra, G.; Mishra, S. Analysis of spectral properties of harmonic undulator radiation of anelectromagnet undulator. Optik 2016, 127, 1639–1643. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. The Physics of Free Electron Lasers; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373. [Google Scholar] [CrossRef]
- Bonifacio, R.; De Salvo, L.; Pierini, P. Large harmonic bunching in a high-gain free-electron laser. Nucl. Instrum. A 1990, 293, 627. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Three-dimensional analysis of harmonic generation in high-gain free-electron lasers. Phys. Rev. E 2000, 62, 7295. [Google Scholar] [CrossRef] [PubMed]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Study of a noise degradation of amplification process in a multistage HGHG FEL. Opt. Commun. 2002, 202, 169–187. [Google Scholar] [CrossRef]
- Shatan, T.; Yu, L.-H. High-gain harmonic generation free-electron laser with variable wavelength. Phys. Rev. E 2005, 71, 046501. [Google Scholar] [CrossRef] [PubMed]
- Dattoli, G.; Giannessi, L.; Ottaviani, P.L.; Ronsivalle, C. Semi-analytical model of self-amplified spontaneous-emission free-electron lasers, including diffraction and pulse-propagation effects. J. Appl. Phys. 2004, 95, 3206–3210. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Nonlinear harmonic generation in high-gain free-electron lasers. J. Appl. Phys. 2005, 97, 113102. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Booklet for FEL Design; ENEA Pubblicazioni: Frascati, Italy, 2007. [Google Scholar]
- Zhukovsky, K.V. Generation of Coherent Radiation in the Near X-ray Band by a Cascade FEL with a Two-Frequency Undulator. Mosc. Univ. Phys. Bull. 2018, 73, 364–371. [Google Scholar] [CrossRef]
- Zhukovsky, K. Compact single-pass X-ray FEL with harmonic multiplication cascades. Opt. Commun. 2018, 418, 57–64. [Google Scholar] [CrossRef]
- Zhukovsky, K. Soft X-ray generation in cascade SASE FEL with two-frequency undulator. EPL 2017, 119, 34002. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Generation of X-Ray Radiation in Free-Electron Lasers with Two-Frequency Undulators. Russ. Phys. J. 2018, 60, 1630–1637. [Google Scholar] [CrossRef]
- Zhukovsky, K. Generation of coherent soft X-ray radiation in short FEL with harmonic multiplication cascades and two-frequency undulator. J. Appl. Phys. 2017, 122, 233103. [Google Scholar] [CrossRef]
- Zhukovsky, K. High-harmonic X-ray undulator radiation for nanoscale-wavelength free-electron lasers. J. Phys. D 2017, 50, 505601. [Google Scholar] [CrossRef]
- Zhukovsky, K.; Potapov, I. Two-frequency undulator usage in compact self-amplified spontaneous emission free electron laser in Roentgen range. Laser Part. Beams 2017, 35, 326. [Google Scholar] [CrossRef]
- Tetsuya, I.; Hideki, A.; Takao, A.; Yoshihiro, A.; Noriyoshi, A.; Teruhiko, B.; Hiroyasu, E.; Kenji, F.; Toru, F.; Yukito, F.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar]
- Owada, S.; Togawa, K.; Inagaki, T.; Hara, T.; Tanaka, T.; Joti, Y.; Koyama, T.; Nakajima, K.; Ohashi, H.; Senba, Y.; et al. Soft X-ray free-electron laser beamline at SACLA: The light source, photon beamline and experimental station. J. Synchrotron Rad. 2018, 25, 282–288. [Google Scholar] [CrossRef]
- Ego, H. RF system of the SPring-8 upgrade project. In Proceedings of the IPAC2016, Busan, Korea, 8−13 May 2016. [Google Scholar]
- Tono, K.; Hara, T.; Yabashi, M.; Tanaka, H. Multiple-beamline operation of SACLA. J. Synchrotron Rad. 2019, 26, 595–602. [Google Scholar] [CrossRef]
- Ichiro, I. Generation of narrow-band X-ray free-electron laser via reflection self-seeding. Nat. Photonics 2019, 13, 319–322. [Google Scholar]
- Tono, K.; Togashi, T.; Inubushi, Y.; Sato, T.; Katayama, T.; Ogawa, K.; Ohashi, H.; Kimura, H.; Takahashi, S.; Takeshita, K.; et al. Beamline, experimental stations and photon beam diagnostics for the hard X-ray free electron laser of SACLA. New J. Phys. 2013, 15, 083035. [Google Scholar] [CrossRef]
- Yabashi, M. Overview of the SACLA facility. J. Synchrotron Rad. 2015, 22, 477–484. [Google Scholar] [CrossRef]
- Yabashi, M.; Tanaka, H.; Tono, K.; Ishikawa, T. Status of the SACLA Facility. Appl. Sci. 2017, 7, 604. [Google Scholar] [CrossRef]
- Takashi, T.; Shunji, G.; Toru, H.; Takaki, H.; Haruhiko, O.; Kazuaki, T.; Makina, Y.; Hitoshi, T. Undulator commissioning by characterization of radiation in X-ray free electron lasers. Phys. Rev. ST-AB 2012, 15, 110701. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).