Abstract
Creative digital artwork is usually the outcome of a long period of intellectual creation and labor of an artist. Similarly, computer-created digital artwork is an outcome of a large amount of machine time and computational resources. However, such intellectual properties can be easily copied by illegal users. Copyright protection of digital art is increasingly more important than before. Recently, using a computational approach to generate string art tends to be popular and attractive. To protect the illegal usage of the digital form of string art, we propose a data hiding algorithm specifically designed for string art. A digital string art image consists of a sequence of string lines, each specified by two nails fixed at the two ends of that line. The encrypted secret data (the watermark) is embedded into the list of line segments by odd–even modulation, where a bit ‘1’ is embedded by forcing the next node to be an odd node, and a bit ‘0’ is embedded by forcing the next node to be an even node. To minimize the impact of data embedding on the quality of the original string art image, a local optimization algorithm is developed to select the nodes that produce minimal distortion. To quantify the embedding distortion, we introduce a smoothing filter model for the human vision system (HVS) specifically tailored to string art image. Experimental results show that using the proposed algorithm, the distortion between the original string art image and the watermarked string art image is unnoticeable. The modified string art image is statistically indistinguishable from the original string art, and hence is secure under steganalysis. To our best knowledge, this is the first work towards data hiding and copyright protection of digital string art.
1. Introduction
String art is a new form of abstract art that employs strings to render a natural image or simple patterns [1,2]. It was first proposed by artist Petros Vrellis in 2016 [3], who uses a private algorithm to generate monochrome and color string art. The first work on using a computer algorithm to generate string art was published in 2018 by M. Birsak et al. They designed and published an optimization algorithm to generate string art from a given digital image [4]. However, their manufacturing machine is an industry robotic arm that is not accessible to the general public. In 2019, S. Je et al. designed a low-cost fabrication machine and a spider-web-inspired algorithm to generate string art images. In addition to its artistic value, the generation process of the string art is very useful for studying the fabrication process. In 2020, I. Ostanin applied the string art to the design and manufacturing of composite materials and structures [5]. The manufactured string art can be used for interior and public space decoration. Furthermore, the manufacturing process using a robotic arm is very attractive for showing to the general public what a robotic arm can do in a public exhibition [6].
Both the design process and the manufacturing process of string art images are time-consuming. A completed string art is an accumulation of a large amount of creative work and labor, and hence is intellectual property. To protect it from illegal copying and usage, the creator or the owner of the digital art may need to embed his personal identification information into it before releasing to public. The same concern may be raised after the string art is extended to composite material design [5], since these composite materials are usually protected by laws of intellectual property right. Data hiding and watermarking have been shown to be a very powerful tool to protect the copyright of digital multimedia works [7].
Data hiding in multimedia signals has been developed for more than three decades [7,8,9,10]. Starting from the digital image, the type of host (to which the data are embedded) signal was extended to video, speech, audio, 3D mesh model and point clouds, etc. [11,12,13,14,15]. For the general data hiding problem, embedding rate and embedding distortion are two major performance metrics. According to application requirements, two types of systems can be adopted: irreversible data hiding and reversible data hiding [16]. For irreversible data hiding, secret data are embedded into host signal by irreversible operations such as addition (such as spread spectrum approach) [17,18,19,20], or quantization (such as quantization index modulation) [21,22,23,24]. Reversible watermarking explores the inherent redundancy in multimedia signals [25,26]: space/time correlation, entropy redundancy, etc., to find room for hiding extra data. This technique is further extended to encrypted images and secret sharing, hence is applicable to cloud storage and cloud computing [27,28,29,30].
However, all these available data hiding algorithms cannot be directly used for string art images. While existing digital multimedia signals use pixels/voxels as basic elements [31], the string art image uses overlapped line segments as basic elements [4]. The relationship between the line elements and the rendered image is more complicated than digital images. Thus, controlling the embedding distortion for string art images is a challenging problem. To our best knowledge, currently there are no data hiding algorithms developed specifically for this type of host signal.
The contributions of our work can be summarized and highlighted as follows:
- This work is the first work addressing data hiding in string art images for copyright protection and secure communication.
- In order to minimize embedding distortion, a data hiding framework by odd–even modulation on node histogram is proposed, which gives sufficient freedom in choosing a string segment pair to modify.
- Four data embedding algorithms are designed in the proposed framework, in an effort to minimize the embedding distortion at low computational complexity.
This paper is organized as follows. Section 2 introduces the data structure of string art image. The embedding and extraction algorithms are described in Section 3. Experiments are discussed in Section 4. Finally, we conclude this paper in Section 5.
Notation: Unless otherwise stated, scalars are denoted as lower-case letters, such as a variable n. Vectors and matrices are represented as low-case and upper-case boldface letters, respectively, such as a vector and a matrix . Functions that operate on an entire image are represented as calligraphic form, such as operators and . Set is represented in upper case San-serif font, such as a set .
2. The Digital String Art
A string art image is usually formed by passing a string through an array of nails fastened on a wooden plate. There are other variations of this basic form. For example, the nails can be replaced by teeth-shaped ends carved from an acrylic sheet [32]. Depending on whether the nails are regularly spaced or irregularly spaced, the string art can be classified into two types.
- Regularly Spaced Nails. For this type, the nails are regularly spaced on a wooden plate. The most popular arrangement of the nail positions is to put the nails on a circle. This will be the focus of our work. Other regular arrangements of nails are also possible, for example, by placing nails on a two-dimensional grid.
- Irregularly Spaced Nails. To better render the original image, the feature of the original image should be used to guide the placement of the nails. For example, in regions with more texture or structure, more nails should be placed.
2.1. Data Structure for Digital String Art Images
Before fabricating the digital string art image into a real string art, the digital string art image is stored in a text file. Unlike the ordinary digital image where the pixels are stored as a matrix, a string art image is stored as a sequence of line segments, connected heads to tails. For a string art image with N nodes and L line segments, we have L rows and two columns, as illustrated in Table 1. A toy example of the data structure for string art image is shown in Figure 1a. The corresponding string art image is rendered as shown in Figure 1b.

Table 1.
Data structure for string art image.
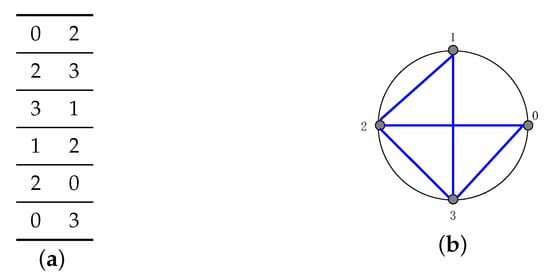
Figure 1.
Rendered string art image for a toy example. (a) Data structure, and (b) rendered result.
Each line segment starts from node and ends at , where and are two node numbers. Let be the set of node indices, then , and in general . To make the line segments connected sequentially, the ending point of line segment i must be the starting point of the next line segment, i.e., . The node is called the joint of two line segments and .
For convenience, we will use a matrix to record this data structure. Each row of this matrix corresponds to one row of Table 1. So we have and , for all . Since this matrix has the same structure as a string art file, we will use the term string art to denote either the file or the data structure as a matrix.
To describe our algorithm, we need to fix the following terms and notations.
- Node: A node of a string art image corresponds to one of the nails fastened at the edge of the circular plate. Each node is specified by its index number .
- Segment: A line segment is determined by two nodes. For example, for a line segment starting at node m and ending at node n, it is denoted as .
- Joint: A joint is a common node shared by two adjacent line segments. For example, for two line segments and , the node n is a joint between them. For example, the node 2 is a joint for line segments and .
- Segment pair: Two line segments connected by a joint. For example, a segment pair formed by lines and is denoted as .
3. Data Hiding by Odd–Even Modulation
In this section, we describe our data hiding framework by utilizing odd–even modulation in string art images. For a string art image having N nodes, this algorithm can hide up to bits. The basic idea is to let the number of visits of each node reflect the hidden message bits. The overall block diagram of the proposed system is shown in Figure 2. It consists of two stages: data embedding and data extraction. In the data embedding stage, encrypted secret data is embedded into string art image to generate modified string art image . During data extraction, the secret data is extracted from the modified string art image . The critical problems here are (1) minimizing distortion between and , and (2) keeping and statistically indistinguishable. To achieve these, our framework is based on a special histogram, node histogram, that we proposed for string art.
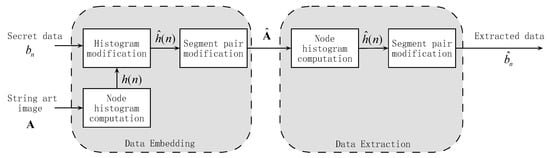
Figure 2.
The overall block diagram of the proposed data hiding system.
3.1. Node Histogram
A node histogram for string art image records the number of visits of each node. This is similar to the image histogram that records the number of occurance of values that pixels can take in a given image.
The node histogram can be obtained by sequentially visiting the entries of the matrix and recording the number of occurance of the node indices. After checking the line segment matrix , we may notice that except for the first node and the last node , all other nodes appear even number of times. This is because each of these nodes appear twice in two connected segments, i.e., .
Let be the number of occurrence of node n in the entries of , then the node histogram can be calculated by:
where the ceiling function returns the nearest integer towards . The node stored in is the ending node of the whole string art image.
For example, given a string art image Mona Lisa, the corresponding node histogram is shown in Figure 3. Two observations can be made from Figure 3b. First, the node histogram is correlated with the local blackness of the image near the node. For example, the nodes near the top-left corner of the image have lower histogram bins because the top-left corner is bright. Second, the node histogram exhibits local similarity, i.e., adjacent bins have similar heights. This local smoothness reflects the local smoothness of the string art image, which comes from the local smoothness of the original Mona Lisa image. This local smoothness is crucial to ensure that our algorithm is secure under steganalysis, as will be shown in Section 4.5.
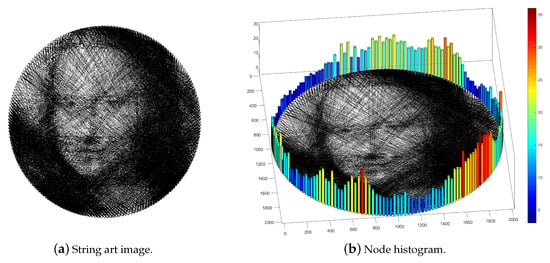
Figure 3.
Node histogram of the string art Mona Lisa. (a) String art image Mona Lisa. (b) The Node histogram of (a).
3.2. Data Embedding
The basic idea of our data hiding algorithm is to let the height of the histogram bin reflect the hidden message. More specifically, given a sequence of secret message , , we let the parity of the histogram bin be equal to , i.e.,
This is equivalent to replacing the least significant bit (LSB) of by :
where B is the bit depth of and is the -th bit of . If the parity of is equal to , then no changes of line segments connected to node n are needed. But, if the parity of is different from , then we need to move the common end of two line segments connected to node n to another node.
To increase security, a random node is selected as the first node. This initial node can be used as a secret key and should be shared between the embedder and the extractor. Without loss of generality, suppose that the node k is chosen as the first node. Then we sequentially embed into the node , i.e.,
To enforce the parity as determined in Equation (4), we need to move line joint from one node to other nodes. If , then we need to choose one line joint from the line joints at node . Two technical issues need to be solved at this stage. (1) Which joint in the current node should be moved? and (2) where to move this joint to? As with data hiding in an image, modifying the string art causes distortion to the rendered image. So, when embedding data, we should try to minimize the introduced distortion.
Ideally, we may formulate the embedding as an optimization problem. Let be a rendering function that renders the line segment matrix into an image. This involves either physically manufacturing the string art image or simulating the string art image as a two-dimensional digital image.
To measure distortion introduced by data hiding, we also need to introduce a metric. Given two rendered digital images, this metric should mimic the behavior of a human vision system (HVS) in evaluating the fidelity of the modified image with respect to the original image. Many available HVS models describe the low-pass behavior of the HVS, for example, the Gaussian low-pass model [33]. Without loss of generality, we set the initial node when discussing non-security related aspects of our algorithm. So, the data hiding problem can be formulated as:
where is the node histogram of the modified string art .
On average, only half of the N nodes may fail to meet the requirement that . So we need to find one joint from each of these nodes and move it to another such node. The number of solutions (i.e., the space of feasible solutions) can be estimated as follows. Let the set of nodes to be and we choose one joint from each of these nodes, then the number of choices is
Considering the worst case, where the node histogram is uniform, this number of combinations is:
For typical parameters and , this number is , which is prohibitive to exhaust if a brute-force approach is used to search the space of feasible solutions.
To reduce the computational complexity, we resort to heuristic local greedy searching approaches. In this paper, we consider the following solutions: (1) random deletion, (2) random selection, and (3) minimal distance selection.
3.3. Random Deletion
If , then we randomly choose a joint from the node n and delete it from the list. Let be a segment pair passing through the node n, then we remove the two segments and from the list and add a new line segment . A drawback of this approach is that the newly added line segment may be quite different from the original line segments and . For example, referring to Figure 1, the two segments and are near the edge of the image, but the new segment passes through the center of the string art image.
3.4. Random Selection
For this approach, we randomly select one joint from the current node and move it to the node next to it. The rationality behind it is that adjacent nodes are closely located with each other. So, when randomly moving a joint from one node to its adjacent neighbor, the impact to the visual quality is limited to a small region which can then be smoothed by HVS. Furthermore, since the node histogram is smooth, moving a node to its neighbor has the least impact on the histogram. As a result, it ensures security against steganalysis.
More specifically, let the current node to be n and that . For each node, we maintain a table that records all the line segments connected to that node. This table can be represented as a list of row indices of with node n as the destination node:
where L is the total number of line segments. To move a joint from node n to node , we randomly select one joint from :
where denotes uniform distribution over the set B, and ∼ denotes sampling operation. Then we modify the line segment list by letting and keeping other entries unchanged.
3.5. Minimal Distance Selection
The string art images are mostly portraits of human faces. So the central region of the image is more visually important than the regions near nodes. When modifying the image, we should try not to change the line segments passing through the central part and should prefer line segments near the edges. The distance from the center of the circular plate to the line segment should be maximized when choosing line segments to move.
For convenience, we set the origin of the coordinate system to be the center of the circular plate. Given a segment and the radius r of the circular plate, we first determine the coordinates of the two nodes and : , where is the angle between two adjacent nodes and can be found by . The parameter N is the number of nodes. Thus, the distance between the plate center and this segment can be calculated by
For a segment pair , the sum of distances should be maximized in order to choose a pair far away from the center of the plate. Furthermore, for a given sum , we should choose the pair with similar lengths. Combining the two requirements, we can formulate the segment pair selection problem as an optimization problem
where and are two positive numbers and . The denominators and are normalizing terms. The second term is a penalty term that favors segment pairs consisting of two line segments with similar lengths. Thus, a parameter controlling the strength of the penalties should be applied. The set consists of all segment pairs at node n:
and is the entry of matrix .
For example, given a hypothetical string art image having four nodes () and the following string art matrix:
we can find the set as
3.6. Simplified Minimum Distance Selection
The computational load of the optimization problem in Equation (11) consists of the following:
- Calculating the distances and .
- Searching the space of feasible solutions.
To calculate the distance , we need to calculate the coordinates first. But the distance calculation in Equation (10) involves division that is more costly than addition/subtraction. The radius should also be known. It can be observed from the string art image in Figure 3a that if two consecutive line segments are near the edge, then both of them are short. So, the sum of the lengths should be a reasonable measure for thread selection. The computation of can be replaced by the index distance as defined below.
For any two nodes m and n, their index distance is the absolute difference between the two indices, i.e., . But since the nodes are placed along a circle, the index distance should be adjusted to account for this. Referring to Figure 4, the node ‘0’ is located on the x-axis (horizontal axis) and the indices increase counter-clockwise. Let the current node be node n, then the index distance between n and m can be calculated directly as . But the index distance between n and ℓ should be smaller than . Considering this, we define the index distance as:
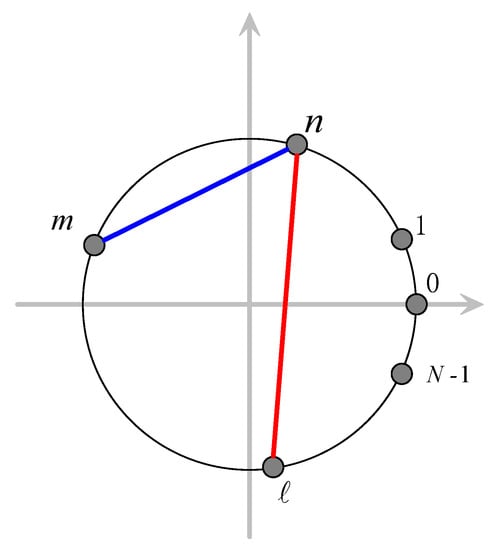
Figure 4.
Calculation of index distance.
Using the index distance, we can re-formulate the segment pair selection problem as
where , and . The denominators N and are maximum values of and , respectively. They are included in Equation (16) to normalize each term before weighted summing. Please note that now we have a minimization problem to solve, while Equation (11) is a maximization problem. The distance calculation in Equation (15) operates on integers and does not involve trigonometric function or division, nor does it need to know the radius of the plate. The divisions in Equation (16) can be included into the coefficients and , and can be pre-calculated. This accelerates the distance calculation significantly.
To show that the index distance is related to distance , we plot the ∼ curve for and , as shown in Figure 5. The radius is set as 180 mm [32]. Figure 5a shows that as n increases from 1 to 100, the distance D increases accordingly. When n increases from 101 to 200, the distance D decreases accordingly. The trend of D is opposite to the trend of L. Figure 5b shows that L decreases monotonically as D increases. Thus, by minimizing D, the distance L can be maximized.
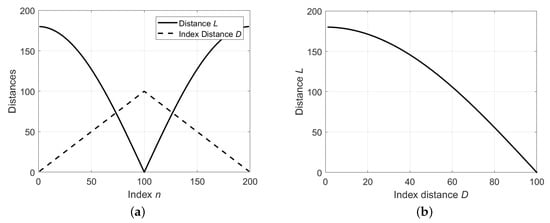
Figure 5.
Relationship between distance L and index distance D. (a) Plotting and as a function of index n. (b) Plotting of vs. .
3.7. Data Extraction
During data extraction, the modified string art file is given and we need to extract the embedded secret data. From the modified string art image, we first construct the the modified string art matrix , as described in Section 2.1. Then, the node histogram can be constructed as:
where the ceiling function returns the nearest integer towards , and records the number of occurrence of node n in the entries of . The embedded bits can be extracted by calculating the parity of :
If the bits were encrypted before embedding, a decryption operation needs to be applied to the extracted bits , in order to recover the plain text.
4. Experimental Evaluation
4.1. Performance Metric
As a typical data hiding system, rate and distortion are two main performance indices. Rate is defined as the number of bits embedded per dimension. For string art image, ‘dimension’ is related to the number of nodes since more nodes lead to better visual quality. For the proposed system, we embed bits into N nodes, so the rate R is a constant
This rate increases with N and approaches 1 bit/node in the limit .
Distortion measures the difference between the perceptual quality of the original string art image and the modified string art image . Let and be rendered string art images. We use HPSNR (Human Peak Signal to Noise Ratio) to measure the distortion of with respect to [34]. First, a Gaussian low-pass filter is used to smooth and . This filter models the low-pass behavior of a human vision system (HVS), which is widely used in digital halftoning. The kernel of this filter is:
where is the parameter of this HVS model. The smoothed images are denoted as and , respectively. Then the HPSNR can be calculated as:
where and are the number of rows and the number of columns of the rendered images, respectively.
As the central region of the rendered string art image is more visually important than region near the border, a weighted HPSNR can be designed to emphasize the central region. Before calculating the HPSNR, each filtered image is further multiplied by a weighting mask. Such a mask is shown in Figure 6.

Figure 6.
A Gaussian weighting mask for calculating weighted Human Peak Signal to Noise Ratio (HPSNR).
For a symmetric string art image, we use a Gaussian mask with standard deviation , such that the rendered image covers range of the Gaussian mask. The corresponding weighted HPSNR can be calculated as in Equation (21) using weighted and smoothed images.
To further characterize the structure distortion, we employ the SSIM (structure similarity measure) metric [35]. After applying the weighting mask as in Figure 6, we also get a weighted SSIM that emphasizes the central region of a string art before comparison.
4.2. Parameter Setup and Optimization
Several parameters of the proposed algorithms need to be set in our experiment. First, we summarize the chosen parameter values in Table 2, and then we present the rationality of these choices.

Table 2.
Parameter setting.
For the original string art, we use nodes and line segments as suggested in [32]. Increasing N may bring us a string art with more details, but it will increase the computational time and fabrication time [6]. For , using more line segments other than brings us less improvement in the quality of the rendered image [32]. Using a plate of radius mm is suitable for manual knitting since the human arm feels comfortable when working in this range while the artist may need to spend several hours knitting the string art. The parameters for the proposed data hiding algorithm are also summarized Table 2 (rows 5 to 7). For calculating HPSNR, we set as suggested in [34]. This value is suitable for observing a digital image displayed on a screen. The size of the smoothing kernel is set as to make sure that the kernel can cover range of the kernel [34].
To implement the Minimal Distance Selection (Section 3.5) and Simplified Minimal Distance Selection (Section 3.6), we must determine the parameters , , and , where , and . So only two parameters and need to be set. Using a set of 4 typical string art images as testing images, we plot the average weighted HPSNR as and increase from 0 to 1. For each image, random secret bits are generated and embedded 10 times.
The testing string art images are shown in Figure 7. They are produced using the algorithm in [32] that are designed for a low-cost string art image printer.

Figure 7.
The four testing string art images that are used in parameter optimization. These images are generated using the algorithm in [32]. (a) Mona Lisa, (b) Lena, (c) Fab, and (d) Odry.
The result is shown in Figure 8. For Simplified Minimal Distance Selection, we observe a jump of weighted HPSNR as increases from 0.5 to 0.6. This can be explained as follows. If is small, then the optimization process selects line segment pairs with similar lengths. So more selected segment pairs may pass through the central region of the string art image, thus producing more visually salient distortion. As , segment pairs having a small total length are preferred. For , the weighted HPSNR reaches its maximum. Therefore, we set in the following experiments. Similar observations can be get from Figure 8a, but now the optimal .
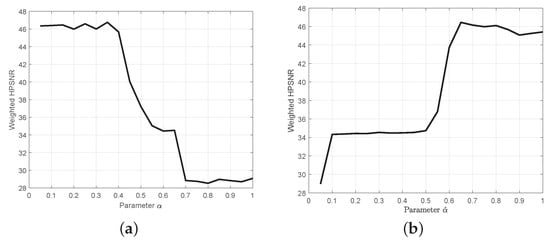
Figure 8.
The weighted PSNR as a function of the weighting parameter or . (a) Weighted HPSNR vs. for minimum distance selection algorithm. (b) Weighted HPSNR vs. for simplified minimum distance selection algorithm.
4.3. Distortion Testing and Comparison
In this experiment, we test the distortion introduced by data hiding to rendered string art images. We implemented the four algorithms designed in Section 3: random deletion, random selection, minimum distance selection, and simplified minimum distance selection. Totally, bits are embedded. All these bits can be extracted correctly from the modified string art.
For the string art image Mona Lisa, the rendered string art images after data embedding are shown in Figure 9. We also included the original string art image for reference. Close inspection reveals that (1) Both the random deletion and random selection algorithm modify line segments crossing the central region of the image, and (2) The minimum distance selection and simplified minimum distance selection algorithms select line segments near the circumference. This observation is supported by the weighted HPSNR metrics. Random deletion and random selection have similar weighted HPSNR and both of them are around 30 dB. In contrast, the minimum distance selection and simplified minimum distance selection algorithms have a much higher weighted HPSNR. Both of them are around 47 dB, a 17 dB improvement. Repeated experiment using other randomly generated secret bits b gives a similar result.

Figure 9.
The rendered string art images of Mona Lisa before and after data hiding. (a) Original string art image, (b) random deletion (weighted HPSNR = 30.92 dB), (c) random selection (weighted HPSNR = 31.56 dB), (d) minimum distance selection (weighted HPSNR = 47.19 dB), and (e) simplified minimum distance selection (weighted HPSNR = 47.15 dB).
To show that the distortion comparisons are consistent across different string art images, we use the four testing images as shown in Figure 7, and test the four algorithms on each image. The resulting weighted HPSNRs and weighted SSIMs are plotted in Figure 10. From Figure 10, we observe that the two minimum distance selection algorithms outperform random deletion and random selection consistently on four testing string art images. Even though a simplified distance calculation is adopted in the simplified minimum distance selection algorithm, its performance is comparable to the original minimum distance selection algorithm.
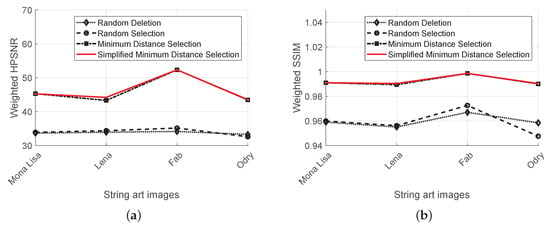
Figure 10.
Comparing distortion for four typical string arts. (a) Weighted HPSNR, and (b) weighted structure similarity measure (SSIM).
Furthermore, we observe a close correlation between the two distortion measures. The (simplified) minimum distance selection algorithms outperforms random deletion and random selection in terms of both weighed HPSNR and weighted SSIM.
A batch test is also conducted on a set of string art generated for human faces. To avoid possible copyright issues, we employ the styleGAN algorithm to generate a set of artificial faces [36]. This data set consists of 20 faces, as shown in Figure 11a. The host string arts for data embedding are then prepared using the StringArtGenerator package [37] as shown in Figure 11b, where , and the sizes of the rendered images are .

Figure 11.
Data set for batch test. (a) A set of faces generated by styleGAN [36]. (b) The corresponding string art images ready for data embedding.
The distortion testing result is shown in Figure 12. It is evident that the two minimum selection algorithms consistently outperform the random deletion and random selection algorithms, both in terms of weighted HPSNR and weighted SSIM.
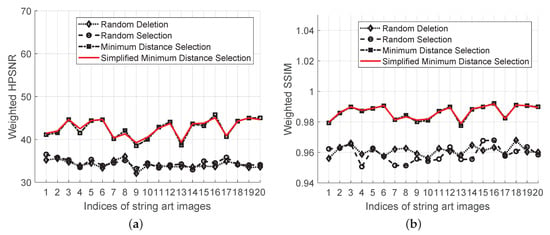
Figure 12.
Batch test for distortion on a data set consisting of 20 string arts. (a) Weighted HPSNR, and (b) weighted SSIM.
To further investigate the coherence between the two distortion measures, we use a scatter plot to show how the weighted SSIM varies with weighted HPSNR, as shown in Figure 13. For random deletion and random selection algorithms, the correlation coefficient is relatively low, only 0.21 and 0.37. These low coefficients can be attributed to the random behavior of these two algorithms. Since a random line segment is selected or deleted, its impact on weighted SSIM and weighted HPSNR is not coherent. Close inspection of some selected or deleted line segments reveals that, for some selection/deletion, it affects tone similarity more than structure similarity. But for other selection/deletion, the reverse is true. However, for the two minimum distance selection algorithms, the correlation coefficients are 0.94 and 0.95, respectively. Using the minimum distance selection, we avoid changes of line segments across the central region of the string art. Thus, it improves not only the metrics but also their coherence. Furthermore, the correlation coefficient for all the four algorithms is 0.96.
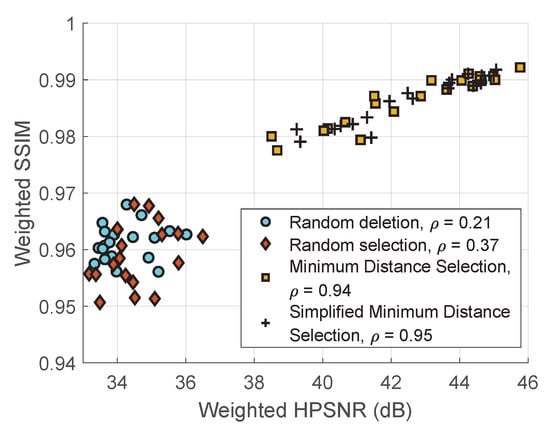
Figure 13.
Correlation coefficient between two distortion measures: weighted HPSNR and weighted SSIM. The overall correlation coefficient for all algorithms is 0.96.
Even though most string arts are designed for human portraits, it would be interesting to extend them to other types of images. We also test our algorithm on a set of biomedical images, as suggested by one of our reviewers. Three typical biomedical images are taken from an online data set [38]. The original image, the string art, and the string art after data embedding are shown in Figure 14, respectively. We use the simplified minimum distance selection algorithm, which is the best among the four proposed algorithms. Please note that our focus here is data embedding, not designing string art to resemble the original image. So, we will focus on distortion between the original string art and the modified string art. The weighted HPSNRs are 45.6 dB, 40.2 dB, and 40.8 dB, respectively. For weighted SSIM, we get 0.99, 0.98, and 0.98, respectively. This test shows that our algorithm can be applied to any type of image once it is rendered as a string art image.
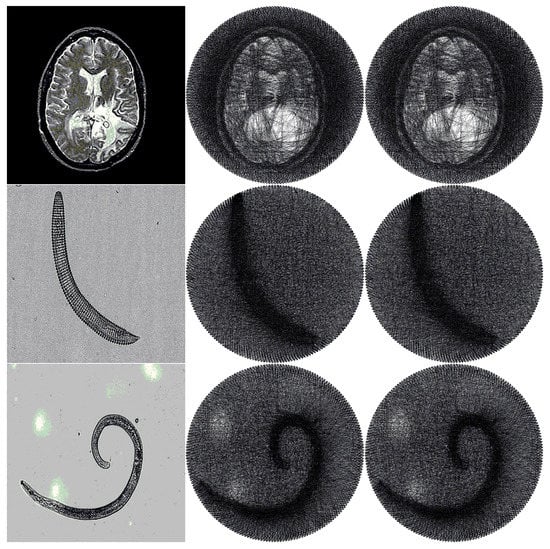
Figure 14.
Testing result for three biomedical images. The first column contains the original images. The second column contains the corresponding string art. The last column contains the string art after data embedding.
4.4. Machine Time
In this experiment, we compare the two minimum distance selection algorithms for time efficiency. As analyzed in Section 3.5 and Section 3.6, using index distance may reduce the distance computation load. Since distance computation is called frequently when finding the optimal segment pairs to modify, we expect that reducing the computational complexity of distance calculation may reduce the machine time of the implementations. We focus on the machine time on computing the distances in Equations (10) and (15), which avoids the influence of machine time of other parts of the whole algorithm. Using the four testing images, we embed random bits 100 times and record the average machine time of both algorithms. The result is shown in Table 3. On average, a 23.4% reduction of machine time can be achieved by using the simplified distance calculation.

Table 3.
Machine time comparison on distances calculation.
4.5. Security
Security of the embedded data can be ensured by encrypting it before embedding. To resist steganalysis, we have to ensure that the statistical properties of the modified string art image are indistinguishable from the original image. In this section, we show that, for the testing images, their node histograms after data embedding are statistically indistinguishable from the original node histograms.
To see the similarity between the two node histograms and , we find the emperical cumulative distribution functions (CDFs) first, which are:
Then, we plot against , as shown in Figure 15 for string art image Mona Lisa. We observe a curve that is almost a straight line, indicating that the two distributions and are nearly indistinguishable.
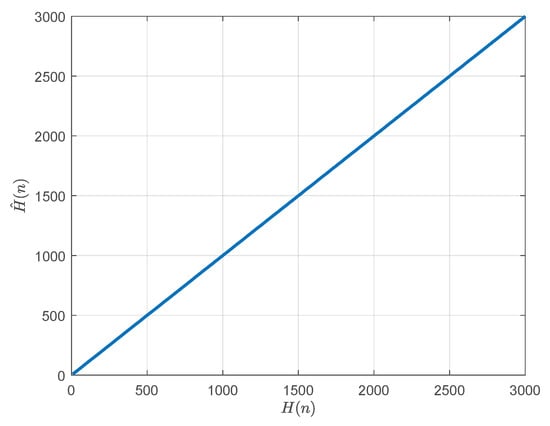
Figure 15.
Plotting two empirical cumulative distribution functions (CDFs) vs. .
To test if the two string art node lists come from the same underlying distribution, we employ the two-sample Kolmogorov–Smirnov test, where the test statistic is:
The significance level is set as 0.05. The null hypothesis is that the two node lists come from the same underlying distribution. All the four images pass this hypothesis testing with a p-value 1, indicating that the two node histograms and are indistinguishable. Thus, we conclude that using the testing images in this paper, the node histogram after embedding is indistinguishable from the node histogram before embedding.
4.6. Qualitative Comparison with Other Copyright Protection Approaches
This paper focuses on using data hiding for copyright protection of string art. There are other approaches that one can employ for this purpose, such as a registration-based approach and visible watermarking [39,40,41,42,43]. In this section, we compare these three approaches qualitatively and demonstrate the superiority of the data hiding approach. The comparison result is summarized in Table 4.

Table 4.
Qualitative comparison with other copyright protection approaches.
- Visible watermarking: Visible watermarking overlays a small-sized image (watermark) on the image to be protected, for notifying users of copyright issues [39,40]. This overlay brings high distortion to the original image. Furthermore, its security is low since the very existence of the watermark is known to everyone. This approach has higher flexibility than a registration-based approach since the owner is free to change his/her watermark.
- Registration-based approach: This approach is widely used in digital rights management (DRM) of multimedia signals shared over networks, such as Internet, DVD and CCTV (Closed Circuit Television) [41,42,43]. A salient feature of this approach is that the quality of the media signal is not affected. Furthermore, it has high security and is supported by display devices from various vendors. However, this approach is not flexible since the owner of the content needs to register his/her media to a centralized organization.
- Data hiding approach: Compared with visible watermarking, data hiding brings low distortion to the multimedia signal. Furthermore, it has higher security than visible watermarking since the watermark is hidden and encrypted. Compared with the registration-based approach, the data hiding approach has higher flexibility because the copyright message is embedded in the media signal itself. No centralized organization is needed to extract the copyright message.
5. Conclusions
To address the problem of data hiding in string art images, we proposed a framework based on odd–even modulation of the node histogram. Four algorithms were designed to minimize the embedding distortion at a low computational cost. The experimental results show that these algorithms can successfully embed secret data into a string art, without bringing perceptual distortion to the host string art. Using the minimum distance selection, an average of 17 dB reduction of weighted HPSNR is obtained on a set of testing images. The superiority of the minimum distance selection algorithm is also confirmed from the weighted SSIM metric. The two distortion metrics show close correlation for minimum distance selection algorithms. Furthermore, the simplified minimum distance selection approach leads to an average of 23.4% reduction of execution time. The modified node histograms after data embedding are indistinguishable from the corresponding original node histograms. Thus, the proposed algorithms are also secure under steganalysis.
One limitation of the proposed algorithm is that the payload of the data is relatively small. It can be improved by embedding into the connection sequence of line segments, instead of embedding into nodes. Another limitation is that the current algorithms are designed for black thread, which are not directly applicable to color threads.
The proposed embedding framework and algorithms can be extended to a string art image having irregularly-placed nodes. The node histogram can be applied to it directly. But since there is no natural ordering for the nodes, the embedding algorithm has to find a node near the current node as the target node. Our future work will focus on improving the embedding payload and designing the embedding algorithm for irregular string art.
Author Contributions
Conceptualization, Y.-S.Y., B.Y.; software, H.-L.C., B.Y.; Methodology, Y.-S.Y., B.Y.; Writing–original draft, Y.-S.Y., H.-L.C., B.Y.; Writing–review & editing, H.-L.C., B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Innovation and Entrepreneurship Training Program of University of Science and Technology Liaoning (No. 202010146561): Computer-Aided Design and Manufacturing of String Art. It is also partially supported by the National Natural Science Foundation of China (NSFC) (No. 61272432), Shandong Provincial Natural Science Foundation (No. ZR2014JL044), and MOE (Ministry of Education in China) Project of Humanities and Social Sciences (Project No. 18YJAZH110)
Acknowledgments
The authors would like to thank Molefi Itumeleng Alice for proof-reading the whole manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stoppel, S.; Bruckner, S. LinesLab: A Flexible Low-Cost Approach for the Generation of Physical Monochrome Art. Comput. Graph. Forum 2019, 38, 110–124. [Google Scholar] [CrossRef]
- Blanken, R. String Art Magic: Secrets to Crafting Geometric Art with String and Nail; Spring House Press: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Vrellis, P. A New Way to Knit. Available online: http://artof01.com/vrellis/works/knit.html (accessed on 12 July 2020).
- Birsak, M.; Rist, F.; Wonka, P.; Musialski, P. String Art: Towards Computational Fabrication of String Images. Comput. Graph. Forum 2018, 37, 263–274. [Google Scholar] [CrossRef]
- Ostanin, I. “String art” approach to the design and manufacturing of optimal composite materials and structures. Compos. Struct. 2020, 246, 112396. [Google Scholar] [CrossRef]
- Jovanović, M.; Vučić, M.; Tepavčević, B.; Raković, M.; Tasevski, J. Robotic Knitting in String Art as a Tool for Creative Design Processes. Advances in Service and Industrial Robotics. RAAD 2019. In Advances in Intelligent Systems and Computing; Berns, K.G.D., Ed.; Springer: Cham, Switzerland, 2019; Volume 980. [Google Scholar]
- Barni, J.; Bartolini, F. Watermarking Systems Engineering: Enabling Digital Assets Security and Other Applications; Marcel Dekker Inc.: New York, NY, USA, 2004. [Google Scholar]
- Bender, W.; Gruhl, D.; Morimoto, N.; Lu, A. Techniques for data hiding. IBM Syst. J. 1996, 35, 313–336. [Google Scholar] [CrossRef]
- Cox, I.; Miller, M.; Bloom, J.; Fridrich, J.; Kalker, T. Digital Watermarking and Steganography, 2nd ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2007. [Google Scholar]
- Pan, J.S.; Li, W.; Yang, C.S.; Yan, L.J. Image steganography based on subsampling and compressive sensing. Multimed. Tools Appl. 2015, 74, 9191–9205. [Google Scholar] [CrossRef]
- Cox, I.J.; Kilian, J.; Leighton, T.; Shamoon, T. Secure spread spectrum watermarking for images, audio and video. In Proceedings of the 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; Volume 3, pp. 243–246. [Google Scholar]
- Wu, H.; Cheung, Y.; Wang, Y. Data Hiding on 3D Meshes Based on Dither Modulation. In Proceedings of the 2006 World Automation Congress, Budapest, Hungary, 24–26 July 2006; pp. 1–6. [Google Scholar]
- Jiang, R.; Zhou, H.; Zhang, W.; Yu, N. Reversible Data Hiding in Encrypted Three-Dimensional Mesh Models. IEEE Trans. Multimed. 2018, 20, 55–67. [Google Scholar] [CrossRef]
- Hao, L.; Yan, B.; Pan, J.; Chen, N.; Yang, H.; Acquah, M.A. Adaptive Unified Data Embedding and Scrambling for Three-Dimensional Mesh Models. IEEE Access 2019, 7, 162366–162386. [Google Scholar] [CrossRef]
- Luo, H.; Lu, Z.; Pan, J. A Reversible Data Hiding Scheme for 3D Point Cloud Model. In Proceedings of the 2006 IEEE International Symposium on Signal Processing and Information Technology, Vancouver, BC, Canada, 27–30 August 2006; pp. 863–867. [Google Scholar]
- Celik, M.U.; Sharma, G.; Tekalp, A.M.; Saber, E. Reversible data hiding. Proc. Int. Conf. Image Process. 2002, 2, II156–II160. [Google Scholar]
- Cox, I.J.; Kilian, J.; Leighton, F.T.; Shamoon, T. Secure spread spectrum watermarking for multimedia. IEEE Trans. Image Process. 1997, 6, 1673–1687. [Google Scholar] [CrossRef]
- Yan, B.; Guo, Y.J.; Wang, X.M. Performance Of Spread Spectrum Watermarking In Autoregressive Host Model Under Additive White Gaussian Noise Channel. J. Meas. Sci. Instrum. 2010, 1, 271–275. [Google Scholar]
- Cheng, Q.; Sorensen, S. Spread Spectrum Signaling For Speech Watermarking. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; Volume 3, pp. 1337–1340. [Google Scholar]
- Garcia, R.A. Digital Watermarking Of Audio Signals Using A Psychoacoustic Auditory Model And Spread Spectrum Theory. Master’s Thesis, Music Engineering Technology, University of Miami, Miami-Dade County, FL, USA, 1999. [Google Scholar]
- Chen, B.; Wornell, G.W. Quantization index modulation: A class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inf. Theory 2001, 47, 1423–1443. [Google Scholar] [CrossRef]
- Lu, Z.M.; Xing, W.; Xu, D.G.; Sun, S.H. Digital Image Watermarking Method Based On Vector Quantization With Labeled Codewords. IEICE Trans. In. Syst. 2003, E86-D, 2786–2789. [Google Scholar]
- Lu, Z.M.; Xu, D.G.; Sun, S.H. Multipurpose Image Watermarking Algorithm Based on Multistage Vector Quantization. IEEE Trans. Image Process. 2005, 14, 822–831. [Google Scholar] [PubMed]
- Moriya, T.; Takashima, Y.; Nakamura, T.; Iwakami, N. Digital Watermarking Schemes Based On Vector Quantization. In Proceedings of the IEEE Workshop on Speech Coding For Telecommunications, Pocono Manor, PA, USA, 7–10 September 1997; pp. 95–96. [Google Scholar]
- Shi, Y.; Li, X.; Zhang, X.; Wu, H.; Ma, B. Reversible data hiding: Advances in the past two decades. IEEE Access 2016, 4, 3210–3237. [Google Scholar] [CrossRef]
- Weng, S.; Chen, Y.; Ou, B.; Chang, C.; Zhang, C. Improved K-Pass Pixel Value Ordering Based Data Hiding. IEEE Access 2019, 7, 34570–34582. [Google Scholar] [CrossRef]
- Zhang, X. Reversible Data Hiding in Encrypted Image. IEEE Signal Process. Lett. 2011, 18, 255–258. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, X. Reversible Data Hiding in Encrypted Images With Distributed Source Encoding. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 636–646. [Google Scholar] [CrossRef]
- Yan, X.; Lu, Y.; Liu, L.; Song, X. Reversible Image Secret Sharing. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3848–3858. [Google Scholar]
- Zhang, W.; Wang, H.; Hou, D.; Yu, N. Reversible Data Hiding in Encrypted Images by Reversible Image Transformation. IEEE Trans. Multimed. 2016, 18, 1469–1479. [Google Scholar] [CrossRef]
- Jain, A.K. Fundamentals of Digital Image Processing; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Je, S.; Abileva, Y.; Bianchi, A.; Bazin, J.C. A computational approach for spider web-inspired fabrication of string art. Comput. Animat. Virtual Worlds 2019, 30, e1904. [Google Scholar] [CrossRef]
- Lau, D.; Arce, G. Modern Digital Halftoning, 2nd ed.; Taylor & Francis: Boca Raton, FL, USA, 2001. [Google Scholar]
- Liu, Y.; Guo, J.; Lee, J. Inverse Halftoning Based on the Bayesian Theorem. IEEE Trans. Image Process. 2011, 20, 1077–1084. [Google Scholar] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Karras, T.; Laine, S.; Aittala, M.; Hellsten, J.; Lehtinen, J.; Aila, T. Analyzing and Improving the Image Quality of StyleGAN. arXiv 2019, arXiv:cs.CV/1912.04958. [Google Scholar]
- String Art Generator. [EB/OL]. Available online: http://github.com/halfmonty/StringArtGenerator/ (accessed on 12 July 2020).
- Biomedical Image Data Set. [EB/OL]. Available online: http://decsai.ugr.es/cvg/dbimagenes/index.php/ (accessed on 12 July 2020).
- Huang, C.-H.; Wu, J.-L. Attacking visible watermarking schemes. IEEE Trans. Multimed. 2004, 6, 16–30. [Google Scholar] [CrossRef]
- Hu, Y.; Kwong, S. Wavelet domain adaptive visible watermarking. Electron. Lett. 2001, 37, 1219–1220. [Google Scholar] [CrossRef]
- Ma, Z. Digital rights management: Model, technology and application. China Commun. 2017, 14, 156–167. [Google Scholar]
- Camp, L. Access denied [digital rights management]. IEEE Secur. Priv. 2003, 1, 82–85. [Google Scholar] [CrossRef]
- Subramanya, S.R.; Yi, B.K. Digital rights management. IEEE Potentials 2006, 25, 31–34. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).