Stability and Boundedness of the Solutions of Multi-Parameter Dynamical Systems with Circulatory Forces

Abstract

We consider a linear dynamical system under the action of potential and circulatory forces. The matrix of potential forces is positive definite, and the main question is when the circulatory forces induce instability to the system. Different approaches to studying the problem are discussed and illustrated by examples. The case of multiple eigenvalues also is considered, and sufficient conditions of instability are obtained. Some issues of the dynamics of a nonlinear system with an unstable linear approximation are discussed. The behavior of trajectories in the case of unstable equilibrium is investigated, and an example of the chaotic behavior versus the case of bounded solutions is presented and discussed.

1. Introduction

In the theory of dynamical systems, interest in the properties of symmetry is steadily growing. In recent decades, a systematic study of systems possessing the so-called reversible symmetry has become widespread [1,2,3,4,5]. Consider an autonomous dynamical system with continuous time, governed by the ordinary differential equation:

$$\frac{d\mathit{x}}{dt}=\mathit{f}\left(\mathit{x}\right).$$

(1)

It is said [1] that the map $\mathit{S}:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is a reversing symmetry of (1) if:

$$\frac{d}{dt}\left(\mathit{Sx}\right)=-\mathit{f}\left(\mathit{Sx}\right).$$

In this case, System (1) is invariant with respect to transformation $(t,\mathit{x})\to (-t,\mathit{Sx}).$

The stability problem for non-conservative dynamical systems is one of the fundamental problems in modern science and technology. It is related to many real-life applications and is mainly matched with the response of mechanical systems to parametric excitation and flutter phenomenon exhibited by aerospace systems undergoing interaction between a structure and fluid flows, as well as playing a crucial role in the control of walking robots and many others [6,7,8,9,10,11].

In this paper, we study a generic canonical form of a finite-dimensional system governed by the second order ODEs presented in the Euler–Lagrange form:

$$\frac{d}{dt}\frac{\partial \mathcal{K}}{\partial {\dot{q}}_j}-\frac{\partial \mathcal{K}}{\partial q_j}=\frac{\partial \Pi }{\partial q_j}+Q_j(j=1,\cdots ,n),$$

where $\mathcal{K},\Pi$ are the kinetic and potential energies of the system, respectively, and $Q_j$ represent the generalized non-potential forces. The dynamics of such a system in the vicinity of equilibrium is described by linearized equations:

$$M\ddot{x}+(D+G)\dot{x}+(K+N)x=0,$$

(2)

which is often referred to as the MDGKNsystem [12,13]. The symmetrical matrices $M,D,K$ stand for the inertia, dissipative, and stiffness matrices, respectively, and the skew-symmetric ones $G,N$ are associated with gyroscopic and non-conservative positional or circulatory forces.

A “strange” property of some non-conservative systems is that the influence of damping can make the system unstable. This property is often referred to as Ziegler’s paradox [14], since adding a viscous damping to the joints of a double pendulum subjected to the follower force destabilizes the system. After the publication of Ziegler in 1952, investigations of the destabilizing effect of damping have attracted the attention of numerous researchers [15,16,17,18,19,20] and are continued to this day [5,21,22]. Furthermore, an additional interesting feature of the “reciprocal” damping effect follows: when adding a damping to unstable non-conservative system, this yields stabilization of an unstable system (in the Lyapunov sense), and the further increasing of damping leads back to instability [23]. A general stability problem of equilibrium of different mechanical non-conservative (both dissipative and circulatory) systems was studied in numerous papers [12,13,24,25,26]. Reviews of the problem for dissipative systems may be found in the works of Bolotin [27], Langthjem and Sugiyama [28], the monograph of Kirillov [11], and the recent work by Bigoni and Kirillov [5].

However, in our study, we shall focus on the undamped non-gyroscopic systems of the $MKN$-type (which are reversible systems). The eigenvalues of such a system are symmetrically located on the complex plane with respect to the imaginary axis; thus, stability is possible only if all of them are situated on this axis. The $MKN$ systems were studied in works [29,30,31,32,33,34]. Since the matrix M is positive definite and symmetric, there exists [35,36] a non-singular transformation, which transforms this system to the $I{K}_{0}N$ form, where I is an identity matrix and $K_0$ has a diagonalized form. For this reason, some authors [32,33,34] consider the $I{K}_{0}N$ systems. Though this simplification is justified from the theoretical point of view, often the elements of matrices are functions of physical parameters, and such a reduction is not of great utility. We shall use this form, as well as the more general form $MKN$ below.

The paper is organized as follows. Section 2 describes three main approaches to the study of the stability problem of the linear circulation systems. Section 3 deals with a multi-parameter system with three degrees of freedom. To find the conditions of stability, the approaches described in Section 2 are used. Their advantages and disadvantages are compared. As an example, we consider the problem of a three link pendulum to which a tracking force is applied. Section 4 examines the special case where the system has multiple roots. Such systems are found in applications, and often, the influence of an arbitrarily small circulation force leads to the instability of the motion. In addition, for systems of high dimensionality, the determination of the stability conditions by a standard procedure may be associated with serious computational difficulties. A theorem is proven, which makes it possible to simply find sufficient conditions for the flutter instability and to detect “dangerous” zones in the system parameter space. Illustrative examples for systems with four and five degrees of freedom are given. Section 5 discusses the influence of nonlinear terms of the differential equations of motion on the system dynamics in the context of the conditions of the above theorem. It is noted that for a nonlinear system, the presence of a positive Lyapunov exponent does not necessarily lead to chaotic behavior. Although the motion is unstable in the Lyapunov sense, it can however be bounded, which can prove to be acceptable enough in engineering applications.

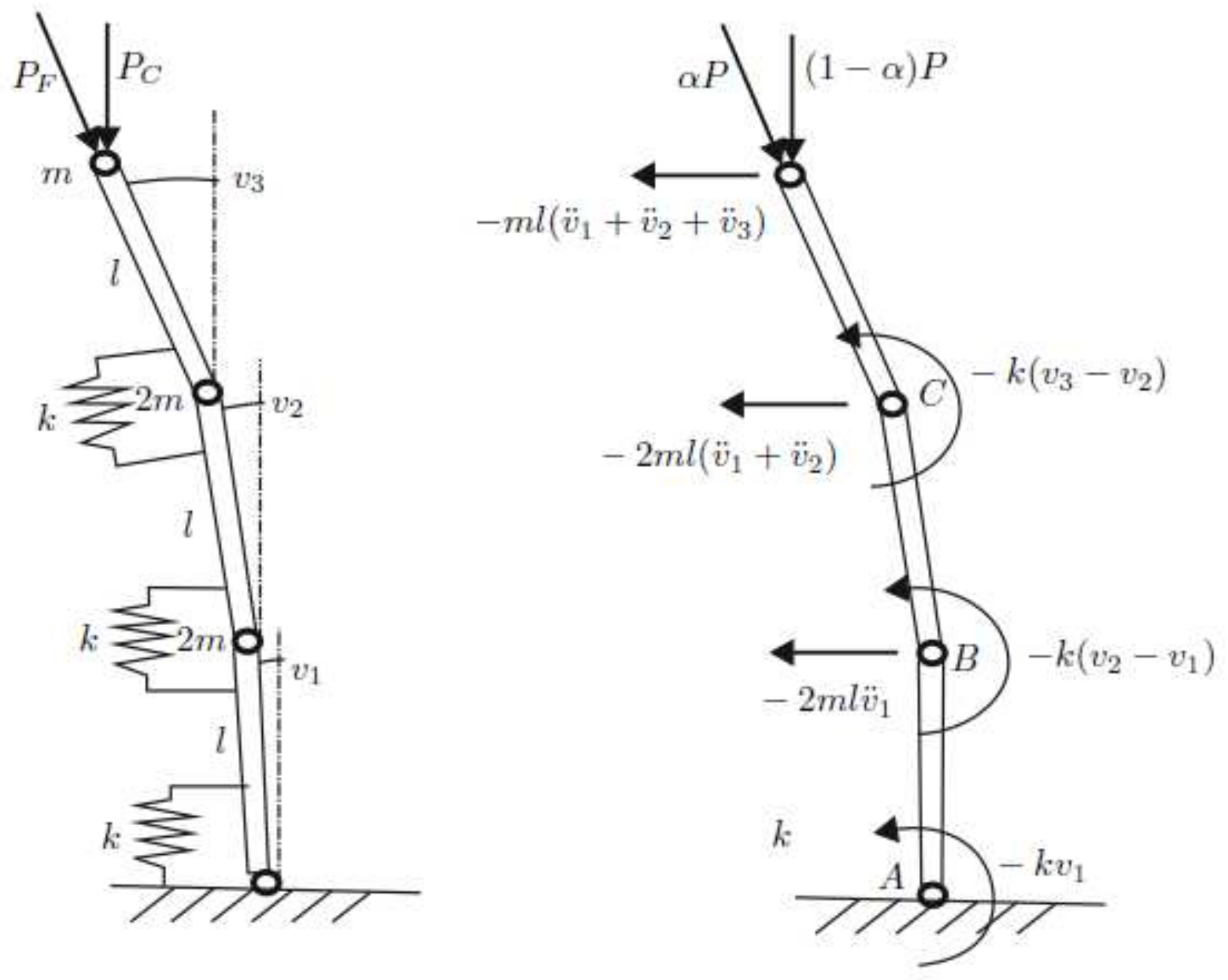
2. Formulation of the Problem

The non-conservative undamped linear systems are mostly presented in the following form:

$$M\ddot{x}+(K+N)x=0$$

(3)

where M and K are positive definite symmetric real square matrices, N is real skew-symmetric, and $x\in R^n$ represents a state vector. In order to underline the absence of damping, such a system is called an undamped non-conservative or circulatory system. Because 3 is a linear autonomous ODE system, its characteristic polynomial $f\left(\lambda \right)$ has order $2n$ and contains only even degrees of $\lambda .$ Consequently, the system (3) is stable if all roots of the polynomial:

$$f(\Lambda )=a_n{\Lambda }^n+a_{n-1}{\Lambda }^{n-1}+\cdots +a_1\Lambda +a_0$$

(4)

are real and negative, $\Lambda ={\lambda }^2$. The polynomial (4) is referred to as the reduced characteristic polynomial related to (3).

Three main cases are possible:

(1) The system is marginally or weakly stable (Lyapunov stability) if all solutions $x\left(t\right)$ of (3) are bounded for $t\in [0,+\infty )$. This means that every eigenvalue ${\lambda }_j$ is on the imaginary axis and semi-simple (there are s linearly independent eigenvectors associated with the eigenvalue of multiplicity s);

(2) The system (3) is unstable by flutter (or oscillatory unstable) if at least one of the eigenvalues ${\lambda }_j$ is complex with the nonzero real part (there exists an oscillating motion with exponentially growing amplitude);

(3) The system (3) is unstable by divergence (or statically unstable) if all of the $\Lambda$ are real and at least one of them is real positive (there is an aperiodic, exponentially growing motion).

The negativeness of the roots ${\Lambda }_j(j=1,\cdots ,n)$ may be validated with the help of Routh–Hurwitz or Lienard–Chipard criteria, and the absence of complex roots may be detected by at least three approaches. Below, we give their brief description.

The first approach will be referred to as the DM-approach and is based on analysis of the so called “discriminant matrix” [30,37].

Definition 1.

The discriminant matrix (in [37], the term “discrimination matrix” is used) of the polynomial (4) is the square$2n\times 2n$matrix of the following form:

$$D=\left(\begin{array}{cccccccc}{a}_n& a_{n-1}& a_{n-2}& \cdots & a_0& 0& \cdots & 0\\ 0& n{a}_n& (n-1)a_{n-1}& \cdots & a_1& 0& \cdots & 0\\ 0& a_n& a_{n-1}& a_{n-2}& \cdots & a_0& \cdots & 0\\ 0& 0& n{a}_n& \cdots & 2a_2& a_1& \cdots & 0\\ ·& ·& ·& ·& ·& ·& ·& ·\\ 0& \cdots & 0& a_n& a_{n-1}& a_{n-2}& \cdots & a_0\\ 0& \cdots & 0& 0& n{a}_n& (n-1)a_{n-1}& \cdots & a_1\end{array}\right).$$

(5)

Definition 2.

The sequence$\{D_1,D_2,\cdots ,D_s\},$where$D_j(j=1,\cdots ,s)$is the leading principal minor (upper left diagonal minor) of order$2j,$is called a discriminant sequence of the polynomial (4) (minors$D_j$sometimes are called “sub-discriminants” or “principal sub-resultants of$f\left(\lambda \right)$and$f\left(\lambda \right)$”).

Theorem 1.

[29,37]. Given a polynomial$f(\Lambda )$with real coefficients, a necessary and sufficient condition for the polynomial to have only real roots is that the elements of the discriminant sequence are all non-negative$D_j\ge 0,j=1,\cdots ,n$.

The second approach (B-approach [31,32]) is connected with consideration of the quadratic form $x^{\tau }Px,$ where:

$$P=\left(\begin{array}{ccccc}n& p_1& p_2& \cdots & p_{n-1}\\ p_1& p_2& p_3& \cdots & p_n\\ p_2& p_3& p_4& \cdots & p_{n+1}\\ ·& ·& ·& ·& ·\\ p_{n-1}& p_n& p_{n+1}& \cdots & p_{2n-2}\end{array}\right),p_m={(-1)}^m\mathrm{Tr}{(K+N)}^m,m=1,\cdots ,2n-2.$$

Note that the elements $p_j$ are connected with the coefficients of $f(\Lambda )$ by the following formulas:

$$p_j=-(p_{j-1}{a}_{n-1}+\cdots +p_1{a}_{n-j+1}+j{a}_{n-j}),j=1,\cdots ,n.$$

(6)

Theorem 2.

(Bulatovic [33]). (a) The system (3) is spectrally stable (zero values for Λ are allowed) iff$P\ge 0$, and$a_j\ge 0,j=1,\cdots ,n.$

(b) The system (3) is unstable by divergence iff$P\ge 0$, and$\exists a_j<0.$

(c) The system (3) is unstable by flutter iff$x^{\tau }Px,$can take negative values.

The third approach (G-approach [35]) is based on the use of a catalecticant matrix (Hankel matrix) of a special kind. Suppose that numbers ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_q$ are distinct roots of the polynomial (4) with multiplicities $n_1,n_2,\cdots ,n_q(n_1+n_2+\cdots +n_q=n):$

$$f(\Lambda )=a_n{(\Lambda -{\alpha }_1)}^{n_1}{(\Lambda -{\alpha }_2)}^{n_2}{(\Lambda -{\alpha }_q)}^{n_q}.$$

Introducing the Newton sums:

$$s_k=\sum _{j=1}^q{n}_j{\alpha }_j^k(k=0,1,2,\cdots ),$$

let us compose the matrix into the following form:

$$S={\left(\begin{array}{cccccc}{s}_0& s_1& s_2& \cdots & s_{n-2}& s_{n-1}\\ s_1& s_2& s_3& \cdots & s_{n-1}& s_n\\ s_2& s_3& s_4& \cdots & s_n& s_{n+1}\\ ·& ·& ·& ·& ·& ·\\ s_{n-1}& s_{n-2}& s_{n-3}& \cdots & s_{2n-3}& s_{2n-2}\end{array}\right)}_{n\times n}.$$

(7)

The elements of matrix S are connected with the coefficients of f by Newton recurrence relations:

$$s_0=n,s_1=-\frac{a_{n-1}}{a_n},s_k=-\frac{1}{a_n}(a_{n-1}{s}_{k-1}+a_{n-2}{s}_{k-2}+\cdots +a_{n-k+1}{s}_1+$$

$$+a_{n-k}k)(k\le n),s_k=-\frac{1}{a_n}(a_{n-1}{s}_{k-1}+a_{n-2}{s}_{k-2}+\cdots +a_0{s}_{k-n})(k>n).$$

(8)

For example, for $n=3$, these formulas take the form (with $a_3=1$):

$$s_0=3,s_1=-a_2,s_2=-(a_2{s}_1+2a_1)=a_2^2-2a_1,s_3=-(a_2{s}_2+a_1{s}_1+3a_0)=$$

$$=-a_2^3+3a_1{a}_2-3a_0,s_4=a_2^4-4a_1{a}_2^2+4a_2{a}_0+2a_1^2.$$

(9)

Theorem 3.

(Gantmakher [35]). (A) The number of roots of polynomial (4) different from each other is equal to the rank of the matrix$S$. (B) The number of distinct real roots of this polynomial is equal to the signature of the real quadratic form with matrix$S$.

For application purposes, the following corollary is helpful:

Corollary 1.

The number of real roots of the polynomial (4) (with real coefficients) different from each other is equal to${\mu }_S-{\nu }_S,$where${\mu }_S$is the “sign permanence” index and${\nu }_S$is the “sign variability” index (i.e., quantities of the values with the same sign and changes of the sign, respectively) in the sequence (in fact, the first element of the sequence is one, and it is followed by sequentially recorded principal minors${\Delta }_S^{\left(j\right)}$of matrix S till order$2r-2$):

$$1,s_0,\left(\begin{array}{cc}{s}_0& s_1\\ s_1& s_2\end{array}\right),\left(\begin{array}{ccccc}{s}_0& s_1& s_2& \cdots & s_{r-1}\\ s_1& s_2& s_3& \cdots & s_r\\ s_2& s_3& s_4& \cdots & s_{r+1}\\ ·& ·& ·& ·& ·\\ s_{r-1}& s_{r-2}& s_{r-3}& \cdots & s_{2r-2}\end{array}\right).$$

(10)

Here, r is the rank of the Hankel form:

$$S_n(x,x)=\sum _{j=1,k}^n{s}_{jk}{x}_j{x}_k,(s_{jk}=s_{kj}=s_{j+k-2})$$

for polynomial$f\left(\lambda \right)$.

Corollary 2.

Polynomial$f\left(\lambda \right)$has n distinct real roots if and only if$r=n,$and${\Delta }_S^j>0,j=2,\cdots ,n$.

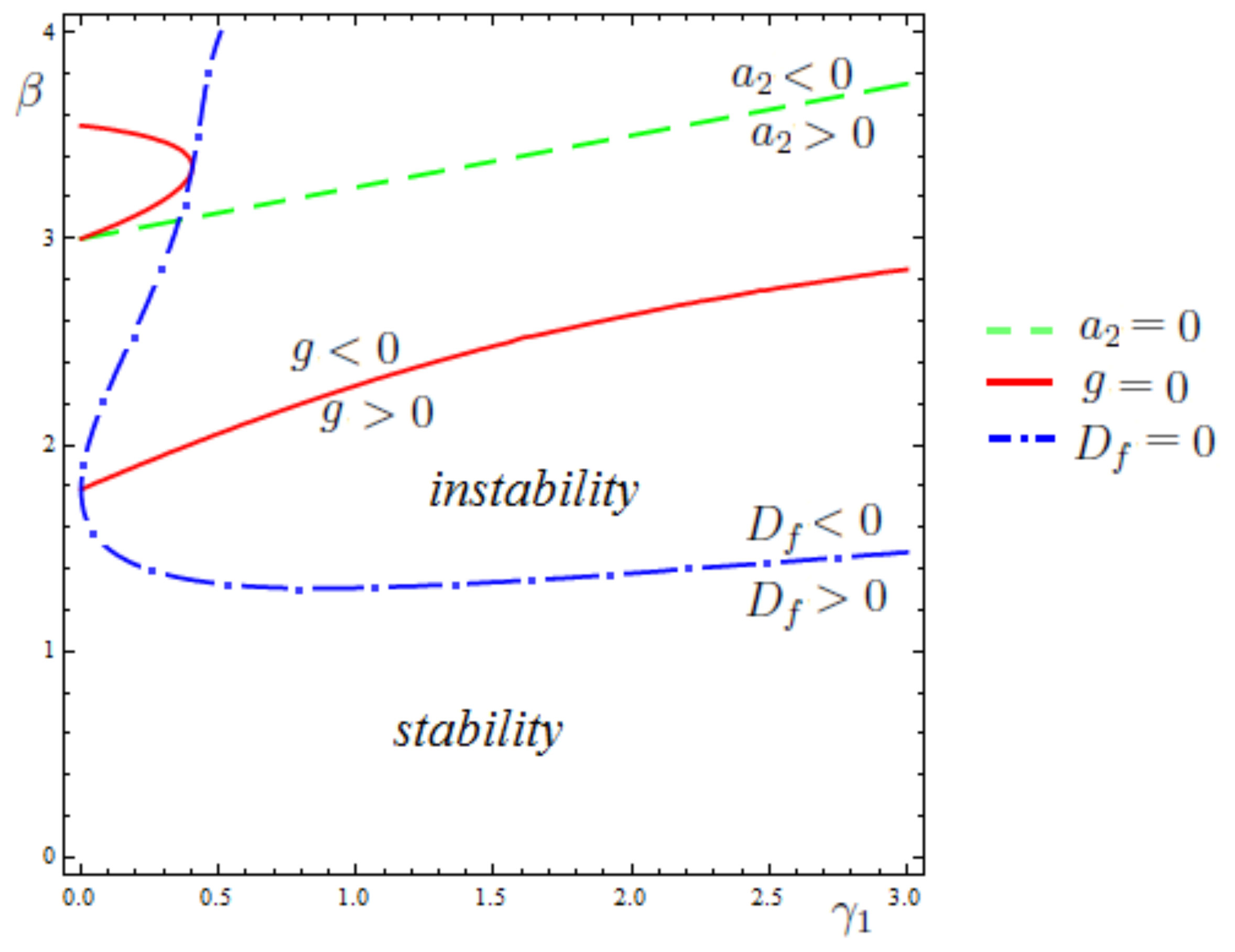
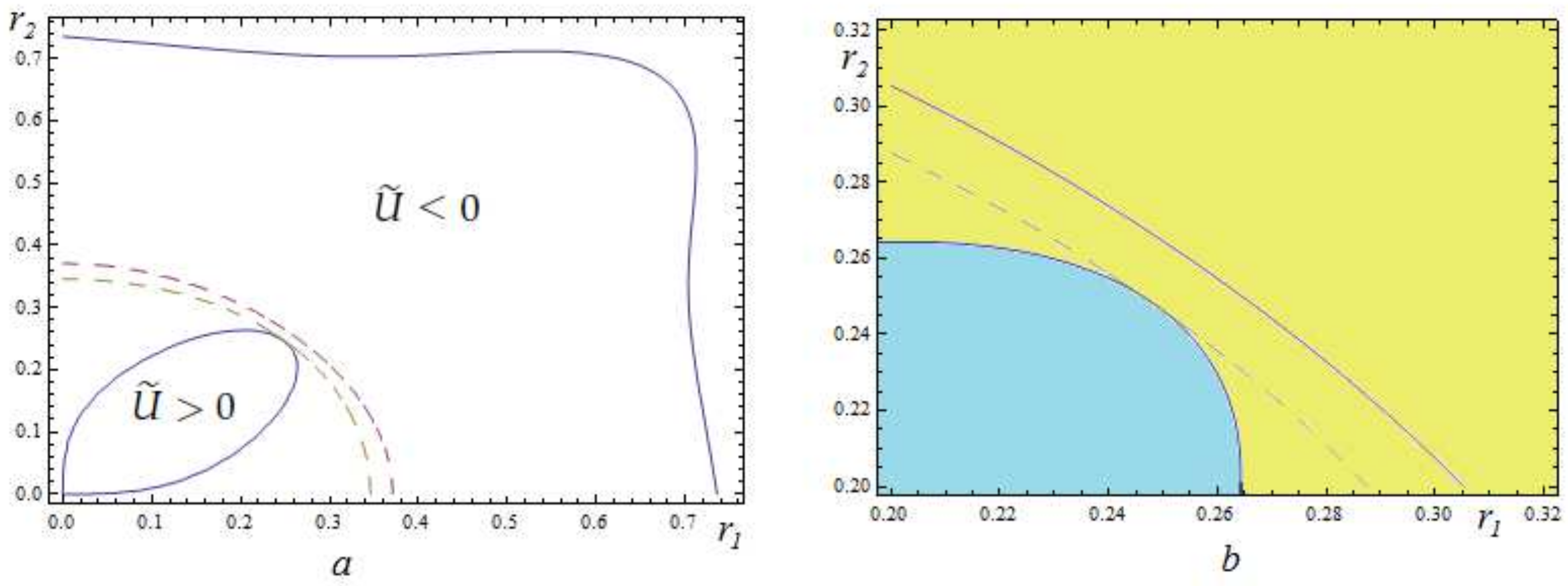
3. Main Results: Circulatory System with Three Degrees of Freedom

Let us consider the system (3) with the following matrices:

$$M=I_3,\tilde{K}=diag(k_1,k_2,k_3),\tilde{N}=\left(\begin{array}{ccc}0& n_{12}& n_{13}\\ -n_{12}& 0& n_{23}\\ -n_{13}& -n_{23}& 0\end{array}\right).$$

Firstly, we try the B-approach. The coefficients $a_j$ are:

$$a_3=1,a_2=k_1+k_2+k_3),a_1=k_1{k}_2+k_1{k}_3+k_2{k}_3+n_{12}^2+n_{13}^2+n_{23}^2,$$

$$a_0=k_1{k}_2{k}_3+k_1{n}_{23}^2+k_2{n}_{13}^2+k_3{n}_{12}^2.$$

(11)

The expressions for elements $p_j,$ according to their definition, are:

$$p_2={\parallel K\parallel }^2-{\parallel N\parallel }^2,p_3=\mathrm{Tr}{K}^3-3\mathrm{Tr}K{N}^2,$$

$$p_4=\parallel K^2{\parallel }^2+\parallel N^2{\parallel }^2-4{\parallel KN\parallel }^2+2\mathrm{Tr}\left({\left(KN\right)}^2\right),$$

(12)

where $\parallel \ast \parallel$ is the Frobenius norm of a matrix ∗, i.e., $\parallel K\parallel =\sqrt{{\sum }_{j,s=1}^n{k}_{js}^2}$.

These formulas give some idea of how the matrices K and N influence the elements $p_j,$ and allow describing stability/instability conditions in terms related to the structure of these matrices (for a 2-DOF system, such conditions were given in [19,31]). However, when $n\ge 3,$ for computational purposes, it is more convenient to express $p_4$ by the coefficients of $f(\Lambda )$ and after that by $p_1,p_2,p_3$ according to Formula (6). Because all coefficients of $f(\Lambda )$ are positive, Case (b) of Theorem 2 is unachievable, and the semi-positiveness of matrix P defines which, Case (a) or (c), takes place. With this observation, we have two expressions to analyze: ${\Delta }_2=3p_2-p_1^2$ and:

$${\Delta }_3=\mathsf{det}P==-3p_3^2+p_3(6p_1{p}_2-\frac{4}{3}{p}_1^3)-\frac{1}{6}{p}_1^6-\frac{7}{2}{p}_1^2{p}_2^2+\frac{3}{2}{p}_1^4{p}_2+\frac{1}{2}{p}_2^3.$$

(13)

Obviously, if $p_2\le 0$, then System (3) is unstable. Noting, in addition, that ${\Delta }_3$ may be presented in the form:

$${\Delta }_3=-\frac{1}{3}{(3p_3-p_1{\Delta }_2-\frac{1}{9}{p}_1^3)}^2+\frac{1}{54}{\left({\Delta }_2\right)}^3,$$

and if ${\Delta }_2\le 0,$ then ${\Delta }_3\le 0$ as well. This means that the positiveness of ${\Delta }_3$ implies the positiveness of ${\Delta }_2,$ and Case (a) takes place if $p_2>0,{\Delta }_3\ge 0$.

Considering the expression (13) as a polynomial of second order with respect to $p_3;$ its positiveness leads to the following inequalities:

$$p_1{p}_2-\frac{2}{9}{p}_1^3-\frac{\sqrt{2}}{18}{(3p_2-p_1^2)}^{3/2}<p_3<p_1{p}_2-\frac{2}{9}{p}_1^3+\frac{\sqrt{2}}{18}{(3p_2-p_1^2)}^{3/2},$$

and requirement $p_2>p_1^2/3$ or:

$${\parallel K\parallel }^2-{\parallel N\parallel }^2-\frac{1}{3}{\left(\mathrm{Tr}K\right)}^2>0$$

stands for the necessary condition of stability.

To compare the effectiveness of the B-approach, let us apply the technique of the G-approach. Taking into account the formulas (9), we get:

$${\Delta }_S^{\left(2\right)}=2(a_2^2-3a_1),{\Delta }_S^{\left(3\right)}=-27a_0^2+a_0(18a_1{a}_2-4a_2^3)-4a_1^3+a_1^2{a}_2^2.$$

Note that ${\Delta }_S^{\left(3\right)}$ is a quadratic polynomial on $a_0$ with a negative coefficient. Then, independently of other coefficients, the necessary condition of the positiveness of ${\Delta }_S^{\left(3\right)}$ is the non-negativeness of its discriminant (with respect to $a_0$): $d_1=16{(a_2^2-3a_1)}^3\ge 0$. Because of this fact and taking into account that $a_1>a_2^2/3,$ both ${\Delta }_S^{\left(2\right)}$ and ${\Delta }_S^{\left(3\right)}$ are negative. This means that there is no possibility of sign sequence $\{++-+\}.$ Therefore, if $r=3,$ consequently $d_f$ (discriminant of $f\left(\lambda \right)$) is not equal to zero, and there are only two possible sign combinations: $\{++++\}$ and $\{++--\}$. In the first case, $\mu =3,\nu =0,$ so f has three distinct real roots. The second case follows as $\mu =2,\nu =1,$ and f has one real root and a pair of complex conjugate roots.

Eventually, we come to the single condition of stability ${\Delta }_S^{\left(3\right)}>0$. Substituting the coefficients (11), we have:

$$D\left(f\right)=-4{(n_{12}^2+n_{13}^2+n_{23}^2)}^3+n_{12}^4[3{(k_1-k_2)}^2-2{(k_1+k_2-2k_3)}^2]+$$

$$+n_{13}^4[3{(k_1-k_3)}^2-2{(k_1+k_3-2k_2)}^2]+n_{23}^4[3{(k_2-k_3)}^2-2{(k_2+k_3-2k_1)}^2]+$$

$$+\frac{1}{2}{n}_{12}^2{n}_{13}^2[{(2k_1-k_2-k_3)}^2+39{(k_2-k_3)}^2]+\frac{1}{2}{n}_{12}^2{n}_{23}^2[{(2k_2-k_1-k_3)}^2+39{(k_1-k_3)}^2]+$$

$$+\frac{1}{2}{n}_{13}^2{n}_{23}^2[{(2k_3-k_2-k_1)}^2+39{(k_2-k_1)}^2]+n_{12}^2(k_1-k_3)(k_2-k_3)[3{(k_1-k_2)}^2-$$

$$-{(2k_3-k_1-k_2)}^2]+n_{13}^2(k_1-k_2)(k_3-k_2)[3{(k_1-k_3)}^2-{(2k_2-k_1-k_3)}^2]+$$

$$+n_{23}^2(k_2-k_1)(k_3-k_1)\left[3{(k_2-k_3)}^2\right)-{(2k_1-k_2-k_3)}^2]+{(k_1-k_2)}^2{(k_1-k_3)}^2{(k_2-k_3)}^2.$$

The current expression is large enough for direct analysis, though it has a symmetric form (is invariant toward cyclic permutation of the indexes $1,2,3$). Suppose that:

$$k_1<k_2<k_3.$$

(14)

Introducing the parameter transformation:

$$n_{12}^2=\frac{1}{4}{\parallel N\parallel }^4\frac{p_1}{k_3-k_1},n_{13}^2=\frac{1}{4}{\parallel N\parallel }^4\frac{q_2-q_1}{k_2-k_1},k_j=k_1+\frac{\sqrt{2}}{4}\parallel N\parallel [b_1+{(-1)}^{j+1}\sqrt{b_2}],$$

$$\lambda =\frac{\sqrt{2}}{4}\parallel N\parallel \tilde{\lambda },b_{j-1}\ge 0,j=2,3;b_2\le b_1^2,$$

(15)

and regarding:

$$n_{23}^2=\frac{1}{2}\parallel N\parallel -n_{12}^2-n_{13}^2,$$

we come to the following expression for discriminant (with respect to $\tilde{\lambda }$):

$$D=-27p_2^2+\frac{b_1}{2}{p}_2(b_1^2-9b_2+36)-\frac{1}{16}(4-b_2){(b_1^2-b_2+4)}^2.$$

(16)

Being considered as the quadratic polynomial with respect to $p_2,$ discriminant D may be positive only if expression:

$$D_{p_2}=b_1^2{(b_1^2-9b_2+36)}^2-27(4-b_2){(b_1^2-b_2+4)}^2={(b_1^2+3b_2-12)}^3$$

is positive. Then, the condition $D>0$ is equivalent to:

$$\frac{1}{108}[b_1(b_1^2-9b_2+36)-{(b_1^2+3b_2-12)}^{3/2}]<q_2<\frac{1}{108}[b_1(b_1^2-9b_2+36)-$$

$$-{(b_1^2+3b_2-12)}^{3/2}],$$

(17)

where parameters $b_1,b_2,q_2$ are connected to the coefficients of System (3) by Formula (15). The bounding surfaces from (17) are presented in Figure 1.

Finally, when $d=0,$ the polynomial f has three real roots, i.e., one of multiplicity two, if ${\Delta }_S^{\left(2\right)}\ne 0$$(\mu =2,\nu =0),$ and of multiplicity three, if ${\Delta }_S^{\left(2\right)}=0$.

To demonstrate the approach suggested, let us consider an example of a mechanical system. There are not many systems in the form of (3) with uncertain parameters for $n>2$ in the literature (with the analytical study of stability conditions) [30,38], so in order to underline the key-points, we take an example from [30].

Example 1.

Let us consider a three link pendulum subjected to the follower force. The last has two components: tangential$P_F$and constant non-tangential$P_C$(Figure 2, non-dissipative case). In the small vicinity of equilibrium${\theta }_j=0,j=1,2,3$, the linearized motion equations lead to System (3) with matrices:

$$M=m{l}^2\left(\begin{array}{ccc}9& 7& 3\\ 4& 4& 2\\ 1& 1& 1\end{array}\right),K+N=\left(\begin{array}{ccc}k-Pl& -Pl& Pl(3\alpha -1)\\ -k& k-Pl& Pl(2\alpha -1)\\ 0& -k& Pl(\alpha -1)+k\end{array}\right).$$

(18)

The dimensionless characteristic equation contains two parameters: α and$\beta =Pl/k$. By the help of the MD-approach, the stability domain was obtained, and six expressions$a_2(\alpha ,\beta ),a_1(\alpha ,\beta ),$$a_0(\alpha ,\beta ),D_1(\alpha ,\beta ),D_2(\alpha ,\beta ),D_3(\alpha ,\beta )$were involved in the process. Using the G-approach, only three expressions$a_2,a_2{a}_1-a_3{a}_0$, and$D=D_3$are needed. In order to bring some contrast to the results of [30], we assume that$P_C=0$(hence,$\alpha =1$), but at the same time, the stiffnesses of the joints$k_1,k_2,k_3$differ from one another. Introducing the dimensionless parameters and time:

$$\beta =\frac{Pl}{k_1},{\gamma }_1=\frac{k_2}{k_1},{\gamma }_2=\frac{k_3}{k_1},\tau =\frac{1}{l}\sqrt{\frac{k_1}{m}}t,$$

(19)

we have the following reduced characteristic polynomial:

$$f(\Lambda )=4{\lambda }^3+(2{\gamma }_1+10{\gamma }_2+14-8\beta ){\lambda }^2+[{\gamma }_1{\gamma }_2+6{\gamma }_1+19{\gamma }_2-2({\gamma }_1+3{\gamma }_2+5)\beta +$$

$$+3{\beta }^2]\lambda +{\gamma }_1{\gamma }_2.$$

The domain of stability is formed as the intersection of three sets:$a_2>0,$

$$g(\beta ,{\gamma }_1,{\gamma }_2)=-24{\beta }^3+(122+22{\gamma }_1+78{\gamma }_2){\beta }^2-4({\gamma }_1^2+10{\gamma }_1{\gamma }_2+15{\gamma }_2^2+24{\gamma }_1+84{\gamma }_2+$$

$$+35)\beta +2{\gamma }_1{\gamma }_2({\gamma }_1+5{\gamma }_2)+12{\gamma }_1^2+108{\gamma }_1{\gamma }_2+190{\gamma }_2^2+84{\gamma }_1+266{\gamma }_2>0,$$

and$D_f>0$(the corresponding expression is given in Appendix A).

The discriminant is the polynomial of sixth order and does not allow for any analytical reduction. Nevertheless, the corresponding 3D surfaces are smooth enough, and plotting does not present difficulties. The results are presented in Figure 3.

With the standard assumption of the equal stiffnesses at the joints$k_1=k_2=k_3,$the value of${\beta }_{crit}\approx 1.305$(Figure 3). With different values of$k_j$, this value can be markedly increased (up to 1.5 times). The optimal configuration is when$k_3$is bigger and$k_2$is smaller than$k_1$(see Figure 4).

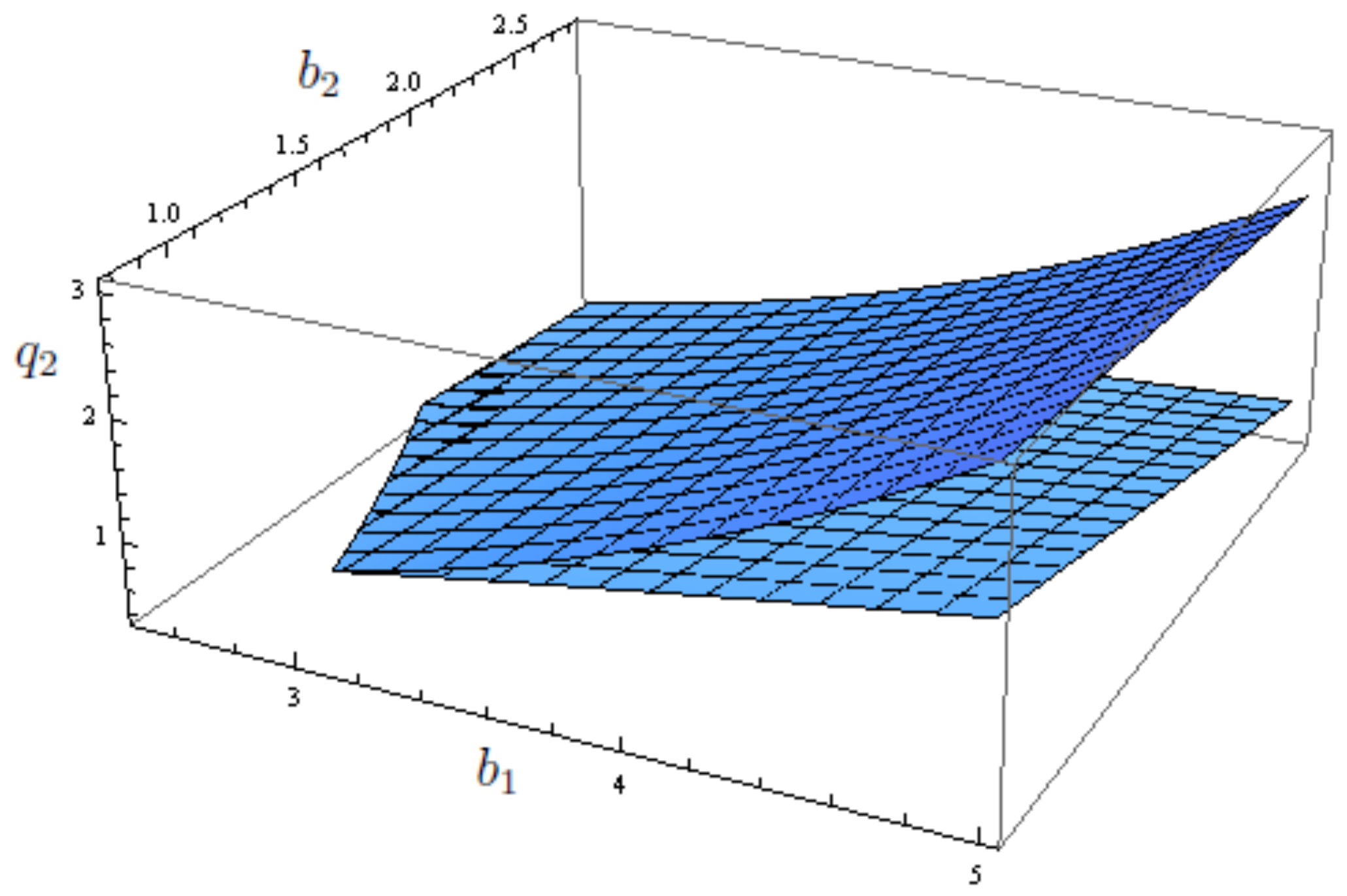
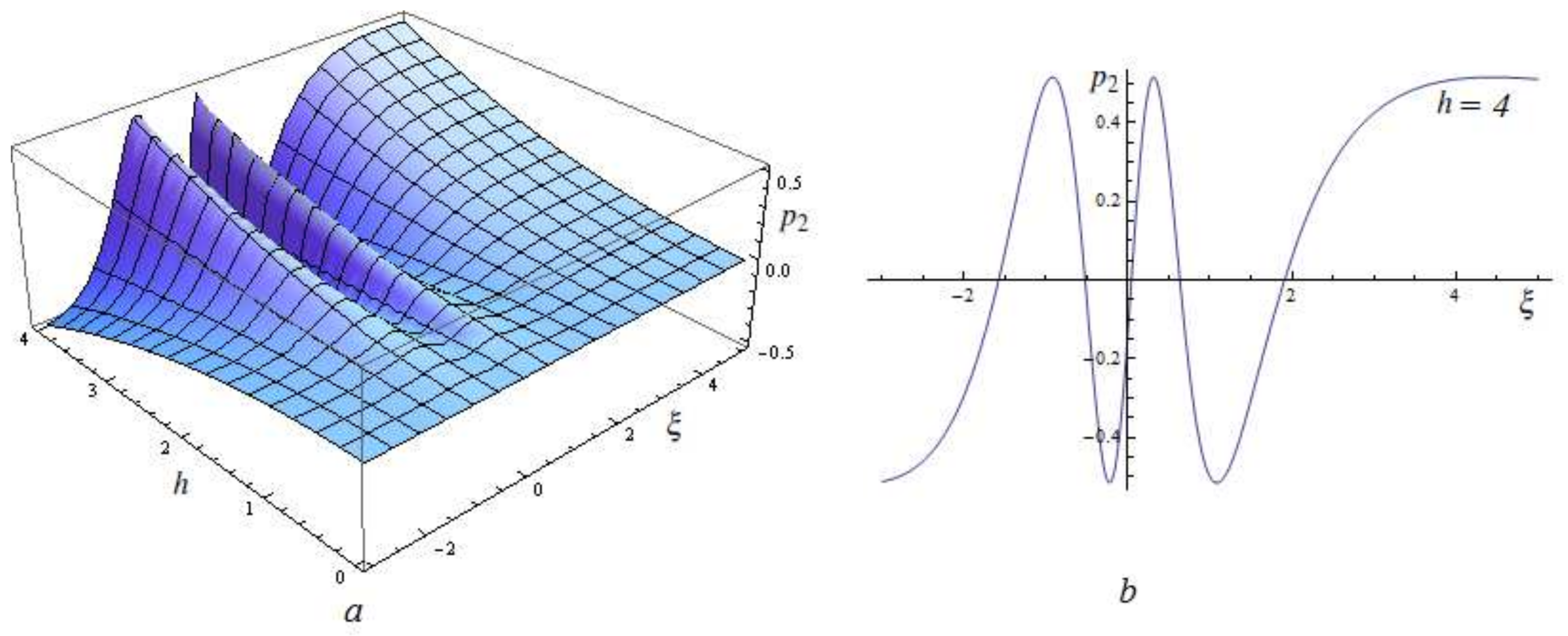
4. Special Case: Multiple Eigenvalues of Matrix K

This section was inspired by the recent publication of F. Udwadia [34], where he generalized the well-known theorem of Merkin [24]. The last one states that when matrix K has eigenvalue $\Lambda$ of multiplicity $n,$ an arbitrary small circulatory force brings flutter instability to the system. In order to generalize this theorem, as it was pointed out by Udwadia, the commutativity of matrices K and N is required. Note that the condition of instability in case $KN=NK$ was first obtained by Bulatovic [29].

Definition 3.

[34]. Consider an n-by-n block diagonal matrix:

$$A=\mathrm{diag}(A_1,A_2,\cdots ,A_k)$$

in which the s-th (square) diagonal block$A_s$has dimensions$i_s$by$i_s$with$i_1\ge i_2\ge \cdots \ge i_k,$and another n-by-n block diagonal matrix:

$$B=\mathrm{diag}(B_1,B_2,\cdots ,B_r)$$

for which the p-th (square) diagonal block$B_p$has dimensions$j_p$by$j_p$with$j_1\ge j_2\ge \cdots \ge j_r.$We shall say that matrices A and B have the same block diagonal structure if:

$$k=r,i_s=j_{s}s=1,\cdots ,k.$$

(20)

Theorem 4.

[34]. Let$K={\lambda }_1{I}_1+{\lambda }_2{I}_2+\cdots +{\lambda }_k{I}_k,$and T be the orthogonal transformation such that the diagonal matrix$\Omega =T^{\tau }KT$has repeated eigenvalues. The matrix$N=\mathsf{diag}(N_1,\cdots ,N_k)$that has the same block diagonal structure as Ω and where$N_j,j=1,\cdots ,k$are arbitrary skew-symmetric matrices will always commute with$\Omega ,$and the matrix$N_T=TN{T}^{\tau }$will always commute with$K.$Arbitrarily small elements in the matrices$N_j$will lead to a flutter instability of the system$\ddot{y}+(K+N_T)y=0.$

Though this result is interesting from a mathematical viewpoint, at first blush, it seems not to be very helpful in direct applications. The reason is that for the system (3) (as $M=I$), the requirement of the same block diagonal structure implies the decomposition of the whole system into unstable and stable (probably) subsystems. This observation yields the question: Why not consider each subsystem separately?

However, on second thought, the sense of this result opens the possibility to detect the instability for non-linear dynamical systems, especially systems of high dimension and/or multi-parameter ones. Here, the instability of a small (say, $k=2,3$) subsystem as a rule leads to the instability of the whole system, which may lead to serious reduction of the computational effort. Bearing this idea in mind, we shall try to introduce some modifications of the above-mentioned result based on the following way.

Let $B={(b_1,b_2,\cdots ,b_n)}^{\tau }$ be a rectangular matrix and $b_j(j=1,\cdots ,n)$ the rows. We “bisect” matrix B into two sub-matrices with q and $n-q$ rows, respectively, and shall use the notation $B_q,B\backslash B_q$ for them below.

Suppose that system $MKN$ allows the representation:

$$M=M_1⨁M_2,K=K_1⨁K_2,N=N_1⨁N_2,$$

where matrices $M_j,K_j(j=1,2)$ are square symmetric and positive definite and $N,N_j$ for skew-symmetric matrices. The dimensions of matrices $M_1,K_1,N_1$ are equal to $l\le n,$ and symbol “⨁” denotes the direct sum of matrices. Let further $J_{M_1}$ be the Jordan normal form of the matrix $M_1,$ i.e., $M_1=T_{M_1}{J}_{M_1}{\left(T_{M_1}\right)}^{-1},$ where the columns of transformation matrix $T_{M_1}$ are eigenvectors of $M_1.$ If $T_{M_1}$ is chosen in its counterpart orthogonal form, then ${\left(T_{M_1}\right)}^{-1}={\left(T_{M_1}\right)}^{\tau },$ and the matrix:

$${\tilde{K}}_1={\left(J_{M_1}\right)}^{-1/2}{T}_{M_1}^{\tau }{K}_1{T}_{M_1}{\left(J_{M_1}\right)}^{-1/2}$$

is symmetric and positive definite. Consequently, there exists an orthogonal matrix $T_{{\tilde{K}}_1}$ such that ${\tilde{K}}_1=T_{{\tilde{K}}_1}{J}_{{\tilde{K}}_1}{(T_{{\tilde{K}}_1})}^{\tau }.$ The following sufficient condition of instability for system $MKN$ is given by the following theorem.

Theorem 5.

Let the equation$det(M_1\Lambda +K_1)=0$have root${\Lambda }_1$of multiplicity$q\le l$(in other words, matrix$M_1^{-1/2}{K}_1{M}_1^{-1/2}$has the eigenvalue (semi-simple) of multiplicity q). Denote by$T_{M_1}$and$T_{{\tilde{K}}_1}$orthogonal matrices, the columns of which are formed by the eigenvectors of the corresponding matrix, and the first q columns are associated with multiple eigenvalues. Let the matrix equality:

$$T_{q}N{(T\backslash T_q)}^{\tau }=0,T=T_{M_1}^{\tau }{\left(J_{M_1}\right)}^{-1/2}{T}_{{\tilde{K}}_1}$$

(21)

hold. Then, if:

$$N_1^{\star }\triangleq T_{q}N{T}_q^{\tau }\ne 0,$$

(22)

the system$MKN$is unstable (flutter instability).

Proof. 

We remind that as block matrices $M_1,K_1$ are symmetric and positive definite, there eigenvalues determine the transformation matrices $T_{M_1},T_{{\tilde{K}}_1},$ and:

$$M_1=T_{M_1}{J}_{M_1}{\left(T_{M_1}\right)}^{-1},K_1=T_{{\tilde{K}}_1}{J}_{K_1}{(T_{{\tilde{K}}_1})}^{-1},$$

where $J_{M_1}{J}_{K_1}$ are Jordan normal forms of those matrices.

These forms are diagonal, and without loss of generality, we may count left upper cells of dimension q as containing proportional elements corresponding to eigenvalue ${\Lambda }_1.$ As matrices $T_{M_1},T_{{\tilde{K}}_1}$ are orthogonal, then their inverse matrices are equal to transpose ones; therefore, systems: $M_1\dot{y}+(K_1+N_1)y=0$ and:

$$J_{M_1}\dot{\xi }+T_{M_1}^{\tau }(K_1+N_1)T_{M_1}\xi =0,\xi \in R^l$$

(23)

are equivalent, i.e., have the identical fundamental matrices. According to the assumption, we have $J_{{\tilde{K}}_1}={\Lambda }_1{I}_q⨁\mathrm{diag}({\Lambda }_{q+1},\cdots ,{\Lambda }_l)$. Moreover, the linear nonsingular transformation $\xi ={\left(J_{M_1}\right)}^{-1/2}{T}_{{\tilde{K}}_1}{e}^{-{\Lambda }_{1}t}\eta$ leads to the following system:

$$\dot{\eta }+(J_{K_1}-{\Lambda }_1{I}_l+{\tilde{N}}_1)\eta =0,$$

(24)

and due to condition (21) ${\left(N_1\right)}_q=N_1^{\star }⨁0_q,$ the equality holds. This means that subsystem:

$${\dot{\eta }}_q+N_1^{\star }{\eta }_q=0$$

(25)

is separated. Using the Lyapunov function $V={\eta }_q^{\tau }{\eta }_q$, one may see that:

$$\frac{dV}{dt}{\mid }_{\left(25\right)}=-{\eta }_q^{\tau }{\left(N_1^{\star }\right)}^{\tau }{\eta }_q-{\eta }_q^{\tau }{N}_1^{\star }{\eta }_q=0,$$

but because of $\mathrm{rank}{N}_1^{\star }\ne 0,$ the system (25) has at least one pair of purely imaginary eigenvalues. This implies the existence of complex eigenvalues for System (24) and resulting in the flutter instability of System (3). □

Now, the calculation procedure will be explained by the following case study.

Example 2.

Consider the system (3) with:

$$M_1=\frac{1}{2}\left(\begin{array}{cccc}15& -9& 0& 0\\ -9& 15& 0& 0\\ 0& 0& 6& 0\\ 0& 0& 0& 6\end{array}\right),K_1=2\left(\begin{array}{cccc}9& -3& -\sqrt{2}& \sqrt{2}\\ -3& 9& -\sqrt{2}& \sqrt{2}\\ -\sqrt{2}& -\sqrt{2}& 7& 0\\ \sqrt{2}& \sqrt{2}& 0& 5\end{array}\right),$$

$$N_1=\left(\begin{array}{cccc}0& 2\sqrt{2}{n}_1& n_1-2n_2& -2n_1-n_2\\ -2\sqrt{2}{n}_1& 0& -n_1-2n_2& 2n_1-n_2\\ -n_1+2n_2& n_1+2n_2& 0& 2\sqrt{2}{n}_2\\ 2n_1+n_2& -2n_1+n_2& -2\sqrt{2}{n}_2& 0\end{array}\right),$$

(26)

where$n_1,n_2$are unknown parameters.

The eigenvalues of$M_1,K_1$are$12,3,3,3$and$6,12,18,24$, respectively. Since the matrices$T_{M_1},J_{M_1},{\tilde{K}}_1$are:

$$T_{M_1}=\frac{\sqrt{2}}{2}\left(\begin{array}{cc}1& 1\\ -1& 1\end{array}\right)⨁I_2,{\left(J_{M_1}\right)}^{-1/2}=\mathrm{diag}(\frac{1}{2},1,1,1),{\tilde{K}}_1=2\left(\begin{array}{cccc}3& 0& 0& 0\\ 0& 6& -2& 2\\ 0& -2& 7& 0\\ 0& 2& 0& 5\end{array}\right),$$

then:

$$T_{{\tilde{K}}_1}=\frac{1}{3}\left(\begin{array}{cccc}3& 0& 0& 0\\ 0& 2& 1& 2\\ 0& 1& 2& -2\\ 0& -2& 2& 1\end{array}\right),T^{\tau }=\frac{\sqrt{2}}{6}\left(\begin{array}{cccc}\frac{3}{2}& 2& 1& 2\\ -\frac{3}{2}& 2& 1& 2\\ 0& \sqrt{2}& 2\sqrt{2}& -2\sqrt{2}\\ 0& -2\sqrt{2}& 2\sqrt{2}& \sqrt{2}\end{array}\right).$$

Finally, because:

$$\left(\begin{array}{cccc}\frac{3}{2}& -\frac{3}{2}& 0& 0\\ 2& 2& \sqrt{2}& -2\sqrt{2}\end{array}\right)N_1{\left(\begin{array}{cccc}1& 1& 2\sqrt{2}& 2\sqrt{2}\\ 2& 2& -2\sqrt{2}& \sqrt{2}\end{array}\right)}^{\tau }=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right),$$

the equality (21) is satisfied, and to verify the condition (22), we get:

$$\left(\begin{array}{cccc}3& -3& 0& 0\\ 2& 2& \sqrt{2}& -2\sqrt{2}\end{array}\right)N_1{\left(\begin{array}{cccc}3& -3& 0& 0\\ 2& 2& \sqrt{2}& -2\sqrt{2}\end{array}\right)}^{\tau }=54\sqrt{2}{n}_1\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right).$$

According to the statement of Theorem 5, if$n_1\ne 0,$the system (26) is unstable, independently of the value of$n_2$.

Remark 1.

As follows from the formulation of the theorem, it gives the sufficient condition of instability. If the condition (22) is not satisfied, the stability of the system depends on the other components of matrix$N$. For instance, in Example 2, the roots of$f(\Lambda )$are:

$${\Lambda }_{1,2}=-1\pm \frac{\sqrt{2}}{4}i{n}_1,{\Lambda }_{3,4}=\frac{1}{2}(-5\pm \sqrt{1-2n_2^2}),$$

and if$n_1=0,$the system (26) is stable when$n_2^2<1/2$(is spectrally stable when$n_2=\pm \sqrt{2}/2$).

Example 3.

We consider one more example, which differs from the previous one. System (3) has a high dimension, and to avoid unnecessary conversions, we take$M=I$. Matrices$K,N$are:

$$K=\left(\begin{array}{ccccc}16& -4& 0& 0& -4\\ -4& 21& -5& 3& -1\\ 0& -5& 17& -3& 5\\ 0& 3& -3& 33& -3\\ -4& -1& 5& -3& 21\end{array}\right),N=\left(\begin{array}{ccccc}0& 0& n_{13}& n_{14}& 0\\ 0& 0& 0& n_{24}& -n_{13}\\ -n_{13}& 0& 0& n_{34}& 0\\ -n_{14}& -n_{24}& -n_{34}& 0& n_{45}\\ 0& n_{13}& 0& -n_{45}& 0\end{array}\right).$$

Even in this case, when matrices$M,K$are known, the dimension$n=5$, and more importantly, the presence of five uncertain parameters may cause a serious obstacle for finding the stability conditions. The potential system has two pairs of multiple eigenvalues, and from a common viewpoint, it raises a query about the existence of a such matrix N (even with$\parallel N\parallel \ll 1$), which would not bring the flutter instability. Again, the direct analysis of the characteristic polynomial is not so optimistic, i.e., the algorithm described in Section 3 still works, but the expressions calculated are very bulky. In order to omit the problem occurring, we try to employ Theorem 5.

The eigenvalues and eigenvectors of matrix K are as follows:

$${\Lambda }_{1,2}=12,{\beta }_1={(1,1,1,0,0)}^{\tau },{\beta }_2={(1,0,-1,0,1)}^{\tau },{\Lambda }_{3.4}=24,{\beta }_3={(-1,1,0,0,1)}^{\tau },$$

$${\beta }_4={(1,-2,1,1,0)}^{\tau },{\Lambda }_5=36,{\beta }_5={(0,-1,1,-3,1)}^{\tau }.$$

As matrix$\tilde{K}=K$has two different multiple eigenvalues, we have to choose one of them to determine block-matrix$K_1$. Let this matrix correspond to${\Lambda }_1=12,$(actually, there is no difference; the choice of$\Lambda =24$leads to the same conditions), then with transformation matrix T and taking into account that$q=2,$the equality (21) of the theorem imposes the following restrictions$n_{34}=-n_{14}-n_{24},n_{45}=2n_{14}+n_{24},$and hence, the condition (22) takes the form:

$$T_{q}N{T}_q^{\tau }=n_{13}\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right).$$

Thereby, if$n_{13}\ne 0,$the system (MKN) is unstable (even with an infinitely small magnitude of circulatory force). However, if$n_{13}=0,$components$n_{14},n_{24}$are responsible for stability or instability. As the system is decomposed, the characteristic polynomial is reduced to third order form:

$${\lambda }^3+7{\lambda }^2+[16+3{(n_{14}+n_{24})}^2]\lambda +12+\frac{51}{4}{n}_{14}^2+12n_{14}{n}_{24}+6n_{24}^2.$$

Its coefficients are positive, and its discriminant:

$$D=\frac{16}{3}[-4608n_{14}^6-13824n_{14}^5{n}_{24}+(543-20736n_{24}^2)n_{14}^4+(816-18432n_{24}^2)n_{14}^3{n}_{24}-$$

$$-(16-600n_{24}^2+10368n_{24}^4)n_{14}^2+(192-3456n_{24}^2)n_{14}{n}_{24}^3+48n_{24}^4-576n_{24}^6]$$

is positive in the domains shown in Figure 5. This result can be interpreted in the following way: when the potential system has multiple eigenvalues, the circulatory forces may contain “harsh” components, which break the stability no matter how small they are, and “soft” components are “dangerous” only if they are high enough.

5. Nonlinear Systems with Unstable Equilibrium

5.1. Some General Remarks

Theorem 5 leads to the following remarkable consequence: if the linear part of the nonlinear dynamical system:

$$M\ddot{x}+(D+G)\dot{x}+(K+N)x=F(x,\dot{x})$$

is decomposed into unstable and stable (even asymptotically stable) subsystems and these subsystems are connected by nonlinear terms, then the equilibrium of the system is unstable. Moreover, the linearly stable component may bring more “discords” into nonlinear dynamics. Let us explain this by employing the following example:

$$M=I_4,K=\mathsf{diag}(1,1,2,3),N=n_1\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)⨁n_2\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right),$$

(27)

$$D=0,G=0,F_1={(1.2x_1{x}_4,-0.5x_3^2,-n_2{x}_2{x}_4^2,n_2{x}_1{x}_3^2)}^{\tau }.$$

The linear part of System (27) is taken from Example 2 (with $n_1\ne 0$), so it is “semi-stable”, i.e., it consists of unstable and stable subsystems, and their eigenvalues are presented in Remark 1. To be able to perform numerical integration of the equations considered, we take $n_1=0.1,n_2=0.3,$ then ${\lambda }_{1,2,3,4}=\pm 0.0499\pm 1.0012\mathit{i},{\lambda }_{5,6}=\pm 1.7029\mathit{i},$${\lambda }_{7,8}=\pm 1.4491\mathit{i}$. If the initial perturbations are sufficiently small, then for a period of time, the motion is regular. For System (27) with initial values $x\left(0\right)={(0.001,0.03,-0.001,0.001)}^{\tau },\dot{x}\left(0\right)={(0.01,0.012,0.001,0.02)}^{\tau }$, this interval is approximately estimated as $[0,110]$. The maximal Lyapunov exponent is not very big (≈0.05), and the behavior with respect to $x_1,x_2$ is similar to linear instability (flutter). However, at some point, $t_{crit}\approx 111,$ the system dynamics very rapidly becomes chaotic, and in a few seconds, the trajectory whirls away (leaves the visible limits; and the computation is interrupted). The clear sign of chaotic behavior is the fact that the very small change of even one initial value ($x_1\left(0\right)$ from 0.001 to −0.001) leads to the divergence of trajectories (see Figure 6).

However, in applied research, Lyapunov’s instability is not always a “desperate” case. Often, for reliable operation of the device, the growth of solutions is allowed in some limits. In this case, even the positive Lyapunov exponent does not necessarily lead to the failure of the system. In order to illustrate the latter statement, let us consider the following system:

$${\ddot{x}}_1+x_1(1+x_2^2)+n{x}_2=0,{\ddot{x}}_2-n{x}_1+x_2(1+x_1^2)+n{x}_2=0,$$

$${\ddot{x}}_3+d{\dot{x}}_3(0.48-x_1^2-x_2^2)+2x_3(1-x_1^2)=0.$$

(28)

Its equilibrium $x=0,\dot{x}=0$ is unstable; however, numerical simulations show that the motions are bounded, if the initial perturbations are small enough (see Figure 7 and Figure 8). Furthermore, the behavior of component $x_3$ is remarkable. Contrary to Example 2, the motion is “almost” asymptotically stable with respect to this coordinate and its velocity. Speaking more strictly, it is unstable, but tends to zero as time increases. Note that time to time, there appear short intervals where the amplitude increases during two-three oscillations more then 50 times; nevertheless, it very quickly returns to small values (Figure 9).

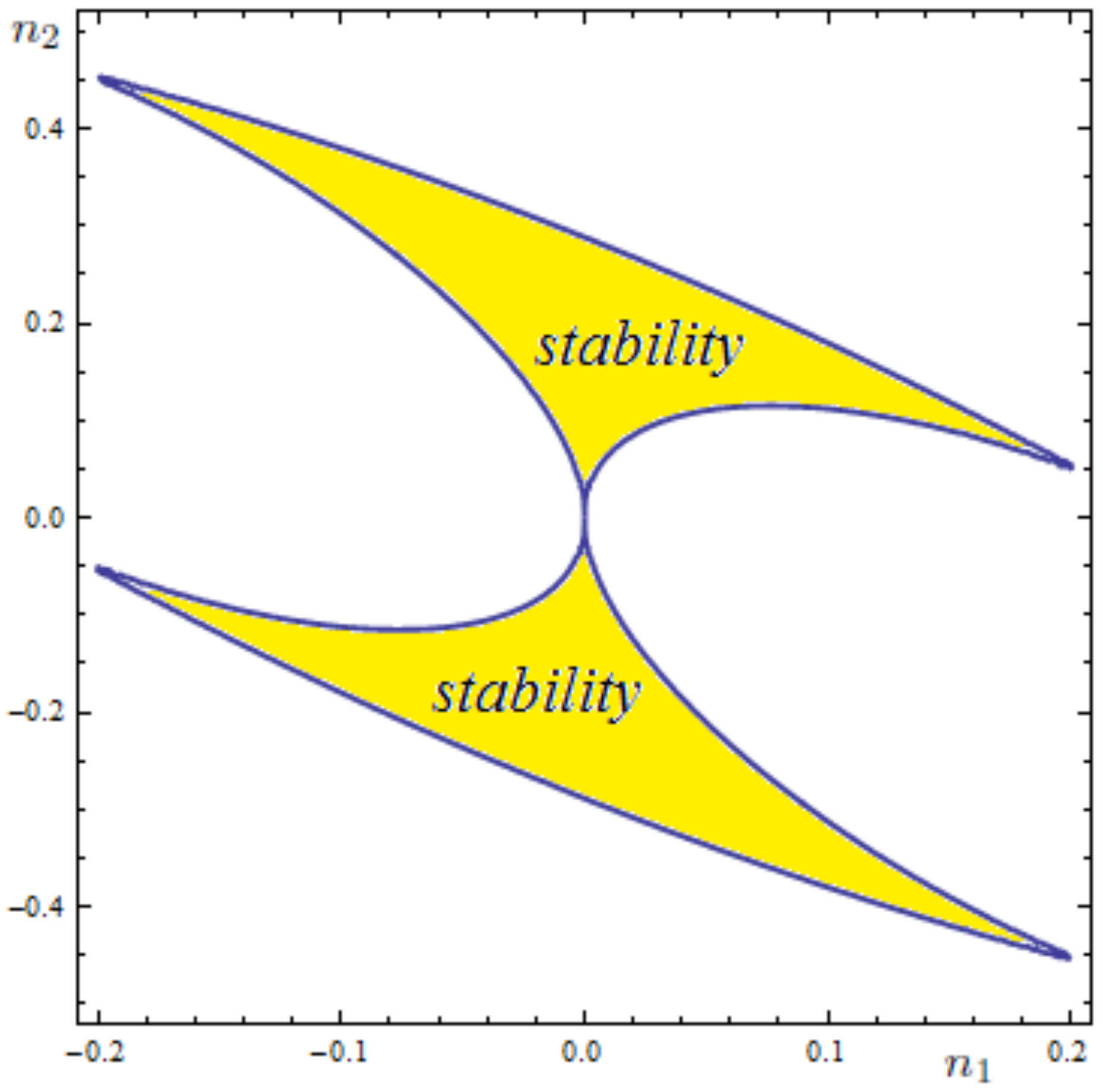
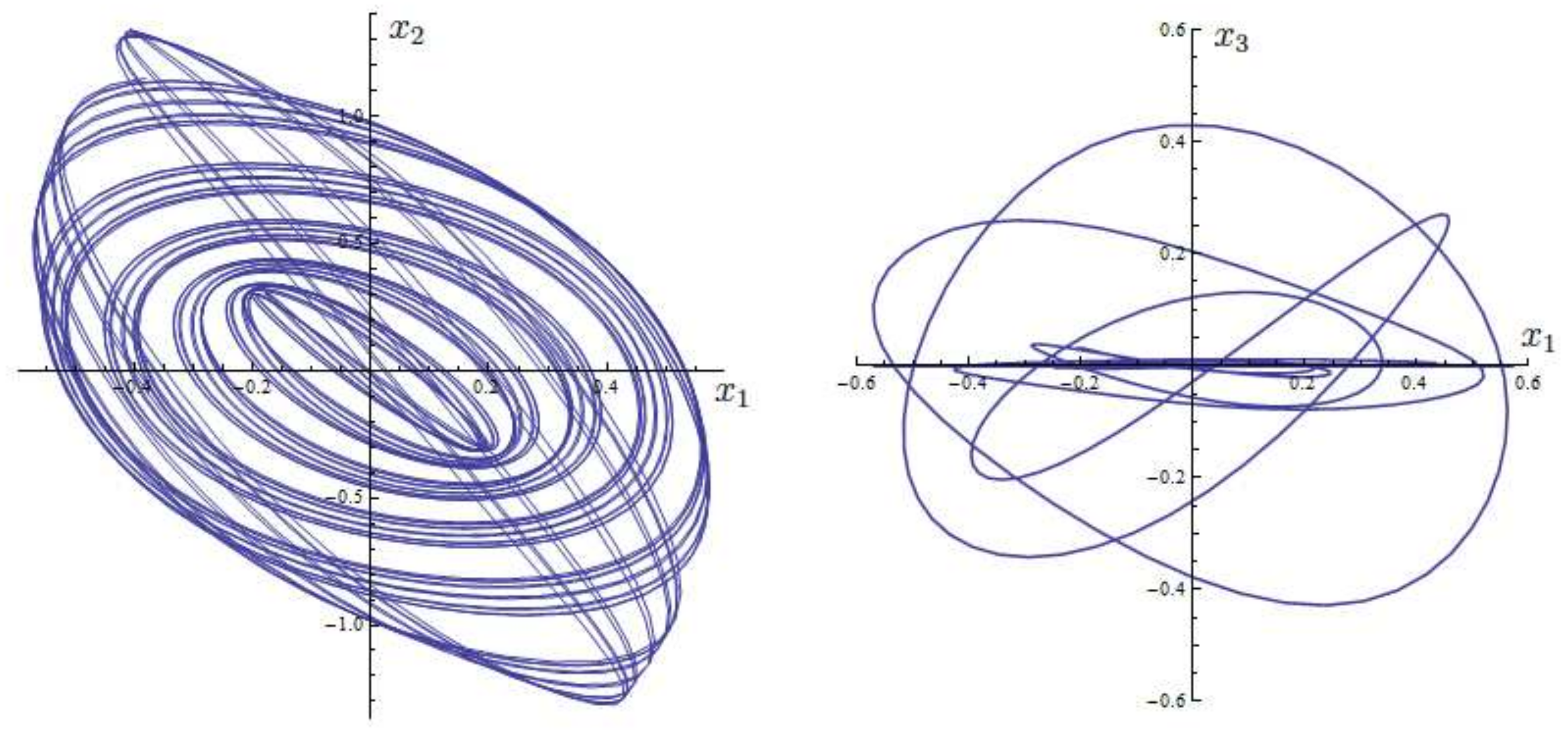
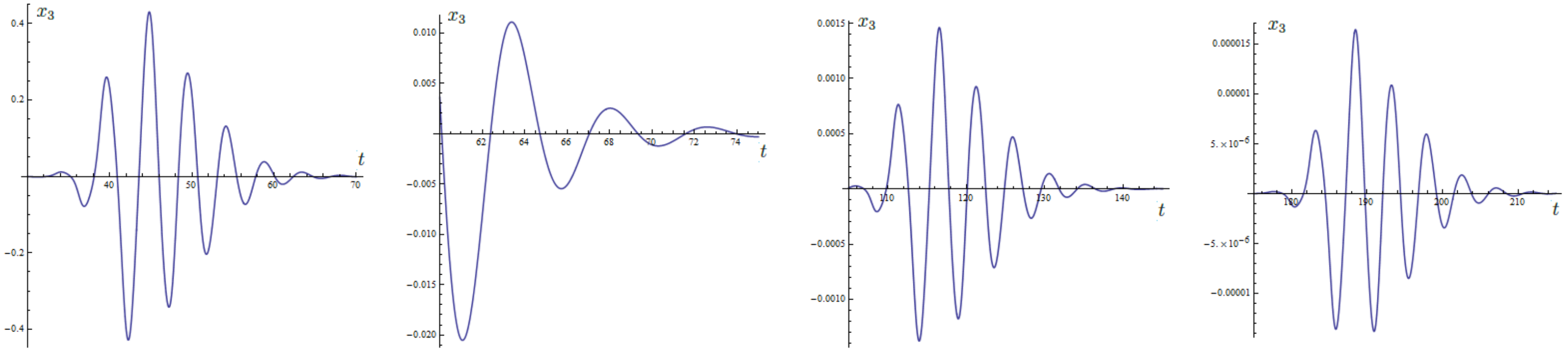
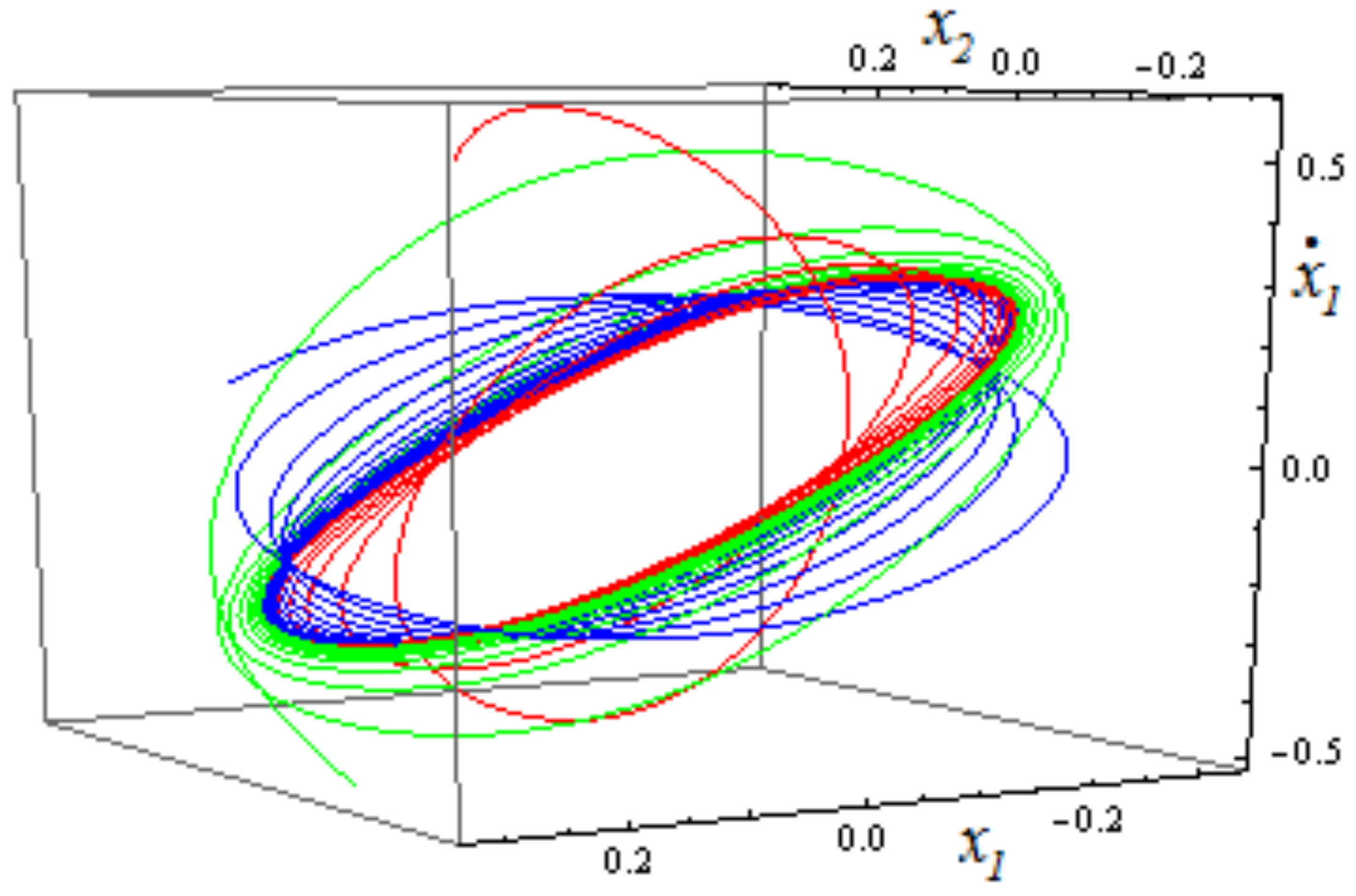
5.2. A Case Study: The Bounded Solutions of a 2-DoF System with Unstable Origin

Let D be some domain of $R^m$ containing the origin. Consider an ODE system:

$$\frac{d\mathit{x}}{dt}=\mathit{F}(t,\mathit{x}),\mathit{x}\left(t_0\right)={\mathit{x}}_0.$$

(29)

We assume that the function $\mathit{F}$ is continuous, and the Cauchy problem for (29) has a unique solution $\mathit{x}(t,t_0,{\mathit{x}}_0)$ that continuously depends on the initial values.

For any $t\in I=[t_0,+\infty )$, we consider the domains $D_1\left(t\right),D_2\left(t\right)$ containing the origin $\mathit{x}=\mathbf{0},$ such that their boundaries $\partial D_1,\partial D_2$ are continuous functions of time and $\partial D_l\left(t\right)\subset D_2\left(t\right)$. The following statement holds.

Lemma 1.

[39]. Assume that there exists a continuously differentiable function$U(t,\mathit{x}):I\times D_2\to R$and a continuous function$U_0(t,\mathit{x})\le U(t,\mathit{x})$such that:

(A) For any$t\ge t_0$, the function$U(t,\mathit{x})$is bounded for$\mathit{x}\in \partial D_1\left(t\right);$

(B) for any$(t,\mathit{x})\in I\times D_2\left(t\right)\backslash D_1\left(t\right)$, the time derivative of the function$U(t,\mathit{x})$with respect to system (1) is non-positive;

(C) for any pair$t_l,t_2(t_2>t_1)$from I, the following inequality holds:

$$\underset{\mathit{x}\in \partial D_1\left(t_1\right)}{sup}U(t_1,\mathit{x})<\underset{\mathit{x}\in \partial D_2\left(t_2\right)}{inf}{U}_0(t_2,\mathit{x}).$$

Then, for any$t_0\in I$, the premise${\mathit{x}}_0\in D_1\left(t_0\right)$implies that$\mathit{x}(t,t_0,\mathit{x})\in D_2\left(t\right)$.

This statement may be applied for different purposes: to prove the stability (marginal or asymptotic), the boundedness of the solutions, the estimation of the rate of the asymptotic behavior, etc.

To illustrate it, let us consider the following system:

$${\ddot{x}}_1+h{\dot{x}}_1{x}_1^2+x_1(k_1-k_2{x}_1^2)+n{x}_2=0,{\ddot{x}}_2+h{\dot{x}}_2{x}_2^2-n{x}_1+x_2(k_1-k_2{x}_2^2)=0,$$

(30)

Here, $h,k_1,k_2,n$ are some positive dimensionless parameters. System (30) may be considered as the equations of motion of two identical non-linear oscillators connected due to the influence of circulatory force. This system has a single equilibrium $\mathit{x}=\mathbf{0},\dot{\mathit{x}}=\mathbf{0}$, which is asymptotically stable if $n=0$ and is unstable for any arbitrary small non-zero value of $n.$ The eigenvalues of the linearized system are located at the tops of the square in the complex plane; their values are:

$${\lambda }_{1,2}=\frac{1}{\sqrt{2}R}[n\pm i(k_1+R)],{\lambda }_{3,4}=\frac{1}{\sqrt{2}R}[-n\pm i(k_1+R)],R=\sqrt{k_1+\sqrt{k_1^2+n^2}}.$$

(31)

Thus, the maximal Lyapunov exponent is equal to $n/\sqrt{2}R,$ and the origin is exponentially unstable. However, if the ratio $n/k_1$ is small enough, then all trajectories incipient in the vicinity of the origin are bounded. To prove this fact, we shall use the lemma.

First of all, we realign the variables, parameters, and time according to formulas:

$$x_j=\sqrt{\frac{k_1}{k_2}}{\tilde{x}}_j(j=1,2),h=\frac{k_2}{\sqrt{k_1}}\tilde{h},t=\frac{\tilde{t}}{\sqrt{k_1}}.$$

(32)

This allows formally putting the values of $k_1$ and $k_2$ in Equation (30) equal to one (for convenience, the symbol “∼” is omitted below). As the system considered is autonomous, we shall seek the polynomial positive definite auxiliary function as the sum of the quadratic part and the form of fourth order: $U(\mathit{x},\dot{\mathit{x}})=U^{\left(2\right)}+U^{\left(4\right)}.$ Obviously, it is impossible to achieve the negative definiteness of ${\dot{U}}^{\left(2\right)}$ (the presence of a positive Lyapunov exponent); thus, we aim for the negativeness of ${\dot{U}}^{\left(4\right)}$ to satisfy Condition (B) of the lemma. The function U is taken in the following form:

$$U(x_1,x_2,{\dot{x}}_1,{\dot{x}}_2)=x_1^2+x_2^2+{\dot{x}}_1^2+{\dot{x}}_2^2-\frac{1}{16}[3{\dot{x}}_1^4+6x_1^2{\dot{x}}_1^2-5x_1^4+3{\dot{x}}_2^4+$$

(33)

$$+6x_2^2{\dot{x}}_2^2-5x_2^4-4h[{\dot{x}}_1{x}_1({\dot{x}}_1^2+x_1^2)+{\dot{x}}_2{x}_2({\dot{x}}_2^2+x_2^2)],$$

and its time derivative with respect to System (30) is:

$$\dot{U}=2n({\dot{x}}_1{x}_2-{\dot{x}}_2{x}_1)-\frac{1}{4}h[{({\dot{x}}_1^2+x_1^2)}^2+{({\dot{x}}_2^2+x_2^2)}^2+n{x}_1{x}_2(x_1^2-x_2^2-3{\dot{x}}_1^2+3{\dot{x}}_2^2)]+$$

$$+\frac{3}{4}n[{\dot{x}}_1{x}_2({\dot{x}}_1^2+x_1^2)-{\dot{x}}_2{x}_1({\dot{x}}_2^2+x_2^2)]-\frac{1}{4}[h{x}_1^2(3{\dot{x}}_1^4+6{\dot{x}}_1^2{x}_1^2-x_1^4)+$$

(34)

$$+h{x}_2^2(3{\dot{x}}_2^4+6{\dot{x}}_2^2{x}_2^2-x_2^4)+(3-h^2)({\dot{x}}_1{x}_1^5+{\dot{x}}_2{x}_2^5)+(3+h^2)({\dot{x}}_1^3{x}_1^3+{\dot{x}}_2^3{x}_2^3)]$$

The upper bound for derivative $\dot{U}(\mathit{x},\dot{\mathit{x}})$ may be derived in the form:

$$\dot{U}\le \tilde{U}(r_1,r_2)\triangleq -\frac{1}{4}\{-n{r}_1{r}_2(4+r_1^2+r_2^2)+h(r_1^4+r_2^4)-$$

(35)

$$-\frac{3}{4}n{p}_1{(r_1^2+r_2^2)}^2-[4h+\sqrt{h^4+21h^2+36}+p_2](r_1^6+r_2^6)\}.$$

Here, $r_j=\sqrt{x_j^2+{\dot{x}}_j^2}(j=1,2),p_1\approx 1.4,$ and the value of $p_2\left(h\right)$ depends on parameter h and is defined as:

$$p_2\left(h\right)=h\underset{\xi \in R}{max}\frac{{\xi }^6-15{\xi }^4+15{\xi }^2-1+2h\xi (3{\xi }^4-10{\xi }^2+3)}{{({\xi }^2+1)}^3}.$$

(36)

The surface $p=p_2(h,\xi )$ is presented in Figure 10.

From the other side, the function U satisfies the following inequalities:

$$\begin{array}{cc}\hfill U_0\triangleq r_1^2+r_2^2& -\frac{1}{16}(\sqrt{h^2+1}+4)(r_1^4+r_2^4)\le U(\mathit{x},\dot{\mathit{x}})\le r_1^2+r_2^2\hfill \\ \hfill & -\frac{1}{16}(\sqrt{h^2+1}+4)(r_1^4+r_2^4)\triangleq U_1.\hfill \end{array}$$

(37)

In the vicinity of the origin of the first quadrant of the plane $O{r}_1{r}_2$, the boundary of the set $\tilde{U}(r_1,r_2)=0$ is formed by two branches (solid lines in Figure 11a). The smaller one bounds the domain $\tilde{U}>0$. Thus, we should choose the domain $D_1$ in such a way that $\partial D_1$ belongs to domain $\tilde{U}\le 0$. It can be taken as $U_1(r_1,r_2)\le \alpha (h,n),$ where $\alpha$ is some constant number. Then, the boundary of $D_2$ may be given by condition $U_0=\alpha +\epsilon ,$ where $\epsilon$ is an arbitrary small positive number. Therefore, all conditions of the lemma are fulfilled, and all trajectories starting in $D_1$ are limited by the threshold of $\partial D_2.$ For values $h=4,n=0.1$, these domains are presented in Figure 11.

This conclusion is confirmed by numerical integration of System (30). For different starting points of the phase space, the trajectories go to the limit cycle (Figure 12). In fact, the estimation shown in Figure 11 is accurate enough.

6. Concluding Remarks

In this paper, we discussed some stability problems for circulatory dynamical systems. Although existing analytical methods allow us to solve the problem (obtaining stability conditions in the closed form) in the case of high order systems with uncertain parameters, these conditions may turn out to be too cumbersome for analysis. Therefore, it is advisable to use optimized algorithms from the point of view of avoiding “unnecessary” computational procedures, which allows reducing the computation time and, possibly, obtaining stability conditions in a simpler form. Some of these procedures were discussed in Section 2 and tested in Section 3. In Section 4, a case of multiple eigenvalues was studied. It is interesting from a theoretical viewpoint as well, as this case often occurs in different applications. A sufficient condition of instability was formulated. In Section 5, some interesting examples of nonlinear dynamics were considered. Then, it was demonstrated that the flutter instability of the linearized system may lead to various results, namely the motion may become chaotic with overwhelming growth of the amplitude and may be bounded. Actually, it may be even asymptotically stable with respect to part of the variables. However, the rigorous study of this question is based on the use of Lyapunov functions for a nonlinear multi-parameter system, which leads to extremely complicated transformations and requires a separate study.

The future research will consider the problem of free flexural vibrations and dynamic loads in an elastic rod with stepwise-changing stiffness, as well as the application of the stated results to the hemivariational principles such as damage [40,41].