Binary Context-Free Grammars

Abstract

A binary grammar is a relational grammar with two nonterminal alphabets, two terminal alphabets, a set of pairs of productions and the pair of the initial nonterminals that generates the binary relation, i.e., the set of pairs of strings over the terminal alphabets. This paper investigates the binary context-free grammars as mutually controlled grammars: two context-free grammars generate strings imposing restrictions on selecting production rules to be applied in derivations. The paper shows that binary context-free grammars can generate matrix languages whereas binary regular and linear grammars have the same power as Chomskyan regular and linear grammars.

1. Introduction

A “traditional” phrase-structure grammar (also known as a Chomskyan grammar) is a generative computational mechanism that produces strings (words) over some alphabet starting from the initial symbol and sequentially applying production rules that rewrite sequences of symbols [1,2,3]. According to the forms of production rules, phrase-structure grammars and their languages are divided into four families: regular, context-free, context-sensitive, and recursively enumerable [4,5].

Regular and context-free grammars, which have good computational and algorithmic properties, are widely used in modeling and studying of phenomena appearing in linguistics, computer science, artificial intelligence, biology, etc. [6,7]. However, many complex structures such as duplication ($ww$), multiple agreements ($a^n{b}^n{c}^n$) and crossed agreements ($a^n{b}^m{c}^n{d}^m$) found in natural languages, programming languages, molecular biology, and many other areas cannot be represented by context-free grammars [6]. Context-sensitive grammars that can model these and other “non-context-free" structures are too powerful in order to be used in applications [5,8]. In addition many computational problems related to context-sensitive grammars are undecidable, and known algorithms for decidable problems concerning to these grammars have exponential complexities [4,5,6,9].

An approach to overcome this problem is to define “in-between’’ grammars that are powerful than context-free grammars but have similar computational properties. Regulated grammars are such types of grammars that are defined by adding control mechanisms to underlying context-free grammars in order to select specific strings for their languages [5]. Several variants of regulated grammars, such as matrix, programmed, ordered, context-conditional, random-context, tree-controlled grammars, have been defined according to control mechanisms used with the grammars [5,6,8]. Regulated grammars are classified into two main categories: rule-based regulated grammars that generate their languages under various production-related restrictions, and context-based regulated grammars that produce their languages under different context-related restrictions [10].

Though this type of the classification of regulated grammars allows us to understand the nature of restrictions imposed on the grammars, it does not clarify the role of control mechanisms from the aspect of the computational power. If we observe the control mechanisms used in both categories of regulated grammars, we can see that they consist of two parts [6]: (1) a “regular part", which is represented by a regular language of the labels of production rules (in rule-based case) or a regular language over the nonterminal and/or terminal alphabets (in context-based case) and (2) an “irregular part", which is represented by appearance checking (in rule-based case) and forbidding context (in context-based case), provides an additional power to the regular part.

If a regular part is solely used, the regulated grammars can generate small subsets of context-sensitive languages. On the other hand, if the both of regulations are used, then most regulated grammars generate all context-sensitive languages [6,10]. At this point, we again return to the same computational problems related to context-sensitive grammars, which we discussed early. Thus, we need to consider such regulation mechanisms that can grant to extend the family of context-free languages only to required ranges that cover necessary aspects of modeled phenomena. One of the possibilities to realize this idea can be the combination of several regular control mechanisms. One can consider a matrix of matrices or a matrix conditional context as combined regulation mechanisms. For instance, paper [11] studied simple-semi-conditional versions of matrix grammars with this approach. The problem in this case is that the combinations of such control mechanisms are, firstly, not natural and, secondly, they are too complex.

We propose, as a solution, an idea of imposing multiple regulations on a context-free grammar without combining them. We realize this idea by using relational grammars. A relational grammar is an n-ary grammar, i.e., a system of n terminal alphabets, n nonterminal alphabets, a set of n-tuples of productions and the initial n-tuple of nonterminals that generates the language of relations, i.e., tuples of strings over the terminal alphabets. On the other hand, a relational grammar can be considered of a system of n grammars in which each grammar generates own language using the corresponding productions enclosed in n-tuples. Thus, we can redefine a relational grammar as a system of mutually controlled n grammars where the grammars in relation generate their languages imposing restrictions on the applications of productions of other grammars. If we specify one grammar as the main, the other grammars in the system can be considered to be the regulation mechanisms controlling the generative processes of the main grammar.

This work is a preliminary work in studying mutually controlled grammars. In this paper, we define binary context-free grammars and study their generative power. We show that even mutually controlled two grammars can be as powerful as matrix grammars or other regulated grammars without appearance checking or forbidding context.

The paper is organized as follows. Section 2 surveys on regulated, parallel and relational grammars that are related to the introduced grammars. Section 3 contains necessary notions and notations used throughout the paper. Section 4 defines binary strings, languages and grammars Section 5 introduces synchronized normal forms for binary grammars and shows that for any binary context-free (regular, linear) grammar there exists an equivalent binary grammar in synchronized form. Section 6 investigate the generative powers of binary regular, linear and context-free grammars. Section 7 discusses the results of the paper and the power of mutually controlled grammars, and indicates to possible topics for future research.

2. Regulated, Parallel and Relational Grammars

In this section, we briefly survey some variants of regulated grammars with respect to the control mechanisms associated with them, parallel grammars as well as relational grammars, which are related to the introduced mutually controlled grammars.

The purpose of regulation is to restrict the use of the productions in a context-free grammar to select only specific terminal derivations successful hence to obtain a subset of the context-free language generated in usual way. Various regulation mechanisms used in regulated grammars can be classified into general types by their common features.

Control by prescribed sequences of production rules where the sequence of productions applied in a derivation belong to a regular language associated with the grammar:

• matrix grammars [12]—the set of production rules is divided into matrices and if the application of a matrix is started, a second matrix can be started after finishing the application of the first one, as well as the rules have to been applied in the order given a matrix;
• vector grammars [13]—in which a new matrix can be started before finishing those which have been started earlier;
• regularly controlled grammars [14]—the sequence of production rules applied in a derivation belong to a given regular language associated with the grammar.

Control by computed sequences of production rules where a derivation is accompanied by a computation, which selects the allowed derivations:

• programmed grammars [15]—after applying a production rule, the next production rule has to be chosen from its success field, and if the left hand side of the rule does not occur in the sentential form, a rule from its failure field has to be chosen;
• valence grammars [16]—where with each sentential form an element of a monoid is associated, which is computed during the derivation and derivations where the element associated with the terminal word is the neutral element of the monoid are accepted.

Control by context conditions where the applicability of a rule depends on the current sentential form and with any rule some restrictions are associated for sentential forms which have to be satisfied in order to apply the rule:

• random context grammars [17]—the restriction is the belonging to a regular language associated with the rule;
• conditional grammars [18]—the restriction to special regular sets;
• semi-conditional grammars [19]—the restriction to words of length one in the permitting and forbidden contexts;
• ordered grammars [18]—a production rule can be applied if there is no greater applicable production rule.

Control by memory where with any nonterminal in a sentential form, its derivation is associated:

• indexed grammars [20]—the application of production rules gives sentential forms where the nonterminal symbols are followed by sequences of indexes (stack of special symbols), and indexes can be erased only by rules contained in these indexes but erasing of the indexes is done in reverse order of their appearance.

Control by external mechanism where a mechanism used to select derivations does not belong to the grammar:

• graph-controlled grammars [21,22]—the sequence of productions applied in a derivation to obtain a string corresponds to a path, whose nodes represent the production rules, in an associated bicolored digraph;
• Petri net controlled grammars [23,24]—the sequence of productions used to obtain a string of the language of a grammar corresponds to a firing sequence of transitions, which are labeled by the productions, from the initial marking to a final marking.

Parallelism is another nontraditional approach used with grammars where, instead of rewriting a single symbol in each derivation step, several symbols can be rewritten simultaneously. There are two main variants of parallel mechanisms associated with grammars. The first is total parallelism, which is used in the broad varieties of (Deterministic Extended Tabled Zero-Sided) Lindenmayer systems [5,25] where all symbols of strings including terminals are in each step rewritten by productions. The second is partial parallelism where all or some nonterminal symbols (not terminal symbols) are written in each step of the derivations:

• absolutely parallel grammars [26]—all nonterminals of the sentential form are rewritten in one derivation step;
• Indian parallel grammars [27]—all occurrences of one letter are replaced (according to one rule);
• Russian parallel grammars [28]—which combines the context-free and Indian parallel feature;
• scattered context grammars [29]—in which only a fixed number of symbols can be replaced in a step but the symbols can be different;
• concurrently controlled grammars [30]—the control over a parallel application of the productions is realized by a Petri net with different parallel firing strategies.

Another perspective in using the notion of parallelism with grammars is a grammar system, which is a system of several phrase-structure grammars with own axioms, symbols and rewriting productions that can work simultaneously and generate own strings. One of such grammar systems is a parallel communicating grammar system [31,32], where the grammars start from separate axioms, work parallelly rewriting their own sentential forms, and also communicate with each other by request. The language of one distinguished grammar in the system is considered the language of the system.

A relational grammar (an n-ary grammar) can be considered to be another type of grammar systems consisting of several grammars that work by applying productions synchronously or asynchronously [33,34]. More precisely, an n-ary grammar (where n is a positive integer) is a system of n terminal alphabets, n nonterminal alphabets, a set of productions and an initial n-tuple of nonterminals. Each production is an n-tuple of common productions or empty places. An n-ary grammar generates the language of relations, i.e., n-tuples of strings over the terminal alphabets. Work [33] showed that classes of languages generated by relational grammars forms a hierarchy between the family of context-free languages and the family of context-sensitive languages. Paper [34] studied closure, projective and other properties of relational grammars, and generalized the Chomsky’s classification for n-ary grammars. Several other papers [35,36,37,38,39,40] also investigated the properties of relational grammars and applied in solving problems appeared in natural and visual language processing.

3. Notions and Notations

Throughout the paper, we assume that the reader is familiar with the basic concepts and results of the theory of formal languages, Petri nets and relations; for details we refer to [4,9,41] (formal languages, automata, computation), [6,10] (regulated rewriting systems), [42,43] (Petri nets), [23,24,44] (Petri net controlled grammars), and [33,34,45,46,47,48] (finitary relations). Though, in this section, we recall all necessary notions and notations that are important for understanding this paper.

Basic conventions: the inclusion is denoted by ⊆ and the strict (proper) inclusion is denoted by ⊂. The symbol ∅ denotes the empty set. The powerset of a set X is denoted by $\mathcal{P}\left(X\right)$, while its cardinality is denoted by $\left|X\right|$. An ordered sequence of elements $a,b$ is called a pair and denoted by $(a,b)$. Two pairs $(a_1,a_2)$ and $(b_1,b_2)$ are equal iff $a_1=b_1$ and $a_2=b_2$. Let $X,Y$ be sets. The set of all pairs $(a,b)$, where $a\in X$ and $b\in Y$, is called the Cartesian product of X and Y, and denoted by $X\times Y$. Then, $X\times X=X^2$. A binary relation on sets $X,Y$ is a subset of the Cartesian product $X\times Y$.

Strings, Languages and Grammars

We first recall the fundamental concepts of the formal language theory such as an alphabet, a string and a language from [41]:

Definition 1.

An alphabet is a nonempty set of abstract symbols.

Definition 2.

A string (or a word) over an alphabet Σ is a finite sequence of symbols from Σ. The sequence of zero symbols is called the empty string, and denoted by λ. The set of all strings over Σ is denoted by ${\Sigma }^{*}$. The set ${\Sigma }^{*}-\left\{\lambda \right\}$ is denoted by ${\Sigma }^{+}$.

Definition 3.

A subset of ${\Sigma }^{*}$ is called a language.

Definition 4.

The number of the occurrences of symbols in $w\in {\Sigma }^{*}$ is called its length and denoted by $\left|w\right|$. The number of occurrences of a symbol x in a string w is denoted by ${\left|w\right|}_x$.

Example 1.

Let $\Sigma =\{a,b,c\}$ be an alphabet. Then, $w=aaabbbcc$ is a string over Σ where $\left|w\right|=8$ and ${\left|w\right|}_a={\left|w\right|}_b=3$, ${\left|w\right|}_c=2$. We can notice that w belongs to $L=\{a^n{b}^n{c}^m\mid n\ge 1,m\ge 1\}$, which is a language over Σ.

Next, we cite the definitions of context-free, matrix grammars and related notations which are more detailly given in [4,6].

Definition 5.

A context-free grammar is a quadruple $G=(V,\Sigma ,S,R)$ where V and Σ are disjoint alphabets of nonterminal and terminal symbols, respectively, $S\in V$ is the start symbol and $R\subseteq V\times {(V\cup \Sigma )}^{*}$ is a finite set of (production) rules. Usually, a rule $(A,x)$ is written as $A\to x$. A rule of the form $A\to \lambda$ is called an erasing rule, and a rule of the form $A\to x$, where $x\in {\Sigma }^{*}$, is called terminal.

Definition 6.

Let $G=(V,\Sigma ,S,R)$ be a context-free grammar. If $R\subseteq V\times {\Sigma }^{*}(V\cup \left\{\lambda \right\})$, then G is called regular, and if $R\subseteq V\times {\Sigma }^{*}(V\cup \left\{\lambda \right\}){\Sigma }^{*}$, then it is called linear.

The families of regular, linear and context-free languages are denoted by $\mathcal{L}\left(\mathsf{REG}\right)$, $\mathcal{L}\left(\mathsf{LIN}\right)$ and $\mathcal{L}\left(\mathsf{CF}\right)$, respectively.

Definition 7.

Let $G=(V,\Sigma ,S,R)$ be a context-free grammar.

• The string $x\in {(V\cup \Sigma )}^{+}$ directly derives $y\in {(V\cup \Sigma )}^{*}$, written as $x\to y$, if and only if there is a rule $r=A\to \alpha \in R$ such that $x=x_{1}A{x}_2$ and $y=x_1\alpha x_2$.
• The reflexive and transitive closure of the relation ⇒ is denoted by ${\Rightarrow }^{*}$.
• A derivation using the sequence of rules $\tau =r_1{r}_2\cdots r_n$ is denoted by $\stackrel{\tau }{\Rightarrow }$ or $\stackrel{r_1{r}_2\cdots r_n}{\Rightarrow }$.
• The language generated by a grammar G is defined by $L\left(G\right)=\{w\in {\Sigma }^{*}\mid S{\Rightarrow }^{*}w\}$.

Example 2.

$G_1=(\{S,A,B\},\{a,b,c\},S,R)$ where R contains the productions:

$$r_0:S\to AB,r_1:A\to aAb,r_2:A\to ab,r_3:B\to cB,r_4:B\to c$$

is a context-free grammar, and it generates the language L in Example 1.

Definition 8.

A matrix grammar is a quadruple $G=(V$, Σ, S, $M)$ where $V,\Sigma ,S$ are defined as for a context-free grammar, M is a finite set of matrices which are finite strings over a set of context-free rules (or finite sequences of context-free rules). The language generated by a matrix grammar G is defined by $L\left(G\right)=\{w\in {\Sigma }^{*}\mid S\stackrel{\sout{\pi }}{\Rightarrow }w\mathrm{and}\pi \in M^{*}\}$.

Example 3.

$G^{\prime }=(\{S,A,B\},\{a,b,c\},S,M)$ where M contains the matrices:

$$m_0:(S\to AB),m_1:(A\to aAb,B\to cB),m_2:(A\to ab,B\to c)$$

is a matrix grammar, and it generates the language $\{a^n{b}^n{c}^n\mid n\ge 1\}$.

The family of languages generated by matrix grammars is denoted by $\mathcal{L}\left(\mathsf{MAT}\right)$.

Lastly, we retrieve the notions of a Petri net, a context-free Petri net and a Petri net controlled grammar from [23,24,44].

Definition 9.

A Petri net is a construct $N=(P,T,F,\varphi )$ where P and T are disjoint finite sets of places and transitions, respectively, $F\subseteq (P\times T)\cup (T\times P)$ is a set of directed arcs, $\varphi :(P\times T)\cup (T\times P)\to \{0,1,2,\cdots \}$ is a weight function, where $\varphi (x,y)=0$ for all $(x,y)\in \left(\right(P\times T)\cup (T\times P\left)\right)-F$.

A Petri net can be represented by a bipartite directed graph with the node set $P\cup T$ where places are drawn as circles, transitions as boxes and arcs as arrows with labels $\varphi (p,t)$ or $\varphi (t,p)$. If $\varphi (p,t)=1$ or $\varphi (t,p)=1$, the label is omitted. A mapping $\mu :P\to \{0,1,2,\dots \}$ is called a marking. For each place $p\in P$, $\mu \left(p\right)$ gives the number of tokens in p.

Definition 10.

A context-free Petri net (in short, a cf Petri net) with respect to a context-free grammar $G=(V,\Sigma ,S,R)$ is a tuple $N=(P,T,F,\varphi ,\beta ,\gamma ,\iota )$ where

(1)

$(P,T,F,\varphi )$ is a Petri net;

(2)

labeling functions $\beta :P\to V$ and $\gamma :T\to R$ are bijections;

(3)

there is an arc from place p to transition t if and only if $\gamma \left(t\right)=A\to \alpha$ and $\beta \left(p\right)=A$. The weight of the arc $(p,t)$ is 1;

(4)

there is an arc from transition t to place p if and only if $\gamma \left(t\right)=A\to \alpha$ and $\beta \left(p\right)=x$ where $x\in V$ and ${\left|\alpha \right|}_x>0$. The weight of the arc $(t,p)$ is ${\left|\alpha \right|}_x$;

(5)

the initial marking ι is defined by $\iota \left({\beta }^{-1}\left(S\right)\right)=1$ and $\iota \left(p\right)=0$ for all $p\in P-\left\{{\beta }^{-1}\left(S\right)\right\}$.

The following example ([23]) explains the construction of a cf Petri net.

Example 4.

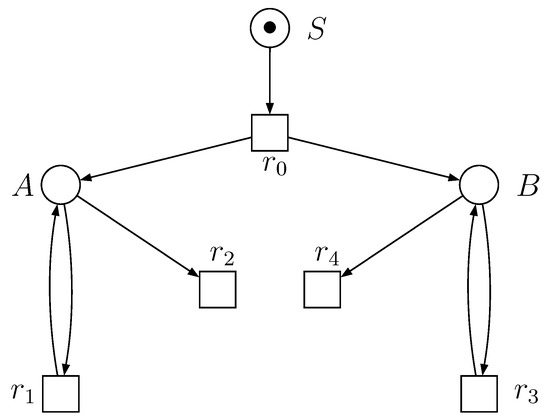
Let $G_1$ be a context-free grammar defined in Example 2. Figure 1 illustrates a cf Petri net N with respect to the grammar $G_1$.

Definition 11.

A Petri net controlled grammar is a tuple $G=(V,\Sigma ,S,R,N,\gamma ,M)$ where V, Σ, S, R are defined as for a context-free grammar and the construct $N=(P,T,F,\varphi ,\iota )$ is a Petri net, $\gamma :T\to R\cup \left\{\lambda \right\}$ is a labeling function and M is a set of final markings. The language generated by a Petri net controlled grammar G, denoted by $L\left(G\right)$, consists of all strings $w\in {\Sigma }^{*}$ such that there is a derivation $S\stackrel{r_1{r}_2\cdots r_k}{\Rightarrow }w$ and an occurrence sequence $\nu =t_1{t}_2\cdots t_s$ which is successful for M such that $r_1{r}_2\cdots r_k=\gamma (t_1{t}_2\cdots t_s)$.

The family of languages generated by Petri net controlled grammars is denoted by $\mathcal{L}\left(\mathsf{PN}\right)$.

The hierarchical relationships of the language families defined above are summarized as follows.

Theorem 1.

$\mathcal{L}\left(\mathsf{REG}\right)\subset \mathcal{L}\left(\mathsf{LIN}\right)\subset \mathcal{L}\left(\mathsf{CF}\right)\subset \mathcal{L}\left(\mathsf{MAT}\right)=\mathcal{L}\left(\mathsf{PN}\right).$

The correctness of inclusions $\mathcal{L}\left(\mathsf{REG}\right)\subset \mathcal{L}\left(\mathsf{LIN}\right)\subset \mathcal{L}\left(\mathsf{CF}\right)$ was first shown in [1,3]. The proof of the strict inclusion $\mathcal{L}\left(\mathsf{CF}\right)\subset \mathcal{L}\left(\mathsf{MAT}\right)$ can be found in [41]. The equality $\mathcal{L}\left(\mathsf{MAT}\right)=\mathcal{L}\left(\mathsf{PN}\right)$ was established in [23].

4. Binary Strings, Languages and Grammars

In this section, we define binary strings, languages and grammars by modifying the n-ary counterparts initially studied in [33,34].

Definition 12.

A pair of strings $u_1,u_2$, is called an binary string over V and denoted by $u=(u_1,u_2)$. The binary empty string is denoted by $(\lambda ,\lambda )$.

Definition 13.

A subset L of ${\left(V^{*}\right)}^2$ is called a binary language.

Definition 14.

The concatenation of binary strings $u=(u_1,u_2)\in {\left(V^{*}\right)}^2$ and $v=(v_1,v_2)\in {\left(V^{*}\right)}^2$ is defined as $uv=(u_1{v}_1,u_2{v}_2)$.

Definition 15.

For two binary languages $L_1,L_2\in {\left(V^{*}\right)}^2$, their

• union is defined as $L_1\cup L_2=\{w\mid w\in L_1\mathrm{or}w\in L_2\},$
• concatenation is defined as $L_1{L}_2=\{uv\mid u\in L_1\mathrm{and}v\in L_2\}.$

Definition 16.

For $L\in {\left(V^{*}\right)}^2$, its Kleene star is defined as

$$L^{*}=L^0\cup L^1\cup L^2\cup \cdots$$

where $L^0=\left\{(\lambda ,\lambda )\right\}$ and $L^i=L^{i-1}L$, $i\ge 1$.

Definition 17.

A binary context-free grammar is a quadruple

$$G=(V_1\times V_2,{\Sigma }_1\times {\Sigma }_2,(S_1,S_2),R)$$

where

(1)

$V_i$, $i=1,2$, are sets of nonterminal symbols,

(2)

${\Sigma }_i$, with $V_i\cap {\Sigma }_i=\varnothing$, $i=1,2$, are sets of terminal symbols,

(3)

$(S_1,S_2)\in V_1\times V_2$ is the start (initial) pair, and

(4)

R is a finite set nonempty set of binary productions (rules).

A binary production is a pair $(r_1,r_2)$ where $r_i$, $i=1,2$, is either empty or it is a context-free production, i.e., $r_i\in V_i\times {(V_i\cup {\Sigma }_i)}^{*}$.

Remark 1.

A binary production $(r_1,r_2)$ can be written as $u\to v$ where $u=(u_1,u_2)$, $v=(v_1,v_2)$ and $u_i\to v_i$ if $r_i\ne \varnothing$, $u_i=v_i=\lambda$, if $r_i=\varnothing$. For production $r_i=u_i\to v_i$, to indicate its left-hand side and right-hand side, we also use notations $lhs\left(r_i\right)$ and $rhs\left(r_i\right)$, i.e., $lhs(\left(r_i\right)=u_i$ and $rhs(\left(r_i\right)=v_i$.

Remark 2.

In Definition 17, if each nonempty $r_i$ is regular production, then the grammar G is called regular and if each nonempty $r_i$ is linear production, then it is called linear.

Remark 3.

We say $G_l=(V_1,{\Sigma }_1,S_1,R_1)$ and $G_r=(V_2,{\Sigma }_2,S_2,R_2)$ are left and right grammars with respect to the binary grammar G, respectively, where

$$R_1=\{r_1\mid (r_1,r_2)\in R\mathrm{and}{r}_1\ne \varnothing \}\mathrm{and}{R}_2=\{r_2\mid (r_1,r_2)\in R\mathrm{and}{r}_2\ne \varnothing \}.$$

Definition 18.

Let G be a binary context-free grammar. Let $u,v$ be pairs in ${(V_1\cup {\Sigma }_1)}^{*}\times {(V_2\cup {\Sigma }_2)}^{*}$. We say that u directly derives v, written as $u\to v$, if there exist pairs $x,z\in {(V_1\cup {\Sigma }_1)}^{*}\times {(V_2\cup {\Sigma }_2)}^{*}$ and a production $y\to w\in R$ such that $u=xyz$ and $v=xwz$. The reflexive and transitive closure of → is denoted by ${\to }^{*}$.

Definition 19.

The binary language generated by a binary context-free grammar G is defined as

$$L\left(G\right)=\{(w_1,w_2)\in ({\Sigma }_1^{*}\times {\Sigma }_2^{*})\mid (S_1,S_2){\to }^{*}(w_1,w_2)\}.$$

Definition 20.

The left and right languages are defined as

$$L_l\left(G\right)=\{w_1\mid (w_1,w_2)\in L\left(G\right)\}\mathrm{and}{L}_r\left(G\right)=\{w_2\mid (w_1,w_2)\in L\left(G\right)\},$$

i.e., the sets of left and right strings in all binary strings of $L\left(G\right)$, respectively.

Example 5.

Consider the binary grammar

$$G_2=(\left\{S_1\right\}\times \left\{S_2\right\},\{a,b\}\times \{a,b\},(S_1,S_2),R)$$

where R consists of the following productions

$$(S_1,S_2)\to (S_1{S}_1,a{S}_2),(S_1,S_2)\to (\lambda ,b{S}_2),(S_1,S_2)\to (\lambda ,\lambda ).$$

It is not difficult to see that, after n steps, the first production produces the pair $(S_1^{n+1},a^n{S}_1)$. Then in order to eliminate all $S_1^{\prime }$s, we apply the second production n times, and terminate derivation with applying the third production, which generates the pair string $(\lambda ,a^n{b}^n)$. Thus, $L\left(G_2\right)=\{(\lambda ,a^n{b}^n)\mid n>0\}$, and $L_r\left(G_2\right)=\{a^n{b}^n\mid n>0\}\in \mathcal{L}\left(\mathsf{CF}\right)$.

Example 6.

The grammar

$$G_3=(\{S_1,A,B,C\}\times \{S_2,X,Y,Z\},{\{a,b,c\}}^2,(S_1,S_2),R)$$

where R consists of the productions

$$\begin{array}{c}(S_1\to ABC,S_2\to X),\hfill \\ (A\to aA,X\to Y),\hfill & (B\to bB,Y\to Z),\hfill & (C\to cC,Z\to X),\hfill \\ (A\to a,X\to Z),\hfill & (B\to b,Z\to Y),\hfill & (C\to c,Y\to \lambda ),\hfill \end{array}$$

generates the language $L\left(G_3\right)=\{(\lambda ,a^n{b}^n{c}^n)\mid n>0\}$ where the right language $L_r\left(G_3\right)=\{a^n{b}^n{c}^n\mid n>0\}\notin \mathcal{L}\left(\mathsf{CF}\right)$.

Example 6 illustrates that binary context-free grammars can generate non-context-free languages, which implies that binary context-free grammars are more powerful than the Chomskyan context-free grammars. Thus, binary context-free grammars can be used in studying non-context-free structures such as cross-serial dependencies appearing in natural and programming languages using “context-free” tools such as parsing (derivation) trees.

We denote the families of binary languages generated by binary grammars with left and right grammars of type $\mathsf{X},\mathsf{Y}\in \{\mathsf{REG},\mathsf{LIN},\mathsf{CF}\}$ by $\mathcal{B}(\mathsf{X},\mathsf{Y})$. We also denote the the families of the left and right languages generated by binary grammars by $\mathcal{B}\left(\mathsf{X}\right)$, $\mathsf{X}\in \{\mathsf{REG},\mathsf{LIN},\mathsf{CF}\}$.

5. Synchronized Forms for Binary Grammars

In a binary grammar, the derivation of a string in the left or right grammar can pause or stop while the other still continues because of the rules of the forms $(\varnothing ,r_2)$ and $(r_1,\varnothing )$. However, we show that the both first and second derivations by binary context-free grammars can be synchronized, i.e., in each derivation step, some pair of nonempty productions is applied and both derivations stop at the same time.

Definition 21.

A binary context-free (regular, linear) grammar G is called synchronized if it does not have any production of the form $(\varnothing ,r_2)$ or $(r_1,\varnothing )$.

Lemma 1.

For every binary context-free grammar, there exist an equivalent synchronized binary context-free grammar.

Proof. 

Let $G=(V_1\times V_2,{\Sigma }_1\times {\Sigma }_2,(S_1,S_2),R)$ be a binary context-free grammar. Let

$$R_{\varnothing }=\{(r_1,r_2)\in R\mid r_1=\varnothing \mathrm{or}{r}_2=\varnothing \}.$$

We define the binary cf grammar $G^{\prime }=(V_1^{\prime }\times V_2^{\prime },{\Sigma }_1\times {\Sigma }_2,(S_1^{\prime },S_2^{\prime }),R^{\prime })$ where $V_i^{\prime }=V_i\cup \{X,S_1^{\prime },S_2^{\prime }\}$, $i=1,2$, where X, $S_1^{\prime }$ and $S_2^{\prime }$ are new nonterminals, and

$$\begin{array}{cc}\hfill R^{\prime }=& (R-R_{\varnothing })\hfill \\ \hfill & \cup \{(X\to X,r_2)\mid (\varnothing ,r_2)\in R\}\hfill \\ \hfill & \cup \{(r_1,X\to X)\mid (r_1,\varnothing )\in R\}\hfill \\ \hfill & \cup \{(S_1^{\prime }\to S_{1}X,S_2^{\prime }\to S_{2}X),(X\to \lambda ,X\to \lambda )\}.\hfill \end{array}$$

Then, the equality $L\left(G\right)=L\left(G^{\prime }\right)$ is obvious. □

The proof of Lemma 1 cannot be used for showing that there is also a synchronized form for a binary regular or linear grammar. The next lemma illustrates the existence of an equivalent synchronized form for any binary regular grammar too.

Lemma 2.

For every binary regular grammar, there exist an equivalent synchronized binary regular grammar.

Proof. 

Let $G=(V_1\times V_2,{\Sigma }_1\times {\Sigma }_2,(S_1,S_2),R)$ be a binary regular grammar. Let $R_{\varnothing }=\{(r_1,r_2)\in R\mid r_1=\varnothing \mathrm{or}{r}_2=\varnothing \}$ and

$$\begin{array}{cc}\hfill R_1=& \{(r_1,r_2)\in R\mid \mathsf{rhs}\left(r_1\right)\in T_1^{*},\mathsf{rhs}\left(r_2\right)\in T_2^{*}\},\hfill \\ \hfill R_2=& \{(r_1,r_2)\in R\mid \mathsf{rhs}\left(r_1\right)\in T_1^{*}{N}_1,\mathsf{rhs}\left(r_2\right)\in T_2^{*}{N}_2\}.\hfill \end{array}$$

The proof of the lemma consists of two parts. First, we replace all binary productions of the form $(A_1\to x_1,r_2)$ and $(r_1,A_2\to x_2)$ with the productions $(A_1\to x_{1}E,r_2)$ and $(r_1,A_2\to x_{2}E)$ where E is a new nonterminal, $x_i\in T_1^{*}\cup T_2^{*}$ and $\mathsf{rhs}\left(r_i\right)\notin T_1^{*}\cup T_2^{*}$, $i=1,2$. By this change, the early stop of one of derivations by the left and right grammars is prevented. Let

$$\begin{array}{cc}\hfill R_3=& \{(r_1,r_2)\in R\mid \mathsf{rhs}\left(r_1\right)\in T_1^{*},\mathsf{rhs}\left(r_2\right)\notin T_2^{*}\},\hfill \\ \hfill R_4=& \{(r_1,r_2)\in R\mid \mathsf{rhs}\left(r_1\right)\notin T_1^{*},\mathsf{rhs}\left(r_2\right)\in T_2^{*}\}.\hfill \end{array}$$

We set $V_1^{\prime }=V_1\cup \left\{E\right\}$, $V_2^{\prime }=V_2\cup \left\{E\right\}$ and

$$\begin{array}{cc}\hfill R_3^{\prime }=& \{(A_1\to x_{1}E,r_2)\mid (A_1\to x_1,r_2)\in R_3\},\hfill \\ \hfill R_4^{\prime }=& \{(r_1,A_2\to x_{2}E)\mid (r_1,A_2\to x_2)\in R_4\}\hfill \end{array}$$

and $R^{\prime }=(R-(R_3\cup R_4))\cup R_3^{\prime }\cup R_4^{\prime }$.

Second, in order to eliminate empty productions, we replace all binary production rules of the form $(A_1\to x_1{B}_1,\varnothing )$ and $(\varnothing ,A_2\to x_2{B}_2)$ with the pairs of production rules $(A_1\to A_r,A_2\to A_r)$, $(A_r\to x_1{B}_1,A_r\to A_2)$ and $(A_1\to A_r,A_2\to A_r)$, $(A_r\to A_1,A_r\to x_2{B}_2)$, respectively, where $A_r$s are new nonterminals. Thus, we define the following sets of new productions:

$$\begin{array}{cc}\hfill R_5=\{& (A_1\to A_r,A_2\to A_r),(A_r\to A_1,A_r\to x{B}_2)\mid \hfill \\ \hfill & r=(\varnothing ,A_2\to x{B}_2)\in R^{\prime }\mathrm{and}(A_1,A_2)\in V_1^{\prime }\times V_2^{\prime }\},\hfill \\ \hfill R_6=\{& (A_1\to A_r,A_2\to A_r),(A_r\to x{B}_1,A_r\to A_2)\mid \hfill \\ \hfill & r=(A_1\to x{B}_1,\varnothing )\in R^{\prime }\mathrm{and}(A_1,A_2)\in V_1^{\prime }\times V_2^{\prime }\}\hfill \end{array}$$

where $A_r$s are new nonterminal symbols introduced for each production $r=(A_1\to {\alpha }_1,\varnothing )$ or $r=(\varnothing ,A_2\to {\alpha }_2)$ in $R^{\prime }$. Let

$$V_{R,1}=\{A_r\mid r=(\varnothing ,A_2\to x{B}_2)\in R^{\prime }\}$$

and

$$V_{R,2}=\{A_r\mid r=(A_1\to x{B}_1,\varnothing )\in R^{\prime }\}.$$

We define the binary regular grammar $G^{″}=(V_1^{″}\times V_2^{″},{\Sigma }_1\times {\Sigma }_2,(S_1,S_2),R^{″})$ as follows:

$$\begin{array}{cc}\hfill V_1^{″}=& V_1^{\prime }\cup V_{R,1},\hfill \\ \hfill V_2^{″}=& V_2^{\prime }\cup V_{R,2},\hfill \\ \hfill R^{″}=& R_1\cup R_2\cup R_5\cup R_6\cup \left\{(E\to \lambda ,E\to \lambda )\right\}.\hfill \end{array}$$

First, we show that $L\left(G\right)\subseteq L\left(G^{″}\right)$. Consider a derivation

$$(S_1,S_2)=(w_{1,0},w_{2,0})\Rightarrow (w_{1,1},w_{2,1})\Rightarrow \cdots \Rightarrow (w_{1,n},w_{2,n})=(w_1,w_2)$$

in G where $(w_1,w_2)\in {\Sigma }_1^{*}\times {\Sigma }_2^{*}.$

For a derivation step $(w_{1,i-1},w_{2,i-1})\Rightarrow (w_{1,i},w_{2,i})$, $1\le i\le n$, the following cases are possible:

Case 1: the right-hand side is obtained by applying a production from $R_1\cup R_2\cup \left\{(E\to \varnothing ,E\to \varnothing )\right\}$. Then, the same rule is also applied in the corresponding step in the simulating derivation of $G^{″}$.

Case 2: the right-hand side is obtained by applying a production of the form $r=(\varnothing ,A_2\to {\alpha }_2)$ or $r=(A_1\to {\alpha }_1,\varnothing )$. Then, the production sequence $(A_1\to A_r,A_2\to A_r),(A_r\to A_1,A_r\to x{B}_2)\in R_5$ or the production sequence $(A_1\to A_r,A_2\to A_r),(A_r\to x{B}_1,A_r\to A_2)\in R_6$ is applied in the corresponding step in the simulating derivation of $G^{″}$.

Case 3: the right-hand side is obtained by applying a rule of the form $(A_1\to x_1,r_2)$, $\mathsf{rhs}\left(r_2\right)\ne \varnothing$ or $(r_1,A_2\to x_2)$, $\mathsf{rhs}\left(r_1\right)\ne \varnothing$. Then, the rule $(A_1\to x_{1}E,r_2)$ or $(r_1,A_2\to x_{2}E)$ is applied in the corresponding step in the simulating derivation in $G^{″}$, and the derivation terminates with applying $(E\to \varnothing ,E\to \varnothing )$.

The inclusion $L\left(G^{″}\right)\subseteq L\left(G\right)$ is obvious:

(1) the application of a rule of the form $(A_1\to x_{1}E,r_2)$, $\mathsf{rhs}\left(r_2\right)\ne \varnothing$, or $(r_1,A_2\to x_{2}E)$, $\mathsf{rhs}\left(r_1\right)\ne \varnothing$, can be immediately replaced with the pair $(A_1\to x_1,r_2)$ or $(r_1,A_2\to x_2)$, respectively;

(2) if a rule of the form $(A_1\to A_r,A_2\to A_r)$ or $(A_1\to A_r,A_2\to A_r)$ is applied at some derivation step, the only applicable pair of productions then is $(A_r\to A_1,A_r\to x{B}_2)$ or $(A_r\to x{B}_1,A_r\to A_2)$, respectively, since $A_r$ is the unique for each pair of productions. Thus, the sequence of pairs of productions $(A_1\to A_r,A_2\to A_r)$ and $(A_r\to A_1,A_r\to x{B}_2)$ or $(A_1\to A_r,A_2\to A_r)$ and $(A_r\to x{B}_1,A_r\to A_2)$ are replaced with $r=(\varnothing ,A_2\to {\alpha }_2)$ or $r=(A_1\to {\alpha }_1,\varnothing )$, respectively. □

Using the same arguments of the proof of Lemma 2, one can show that the similar fact also holds for binary linear grammars.

Lemma 3.

For every binary linear grammar, there exist an equivalent synchronized binary linear grammar.

6. Generative Capacities of Binary Grammars

In this section, we discuss the generative capacities of binary regular, linear and context free grammars.

The following two lemmas immediately follows from the definitions of binary languages.

Lemma 4.

$\mathcal{B}(\mathsf{X},\mathsf{Y})=\mathcal{B}(\mathsf{Y},\mathsf{X})$, $\mathsf{X}\in \{\mathsf{REG},\mathsf{LIN},\mathsf{CF}\}$.

Lemma 5.

$\mathcal{B}\left(\mathsf{REG}\right)\subseteq \mathcal{B}\left(\mathsf{LIN}\right)\subseteq \mathcal{B}\left(\mathsf{CF}\right).$

Lemma 6.

$\mathcal{L}\left(\mathsf{REG}\right)\subseteq \mathcal{B}\left(\mathsf{REG}\right),\mathcal{L}\left(\mathsf{LIN}\right)\subseteq \mathcal{B}\left(\mathsf{LIN}\right),\mathcal{L}\left(\mathsf{CF}\right)\subseteq \mathcal{B}\left(\mathsf{CF}\right).$

Proof. 

Let $G=(V,\Sigma ,S,R)$ be a context-free (regular, linear) grammar. Then, we define the binary context-free (regular, linear) grammar $G^{\prime }=(V\times V,\Sigma \times \Sigma ,R^{\prime },(S,S))$ by setting, for each production $r=A\to \alpha \in R$, the production $r^{\prime }=(\varnothing ,A\to \alpha )$ in $R^{\prime }$. Then, it is not difficult to see that $L\left(G\right)=L_r\left(G^{\prime }\right)$. In the same way, we can also show that $L\left(G\right)=L_l\left(G^{\prime }\right)$. □

Now we show that binary regular and linear grammars generate regular and linear languages, respectively.

Lemma 7.

$\mathcal{B}\left(\mathsf{LIN}\right)\subseteq \mathcal{L}\left(\mathsf{LIN}\right).$

Proof. 

Let $G=(V_1\times V_2,{\Sigma }_1\times {\Sigma }_2,(S_1,S_2),R)$ be a binary linear grammar. Without loss of generality, we can assume that the grammar G is synchronized. We set $V=\{[A_1,A_2]\mid (A_1,A_2)\in V_1\times V_2\}$ where $[A_1,A_2]$, $(A_1,A_2)\in V_1\times V_2$, are new nonterminals, and we define

$$\begin{array}{cc}\hfill R^{\prime }=& \{[A_1,A_2]\to x_2[B_1,B_2]y_2\mid (A_1\to x_1{B}_1{y}_1,A_2\to x_2{B}_2{y}_2)\in R\}\hfill \\ \hfill & \cup \{[A_1,A_2]\to x_2\mid (A_1\to x_1,A_2\to x_2)\in R\}.\hfill \end{array}$$

Then, $G^{\prime }=(V,{\Sigma }_2,[S_1,S_2],R^{\prime })$ is a linear grammar, and $L_r\left(G\right)=L\left(G^{\prime }\right)$ is obvious. Hence, $L_r\left(G\right)$ is linear, i.e., $\mathcal{B}\left(\mathsf{LIN}\right)\subseteq \mathcal{L}\left(\mathsf{LIN}\right)$. □

Corollary 1.

$\mathcal{B}\left(\mathsf{REG}\right)\subseteq \mathcal{L}\left(\mathsf{REG}\right).$

Next, we show that binary context-free grammars are more powerful than Chomskyan context-free grammars.

Lemma 8.

$\mathcal{L}\left(\mathsf{CF}\right)\subset \mathcal{B}\left(\mathsf{CF}\right)$.

Proof. 

By Lemma 6, $\mathcal{L}\left(\mathsf{CF}\right)\subseteq \mathcal{B}\left(\mathsf{CF}\right)$. Let us consider a binary context-free grammar $G_4=(\{S,C,D,E\}\times \{S,A,B\},{\{a,b,c\}}^2,(S,S),R)$ where R consists of the following productions:

$$\begin{array}{c}\left(1\right)(S\to S,S\to AB),\hfill \\ \left(2\right)(S\to C,A\to aA),\hfill & (C\to S,B\to aB),\hfill \\ \left(3\right)(S\to D,A\to bA),\hfill & (D\to S,B\to bB),\hfill \\ \left(4\right)(S\to E,A\to \lambda ),\hfill & (E\to a,B\to \lambda ),\hfill \end{array}$$

Any successful derivation starts with production $\left(1\right)$. For each production sequence $\left(i\right)$, $2\le i\le 4$, if the first production is applied, then, the only applicable production in the derivation is the second one. If after $\left(1\right)$, production sequence $\left(4\right)$ is applied, then the derivation generates the binary string $(a,\lambda )$. Else, after some steps, the derivation results in $(S,wAwB)$, $w\in {\{a,b\}}^{+}$, by applying production sequences $\left(2\right)$ or/and $\left(3\right)$, and then, it terminates by applying production sequence $\left(4\right)$. Thus,

$$L\left(G_4\right)=\{(a,ww)\mid w\in {\{a,b\}}^{*}\}.$$

Since $L_r\left(G_4\right)\notin \mathcal{L}\left(\mathsf{CF}\right)$, we have the strict inclusion $\mathcal{L}\left(\mathsf{CF}\right)\subset \mathcal{B}\left(\mathsf{CF}\right)$. □

Next, we show that binary context-free grammars are at least as powerful as matrix grammars.

Lemma 9.

$\mathcal{L}\left(\mathsf{MAT}\right)\subseteq \mathcal{B}\left(\mathsf{CF}\right).$

Proof. 

Let $G=(V,\Sigma ,S,M)$ be a matrix grammar where M consists of matrices $m_1,m_2,\dots ,m_n$ with $m_i:(r_{i,1},r_{i,2},\dots ,r_{i,k\left(i\right)})$, $1\le i\le n$. We set the following sets of new nonterminals

$$\begin{array}{cc}\hfill V_1=& \{Y_i\mid 1\le i\le n\}\cup \{Z_{i,j}\mid 1\le i\le n,1\le j\le k\left(i\right)\}\cup \{S_1,X\},\hfill \\ \hfill V_2=& V\cup \left\{S_2\right\},\hfill \end{array}$$

We construct the following binary productions

(1)

the start production: $(S_1\to X,S_2\to S),$

(2)

the matrix entry productions: $(X\to Y_i,\varnothing ),1\le i\le n,$

(3)

the matrix processing productions:

$$\left(Y_i\to Z_{i,1},r_{i,1}\right),(Z_{i,1}\to Z_{i,2},r_{i,2}),\dots ,(Z_{i,k\left(i\right)-1}\to Z_{i,k\left(i\right)},r_{i,k\left(i\right)})$$

where $1\le i\le n$,

(4)

the matrix exit productions: $(Z_{i,k\left(i\right)}\to X,\varnothing ),1\le i\le n.$

(5)

the terminating production: $(X\to \lambda ,\varnothing ).$

We define the binary context-free grammar $G^{\prime }=(V_1\times V_2,\Sigma \times \Sigma ,(S_1,S_2),R)$ where R consists of all productions (1)–(5) constructed above.

Claim 1: $L\left(G\right)\subseteq L\left(G^{\prime }\right)$. Let

$$D:S=w_0\stackrel{m_{i_1}}{\Rightarrow }{w}_1\stackrel{m_{i_2}}{\Rightarrow }{w}_2\cdots \stackrel{m_{i_k}}{\Rightarrow }{w}_k=w\in {\Sigma }^{*}$$

be a derivation in G. We construct the derivation $D^{\prime }$ in $G^{\prime }$ that simulates D. The derivation starts with the step:

$$(S_1,S_2)\Rightarrow (X,S).$$

Since, $m_{i_1}$ is the first matrix applied in derivation D, the next step in $D^{\prime }$ is

$$(X,S)\Rightarrow (Y_{i_1},S).$$

Furthermore,

$$(Y_{i_1},S)\stackrel{(Y_{i_1}\to Z_{i_1},r_{i_1})}{\Rightarrow }\cdots \stackrel{(Z_{i_1,k\left(i_1\right)-1}\to Z_{i_1,k\left(i_1\right)},r_{i_1,k\left(i_1\right)})}{\Rightarrow }{w}_1.$$

By applying $(Z_{i_1,k\left(i_1\right)}\to X,\varnothing )$,

$$w_1\stackrel{(Z_{i_1,k\left(i_1\right)}\to X,\varnothing )}{\Rightarrow }{w}_1,$$

we return X to the derivation, and then, we can continue the simulation of the application of the matrix $m_{i_2}$ in the same manner. Thus, $D^{\prime }$ simulates D, and $L\left(G\right)\subseteq L\left(G^{\prime }\right)$.

Claim 2: $L\left(G\right)\subseteq L\left(G^{\prime }\right)$. Any successfully terminating derivation in $G^{\prime }$ starts by applying production $(S_1\to X,S_2\to S)$, followed by applying $(X\to Y_i,\varnothing )$ for some $1\le i\le n$. Then only possible productions to be applied are matrix processing productions of the form (3). When the application of the productions in the currently active sequence starts, the productions of another sequence of the form (3) cannot be applied. In order to switch to another sequence of productions of the form (3), the corresponding production of the form (4) must be applied after finishing the application of all productions in the current sequence in the given order. To successfully terminate the derivation, the productions of the forms (4) and (5) must be applied. By construction, each sequence of productions of the form (3) simulates some matrix from G, any successful derivation in $G^{\prime }$ can be simulated by a successful derivation in G. Thus, $L\left(G^{\prime }\right)\subseteq L\left(G\right)$. □

The lemma above shows that any matrix language can be generated by a binary grammar where one of its grammars is regular and the other is context-free. Here, the natural question arises whether there is a binary grammar with both grammars are context-free that generates a non-matrix language or not. Next lemma shows that binary context-free grammars can only generate matrix languages even if their both grammars are context-free.

Lemma 10.

$\mathcal{B}\left(\mathsf{CF}\right)\subseteq \mathcal{L}\left(\mathsf{MAT}\right).$

Proof. 

Let $G=(V_1\times V_2,{\Sigma }_1\times {\Sigma }_2,(S_1,S_2),R)$ be a binary context-free grammar. Without loss of generality, we assume that G is in a synchronized form. Let $R_2=\{r_2\mid (r_1,r_2)\in R\}$. The proof idea is as follows: First, we will construct a context-free Petri net N with respect to G. Second, we define a Petri net controlled grammar $G^{\prime }$ where the underlying right grammar $G_r=(V_2,{\Sigma }_2,S_2,R_2)$ is controlled by the Petri net N. Then we show that $L_r\left(G\right)=L\left(G^{\prime }\right)$, i.e., $\mathcal{B}\left(\mathsf{CF}\right)\subseteq \mathcal{L}\left(\mathsf{PN}\right)$.

Part 1: We construct the cf Petri net $N=(P,T,F,\varphi ,\beta ,\gamma ,\iota )$ with respect to the nonterminals of the left grammar and productions of the grammar G by setting its components in the following way:

• $(P,T,F,\varphi )$ is a Petri net;
• the labeling functions $\beta :P\to V_1$ and $\gamma :T\to R$ are bijections;
• there is an arc from place p to transition t if and only if $\gamma \left(t\right)=(r_1,r_2)$ and $\beta \left(p\right)=\mathsf{lhs}\left(r_1\right)$. The weight of the arc $(p,t)$ is 1;
• there is an arc from transition t to place p if and only if $\gamma \left(t\right)=(r_1,r_2)$ and $\beta \left(p\right)=X$ where $X\in V_1$ and $|\mathsf{rhs}\left(r_1\right){|}_X>0$. The weight of the arc $(t,p)$ is $|\mathsf{rhs}\left(r_1\right){|}_X$;
• the initial marking $\iota$ is defined by $\iota \left({\beta }^{-1}\left(S_1\right)\right)=1$ and $\iota \left(p\right)=0$ for all $p\in P-\left\{{\beta }^{-1}\left(S_1\right)\right\}$.

Part 2: Using the right grammar $(V_2,{\Sigma }_2,R_2,S_2)$, we define the PN controlled grammar $G^{\prime }=(V_2,{\Sigma }_2,R_2,S_2,N,\eta ,M)$ where $N=(P,T,F,\varphi ,\beta ,\gamma ,\iota )$ is the cf Petri net defined above, $\eta :T\to R_2$ is a labeling function and M is a set of final markings. We set $M=\varnothing$ and $\eta \left(t\right)=r_2$ if and only if $\gamma \left(t\right)=(r_1,r_2)$.

Part 3: Now we show that $L_r\left(G\right)=L\left(G^{\prime }\right)$. Let

$$D:(S_1,S_2)\stackrel{(r_{1,1},r_{2,1})}{\Rightarrow }(w_{1,1},w_{2,1})\stackrel{(r_{1,2},r_{2,2})}{\Rightarrow }\cdots \stackrel{(r_{1,k},r_{2,k})}{\Rightarrow }(w_{1,k},w_{2,k})$$

be a derivation in G where $(w_{1,k},w_{2,k})\in {\Sigma }_1^{*}\times {\Sigma }_2^{*}$. We show that the derivation D can be simulated by the derivation $D^{\prime }$ in the grammar $G^{\prime }$ constructed as follows. $D^{\prime }$ starts with $S_2$, and by definition of N, $\iota \left({\beta }^{-1}\left(S_1\right)\right)=1$, thus, transition $t_1={\gamma }^{-1}\left((r_{1,1},r_{2,1})\right)$ is enabled. In the first step, we obtain

$$D^{\prime }:S_2\stackrel{r_{2,1}}{\Rightarrow }{w}_{2,1}\mathrm{where}\eta \left(t_1\right)=r_{2,1}.$$

When transition $t_1$ occurs the place in N corresponding to each nonterminal in $\mathsf{rhs}\left(r_{1,1}\right)=w_{1,1}$ receive the tokens whose number is equal to the number of the occurrence of the nonterminal in $\mathsf{rhs}\left(r_{1,1}\right)$.

Suppose that for some $1\le i<k$, we constructed the first i steps of the derivation $D^{\prime }$:

$$D^{\prime }:S_2\stackrel{r_{2,1}}{\Rightarrow }{w}_{2,1}\stackrel{r_{2,2}}{\Rightarrow }\cdots \stackrel{r_{2,i}}{\Rightarrow }{w}_{2,i}$$

with $r_{2,1}{r}_{2,2}\cdots r_{2,i}=\eta (t_1{t}_2\cdots t_i)$ where $(r_{1,1},r_{2,1})(r_{1,2},r_{2,2})\cdots (r_{1,i},r_{2,i})=\gamma (t_1{t}_2\cdots t_i)$, which corresponds to the first i steps of D. By definition, $\gamma \left(t_i\right)=(r_{1,i},r_{2,i})$ and $\eta \left(t_i\right)=r_{2,i}$. When transition $t_i$ fires, a token moves from the input place of $t_i$, that is labeled by the left-hand side of $r_{1,i}$, to its output places, that are labeled by the nonterminals occurring in the right-hand side of $r_{1,i}$. Thus, these nonterminals are also occur in $w_{1,i}$. The next step in D occurs by applying the pair $(r_{1,i+1},r_{2,i+1})$:

$$(w_{1,i},w_{2,i})\stackrel{(r_{1,i+1},r_{2,i+1})}{\Rightarrow }(w_{1,i+1},w_{2,i+1}).$$

Since production $r_{1,i+1}$ is applicable in the current step, its left-hand side occurs in $w_{1,i}$. It follows that the transition $t_{i+1}$, $\gamma \left(t_{i+1}\right)=(r_{1,i+1},r_{2,i+1})$, can fire. Consequently, we choose the production $r_{2,i+1}$ with $\eta \left(t_{i+1}\right)=r_{2,i+1}$, in $D^{\prime }$, and obtain

$$w_{2,i}\stackrel{r_{2,i+1}}{\Rightarrow }{w}_{2,i+1}.$$

The last step in D results in $(w_{1,k},w_{2,k})\in {\Sigma }_1^{*}\times {\Sigma }_2^{*}$ that is obtained by applying the pair $(r_{1,k},r_{2,k})$. Then, we choose $r_{2,k}$ with $\eta \left(t_k\right)=r_{2,k}$ in $D^{\prime }$. Since $w_{1,k}\in {\Sigma }_1^{*}$, i.e., it does not contain nonterminals, all places of N have no tokens. Thus, $M=\varnothing$. It shows that $L_r\left(G\right)\subseteq L\left(G^{\prime }\right)$.

Let

$$D^{\prime }:S_2\stackrel{r_{2,1}}{\Rightarrow }{w}_{2,1}\stackrel{r_{2,2}}{\Rightarrow }\cdots \stackrel{r_{2,k}}{\Rightarrow }{w}_{2,k}$$

with $r_{2,1}{r}_{2,2}\cdots r_{2,k}=\eta (t_1{t}_2\cdots t_k)$. By definition, we immediately obtain $\gamma (t_1{t}_2\cdots t_k)=(r_{1,1},r_{2,1})(r_{2,2},r_{2,2})\cdots (r_{1,k},r_{2,k})$ for some $(r_{1,i},r_{2,i})\in R$, $1\le i\le k$. Then, we can construct the derivation D in the grammar G

$$D:(S_1,S_2)\stackrel{(r_{1,1},r_{2,1})}{\Rightarrow }(w_{1,1},w_{2,1})\stackrel{(r_{1,2},r_{2,2})}{\Rightarrow }\cdots \stackrel{(r_{1,k},r_{2,k})}{\Rightarrow }(w_{1,k},w_{2,k}),$$

which shows that $L\left(G^{\prime }\right)\subseteq L_r\left(G\right)$. Thus, $\mathcal{B}\left(\mathsf{CF}\right)\subseteq \mathcal{L}\left(\mathsf{PN}\right)$. By Theorem 1, $\mathcal{B}\left(\mathsf{CF}\right)\subseteq \mathcal{L}\left(\mathsf{MAT}\right)$ □.

We summarize the results obtained above in the following theorem.

Theorem 2.

$$\mathcal{B}\left(\mathsf{REG}\right)=\mathcal{L}\left(\mathsf{REG}\right)\subset \mathcal{B}\left(\mathsf{LIN}\right)=\mathcal{L}\left(\mathsf{LIN}\right)\subset \mathcal{L}\left(\mathsf{CF}\right)\subset \mathcal{L}\left(\mathsf{MAT}\right)=\mathcal{B}\left(\mathsf{CF}\right).$$

7. Conclusions

In this paper, we redefined binary grammars as mutually controlled grammars where either grammar in a relation generates own language imposing restriction to the other.

Though binary grammars are asynchronous systems by their definitions, we showed that they can also work in synchronized mode (Lemmas 1–3), i.e., the both grammars in a binary relation generate strings with derivations where the grammars apply some productions in each step, and stop at the same time. This feature of binary grammars allows using one grammar in a relation as a regulation mechanism for the other.

We have studied the generative capacity of binary context-free grammars, and showed that binary regular and linear grammars have the same power as their Chomskyan alternatives, i.e., traditional regular and linear grammars, respectively (Lemmas 6 and 7 and Corollary 1). On the other hand, we have proved that binary context-free grammars are much more powerful than traditional context-free grammars (Lemma 8), that is, they generate all matrix languages even if binary grammars consist of regular and context-free pairs (Lemma 9). Moreover, we established that using context-free grammars as the components of relations does not increase the computational power of binary context-free grammars, i.e., they remain equivalent to matrix grammars (Lemma 10). Using the inclusion hierarchies in Theorem 1 and the results of the paper, we obtained the comparative hierarchy for binary regular, linear and context-free grammars (Theorem 2). We have also illustrated that binary grammars have practical significance: Example 6, and Lemma 8 show that cross-serial dependencies such as duplication and multiple agreements—non-context-free syntactical structures appearing in natural and programming languages—can be expressed with binary grammars.

Here, we emphasize that ternary or higher degree relational context-free grammars are more powerful than binary ones, and can be used in modeling “nested” cross-serial dependencies. Let us assume that a ternary context-free grammar is defined similarly to binary grammars. Then, the reader can convince himself that the following language

$$\left\{{\left(a_1^{n_1}{b}_1^{n_1}{c}_1^{n_1}\right)}^n{\left(a_2^{n_2}{b}_2^{n_2}{c}_2^{n_2}\right)}^n{\left(a_3^{n_3}{b}_3^{n_3}{c}_3^{n_3}\right)}^n\mid n,n_1,n_2,n_3\ge 1\right\},$$

the language of nested mutual agreements, can be generated by a ternary context-free grammar

$$G=(\{S_1,S_2,S_3\},\{a_i,b_i,c_i\mid i=1,2,3\},(S_1,S_2,S_3),R)$$

where R consists of the following tuples of productions:

$$\begin{array}{cc}(S_1\to X_1,S_2\to X_2,S_3\to A_1{A}_2{B}_1{B}_2{C}_1{C}_2),\hfill & (X_1\to X_1,X_2\to X_2^{\prime },A_1\to a_1{A}_1{b}_1),\hfill \\ (X_1\to X_1,X_2^{\prime }\to X_2,A_2\to c_1{A}_2),\hfill & (X_1\to Y_1,X_2^{\prime }\to Y_2,A_2\to c_1{A}_2),\hfill \\ (Y_1\to Y_1,Y_2\to Y_2^{\prime },B_1\to a_2{B}_1{b}_2),\hfill & (Y_1\to Y_1,Y_2^{\prime }\to Y_2,B_2\to c_2{B}_2),\hfill \\ (Y_1\to Z_1,Y_2^{\prime }\to Z_2,B_2\to c_2{B}_2),\hfill & (Z_1\to Z_1,Z_2\to Z_2^{\prime },C_1\to a_3{C}_1{b}_3),\hfill \\ (Z_1\to Z_1,Z_2^{\prime }\to Z_2,C_2\to c_3{C}_2),\hfill & (Z_1\to X_1,Z_2^{\prime }\to X_2,C_2\to c_3{C}_2),\hfill \\ (X_1\to X_1,X_2\to X_2^{\prime },A_1\to a_1{b}_1),\hfill & (X_1\to Y_1,X_2^{\prime }\to Y_2,A_2\to c_1),\hfill \\ (Y_1\to Y_1,Y_2\to Y_2^{\prime },B_1\to a_2{b}_2),\hfill & (Y_1\to Z_1,Y_2^{\prime }\to Z_2,B_2\to c_2),\hfill \\ (Z_1\to Z_1,Z_2\to Z_2^{\prime },C_1\to a_3{b}_3),\hfill & (Z_1\to \lambda ,Z_2^{\prime }\to \lambda ,C_2\to c_3).\hfill \end{array}$$

The detailed study of higher degree relational grammars as mutually controlled grammars will be the topic of our next investigation.