Abstract
We define helical (i.e., helicoidal) hypersurfaces depending on the axis of rotation in Minkowski four-space . There are three types of helicoidal hypersurfaces. We derive equations for the curvatures (i.e., Gaussian and mean) and give some examples of these hypersurfaces. Finally, we obtain a theorem classifying the helicoidal hypersurface with timelike axes satisfying .
1. Introduction
Chen [1] served the problem of classifying finite type surfaces in the 3-dimensional Euclidean space . If its coordinate functions are a finite sum of eigenfunctions of its Laplacian , a Euclidean submanifold is called of Chen finite type.
Moreover, the notion of finite type may be extended to any smooth function on a submanifold of a Euclidean space or a pseudo-Euclidean space. The submanifolds theory of finite type has been discussed by mathematicians.
Takahashi [2] obtained that minimal surfaces and spheres are the only surfaces in satisfying the condition Ferrandez, Garay, and Lucas [3] introduced the surfaces of satisfying , are either minimal, or an open piece of sphere or of a right circular cylinder. Choi and Kim [4] worked the minimal helicoid in terms of pointwise 1-type Gauss map of the first kind.
Dillen, Pas, and Verstraelen [5] gave the only surfaces in satisfying are the minimal surfaces, the spheres and the circular cylinders. Dillen, Fastenakels, and Van der Veken [6] studied rotation hypersurfaces of and Beneki, Kaimakamis, and Papantoniou [7] worked helicoidal surfaces with spacelike, timelike and lightlike axis in three-dimensional Minkowski space. Senoussi and Bekkar [8] focused helicoidal surfaces in which are of finite type in the sense of Chen with respect to the fundamental forms and
The right helicoid (resp. catenoid) is the only ruled (resp. rotational) surface which is minimal. Hence, we meet Bour’s theorem in [9]. Do Carmo and Dajczer [10] proved that, by using Bour [9], there exists a two-parameter family of helicoidal surfaces isometric to a given helicoidal surface. Güler and Vanlı [11] worked Bour’s theorem in Minkowski three-space. Using Bour’s theorem in Minkowski geometry, Güler [12] investigated helicoidal surface with lightlike profile curve. Mira and Pastor [13] studied helicoidal maximal surfaces in Lorentz–Minkowski three-space.
Lawson [14] gave the general definition of the Laplace–Beltrami operator. Magid, Scharlach, and Vrancken [15] introduced the affine umbilical surfaces in . Hasanis and Vlachos [16] considered hypersurfaces in 4-space with harmonic mean curvature vector field. Scharlach [17] studied the affine geometry of surfaces and hypersurfaces in . Cheng and Wan [18] considered complete hypersurfaces of four-space with CMC. Arslan, Deszcz, and Yaprak [19] studied Weyl pseudosymmetric hypersurfaces. Turgay and Upadhyay [20] considered biconservative hypersurfaces in 4-dimensional Riemannian space forms.
Arvanitoyeorgos, Kaimakamis, and Magid [21] showed that if the mean curvature vector field of satisfies the equation ( is a constant), then has CMC in Minkowski four-space .
General rotational surfaces in were originated by Moore [22,23]. Ganchev and Milousheva [24] considered the counterpart of these hind surfaces in the Minkowski four-space. Kim and Turgay [25] focused surfaces satisfying -pointwise 1-type Gauss map in . Moruz and Munteanu [26] gave minimal translation hypersurfaces in Verstraelen, Walrave, and Yaprak [27] studied minimal translation surfaces in . Özkaldı et al. [28] worked LC helix on hypersurfaces in Minkowski space .
Güler, Magid, and Yaylı [29] defined helicoidal hypersurface and studied the Laplace–Beltrami operator of the hypersurface in . Güler, Hacısalihoğlu, and Kim [30] introduced Gauss map and the third Laplace–Beltrami operator of the rotational hypersurface in Moreover, Güler and Turgay [31] studied Cheng–Yau operator and Gauss map using rotational hypersurfaces in four-space. Güler and Kişi [32] worked Dini-type helicoidal hypersurfaces with timelike axis in Minkowski four-space.
In this paper, we introduce the helicoidal hypersurfaces in Minkowski four-space . We give some basic notions of the four dimensional Minkowski geometry in Section 2. In Section 3, we give the definition of a helicoidal hypersurface with spacelike axis (resp., with timelike axis in Section 4, with lightlike axis in Section 5.), then calculate the curvatures of it. We describe the helicoidal hypersurfaces with timelike axis satisfying in in Section 6. Finally, we give some open problems in the last section.
2. Preliminaries
In this section, we introduce the first and the second fundamental forms, matrix of the shape operator Gaussian curvature K, and the mean curvature H of hypersurface in Minkowski four-space . Throughout the paper, we shall identify a vector (a,b,c,d) with its transpose (a,b,c,d)
Let be an isometric immersion of a hypersurface from to where is an element of length (Lorentz metric) and are the pseudo-Euclidean coordinates of type . The vector product of in is defined as follows
For a hypersurface in , we have
where e is the Gauss map (i.e., the unit normal vector)
gives the matrix of the shape operator . Now, we have the formulas of the Gaussian curvature and the mean curvature , respectively, as follows
and
A hypersurface is minimal if identically on .
Let be a curve in a plane and ℓ be a straight line in of . A rotational hypersurface in is defined as a hypersurface rotating a curve (profile) around a line (axis) ℓ. When the profile curve rotates around the axis ℓ, it simultaneously displaces parallel lines orthogonal to the axis ℓ, so that the speed of displacement is proportional to the speed of rotation. Resulting hypersurface is called the helicoidal hypersurface with axis ℓ and pitches .
Therefore, we introduce three type of the helicoidal hypersurfaces in throughout next three sections.
3. Helicoidal Hypersurfaces with Spacelike Axis
Supposing is the line spanned by the spacelike vector , the orthogonal matrix is given by
where The matrix can be found by solving the following equations, simultaneously,
where When the axis of rotation is , there is an Minkowskian transformation by which the axis is transformed to the -axis of . A parametrization of the profile curve is given by
where is a differentiable function for all . Thus, the helicoidal hypersurface which is spanned by the vector with pitches , is
in where If we get helicoidal surface with spacelike axis as in the three dimensional Minkowski space .
When , the surface is just a rotational hypersurface with timelike axis:
Next, we obtain the curvatures of a helicoidal hypersurface with spacelike axis
where and See Figure 1 and Figure 2 to projections of with spacelike axis into three-space.
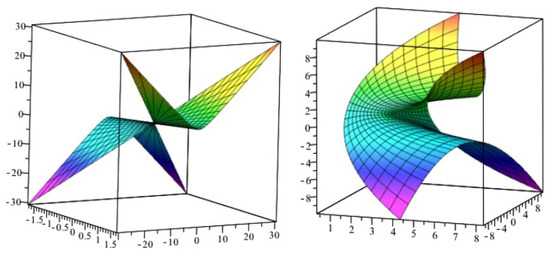
Figure 1.
Projections of (1), , into (Left) space, (Right) space.
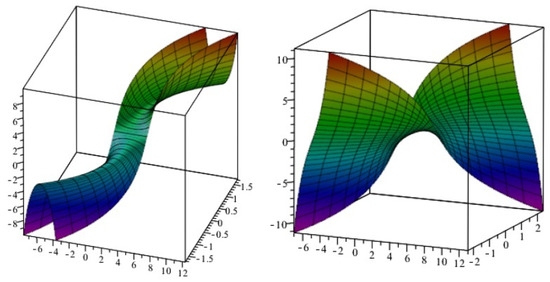
Figure 2.
Projections of (1), , into (Left) space, (Right) space.
Computing the first differentials of (1), we get the first quantities as follows
where Thus, we have
With the second differentials with respect to we obtain the second quantities as follows
and
Hence, the Gauss map of the helicoidal hypersurface is given by
Finally, we calculate the Gaussian curvature and the mean curvature of the helicoidal hypersurface with spacelike axis and state the results in the following propostion:
Proposition 1.
For a helicodal hypersurface with spacelike axis in the Gaussian and mean curvatures, respectively, are as follows
where
Corollary 1.
When we get
Corollary 2.
When and we have
4. Helicoidal Hypersurfaces with Timelike Axis
Taking is the line spanned by the timelike vector , the orthogonal matrix is given by
where The matrix can be found by
where When the axis of rotation is , there is an Minkowskian transformation by which the axis is transformed to the -axis of . Parametrization of the profile curve is given by
where is a differentiable function for all . Thus, the helicoidal hypersurface which is spanned by the vector with pitches , is as follows
in where If we get helicoidal surface with timelike axis as in the three dimensional Minkowski space .
When , the surface is just a rotational hypersurface with timelike axis as follows
Now, we obtain the mean curvature and the Gaussian curvature of a helicoidal hypersurface with timelike axis
where and See Figure 3 and Figure 4 to projections of with timelike axis into three-space.
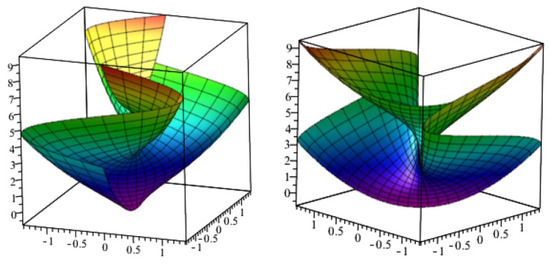
Figure 3.
Projections of (2), into (Left) space, (Right) space.
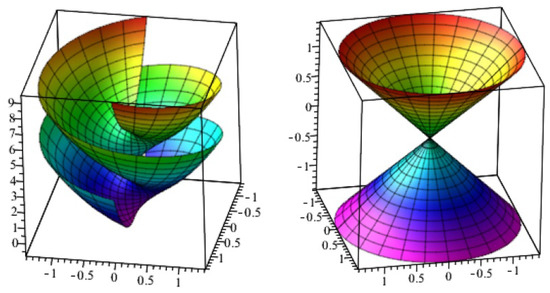
Figure 4.
Projections of (2), into (Left) space, (Right) space.
Computing the first differentials of (2), we find the first quantities
where Then, we get
With the second differentials with respect to we have the second quantities
and
Then, the Gauss map of the helicoidal hypersurface is given by
Finally, we calculate the Gaussian curvature and the mean curvature of the helicoidal hypersurface with timelike axis and state the results in the following propostion.
Proposition 2.
For a helicodal hypersurface with timelike axis in the Gaussian and mean curvatures, respectively, are as follows
where
Corollary 3.
When then we have
Corollary 4.
When and we have the same situation of Corollary 2, i.e., K and H vanish.
5. Helicoidal Hypersurfaces with Lightlike Axis
Considering is the line spanned by the lightlike vector , the orthogonal matrix is given by
where The matrix can be found by
where When the axis of rotation is , there is an Minkowskian transformation by which the axis is transformed to the -axis of . Parametrization of the profile curve is given by
where is a differentiable function for all . So, the helicoidal hypersurface which is spanned by the lightlike vector with pitches , is as follows:
in where When we get helicoidal surface with lightlike axis as in the three dimensional Minkowski space .
When , the surface is just a rotational hypersurface with lightlike axis as follows
Next, we obtain the curvatures of a helicoidal hypersurface with lightlike axis
where and See Figure 5 and Figure 6 to projections of with lightlike axis into three-space.
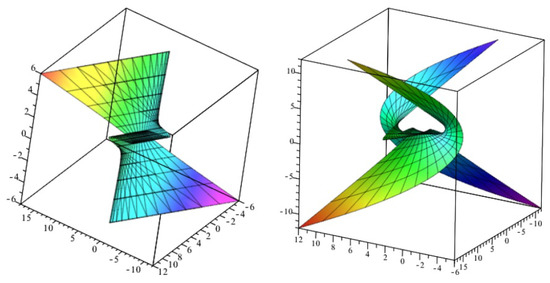
Figure 5.
Projections of (3) into (Left) space, (Right) space.
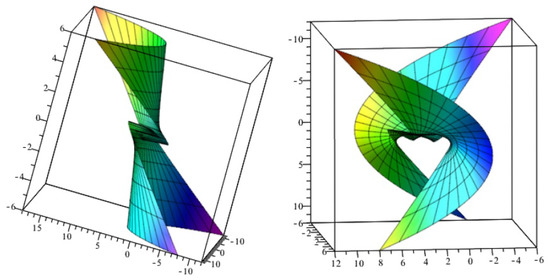
Figure 6.
Projections of (3), into (Left) space, (Right) space.
Calculating the first differentials of (3), we obtain the first quantities
where Then, we have
With the second differentials with respect to we have the second quantities
Hence, the Gauss map of the hypersurface is given by
where Finally, we calculate the Gaussian curvature and the mean curvature of the helicoidal hypersurface with lightlike axis, respectively, as follows
and
We assume that Therefore, the problem now is reduced to finding the solution of this differential equation in , where the function is the known smooth function given.
Next, we will examine Equation (4). Let , then and Hence, (4) reduces to
where
In order to get an idea for these hypersurfaces, we study , and for some special functional forms of the curvatures.
Case 1. Equation (6) takes the form
Suppose that
Then Equation (7) reduces to
The solution of this equation is given by
From Equation (8) we get
Hence, we have
If , then and find
Moreover, we define following one-parameter family of curves
Therefore, the equation of these helicoidal hypersurfaces is given by
where
If then and we obtain
Then, we define following two-parameter family of curves
Hence, the equation of these helicoidal hypersurfaces is given by
Finally, we observe that given the function , we can determine a one or two-parameter family of curves given by (9) or (11), respectively, and define the corresponding Equations (10) or (12) of the helicoidal hypersurfaces with lightlike axis immersed in
Case 2(a). When and Equation (6) takes the form
which is satisfied by the function and therefore , where So, given the function by (13) following the same process there exists a family of helicoidal hypersurfaces immersed in the equation of which is
Similarly, when and Equation (6) reduces to
Case 2(b). Equation (6) takes the form
which is satisfied by the function and therefore , where So, given the function by (14) following the same process there exists a family of helicoidal hypersurfaces immersed in the equation of which is
Case 2(c). We consider , Then we get
Using the substitution the equation reduces to
We could not compute this equation using analytical methods. It is the future problem for us.
Case 3. Now, we think such that for every So, we can consider the inverse function . Then, Equation (6) can be written as
Taking it takes the form
If we do not know some particular solution, we can not get its general solution.
Case 4. The mean curvature of the helicoidal hypersurface given by (3) in the Minkowski space is given by (5). The problem now is to find the solution of this equation in , where the function is the known smooth function given. Since we may give the solution of the equation
we can find the helicoidal minimal hypersurfaces. Taking then this equation takes the form
where So, using it reduces to
Setting we get
Solution of above equation is
Therefore, we see that (resp. ) satisfy the following equations:
and
Hence, for every function which satisfies the last equation, there exists a helicoidal minimal hypersurface with lightlike axis in whose parametric representation is given by (3).
We were not able to find the solution of Equation (5) by using analytical methods, so, it is for us, an open problem. Nevertheless, one could consider special values for the function as we did earlier for the function , and then give solutions of the corresponding equations. For example, if
where then (5) reduces to
This equation is satisfied by the function and then Here, when then So, we have
Given the function by (15), there exists a helicoidal hypersurface with lightlike axis immersed in the equation of which is given by
Finally, we give the following theorem:
Theorem 1.
Let , be a profile curve of the helicoidal hypersurface immersed in given by (3). Then the Gaussian and the mean curvature at the point are functions of the same variable u, i.e., . Moreover, given constants , and a smooth function (resp. ), we define the family of curves (resp. ).
6. Helicoidal Hypersurface with Timelike Axis satisfying in
The Gauss map of the helicoidal hypersurface with timelike axis (2) is clearly given by
where We use
and we get
where A is a matrix, and The equation by means of the first quantities and leads to the following system of ODEs:
Differentiating ODE’s twice with respect to we have
From (16), we get
cosine and sine are linearly independent functions of v, then we see . Since , we have . Consequently, is a minimal hypersurface with timelike axis.
Therefore, we have following theorem:
Theorem 2.
Let timelike : ⟶ be an isometric immersion given by (2). Then where A is a matrix iff the mean curvature of vanishes.
7. Open Problems
An umbilical point is an significant geometric qualification, related to lines of curvature. Since a line of curvature will end at such points, it is a singularity of a line of curvature. It can partially be because there is an powerful criterion for a smooth (hyper)surface defined by a formula, for both parametric or implicit (hyper)surfaces:
Lemma 1.
A point is an umbilical point iff at this point.
Finding the umbilic points, we calculate , and also we use the equation in Lemma 1 for three hypersurfaces in this paper. Hence, we have following problems:
Problem 1.
Solve following differential equation for helicoidal hypersurface with spacelike axis (1):
Problem 2.
Solve following differential equation for helicoidal hypersurface with timelike axis (2):
Problem 3.
Solve following differential equation for helicoidal hypersurface with lightlike axis (3):
All solutions in the problems will give umbilic points of the hypersurfaces.
Author Contributions
E.G. gave the idea for the helical hypersurfaces problem in Minkowski geometry . He also checked and polished the draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank Martin Magid, George Kaimakamis, and also Reviewers to valuable comments.
Conflicts of Interest
The author declares that there is no conflict of interests regarding the publication of this paper.
References
- Chen, B.Y. Total Mean Curvature and Submanifolds of Finite Type; World Scientific: Singapore, 1984. [Google Scholar]
- Takahashi, T. Minimal immersions of Riemannian manifolds. J. Math. Soc. Jpn. 1966, 18, 380–385. [Google Scholar] [CrossRef]
- Ferrandez, A.; Garay, O.J.; Lucas, P. On a Certain Class of Conformally at Euclidean Hypersurfaces. In Global Differential Geometry and Global Analysis; Lecture Notes in Math., n. 1481; Springer: Berlin, Germany, 1991; pp. 48–54. [Google Scholar]
- Choi, M.; Kim, Y.H. Characterization of the helicoid as ruled surfaces with pointwise 1-type Gauss map. Bull. Korean Math. Soc. 2001, 38, 753–761. [Google Scholar]
- Dillen, F.; Pas, J.; Verstraelen, L. On surfaces of finite type in Euclidean three-space. Kodai Math. J. 1990, 13, 10–21. [Google Scholar] [CrossRef]
- Dillen, F.; Fastenakels, J.; Van der Veken, J. Rotation hypersurfaces of × and × . Note Mater. 2009, 29, 41–54. [Google Scholar]
- Beneki, C.C.; Kaimakamis, G.; Papantoniou, B.J. Helicoidal surfaces in three-dimensional Minkowski space. J. Math. Anal. Appl. 2002, 275, 586–614. [Google Scholar] [CrossRef]
- Senoussi, B.; Bekkar, M. Helicoidal surfaces with ΔJr = Ar in 3-dimensional Euclidean space. Stud. Univ. Babeş-Bolyai Math. 2015, 60, 437–448. [Google Scholar]
- Bour, E. Théorie de la déformation des surfaces. J. l’Êcole Imp. Polytech. 1862, 22, 1–148. [Google Scholar]
- Do Carmo, M.; Dajczer, M. Helicoidal surfaces with constant mean curvature. Tohoku Math. J. 1982, 34, 351–367. [Google Scholar] [CrossRef]
- Güler, E.; Vanlı, A. Bour’s theorem in Minkowski three-space. J. Math. Kyoto Univ. 2006, 46, 47–63. [Google Scholar] [CrossRef]
- Güler, E. Bour’s theorem and lightlike profile curve. Yokohama Math. J. 2007, 54, 55–77. [Google Scholar]
- Mira, P.; Pastor, J.A. Helicoidal maximal surfaces in Lorentz-Minkowski space. Monatsh. Math. 2003, 140, 315–334. [Google Scholar] [CrossRef]
- Lawson, H.B. Lectures on Minimal Submanifolds, 2nd ed.; Mathematics Lecture Series 9; Publish or Perish, Inc.: Wilmington, DE, USA, 1980; Volume I. [Google Scholar]
- Magid, M.; Scharlach, C.; Vrancken, L. Affine umbilical surfaces in . Manuscr. Math. 1995, 88, 275–289. [Google Scholar] [CrossRef]
- Hasanis, T.; Vlachos, T. Hypersurfaces in with harmonic mean curvature vector field. Math. Nachr. 1995, 172, 145–169. [Google Scholar] [CrossRef]
- Scharlach, C. Affine Geometry of Surfaces and Hypersurfaces in . In Symposium on the Differential Geometry of Submanifolds; Dillen, F., Simon, U., Vrancken, L., Orgs, U., Eds.; Valenciennes: Valenciennes, France, 2007; Volume 124, pp. 251–256. [Google Scholar]
- Cheng, Q.M.; Wan, Q.R. Complete hypersurfaces of with constant mean curvature. Monatsh. Math. 1994, 118, 171–204. [Google Scholar] [CrossRef]
- Arslan, K.; Deszcz, R.; Yaprak, S. On Weyl pseudosymmetric hypersurfaces. Colloq. Math. 1997, 72, 353–361. [Google Scholar] [CrossRef]
- Turgay, N.C.; Upadhyay, A. On biconservative hypersurfaces in 4-dimensional Riemannian space forms. Math. Nachr. 2019, 292, 905–921. [Google Scholar] [CrossRef]
- Arvanitoyeorgos, A.; Kaimakamis, G.; Magid, M. Lorentz hypersurfaces in satisfying ΔH = αH. Ill. J. Math. 2009, 53, 581–590. [Google Scholar] [CrossRef]
- Moore, C. Surfaces of rotation in a space of four dimensions. Ann. Math. 1919, 21, 81–93. [Google Scholar] [CrossRef]
- Moore, C. Rotation surfaces of constant curvature in space of four dimensions. Bull. Am. Math. Soc. 1920, 26, 454–460. [Google Scholar] [CrossRef]
- Ganchev, G.; Milousheva, V. General rotational surfaces in the 4-dimensional Minkowski space. Turkish J. Math. 2014, 38, 883–895. [Google Scholar] [CrossRef]
- Kim, Y.H.; Turgay, N.C. Surfaces in with L1-pointwise 1-type Gauss map. Bull. Korean Math. Soc. 2013, 50, 935–949. [Google Scholar] [CrossRef]
- Moruz, M.; Munteanu, M.I. Minimal translation hypersurfaces in . J. Math. Anal. Appl. 2016, 439, 798–812. [Google Scholar] [CrossRef]
- Verstraelen, L.; Walrave, J.; Yaprak, S. The minimal translation surfaces in Euclidean space. Soochow J. Math. 1994, 20, 77–82. [Google Scholar]
- Özkaldi Karakuş, S.; Şenol, A.; Ghadami, R.; Yayli, Y. LC Helix on hypersurfaces in Minkowski space . Int. J. Pure Appl. Math. 2013, 86, 471–485. [Google Scholar]
- Güler, E.; Magid, M.; Yaylı, Y. Laplace–Beltrami operator of a helicoidal hypersurface in four-space. J. Geom. Symmetry Phys. 2016, 41, 77–95. [Google Scholar] [CrossRef]
- Güler, E.; Hacısalihoğlu, H.H.; Kim, Y.H. The Gauss map and the third Laplace–Beltrami operator of the rotational hypersurface in four-space. Symmetry 2018, 10, 398. [Google Scholar] [CrossRef]
- Güler, E.; Turgay, N.C. Cheng-Yau operator and Gauss map of rotational hypersurfaces in four-space. Mediterr. J. Math. 2019, 16, 1–16. [Google Scholar] [CrossRef]
- Güler, E.; Kişi, Ö. Dini-type helicoidal hypersurfaces with timelike axis in Minkowski four-space . Mathematics 2019, 7, 205. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).