Neutrosophic Modeling of Talcott Parsons’s Action and Decision-Making Applications for It

Abstract

The grand theory of action of Parsons has an important place in social theories. Furthermore, there are many uncertainties in the theory of Parsons. Classical math logic is often insufficient to explain these uncertainties. In this study, we explain the grand theory of action of Parsons in neutrosociology for the first time. Thus, we achieve a more effective way of dealing with the uncertainties in the theory of Parsons as in all social theories. We obtain a similarity measure for single-valued neutrosophic numbers. In addition, we show that this measure of similarity satisfies the similarity measure conditions. By making use of this similarity measure, we obtain applications that allow finding the ideal society in the theory of Parsons within the theory of neutrosociology. In addition, we compare the results we obtained with the data in this study with the results of the similarity measures previously defined. Thus, we have checked the appropriateness of the decision-making application that we obtained.

1. Introduction

There are many uncertainties in the world. Classical math logic is usually insufficient to explain uncertainties. Thus, we are not always able to say for a situation or an event whether it is true or wrong in an absolute manner. For example, we cannot always say the weather is hot or cold. While the weather is hot according to some, it may be cold for others. Therefore, Smarandache obtained the neutrosophic logic and neutrosophic set to deal with uncertainties more objectively in 1998 [1]. ‘T’ is the membership degree, ‘I’ is the uncertainty degree and ‘F’ is the non-membership degree in the neutrosophic logic and neutrosophic sets. “T, I, F” are defined independently. In addition, a neutrosophic number has the form (T, I, F). Furthermore, neutrosophic logic is a generalization of fuzzy logic [2] and intuitionistic fuzzy logic [3] since fuzzy and intuitionistic fuzzy logic’s membership, non–membership degrees are defined dependently. Thus, many researchers have obtained new structures and new applications on neutrosophic logic and sets [4,5,6,7,8,9,10,11,12,13,14,15].

In Section 2 of this study, we provide a literature review. In Section 3, we give related works. In Section 4, we include the definitions of neutrosophic sets [1], single-valued sets [6], similarity measures in [7] and [16], the theory of social action of Parsons [17], Hausdorff measure [18] and Hamming measure [18]. In Section 5, we re-model the social action theory of Parsons which is modeled in neutrosociology. In Section 6, we obtain a similarity measure for single-valued neutrosophic sets and prove that this measure meets the requirements of the similarity measure. In Section 7, we create the decision-making algorithm that we can choose the ideal society among the societies for the social action theory of Parsons in neutrosociology with the help of similarity measure in Section 6. In Section 8, we give sensitivity analysis for numeric example in Section 7; in Section 9, we give comparison methods. We compare the results we obtained with the data in this study with the results of the similarity measures previously defined. Thus, we have checked the appropriateness of the decision-making application we obtained; in Section 10, we discuss what we obtained in this study and make suggestions for studies that can be obtained by making use of this study; in Section 11, we give conclusions.

2. Literature Review

Similarity measure and decision-making practices emerge as an important application theory, especially after the definition of the fuzzy sets and neutrosophic sets. Many researchers have tried to deal with uncertainties by making new applications on neutrosophic sets, using similarity measures, TOPSIS method, VIKOR method, multicriteria method, Maximizing deviation method, decision tree methods, gray relational analysis method, etc. Recently, Şahin et al. studied combined classic neutrosophic sets and double neutrosophic sets [19]; Şahin et al. obtained decision-making applications for professional proficiencies in neutrosophic theory [16]; Uluçay et al. introduced decision-making applications for neutrosophic soft expert graphs [20]; Olgun et al. studied neutrosophic logic on the decision tree [21]; Wang et al. studied an extended VIKOR method with triangular fuzzy neutrosophic numbers [22]; Biswas et al. introduced TOPSIS method for decision–making applications [23]; Şahin et al. obtained a maximizing deviation method in neutrosophic theory [24]; Biswas et al. studied gray relational analysis method for decision-making applications [25].

3. Related Works

Smarandache claims that sociopolitical events can be studied mathematically [4]. In addition, he claims that it is possible to design a tool to describe an equation, an operator, a mathematical structure or a social phoneme. Studying the past gives us an idea about the future, at least partially. For this reason, we need to construct neutrosophic theories that may describe the new possible types of social structures with a neutrosophic number form. Since the social word contains a high degree of subjectivity that causes a low level of unanimity, these theories necessarily address uncertainty. Most of the data we come across in the field of sociology may be vague, incomplete, contradictory, biased, hybrid, ignorant, redundant, etc. Therefore, they are neutrosophic in nature and neutrosophic sciences dealing with indeterminacy should be involved in the study of sociology [4].

For the very same reasons, Smarandache proposed a model to be used in neutrosophic studies. He states that a neutrosophic extension of an element x with a neutrosophic number form.

Parsons, who built his theory on methodological and meta-theoretical debates in the field of social science, also paid special attention to hermeneutic to explain the extent of the individual’s voluntary involvement in action [26]. He made structural and functional explanations to maintain social balance and harmony [21]. While Parsons saw culture as values and norms that guide the actions of individuals in social life, he conceptualized the structure as a system of intertwined and independent parts [27]. According to Parsons, cultural objects are autonomous. He did this by distinguishing between the cultural and social systems. He also viewed society as a general system of action. In addition, many researchers have studied Parsons’s social action theory [26,27,28,29,30,31,32,33,34,35,36].

In this study, Parsons’s social action theory was aimed to re-model neutrosociology. As in all social theories, the social action theory of Parsons could not escape uncertainty [21]. Hence, the handling of it in neutrosociology theory would make this theory more useful. Therefore, we have obtained a similarity measure with single-valued neutrosophic numbers and included applications where this measure can be used as the neutrosophic equivalent of the ideal society in this theory.

4. Preliminaries

This section includes the definitions of neutrosophic sets [1], single-valued neutrosophic sets [6], similarity measures [7,16] and theory of social action of Parsons [17], Hausdorff measure [18] and Hamming measure [18].

Definition 1

([17]). Parsons, who built his theory on methodological and meta-theoretical debates in the field of social science, also paid special attention to hermeneutic to explain the extent of the individual’s voluntary involvement in action (so, which is neutrosophic). He made structural and functional explanations to maintain social balance and harmony. While Parsons saw culture as values and norms that guide the actions of individuals in social life, he conceptualized the structure as a system of intertwined and independent parts. According to Parsons, cultural objects are autonomous. He did this by distinguishing between the cultural and social systems. He also viewed society as a general system of action.

Definition 2

([1]). Let X be a universal set. Neutrosophic set S; is identified as S = {(x:$T_{A\left(x\right)}$, $I_{A\left(x\right)}$, $F_{A\left(x\right)}$>, x $\in$ X}. Where; on the condition that 0⁻$\le T_{A\left(x\right)}$ + $I_{A\left(x\right)}$ + $F_{A\left(x\right)}\le$3⁺; the functions T:U $\to$ ]0⁻,1⁺[ is truth function, I:U $\to$ ]0⁻,1⁺[ is uncertain function and F:U $\to$ ]0⁻,1⁺[ is falsity function.

Definition 3

([6]). Let X be a universal set. Single-valued neutrosophic number set S; is identified as S = {(x:$T_{A\left(x\right)}$, $I_{A\left(x\right)}$, $F_{A\left(x\right)}$>, x $\in$ X}. Where; on condition that 0$\le T_{A\left(x\right)}$ + $I_{A\left(x\right)}$ + $F_{A\left(x\right)}\le$3; the functions T:X $\to$ [0,1] is truth function, I:X $\to$ [0,1] is uncertainly function and F:X $\to$ [0,1] is falsity function.

Definition 4

([6]). Let A = {(x:<$T_{A\left(x\right)}$, $I_{A\left(x\right)}$, $F_{A\left(x\right)}$>} and B = {(x:<$T_{B\left(x\right)}$, $I_{B\left(x\right)}$, $F_{B\left(x\right)}$>} are single-valued neutrosophic numbers. If A = B; then $T_{A\left(x\right)}$ = $T_{B\left(x\right)}$, $I_{A\left(x\right)}$ = $I_{B\left(x\right)}$ and $F_{A\left(x\right)}$ = $F_{B\left(x\right)}$.

Definition 5

([6]). Let A = {(x:<$T_{A\left(x\right)}$, $I_{A\left(x\right)}$, $F_{A\left(x\right)}$>} and B = {(x:<$T_{B\left(x\right)}$, $I_{B\left(x\right)}$, $F_{B\left(x\right)}$>} are single-valued neutrosophic sets for x $\in$ U. If A < B; then for ∀ x $\in$ U; $T_{A\left(x\right)}$ < $T_{B\left(x\right)}$, $I_{A\left(x\right)}$ < $I_{B\left(x\right)}$ and $F_{A\left(x\right)}$ < $F_{B\left(x\right)}$.

Properties 1

([7]). Let $A_1, A_2$ and $A_3$ are three single-valued neutrosophic numbers and S be a similarity measure. S provides the following conditions.

• $0\le \mathrm{S}\left(A_1, A_2\right)\le 1$
• $\mathrm{S}\left(A_1, A_2\right)$ = $\mathrm{S}\left(A_2, A_1\right)$
• $\mathrm{S}\left(A_1, A_2\right) = 1$$\iff A_1=A_2$.
• If$A_1 \le$$A_2$$\le$$A_3$then,$\mathrm{S}\left(A_1, A_3\right) \le$$\mathrm{S}\left(A_1, A_2\right)$.

Definition 6

([16]). Let $A_1$ = <$T_1,$ $I_1,$ $F_1$> and $A_2$ = <$T_2,$ $I_2,$ $F_2$> be two single-valued neutrosophic numbers.

$$\begin{gathered} S_N(A_1, A_2)= \\ 1-(2/3)[\frac{min\{\left|3(T_1-T_2)-2\left(F_1-F_2\right)\right|,\left|F_1-F_2\right|\}}{\{max\{\left|3(T_1-T_2)-2\left(F_1-F_2\right)\right|,\left|F_1-F_2\right|\}/5\}+1}+ \\ \frac{min\{\left|4(T_1-T_2)-3\left(I_1-I_2\right)\right|,\left|I_1-I_2\right| \}}{\{max\{\left|4(T_1-T_2)-3\left(I_1-I_2\right)\right|,\left|I_1-I_2\right|\}/7\}+1}+ \\ \frac{min\{\left|5(T_1-T_2)-2\left(F_1-F_2\right)-3\left(I_1-I_2\right)\right|,\left|T_1-T_2\right|\}}{\{max\{\left|5(T_1-T_2)-2\left(F_1-F_2\right)-3\left(I_1-I_2\right)\right|,\left|T_1-T_2\right|\}/10\}+1}] \end{gathered}$$

is a similarity measure.

Definition 7

([18]). Let $A_1$ = <$T_1,$ $I_1,$ $F_1$> and $A_2$ = <$T_2,$ $I_2,$ $F_2$> be two single-valued neutrosophic numbers.

$$S_h\left(A_1,A_2\right)=1-max\{\left|T_1-T_2\right|,\left|I_1-I_2\right|,\left|F_1-F_2\right|\}$$

is a Hausdorff similarity measure.

Definition 8

([18]). Let $A_1$ = <$T_1,$ $I_1,$ $F_1$> and $A_2$ = <$T_2,$ $I_2,$ $F_2$> be two single-valued neutrosophic numbers.

$$S_H\left(A_1,A_2\right)=1-\left(\left|T_1-T_2\right|+\left|I_1-I_2\right|+\left|F_1-F_2\right|\right)/3$$

is a Hamming similarity measure.

5. Neutrosophic Modeling of Parson’s Theory of Action

According to the perfection of action categories of Parsons, it is inevitable to have deep doubts in every society and between layers of a particular society. However, “there is no ideal society in the sense that Marx defines, within each society the definition of ideal changes according to the place of a person within the society. By those who are at the top layer, the society is defined as ideal, by those at the lowest layer, it is far from being ideal, and by those in the mid-layer, who can sometimes be completely ignorant of what is an ideal society, it can be described as a fluctuating phenomenon depending on circumstances. Therefore, we always have a neutrosophic ideal society with an opposite and neutral triad. Naturally, this is valid for all societies since there are always people with more privileges than the others. Even in any a democratic society, some people have more privileges although they may form a small minority” [4].

Parsons developed a theory of action to explain how the macro and micro aspects of a particular social order show structural integrity together with the participation of its members. He took into account the voluntary participation of the individual in the social life on one hand, and structural continuity on the other. Here, it is assumed that the individual acts under the motivation of the social structure while taking action. According to him, social sciences should consider a trio considering the purposes, ends and ideals when examining actions.

Grand Theory of Action

The basic paradigm of Parson viewed society as a general system of action is based on the understanding of ‘rational social action’ of Weber [28]. However, according to Weber, sociology is a science that tries its interpretive understanding of social action to achieve a causal explanation of its course and its effects [36].

This interpretation is enriched from the perspective of the sociologist. Thus, social actions become neutrosophic. Others may agree, partially agree or disagree (1, 0, 0). Likewise, in the theory of Parson, the possibility of all members of society to participate in social values and norms that regulate, and guide human relations rather than individual activities is questionable, uncertain. Here we must see neutrosophic triplets.

According to Parson’s theory, all social actions are based on five pattern variables. These:

• Affectivity versus affective neutrality;
• Self-orientation versus collective orientation;
• Universalism versus particularism;
• Quality versus performance;
• Specificity versus diffuseness.

Parsons believes that these variables classify expectations and the structure of relationships, making the intangible action theory more understandable. However, according to Parsons, pattern variables are twofold, and each pattern variable indicates a problem or riddle that must be solved by the actor before the action can be performed. At the same time, there is a wide variety between the traditional society and the modern society. However, these can be seen as binary for neutrosophic sociological analysis (1, 0), it is very difficult to determine which of the individual’s behaviors are modern or traditional. Therefore, each of them should be considered as triple neutrosophic (1, 0, 0). The feminists’ response to Parsons’ family view can be given as an example. According to Parsons, the instrumental leadership role in the family structure in modern societies should be given to the spouse–father, on which the family’s reputation and income are based [32]. However, according to feminists, this statement by Parsons is nothing more than the continuation of the status quo [35]. In addition, these pattern variables (stereotypes) do not say how people will behave when faced with role conflict, and we will once again encounter uncertainty. This uncertainty can only be answered by neutrosociology.

The society model that Parsons has compared to the biologic model of an organism is based on the understanding of “living systems” that continues in a balanced way. According to him, a change in any part of the social system leads to adaptive changes in other parts [33]. There are four main problems an all-action system must solve. These are adaptation, goal-attainment, integration and latent pattern maintenance (AGIL). In short, these are referred to as AGIL in Table 1.

Table 1. Pure adaptation, goal-attainment, integration and latent pattern maintenance (AGIL) model for all living systems [33].

A	Instrumental	Consummatory	G
External	Adaptation	Goal-attainment
Internal	Latent pattern maintenance	Integration
L			I

“Adaptation” (A) is concerned with meeting the needs of the system from its environment and how resources are distributed within the system. Here, the system should provide sufficient resources from the environment and distribute it within itself. Social institutions are related to interrelated social rules and roles system that will meet social needs or functions and help solve social system problems. For example, economy, political order, law, religion, education and family are basic institutions for these. If a social system will continue to live, it needs structures and organizations that will function to adapt to its environment. The most dominant of these institutions is the economy. In “achieving the goal” (G), it is determined that the system reaches the specific target and which of these targets has priority. In other words, it should mobilize the resources and energies of the system and determine the priorities among them. “Integration” (I) refers to the coordination and harmony of parts of the system so that the system functions as a whole. To keep the system running, it must coordinate, correct, and regulate the relationships between the various actors or units in the system. “Latent pattern maintenance” (L) shows how to ensure the continuity of the action within the system according to a certain order or norm. The system should protect its values from deterioration and ensure the transfer of social values. Thus, it ensures the compliance of the members of the system. Especially family, religion, media and education have basic functions. Thanks to these, individuals gain a moral commitment to values shared socially [30].

The General Action Level is as follows in Table 2:

Table 2. General Action Level [30].

A		G
	The behavioral organism	The personality system
	The cultural system	The social system
L			I

Ultimately we get this series: The social the system, the fiduciary the cognitive.

Let us rebuild this series neutrosociology: (1, 0, 0) (1, 0, 0) (1, 0, 0).

If we go back to the beginning, “Behavioral organic, Personality system, Cultural system and Social system” must work continuously to ensure social balance. This will be through “socialization” and “social control”. If socialization “works”, all members of the society will adhere to shared values, make appropriate choices between pattern variables, and do what is expected of them in harmony, integration and other issues. For example, people will marry and socialize their children (L), and the father in the family will gain bread as it should be (A) [35].

6. A New Measurement of Similarity for Single-Valued Neutrosophic Numbers

Definition 9.

Let$A_1$= <$T_1,$$I_1,$$F_1$>,$A_2$= <$T_2,$$I_2,$$F_2$> be two single-valued neutrosophic numbers. We define measure of similarity between$A_1$and$A_2$as follows

$$\begin{gathered} S_N(A_1, A_2)=1 - (2/3)[\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}] \end{gathered}$$

We show that the measure of similarity in Definition 9 meets the requirements in Properties 1.

Theorem 1.

Let$S_N$be the measure of similarity in Definition 9.$S_N$provides the following features.

• $0\le S_N\left(A_1, A_2\right)\le 1$
• $S_N\left(A_1, A_2\right) =$$S_N\left(A_2, A_1\right)$
• $S_N\left(A_1, A_2\right) =1$if and only if$A_1=A_2$.
• If$A_1\le$$A_2$$\le$$A_3$, then$S_N\left(A_1, A_3\right)\le$$S_N\left(A_1, A_2\right)$.

Proof: 

(i) Since $A_1$ and $A_2$ are single-valued neutrosophic numbers, we have

$$\begin{gathered} max\{\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1}\}=½, \\ min\{\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1}\}=0, \\ max\{\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1}\}=½, \\ min\{\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1}\}=0, \\ max\{\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}\}=\mathrm{½}, \\ min\{\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}\}=0. \end{gathered}$$

Therefore,

$$\begin{gathered} min\{S_N\left(A_1, A_2\right)\}=1-2/3(1/2+1/2+1/2)=1-1=0, \\ max\{S_N\left(A_1, A_2\right)\}=1-2/3(0 + 0 + 0)=1-0=1. \end{gathered}$$

Hence, 0$\le S_N\left(A_1, A_2\right)\le$1.

(ii)

$$\begin{gathered} S_N(A_1, A_2)=1-(2/3)[\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}] \\ =1-2/3. \{\frac{min\{\sqrt{3{(T_2-T_1)}^2+{(I_2-I_1)}^2}, \left|2\left(T_2-T_1\right)-\left(I_2-I_1\right)\right|/3\}}{\{max\{\sqrt{3{(T_2-T_1)}^2+{(I_2-I_1)}^2}, \left|2\left(T_2-T_1\right)-\left(I_2-I_1\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_2-T_{12})}^2+{(F_2-F_1)}^2}, \left|2\left(T_2-T_1\right)-\left(F_2-F_1\right)\right|/3\}}{\{max\{\sqrt{3{(T_2-T_1)}^2+{(F_2-F_1)}^2}, \left|2\left(T_2-T_1\right)-\left(F_2-F_1\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_2-T_1)}^2+{(I_2-I_1)}^2+{(F_2-F_1)}^2}, \left|3\left(T_2-T_1\right)-\left(I_2-I_1\right)-\left(F_2-F_1\right)\right|/5\}}{\{max\{\sqrt{2{(T_2-T_1)}^2+{(I_2-I_1)}^2+{(F_2-F_1)}^2}, \left|3\left(T_2-T_1\right)-\left(I_2-I_1\right)-\left(F_2-F_1\right)\right|/5\}/2\}+1}\} \\ =S_N(A_2, A_1). \end{gathered}$$

(iii) We assume that

$$\begin{gathered} S_N(A_1, A_2)=1-(2/3)[\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}]=1 \end{gathered}$$

Therefore,

$$\begin{gathered} -(2/3)[\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}]=0 \end{gathered}$$

So,

$$\begin{gathered} \frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1}=0 \mathrm{and} \\ \frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1}=0, \\ \frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}=0. \end{gathered}$$

Therefore,

$$\begin{gathered} min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}=0, \\ min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}=0, \\ min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-(I_1-I_2)-\left(F_1-F_2\right)\right|/5\}=0. \end{gathered}$$

Now, we write all the cases that can make these statements 0 one-by-one.

(a) We assume that

$$\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}=0.$$

(1)

Therefore, it is

$$2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2=0.$$

Here, it is obtained that $T_1-T_2$ = 0, $I_1-I_2$ = 0 and $F_1-F_2$ = 0. Hence, we get $T_1=T_2, I_1=I_2$ and $F_1=F_2$. By Definition 4, $A_1$ = $A_2$.

(b) Let

$$\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}=0,$$

(2)

$$\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}=0.$$

(3)

By (2) and (3), we obtain $3{(T_1-T_2)}^2+{(I_1-I_2)}^2$ = 0 and $3{(T_1-T_2)}^2+{(F_1-F_2)}^2$ = 0.

Therefore, we obtain $T_1-T_2$ = 0, $I_1-I_2$ = 0 and $F_1-F_2$ = 0. Hence, we obtain $T_1=T_2, I_1=I_2$ and $F_1=F_2$. By Definition 4, $A_1$ = $A_2$.

(c) We assume that

$$\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}=0,$$

(4)

$$\left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|=0,$$

(5)

By $\left(4\right)$, we have

$$T_1-T_2=0 \mathrm{and} I_1-I_2=0.$$

(6)

Hence, we obtain that $F_1-F_2$ = 0 by (5) and (6).

Hence, $T_1=T_2, I_1=I_2$ and $F_1=F_2$. By Definition 4, we get $A_1$ = $A_2$.

(d) We assume that

$$\left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3=0,$$

(7)

$$\left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3=0,$$

(8)

$$\left|3\left(T_1-T_2\right)-(I_1-I_2)-\left(F_1-F_2\right)\right|/5=0.$$

(9)

By (7) and (8), we obtain

$$T_1-T_2=I_1-I_2=F_1-F_2.$$

(10)

Hence, $T_1-T_2$ = 0 by (9) and (10).

Hence, $T_1=T_2,I_1=I_2 \mathrm{and} F_1=F_2$. By Definition 4, $A_1$ = $A_2$.

We assume that $A_1$ = $A_2$. Therefore, by Definition 4, it is $T_1$ = $T_2$, $I_1$ = $I_2$, $F_1$ = $F_2$. Because of this, we have

$$\begin{gathered} S_N(A_1, A_2)=1-(2/3)[\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}]=0 \end{gathered}$$

(iv) We assume that $A_1$ ≤ $A_2$ ≤ $A_3$. By Definition 5, it is $T_1$ ≤ $T_2$ ≤ $T_3$, $I_1$ ≥ $I_2$ ≥ $I_3$, $F_1$ ≥ $F_2$ ≥ $F_3$. Hence, we obtain that

$$\begin{gathered} min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}\le 1, \\ max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}\le 1, \\ min\{\sqrt{3{(T_1-T_3)}^2+{(I_1-I_3)}^2}, \left|2\left(T_1-T_3\right)-\left(I_1-I_3\right)\right|/3 \}\le 1, \\ max\{\sqrt{3{(T_1-T_3)}^2+{(I_1-I_3)}^2}, \left|2\left(T_1-T_3\right)-\left(I_1-I_3\right)\right|/3\}/2\}\le 1. \end{gathered}$$

Therefore, we have

$$\begin{gathered} min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}\le \\ min\{\sqrt{3{(T_1-T_3)}^2+{(I_1-I_3)}^2}, \left|2\left(T_1-T_3\right)-\left(I_1-I_3\right)\right|/3 \}, \\ max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}\le \\ max\{\sqrt{3{(T_1-T_3)}^2+{(I_1-I_3)}^2}, \left|2\left(T_1-T_3\right)-\left(I_1-I_3\right)\right|/3\}/2\}. \end{gathered}$$

Hence,

$$\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1}\le$$

$$\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1}.$$

(11)

In addition,

$$\begin{gathered} min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}\le 1, \\ max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}\le 1 \\ min\{\sqrt{3{(T_1-T_3)}^2+{(F_1-F_3)}^2}, \left|2\left(T_1-T_3\right)-\left(F_1-F_3\right)\right|/3\}\le 1, \\ max\{\sqrt{3{(T_1-T_3)}^2+{(F_1-F_3)}^2}, \left|2\left(T_1-T_3\right)-\left(F_1-F_3\right)\right|/3\}/2\}\le 1 \end{gathered}$$

Therefore, we obtain that

$$\begin{gathered} min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}\le \\ min\{\sqrt{3{(T_1-T_3)}^2+{(F_1-F_3)}^2}, \left|2\left(T_1-T_3\right)-\left(F_1-F_3\right)\right|/3\}, \\ max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}\le \\ max\{\sqrt{3{(T_1-T_3)}^2+{(F_1-F_3)}^2}, \left|2\left(T_1-T_3\right)-\left(F_1-F_3\right)\right|/3\}/2\}. \end{gathered}$$

Hence,

$$\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3 \}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1}\le$$

$$\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1}.$$

(12)

In addition,

$$\begin{gathered} min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-(I_1-I_2)-\left(F_1-F_2\right)\right|/5\}\le 1 \\ max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-(I_1-I_2)-\left(F_1-F_2\right)\right|/5\}/3\le 1, \\ min\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-(I_1-I_3)-\left(F_1-F_3\right)\right|/5\}\le 1 \\ max\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-(I_1-I_3)-\left(F_1-F_3\right)\right|/5\}/3\le 1, \end{gathered}$$

Hence, we have

$$\begin{gathered} min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-(I_1-I_2)-\left(F_1-F_2\right)\right|/5\}\le \\ min\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-(I_1-I_3)-\left(F_1-F_3\right)\right|/5\}, \\ max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-(I_1-I_2)-\left(F_1-F_2\right)\right|/5\}/2\le 1, \\ max\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-(I_1-I_3)-\left(F_1-F_3\right)\right|/5\}/2. \end{gathered}$$

Hence,

$$\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\}/2\}+1}\le$$

$$+\frac{min\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-\left(I_1-I_3\right)-\left(F_1-F_3\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-\left(I_1-I_3\right)-\left(F_1-F_3\right)\right|/5\}/2\}+1}.$$

(13)

By (11), (12) and (13), we have

$$\begin{gathered} 1-(2/3)[\frac{min\{\sqrt{3{(T_1-T_3)}^2+{(I_1-I_3)}^2}, \left|2\left(T_1-T_3\right)-\left(I_1-I_3\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_3)}^2+{(I_1-I_3)}^2}, \left|2\left(T_1-T_3\right)-\left(I_1-I_3\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_1-T_3)}^2+{(F_1-F_3)}^2}, \left|2\left(T_1-T_3\right)-\left(F_1-F_3\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_3)}^2+{(F_1-F_3)}^2}, \left|2\left(T_1-T_3\right)-\left(F_1-F_3\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-\left(I_1-I_3\right)-\left(I_1-I_3\right)-\left(F_1-F_3\right)\right|/5\}}{\{max\{\sqrt{2{(T_1-T_3)}^2+{(I_1-I_3)}^2+{(F_1-F_3)}^2}, \left|3\left(T_1-T_3\right)-\left(I_1-I_3\right)-\left(F_1-F_3\right)\right|/5\}/2\}+1}]\le \\ 1-(2/3)[\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(I_1-I_2)}^2}, \left|2\left(T_1-T_2\right)-\left(I_1-I_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}}{\{max\{\sqrt{3{(T_1-T_2)}^2+{(F_1-F_2)}^2}, \left|2\left(T_1-T_2\right)-\left(F_1-F_2\right)\right|/3\}/2\}+1} \\ +\frac{min\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_3\right)\right|/5\}}{\{max\left\{\sqrt{2{(T_1-T_2)}^2+{(I_1-I_2)}^2+{(F_1-F_2)}^2}, \left|3\left(T_1-T_2\right)-\left(I_1-I_2\right)-\left(F_1-F_2\right)\right|/5\right\}/2\}+1}]. \end{gathered}$$

Hence, we get $S_N\left(A_1, A_3\right)$ ≤ $S_N\left(A_1, A_2\right)$ as desired. □

7. Decision-Making Applications for Neutrosophic Modeling of Talcott Parsons’s Action

In this section, we give an algorithm for applications that allow us to find the ideal society in the grand theory of action of Parsons by taking advantage of the similarity measure in Definition 9. In addition, we give a numeric example to this algorithm.

7.1. Algorithm

1. Step: To find out which societies are closer to the ideal society, the criteria to be considered are determined. The criteria of the ideal society in the grand theory of action of Parsons [17] are taken as below:

• c₁ = affectivity versus affective neutrality
• c₂ = self-orientation versus collective orientation
• c₃ = universalism versus particularism
• c₄ = quality versus performance
• c₅ = specificity versus diffuseness

Let the set of these criteria be C = {$c_1$, $c_2$, …, $c_5$}.

2. Step: Let the set of weighted values of the criteria be W = {w₁, w₂, …, w_m} and let the weighted values be taken as below:

• the weighted value of the criterion c₁ is w₁,
• the weighted value of the criterion c₂ is w₂,
• the weighted value of the criterion c₃ is w₃,
• the weighted value of the criterion c₄ is w₄ and
• the weighted value of the criterion c₅ is w₅.

In addition, it must be ${{\displaystyle \sum }}_{i=1}^m{w}_i$ = 1 and $w_1$, $w_2$, …, $w_m$ $\in$ [0,1].

In this study, we will take the weighted value of each criterion as equal. If necessary, different weighted values can be selected for each criterion.

3. Step: Each society that will be taken into ideal society assessment should be evaluated by sociologists determined as a single-valued neutrosophic number. Let T = {$t_1$, $t_2$, …, $t_n$} be set of societies. Symbolic representation of societies as single-valued neutrosophic sets are denoted as:

$$\begin{gathered} t_1=\{c_1:<T_{t_1\left(c_1\right)}, I_{t_1\left(c_1\right)},F_{t_1\left(c_1\right)}>, c_2:<T_{t_1\left(c_2\right)}, I_{t_1\left(c_2\right)},F_{t_1\left(c_2\right)}>,\dots , c_5:<T_{t_1\left(c_5\right)}, I_{t_1\left(c_5\right)},F_{t_1\left(c_5\right)}>; c_i\in \mathrm{C} (\mathrm{i}=1, 2, \dots , 5)\}, \\ {t}_2=\{c_1:<T_{t_2\left(c_1\right)}, I_{t_2\left(c_1\right)},F_{t_2\left(c_1\right)}>, c_2:<T_{t_2\left(c_2\right)}, I_{t_2\left(c_2\right)},F_{t_2\left(c_2\right)}>,\dots , c_5:<T_{t_2\left(c_5\right)}, I_{t_2\left(c_5\right)},F_{t_2\left(c_5\right)}>; c_i\in \mathrm{C} (\mathrm{i}=1, 2, \dots , 5)\}, \\ {t}_3=\{c_1:<T_{t_3\left(c_1\right)}, I_{t_3\left(c_1\right)},F_{t_3\left(c_1\right)}>, c_2:<T_{t_3\left(c_2\right)}, I_{t_3\left(c_2\right)},F_{t_3\left(c_2\right)}>,\dots , c_5:<T_{t_3\left(c_5\right)}, I_{t_3\left(c_5\right)},F_{t_3\left(c_5\right)}>; c_i\in \mathrm{C} (\mathrm{i}=1, 2, \dots , 5)\}, \\ {t}_n=\{c_1:<T_{t_n\left(c_1\right)}, I_{t_n\left(c_1\right)},F_{t_n\left(c_1\right)}>, c_2:<T_{t_n\left(c_2\right)}, I_{t_n\left(c_2\right)},F_{t_n\left(c_2\right)}>,\dots ,c_5:<T_{t_n\left(c_5\right)}, I_{t_n\left(c_5\right)},F_{t_n\left(c_5\right)}>; c_i\in \mathrm{C} (\mathrm{i}=1, 2, \dots , 5)\}. \end{gathered}$$

Here, $c_1$, $c_2$, …, $c_5$ are the criteria in Step 1. Thus, each society will be obtained as a single-valued neutrosophic number according to the given criteria.

4. Step: To compare how close the societies are to ideal society in the theory of Parsons, an imaginary perfect society is determined. Perfect society under the similarity measure we have obtained should be as

$$\mathrm{I}=\{c_1:<1, 0, 0>, x_2:<1, 0, 0>, \dots , c_5: <1, 0, 0>; c_i\in \mathrm{C} (\mathrm{i}=1, 2, \dots , 5) \}.$$

Hence, we will accept the existence of an imaginary society that includes 100% truth, 0% uncertainty and 0% falsity according to each criterion.

5. Step: We express the societies given as a single-valued neutrosophic set in step 3 in a table according to criteria. Thus, we will obtain Table 3.

Table 3. Criteria table of societies.

	c1	c2	c3	c4	c5
t1	<$T_{t_1\left(c_1\right)}$, $I_{t_1\left(c_1\right)}$, $F_{t_1\left(c_1\right)}$>	…	<$T_{t_1\left(c_3\right)}$, $I_{t_1\left(c_3\right)}$, $F_{t_1\left(c_3\right)}$>	…	<$T_{t_1\left(c_5\right)}$, $I_{t_1\left(c_5\right)}$, $F_{t_1\left(c_5\right)}$>
t2	<$T_{t_2\left(c_1\right)}$, $I_{t_2\left(c_1\right)}$, $F_{t_2\left(c_1\right)}$>	…	<$T_{t_2\left(c_3\right)}$, $I_{t_2\left(c_3\right)}$, $F_{t_2\left(c_3\right)}$>	…	<$T_{t_2\left(c_5\right)}$, $I_{t_2\left(c_5\right)}$, $F_{t_2\left(c_5\right)}$>
⋮	⋮	…	⋮	…	⋮
tn	<$T_{t_n\left(c_1\right)}$, $I_{t_n\left(c_1\right)}$, $F_{t_n\left(c_1\right)}$>	…	<$T_{t_n\left(c_3\right)}$, $I_{t_n\left(c_3\right)}$, $F_{t_n\left(c_3\right)}$>	…	<$T_{t_n\left(c_5\right)}$, $I_{t_n\left(c_5\right)}$, $F_{t_n\left(c_5\right)}$>

6. Step: We will process each criterion values given for each society separately and each criterion values of the perfect society I in Step 4 separately with similarity measure. Hence, we will obtain Table 4.

Table 4. Similarity table for each social criteria to perfect society criteria.

	c1	c2	c3	c4	c5
t1	$S_N$($I_{c_1}$, $t_{1_{c_1}}$)	…	$S_N$($I_{c_3}$, $t_{1_{c_3}}$)	…	$S_N$($I_{c_5}$, $t_{1_{c_5}}$)
t2	$S_N$($I_{c_1}$, $t_{2_{c_1}}$)	…	$S_N$($I_{c_3}$, $t_{2_{c_3}}$)	…	$S_N$($I_{c_5}$, $t_{2_{c_5}}$)
⋮	⋮	…	⋮	…	⋮
tn	$S_N$($I_{c_1}$, $t_{n_{c_1}}$)		$S_N$($I_{c_3}$, $t_{n_{c_3}}$)	…	$S_N$($I_{c_5}$, $t_{n_{c_5}}$)

7. Step: In this step, we will obtain a weighted similarity table (Table 5).

Table 5. Weighted similarity table for each social criteria to perfect society criteria.

	w1c1	w2c2	w3c3	w4c4	w5c5
t1	$w_1{S}_N$($I_{c_1}$, $t_{1_{c_1}}$)	…	$w_3{S}_N$($I_{c_3}$, $t_{1_{c_3}}$)	…	$w_5{S}_N$($I_{c_5}$, $t_{1_{c_5}}$)
t2	$w_1{S}_N$($I_{c_1}$, $t_{2_{c_1}}$)	…	$w_3{S}_N$($I_{c_3}$, $t_{2_{c_3}}$)	…	$w_5{S}_N$($I_{c_5}$, $t_{2_{c_5}}$)
⋮	⋮	…	⋮	…	⋮
tn	$w_1{S}_N$($I_{c_1}$, $t_{n_{c_1}}$)		$w_3{S}_N$($I_{c_3}$, $t_{n_{c_3}}$)	…	$w_5{S}_N$($I_{c_5}$, $t_{n_{c_5}}$)

In this study, this step is not needed since we take the same weighted value of each criterion. More precisely, Table 5 and Table 4 will be the same since the weighted values are equal. This step can be used if necessary.

8. Step:

In this last step, we will obtain a similarity value table (Table 6) by applying $S_{Nk}$($t_k$, I) = ${{\displaystyle \sum }}_{i=1}^n{w}_i.S_N(I_{c_i}, t_{k_{c_i}})$.

Table 6. Similarity value table of societies to the perfect society.

	The Similarity Value
t1	SN1(t1, I)
t2	SN2(t2, I)
⋮	⋮
tn	SNn(tn, I)

See Figure 1.

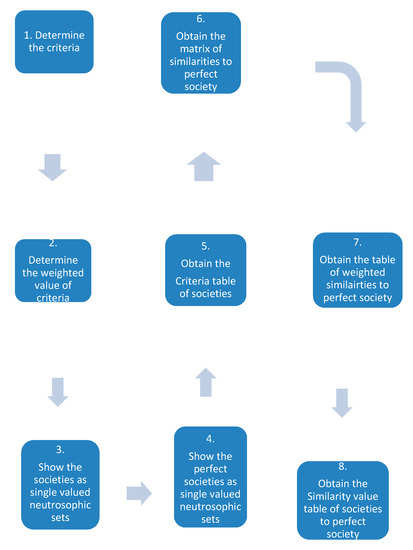
Figure 1. Diagram of the algorithm.

7.2. Numeric Example

Using the steps in Section 7.1, we show how close the 4 societies are to the ideal society.

1. Step: Let the criteria of an ideal society in the theory of Parsons be as it is in Step 1 of Section 7.1;

• c₁ = affectivity versus affective neutrality
• c₂ = self-orientation versus collective orientation
• c₃ = universalism versus particularism
• c₄ = quality versus performance
• c₅ = specificity versus diffuseness

Let C = {c₁, c₂, …, c₅} be the set of criteria.

2. Step: In this example, we will take the weight values of each criterion equal so that w₁ = w₂ = … = w₅ = 0.2.

3. Step: Let the set of societies be T = {t₁, t₂, t₃, t₄}. We assume that the single-valued neutrosophic set with evaluation of societies by sociologists according to the criteria in Step 1 will be as below:

$$\begin{gathered} t_1=\{c_1:<0.6, 0.2, 0.1 >, c_2:<0.7, 0.2, 0.1 >, c_3:<0.4, 0.1, 0.2 >, c_4:<0.8, 0.1, 0 >, c_5:< 0.5, 0.1, 0.2 >\} \\ {t}_2=\{c_1:<0.5, 0.2, 0.3 >, c_2:<0.6, 0.1, 0.3 >, c_3:<0.8, 0.1, 0.2 >, c_4:<0.4, 0.1, 0.4 >, c_5:<0.9, 0, 0.1 >\} \\ {t}_3=\{c_1:<0.5, 0.2, 0.1 >, c_2:<0.8, 0.1, 0.1 >, c_3:<0.8, 0.1, 0 >, c_4:<0.7, 0.2, 0.1 >, c_5:<0.7, 0.2, 0.3 >\} \\ {t}_4=\{c_1:<0.7, 0.2, 0.1>, c_2:<0.6, 0.2, 0.2 >, c_3:<0.7, 0.2, 0.1 >, c_4:<0.7, 0.1, 0.2 >, c_5:<0.8, 0.1, 0.1 >\} \end{gathered}$$

4. Step: Let the dream perfect society that we compare societies be

$$\mathrm{I}=\{c_1:<1, 0, 0>, c_2:< 1, 0, 0>, c_3: <1, 0, 0>, c_3:<1, 0, 0>, c_4:< 1, 0, 0>, c_5: <1, 0, 0>\}.$$

5. Step: Let us express the societies as a single-valued neutrosophic set in Step 3 in Table 7.

Table 7. The criteria table of societies.

	c1	c2	c3	c4	c5
t1	<0.6, 0.2, 0.1>	<0.7, 0.2, 0.1>	<0.4, 0.1, 0.2>	<0.8, 0.1, 0>	<0.5, 0.1, 0.2>
t2	<0.5, 0.2, 0.3>	<0.6, 0.1, 0.3>	<0.8, 0.1, 0.2>	<0.4, 0.1, 0.4>	<0.9, 0, 0.1>
t3	<0.5, 0.2, 0.1>	<0.8, 0.1, 0.1>	<0.8, 0.1, 0>	<0.7, 0.2, 0.1>	<0.7, 0.2, 0.3>
t4	<0.7, 0.2, 0.1>	<0.6, 0.2, 0.2>	<0.7, 0.2, 0.1>	<0.7, 0.1, 0.2>	<0.8, 0.1, 0.1>

6. Step: Using the similarity measure, we obtain the similarity table (Table 8) which is the similarity of the criteria of societies to the criteria of the perfect society.

Table 8. The similarity table of the criteria of societies to the criteria of the perfect society.

	c1	c2	c3	c4	c5
t1	0.5351	0.6088	0.4121	0.7489	0.4700
t2	0.4263	0.5132	0.6930	0.3734	0.8494
t3	0.4700	0.7196	0.7489	0.6088	0.5610
t4	0.6088	0.5112	0.6088	0.6088	0.7196

7. Step: In this example, there is no need to make any changes in Table 8 since we take the weighted value of each criterion as equal.

8. Step: In this step, we obtain similarity values of the societies in Table 8 to the perfect society.

Now, we obtain the similarity values of the societies in Table 9 and we obtain Table 10 by dividing the values in Table 9 by 5, taking the weighted values as equal for each society on 5 criteria and, hence, getting the results in the range [0,1].

Table 9. The similarity value table of the societies to the perfect society.

	The Similarity Value
t1	SN1(t1, I) = 2.7749
t2	SN2(t2, I) = 2.8553
t3	SN3(t3, I) = 3.1083
t4	SN4(t4, I) = 3.0572

Table 10. The similarity rate of the societies to the perfect society.

	The Similarity Value
t1	SN1(t1, I) = 0.5549
t2	SN2(t2, I) = 0.5710
t3	SN3(t3, I) = 0.6216
t4	SN4(t4, I) = 0.6114

In addition, the similarity value of each society to the perfect society in Table 10 is obtained. The result of the evaluation is given. Thus, societies closest to the perfect society are obtained as t₃, t₄, t₂ and t₁ respectively.

8. Sensitivity Analysis

In 7.1 Numeric example, we take the weighted values of criteria W = {w₁, w₂, …, w_m} equal such that

• the weighted value of c₁ criteria w₁ = 0.2
• the weighted value of c₂ criteria w₂ = 0.2
• the weighted value of c₃ criteria w₃ = 0.2
• the weighted value of c₄ criteria w₄ = 0.2
• the weighted value of c₅ criteria w₅ = 0.2

Thus, societies closest to the perfect society are obtained as t₃, t₄, t₂, t₁ respectively.

(a) If we take the W = {w₁ = 0.1, w₂ = 0.3, w₃ = 0.2, w₄ = 0.2, w₅ = 0.2}, then we obtain that societies closest to the perfect society are obtained as t₃, t₄, t₂ and t₁ respectively (Table 11).

Table 11. The similarity rate of the societies to the perfect society for W = {w₁ = 0.1, w₂ = 0.3, w₃ = 0.2, w₄ = 0.2, w₅ = 0.2}.

	The Similarity Value
t1	SN1(t1, I) = 0.55235
t2	SN2(t2, I) = 0.57975
t3	SN3(t3, I) = 0.64662
t4	SN4(t4, I) = 0.60168

Thus, we obtain the same result with the Numeric Example 7.1.

(b) If we take the W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.3, w₄ = 0.1, w₅ = 0.2}, then we obtain that societies closest to the perfect society are obtained as t₃, t₄, t₂ and t₁ respectively respectively (Table 12).

Table 12. The similarity rate of the societies to the perfect society for W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.3, w₄ = 0.1, w₅ = 0.2}.

	The Similarity Value
t1	SN1(t1, I) = 0.5213
t2	SN2(t2, I) = 0.60302
t3	SN3(t3, I) = 0.63567
t4	SN4(t4, I) = 0.61144

Thus, we obtain same result with Numeric Example 7.1.

(c) If we take the W = {w₁ = 0.3, w₂ = 0.1, w₃ = 0.2, w₄ = 0.2, w₅ = 0.2}, then we obtain that societies closest to the perfect society are obtained as t₄, t₃, t₂ and t₁ respectively respectively (Table 13).

Table 13. The similarity rate of the societies to the perfect society for W = {w₁ = 0.3, w₂ = 0.1, w₃ = 0.2, w₄ = 0.2, w₅ = 0.2}.

	The Similarity Value
t1	SN1(t1, I) = 0.54761
t2	SN2(t2, I) = 0.56237
t3	SN3(t3, I) = 0.5967
t4	SN4(t4, I) = 0.6212

Thus, we obtain a different result from Numeric Example 7.1.

(d) If we take the W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.1, w₄ = 0.3, w₅ = 0.2}, then we obtain that societies closest to the perfect society are obtained as t₄, t₁, t₂ and t₃ respectively respectively (Table 14).

Table 14. The similarity rate of the societies to the perfect society for W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.1, w₄ = 0.3, w₅ = 0.2}.

	The Similarity Value
t1	SN1(t1, I) = 0.58866
t2	SN2(t2, I) = 0.5391
t3	SN3(t3, I) = 0.36379
t4	SN4(t4, I) = 0.61144

Thus, we obtain a different result with Numeric Example 7.1.

(e) If we take the W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.2, w₄ = 0.3, w₅ = 0.1}, then we obtain that societies closest to the perfect society are obtained as t₃, t₄, t₁, and t₂ respectively respectively (Table 15).

Table 15. The similarity rate of the societies to the perfect society for W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.2, w₄ = 0.3, w₅ = 0.1}.

	The Similarity Value
t1	SN1(t1, I) = 0.58287
t2	SN2(t2, I) = 0.52346
t3	SN3(t3, I) = 0.62644
t4	SN4(t4, I) = 0.60036

Thus, we obtain a different result from Numeric Example 7.1.

(f) If we take the W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.2, w₄ = 0.1, w₅ = 0.3}, then we obtain that societies closest to the perfect society are obtained as t₄, t₂, t₃, and t₁ respectively respectively (Table 16).

Table 16. The similarity rate of the societies to the perfect society for W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.2, w₄ = 0.1, w₅ = 0.3}.

	The Similarity Value
t1	SN1(t1, I) = 0.52709
t2	SN2(t2, I) = 0.61866
t3	SN3(t3, I) = 0.61688
t4	SN4(t4, I) = 0.62252

Thus, we obtain a different result from Numeric Example 7.1.

Now, we give results in (a), (b), (c), (d), (e) and (f) in Table 17.

Table 17. Ideal societies according to weighted values.

	Ideal Societies Respectively
W = {w1 = 0.2, w2 = 0.2, w3 = 0.2, w4 = 0.1, w5 = 0.3}	t3, t4, t1, t2
W = {w1 = 0.2, w2 = 0.2, w3 = 0.2, w4 = 0.3, w5 = 0.1}	t4, t3, t2, t1
W = {w1 = 0.2, w2 = 0.1, w3 = 0.3, w4 = 0.2, w5 = 0.2}	t3, t4, t2, t1
W = {w1 = 0.2, w2 = 0.3, w3 = 0.1, w4 = 0.2, w5 = 0.2}	t4, t1, t2, t3
W = {w1 = 0.3, w2 = 0.1, w3 = 0.2, w4 = 0.2, w5 = 0.2}	t4, t3, t2, t1
W = {w1 = 0.1, w2 = 0.3, w3 = 0.2, w4 = 0.2, w5 = 0.2}	t3, t4, t2, t1

As seen in Table 17, if we take W = {w₁ = 0.2, w₂ = 0.2, w₃ = 0.2, w₄ = 0.1, w₅ = 0.3} or W = {w₁ = 0.1, w₂ = 0.3, w₃ = 0.2, w₄ = 0.2, w₅ = 0.2}, then we obtain same result with Numeric Example 7.1. In other cases, we obtain different results from Numeric Example 7.1.

9. Study Comparison Methods

In this section, we have compared the obtained results of the data in our Example 1 with the results of the similarity measures, Hausdorff measure [18], Hamming measure [18] and the previously defined similarity measure [16].

1. If we use the similarity measure in Definition 6 [16] for Example 1, we obtain Table 18 as a result.

Table 18. The similarity rate according to similarity measure, in Definition 6 [16], of the societies to the perfect society.

	The Similarity Value
t1	SN1(t1, I) = 0.661445
t2	SN2(t2, I) = 0.639916
t3	SN3(t3, I) = 0.691014
t4	SN4(t4, I) = 0.678023

Thus, societies closest to the perfect society are obtained as t₃, t₄, t₁ and t₂ respectively according to similarity measure in Definition 6 [16].

2. If we use the Hausdorff measure [18] for Example 1, we obtain Table 19 as a result.

Table 19. The similarity rate according to Hausdorff measure, in Definition 7 [18], of the societies to the perfect society.

	The Similarity Value
t1	Sh(t1, I) = 0.6
t2	Sh(t2, I) = 0.64
t3	Sh(t3, I) = 0.7
t4	Sh(t4, I) = 0.7

Thus, societies closest to the perfect society are obtained as t₃ = t₄, t₂ and t₁ respectively according to Hausdorff similarity measure in Definition 7 [18].

3. If we use the Hamming measure [18] for Example 1, we obtain Table 20 as a result.

Table 20. The similarity rate according to Hamming similarity measure, in Definition 8 [18], of the societies to the perfect society.

	The Similarity Value
t1	SH(t1, I) = 0.78
t2	SH(t2, I) = 0.76
t3	SH(t3, I) = 0.806667
t4	SH(t4, I) = 0.8

Thus, societies closest to the perfect society are obtained as t₃, t₄, t₁ and t₂ respectively according to Hamming similarity measure, in Definition 8 [18].

As a result,

• according to our similarity measure, the perfect society is obtained as t₃, t₄, t₂, t₁ respectively;
• according to similarity measure [16], the perfect society is obtained as t₃, t₄, t₁, t₂ respectively;
• according to Hausdorff measure [18], the perfect society is obtained as t₃ = t₄, t₂, t₁ respectively;
• according to Hamming measure [18], the perfect society is obtained as t₃, t₄, t₁, t₂ respectively.

10. Discussions

In this study, we explained the grand theory of action of Parsons, which has an important place in social theories, for the first time in neutrosociology. Thus, like all social theories, we have achieved a more effective way of dealing with uncertainties in the theory of Parsons. In addition, we have obtained a similarity measure for single-valued neutrosophic numbers. By making use of this similarity measure, we have obtained applications that allow finding the ideal society in the theory of Parsons within the theory of neutrosociology. Hence, we have added a new structure to neutrosophic theory, neutrosociology theory. In addition, by utilizing this study, other social theories can be explained in neutrosociology. Thus, the uncertainties encountered can be dealt with more easily. In addition, by using neutrosophic numbers and sets related to other social theories, new similarity measures can be obtained, and the consistency of these measures can be checked.

11. Conclusions

In Section 9, we obtained different results for the similarity measure [16]; Hausdorff measure [18]; and Hamming measure [18]. In addition, we give a comparison in Table 21.

Table 21. Comparison methods.

	Ideal Societies, Respectively
Similarity measure in definition 9	t3, t4, t1, t2
Similarity measure in definition 6 [16]	t3, t4, t1, t2
Hausdorff measure in definition 7 [18]	t3 = t4, t2, t1
Hamming measure in definition 8 [18]	t3, t4, t1, t2