Enzymatic Degradation of 2,4,6-Trichlorophenol in a Microreactor using Soybean Peroxidase

Abstract

Soybean peroxidase is an enzyme extracted from soybean seed hulls. In the presence of hydrogen peroxide, the enzyme has the potential to catalyze the biodegradation of toxic substances like chlorophenols. For this reason, its use in wastewater treatment processes is environmentally friendly since the enzyme can be obtained from a renewable and abundant raw material. In this work, enzymatic biodegradation of 2,4,6-trichlorophenol performed by soybean peroxidase in a microreactor was studied experimentally and theoretically. The experimental data set was obtained with a volume of 250 μL by using different soybean peroxidase concentrations and different reaction times. The fluid dynamics of the microreactor was modeled as well, using ANSYS CFX. The simulations exhibited secondary flows, which enhanced mixing. Although the laminar flow was developed, it can be assumed to be a well-mixed medium. The kinetic data were evaluated through a mechanistic model, the modified bi-bi ping-pong model, which is adequate to represent the enzymatic degradation using peroxidases. The model was composed of an initial value problem for ordinary differential equations that were solved using MATLAB. Some kinetic constants were estimated using the least square function. The results of the model fit well the experimental data.

1. Introduction

After an indiscriminate use of finite natural resources, the human being has finally come to realize that limits must be imposed. For instance, guidelines have finally been proposed to regulate human actions and ensure the planet’s sustainability [1]. Chemists and chemical engineers should also contribute to this effort, i.e., by developing processes that minimize waste, increase recycling, and improve sustainability [2]. There are also some initiatives in this direction, such as Responsible Care^® [3], which works with national industry associations to improve the industry’s health, safety, and environmental performance.

The removal of undesirable substances from water may be classified under physical, chemical, and biological treatments [4]. However, these treatments are not always suitable for recalcitrant chemicals, such as aromatics and other complex molecules deriving from industrial waste or personal care products. In several cases, the use of enzymes as catalysts was successfully proposed [5,6,7,8,9]. In particular, enzymes belonging to the oxidoreductase family, like peroxidases and laccases, showed good potential for this use.

Peroxidases (E.C. 1.11.1.7) are heme proteins that belong to the oxidoreductase family. They catalyze the oxidation of several substrates by using peroxides as electron acceptors. Peroxidases are found in animals and plants and some of them can be processed at low cost from renewable feedstocks [10], the seventh principle of green chemistry [11,12]. Soybean peroxidase (SBP) can be extracted from the soybean (Glycine max) seed hulls; therefore, it is environmentally friendly, and it is an abundant raw material in Brazil, which in 2013 became the world’s largest soybean producer in the world. In 2019, the overall production of soybean was 336 million metric tons, 131 of which was produced in Brazil [13].

Many authors showed the effectiveness of SBP in the oxidation of chlorophenols [14,15,16,17,18]. The ability of SBP in the degradation of 2,4,6-trichlorophenol (TCP) was previously studied by Calza et al. [19] using composite material under UV irradiation. Nevertheless, the goal of this present work is to study the enzymatic degradation of TCP in a microreactor using SBP as a catalyst.

Microreactors are devices with microscopic dimensions, for instance, a width of 200 μm and a volume of 250–1000 μL. This design allows the development of well-controlled very fast reactions, highly exothermic and endothermic reactions, and some multiphase flows. In microreactors, small quantities of reagents were used, thus leading to lower costs, lower consumption of raw materials, and a greener process. They have been used to develop new pharmaceutical and fine chemical routes [20] or as tools for organic synthesis [21] and intensive chemical processes. Microreactor devices were also extensively used to study enzymatic reactions, as reviewed before [22,23], for instance, to hydrolyze the soybean oil catalyzed with Thermomyces lanuginosus lipase [24] or to degrade p-chlorophenol in a two-phase flow microchannel system [25].

In this work, a microreactor with a volume of 250 μL was employed in the study of enzymatic degradation of TCP. The fluid dynamics of the microreactor was modeled as well. By using the ANSYS CFX tool, the simulations showed the existence of secondary flows, which enhanced mixing. Although the laminar flow was developed, it can be assumed to be a well-mixed medium. The kinetic data were evaluated through a mechanistic model using the bi-bi ping-pong model, which was adequate to represent peroxidase degradation. Finally, the results presented here increase the current knowledge and demonstrate the possibility of efficient TCP degradation performed by an abundant and low-cost enzyme, also contributing to the future development of cost-effective industrial processes for the treatment of wastewaters containing recalcitrant toxic pollutants. It is an innovative, environmentally friendly wastewater treatment method.

2. Materials and Methods

2.1. Reagents

The reagents used were 2,4,6–trichlorophenol (C₆H₃Cl₃O), provided by Sigma-Aldrich (purity 98%); hydrochloric acid, provided by Synth (37% v/v); acetonitrile and acetic acid (100% v/v), provided by Tedia. SBP was purchased by Bio-Research Products Inc., Iowa, USA, and used as is.

2.2. Experimental Setup

The experimental data were obtained in the Syrris ASIA Microsystem (shown in Figure 1) equipped with two syringe pumps, a heater system for temperature control, and a Dolomite glass microchip (length, 2500 mm; volume, 250 μL; maximum operating pressure, 30 bar). The mixing of SBP and substrates occurs in a double T-junction placed immediately before the microreactor.

The oxidation of TCP (0.25 mM) was developed in the presence of H₂O₂ (0.3 mM) at 25 °C in phosphate buffer solution 0.1 M (pH = 5.4) and different concentrations of SBP from 0.5 to 2 μg/mL. The flow rate was set in the range of values from 12.5 to 250 μL/min depending on the desired reaction time. Samples of 0.1 mL each were collected from the output of the microreactor and 0.9 mL of HCl 0.1 M were immediately added to the sample in order to stop the reaction. Each measurement was performed in triplicate.

The concentration of TCP in the samples was determined by Ultra Performance Liquid Chromatography with a Shimadzu LC-20AD Prominence UPLC equipped with a LICHROSPHER 100 RP-18 5 μm 125 × 4 mm column (elution with acetonitrile/acetic acid 2%–60/40% v/v; flow rate 0.6 mL/min, temperature 40 °C, analytical detector wavelength, 220 nm).

2.3. Mathematical Method

The classical model for enzymatic reactions, proposed by Michaelis-Menten (Equation (1)), is inadequate for peroxidase reactions. Indeed, peroxidase reactions follow a modified bi-bi ping-pong mechanism, involving a sequence of reactions with enzyme oxidized intermediates. The general bi-bi ping-pong mechanism is represented below (Equations (2) and (3)) [26]:

$$\mathrm{E}+\mathrm{S}\underset{}{\overset{}{\rightleftarrows }}\mathrm{E}\mathrm{S}\stackrel{}{\to }\mathrm{E}+\mathrm{P}$$

(1)

$$\mathrm{E}+\mathrm{A}\underset{}{\overset{}{\rightleftarrows }}\mathrm{E}\mathrm{A}\underset{}{\overset{}{\rightleftarrows }}\mathrm{E}\mathrm{P}+\mathrm{Q}$$

(2)

$$\mathrm{EP}+\mathrm{B}\underset{}{\overset{}{\rightleftarrows }}\mathrm{EPB}\underset{}{\overset{}{\rightleftarrows }}\mathrm{E}+\mathrm{P}$$

(3)

In these reactions, E is the enzyme; EP is a modified form of the enzyme; ES, EA, and EPB are enzyme-substrate complexes; S, A, and B are the substrates; and P and Q are the products.

Peroxidases in the presence of H₂O₂ catalyzed the dehydrogenation of compounds, such as phenols and amines, following a modified ping-pong mechanism, also known as the peroxidase mechanism (Figure 2):

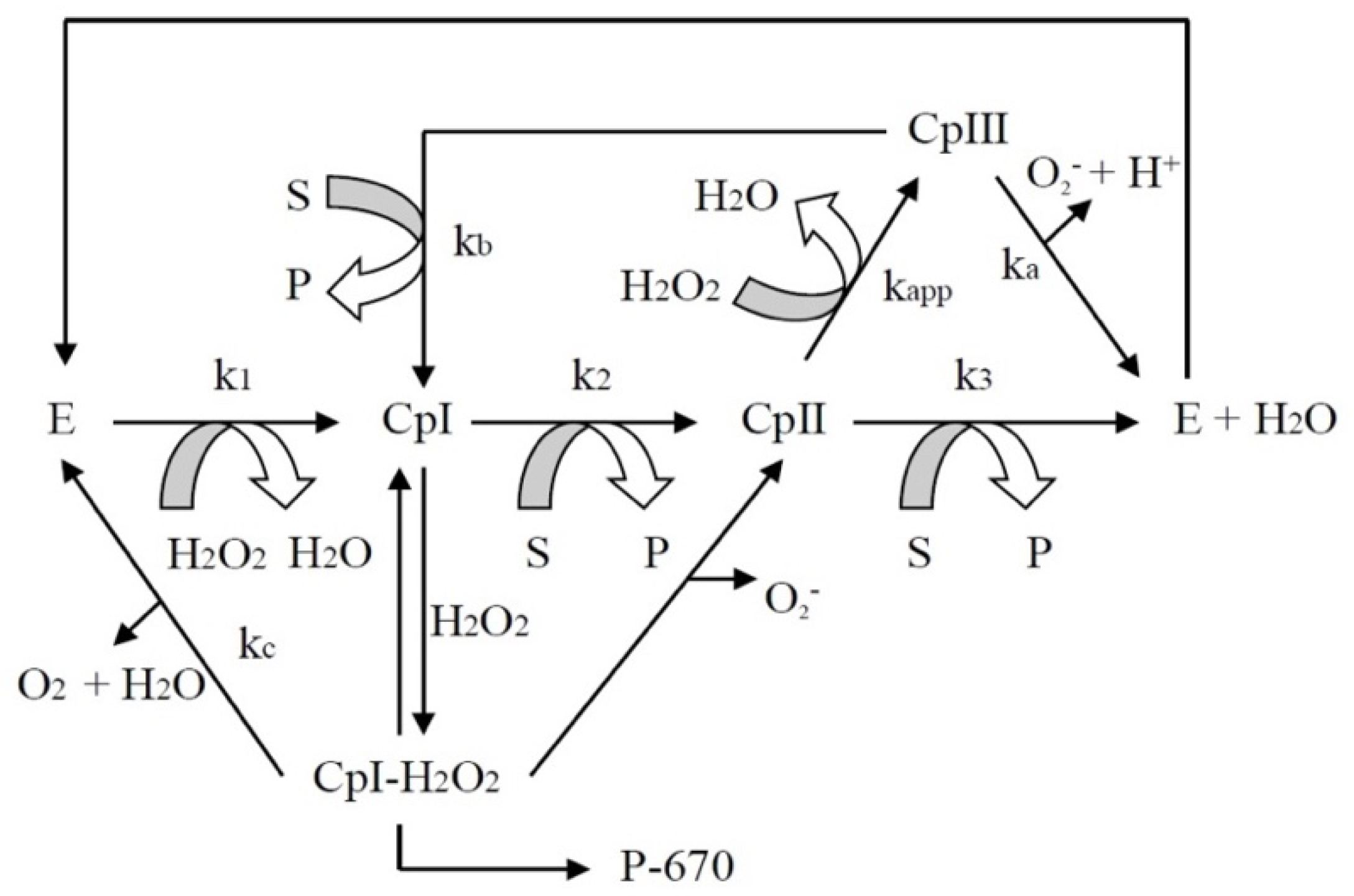
In this mechanism, the enzyme native form (E) is oxidized by the two-electron transfer from H₂O₂ to the heme, creating an oxidized form of the enzyme called “Compound I” (CpI). Successive one-electron reductions return the enzyme to its native or reduced state via another enzyme oxidized intermediate called “Compound II” (CpII). Other pathways can be performed, involving “Compound III” (CpIII), Compound I-H₂O₂ intermediate (CpI-H₂O₂), and an inactive form called verdo hemo protein (P-670). S is the substrate and P is the radical product generated. This mechanism will be covered in more detail in the next section, where the model development is discussed.

Miložič et al. [23] proposed a mathematical model to simulate the enzyme catalyzed reaction, in which the enzyme was immobilized in the inner walls of the microreactor. The kinetics was represented by a ping-pong bi-bi mechanism. The model well simulated two consecutively connected microreactors coated with N-SBM-ATA-wt.

2.4. Modeling and Parameter Estimation

The representation of the enzymatic kinetic model, as with other models of chemical reactions, was performed by mathematical systems composed by differential and/or algebraic equations of the process variables, such as the concentrations, in a way that predictions based on the model response can be obtained. These predictions allowed the simulation, design, and optimization of the process.

The parameter estimation procedure consisted of adjusting the model parameters by the minimization of an objective function, which is a measure of the distance between the experimental data and the model predictions. The weighted least squares function, which measures the sum of the quadratic deviations of the model in relation to the experiment, was used. Once the objective function had been defined, the next step was to minimize it by adjusting the parameters. In this work, the computational simulations were performed using the MATLAB software.

2.5. Computational Fluid Dynamics

The computational fluid dynamics (CFD) is the numerical branch of fluid mechanics. The basic equations of mass, momentum, and energy balances are differential equations that may mathematically represent, through the models, a huge number of physical phenomena, such as multiphase flows [27], reactive flows [28,29], and industrial equipment [30].

Therefore, what characterizes each phenomenon specifically is the geometry, the boundary, and the initial conditions related to each specific situation. From this point, it is possible to solve the system of partial differential equations that represents each prototype. Thus, the CFD simulation can be seen as a set composed of three issues: (1) the geometry that represents the phenomenon and the associated mesh; (2) the mathematical solution of differential equations, constitutive equations, and boundary conditions connected with the phenomenon; and (3) the visual presentation of the results.

In this work, the CFD simulations were carried out using ANSYS CFX 16.0. The discretization of microfluidic elements was performed with hexahedral and prismatic elements since the total number of elements was reduced if compared to tetrahedral meshes.

The mesh was considered converged comparing head losses with flow of 2000 μL/min, which generated a more complex velocity distribution. The steady state was assumed. The fluid considered was water at 25 °C.

The flow in the microchannels under the conditions analyzed was laminar, since the greatest Reynolds number was equal to 100 calculated on the Dolomite microchip, considering the T-mixer, double T and reaction section. The laminar flow was composed of several laminar layers that do not mix; thus, exchange occurred only by slow diffusion at the interfaces. The Dolomite microchip used in this work encompasses a double T-junction and a mixing sector, so a pre-mixing of different inputs may occur. The various curves present in the reaction sector developed secondary flows resulting from the centrifuge force, the Dean effect. The crossing of streamlines led to better mixing of the reaction medium.

2.6. Kinetic Model Development

The peroxidase reactions follow the bi-bi ping-pong mechanism described in Section 2.3, which involves almost three steps described by Equations (4)–(6) (where k₁, k₂, and k₃ are the apparent kinetic constants).

$$\mathrm{SBP}+{\mathrm{H}}_2{\mathrm{O}}_2\stackrel{k_1}{\to }\mathrm{CpI}+{\mathrm{H}}_2\mathrm{O}$$

(4)

$$\mathrm{CpI}+\mathrm{TCP}\stackrel{k_2}{\to }\mathrm{CpII}+\mathrm{P}$$

(5)

$$\mathrm{CpII}+\mathrm{TCP}\stackrel{k_3}{\to }\mathrm{SBP}+\mathrm{P}+{\mathrm{H}}_2\mathrm{O}$$

(6)

Further, the overall reaction can be expressed in Equation (7).

$${\mathrm{H}}_2{\mathrm{O}}_2+2\mathrm{TCP}\stackrel{\mathrm{SBP}}{\to }2\mathrm{P}+{\mathrm{H}}_2\mathrm{O}$$

(7)

However, peroxidase can be deactivated due to excess H₂O₂, generating a third oxidized enzyme intermediate (CpIII) as in Equation (8):

$$\mathrm{CpII}+{\mathrm{H}}_2{\mathrm{O}}_2\stackrel{k_{app}}{\to }\mathrm{CpIII}+{\mathrm{H}}_2\mathrm{O}$$

(8)

Although CpIII is catalytically inactive, it can be decomposed back to the enzyme native form (Equation (9)) or can also be reduced to CpI (Equation (10)), which can be oxidized back to the enzyme native form (Equation (11)) [31].

$$\mathrm{CpIII}\stackrel{k_a}{\to }\mathrm{SBP}+{\mathrm{O}}_2{}^{-}+{\mathrm{H}}^{+}$$

(9)

$$\mathrm{CpIII}+\mathrm{TCP}\stackrel{k_b}{\to }\mathrm{CpI}+\mathrm{P}$$

(10)

$$\mathrm{CpI}+{\mathrm{H}}_2{\mathrm{O}}_2\stackrel{k_C}{\to }\mathrm{SBP}+{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}$$

(11)

Nicell [32] demonstrated that the enzyme inactivation occurs mostly because of other factors such as free radical inactivation and adsorption or entrapment on the end product polymers. Once the reaction has gone to completion, the number of phenolic compounds molecules oxidized per molecule of the enzyme in solution is constant. By this way, SBP can be treated as a pseudo-substrate of the reaction, as represented below in Equation (12):

$$\mathrm{SBP}+Ks\mathrm{TCP}\to {\mathrm{SBP}}_{(inactive)}+\mathrm{Products}$$

(12)

Ks is the number of TCP molecules removed per enzyme molecule after a complete reaction, also known as the turnover number of an enzyme, and is calculated by Equation (13):

$$Ks=\frac{{[\mathrm{TCP}]}_0-{[\mathrm{TCP}]}_{final}}{{[\mathrm{SBP}]}_0}$$

(13)

Then the amount of permanently inactivated enzyme can be calculated by Equation (14):

$${\mathrm{SBP}}_{(inactive)}=\frac{{[\mathrm{TCP}]}_0-[\mathrm{TCP}]}{Ks}$$

(14)

However, it is important to emphasize that Nicell’s [32] studies were focused on horseradish peroxidase (HRP) and not SBP. Although these two proteins are similar, a different behavior on these aspects cannot be excluded in the absence of experimental evidence.

The process modeling is obtained by the mass balance of all species, according to reactions (4), (5), (6), (8), (9), (10), and (11). The mass balance of the enzyme forms, substrates, and products are shown in Equations (15)–(21).

$$\frac{d[\mathrm{SBP}]}{dt}=-k_1[\mathrm{SBP}][{\mathrm{H}}_2{\mathrm{O}}_2]+k_3[\mathrm{CpII}][\mathrm{TCP}]+k_a[\mathrm{CpIII}]+k_c[\mathrm{CpI}][{\mathrm{H}}_2{\mathrm{O}}_2]$$

(15)

$$\frac{d[\mathrm{CpI}]}{dt}=k_1[\mathrm{SBP}][{\mathrm{H}}_2{\mathrm{O}}_2]-k_2[\mathrm{CpI}][\mathrm{TCP}]+k_b[\mathrm{CpIII}][\mathrm{TCP}]-k_c[\mathrm{CpI}][{\mathrm{H}}_2{\mathrm{O}}_2]$$

(16)

$$\frac{d[\mathrm{CpII}]}{dt}=k_2[\mathrm{CpI}][\mathrm{TCP}]+k_3[\mathrm{CpII}][\mathrm{TCP}]-k_{app}[\mathrm{CpII}][{\mathrm{H}}_2{\mathrm{O}}_2]$$

(17)

$$\frac{d[\mathrm{CpIII}]}{dt}=k_{app}[\mathrm{CpII}][{\mathrm{H}}_2{\mathrm{O}}_2]-k_a[\mathrm{CpIII}]-k_b[\mathrm{CpIII}][\mathrm{TCP}]$$

(18)

$$\frac{d[{\mathrm{H}}_2{\mathrm{O}}_2]}{dt}=-k_1[\mathrm{SBP}][{\mathrm{H}}_2{\mathrm{O}}_2]-k_{app}[\mathrm{CpII}][{\mathrm{H}}_2{\mathrm{O}}_2]-k_c[\mathrm{CpI}][{\mathrm{H}}_2{\mathrm{O}}_2]$$

(19)

$$\frac{d[\mathrm{TCP}]}{dt}=-k_2[\mathrm{CpI}][\mathrm{TCP}]-k_3[\mathrm{CpII}][\mathrm{TCP}]-k_b[\mathrm{CpIII}][\mathrm{TCP}]$$

(20)

$$\frac{d[\mathrm{P}]}{dt}=k_2[\mathrm{CpI}][\mathrm{TCP}]+k_3[\mathrm{CpII}][\mathrm{TCP}]+k_b[\mathrm{CpIII}][\mathrm{TCP}]$$

(21)

This system of ordinary differential equations (ODEs) represents a transient-state model. A pseudo-steady-state model can also be obtained by assuming steady state for all the enzyme forms (they quickly reach this condition), as shown in Equation (22):

$$\frac{d[\mathrm{CpI}]}{dt}=\frac{d[\mathrm{CpII}]}{dt}=\frac{d[\mathrm{CpIII}]}{dt}=0$$

(22)

Equations (16)–(18) may be simplified for CpI, CpII, and CpIII concentrations, generating Equations (23)–(25):

$$[\mathrm{CpI}]=\frac{k_1[\mathrm{SBP}][{\mathrm{H}}_2{\mathrm{O}}_2]+k_b[\mathrm{CpIII}][\mathrm{TCP}]}{k_2[\mathrm{CpI}][\mathrm{TCP}]+k_c[{\mathrm{H}}_2{\mathrm{O}}_2]}$$

(23)

$$[\mathrm{CpII}]=\frac{k_2[\mathrm{CpI}][\mathrm{TCP}]}{k_3[\mathrm{CpII}][\mathrm{TCP}]+k_{app}[{\mathrm{H}}_2{\mathrm{O}}_2]}$$

(24)

$$[\mathrm{CpIII}]=\frac{k_{app}[\mathrm{CpII}][{\mathrm{H}}_2{\mathrm{O}}_2]}{k_a+k_b[\mathrm{CpIII}][\mathrm{TCP}]}$$

(25)

The total (initial) amount of enzyme is given by Equation (26):

$${[\mathrm{SBP}]}_0=[\mathrm{SBP}]+[\mathrm{CpI}]+[\mathrm{CpII}]+[\mathrm{CpIII}]+{[\mathrm{SBP}]}_{inactive}$$

(26)

In this case, a differential-algebraic system of equations (DAEs) is obtained, considering Equations (19)–(21), (23)–(26).

The reaction constants listed in

Table 1. Reaction constants used in model development.

Constant	Value	Unit	Reference
k1	2.0 × 107	M−1 s−1	[33]
k2	1.13 × 107	M−1 s−1	[34]
k3	1.1 × 106	M−1 s−1	[35]
kapp	2.0 × 101	M−1 s−1	[36]
ka	4.2 × 10−3	s−1	[37]
kb	9.5 × 10−1	M−1 s−1	[38]
kc	1.0 × 103	M−1 s−1	[37]

were used as a reference in the development of the model. All of these rate constants were obtained for HRP at 25 °C and pH 7.

2.7. Kinetic Data Analysis

The kinetic model used here was a system of initial value problem (IVP) for the differential-algebraic system of equations (DAEs). The mass balance was considered for substrates (TCP and H₂O₂), product (P), enzyme (SBP), and enzyme oxidized intermediates (CpI, CpII, and CpIII). The following restrictions on parameters was also considered [32]: k₁ > k₂ > k₃ >> k_app, k_a, k_b, k_c.

All simulations were performed on MATLAB version R2015a. The mathematical model solutions were obtained by ode15s solver (BDF, backward differentiation formula, method). The parameter estimation procedures were carried out using the fmincon optimizer considering the interior point method. The objective function was the weighted least squares between the experimental data and the values predicted by the model. The model fit was evaluated by the plots of model prediction and experimental data, and the calculated values of root-mean-square error (RMSE), as Equation (27), and the adjusted coefficient of determination ($R_{adjusted}^2$), as Equation (28):

$$\mathrm{RSME}={\displaystyle \sum _{i=1}^n\frac{{({\hat{u}}_i-u_i)}^2}{n}}$$

(27)

$$R_{adjusted}^2=1-\frac{(1-R^2)(n-1)}{n-(p+1)}$$

(28)

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^n{({\hat{u}}_i-u_i)}^2}}{{\displaystyle \sum _{i=1}^n{({\hat{u}}_i-{\overline{u}}_i)}^2}}$$

(29)

In these equations ${\hat{u}}_i$ is the value predicted by the model, u_i is the experimental data, ${\overline{u}}_i$ is the average experimental data, n is the number of points, and p is the number of model parameters.

3. Results

Three set of results are presented here. First, the CFD simulations of the 250 µL microchip are showed, followed by the experimental data of the degradation of TCP. Finally, the ping-pong model was assumed to represent the experimental data, and the system of IVP-ODE was solved by using MATLAB.

3.1. CFD Simulations

The first necessary step is to define the mesh. The optimum number of mesh elements was obtained by evaluating the pressure drop for an inlet flow rate of 2000 L/min. The mesh was considered converged when the pressure drop differs less than 1% for average cell edge size smaller than 17.5 μm, equivalent to 1.2 million elements.

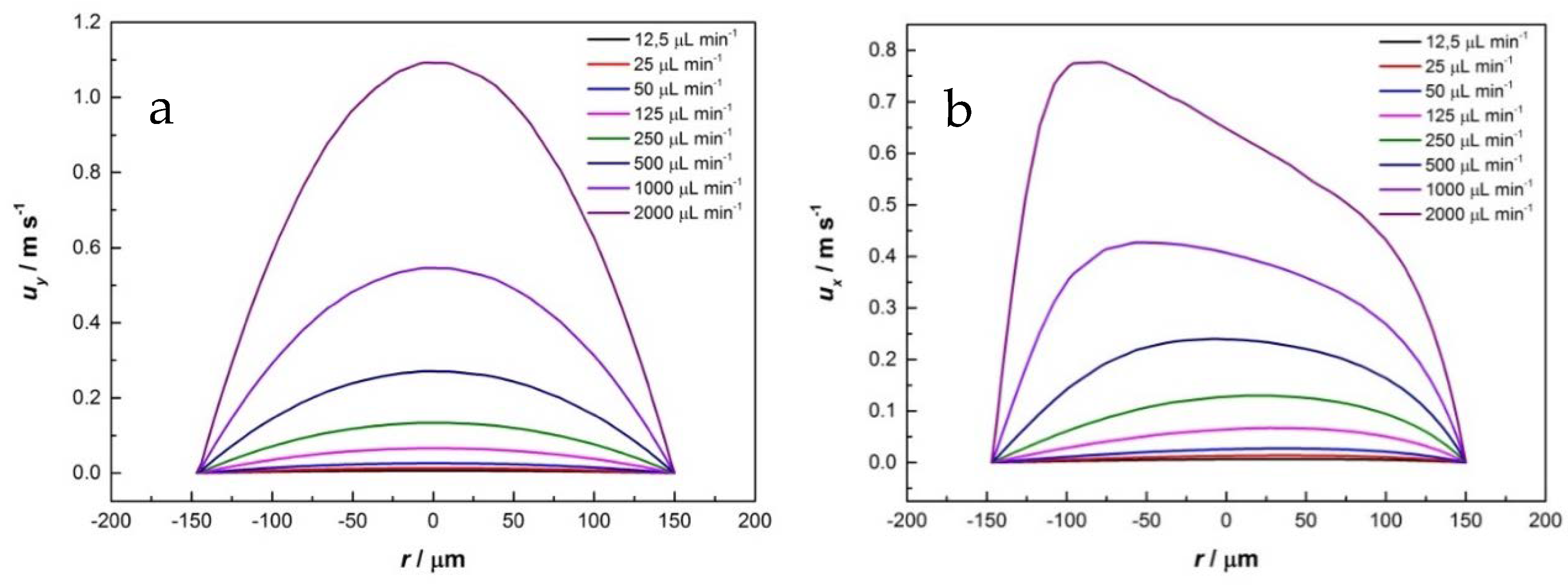
The flow was laminar since the Reynolds number was about 100. Therefore, the axial velocity profile had a parabolic shape in the straight-line portion, as can be seen in Figure 3a. Although the system has reduced dimensions and low rate-flows, the velocity allowed values of 1 m/s. Centripetal force interfered with the distribution of the velocity profile: the fluid accelerated toward the outside of the channel at the curve segments, and the maximum velocity point was shifted in this direction as well, as shown in Figure 3b.

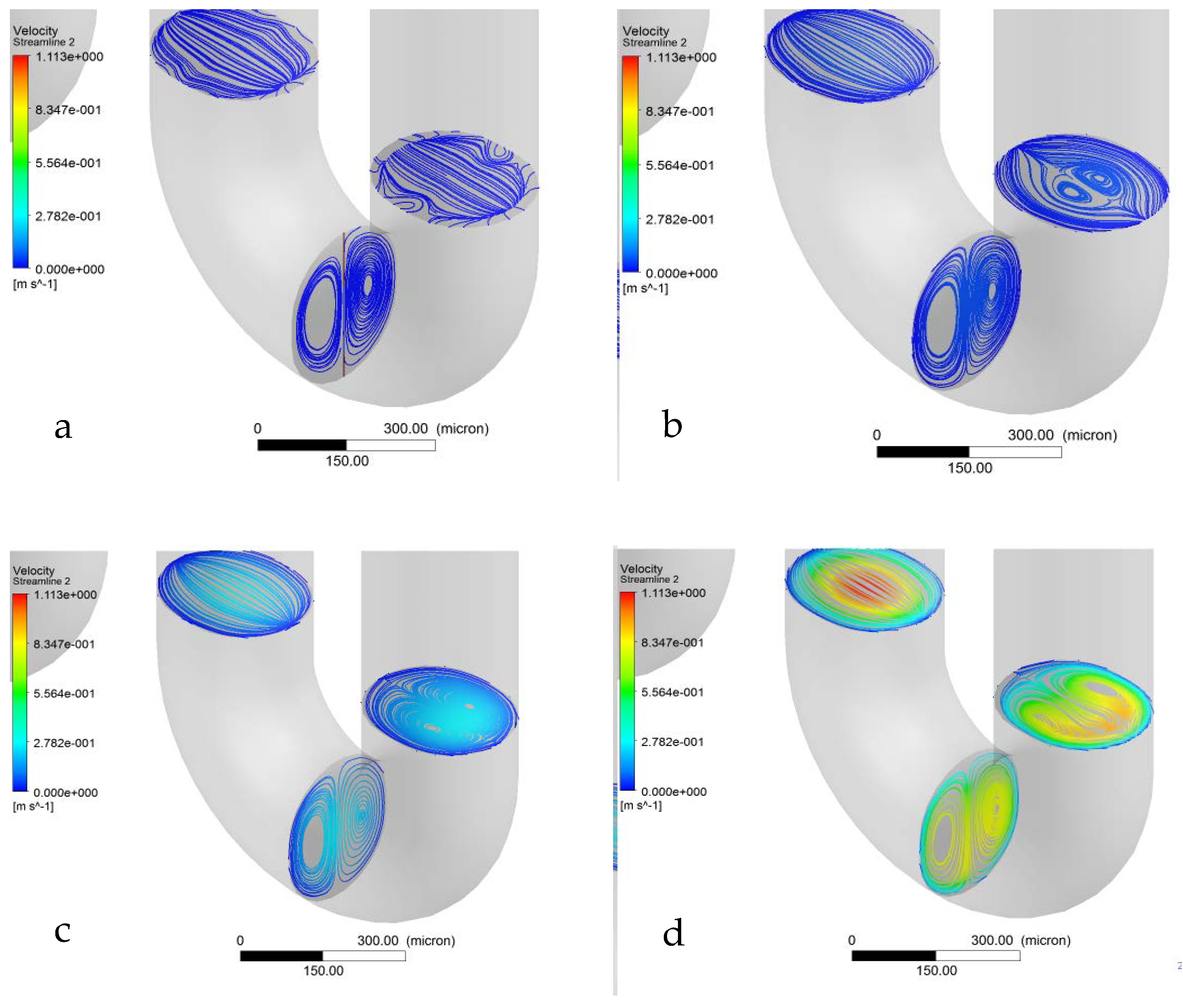
Another effect of the centripetal force was the formation of secondary flows in curved segments. This force interacted with the viscous forces generating a double vortex at the curved segments. Figure 4 presents the vortexes for the curved segment between the 6° and 7° channels and the flow of 12 µL/min. This is the Dean flow, which is inevitably formed in curve and spiral channels. This secondary flow can be evaluated from the Dean number (De), which relates inertial forces, centripetal forces, and viscous forces. If De < 140, only one vortex is formed in curve pipes [39], which was also observed here. The secondary flow contributed to diffuse flows and to improve microchannel mixing. It is important to point out that the secondary flows are very similar but are not the turbulence structure. However, the secondary flows are as effective as turbulence flows to promote better mixing [40,41].

3.2. TCP Degradation Experiments

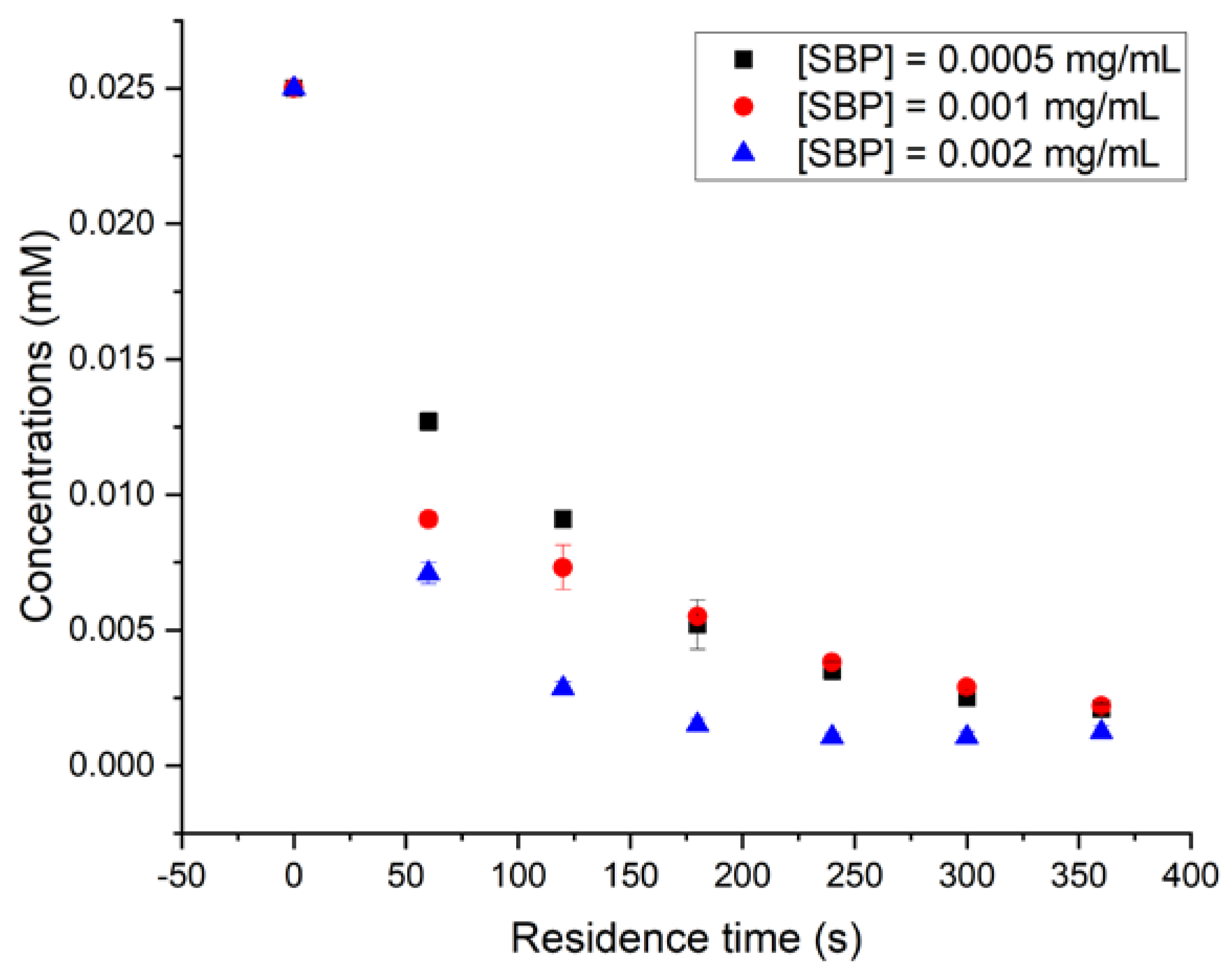
The experimental data relative to the TCP degradation using SBP are summarized in Figure 5 for three different enzyme concentrations (0.0005, 0.001, and 0.002 mg/mL). Due to well-mixing, the residence time can be assumed equal to one point of the kinetic curve (t_i, C_i). The results presented in Figure 5 and Figure 6 also show short values of residence times. The final conversions of substrate found for the three concentrations, as seen in Figure 5, were approximately 90%, which were reached in a few hundred seconds, indicating that a limit of degradation was achieved. These results indicate that biodegradation of TCP is efficient even at low enzyme concentrations.

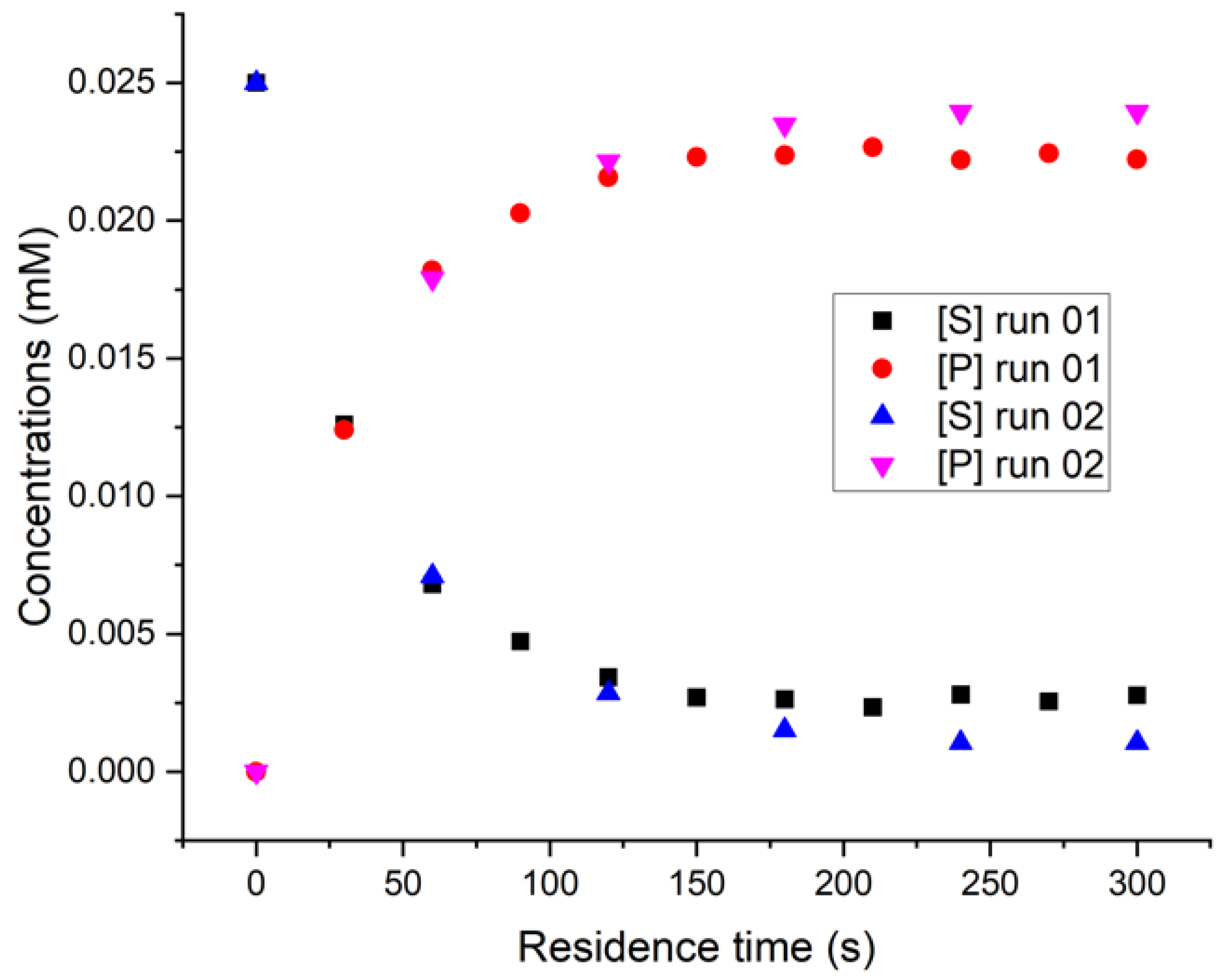
Additionally, the same operational conditions were performed at different times to evaluate the reproducibility of data. The curves in Figure 6 point out to a quite good agreement.

3.3. Data Analysis

The kinetic data were evaluated through a mechanistic model, the ping-pong model, which is adequate to represent peroxidase degradation. The model was composed of an initial value problem for ordinary differential equations that was solved using a MATLAB tool. The model solution was calculated by the BDF method (ode15s solver). In all these cases, both the ODE’s system and the DAE’s system were considered, but the second one presented a solution less sensitive to the initial estimates so only these results are presented.

Parameter estimation in MATLAB was performed using the main routine that reads all the experimental reaction data, and from an initial estimate for the model parameters, based on the reference values found in the literature (Table 1). The optimization was performed using the fminsearch optimizer. This procedure considers an objective function and the mathematical model, which were implemented in two respective subroutines. The objective function was minimized by the weighted least squares between the calculated values for the variable (substrate) obtained by the model and their respective experimental values.

Table 2. Estimated parameters and model fit evaluation.

Parameter	Value	Unit
k1	2.0 × 107	M−1 s−1
k2	6.79 × 106	M−1 s−1
k3	2.75 × 106	M−1 s−1
kapp	6.6	M−1 s−1
ka	1.09 × 10−2	s−1
kb	9.3 × 10−1	M−1 s−1
kc	8.99 × 102	M−1 s−1
Fobj	5.6276 × 10−2
RMSE	8.1177 × 10−10
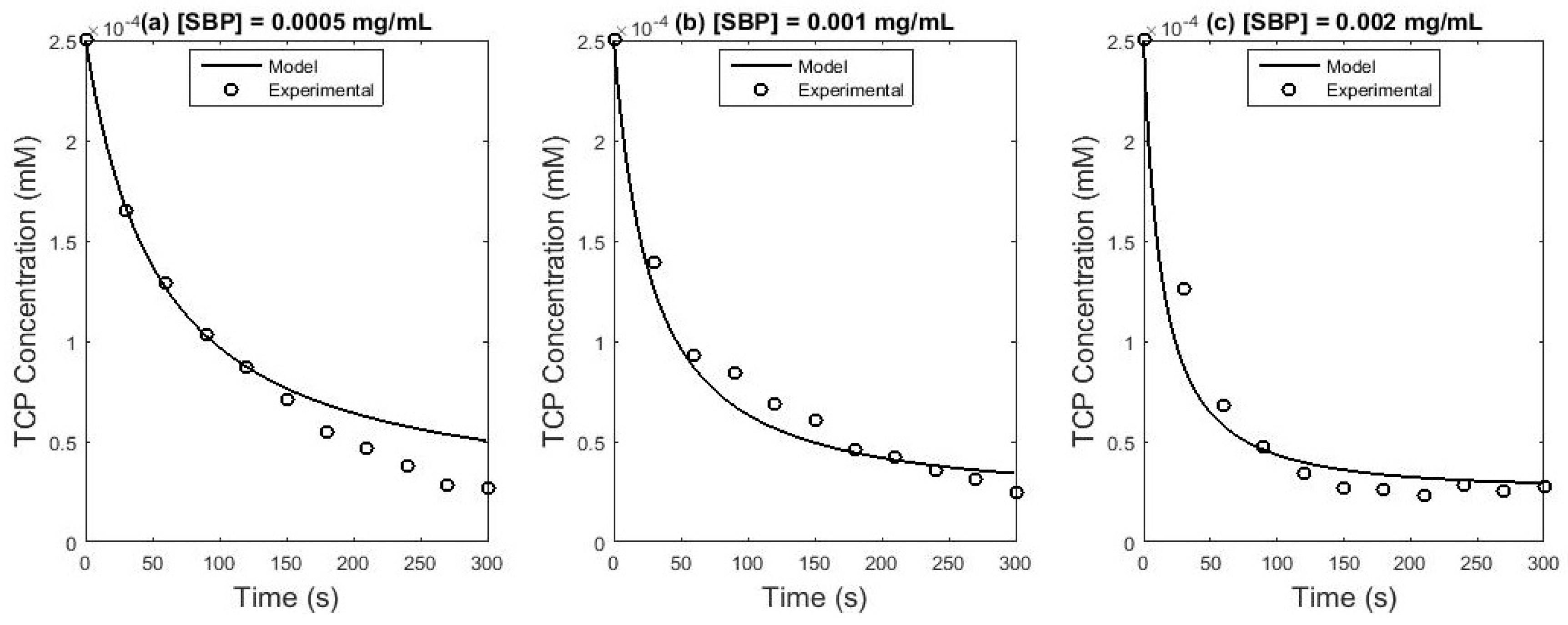
$R_{adjusted}^2$	95.06%

presents the estimated parameters and in Figure 7 the model prediction and experimental data were shown.

In all the experiments, the initial H₂O₂ and TCP concentrations were fixed at 0.3 mM and 0.25 mM, respectively. The influence of SBP concentration was evaluated by performing the reaction increasing the amount of SBP, considering the following concentrations: 0.0005 mg/mL, 0.001 mg/mL, and 0.002 mg/mL. It can be seen in Figure 7 that, with a higher SBP concentration, the TCP degradation increases. This confirms that SBP can perform TCP degradation in the presence of H₂O₂.

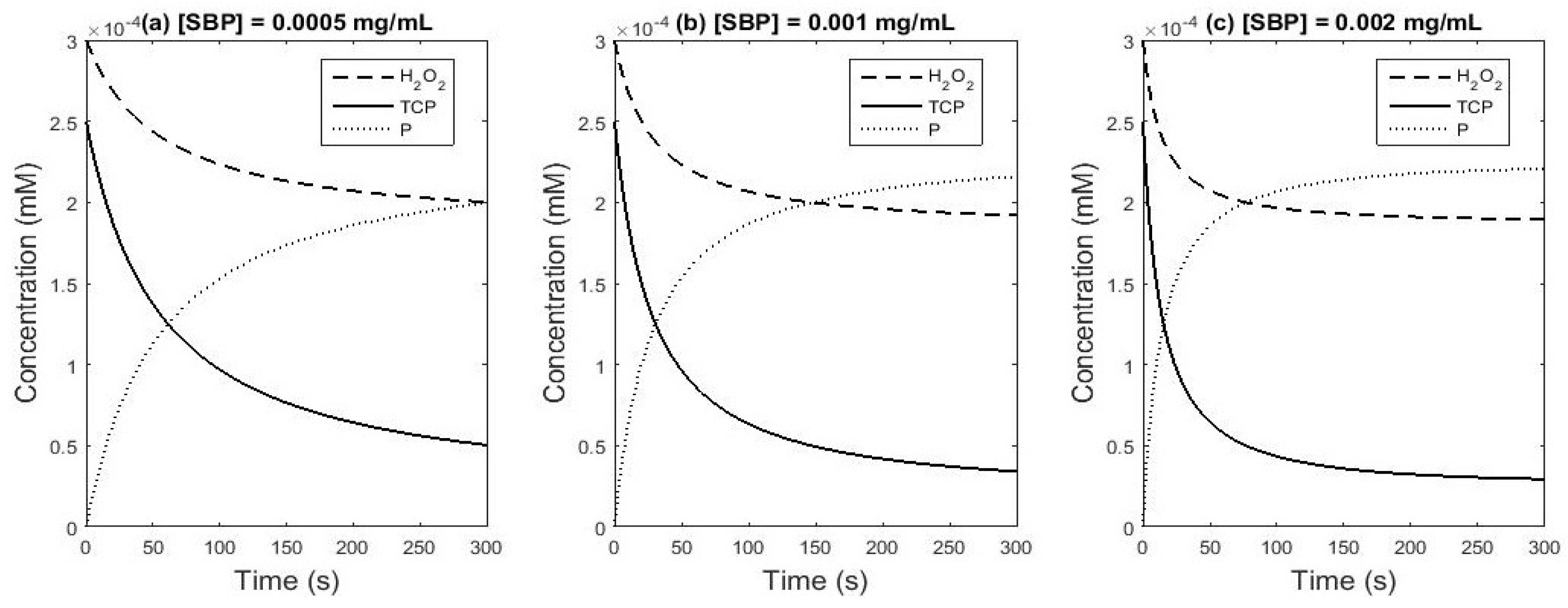
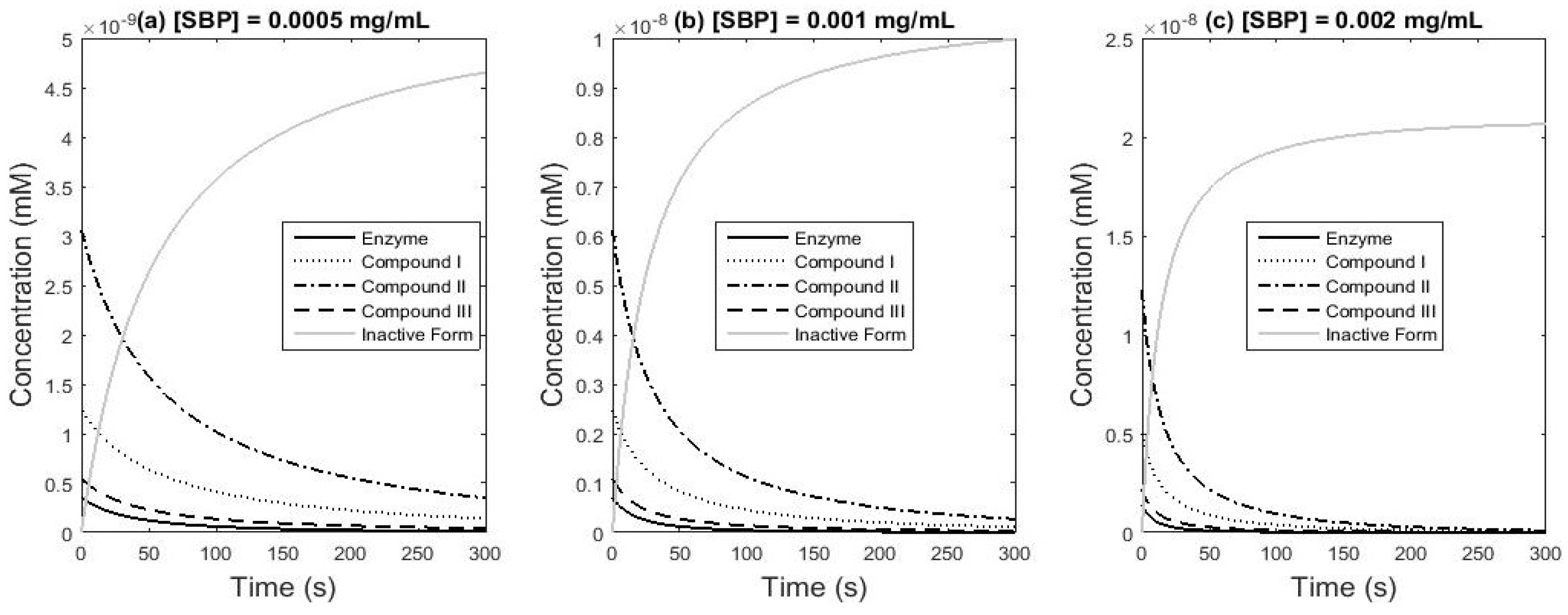
Based on the RSME, R²_adjusted values, and the predictions observed in Figure 7, it can be inferred that the model fit the experimental data reasonably well. It was also performed the model simulation of the process variables, based on the estimated parameters. Figure 8 presents the simulation of the substrates and products concentrations and Figure 9 presents the simulation of enzyme forms concentrations. The behavior of the curves is consistent with the expected results.

It is important to emphasize that several possibilities were tested before obtaining the presented model, including the Michaelis-Menten model (considering only TCP as substrate); other models considering different combinations of the reaction intermediate complexes; whether or not reverse reactions, considering of not Compound III formation and considering or not the enzyme inactivation model. First it was considered a large set of parameters, but this did not allow obtaining a single set of parameters in the estimation procedure.

4. Conclusions

The presented study confirms the potential of SBP in degrading harmful compounds, such as chlorinated phenolics. SBP is an enzyme that can be extracted from soybean hulls in a sustainable and cost-effective process, being a promising bioremediation method for wastewater treatment. The fluid dynamic evaluation (CFD analysis) confirmed the presence of secondary flows in the 250 μL microchip curves, which resulted in diffusion mixing and promoted better mixing. The experimental method used here to study the degradation of TCP using SBP proved to be efficient. It was possible to collect reaction samples with residence times in the order of seconds, with good repeatability and reproducibility of data obtained under different experimental conditions. The conversion of the substrate allowed about 90% for the three concentrations, indicating that a limit of degradation was achieved.

The kinetic data were evaluated through a mechanistic model, the bi-bi ping-pong model, which is adequate to represent peroxidase degradation. The model was composed by an initial value problem for ordinary differential equations that were solved using MATLAB. Some kinetic constants were estimated using the least square function. The results of the model fitted the experimental data reasonably well.

In conclusion, this work indicates that it is possible to design a preliminary industrial process for the degradation of toxic pollutants using the low-cost enzyme SBP. This is an innovative, environmentally friendly, and potentially efficient wastewater treatment strategy.