1. Introduction
The generalized Hamiltonian dynamics (hereafter GHD) was developed by Dirac 70 years ago [
1,
2,
3]. While the conventional Hamiltonian dynamics employs an assumption that the momenta are independent functions of velocities, Dirac considered a more general situation where momenta are not independent functions of velocities [
1,
2,
3]. From the physical point of view, the GHD is a purely classical formalism for constrained systems: in the GHD, constraints are incorporated into the Hamiltonian. Dirac developed the GHD with the purpose to apply it to quantum field theory [
3].
For the application to the quantum field theory and statistical mechanics, Dirac’s GHD was further developed by a number of authors—see, e.g., papers by Sergi [
4,
5,
6,
7] and references therein. The focus of Sergi’s works [
4,
5,
6,
7] was on non-Hamiltonian mathematical structures, including non-Hamiltonian commutators.
In search of a purely classical formalism that can be applied to atomic and molecular physics and can reproduce quantum results classically, Oks and Uzer, in 2002 [
8], brought up an idea of choosing integrals of the motion as the constraints. The authors of paper [
8] first provided a general description of their formalism. Then they considered hydrogenic atoms as an example. The authors of paper [
8] demonstrated that this purely classical formalism allows the existence of classical non-radiating states, so that such states are stable. Remember that, according to the usual classical formalism (including classical electrodynamics), the electron would lose the energy through the radiation and fall into the nucleus: this failure of the usual classical formalism was one of the primary reasons for the birth of quantum mechanics. In distinction, in the purely classical formalism from paper [
8] the electron does not fall into the nucleus.
Further, the authors of paper [
8] derived the formula for the energy of such classical non-radiating states. They showed that this set of classical energies coincides with the energies of the corresponding quantal stationary states. While obtaining this result, the authors of paper [
8] did not “forcefully” quantize any physical quantity describing the atom.
It should be emphasized that the physical interpretation was that the existence of these classical non-radiating states is due to a new kind of a time dilation. This new kind of the time dilation is non-Einsteinian (see paper [
9] and book [
10]): it has nothing to do with the time-dilation in the theory of relativity.
The purpose of the present paper is to present another application of the Oks–Uzer purely classical formalism [
8] within atomic and molecular physics, i.e., to microscopic systems of discrete (rather than continuous) charges. Before proceeding with our presentation, we note in passing that, outside atomic and molecular physics, some authors studied whether there are continuous moving charge distributions that would not radiate—see, e.g., the paper by Goedecke [
11] and references therein. It was found that certain continuous charge distributions would not radiate. However, first, the radius of their “orbit” should be less than the size of the charge distribution (so that the the distribution would only “wobble”). Second, this result is valid only for continuous charge distributions, so that atoms and molecules do not qualify.
In our view, the most interesting (and potentially relevant to atomic physics) paper of that series was published by Raju [
12]. He considered classical circular orbits of the electron and of the proton in a hydrogen atom. He took into account the relativistic effect of the retardation, due to which the force on the electron is at the “last-seen” position of the proton, while the proton has moved since then. This results in a torque that would initially accelerate the electron and later on decelerate the electron and so on. Then Raju [
12] added radiative damping into the consideration, which provides a decelerating torque for the electron. Raju [
12] found sets of parameters for which the initially accelerating torque due to the retardation would be totally compensated by the decelerating torque due to the radiative damping. Then Raju [
12] stated that “it was prematurely concluded that radiative damping makes the classical hydrogen atom unstable”. However, this statement seems to be incorrect. In reality, within Raju’s concept [
12], the radiative damping does make the classical hydrogen atom unstable. Indeed, when the retardation torque compensates the radiative damping torque, this means only that the tangential acceleration of the electron vanishes, but the centripetal acceleration of the electron remains and so does the radiation. Another view of this situation is that the two torques can compensate each other, but one of them is due to the radiation, which carries the energy away from the electron. The electron would therefore continuously lose energy and would fall into the proton. Thus, the concept by Raju [
12] did not lead to a non-radiating state of hydrogen atoms.
To avoid any confusion, we also mention that there were attempts to find stable states of hydrogen atoms in frames of a so-called stochastic electrodynamics, where the interaction with the zero-point fluctuations of a vacuum were added into the system to counterbalance the effect of the radiative damping—see, e.g., papers by Puthoff [
13], Cole and Zou [
14], as well as by Nieuwenhuizen [
15], and references from these papers. However, first and foremost, the zero-point fluctuations are purely quantum effects. These kind of works are thus beyond the scope of the present paper devoted to purely classical description of microscopic systems. Second, the study by Nieuwenhuizen [
15] (the latest out of the above three works) showed that this concept leads to the self-ionization of hydrogen atoms from states of relatively low (by absolute value) energy. Thus, this mixed quantum–classical concept actually does not explain the stability of all states of hydrogen atoms.
In the present paper, we apply the GHD to a charged Spherical Harmonic Oscillator (hereafter SHO). The SHO is important both fundamentally and practically. From the theoretical point of view, the SHO is one of the two fundamental microscopic systems (the other one being hydrogenic atoms), characterized by higher-than-geometrical symmetry (i.e., algebraic symmetry) and thus having conserved quantities beyond energy and the angular momentum. The algebraic symmetries of these two fundamental microscopic systems manifest classically by closed orbits and quantally by an “additional” degeneracy of their energy levels. From the practical point of view, the SHO is employed, e.g., in nuclear physics in nuclear shell models.
According to classical physics, the charged SHO is unstable with respect to radiating electromagnetic waves: it would lose its energy and end up in the state of zero energy. Of course, this is contrary to quantum mechanics, according to which the charged SHO has relatively stable stationary states. We show that, similarly to the Oks–Uzer results [
8], the GHD—the purely classical formalism—allows the existence of, generally speaking, an infinite number of classical non-radiating states of the SHO.
2. Overview of the General Formalism and of Its Application to Hydrogenic Atoms
This overview is absolutely necessary for readers to facilitate their understanding of the new results (presented in
Section 3) and of the conclusions (
Section 4). The alternative would be to simply refer to our previous publications [
8,
10], but, in this case, readers would have to spend lots of time searching through our paper [
8] and book [
10]. Therefore, out of the respect to readers, we provide here excerpts from our two previous publications [
8,
10] as quotations (enclosed in the quotation marks).
“Dirac [
1,
2,
3] considered a dynamical system of N degrees of freedom characterized by generalized coordinates q
n and velocities v
n = dq
n/dt, where n = 1, 2, ..., N. From the Lagrangian of the system
momenta are defined as
“The quantities qn, vn, pn can be varied by small amounts δqn, δvn, δpn, respectively. The latter small quantities are of the order of ε and the variation should be worked to the accuracy of ε. As a result of the variation, the set of Equation (2) would not be satisfied any more. This is because their right side would differ from the corresponding left side by a quantity of the order of ε.
Further, Dirac made a distinction between two types of equations. One type is equations that do not hold after the variation, such as the set of Equation (2). Dirac called them “weak” equations. Below for weak equations, following Dirac, we use an equality sign ≅ different from the usual equality sign. Another type constitute equations that hold exactly even after the variation, such as Equation (1). Dirac called them “strong” equations. If quantities ∂L/∂v
n are not independent functions of velocities, it is possible to exclude velocities v
n from the set of Equation (2) and obtain one or several weak equations
containing only the sets of q and p (here and below we skip the suffix of quantities q and p).”
“In his formalism, Dirac [
1,
2,
3] used the following complete system of independent Equations of the type (3):
Here the word “independent” means that neither of the φ’s can be expressed as a linear combination of the other φ’s with coefficients depending on q and p. The word “complete” means that any function of q and p, which would become zero with the allowance for Equation (4) and which would change by ε under the variation, should be a linear combination of the functions φm(q, p) from Equation (4) with coefficients depending on q and p.
Finally, proceeding from the Lagrangian to a Hamiltonian, Dirac [
1,
2,
3] obtained the following primary result:
(here and below, the summation over a twice repeated suffix is understood).”
“Equation (5) is a strong equation expressing a relation between the generalized Hamiltonian Hg and the conventional Hamiltonian H (q, p). Quantities um are coefficients to be determined.”
“Generally, they are functions of q, v, and p; by using the set of Equation (2), they could be made functions of q and p. It should be emphasized that Hg ≅ H(q, p) would be only a weak equation - in distinction to Equation (5).
From Equation (5) it is seen that the Hamiltonian is not uniquely determined, because a linear combination of φ’s may be added to it. Equation (4) are called constraints. The distinction between constraints (i.e., weak equations) and strong equations, described above, can be reformulated as follows.
Constraints must be employed in accordance to certain rules. Constraints can be added. Constraints can be multiplied by factors (depending on q and p), but only on the left side, so that these factors must not be used inside Poisson brackets.
If f is some function of q and p, then df/dt (i.e., a general equation of motion) in the Dirac’s GHD is
where [f, g] is the usual Poisson bracket. Substituting φ
m’ in Equation (6) instead of f and taking into account the set of Equation (4), one obtains:
these consistency conditions allow determining the coefficients u
m.”
“It should be emphasized that the GHD was designed by Dirac specifically for applications to quantum field theory [
3], that is, for the purpose totally different from the purpose of Oks-Uzer work [
8].”
“The authors of paper [
8] reformulated the GHD for atomic and molecular physics where many systems have a higher than geometrical symmetry and therefore possess additional integrals of the motion. Oks and Uzer [
8] suggested using integrals of the motion as the constraints in the GHD.
In their general formalism, they considered a classical atomic or molecular system of N degrees of freedom, possessing M classical integrals of the motion A
m (q, p), m = 1, 2, ..., M. They wrote the generalized Hamiltonian in the form (see Equations (4) and (5)):
Here A
0m is the value of A
m (q, p) in a particular state of the motion, so that in this state
Since the quantities A
m(q, p) are integrals of the motion, their Poisson bracket with H(q, p) vanishes and the consistency condition (7) reduces to the form
“The set of Equation (10) allows determining the coefficients um.
Specifically, for a hydrogenic atom of the nuclear charge Z, the integrals of the motion (other than the energy) are the angular momentum
L =
r□
p and the Runge-Lenz vector (see, e.g., [
16])
A(
r,
p) = {
rp
2 −
p(
r·p)}/(μZe
2) −
r/r, where μ is the reduced mass. Therefore, Oks and Uzer [
8] presented the generalized Hamiltonian in the form:
Here
L0,
A0, and the energy H
0 are connected by the well-known relation [
16]:
“The consistency conditions [
r□
p, H
g] ≅ 0, [
A(
r,
p), H
g] ≅ 0 resulted into the following equations for the unknown vector-coefficients
u and
w:
By using the consistency Equation (13), Oks and Uzer [
8] reduced the number of yet unknown coefficients to just one, which they denoted as B. Of course, B was yet unknown function of energy H
0 in the particular state of the atom. Oks and Uzer [
8] showed that in terms of B(H
0), the generalized Hamiltonian and the equations of the motion take the following form:
“The Equation of the motion (15) differ from their conventional form only by the factor {1 + B(H
0, A
0)}. Therefore, the transformation of the time
the equations of the motion with respect to the new time t′ would be formally brought back to their conventional form.
Thus the authors of paper [
8] came to the following central point. In the above generalized formalism, the trajectory of the atomic electron remains the same as in the conventional formalism. However, the generalized period T
g and the generalized frequency ω
g differ from their conventional values T
0 and ω
0 as follows:
(in Equation (18), the explicit expression for the Kepler frequency ω
0 has been used).”
“Equation (18) clearly demonstrates that the generalized formalism allows the existence of such state (or states) of the motion, where ωg = 0 despite H0 ≠ 0 (the conventional formalism allows to be ω0 = |2H0|3/2/D1/2 = 0 only for H0 = 0). This is a state (or states) where B(H0) = −1. Therefore, such state or states would not emit the electromagnetic radiation, would not lose energy for the radiation, and would thus constitute stable states of the classical atom.”
The authors of paper [
8] showed that there is infinite number of the energies of the classical stationary states—just as in the corresponding quantum solution.
“Oks and Uzer [
8] pointed out that in a classical non-radiating stable state, one has d
r/dt = d
p/dt = 0, so that
r(t) =
r0 and
p(t) =
p0, where
r0 and
p0 are some vector constants. Thus, the electron is motionless, but its momentum differs from zero. This is not surprising: the momentum
p is a more complex physical quantity than the velocity
v ≡ d
r/dt. For example, for a charge in an electromagnetic field characterized by a vector-potential
A, it is also possible to have
v = [
p − e
A/(mc)]/m = 0 while
p = e
A/(mc) ≠ 0 [
17].
It is also very important to emphasize that the physics behind such classical non-radiating states is a new kind of time-dilation expressed by Equation (16): a non-Einsteinian time-dilation, as pointed out in book [
10]. The closer the energy of the system to the energy of the classical non-radiating state, the more dilates the time. At the classical non-radiating state, the time gets dilated infinitely, so that the frequency ω
g in Equation (18) vanishes and so does the radiation.”
3. New Results
We consider a charged Spherical Harmonic Oscillator (SHO). The “conventional” conserved quantities are the energy E and the angular momentum vector
M, the conservation of the latter following from the geometrical (spherical) symmetry of this system. It is well-known that the SHO also possesses another set of conserved quantities, whose conservation is the consequence of the higher-than-geometric (algebraic) symmetry:
Here, p
m and x
m are the Cartesian components of the momentum
p and of the radius-vector
r, respectively; μ is the mass of the SHO. Obviously, I
nm = I
mn, so that there are generally only six independent conserved quantities I
mn. The unperturbed Hamiltonian H can be actually expressed via some of the conserved quantities from Equation (19) as follows:
It is well known that the motion is limited to a plane. We choose the x3-axis (the z-axis) perpendicular to the orbital plane. Then, the dynamical variables are x1, p1, x2, p2.
In order to study whether classical non-radiative states of the SHO are possible, it should be sufficient to consider the generalized Hamiltonian H
g, which differs from H only by the addition of the constraints corresponding to the conserved quantities responsible for the algebraic symmetry, i.e., the conserved quantities from Equation (19), but only those of them that are relevant to the motion in the orbital plane:
where I
mn,0 are the values of these conserved quantities in the particular state of the system; E is the energy of the system in a particular state of the motion.
The conserved quantities I
mn “commute” with each other: the Poisson bracket of any two of them vanishes. Therefore, the consistency conditions from Equation (10) in this case reduce to equating to zero the Poisson brackets of the components of the angular momentum
M with the second term in the right side of Equation (21):
where e
ijq is the Levi-Civita symbol.
The calculations of the Poisson brackets from Equation (22), with the subsequent substitution of I
mn by I
mn,0 (as required by the GHD), lead to the following equations:
From Equation (19), it is obvious that the quantities I11 and I22 are non-negatively defined.
For definiteness, we assume that I
11,0 differs from zero, i.e., I
11,0 > 0. Then, from Equations (23) and (24), it is easy to obtain
Thus, the consistency conditions help reduce the unknown coefficients in the generalized Hamiltonian H
g from three to one, so that H
g can be represented in the form:
Based on the Hamiltonian H
g from Equation (26) and using dx
i/dt = ∂H
g/∂p
i, dp
i/dt = −∂H
g/∂x
i, we find the following equations of motion:
By differentiation of Equation (27) with respect to time and substituting Equation (28) into the outcome, we obtain the following system of equations:
where
is the “unperturbed” frequency of the oscillator.
We seek a solution of system (29) in the form:
here, ω
g is the (yet unknown) generalized frequency of the oscillator.
Substituting x
1 and x
2 from Equation (31) into the first equation in Formula (29), we obtain:
Substituting x
1 and x
2 from Equation (31) into the second equation in Formula (29), we obtain:
For Equations (32) and (33), which have the same left sides, to be compatible with each other, their right sides should also be equal to each other. By equating the right sides of Equations (32) and (34), after some simplifications, we find that the parameter α must satisfy the following quadratic equation:
The two solutions of Equation (34) are
Obviously, α+ > 0 while α− < 0. Physically, these two solutions correspond to the two opposite directions of the revolution along the orbit (see Equation (31)).
Equation (33) can be represented in a more explicit form:
where we temporarily introduce the following notation:
Using Equation (35), it is easy to find out that
so that Equation (35) simplifies to
which is equivalent to the following:
Coming back to the original notations, we rewrite Equation (40) in the form
where we have restored the argument E of the coefficient B
11(E). It is seen that, for each direction of the revolution of the charged particle in the orbital plane, there is a value of B
11(E), for which the generalized frequency is ω
g vanishes and so is the radiation. These non-radiating (stationary) states correspond explicitly to the following values, B
11+(E
st) and B
11– (E
st) of B
11(E), where the subscript “st” stands for “stationary”:
for α = α
+ and
for α = α
–. Remember that α
± (γ) is given by Equation (35), where γ = (I
22,0 − I
11,0)/I
12,0.
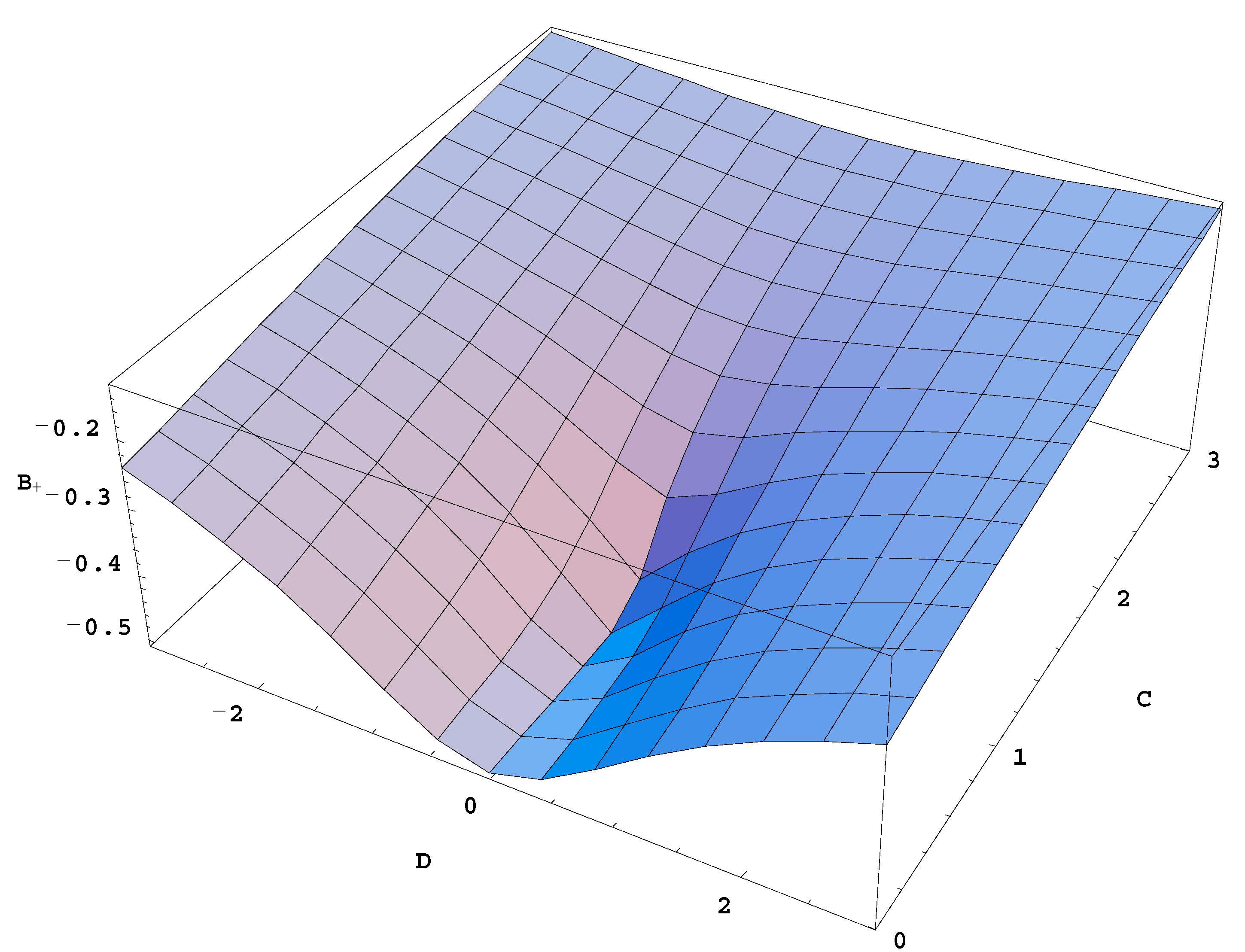
Figure 1 shows a three-dimensional plot of B
11+ (denoted in the plot for brevity as B
+) versus I
22,0/I
11,0 (denoted in the plot as C) and I
12,0/I
11,0 (denoted in the plot as D).
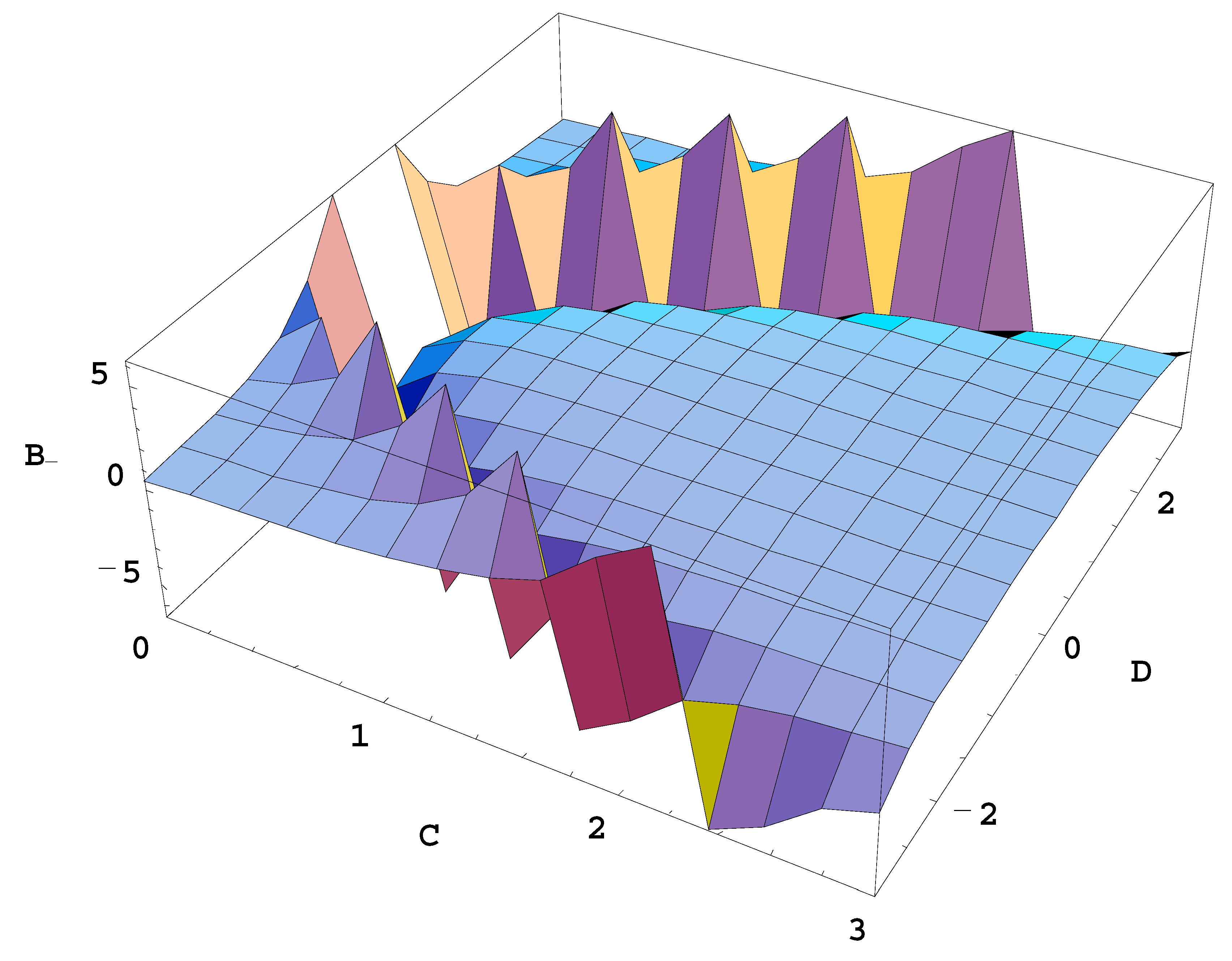
Figure 2 shows a three-dimensional plot of B
11– (denoted in the plot for brevity as B
–) versus I
22,0/I
11,0 (denoted in the plot as C) and I
12,0/I
11,0 (denoted in the plot as D).
Here is an intermediate summary of the above results. By employing the GHD, we have proven the existence of the classical non-radiating states of the charged spherical harmonic oscillator—similarly to the corresponding results of paper [
8] for hydrogenic atoms.
Physically, this is the manifestation of a non-Einsteinian time-dilation. Time dilates more and more as the energy of the system becomes closer and closer to the energy of the classical non-radiating state:
At the classical non-radiating state, the time gets dilated infinitely. As a result, the frequency of the revolution along an elliptical orbit ωg in Equation (41) vanishes—consequently, the radiation also vanishes.
In the important particular case of I
22,0 = I
11,0, corresponding to the circular orbits, the above formulas can be simplified as follows. In this case, from Equation (34) follows γ = 0, so that from Equation (35) we get α
+ = 1 and α
– = −1, as it should be for the circular orbits (see Equation (31)). Then Equation (36) simplifies to
where the plus sign corresponds to α = 1 and the minus sign corresponds to α = −1.
It is seen that, in this particular case, the generalized frequency ω
g vanishes (and so does the radiation) at the following values of B
11(E):
and
Obviously, Equation (47) is valid, except if |I12,0|/I11,0 = 2. In the exceptional case, Equation (45) yields a trivial result: ωg = ω0.
The primary result for the circular orbits is non-trivial. Namely, there are classical non-radiating states, corresponding to B11(E) = B11+(Est) for α = 1 or B11(E) = B11−(Est) for α = −1.
Thus, for each direction of the revolution of the charged particle in the orbital plane, there is one value of B11(E)—given by Equations (42) and (43) in the general case of the elliptical orbits or by Equations (46) and (47) for the particular case of the circular orbits—for which the radiation vanishes. The fact that, for each direction of the revolution, there is only one value of B11(E), does not mean that there is only one classical stationary state. Indeed, if the dependence of B11 on the energy E is oscillatory (with the amplitude greater than or equal to the absolute value of the right side of Equation (42) for α = α+, or with the amplitude greater than or equal to the absolute value of the right side of Equation (43) for α = α–), then there would be an infinite number of the energies of the classical stationary states Est—just as in the corresponding quantum solution.
Here is an example, illustrating the statement from the previous sentence for the case of circular orbits—for the subcase of α = 1 chosen for definiteness. Let us consider the following dependence of B
11+ on the energy E:
where E
st,0 is the energy of the lowest non-radiating state (the ground state) and both E and E
st,0 are measured in units of ħω
0. In Equation (48), C is a constant, which is an analog of the Maslov index [
18], which, for spherically symmetric potentials, is equal to 1/2 (see, e.g., the textbook [
19]). With C = 1/2, Equation (48) takes the form
From Equation (49), it is easy to find out that E = E
st,n, where
where the quantity B
11+ satisfies Equation (46), so that the sequence of values E
st,n from Equation (50) is the sequence of the energies of the classical non-radiating stationary states. More explicitly,
If Est,0 = 3/2, then the sequence of values Est,n from Equation (51) would coincide with the corresponding quantum results.