Abstract
The experience of disruptive events causing supply chain vulnerability and business downturns has motivated manufacturing purchasers to consider resilience capability when selecting suppliers. However, this problem is complex, mainly due to difficulties in obtaining precise data on supplier performance. Disruptions are viewed as low-possibility events, leading to incomplete or insufficient evidence to support assessment. A literature review presented in this paper identifies a list of prospective criteria for resilient supplier selection, within the electronics market, considering both quantitative and qualitative aspects in a symmetrical way. A new hybrid methodology, able to handle various forms of uncertain and incomplete data, is proposed to facilitate the supplier selection process. Evidence theory, which suggests the assignment of degrees of belief, instead of traditional probabilities, to expected results, is adopted to construct a decision matrix. The rule-based transformation technique is then employed to transform various forms of the assessment results into a unified format before further aggregation by the modified Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method. The proposed methodology is tested with a case of resilient supplier selection in a company producing computer hardware components. The proposed decision-making methodology can be applied not only by electronics purchasers but also by practitioners in other industries to logically and straightforwardly model the uncertainty and incompleteness of the available information.
1. Introduction
Concerns about supply disruptions that may be man-made (e.g., due to labour strikes, terrorist attacks, political instability, or accidents at plants) or caused by natural disasters (e.g., floods, earthquakes, or epidemic diseases) are increasing among business firms [1,2]. A number of disruptive events in the past caused many buying firms to experience a downturn in their businesses because of shortages of raw materials [3]. For example, a fire at a microchip plant, owned by Philips, in New Mexico caused its production shutdown in 2000, significantly affecting its buyers’ operations. Ericsson, one of the buyers, lost potential income of around 400 million dollars from this event [4]. The Japanese earthquake and tsunami of 2011 considerably affected Apple’s supply chain as a number of its suppliers were temporarily shut down. This caused delays in the availability of components for iPad2 for some time [2]. Currently, the COVID-19 outbreak is severely disrupting supply chain and manufacturing operations all over the world, and it is predicted that thousands of assembly plants in the United States and Europe would have to be temporarily shut down since they rely heavily on suppliers in China [5]. The recognition of supply chain continuity has prompted manufacturing companies to increasingly focus on resilience as a criterion for selecting suppliers [6].
Resilience can be defined as the ability of the supply chain to adapt itself to and prepare for unexpected disruptive events, as well as its ability to recover quickly to return to normal operations [1,7]. The effective planning of resilience strategies is now a priority for manufacturers to mitigate business uncertainties and to sustain themselves in an environment of global competition [8].
Supplier selection significantly influences a buyer’s business success and competitive advantage [2,6,9,10]. It is a challenging decision-making process that involves various criteria for consideration. The multi-criteria decision-making (MCDM) approach introduces different methods to solve selection problems when multiple criteria and alternatives are involved. In general, the application of MCDM methods to handle the supplier selection process involves three basic steps. The first is the identification of the criteria for consideration. The second step is the assessment of candidate suppliers based on the previously selected criteria, and the final step is aggregation or analysis of the suppliers’ composite performance under multiple criteria to eventually rank them.
Resilient supplier selection can be defined as the selection of a potential supplier that can provide the best support in the face of disruptive scenarios and reduce the overall risk of supply chain interruption [3,11,12]. Resilient supplier selection is considered a more complex problem than traditional selection problems for several reasons. The resilience capability of a supplier is multidisciplinary, and its complete assessment through quantitative indicators is considered unrealistic. Subjective judgement is always involved in the assessment process due to the inclusion of many qualitative criteria [7,13]. As stressed by Levary [14] and Rajesh and Ravi [15], a method for assessing and ranking suppliers must incorporate input information of both tangible and intangible criteria. Moreover, the risk of supply disruption needs to be considered in modern supply chain management. When the disruption risk is associated with the supplier selection problem, it is unrealistic to expect that complete information regarding all criteria or the decision-maker’s full understanding of the problem is available. Disruptive events normally occur with low probability (but high intensity), and they can be considered inherent uncertainties in the supply chain system. Rare or low-probability events imply incompleteness or a lack of evidence to support the assessment of a supplier’s performance under disruptive situations. Suppliers may have no relevant experience to deal with some events that might never have happened in the past. This also implies that a supplier’s performance in some criteria may be truly unknown at the assessment date. Clear and precise data, therefore, may be unavailable or impossible to find for modelling supplier performance under uncertain scenarios [1,2,7,12]. The probability of events and unknown information, thus, should be used as inputs in the decision-making model to reflect reality and avoid losing meaningful information. From the three basic steps of supplier selection mentioned earlier, questions arise as to what the criteria widely used for resilient supplier selection are and how to logically make such a decision when precise and complete sources of information are unavailable.
This study, therefore, aims to identify commonly used criteria for resilient supplier selection based on a review of the relevant literature and to propose a new decision-making method that can handle uncertainty and incompleteness of information arising from unexpected disruptive situations. ‘Uncertainty’ is defined here as a fluctuation of a supplier’s performance due to possibly changed circumstances, while ‘incompleteness’ means a lack of comprehensive evidence and knowledge that can perfectly explain its performance. The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is adopted as a fundamental basis of the proposed method for several reasons. First, it is one of the most widely used MCDM methods for alternative selection. Additionally, its logic is straightforward and easy to understand; it assigns a high composite score to an alternative whose performance is simultaneously the most distant from the negative-ideal solution and the least distant from the best or the positive-ideal solution. At the end of the process, the TOPSIS method simply gives the closeness coefficient to the ideal solutions for each alternative, which can be viewed as a composite index to rank them [16,17,18]. However, according to the original TOPSIS introduced by Hwang and Yoon [19], input information must be numeric, definite, monotonically decreasing and increasing, and share a commensurable unit [16]. This means that the original technique is unable to handle qualitative criteria that are difficult to assess precisely, and it cannot tackle incompleteness and uncertainty of the assessment information. In 2018, Sureeyatanapas et al. [17] extended the ability of traditional TOPSIS to be able to determine a composite score of each alternative from a range of possible values, rather than allowing only crisp data to be considered. This current study aims to propose a generalised version of that extended TOPSIS by providing a solution when the assessment of performance is better described through probabilities of occurrence.
A review of the literature addressing resilient supplier selection showed that many studies have integrated fuzzy logic into MCDM methods to handle uncertainties caused by decision makers’ subjective judgements. However, the employment of fuzzy logic still raises a number of concerns and impracticalities. Firstly, fuzzy numbers are linked to linguistic variables used in the assessment of supplier performance and lead to the questions of what is the most appropriate set of fuzzy numbers to represent each variable, and who is the appropriate person to determine it. In addition, linguistic scales used for assessment still lack standardisation and are open to personal bias. Moreover, the aggregated results are still in fuzzy form and need to be defuzzified for the final decision making, and the best alternative is sometimes sensitive to the chosen defuzzification method. Furthermore, most previous studies propose a fuzzy method to handle both quantitative and qualitative criteria, although the former can be simply and straightforwardly assessed using a precise form. In general, there is no need to transform such data into fuzzy numbers, but most previous studies do not present a solution to handling both certain and fuzzy information simultaneously [17]. According to Hasan et al. [13], fuzzy logic lacks sophistication in processing quantitative information. In addition, fuzzy sets lack the ability to model the uncertainty caused by inadequate knowledge or the absence of supportive evidence [20]. The application of fuzzy logic has also been criticised as it unnecessarily increases the complexity of the decision-making process since the results generated by fuzzy methods are usually not different from those calculated by traditional processes [21]. Equally importantly, many studies have proposed methods to solve alternative selection problems by limiting the types of input information. This restriction may result in the loss of meaningful information during the assessment process. Therefore, instead of applying fuzzy logic, this study aims to model the uncertainty and incompleteness of information, arising from unexpected disruptive events, through degrees of belief (according to evidence theory) and evidence-based evaluation grades. Various forms of input information are transformed into a unified format through rule-based transformation. To this end, a solution for logically handling uncertain and incomplete information in MCDM problems is developed and proposed for practical applications.
In this study, the applicability of the proposed solution is demonstrated through the case of resilient supplier selection in electronic components procurement. The electronics industry is chosen for a number of reasons. First, it is one of the significant sectors influencing the global economy. Second, most electronic products (e.g., computers, televisions, and mobile phones) are assembled from a variety of sub-components. Purchasing and supplier selection strategies are, therefore, the critical functions that influence production quality and cost. As stressed by Bharadwaj [22], electronics manufacturers generally spend up to 22–53% of their revenue on the procurement of materials and services from various suppliers. Third, the industry relies heavily on technology that is fast-changing and products with short life cycles. Many electronics manufacturers, therefore, focus on establishing buyer-supplier partnerships, such as technological collaboration, purchase contracts, and strategic alliances, to lower costs and survive global competition [23]. These factors attest to the significance of supplier selection strategy in the electronics industry.
This paper is organised as follows. After the introduction, Section 2 presents a review of previous studies. Section 3 then proposes a new TOPSIS-based methodology. In Section 4, the proposed methodology is applied to a case study of a large-scale manufacturer of computer hardware components. At the end of Section 4, the obtained ranking of candidate suppliers is cross-compared to that determined by the evidential reasoning (ER) approach for validation. Conclusions are drawn in Section 5.
2. Literature Review
This section presents a review of previous studies in four sub-sections. Section 2.1 presents trends in supplier selection. Section 2.2 then reviews previous studies relating to resilient supplier selection by focusing on the criteria and methods employed. Section 2.3 reviews supplier selection criteria generally used in the electronics industry, and Section 2.4 suggests a list of criteria for resilient supplier selection for electronic components procurement.
2.1. Trends in Supplier Selection
Based on review articles and surveys published from 1966 to 2016, Sureeyatanapas et al. [17] reviewed the criteria and methods generally used for supplier selection, without reporting a specific industry or business sector. They concluded that product price was the most commonly used criterion for supplier selection. However, when reviewing the level of importance of each criterion as rated by the respondents in these studies, price was generally not perceived as the most important criterion. Product quality, service, and delivery performance were among the criteria rated as highly important by most business practitioners. They also concluded that the list of criteria for supplier selection was dynamic and likely to change according to current trends in business management strategies. For example, just-in-time manufacturing led to the emergence of criteria relating to geographical location; the trend in supply-chain management introduced many new criteria, such as the supplier’s flexibility, responsiveness, and information and communication technology; the advent of sustainability strategy then encouraged businesses to select suppliers based on their environmental and social responsibility. In the case of the current trend in supplier selection, resilience capabilities have been in the spotlight recently. According to the available literature, the number of SCOPUS-indexed articles with the term ‘resilient supplier selection’ in their titles, abstracts and keywords is increasing every year, from only two articles in 2012 to 45 articles at the end of 2019, indicating the growing interest in this topic in academia, which is also a reflection of the interest among business firms.
According to studies in supply chain performance analysis [24,25,26,27], decision-making models supporting the assessment of supply chain performance must consider comprehensive elements in the supply network, covering not only cost and technical capabilities, but also qualitative aspects. For the sake of supplier evaluation and selection, various aspects were emphasised, such as the supplier’s capacity in production, storage, handling and transportation, safety stock, delivery time to the recipient, service quality, supply reliability, safety factors regarding their geographical location, as well as their flexibility or ability to adapt to customer requirements and unexpected circumstances.
In terms of the generally used methods for supplier selection, the review by Sureeyatanapas et al. [17] found that the analytic hierarchy process (AHP), TOPSIS, and data envelopment analysis (DEA) are among the most popular methods employed to solve supplier selection problems. Similar results were obtained in another recently published review article by Aouadni et al. [28] who presented a systematic literature review on supplier selection from 2000 to 2017. They showed that AHP and TOPSIS were the most commonly used methods; hybrid methods also received considerable attention in the last five years of the study. Regarding the TOPSIS, which is selected as a fundamental method for this study, Behzadian et al. [16], who conducted a survey on application of TOPSIS in 266 articles from 103 journals between 2000 and 2011, found that the primary sectors applying TOPSIS were supply chain management and logistics, followed closely by engineering and manufacturing systems. Within the area of supply chain and logistics management, most studies focused on problems of supplier selection as well as transportation and location selection. Most of the studies reviewed proposed a combination of TOPSIS with other methods, rather than applying classical TOPSIS. Fuzzy set theory, group decision-making techniques, and AHP were the top three approaches combined with TOPSIS.
AHP and DEA, the other two widely used methods for ranking alternatives, are not adopted here for several reasons. First, AHP and fuzzy AHP are highly dependent on subjective judgements in pairwise comparisons, regardless of any utilisation of quantitative information that may be available. Moreover, they require a large number of judgements and are therefore not practical methods when many criteria and alternatives are considered since it is difficult to obtain consistent judgements from all subjective comparisons [17]. Furthermore, AHP needs to be adopted with caution as there are some technical issues to it, such as the rank reversal problem [29,30] and the violation of the Pareto optimality axiom [31,32]. DEA also raises several concerns. First, it relies on a generally adopted rule of thumb, stating that to optimise the discrimination power of the method the number of alternatives should be at least twice the number of the criteria [33,34]. This requirement is often unrealistic in supplier selection problems. In addition, DEA often gives more than one efficient alternative, and decision makers need to identify another solution to select the best one. It may suit the purpose of performance analysis but not of alternative selection [17].
As seen in these review articles [16,17,28], issues concerning uncertainties in the assessment of supplier performance became the focus of most published articles in the late years of their periods reviewed. The literature relating to supplier management also mentions issues of inherent uncertainties and incompleteness of information in procurement and inventory management processes. Sari [35], for example, addressed the significance of vendor managed inventory (VMI) and collaborative planning, forecasting and replenishment (CPFR) to optimise material and information flow. However, in most VMI implementations, communications between all partners are usually incomplete due to the unavailability or inadequacy of retail-level information. The unique knowledge of retailers is generally not utilised in inventory and purchasing decisions. The implementation of CPFR also faces difficulties due to the intensive requirement of organisational resources and the lack of mutual trust among all supply chain members about sharing information. Similar to Niranjan et al. [36], poor information sharing and data integrity, as well as data inaccuracies, are some of the impediments to successful VMI implementations, as reported in their case studies. Aloini et al. [37] proposed a conceptual design of a ‘last-mile’ logistics solutions (e.g., drones and automation technologies in transportation) to improve the efficiency of the procurement process. Such a concept also faced difficulty from the variability and unpredictability of related information. Additionally, Ravindran et al. [38] stressed that supplier selection problems, particularly in global supply chains, always connected to uncertainties that arise from diverse conditions (e.g., different locations, control capabilities, trade restrictions). The literature shows that most studies employed fuzzy logic to model existing uncertainties [16,17]. However, fuzzy logic may not be the best solution to tackle uncertainties, as described in the introduction.
2.2. Resilient Supplier Selection
The topic of resilient supplier selection has received increasing attention during the past decade. Nourbakhsh et al. [4] proposed a new model to support the supplier selection process by considering both conventional selection criteria (quality, delivery, price, and capacity) and supply risks. In their study, the risks, which were linked to supplier reliability, were grouped into three categories: (i) production (failure of facilities, unavailability of raw materials and labour strikes); (ii) transportation (failure of vehicles and route insecurity); and (iii) communication (failure of communication that disables further operations and transactions). They employed DEA to determine efficient suppliers based on the conventional criteria, while they used an artificial neural network, trained by expert opinion of the risk factors, for estimating reliability scores. The efficiencies and reliability scores were eventually combined to determine the list of non-dominated suppliers.
Several studies have developed mathematical programming models to find the best compromised solution for supplier management that considers supply disruptions. For instance, Sawik [12] proposed a mathematical programming model to select part suppliers and allocate the order quantity by considering the resilient supply portfolio (suppliers capable of supplying parts during disruptive events). The disruption probability for each supplier was utilised in the proposed model. Ravindran et al. [38] developed a multi-criteria supplier selection model to screen out a large set of initial suppliers (Phase I) and then to allocate the order quantity to the remaining ones (Phase II) under the risk of disruptions. Fourteen criteria were employed for the first phase, while only four significant criteria were used for Phase II, including lead time, quality, cost and risk. Similarly, Torabi et al. [2] proposed a two-stage stochastic programming model to solve supplier selection and order allocation problems under disruption risks. They suggested several proactive strategies, such as consideration of the supplier’s business continuity plans (BCP) and its contracts with backup suppliers. Chen et al. [8] developed a multi-objective programming model for determining the best supplier and the most appropriate supplier location in a particular region, under supply risks caused by natural or man-made disasters. They used an automotive company as a case study. Various criteria were classified into eight groups: safety, quality, delivery, cost, people, environment, cash flow, and risks.
MCDM methods were generally proposed to tackle resilient supplier selection problems. Haldar et al. [1] proposed the application of a fuzzy TOPSIS method to rank suppliers under resilience scenarios in automobile manufacturing. Five basic criteria—quality, product reliability, product functionality, customer satisfaction, and price—were adopted in combination with three resiliency strategy criteria—investment in capacity buffers, responsiveness, and capacity for holding inventory stocks for crises. Sahu et al. [11] applied the fuzzy VIKOR method to handle the vagueness of assessment information in resilient supplier selection problems and to calculate a final score for each candidate supplier. Their list of selection criteria was adopted from Haldar et al. [1]. Rajesh and Ravi [15] utilised a grey relational analysis approach to solve the resilient supplier selection problem. In this study, the issues of imprecise and limited information were mentioned, and the grey relational analysis employed linguistic scales to facilitate the assessment and handle such issues. Thirteen criteria were used in the supplier selection problem, and they were classified into five groups: primary criteria, responsiveness, risk reduction, technical support, and sustainability.
AHP was employed in various studies. Levary [14] applied AHP to rank suppliers by considering the supply risk. Four criteria were employed, including supplier reliability (potential of strikes and loss of client’s proprietary information), country risk (risk of political issues, currency conversion, natural and man-made disasters), transportation reliability, and reliability of the supplier’s suppliers. Pramanik et al. [7] integrated fuzzy TOPSIS with AHP and quality function deployment (QFD) methods to facilitate the resilient supplier selection process. Similar to a number of previous studies, this study suggested consideration of both general criteria and resilience criteria for selection. According to their methodology, suppliers were initially screened by TOPSIS and AHP using general criteria (quality, delivery time, reliability, processing time, and profit margin). Suppliers whose performance was above the predefined cut-off value passed into the second stage where both the manufacturer’s critical criteria and resilience criteria were considered. The critical criteria included conformity of production, fitments of a product, and mean time between failures, while the resilience criteria covered buffer capacity, the number of critical nodes, responsiveness, re-engineering, and adaptive capability. AHP and QFD were integrated to construct a subjective factor measure (SFM) for each supplier. The objective factor measure (OFM) was then determined for each supplier for several cost factors. The SFM and OFM were then combined to construct the supplier selection index for ranking the suppliers. Mohammed et al. [39] applied AHP and fuzzy TOPSIS to evaluate and select suppliers based on their performance in green and resilience criteria. AHP was used to determine the importance weight of the criteria, and candidate suppliers were then ranked through the fuzzy TOPSIS method. The adopted criteria were categorised into three groups: (i) traditional (cost, quality, delivery, performance history, turnover, lead time, and capacity); (ii) green (environmental management system, waste management, and environmental certificate); and (iii) resilience (robustness, agility, leanness, visibility, and flexibility).
Hosseini and Khaled [6] divided suppliers’ resilience capacities into three categories: (i) absorptive capacity (the supplier’s preparedness to absorb damage and minimise negative consequences of disruptive events, including surplus inventory, location separation, backup supplier contracting, physical protection, and reliability); (ii) adaptive capacity (the supplier’s ability to adapt to unexpected scenarios, including rerouting and reorganisation); and (iii) restorative capacity (the supplier’s capacity to recover from disruptions and return to the normal stage of operation). Data mining, logistic regression, and neural network approaches were employed to predict the resilience capability of each supplier, and AHP was then used to rank them. The proposed hybrid methodology was applied in a case study of plastic supplier selection by a manufacturer in the United States. Gan et al. [3] also proposed a hybrid approach, called GMo-RTOPSIS, that combines the fuzzy best–worst method and TOPSIS to solve resilient supplier selection problems in random environments. The same set of criteria introduced by Hosseini and Khaled [6] was employed. Davoudabadi et al. [20] introduced a new interval-valued intuitionistic fuzzy evaluation framework for solving resilient supplier selection problems. The criteria weights were determined based on the entropy method. The proposed method was applied to the same case studies used by Haldar et al. [1] and Sahu et al. [11] for comparison. Recently, Hasan et al. [13] also employed fuzzy TOPSIS to rank alternative suppliers in resilient supplier selection for the logistics 4.0 industry. The originality of this work lies in the fact that the probability-possibility consistency principle was used to determine triangular fuzzy numbers from large-scale temporal data; goal programming was used to determine optimal order allocation for each supplier.
2.3. Supplier Selection in the Electronics Industry
Due to the fact that the list of decision criteria for supplier selection differs by product category [22], this section reviews previous studies addressing supplier selection problems in the electronics industry to capture the critical criteria generally employed within this industry. Using a questionnaire-based survey, Hirakubo and Kublin [40] compared the relative importance of several criteria adopted by Japanese electronics companies when purchasing switches and printed circuit boards. In general, price was the most critical criterion for Japanese electronics purchasers due to the intense competition in electronic products. A number of other criteria were also identified as important for this industry, including quality, delivery, technology, design, and manufacturing capabilities, as well as experience and reputation. Based on a survey, Bharadwaj [22] also explored a ranking of key buying criteria used by electronics manufacturers. The list of criteria was initially drawn up from a literature review and validated by purchasing managers in the electronics industry. This resulted in a variety of criteria that were then classified into four groups. They were ranked in order of importance from the highest to lowest, based on group means for ratings, as follows: product quality, delivery, price, and post-sales service. The survey results for two different product groups also indicated that the importance of decision criteria was generally similar across an array of electronic component parts.
Gencer and Gürpinar [41] proposed a supplier selection model based on the analytic network process (ANP) and applied the model to a company producing electronic products. A large number of selection criteria were identified and classified into three clusters: supplier’s business structure, manufacturing capability, and quality system. Chiou et al. [42] employed fuzzy AHP to determine and compare the relative importance of criteria for green supplier selection by American, Japanese, and Taiwanese electronics manufacturers in China. More than 20 criteria were identified and classified into six groups, including a group for the supply chain base (cost, quality, delivery, and service) and five other groups relating to environmental performance and social responsibility. The comparative results showed that the supply chain base criteria were rated as of the highest importance, with the relative weights greater than 0.33 for all three groups of respondents.
Lee et al. [23] identified four strategic criteria influencing buyer-supplier relationships in the electronics industry, with a case study of a company manufacturing hard disks in Taiwan. The four strategies were cost reduction, quality improvement, stabilised supply, and research and development (R&D) facilitation. Various supplier evaluation criteria were also identified in their study. Chang et al. [10] designed a questionnaire, by applying a fuzzy decision-making trial and evaluation laboratory (DEMATEL) technique, to survey key criteria for supplier selection in the electronics industry, as well as to analyse causal relationships between criteria. The results showed that the criteria of high importance for this industry included product quality, stable delivery, reaction to demand change in time, and service.
2.4. Suggested List of Criteria for Resilient Supplier Selection in the Electronics Industry
From the reviews in Section 2.2 and Section 2.3, the large number of criteria suggested in the literature for resilient supplier selection in the electronics industry was synthesised into 17 criteria. They were classified into two groups: resilience capabilities and general criteria (Table 1). Note that the names of criteria shown in Table 1 may not be the same as in the original sources. The names were generated based on the authors’ interpretation.

Table 1.
Synthesised criteria for resilient supplier selection in the electronics industry.
3. Extension of TOPSIS
The ideal scenario for supplier selection is one in which the suppliers’ performance can be precisely assessed with sufficient sources of information. When their performance in all criteria is available and stable, the assessor can be confident enough to assign a single value to each supplier for a quantitative criterion, or precisely rate each supplier with a specific set of rating scales or evaluation grades for a qualitative criterion. However, this is not always the case in reality. When a supplier’s performance in a particular criterion fluctuates or is uncertain, it may be more rational to determine the probability of occurrence for each outcome based on historical information or logical prediction. For example, when assessing supplier X on the criterion ‘service and support’ with a set of evaluation grades (very poor, poor, fair, good and excellent), according to past experience, most of their staff members were able to instantly solve a technical problem with competence and always with a good attitude in assisting and supporting. However, a few were still not competent enough and could not solve problems without asking for help from colleagues and consequently spent a long time in completing tasks. With this type of information, the assessor is only 80% sure that the performance is ‘excellent’ and 20% sure it is ‘good’. Because of the completeness of historical information, the probabilities assigned to all grades sum to one. Uncertainty also exists in quantitative assessments, for instance, for product prices that are periodically adjusted because they are influenced by many global factors. For example, based on information from the previous 12 months, the price is changed every three months, starting from 10 Baht in the first quarter to 9.5 Baht and then to 9.2 Baht in the second and third quarters before raising it to 11 Baht in the last quarter. This information leads the assessor to assign a probability of 0.25 (or 25%) to each price (10, 9.5, 9.2, and 11 Baht). Instead of the allocation of 100% probability to the average value (9.925 Baht), the distribution of probabilities of occurrence to the quarterly values provides a more comprehensive picture of price fluctuation and preserves the original features of the data [43].
Nevertheless, a supplier’s past performance may not be completely known, and on-hand sources of information may help the assessor to predict only some parts of future performance. In this case, full confidence cannot be given by the assessor to the supporting information or evidence due to its incompleteness. For example, for the criterion ‘invulnerable location’, the available information based on geology may lead the assessor to be 90% certain that the supplier’s current location is safe from flooding, earthquakes, and other kinds of natural disasters. The assessor, however, still leaves 10% for unpredictable incidents due to the incompleteness of the information. This 10% is the degree of global ignorance [44]. This means that if the same set of evaluation grades (very poor, poor, fair, good and excellent) is employed, the probability of 0.1 is not assigned to any grade, and the probabilities assigned to all the grades do not sum to one. This case, in fact, does not conform to probability theory which states that the probabilities of all possible events must sum to one. Due to non-conformance with probability theory, this study, therefore, employs evidence theory to model the assessment results instead of the traditional probability theory. Another possible situation in real-life practice is the assessor completely lacking information for an assessment—a case of complete ignorance [44]. Evidence theory also provides a solution to handle such circumstances. The theory and its application to resilient supplier selection problems are described in Section 3.1.
With several types of results possibly emerging from the assessment of qualitative and quantitative criteria, the results need to be transformed into a unified format to enable the aggregation of data for TOPSIS. This study employs the rule-based information transformation technique to handle the task. Section 3.1 introduces the basic principle of evidence theory and the formation of a generalised decision matrix, and Section 3.2 describes the rule-based information transformation technique that has been modified for this study. Section 3.3 presents the integration of the generalised or transformed decision matrix into the extended TOPSIS method.
3.1. Evidence Theory and Generalised Decision Matrix
Evidence theory was originally developed by Arthur P. Dempster in 1967 [45] and was later formalised by Glenn Shafer in 1976 [46]. It is also known as the Dempster-Shafer theory or D-S theory. Evidence theory is a generalisation of traditional probability theory. The latter allows probabilities to be assigned to only mutually exclusive singletons, or individual answers; in contrast, in the former, probabilities can be assigned to subsets of answers to model uncertainties and ignorance. Evidence theory gives way to probability theory when adequate evidence is available, leading to the assignment of probabilities to only single answers [47].
Evidence theory considers belief functions instead of probability functions. According to this, for each source of information or piece of evidence, a decision maker can express a degree of belief or probabilistic opinion in either an individual answer in the space or a set of possible answers, or both. The assignment of degrees of belief to a set of answers implies that the evidence does not have sufficient information to precisely specify the single right answer. After considering all pieces of evidence, the degrees of belief assigned to all possible answers do not necessarily sum to one, and the sum can be less than one. In the case of the latter, the remainder denotes the degree of incompleteness of the evidence. In other words, the available sources of information are unable to provide a complete picture of the situation [48].
Based on evidence theory, Yang and Singh [49] and Yang [43] proposed a generalised decision matrix to model MCDM problems, in which each criterion is assessed and then reported in the form of a belief structure, or a belief distribution. For an MCDM problem considering M number of alternatives al (l = 1,…, M) for each of L number of criteria ei (i = 1,…, L), each criterion is assessed using a set of evaluation grades Hn (n = 1,…, N) called a frame of discernment, with the grades being mutually exclusive and collectively exhaustive. The relative weight of criterion ei is denoted by wi under the conditions, 0 ≤ wi ≤ 1 and . In evidence theory, each grade is considered an individual answer, and the criterion is considered a piece of evidence or a source of information. The finite set of distinctive grades can be defined by:
where is preferred to . This means that and are the worst and the best grades, respectively. Then, a generalised decision matrix can be constructed as shown in Table 2.

Table 2.
Generalised decision matrix in the form of belief structures.
denotes a generalised belief structure, which is the assessment result for alternative for criterion . It can be expressed as shown below.
where denotes a degree of belief in which an alternative is assessed as grade when considering criterion , and and . If , the assessment is considered complete; otherwise, it is incomplete. The case of complete ignorance emerges when . represents the degree of global ignorance implying that, for a criterion , an alternative could be assessed as any grade in the set due to the lack of supporting evidence. Thus, the following conditions are applied: and . This means that represents the lower bound of the probability that is assessed as Hn, while becomes the upper bound [43,44,50].
A strict condition required by evidence theory for combining information is that elements defined by all pieces of evidence must be members of the same frame of discernment [51,52]. In general, when it is applied to MCDM problems, all criteria must be assessed by the same set of evaluation grades; otherwise, the performance of an alternative for different criteria cannot be aggregated. This condition may not be practical in reality. For example, it may be more sensible and practical to assess quantitative criteria using numerical measurement values, rather than by employing subjective grading or rating scales. For qualitative criteria, although rating scales or a set of grades can be employed to facilitate evaluation, each grade should be attached to a clear description connected to evidence or feasible situations to minimise inconsistency in subjective grading as well as to standardise the assessment. Under this concept, it may be unrealistic to employ the same set of grades for all qualitative criteria since the number of grades for each criterion should depend on how many distinct levels of feasible practices exist to ensure that the grades are collectively exhaustive [17,53]. The next section, therefore, describes how various forms of assessment results can be transformed into the same standards, which are in the form of generalised belief structures as defined by Table 2 and Equation (2). The generalised belief structures all employ the same set of grades, hereafter called the ‘general’ set of grades, as shown in Equation (1).
Table 3 summarises eight possible forms of assessment results considered in this study. For qualitative assessment, denotes a belief structure which is the assessment result of alternative for criterion using its own set of evaluation grades, , which is not in the form of the general grades yet. represents a degree of belief in which an alternative is assessed as grade when considering a criterion . In terms of quantitative assessment, denotes a belief structure that is the assessment result of alternative for criterion in the form of numerical measurement values, or , and is the degree of belief that an alternative is assessed to a value for criterion . As previously stated, these possible forms of the assessment results need to be transformed into the same standards before aggregation.

Table 3.
Original forms of the assessment results.
3.2. Rule-Based Information Transformation Technique
The rule-based information transformation technique was introduced by Yang [43] to transform various forms of assessment information into a unified format, as a normalisation process in traditional MCDM, before the aggregation of multiple criteria for each alternative. Such a technique is readily applicable to various forms of assessment results defined for this study, as summarised in Table 3. The proposed technique requires a decision-maker to construct ‘rules of equivalence’ based on his/her knowledge and experience. The explanation of the rule-based transformation technique, mainly adapted from Yang [43], is given in two parts below for qualitative and quantitative assessments.
3.2.1. Rule-Based Transformation Technique for Qualitative Assessment
Let each qualitative criterion be assessed using its own set of grades, . The original assessment of alternative for criterion , or , can be defined by Equation (3).
where . Then, each grade can be transformed into any grades in the general set , where based on their equivalence which is determined by the form of rules. The simplest idea is that both sets have an equal number of grades, or , and each grade completely means or is equivalent to a grade in . In this case, can be easily transformed into a generalised belief structure defined by Equation (4).
However, as mentioned before, this may not be practical for actual assessment according to the different characteristics of various criteria. In general, it may be the case that , and a grade in does not exactly mean a single grade in , but a number of grades in to some degrees of equivalence. To avoid confusion from a duplicate parameter, only for qualitative assessment, the generalised belief structure defined by (4) is revised as shown in (5).
Let in be equivalent to grade in to a degree , where and . Then, the equivalence rules can be defined, using symbol to represent the equivalence, as follows:
Equivalence implies that the underlying utility, based on the decision-maker’s preference, of is equal to the expected utility of . After all the rules for equivalence are determined, the original assessment can be transformed into the generalised belief structure , and can be calculated as follows:
3.2.2. Rule-Based Transformation Technique for Quantitative Assessment
To transform numerical values into the generalised belief structure in the form of a general set of grades , let be the numerical value equivalent to the general grade , as defined by (8).
Suppose value is an assessment result of alternative for criterion with a belief degree of , the original assessment can be defined as in Equation (9).
where and . In the case of precise assessment where there is only one , . The assessment value is not necessarily equal to value , and it can fall between the two values and as exemplified by Figure 1.
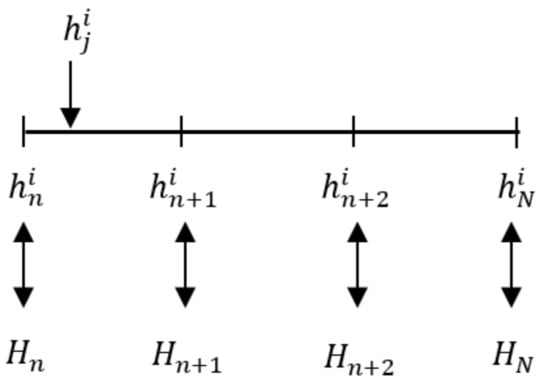
Figure 1.
Case in which falls between and , when N = 4.
In Figure 1, the belief degree is distributed to both of the general grades and . The closer the distance, the higher the degree of belief allocated to both grades. As seen in Figure 1, a higher degree of belief is given to . denotes the degree of belief allocated based on value to grade for alternative and criterion ; it can be calculated as follows:
When the assessment is uncertain, or when the number of is equal to , and each holds a belief degree equal to , can be calculated by the following equation:
From the proposed formulation, can be transformed into the generalised belief structure shown in Equation (14).
Transformation using rules of equivalence preserves the original features of complete and incomplete assessment. Based on the rule-based transformation technique, various forms of the original assessments shown in Table 3 can be transformed into the generalised belief structure shown in Table 4. is the degree of global ignorance that exists when an alternative could be assessed to any grades in the set , which is a consequence of unavailable or incomplete information.

Table 4.
Generalised belief structures after rule-based transformation.
3.3. Integration of a Generalised Decision Matrix Into TOPSIS
After transformation, the generalised decision matrix (Table 2) can be constructed. The belief distribution shown in the matrix describes a comprehensive picture of the assessment result for each alternative for each criterion. These, however, are still difficult and not straightforward for comparing and ranking the alternatives. Yang [43] suggested the comparison of alternatives based on their utility, which reflects the degree of a decision-maker’s preferences for the values being considered; utility is based on his/her attitude towards risk [54]. The utility of a general grade , denoted by , is a function between 0 and 1, where When the utility of all grades is determined, the expected utility of an alternative for criterion can be defined by Equation (15).
Nevertheless, when an assessment is incomplete, with an unassigned belief degree or , the expected utility of an alternative cannot be straightforwardly determined; therefore, a utility interval for that alternative needs to be established, instead. The maximum and minimum of the interval can be set by simply assuming that is transferred to either the best grade ( or the worst grade (, respectively. The maximum and minimum utility of each alternative can be calculated by Equations (16) and (17), as adapted from Yang [43].
If all assessments are complete, or , the maximum utility and the minimum utility are equal. This process results in a new decision matrix, hereafter called an interval decision matrix, which becomes a starting point for applying the extended TOPSIS method proposed by Sureeyatanapas et al. [17]. The extended TOPSIS is briefly described below.
Table 5 shows an interval decision matrix for an MCDM problem with number of alternatives for number of criteria . The meaningful concept of TOPSIS is to give the highest composite score to an alternative with the shortest distance from the positive ideal solution (PIS) and the longest distance from the negative ideal solution (NIS). The composite score, called the closeness coefficient to the ideal solution , is calculated for each alternative for the purpose of comparing and ranking the alternatives. The extended TOPSIS was developed to enhance the ability of the traditional TOPSIS method to be able to handle uncertain information in the form of interval values. The basic concept of the interval is that the actual data point, which is currently unknown, can fall into any value in the specified range at the date of decision making. The extended TOPSIS clarifies that when the input information is uncertain, the output is consequently uncertain. Thus, instead of giving a single to an alternative , the minimum and the maximum are computed, hereafter called min and max , respectively.

Table 5.
Interval decision matrix in the form of utility intervals.
To calculate min for an alternative , all of its performances, or all , , must be at the minimum level, and performances of other alternatives or all for and are at the maximum level. The same concept is applied when determining max , that is an alternative will reach the maximum composite score only when all of its are at the highest level, and all for are at the lowest level, as specified by Equations (18) and (19). Based on this concept, the interval decision matrix, which is a matrix of , is converted back into a matrix , which is in a common form for . Then, the problem can be simply solved by the traditional TOPSIS method, as described by (20)–(25). This means that calculations are made times when comparing alternatives (twice for calculating min and max for each alternative ).
To select the best alternative, two approaches can be adopted. The first is to rank the alternatives based on the average of their min and max . The average is denoted by avg for alternative . The alternative with the highest avg is recommended. This approach, however, may not be decisive or convincing due to its potential loss of meaningful information. Another approach is to integrate the decision-maker’s risk attitude into the judgement. For example, if the decision maker is risk seeking, an alternative with the highest max may be preferred to the others, although its avg may not be the highest. On the other hand, a person who is risk averse may avoid selecting an alternative with the lowest min , although its avg or max is superior to that of the others, in order to avoid the possibility of very low performance by the selected alternative [17,54].
The procedure for the implementation of the proposed methodology can be summarised as follows. Note that our assumption is that the weights of decision criteria are certain and available; the weighting process is thus not mentioned in this paper.
- Conduct an assessment of quantitative criteria through numerical measurement and qualitative criteria with a specified set of evaluation grades. Degrees of belief are assigned to numerical values for quantitative criteria and grades that best describe the actual situation for qualitative criteria. Note that more than one value or a grade could be assigned if the situation is uncertain, and the total degree of belief could be less than one if the supporting information is insufficient or incomplete. The results can eventually be in various forms, as defined in Table 3.
- Identify a general set of grades and construct the equivalence rules between the assessment scales of each criterion and the general grades.
- Transform the original assessment results, using the rule-based transformation technique, into the generalised belief structure for each alternative for each criterion , and then draw the generalised decision matrix, as exemplified by Table 2.
- Convert the belief structures into utility intervals, and then construct the interval decision matrix, as shown in Table 5.
- Calculate the min and max for each alternative based on extended TOPSIS.
- Select the best alternative based solely on avg or in combination with the decision-maker’s risk attitude.
4. Application of the Proposed Methodology in a Resilient Supplier Selection Problem
To demonstrate the applicability of the proposed hybrid methodology, a case of resilient supplier selection in electronic components procurement was employed. The case study was a large-scale company producing various components of computer hardware in Thailand. First, a purchasing manager was asked to select criteria, from the list in Table 1, for resilient supplier selection for the purchase of one particular product. The manager chose seven criteria, including responsiveness , backup supplier contracts , restoration , risk of losing information and communication , service and support , innovation and technology , and product quality . The number of chosen criteria is considered appropriate, as suggested by the literature on supplier selection, which states that it is difficult for buyers to simultaneously consider more than seven to nine criteria in their supplier selection process [22]. Next, an interview was conducted with the same manager and a purchasing engineer for defining the assessment scale for each criterion. A suitable indicator and its measurement unit were set for each quantitative criterion (, , and ). For each qualitative criterion (, , , and ), the definition of each evaluation grade was clarified to ensure the whole set of grades covered all feasible situations. The defined assessment scales are shown in Table 6. Note that this study does not aim to generalise the important criteria for resilient supplier selection and the appropriate assessment scales since these types of information tend to vary by decision-makers’ experiences and preferences on a case-by-case basis. We do not claim the information in Table 6 to be the most appropriate way of assessment since it was identified by only two staff members of the case-study company.

Table 6.
Examples of assessment scales for criteria chosen for resilient supplier selection.
A set of general grades, or , was identified for this study: = {very poor, poor, fair, good, excellent}. Then, the equivalence rules between the assessment scales of each criterion and the general grades were constructed based on the manager’s perception. The rules are presented following Equation (6) for quantitative criteria and Equation (8) for qualitative criteria in Table 7. For example, to transform a supplier’s responsiveness, it was assumed that if their responsiveness was graded ‘A’, then their performance was ‘excellent’, but if responsiveness was grade ‘B’, their performance was ‘excellent’ only at 0.4 degrees of belief, and it was ‘good’ at 0.6 degrees of belief.

Table 7.
Equivalence rules for the chosen criteria.
Next, three candidate suppliers were assessed for the seven criteria via interview of the purchasing manager. He was concerned about confidential information and was informed that this study did not need real information, and only close or estimated values were sufficient to demonstrate the application of the proposed method. Furthermore, he could assign probabilities to a case that he was uncertain about or when the supplier’s performance fluctuated. He was also recommended to consider a new candidate supplier whose performance on some criteria was unavailable or unknown for representing a case of complete ignorance. The weights of the criteria were determined by asking the manager to directly assign a score of 0–100 to reflect the level of importance of each criterion. The weights were then normalised to make them sum to one. The assessment results for the three suppliers and criteria weights are shown in Table 8. Incomplete assessments were obtained for the performance of suppliers 2 and 3 for criterion . As stated by the manager, he had only partial information for the technologies employed by these two companies since the information was considered partly confidential even for their customers, while he was quite confident about those of supplier 1 since he had visited their plant many times. Complete ignorance was reported for supplier 3′s product quality (DPPM) or . This is because the company had never purchased this particular product from supplier 3, and their performance on other criteria was inferred from experience of purchasing other product models.

Table 8.
Original assessment results for the three candidate suppliers.
From the original assessment results and the constructed rules of equivalence, the suppliers’ performance was transformed with rule-based transformation. The results are shown in Table 9. As an example, supplier 1′s responsiveness is transformed according to Equation (7) as follows:

Table 9.
Transformed assessment results for the three candidate suppliers.
For quantitative transformation, the calculation of supplier 1′s product quality
following Equations (10)–(13), is given as an example.
The next step was to convert the generalised belief structures into utility intervals using Equations (16)–(17). For this case study, suppose the utility of each of the general grades is estimated as a linear function as follows: = 0, = 0.25, = 0.5, = 0.75, = 1.0. Table 10 shows the interval decision matrix obtained. Examples of the calculation for supplier 2′s innovation and technology are shown below. Note again that the minimum utility and maximum utility are equal for a complete assessment.

Table 10.
Utility intervals for the three candidate suppliers.
The min , max , and avg of each of the three candidate suppliers can be derived from their utility intervals with Equations (18)–(25). The results (Table 11) clearly indicate that, according to the avg , supplier 3 should be selected as the best compromise choice, with supplier 2 next and supplier 1 last. The rankings were all the same whether the decision maker was risk averse or risk seeking. However, due to the effect of uncertain and incomplete information, the recommendation is not conclusive, as there was some overlap of the utility intervals of the three suppliers. The max of supplier 1, who was the worst based on the average, was still higher than the min of the other two suppliers. If all sources of information are complete and precise, it is possible that supplier 1 could be the best.

Table 11.
Closeness coefficient to the ideal solution ( ) of the three suppliers derived by the proposed methodology.
The proposed methodology can be validated by comparing the ranking order of the three candidates to the results determined by other MCDM methods. The ER approach, developed by Yang and Singh [49], was chosen for this purpose due to its ability to tackle data in the form of belief distribution. The ER algorithm is given in Yang and Singh [49] and Yang [43]. The final results given by the ER method are in the form of the utility interval, denoted by and for alternative . The average or can also be used for decision making. The results of the ER method are shown in Table 12.

Table 12.
Minimum, average, and maximum utility of the three suppliers derived by the evidential reasoning method.
Based on average utility, the ER method also chose supplier 3. In addition, it is highly likely for a risk-seeking person to consider supplier 3 as the best compromise choice. However, a risk-averse person may prefer supplier 2 due to their highest minimum score. By comparing the decisions determined by the two methodologies, the differences can be summarised as follows.
- Although both methodologies provide a compensatory process of aggregation, they employ different approaches to derive the composite scores for each alternative. The proposed hybrid methodology is based on the principle of the TOPSIS method, which derives the score from the distances between the performance of the alternative and the best and worst values within the peer group, while the ER method conforms to conjunctive reasoning by seeking joint support from all criteria. This means that the composite score of an alternative derived by the ER method is independent of the performance of other alternatives; however, this is not the case for the TOPSIS-based methodology.
- According to the different approaches described in (1), the ER method did not assign an interval to supplier 1′s composite score since the interval only reflected the incompleteness of the information which emerged solely from suppliers 2 and 3. This implies that supplier 1′s overall performance did not change whether or not the other suppliers’ performance fluctuated. On the other hand, the TOPSIS method gave an interval to supplier 1′s composite score due to the fact that the other suppliers’ performance was uncertain because of incomplete or unknown information, and the overall performance of an alternative was dependent on the changes in performance of the others. Therefore, the proposed TOPSIS methodology is more rational, and provides a more comprehensive picture for ranking and choosing alternatives. The ER method seems to be more appropriate for constructing a self-assessment model for analysing and monitoring overall performance. The performance analysis of a single element without another alternative for comparison is an obvious limitation of the TOPSIS-based methodology.
- When considering minimum composite scores derived by the two methodologies, supplier 2 received a lower score than supplier 3 in the TOPSIS method, while the opposite result was obtained by the ER method. Such a difference was mainly caused by the high level of incompleteness in supplier 3′s performance (in criteria and ). The incompleteness means that the performance can be assigned to any value or any grade in the frame of discernment, such that its utility can range from 0 to 1. In the extended TOPSIS method, when calculating the minimum score for each alternative, its performance is assumed at the lowest level while the performance of the others is set at the highest level. This means that when calculating min , supplier 3′s utility was assumed at 0.7 and 1 in criteria and , respectively. This considerably downgraded supplier 2′s score due to the large distance between its minimum performance and the assumed excellent performance of supplier 3. Although the same method was applied when calculating min , the effects were not significant since only a short distance between supplier 3′s minimum utility and the highest utility of other suppliers was reported.
- Based on the explanation in (3), each alternative’s range derived by the proposed TOPSIS methodology is not sensitive to the incompleteness and uncertainty of its own assessment data, but to those of the other alternatives. In contrast, in the ER approach, each alternative’s range is a true reflection of the incompleteness of its own data.
In summary, both methodologies provide meaningful results for decision making through different approaches. Understanding the underlying concepts of each method is, therefore, necessary. As previously stated, the TOPSIS-based methodology tends to be a more rational solution for selecting the best choice from a finite set of alternatives. In the example, supplier 3 ultimately seemed to be the best choice. To improve the quality of outcomes, the decision maker should try to reduce the incompleteness of supporting information to narrow the range of the utility interval for making the final choice more robust.
5. Conclusions
This study identified a set of criteria for supplier selection in relation to the supplier’s ability to prepare itself to cope with any disruptive events. Seventeen criteria were gathered and synthesised from a review of published articles focusing on resilient supplier selection as well as general supplier selection problems within the electronics industry. The list of criteria was divided into two groups: (i) resilience capability and (ii) general criteria commonly considered critical for electronic components procurement. Our study makes several contributions, the first being that it fills the gap in research regarding resilient supplier selection in the electronics market. Our list, particularly the group of resilience capability criteria, can also be used as a starting point for practitioners in other industries, as well as for researchers in future studies, to formulate their own lists for the purpose of resilient supplier selection.
Another contribution of this study is the proposed hybrid methodology to facilitate the supplier selection process when there is uncertainty and incompleteness in supporting information. This issue is considered to be highly likely in assessments of supplier performance that include, in particular, consideration of disruptive situations that have never happened. This study is the first of its kind to integrate evidence theory and the rule-based information transformation technique into TOPSIS. Evidence theory involves the assignment of degrees of belief, instead of probabilities, during the assessment process. Consequently, the incompleteness of on-hand information can be modelled since the theory allows that subjective probabilities do not necessarily have to sum to one, but the sum can be less than one. Incompleteness is modelled here in the form of ‘global ignorance’, implying that the right answer can be any element in the frame of discernment. The rule-based technique was employed to transform various forms of possible assessment results into a unified format (a set of general grades) based on utility equivalence. After the completion of these processes, the transformed data are readily applicable to the extended TOPSIS method to determine a range of possible values of the composite score for each candidate supplier. This study provides a convenient method of aggregation in which various forms of uncertainties and incompleteness in the original assessment results can be used for further analysis. The uncertainty of the data is still preserved in the final form of the results to minimise the inaccuracy of a composite score and to frame guidelines for further discussion. The results obtained are considered to be more realistic and convincing than those provided by other methods constrained by the assumption of a combined precise value (as a consequence of managing uncertainty) or ignoring missing information. In this study, the final results are expressed as a range of possible scores, which also allows decision makers to integrate their risk attitudes to reach the best compromise solution. The recommended choice in the case study is mostly comparable to that derived by the ER method whose algorithm is viewed as more complicated. There is only a slight difference between the results of the two methodologies due to their dissimilar approaches to decision making.
This study enables manufacturers, acting as purchasers, to devise a resilience strategy to minimise the vulnerability of their business processes to any disruptions. The proposed hybrid methodology is applicable not only to electronic components procurement, but also to any cases of MCDM applied to other industries, particularly when decision makers perceive insufficient evidence or unavailable information as an obstacle for assessing alternatives.
The TOPSIS-based hybrid methodology presented here, however, still does not provide a solution for a case where the incompleteness (unassigned belief degree) is not assigned to the whole range of grades but only to subsets of the frame of discernment (which is not a singleton and the set itself) based on known or partially known information. This can be regarded as the degree of ‘local ignorance’. Future studies may extend the proposed methodology to create a solution for these new types of assessment results.
Author Contributions
Conceptualisation, P.S. and N.W.; methodology, P.S.; validation, P.S.; formal analysis, P.S. and N.W.; investigation, P.S. and N.W.; resources, P.S.; data curation, N.W.; writing—original draft preparation, P.S.; writing—review and editing, S.A. and T.N.; supervision, P.S.; project administration, P.S.; funding acquisition, P.S., S.A. and T.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Supply Chain and Logistics System Research Unit and the Faculty of Engineering, Khon Kean University.
Acknowledgments
This research was supported by Research Administration Division, Khon Kean University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haldar, A.; Ray, A.; Banerjee, D.; Ghosh, S. Resilient supplier selection under a fuzzy environment. Int. J. Manag. Sci. Eng. Manag. 2014, 9, 147–156. [Google Scholar] [CrossRef]
- Torabi, S.A.; Baghersad, M.; Mansouri, S.A. Resilient supplier selection and order allocation under operational and disruption risks. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 22–48. [Google Scholar] [CrossRef]
- Gan, J.; Zhong, S.; Liu, S.; Yang, D. Resilient supplier selection based on fuzzy BWM and GMo-RTOPSIS under supply chain environment. Discret. Dyn. Nat. Soc. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Nourbakhsh, V.; Ahmadi, A.; Mahootchi, M. Considering supply risk for supplier selection using an integrated framework of data envelopment analysis and neural networks. Int. J. Ind. Eng. Comput. 2013, 4, 273–284. [Google Scholar] [CrossRef]
- Haren, P.; Simchi-Levi, D. How Coronavirus could impact the global supply chain by mid-March. In Harvard Business Review; Harvard Business Publishing: Brighton, MA, USA, 2020; Available online: https://hbr.org/2020/02/how-coronavirus-could-impact-the-global-supply-chain-by-mid-march (accessed on 4 April 2020).
- Hosseini, S.; Khaled, A.A. A hybrid ensemble and AHP approach for resilient supplier selection. J. Intell. Manuf. 2019, 30, 207–228. [Google Scholar] [CrossRef]
- Pramanik, D.; Haldar, A.; Mondal, S.C.; Naskar, S.K.; Ray, A. Resilient supplier selection using AHP-TOPSIS-QFD under a fuzzy environment. Int. J. Manag. Sci. Eng. Manag. 2017, 12, 45–54. [Google Scholar] [CrossRef]
- Chen, A.; Hsieh, C.-Y.; Wee, H.M. A resilient global supplier selection strategy-a case study of an automotive company. Int. J. Adv. Manuf. Technol. 2016, 87, 1475–1490. [Google Scholar] [CrossRef]
- Bhutta, K.S.; Huq, F. Supplier selection problem: A comparison of the total cost of ownership and analytic hierarchy process approaches. Supply Chain Manag. Int. J. 2002, 7, 126–135. [Google Scholar] [CrossRef]
- Chang, B.; Chang, C.-W.; Wu, C.-H. Fuzzy DEMATEL method for developing supplier selection criteria. Expert Syst. Appl. 2011, 38, 1850–1858. [Google Scholar] [CrossRef]
- Sahu, A.K.; Datta, S.; Mahapatra, S.S. Evaluation and selection of resilient suppliers in fuzzy environment: Exploration of fuzzy-VIKOR. Benchmarking Int. J. 2016, 23, 651–673. [Google Scholar] [CrossRef]
- Sawik, T. Selection of resilient supply portfolio under disruption risks. Omega 2013, 41, 259–269. [Google Scholar] [CrossRef]
- Hasan, M.M.; Jiang, D.; Ullah, A.M.M.S.; Noor-E-Alam, M. Resilient supplier selection in logistics 4.0 with heterogeneous information. Expert Syst. Appl. 2020, 139, 1–24. [Google Scholar] [CrossRef]
- Levary, R.R. Using the analytic hierarchy process to rank foreign suppliers based on supply risks. Comput. Ind. Eng. 2008, 55, 535–542. [Google Scholar] [CrossRef]
- Rajesh, R.; Ravi, V. Supplier selection in resilient supply chains: A grey relational analysis approach. J. Clean. Prod. 2015, 86, 343–359. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Sureeyatanapas, P.; Sriwattananusart, K.; Niyamosoth, T.; Sessomboon, W.; Arunyanart, S. Supplier selection towards uncertain and unavailable information: An extension of TOPSIS method. Oper. Res. Perspect. 2018, 5, 69–79. [Google Scholar] [CrossRef]
- Wang, C.-N.; Tsai, H.-T.; Nguyen, V.T.; Nguyen, V.T.; Huang, Y.-F. A hybrid fuzzy analytic hierarchy process and the technique for order of preference by similarity to ideal solution supplier evaluation and selection in the food processing industry. Symmetry 2020, 12, 211. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making—Methods and Application: A State-of-the-Art Survey; Springer-Verlag: New York, NY, USA, 1981. [Google Scholar]
- Davoudabadi, R.; Mousavi, S.M.; Mohagheghi, V.; Vahdani, B. Resilient supplier selection through introducing a new interval-valued intuitionistic fuzzy evaluation and decision-making framework. Arab. J. Sci. Eng. 2019, 44, 7351–7360. [Google Scholar] [CrossRef]
- Govindan, K.; Rajendran, S.; Sarkis, J.; Murugesan, P. Multi criteria decision making approaches for green supplier evaluation and selection: A literature review. J. Clean. Prod. 2015, 98, 66–83. [Google Scholar] [CrossRef]
- Bharadwaj, N. Investigating the decision criteria used in electronic components procurement. Ind. Mark. Manag. 2004, 33, 317–323. [Google Scholar] [CrossRef]
- Lee, A.H.I.; Chang, H.-J.; Lin, C.-Y. An evaluation model of buyer-supplier relationships in high-tech industry-the case of an electronic components manufacturer in Taiwan. Comput. Ind. Eng. 2009, 57, 1417–1430. [Google Scholar] [CrossRef]
- Jacyna-Gołda, I. Decision-making model for supporting supply chain efficiency evaluation. Arch. Transp. 2015, 33, 17–31. [Google Scholar] [CrossRef][Green Version]
- Izdebski, M.; Jacyna-Gołda, I.; Markowska, K.; Murawski, J. Heuristic algorithms applied to the problems of servicing actors in supply chains. Arch. Transp. 2017, 44, 25–34. [Google Scholar] [CrossRef]
- Bieniek, M. Service level in model of inventory location with stochastic demand. Arch. Transp. 2014, 31, 7–21. [Google Scholar] [CrossRef]
- Jacyna-Gołda, I.; Izdebski, M.; Szczepański, E.; Gołda, P. The assessment of supply chain effectiveness. Arch. Transp. 2018, 45, 43–52. [Google Scholar] [CrossRef]
- Aouadni, S.; Aouadni, I.; Rebaï, A. A systematic review on supplier selection and order allocation problems. J. Ind. Eng. Int. 2019, 15, S267–S289. [Google Scholar] [CrossRef]
- Belton, V.; Gear, T. On a short-coming of Saaty’s method of analytic hierarchies. Omega 1983, 11, 228–230. [Google Scholar] [CrossRef]
- Barzilai, J.; Golany, B. AHP rank reversal, normalization and aggregation rules. Inf. Syst. Oper. Res. 1994, 32, 14–20. [Google Scholar] [CrossRef]
- Ramanathan, R.; Ganesh, L.S. Group preference aggregation methods employed in AHP: An evaluation and an intrinsic process for deriving members’ weightages. Eur. J. Oper. Res. 1994, 79, 249–265. [Google Scholar] [CrossRef]
- Van Den Honert, R.C.; Lootsma, F.A. Group preference aggregation in the multiplicative AHP: The model of the group decision process and Pareto optimality. Eur. J. Oper. Res. 1996, 96, 363–370. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Poh, K.L. A survey of data envelopment analysis in energy and environmental studies. Eur. J. Oper. Res. 2008, 189, 1–18. [Google Scholar] [CrossRef]
- Ramanathan, R. Data envelopment analysis for weight derivation and aggregation in the analytic hierarchy process. Comput. Oper. Res. 2006, 33, 1289–1307. [Google Scholar] [CrossRef]
- Sari, K. On the benefits of CPFR and VMI: A comparative simulation study. Int. J. Prod. Econ. 2008, 113, 575–586. [Google Scholar] [CrossRef]
- Niranjan, T.T.; Wagner, S.M.; Nguyen, S.M. Prerequisites to vendor-managed inventory. Int. J. Prod. Res. 2012, 50, 939–951. [Google Scholar] [CrossRef]
- Aloini, D.; Benevento, E.; Stefanini, A. Conceptual design of a tool supporting the “last mile” logistics in hospitals. In Proceedings of the 12th IADIS International Conference Information Systems, Utrecht, The Netherlands, 11–13 April 2019. [Google Scholar]
- Ravindran, A.R.; Bilsel, R.U.; Wadhwa, V.; Yang, T. Risk adjusted multicriteria supplier selection models with applications. Int. J. Prod. Res. 2010, 48, 405–424. [Google Scholar] [CrossRef]
- Mohammed, A.; Harris, I.; Soroka, A.; Mohamed, N.; Ramjaun, T. Evaluating green and resilient supplier performance: AHP-fuzzy Topsis decision-making approach. In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems, Madeira, Portugal, 24–26 January 2018. [Google Scholar]
- Hirakubo, N.; Kublin, M. The relative importance of supplier selection criteria: The case of electronic components procurement in Japan. J. Supply Chain Manag. 1998, 34, 19–24. [Google Scholar] [CrossRef]
- Gencer, C.; Gürpinar, D. Analytic network process in supplier selection: A case study in an electronic firm. Appl. Math. Model. 2007, 31, 2475–2486. [Google Scholar] [CrossRef]
- Chiou, C.Y.; Hsu, C.W.; Hwang, W.Y. Comparative investigation on green supplier selection of the American, Japanese and Taiwanese electronics industry in China. In Proceedings of the 2008 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 8–11 December 2008. [Google Scholar]
- Yang, J.B. Rule and utility based evidential reasoning approach for multiple attribute decision analysis under uncertainty. Eur. J. Oper. Res. 2001, 131, 31–61. [Google Scholar] [CrossRef]
- Wang, Y.M.; Yang, J.B.; Xu, D.L. Environmental impact assessment using the evidential reasoning approach. Eur. J. Oper. Res. 2006, 174, 1885–1913. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Sentz, K.; Ferson, S. Combination of evidences in Dempster-Shafer theory. In Sandia Report; SAND2002-0835; Sandia National Laboratories: Albuquerque, NM, USA, 2002. [Google Scholar]
- Lowrance, J.D.; Garvey, T.D.; Strat, T.M. A framework for evidential-reasoning systems. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Yager, R.R., Liu, L., Eds.; Springer: New York, NY, USA, 2008; pp. 419–434. [Google Scholar]
- Yang, J.B.; Singh, M.G. An evidential reasoning approach for multiple attribute decision making with uncertainty. IEEE Trans. Syst. ManCybern. 1994, 24, 1–18. [Google Scholar] [CrossRef]
- Yang, J.B.; Xu, D.L. Introduction to the ER rule for evidence combination. In Integrated Uncertainty in Knowledge Modelling and decision Making; Tang, Y., Huynh, V.N., Lawry, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 7–15. [Google Scholar]
- Florea, M.C.; Jousselme, A.L.; Bossé, É.; Grenier, D. Robust combination rules for evidence theory. Inf. Fusion 2009, 10, 183–197. [Google Scholar] [CrossRef]
- Dezert, J. Foundations for a new theory of plausible and paradoxical reasoning. Inf. Secur. Int. J. 2002, 9, 13–57. [Google Scholar] [CrossRef][Green Version]
- Sureeyatanapas, P.; Yang, J.B.; Bamford, D. The sweet spot in sustainability: A framework for corporate assessment in sugar manufacturing. Prod. Plan. Control 2015, 26, 1128–1144. [Google Scholar] [CrossRef]
- Winston, W.L. Operations Research: Applications and Algorithms, 4th ed.; Thomson Learning: Toronto, ON, Canada, 2004. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).