1. Introduction
In recent years, there has been a continuous interest in the so-called Bopp–Podolsky theory [
1,
2,
3,
4,
5,
6,
7], a first-order linear gradient theory of electrodynamics. The theory was introduced in the early 1940s by Bopp and Podolsky [
8,
9,
10] as a method to remove singularities in classical Maxwell electrodynamics and to obtain a consistent Lorentz and gauge-invariant theory of point charges with finite self-energy (see also [
11]), thereby proposing an alternative to earlier theories that achieved the same goal through a nonlinear generalization of electrodynamics [
12]. While the motivation was ultimately the quantization of the theory (e.g., [
13]), it is, first of all, a classical field theory. Through the introduction of an additional gradient term in the Lagrangian, the generalized Maxwell equations yield linear partial differential equations of fourth order for the electromagnetic potentials. Along with the additional term, a new constant has to be introduced, the Bopp–Podolsky length scale parameter
ℓ, which by the original idea was supposed to be related to the electron self-energy. Indeed, Iwanenko and Sokolow [
14], Kvasnica [
15] and Cuzinatto et al. [
16] reasoned that the Bopp–Podolsky length scale parameter
ℓ is of the order of ∼
m which is the order of the classical electron radius; however, Accioly and Mukai [
17], and Carley et al. [
3] argued that the Bopp–Podolsky length scale parameter
ℓ should be equal to or smaller than ∼
m. From the mathematical point of view the length scale parameter
ℓ plays the role of a regularization parameter. The regularization through the higher-order field equations provides a finite self-energy for the point charge, and its electrostatic potential is finite and nonsingular; its electric field is finite, but with a directional discontinuity. Additionally, in Bopp–Podolsky electrodynamics the electromagnetic fields of a non-uniformly moving point charge possess a directional discontinuity on the light cone. In order to obtain electromagnetic fields of a non-uniformly moving point charge with no directional discontinuity on the light cone, the theory of second gradient electrodynamics has recently been proposed and used in [
18]. Further important advantages of gradient electrodynamics in comparison to the classical Maxwell electrodynamics are: no infamous “4/3-problem”, no unphysical runaway solutions to the equation of motion of a moving charged particle (the analogue of the Lorentz-Dirac equation), no singularities of the electromagnetic fields on the light cone, the self-force of a non-uniformly moving charged particle is regular (see also the discussion in [
18]).
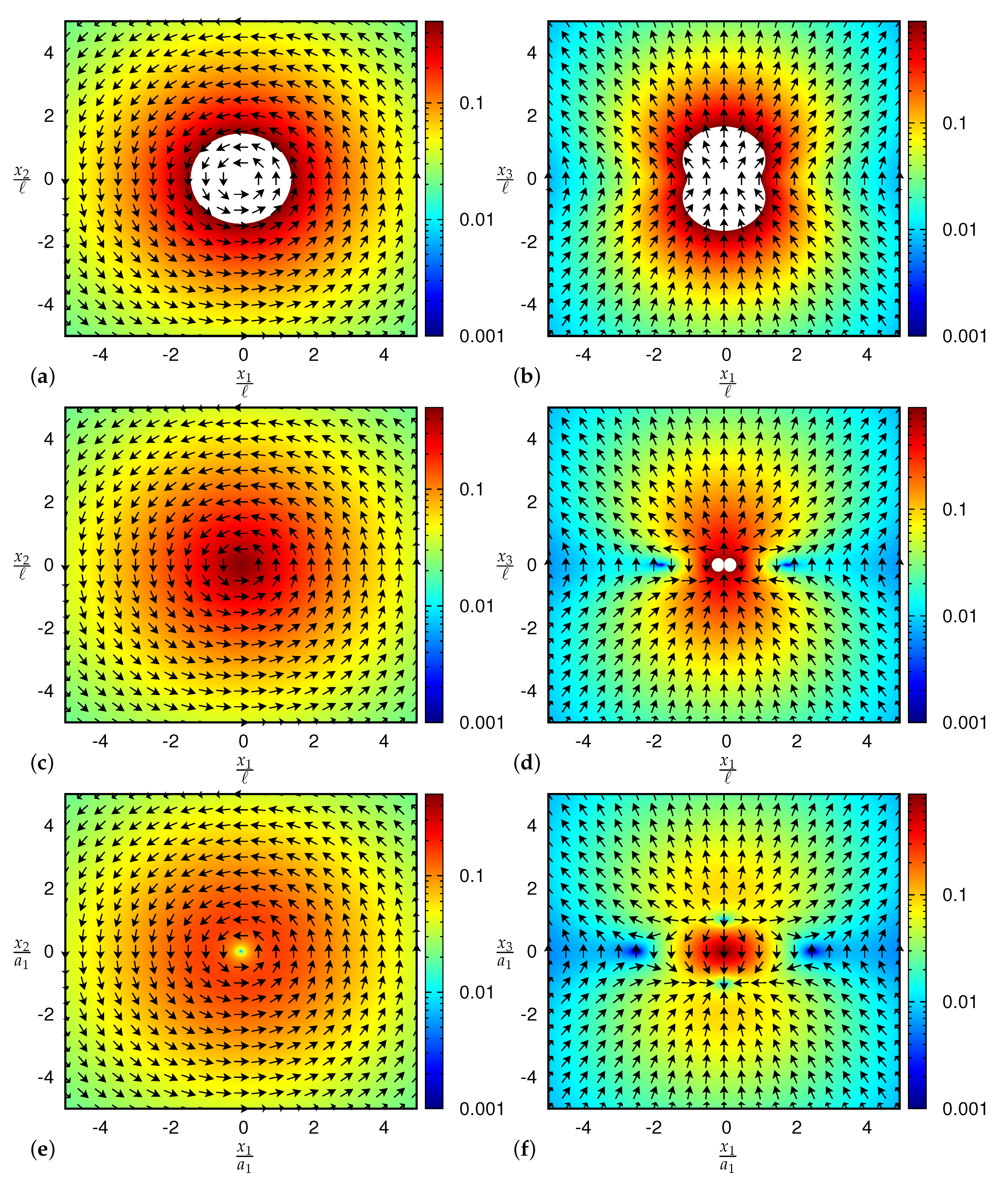
Besides the point charge, other important textbook examples of the Maxwell theory are the electrostatic and magnetostatic dipoles possessing typical dipole singularities (
and Dirac delta-singularity) in the electromagnetic fields [
19,
20,
21,
22]. In the mathematical literature, there is an interest in the regularization of the dipole singularities arising from the second-order derivatives of
in the sense of generalized functions (see, e.g., [
23,
24,
25]). The ideal magnetostatic dipole in first-order gradient electrodynamics was already studied by Landé and Thomas [
26], giving the magnetic fields and a finite self-energy. The latter result, however, turns out to be erroneous. Using the Bopp–Podolsky theory, the electric and magnetic fields of electrostatic and magnetostatic dipoles are still singular and their self-energy is also infinite, as will be shown in this paper.
Our purpose is to investigate the theory of second gradient electromagnetostatics which is the static version of the theory of second gradient electrodynamics [
18]. We will study the textbook examples of electric point charge, electrostatic dipole and magnetostatic dipole in the framework of generalized electrodynamics, and show that second gradient electromagnetostatics yields nonsingular dipole fields and gives a straightforward regularization of the dipole singularities based on higher-order partial differential equations.
In general, in generalized electrodynamics, the electromagnetic fields (electric and magnetic potential, electric and magnetic field strengths) should satisfy the following conditions:
The field must be finite at ;
The field must be everywhere continuous;
The self-energy of the field must be finite.
As mentioned, not all conditions can be satisfied for an electric point charge, an electrostatic dipole and a magnetostatic dipole using Bopp–Podolsky electrodynamics.
Nowadays, generalized continuum theories and in particular gradient continuum theories are very popular in physics, applied mathematics, material science and engineering science. Gradient continuum theories are continuum theories which might possess characteristic length scales and characteristic time scales in order to describe size effects and memory effects, respectively. In particular, gradient theories are continuum theories valid at small scales, unlike classical continuum theories such as Maxwell electrodynamics. Because classical continuum theories are not valid at small scales, they lead to unphysical singularities at such scales. Thus, we are forced to regularize at short distances the classical continuum theories by means of generalized continuum theories. Gradient continuum theories provide nonsingular solutions of the field equations and a regularization of classical singularities is achieved. In physics, the most popular gradient continuum theory is the Bopp–Podolsky theory [
8,
9], which is the first-order gradient version of the theory of electrodynamics as mentioned above. In engineering science, a very popular gradient continuum theory is Mindlin’s theory of first strain gradient elasticity [
27]. An advantage of gradient elasticity theory is that it can be connected with atomistic theories and all material parameters, including the appearing length scale parameters, can be determined from ab initio calculations and using atomistic potentials (see, e.g., [
28,
29,
30]). Exciting gradient effects, which are important for applications in material science, exist due to the coupling between gradient elasticity and gradient electricity in gradient electroelasticity [
31], like flexoelectricity in solids [
32], which is the property of a dielectric material whereby it exhibits a spontaneous electrical polarization induced by an elastic strain gradient (see also the papers on flexoelectricity published in this Special Issue on
Recent Advances in the Study of Symmetry and Continuum Mechanics). Furthermore, Mindlin [
33] introduced the theory of second strain gradient elasticity (see also [
34,
35,
36]). Mindlin’s theory of second strain gradient elasticity involves additional material constants, in addition to the elastic constants, which can be determined from atomistic potentials (see [
37]). Second strain gradient elasticity provides better modelling of atomistics than first strain gradient elasticity. Using a simplified version of second gradient elasticity, it was possible to obtain nonsingular solutions for the elastic field produced by point defects which are elastic dipoles in solids [
38]. The theory of second gradient electrodynamics has been recently proposed by Lazar [
18]. It turns out that second gradient electrodynamics provides better mathematical modeling of electromagnetic fields at small distances than the Bopp–Podolsky electrodynamics (first gradient electrodynamics). In this paper, we study the static version of it called second gradient electromagnetostatics. Of course, the coupling between second strain gradient elasticity and second gradient electromagnetostatics may lead to many interesting gradient effects of higher order which will be worth studying more in detail in future work. Therefore, gradient continuum theories are very exciting research areas of physics on small scales.
While structurally, as mathematical theories, gradient electrodynamics and gradient elasticity of
n-th order are analogous, their physical significance differs slightly. Both can serve the purpose of regularization at small scales, but while gradient elasticity can be interpreted to describe microstructure and can, for example, also be derived as an approximation of lattice theories (see, e.g., [
33,
39]), in gradient electrodynamics analogous interpretations are not as clear. Moreover, the length scale for gradient elasticity is of the order of
, and thus, as mentioned above, can be compared with atomistic simulations; however, in gradient electrodynamics the smallness of the length scale parameter has so far eluded experimental verification. While possible approaches have been suggested (e.g., [
16]), so far none has reached the scale of
or smaller for the Bopp–Podolsky parameter, and comparisons with quantum mechanical effects have yielded upper estimates for the length scale parameter (e.g., [
3,
17]). However, gradient electrodynamics remain an interesting subject, as a candidate for a consistent classical field theory of electrodynamics including point charges (see also [
40]), as a candidate for a generalized quantum electrodynamics (see, e.g., [
41,
42]) and in comparison with other mathematical techniques of regularization.
The outline of this paper is as follows. In
Section 2, the theory of second gradient electromagnetostatics is presented. In
Section 3, we give the collection of all relevant Green functions and their derivatives. In
Section 4, the nonsingular electromagnetic fields of a point charge, an electrostatic dipole and a magnetostatic dipole are computed in the framework of second gradient electromagnetostatics. The limits of those electromagnetic fields to the Bopp–Podolsky theory and to the classical Maxwell theory are given in
Section 5 and
Section 6, respectively. The conclusions are given in
Section 7.
2. Second Gradient Electromagnetostatics
In this Section, we provide the theoretical framework of second gradient electromagnetostatics. Second gradient electromagnetostatics is the static version of second gradient electrodynamics given in [
18] (for details of second gradient electrodynamics we refer to [
18]). In the theory of second gradient electromagnetostatics, the electrostatic and magnetostatic fields are described by the Lagrangian density
with the notation
,
and
. Here
is the electrostatic scalar potential,
is the magnetostatic vector potential,
is the electrostatic field strength vector,
is the magnetostatic field strength vector,
is the electric charge density and
is the electric current density vector.
is the electric constant and
is the magnetic constant (also called permittivity of vacuum and permeability of vacuum, respectively). Moreover,
and
are the two (positive) characteristic length scale parameters in second gradient electrodynamics and ∇ is the vector operator Del (or Nabla). In addition to the classical terms, first and second spatial derivatives of the (static) electromagnetic field strengths (
,
) multiplied by the characteristic lengths
and
appear in Equation (
1) describing a weak nonlocality in space.
While in classical electrodynamics and electromagnetostatics the requirements of isotropy and gauge invariance lead to a unique choice for the Lagrangian, we here only have uniqueness up to null-Lagrangians (cf. [
43]). Bopp [
8] and Podolsky [
9] introduced first-order gradient electrodynamics using different Lagrangians both being equal up to null-Lagrangians and leading to identical field equations. Our choice of Lagrangian is closer to Bopp’s convention, using contractions of field gradients rather than divergences. Of course, with the introduction of higher-order terms the number of possible null-Lagrangians increases.
Note that, as is the case in classical electromagnetostatics with linear constitutive relations, the Lagrangian (
1) is a sum of two purely electrostatic or magnetostatic terms. In consequence, unlike in Born-Infeld electromagnetostatics [
44], it is obvious that electrostatics and magnetostatics are separated: electric currents do not produce electric fields and electric charges do not produce magnetic fields. Additionally, note that the two energy densities are positive definite, which results in positive definite energy functionals and thus in well-posed variational problems. While in the second gradient term the positive sign is both necessary and sufficient for positivity of the energy functional, in the first term it is only sufficient. As long as
, a negative sign could be allowed from the mathematical point of view; however, as will be seen below (case (3)), this would be unphysical. While the static theory works formally with this choice of parameters, the dynamic generalization contains serious problems. Additionally, the Lagrangian with a negative sign in the first gradient term would not be a generalization of the Bopp–Podolsky theory where the positive sign is mandatory.
In electromagnetostatics, the electromagnetic field strengths (
,
) can be expressed in terms of the static electromagnetic potentials (
,
)
because they satisfy the two electromagnetostatic Bianchi identities
which are known as the homogeneous Maxwell equations. Equation (
4) states that the electrostatic field
is irrotational, and Equation (5) states that the magnetostatic field
has no scalar sources.
The Euler–Lagrange equations of the Lagrangian (
1) with respect to the scalar potential
and the vector potential
give the electromagnetic field equations
respectively, and the scalar differential operator of fourth order is given by
where
is the Laplacian. Equations (
6) and (7) are the generalized inhomogeneous Maxwell equations in second gradient electromagnetostatics, which are partial differential equations of fifth order. Equation (
6) represents the generalized Gauss law, and Equation (7) represents the generalized Ampère law. The electric current density vector fulfills the equation of continuity
If we use the variational derivative with respect to the electromagnetic fields (
,
), then we obtain the (isotropic) constitutive relations in second gradient electromagnetostatics for the response quantities (
,
) in vacuum
where
is the electric excitation vector and
is the magnetic excitation vector. Therefore, in second gradient electromagnetostatics the (isotropic) constitutive relations (
10) and (11) involve an invariant scalar constitutive operator of fourth order,
, in addition to the scalar constitutive parameters
and
. The constitutive operator
is the only linear scalar isotropic operator of fourth order, a fact that is related to the uniqueness up to null-Lagrangians of the Lagrangian for the theory. Constitutive operators of this form already showed up in second strain gradient elasticity (e.g., [
33,
35,
38]). The higher-order terms in Equations (
10) and (11) describe the polarization of the vacuum present in second gradient electrodynamics (see, e.g., [
18,
45]). Using the constitutive relations (
10) and (11), the Euler–Lagrange Equations (
6) and (7) can be rewritten in the form of inhomogeneous Maxwell equations
From Equations (
6) and (7), the following inhomogeneous partial differential equations, being partial differential equations of sixth order, can be derived for the static electromagnetic field strengths
Using the generalized Coulomb gauge condition (here the standard Coulomb gauge yields the same results; the necessity for the generalized condition only arises in quantum field theories corresponding to the theory presented here) (see [
4,
46,
47]),
the electromagnetic gauge potentials fulfill the following inhomogeneous partial differential equations of sixth order
The differential operator of fourth order (
8) can be written in the form as product of two Helmholtz operators with two length scale parameters
and
, which is called bi-Helmholtz operator,
with
and
The two length scales
and
may be real or complex. In the theory of second gradient electromagnetostatics, the condition for the character, real or complex, of the two lengths
and
is the condition for the discriminant in Equation (
22),
, to be positive or negative. Depending on the character of the two length scales
and
one can distinguish between the following cases:
- (1)
:
The length scales
and
are real and distinct and they read
with
. The limit to the Bopp–Podolsky theory is given by
.
- (2)
:
The length scales
and
are real and equal,
There is no limit to the Bopp–Podolsky theory. This case can lead to Green functions having a time dependence that increases or decreases slowly, which can give rise to unphysical results (e.g., [
18,
48]).
- (3)
:
The two length scales
and
are complex conjugate,
with
There is no limit to the Bopp–Podolsky theory. For generalized electrodynamics, this case leads to Green functions having a time dependence that increases exponentially, an acausal propagation and complex mass terms (e.g., [
18,
48,
49]). The dispersion relations of the vacuum, analogous to those computed in [
45], have complex coefficients, suggesting instabilities or dissipation in the vacuum.
The possible negative sign in the first gradient term of the Lagrangian mentioned above also yields complex and and thus has similar consequences.
Therefore, the case (1) is the physical one and is the generalization of the Bopp–Podolsky theory (first gradient electromagnetostatics) towards second gradient electromagnetostatics.
3. Green Functions in Second Gradient Electromagnetostatics
Second gradient electromagnetostatics is a linear theory with partial differential equations of sixth order, and the method of Green functions (fundamental solutions) can be used.
The Green function
of the sixth order differential operator
is defined by
where
and
is the Dirac delta-function. The partial differential equation of sixth order (
27) can be written as an equivalent system of partial differential equations of lower order
or alternatively
where
is the Green function of the Laplace operator (29) and
is the Green function of the bi-Helmholtz operator (31).
Using partial fraction decomposition, the inverse differential operators
and
with Equation (
19) read in the formal operator notation (see also [
50])
and
This formal notation directly translates into relations for the Green functions so that the Green function
can be written as a linear combination of two Green functions
and
corresponding to the two length scale parameters
and
and Helmholtz operators
and
,
Similarly, the Green function
can be written as a linear combination of the Green function
of the Laplace operator and the two Green functions
and
corresponding to the two length scale parameters
and
,
Note that the foregoing is essentially an application of proposition 1.4.4 in [
51] and could analogously be applied in linear gradient theories of any order. Using Equation (
34), the Green function of the bi-Helmholtz equation might be derived from the Green function of the Helmholtz equation (see, e.g., [
50,
52,
53]). Sometimes, the differential operator
is called modified Helmholtz operator [
52] or metaharmonic operator [
54]. Therefore, the bi-Helmholtz field is a superposition of two Helmholtz fields with length scales
and
. Using Equation (
35), the Green function of the bi-Helmholtz-Laplace equation might be derived by using the expressions of the Green function of the Laplace operator (see, e.g., [
50,
55,
56]) and the Green function of the Helmholtz operator (see, e.g., [
50,
52,
53]). Therefore, the bi-Helmholtz-Laplace field is a superposition of the Laplace field and two Helmholtz fields.
On the other hand, resulting from the decomposition into the systems Equations (
28) and (29), or (
30) and (31), the Green function of the bi-Helmholtz-Laplace operator can be written as the convolution of the Green function of the Laplace operator and the Green function of the bi-Helmholtz equation
Here, the symbol ∗ denotes the spatial convolution. Therefore, the Green function
plays the role of the regularization function in second gradient electromagnetostatics. Moreover, the Green function of the bi-Helmholtz equation can be written as convolution of the Green functions of the two Helmholtz operators
satisfying Equations (31) and (
19).
3.1. Green Functions
The (three-dimensional) Green functions (or fundamental solutions) of the Laplace operator (29), the Helmholtz operator with length parameter
, the bi-Helmholtz operator (31) and the bi-Helmholtz-Laplace operator are given by
Equation (40) is obtained by substituting Equation (39) into Equation (
34), and Equation (41) is obtained by substituting Equations (
38) and (39) into Equation (
35). Moreover, the Green function (41) may be written as
with the auxiliary function
The series expansion (near field) of the auxiliary function (
43) reads as
Therefore, the function
regularizes up to a
-singularity towards a nonsingular field expression. Indeed, the Green function (41) is nonsingular and finite at
, namely
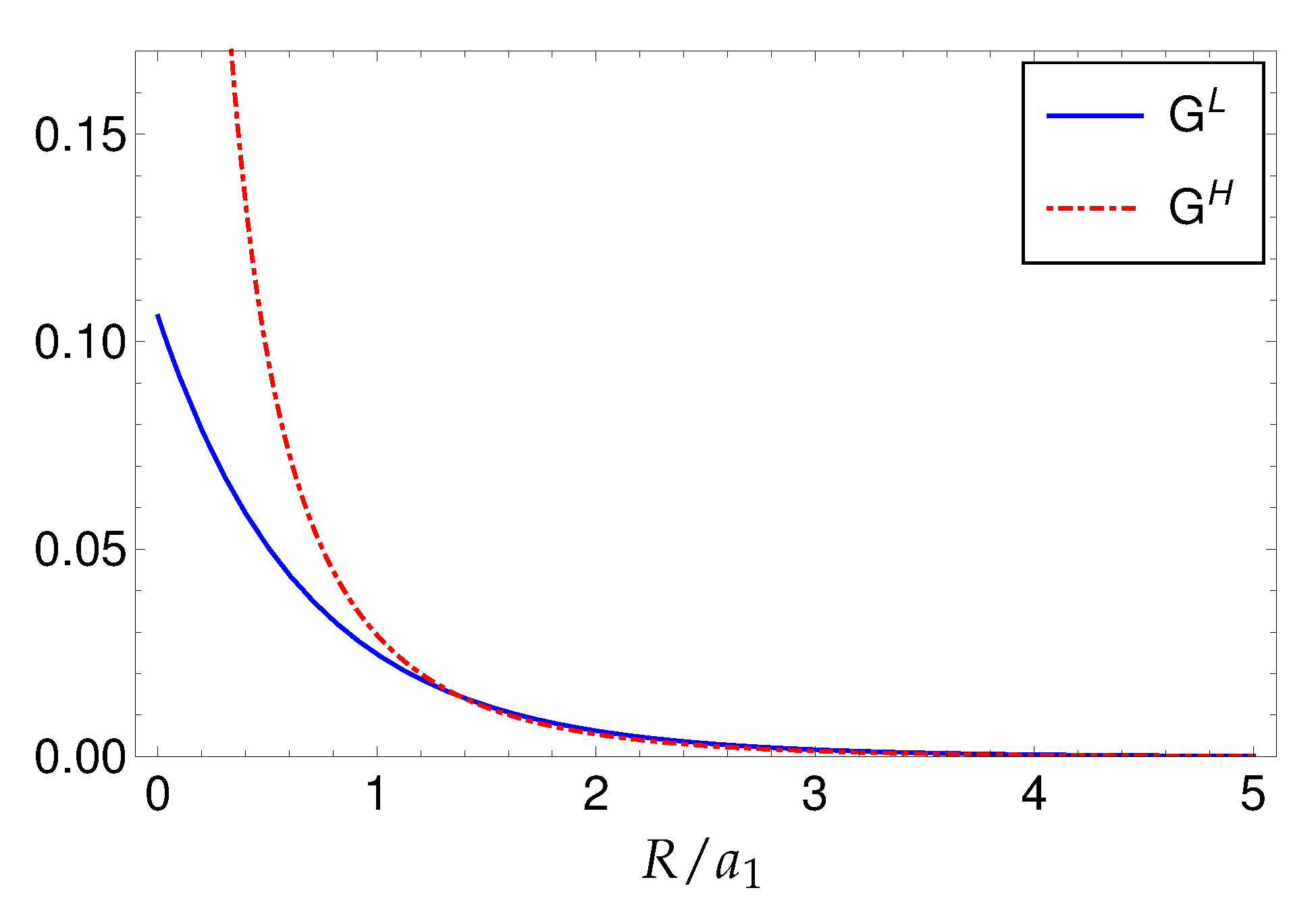
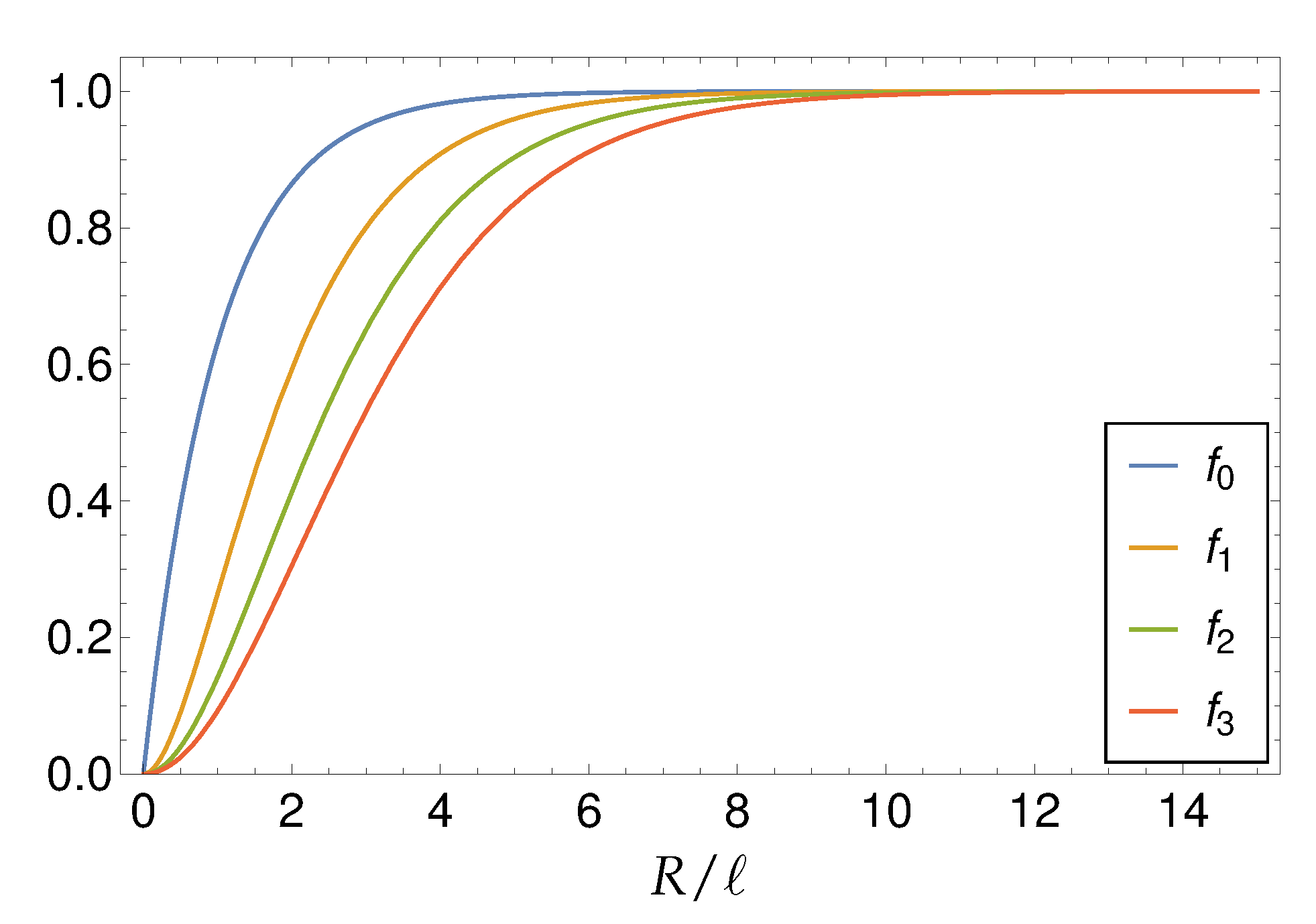
On the other hand, the Green function (40) is nonsingular and possesses a maximum value at
, namely (see
Figure 1)
Moreover, the Green function (40) is a Dirac-delta sequence with parametric dependence
and
with
where the limit is to be understood in the weak sense for distributions. The Green functions (39) and (40) are plotted in
Figure 1.
3.2. Derivatives of the Green Function
Now, we calculate the first, second and third gradients of the Green function
. The first, second and third gradients of the Green function (41) are obtained as (the expression
means
)
and (cf. Equation (
30))
with the auxiliary functions
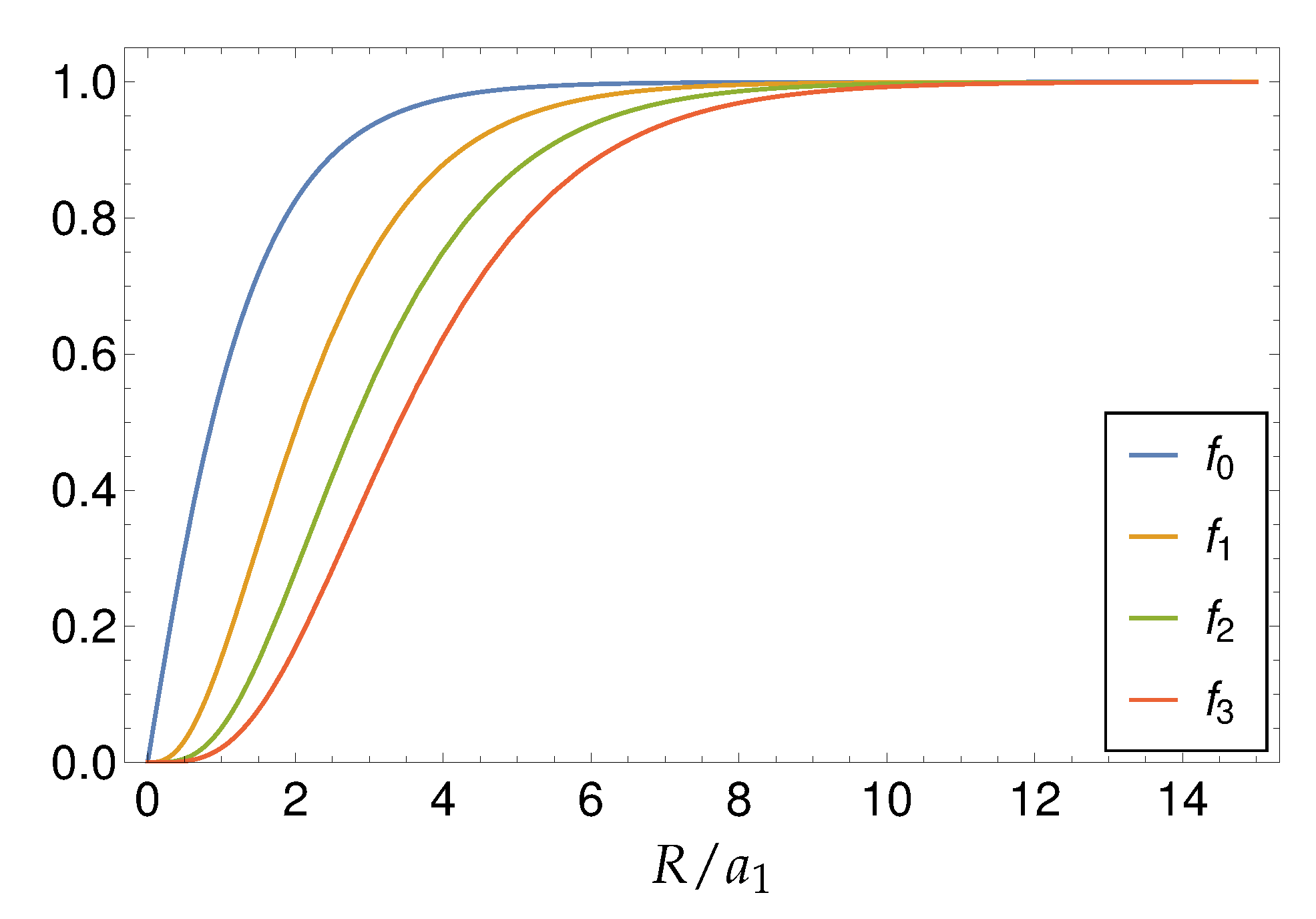
Note that the auxiliary functions for the gradients of a Green function in the form (
42) obey
for
. This procedure might even carry on to higher orders of the derivatives in an approach to Equation (
42) similar to the results of [
57], but this level of generality is not needed here. This relation has direct consequences for the series expansions (the
are analytic and can be differentiated term by term):
has no linear term,
neither linear nor cubic,
no
R,
and
-term, and so forth. Therefore, the first non-vanishing term of even order in
, which here is the fourth-order term, determines the strength of the regularization.
The relevant series expansions of the auxiliary functions (
54)–(56) (near fields) read as
In Equations (
58)–(60), it can be seen that the function
regularizes up to a
-singularity and the functions
and
regularize up to a
-singularity towards nonsingular field expressions.
The auxiliary functions (
43), (
54)–(56) are plotted in
Figure 2. In the far field, the auxiliary functions (
43), (
54)–(56) approach the value of 1 and in the near field, they are modified due to gradient parts and approach the value of 0 at the position
(see
Figure 2).
7. Conclusions
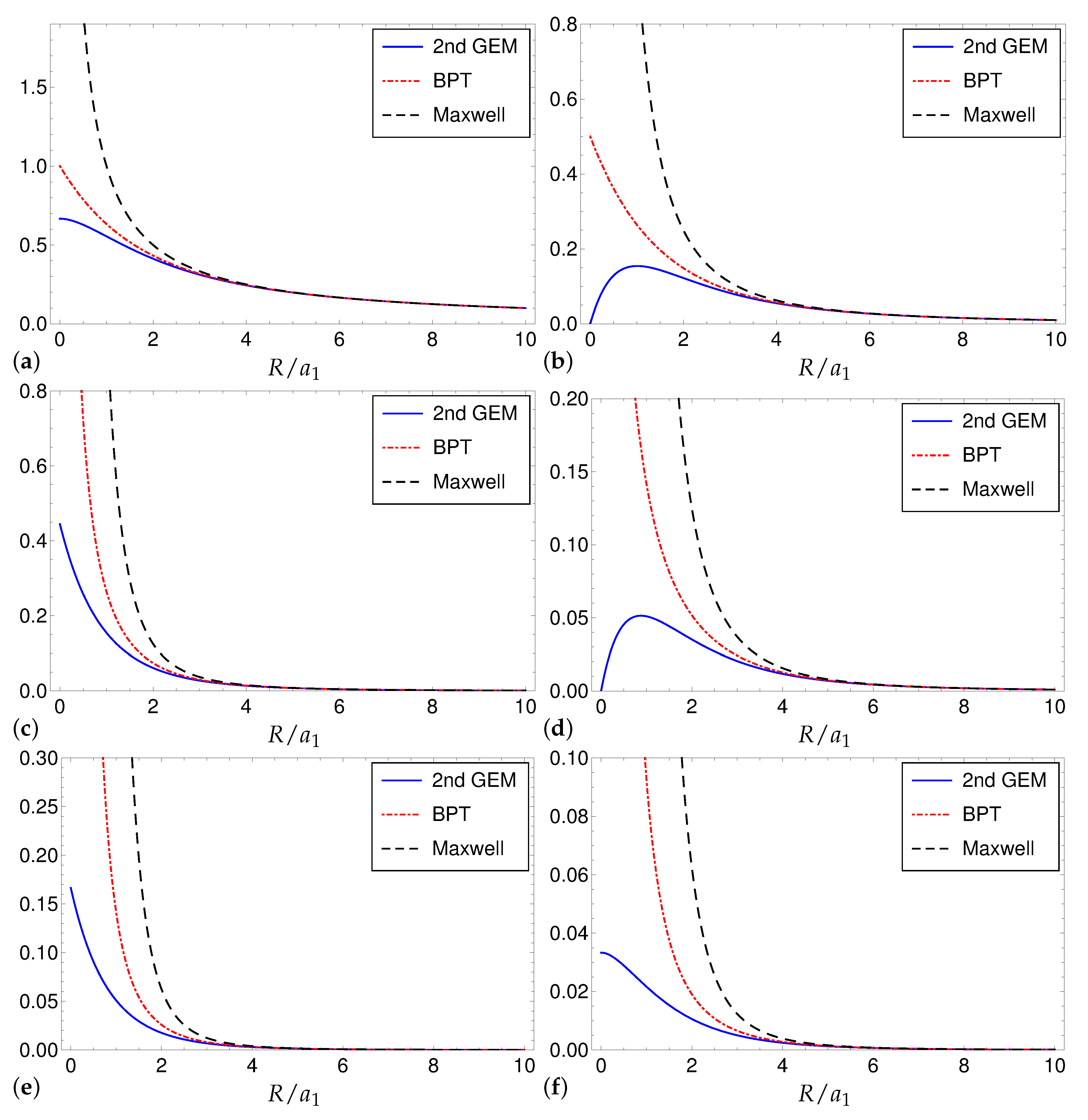
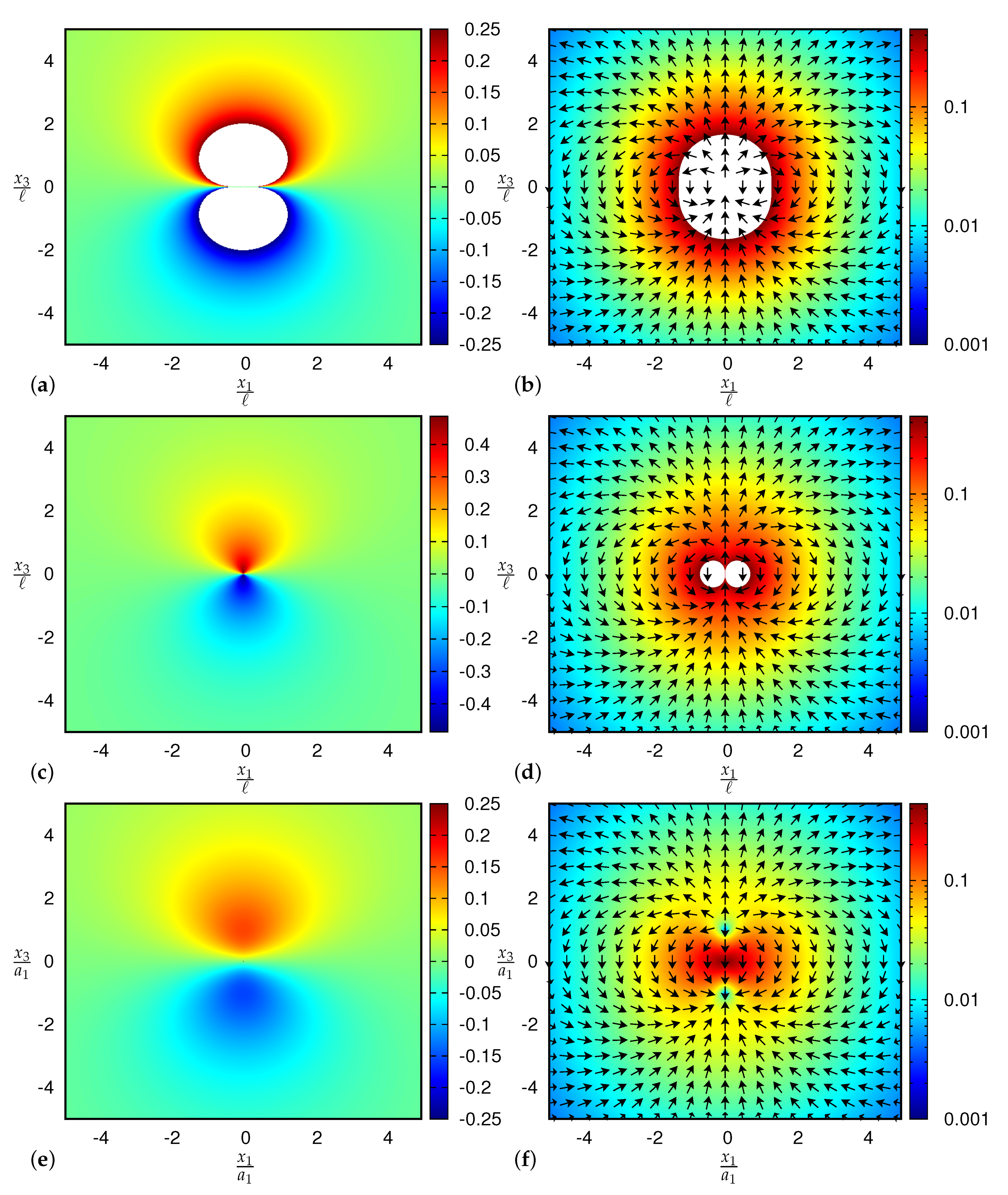
We have presented second gradient electromagnetostatics, which is the static version of second gradient electrodynamics, a generalization of Bopp–Podolsky electrodynamics, as a singularity-free field theory of electromagnetic fields, in particular, for an electrostatic point charge, an electrostatic dipole and a magnetostatic dipole. Through linear field equations of sixth order, second gradient electromagnetostatics yields an even stronger regularization than the Bopp–Podolsky theory: The field of a point charge is nonsingular and zero at the origin, the fields of electric and magnetic dipoles are nonsingular as well and dipoles have a finite self-energy, which diverges in the limit to Bopp–Podolsky electrodynamics (see
Table 1).
The regularization stems from the fact that the Green function of the bi-Helmholtz-Laplace operator appearing in second gradient electromagnetostatics and its first, second, and third gradients are singularity-free:
In every single problem studied, we were able to recover the Bopp–Podolsky results and the Maxwell results in the proper limits, when the length scale parameter (or ) goes to zero and the Bopp–Podolsky length scale parameter ℓ goes to zero, respectively.
We have also demonstrated that, much like in Bopp–Podolsky electrodynamics, the above results can be obtained through a special ansatz for extended charge distributions in classical electrostatics instead of an invariant generalized field theory. This is due to the structure of the Green function, a convolution of multiple Green functions to second-order operators, some of which can be attributed to a charge distribution in this interpretation.
Another interesting detail in second gradient electromagnetostatics is the existence of stable equilibria of three point charges. While in classical electrodynamics the maximum principle for the Poisson equation forbids such states (this is sometimes referred to as Earnshaw’s theorem), the higher-order generalized analogue to the Poisson equation has no maximum principle. The same is true for the fourth-order equation for the potential in Bopp–Podolsky electrostatics, although a stable configuration of point charges might be harder to construct there.
Finally, we conclude that the theory of second gradient electromagnetostatics provides a singularity-free, generalized continuum theory of electromagnetostatics with generalized Gauss law and generalized Ampère law valid down to short distances. The covariant form of second gradient electrodynamics and its meaning as a nonsingular relativistic field theory will be given in a forthcoming publication.