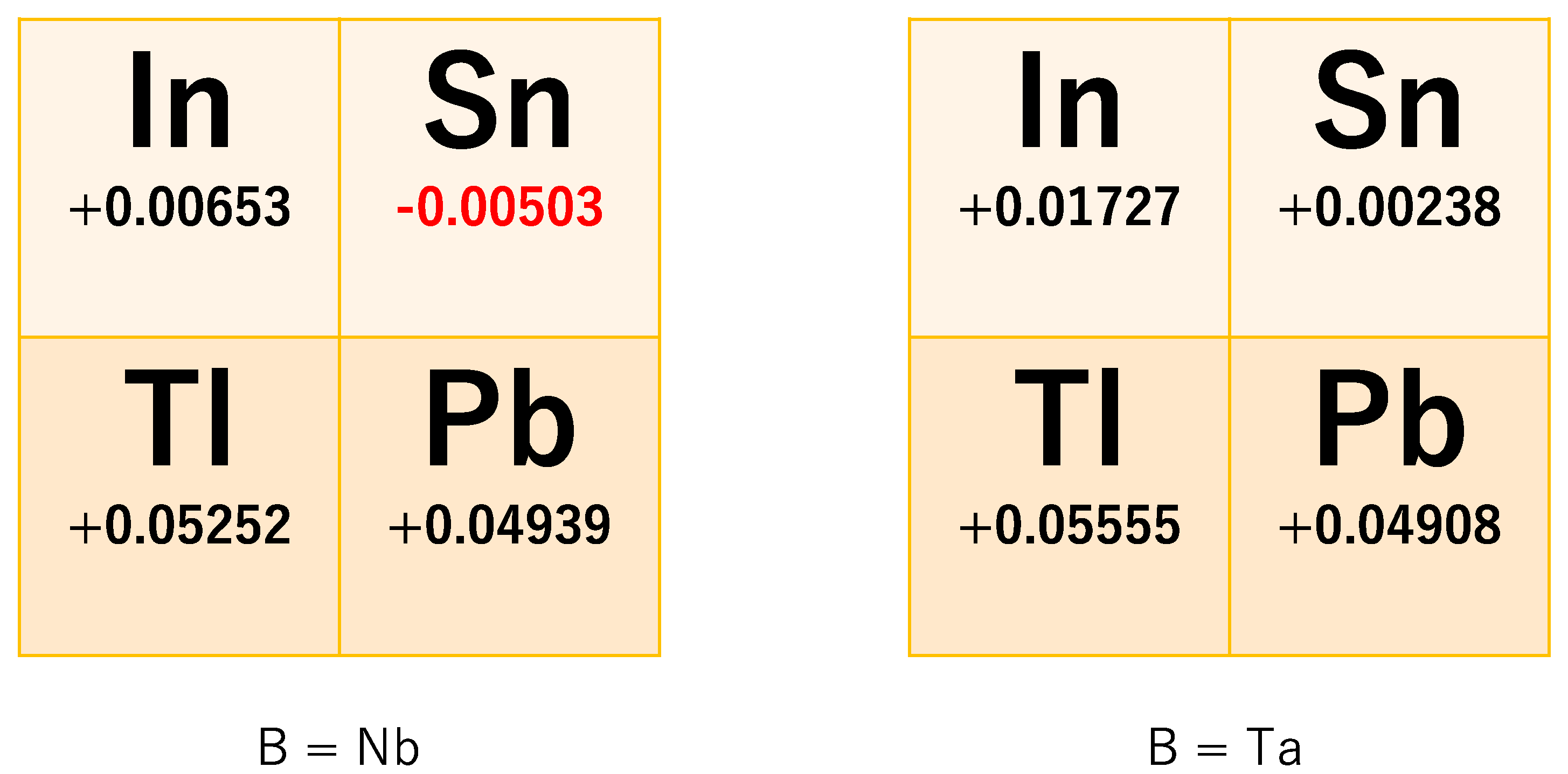1. Introduction
Topologically non-trivial states in materials have been paid much attention in the last decades. Among them, topological insulators (TIs) have attracted attention, not only from a basic but also from an application point of view. In TI, while the bulk is insulating, the surface has a metallic state. Since this surface state is robust against perturbations that do not violate the time reversal symmetry, it has been pointed out that it can be applied to a quantum computing device. Considering such applications, the material is desired to be three-dimensional and stable in the air, namely oxide. However, very little is known about oxides that are candidates for TI.
Outstanding works by Kane and Mele [
1,
2] have revealed that graphene may show a quantum spin Hall (QSH) effect if the spin–orbit coupling (SOC) is sufficiently strong. This effect can be explained as follows: Graphene has Dirac points that are protected by space–group symmetry, and this degeneracy is lifted by the SOC. This SOC opens a gap and makes the system a TI. A conventional (quantum) Hall effect is caused by an external magnetic field, while in this case the SOC plays the role of “magnetic field”, depending on the direction of the electron spin. Although the SOC in real graphene is too small to open a gap, subsequent works predicted that the HgTe–CdTe quantum well is a good candidate showing a QSH effect [
3]. This prediction has been subsequently verified experimentally [
4].
Later on, the Kane–Mele model [
1,
2] has been extended to other lattice models. Guo and Franz applied this model to a two-dimensional (2D) Kagome lattice [
5] and three-dimensional (3D) pyrochlore lattice [
6]. Both of these models are known to have a flat band (FB) that has no energy dispersion when only the nearest neighbor transfer is considered. Adding SOC with the type of Kane–Mele model, these lattice models show various topological properties.
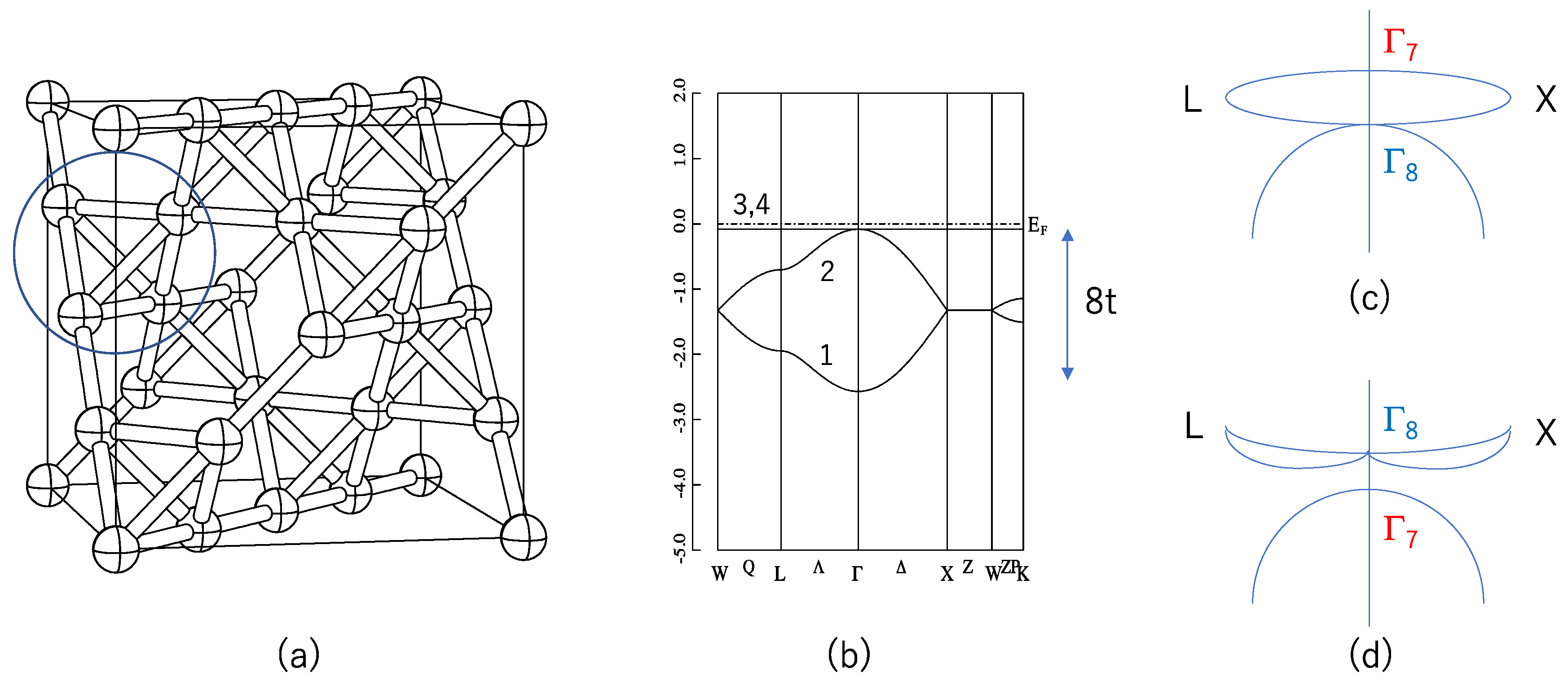
The Guo and Franz (GF) model can be described as follows [
6]:
where the first term of Equation (1) denotes the non-interacting tight-binding Hamiltonian, and <
ij> denotes the nearest neighbors. This lattice sum is taken on the pyrochlore lattice shown in
Figure 1a. This term can also be regarded as the Mielke model without an electron–electron interaction [
7,
8]. The second term denotes SOC with an effective coupling constant λ.
σαβ denotes the spin
αβ component of the Pauli matrices. In the pyrochlore lattice there are four sites in the primitive cell, and we obtain four bands. Here,
dij1,2 denote the nearest-neighbor vectors traversed between the second neighbor sites
i and
j. The summation <<
ij>> is taken for these second neighbor sites. In case of λ = 0, this Hamiltonian is rigorously diagonalized and the eigenvalues are
where
.
E3 and
E4 do not depend on the wave vector
k, so they are called flat bands (FBs). These energy eigenvalues are shown in
Figure 1b. Note that these FBs touch the dispersive band
at
k = 0. In other words, the state at
k = 0 is three-fold (six-fold if we consider spin) degenerated. Therefore, in case of half-filling, i.e., two of the four bands are filled, the system is a zero-gap semiconductor. FB itself induces many attractive physical properties [
7,
8,
9,
10], but in this paper we focus on the topological aspect of this model.
Next, we include SOC. This SOC lifts the abovementioned six-fold degeneracy into two-fold (Γ
7) and four-fold (Γ
8) degenerated states. Which of these states have higher energy depends on the sign of λ. A schematic picture is shown in
Figure 1c,d. When λ > 0, the energy of Γ
7 is higher than that of Γ
8, i.e.,
E(Γ
7) >
E(Γ
8). In this case, four-fold degenerated FBs split into Γ
7 and Γ
8 at the Γ point, but are still degenerated at the zone boundary points X and L. Therefore, the system remains gapless when λ > 0. On the contrary when λ < 0, the energy of Γ
7 is lower than that of Γ
8, i.e.,
E(Γ
7) <
E(Γ
8). In case of half-filling and λ < 0, the system has a band gap Δ = 24 |λ|. Guo and Franz [
6] have shown that this is a 3D strong TI having topological indices (1;000), where (ν
0;ν
1ν
2ν
3) denote the four-component
Z2 topological indices [
11,
12]. Each ν
i has a binary value 0 or 1, and if all ν
i are zero, i.e., (0;000), the system is an ordinary band insulator; if ν
0 = 1 it is a strong TI, which means topologically protected surface states exist on all surfaces and they are robust with regard to non-magnetic disorder.
It is very important to apply these results to real materials. In this sense, the GF model defined on the pyrochlore lattice is very attractive since the pyrochlore oxides A
2B
2O
7 include two independent pyrochlore sublattices [
13]. However, even though there are hundreds of pyrochlore oxides [
13], there are very few compounds whose electronic states near the Fermi level (
EF) can be approximated by the GF model. The reason for this is as follows: In the GF model, the transfer integral
t is isotropic, while in most of the pyrochlore oxides the relevant orbital is an anisotropic d- or f- orbital.
In previous papers [
14,
15,
16] we have shown that six pyrochlore oxides A
2B
2O
7 (A = Sn, Pb, Tl; B = Nb, Ta) have band structures that are well described in the GF model. In those papers, we mainly focused on the possible ferromagnetism induced by the quasi-FB. We have already shown [
14] that Sn
2Nb
2O
7 has
E(Γ
7) <
E(Γ
8), i.e., λ < 0. On the other hand, Sn
2Ta
2O
7 has λ > 0. It means that Sn
2Nb
2O
7 is a good candidate for a strong TI when the holes are sufficiently doped (Sn
2Nb
2O
7 itself is away from half-filling), but Sn
2Ta
2O
7 is not. After this work, Zhou et al. proposed a novel topological state for ferromagnetic Sn
2Nb
2O
7 induced by quasi-FB [
17], and Zhang et al. proposed that Tl
2Nb
2O
6+x (0 ≤ x ≤ 1) leads to various topological phases accompanied with lattice distortion [
18].
The purpose of this paper is to extend the above discussion to other pyrochlore oxides of which the band structure near EF is approximated by the GF model. We calculated the band structure of six pyrochlore oxides A2B2O7 (A = Sn, Pb, Tl; B = Nb, Ta) from first principles. Additionally, we calculated the band structure of three hypothetical compounds, In2Nb2O7, In2Ta2O7 and Sn2Zr2O7, which may be potential candidates for a TI. We found that only Sn2Nb2O7 and Sn2Zr2O7 gives λ < 0, though the band structure of Sn2Zr2O7 cannot fit very well with the GF model.
This paper is organized as follows.
Section 2 explains the method of calculation. The main results and discussions are shown in
Section 3. Conclusions are given in
Section 4.
2. Materials and Computational Methods
We calculated six pyrochlore oxides with the composition A
2B
2O
7 (A = Sn, Pb, Tl; B = Nb, Ta) from first principles. We used the density-functional theory (DFT) and a linearized augmented plane wave with the addition of a local orbital (LAPW+lo) scheme (WIEN2k code [
19]). The exchange-correlation potential was constructed within the general gradient approximation [
20]. The
k-point mesh was set so that the total number of the mesh was about 1000 in the first Brillouin zone. The parameter
RKmax, which is a product of the maximum radius of the muffin-tin spheres
R and the cut-off wave number of the plane-wave basis
Kmax, was set to be 7.0. For simplicity, we assumed that the calculated compounds all have an ideal A
2B
2O
6O’ pyrochlore structure with the space group Fd-3m (#227). Since oxygen atoms occupy two crystallographic sites, we named these sites as O and O’ to distinguish between them. The atomic positions are A(0, 0, 0), B(1/2, 1/2, 1/2), O(
u, 1/8, 1/8) and O’(1/8, 1/8, 1/8). This pyrochlore structure contains 88 atoms in the conventional cubic unit cell. In this work we focus on the A atoms, which form the pyrochlore lattice shown in
Figure 1a. O’ atoms are at the center of the A
4 tetrahedron shown by a circle in
Figure 1a. We optimized this parameter
u by minimizing the Hellmann–Feynman force
, where
H denotes the one-electron Hamiltonian for the atomic coordinates
R, and
is its eigenfunction. The convergence of the atomic positions was judged by this Hellmann–Feynman force working on each atom, which was to be less than 1.0 mRy/a.u. We also optimized the lattice constant
a for Tl
2Ta
2O
7. The optimized value
a = 10.716 Å well agreed with an experimental value
a = 10.56 Å [
21] or 10.651 Å [
22]. For the other five compounds, we used the experimental lattice constant.
After the relaxation of the atomic position and lattice constant, a spin–orbit interaction (SOI) is included via a second-variational step using a scalar-relativistic eigenfunction as the basis [
23,
24]. Hereafter, we distinguish between SOI and SOC. The former is essentially an on-site term, explicitly included in the band calculation [
19,
23,
24]. The latter is the term introduced in the Kane–Mele model [
1] and GF model [
6], which is essentially a non-local term. We can estimate the SOC from the band calculation by fitting the bands to the GF model, or more simply, just see the energy splitting at the Γ point Δ
SO =
E(Γ
7) –
E(Γ
8) and use the relation Δ
SO = 24 λ [
6].
In order to understand the electronic structure of this A
2B
2O
7 system, we also performed band calculations on the virtual compounds In
2Nb
2O
7, In
2Ta
2O
7 and Sn
2Zr
2O
7. For these compounds, we relaxed both of the lattice constant and the atomic positions. The obtained lattice constant is
a = 10.611, 10.631 and 10.618 Å for In
2Nb
2O
7, In
2Ta
2O
7 and Sn
2Zr
2O
7, respectively. They are all within the normal range of the lattice constants of pyrochlore oxides [
13].
3. Results and Discussions
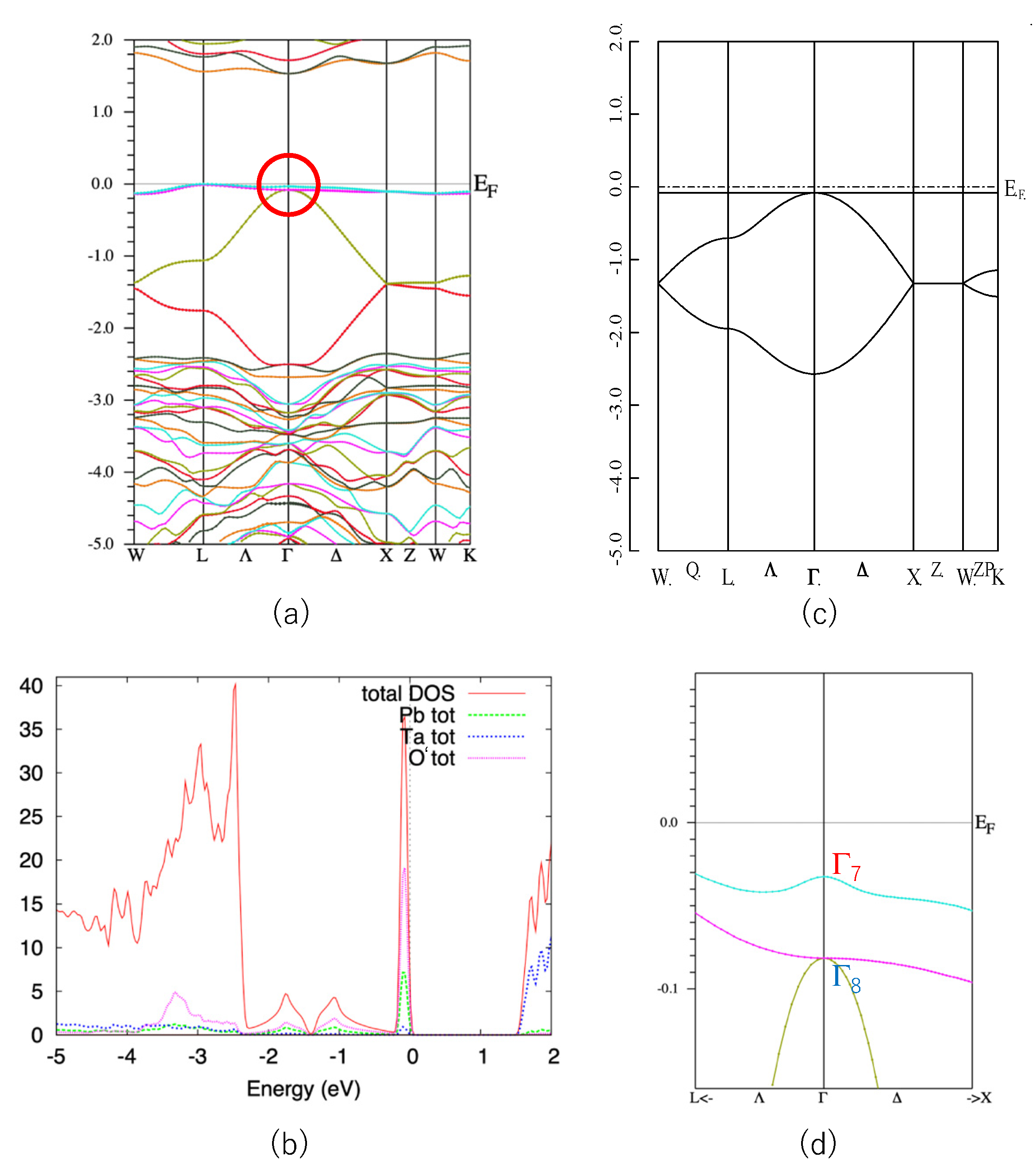
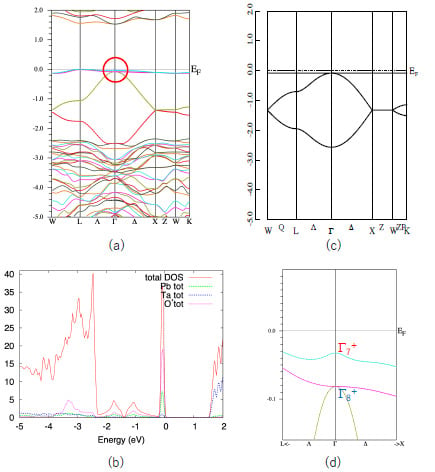
First, we show the band structure of Pb
2Ta
2O
7 in
Figure 2a. Similar to other quasi-FB oxides [
14,
15,
16,
17,
18], this compound also shows a characteristic quasi-FB just below
EF. The origin of this quasi-FB is explained as follows. The formal chemical valences of Pb
2Ta
2O
7 are denoted as Pb
2+2Ta
5+2O
2−7. Since Ta
5+ and O
2− form closed shells, we see that only Pb
2+ is chemically active in the first approximation. The electron configuration of Pb
2+ is (6s)
2, so we can expect that the band gap is opened between the Ta5d band and Pb6s band. This is verified by density-of-states (DOS) analysis shown in
Figure 2b. We see that the sharp peak coming from quasi-FB mainly consists of the Pb-s and O’-p components.
As is explained in
Section 1, a simple nearest-neighbor tight-binding model on a pyrochlore lattice gives a flat band as in Equation (2). We show the energy dispersion of this model in
Figure 2c. The agreement between the actual valence band of Pb
2Ta
2O
7 and the simple GF model is quite good, considering that the GF model includes only one parameter,
t (in
Figure 2c we set λ = 0). Since the s-orbital is isotropic, the hopping integral
t in Equation (1) is also isotropic. Note that in most of the pyrochlore oxides the relevant (frontier) orbitals are d- or f-orbitals, which are anisotropic. We can also show that the more precise 10-orbital model, including four Pb-s and 6 O’-p orbitals, also have a FB [
14]. However, we deal with the minimal 4-orbital model because we can utilize the results for the GF model.
Note that the top of the valence band of Pb2Ta2O7 is not a complete FB but a quasi-FB. This small dispersion (about 0.2 eV) is attributed to the hopping terms other than the nearest neighbor one, such as next-nearest-neighbor hopping. However, this small dispersion does not change the topology of the band structure and we can use the result for the GF model.
We can see that the quasi-FB in Pb
2Ta
2O
7 is slightly split due to the SOI. Other bands, e.g., the bands at energy ~1.5 eV, split more than the quasi-FB at the valence band. This is because the conduction band mostly consist of Ta5d orbitals in which the SOI is large. If the valence band purely consists of Pb6s orbitals, the SOI should be zero. Small splitting of the quasi-FB in Pb
2Ta
2O
7 is due to the hybridization of the other orbitals. In
Figure 2d we show a blow-up of the band structure of the Pb
2Ta
2O
7 near
EF (shown by a circle in
Figure 2a).
As shown in Reference [
6], the GF model in the half-filled case has a band gap at the Γ point when the SOC is switched on and λ < 0; in this case the system becomes a strong TI with
Z2 indices (1;000). On the other hand, it does not have a band gap when λ > 0. We see that
E(Γ
7) is larger than
E(Γ
8), i.e., λ > 0 in Pb
2Ta
2O
7. This situation corresponds to the case in
Figure 1c. Note that these
Z2 indices are purely topological ones and robust for the small perturbations. Therefore, we can expect that these indices are unchanged in the real compounds we calculated, unless there are extra band crossings. Above these reasons, we can investigate the topological properties of the A
2B
2O
7 compounds by calculating the energy difference Δ
SO =
E(Γ
7) −
E(Γ
8) at the Γ point (
k = 0).
Figure 3 shows the energy difference Δ
SO =
E(Γ
7) −
E(Γ
8) in eight pyrochlore oxides A
2B
2O
7 (A = In, Sn, Tl, Pb; B = Nb, Ta), including two virtual oxides, In
2Nb
2O
7 and In
2Ta
2O
7. Apparently, only Sn
2Nb
2O
7 has a band gap, and the other seven oxides do not have a band gap. This result shows that Sn
2Nb
2O
7 may become a strong TI when the chemical potential is put in this band gap by heavily doping the holes. At present, hole doping in Sn
2Nb
2O
7 has been successful [
25], but such a heavy doping is difficult. As for Sn
2Nb
2O
7, combining the topological band structure and the possible ferromagnetism due to quasi-FB, the existence of a novel three-dimensional Weyl point is suggested [
17].
As seen in
Figure 3, Δ
SO (or effective SOC coefficient λ = Δ
SO/24) is material-dependent, even in its sign. We can see some trends in this figure:
When A is the period-6 element of the periodic table, ΔSO is large, and when it is a period-5 element, ΔSO is small. The difference of ΔSO is about 40–50 meV.
When A is the group-13 element of the periodic table, ΔSO is large, and when it is a period-14 element, ΔSO is small. The difference of ΔSO is about 3–15 meV.
ΔSO does not so much depend on the B element. The difference of ΔSO is about −0.3–10 meV.
Among these three trends, the first one is most crucial. It suggests that element A should be period-5 like In or Sn for obtaining a small Δ
SO. In order to realize a TI in pyrochlore oxide, we should also tune the chemical potential. Half-filling of the 4-orbital GF model means that two of the four bands are occupied, i.e., there are four electrons in the primitive unit cell. Since there are four atomic sites, it turns so that the outermost electron configuration in the real compound is (5s)
1 or (6s)
1, which means there is one electron in the outermost s-orbital. We call this type of compound the “s1 compound”. This includes Tl
2Nb
2O
7 and so on. A famous mother compound of the high-
Tc superconductor BaBiO
3 is also an s1 compound [
26,
27,
28,
29], but Tl
2Nb
2O
7 has a quasi-FB due to the strong geometric frustration of the pyrochlore lattice. This strong frustration may prevent forming a charge-density wave, which is seen in BaBiO
3. On the contrary, a compound containing two electrons in the outermost s-orbital is called the “s2 compound”. As for realizing the TI, the s1 compound is desirable in order to realize the TI, though in general the s1 compound is not so stable.
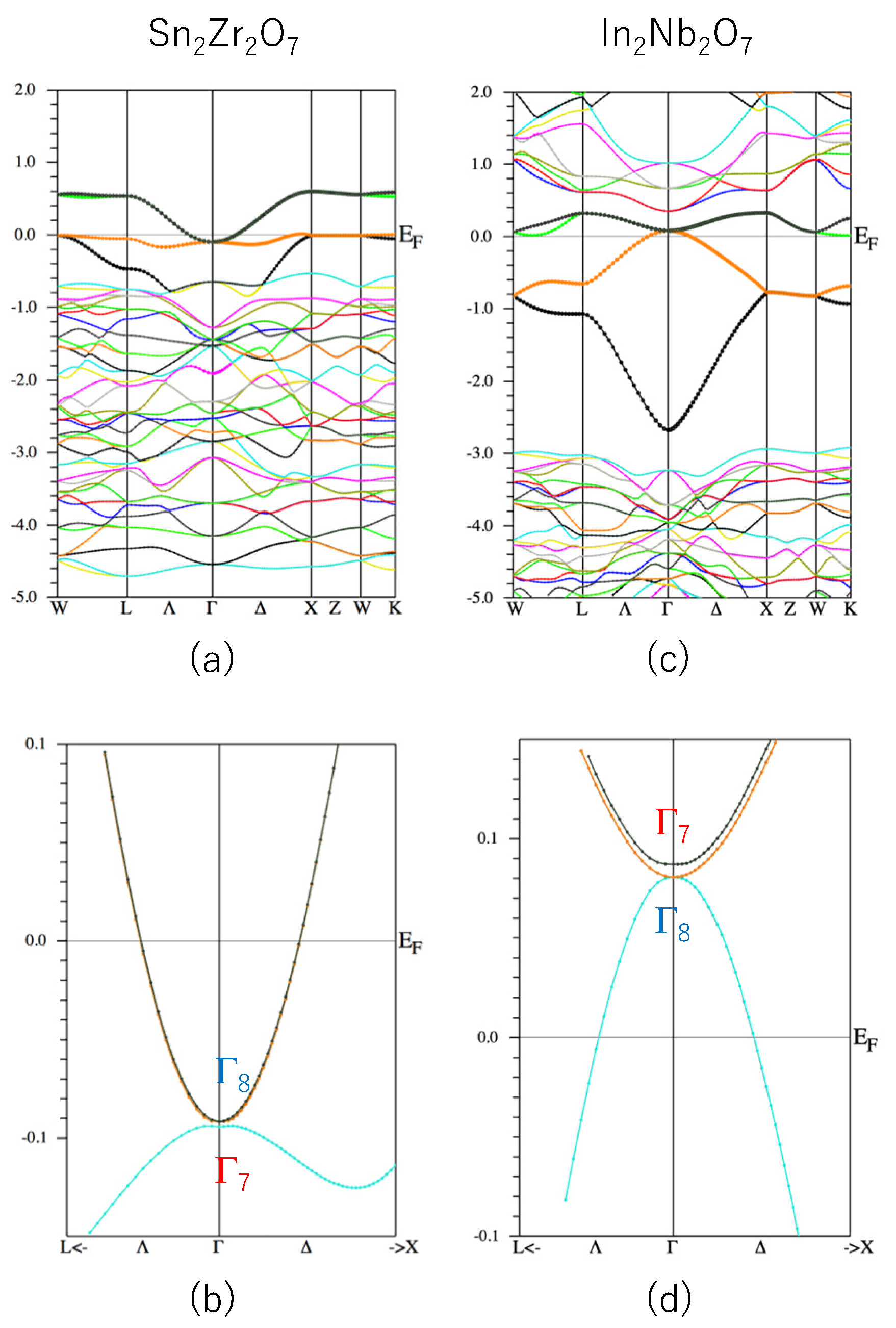
From the above discussion, we consider that a virtual compound Sn
2Zr
2O
7 may be a good candidate for a TI because it is formally described as Sn
3+2Zr
4+2O
2−7, having an s1 ion Sn
3+ and the other ions form a closed shell. This compound may also have small λ since it contains an Sn atom on the A site. The calculated band structure of the Sn
2Zr
2O
7 is shown in
Figure 4a,b. As is expected, we found Δ = 2.5 meV, which means there is a band gap at the Γ point. However, the valence band Sn
2Zr
2O
7 is apparently not described well by the GF model, as shown in
Figure 4a. The reason why Sn
2Zr
2O
7 has such a band structure is not clear, but we note that the band structure of the other pyrochlore oxides with a formal ionic valence A
3+2B
4+2O
2−7 (e.g., Bi
2Ti
2O
7) are not described well by the GF model (or non-interacting Mielke model) [
15].
On the other hand, another virtual compound, In
2Nb
2O
7, has a band structure like the GF model (see
Figure 4c), but λ > 0 (though not too large, see
Figure 3). Sn
2Zr
2O
7 has λ < 0 but the band structure is not like the GF model. Therefore, we propose that a co-doped system, (In,Sn)
2(Nb,Zr)
2O
7, may have both of the desired properties for a TI, namely, a GF-model-like band and λ < 0.
Finally, we comment on the possibility of lattice distortion in the pyrochlore oxides. For example, though in Sn
2Nb
2O
7 there is no experimental signature of lattice distortion from the cubic phase, Pb
2Nb
2O
7 suffers a lattice distortion in low temperature [
30]. Lattice distortion can greatly affect the topological properties. Zhang et al. have shown that Tl
2Nb
2O
7 can transform from a semi-metal to a TI by in-plane strain [
18]. Since the topological properties are not dependent on the detail of the band structure, it is highly possible that the TI is also induced by in-plane strain in Tl
2Ta
2O
7, In
2Nb
2O
7 and In
2Ta
2O
7, which have similar band structures.