Intuitionistic Fuzzy Three-Way Decision Model Based on the Three-Way Granular Computing Method
Abstract
1. Introduction
- (1)
- The concepts of membership state possibility and non-membership state possibility are defined, and their related properties are proved. Then, according to the relationship between the state probability distribution and the probability distribution, we give an approximate division rule for the object information granularity.
- (2)
- By combining object information granules and dominance relation, we propose superiority-compatibility relation and inferiority-compatibility relation. Furthermore, we deduced the IFTWD model on the basis of the superiority-compatibility class and inferiority-compatibility class.
- (3)
- To objectively evaluate the decision-making results and analyze the potential symmetrical relationship between decision costs, we define the concepts of advantage cost and disadvantage cost, and create a secondary decision strategy for boundary domain objects.
2. Preliminaries
2.1. Pawlak Rough Set
2.2. Three-Way Decision
2.3. Intuitionistic Fuzzy Set and Dominance Relation
- (1).
- (2).
- (3).
- (4).
- (5).
- (1).
- , .
- (2).
- .
3. IFTWD Derived from the Three-Way Granular Computing Method
3.1. State Possibility and Information Granularity
- (1)
- Satisfy the weak and strong conditions of (M4) and (M5). Specifically, there is always a possibility that (1,0) satisfies the enhanced membership state and (0,1) satisfies the weakened non-membership state.
- (2)
- The following two state values need special consideration to make the calculation results meaningful.Case 1: when the state value is (1,0), we only need to consider the membership state possibility.Case 2: when the state value is (0,1), we only need to consider the non-membership state possibility.
- (3)
- When the state value is , the conversion of hesitation degree is completely uncertain. Relative to the determined membership and non-membership degrees, the intuitionistic fuzzy index is caused by the existence of a variety of unknown information. For the sake of analysis, it is assumed that these unknown factors are independent. According to the central limit theorem, these independent unknown factors obey the Gaussian distribution (hypothetical standard Gaussian distribution), and then the transformation degree of the intuitionistic fuzzy index can be expressed as follows:
- (1).
- If and , then .
- (2).
- If and , or and , then .
- (3).
- If and , then .
| Algorithm 1 Granularity classification of objects in the universe of discourse |
| 1: Input , , , 2: Initialization (1) parameters: , 3: functions: (1) 4: (2) 5: (3) 6: Output Granularity category of each object. 7: BEGIN 8: for Calculate the possibility of membership status and non-membership status do 9: , 10: if then 11: . // maximum hesitation probability state value 12: end if 13: end for 14: for Calculate the information granularity of each object do 15: // Get the hesitation factor impact 16: then // Get the granularity value 17: while Calculate the relationship between the granularity value and do 18: , 19: if then 20: Object is Fine-grained: // satisfies both and 21: if then 22: Object is Medium-grained: // satisfies either or 23: else 24: Object is Coarse-grained: // satisfies neither nor 25: end if 26: end if 27: end while 28: end for 29: END BEGIN |
3.2. Superiority-Compatibility Relation and Decision Evaluation
- (1) .
- Ifare superiority-compatibility classes on, thenmakeshold, whererepresents the largest superiority-compatibility classes.
- (2) .
- Ifare inferiority-compatibility classes on, then makeshold, whererepresents the largest inferiority-compatibility classes.
- (1).
- , .
- (2).
- , .
- (3).
- , .
- (4).
- , .
- (5).
- .
| Algorithm 2 Intuitionistic fuzzy three-way decision model based on three-way granular computing method |
| 1: Input (1) , , 2: (2) granular information: ,, 3: Initialization relations: (1) 4: 5: parameters: , 6: Output (1) three-way decision result: POS, NEG and BND (2) secondary decision result 7: BEGIN 8: for Calculate the advantages-compatible and disadvantage-compatible classes of each object do 9: , 10: then Calculate the dominance cost and disadvantages cost of each object do 11: , , 12: end for 13: for Get the advantages and disadvantages degree of each object do 14: , 15: do // Object in the boundary domain 16: if then 17: // having the maximum superiority degree 18: if then 19: // having the maximum inferiority degree 20: end if 21: end if 22: while // Executed if the number of BND elements is smaller than one. 23: if then 24: // case of 25: else 26: 27: end if 28: end for 29: END BEGIN |
4. An Illustrative Example
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Liu, K.Y.; Yang, X.B.; Yu, H.L.; Mi, J.S.; Wang, P.X.; Chen, X.J. Rough set based semi-supervised feature selection via ensemble selector. Knowl. Based Syst. 2019, 165, 282–296. [Google Scholar] [CrossRef]
- Jia, X.Y.; Li, W.W.; Shang, L. A multiphase cost-sensitive learning method based on the multiclass three-way decision-theoretic rough set model. Inf. Sci. 2019, 485, 248–262. [Google Scholar] [CrossRef]
- Greco, G.; Jipsen, P.; Manoorkar, K.; Palmigiano, A.; Tzimoulis, A. Logics for Rough Concept Analysis; ICLA 2019, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2019; pp. 144–159. [Google Scholar]
- Shao, M.W.; Guo, L.; Wang, C.Z. Connections between two-universe rough sets and formal concepts. Int. J. Mach. Learn. Cybern. 2018, 9, 1869–1877. [Google Scholar] [CrossRef]
- Wang, F.G.; Wang, N.B.; Cai, S.B.; Zhang, W.L. A similarity measure in formal concept analysis containing general semantic information and domain information. IEEE Access. 2020, 8, 75303–75312. [Google Scholar] [CrossRef]
- Yang, J.; Wang, G.Y.; Zhang, Q.H. Knowledge Distance Measure for the Multi-granularity Rough Approximations of a Fuzzy Concept. IEEE Trans. Fuzzy Syst. 2020, 28, 706–717. [Google Scholar] [CrossRef]
- Santra, D.; Basu, S.K.; Mandal, J.K.; Goswami, S. Rough set based lattice structure for knowledge representation in medical expert systems: Low back pain management case study. Expert Syst. Appl. 2020, 145, 113084. [Google Scholar] [CrossRef]
- Luqman, A.; Akram, M.; Koam, A.N.A. An m-Polar fuzzy hypergraph model of granular computing. Symmetry 2019, 11, 483. [Google Scholar] [CrossRef]
- Singh, P.; Huang, Y.P. A four-way decision-making approach using interval-valued fuzzy sets, rough set and granular computing: A new approach in data classification and decision-making. Granul. Comput. 2019, 1–13. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets: Theoretical Aspects of Resoning about Data; Kluwer Academic: Boston, MA, USA, 1991. [Google Scholar]
- Zhan, J.M.; Sun, B.Z.; Alcantud, J.C.R. Covering based multigranulation (I,T)-fuzzy rough set models and applications in multi-attribute group decision-making. Inf. Sci. 2019, 476, 290–318. [Google Scholar] [CrossRef]
- Yao, Y.Y.; Wong, S.K.M.; Lingras, P. A Decisions-Theoretic Rough Set Model. In 5th International Symposium of Methodologies for Intelligent Systems Held 25–27 October; North-Holland: New York, NY, USA, 1990; pp. 17–25. [Google Scholar]
- Li, M.M.; Chen, M.H.; Xu, W.H. Double-quantitative multigranulation decision-theoretic rough fuzzy set model. Int. J. Mach. Learn. Cybern. 2019, 10, 3225–3244. [Google Scholar] [CrossRef]
- Yu, J.H.; Li, Y.Q.; Chen, M.H.; Zhang, B.; Xu, W.H. Decision-theoretic rough set in lattice-valued decision information system. J. Intell. Fuzzy Syst. 2019, 36, 3289–3301. [Google Scholar] [CrossRef]
- Diker, M. Textures and fuzzy unit operations in rough set theory: An approach to fuzzy rough set models. Fuzzy Sets Syst. 2018, 336, 27–53. [Google Scholar] [CrossRef]
- Yao, Y.Y. Three-Way Decision: An Interpretation of Rules in Rough Set Theory. In Proceedings of the 4th International Conference on Rough Sets and Knowledge Technology, Gold Coast, Australia, 14–16 July 2009; pp. 642–649. [Google Scholar]
- Yao, Y.Y. Three-way decisions with probabilistic rough sets. Inf. Sci. 2010, 180, 341–353. [Google Scholar] [CrossRef]
- Yao, Y.Y. An Outline of a Theory of Three-Way Decisions. In Proceedings of the International Conference on Rough Sets and Current Trends in Computing, Chengdu, China, 17–20 August 2012; Volume 7413, pp. 1–17. [Google Scholar]
- Zhai, J.H.; Zhang, S.F. Three-way decisions model based on rough fuzzy set. J. Intell. Fuzzy Syst. 2018, 34, 2051–2059. [Google Scholar] [CrossRef]
- Zhao, X.R.; Hu, B.Q. Three-way decisions with decision-theoretic rough sets in multiset-valued information tables. Inf. Sci. 2020, 507, 684–699. [Google Scholar] [CrossRef]
- Yang, X.P.; Tan, A.H. Three-Way Decisions Based on Intuitionistic Fuzzy Sets. In Proceedings of the International Joint Conference on Rough Sets, Olsztyn, Poland, 3–7 July 2017; Springer: Cham, Switzerland, 2017; pp. 290–299. [Google Scholar]
- Liang, D.C.; Xu, Z.S.; Liu, D. Three-way decisions based on decision-theoretic rough sets with dual hesitant fuzzy information. Inf. Sci. 2017, 396, 127–143. [Google Scholar] [CrossRef]
- Liang, D.C.; Xu, Z.S.; Liu, D. Three-way decisions with intuitionistic fuzzy decision-theoretic rough sets based on point operators. Inf. Sci. 2017, 375, 183–201. [Google Scholar] [CrossRef]
- Gao, Y.; Li, D.S.; Zhong, H. A novel target threat assessment method based on three-way decisions under intuitionistic fuzzy multi-attribute decision making environment. Eng. Appl. Artif. Intell. 2020, 87, 103276. [Google Scholar] [CrossRef]
- Yang, X.P.; Li, T.J.; Tan, A.H. Three-way decisions in fuzzy incomplete information systems. Int. J. Mach. Learn. Cybern. 2020, 11, 664–674. [Google Scholar] [CrossRef]
- Liu, D.; Liang, D.C.; Wang, C.C. A novel three-way decision model based on incomplete information system. Knowl. Based Syst. 2016, 91, 32–45. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Yang, S.Y.; Ma, J.M. Ranking interval sets based on inclusion measures and applications to three-way decisions. Knowl. Based Syst. 2016, 91, 62–70. [Google Scholar] [CrossRef]
- Wang, T.X.; Li, H.X.; Zhang, L.B.; Zhou, X.Z.; Huang, B. A Three-Way Decision Model Based on Cumulative Prospect Theory. Inf. Sci. 2020, 519, 74–92. [Google Scholar] [CrossRef]
- Yang, X.; Li, T.R.; Fujita, H.; Liu, D. A sequential three-way approach to multi-class decision. Int. J. Approx. Reason. 2019, 104, 108–125. [Google Scholar] [CrossRef]
- Qi, J.J.; Wei, L.; Yao, Y.Y. Three-Way Formal Concept Analysis. In Proceedings of the International Conference on Rough Sets and Knowledge Technology, Shanghai, China, 24–26 October 2014; Spring: Berlin/Heidelberg, Germany, 2014; pp. 732–741. [Google Scholar]
- Yu, H.Y.; Li, Q.G.; Cai, M.J. Characteristics of three-way concept lattices and three-way rough concept lattices. Knowl. Based Syst. 2018, 146, 181–189. [Google Scholar] [CrossRef]
- Yu, H.; Wang, X.C.; Wang, G.Y.; Zeng, X.H. An active three-way clustering method via low-rank matrices for multi-view data. Inf. Sci. 2020, 507, 823–839. [Google Scholar] [CrossRef]
- Wang, P.X.; Yao, Y.Y. CE3: A three-way clustering method based on mathematical morphology. Knowl. Based Syst. 2018, 155, 54–65. [Google Scholar] [CrossRef]
- Xu, J.F.; Zhang, Y.J.; Miao, D.Q. Three-way confusion matrix for classification: A measure driven view. Inf. Sci. 2020, 507, 772–794. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Miao, D.Q.; Wang, J.Q.; Zhang, Z.F. A cost-sensitive three-way combination technique for ensemble learning in sentiment classification. Int. J. Approx. Reason. 2019, 105, 85–97. [Google Scholar] [CrossRef]
- Ma, X.A.; Zhao, X.R. Cost-sensitive three-way class-specific attribute reduction. Int. J. Approx. Reason. 2019, 105, 153–174. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yang, J.L.; Tang, L.Y. Three-way class-specific attribute reducts from the information viewpoint. Inf. Sci. 2020, 507, 840–872. [Google Scholar] [CrossRef]
- Fang, Y.; Min, F. Cost-sensitive approximate attribute reduction with three-way decisions. Int. J. Approx. Reason. 2019, 104, 148–165. [Google Scholar] [CrossRef]
- Liang, D.C.; Wang, M.W.; Xu, Z.S.; Liu, D. Risk appetite dual hesitant fuzzy three-way decisions with TODIM. Inf. Sci. 2020, 507, 585–605. [Google Scholar] [CrossRef]
- Xue, Z.A.; Xin, X.W.; Yuan, Y.L.; Xue, T.Y. Intuitionistic fuzzy possibility measure-based three-way decisions for incomplete data. J. Intell. Fuzzy Syst. 2018, 35, 5657–5666. [Google Scholar] [CrossRef]
- Yao, Y.Y. Three-way conflict analysis: Reformulations and extensions of the Pawlak model. Knowl. Based Syst. 2019, 180, 26–37. [Google Scholar] [CrossRef]
- Sun, B.Z.; Chen, X.T.; Zhang, L.Y.; Ma, W.M. Three-way decision making approach to conflict analysis and resolution using probabilistic rough set over two universes. Inf. Sci. 2020, 507, 809–822. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 90, 111–127. [Google Scholar] [CrossRef]
- Yao, Y.Y. A Unied Framework of Granular Computing. Handbook of Granular Computing; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 401–410. [Google Scholar]
- Yao, Y.Y. A triarchic theory of granular computing. Granul. Comput. 2016, 1, 145–157. [Google Scholar] [CrossRef]
- Leng, J.W.; Chen, Q.X.; Mao, N.; Jiang, P.Y. Combining granular computing technique with deep learning for service planning under social manufacturing contexts. Knowl. Based Syst. 2018, 143, 295–306. [Google Scholar] [CrossRef]
- Loia, V.; Orciuoli, F.; Pedrycz, W. Towards a granular computing approach based on formal concept analysis for discovering periodicities in data. Knowl. Based Syst. 2018, 146, 1–11. [Google Scholar] [CrossRef]
- Lu, W.; Zhou, W.; Shan, D.; Zhang, L.Y.; Yang, J.H.; Liu, X.D. The linguistic modeling of interval-valued time series: A perspective of granular computing. Inf. Sci. 2019, 478, 476–498. [Google Scholar] [CrossRef]
- Fang, Y.; Gao, C.; Yao, Y.Y. Granularity-driven sequential three-way decisions: A cost-sensitive approach to classification. Inf. Sci. 2020, 507, 644–664. [Google Scholar] [CrossRef]
- Yao, Y.Y. Three-way decision and granular computing. Int. J. Approx. Reason. 2018, 103, 107–123. [Google Scholar] [CrossRef]
- Yao, Y.Y. Three-way granular computing, rough sets, and formal concept analysis. Int. J. Approx. Reason. 2020, 116, 106–125. [Google Scholar] [CrossRef]
- Yao, Y.Y. Tri-level thinking: Models of three-way decision. Int. J. Mach. Learn. Cybern. 2019, 1–13. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Greco, S.; Matarazzo, B.; Slowinski, R. Rough approximation by dominance relations. Int. J. Intell. Syst. 2002, 17, 153–171. [Google Scholar] [CrossRef]
- Liu, J.B.; Zhou, X.Z.; Huang, B.; Li, H.X. A Three-Way Decision Model Based on Intuitionistic Fuzzy Decision Systems. In Proceedings of the International Joint Conference on Rough Sets, Olsztyn, Poland, 3–7 July 2017; Springer: Cham, Switzerland, 2017; pp. 249–263. [Google Scholar]
- Xu, Z.S.; Yager, R.R. Dynamic intuitionistic fuzzy multi-attribute decision making. Int. J. Approx. Reason. 2008, 48, 246–262. [Google Scholar] [CrossRef]
- Liang, D.C.; Liu, D. Deriving three-way decisions from intuitionistic fuzzy decision-theoretic rough sets. Inf. Sci. 2015, 300, 28–48. [Google Scholar] [CrossRef]
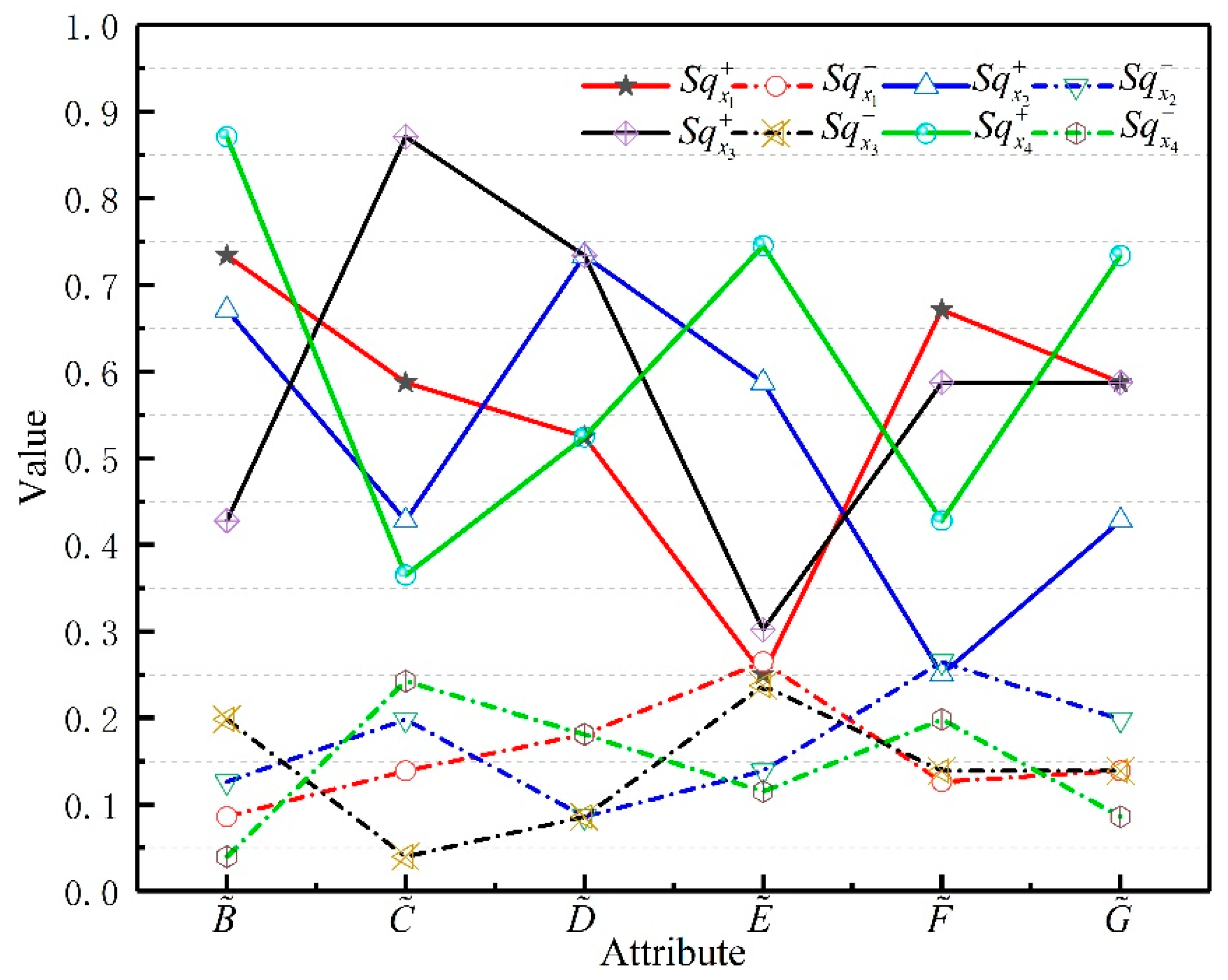
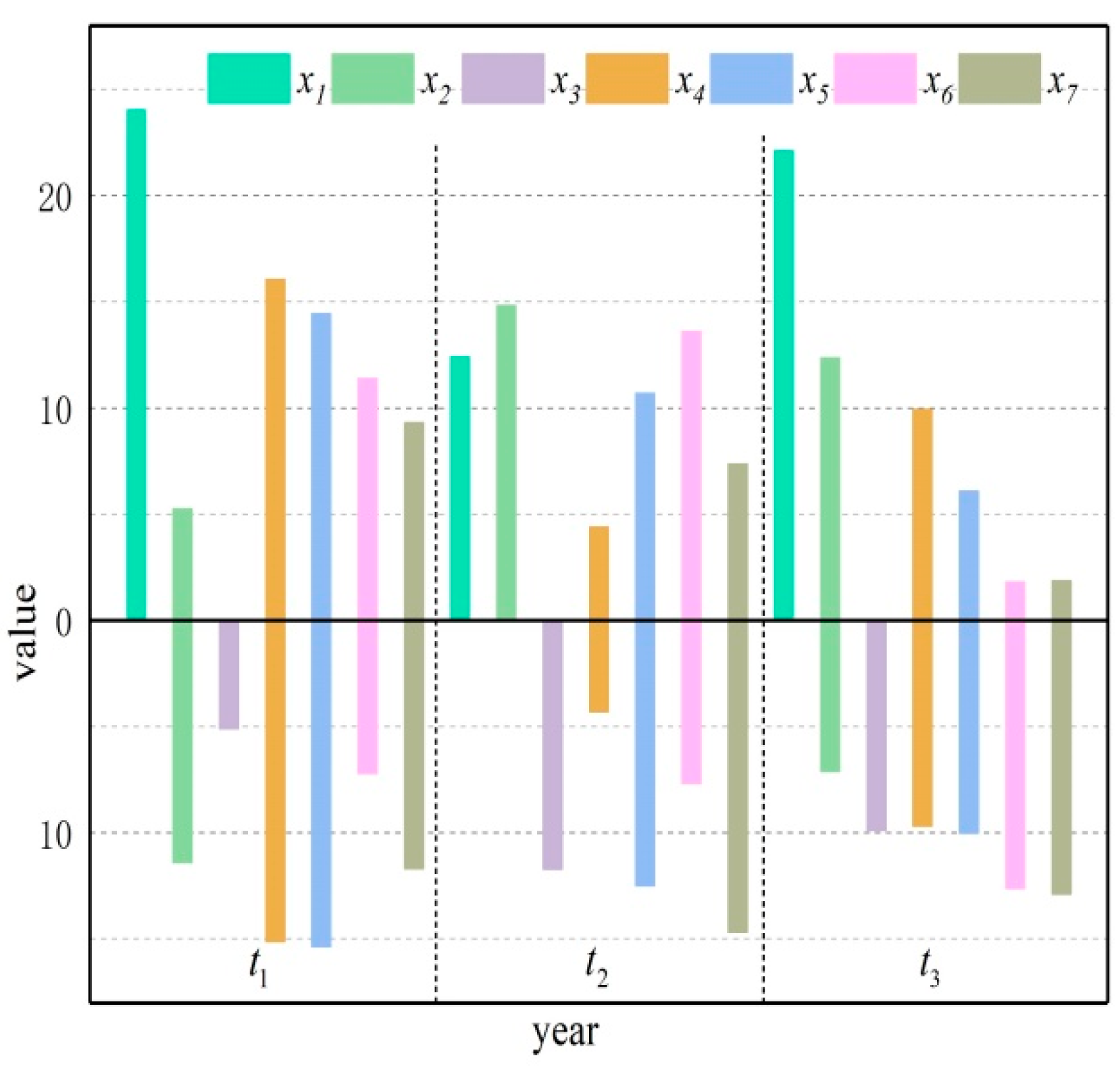

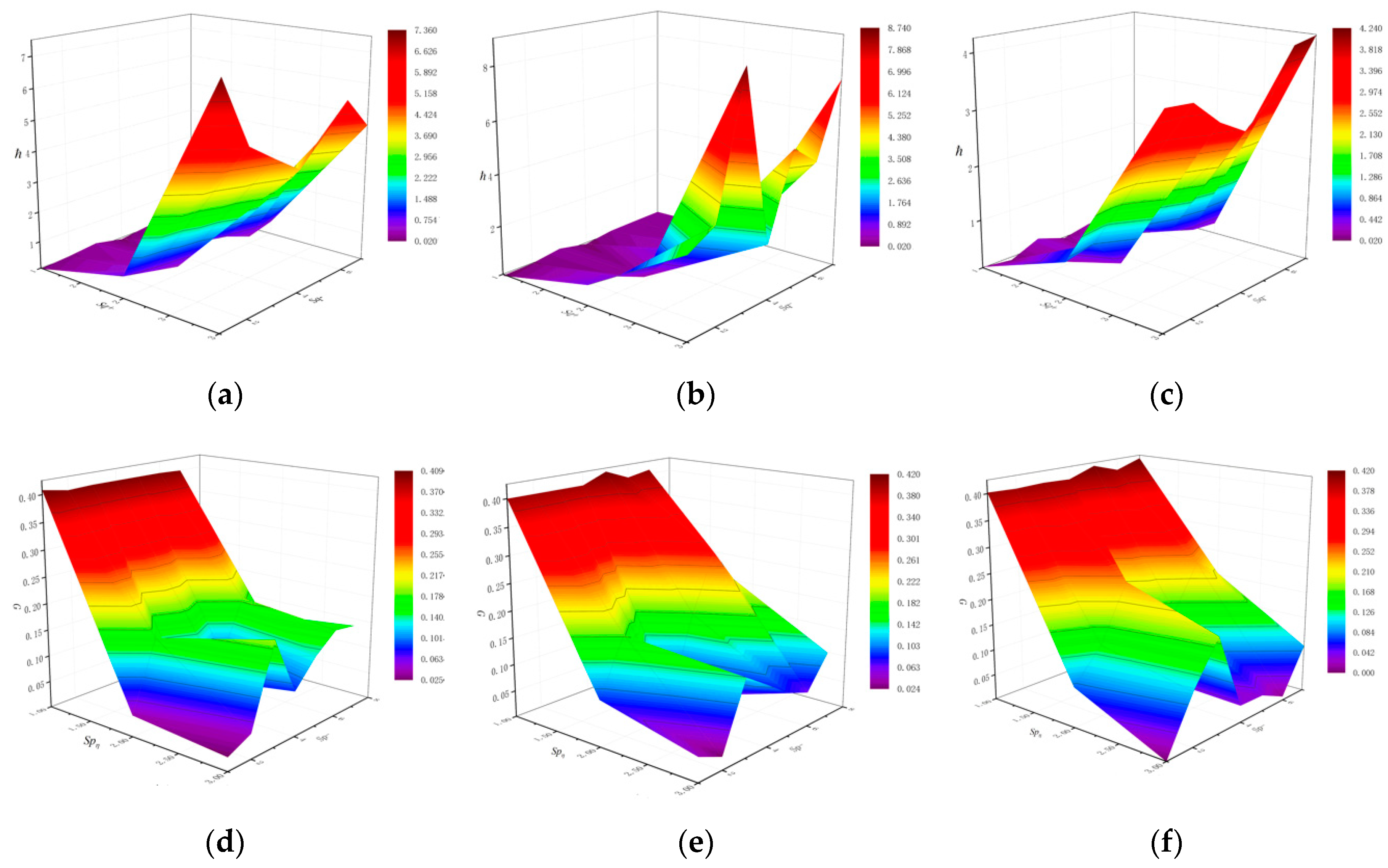
| Action | Cost Function | |
|---|---|---|
| (0.8, 0.2) | (0.7, 0.3) | (0.6, 0.3) | (0.5, 0.5) | (0.7, 0.2) | (0.7, 0.3) | |
| (0.7, 0.2) | (0.6, 0.4) | (0.8, 0.2) | (0.7, 0.3) | (0.5, 0.5) | (0.6, 0.4) | |
| (0.6, 0.4) | (0.9, 0.1) | (0.8, 0.2) | (0.4, 0.6) | (0.7, 0.3) | (0.7, 0.3) | |
| (0.9, 0.1) | (0.4, 0.2) | (0.6, 0.3) | (0.7, 0.1) | (0.6, 0.4) | (0.8, 0.2) |
| Comparison and Classification of Values | Probability Distributions | |
|---|---|---|
| Fine-grained: | O | O |
| Medium-grained: | O() | (O) |
| Coarse-grained: |
| 0.86 | 0.27 | 0.24 | 0.52 | 0.16 | ||
| 0.86 | 0.27 | 0.27 | 0.48 | 0.13 | ||
| 0.92 | 0.14 | 0.27 | 0.62 | 0.13 | ||
| 0.92 | 0.14 | 0.22 | 0.67 | 0.18 |
| Classification | |||||
|---|---|---|---|---|---|
| P | Classification | ||||
|---|---|---|---|---|---|
| 0.07 | POS | ||||
| 0.15 | BND | ||||
| 0.2 | NEG | ||||
| 0.08 | BND | ||||
| 0.1 | BND | ||||
| 0.15 | BND | ||||
| 0.25 | BND |
| Classification | |||||
|---|---|---|---|---|---|
| 0.08 | POS | ||||
| 0.09 | POS | ||||
| 0.14 | NEG | ||||
| 0.11 | BND | ||||
| 0.16 | BND | ||||
| 0.22 | BND | ||||
| 0.20 | BND |
| Classification | |||||
|---|---|---|---|---|---|
| 0.06 | POS | ||||
| 0.08 | BND | ||||
| 0.17 | NEG | ||||
| 0.09 | BND | ||||
| 0.14 | BND | ||||
| 0.24 | BND | ||||
| 0.22 | BND |
| Initialization | First Cycle | Second Cycle | Final Result | |
|---|---|---|---|---|
| POS | ||||
| BND | ||||
| NEG |
| Initialization | First Cycle | Second Cycle | Final Result | |
|---|---|---|---|---|
| POS | ||||
| BND | ||||
| NEG |
| Initialization | First Cycle | Second Cycle | Final Result | |
|---|---|---|---|---|
| POS | ||||
| BND | ||||
| NEG |
| Region | |||||||
|---|---|---|---|---|---|---|---|
| Decision | POS | POS | NEG | POS | NEG | NEG | NEG |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, X.; Song, J.; Peng, W. Intuitionistic Fuzzy Three-Way Decision Model Based on the Three-Way Granular Computing Method. Symmetry 2020, 12, 1068. https://doi.org/10.3390/sym12071068
Xin X, Song J, Peng W. Intuitionistic Fuzzy Three-Way Decision Model Based on the Three-Way Granular Computing Method. Symmetry. 2020; 12(7):1068. https://doi.org/10.3390/sym12071068
Chicago/Turabian StyleXin, Xianwei, Jihua Song, and Weiming Peng. 2020. "Intuitionistic Fuzzy Three-Way Decision Model Based on the Three-Way Granular Computing Method" Symmetry 12, no. 7: 1068. https://doi.org/10.3390/sym12071068
APA StyleXin, X., Song, J., & Peng, W. (2020). Intuitionistic Fuzzy Three-Way Decision Model Based on the Three-Way Granular Computing Method. Symmetry, 12(7), 1068. https://doi.org/10.3390/sym12071068




