ECCPoW: Error-Correction Code based Proof-of-Work for ASIC Resistance

Abstract

Bitcoin is the first cryptocurrency to participate in a network and receive compensation for online remittance and mining without any intervention from a third party, such as financial institutions. Bitcoin mining is done through proof of work (PoW). Given its characteristics, the higher hash rate results in a higher probability of mining, leading to the emergence of a mining pool, called a mining organization. Unlike central processing units or graphics processing units, high-cost application-specific integrated circuit miners have emerged with performance efficiency. The problem is that the obtained hash rate exposes Bitcoin’s mining monopoly and causes the risk of a double-payment attack. To solve this problem, we propose the error-correction code PoW (ECCPoW), combining the low-density parity-check decoder and hash function. The ECCPoW contributes to the phenomenon of symmetry in the proof of work (PoW) blockchain. This paper proposes the implementation of ECCPoW, replacing the PoW in Bitcoin. Finally, we compare the mining centralization, security, and scalability of ECCPoW and Bitcoin.

1. Introduction

We use digital signatures from third-party trust agencies to promote trust in Internet commerce. We warrant proof of data forgery using middlemen. Satoshi Nakamoto proposed an electronic money system without a middleman in a peer-to-peer (P2P) network through a Bitcoin white paper [1]. Bitcoin applies blockchain technology to electronic monetary systems to guarantee transactions without intermediaries (e.g., banks). Blockchain is a ledger management technology based on a distributed computing technology that cannot be arbitrarily modified by storing the transaction content in a chain-based distributed data storage environment in the form of a block [2,3].

The blockchain stores the same ledger on a global network and is designed to pay certain rewards to maintain the block. This is called mining, and mining creates blocks and obtains cryptocurrency by executing a hash function. Miners belong to mining pools because of the probability and convenience of being rewarded for mining cryptocurrency [4,5].

The hash rate is the number of hash values calculated per second as a measure of computational processing power for mining cryptocurrency. The hash rate of cryptocurrency is determined by the total number of the participating nodes. Most miners belong to a hash pool and occupy a high percentage of the hash rate. We should be concerned about the risk of a double-payment attack if the mining pool in the blockchain accounts for a high percentage of the total hash rate of cryptocurrency [6]. A double-payment attack occurs when the mining pool seizes at least 51% of the total hash rate to determine the branch of the blockchain to the desired side. Recent studies have shown that a double-payment attack can be made to benefit from a low share of the hash rate [7].

Bitcoin miners receive blockchain information (version, previous block hash, Merkle root, bits, and others) and execute hash functions (e.g., the secure hash algorithm (SHA 256). Miners create a block if the output value of the hash function is less than the target level of difficulty. Currently, Bitcoin requires an increasingly high operation to create blocks. Miners purchase application-specific integrated circuits (ASICs) with high per-second computing power to mine Bitcoin and join the mining pool. Low-power miners using central or graphics processing units (CPUs or GPUs) have difficulty mining.

Bitcoin uses the number of zeros in the front digits of the output from the SHA 256 function to generate blocks. The mining difficulty increases with the number of zeros. Miners buy ASICs to compute SHA functions quickly. The mining machine Antminer S9 (13,000 MH/s) is approximately 8800 times faster than GTX1060 (1478 MH/s). The recently released S19 has a speed of 95 TH/s, and S19Pro exhibits performance of 110 TH/s [8]. Miners using CPUs or GPUs in Bitcoin, and miners using ASIC chips do not have equal chances for success because ASIC miners have an 8800-fold greater chance of success in mining.

Blockchain was proposed to allow nodes to participate as miners freely and to share mining rewards fairly. Blockchain is not free to participate in as a miner. The participating miners compete against equity. Several methods have been proposed to curb the development of ASIC miners, but in the end, these methods have not prevented ASIC development. As a new mining function to prevent the development of ASIC miners, we proposed the error-correction code proof of work (ECCPoW) concept, which combines the low-density parity-check (LDPC) decoder and hash function [9]. In addition, we analyzed the hash cycle of ECCPoW and demonstrated that it could be used for blockchain mining.

This paper contributes to the phenomenon of symmetry in the proof of work (PoW) blockchain. The PoW blockchain tends to increase the hash rate along with the total size of the blockchain. The size of the hash rate is related to the computing power required by block generation. Some people take issue with the large amount of wasted power used to create the PoW blockchain. However, the PoW blockchain guarantees high stability with the power required to create the block. The transition to other PoWs due to problems in the PoW blockchain causes dangerous problems. Thus, ECCPoW mitigates the power problems in the PoW blockchain and helps reduce the symmetry of the hash rate, which increases in proportion to the size of the blockchain in the PoW blockchain.

The contribution of this paper is two-fold. It introduces the proposed ECCPoW and proposes an implementation method. The second contribution is to introduce the process of experimenting in Bitcoin by replacing the SHA 256 function with the ECCPoW function. This paper proposes the creation of a cryptographic puzzle that changes every block and shows how to apply the crypto puzzle decoder to the solution. We present the implementation of the proposed method by replacing ECCPoW in Bitcoin. We also measure the block generation time of the ECCPoW. Finally, we compare ECCPoW and Bitcoin by implementing them in the same environment.

This study contributes to the previous literature on ASIC resistance in PoW blockchain. Previous studies have used forced memory access, leading to the inefficient behavior of ASICs. Another method is to make ASICs challenging to produce using various hash functions. The last method is to change the existing hash function to another hash function when ASICs are released. Therefore, ECCPoW combines the LDPC decoder with a hash function to create the effect of releasing different hash functions in each block. Implementing ASICs is difficult for the LDPC decoder due to cost issues. Furthermore, the PoW blockchain without ASICs reduces the mining centralization. In addition, ECCPoW can reduce power consumption by maintaining the advantages of the PoW.

This paper is structured as follows. Section 2 introduces the relevant research on the development of the prevention of ASIC miners. Section 3 presents ECCPoW and development methods. Section 4 reveals the results of the experiment by loading the ECCPoW into Bitcoin. Section 5 evaluates the mining centralization, security, and scalability of the ECCPoW. Finally, Section 6 presents the conclusion of the paper.

2. Related Work

2.1. Ethereum

Ethereum is a distributed computing platform developed to implement smart contract functions based on blockchain technology. In July 2015, Vitalik Buterin developed Ethereum in the C++ and Go languages. Ethereum uses the Ethash algorithm. Ethereum plans to change from a PoW to a proof of stake in the future [10]. Ether Solarium is against the use of the nonlinear directed acyclic graph (DAG) in ASICs. The initial size of the DAG was about 1 GB, and it was designed to increase in size linearly over time. In October 2019, the size of the DAG was 3.99 GB, which was maintained until December 20, 2020 [11,12].

Ethereum approved the application of programmatic proof of work (ProgPoW) [13] to respond to the centralization of mining in ASIC in 2019. First, ProgPoW regularly changes mining problems to a problem in which GPUs can adapt quickly. Second, ProgPoW makes the most of all the components of the graphics card for mining. Moreover, ProgPoW uses randomly generated problems based on block numbers and is designed for the efficient operation of GPUs. This reduces performance differences compared to ASICs.

2.2. The X-11 Series

The X-11 series is a cryptocurrency mining algorithm that uses as many hash functions as the number indicated behind the X [14]. The X-11 series used hash functions to add depth and complexity to curb ASICs. The X-11 series connects several hash functions and uses the output value of the hash as the input value of the next hash. Typically, the algorithm is used in Dash. The concept of the X-11 series uses multiple hashes to increase security and prevent ASIC mining. Currently, however, the X-11 series has been upgraded to increase the number of hash functions, such as X-13, X-14, X-15, X-16R, and X-17 because ASIC mining is still possible.

2.3. CryptoNote

CryptoNote was designed to be more inefficiently executed with a GPU than a CPU [15] to prevent ASIC mining. The performance of CryptoNote is susceptible to memory latency because memory creation and subsequent read operations occur repeatedly. This is similar to Etherium’s Ethash function. CryptoNote creates blocks by determining the hash function to be used after memory-intensive tasks.

Despite such attempts, Bitmain released ASICs optimized for CryptoNote algorithms in March 2018. Monero uses CryptoNote to change its mining algorithm twice a year to prevent ASICs. Monero’s algorithm change has prevented the use of ASICs. However, the frequent hard fork execution (radical changes) caused participants to break away from mining. In the end, there was a risk of the centralization of mining. To prevent frequent hard forks, RandomX proposed a key block concept that periodically changes mining methods [16].

3. The Proposed Method

This chapter provides an overview of and the implementation method of the proposed ECCPoW. We proposed the concept of ECCPoW to increase the resistance to ASIC, using a hash function that makes ASIC development difficult. Moreover, ASIC resistivity research reviews methods of inducing the loading of memory; for example, Ethereum uses several hash algorithms, such as X-11. However, ASICs for Ethereum and the X-11 series have been developed. Thus, ECCPoW is a method for miners to release different hash functions for each block to curb the emergence of ASICs.

The ECCPoW can help ease the centralization of mining. The conversion to ASICs in mining is made by ordinary people to avoid being excluded from mining and by a small group of people with capital power to monopolize mining. Mining centralization of a small group is likely to lead to mining blocks for malicious purposes and forging and tampering with the mined blocks. The implementation of ASICs in the LDPC decoder lacks flexibility due to structural cost issues [17]. Moreover, ECCPoW proposes a method of combining the LDPC decoder with a hash function. We help reduce the risk in the blockchain by mitigating mining centralization.

3.1. ECCPoW Overview

The ECCPoW is a POW that uses the ECC decoder that is used in communication, which can be implemented using ASICs. As a simple example, cell phones use ASICs to implement an ECC decoder quickly and at low power. The parity-check Matrix H determines the design of the ECC decoder based on ASICs. In other words, ASIC equipment can produce a decoder using parity-check matrices. For mobile phones, ASICs have standardized parity-check matrices that allow an ECC decoder design. Building ASICs to match the decoder supporting countless parity-check matrices is difficult due to cost problems and decoder size problems.

Randomly, ECCPoW changes each block parity-check matrix (i.e., ECCPoW uses an infinite number of parity-check matrices). As a result, ECCPoW inhibits the development of ASICs for ECC decoders. The ECC decoding algorithm only runs on a CPU or GPU. For example, even if the SHA function used in the PoW is executed quickly, a bottleneck occurs in the execution of ECC decoding algorithms.

3.2. Create a Cryptographic Puzzle That Changes Every Block

The ECCPoW aims to create a cryptographic puzzle that changes every block. We changed the composite function used to create the cryptographic puzzle using the generation method by Gallagher [18] and the previous hash value. In other words, ECCPoW randomly generates an LDPC matrix used by the decoder of the composite function. The Gallagher method requires variables.

Table 1. Variables in the low-density parity-check Matrix H.

Variables	Definition
n	Number of columns in H
m	Number of rows in H
wc	Number of 1s in each column
wr	Number of 1s in each row

displays the definition of the variables used in the LDPC.

The LDPC matrix satisfies the equation $n{w}_c=(n-k)w_r$, where k is n − m and $2^k$ is the total number of symbols that can be generated. When the variables are given, the LDPC Matrix H of size A is generated by the following method:

Step 1: Create a partial matrix of size $\frac{m}{w_c}\times n$

$$A_1:=\left[\begin{array}{cccc}\underset{w_r}{\underbrace{1 1 \cdots 1}}& & & \\ & \underset{w_r}{\underbrace{1 1 \cdots 1}}& & \\ & & \ddots & \\ & & & \underset{w_r}{\underbrace{1 1 \cdots 1}}\end{array}\right]\in {\left\{0,1\right\}}^{\frac{m}{w_c}\times n}$$

Step 2: Generate $w_c-1$ submatrices by randomly permutating the following matrices:

$$A_i:=\prod i(A_i)\in {\{0,1\}}^{\frac{m}{w_c}\times n},$$

where $\prod i$ is the ith sequence, and $i=2,3,\cdots ,w_c$.

Step 3: Construct the final LDPC matrix using all submatrices above:

$$\mathrm{H}:=\left[\begin{array}{cccc}{A}_1^T& A_2^T& \cdots & A_{w_c}^T\end{array}\right]\in {\left\{0,1\right\}}^{m\times n}.$$

Moreover, ECCPoW changes the sequence of permutations through the previous hash values and uses the previous hash value as the seed value to determine the sequence of permutations. The sequence of permutations is random because the hash values are random. The code is implemented in Reference [19].

Table 2. Form of the resulting Matrix H using different hash values.

Generated Matrix H n = 24 m = 16 wc = 3 wr = 4
Previous hash value	0x00000000000000000000000000000001
Generated Matrix H n = 24 m = 16 wc = 3 wr = 4
Previous hash value	0x00000000000000000000000000000002

compares Matrix H produced using different hash values. The lower part of the generated Matrix H in Table 2 is different.

3.3. Crypto Puzzle Decoder That Changes Every Block

The LDPC decoder of ECCPoW was developed using a message-passing algorithm. The decoder receives an $m\times n$ LDPC matrix of hash values $r\in {\{0,1\}}^n$ of length n as input values. The decoder outputs a value $c\in {\{0,1\}}^n$ of length n. The decoder can produce two types of answers depending on the input hash value r. The decoder outputs a sign $D_{MP}:\left\{r,H\right\}\mapsto c_i$ if the entered hash value r satisfies $\Vert r-c_i{\Vert }_h\le t$ for any sign $c_i$, where t is the value determined by the LDPC matrix. If not satisfied, the decoder outputs a random vector $c\in {\{0,1\}}^n$. The code is implemented in Reference [19].

The two conditions for determining whether to solve a cryptographic puzzle are listed in

Table 3. Conditions for the determination of crypto puzzle resolution.

Condition 1	(Original method) If the result of the decoder is code and has a specific Hamming weight, the problem is solved.
Condition 2	(Existing proof of work) If the result of rehashing the result of the decoder is less than a specific value, the problem is solved.

. Condition 1 determines that the cryptographic puzzle has been solved if the decoder’s output value c satisfies the conditions. In Condition 1, the output value is the code. Condition 1 is possible because the output value is less likely to code when the value is any input to the decoder. For example, there is a low probability of finding an answer to any input in SHA 256. In Condition 2, the Hamming weight of the output value is an element of the given set S. Set S is the range value of the output value. Condition 2 occurs because the Hamming weights of the possible codes may differ when Matrix H is given.

The satisfactory probability of Condition 1 requires a minimum Hamming distance value of H. To calculate this value, all distinct codes in $2^k$ must be considered, which is possible when the number of codes is small, but it is impossible when the number is large. Litsyn [20] reported the upper and lower bounds of the minimum Hamming distance value of H at specific $w_c$ and $w_r$ values.

Table 4. Probability of finding a code according to the variables of the low-density parity-check matrix.

wc = 4, wr = 5	p1 Upper Bounds	p1 Lower Bounds
n = 80, k = 12	6.32 × 10−5	2.12 × 10−8
n = 120, k = 24	1.65 × 10−8	1.49 × 10−13
n = 160, k = 32	4.06 × 10−10	1.34 × 10−17

reveals the probability of finding the codes according to the variables in the LDPC matrix. In this way, the upper bound of the probability is small. This makes it less likely for the decoder to meet Condition 1 when any value is entered.

Condition 2 is used to increase the difficulty of cryptographic puzzles when variables n, m, w_c, and w_r are fixed.

Table 5. The probability that Condition 2 is satisfied.

Hamming Weight	Probability	Element of the Set S	Probability that Condition 2 is Satisfied
98	≈5 × 10−5	98	≈5 × 10−5
…	…	…	…
128	≈9.7 × 10−2	98, 100, …, 126	≈4 × 10−1
128	≈1 × 10−1	98, 100, …, 126, 128	≈5 × 10−1

displays the probability that Condition 2 is satisfied when given a set S and part of the distribution of Hamming weights of the codes that can be generated when n = 256, m = 192, and w_c, w_r = 5 are given.

The probability of satisfying both Conditions 1 and 2 is as follows:

$$p:=Pr\left\{c|\mathrm{Hc}=0\right\}\times Pr\{\Vert c{\Vert }_h\in S\}.$$

We produced the difficulty table, as shown in

Table 6. Difficulty table for ECCPoW.

Lv.	n	wc	wr	Set S	p
1	32	3	4	{10, 12, …, 20, 22}	≈3.07 × 10−5
2	32	3	4	{10, 12, …, 14, 16}	≈2.02 × 10−5
…
379	128	3	4	{34, 94}	≈5.12 × 10−23
380	128	3	4	{34}	≈2.60 × 10−23

, by calculating the probability of meeting Conditions 1 and 2 at the same time when the variables n, w_c, and w_r and the set S are given. The probability value p in Table 6 is the difficulty level of the cryptographic puzzle. The closer the probability value is to zero, the higher the difficulty of the cryptographic puzzle.

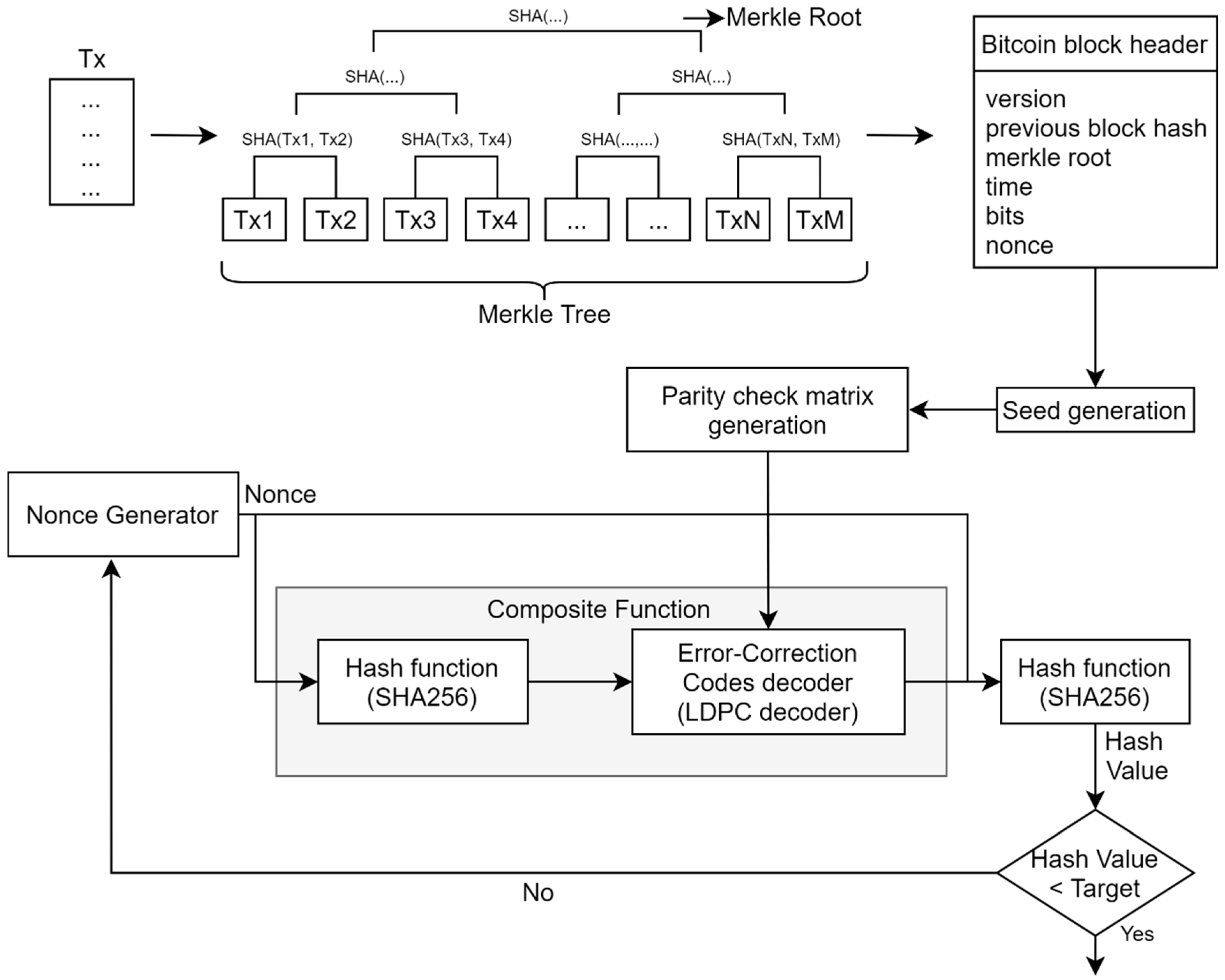
Condition 2 determines the resolution of the cryptographic puzzle by comparing the output value of the decoder with the result value and comparing the nonce with the target. Figure 1 illustrates Condition 2 for determining whether ECCPoW cryptographic puzzles are resolved. If the composite function and the hash algorithm are recognized as one hash function, Figure 1 has the same structure as Bitcoin, so the difficulty control function of Bitcoin can be used.

4. Experiment

This chapter presents experiments to verify ECCPoW. In the single-node experiment, the Bitcoin consensus algorithm was replaced by ECCPoW to verify the block generation function. In the multi-node experiment, we experimented with checking whether block generation, block synchronization, and transaction creation and transmission were performed correctly in a multi-node environment. In addition, the block generation time was tested in Bitcoin and Ethereum.

4.1. ECCPoW Operation Single/Multiple Node Experiment

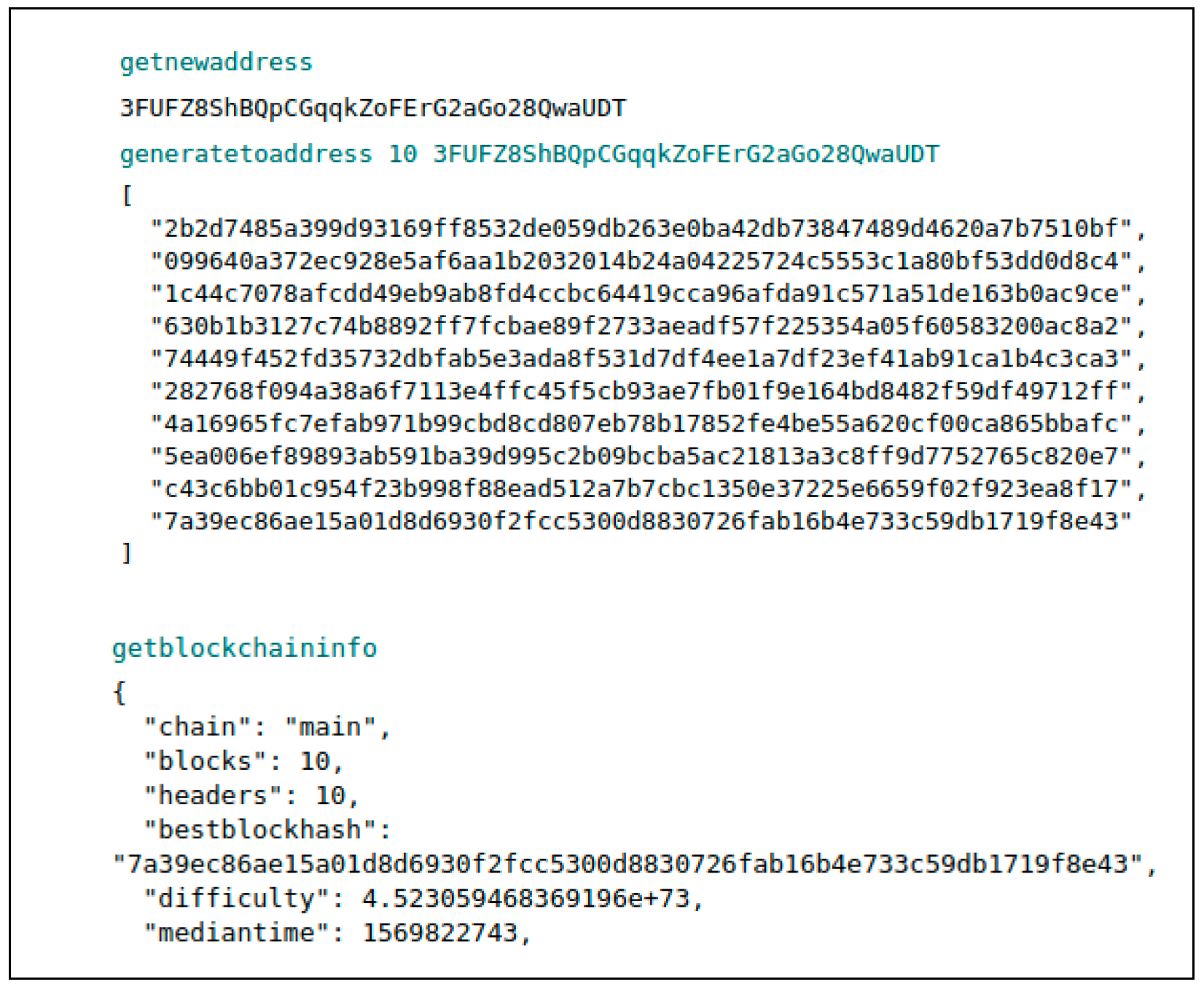
We replaced Bitcoin’s consensus algorithm with ECCPoW. The single-node experiment is a block generation experiment of the ECCPoW blockchain. Bitcoin uses the “generatetoaddress” command for block generation and receives the current address of the blockchain as a parameter. Then, a new block address is created using the “getnewaddress” command, and 10 blocks are created using “generatetoaddress.” Figure 2 illustrates the change in 10 of the “blocks” after block generation.

Multiple node experiments use three random nodes (Nodes 1, 2, and 3) to experiment with block synchronization, to transmit transactions, and to verify them. This experiment demonstrates that each node mines different numbers of blocks, synchronizing to a long blockchain. Figure 3 indicates the results of mining and checking the blocks in Node 1.

Figure 4 reveals the results of mining and checking blocks on Node 2, and Figure 5 demonstrates the results of mining and checking blocks on Node 3.

Node 3 connects Node 1 (192.168.232.128) and Node 2 (192.168.232.129) using the “addnode” command. Then, Node 3 uses the “getadnednodeinfo” command to check the information on the connected nodes. Figure 6 illustrates the connection between Node 1 (192.168.232.128) and Node 2 (192.168.232.129) using the “addnode” command. Next, Figure 6 indicates the connected node information using the “getadnednodeinfo” command. Bitcoin’s nodes synchronize to nodes that hold many blocks, and Bitcoin determines that nodes with many blocks are highly reliable. In the current experiment, Node 3 had the largest number of blocks. Nodes 1 and 2 synchronize to the blocks of Node 3, and these results are displayed in Figure 7.

We checked the behavior of the blockchain by checking the synchronization. We sent the transactions between linked Nodes 2 and 3. Figure 8 indicates the balances held by Nodes 2 and 3. Currently, Node 2 has zero, and Node 3 has 1000.

Figure 9 displays the address of Node 2 (in the Pay-To field) and the amount of coin to send (in the Amount field) for Node 3 to transmit 500 coins to Node 2. A transaction fee was set to the minimum cost of 0.00001. Figure 10 reveals the transaction transfer by identifying the amount of coin in Node 2 and displaying the recent transaction records. Figure 11 illustrates that the number of coins in Node 3 and the recent transaction record decreased.

4.2. Block Generation Time

Figure 12 reveals the time-by-time block generation of Bitcoin with ECCPoW, using the difficulty table proposed in Section 3. Block generation time should be able to meet the target generation time for a stable blockchain. The blockchain adjusts the target block generation time by adjusting the difficulty level over time. The experimental environment used block generation with one node. As shown in Figure 12, the block generation time is unstable in the experiment. Sufficient nodes can confirm the stability of the block generation time. The difficulty table must be finely adjusted.

5. Evaluation

We evaluated the mining centralization, security, and scalability of ECCPoW using Amazon Web Services.

Table 7. Implementation environment of the evaluation.

No	Role	CPU	Memory (GB)	HDD/SSD (GB)	Volume
1	Monitoring PC	Intel i7-8700 3.20 GHz	16	SSD 256	1
2	Seed Instance	AWS m5.xlarge vCPU 2	8	HDD 20	6
3	Mining Instance	AWS m5.xlarge vCPU 2	8	HDD 20	40

presents the evaluation environment. A monitoring computer checked the network test results. The seed instance made the blockchain network connections between nodes. The mining instance was responsible for block mining. The implementation environment for each node was a Ubuntu Server 18.04 LTS, m5.large (vCPU processor 2 core with 8 GB of RAM, and a 20 GB solid-state drive).

The blockchain trilemma problem is that trade-off relationships occur in the evaluation characteristics of the blockchain. The trilemma elements of a blockchain are decentralization, scalability, and security. Thus, we compared Bitcoin in terms of these elements (mining centralization instead of decentralization).

Table 8. Description of evaluation features.

Evaluation Features	Unit of Measurement	Evaluation Standards	Evaluation Goal
Mining centralization	Distribution of mining success rate	40% (Estimate) (Bitcoin, Oct.–Dec. 2018)	40%
Security	Security of Bitcoin contrast	100% (Bitcoin)	100%
Scalability	Scalability of Bitcoin contrast	100% (Bitcoin)	100%

displays the evaluation standards and goals for evaluation.

Bitcoin has a total hash rate of approximately 90 TH/s (March 2020). It is impossible to compare the current version of Bitcoin with ECCPoW. Moreover, ECCPoW (ver. 0.1.2) replaced the Bitcoin 0.17 version [21] of SHA 256 [22]. We compared two completely initialized blockchains (block count zero).

We compared the Bitcoin and ECCPoW initialized to set the evaluation environment (difficulty change cycle, target block generation time, 23 instances, among others). The blockchain typically sets a difficulty change cycle of 60 min and a target block creation time of 3 min for experimentation.

5.1. Mining the Centralization Evaluation

Mining centralization is when a network is no longer centralized and operates autonomously within a blockchain. We define mining centralization as when the nodes are fairly mined with the same performance. The indicators used in the mining centralization evaluation include the distribution of the mining success rates, which are defined by the formula below. According to the formula, the lower the dispersion of the probability of mining success, the higher the distribution of mining success. In other words, the distribution of mining success rates is higher for each participating node to have a uniform distribution of mining success rates, which means better dispersion. Bitcoin is estimated to have a 40% distribution of mining success rates (October to December 2018). Moreover, ECCPoW targets 40% dispersion:

$$A=\frac{C}{\sqrt{B+C^2}}\times 100A=\mathrm{The} \mathrm{distribution} \mathrm{of} \mathrm{mining} \mathrm{success} \mathrm{rate} (\%),$$

$$B=\mathrm{The} \mathrm{dispersion} \mathrm{of} \mathrm{mining} \mathrm{success} \mathrm{rate},$$

$$\mathrm{C}=\mathrm{Average} \mathrm{of} \mathrm{the} \mathrm{mining} \mathrm{success} \mathrm{rate}.$$

We created three seed nodes for the ECCPoW blockchain and composed 20 mining nodes.

Table 9. The number of mining success and number of nodes.

Number of Mining Nodes	Number of Mining Success	Number of Mining Nodes	Number of Mining Success
1	4	11	7
2	9	12	4
3	3	13	12
4	4	14	5
5	6	15	11
6	4	16	2
7	6	17	7
8	6	18	6
9	5	19	10
10	5	20	8

lists the number of mining successes of each mining node at the time of 100 blocks being mined.

Table 10. Evaluation results of the mining centralization evaluation features.

Total Number of Mining Successes	Average Mining Successes	Square of the Average Number	Dispersion of the Average Number	Distribution of Mining Successes
124	6.2	38.44	6.76	92.21944

indicates the distribution of mining success.

The dispersion of ECCPoW was measured by the distribution of the mining success rate and measured at 92.22%, which was 32% higher than the assessment target of 60% (Table 10). The results of the experiment revealed that the ECCPoW miner is more likely to be rewarded than a Bitcoin miner in an ideal environment where participating nodes exhibit the same performance. In other words, ECCPoW is stronger in mining centralization than Bitcoin.

5.2. Security Evaluation

Security is associated with the difficulty of the blockchain being altered by a miner’s attack. A typical attack on the blockchain is the double-payment issue. One of the causes of double-payment problems occurs in the branch of the blockchain. An orphan chain is a chain that has a branch other than the main chain, and an orphan block is a block belonging to an orphan chain. We assess the security as the ratio of orphaned blocks to the total number of blocks in the blockchain. The security assessment calculates the orphan block ratio of Bitcoin and ECCPoW using the expression below. We evaluated the security of ECCPoW based on the security of Bitcoin at 100%.

$$Orphan block ratio=\frac{number of orphan blocks}{Total Height of Blockchain}\times 100$$

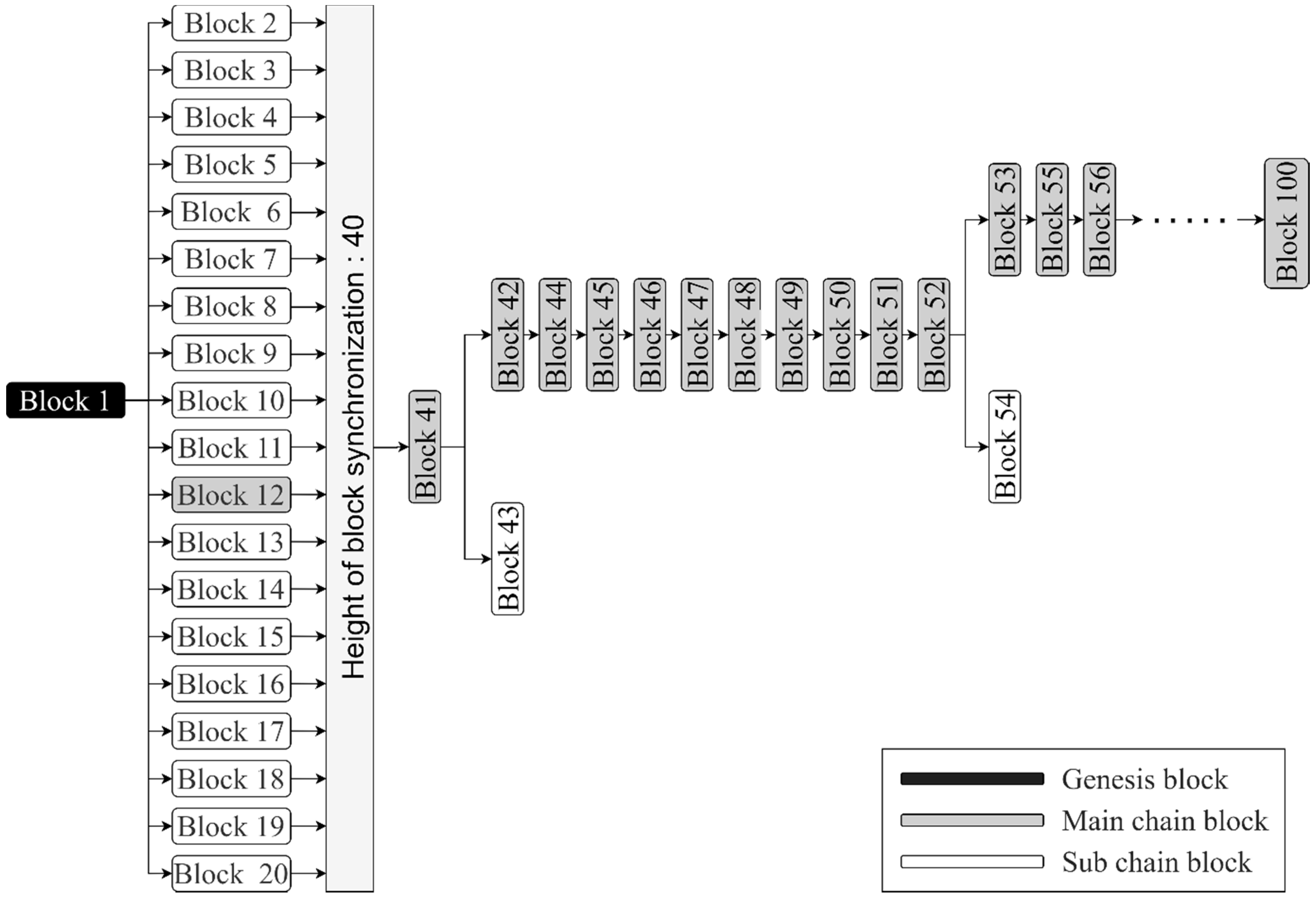
We configured the blockchain test environment with three seed nodes and 20 mining nodes. In addition, we mined 100 blocks in the blockchain and checked the orphan blocks. Figure 13 depicts the orphan block identification for the security assessment. After mining 40 blocks, the evaluation identified blocks for stable synchronization of the blockchain. In the experiment, orphan blocks of a height of one frequently occurred in both environments. In our experiment, we classified the height of subchains of two or higher as orphan blocks. In Figure 13, orphan blocks correspond to Blocks 13, 14, 15, 16, and 18.

Figure 14 demonstrates the blockchain status based on the results of the security assessment in the Bitcoin environment.

Figure 15 reveals the blockchain status according to the results of the security assessment in the ECCPoW environment.

All blockchains were measured at 0% because of the assessment. The security of ECCPoW was the same on a Bitcoin and orphan block basis. Blockchain measurements inhibited the generation of orphan blocks.

5.3. Scalability Evaluation

Scalability is the extent to which a system can flexibly respond to an increase in the number of users. Blockchain scalability is related to the transaction processing speed of blockchain. Transactions per second (TPS) is the transaction processing speed of the blockchain. Thus, we evaluated the scalability of the blockchain using TPS. The following equation defines how to obtain TPS using transactions in blocks.

$$\mathrm{TPS}=\frac{Total number of transactions in block}{Generation time of total block}.$$

We configured the blockchain test environment with three seed nodes and 20 mining nodes. Transaction generation occurs continuously from height 91 to 100—the blockchain mines 100 blocks. We checked the number of transactions in the height blocks of the blockchain from 91 to 100. We calculated the TPS of the blockchain.

Table 11. The evaluation result of Bitcoin scalability.

Number	Height	Block Generation Time (Seconds)	Number of Transactions
1	91	719	672
2	92	19	22
3	93	94	88
4	94	144	141
5	95	275	263
6	96	40	40
7	97	313	296
8	98	6	11
9	99	574	534
10	100	146	137
Total		2330	2204
TPS		0.945922747 TPS

lists the generation time and number of transactions of blocks of height 91 to 100 in Bitcoin.

Table 12. Evaluation results of ECCPoW scalability.

Number	Height	Block Generation Time (Seconds)	Number of Transactions
1	91	151	140
2	92	192	182
3	93	369	351
4	94	361	331
5	95	156	151
6	96	214	205
7	97	124	120
8	98	267	250
9	99	585	548
10	100	514	480
Total		2933	2758
TPS		0.940334129 TPS

displays the generation time and the number of transactions of blocks of height 91 to 100, in ECCPoW. The evaluation results revealed that Bitcoin’s TPS is 0.95, and ECCPoW’s average TPS is 0.94. Moreover, ECCPoW’s scalability was measured at 98.95%, which was down 1.02% from Bitcoin’s scalability. In addition, ECCPoW added a process to Bitcoin to resist ASICs. However, the scalability values of ECCPoW and Bitcoin were assessed at a similar level.

5.4. Comparison to Related Work

This section compares the features with the existing studies on ASIC resistance.

Table 13. Comparison results of the related work.

Comparison Features	Proposed Method	Memory Approach	Hash Function Overlay	Periodic Hash Function Replacement
Applied cryptocurrency	-	Ethereum, Bytecoin	X-11 series	Monero (2019.9, RandomX), Ethereum (2020.7 applying scheduled, ProgPoW)
Characteristic	Change hash function every block	Force memory access	Overlapping multiple hash functions	Hard fork manually or automatically with a hash function
Algorithm	ECCPoW	Ethash, ProgPoW, CryptoNight	Blake, Bmw, Groetl, etc.	RandomX, ProgPoW
ASIC appearance	-	Yes	Yes	Unknown
ASIC resistance induction method	Use of ASIC resistance by connecting the LDPC decoder and hash function	Induce cache miss when creating blocks (using a DAG, etc.)	Overlapping the difficulty of known hash functions	Hard fork every six months (formerly Monero). Convert the hash function for a period using the key-block concept (currently Monero)

compares the proposed method and existing relevant research on ASIC resistance. The ASIC resistance study for the PoW blockchain has three approaches. The first method causes bottlenecks using memory access in a hash function—for example, Ethereum (Ethash) and Bytecoin. The second method prevents the generation of ASICs using a hash function overlay, for example, the X-11 series. Finally, the third method uses periodic hash function replacement for ASICs, for example, in Monero (2019.9, RandomX algorithm) and Ethereum (2020.7 applying scheduled, ProgPoW).

The resistance induction of each ASIC in the existing studies is as follows. The memory approach induces a cache miss (using DAG, among others) when creating blocks. This method degrades ASIC performance as memory access increases. The hash function overlay method uses the overlap of the difficulty of known hash functions. This method relies on the security of the applied hash function. The periodic hash function replacement method periodically changes the hash function manually or automatically.

6. Conclusions

In this paper, we explained ECCPoW and applied the proposed method to Bitcoin. This paper addressed the problem of centralization of mining due to the emergence of ASICs. We proposed a PoW concept based on error-correction codes to solve this problem. The core of the ECCPoW is the connection of the hash function with the LDPC decoder. Blockchain applied with the ECCPoW determines the completion of the POW using the output value of the decoder. In addition, ASIC suppression is possible because ASICs use the LDPC decoder.

This paper contributes to the phenomenon of symmetry in the PoW blockchain. The total block size of the PoW blockchain symmetrically influences the hash rate. The PoW blockchain increases stability as the hash rate increases in size. However, a high hash rate causes the waste of computing power in block generation. Thus, we mitigate the causes of a high hash rate using ASIC resistance.

The ECCPoW offers a method of solving different puzzles in each block to avoid ASICs. This maximizes the benefits of how existing studies use a limited number of hash functions to solve each block of different hash functions. The proposed method offers more effective connections and the use of multiple hash functions. We presented the difficulty control, parity-check matrix generation method, hash vector generation, and code determination methods for implementing ECCPoW. Furthermore, ECCPoW was applied to Bitcoin to verify the proposed method. We assessed the mining centralization, security, and scalability of ECCPoW and Bitcoin. We found that ECCPoW maintained security and scalability, showing 32% higher mining centralization than Bitcoin. Using the proposed method, ECCPoW does not require high hash rates, and miners can compete more fairly.

This study contributes to the previous literature on ASIC resistance in the PoW blockchain. The ASIC resistance study of the PoW blockchain was conducted in response to hardware development by ASIC manufacturers. One of the studies on ASIC resistance induced forced access to memory in the hash function, thereby lowering the performance of ASICs. Other studies have suggested periodically altering the hash function to render ASICs useless. The ECCPoW provides a method of releasing different hash functions for each block, rather than changing the periodic hash function.

The ECCPoW revealed the limit of block generation time in the experiment. For the stable operation of the blockchain, the block generation time of the ECCPoW must be stable and controllable. The results of the block generation time test were unstable in the experiment using one node. Thus, ECCPoW requires further research regarding the difficulty of block generation for stable operation. We also need to increase the number of nodes in the ECCPoW to carry out mining.