q-Rung Orthopair Fuzzy Prioritized Aggregation Operators and Their Application Towards Green Supplier Chain Management

Abstract

Supply management and environmental concerns are becoming increasingly relevant to scientific decision analysis around the world. Several companies have implemented the green supply chain management (GSCM) approach for attaining economic advantages while retaining sustainable growth for the environment. Green supplier selection has also been analyzed in many literary works as an important part of GSCM, which is considered an important multi-criteria group decision making (MCGDM) problem. The lack of consideration of the relationships of alternatives to the uncertain environment will be the main reason for weak conclusions in some MCGDM problems. To address these drawbacks, we introduce a new approach for selecting green suppliers with the q-rung orthopair fuzzy information, in which the input assessment is considered by using q-rung orthopair fuzzy numbers (q-ROFNs). A q-ROFN is extremely valuable in representing vague information that occurs in these real-world circumstances. The priority relationship of the alternatives to q-rung orthopair fuzzy information is very helpful to deal with GSCM. Consequently, we develop some prioritized operators with q-ROFNs named the q-rung orthopair fuzzy prioritized weighted average (q-ROFPWA) operator and q-rung orthopair fuzzy prioritized weighted geometric (q-ROFPWG) operator. Several important characteristics of these operators such as idempotents, boundary, and monotonicity are also well proven. Finally, an application of the proposed operators is presented for green supplier selection in GSCM. The scientific nature of the proposed methodology is illustrated by a numerical example to validate its rationality, symmetry, and superiority.

1. Introduction and Literature Review

Several researchers have now adopted the GSCM approach to greening their supply chains and are willing to learn more about the key performance measures that are accountable for their implementation. In view of environmental legislation and the increasing demand from overseas consumers for many environmentally friendly products, many companies around the world are adopting environmentally friendly products as their business strategy for future sustainability is gaining a competitive advantage over others. Government companies and some non-governmental organizations are working in a number of countries to buy eco-products that would eventually support the world and thus civilization. Limiting environmental degradation will be the biggest challenge facing society in the coming years [1]. In recent decades, more attention has been paid to environmental concerns; some industries, in particular in emerging countries, have taken great care to cope with environmental constraints in the area of green growth and pollution reduction. Government rules and regulations have been enacted to restrict the conduct of business; consumers can take into account the environmental impacts of different firms when making their choice [2]. More and more organizations are now using the new GSCM environmental sustainability mode to reduce emissions during supply chain operations. GSCM covers many facets of the supply chain, such as product design, vendor selection, processing, storage, shipping, marketing, and recycling. The initial linkage of the supply chain and the impact on the productivity and environmental performance of the supply chain are between the different segments. Green suppliers therefore play a crucial role in selecting a green supplier from GSCM. In general, the selection of green suppliers can be seen as a question of a variety of MCGDM evaluating different possible green suppliers with respect to other requirements in order to decide the best option. The assessment details can in practice be ambiguous and incomplete. Green architecture, green construction, green production, green transport, and reverse logistics are the main pursuits involved in GSCM.

The remaining article is structured in the following manner. In Section 2, the basic definitions of the q-ROFN score function, q-ROFN accuracy function, and basic aggregation operators are presented. In Section 3, some q-rung orthopair fuzzy prioritized aggregation operators are developed. We present an MCGDM approach related to the proposed operators in Section 4. The case study of GSCM is discussed in Section 5, and a numerical example is given as well. Section 6 summarizes the main results of the current research work.

1.1. Green Supplier Selection Approaches

Throughout recent years, GSCM’s cross-disciplinary research area has included both academia and industry. This trend is attested by the preponderance of special issues devoted exclusively to this subject in leading operations and supply chain management (SCM) journals. The ongoing academic development and further advancement in this inchoate field include developing new ideas and awareness. Suppliers deliver raw materials, products, or services, which cannot be offered by a company. The manufacturer is an integral aspect of the modern business process for supply chains, and the best manufacturer should provide the client with the correct quality and quantity of goods at fair prices and at the required time. In the past few years, environmental factors have been dramatically reemerging as an important problem for decision makers. Waste electrical and electronic equipment (WEEE), restriction of hazardous substances (RoHS), and eco-design requirements for energy using products (EUP) are the three main European Union directives that concern the electronic businesses. The three guidelines demonstrate EU concern for recycling, no-hazardous pollutants, low energy, and resource waste. Rao [3] defined GSCM as involving environmental performance based screening providers and complying with environmental regulations and standards. The selection of suppliers in GSCM is clearly a crucial purchasing practice, since its suppliers can demonstrate environmental and ecological efficiency. As an enterprise becomes completely dependent on suppliers, an effective approach to the evaluation of the performance of suppliers is necessary. The selection of suppliers needs several goals to be considered; hence, the choice of suppliers suggested by Bhutta and Huq [4] in 2002 can be seen as an MCDM.

As the MCGDM issue has become more complex, a number of new approaches have been explored purely on the basis of MCGDM and soft computing techniques. Comparably, owing to the characteristics of GSM, many scientists have considered the green supplier selection process to be a complicated MCGDM problem; therefore, a number of MCGDM methods have been used in GSCM research under fuzzy circumstances. Lee et al. [5] developed the GSCM analytical hierarchy process (AHP). Both Chen et al. [6] and Yazdani [7] developed an integrated MCDM strategy to get the best green supplier (BGS) consisting of fuzzy AHP and the technique for order performance by similarity to ideal solution (TOPSIS). By using the data envelopment analysis (DEA) process, Dobos and Vörösmarty [8] decided on BGS. Kuo et al. [9] utilized the decision making trial and evaluation laboratory (DEMATEL) process and the VIKOR (vlse kriterijumska optimizacija Kompromisno Resenje) technique to examine the relationships among criteria and calculate criteria weights, then select BGS. Banaeian et al. [10] analyzed green providers in the agri-food industry using TOPSIS and VIKOR to address the applications of fuzzy green suppliers. Govindan et al. [11] suggested a method of selecting the BGS based on the revised Simos procedure and preference ranking organization method for enrichment evaluation (PROMETHEE) technique. Quan et al. [12] analyzed BGS selection with a broad decision maker community and established an integrated process combined with ant colony algorithms and multi-objective optimizations by ratio analysis plus the full multiplicative form (MULTIMOORA) method. Young and Kielkiewicz [13] investigated the sustainable supply network management systems. Wang and Li [14] introduced a novel approach for green supplier selection using q-rung orthopair fuzzy numbers (q-ROFNs). Wang et al. [15,16] established models for green supplier selection with some two-tuple linguistic neutrosophic number Bonferroni mean operators and q-rung interval-valued orthopair fuzzy information. Srivastava [17] presented green supply chain management and introduced a brief literature review. Sharfman et al. [18] established the supply-chain environmental management strategies. Rath [19] described GSCM as a catalyst of organizational sustainable growth. Min and Galle [20] with Murphy and Poist [21] presented some modified green purchasing strategies. Curz and Matsypura [22] presented supply chain networks with corporate social responsibility through integrated environmental decision making. Khan et al. [23] worked on measuring the performance of green supply chain management. Mangla et al. [24] presented the analysis of flexible decision strategies for a sustainability focused green product recovery system.

1.2. Indicators for Green Supplier Selection

First, we discuss the indicators for common supplier selection, in order to carry out an appropriate company performance assessment. Dickson [25] performed a survey and provided 23 specific attributes. Quality, delivery, and performance history were the top three indicators. While Dickson introduced the 23 parameters 20 years ago, the majority of them in the literature to date are still covered [26]. In a new analysis, Hu [27] reviewed 24 published papers after 1991. The most important criteria for vendor assessment approaches include cost, quality, production capability, and production. Çelebi and Bayraktar [28] proposed 37 criteria to be more realistic in selecting suppliers and advanced the theory of the integration of neural network and data envelopment analysis for provider evaluation on the basis of inadequate assessment criteria details. The fourdimensions of the criterion were classified. These are cost, quality, service, and delivery. When we talk about indicators for green supplier selection, Seuring and Müller [29] reviewed 191 articles and established two specific strategies, supplier risk management and supply chain management for sustainable products. In addition, a number of researchers analyzed renewable supplier assessment indicators in order to comply with environmental standards. Noci [30] applied the AHP model to help decision makers choose the most efficient vendor from an environmental perspective. In addition, Handfield et al. [31,32] used the Delphi approach to obtain the point of view of professionals from IBM, Ford, Mascotech, Cone Drive, and Herman Miller Company to determine the structure of the criteria and used the AHP method to determine the efficiency of the supplier. That structure was applied to three kinds of factories. The findings showed that the automotive industry and the ready-made garment industry would select the most desirable suppliers. Humphreys et al. [33] thought environmental costs had little emphasis; therefore, they suggested other more established selection criteria. ANPwas used by Sarkis [34] to develop a six-dimensional strategic GSCM decision making system. Sarkis et al. [35] established an organizational theoretic review of green supply chain management literature. The relevant criteria proposed by each researcher are listed in

Table 1. The relevant criteria proposed by different researchers.

Researchers and References	Criteria
Noci [30]	Green competencies,
	the green picture of the manufacturer,
	efficiency at the current location, and
	cost of the net life-cycle.
Handfield et al. [31]	Logistics for packaging, managing waste,
	brand attributes’ certification,
	environmental policy, and
	rules and regulations of government.
Haumphreys et al. [33]	Production of environmental impacts,
	environmental planning, eco-friendly,
	systems of environmental protection,
	skills in management, and eco-friendly skills green pic.
Sarkis [34]	Enhance procedures of GSC,
	quality standards for the company,
	organizational practices that are socially positive,
	and GSC’s program substitutes.
Hsu and Hu [36]	Control of procurement,
	controlling inbound price,
	management of research and development,
	systems of management, and control of procedures.

.

1.3. MCDM Based Uncertain Data Modeling

For many years, the issue of vague and imperfect information has been at the forefront. Information aggregation is the key factor for the decision management in the areas of business, management, engineering, psychology, social sciences, medical sciences, and artificial intelligence. Traditionally, the information about an alternative has been believed to be considered as a crisp number or linguistic number. Nevertheless, information cannot be aggregated in a simple form due to its uncertainty. It is very important to address this problem, in order to deal with uncertainty. Zadeh [37] initiated the notion of fuzzy set theory. After Zadeh, Atanassov [38] introduced intuitionistic fuzzy sets (IFSs) as an extension of fuzzy sets. Consequently, Yager [39,40] introduced Pythagorean fuzzy sets (PFSs) as an extension of IFS. After that, he introduced [41,42] another generalization of IFSs and PFSs named q-rung orthopair fuzzy sets (q-ROFSs). Additionally, a Pythagorean fuzzy number (PFN) is superior to an intuitionistic fuzzy number (IFN) towards uncertainty. A q-ROFN is superior to both IFN and PFN because both are q-ROFN, but not conversely (see [40,41,42,43]). Many works have researched the TOPSIS approach for the problem of decision making: Li and Nan [44], Boran et al. [45], Zhang and Xu [46], and Selvachandran and Peng [47]. Xu et al. [48] established some q-rung dual hesitant fuzzy Heronian mean operators with their application to MAGDM.

Xu et al. [49,50,51] introduced weighted averaging operators, geometric operators, and induced generalized operators based on intuitionistic fuzzy numbers (IFNs). Hashmi et al. [52] introduced the notion of the m-polar neutrosophic set and m-polar neutrosophic topology and their applications to multi-criteria decision making (MCDM) in medical diagnosis and clustering analysis. Hashmi and Riaz [53] introduced a novel approach to the census process by using Pythagorean m-polar fuzzy Dombi aggregation operators. Riaz and Hashmi [54,55] introduced the notion of linear Diophantine fuzzy Set (LDFS) and its applications to the MCDM problem. The linear Diophantine fuzzy set (LDFS) is superior to IFSs, PFSs, and q-ROFSs. The novel concepts of soft rough Pythagorean m-polar fuzzy sets and Pythagorean m-polar fuzzy soft rough sets with application to decision making problems were introduced. Riaz et al. [56] presented a robust q-rung orthopair fuzzy information aggregation using Einstein operations with applications to sustainable energy planning decision management. Riaz and Tehrim [57] established the idea of a cubic bipolar fuzzy set and cubic bipolar fuzzy ordered weighted geometric aggregation operators and their application using internal and external cubic bipolar fuzzy data. Naeem et al. [58] established Pythagorean fuzzy soft MCGDM methods based on TOPSIS, VIKOR, and aggregation operators.

Feng et al. [59] introduced MADM models in the environment of generalized IFsoft sets. Ye [60] introduced prioritized aggregation operators in the context of IVHFSand worked on its MAGDM. Zhang et al. [61] introduced aggregation operators with MCDM by using interval-valued FNS(IVFNS). Zhao et al. [62] worked on generalized aggregation operators in the context of IFS. Wang and Liu [63] introduced the Einstein operators on IFSs. Garg [64] introduced Pythagorean Einstein operators and presented their applications. Liu and Wang [65] established some q-rung orthopair fuzzy aggregation operators and presented their application to multi-attribute decision making. Yager [66] introduced several prioritized aggregation operators. According to Yager, when considering the situation in which we choose a bicycle for a child based on safety and cost attributes, we should not allow a cost-related advantage to compensate for a safety loss. Then, we have a sort of relationship of prioritization over these two attributes, and protection is of higher importance. This situation can be called a problem of aggregation, where the relationship of priority exists over the attributes. Since we want to consider the satisfaction of the higher priority attributes, such as safety in the example above, it is no longer feasible for the aggregation operators in question, such as the weighted average operator and the weighted geometric operator. In such a case, Yager [66] provided the prioritized aggregation operators by modeling attribute prioritization regarding the weights associated with the attributes based on the satisfaction of the higher priority attributes. Si et al. [67] presented a novel approach for the ranking of picture fuzzy numbers. Yusifov et al. [68] established multi-criteria evaluations and a positional ranking approach for candidate selection in E-voting.

1.4. Motivation, Highlights, and Focus of the Study

In this subsection, we put a light on the scope, motivation, and novelty of the proposed work.

• This article includes two major issues: a theoretical model of the problem and decision making application.
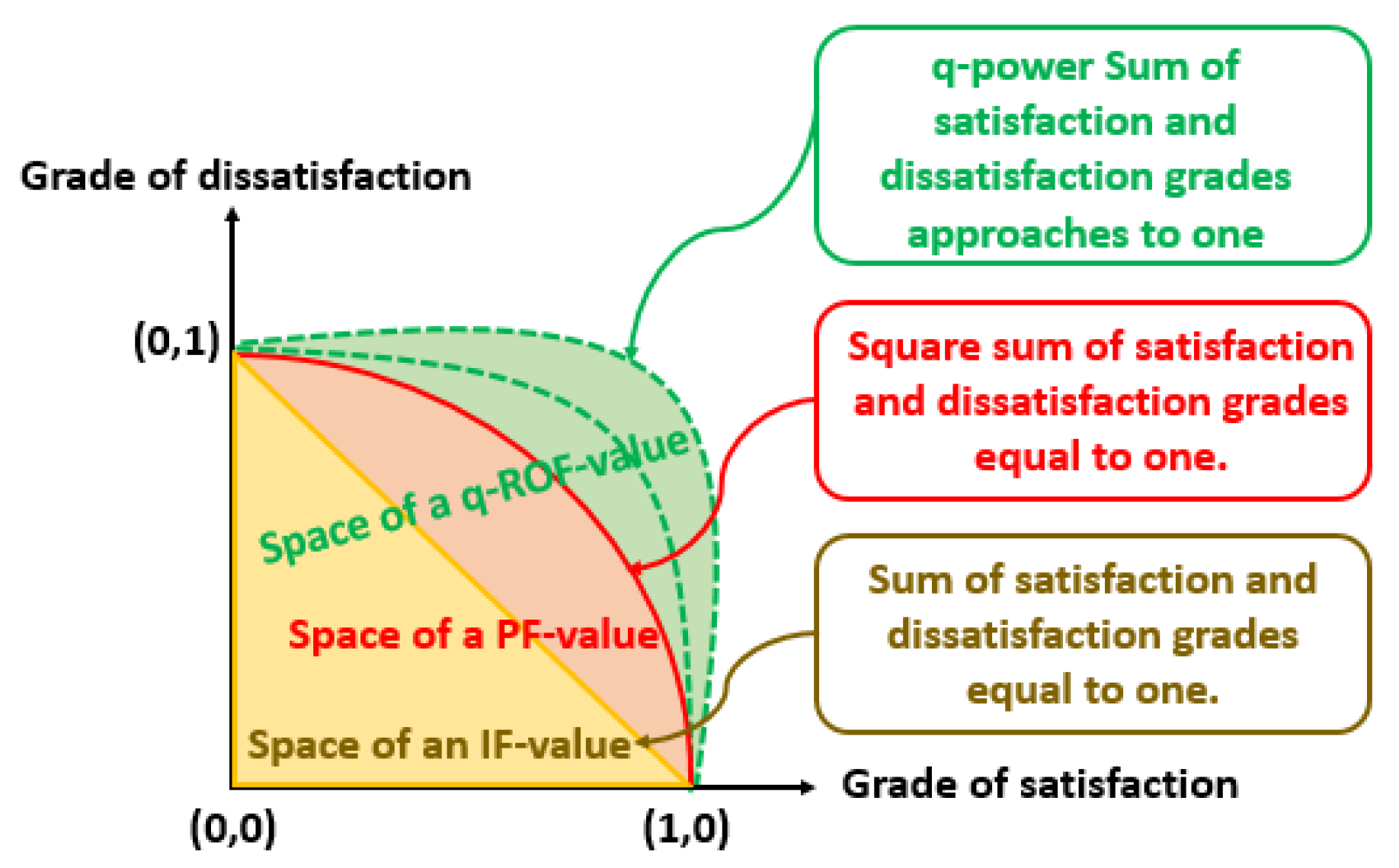
• The proposed models of aggregated operators are authentic, valid, flexible, and superior to others because they are based on the generalized structure of q-ROFNs. If we apply the proposed operators in the context of IFNs or PFNs, then the results will be imprecise due to the loss of information in the input data. This loss is due to the constraints based on the membership and non-membership grades of IFNs and PFNs (see Figure 1). The IFNs and PFNs become special cases of q-ROFNs when $q=1$ and $q=2$, respectively.
• The vital objective is to construct a strong relationship between the proposed operators with the multi-criteria decision making problems. The application based on the green supplier selection in GSCM communicates the effectiveness, interpretation, and motivation of the proposed aggregated operators.
• This research fills the research gap and provides us a wide domain for the input data selection in medical, business, artificial intelligence, agriculture, and engineering. We can tackle those problems that contain ambiguity and uncertainty due to its limitations. The results obtained by using proposed operators and q-ROFNs will be superior and profitable in decision making techniques.

2. Some Basic Concepts

We keep in mind a few fundamentals of q-ROFS, the operational laws of q-ROFNs, and score and accuracy functions in this section.

Definition 1

([42,43]). Let $q\ge 1$. A q-rung orthopair fuzzy set $\mathcal{O}$ in $\mathcal{Q}$ is defined as:

$$\mathcal{O}=\{\langle \varsigma ,{\mathcal{Y}}_{\mathcal{O}}\left(\varsigma \right),{\mathcal{X}}_{\mathcal{O}}\left(\varsigma \right)\rangle :\varsigma \in \mathcal{Q}\}$$

where ${\mathcal{Y}}_{\mathcal{O}},{\mathcal{X}}_{\mathcal{O}}:\mathcal{Q}\to [0,1]$ defines the membership and non-membership of the alternative $\varsigma \in \mathcal{Q}$, and for every ς, we have:

$$0\le {\mathcal{Y}}_{\mathcal{O}}^q\left(\varsigma \right)+{\mathcal{X}}_{\mathcal{O}}^q\left(\varsigma \right)\le 1.$$

Furthermore, ${\pi }_{\mathcal{O}}\left(\varsigma \right)={\left(1-{\mathcal{Y}}_{\mathcal{O}}^q\left(\varsigma \right)-{\mathcal{X}}_{\mathcal{O}}^q\left(\varsigma \right)\right)}^{1/q}$ is called the indeterminacy degree of ς to $\mathcal{O}$.

Liu further suggested to combine the q-ROFN information with the following operational rules.

Definition 2

([65]). Let ${\mathcal{G}}_1=\langle {\mathcal{Y}}_1,{\mathcal{X}}_1\rangle$ and ${\mathcal{G}}_2=\langle {\mathcal{Y}}_2,{\mathcal{X}}_2\rangle$ be q-ROFNs. Then,

(1) $\overline{{\mathcal{G}}_1}=\langle {\mathcal{X}}_1,{\mathcal{Y}}_1\rangle$

(2) ${\mathcal{G}}_1\vee {\mathcal{G}}_2=\langle max\{{\mathcal{Y}}_1,{\mathcal{X}}_1\},min\{{\mathcal{Y}}_2,{\mathcal{X}}_2\}\rangle$

(3) ${\mathcal{G}}_1\wedge {\mathcal{G}}_2=\langle min\{{\mathcal{Y}}_1,{\mathcal{X}}_1\},max\{{\mathcal{Y}}_2,{\mathcal{X}}_2\}\rangle$

(4) ${\mathcal{G}}_1\oplus {\mathcal{G}}_2=\langle {({\mathcal{Y}}_1^q+{\mathcal{Y}}_2^q-{\mathcal{Y}}_1^q{\mathcal{Y}}_2^q)}^{1/q},{\mathcal{X}}_1{\mathcal{X}}_2\rangle$

(5) ${\mathcal{G}}_1\otimes {\mathcal{G}}_2=\langle {\mathcal{Y}}_1{\mathcal{Y}}_2,{({\mathcal{X}}_1^q+{\mathcal{X}}_2^q-{\mathcal{X}}_1^q{\mathcal{X}}_2^q)}^{1/q}\rangle$

(6) $\sigma {\mathcal{G}}_1=\langle {(1-{(1-{\mathcal{Y}}_1^q)}^{\sigma })}^{1/q},{\mathcal{X}}_1^{\sigma }\rangle$

(7) ${\mathcal{G}}_1^{\sigma }=\langle {\mathcal{Y}}_1^{\sigma },{(1-{(1-{\mathcal{X}}_1^q)}^{\sigma })}^{1/q}\rangle$

Definition 3.

Suppose $\tilde{\Re }=\langle \mathcal{Y},\mathcal{X}\rangle$ is a q-ROFN, then a score function $\mathfrak{E}$ of $\tilde{\Re }$ is defined as:

$$\mathfrak{E}\left(\tilde{\Re }\right)={\mathcal{Y}}^q-{\mathcal{X}}^q$$

$\mathfrak{E}\left(\tilde{\Re }\right)\in [-1,1]$. The score of a q-ROFN defines its ranking, i.e., a high score defines the high preference of q-ROFN. However, the score function is not useful in many cases of q-ROFN. For example, let us consider ${\mathcal{G}}_1=\langle 0.6138,0.2534\rangle$ and ${\mathcal{G}}_2=\langle 0.7147,0.4453\rangle$ to be two q-ROFNs, if we take the value of q to be two. Then, $\mathfrak{E}\left({\mathcal{G}}_1\right)=0.3125=\mathfrak{E}\left({\mathcal{G}}_2\right)$, i.e, the score functions of ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ are the same. Therefore, to compare the q-ROFNs, it is not necessary to rely on the score function. We add a further method, the accuracy function, to solve this issue.

Definition 4.

Suppose $\tilde{\Re }=\langle \mathcal{Y},\mathcal{X}\rangle$ is a q-ROFN, then an accuracy function $\mathfrak{R}$ of $\tilde{\Re }$ is defined as:

$$\mathfrak{R}\left(\tilde{\Re }\right)={\mathcal{Y}}^q+{\mathcal{X}}^q$$

$\mathfrak{R}\left(\tilde{\Re }\right)\in [0,1]$. The high value of accuracy degree $\mathfrak{R}\left(\tilde{\Re }\right)$ defines the high preference of $\tilde{\Re }$.

Again, consider ${\mathcal{G}}_1=\langle 0.6138,0.2534\rangle$ and ${\mathcal{G}}_2=\langle 0.7147,0.4453\rangle$ to be two q-ROFNs. Then, their accuracy functions are $\mathfrak{R}\left({\mathcal{G}}_1\right)=0.4410$ and $\mathfrak{R}\left({\mathcal{G}}_2\right)=0.4410$, so by the accuracy function, we have ${\mathcal{G}}_1<{\mathcal{G}}_2$.

Definition 5.

Let $\mathcal{Y}=\langle {\mathcal{Y}}_{\mathcal{Y}},{\mathcal{X}}_{\mathcal{Y}}\rangle$ and $\mathfrak{M}=\langle {\mathcal{Y}}_{\mathfrak{M}},{\mathcal{X}}_{\mathfrak{M}}\rangle$ be any two q-ROFN and $\mathfrak{E}\left(\mathcal{Y}\right),\mathfrak{E}\left(\mathfrak{M}\right)$ be the score function of $\mathcal{Y}$ and $\mathfrak{M}$, while $\mathfrak{R}\left(\mathcal{Y}\right),\mathfrak{R}\left(\mathfrak{M}\right)$ are the accuracy functions of $\mathcal{Y}$ and $\mathfrak{M}$, respectively, then:

(1) If $\mathfrak{E}\left(\mathcal{Y}\right)>\mathfrak{E}\left(\mathfrak{M}\right)$, then $\mathcal{Y}>\mathfrak{M}$

(2) If $\mathfrak{E}\left(\mathcal{Y}\right)=\mathfrak{E}\left(\mathfrak{M}\right)$, then

if $\mathfrak{R}\left(\mathcal{Y}\right)>\mathfrak{R}\left(\mathfrak{M}\right)$, then $\mathcal{Y}>\mathfrak{M}$,

if $\mathfrak{R}\left(\mathcal{Y}\right)=\mathfrak{R}\left(\mathfrak{M}\right)$, then $\mathcal{Y}=\mathfrak{M}$.

It should always be noticed that the value of score function is between –1 and one. We introduce another score function, to support the following research, $\mathcal{H}(\Re )=\frac{1+{\mathcal{Y}}_{\Re }^q-{\mathcal{X}}_{\Re }^q}{2}$. We can see that $0\le \mathcal{H}(\Re )\le 1$. This new score function satisfies all properties of the score function defined by Yager [41].

2.1. q-rung Orthopair Fuzzy Aggregation Operators

Definition 6

([65]). Assume that ${\breve{\mathcal{G}}}_k=\langle {\mathcal{Y}}_k,{\mathcal{X}}_k\rangle$ is a family of q-ROFNs, and q-ROFWA $:{\mathsf{\Lambda }}^n\to \mathsf{\Lambda }$, if:

$$\begin{array}{cc}\hfill q-ROFWA({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)& =\sum _{k=1}^n{\mathfrak{F}}_k{\breve{\mathcal{G}}}_k\hfill \\ \hfill & ={\mathfrak{F}}_1{\breve{\mathcal{G}}}_1\oplus {\mathfrak{F}}_2{\breve{\mathcal{G}}}_2\oplus ,\dots ,{\mathfrak{F}}_n{\breve{\mathcal{G}}}_n\hfill \end{array}$$

where ${\mathsf{\Lambda }}^n$ is the set of all q-ROFNs, and $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)$, such that $0⩽{\mathfrak{F}}_k⩽1$ and ${\sum }_{k=1}^n{\mathfrak{F}}_k=1$. Then, the q-ROFWA is called the q-rung orthopair fuzzy weighted average operator.

Based on q-ROFNs operational rules, we can also consider q-ROFWA by the theorem below.

Theorem 1

([65]). Let ${\breve{\mathcal{G}}}_k=\langle {\mathcal{Y}}_k,{\mathcal{X}}_k\rangle$ be the family of q-ROFNs; we can find $q-ROFWA$ by:

$$q-ROFWA({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)={\displaystyle \langle }\sqrt[q]{(1-{\prod }_{k=1}^n{(1-{\mathcal{Y}}_k^q)}^{{\mathfrak{F}}_k})},\prod _{k=1}^n{\mathcal{X}}_k^{{\mathfrak{F}}_k}{\displaystyle \rangle }$$

Definition 7

([65]). Assume that ${\breve{\mathcal{G}}}_k=\langle {\mathcal{Y}}_k,{\mathcal{X}}_k\rangle$ is the family of $q-ROFN$, and $q-ROFWG:{\mathsf{\Lambda }}^n\to \mathsf{\Lambda }$, if:

$$\begin{array}{cc}\hfill q-ROFWG({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)& =\sum _{k=1}^n{\breve{\mathcal{G}}}_k^{{\mathfrak{F}}_k}\hfill \\ \hfill & ={\breve{\mathcal{G}}}_1^{{\mathfrak{F}}_1}\otimes {\breve{\mathcal{G}}}_2^{{\mathfrak{F}}_2}\otimes ,\dots ,{\breve{\mathcal{G}}}_n^{{\mathfrak{F}}_n}\hfill \end{array}$$

where ${\mathsf{\Lambda }}^n$ is the set of all $q-ROFNs$ and $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)$, such that $0⩽{\mathfrak{F}}_k⩽1$ and ${\sum }_{k=1}^n{\mathfrak{F}}_k=1$. Then, the $q-ROFWG$ is called the q-rung orthopair fuzzy weighted geometric operator.

Based on q-ROFNs operational rules, we can also consider q-ROFWG by the theorem below.

Theorem 2

([65]). Let ${\breve{\mathcal{G}}}_k=\langle {\mathcal{Y}}_k,{\mathcal{X}}_k\rangle$ be the family of q-ROFNs; we can find $q-ROFWG$ by:

$$q-ROFWG({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)={\displaystyle \langle }\prod _{k=1}^n{\mathcal{Y}}_k^{{\mathfrak{F}}_k},\sqrt[q]{(1-{\prod }_{k=1}^n{(1-{\mathcal{X}}_k^q)}^{{\mathfrak{F}}_k})}{\displaystyle \rangle }$$

2.2. Superiority and Comparison of q-ROFNs with Some Existing Theories

In this part, we discuss the superiority and comparison of q-ROFNs with some existing structures such as fuzzy numbers (FNs), IFNs, and PFNs. In the decision making problem, if we take the input information by using FNs, then we cannot talk about the dissatisfaction part of the alternatives or decision makers’ opinion. If we use IFNs and PFNs, then we cannot take the membership and nonmembership values with the open choice of the real world situation. The constraints restrict them to limited criteria. For example, $0.8+0.7=1.5>1$ and ${0.8}^2+{0.7}^2=1.13>1$, which contradicts the conditions of IFNs and PFNs. However, if we select $q=3$, then for 3-ROFN, the constraint implies that ${0.8}^3+{0.77}^3=0.855<1$. This criteria satisfies the fuzzy criteria, and we can handle the decision making input with a wide domain.

Table 2. Comparison of q-ROFS with some existing theories.

Set	Truth	Falsity	Advantages	Limitations
Theory	Information	Information
Fuzzy sets [37]	✓	×	can handle uncertainty	do not give any information about
			using fuzzy interval	the non-membership grades in input data
Intuitionistic	✓	✓	can handle uncertainty	cannot deal with the problems satisfying
Fuzzy sets [38]			using membership	0 ≤ membership + non-membership > 1
			and non-membership grades
Pythagorean	✓	✓	larger valuation space	cannot deal with the problems satisfying
Fuzzy sets [39,40,41]			than IFNs	0 ≤ membership2 + non-membership2 > 1
q-rung orthopair	✓	✓	larger valuation space	cannot deal with the problems
Fuzzy sets [42,43]			than IFNs and PFNs	when membership=1 and nonmembership=1

represents the brief comparison of the advantages and limitations of q-ROFN with some exiting theories.

3. q-Rung Orthopair Fuzzy Prioritized Aggregation Operators

Within this section, we present the notion of the q-rung orthopair fuzzy prioritized weighted average (q-ROFPWA) operator and q-rung orthopair fuzzy prioritized weighted geometric (q-ROFPWG) operator. Then, we discuss other attractive properties of the proposed operators like idempotency, boundary, and monotonicity in detail.

3.1. q-ROFPWA Operator

Definition 8.

Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs, and $q-ROFPWA:{\mathsf{\Lambda }}^n\to \mathsf{\Lambda }$, being a n-dimensional mapping. If:

$$q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)=\frac{{\breve{\mathcal{T}}}_1}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}{\breve{\mathcal{G}}}_1\oplus \frac{{\breve{\mathcal{T}}}_2}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}{\breve{\mathcal{G}}}_2\oplus ,\dots ,\oplus \frac{{\breve{\mathcal{T}}}_n}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}{\breve{\mathcal{G}}}_n$$

(1)

then the mapping q-ROFPWA is called the q-rung orthopair fuzzy prioritized weighted averaging (q-ROFPWA) operator, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN.

Based on q-ROFN operational rules, we can also consider q-ROFPWA by the theorem below.

Theorem 3.

Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs; we can find q−ROFPWA by:

$$q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)={\displaystyle \langle }\sqrt[q]{(1-{\prod }_{j=1}^n{(1-{\mathcal{Y}}_j^q)}^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}},\prod _{j=1}^n{\mathcal{X}}_j^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}{\displaystyle \rangle }$$

(2)

Proof. 

See Appendix A. □

Below, we define some of q-ROFPWA’s appealing properties.

Theorem 4.

(Idempotency) Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN. If all ${\breve{\mathcal{G}}}_j$ are equal, i.e., ${\breve{\mathcal{G}}}_j=\breve{\mathcal{G}}$ for all j, then:

$$q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)=\breve{\mathcal{G}}$$

Proof. 

See Appendix A.1. □

Corollary 1.

If ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$$j=(1,2,\dots ,n)$ is the family of the largest q-ROFNs, i.e., ${\breve{\mathcal{G}}}_j=(1,0)$ for all j, then:

$$q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)=(1,0)$$

Proof. 

We can easily obtain the corollary similar to Theorem 4. □

Corollary 2.

(Non-compensatory) If ${\breve{\mathcal{G}}}_1=\langle {\mathcal{Y}}_1,{\mathcal{X}}_1\rangle$ is the smallest q-ROFN, i.e., ${\breve{\mathcal{G}}}_1=(0,1)$, then:

$$q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)=(0,1)$$

Proof. 

See Appendix A.2. □

Corollary 4 means that, if the higher priority criteria are met by the smallest q-ROFN, rewards will not be received by other criteria even though they are fulfilled.

Theorem 5

(Monotonicity). Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ and ${\breve{\mathcal{G}}}_j^{*}=\langle {\mathcal{Y}}_j^{*},{\mathcal{X}}_j^{*}\rangle$ are the families of q-ROFNs, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$, ${\breve{\mathcal{T}}}_j^{*}={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k^{*}\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, ${\breve{\mathcal{T}}}_1^{*}=1$, $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of ${\breve{\mathcal{G}}}_k$ q-ROFN, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k^{*}\right)$ is the score of ${\breve{\mathcal{G}}}_k^{*}$ q-ROFN. If ${\mathcal{Y}}_j^{*}\ge {\mathcal{Y}}_j$ and ${\mathcal{X}}_j^{*}\le {\mathcal{X}}_j$ for all j, then:

$$q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\le q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1^{*},{\breve{\mathcal{G}}}_2^{*},\dots ,{\breve{\mathcal{G}}}_n^{*})$$

Proof. 

See Appendix A.3. □

Theorem 6.

(Boundary) Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs, and:

$${\breve{\mathcal{G}}}^{-}=(mi{n}_j\left({\mathcal{Y}}_j\right),ma{x}_j\left({\mathcal{X}}_j\right))\mathit{and}{\breve{\mathcal{G}}}^{+}=(ma{x}_j\left({\mathcal{Y}}_j\right),mi{n}_j\left({\mathcal{X}}_j\right))$$

Then,

$${\breve{\mathcal{G}}}^{-}\le q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\le {\breve{\mathcal{G}}}^{+}$$

where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN.

Proof. 

See Appendix A.4. □

Theorem 7.

Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ and ${\beta }_j=\langle {\varphi }_j,{\phi }_j\rangle$ are two families of q-ROFNs, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN. If $r>0$ and $\beta =\langle {\mathcal{Y}}_{\beta },{\mathcal{X}}_{\beta }\rangle$ is an q-ROFN, then,

1. $q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1\oplus \beta ,{\breve{\mathcal{G}}}_2\oplus \beta ,\dots ,{\breve{\mathcal{G}}}_n\oplus \beta )=q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\oplus \beta$

2. $q-\mathit{ROFPWA}(r{\breve{\mathcal{G}}}_1,r{\breve{\mathcal{G}}}_2,\dots ,r{\breve{\mathcal{G}}}_n)=rq-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)$

3. $q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1\oplus {\beta }_1,{\breve{\mathcal{G}}}_2\oplus {\beta }_2,\dots ,{\breve{\mathcal{G}}}_n\oplus {\beta }_n)=q-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\oplus q-\mathit{ROFPWA}$$({\beta }_1,{\beta }_2,\dots ,$${\beta }_n)$

4. $q-\mathit{ROFPWA}(r{\breve{\mathcal{G}}}_1\oplus \beta \oplus r{\breve{\mathcal{G}}}_2\oplus \beta ,\dots ,\oplus r{\breve{\mathcal{G}}}_n\oplus \beta )=rq-\mathit{ROFPWA}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\oplus \beta$

Proof. 

See Appendix A.5. □

3.2. q-ROFPWG Operator

Definition 9.

Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs, and $q-ROFPWG:{\mathsf{\Lambda }}^n\to \mathsf{\Lambda }$, being an n-dimensional mapping. If:

$$q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)={\breve{\mathcal{G}}}_1^{\frac{{\breve{\mathcal{T}}}_1}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}\otimes {\breve{\mathcal{G}}}_2^{\frac{{\breve{\mathcal{T}}}_2}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}\otimes ,\dots ,\otimes {\breve{\mathcal{G}}}_n^{\frac{{\breve{\mathcal{T}}}_n}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}$$

(3)

then the mapping q-ROFPWG is called the q-rung orthopair fuzzy prioritized weighted geometric (q-ROFPWG) operator, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN.

Based on q-ROFNs operational rules, we can also consider q-ROFPWG by the theorem below.

Theorem 8.

Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs; we can find q−ROFPWG by:

$$q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)={\displaystyle \langle }\prod _{j=1}^n{\mathcal{Y}}_j^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}},\sqrt[q]{(1-{\prod }_{j=1}^n{(1-{\mathcal{X}}_j^q)}^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}}{\displaystyle \rangle }$$

(4)

Proof. 

See Appendix B. □

Below, we define some of the q-ROFPWG operator’s appealing properties.

Theorem 9

(Idempotency). Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN. If all ${\breve{\mathcal{G}}}_j$ are equal, i.e., ${\breve{\mathcal{G}}}_j=\breve{\mathcal{G}}$ for all j, then:

$$q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)=\breve{\mathcal{G}}$$

Proof. 

See Appendix B.1. □

Corollary 3.

If ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$$j=(1,2,\dots ,n)$ is the family of the largest q-ROFNs, i.e., ${\breve{\mathcal{G}}}_j=(1,0)$ for all j, then:

$$q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)=(1,0)$$

Proof. 

We can easily obtain the corollary similar to Theorem 4. □

Corollary 4

(Non-compensatory). If ${\breve{\mathcal{G}}}_1=\langle {\mathcal{Y}}_1,{\mathcal{X}}_1\rangle$ is the smallest q-ROFN, i.e., ${\breve{\mathcal{G}}}_1=(0,1)$, then:

$$q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)=(0,1)$$

Proof. 

See Appendix B.2. □

Corollary 4 means that, if the higher priority criteria are met by the smallest q-ROFN, rewards will not be received by other criteria even though they are fulfilled.

Theorem 10

(Monotonicity). Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ and ${\breve{\mathcal{G}}}_j^{*}=\langle {\mathcal{Y}}_j^{*},{\mathcal{X}}_j^{*}\rangle$ are the families of q-ROFNs, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$, ${\breve{\mathcal{T}}}_j^{*}={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k^{*}\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, ${\breve{\mathcal{T}}}_1^{*}=1$, $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of ${\breve{\mathcal{G}}}_k$ q-ROFN, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k^{*}\right)$ is the score of ${\breve{\mathcal{G}}}_k^{*}$ q-ROFN. If ${\mathcal{Y}}_j^{*}\ge {\mathcal{Y}}_j$ and ${\mathcal{X}}_j^{*}\le {\mathcal{X}}_j$ for all j, then:

$$q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\le q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1^{*},{\breve{\mathcal{G}}}_2^{*},\dots ,{\breve{\mathcal{G}}}_n^{*})$$

Proof. 

See Appendix B.3. □

Theorem 11

(Boundary). Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ is the family of q-ROFNs, and:

$${\breve{\mathcal{G}}}^{-}=(mi{n}_j\left({\mathcal{Y}}_j\right),ma{x}_j\left({\mathcal{X}}_j\right))\mathit{and}{\breve{\mathcal{G}}}^{+}=(ma{x}_j\left({\mathcal{Y}}_j\right),mi{n}_j\left({\mathcal{X}}_j\right))$$

Then,

$${\breve{\mathcal{G}}}^{-}\le q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\le {\breve{\mathcal{G}}}^{+}$$

where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN.

Proof. 

The proof of this theorem is the same as Theorem 6. □

Theorem 12.

Assume that ${\breve{\mathcal{G}}}_j=\langle {\mathcal{Y}}_j,{\mathcal{X}}_j\rangle$ and ${\beta }_j=\langle {\varphi }_j,{\phi }_j\rangle$ are two families of q-ROFNs, where ${\breve{\mathcal{T}}}_j={\prod }_{k=1}^{j-1}\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$$(j=2,\dots ,n)$, ${\breve{\mathcal{T}}}_1=1$, and $\mathcal{H}\left({\breve{\mathcal{G}}}_k\right)$ is the score of the $k^{\mathrm{th}}$ q-ROFN. If $r>0$ and $\beta =\langle {\mathcal{Y}}_{\beta },{\mathcal{X}}_{\beta }\rangle$ is an q-ROFN, then,

1. $q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1\oplus \beta ,{\breve{\mathcal{G}}}_2\oplus \beta ,\dots ,{\breve{\mathcal{G}}}_n\oplus \beta )=q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\oplus \beta$

2. $q-\mathit{ROFPWG}(r{\breve{\mathcal{G}}}_1,r{\breve{\mathcal{G}}}_2,\dots ,r{\breve{\mathcal{G}}}_n)=rq-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)$

3. $q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1\oplus {\beta }_1,{\breve{\mathcal{G}}}_2\oplus {\beta }_2,\dots ,{\breve{\mathcal{G}}}_n\oplus {\beta }_n)=q-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\oplus q-\mathit{ROFPWG}({\beta }_1,{\beta }_2,\dots ,{\beta }_n)$

4. $q-\mathit{ROFPWG}(r{\breve{\mathcal{G}}}_1\oplus \beta \oplus r{\breve{\mathcal{G}}}_2\oplus \beta ,\dots ,\oplus r{\breve{\mathcal{G}}}_n\oplus \beta )=rq-\mathit{ROFPWG}({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)\oplus \beta$

Proof. 

The proof of this theorem is the same as Theorem 7. □

4. Proposed Methodology

Consider a set of alternatives $\mathcal{A}=\{{\mathcal{A}}_1,{\mathcal{A}}_2,\dots ,{\mathcal{A}}_m\}$ with m elements; $\mathfrak{O}=\{{\mathfrak{O}}_1,{\mathfrak{O}}_2,\dots ,{\mathfrak{O}}_n\}$ is the finite set of criteria with n elements; and prioritization is given between the criteria presented by the linear order ${\mathfrak{O}}_1\succ {\mathfrak{O}}_2\succ {\mathfrak{O}}_3\dots {\mathfrak{O}}_n$ indicating that criteria ${\mathfrak{O}}_J$ have a higher priority than ${\mathfrak{O}}_i$ if $j>i$. $\mathfrak{K}=\{{\mathfrak{K}}_1,{\mathfrak{K}}_2,\dots ,{\mathfrak{K}}_p\}$ is the group of decision makers, and decision makers (DMs) do not have equal importance. Prioritization is given between the DMs presented by the linear order ${\mathfrak{K}}_1\succ {\mathfrak{K}}_2\succ {\mathfrak{K}}_3\dots {\mathfrak{K}}_p$ indicating DM ${\mathfrak{K}}_{\zeta }$ has a higher priority than ${\mathfrak{K}}_{\varrho }$ if $\zeta >\varrho$. Decision makers provide a matrix of their own opinion $D^{\left(p\right)}={\left({\mathcal{B}}_{ij}^{\left(p\right)}\right)}_{m\times n}$, where ${\mathcal{B}}_{ij}^{\left(p\right)}$ is given for the alternatives ${\mathcal{A}}_i\in \mathcal{A}$ with respect to the criteria ${\mathfrak{O}}_j\in \mathfrak{O}$ by the ${\mathfrak{K}}_p$ decision maker in the form of q-ROFNs. If all criteria are the same types, there is no need for normalization, but there are two types of criteria (benefit type attributes ${\tau }_b$ and cost type attributes ${\tau }_c$ ) in MCGDM; in this case, using the normalization formula the matrix $D^{\left(p\right)}$ has been changed into normalizing matrix $Y^{\left(p\right)}={\left({\mathcal{P}}_{ij}^{\left(p\right)}\right)}_{m\times n}$,

$${\left({\mathcal{P}}_{ij}^{\left(p\right)}\right)}_{m\times n}=\left\{\begin{array}{cc}{\left({\mathcal{B}}_{ij}^{\left(p\right)}\right)}^c;\hfill & j\in {\tau }_c\hfill \\ {\mathcal{B}}_{ij}^{\left(p\right)};\hfill & j\in {\tau }_b.\hfill \end{array}\right.$$

(5)

where ${\left({\mathcal{B}}_{ij}^{\left(p\right)}\right)}^c$ show the compliment of ${\mathcal{B}}_{ij}^{\left(p\right)}$.

We then use the q-ROFPWA operator or q-ROFPWA operator to implement an MCGDM approach in q-ROF circumstances.

The proposed operators will be applied to the MCGDM, which involves the following steps given in Algorithm 1.

Algorithm 1 Selection of green supplier chain management.

Input:

Step 1:

Acquire a decision matrix $D^{\left(p\right)}={\left({\mathcal{B}}_{ij}^{\left(p\right)}\right)}_{m\times n}$ in the form of q-ROFNs from the decision makers. $$\begin{array}{cccccc}\hfill cccccc& & {\mathfrak{O}}_1\hfill & {\mathfrak{O}}_2& & {\mathfrak{O}}_n\\ \hfill \begin{array}{c}\hfill cc\left[cccc\right]{\mathfrak{K}}_1\end{array}& {\mathcal{A}}_1& ({\mathcal{Y}}_{11}^1,{\mathcal{X}}_{11}^1)\hfill & ({\mathcal{Y}}_{12}^1,{\mathcal{X}}_{12}^1)& \cdots \cdots & ({\mathcal{Y}}_{1n}^1,{\mathcal{X}}_{1n}^1)\left[t\right]\\ \hfill & {\mathcal{A}}_2& ({\mathcal{Y}}_{21}^1,{\mathcal{X}}_{21}^1)\hfill & ({\mathcal{Y}}_{22}^1,{\mathcal{X}}_{22}^1)& \cdots \cdots & ({\mathcal{Y}}_{2n}^1,{\mathcal{X}}_{2n}^1)\\ \hfill & & ⋮\hfill & ⋮& \ddots \ddots & ⋮\\ \hfill & {\mathcal{A}}_m& ({\mathcal{Y}}_{m1}^1,{\mathcal{X}}_{m1}^1)\hfill & ({\mathcal{Y}}_{m2}^1,{\mathcal{X}}_{m2}^1)& \cdots \cdots & ({\mathcal{Y}}_{mn}^1,{\mathcal{X}}_{mn}^1)\left[b\right]\\ \hfill {\mathfrak{K}}_2& {\mathcal{A}}_1& ({\mathcal{Y}}_{11}^2,{\mathcal{X}}_{11}^2)\hfill & ({\mathcal{Y}}_{12}^2,{\mathcal{X}}_{12}^2)& \cdots \cdots & ({\mathcal{Y}}_{1n}^2,{\mathcal{X}}_{1n}^2)\left[t\right]\\ \hfill ⋮& {\mathcal{A}}_2& ({\mathcal{Y}}_{21}^2,{\mathcal{X}}_{21}^2)\hfill & ({\mathcal{Y}}_{22}^2,{\mathcal{X}}_{22}^2)& \cdots \cdots & ({\mathcal{Y}}_{2n}^2,{\mathcal{X}}_{2n}^2)\\ \hfill & & ⋮\hfill & ⋮& \ddots \ddots & ⋮\\ \hfill & {\mathcal{A}}_m& ({\mathcal{Y}}_{m1}^2,{\mathcal{X}}_{m1}^2)\hfill & ({\mathcal{Y}}_{m2}^2,{\mathcal{X}}_{m2}^2)& \cdots \cdots & ({\mathcal{Y}}_{mn}^2,{\mathcal{X}}_{mn}^2)\left[b\right]\\ \hfill {\mathfrak{K}}_p& {\mathcal{A}}_1& ({\mathcal{Y}}_{11}^p,{\mathcal{X}}_{11}^p)\hfill & ({\mathcal{Y}}_{12}^p,{\mathcal{X}}_{12}^p)& \cdots \cdots & ({\mathcal{Y}}_{1n}^p,{\mathcal{X}}_{1n}^p)\left[t\right]\\ \hfill & {\mathcal{A}}_2& ({\mathcal{Y}}_{21}^p,{\mathcal{X}}_{21}^p)\hfill & ({\mathcal{Y}}_{22}^p,{\mathcal{X}}_{22}^p)& \cdots \cdots & {({\mathcal{Y}}_{2n}^p,{\mathcal{X}}_{2n})}^p\\ \hfill & & ⋮\hfill & ⋮& \ddots \ddots & ⋮\\ \hfill & {\mathcal{A}}_m& ({\mathcal{Y}}_{m1}^p,{\mathcal{X}}_{m1}^p)\hfill & ({\mathcal{Y}}_{m2}^p,{\mathcal{X}}_{m2}^p)& \cdots \cdots & ({\mathcal{Y}}_{mn}^p,{\mathcal{X}}_{mn}^p)\left[b\right]\end{array}$$

Step 2:

Two types of criteria are specified in the decision matrix, namely cost type criteria $\left({\tau }_c\right)$ and benefit type criteria $\left({\tau }_b\right)$. If all criteria are the same types, there is no need for normalization, but there are two types of criteria in MCGDM. In this case, using the normalization formula Equation (5), the matrix is changed into transformed response matrix $Y^{\left(p\right)}={\left({\mathcal{P}}_{ij}^{\left(p\right)}\right)}_{m\times n}$.

Calculations:

Step 3:

Calculate the values of ${\breve{\mathcal{T}}}_{ij}^{\left(p\right)}$ by the following formula. $${\breve{\mathcal{T}}}_{ij}^{\left(p\right)}=\prod _{k=1}^{p-1}\mathcal{H}\left({\mathcal{P}}_{ij}^{\left(k\right)}\right)(p=2,\dots ,n),$$ (6) $${\breve{\mathcal{T}}}_{ij}^{\left(1\right)}=1$$

Step 4:

Use one of the suggested aggregation operators. $${\mathcal{W}}_{ij}=\mathrm{q}-\mathrm{ROFPWA}({\mathcal{P}}_{ij}^{\left(1\right)},{\mathcal{P}}_{ij}^{\left(2\right)},\dots ,{\mathcal{P}}_{ij}^{\left(p\right)})={\displaystyle \langle }\sqrt[q]{(1-{\prod }_{z=1}^p(1-{\left({\left({\mathcal{Y}}_{ij}^q\right)}^z\right)}^{\frac{{\breve{\mathcal{T}}}_j^z}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j^z}}},\prod _{z=1}^p{\left({\left({\mathcal{X}}_{ij}^q\right)}^z\right)}^{\frac{{\breve{\mathcal{T}}}_j^z}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j^z}}{\displaystyle \rangle }$$ (7) or: $${\mathcal{W}}_{ij}=\mathrm{q}-\mathrm{ROFPWA}({\mathcal{P}}_{ij}^{\left(1\right)},{\mathcal{P}}_{ij}^{\left(2\right)},\dots ,{\mathcal{P}}_{ij}^{\left(p\right)})={\displaystyle \langle }\prod _{z=1}^p{\left({\left({\mathcal{Y}}_{ij}^q\right)}^z\right)}^{\frac{{\breve{\mathcal{T}}}_j^z}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j^z}},\sqrt[q]{(1-{\prod }_{z=1}^p(1-{\left({\left({\mathcal{X}}_{ij}^q\right)}^z\right)}^{\frac{{\breve{\mathcal{T}}}_j^z}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j^z}}}{\displaystyle \rangle }$$ (8) to aggregate all individual q-ROF decision matrices $Y^{\left(p\right)}={\left({\mathcal{P}}_{ij}^{\left(p\right)}\right)}_{m\times n}$ into one cumulative assessments matrix of the alternatives $W^{\left(p\right)}={\left({\mathcal{W}}_{ij}\right)}_{m\times n}$

Step 5:

Calculate the values of ${\breve{\mathcal{T}}}_{ij}$ by the following formula. $${\breve{\mathcal{T}}}_{ij}=\prod _{k=1}^{j-1}\mathcal{H}\left({\mathcal{W}}_{ik}\right)(j=2,\dots ,n),$$ (9) $${\breve{\mathcal{T}}}_{i1}=1$$

Step 6:

Aggregate the q-ROF values ${\mathcal{W}}_{ij}$ for each alternative ${\mathcal{A}}_i$ by the q-ROFPWA (or q-ROFPWG) operator: $${\mathcal{W}}_i=\mathrm{q}-\mathrm{ROFPWA}({\mathcal{P}}_{i1},{\mathcal{P}}_{i2},\dots ,{\mathcal{P}}_{in})={\displaystyle \langle }\sqrt[q]{(1-{\prod }_{j=1}^n(1-{\left({\mathcal{Y}}_{ij}^q\right)}^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}},\prod _{j=1}^n{\left({\mathcal{X}}_{ij}^q\right)}^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}{\displaystyle \rangle }$$ (10) or: $${\mathcal{W}}_i=\mathrm{q}-\mathrm{ROFPWG}({\mathcal{P}}_{i1},{\mathcal{P}}_{i2},\dots ,{\mathcal{P}}_{in})={\displaystyle \langle }\prod _{j=1}^n{\left({\mathcal{Y}}_{ij}^q\right)}^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}},\sqrt[q]{(1-{\prod }_{j=1}^n(1-{\left({\mathcal{X}}_{ij}^q\right)}^{\frac{{\breve{\mathcal{T}}}_j}{{\sum }_{j=1}^n{\breve{\mathcal{T}}}_j}}}{\displaystyle \rangle }$$ (11)

Output:

Step 7:

Evaluate the score of all cumulative alternative assessments.

Step 8:

Rank the alternatives by the score function and ultimately choose the most appropriate alternative.

5. Case Study

Environmental problems have grown and spread faster in recent decades, such forest fires, with respect to country by area and worldwide territory, which are a leading cause of weather change and world wide warming. In addition, environmental scarcity and air and water pollution have serious implications for flora and fauna and human life, with various diseases, such as ischemic cardiovascular disease, lung cancer, pulmonary chronic obstruction, stroke, dracunculiasis, cholera, tuberculosis, and typhoid. These are also of serious concern. The green supply chain definition aims to mitigate environmental degradation and to regulate air, water, and waste pollution through green business practices. The core philosophy behind the green concept is certainly one of improved environmental protection. However, companies adopt the green concept of “killing two birds with one stone” because the green supply chains will minimize environmental pollution and manufacturing costs and thus promote economic growth. Sustainability or the green supply chain relates to the notion that sustainable practices should be integrated into the conventional supply chain [24]. This involves the procurement, order, design, production, assembly, distribution, and end-of-life management of the supplier. 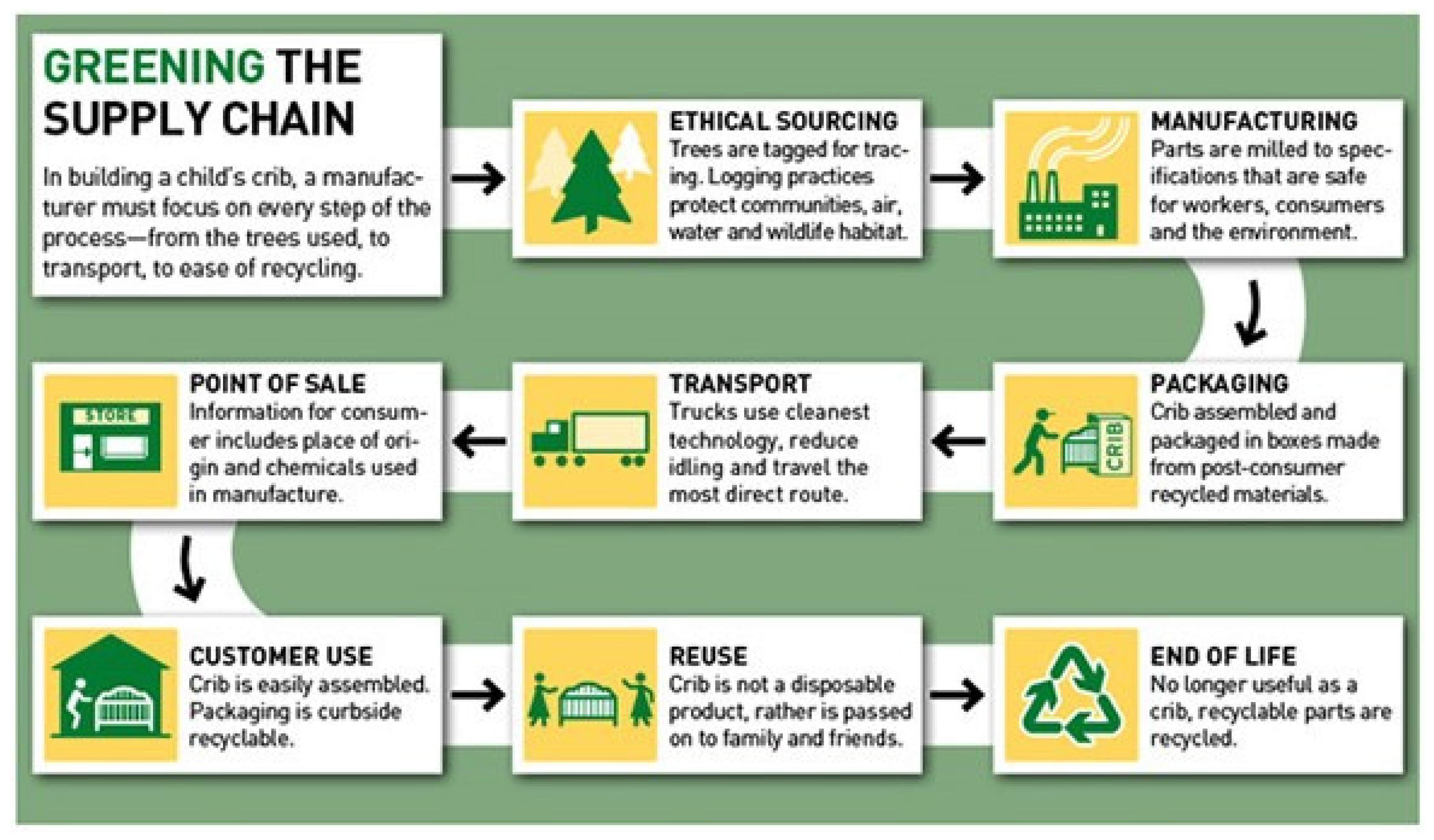Figure 2 shows an example of a GSCM for a vendor of baby cribs.

In the world, as environmental consciousness grows, businesses face intense pressure on their damaging impact on the environment from various stakeholders, including governments and clients. Indeed, the industry sector must consider incorporating its operating practices with sustainability into the service and manufacturing industry and rising end-to-end supply chain costs in order for it to have a competitive advantage. During the past few decades, the growing effects of global warming, climate change, waste, and air pollution have driven experts around the world to think more environmentally friendly [69]. Rath [19] described GSCM as a catalyst of organizational sustainable growth. GSCM needs a permanent collective interest in developing nations, as environmental issues continue to grow. In addition, the developing countries have recently become part of the green movement. Administrators of the green supply chain shall be incorporated into the management of the supply chain, including the design, procurement, and selection of goods, the production process, the distribution of the finished product to customers, and the end of the product’s life.

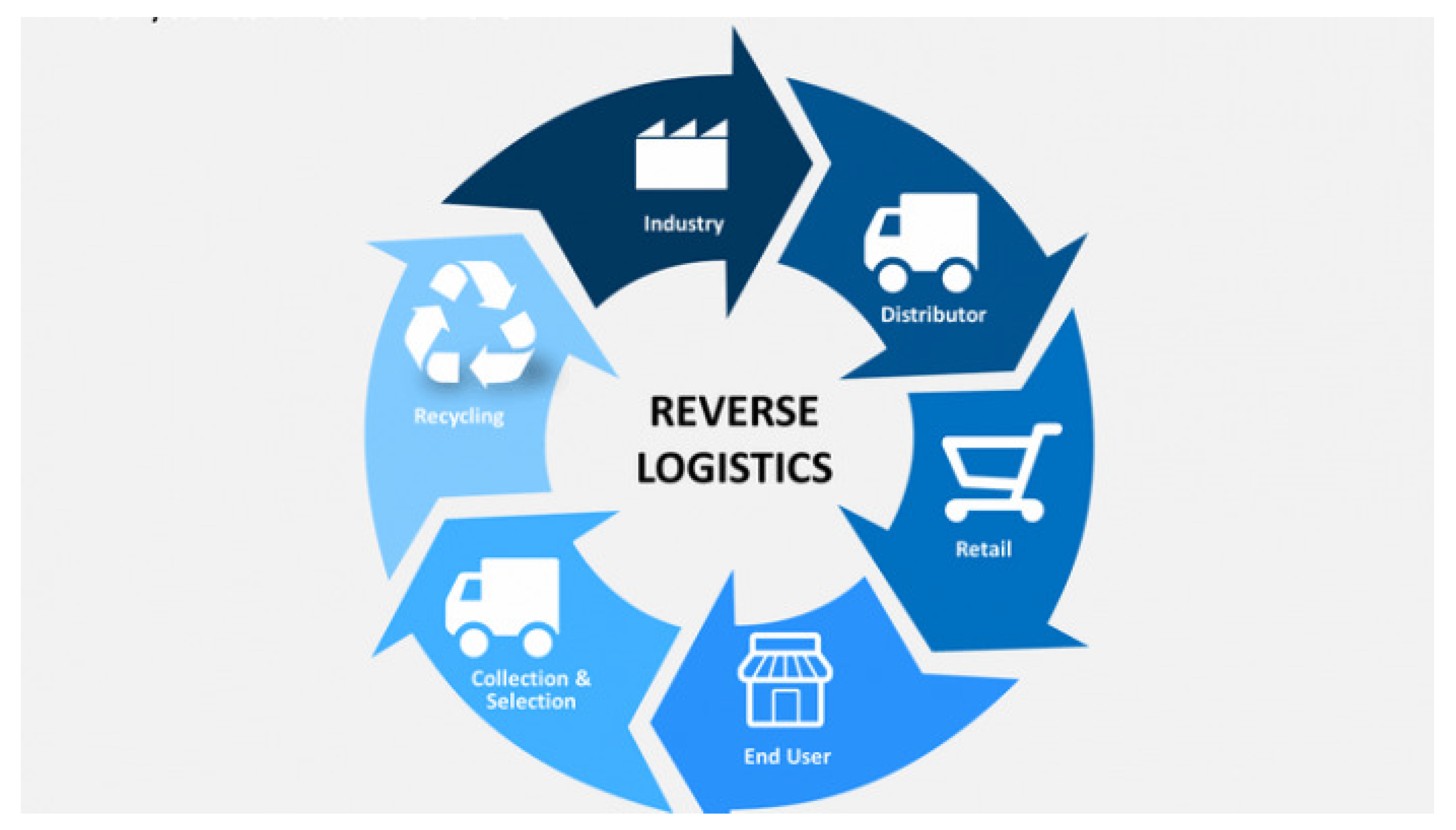
The model of reverse logistic activities plays a major role in enhancing green supply chain environmental, social, and economic performance. However, incorporating reverse logistics into the GSCM strategy is not a trivial task. Reverse logistics is characterized as the process of moving goods for things like reutilization, capture, or proper disposal outside their typical destination. Products flow from suppliers to end users in supply chain networks. The efficiency of the flow is calculated by the time delivery metric by supply chain managers. This is a standard metric of the supply chain aimed at ensuring a fast and efficient distribution to the end customer from the moment he/she places an order. Reverse logistics are more complex and are more of a concern than forward-looking logistics, which are more coordinated and also part of the scheduled methodologies of any company in the manufacturing, sales, storage, distribution, and servicing of its goods. Historically, reverse logistics has been one field that is often disorganized and disregarded by any manufacturing company. However, this is no longer so. For a company that does not have a planned reverse logistics strategy, the trends in its financial performance and market share may be a gloomy picture. Figure 3 shows the short summary of reverse logistics.

The implementation of ecological management values is necessary across the entire client order cycle, such as design, procurement, manufacture and assembly, packaging, transport, and delivery [32]. GSCM integrates eco-friendly concepts into supply chain management to improve environmental sustainability through a variety of green practices, including green purchasing, green distribution and storage, green transport using biofuels, green manufacturing processes, and end-of-life products [23]. There are several differences in its definition and terminology over the years [35], as we see in the definition of GSCM. Some words characterizing this definition are included in a detailed list below.

• Sustainable management of the supply network [13].
• Sustainability of supply and requirement across corporate social responsibility networks [22].
• Environmental supply chain management [18].
• Green purchasing [20].
• Green logistics [21].

A comprehensive definition of GSCM was given by Srivastava [17], “The GSCM is a aspect of environmental thought into the management of the supply chain including product design and material procurement, selection, manufacturing processes, the distribution and end-of-life management of the product to the customer”.

For an enterprise, GSCM has many advantages. The myth that greening would lead to lower sales and higher operating costs has vanished as many companies have now recognized that it will not be terrible and have been able to satisfy customers’ desires to incorporate environmental initiatives in their supply chains and turn them into higher profits. There is a connection between better environmental sustainability and financial incentives established by a number of businesses. Firms have gained an insight into their supply chains and found places where changes in the way they work can lead to increased income. Green logistics helps to reduce the emissions of many kinds such as CO₂ and CO. The use of non-fossil fuels such as for electric cars helps to reduce air pollution that affects human health when breathing the air. Various forms of fossil fuel are destroying the atmosphere because of pollution. For example, for marine life, aviation impacts the air quality due to diesel consumption. The same occurs on land using various types of transportation. Collectively, this impacts the environment, agriculture, and human health. Green logistics does help with these problems, however. In a company, green logistics, depending on the sector, is very beneficial. For example, trucks are used to transport products from A to B. The final destination will take days to get to. For the whole journey, the motorists and the cases of idling are more detrimental than driving the trucks. It costs much money to use petrol at the same time. Fuel consumption and energy costs will be reduced as trucks receive alternative or additional power for critical things such as lights and AC while idling. As less energy use = renewable resources, the company or organization will not invest in sustainability.

In the literature review, we discussed criteria for green supplier selection according to different researchers. In this paper, the criteria for the selection of green suppliers are considered as in

Table 3. Criteria for evaluating the best alternative. WEEE, waste electrical and electronic equipment; RoHS, restriction of hazardous substances.

	Criteria	Definition
${\mathfrak{O}}_1$	Quality	Reject rate, commitment to excellence in leadership,
		process improvement, warranty coverage and claims,
		and quality assurance.
${\mathfrak{O}}_2$	Cost	Value for price performance, compliance with demand,
		actions in the sector, and transportation cost.
${\mathfrak{O}}_3$	Delivery	Order fulfill rate, lead time, and order frequency.
${\mathfrak{O}}_4$	Service	Responsibility, inventory management, willingness,
		and design capability.
${\mathfrak{O}}_5$	Environment	Eco-design specifications, ozone depleting chemicals (ODC),
		WEEE, and RoHS.
${\mathfrak{O}}_6$	Corporate social responsibility	Employee privileges and rights,
		stakeholder rights, information disclosure,
		and respect for the policy.

.

5.1. Numerical Example

Consider a set of alternatives $\mathcal{A}=\{{\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_4,{\mathcal{A}}_5\}$, and $\mathfrak{O}=\{{\mathfrak{O}}_1,{\mathfrak{O}}_2,{\mathfrak{O}}_3,{\mathfrak{O}}_4,{\mathfrak{O}}_5,{\mathfrak{O}}_6\}$ is the finite set of criteria given in Table 3. Prioritization is given between the criteria presented by the linear order ${\mathfrak{O}}_1\succ {\mathfrak{O}}_2\succ {\mathfrak{O}}_3\dots {\mathfrak{O}}_6$ indicating criteria ${\mathfrak{O}}_J$ have a higher priority than ${\mathfrak{O}}_i$ if $j>i$. $\mathfrak{K}=\{{\mathfrak{K}}_1,{\mathfrak{K}}_2,{\mathfrak{K}}_3\}$ is the group of decision makers, and decision makers (DMs) do not have equal importance. Prioritization is given between the DMs presented by the linear order ${\mathfrak{K}}_1\succ {\mathfrak{K}}_2\succ {\mathfrak{K}}_3$ indicating DM ${\mathfrak{K}}_{\zeta }$ has a higher priority than ${\mathfrak{K}}_{\varrho }$ if $\zeta >\varrho$. Decision makers provide a matrix of their own opinion $D^{\left(p\right)}={\left({\mathcal{B}}_{ij}^{\left(p\right)}\right)}_{m\times n}$, where ${\mathcal{B}}_{ij}^{\left(p\right)}$ is given for the alternatives ${\mathcal{A}}_i\in \mathcal{A}$ with respect to the criteria ${\mathfrak{O}}_j\in \mathfrak{O}$ by the ${\mathfrak{K}}_p$ decision maker in the form of q-ROFNs. We take $q=3$.

Step 1: Acquire a decision matrix $D^{\left(p\right)}={\left({\mathcal{B}}_{ij}^{\left(p\right)}\right)}_{m\times n}$ in the form of q-ROFNs from three decision makers given as

Table 4. q-ROF decision matrix for ${\mathfrak{K}}_1$.

	${\mathfrak{O}}_1$	${\mathfrak{O}}_2$	${\mathfrak{O}}_3$	${\mathfrak{O}}_4$	${\mathfrak{O}}_5$	${\mathfrak{O}}_6$
${\mathcal{A}}_1$	(0.90, 0.00)	(0.65, 0.35)	(0.75, 0.15)	(0.95, 0.15)	(0.75, 0.00)	(0.45, 0.25)
${\mathcal{A}}_2$	(0.95, 0.25)	(0.80, 0.30)	(0.55, 0.25)	(0.75, 0.15)	(0.45, 0.45)	(0.35, 0.15)
${\mathcal{A}}_3$	(0.85, 0.15)	(0.35, 0.55)	(0.75, 0.25)	(0.55, 0.00)	(0.65, 0.35)	(0.45, 0.00)
${\mathcal{A}}_4$	(0.75, 0.35)	(0.81, 0.25)	(0.65, 0.15)	(0.35, 0.25)	(0.75, 0.25)	(0.35, 0.75)
${\mathcal{A}}_5$	(0.80, 0.25)	(0.60, 0.00)	(0.25, 0.15)	(0.15, 0.65)	(0.65, 0.15)	(0.25, 0.65)

,

Table 5. q-ROF decision matrix for ${\mathfrak{K}}_2$.

	${\mathfrak{O}}_1$	${\mathfrak{O}}_2$	${\mathfrak{O}}_3$	${\mathfrak{O}}_4$	${\mathfrak{O}}_5$	${\mathfrak{O}}_6$
${\mathcal{A}}_1$	(0.75, 0.25)	(0.55, 0.30)	(0.85, 0.15)	(0.95, 0.15)	(0.80, 0.25)	(0.90, 0.15)
${\mathcal{A}}_2$	(0.55, 0.15)	(0.60, 0.35)	(0.45, 0.15)	(0.75, 0.35)	(0.65, 0.30)	(0.75, 0.00)
${\mathcal{A}}_3$	(0.90, 0.60)	(0.65, 0.20)	(0.25, 0.55)	(0.65, 0.55)	(0.15, 0.25)	(0.70, 0.30)
${\mathcal{A}}_4$	(0.50, 0.00)	(0.55, 0.40)	(0.15, 0.10)	(0.50, 0.60)	(0.10, 0.15)	(0.60, 0.35)
${\mathcal{A}}_5$	(0.85, 0.35)	(0.70, 0.30)	(0.65, 0.55)	(0.25, 0.50)	(0.50, 0.30)	(0.50, 0.25)

and

Table 6. q-ROF decision matrix for ${\mathfrak{K}}_3$.

	${\mathfrak{O}}_1$	${\mathfrak{O}}_2$	${\mathfrak{O}}_3$	${\mathfrak{O}}_4$	${\mathfrak{O}}_5$	${\mathfrak{O}}_6$
${\mathcal{A}}_1$	(0.90, 0.15)	(0.85, 0.25)	(0.80, 0.00)	(0.70, 0.35)	(0.80, 0.20)	(0.70, 0.30)
${\mathcal{A}}_2$	(0.80, 0.25)	(0.55, 0.15)	(0.60, 0.25)	(0.50, 0.30)	(0.60, 0.30)	(0.60, 0.30)
${\mathcal{A}}_3$	(0.75, 0.15)	(0.65, 0.25)	(0.35, 0.00)	(0.50, 0.35)	(0.75, 0.30)	(0.35, 0.25)
${\mathcal{A}}_4$	(0.35, 0.35)	(0.50, 0.35)	(0.45, 0.25)	(0.55, 0.45)	(0.25, 0.25)	(0.65, 0.00)
${\mathcal{A}}_5$	(0.65, 0.25)	(0.65, 0.25)	(0.60, 0.15)	(0.65, 0.25)	(0.65, 0.55)	(0.45, 0.40)

.

Step 2: Normalize the decision matrices acquired by DMs using Equation (5). In Table 3, there are two types of criteria. ${\mathfrak{O}}_2$ is the cost type criteria, and the other is the benefit type criteria. The normalized Tables for all the decision-makers are represented as

Table 7. Normalized q-ROF decision matrix from ${\mathfrak{K}}_1$.

	${\mathfrak{O}}_1$	${\mathfrak{O}}_2$	${\mathfrak{O}}_3$	${\mathfrak{O}}_4$	${\mathfrak{O}}_5$	${\mathfrak{O}}_6$
${\mathcal{A}}_1$	(0.90, 0.00)	(0.35, 0.65)	(0.75, 0.15)	(0.95, 0.15)	(0.75, 0.00)	(0.45, 0.25)
${\mathcal{A}}_2$	(0.95, 0.25)	(0.30, 0.80)	(0.55, 0.25)	(0.75, 0.15)	(0.45, 0.45)	(0.35, 0.15)
${\mathcal{A}}_3$	(0.85, 0.15)	(0.55, 0.35)	(0.75, 0.25)	(0.55, 0.00)	(0.65, 0.35)	(0.45, 0.00)
${\mathcal{A}}_4$	(0.75, 0.35)	(0.25, 0.81)	(0.65, 0.15)	(0.35, 0.25)	(0.75, 0.25)	(0.35, 0.75)
${\mathcal{A}}_5$	(0.80, 0.25)	(0.00, 0.60)	(0.25, 0.15)	(0.15, 0.65)	(0.65, 0.15)	(0.25, 0.65)

,

Table 8. Normalized q-ROF decision matrix from ${\mathfrak{K}}_2$.

	${\mathfrak{O}}_1$	${\mathfrak{O}}_2$	${\mathfrak{O}}_3$	${\mathfrak{O}}_4$	${\mathfrak{O}}_5$	${\mathfrak{O}}_6$
${\mathcal{A}}_1$	(0.75, 0.25)	(0.30, 0.55)	(0.85, 0.15)	(0.95, 0.15)	(0.80, 0.25)	(0.90, 0.15)
${\mathcal{A}}_2$	(0.55, 0.15)	(0.35, 0.60)	(0.45, 0.15)	(0.75, 0.35)	(0.65, 0.30)	(0.75, 0.00)
${\mathcal{A}}_3$	(0.90, 0.60)	(0.20, 0.65)	(0.25, 0.55)	(0.65, 0.55)	(0.15, 0.25)	(0.70, 0.30)
${\mathcal{A}}_4$	(0.50, 0.00)	(0.40, 0.55)	(0.15, 0.10)	(0.50, 0.60)	(0.10, 0.15)	(0.60, 0.35)
${\mathcal{A}}_5$	(0.85, 0.35)	(0.30, 0.70)	(0.65, 0.55)	(0.25, 0.50)	(0.50, 0.30)	(0.50, 0.25)

and

Table 9. Normalized q-ROF decision matrix from ${\mathfrak{K}}_3$.

	${\mathfrak{O}}_1$	${\mathfrak{O}}_2$	${\mathfrak{O}}_3$	${\mathfrak{O}}_4$	${\mathfrak{O}}_5$	${\mathfrak{O}}_6$
${\mathcal{A}}_1$	(0.90, 0.15)	(0.25, 0.85)	(0.80, 0.00)	(0.70, 0.35)	(0.80, 0.20)	(0.70, 0.30)
${\mathcal{A}}_2$	(0.80, 0.25)	(0.15, 0.55)	(0.60, 0.25)	(0.50, 0.30)	(0.60, 0.30)	(0.60, 0.30)
${\mathcal{A}}_3$	(0.75, 0.15)	(0.25, 0.65)	(0.35, 0.00)	(0.50, 0.35)	(0.75, 0.30)	(0.35, 0.25)
${\mathcal{A}}_4$	(0.35, 0.35)	(0.35, 0.50)	(0.45, 0.25)	(0.55, 0.45)	(0.25, 0.25)	(0.65, 0.00)
${\mathcal{A}}_5$	(0.65, 0.25)	(0.25, 0.65)	(0.60, 0.15)	(0.65, 0.25)	(0.65, 0.55)	(0.45, 0.40)

.

Step 3: Calculate the values of ${\breve{\mathcal{T}}}_{ij}^{\left(p\right)}$ by Equation (6).

$${\breve{\mathcal{T}}}_{ij}^{\left(1\right)}=\left(\begin{array}{cccccc}1& 1& 1& 1& 1& 1\\ 1& 1& 1& 1& 1& 1\\ 1& 1& 1& 1& 1& 1\\ 1& 1& 1& 1& 1& 1\\ 1& 1& 1& 1& 1& 1\end{array}\right)$$

$${\breve{\mathcal{T}}}_{ij}^{\left(2\right)}=\left(\begin{array}{cccccc}0.8645& 0.3841& 0.7093& 0.9270& 0.7109& 0.5378\\ 0.9209& 0.2575& 0.5754& 0.7093& 0.5000& 0.5198\\ 0.8054& 0.5618& 0.7031& 0.5832& 0.6159& 0.5456\\ 0.6895& 0.2421& 0.6356& 0.5136& 0.7031& 0.3105\\ 0.7482& 0.3920& 0.5061& 0.3644& 0.6356& 0.3705\end{array}\right)$$

$${\breve{\mathcal{T}}}_{ij}^{\left(3\right)}=\left(\begin{array}{cccccc}0.6078& 0.1653& 0.5629& 0.8593& 0.5319& 0.4640\\ 0.5355& 0.1065& 0.3062& 0.4891& 0.3119& 0.3695\\ 0.6092& 0.2060& 0.2985& 0.3232& 0.3042& 0.3590\\ 0.3878& 0.1087& 0.3186& 0.2334& 0.3507& 0.1821\\ 0.5878& 0.1341& 0.2804& 0.1623& 0.3489& 0.3526\end{array}\right)$$

Step 4: Use q-ROFPWA to aggregate all individual q-ROF decision matrices $Y^{\left(p\right)}={\left({\mathcal{P}}_{ij}^{\left(p\right)}\right)}_{m\times n}$ into one cumulative assessments matrix of the alternatives $W^{\left(p\right)}={\left({\mathcal{W}}_{ij}\right)}_{m\times n}$ using Equation (7) given in

Table 10. Collective q-ROF decision matrix.

	${\mathfrak{O}}_1$	${\mathfrak{O}}_2$	${\mathfrak{O}}_3$	${\mathfrak{O}}_4$	${\mathfrak{O}}_5$	${\mathfrak{O}}_6$
${\mathcal{A}}_1$	(0.8648, 0.0000)	(0.3304, 0.6417)	(0.7997, 0.0000)	(0.9171, 0.1948)	(0.7796, 0.0000)	(0.7312, 0.2273)
${\mathcal{A}}_2$	(0.8611, 0.2064)	(0.3044, 0.7359)	(0.5343, 0.2138)	(0.7153, 0.2300)	(0.5512, 0.3752)	(0.5835, 0.0000)
${\mathcal{A}}_3$	(0.8600, 0.2382)	(0.3048, 0.7192)	(0.6288, 0.0000)	(0.5794, 0.0000)	(0.6081, 0.3474)	(0.5470, 0.0000)
${\mathcal{A}}_4$	(0.6472, 0.0000)	(0.2988, 0.7269)	(0.5491, 0.1429)	(0.4394, 0.3498)	(0.6184, 0.2099)	(0.4825, 0.0000)
${\mathcal{A}}_5$	(0.7936, 0.2784)	(0.2091, 0.6309)	(0.5051, 0.2167)	(0.3400, 0.5516)	(0.6124, 0.2353)	(0.3821, 0.4793)

.

Step 5: Evaluate the values of ${\breve{\mathcal{T}}}_{ij}$ by using Equation (9).

$${\breve{\mathcal{T}}}_{ij}=\left(\begin{array}{cccccc}1& 0.8234& 0.3178& 0.2402& 0.2118& 0.1561\\ 1& 0.8149& 0.2565& 0.1466& 0.0992& 0.0553\\ 1& 0.8113& 0.2663& 0.1663& 0.0993& 0.0587\\ 1& 0.6356& 0.2042& 0.1187& 0.0618& 0.0379\\ 1& 0.7391& 0.2801& 0.1567& 0.0683& 0.0415\end{array}\right)$$

Step 6: Aggregate the q-ROF values ${\mathcal{W}}_{ij}$ for each alternative ${\mathcal{A}}_i$ by the q-ROFPWA operator using Equation (10) given in

Table 11. q-ROF aggregated values ${\mathcal{W}}_i$.

${\mathcal{W}}_1$	(0.7899, 0.0000)
${\mathcal{W}}_2$	(0.7319, 0.0000)
${\mathcal{W}}_3$	(0.7299, 0.0000)
${\mathcal{W}}_4$	(0.5614, 0.0000)
${\mathcal{W}}_5$	(0.6576, 0.3704)

.

Step 7: Calculate the score of all q-ROF aggregated values ${\mathcal{W}}_i$.

$$\mathcal{H}\left({\mathcal{W}}_1\right)=0.7464$$

$$\mathcal{H}\left({\mathcal{W}}_2\right)=0.6960$$

$$\mathcal{H}\left({\mathcal{W}}_3\right)=0.6944$$

$$\mathcal{H}\left({\mathcal{W}}_4\right)=0.5885$$

$$\mathcal{H}\left({\mathcal{W}}_5\right)=0.6168$$

Step 8: Rank by the score function values.

$${\mathcal{W}}_1\succ {\mathcal{W}}_2\succ {\mathcal{W}}_3\succ {\mathcal{W}}_5\succ {\mathcal{W}}_4$$

Therefore,

$${\mathcal{A}}_1\succ {\mathcal{A}}_2\succ {\mathcal{A}}_3\succ {\mathcal{A}}_5\succ {\mathcal{A}}_4$$

5.2. Discussion and Symmetrical Analysis

In this part, we discuss the final results obtained from the calculations of green supplier selection by using the proposed aggregation operators.

Table 12. Results obtained via the proposed aggregation operators.

Alternatives	Ranking Order	Final Decision
q-ROFPWA	${\mathcal{A}}_1\succ {\mathcal{A}}_2\succ {\mathcal{A}}_3\succ {\mathcal{A}}_5\succ {\mathcal{A}}_4$	${\mathcal{A}}_1$
q-ROFPWG	${\mathcal{A}}_1\succ {\mathcal{A}}_2\succ {\mathcal{A}}_3\succ {\mathcal{A}}_4\succ {\mathcal{A}}_5$	${\mathcal{A}}_1$

represents the ranking of alternatives via the q-ROFPWA and q-ROFPWG aggregation operators. The beauty of the proposed algorithm and operators is that both produce the same results. These operators show the symmetry in the results and provide us an appropriate optimal solution for the decision making problem.

For the worst alternatives, we can observe some changes in the ranking results of both operators. This change is due to different formulating strategies and operations in the aggregation operators. Otherwise, the final optimal decision remains the same. This phenomenon represents the validity, flexibility, authenticity, and symmetry of proposed operators.

6. Conclusions

This manuscript proposed a novel approach to the selection of green suppliers under the q-ROF framework to address the complexities of the problems of the selection of green suppliers in practice. The lack of consideration of the relationships of attributes to an uncertain environment may affect the conclusions in some MCGDM problems. To address these drawbacks, we introduced a new approach for selecting green suppliers with the q-ROF information, in which the decision makers’ assessment was considered by the q-rROFNs. The q-ROFNs were used to express the assessment of decision makers, and the vagueness and incompleteness of the information were effectively addressed. Meanwhile, we developed prioritized aggregation operators named the q-ROFPWA and q-ROFPWG aggregation operators. Based on these operators, we developed an important MCGDM approach for GSCM. Moreover, a practical example was illustrated for choosing green suppliers to demonstrate the feasibility of the proposed operators. In the case of numerous complicated issues in the selection of green suppliers, the proposed approach could effectively address many areas, such as providing decision makers with a comfortable climate of assessment, fostering a comparatively high level of consensus among decision makers, and fully assessing the weights of decision makers. This paper, therefore, provided a more practical and efficient approach for selecting green suppliers for the companies in practice.

In further research, considering the superiority of new q-ROFNs, one can extend them to some other aggregation operators, such as power mean aggregation operators, Dombi’s aggregation operators, Bonferroni mean operators, Heronian mean operators, and so on. We hope our findings will be fruitful for the researchers working in supply chain and GSCM analysis, information aggregation, decision analysis, supply management, and environmental science. The methodological advances for supply chain and GSCM analysis are promising areas for future studies. We believe that there are substantial growth and opportunities to understand our world in the convergence of these key climate-centric organizational research fields.