Abstract
It has been shown recently by Saad, Shenker and Stanford that the genus expansion of a certain matrix integral generates partition functions of Jackiw-Teitelboim (JT) quantum gravity on Riemann surfaces of arbitrary genus with any fixed number of boundaries. We use an extension of this integral for studying gas of baby universes or wormholes in JT gravity. To investigate the gas nonperturbatively we explore the generating functional of baby universes in the matrix model. The simple particular case when the matrix integral includes the exponential potential is discussed in some detail. We argue that there is a phase transition in the gas of baby universes.
1. Introduction
It has been shown by Saad, Shenker and Stanford [1] that the genus expansion of a certain matrix integral generates the partition functions of Jackiw-Teitelboim (JT), [2,3], quantum gravity on Riemann surfaces of arbitrary genus with an arbitrary fixed number of boundaries. It is shown in [1] that an important part of JT quantum gravity is reduced to computation of the Weil-Petersson volumes of the moduli space of hyperbolic Riemann surfaces with various genus and number of boundaries for which Mirzakhani [4] established recursion relations. Eynard and Orantin [5,6] proved that Mirzakhani’s relations are a special case of random matrix recursion relations with the spectral curve . This is a natural extension of results on topological gravity [7,8,9,10]. Relation of random matrices and gravity, including black hole description, has a long history, see [11,12] and refs therein.
The results of [1] provide a nonperturbative approach to JT quantum gravity on Riemann surfaces of various genus and perturbative description of boundaries. We use an extension of this result for nonperturbative studying of gas of baby universes in JT gravity. To investigate the boundaries nonperturbatively we explore the generating functional of boundaries in the matrix model and in JT gravity. One interprets the generating functional as the partition function of gas of baby universes in grand canonical ensemble in JT multiverse with the source function describing the distribution of boundaries being treated as the chemical potential. The interaction is presented by splitting and joining of baby universes. One can compare this picture with string interactions and using this analogy closed strings describe baby universes without boundaries, meanwhile the baby universes with boundary correspond to open strings. An analogue of matrix theory is given by string field theory (SFT) [13,14,15]. As has been noted in [1] there is an essential difference in coupling constant in SFT and JT.
Let be the JT gravity path integral for Riemann surface of genus with n boundaries with lengths . Consider a generating function for these functions
where is a constant which in notations of [1] is .
The following remarkable relation between correlation functions in matrix model and JT gravity holds [1]:
Here is the double scaling (d.s.) limit of the correlation function in a matrix model with the spectral curve mentioned above. This form of the curve was obtained in [1] by computing the JT path integral for the disc.
In this note we consider the generating functional for the gravitational correlation functions
where is a source function. An appropriate generating functional in matrix theory has the form
Here and M is a random Hermitian matrix. This amounts to a shift of the potential in the matrix model , where is the Laplace transform of , see Section 2.
We define the generating functional for connected correlation functions
take the double scaling limit introducing the parameter and obtain the relation between JT gravity and the matrix model in terms of the generating functionals:
The “≃” symbol indicates the equality in the sense of formal series.
The paper is organized as follows. In Section 2 the generating functional in matrix theory is discussed. In Section 3 the generating functional of boundaries in JT gravity is considered. In Section 4 we investigate the double scaling limit in matrix models with a particular choice of the source which leads to the change of the potential . In Section 5 the matrix model with the exponential potential is investigated. In Section 6 the matrix model with the spectral curve and the source is discussed and phase transition is observed. In Section 7 the discussion of obtained results is presented.
2. Generating Functional in Matrix Models
Generating functional. We consider ensemble of Hermitian matrices [16,17,18,19] with potential . Let
where are eigenvalues of the matrix M. The n-point correlation function of in the matrix model is given by
Its generating functional can be presented as [20]
or
where
This amounts to shift the potential .
One expands to get the connected correlation functions
Particular case. We consider a special case
In this case the consideration of is equivalent to dealing with the matrix model with a deformed potential
In this case the singular integral equation (See [21,22] for the theory of singular integral equations.) defining the eigenvalues distribution has the form
and the spectral density is
Double scaling limit. This limit in matrix models has been introduced in [23], see [24,25,26] for review and refs therein. All the correlation functions in principle could be derived if the potential or the spectral density/spectral curve is known. To get a connection of the matrix model with JT gravity one has to go to the double scaling limit, see [1]. Consider a matrix model with a non-normalized spectral density
where is a constant. Now, shifting and sending we get the spectral density of the double-scaled matrix model
and the correlation functions in the double scaled limit
The limiting correlation functions have an expansion of the form
The double scaling limit of the generating functional is
The correlation functions and the constant will be used in the next section to describe the connection of the matrix model with JT gravity. The double scaling limit will be discussed also in Section 4.
Resolvents. Similarly one has generating functional for correlation functions of resolvents
where is a test function and
Expanding in the series on f one gets connected correlation functions . We perform the double scaling limit
which admits an expansion
One defines the correlation functions
which satisfy the loop equations [20,27,28] and will be used in the next section, and the generating functional
3. Generating Functional in JT Gravity
The Euclidean action of JT gravity [2,3,29] has the form
Here is a metric on a two dimensional manifold , is a scalar field (dilaton) and the constant was mentioned in the previous section. The path integral for Riemann surface of genus with n boundaries with lengths reads
where is the Euler characteristic and is the JT action with the first term left out.
The following relation between the matrix model and JT gravity holds [1]:
or
where
It was found in [1] that the partition function has the form
where is the Weil-Petersson volume of the moduli space of a genus g Riemann surface with n geodesic boundaries of lengths and
From this we get
where
and the generating functional
Finally, one obtains the relation
Similarly, the correlation functions are related with volumes of the moduli spaces as
The generating functional is
Baby universes. In cosmology [30,31,32,33,34,35,36,37,38], one usually deals with baby universes that branch off from, or join onto, the parent(s) Universe(s). In matrix theories one parent is a connected Riemann surface with arbitrary number of handles and at least one boundary. We assume that the lengths of boundaries of baby universities are small as compare with the boundary length of the parent, see Figure 1. Baby universes are attached to the parent by necks that have restricted lengths of geodesics at which the neck is attached to the parent, We assume that the lengths of the boundaries of baby universes are small compared to the length of the boundary of the parent, see Figure 1. Baby universes are attached to the parent with the help of thin necks. Thickness of the neck is defined as the geodesic length of the loop located at the thinness point of the neck, and this length is assumed to be essentially smaller than the length of theboundary of the parent, see Figure 1b,c. There are also restrictions on the area of the surface of baby universes, see [39,40] for more precise definitions. Cosmological baby universes in the parent-baby universe approximation interact only via coupling to the parent universes, that themselves interact via wormholes. In matrix models the baby universes always interact via their parents too and parents interact via wormholes, Figure 1b,c). One can expect that at large number of baby universes interaction between different parts of the system increases and this leads to phase transition (an analog of the the nucleation of a baby universe in [32]). We interpret the matrix partition function , defined by equation (22) as a partition function of the gas of baby universes.
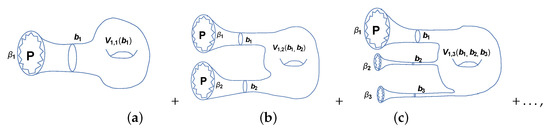
Figure 1.
Gas of baby universes. (a) One parent, (b) two parents connected by the wormhole, (c) three parents by the wormhole. Here for and for .
4. Double Scaling Limit for the GUE
There are various notions of the double scaling limit in matrix theory [23,24,25,26,41,42,43,44,45,46,47,48,49,50,51]. A special double scaling limit was considered in [1] at the level of spectral density. Here we discuss it at the level of the potentials. We will see that the linear term in the potential plays a special role.
Let us start with the Wigner distribution for the Gaussian Unitary Ensemble (GUE) [16,17,18,19]. The ordinary Wigner distribution is supported on the interval and is obtained from a matrix model with the potential , where . We want to make a shift and get a distribution on the interval , To this end we consider the gaussian model with an external source. Note that the Gaussian matrix model with an arbitrary matrix source has been studied in [52]. Here we consider the case corresponding in notations [52] to , I is the unit matrix.
and we make parameters m and j depending on to put the measure support on . The singular integral equation defining the density takes the form
Here means the Cauchy principal value of the integral. The solution of (42) is given by the shifted Wigner distribution
Note that the constant j from the linear term in the potential does not enter into the expression for the spectral density. This is valid for any potential. The constant appears only throughout the normalization and consistency conditions that in this case read: We get that the eigenvalue density (43) is supported by the potential in the sense that
in (44) means averaging with potential
Now we take the limit and write
where . So, we get an expected result in two steps. First we send and then .
One can use also another procedure. Set and in this case one has
5. Deformation by an Exponential Potential
Here we consider a deformation of the Wigner distribution by the insertion of the exponential potential. It is interesting to compare this model with the model [53] that represents planar graphs with dynamical holes of arbitrary sizes. In this model there is spontaneous tearing of the world sheet, associated with the planar graph, which gives a singularity at zero coupling constant of string interaction.
There are 4 different choices of signs of J and , see Figure 2. There is no instability for , see Figure 2a,b. Only may produce some non trivial effects due to an appearance of potential instability, Figure 2c,d. The choice of sign of is irrelevant. Instability regions also appeared in Higgs-type models [54,55,56].
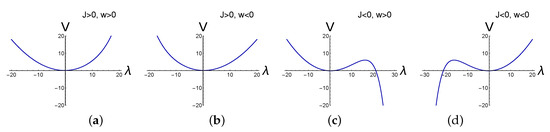
Figure 2.
Four different choices of perturbations of the gaussian ensemble by the exponential potential : (a) ; (b) ; (c) ; (d) .
The shift of in the potential (47) produces the linear term in the potential and multiplies the current J on the constant . We parametrize our potential as
and fix the parameters in (48) in an agreement with the measure localization on the segment . To this purpose we first find the non-normalized measure as a sum of non-normalized ones corresponding to the shifted Wigner and exponential potential distributions and .
The forms of non-normalized measures for positive and negative w are presented in Figure 3.
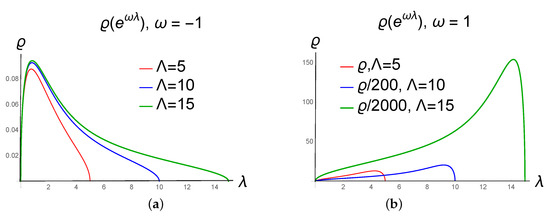
Figure 3.
Non–normalized density plot for the exponential potential with negative (a) and positive (b) and different regularization parameter .
We can compare the contribution to the non-normalized density from the Wigner semi-circle for mass equal to 1 and the exponential potential taken with arbitrary current J. We see that this sum always defines the positive density for and becomes negative for . Then for we find relation between and and J from normalization condition.
In Figure 4 the appearance of the phase transition at negative J is presented. In Figure 5a relations between and J for fixed and are shown for and in Figure 5b. More plots for different one can find in the extended version of this paper [57].
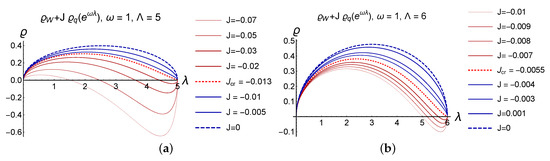
Figure 4.
The plot of non–normalized density for the quadratic potential deformed by the exponential potential for and different values of the regularization parameter : for (a) and for (b).
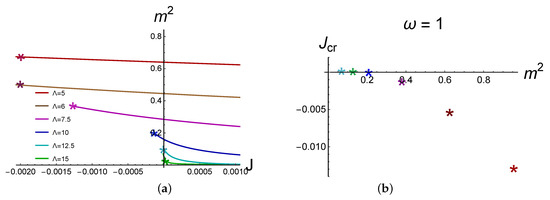
Figure 5.
(a) Relations between and J for fixed and . (b) vs at . The legend is the same as at (a).
We can present the eigenvalues distribution corresponding to the potential (48) as a sum. Note that the potential does not have a solution to the singular equation and does not itself defines the eigenvalues distribition, but does in the case . By we mean this distribution with corresponding choice of the linear term.
and fix constant C and from the consistency condition and normalization, respectively,
The forms of non-normalized measures for positive and negative w presented are presented in Figure 3. We see that these two segment distributions are nonsymmetric under the centre of the segment. The distribution of eigenvalues for the case of negative is pressed to the left boundary of the segment, and the for the case of positive it is pressed to the right one. Applying this deformation with a positive J to the GUE we “activate” the left or right part of of eigenvalues. Applying the same with negative J we can destroy the constructed solution. We compare the contribution to the non-normalized density from the Wigner semi-circle for mass equal to 1 and the exponential potential taken with arbitrary current J. We see the this sum always define the positive density for and becomes negative for . Then we find relation between and , and J from normalization condition.
In Figure 4 is presented the appearance of the phase transition at negative J for different . We see that for chosen parameters, the critical decreases with increasing . To find the real mass that supports the normalized solution,
we find from the normalization condition, so that and assume that the mass is given by .
In Figure 5a the dependence of on J for fixed and is shown for different values of . Here . We see that mass (in our parametrization of the potential of the model) decreases with increasing J. The slope of the mass is more fast for larger .
In Figure 5b the dependence of the critical current on mass is shown. We see that goes to zero when goes to zero, that corresponds to increasing .
Fine tuning. It is obvious that fixing from the beginning the location of the eigenvalue one immediately gives restrictions on parameters of the potential of the matrix model. If we want to shift the location of the eigenvalues, we have to make a shift in the potential, . For the quadratic potential this shift produces the linear term and j can be determined from the location of the left point of the cut. For higher polynomial interaction the shift produces the linear term in the LHS of singular equation, as well as change of coupling constants. The shift in the exponential potential produces just a multiplication on positive constant.
We have also seen that if we want to deform a given distribution by a new potential, that has the same locations of eigenvalues, we can just take the sum of the given two distributions and multiply all coupling constants of two initial model on the same parameter to fix the normalization condition for the distributions that is the some of given two distributions. As to the consistency condition it follows from consistency conditions of individual distributions. More precisely, if we know that
Note that in both integrals the segment is the same. Taking
we can claim that solves equations
The consistency condition is automatically satisfied.
One can put a coupling constant in front of the second potential, say J. In our previous example this were the coupling constant g in the perturbation of Gaussian model by qubic term, or J in the case of the exponential potential. For positive J we keep the positivity condition for the sum of two distribution, meanwhile we can lost it for the case of big negative current. This loss of positivity leads to the destruction of the large N expansion of the model and can be interpreted as a phase transition.
As to double scaling limit, we can consider it in three steps. First we bring the support of the eigenvalue distribution on the interval by fine tuning the linear term in the potential. Then one goes to the limit and after that .
6. Matrix Model for JT Gravity
6.1. Potentials for Non-Normalized Density Distribution
For fixed we consider the eigenvalue distribution normalized to 1
This form of the eigenvalue distribution in the Sachdev-Ye-Kitaev (SYK) model has been obtained in [58,59] and is nothing but the Bethe formula for the nuclear level density [60]. For large one has . The distribution normalized to N has the form
compare with (19). It is evident that
To recover the potential that supports the distribution , we write
where is defined by
This gives
Here Ei is the exponential integral that for real non zero values of x is defined as
The potential up to a constant is
and it is presented in Figure 6.
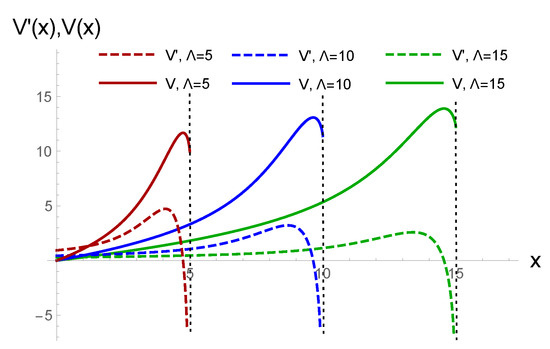
Figure 6.
The potential supported the density for different parameter .
6.2. Effective Energy
The effective energy , [18], is evaluated on the normalized density and it is given by the following formula
In Figure 7 the effective action as function of is shown. We see that it can be approximated by a log . The next approximation is given by the double-log, .
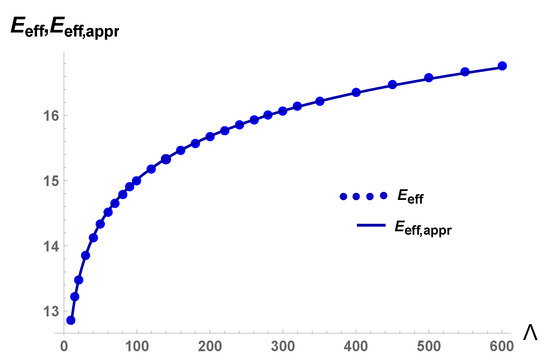
Figure 7.
as function of and its approximation .
6.3. Phase Transition
To study the phase transition we consider the deformation of by
It is interesting to compare this density with the density
where
In Figure 8 we plot the density (66) and (67) for and different J and . We see that for negative on the segment domains, where and become negative, appear. Note that the critical value are the same for and . In Figure 9 the locations of critical points depending on are shown. This broken of positivity of the density means an instability of the solution (phase) under a perturbation by the exponential potential. We interpret this instability as an appearance of a phase transition at .
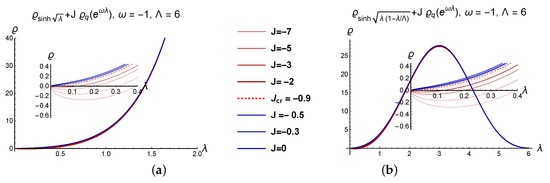
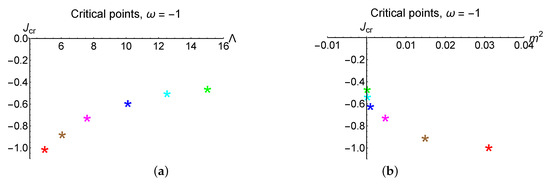
Figure 9.
(a) The points show the values of for given by (66) for different . (b) vs for the same set of as at (a). are shown by red, brown, magenta, blue, cyan and green colors. Here .
7. Discussion and Conclusions
The generating functional for the correlation functions of the boundaries of the Riemann surfaces is considered in JT gravity and in matrix theory. The matrix integral [1] provides a nonperturbative completion of the genus expansion in JT gravity on Riemann surfaces with fixed number of boundaries for all genus. The generating functional considered in this paper, gives completion also for infinitely many number of boundaries.
By using this formulation several matrix models, including double scaling limit for the Gaussian model relevant to topological gravity, cubic model, and JT gravity are investigated in this paper. In all these cases, indications to phase transitions are found. In particular, in JT gravity the phase transition in the gas of baby universes has been establised. By analogy with phase transitions between different states of matter, it can be expected that the phase transition discussed above describes the transition from the gaseous state of the JT multiverse to the liquid state.
To study this phase transition, we consider generating functional that we associate with baby universes. The generating functional for a matrix model with potential is obtained from the partition function of the model just by shift where is the Laplace transform of . Baby universes should look as point-like objects with very small length of the boundary. Therefore the distribution should have a peak somewhere near zero. In our model with baby universes correspond to small . The shifted potential in this case is . Note that one could expect for large n similarly to the infinite replica number limit considered in [61].
We have obtained that in all considered cases there are critical negative , such that for the corresponding solution is destroyed. The mass at the critical points decreases with increasing of . In this paper we have considered the deformation of the density function by the exponential potential, but is also possible to study all momenta deformations, as well as , compare with [62,63], as well matrix models with other potentials considered in [64].
The holographic boundary dual of the JT gravity in spacetime with M boundaries is the M-replica SYK model in the low energy limit [65,66,67,68]. The studies of [61,69,70,71,72,73] show that the nonperturbative completion of SYK involves nontrivial replica-nondiagonal saddle points. The replica-nondiagonal structures in SYK with replica interaction [73,74,75,76] demonstrate nontrivial phase structures and symmetry breaking patterns.
Note that the deformation of potential by the linear term or nonlinear ones as a tool for investigation of phase transitions and spontaneous symmetry breaking in SYK-like models was used in [69,70,73]. In particular, a nonlocal interacting of two-replica by a nonlocal term proportional to an external current permits to reveal nonperturbative effects in the SYK model. This nonlocality in some sense is analogous to an external nonlocal source (cosmological daemon) in cosmology [77], there it specified boundary conditions.
There are numerous investigations of wormholes and baby universes in cosmology and particle physics, including the Giddings–Strominger wormhole solution [32] and Coleman’s approach to the cosmological constant problem [36]. There are many open questions in theory of wormholes and baby universes. In particular, it would be interesting to see whether in JT gravity or its generalizations there is a mechanism of suppression [78] the probability of creation of giant wormholes and big baby universes. By using the wormhole/baby universe approach it was found that the probability for the universe to undergo a spontaneous compactification down to a four-dimensional spacetime is greater than to remain in the original homogeneous multidimensional state [37]. It is interesting to find an analog of this in the context of JT gravity.
In the study of SYK from gravity perspective, a crutial role plays consideration of wormholes in JT gravity [74,76,79,80,81,82,83]. A interplay between baby universes and wormholes could lead to nontrivial effects and this subject requires further investigations.
Using the recent result of [84] according which JT gravity in is an analytic continuation of JT gravity in Euclidean it would be interesting to understand the meaning of the phase transition considered here in the dS case.
It would be also interesting to compare the Hartle-Hawking construction of string baby universes related with geometry, using free fermionic formulation [85] with the fermionic interpretation of determinant in matrix models, and also find a slot for baby universes in an quasi-classical [86,87] or exact quantization of JT proposed in [88].
Author Contributions
Conceptualization, methodology, investigation, I.A., I.V.; writing—original draft preparation, I.V.; writing—review and editing, I.A., I.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Russian Science Foundation (project 19-11-00320, Steklov Mathematical Institute).
Acknowledgments
The authors are grateful to M. Khramtsov for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saad, P.; Shenker, S.H.; Stanford, D. JT gravity as a matrix integral. arXiv 2019, arXiv:1903.11115. [Google Scholar]
- Jackiw, R. Lower Dimensional Gravity. Nucl. Phys. B 1985, 252, 343–356. [Google Scholar] [CrossRef]
- Teitelboim, C. Gravitation and Hamiltonian Structure in Two Space-Time Dimensions. Phys. Lett. B 1983, 126, 41–45. [Google Scholar] [CrossRef]
- Mirzakhani, M. Growth of Weil-Petersson volumes and random hyperbolic surface of large genus. J. Differ. Geom. 2013, 94, 267–300. [Google Scholar] [CrossRef]
- Eynard, B.; Orantin, N. Invariants of algebraic curves and topological expansion. arXiv 2007, arXiv:math-ph/0702045. [Google Scholar] [CrossRef]
- Eynard, B.; Orantin, N. Weil-Petersson volume of moduli spaces, Mirzakhani’s recursion and matrix models. arXiv 2007, arXiv:0705.3600. [Google Scholar]
- Witten, E. Two-dimensional gravity and intersection theory on moduli space. Surv. Diff. Geom. 1991, 1, 243–310. [Google Scholar]
- Kontsevich, M. Intersection theory on the moduli space of curves and the matrix airy function. Commun. Math. Phys. 1992, 147, 1–23. [Google Scholar] [CrossRef]
- Manin, Y.I.; Zograf, P. Invertible Cohomological Field Theories and Weil-Petersson volumes. arXiv 1999, arXiv:math/9902051. [Google Scholar] [CrossRef]
- Dijkgraaf, R.; Witten, E. Developments in Topological Gravity. Int. J. Mod. Phys. A 2018, 33, 1830029. [Google Scholar] [CrossRef]
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black Holes and Random Matrices. J. High Energy Phys. 2017, 2017, 118. [Google Scholar] [CrossRef]
- Saad, P.; Shenker, S.H.; Stanford, D. A semiclassical ramp in SYK and in gravity. arXiv 2018, arXiv:1806.06840. [Google Scholar]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory; Cambridge University Press: Cambridge, UK, 1987; 469p. [Google Scholar]
- Witten, E. Noncommutative Geometry and String Field Theory. Nucl. Phys. B 1986, 268, 253–294. [Google Scholar] [CrossRef]
- Aref’eva, I.Y.; Volovich, I.V. Two-dimensional gravity, string field theory and spin glasses. Phys. Lett. 1991, 255, 197–201. [Google Scholar] [CrossRef]
- Wigner, E.P. On the statistical distribution of the widths and spacings of nuclear resonance levels. Proc. Cambr. Philos. Soc. 1951, 47, 790–798. [Google Scholar] [CrossRef]
- Dyson, F.J. A Class of Matrix Ensembles. J. Math. Phys. 1972, 13, 90–97. [Google Scholar] [CrossRef]
- Brezin, E.; Itzykson, C.; Parisi, G.; Zuber, J.-B. Planar diagrams. Commun. Math. Phys. 1978, 50, 35–51. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices, 2nd ed.; Academic Press: New York, NY, USA, 1991. [Google Scholar]
- Migdal, A. Loop equations and 1/N expansion. Phys. Rep. 1983, 102, 199. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Singular Integral Equations; Noordhoff: Groningen, The Netherlands, 1953. [Google Scholar]
- Gakhov, F.D. Boundary Problems; Fizmatgiz: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Brézin, E.; Kazakov, V.A. Exactly Solvable Field Theories of Closed Strings. Phys. Lett. B 1990, 236, 144. [Google Scholar] [CrossRef]
- di Francesco, P.; Ginsparg, P.; Zinn-Justin, J. 2-D Gravity and random matrices. Phys. Rep. 1995, 254, 1–133. [Google Scholar] [CrossRef]
- Marino, M. Les Houches lectures on matrix models and topological strings. arXiv 2004, arXiv:hep-th/0410165. [Google Scholar]
- Eynard, B.; Kimura, T.; Ribault, S. Random matrices. arXiv 2004, arXiv:1510.04430. [Google Scholar]
- Ambjorn, J.; Jurkiewicz, J.; Makeenko, Y.M. Multiloop correlators for two-dimensional quantum gravity. Phys. Lett. B 1990, 251, 517–524. [Google Scholar] [CrossRef]
- Eynard, B. Topological expansion for the 1-Hermitian matrix model correlation functions. J. High Energy Phys. 2004, 2004, 31. [Google Scholar] [CrossRef]
- Almheiri, A.; Polchinski, J. Models of AdS2 backreaction and holography. J. High Energy Phys. 2015, 2015, 14. [Google Scholar] [CrossRef]
- Hawking, S.W.; Laflamme, R. Baby universes and the non-renormalizability of gravity. Phys. Lett. 1988, 209, 39–41. [Google Scholar] [CrossRef]
- Lavrelashvili, G.V.; Rubakov, V.A.; Tinyakov, P.G. Disruption of Quantum Coherence upon a Change in Spatial Topology in Quantum Gravity. JETP Lett. 1987, 46, 167. [Google Scholar]
- Giddings, S.B.; Strominger, A. Axion Induced Topology Change in Quantum Gravity and String Theory. Nucl. Phys. B 1988, 306, 890–907. [Google Scholar] [CrossRef]
- Strominger, A. Baby Universes. In Quantum Cosmology and Baby Universes; World Scientific: Singapore, 1991; pp. 269–346. [Google Scholar]
- Hawking, S.W. Quantum coherence down the wormhole. Phys. Lett. B. 1987, 195, 337–343. [Google Scholar] [CrossRef]
- Giddings, S.B.; Strominger, A. Baby Universes, Third Quantization and the Cosmological Constant. Nucl. Phys. B 1989, 321, 481–508. [Google Scholar] [CrossRef]
- Coleman, S.R. Why There Is Nothing Rather than Something: A Theory of the Cosmological Constant. Nucl. Phys. B 1988, 310, 643–668. [Google Scholar] [CrossRef]
- Volovich, I.V. Baby universes and the dimensionality of spacetime. Phys. Lett. B 1989, 219, 66–70. [Google Scholar] [CrossRef]
- Hebecker, A.; Mikhail, T.; Soler, P. Euclidean wormholes, baby universes, and their impact on particle physics and cosmology. Front. Astron. Space Sci. 2018, 5, 35. [Google Scholar] [CrossRef]
- Jain, S.; Mathur, S.D. World sheet geometry and baby universes in 2-D quantum gravity. Phys. Lett. B 1992, 286, 239–246. [Google Scholar] [CrossRef]
- Ambjorn, J.; Barkley, J.; Budd, T.; Loll, R. Baby Universes Revisited. Phys. Lett. B 2011, 706, 86–89. [Google Scholar] [CrossRef][Green Version]
- Douglas, M.R.; Shenker, S.H. Strings in Less than One-Dimension. Nucl. Phys. B 1990, 335, 635–654. [Google Scholar] [CrossRef]
- Gross, D.J.; Migdal, A.A. Nonperturbative Two-Dimensional Quantum Gravity. Phys. Rev. Lett. 1990, 64, 127. [Google Scholar] [CrossRef]
- Brezin, E.; Zee, A. Universality of the correlations between eigenvalues of large random matrices. Nucl. Phys. B 1993, 402, 613–627. [Google Scholar] [CrossRef]
- Bowick, M.; Brezin, E. Universal scaling of the tail of the density of eigenvalues in random matrix models. Phys. Lett. B 1991, 268, 21. [Google Scholar] [CrossRef]
- Bleher, P.M.; Its, A.R. Double scaling limit in the random matrix model: The Riemann-Hilbert approach. Commun. Pure Appl. Math. 2003, 56, 433–516. [Google Scholar] [CrossRef]
- De Monvel, A.B.; Pastur, L.; Shcherbina, M. On the statistical mechanics approach in the random matrix theory: Integrated density of state. J. Stat. Phys. 1995, 79, 585–611. [Google Scholar] [CrossRef]
- Pastur, L.; Shcherbina, M. Universality of the Local Eigenvalue Statistics for a Class of Unitary Invariant Random Matrix Ensembles. J. Stat. Phys. 1997, 86, 109–147. [Google Scholar] [CrossRef]
- Tracy, C.; Widom, H. Level-Spacing Distributions and the Airy Kernel. Commun. Math. Phys. 1994, 159, 151–174. [Google Scholar] [CrossRef]
- Tracy, C.; Widom, H. Fredholm Determinants, Differential Equations and Matrix Models. Commun. Math. Phys. 1994, 163, 33–72. [Google Scholar] [CrossRef]
- Kuijlaars, A.B.J.; McLauglin, K.T.-R. Generic behavior of the density of states in random matrix theory and equilibrium problems in the presence of real analytic external field. Commun. Pure Appl. Math. 2000, 53, 736–785. [Google Scholar] [CrossRef]
- Deift, P.; Kriecherbauer, T.; McLaughlin, K.T.-R.; Venakides, S.; Zhou, X. Uniform asymptotics for polynomials orthogonal with respect to varying exponential weights and applications to universality questions in random matrix theory. Commun. Pure Appl. Math. 1999, 52, 1335–1425. [Google Scholar] [CrossRef]
- Brezin, E.; Hikami, S. Random Matrix Theory with an External Source; Springer: Singapore, 2016. [Google Scholar]
- Kazakov, V.A. A simple solvable model of quantum field theory of open strings. Phys. Lett. B 1990, 237, 212–216. [Google Scholar] [CrossRef]
- Arefeva, I.Y.; Ilchev, A.C.; Mitruchkin, B.K. Phase structure of matrix NxN Goldstoune model in the large N limit. In Proceedings of the III International Symposium on Selected Topics in Statistical Mechanics, Dubna, Russia, 22–26 August 1984; pp. 20–26. [Google Scholar]
- Cicuta, G.M.; Molinari, L.; Montaldi, E. Large N phase transition in low dimensions. Mod. Phys. Lett. A 1986, 1, 125–129. [Google Scholar] [CrossRef]
- Crnkovic, C.; Moore, G. Multicritical multi-cut matrix models. Phys. Lett. B 1991, 257, 322–328. [Google Scholar] [CrossRef]
- Aref’eva, I.; Volovich, I. Gas of baby universes in JT gravity and matrix models. arXiv 2019, arXiv:1905.08207. [Google Scholar]
- Bagrets, D.; Altland, A.; Kamenev, A. Sachdev-Ye-Kitaev Model as Liouville Quantum Mechanics. Nucl. Phys. B 2016, 911, 191–205. [Google Scholar] [CrossRef]
- Stanford, D.; Witten, E. Fermionic Localization of the Schwarzian Theory. J. High Energy Phys. 2017, 2017, 8. [Google Scholar] [CrossRef]
- Bethe, H.A. An Attempt to Calculate the Number Energy Levels of a Heavy Nucleus. Phys. Rev. 1936, 50, 332. [Google Scholar] [CrossRef]
- Aref’eva, I.; Khramtsov, M.; Tikhanovskaya, M.; Volovich, I. Replica-nondiagonal solutions in the SYK model. J. High Energy Phys. 2019, 2019, 113. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.M.; Jia, Y.; Verbaarschot, J.J.M. Exact moments of the Sachdev-Ye-Kitaev model up to order 1/N2. J. High Energy Phys. 2018, 2018, 146. [Google Scholar] [CrossRef]
- Garca-Garca, A.M.; Zacaras, S. Quantum Jackiw-Teitelboim gravity, Selberg trace formula, and random matrix theory. arXiv 2019, arXiv:1911.10493. [Google Scholar]
- McGuigan, M. Dark Horse, Dark Matter: Revisiting the SO(16)x SO(16)’ Nonsupersymmetric Model in the LHC and Dark Energy Era. arXiv 2019, arXiv:1907.01944. [Google Scholar]
- Jensen, K. Chaos in AdS2 Holography. Phys. Rev. Lett. 2016, 117, 111601. [Google Scholar] [CrossRef]
- Engelsy, J.; Mertens, T.G.; Verlinde, H. An investigation of AdS2 backreaction and holography. J. High Energy Phys. 2016, 2016, 139. [Google Scholar] [CrossRef]
- Maldacena, J.; Stanford, D.; Yang, Z. Conformal symmetry and its breaking in two dimensional Nearly Anti-de-Sitter space. Prog. Theor. Exp. Phys. 2016, 2016, 12C104. [Google Scholar] [CrossRef]
- Harlow, D.; Jafferis, D. The Factorization Problem in Jackiw-Teitelboim Gravity. J. High Energy Phys. 2020, 2020, 1–32. [Google Scholar] [CrossRef]
- Aref’eva, I.; Volovich, I. Notes on the SYK model in real time. Theor. Math. Phys. 2018, 197, 1650–1662. [Google Scholar] [CrossRef]
- Aref’eva, I.; Volovich, I. Spontaneous symmetry breaking in fermionic random matrix model. J. High Energy Phys. 2019, 2019, 114. [Google Scholar] [CrossRef]
- Okuyama, K. Replica symmetry breaking in random matrix model: A toy model of wormhole networks. Phys. Lett. B 2020, 803, 135280. [Google Scholar] [CrossRef]
- Wang, H.; Bagrets, D.; Chudnovskiy, A.L.; Kamenev, A. On the replica structure of Sachdev-Ye-Kitaev model. J. High Energy Phys. 2019, 2019, 57. [Google Scholar] [CrossRef]
- Aref’eva, I.; Khramtsov, M.; Volovich, I. Revealing nonperturbative effects in the SYK model. Theor. Math. Phys. 2019, 201, 1585–1605. [Google Scholar] [CrossRef]
- Maldacena, J.; Qi, X.-L. Eternal traversable wormhole. arXiv 2018, arXiv:1804.00491. [Google Scholar]
- Kim, J.; Klebanov, I.R.; Tarnopolsky, G.; Zhao, W. Symmetry Breaking in Coupled SYK or Tensor Models. Phys. Rev. X 2019, 9, 021043. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.M.; Nosaka, T.; Rosa, D.; Verbaarschot, J.J.M. Quantum chaos transition in a two-site SYK model dual to an eternal traversable wormhole. Phys. Rev. D 2019, 100, 026002. [Google Scholar] [CrossRef]
- Aref’eva, I.Y.; Volovich, I.V. Cosmological daemon. J. High Energy Phys. 2011, 2011, 102. [Google Scholar] [CrossRef]
- Coleman, S.R.; Lee, K. Escape From the Menace of the Giant Wormholes. Phys. Lett. B 1989, 221, 242–249. [Google Scholar] [CrossRef]
- Maldacena, J.; Turiaci, G.J.; Yang, Z. Two dimensional Nearly de Sitter gravity. arXiv 2019, arXiv:1904.01911. [Google Scholar]
- Lin, H.W.; Maldacena, J.; Zhao, Y. Symmetries Near the Horizon. J. High Energy Phys. 2019, 2019, 49. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, P. Entanglement Entropy of Two Coupled SYK Models and Eternal Traversable Wormhole. J. High Energy Phys. 2019, 2019, 33. [Google Scholar] [CrossRef]
- Freivogel, B.; Godet, V.; Morvan, E.; Pedraza, J.F.; Rotundo, A. Lessons on Eternal Traversable Wormholes in AdS. J. High Energy Phys. 2019, 2019, 122. [Google Scholar] [CrossRef]
- Betzios, P.; Kiritsis, E.; Papadoulaki, O. Euclidean Wormholes and Holography. J. High Energy Phys. 2019, 2019, 42. [Google Scholar] [CrossRef]
- Cotler, J.; Jensen, K.; Maloney, A. Low-dimensional de Sitter quantum gravity. arXiv 2019, arXiv:1905.03780. [Google Scholar]
- Dijkgraaf, R.; Gopakumar, R.; Ooguri, H.; Vafa, C. Baby universes in string theory. Phys. Rev. D 2006, 73, 066002. [Google Scholar] [CrossRef]
- Blommaert, A.; Mertens, T.G.; Verschelde, H. Fine Structure of Jackiw-Teitelboim Quantum Gravity. J. High Energy Phys. 2019, 2019, 66. [Google Scholar] [CrossRef]
- Blommaert, A.; Mertens, T.G.; Verschelde, H. Clocks and Rods in Jackiw-Teitelboim Quantum Gravity. J. High Energy Phys. 2019, 2019, 60. [Google Scholar] [CrossRef]
- Iliesiu, L.V.; Pufu, S.S.; Verlinde, H.; Wang, Y. An exact quantization of Jackiw-Teitelboim gravity. J. High Energy Phys. 2019, 2019, 91. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).