Abstract
With the emergence of increasingly computing-intensive and delay-sensitive tasks, the processing of computing tasks on cloud servers cannot meet the current needs any longer. The emergence of mobile edge computing (MEC) technology and the popularity of 5G applications can solve these demands. Offloading tasks to the MEC server reduces the energy consumption of local devices, and also has a lower latency than offloading to the cloud server. In this paper, an MEC–edge cloud server collaborative system model with energy harvesting technology is designed to minimize the processing delay of computing tasks by allocating computing resources. We propose an optimal integer linear programming (OILP) algorithm with two steps. Firstly, we propose a Lyapunov stability optimization algorithm based on task priority. With the constraints of local mobile device power stability, the divide-and-conquer idea is used for solving the target values of the processing tasks locally, and the MEC and edge cloud servers separately. Therefore, the objective problem is transformed into an integer linear programming problem, and then an integer linear programming algorithm based on CPU utilization optimization is proposed to obtain a resource allocation scheme. Simulation results show that the proposed OILP algorithm can further reduce the delay, improve the CPU’s utilization of the MEC server, and reduce the number of the tasks that cannot be processed under the condition of the energy stability of the local device.
1. Introduction
With the development of mobile communication technology and the popularization of smart mobile devices, such as smart phones and smart watches, various network services and applications are constantly emerging [1,2]. These new mobile applications, such as e-health, biometric recognition [3], surveillance, and augmented reality/virtual reality (AR/VR), require not only a large amount of computing, but also a high energy consumption [4]. Benefiting from the widespread application of “Internet of Things” (IoT) and “cloud computing” technologies, mobile cloud computing (MCC) has become a potential solution to enhance the computing capabilities of IoT applications, shifting the computing tasks of IoT devices to those with sufficient computing and storage capabilities on a centralized cloud server [5]. However, users accessing the remote centralized cloud computing and storage resources through the internet will cause a relatively long delay, which makes MCC unable to meet the conditions of some delay-sensitive applications.
The European Telecommunications Standardization Institute (ETSI) proposed mobile edge computing (MEC) in 2014 to solve the problems of cloud computing models. Mobile edge computing (MEC) provides cloud computing capabilities in the radio access network (RAN), with a new paradigm for mobile devices to liberate them from the heavy computing workloads [6]. As a result, the services provided by the MEC server and the cloud server can be considered to be symmetrical. Owing to the development of 5G technology, users can offload tasks to the MEC server for processing through wireless and cellular networks. This can reduce the processing delay from the local to the cloud server; in addition, it can improve the task processing capacity and extend the life of the local devices. To further improve the battery capacity of local equipment, energy harvesting (EH) is a promising technology to solve these problems. It can capture environmentally recyclable energy [7], including solar radiation, wind, and energy captured through radio frequency (RF) [8], so that the system can continue to run for a long time [9].
At present, more and more people are very interested in the research about offloading strategies for computing tasks in MEC systems. First, the different system models are proposed for the different scenarios, e.g., single MEC servers [10,11], multiple MEC servers [12,13], binary tasks [14,15], partial tasks [16,17], and energy harvesting MEC systems [18,19], etc. Then, the different target problem models are formulated based on the different scenarios, e.g., minimizing equipment energy consumption under the time delay constraints [20] and weighing trade-off energy consumption and the time delay. Finally, different algorithm strategies are designed to solve the problems of offloading decisions, links, and computing resource allocation [21]. The optimal strategies have been used for meeting the specified goals to achieve the design requirements. However, many people’s research only considers the resource allocation of the local device and the MEC server, and rarely considers the collaborative model of the cloud server; many models do not consider the capacity limit of the MEC server. In addition, the excessive usage problem of the CPUs of the MEC servers also need to be considered, because in actual applications, the continuously high CPU usage of the server may cause a series of problems, e.g., server downtime, which will cause offload tasks to be blocked, and seriously affect QoS. We therefore consider these issues in this article:
- (1)
- Propose a local, MEC server, and edge cloud server collaborative processing task system, reasonably allocate energy and computing resources, and improve system performance, e.g., task processing capacity;
- (2)
- Use Lyapunov stability theory for local mobile device power stability and task processing delay as optimization goals, and jointly consider the local mobile device’s energy collection, computing power allocation, wireless link transmit power allocation, and MEC–edge cloud server resource allocation problem. In order to solve this problem, a Lyapunov algorithm based on task priority is first proposed to decompose this NP-hard problem into an integer programming problem. The task priority attribute can improve the performance of the system, and then an integer programming algorithm based on CPU utilization optimization is proposed to obtain the optimal resource allocation strategy. By comparing and analyzing with the integer linear programming (ILP) algorithm, the optimal integer linear programming (OILP) algorithm proposed has the lower latency and higher resource utilization;
- (3)
- Considering that MEC server resources are scarce, especially during the peak traffic, the CPU computing resources provided by the server through virtualization technology may not be utilized effectively. When the CPU resources are insufficient to handle the entire unload task, the proposed algorithm will split the task into two parts, one of which will be processed on the local device, and the other on the MEC server. This not only increases server resource utilization, but also reduces the number of tasks that cannot be processed. The simulation results show that the number of unprocessed tasks can be optimized by more than 10%.
In Section 2, we review related research work from recent years. The system model and the objective problem of Lyapunov optimization are described in Section 3. In order to solve the objective problem, an optimal integer linear programming (OILP) algorithm is proposed in Section 4, which includes the Lyapunov optimization, based on task priority, and the integer linear programming algorithm, based on the CPU utilization optimization strategy. In Section 5, we analyze the simulation results. Finally, in Section 6 we summarize this article and look forward to future work.
2. Related Work
In recent years, the research on the simulation model of computing offloading of MEC systems has attracted the attention of many scholars. In [22], the joint offloading of downlink and uplink edge computing in ultra-dense heterogenous networks (HetNets) is studied, with minimizing the overall task delay and equipment energy consumption as goals. Here, the planning problem is transformed into resource allocation sub-problem and offloading calculation sub-problem. Deng et al. [10] studied the offloading decision between multiple devices and an MEC server. Ahn et al. [16] studied the problems of the partial offloading from the perspective of noncooperative games, and designed an energy-oriented task scheduling scheme. Cheng et al. [23] considered a signal access MEC server system using an orthogonal frequency division multiplexing (OFDMA) transmission mechanism, and optimized offload strategy and radio resource allocation. Ndikumana et al. [24] considered joint computing, caching, communication, and control as an optimization problem, and adopted a block successive, upper-bound minimization method to minimize bandwidth consumption and delay. Zhao et al. [25] took offloading decisions, wireless resource optimization, and computing resource optimization as the key elements to achieve energy-saving goals. In [26], the joint multi-user offloading and transmission power control optimization problems in the multi-channel wireless interference scenarios are studied, and a semi-distributed algorithm is proposed to obtain the optimal solution to minimize the computational overhead of the entire system. In order to avoid the network congestion and load balancing, a joint optimization of data caching and request forwarding was considered by Liu et al. [27]. A Lyapunov stochastic optimization model was used for limiting the network stability and minimizing the average transmission cost.
Due to the limited battery power of mobile devices, low-power local mobile devices cannot offload computing tasks to the MEC server via wireless channels. Therefore, research on systems with battery energy harvesting has also received scholars’ attention. Min et al. [28] proposed an IoT device offloading scheme based on reinforcement learning. The edge device and offloading rate were selected by analyzing the current battery power, the previous radio transmission rate to each edge device, and the predicted harvested energy amount. Zhou et al. [29] applied energy harvesting research based on the radio frequency (RF) to a UAV, multi-user MEC system, and discusses the binary and partial computing offloading methods separately to solve the problem of the maximizing computing speed. Yao et al. [18] considered the importance of battery power stability for local mobile devices, and introduced a Lyapunov optimization model to minimize the processing delay of computing tasks under the constraints of battery power stability of the local mobile devices. However, the model only considers the scenario of one mobile device and one MEC server. Therefore, in [12], a scenario model of multiple mobile devices and multiple MEC servers was proposed, taking into account the capacity limitations of the MEC server and under the condition of guaranteeing QoE, and the tasks were first offloaded to the MEC server for processing. However, in the model, the upper limit of the number of computing tasks offloaded to the MEC server is used as a capacity limit. This design cannot maximize the use of resources, and in real scenarios, the CPU usage of the MEC server will negatively affect task processing when it reaches a certain level. Therefore, we need to consider how to control CPU usage at a safe value. In addition, in terms of resource allocation, the priority of each type of offloading task to obtain resources are different, and the higher priority tasks need to be processed first.
In some cases, due to the limitation of the local device power and the processing capacity, it is also necessary to consider the cloud server and the other means of system offloading. In [30], a scalable vehicle-assisted MEC (SVMEC) paradigm was proposed, and then the offloading decision problem is solved by using integer nonlinear programming. Similarly, the collaboration between the cloud and MEC can further break through the limitation of MEC server capabilities and obtain better processing results. Guo et al. [31] proposed a cloud–MEC collaborative computing offload architecture, using WiFi to access networks. Under this framework, an approximate collaborative computing offloading scheme and a game collaborative computing offloading scheme are proposed to obtain better offloading performance.
3. System Model and Problem Formulation
The system model diagram and the summary of key notations are shown in Figure 1 and Table 1 respectively. In campus, it is assumed that there are local mobile devices with energy collection and small base stations; each small base station deploys a MEC server. The edge cloud servers are deployed near the MEC servers to supplement the computing capability of MEC servers, and the edge cloud service servers have lower latency than the cloud server. The local mobile device is denoted by , and the MEC server is denoted by . Each local device is connected to the MEC server through a wireless link, and each MEC server can be connected to the edge cloud server through a wired link. It is supposed that there are time slots, each time slot interval is , and each device generates one computing task with fixed size (bits) in each time slot. Considering the mobility of the device, at the -th time slot, the distance between the local device and the server is denoted as .
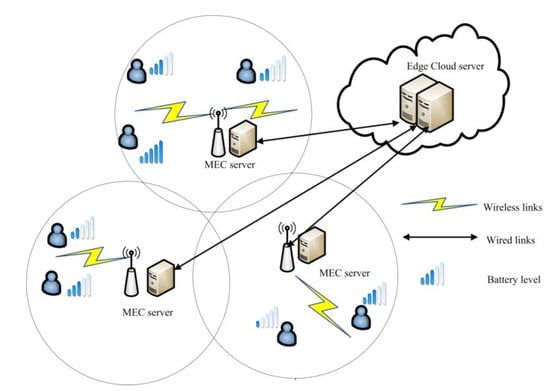
Figure 1.
A mobile edge computing (MEC)–edge cloud server collaborative system with energy harvesting technology.

Table 1.
Summary of key notations.
3.1. Task Offloading Model
Let be the task size (bits) generated by local device at the -th time slot, and be the number of CPU cycles required to process one bit of data, and define as the task priority. If , the task is to be priority processing. At the -th time slot, the task can be chosen to be processed locally, via the MEC or edge cloud servers, or not be processed. This is expressed as
In this system, the computing task can only select one of the modes of processing. That is,
3.2. Computing Model
3.2.1. Local Computing
The first processing mode is that the task is selected to be processed locally. The delay generated is only the processing time of the local device. In order to successfully execute the task generated by the local device at the -th time slot, cycles are required. The frequency arranged for the cycles at the -th time slot is expressed as , which can be achieved by adjusting the chip voltage using DVFS [32]. As a result, the local processing time generated by the local device at the -th time slot is expressed as
Due to the limitation of the local device processing capacity, is defined as the maximum CPU frequency of the local mobile device, so it needs to satisfy
The local processing energy consumption of mobile device at the -th time slot only includes the energy consumption of the task processing locally. In addition, is expressed as the chip’s effective capacitance coefficient, and is expressed as
3.2.2. MEC Server Computing
The second processing mode is that the local device offloads the task to the MEC server for processing through a wireless link. When , the task needs to decide which MEC server to offload, so defining and indicates the connection between and . In addition, each task generated by the local device at -th time slot can only be processed by one MEC server, so needs to satisfy
The task generated by the local device is offloaded to the MEC server through the wireless link. Assuming that wireless channel bandwidths are evenly distributed and do not interfere with each other, the channel transmission rate of the device transmission task to the MEC server is obtained according to Shannon Hartley Formula:
In the above formula, and is the channel gain ( is the fading power gain, is the loss constant, is the relative distance, and is the loss index); is the channel bandwidth; is the transmission power; and is the noise power. The time consumption considers the time costed when the task is transmitted to the MEC server, and the processing time of the MEC server, , is the frequency of MEC server. Then the processing time at the -th time slot when the task is offloaded to the MEC server is expressed as
Since the task offloading to the MEC server via the wireless link requires the energy of the local mobile device, the energy consumption only considers the transmit power of the local device, and the energy consumption of the second processing scenario is expressed as
3.2.3. Edge Cloud Server Computing
The third processing mode occurs when the local device offloads the task to the MEC server through a wireless link; when the MEC server has insufficient CPU resources, the device can upload the task to the edge cloud server for processing through the wired link on the MEC server, so the task processing time at the edge cloud server at the -th time slot is the sum of wireless transmission, wired transmission, and the processing time of the edge cloud server. Let be the backhaul fiber link rate, and the frequency of the edge cloud server is . In particular, considering the congestion of wired links, the links from each MEC server to edge cloud server are divided into to achieve the function of the speed-limiting shunt. Therefore, the processing time is expressed as
Similar to the MEC processing mode, when , the task needs to decide by which MEC server to upload the data to the edge cloud server, so defining , and indicates that the local device offloads the task to the MEC server via wireless link, and then uploads it to the edge cloud server for processing. In addition, needs to satisfy
As for the energy consumption of edge cloud server processing, as far as the local device is concerned, it is consistent with the energy consumption of an MEC server. The local device consumes energy only on wireless transmission, which is expressed as
3.3. Energy Harvesting Model
To sum up, the total energy consumption of mobile device at the -th time slot can be expressed as
Define the battery level of the local device with energy harvesting technology at the -th time slot as , and the maximum power possessed by the local mobile device as ; therefore, the following conditions need to be satisfied:
At the same time, is defined as the energy supplemented by the local device at the -th time slot through energy harvesting technology, and is the maximum energy limit that can be replenished, so the battery level of the device at next time slot is expressed as
3.4. Objective Function Based on Lyapunov Optimization
Through the above analysis of the three processing modes, the total processing time of the mobile devices at -th time slot can be obtained as
It should be noted that the processing time of the task cannot be higher than the time slot interval , which is expressed as
In this paper, the total consumption of all mobile devices at the -th time slot is used as an optimization goal, which is composed of the time delay and the penalty for the task not being processed. The total consumption is expressed as
where the penalty for the task not being processed is . In order to minimize the , the objective function at the -th time slot is defined as
Regarding the constraints, Equation (20) indicates that the CPU usage of the MEC server cannot exceed the maximum value, and the CPU usage of the server at the -th time slot can be expressed as
Equation (21) indicates the upper and lower limits of the device’s transmit power. Equation (22) indicates the limit on the total number of links available for each MEC server to connect to the edge cloud server and act as a speed limit.
Therefore, solving the problem can obtain the result for all mobile device resource allocation at the -th time slot, and the result for the local device can be expressed as
Among these variables, is the decision vector for the task selection processing scenario, which can be expressed as
where is the CPU processing frequency of the local device in the first processing mode, is the wireless transmission power value of the local device to the MEC server when the task is selected to offload to the second or third mode, and is expressed as the decision vector of the local device choosing which MEC server to offload tasks to when . This is similar to when , and indicates that the local device offloads the task to a particular MEC server via wireless link, and then uploads it to the edge cloud server for processing.
where is the energy value collected by the local device at the -th time slot.
However, this goal can be solved without considering the power of the local equipment. Because the system always wants the task to be processed, the power of the local device is always low. Considering that the task is generated by the application of the local mobile device, in order to maintain the stability of the power of the local mobile device, ensure that it has sufficient power to handle tasks that cannot be offloaded, e.g., the call service of mobile phones requires a certain amount of power, but the service task can only be handled locally. This article introduces the Lyapunov function to optimize local device power stability. Through stability analysis [18] for each mobile device, we use the perturbation parameter to define virtual power , which can be expressed as
The perturbation parameter is defined as:
where .
Then the Lyapunov optimization function and the Lyapunov drift function can be expressed as
Using Equation (15), we can obtain
As a result, we have:
where . Equation (33) means that is upper-bounded. In other words, the power of the system can be stabilized.
By analyzing Equations (19) and (33), considering the trade-off between the energy stability of the equipment battery and the processing consumption, the objective function of the resource allocation scheme at the -th time slot is obtained, which is expressed as :
represents the weight of the battery energy stability and delay. This weight can be initialized according to the battery power demand of the local device.
4. Proposed Algorithm
According to the objective function proposed by the above analysis, the purpose is to solve the problem of minimizing the processing delay under the constraint of battery energy stability, which is an NP-hard problem. This is considering that the tasks generated by mobile devices can be processed in three processing modes: local, MEC server, and edge cloud server. A method of solving the problem step-by-step is proposed. First, the target value of each processing scenario is obtained by dividing and conquering. The problem is transformed into an integer linear programming problem, and then an integer programming algorithm is used for finding the optimal target value. In order to get a better solution, this paper proposes an optimal integer linear programming (OILP) algorithm, which is performed in two steps. The first step is to propose a Lyapunov optimization based on task priority, in order to convert the problem into an integer programming problem. The second step is to propose an integer programming algorithm based on the CPU utilization optimization strategy, in order to obtain the optimal resource allocation plan.
4.1. Lyapunov Optimization Based on Task Priority
Divide problem into problems and , according to the divide-and-conquer idea, and solve them separately.
The problem is a linear problem. The value of is determined according to the sign of , and the mobile device energy collection value is solved.
By decomposing the problem into sub-problems for solving the three modes of local, MEC server, and edge cloud server, the decomposition formula is as follows:
The sub-problems , , and are solved as linear problems. By solving the optimization problem for local scene processing, the local processing frequency can be obtained, and the corresponding transmit power can be obtained by solving the optimization problem of the MEC server mode processing [18]. Because the time slot interval can be considered as the maximum time for tasks to complete processing, defining is the penalty value if the task cannot be processed. Therefore, the target value indicating that the task is not processed is expressed as
Therefore, in the end, the value of the decision vector for the task selection processing mode , as well as the decision vectors and of the local device choosing on which MEC server to offload tasks to need to be obtained. This problem is solved by the proposed second-step integer linear programming algorithm.
In addition, because the problem considers the power stability of the local mobile device, the system will not process some tasks that consume power in order to maintain the power stability. Therefore, the Lyapunov stability optimization will give up certain task processing performance. At this time, some tasks will not be processed, which will affect QoS, especially for some tasks that need to be processed urgently. Therefore, a Lyapunov algorithm based on task priority is proposed. This algorithm adds the task priority due to the Lyapunov stability optimization, which can guarantee the processing rate of high-priority tasks. For the task of , it is necessary to increase the penalty value when the task is not processed. Therefore, the target value indicating that the task is not processed is redefined.
where is defined as when the task cannot be processed in any mode under the constraints of local energy and time interval , which is . To ensure that high-priority tasks can be processed, is defined as
This can be guaranteed that when the local mobile device generates a high-priority task, and the task will be processed as long as the current battery is sufficient and the task can be processed within the time interval .
4.2. Integer Programming Algorithm Based on CPU Utilization Optimization Strategy
In order to solve the problem , after obtaining the target values of , , and , the problem can be converted into an integer linear programming problem. Through the integer programming algorithm, a resource allocation scheme can be obtained that minimizes the task processing delay at the -th time slot.
Construct an integer programming problem as follows:
In the above formula, , b, , beq, , are respectively inequality constraint matrix, inequality constraint column vector, equality constraint matrix, equality constraint column vector, lower and upper values. is the problem coefficient matrix, and the target values of , , and which are obtained by the first step, are used as the coefficient matrix element of the problem. This is expressed as
The matrix element is the target value of each scene at the -th time slot by the local device , which is defined as
Therefore, the decision solution obtained at the -th time slot is defined as
This corresponds to the coefficient matrix, which is defined as
Finally, the problem is converted to :
represents reasonable CPU usage value for the MEC server. For security reasons, in the real environment, the server’s CPU resources cannot be fully used for computing tasks, and if the server CPU runs for a long time with high values, problems like downtime will be generated, which will seriously affect QoS. Therefore, it is necessary to control the CPU usage of the server to provide computing resources within a safe range. is introduced to satisfy
The problem can be solved by a integer linear programming algorithm. However, in the case of task density, due to the shortage of CPU resources of the MEC server and the bandwidth resources of the edge cloud link, some tasks will not be processed, especially when the tasks are relatively large, which affects the resource utilization of the MEC server—e.g., when the remaining resources of the MEC server can process only 10 Kb of data, but the amount of work to be processed is 15 Kb, so the task is not processed and the resource utilization is low. Therefore, an integer linear programming algorithm based on CPU utilization optimization is proposed.
Firstly, after solving the P5 problem, the initial resource allocation strategy must be obtained. Then, the unhandled tasks are divided into two parts. Let be the part of the task size (bits) that the local device needs to handle, and let be the part of task size (bits) that the MEC server needs to handle. Finally, the optimal resource allocation scheme can be obtained.
Task sizes satisfy the following formula:
Equation (44) indicates the full use of the MEC server’s resources, and then place the remaining tasks on the local device to process.
The available energy is which has been obtained in the Lyapunov optimization based on the task priority algorithm, satisfies
Therefore, the CPU processing frequency of the local device can be expressed as
Then the processing time at -th time slot is expressed as
Therefore, at the -th time slot, for local devices , the problem is expressed as
Therefore, solving the P6 problem algebraically can obtain and for the local device , so the optimal result of resource allocation at the -th time slot can be obtained.
Algorithm 1 gives the main part of the OILP algorithm.
| Algorithm 1. Optimal integer linear programming (OILP) algorithm. |
| Input: () Output: (,) 1. For t = 1, 2, … T do 2. For i =1, 2, … N do 3. Obtain the values of , , and through the Lyapunov optimization, based on the task priority 4. End for 5. Solve P5 by integer programming algorithm 6. Find the tasks that cannot be processed 7. If the task was not processed due to the insufficient MEC server CPU resources and the edge cloud link resources then 8. Split the task, offload one part to MEC server, process the other locally, and keep the energy consumption as the energy consumed if the total task is offloaded to the MEC server for processing 9. Solve algebraically to obtain , and 10. If then 11. Implement the optimization strategy and update the MEC server CPU usage 12. else 13. Continue to optimize the next unhandled task 14. endif 15. endif 16. 17. End for |
5. Simulation Results
In this section, the proposed system and algorithm are verified by the simulation experiments. The battery energy stability of the local device, the number of unprocessed tasks, the delay of task processing, the CPU utilization of the MEC server, and the impact of task priority on the system were analyzed. Throughout the experimental analysis, the OILP algorithm can improve server utilization, reduce the number of unprocessed tasks, and reduce the time delay while keeping the system power stable.
5.1. System Setting
We used MATLAB for simulation experiments on WIN7 64-bit system. We assumed that each local device generates a computing task with fixed size (bits) in each time slot, and the probability that is . In addition, the wireless link environment parameters were consistent with the literature [18], and the remaining specific parameters are shown in Table 2. If there is no special explanation in the simulation, the parameters in the Table 2 are used in the simulation.

Table 2.
Simulation parameters.
5.2. Results Analysis
As shown in Figure 2, Lyapunov stability optimization can ensure that the power level of the local mobile device is maintained in a stable state. On the one hand, the task can be offloaded based on the battery power. On the other hand, the mobile device can locally have enough power to keep other applications running. In the experiment, the power of the mobile device is initially zero. As the energy is continuously collected and combined with the energy consumption of the task processing, the power will eventually remain in a stable state. Because the OILP algorithm considers the task priority, it will prioritize high-priority tasks at the beginning, and take energy supplement as a secondary consideration, which will lead to a longer time for the battery energy to reach stability, as shown in Figure 2a, when the number of the local device , the number of the MEC server , and the penalty value for the unprocessed tasks . The power of the local mobile devices that use the system and algorithm of this paper tend to be stable at about the 200th time slot. However, when we set the penalty value for the unprocessed tasks , as shown in Figure 2b, the power of the local mobile devices tends to be stable at about the 600th time slot, and is less stable than what is shown in Figure 2a. This is because a high penalty value ignores the local battery energy level, resulting in system energy instability. Therefore, in this paper, the penalty value for ordinary tasks that cannot be processed is the time slot interval , while for the tasks with priority, the consumption of unprocessed tasks is redefined in Equation (36), so as to ensure that the tasks with priority are processed.
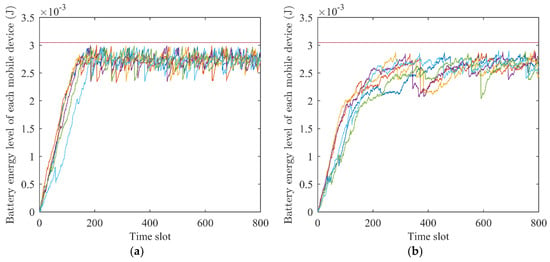
Figure 2.
The battery energy level when and . (a) The penalty value for the unprocessed tasks ; (b) the penalty value for the unprocessed tasks .
The experimental data were obtained by averaging 10 experiments, and the confidence intervals for the number of unprocessed tasks are shown in the locally zoomed, dotted intervals in Figure 3. Considering that the system power is stable after about the 300th time slot in the simulation, in Figure 3a, when the number of the local device and the number of the MEC server , the relationship between the different data size of the task and the number of unprocessed tasks in the 300th to 500th time slots is shown by comparing the integer linear programming (ILP) algorithm with the optimization (OILP) algorithm proposed in this paper. What is more, when the number of the MEC server and the task size , the relationship between the number of the local devices and the number of unprocessed tasks in the 300th to 500th time slots is shown in Figure 3b. From the simulation results, as the size of the tasks and the number of local devices increase, the resources of the MEC server and the edge cloud link become increasingly rare, so the number of unprocessed tasks increases.
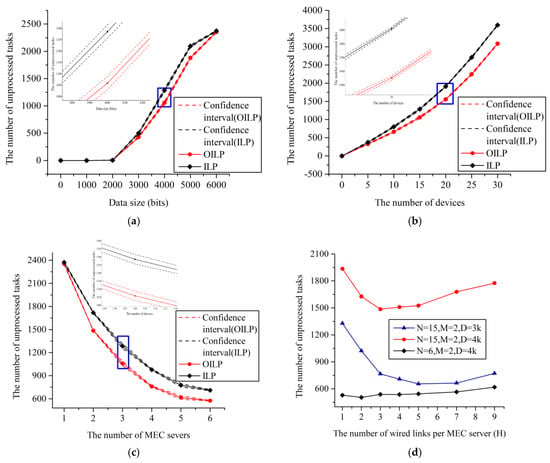
Figure 3.
Comparison of the integer linear programming (ILP) algorithm and the OILP algorithm on the number of unprocessed tasks. (a) The relationship between the number of unprocessed tasks and the data size of the task; (b) the relationship between the number of unprocessed tasks and the number of the local devices; (c) the relationship between the number of unprocessed tasks and the number of MEC servers; (d) the relationship between the number of unprocessed tasks and the number of wired speed limit links of each MEC server.
However, when the number of the local device and the task size , as shown in Figure 3c. As the number of MEC servers increases, the number of unprocessed tasks decreases.
In Figure 3d, we reveal the relationship between the number of unprocessed tasks and the number of wired speed limit links of each MEC server. According to the experimental analysis, in the case of random distribution of mobile devices, to get the lowest number of unprocessed tasks, the value of should not be greater than , i.e., is equivalent to the average number of wired speed limit links per MEC server provided to the local device to connect to the edge cloud server. Since the total bandwidth of wired links is constant, when the number of wired speed limit links is small, although high bandwidth can be provided, the available link connections will be more competitive. When the number of wired speed limit links is large, although the available wired link resources are more abundant, the bandwidth provided by each link is reduced, which will affect the QoS of some applications, resulting in tasks that cannot be processed. As shown in Figure 3d, when the number of the local devices , the number of the MEC servers and the task size , the number of unprocessed tasks is lowest when H = 3. However, when the task size , can be set a little bit higher; this is because, when the task size is small, the transmission of the tasks needs only a small amount of bandwidth to meet the delay requirement, so the number of links can be increased. In addition, the optimal value of is also related to the number of mobile devices. If the number of mobile devices is small, the value of should be set relatively small. In a word, the optimal value of is associated with factors like the number of mobile devices, the number of servers and the size of tasks. Therefore, it makes sense to give the right value.
When the number of the local device and the number of the MEC server , the consumption of all local devices in each time slot was averaged for statistics. As shown in Figure 4, because the OILP algorithm in this paper can reduce the number of unprocessed tasks, the average time delay consumption will also be optimized, especially after the power of the system is stable (after about the 300th time slot), and the optimization effect is particularly obvious.
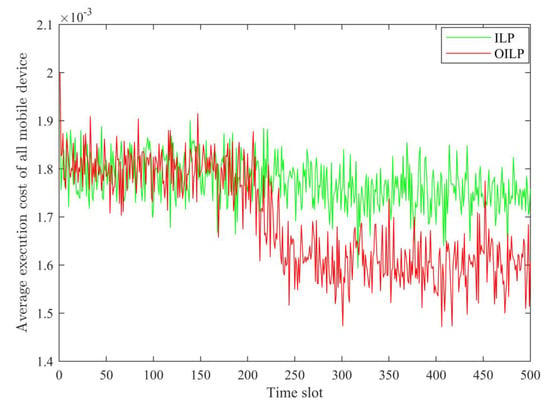
Figure 4.
The average cost of all devices.
Figure 5a,b show the CPU resource utilization of the MEC server. When the local device number , the data size of each task , and the reasonable CPU usage value , then the (OILP) algorithm proposed in this paper can increase the CPU utilization of the MEC servers. Because of the large size of the tasks to be processed, the virtual resources provided by the MEC server cannot handle multiple tasks, but they can be processed by task segmentation, which can improve both resource utilization and the performance. At the same time, the risk of server failures can be reduced by limiting the usage of the CPU resource.
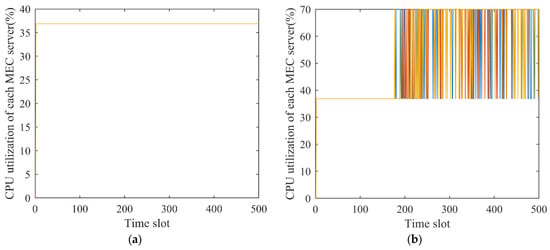
Figure 5.
The CPU usage of each MEC server in each time slot. (a) the CPU resource utilization of the MEC server by ILP algorithm; (b) the CPU resource utilization of the MEC server by OILP algorithm.
In the simulation, the experimental data were obtained by averaging 10 experiments, and the proportion of tasks with priority was simulated by setting the value of , as the value of determines whether the generated tasks have priority or not. When the number of the local device and the number of the MEC server , we analyzed the impact of task priorities on the system. As shown in Figure 6a, as the proportion of tasks marked with priority goes up, the number of tasks that cannot be processed goes down, so the performance of the system can be improved and the (OILP) algorithm can reduce the number of unprocessed tasks by more than the (ILP) algorithm. However, overprioritizing tasks will affect the power stability of the system. As shown in Figure 6b, as the proportion of tasks marked with priority increases, the longer it takes for the system to reach stability. In particular, when , the system will almost always be in a state of low power. This is because the tasks with priority must be processed when the power is sufficient, so the power will be consumed all the time. Therefore, it is necessary to reasonably set the proportion of tasks with priority.
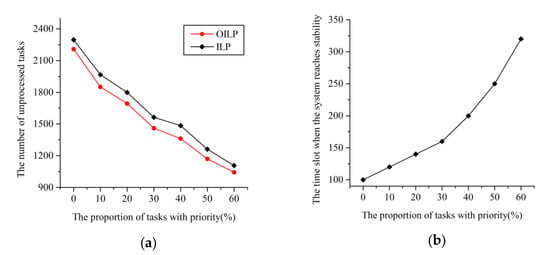
Figure 6.
The impact of the proportion of tasks with priority on the system. (a) The relationship between the number of unprocessed tasks and the proportion of tasks with priority ; (b) the relationship between the time slot when the system reaches stability and the proportion of tasks with priority ().
6. Conclusions
In this article, we propose an MEC–edge cloud server collaborative system model with energy harvesting technology, in order to minimize the processing delay of computing tasks and maximize MEC CPU resource utilization by allocating computing and network resources. We first use the Lyapunov stability theory to propose an objective function for the local device power stability. Then we propose an optimized integer linear programming (OILP) algorithm, which is performed in two steps. Those are the Lyapunov optimization algorithm, based on task priority, and the integer programming algorithm, based on the CPU utilization optimization strategy. Through analysis, the system and algorithm proposed in this paper can improve the utilization of the server and reduce the number of unprocessed tasks and the time delay, while keeping the system power stable. Finally, through simulation experiments, the better effect of the algorithm in this paper was obtained. Even though in an actual environment deployment, the complex environment will bring different parameters, and the different parameters will cause the different results, the idea proposed in this paper is still effective and valuable. In future studies, the attributes and scenarios like partial offloading and the relevance of task processing results need to be considered. In particular, hardware properties like memory and caching need to be studied for heterogeneous systems. In addition, the optimization of wired and wireless backhaul networks is also worth studying.
Author Contributions
Methodology, writing—review and editing, supervision, project administration, funding acquisition, D.L.; software, writing—original draft preparation, Y.J.; validation, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by National Natural Science Foundation of China under Grant 61902205.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CPU | Central Processing Unit |
| QoS | Quality of Service |
| NP | Non-deterministic Polynomial |
| UAV | Unmanned Aerial Vehicle |
| QoE | Quality of Experience |
| DVFS | Dynamic Voltage and Frequency Scaling |
| s.t. | subject to |
References
- Xia, W.; Quek, T.Q.; Zhang, J.; Jin, S.; Zhu, H. Programmable hierarchical C-RAN: From task scheduling to resource allocation. IEEE Trans. Wirel. Commun. 2019, 18, 2003–2016. [Google Scholar] [CrossRef]
- Huang, H.; Xia, W.; Xiong, J.; Yang, J.; Zheng, G.; Zhu, X. Unsupervised learning-based fast beamforming design for downlink MIMO. IEEE Access 2019, 7, 7599–7605. [Google Scholar] [CrossRef]
- Rida, I.; Al-Maadeed, N.; Al-Maadeed, S.; Bakshi, S. A comprehensive overview of feature representation for biometric recognition. Multimed. Tools Appl. 2020, 79, 4867–4890. [Google Scholar] [CrossRef]
- Abbas, N.; Zhang, Y.; Taherkordi, A.; Skeie, T. Mobile edge computing: A survey. IEEE Internet Things J. 2018, 5, 450–465. [Google Scholar] [CrossRef]
- Kumar, K.; Liu, J.; Lu, Y.H.; Bhargava, B. A survey of computation offloading for mobile systems. Mob. Netw. Appl. 2013, 18, 129–140. [Google Scholar] [CrossRef]
- ETSI White Paper. Mobile Edge Computing: A Key Technology towards 5G. Available online: https://infotech.report/Resources/Whitepapers/f205849d-0109-4de3-8c47-be52f4e4fb27_etsi_wp11_mec_a_key_technology_towards_5g.pdf (accessed on 7 June 2020).
- Sudevalayam, S.; Kulkarni, P. Energy harvesting sensor nodes: Survey and implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Tabassum, H.; Hossain, E.; Ogundipe, A.; Kim, D.I. Wireless-Powered cellular networks: Key challenges and solution techniques. IEEE Commun. Mag. 2015, 53, 63–71. [Google Scholar] [CrossRef]
- Ulukus, S.; Yener, A.; Erkip, E.; Simeone, O.; Zorzi, M.; Grover, P.; Huang, K. Energy harvesting wireless communications: A review of recent advances. IEEE J. Sel. Areas Commun. 2015, 33, 360–381. [Google Scholar] [CrossRef]
- Deng, M.; Tian, H.; Lyu, X. Adaptive sequential offloading game for multi-cell Mobile Edge Computing. In Proceedings of the 2016 23rd International Conference on Telecommunications (ICT), Thessaloniki, Greece, 16–18 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, F.; Xu, J.; Wang, X.; Cui, S. Joint offloading and computing optimization in wireless powered mobile-edge computing systems. IEEE Trans. Wirel. Commun. 2018, 17, 1784–1797. [Google Scholar] [CrossRef]
- Zhao, H.; Du, W.; Liu, W.; Lei, T.; Lei, Q. QoE aware and cell capacity enhanced computation offloading for multi-server mobile edge computing systems with energy harvesting devices. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018; pp. 671–678. [Google Scholar] [CrossRef]
- Yang, X.; Yu, X.; Huang, H.; Zhu, H. Energy efficiency based joint computation offloading and resource allocation in multi-access MEC systems. IEEE Access 2019, 7, 117054–117062. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Chen, Y.; Li, Z. Mobile edge computing based task offloading and resource allocation in 5G ultra-dense networks. IEEE Access 2019, 7, 184172–184182. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, Y.J. Computation rate maximization for wireless powered mobile-edge computing with binary computation offloading. IEEE Trans. Wirel. Commun. 2018, 17, 4177–4190. [Google Scholar] [CrossRef]
- Ahn, S.; Lee, J.; Park, S.; Newaz, S.S.; Choi, J.K. Competitive partial computation offloading for maximizing energy efficiency in mobile cloud computing. IEEE Access 2018, 6, 899–912. [Google Scholar] [CrossRef]
- You, C.; Huang, K.; Chae, H.; Kim, B.H. Energy-Efficient resource allocation for mobile-edge computation offloading. IEEE Trans. Wirel. Commun. 2017, 16, 1397–1411. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, J.; Letaief, K.B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices. IEEE J. Sel. Areas Commun. 2016, 34, 3590–3605. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Shen, J.; Jiang, X.; Zhong, X. Dynamic offloading for energy harvesting mobile edge computing: Architecture, case studies, and future directions. IEEE Access 2019, 7, 79877–79886. [Google Scholar] [CrossRef]
- Teng, Y.; Cheng, K.; Zhang, Y.; Wang, X. Mixed-Timescale joint computational offloading and wireless resource allocation strategy in energy harvesting multi-MEC server systems. IEEE Access 2019, 7, 74640–74652. [Google Scholar] [CrossRef]
- Mehrabi, M.; You, D.; Latzko, V.; Salah, H.; Reisslein, M.; Fitzek, F.H. Device-Enhanced MEC: Multi-Access Edge Computing (MEC) aided by end device computation and caching: A survey. IEEE Access 2019, 7, 166079–166108. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, L.; Wang, H.; Li, X.; Xu, P.; Wang, L.; Yang, X. Joint downlink and uplink edge computing offloading in ultra-dense HetNets. Mob. Netw. Appl. 2019, 24, 1452–1460. [Google Scholar] [CrossRef]
- Cheng, K.; Teng, Y.; Sun, W.; Liu, A.; Wang, X. Energy-Efficient joint offloading and wireless resource allocation strategy in multi-MEC server systems. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), IEEE, Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Ndikumana, A.; Tran, N.H.; Ho, T.M.; Han, Z.; Saad, W.; Niyato, D.; Hong, C.S. Joint communication, computation, caching, and control in big data multi-access edge computing. IEEE Trans. Mob. Comput. 2019, 19, 1359–1374. [Google Scholar] [CrossRef]
- Zhao, P.; Tian, H.; Qin, C.; Nie, G. Energy-Saving offloading by jointly allocating radio and computational resources for mobile edge computing. IEEE Access 2017, 5, 11255–11268. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Liu, J.; Lai, J. Joint offloading and transmission power control for mobile edge computing. IEEE Access 2019, 7, 81640–81651. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C. Optimization of network-based caching and forwarding using mobile edge computing. IEEE Access 2019, 7, 181855–181866. [Google Scholar] [CrossRef]
- Min, M.; Xiao, L.; Chen, Y.; Cheng, P.; Wu, D.; Zhuang, W. Learning-Based computation offloading for IoT devices with energy harvesting. IEEE Trans. Veh. Technol. 2019, 68, 1930–1941. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, Y.; Hu, R.Q.; Qian, Y. Computation rate maximization in UAV-enabled wireless-powered mobile-edge computing systems. IEEE J. Sel. Areas Commun. 2018, 36, 1927–1941. [Google Scholar] [CrossRef]
- Pham, X.-Q.; Nguyen, T.-D.; Nguyen, V.; Huh, E.-N. Joint node selection and resource allocation for task offloading in scalable vehicle-assisted multi-access edge computing. Symmetry 2019, 11, 58. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Qin, H. Collaborative mobile edge computation offloading for IoT over fiber-wireless networks. IEEE Netw. 2018, 32, 66–71. [Google Scholar] [CrossRef]
- Liang, J.; Liu, C.; Tan, G.; Yang, L. Joint offloading and frequency scaling technology for mobile edge computing. In Proceedings of the 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Zhangjiajie, China, 10–12 August 2019; pp. 2045–2052. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).