Design of Concentric Ring Antenna Arrays Based on Subarrays to Simplify the Feeding System

Abstract

The global synthesis for antenna arrays that produce a desired radiation pattern is a scientific symmetry problem. This paper deals with the design of concentric ring antenna arrays to simplify the feeding system using a cophasal subarray configuration. This simplification in the feeding network is achieved by the reduction of phase shifters via a proper clustering of radiators applying one amplitude and one phase excitation by subarray in the array system. The array design for this geometry considers an optimization process based in differential evolution to reduce the side-lobe level, resulting in simplification of the feeding network. Simulation results based on CST Microwave Studio and HFSS are provided to verify the accuracy of the array model and to take mutual coupling into account. These simulations are provided using a circular patch as antenna element to generate a scannable array pattern over the elevation plane. Furthermore, an analysis of the manufacturing tolerances was made to verify the reliability of our design.

1. Introduction

The number of devices connected to mobile networks is continually increasing with the use of wireless sensors. One promising solution for overcoming the associated issues is the use of phased antenna arrays at the hardware level of the sensor nodes. The applications of phased array systems are well known and widespread in numerous telecommunications fields. Phase shifters are essential components and are extensively used in modern phased-array antennas [1]. However, with the complexity in the feeding network and its interaction with the radiating elements, the design of phased arrays can be a challenging problem [2,3]. Design cases using a large number of phase shifters can be particularly complicated. In conventional antenna arrays, the beamforming network (with phase and amplitude coefficients) uses one phase shifter (and, often, one phase shifter and one attenuator) per antenna element. In these cases, the beamforming network can be highly complex and limited for applications with a large number of antenna elements.

It is desirable in all applications to ensure low complexity and low cost by using a small number of phase shifters to accomplish the requirements of scanning and side-lobe level. A significant amount of previous literature relates to the reduction of the number of phase shifters. Notably, simplification of the complexity of the feeding system has been undertaken for a large number of applications: mobile earth stations [4], radar systems [5,6,7], vehicular uses [8] and autonomous systems [9].

The conventional method of reducing the number of phase shifters is to divide the array into uniform subarrays (or groups) and feed each group with a single-phase shifter [10,11,12]. However, grating lobes appear in the visible space and cause the side-lobe level to increase abruptly [13,14]. This problem has been dealt in previous work by using overlapping subarrays [15,16,17,18,19,20], aperiodic subarrays [4,21], random feeding networks [2] and interleaved subarrays [3]. The technologies of overlapping subarrays and random feeding networks have been applied recently [2,20].

However, the majority of applications based on overlapping subarrays and random feeding networks consider limited-scan arrays for conventional antenna array structures, such as linear and planar. The application of subarrays to reduce the number of phase shifters in array structures of wide-angle scanning is scarce.

The current paper introduces the design of concentric ring antenna arrays based on subarrays to simplify the feeding system. The choice of concentric ring geometry is not arbitrary. This array structure was chosen considering its applications in technology, including mobile communication, radar system, satellites and medical treatment. In addition, the behavior of the cophasal excitation of this structure facilitates the generation of subarrays.

This paper proposes the design of concentric ring antenna arrays using a cophasal subarray configuration. This array design configuration using a structure of concentric rings can provide desired radiation characteristics with angular scanning and reduces the number of phase shifters employed in the system.

Because the geometry influences the results, the design methodology for this array geometry considers an optimization process based on differential evolution [22] to reduce the side-lobe level, resulting in the simplification of the feeding network. The reduction of phase shifters is achieved via a proper clustering of radiators applying one amplitude and one phase excitation by subarray in the array system.

This paper illustrates a highly nonlinear symmetry problem related to the design of antenna arrays using concentric rings geometry for reducing the number of phase shifters and achieving maximum performance. The novelty of the paper concerns the proposed subarraying technique to reduce phase shifters using the specified array geometry. Amongst the current state-of-the-art approaches, there appears to be no trace of works dealing with the design of antenna arrays to reduce the number of phase shifters using the proposed technique and concentric rings geometry.

Furthermore, simulation results based in CST Microwave Studio and HFSS are provided to verify the accuracy of the array model and to take mutual coupling into account. The CST Microwave Studio simulations consider a circular patch as antenna element to generate a scannable array pattern over the elevation plane.

2. Array Pattern with Cophasal Subarrays

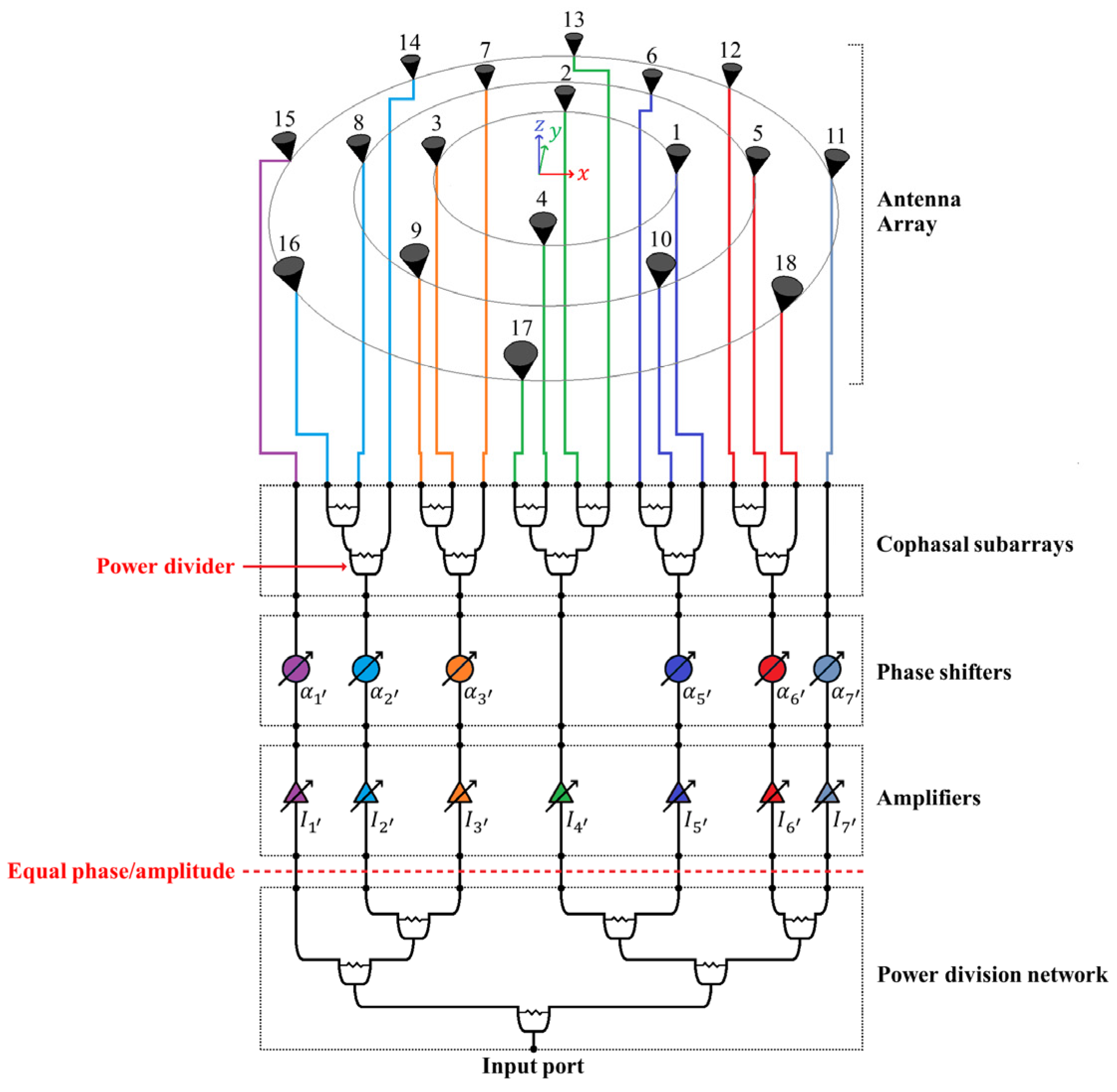
The approach proposed in this paper uses a concentric ring antenna array to generate a radiation pattern over the elevation plane, and to reduce the number of phase shifters employed by applying a cophasal subarray configuration, i.e., for grouping the elements using one amplitude and one phase excitation by each cophasal subarray in the array system.

The array factor of the concentric ring antenna array (see Figure 1) can be expressed as [23,24]:

$$AF={\displaystyle \sum }_{n=1}^{N_r}{\displaystyle \sum }_{m=1}^{N_n}{I}_{nm}\exp \left[j\left(k{r}_{n}sin\theta cos\left(\phi -{\phi }_{nm}\right)+{\alpha }_{nm}\right)\right]$$

(1)

where N_r is the number of circular rings in the array, N_n is the number of antenna elements in the nth circular ring, I_nm and α_nm are the amplitude and phase excitations of the mth antenna element for the nth circular ring, respectively, r_n is the radius of nth circular ring, k is the propagation number, θ is the elevation angle and φ is the azimuth angle. The main beam is scanned to (θ₀,φ₀) by applying a cophasal excitation, therefore, α_nm is given by:

$${\alpha }_{nm}=-k{r}_{n}sin{\theta }_{0}cos\left({\phi }_0-{\phi }_{nm}\right)$$

(2)

The total radiation pattern of the complete system, P(θ,φ), is determined as:

$$P\left(\theta ,\phi \right)=AF\left(\theta ,\phi \right)\times EP\left(\theta ,\phi \right)$$

(3)

where EP(θ,φ) is the pattern of the antenna element.

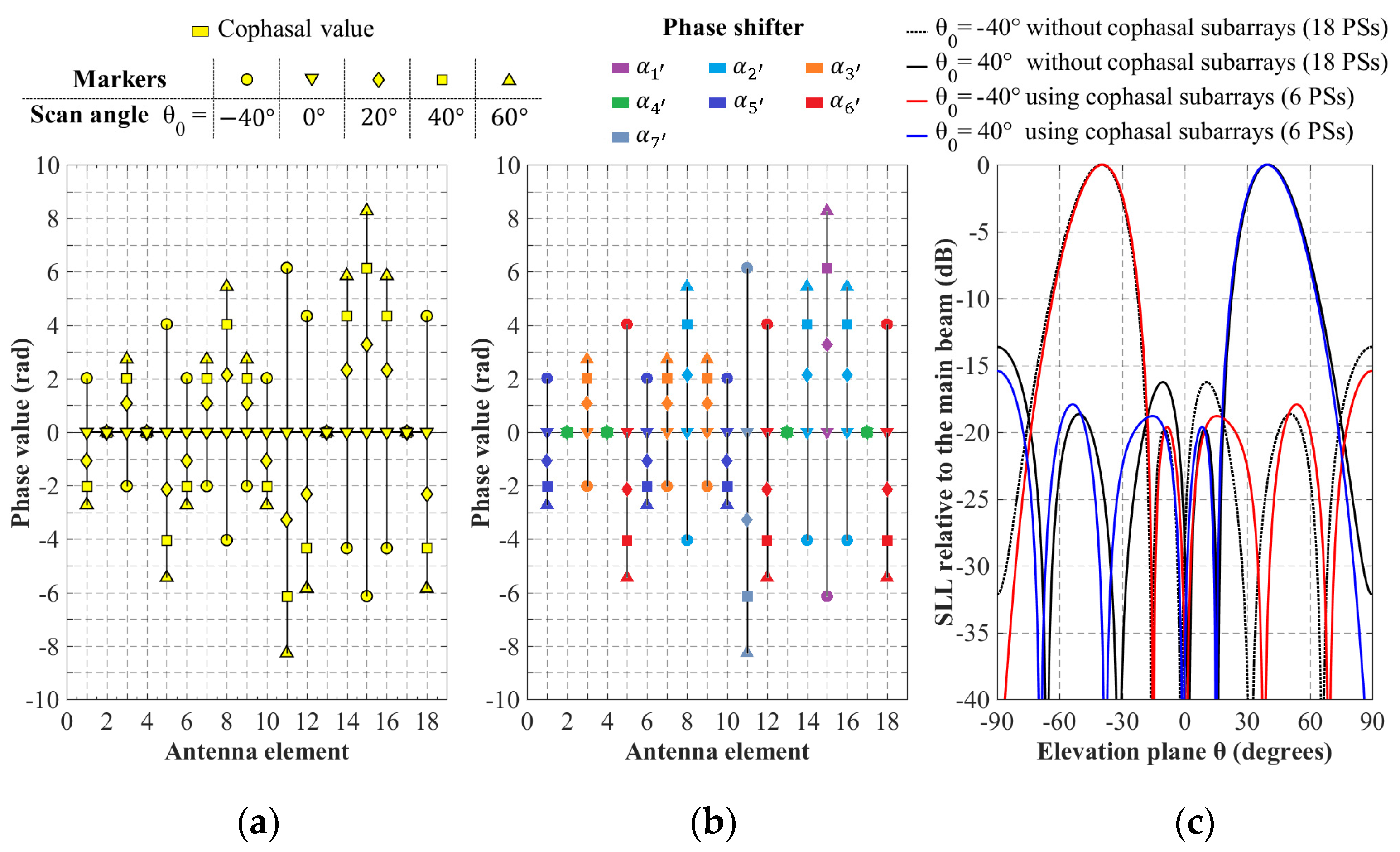
In order to explain the proper clustering of radiators, Figure 2 and Figure 3 show a concentric ring antenna array of three rings with N₁ = 4, N₂ = 6 and N₃ = 8. This configuration uses seven subarrays created strategically considering cophasal excitation. The behavior of the cophasal excitation values in the elevation plane based on Equation (2) is illustrated in Figure 4. This figure illustrates the phase value required by each antenna element to scan the main beam in θ₀ = [−40°, 0°, 20°, 40°, 60°] in the elevation plane in the cut of φ = π. This behavior for this array geometry illustrates that one same phase value (elements with similar phase values) can be assigned to several antenna elements, as shown in Figure 4b. This can be taken as an advantage for grouping the antenna elements in subarrays and reducing the number of phase shifters employed in the antenna system. Therefore, the groups or subarrays are set considering the cophasal excitation required for scanning the main beam; then, this subarray configuration can be named cophasal subarrays configuration. In the case of Figure 2, the amplifiers can be considered variable or fixed during beam scanning. Figure 3 illustrates the subarray configuration proposed for the case of using a distribution of raised cosine amplitude excitation [2].

This amplitude distribution has been shown to be efficient in antenna arrays for the amplitude excitation function [2]. This design case can be useful to evaluate the performance of the optimized case. The case of raised cosine distribution needs 12 (fixed) amplifiers to generate the amplitude excitations across the antenna array [2] for that design configuration, as shown in Figure 3. As shown in the phase values of Figure 4a, four antenna elements {n₂, n₄, n₁₃, n₁₇} represent zero phase values for all scanning directions. In this case, these antenna elements do not require a phase shifter (or these antenna elements could be set in a subarray fed by one phase shifter). The next subarrays that present the same phase value (or similar values) are groups of three elements, the cases of {n₁, n₆, n₁₀}, {n₃, n₇, n₉}, {n₅, n₁₂, n₁₈} and {n₈, n₁₄, n₁₆}, and finally two groups of one antenna element: {n₁₁} and {n₁₅}. The power delivery network can be considered by using a cascaded unequal dividers network [2] (usually with Wilkinson divisors). The power and phase in each element of a same subarray (in our configuration of cophasal subarrays) must be equal. This is achieved by using 1-to-3 and 1-to-4 equal power dividers.

Note that a scannable pattern (see Figure 4c) in the range of −40° ≤ θ₀ ≤ 40° (with a peak side-lobe level of −15 dB) could be generated maintaining the same subarray configuration, i.e., by just varying the value of the phase shifter for each subarray: α_1’, α_2’, α_3’, α_5’, α_6’, α_7’. This configuration represents the case of using the radii values of r₁ = 0.5λ, r₂ = 1.00λ and r₃ = 1.52λ. These radii values were obtained using our previous experience in antenna arrays optimization [25,26,27,28,29,30]. Although it is obvious that different array configurations and scanning angle (such as different radii values) result in different element phase distribution, the same subarray configuration will be retained for a specific array configuration and scanning angle range. This condition is retained because the phase values for each subarray are assigned in a perpendicular way to the scanning elevation plane (x-z plane), i.e., although the phase value changes for each scanning direction the same groups or subarrays are obtained. As commented previously, this is the reason why we chose concentric rings as the array geometry. The behavior of the cophasal excitation of this structure facilitates the generation of subarrays.

The decision variables for this design case are the values of the amplitude and phase excitations feeding each subarray. In our optimization procedure, the optimization goal is to minimize the side-lobe level. The technique of differential evolution was considered based on its versatility for designing antenna arrays and our previous experience. Differential evolution is a well-known state-of-the-art technique; details and implementation procedures can be found in [22,26].

3. Results and Discussion

The method of differential evolution was implemented in MATLAB for optimizing the values of the amplitude and phase excitations using the cophasal subarray configuration for grouping the elements illustrated in Figure 2 (considering N₁ = 4, N₂ = 6 and N₃ = 8). Differential evolution was applied to find the values of the amplitude and phase excitations to generate a scannable array pattern over the elevation plane. We followed the literature and our previous results to set the parameters for the optimization algorithm. We considered the design cases of variable and fixed amplifiers. In addition to these design cases, we make a comparison to the case in which a raised cosine distribution (Figure 3) across the antenna array is used.

3.1. Array Factor Results

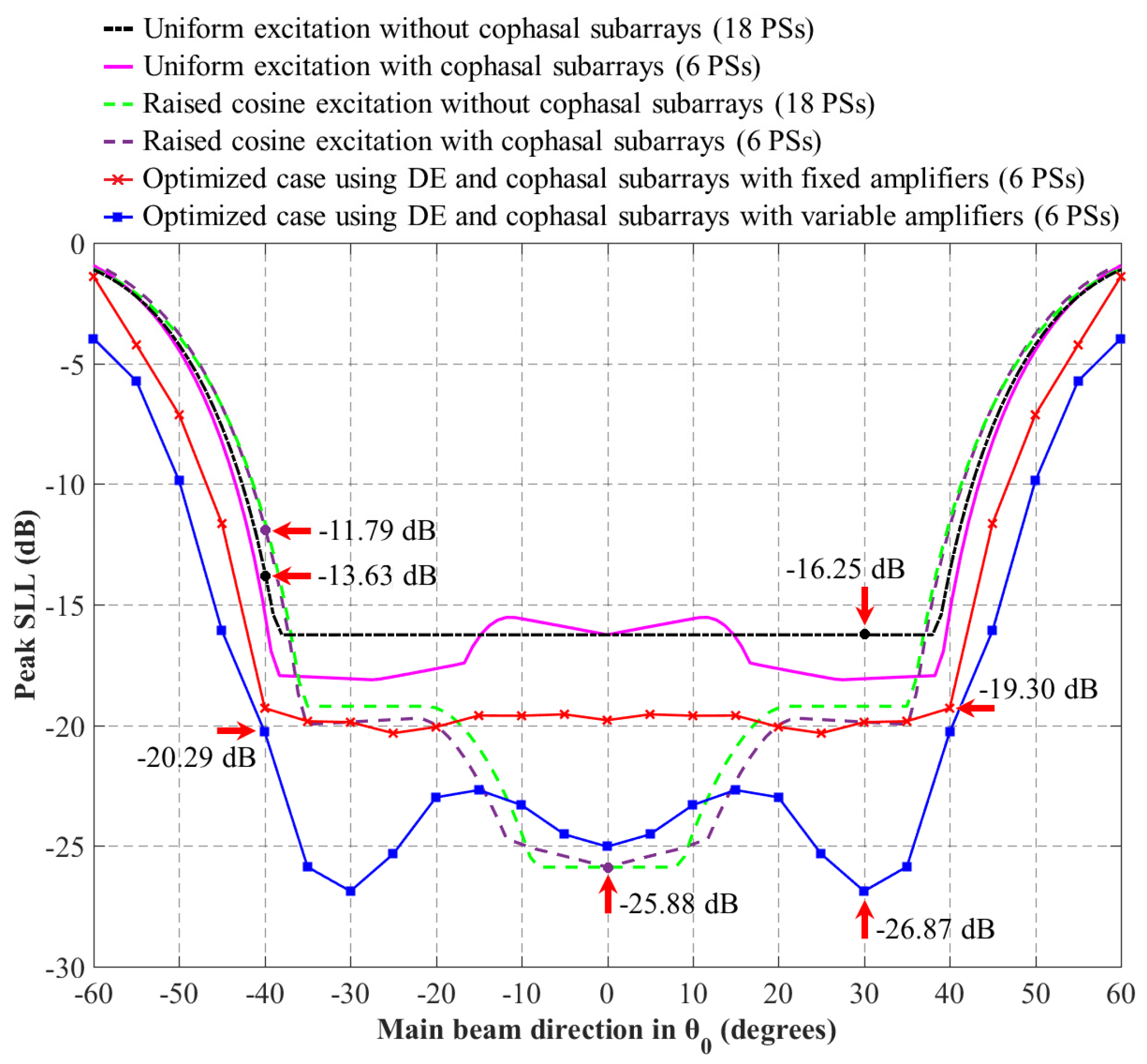
The first case studied using cophasal subarrays was that considering the response of the array factor. In this case, Figure 5 illustrates the behavior of the side-lobe level obtained (for the array factor optimized by differential evolution) versus scanning direction for the concentric ring antenna array using cophasal subarrays with optimization using variable and fixed amplifiers, and its comparison with respect to the design cases using a raised cosine distribution and uniform amplitude excitation. The behavior of the side lobe level as a function of scanning direction in steps of 5° is illustrated. As shown in Figure 5, the optimized case using differential evolution and cophasal subarrays with variable amplifiers provides better side-lobe level values for all of the scanning range. The important aspect is that this side lobe-level behavior in the scanning range is achieved by using only six phase shifters (and seven variable amplifiers), reducing the number of phase shifters from 18 for a conventional array (which uses one phase shifter per antenna element without optimization) to six. This represents a 66.6% reduction in the number of phase shifters used in the array system at the expense of using seven variable amplifiers. The highest or maximum value of the side-lobe level was −26.87 dB found for the array factor in the case of θ₀ = 30°. The minimum value of side-lobe level (in the scanning range) was −20.29 dB found in θ₀ = 40°. There was a reduction in the side-lobe level of almost 10 dB with respect to the conventional array of cophasal excitation, and almost 8 dB with respect to the case using cophasal subarrays without optimization. The optimized case of cophasal subarrays provides a scanning range over the elevation plane of [−45°, 45°] for a peak side-lobe level below −15 dB, and a range of [−50°, 50°] for a peak side lobe level of −10 dB.

The optimized case using fixed amplifiers provides a good design compromise. This design case provides a range of scanning of [−40°, 40°] for a peak side-lobe level of ≅−20 dB, and a range of [−45°, 45°] for a peak side lobe level of ≅−12 dB. It is important to note that this performance is obtained using six phase shifters and seven fixed amplifiers, holding them constant during the beam scanning, and avoiding the use of variable amplifiers. The side-lobe level response is much flatter than the variable amplifier case and the other cases.

Furthermore, it is interesting to note that the case of raised cosine distribution presents similar values of side-lobe level using six or 18 phase shifters. This design case provides a range of scanning of [−10°, 10°] for a peak side-lobe level of ≅−25 dB, a range of [−35°, 35°] for a peak side-lobe level of ≅−20 dB and a range of [−40°, 40°] for a peak side-lobe level of ≅−11 dB. This design case requires 12 fixed amplifiers to adequately generate the amplitude distribution. Depending on the designer criteria this design case could be a good option for cases of limited scanning range.

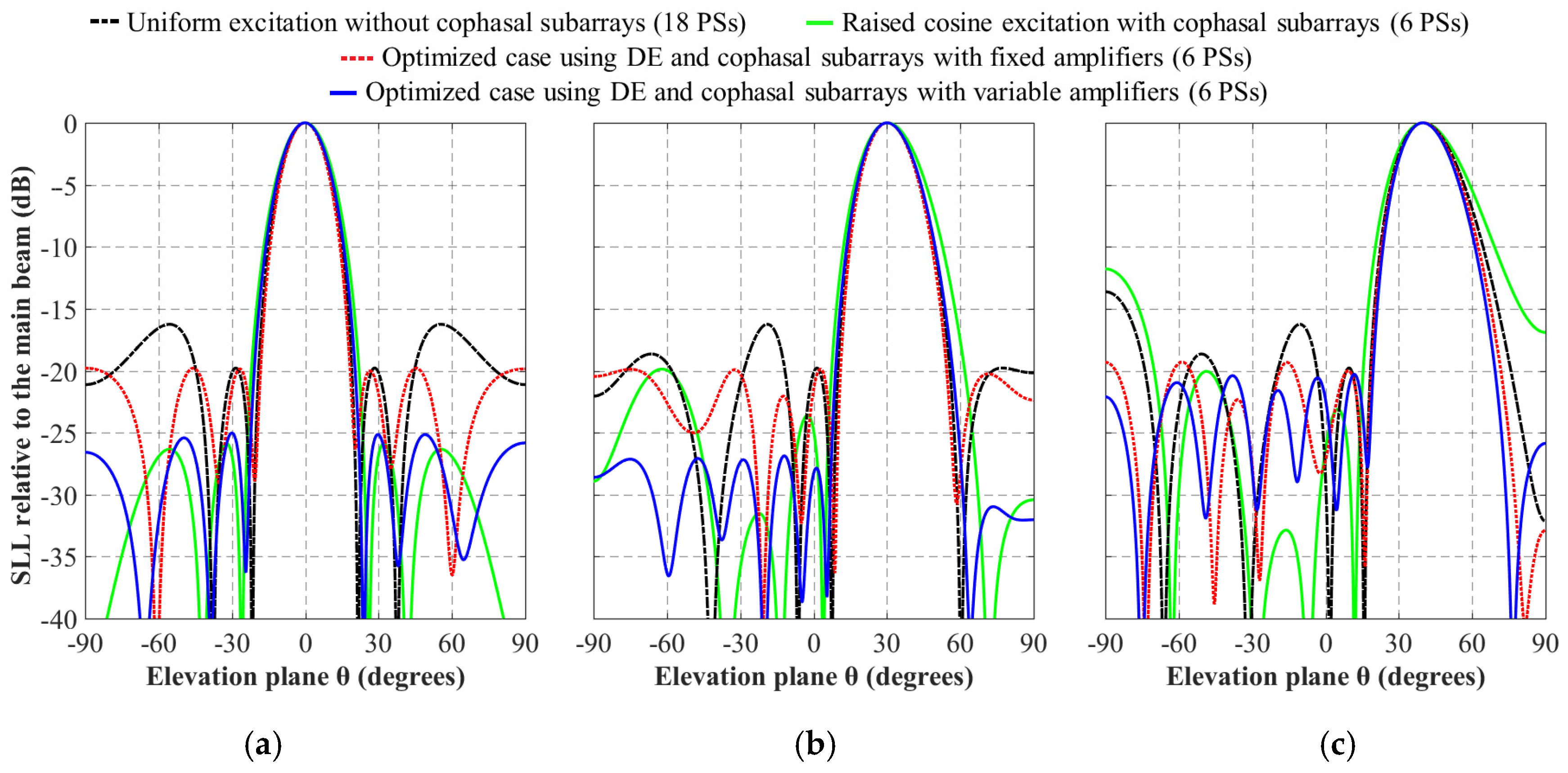
Figure 6 shows some example cases of an array factor optimized with differential evolution and cophasal subarrays using variable and fixed amplifiers, and its comparison with respect to the other design cases, for scanning directions of (a) θ₀ = 0°, (b) θ₀ = 30° and (c) θ₀ = 40°. The method of differential evolution efficiently computes the values of the design variables to generate an array factor with characteristics of low side-lobe level without pattern distortion during beam steering.

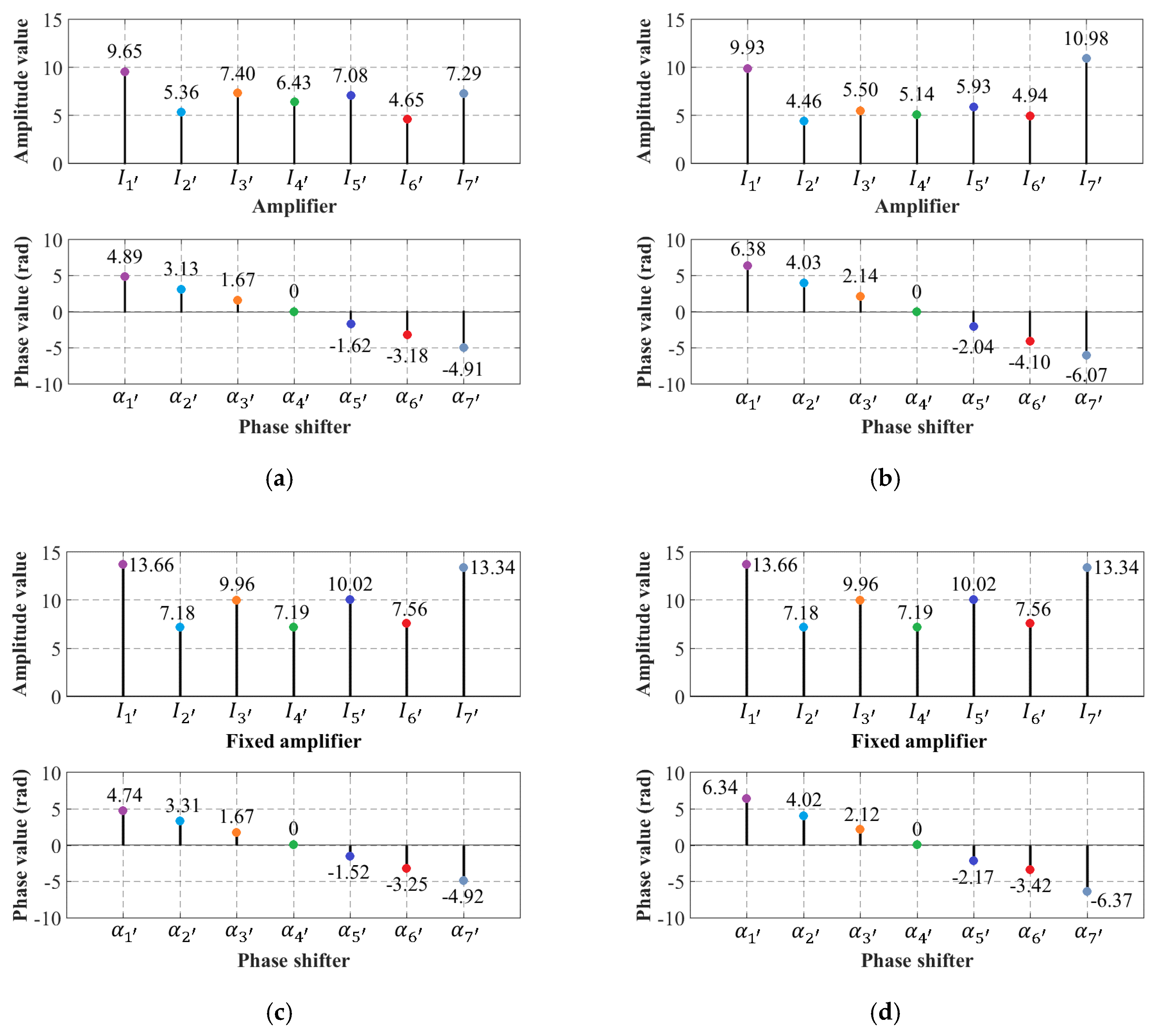
The values of the amplitude and phase excitations for each cophasal subarray were determined by differential evolution for each scanning direction in steps of 5° for the optimized case using variable amplifiers. In the case of fixed amplifiers, the same set of amplitude excitations was held constant during beam scanning. Figure 7 shows the values of the amplitude and phase excitations for the optimized cases using variable and fixed amplifiers with scanning directions of θ₀ = 30° and θ₀ = 40°. The minimum value of the amplitude excitation was 4.46 and the maximum value was 10.98 for the case of variable amplifiers, and 7.18 and 13.66, respectively, using fixed amplifiers. In this case, the amplitude weights could be realized in a real hardware setup rescaling all the complex coefficients before applying them to a real system. In a real system, the amplitudes will be adjusted at every layer in such a way that the conservation law of the energy will be preserved. Furthermore, it is interesting to note that the values of phase excitations obtained follow the behavior of a phase slope, i.e., a progressive phase excitation is obtained similar to phase excitation for linear arrays. This is because the phase values for each subarray are assigned in a perpendicular way to the scanning elevation plane (x-z plane).

3.2. CST Microwave Studio Simulation

In order to verify the accuracy of the array model and to take mutual coupling into account, the optimized design case was simulated in full-wave using CST Microwave Studio. The CST Microwave Studio simulations were run in a high performance server consisting of several GPU cards to accelerate the process. The optimized design case using variable amplifiers was modelled and implemented in CST Microwave Studio using a circular patch as antenna element for an operation frequency of 2.4 GHz with the dimensions: a = 17.27 mm, h = 1.6 mm and p’ = 6.37 mm [31]. The substrate of the circular patch presents characteristics of relative permittivity ε_r = 4.2, μ = 1 and 0.025 of tangential losses, corresponding to FR4 values. We considered full-wave analysis of the feeding network for the phase and amplitude values found in the optimized design (without post-processing the results of the full-wave analysis of the antenna array).

First, we examined the active impedance or active S parameters of the array design. The behavior of the reflection coefficient changes during beam scanning, so we considered a scanning direction far from the natural radiation response of the array (i.e., in θ₀ = −40°). The active reflection coefficient (or scan reflection coefficient) is the reflection coefficient for a single antenna element in the array antenna, in the presence of mutual coupling. 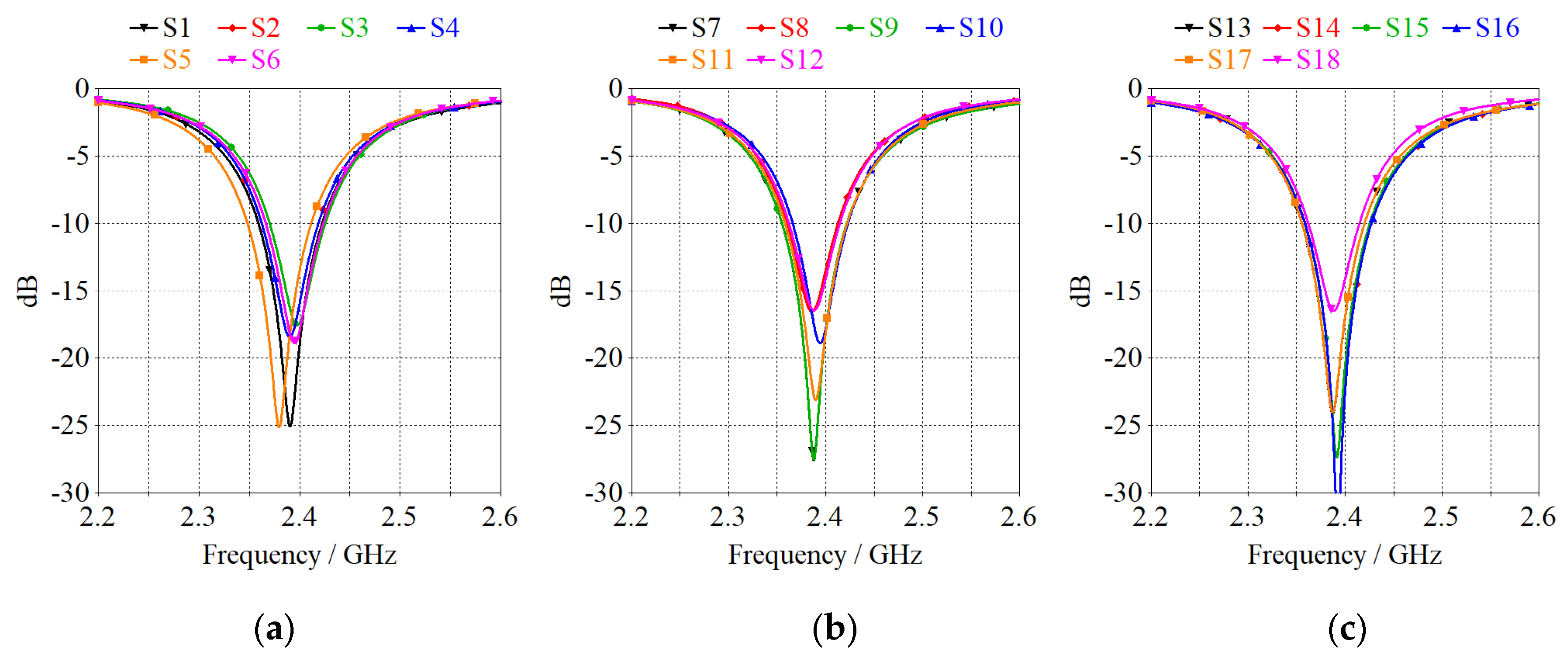The active reflection coefficient is a function of frequency, scanning direction and the excitation of the neighboring elements [32]. Every scanning direction was examined (of the scanning range) far from the natural radiation response of the array. This was challenging, especially for the farthest directions (from the natural radiation response of the array), but the active reflection coefficient of 18 antenna elements remained below −10 dB for all scanning directions [−40°, 40°] at 2.4 GHz.

Figure 8 shows the active reflection coefficient of 18 antenna elements at 2.4 GHz corresponding to the scanning direction of the main beam in θ₀ = −40°. As was expected, the elements show a good matching performance. Furthermore, the reflection coefficient of elements is lower than −10 dB in the frequency of interest, which is acceptable for many applications. This behavior remained around the central frequency of the array from 2.37 to 2.41 GHz with 40 MHz of bandwidth.

Figure 9 illustrates the radiation pattern obtained using CST Microwave Studio and HFSS simulations for the configuration using cophasal subarrays and the circular patch in scanning directions of θ₀ = −40°, −30°, 20° and 40°. As shown in Figure 9, the side-lobe level response was maintained at low values, i.e., a side-lobe level of −19.76 dB with CST and −18.75 dB with HFSS at the most distant scanning directions considering the antenna element based in the circular patch with the characteristics mentioned previously. The two pattern responses (obtained using CST and HFSS) are very similar.

Figure 10 shows the array configuration using circular patches and the 3D radiation pattern obtained using CST Microwave Studio simulation for the case using cophasal subarrays in scanning directions of θ₀ = −40°, θ₀ = 0° and θ₀ = 40°. These simulation results demonstrate that for the proposed configuration of concentric rings array using cophasal subarrays for grouping the elements, the technique of differential evolution shows that the values of the amplitude and phase excitations feeding each cophasal subarray provide a low side-lobe level.

Furthermore, a better side lobe level performance was obtained with a significant reduction in the number of phase shifters compared to a conventional array (that uses one phase shifter per antenna element without optimization). The CST Microwave Studio simulations using the circular patch as antenna element generated a scannable array pattern over the elevation plane in the range [−40°, 40°] without pattern distortion during beam steering.

Table 1. Comparison of the CST simulation results (directivity and side-lobe level) with respect to the theoretical results for the analyzed scanning angles.

Main Beam Direction (θ0)	Array Factor		CST
	Side Lobe Level (dB)	Directivity (dB)	Side Lobe Level (dB)	Directivity (dB)
−40°	−20.29	11.99	−19.76	12.23
−35°	−25.86	12.04	−24.26	12.14
−30°	−26.87	12.22	−27.83	12.28
−25°	−25.34	12.48	−26.79	12.57
−20°	−22.99	12.60	−23.40	12.67
−15°	−22.68	12.63	−23.38	12.68
−10°	−23.31	12.61	−23.78	12.61
−5°	−24.18	12.70	−23.01	12.70
0°	−25.17	12.72	−25.77	12.73
5°	−24.18	12.70	−23.01	12.70
10°	−23.31	12.61	−23.83	12.61
15°	−22.68	12.63	−23.42	12.67
20°	−22.99	12.60	−23.46	12.67
25°	−25.34	12.48	−26.82	12.57
30°	−26.87	12.22	−28.18	12.29
35°	−25.86	12.04	−24.52	12.14
40°	−20.29	11.99	−20.21	12.22

shows a comparison of the CST simulation results (directivity and side-lobe level) with respect to the results without considering mutual coupling. Mutual coupling does not deteriorate the pattern features obtained. The minimum spacing is 0.5 λ among antenna elements. This helps to avoid degradations caused by electromagnetic couplings.

Furthermore,

Table 2. A performance comparison of the design case based in cophasal subarrays for the geometry of concentric rings with respect to other array geometries published in state of art.

	Geometry		Number of Elements	Number of Phase Shifters	Reduction of Phase Shifters (%)	Scanning Range	Peak Sidel Lobe Level
Cophasal subarrays	Concentric rings		18	6	66%	±40°	−20 dB
Conventional case	Concentric rings		18	18	0%	±39°	−15 dB
Uniformly subarrays [2]	Linear array		36	12	66%	±6°	−15 dB
Overlapped subarrays	Planar array	[3]	80	4	95 %	±7°	−20 dB
		[20]	28	14	50%	±24°	−15 dB
			28	7	75%	±11°	−15 dB
Randomly feeding network [2]	Linear array		30	12	60%	±14°	−15 dB
CORPS [33]	Linear array		10	8	20%	±30°	−19 dB
			10	7	30%	±20°	−16 dB

shows a performance comparison of the design case for the geometry of concentric rings with respect to other state-of-the-art array geometries. This comparison is achieved in terms of the array geometry, number of antenna elements, reduction of phase shifters, scanning range and side lobe level. The case of cophasal subarrays presents a reduction in phase shifters of 66% for a scanning range of ±40° with a peak side-lobe level of −20 dB. The case of cophasal subarrays outperforms all cases in terms of the scanning capacity and side-lobe level, and resulting in a good compromise in the reduction of phase shifters by 66%.

3.3. Manufacturing Tolerances

An analysis of the manufacturing tolerances was made to verify the reliability of our design, i.e., the control points (the design variables: amplitude and phase excitations) can differ from the ideal because of manufacturing tolerances [34]. Tolerances in the implementation of the amplitude levels and the phase shifts (produced by the phase shifters) could result in a pattern with relatively high side-lobe level [34]. Therefore, errors in the amplitude and phase values of the excitations were taken into account by means of a probability distribution function where random and statistically independent errors among the array elements were assumed [35], i.e., we can model the manufacturing tolerance errors by considering the amplitude and phase errors as statistically independent functions. These error functions can be modelled by a Rician probability function [35].

Figure 11 shows the error intervals for the ideal values of the amplitude and phase excitations (obtained for main lobe direction of θ₀ = −40°) considering a tolerance of 5%. Figure 11 illustrates that the error is directly proportional to the value of the amplitude and phase excitation, i.e., we have a higher value of error for higher values of amplitude and phase. The maximum error interval is found in the antenna element n₁₅ for the amplitude excitation (from 10.43 to 11.52, $\pm$0.54), and, in the elements n₁₁ and n₁₅ for the phase ($\pm$0.32 radians $\approx \pm$18°).

All scanning directions were examined using 300 iterations with a tolerance of 1% and 5%. Here we illustrate the cases of scanning directions more sensitive to the tolerance errors. Figure 12 illustrates the response of the array factor for all the iterations obtained using the amplitude and phase values with an error tolerance of 1% (Figure 12a) and 5% (Figure 12b) for a scanning direction in θ₀ = −40°, and for a scanning direction in θ₀ = 20° (Figure 12c) with 5% tolerance. 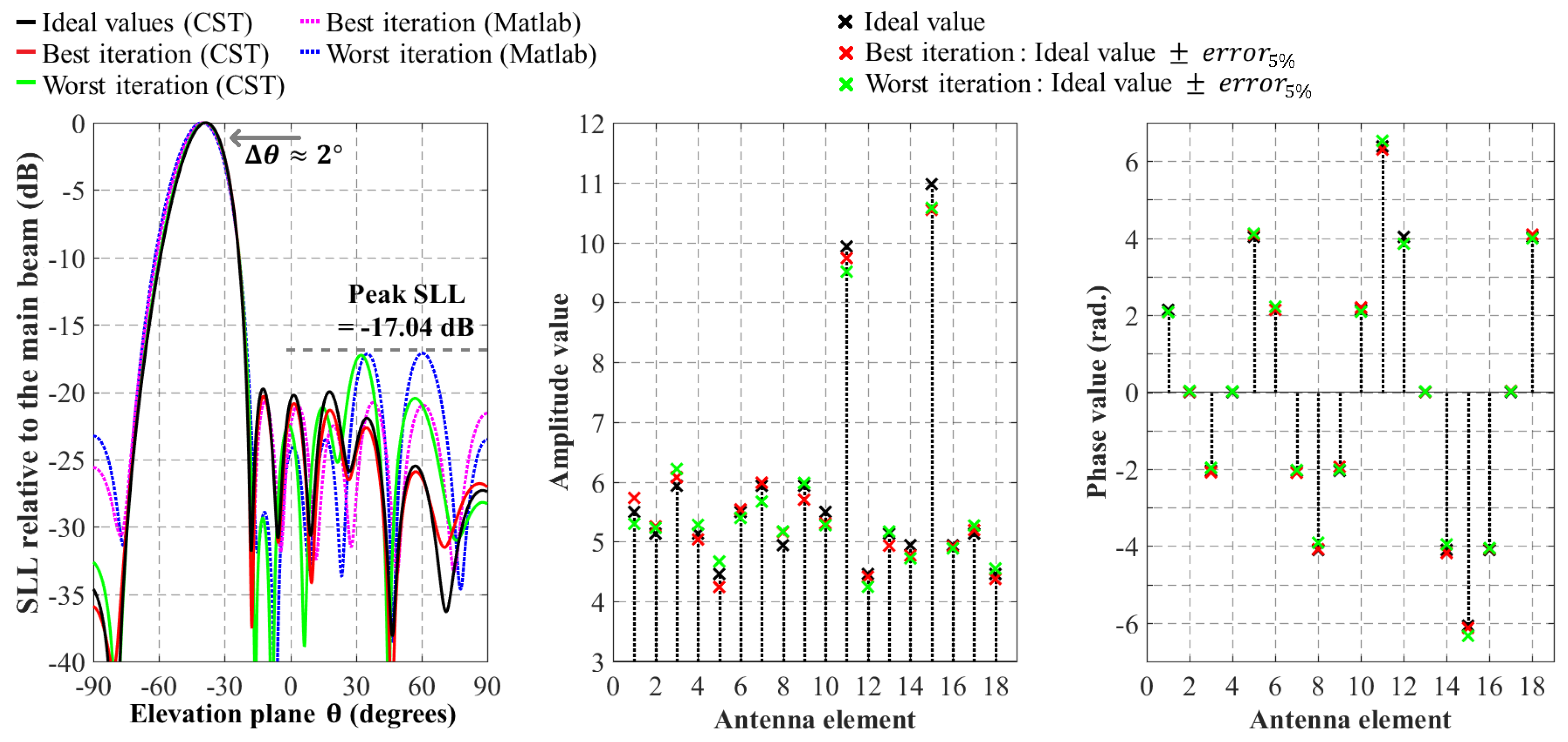As shown in Figure 12, the side-lobe level response remained below a peak value of −17.04 dB for the most sensitive case.

Figure 13 shows an analysis of the manufacturing tolerances using ElectroMagnetic software. The response of the array pattern (considering the iterations corresponding to the lowest and the highest values of side-lobe level) is illustrated using CST Microwave Studio, and their comparison with respect to the results without considering mutual coupling. As expected, the most sensitive case achieved a peak value of −17.04 dB and a misalignment of 2° for the main beam. Therefore, the design values obtained can be considered reliable considering manufacturing tolerances.

Although only the configuration of concentric rings array was analyzed in this paper, other array configurations could be analyzed using cophasal subarrays for reducing the number of phase shifters used in antenna systems.

4. Conclusions

The results derived using CST Microwave Studio illustrated that the design methodology for a concentric rings array based on cophasal subarrays for grouping the elements reduces the number of phase shifters by 66% for a scanning range of ±40° with a peak side-lobe level of −20 dB. The case of cophasal subarrays outperforms previous work cases in scanning capacity and side-lobe level, and results in a good compromise in terms of the reduction of the number of phase shifters. The proposed approach obtained a better side-lobe level performance with a reduction in the number of phase shifters compared to a conventional array (that uses one phase shifter per antenna element without optimization). Furthermore, an analysis of the manufacturing tolerances was made in EM software to verify the reliability of our design. The most sensitive case achieved a peak value of −17.04 dB, therefore, the design values obtained can be considered reliable considering manufacturing tolerances.

Future works will deal with other antenna array configurations using cophasal subarrays for reducing the number of phase shifters used in antenna systems.