Decentralized Broadcast Encryption Schemes with Constant Size Ciphertext and Fast Decryption

Abstract

Broadcast encryption ($\mathsf{BE}$) allows a sender to encrypt a message to an arbitrary target set of legitimate users and to prevent non-legitimate users from recovering the broadcast information. $\mathsf{BE}$ has numerous practical applications such as satellite geolocation systems, file sharing systems, pay-TV systems, e-Health, social networks, cloud storage systems, etc. This paper presents two new decentralized BE schemes. Decentralization means that there is no single authority responsible for generating secret cryptographic keys for system users. Therefore, the scheme eliminates the concern of having a single point of failure as the central authority could be attacked, become malicious, or become unavailable. Recent attacks have shown that the centralized approach could lead to system malfunctioning or to leaking sensitive information. Another achievement of the proposed BE schemes is their performance characteristics that make them suitable for environments with light-weight clients, such as in Internet-of-Things (IoT) applications. The proposed approach improves the performance over existing decentralized BE schemes by simultaneously achieving constant size ciphertext, constant size secret key and fast decryption.

1. Introduction

Broadcast encryption ($\mathsf{BE}$) was first introduced by Fiat and Naor in [1]. $\mathsf{BE}$ enables a sender to encrypt a message for an arbitrary target set of legitimate users and to prevent non-legitimate users from obtaining any information about the broadcast content, even if some or all of them collude. $\mathsf{BE}$ has many concrete application scenarios such as Satellite geolocation systems, Army radio systems, File sharing systems, Pay-TV systems, E-Health, Social networks, Cloud storage systems, etc. We refer the reader to [1,2,3] for more details. The $\mathsf{BE}$ schemes can be divided into two types: inclusive schemes and exclusive schemes (or revoking schemes). In the former, the sender directly determines the set of legitimate users (the target set). In the later, the sender directly determines the set of non-legitimate users, and the target set is then defined as all but non-legitimate users (who are also called the revoked users). When considering a $\mathsf{BE}$ scheme, one of the most important properties we should take into account is the ciphertext size, since the bandwidth is usually restricted. On the other hand, for lightweight devices such as in Internet of Things (IoT) applications, where the power of clients is restricted, two other properties that should also be considered are the key size and the decryption time. Regarding the key size, the key has two separate parts, one is kept secret by user, which is usually called the secret key, and the other is needed for decryption but it does not need to be secret (can be stored and accessed on demand from a non-weak server). The user decryption key includes both parts. Note that in all $\mathsf{BE}$ schemes, the secret key of the user is generated by the central authority.

Due to many recent attacks, the key escrow problem, where the authority generates and hence knows users’ secret keys, becomes a critical challenge for Broadcast encryption as well as other related schemes such as Identity-based encryption [4], Attribute-based encryption [5] and Functional encryption [6]. More precisely, the key escrow problem includes two sub-problems. First, user’s secret key is known by the authority or it is even exposed if the authority is malicious or gets hacked. Note that the user would not be willing to register to a system if he/she knows that his/her secret key can be known by someone. Second is the bottleneck problem arising from having a single point of failure. This problem is caused by the fact that we have only one authority who generates secret keys for all users. If this authority is malfunctioning (e.g., due to server or network problems, virus, denial-of-service attack, etc.), a new user cannot be added to the system. Note that if the authority fails, the system still works as normal except for the functionality of generating secret keys for new users.

Although one may argue that having a central authority may not be a big concern since today’s cloud infrastructures are very secure and extremely reliable, providing more than 99.9% service availability. However, recent market surveys indicate that significant percentage (about two thirds) of organizations still consider security to be the biggest challenge in practice that hinders their adoption of cloud services. In addition, a significant percentage (about one third) of these organizations see unplanned service outages as a challenge limiting their adoption of such services. Therefore, the issue is not only an up-time issue but also a trust issue. Moreover, there is always cost associated with achieving higher-level of security and availability to meet the critical demands of a centralized key management authority.

We currently have two techniques to address the key escrow problem. The first one is called the certificateless scheme [7,8,9] (or the certificate-based scheme). In [7,8] the problem is addressed in the context of identity-based encryption, while [9] addresses the problem in the context of broadcast encryption. In the certificateless scheme, to generate the full secret key, the user first receives a partial secret key from the authority, then chooses some randomnesses to build the full secret key. By this, without knowing randomnesses the authority cannot know user’s full secret key. However, since there is only one authority in the system, the bottleneck problem remains. The second technique is called the decentralized (or multi-authority) scheme [10,11,12,13,14,15,16,17,18,19,20]. In this scheme, the system includes multiple authorities, to generate a user’s full secret key, each authority takes charge of generating a partial secret key, then the full secret key is built from these partial secret keys. Obviously, user’s full secret key can be exposed only if enough number of authorities collude. More precisely, we can identify the following three different levels of construction of the decentralized scheme.

• Level 1: At the setup phase, all users in the system collude to generate the secret key for each user as well as the public parameters of the system. After the setup phase, only the user knows his/her secret key, the collusion of all other users cannot derive his/her secret key. In addition, no more new users can be added to the system after the setup phase.
• Level 2: This is similar to Level 1 except that after the setup phase new users can still be added to the system. More precisely, each user colluding at the setup phase plays the role of an authority to generate a partial secret key for a new user. The full secret key of the new user is built from all of these partial secret keys. This level obviously deals well with the problem of trusting a single authority with the keys, but does not handle the bottleneck problem. The reason is that if anyone of the authorities is malfunctioning, the full secret key of a new user cannot be built. We note that the certificateless scheme [7,8,9] is in fact equivalent to Level 2 since it deals well with the users’ security aspect but does not handle the problem of bottleneck.
• Level 3: To deal with the problem of malfunctioning authority in Level 2, in this level, the system is able to revoke the right of generating partial secret keys for new users from a malfunctioning authority. This leads to the fact that a new user does not need to receive the partial secret key from this failing authority to build his/her full secret key. In other words, new users can still be added to the system despite the presence of malfunctioning authorities. New users could not be added to the system only if all authorities in the system are malfunctioning.

This paper presents decentralized multi-authority $\mathsf{BE}$ schemes that deal with the key escrow problem and address the issues of entrusting a single-authority with cryptographic keys, as well as the problem of bottleneck. In addition, the proposed methods can simultaneously achieve the very desirable properties of constant size ciphertext, constant size secret key and fast decryption, which are particularly important in environments with weak clients (such as mobile phones, smart cards or IoT devices).

1.1. Related Work

Broadcast encryption was first introduced in [1] and then successively proposed in [2,3,21,22,23,24,25,26,27,28,29,30,31,32]. Besides the efficiency of the scheme, some other main research directions that broadcast encryption has taken include addressing the key escrow problem [9,19], dealing with collusion-resistance of malicious users [2,25,30], achieving adaptive security [22,28,29], supporting tracing traitors [3,23,24], and identity-based broadcast encryption [26,32].

As discussed earlier, $\mathsf{BE}$ schemes that deal with the key escrow problem can be categorized as either be certificateless, or decentralized. Recently, Li el al. [9] proposed a certificateless $\mathsf{BE}$ scheme which supports fast decryption and user anonymity (i.e., one cannot know the identities of users in the target set). This scheme, however, has a large ciphertext size which is linear in the number of users in the target set. Reducing the $\mathsf{BE}$ ciphertext size is critical for reducing the bandwidth requirement of the broadcast channel. A decentralized multi-authority $\mathsf{BE}$ scheme was proposed in [19] by combining NNL scheme [3] with group key exchange and public key encryption. Compared to the original NNL scheme, the resulting scheme has a larger public key, which is linear in the maximum number of users in the system.

Similar to $\mathsf{BE}$, attribute based encryption ($\mathsf{ABE}$) [5,33,34] can also encrypt a message to a set of users. Therefore, $\mathsf{ABE}$ can be used in similar modern applications such as File Sharing systems and Cloud Storage systems. In an $\mathsf{ABE}$ scheme, each user possesses a set of attributes and gets the corresponding secret key from the authority. To encrypt a message, the encryptor first chooses an access policy which is a structure of attributes, then encrypts the message under this access policy. A decryptor can decrypt the ciphertext if decryptor’s set of attributes satisfies this access policy. Modern applications require that the $\mathsf{ABE}$ scheme should have fine-grained access policy (described at least as a Boolean formula). Note that if there is only one authority in the system, $\mathsf{ABE}$ scheme suffers from the same key escrow problem as in $\mathsf{BE}$ scheme. To deal with the key escrow problem, decentralized $\mathsf{ABE}$ schemes supporting fine-grained access policy have been introduced in [14,15,17,18,20,35,36]. However, there is no decentralized $\mathsf{ABE}$ scheme that simultaneously achieves all the three important properties of fast decryption, constant size of ciphertext and constant size of secret key. Note that the three schemes [14,15,17] are built on the composite order group, which is quite inefficient.

Functional encryption ($\mathsf{FE}$) was introduced in [6]. In this scheme, the secret key is associated with a function f and it is generated from the master key. Given a ciphertext for m, if the user is in the target set, she can learn the value $f\left(m\right)$ and nothing else about m. Therefore, $\mathsf{FE}$ is a generalization of $\mathsf{BE}$ and is applicable to the context of broadcast encryption (if we set the function $f\left(m\right)=m$). However, the design of a decentralized $\mathsf{FE}$ scheme is still an open problem. Very recently, the authors in [10,11] proposed two decentralized inner product $\mathsf{FE}$ schemes. These schemes represent a very special type of the general $\mathsf{FE}$ scheme in the sense that, each different secret key is associated with a different vector $\overrightarrow{y}$ over ${\mathbb{Z}}_p^{*}$ and the encrypted message m now is also a vector $\overrightarrow{x}$ over ${\mathbb{Z}}_p^{*}$. If the user is in the target set, she can learn the inner product $\langle \overrightarrow{x},\overrightarrow{y}\rangle$ (this value is different for each user) and nothing else about $\overrightarrow{x}$, which means the function $f\left(x\right)=\langle \overrightarrow{x},\overrightarrow{y}\rangle$. This type of scheme is useful for some specific applications but obviously it cannot be directly used to support modern $\mathsf{BE}$ applications such as File sharing systems, Pay-TV systems and Social networks. Note that in a $\mathsf{BE}$ scheme, each different user in the target set possesses a different secret key but can learn the same plaintext m.

1.2. Our Contributions

The innovation of this paper is that our proposed $\mathsf{BE}$ schemes deal with the key escrow problem and address the issues of entrusting a single-authority with cryptographic keys, as well as the problem of bottleneck. In addition, our proposed schemes are the first decentralized $\mathsf{BE}$ schemes which can simultaneously achieve the very desirable properties of constant size ciphertext, constant size secret key and fast decryption, which are particularly important in environments with weak clients (such as mobile phones, smart cards or IoT devices). Concretely, we first propose a $\mathsf{BE}$ scheme which has the following properties:

• constant-size ciphertext;
• constant-size secret key: in our first scheme, the secret key includes a maximum of two elements;
• fast decryption: to decrypt, the user only computes two Pairings in the prime order setting;
• decryption key size is linear in the maximum number of users in the system;
• The scheme is categorized as Level 2.

The first scheme is improved then to obtain the second scheme which is Level 3. However, as a trade-off, the cost we have to pay is on the secret key size and the security of the scheme. More precisely, the secret key size in our second scheme now depends on the number of authorities and the scheme only achieves a weaker level of security. Two important $\mathsf{BE}$ papers that address the key escrow problem in the context of broadcast encryption are [9,19].

Table 1. Performance comparison. S is the number of users in the target set. N is the number of users in the system, r is the number of revoked users, ℓ is the size of the access policy, n is the number of attribute authorities, $\left|\mathcal{U}\right|$ is the number of attributes in the system, $\left|\mathcal{B}\right|$ is the number of attributes belonging to a decryption key. $\left|I\right|$ is the number of attributes belonging to a decryption key that satisfies the access policy, P is the Pairing operation, e and M are exponent and multiplication operations, k is the maximum number of times that one attribute can be reused in an access policy. $De{c}_{\mathsf{PKE}}$ denotes the decryption time of a Public key encryption scheme. We note that the multiplication operation M is very fast compared to the exponential operation e and Parings operation P.

	Ciphertext	Decryption Key	Secret Key	System Public Storage	Dec Time
[19]	$rlogN$	$2N$	$logN$	$2N$	$De{c}_{\mathsf{PKE}}$
[9]	$\left|S\right|+1$	$N+5$	1	$N+4$	$2P+3e+3M$
[18]	$3\ell$	$k\left|\mathcal{B}\right|+4$	$k\left|\mathcal{B}\right|+1$	$3\left|\mathcal{U}\right|+2$	$2P+2\left|I\right|M$
[15]	$3\ell +1$	$k\left|\mathcal{B}\right|+2$	$k\left|\mathcal{B}\right|$	$2N+2$	$2\left|I\right|P+3\left|I\right|e+2\left|I\right|M$
[17]	$2\ell +2$	$kN+n+5$	$k\left|\mathcal{B}\right|+n+2$	$2N+3$	$\left(2\right|I|+1)P+\left|I\right|e+2\left|I\right|M$
[20]	$4\ell +1$	$2\left|\mathcal{B}\right|+4$	$2\left|\mathcal{B}\right|$	$2n+5$	$3\left|I\right|P+\left|I\right|e+3\left|I\right|M$
[14]	$3\ell +1$	$2k\left|\mathcal{B}\right|+3$	$k\left|\mathcal{B}\right|+6$	$2N+n+3$	$4\left|I\right|P+\left|I\right|e+3\left|I\right|M$
[36]	$\ell +1$	$\left|\mathcal{B}\right|+2$	1	$N\left(\right|\mathcal{B}|+2)$	$2P+\left|I\right|M$
Ours 1	2	$N+1$	1	$N^2+N+5$	$2P+rM$
Ours 2	2	$n(N+1)$	n	$N^{2}n-N(n-3)+5$	$2P+rM$

and

Table 2. Comparison of security properties. ROM is random oracle, SM is standard model. In all types of parings, Type 3 is the most efficient one and Composite is the least efficient one. Regrading the hardness of assumption, DDH (Decision Diffie-Hellman) and CBDH (Computational Bilinear Diffie-Hellman) are the best ones, generic group is the worst one and all the others are equivalent.

	Security Model	Pairings	Decentralizing Tech	Assumption
[19]	Adaptive+SM	no	Level 2	DDH
[9]	Adaptive+ROM	Type 1	Level 2	CBDH
[18]	Generic group	Type 1	ABE	Generic group
[15]	Adaptive+ROM	Composite	ABE	Subgroup decision
[17]	Adaptive+SM	Composite	ABE	Subgroup decision
[20]	Selective+ROM	Type 1	ABE	q-DPBDHE2
[14]	Adaptive+SM	Composite	ABE	Subgroup decision
[36]	Selective+SM	Type 1	ABE	Modified-BDHE
Ours 1	Selective+SM	Type 3	Level 2	MBDHE
Ours 2	Weak Selective+SM	Type 3	Level 3	MBDHE

provide a comparison between our schemes and these two schemes. These tables also include comparison with other relevant decentralized $\mathsf{ABE}$ schemes proposed in the literature. The first three columns of Table 1 represent space complexity, while the last column demonstrates time complexity. Some of the terminology used in this paper is described in Appendix

Table A1. Summary of used symbols and abbreviations.

Term	Description	Term	Description
N	Total number of users in the system	$d_i$	Secret key for user i
S	Target set of valid key users	K	Symmetric session key
$\mathcal{R}$	Set of revoked users	$\mathcal{K}$	Session key space
r	Number of revoked users	$\mathsf{param}$	Public parameters
ℓ	Size of the access policy	$\mathcal{A}$	Adversary
n	Number of key users (or attribute authorities)	$\mathcal{C}$	Challenger
$\lambda$	Security parameter	$\mathcal{S}$	Simulator
ABE	Attribute based encryption	BE	Broadcast encryption
LSS	Linear secret sharing	FE	Functional encryption
SM	Standard model	ROM	Random oracle model
DDH	Decision Diffie-Hellman	CBDH	Computational bilinear Diffie-Hellman
BDHE	Bilinear Diffie-Hellman exponent	MBDHE	Modified BDHE

.

Finally, we implement our first and second schemes and present concrete benchmarks in Section 5, which shows that both of our schemes can be used for applications with lightweight devices. Moreover, Section 5 shows that both of our schemes are comparable to the most recent decentralized $\mathsf{BE}$ scheme [9] and decentralized $\mathsf{ABE}$ scheme [36] in term of both size complexity and time complexity. Note that the ciphertext size in [9] is linear in the number of receivers, which is impractical if the target set is large.

1.3. Paper Organization

The definition and security model of our schemes are introduced in the next section. The next section also introduces some useful tools for our constructions and proof of security. We next describe our first and second schemes in Section 3 and Section 4, respectively. We present the implementation of our schemes and two other schemes [9,36], and evaluate them using concrete benchmarks in Section 5. The conclusion is presented in Section 6.

2. Preliminaries

In this section, we first define the security model of our decentralized $\mathsf{BE}$ schemes, we then recall the definition of bilinear maps and linear secret sharing (LSS) matrix, which are needed for the security proof of our schemes. We refer the reader to Appendix Table A1 for a summary of the symbols used throughout this paper.

2.1. Decentralized Broadcast Encryption

In our system, there is no need to have a trusted authority to establish the system. Instead, the system is established by cooperating users in the setup phase. We split two types of users in our system:

• The first type is called key user. Key users take charge of generating partial secret keys for users in the system.
• The second type is called usual user who receives broadcast messages but does not participate in generating partial secret keys.

Formally, our first scheme includes four following probabilistic algorithms:

$\mathbf{Setup}(1^{\lambda },n,N)$: This algorithm is run by n key users $i=1,\cdots ,n$, that takes as $\lambda$ (security parameter), n (number of key users ) and N (the maximum number of users including n key users in the system). Note that $N\ge n$. This algorithm generates the public parameters $\mathsf{param}$ and the secret keys for n key users ${\left\{d_i\right\}}_{i=1,\cdots ,n}$. In this paper we also use the notation $i\in \left[n\right]$ instead of $i=1,\cdots ,n$.

$\mathbf{Extract}(j,{\left\{d_i\right\}}_{i=1,\cdots ,n},\mathsf{param})$: This algorithm takes as input the user j and n secret keys of n key users as well as $\mathsf{param}$, It outputs the secret key of user j.

$\mathbf{Encrypt}(\mathcal{R},\mathsf{param})$: This algorithm takes as input a revoked set of users $\mathcal{R}$ (which can include both key users and usual users) as well as $\mathsf{param}$. It outputs $(\mathsf{Hdr},K)$, where $\mathsf{Hdr}$ encapsulates the session key $K\in \mathcal{K}$. Denote $\mathsf{Hdr}$ the header, which contains the description of $\mathcal{R}$. Here, $\mathcal{K}$ is the session key space.

$\mathbf{Decrypt}(\mathsf{Hdr},d_j,\mathsf{param})$: This algorithm takes as input $\mathsf{Hdr}$ and $d_j$. If $j\notin \mathcal{R}$, the algorithm outputs the session key $K\in \mathcal{K}$. Otherwise, the algorithm returns ⊥.

In our second scheme, when the right of generating partial secret keys for users is revoked from a subset of key users, which can happen due to various reasons such as being malicious or malfunctioning. In this case, public parameters only need a simple update and nothing else. To this aim, we add the following algorithm.

$\mathbf{Revoke}(S,\mathsf{param})$: This algorithm takes as input a set of valid key users S and $\mathsf{param}$, it then revokes the rights of generating partial secret keys of all key users who do not belong to set S.

Note that in practice, we use the session key as a symmetric keys K to encrypt the message M, which generates the ciphertexts $\mathsf{CM}$. So, the full ciphertext to broadcast includes ($\mathsf{Hdr}$, $\mathsf{CM}$). We usually call $\mathsf{Hdr}$ as header and $\mathsf{CM}$ as encrypted payload.

2.2. Security Model

Let $\mathcal{A}$ be an adversary and $\mathcal{C}$ be a challenger. The security model of our decentralized broadcast encryption system is described by the following security game between A and $\mathcal{C}$:

At first, $\mathcal{A}$ sends the revoked target set $\mathcal{R}$ to $\mathcal{C}$.

Setup: In this step, $\mathcal{C}$ relies on $\mathcal{R}$ to run the $\mathbf{Setup}$ algorithm to create the public parameters $\mathsf{param}$ of the system as well as n secret keys ${\left\{d_i\right\}}_{i=1,\cdots ,n}$, it then sends $\mathsf{param}$ to $\mathcal{A}$.

Query phase 1: the adversary $\mathcal{A}$ adaptively asks corruption key query for the users in the revoked set $\mathcal{R}$ which can include both usual user and key user: the challenger $\mathcal{C}$ either uses ${\left\{d_i\right\}}_{i=1,\cdots ,n}$ or runs $\mathbf{Extract}$ algorithm to answer $\mathcal{A}$.

Challenge: the challenger $\mathcal{C}$ runs $\mathbf{Encrypt}(\mathcal{R},$ $\mathsf{param})$ and gets $({\mathsf{Hdr}}^{*},K^{*})$. Next, the $\mathcal{C}$ randomly chooses $b\stackrel{\$}{\leftarrow }\{0,1\}$. If $b=1$, it randomly chooses $K^{*}\stackrel{\$}{\leftarrow }\mathcal{K}$, then returns $({\mathsf{Hdr}}^{*},K^{*})$ to $\mathcal{A}$.

It is easy to see that in case $b=0$ then $K^{*}$ is the real key which is encapsulated in ${\mathsf{Hdr}}^{*}$. In case $b=1$, $K^{*}$ is a random element which is independent of the header.

Query phase 2: the same as in the first phase.

Guess: In this phase, $\mathcal{A}$ outputs the guess for bit b, that is bit $b^{\prime }\in \{0,1\}$.

We say the adversary wins the game if $b^{\prime }=b$, but only if $\mathcal{A}$ corrupts maximum $n-1$ secret keys of key users (note that if $\mathcal{A}$ corrupts all n secret keys of key users, he/she can generate all users’ secret keys in the system, so this is a trivial attack). Let ${\mathbf{Succ}}^{\mathsf{ind}}\left(\mathcal{A}\right)=Pr[b^{\prime }=b]$ be the probability that $\mathcal{A}$ wins the game, and let its advantage be

$$\begin{array}{ccc}\hfill {\mathbf{Adv}}^{\mathsf{ind}}\left(\mathcal{A}\right)& =& 2\times {\mathbf{Succ}}^{\mathsf{ind}}\left(\mathcal{A}\right)-1\hfill \\ & =& Pr[1\leftarrow \mathcal{A}|b=1]-Pr[1\leftarrow \mathcal{A}|b=0].\hfill \end{array}$$

Definition 1

(Selective Security). If the advantage of $\mathcal{A}$ in the above security game is negligible, a decentralized $\mathsf{BE}$ scheme is said to achieves selective security.

We also define the weak selective security game in the sense that the adversary $\mathcal{A}$ must output both the revoked target set $\mathcal{R}$ as well as the set of authorities for which he/she intends to corrupt at the beginning of the game.

We note that in the adaptive security game, the adversary $\mathcal{A}$ outputs the revoked target set $\mathcal{R}$ at the challenge phase instead of doing so at the beginning of the game.

2.3. Bilinear Maps

Let $\mathbb{G}$, $\tilde{\mathbb{G}}$, ${\mathbb{G}}_T$ be three finite multiplicative abelian groups of large prime order p. Let $g,\tilde{g}$ be generators of $\mathbb{G}$ and $\tilde{\mathbb{G}}$, and $e:\mathbb{G}\times \tilde{\mathbb{G}}\to {\mathbb{G}}_T$ be an admissible asymmetric bilinear map. For all $x,y\in {\mathbb{Z}}_p$, we have:

• $e(g^x,{\tilde{g}}^y)=e{(g,\tilde{g})}^{xy}$;
• if $g\ne 1_{\mathbb{G}}$ and $\tilde{g}\ne 1_{\tilde{\mathbb{G}}}$ then $e(g,\tilde{g})\ne 1_{{\mathbb{G}}_T}$;
• we can efficiently compute $e(g,\tilde{g})$.

$(p,\mathbb{G},\tilde{\mathbb{G}},{\mathbb{G}}_T,g,\tilde{g},e)$ is named a bilinear map group system and we have:

• if $\mathbb{G}=\tilde{\mathbb{G}}$, it is in Type 1 Pairings
• if $\mathbb{G}\ne \tilde{\mathbb{G}}$ and there is an efficiently computable homomorphism $\varphi :\mathbb{G}\to \mathbb{G}$, it is in Type 2 Pairings
• if $\mathbb{G}\ne \tilde{\mathbb{G}}$ and there are no efficiently computable homomorphism between $\mathbb{G}$ and $\tilde{\mathbb{G}}$, it is in Type 3 Pairings

Note that recent cryptanalysis of Type 1 Pairings has broken many well-known security assumptions, and among the three types of Pairings, Type 3 Pairings are the most efficient one.

2.4. Linear Secret Sharing Matrix

Let p be a prime and $\mathcal{R}$ be an any Boolean formula with AND-gates, that means $\mathcal{R}=i_1\wedge i_2\wedge \cdots \wedge i_{\ell }$. One can construct a function $\rho$ and a linear secret sharing matrix (LSS matrix) $M\in {\mathbb{Z}}_p^{\ell \times {\ell }^{\prime }}$, where the function $\rho \in \mathcal{F}(\left[\ell \right]\to (i_1,i_2,\cdots ,i_{\ell }))$ which labels the rows of M with $i_j,j=1,\cdots ,\ell$. Note that, to convert from $\mathcal{R}$ to a LSS matrix, we refer the reader to the algorithm in Appendix G of [15].

Assume t is a secret value and vector $\overrightarrow{y}={(t,y_2,\cdots ,y_{{\ell }^{\prime }})}^{\perp }\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p^{{\ell }^{\prime }}$, then $\overrightarrow{\lambda }=M.\overrightarrow{y}$ is called the vector shares. We can then easily compute ${\left\{{\omega }_i\right\}}_{i\in \left[\ell \right]}\in {\mathbb{Z}}_p$ such that for valid shares ${\{{\lambda }_i={(M.\overrightarrow{y})}_i\}}_{i\in \left[\ell \right]}$ of a sharing secret t, ${\sum }_{i\in \left[\ell \right]}{\omega }_i{\lambda }_i=t$. In fact, based on the equation ${\sum }_{i\in \left[\ell \right]}{\omega }_i{M}_i=(1,0,\cdots ,0)$ where $M_i$ is the i-th row of the matrix M, one can compute those constants.

3. First Scheme

In this section, we describe the construction of our first decentralized $\mathsf{BE}$ scheme and its security analysis and efficiency.

3.1. Construction

Our first decentralized $\mathsf{BE}$ scheme is detailed as follows.

$\mathbf{Setup}(1^{\lambda },n,N)$: In this phase, n key users $1,\cdots ,n$ co-operate to generate the public parameter of the system $\mathsf{param}$ as well as the secret key for each key user. More precisely, this algorithm takes as input the security parameter $\lambda$, the number of key users n as well as the maximum number of users in the system N, note that $N\ge n$. It generates $\mathsf{param}$ as well as the secret keys ${\left\{d_i\right\}}_{i=1,\cdots ,n}$ for n key users as follows:

First, all key users $i=1,\cdots ,n$ choose a bilinear group system $(p,\mathbb{G},\tilde{\mathbb{G}},{\mathbb{G}}_T,e(·,·),g,\tilde{g})$

Next, each key user i randomly chooses $N+2$ values ${\alpha }_i,{\beta }_i,r_{i,1},\cdots ,r_{i,N}\in {\mathbb{Z}}_p^{*}$, he/she computes $e{(g,\tilde{g})}^{{\alpha }_i},{\tilde{g}}^{{\alpha }_i},g^{{\beta }_i},{\tilde{g}}^{{\beta }_i}$, then publishes $e{(g,\tilde{g})}^{{\alpha }_i},g^{{\beta }_i},{\tilde{g}}^{{\beta }_i},g^{r_{i,1}},{\tilde{g}}^{r_{i,1}},\cdots ,g^{r_{i,N}},{\tilde{g}}^{r_{i,N}}$. He/she keeps ${\tilde{g}}^{{\alpha }_i}$ secret. Let $\mathsf{param}$ be public parameters and it is set as:

$$\mathsf{param}=(g,g^{\beta },{\tilde{g}}^{\beta },u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N,e{(g,\tilde{g})}^{\alpha },n)$$

where $\beta ={\sum }_{i=1}^n{\beta }_i,\alpha ={\sum }_{i=1}^n{\alpha }_i$ and $u_j=g^{{\sum }_{i=1}^n{r}_{i,j}},{\tilde{u}}_j={\tilde{g}}^{{\sum }_{i=1}^n{r}_{i,j}},j=1,\cdots ,N$.

Each key user j’s secret key is generated as follows.

First, each key user $i,i=1,\cdots ,n,$ picks randomly a different scalar $s_i\in {\mathbb{Z}}_p^{*}$, the i-th partial secret key of user j is $d_j^i=(d_{j_0}^i,d_{j_0}^{{}^{\prime }i},{\left\{d_{j_k}^i\right\}}_{\genfrac{}{}{0pt}{}{k=1,\cdots ,N}{k\ne j}})$ where:

$$\begin{array}{c}\hfill d_{j_0}^i={\tilde{g}}^{{\alpha }_i}·{\tilde{g}}^{\beta ·s_i},d_{j_0}^{{}^{\prime }i}={\tilde{g}}^{s_i},d_{j_k}^i={\tilde{u}}_k^{s_i},k=1,\cdots ,N,k\ne j\end{array}$$

Key user i then sends $d_j^i$ to j. Since user j is a key user, j also generates $d_j^j$ as above, but keeps this value secret.

After receiving all partial secret keys, user j computes his/her full secret key $d_j=(d_{j_0},d_{j_0}^{\prime },{\left\{d_{j_k}\right\}}_{\genfrac{}{}{0pt}{}{k=1,\cdots ,N}{k\ne j}},{\tilde{g}}^{{\alpha }_j})$, where:

$$\begin{array}{c}\hfill d_{j_0}={\tilde{g}}^{\alpha }·{\tilde{g}}^{\beta ·s},d_{j_0}^{\prime }={\tilde{g}}^s,d_{j_k}={\tilde{u}}_k^s,k=1,\cdots ,N,k\ne j,s=s_1+\cdots +s_n\end{array}$$

The decryption key size of key user j is linear in N, however key user j only keeps $(d_{j_0},{\tilde{g}}^{{\alpha }_j})$ secret, the rest of his/her secret key can be stored and accessed on demand from a non-weak server. Hence, the size of key user’s secret key in our first scheme is constant.

$\mathbf{Extract}(j,{\left\{d_i\right\}}_{i=1,\cdots ,n},\mathsf{param})$: The input of this algorithm includes a user $j,n+1\le j\le N$, secret keys of all key users $i=1,\cdots ,n$ and $\mathsf{param}$. The algorithm first computes partial user’s secret keys $d_j^i,i=1,\cdots ,n$ as above, then the full secret key of user j is set: $d_j=(d_{j_0},d_{j_0}^{\prime },{\left\{d_{j_k}\right\}}_{\genfrac{}{}{0pt}{}{k=1,\cdots ,N}{k\ne j}})$, where:

$$\begin{array}{c}\hfill d_{j_0}={\tilde{g}}^{\alpha }·{\tilde{g}}^{\beta ·s},d_{j_0}^{\prime }={\tilde{g}}^s,d_{j_k}={\tilde{u}}_k^s,k=1,\cdots ,N,k\ne j\end{array}$$

Similar to the case of key user, user j just needs to keep $d_{j_0}$ secret. Hence, the size of user j’s secret key is also constant. Note that our scheme is secure against the collusion of revoked users since each secret key has a different randomness s.

$\mathbf{Encrypt}(\mathcal{R},\mathsf{param})$: The input of this algorithm includes a set of revoked users $\mathcal{R}$ (which can include both usual users and key users) and $\mathsf{param}$. It chooses $k\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$, generates the header $\mathsf{Hdr}=(C_1,C_2)$ as follows:

$$C_1=g^k,C_2={\left(g^{\beta }\prod _{i\in \mathcal{R}}{u}_i\right)}^k$$

and the session key $K=e{(g,\tilde{g})}^{\alpha ·k}$. Eventually, the algorithm outputs K and $\mathsf{Hdr}$ which includes the description of $\mathcal{R}$.

$\mathbf{Decrypt}(\mathsf{Hdr},d_j,\mathsf{param})$: The algorithm first checks whether $j\in \mathcal{R}$, if it is the case, the algorithm outputs ⊥. Otherwise, the algorithms computes the session key:

$$\begin{array}{ccc}\hfill K& =& \frac{e(C_1,d_{j_0}{\prod }_{i\in \mathcal{R}}{d}_{j_i})}{e(C_2,d_{j_0}^{\prime })}=\frac{e(g^k,{\tilde{g}}^{\alpha }{\left({\tilde{g}}^{\beta }{\prod }_{i\in \mathcal{R}}{\tilde{u}}_i\right)}^s)}{e({\left(g^{\beta }{\prod }_{i\in \mathcal{R}}{u}_i\right)}^k,{\tilde{g}}^s)}=e{(g,\tilde{g})}^{\alpha ·k}\hfill \end{array}$$

Remark 1.

Regarding the efficiency, both the encryption algorithm and decryption algorithm of our scheme are efficient. In the encryption algorithm, the encryptor just needs to compute two exponential operations and$\left|\mathcal{R}\right|+1$multiplication operations. In the decryption algorithm, the decryptor just needs to compute two Parings operations and$\left|\mathcal{R}\right|+2$multiplication operations.

One can argue that if the set of revoked users $\mathcal{R}$ is too big, our scheme becomes less efficient, however we note that multiplication operation is very fast when compared to the exponential operation and Parings operation. We give in the Table 1, Table 2 and

Table 3. Performance comparison of our schemes and schemes in [9,36]. Encryption and Decryption times are in milliseconds. N is the number of users and r is the number of revoked users. We use type A pairing in the PBC Library and set the security parameter $\lambda =128$. We also consider the case each user in [36] possesses only one attribute. However, in practice to support the flexible access control and anonymity of receivers, each user in [36] must possess many attributes, thus the encryption time and the decryption time of this scheme could be actually longer.

Target Users		[9]		[36]		Ours 1		Ours 2
		Enc Time	Dec Time	Enc Time	Dec Time	Enc Time	Dec Time	Enc Time	Dec Time
$N=100$	$r=10$	$13.1$	3	$105.7$	$1.9$	$2.4$	$1.8$	$2.5$	$1.8$
	$r=20$	$11.4$	3	$94.0$	$2.0$	$2.5$	$1.9$	$2.6$	$1.9$
	$r=30$	$10.1$	$3.1$	$82.5$	$1.9$	$2.6$	2	$2.7$	2
$N=200$	$r=20$	24	3	$210.3$	$1.9$	$2.5$	$1.9$	$2.7$	$1.9$
	$r=40$	$22.8$	3	$186.3$	$1.9$	$2.6$	2	$2.7$	2
	$r=60$	$21.8$	3	$159.1$	$1.8$	$2.6$	$2.1$	$2.8$	$2.1$
$N=400$	$r=40$	$46.9$	3	$422.1$	$1.9$	$2.7$	$2.1$	$2.8$	$2.1$
	$r=80$	$41.5$	3	$374.7$	$1.9$	$2.9$	$2.3$	3	$2.3$
	$r=120$	$36.9$	3	326	$1.9$	$3.1$	$2.5$	$3.2$	$2.5$
$N=800$	$r=80$	$46.9$	$3.1$	841	$1.9$	$2.7$	$2.1$	$2.8$	$2.1$
	$r=160$	45	$3.2$	$745.3$	$2.0$	$2.9$	$2.3$	3	$2.3$
	$r=240$	$39.6$	$3.3$	$651.3$	$1.9$	$3.1$	$2.6$	$3.2$	$2.6$

a detailed comparison between our schemes and other relevant schemes proposed in the literature.

3.2. Security

In this section, we first define a new assumption, which is a simple modification of the well-known $\mathsf{BDHE}$ assumption [2]. We then prove that our first scheme is selectively secure under this new assumption.

Definition 2.

$\mathsf{MBDHE}$problem:Let $(p,\mathbb{G},\tilde{\mathbb{G}},{\mathbb{G}}_T$ $,e)$ be a bilinear group system. Pick $\beta ,t,k,q\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p,$ and two generators $g\in \mathbb{G},\tilde{g}\in \tilde{\mathbb{G}}$. Given

$$\begin{array}{c}\hfill \overrightarrow{Y}=\left(g,\tilde{g},g^{\beta },{\tilde{g}}^{\beta },\cdots ,g^{{\beta }^q},{\tilde{g}}^{{\beta }^q},g^{{\beta }^{q+2}},{\tilde{g}}^{{\beta }^{q+2}},\cdots ,g^{{\beta }^{2q}},{\tilde{g}}^{{\beta }^{2q}},g^{\beta t},{\tilde{g}}^{\beta t},g^{{\beta }^{2}t},{\tilde{g}}^{{\beta }^{2}t},\cdots ,g^{{\beta }^{q}t},{\tilde{g}}^{{\beta }^{q}t},\right.\\ \hfill \left.g^{{\beta }^{q+2}t},{\tilde{g}}^{{\beta }^{q+2}t},\cdots ,g^{{\beta }^{2q}t},{\tilde{g}}^{{\beta }^{2q}t},g^k,g^{k(\beta t+\beta )}\right)\end{array}$$

it is difficult to distinguish between $T=$ $e{(g,\tilde{g})}^{{\beta }^{q+1}k}$ $\in {\mathbb{G}}_T$ or $T=R\stackrel{\$}{\leftarrow }{\mathbb{G}}_T$.

Let $\mathcal{A}$ be an adversary that solves the $\mathsf{MBDHE}$ problem above, and denote $ϵ$ the advantage of $\mathcal{A}$:

$$ϵ\le \left|\mathrm{Pr}\left[\mathcal{A}(\overrightarrow{Y},T=e{(g,\tilde{g})}^{{\beta }^{q+1}k})=0\right]-\mathrm{Pr}\left[\mathcal{A}(\overrightarrow{Y},T=R)=0\right]\right|$$

Definition 3.

If there does not exist any polynomial-time adversary who has a non-negligible advantage in solving the$\mathsf{MBDHE}$problem, then we say that the$\mathsf{MBDHE}$assumption holds.

It is easy to see that to distinguish between $T=$ $e{(g,\tilde{g})}^{{\beta }^{q+1}k}$ $\in {\mathbb{G}}_T$ or $T=R\stackrel{\$}{\leftarrow }{\mathbb{G}}_T$, one needs to have one of the values $g^{{\beta }^{q+1}}$, $g^{{\beta }^{q+1}t}$, ${\tilde{g}}^{{\beta }^{q+1}}$ or ${\tilde{g}}^{{\beta }^{q+1}t}$. However, we do not have these elements in $\overrightarrow{Y}$ and there is also no way to derive one of these elements. Since it is a simple modification of the well-known $\mathsf{BDHE}$ assumption [2], we do not provide the proof of security of $\mathsf{MBDHE}$ assumption in the generic group model.

Theorem 1.

Assume that$q\ge N$, our first scheme is selectively secure under the$\mathsf{MBDHE}$assumption.

Proof. 

Let $\mathcal{S}$ be an adversary against the $\mathsf{MBDHE}$ assumption and $\mathcal{A}$ be an adversary against our first scheme. In this proof, we will show that $\mathcal{S}$ can simulate $\mathcal{A}$ and then use the output of $\mathcal{A}$ to break the security of $\mathsf{MBDHE}$ assumption.

First, $\mathcal{A}$ sends the revoked target set $\mathcal{R}$ to $\mathcal{S}$. Note that $\mathcal{S}$ also has an instance of $\mathsf{MBDHE}$ assumption as well as the number of key users n and the maximum number of users N.

$\mathbf{Setup}$: $\mathcal{S}$ first considers $\mathcal{R}$ as a Boolean formula with AND-gates: $\mathcal{R}={(\wedge i)}_{i\in \mathcal{R}}$, then uses the algorithm in Appendix G in [15] to build a LSS matrix $(M_{\ell \times {\ell }^{\prime }},\rho )$ from $\mathcal{R}$, where $\ell =\left|\mathcal{R}\right|$ and $\ell ,{\ell }^{\prime }\le q$. Note that $\mathcal{R}={\left\{\rho \left(i\right)\right\}}_{i=1,\cdots ,\ell }$.

$\mathcal{S}$ next chooses ${\alpha }^{\prime }\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p^{*}$ and implicitly sets $\alpha ={\alpha }^{\prime }+{\beta }^{q+1}$, generates $e{(g,\tilde{g})}^{\alpha }=e{(g,\tilde{g})}^{{\alpha }^{\prime }}·e(g^{\beta },{\tilde{g}}^{{\beta }^q})$.

To generate $u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N$, $\mathcal{S}$ implicitly sets

$$\overrightarrow{y}={(t,t\beta ,t{\beta }^2,\cdots ,t{\beta }^{{\ell }^{\prime }-1})}^{\perp }\in {\mathbb{Z}}_p^{{\ell }^{\prime }}$$

Let $\overrightarrow{\lambda }=M·\overrightarrow{y}$ be the vector shares, for all $j=1,\cdots ,\ell$ we have

$${\lambda }_j=\sum _{i\in \left[{\ell }^{\prime }\right]}{M}_{j,i}t{\beta }^{i-1}$$

Although $\mathcal{S}$ cannot compute $\overrightarrow{\lambda }$, $\mathcal{S}$ is able to find constants ${\left\{{\omega }_i\right\}}_{1\le i\le \ell }$ satisfying:

$$\sum _{i=1,\cdots ,\ell }{\omega }_i·{\lambda }_i=t$$

Based on the property of LSS matrix, $\mathcal{S}$ is able to find ${\left\{{\omega }_i\right\}}_{1\le i\le \ell }$ satisfying

$$\sum _{i=1,\cdots ,\ell }{\omega }_i·M_i=(1,0,\cdots ,0)$$

or

$$\sum _{i=1,\cdots ,\ell }{\omega }_i·M_{i,1}t=t$$

It is then easy to see that

$$\sum _{i=1,\cdots ,\ell }{\omega }_i·{\lambda }_i=t$$

On the other hand, $\mathcal{S}$ has $g^{t{\beta }^a},{\tilde{g}}^{t{\beta }^a},a\in \left[{\ell }^{\prime }\right]$ (from the assumption, note that $q\ge N\ge {\ell }^{\prime }$) and matrix M, $\mathcal{S}$ thus can generate $u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N$ as follows.

First, for each $u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N$ where there exists $i\in \left[\ell \right]$ satisfying $j=\rho \left(i\right)$ ($\rho$ is an injective function), $\mathcal{S}$ picks randomly scalar $z_j\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ then computes

$$u_j=g^{z_j}·g^{{\omega }_i{\sum }_{a\in \left[{\ell }^{\prime }\right]}{M}_{i,a}t{\beta }^a}=g^{z_j}·g^{\beta {\omega }_i{\lambda }_i}$$

and

$${\tilde{u}}_j={\tilde{g}}^{z_j}·{\tilde{g}}^{{\omega }_i{\sum }_{a\in \left[{\ell }^{\prime }\right]}{M}_{i,a}t{\beta }^a}={\tilde{g}}^{z_j}·{\tilde{g}}^{\beta {\omega }_i{\lambda }_i}$$

Second, for each $u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N$, where there does not exists $i\in \left[\ell \right]$ satisfying $j=\rho \left(i\right)$, $\mathcal{S}$ picks randomly scalar $z_j\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ then computes $u_j=g^{z_j},{\tilde{u}}_j={\tilde{g}}^{z_j}$.

Since all $z_j$ are randomly chosen, $u_1,\cdots ,u_N,$ ${\tilde{u}}_1,\cdots ,{\tilde{u}}_N$ are in the right form.

$\mathcal{S}$ eventually sets $\mathsf{param}$ as

$$\mathsf{param}=(g,\tilde{g},g^{\beta },{\tilde{g}}^{\beta },e{(g,\tilde{g})}^{\alpha },u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N,n)$$

and sends it to $\mathcal{A}$.

Query phase 1:$\mathcal{A}$ can ask the following two types of queries:

• First, $\mathcal{A}$ chooses a usual user or a key user, then requests to know his/her secret key. To avoid the trivial attack, $\mathcal{A}$ can only ask to know at most $n-1$ secret keys of key users, and obviously these key users are in the revoked set $\mathcal{R}$;
• $\mathcal{A}$ requests a part of the secret key of either usual user or key user who does not belong to the revoked set $\mathcal{R}$, that is $(d_{j_0}^{\prime },{\left\{d_{j_i}\right\}}_{\genfrac{}{}{0pt}{}{i=1,\cdots ,N}{i\ne j}})$. The reason why $\mathcal{A}$ is able to make this query is that this part of the secret key is stored in the public server.

To answer the first one, $\mathcal{S}$ first gets $j\in \mathcal{R}$ from $\mathcal{A}$ then constructs a vector $\overrightarrow{x}=(x_1,\cdots ,x_{{\ell }^{\prime }})\in {\mathbb{Z}}_p^{*}$ where $x_1=-1$ and $\forall i=1,\cdots ,\ell ,\rho \left(i\right)\ne j$, the product $\langle \overrightarrow{x}·M_i\rangle =0$. We notice here that such vector exists due to the property of LSS matrix. To continue, $\mathcal{S}$ picks $r\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ then implicitly sets:

$$s=r+x_1{\beta }^q+x_2{\beta }^{q-1}+\cdots +x_{{\ell }^{\prime }}{\beta }^{q-{\ell }^{\prime }+1}$$

Next, $\mathcal{S}$ generates the secret key:

$$d_{j_0}={\tilde{g}}^{{\alpha }^{\prime }}{\tilde{g}}^{\beta r}\prod _{i=2,\cdots ,{\ell }^{\prime }}{\left({\tilde{g}}^{{\beta }^{q+1-i}}\right)}^{x_i}={\tilde{g}}^{\alpha }·{\tilde{g}}^{\beta ·s}$$

Note that $x_1=-1$. It is easy to see that the unknown term ${\tilde{g}}^{{\beta }^{q+1}}$ in ${\tilde{g}}^{\alpha }$ is canceled out, since ${\tilde{g}}^{\beta ·s}$ contains ${\tilde{g}}^{-{\beta }^{q+1}}$. On the other hand, $\mathcal{S}$ knows vector $\overrightarrow{x}$, so he/she can generate:

$$d_{j_0}^{\prime }={\tilde{g}}^s={\tilde{g}}^r\prod _{i=1,\cdots ,{\ell }^{\prime }}{\left({\tilde{g}}^{{\beta }^{q+1-i}}\right)}^{x_i}$$

Next, $\forall 1\le a\le N,a\ne j$ and there does not exist $i\in \left[\ell \right]$ such that $\rho \left(i\right)=a$. $\mathcal{S}$ has $z_a$ at hands (chosen at the setup phase) then he/she is able to generate

$${\tilde{u}}_a^s={\left({\tilde{g}}^s\right)}^{z_a}$$

$\forall 1\le a\le N,a\ne j,$ and there exists $i\in \left[\ell \right]$ such that $\rho \left(i\right)=a$, $\mathcal{S}$ generates

$$\begin{array}{c}\hfill {\tilde{u}}_a^s={\left({\tilde{g}}^s\right)}^{z_a}·{\tilde{g}}^{(r+x_1{\beta }^q+x_2{\beta }^{q-1}+\cdots +x_{{\ell }^{\prime }}{\beta }^{q-{\ell }^{\prime }+1}){\omega }_i{\sum }_{v\in \left[{\ell }^{\prime }\right]}{M}_{i,v}t{\beta }^v}\end{array}$$

The key point for $\mathcal{S}$ to compute ${\tilde{u}}_a^s$ is that the product $\langle \overrightarrow{x}·M_i\rangle =0$. This means $\mathcal{S}$ does not need to know the term ${\tilde{g}}^{{\beta }^{q+1}t}$. For other terms, $\mathcal{S}$ has already known from the assumption. In addition, if $a=j$ and there exists $i\in \left[\ell \right]$ satisfying $\rho \left(i\right)=j$ then $\langle \overrightarrow{x}·M_i\rangle \ne 0$, this leads to the fact that $\mathcal{S}$ cannot generate $u_j^s$, that is exactly the well-known partition technique proof.

In case, user j is a key user, $\mathcal{A}$ also has the right to request ${\tilde{g}}^{{\alpha }_j}$. To answer ${\tilde{g}}^{{\alpha }_j}$, $\mathcal{S}$ picks ${\alpha }_j\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ computes and returns ${\tilde{g}}^{{\alpha }_j}$ to $\mathcal{A}$. The key point here is that $\mathcal{A}$ only has the right to request maximum $n-1$ corrupted secret keys of key users, This means $\mathcal{S}$ is able to pick $n-1$ scalars ${\alpha }_j\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$ as above. To be more clear, if we assume that $\mathcal{A}$ cannot request for key user 1, then we implicitly set ${\alpha }_1=\alpha -{\sum }_{j=2}^n{\alpha }_j$.

To answer the second type of query, note that the unknown element ${\tilde{g}}^{\alpha }$ only appear in $d_{j_0}$. However, fortunately $\mathcal{S}$ just needs to provide to $\mathcal{A}$ the values $(d_{j_0}^{\prime },{\left\{d_{j_i}\right\}}_{\genfrac{}{}{0pt}{}{i=1,\cdots ,N}{i\ne j}})$, this leads to the fact that $\mathcal{S}$ can simply picks $s\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p^{*}$ then generates $(d_{j_0}^{\prime },{\left\{d_{j_i}\right\}}_{\genfrac{}{}{0pt}{}{i=1,\cdots ,N}{i\ne j}})$ and returns to $\mathcal{A}$.

Challenge: The simulator $\mathcal{S}$ computes the session key:

$$K^{*}=T·e(g^k,{\tilde{g}}^{{\alpha }^{\prime }})$$

and

$$\begin{array}{ccc}\hfill C_1^{*}=g^k,C_2^{*}& =& \left(g^{k(\beta +\beta t)}{g}^{{\sum }_{i\in \left[\ell \right]}k{z}_{\rho \left(i\right)}}\right)=\left({(g^{\beta }·\prod _{i\in \left[\ell \right]}{g}^{z_{\rho \left(i\right)}}·g^{\beta {\omega }_i{\lambda }_i})}^k\right)\hfill \\ & =& \left({\left(g^{\beta }\prod _{i\in \left[\ell \right]}{u}_{\rho \left(i\right)}\right)}^k\right)=\left({\left(g^{\beta }\prod _{i\in \mathcal{R}}{u}_i\right)}^k\right)\hfill \end{array}$$

We note that $\mathcal{S}$ knows $g^{k(\beta +\beta t)},g^k$ from the assumption. On the other hand, since all $z_{\rho \left(i\right)}$ have been chosen at the setup phase, it means that $\mathcal{S}$ knows these elements.

Next, in case $T=e{(g,\tilde{g})}^{{\beta }^{q+1}k}$ then it is easy to see that $K^{*}$ is in valid form. Otherwise, $K^{*}$ is a random element in ${\mathbb{G}}_T$.

Query phase 2: Similar to Phase 1

Guess: Eventually, $\mathcal{A}$ returns his/her bit guess $b^{\prime }$ for b. $\mathcal{S}$ checks if $b^{\prime }=b$. If they are equal, it outputs 0 to guess that $T=e{(g,\tilde{g})}^{{\beta }^{q+1}k}$. Otherwise, $\mathcal{S}$ outputs 1, which means that T is a random element in ${\mathbb{G}}_T$.

Because $\mathcal{S}$ never aborts the game, the simulation is perfect or the advantage of $\mathcal{A}$ to break the security of our first scheme is equal to the advantage of $\mathcal{S}$ to break the security of the $\mathsf{MBDHE}$ assumption. In other words, our first scheme is selectively secure under the $\mathsf{MBDHE}$ assumption, which concludes our proof. □

4. Second Scheme

The bottleneck problem still remains in the first scheme since if there is one malfunctioning key user, a new user cannot be added to the system. In the second scheme, we improve the first scheme aiming to deal with this problem.

To this aim, each user in the second scheme stores all n partial secret keys ${\left\{d_j^i\right\}}_{i=1,\cdots ,n}$, and sets the $\mathsf{param}$ as

$$\begin{array}{c}\hfill \mathsf{param}=(g,\tilde{g},g^{\beta },{\tilde{g}}^{\beta },u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N,e{(g,\tilde{g})}^{{\alpha }_1},\cdots ,e{(g,\tilde{g})}^{{\alpha }_n},n)\end{array}$$

Let us assume that the malfunctioning key user is the user n (this can naturally be extended to the case which has more than one malfunctioning key user). To revoke the right of generating partial secret key of user n, the system works as follows.

• First, the system requires that user’s full secret key now includes $n-1$ partial secret keys, which are generated by key users from 1 to $n-1$. This means when a new user is added to the system, this new user does not need to obtain the partial secret key from user n. In other words, even if user n is malfunctioning, we still can add a new user to the system.
• Second, the system updates the $\mathsf{param}$ as

  $$\begin{array}{c}\hfill \mathsf{param}=(g,\tilde{g},g^{\beta },{\tilde{g}}^{\beta },u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N,e{(g,\tilde{g})}^{{\alpha }_1},\cdots ,e{(g,\tilde{g})}^{{\alpha }_{n-1}},n-1)\end{array}$$

Obviously, this approach can be extended to the case of malfunctioning of many key users. As a trade-off, the size of the secret key now is not constant, it in fact depends on the number of key users in the system. In addition, in the proof, simulator must know the set of corrupted authorities in advance to respond adversary’s queries. This lets our scheme be secure under a weaker security model.

Our second scheme is detailed as follows.

$\mathbf{Setup}(\lambda ,n,N)$: It is similar to the first scheme, the only difference is that user’s full secret key includes all n partial secret keys.

$\mathbf{Extract}(j,{\left\{d_i\right\}}_{i=1,\cdots ,n},\mathsf{param})$: It is similar to the first scheme, it is only difference that the algorithm outputs user j’s full secret key which includes all n partial secret keys.

$\mathbf{Revoke}(S,\mathsf{param})$: The input of this algorithm includes a set of non-malfunctioning key users S and $\mathsf{param}$. The algorithm outputs the updated $\mathsf{param}$ as

$$\begin{array}{c}\hfill \mathsf{param}=(g,\tilde{g},g^{\beta },{\tilde{g}}^{\beta },u_1,\cdots ,u_N,{\tilde{u}}_1,\cdots ,{\tilde{u}}_N,{\left\{e{(g,\tilde{g})}^{{\alpha }_i}\right\}}_{i\in S},S)\end{array}$$

$\mathbf{Encrypt}(\mathcal{R},\mathsf{param})$: First, this algorithm computes $e{(g,\tilde{g})}^{\alpha }={\prod }_{i\in S}e{(g,\tilde{g})}^{{\alpha }_i}$. The rest of the algorithm is the same as in the first scheme.

$\mathbf{Decrypt}(\mathsf{Hdr},d_j,\mathsf{param})$: It is similar to the first scheme, except that it first computes the full secret key from n partial secret keys. Note that to reduce the time of decrypting, the full secret key can be computed in advance.

The security of the second scheme is addressed by the following theorem.

Theorem 2.

Assume that $q\ge N$, our second scheme is weak selectively secure under the $\mathsf{MBDHE}$ assumption.

The proof of this theorem is very similar to the proof of the Theorem 1. We therefore think that it is not necessary to repeat it again, we just give here a sketch of the proof of this theorem.

Sketch of the proof. The proof of this theorem easily follows from the proof of Theorem 1. Note that there is only one difference here; that is the full secret key of a user now includes n partial secret keys. However, the adversary must declare a set of authorities at the beginning of the security game for which he/she intends to corrupt. That means the simulator $\mathcal{S}$ knows in advance at least a key user who will not be corrupted, let key user 1 be the uncorrupted key user. $\mathcal{S}$ is able to freely pick ${\alpha }_2,\cdots ,{\alpha }_n\stackrel{\$}{\leftarrow }{\mathbb{Z}}_p^{*}$ then implicitly sets ${\alpha }_1=\alpha -{\sum }_{i=2}^n{\alpha }_i$.

Next, to answer the corrupted full secret key of user j, $\mathcal{S}$ first computes $d_j$ as in the proof of Theorem 1. Second, $\mathcal{S}$ with ${\alpha }_2,\cdots ,{\alpha }_n$ at hands computes $n-1$ corresponding partial keys. Eventually, based on $d_j$ and these $n-1$ partial keys $\mathcal{S}$ can compute the 1-$st$ partial secret key $d_j^1$. As a result $\mathcal{S}$ can compute the full secret keys for all corrupted users. The rest of the proof is the same as in the proof of Theorem 1.

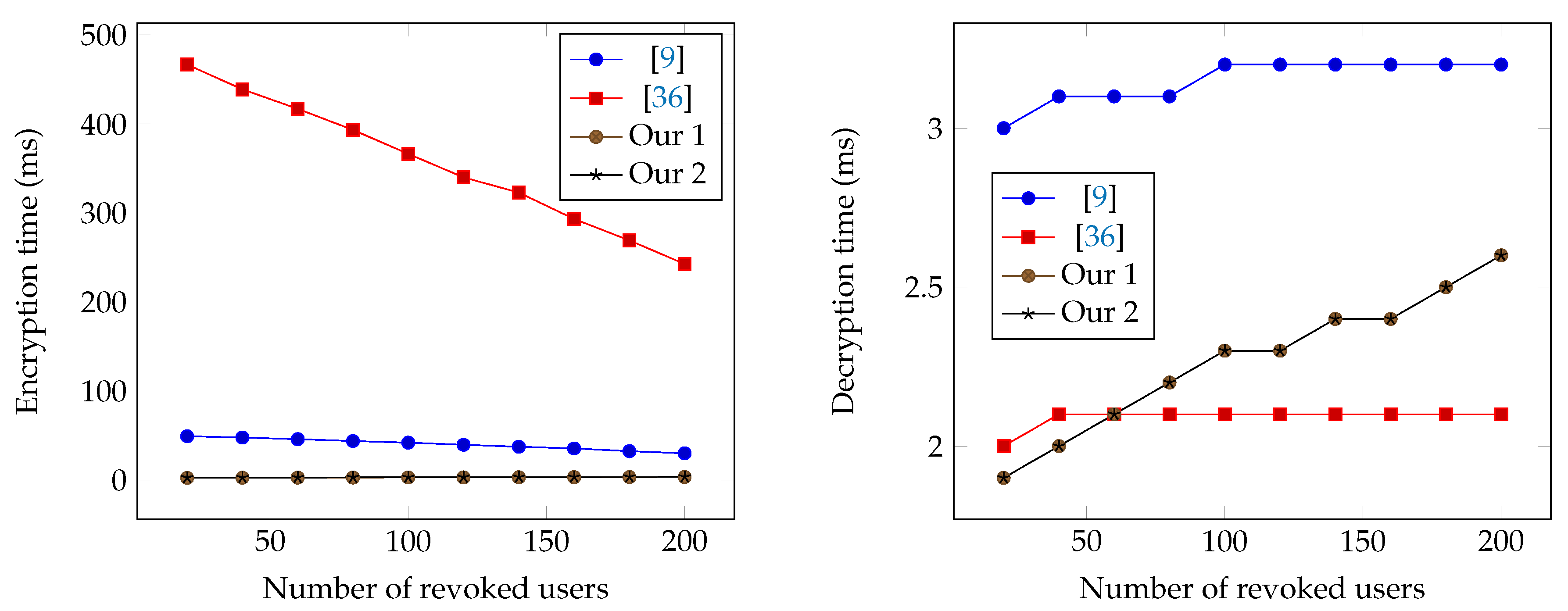
5. Performance Analysis

As shown in Table 1 and Table 2, our proposed schemes are the most efficient decentralized schemes in terms of all important properties: ciphertext size, secret key size and decryption time. Our schemes also use Type 3 Pairings; note that recent cryptanalysis of Type 1 Pairings has broken many well-known security assumptions, and among the three types of Pairings, Type 3 Pairings is the most efficient one. For decentralization, our first and second schemes achieve Level 2 and Level 3, respectively. There are still no known techniques to improve the schemes [9,19] to Level 3. Regarding the used assumptions, we note that the hardness of our assumption is similar to the assumptions of the other schemes listed in Table 1 and Table 2. The weaknesses of our schemes are the large public storage and the selective security (only obtain a weak level of security), these however may not be big problems since:

• the public parameters may not need to be stored permanently on the client and can be accessed on demand from a non-weak server with large computational resources. Moreover, keys are typically much more smaller than the data and/or its ciphertext in real-life scenarios. For example, consider using Broadcast encryption scheme for sharing files in a cloud storage system that encrypts files. The number of users N sharing access to a particular repository is typically limited. Therefore, the files ciphertexts are typically much larger than the public $param$ (which is $O\left(N^2\right)$ for the proposed algorithms) or the constant-size secret key.
• although selective security is more limited than adaptive security, researchers nowadays agree that selective security is also acceptable for practical applications. In fact, many proposed schemes today only achieve this level of security for both broadcast encryption schemes [2,21,26,37] and attribute-based encryption schemes [20,38,39], to name a few. Particularly, the BGW scheme [2] now is used widely in Pay-TV systems. Finally, if we would like to achieve adaptive security, we may make use of some existing tools such as [40] to generically transform a selective security scheme to an adaptive security scheme with a cost to pay in efficiency. Note that Functional encryption ($\mathsf{FE}$) [6] is a generalization of $\mathsf{BE}$, so this technique is directly applied to our proposed schemes. Note that in this paper we focus on the efficiency, so we omit this transformation.

To compare a decentralized $\mathsf{BE}$ scheme to a decentralized $\mathsf{ABE}$ scheme, we note that for several real-life applications such as File sharing systems, Pay-TV systems, E-Health, Social networks and Cloud storage systems, we can use the decentralized $\mathsf{ABE}$ scheme instead of the decentralized $\mathsf{BE}$ scheme. However, we emphasize that if we care about the efficiency property, for example when we deploy applications with lightweight devices (such as IoT devices), a decentralized $\mathsf{BE}$ scheme is the appropriate choice since it addresses the same problem while being much simpler and more efficient than decentralized $\mathsf{ABE}$ schemes. Obviously, a decentralized $\mathsf{ABE}$ scheme is a better choice if applications need to have anonymity of receivers, flexible access control, and high level of security. It is thereby fair to say that our proposed schemes provide an alternative choice offering a trade-off between efficiency on one hand and the properties of flexibility, security and anonymity on the other hand.

We implemented our schemes and the most recent decentralized $\mathsf{BE}$ scheme in [9] and decentralized $\mathsf{ABE}$ scheme in [36] to provide concrete performance evaluation. The results are shown in Table 3 and

Table 4. Comparison of our schemes and the schemes in [9,36] based on required storage (in bytes). We set the security parameter $\lambda =128$ and each user in [36] possesses only one attribute. However, in practice to support the flexible access control and anonymity of receivers, each user in [36] must possess many attributes, thus the user’s public storage in this scheme actually will be much larger. Note that, when $N=800$, each user in our first and second schemes just needs to publicly store about 100KB and 500KB, respectively, which is still appropriate for environments with lightweight devices.

Target Users		Ciphertext		Secret Key			User Public Storage
		[9,36]	Ours 1, 2	[9,36]	Ours 1	Ours 2	[9]	[36]	Ours 1	Ours 2
$N=100$	$r=10$	5915	130	65	65	650	6695	6825	$\mathrm{13,260}$	$\mathrm{71,760}$
	$r=20$	5265
	$r=30$	4615
$N=200$	$r=20$	$\mathrm{11,765}$	130	65	65	650	$\mathrm{13,195}$	$\mathrm{13,325}$	$\mathrm{26,260}$	$\mathrm{143,260}$
	$r=40$	$\mathrm{10,465}$
	$r=60$	9165
$N=400$	$r=40$	$\mathrm{23,465}$	130	65	65	650	$\mathrm{26,195}$	$\mathrm{26,325}$	$\mathrm{52,260}$	$\mathrm{286,260}$
	$r=80$	$\mathrm{20,865}$
	$r=120$	$\mathrm{18,265}$
$N=800$	$r=80$	$\mathrm{46,865}$	130	65	65	650	$\mathrm{52,195}$	$\mathrm{52,325}$	$\mathrm{104,260}$	$\mathrm{572,260}$
	$r=160$	$\mathrm{41,665}$
	$r=240$	$\mathrm{36,465}$

and Figure 1 and Figure 2. The program was written in the C language and the source code is available online (https://github.com/tranvinhduc/dbe). We use the PBC Library [41] for pairing environment.

The experiments were carried out on a computer with the processor Intel Core i7-4600U @ 2.1 GHz. The results are calculated as the average of 100 iterations of measurement.

Table 3 compares the encryption and decryption time of our schemes with the schemes in [9,36]. In our schemes, we fix the number of key users $n=10$. We run the experiments with two parameters: N (maximum number of users) and r (number of revoked users). Therefore, the number of target users is $N-r$. We run the decentralized $\mathsf{ABE}$ scheme [36] with test cases using the size of access policy $\ell =N-r$. The reason is that to support the functionality of encrypting a message to an arbitrary set of users (work as a $\mathsf{BE}$ scheme), the only way is for each user in an $\mathsf{ABE}$ scheme to possess an identity attribute (other users in the system do not possess this attribute). Assuming $A_i$ to be the identity attribute for user i, if the target set is $S=\{1,3,4\}$, then the corresponding access policy would be

$$A_1\vee A_3\vee A_4$$

which means the size of access policy is equal to the number of users in the target set, and the ciphertext size when using the scheme [36] is also linear in the number of users in the target set. Since both the $\mathsf{BE}$ and $\mathsf{ABE}$ schemes can be used to address the similar problems such as File sharing, Pay-TV systems, E-Health, Social networks and Cloud storage systems, it is an interesting question whether or not there exists a $\mathsf{BE}$ scheme that offers a similar decentralized property as in the $\mathsf{ABE}$ scheme [36], but has better efficiency. So, the main difference between our proposed schemes and the $\mathsf{ABE}$ scheme [36] is that our schemes have better efficiency, but the $\mathsf{ABE}$ scheme [36] supports better anonymity of receivers and flexibility of access control.

The encryption and decryption times are shown in Figure 1 and Figure 2. The encryption time of our schemes is dependent slightly on r while the schemes [9,36] are both dependent on $N-r$. Note that in all schemes, the public storage depends only on N not on r, which means the encryption time of our schemes does not depend on the size of the public storage while the schemes [9,36] do. In addition, r is typically smaller than $N-r$ in practice. Therefore, our schemes is expected to have better encryption performance than schemes [9,36]. Regarding the decryption time, our first and second schemes provide similar performance to the scheme in [9], but are slightly slower than the scheme in [36] when r becomes bigger.

Table 4 compares our schemes and the schemes in [9,36] based on the storage size (in bytes) of ciphertext, secret key and user’s public storage. Note that the user’s public storage is the public information for the user to perform encryption and decryption, which includes both the encryption key and the public storage part of the decryption key. Some specific classes of users (for example users in Pay-TV systems) do not need the functionality of encryption. Therefore, they just need to store the decryption key (that is why we specifically mention this property in the caption of Table 1). The values in Table 4 correspond to the worst case scenario when the user needs to perform both encryption and decryption. We also note that the system public storage in Table 1 is the sum of all users’ public storage.

In the experiments, we use type A pairing in the PBC Library, in which each point in the elliptic curve is compressed to 520 bits (corresponding to security parameter $\lambda =128$). Regarding ciphertext size, which is the most important parameter in $\mathsf{BE}$ due to the restricted bandwidth, our schemes are very efficient, and only require a constant size of 130 bytes. The schemes in [9,36] do not have constant size ciphertext, and their ciphertext sizes depend on the number of target users. The secret key size for all schemes is tiny. Regarding the user’s public storage, for simplicity, we consider the case when each user in [36] possesses only one identity attribute. That is why the user’s public storage in this scheme is equivalent to user’s public storage in [9] and both are smaller than in our schemes. However, in the worst case, when $N=800$, each user in our first scheme and second schemes just needs to publicly store about 100KB and 500KB, respectively. Such storage requirements are well within the capacity of lightweight devices. Overall, the experimental results demonstrate that our schemes are efficient and well fit applications with lightweight devices.

6. Conclusions

Recent attacks have shown that a single authority for managing keys creates a single point of failure as this authority could be hacked or could become unavailable. Therefore, key escrow is an important problem for many cryptographic primitives to protect against system malfunctioning or leaking sensitive user information. This paper demonstrates the construction of novel decentralized $\mathsf{BE}$ schemes that eliminate the problems associated with a single authority. Compared to other techniques presented in the literature, the proposed schemes are unique in the sense that they simultaneously achieve constant-size ciphertext, constant-size secret key and fast decryption. More specifically, our first scheme has the following properties:

• constant-size ciphertext;
• constant-size secret key: the secret key includes a maximum of two elements;
• fast decryption: to decrypt, the user only computes two Pairings in the prime order setting;
• decryption key size is linear in the maximum number of users in the system;
• supporting for level 2 decentralization, where new users can be added to the system dynamically.

Our second scheme improves the first scheme in the sense that it supports level 3 decentralization, where new users can be added or access of current users can be revoked after the initial setup phase. The weakness of the proposed schemes is that they only provide the more limited selective security. Our proposed schemes, therefore, provide a trade-off between the efficiency of the scheme (suitable for $\mathsf{BE}$ applications with light-weight users such as mobile and IoT devices) and the required security guarantees.