Abstract
A magic three-qubit Veldkamp line of , i.e., the line comprising a hyperbolic quadric , an elliptic quadric and a quadratic cone that share a parabolic quadric , the doily, is shown to provide an interesting model for the Veldkamp space of the doily. The model is based on the facts that: (a) the 20 off-doily points of form ten complementary pairs, each corresponding to a unique grid of the doily; (b) the 12 off-doily points of form six complementary pairs, each corresponding to a unique ovoid of the doily; and (c) the 15 off-doily points of , disregarding the nucleus of , are in bijection with the 15 perp-sets of the doily. These findings lead to a conjecture that also parapolar spaces can be relevant for quantum information.
1. Introduction
Quantum information theory (QIT), an important branch of quantum physics, is the study of how to integrate information theory with quantum mechanics, by studying how information can be stored in (and/or retrieved from) a quantum mechanical system. Within the last ten to fifteen years it has been gradually realized that finite geometries represent key mathematical concepts of QIT. We here mention finite projective (Hjelmslev) planes, projective lines over certain modular rings and rings of ternions, small generalized polygons (in particular the split Cayley hexagon of order two), factor-group-generated symplectic and orthogonal polar spaces, affine polar spaces of rank three and order two (in particular extended generalized quadrangles with lines of size three), combinatorial Grassmannians, binary Segre varieties and, last but not least, Veldkamp spaces of certain point-line incidence structures with three points per line; for the relevant literature, see recent reviews by Holweck [1] and Keppens [2] aimed, respectively, at both physicists and mathematicians. Among them, the unique triangle-free -configuration (out of 245,342 ones), also known as the Cremona–Richmond configuration and in the sequel referred to as the doily, acquires a special footing. This notable role of the doily stems from the fact that it is isomorphic to three remarkable, conceptually-distinct point-line incidence structures, namely a symplectic polar space of type (whose subgeometries furnish simplest observable proofs of quantum contextuality and justify the existence of the maximal sets of MUBs in the associated Hilbert space of two-qubits [3]), an orthogonal parabolic polar space of type (being the core of the magic three-qubit Veldkamp line of form theories of gravity [4,5,6]) and a generalized quadrangle of type GQ (being a subquadrangle of GQ that entails some important aspects of the so-called black-hole/qubit correspondence [7,8]). Employing the concept of Veldkamp space of a point-line incidence structure, this note aims at shedding some interesting light on how these three geometrical settings are interrelated.
2. Basic Glossary
We shall start with a well-known duad-syntheme model of the doily [9,10]. Given a six-element set , let us call a two-element subset of S a duad, and a set of three duads forming a partition of S a syntheme. The point-line incidence structure whose points are duads and whose lines are synthemes, with incidence being containment, is isomorphic to the doily.
A generalized n-gon ; , is a point-line incidence geometry which satisfies the following two axioms [11]: (a) does not contain any ordinary k-gons for and (b) given two points, two lines, or a point and a line, there is at least one ordinary n-gon in that contains both objects. A finite generalized n-gon is of order , if every line contains points and every point is contained in lines; if , we also say that is of order s. A generalized 4-gon is also called a generalized quadrangle (and abbreviated as GQ).
Next, we will also need particular types of four different kinds of finite polar spaces [12]. The symplectic polar space , , consisting of all the points of PG together with the totally isotropic subspaces in respect to the standard symplectic form
The hyperbolic orthogonal polar space , , formed by all the subspaces of PG that lie on a given nonsingular hyperbolic quadric, with the standard equation
The elliptic orthogonal polar space , , featuring all points and subspaces of PG satisfying the standard equation
where f is irreducible over . And, finally, the parabolic orthogonal polar space , , formed by all points and subspaces of PG satisfying the standard equation
A projective subspace of maximal dimension is called a generator; all generators have the same (vector) dimension r, which is called the rank of the polar space. The rank of each of the above-listed cases is N.
Further, given a point-line incidence geometry , a geometric hyperplane of is a subset of its point set such that a line of the geometry is either fully contained in the subset or has with it just a single point in common; if all the lines passing through a given point lie in the hyperplane, the point in question is called deep. The Veldkamp space of , , is the space [13] in which a point is a geometric hyperplane of and a line is the collection of all geometric hyperplanes H of such that or , where and are distinct points of . For a with three points on a line, all Veldkamp lines are of the form where is the complement of symmetric difference of and , i.e., they form a vector space over . In what follows we shall denote as and call it the Veldkamp sum of and .
Finally, a subset of the point-set of is called a subspace iff any line from L intersects it in zero, one or all of its points. A subspace is called singular if any two of its points are collinear. If p is a point, the symbol denotes the set of all points collinear with it, including the point itself. A point-line incidence structure is called a gamma space iff is a subspace for every point .
3. Veldkamp Space of the Doily
As it is well known [14,15], the doily features three different types of geometric hyperplanes (that is, Veldkamp points), namely six ovoids, fifteen perp-sets and ten grids. An ovoid is a set of points such that each line is incident with exactly one point in it; hence, each ovoid of the doily has five points. Using the duad-syntheme representation of the doily, it can be written as
A perp-set is the set of points collinear with a given point, the point inclusive. If the latter is , and taking
in some order, the corresponding perp-set reads
Finally, the nine points of a grid, , can be represented as
It can readily be verified that and . The doily contains 155 Veldkamp lines that fall into five different families, having the following representatives
4. Three Off-Doily Sectors of the Magic Veldkamp Line and the Doily’s Veldkamp Space
As already mentioned, a magic Veldkamp line of , the symplectic polar space behind the generalized three-qubit Pauli group, consists of a hyperbolic quadric , an elliptic quadric and a quadratic cone that have the doily () in common [4]. Our focus will be on the complements of the doily of the three constituents (to be called sectors in the sequel), in particular on how the points in these sectors are related with geometric hyperplanes of the core doily.
4.1. Grids and Hyperbolic Sector
It is easy to show that the 20 off-doily points of the hyperbolic sector form ten complementary pairs, the two points in any such pair being related to a particular grid of the doily. Let us label these twenty points by three-element subsets of and let be a partition of S. Then the nine lines passing through the point are (In what follows we will use a short-hand notation , , etc.)
and the nine lines through the complementary/conjugate point read
Comparing these two sets of equations with Equation (3) we see that in both cases the lines cut the core doily in the nine points of the same grid, namely the one. Figure 1 illustrates this property for two pairs of complementary points, 146/235 (top) and 136/245 (bottom).
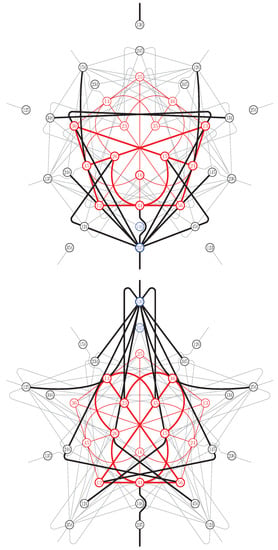
Figure 1.
A model of built around the doily (red); the nine lines (shown in bold) concurrent in an off-doily point (bold blue) cut the doily in a grid (bold red).
4.2. Ovoids and Elliptic Sector
The twelve off-doily points of the elliptic sector form six complementary pairs. If we label these points as and , and regard i and as complementary/conjugate, then the five lines through an off-doily point i or are, respectively, of the form [16]
where , , and . Comparing these expressions with Equation (1) we see that the five points of the doily in both cases correspond to the same ovoid, . Figure 2 serves as an illustration of this fact for points 3 and 3’.
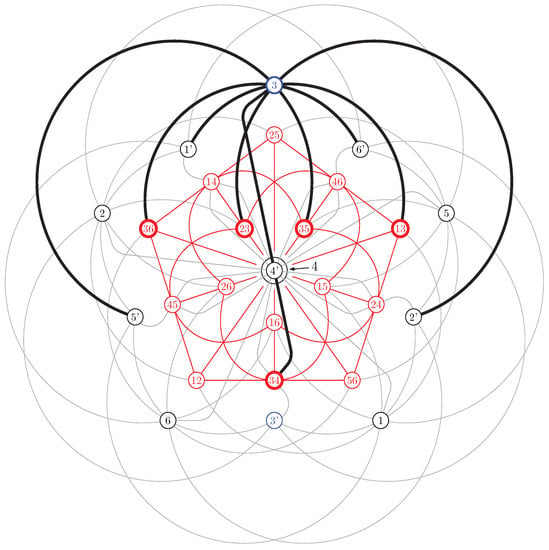
Figure 2.
A model of built around the doily (red); the five lines (shown in bold) concurrent in an off-doily point (bold blue) cut the doily in an ovoid (bold red).
4.3. Perp-Sets and Parabolic Sector
The parabolic sector comprises 16 points of which one has a special footing, being the nucleus of , that is the point common to all tangent hyperplanes of the quadric. If we label this nucleus by 123456 and the remaining 15 points by four-element subsets of S, , then we can set up a natural bijection between these 15 points and the 15 perp-sets of the doily, each being defined by its unique deep point , in the form
4.4. Sectors Image of the Doily’s Veldkamp Space
Based on these findings, we can establish the following correspondence between the geometric hyperplanes of the doily and off-doily points of the three sectors,
from where we readily get the following sectorial counterparts of the five families of Veldkamp lines of the doily (Equations (4)–(8), respectively)
Note that the parabolic sector plays a (slightly) different role than the other two.
5. Towards Parapolar Spaces
There are several interesting implications of this correspondence. We will mention only one that we find particularly intriguing as it concerns so-called parapolar spaces. A point-line incidence geometry is called a parapolar space iff it satisfies the following properties [17,18]: (i) is a connected gamma space, (ii) for every line , is not a singular subspace, and (iii) for every pair of non-collinear points , is either empty, a single point, or a non-degenerate polar space of rank at least two in which case is called a polar pair. And it is the very last property that makes a parapolar space to be a worth exploring concept in QIT. Indeed, as a grid of the doily, being isomorphic to , is, like the doily itself, a non-degenerate polar space of rank two, the corresponding pair of complementary points in the associated hyperbolic sector play in our model the role of polar pairs. Moreover, if we regard as being embedded in some parapolar space like, for example, where is a projective line of size three [19], then such a pair of complementary points becomes a polar pair in this parapolar space. (We note that the last requirement in axiom (iii) of the definition of a parapolar space puts aside pairs of complementary points in the elliptic sector, because an ovoid of the doily is isomorphic to and the latter is a non-degenerate polar space of rank one only (see Section 2).)
The fact that the above-described three-qubit Veldkamp line setting for the Veldkamp space of the doily leads rather straightforwardly to parapolar spaces should not come as a surprise. Parapolar spaces were originally invented to characaterize Lie geometries associated with exceptional algebraic groups [20], the groups that play a very important role in physics. Recently, they were also linked with the properties of the Freudenthal–Tits Magic Square [21], which encodes relation between a certain class of also physically-relevant semi-simple Lie algebras. In light of these facts, the eventual occurrence of parapolar spaces in the context of QIT is a rather viable conjecture. To be more specific, it will be worth exploring parapolar spaces with lines of size three and more, with a particular focus on: dual polar spaces, grassmannian spaces, half-spin geometries, exceptional strong parapolar spaces of type and , metasymplectic spaces, exceptional long root geometries of type , and , and polar grassmannians; this should, for example, lead to a novel hierarchy of quantum contextual configurations that are natural generalizations of the famous Mermin–Peres magic square (two-qubits) and the Mermin pentagram (three-qubits). Furthermore, a closer look at the structure of the exceptional Moufang quadrangles of type that appear as fixed point structures of involutions of metasymplectic spaces over fields of characteristic two, together with examination of improperly embedded symplectic quadrangles of type GQ, may shed further light on ‘peculiarities’ of characteristic two in quantum theory that were already noticed in the behavior of Lagrangian grassmannian mappings between different N-qubit Pauli groups [22].
Author Contributions
Conceptualization and analysis, M.S. and Z.S.; writing—original draft preparation, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Slovak Research and Development Agency under the contract # SK-FR-2017-0002, as well as by the Slovak VEGA Grant Agency, Project # 2/0004/20.
Acknowledgments
We thank all the three anonymous reviewers for their constructive comments/suggestions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Holweck, F. Geometric constructions over and for quantum information. In Quantum Physics and Geometry; Ballico, E., Bernardi, A., Carusotto, I., Mazzucchi, S., Moretti, V., Eds.; Lecture Notes of the Unione Matematica Italiana; Springer Nature: Cham, Switzerland, 2019; Volume 25, pp. 87–124. [Google Scholar]
- Keppens, D. On the history of ring geometry (with a thematical overview of literature). Mitt. Math. Ges. Hambg. 2019, 39, 99. [Google Scholar]
- Planat, M.; Saniga, M. On the Pauli graph of N-qudits. Quantum Inf. Comput. 2008, 8, 127. [Google Scholar]
- Lévay, P.; Holweck, F.; Saniga, M. The magic three-qubit Veldkamp line: A finite geometric underpinning for form theories of gravity and black hole entropy. Phys. Rev. D 2017, 96, 026018. [Google Scholar] [CrossRef]
- Lévay, P.; Szabó, Z. Mermin pentagrams arising from Veldkamp lines for three qubits. J. Phys. Math. Theor. 2017, 50, 095201. [Google Scholar] [CrossRef]
- Saniga, M. A combinatorial Grassmannian representation of the magic three-qubit Veldkamp line. Entropy 2017, 19, 556. [Google Scholar] [CrossRef]
- Lévay, P.; Saniga, M.; Vrana, P.; Pracna, P. Black hole entropy and finite geometry. Phys. Rev. D 2009, 79, 084036. [Google Scholar] [CrossRef]
- Borsten, L.; Duff, M.J.; Lévay, P. The black-hole/qubit correspondence: An up-to-date review. Class. Quantum Gravity 2012, 29, 224008. [Google Scholar] [CrossRef]
- Green, R.M. Combinatorics of Minuscule Representations. Cambridge Tracts in Mathematics, 199; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Payne, S.E.; Thas, J.A. Finite Generalized Quadrangles; Pitman: Boston, MA, USA, 1984. [Google Scholar]
- Van Maldeghem, H. Generalized Polygons; Birkhäuser: Basel, Switzerland, 1998. [Google Scholar]
- Cameron, P.J. Projective and Polar Spaces. QMW Maths Notes, 13; School of Mathematical Sciences, Queen Mary and Westfield College: London, UK, 1992. [Google Scholar]
- Buekenhout, F.; Cohen, A.M. Diagram Geometry: Related to Classical Groups and Buildings; Springer: Berlin, Germany, 2013. [Google Scholar]
- Saniga, M.; Planat, M.; Pracna, P.; Havlicek, H. The Veldkamp space of two-qubits. Symmetry Integr. Geom. Methods Appl. 2007, 3, 75. [Google Scholar] [CrossRef]
- Saniga, M.; Lévay, P.; Planat, M.; Pracna, P. Geometric hyperplanes of the near hexagon L3×GQ(2,2). Lett. Math. Phys. 2010, 91, 93. [Google Scholar] [CrossRef][Green Version]
- Polster, B. A Geometrical Picture Book; Springer: New York, NY, USA, 1991. [Google Scholar]
- Cooperstein, B.N. A characterization of some Lie incidence structures. Geom. Dedicata 1977, 6, 205. [Google Scholar] [CrossRef]
- Shult, E.E. Points and Lines: Characterizing the Classical Geometries; Universitext; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kasikova, A.; Shult, E.E. Point-line characterizations of Lie incidence geometries. Adv. Geom. 2002, 2, 147. [Google Scholar] [CrossRef]
- Cohen, A.M.; Cooperstein, B.N. A characterization of some geometries of exceptional Lie type. Geom. Dedicata 1983, 15, 73. [Google Scholar] [CrossRef]
- Schillewaert, J.; Van Maldeghem, H. On the varieties of the second row of the split Freudenthal–Tits magic square. Ann. Inst. Fourier 2017, 67, 2265. [Google Scholar] [CrossRef]
- Holweck, F.; Saniga, M.; Lévay, P. A notable relation between N-qubit and 2N−1-qubit Pauli groups via binary LGr(N,2N). Symmetry Integr. Geom. Methods Appl. 2014, 10, 41. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).