Symmetry-Breaking for Airflow Control Optimization of an Oscillating-Water-Column System
Abstract
1. Introduction
2. Model Statement
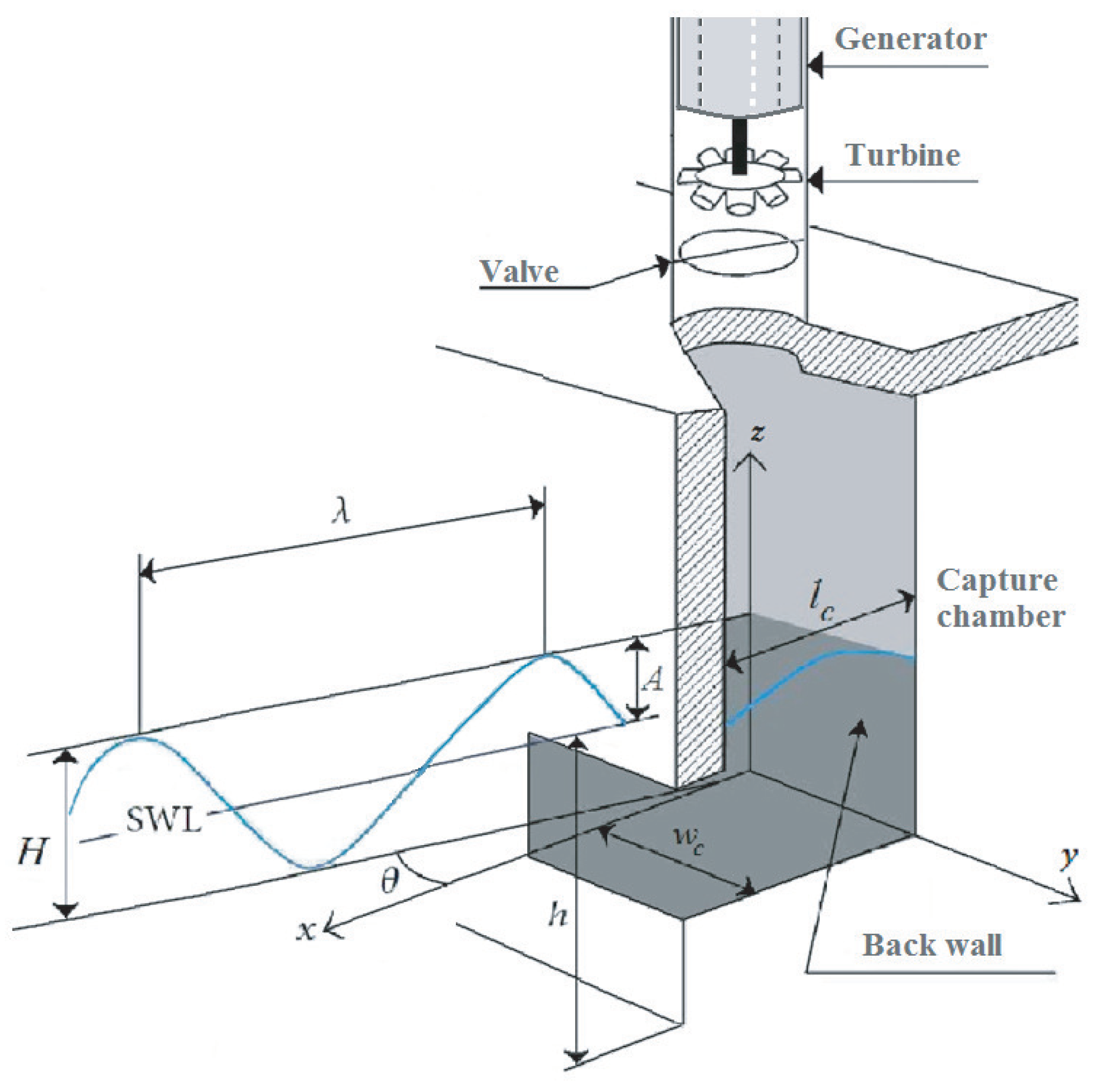
2.1. Wave Surface Dynamics
2.2. Capture Chamber Model
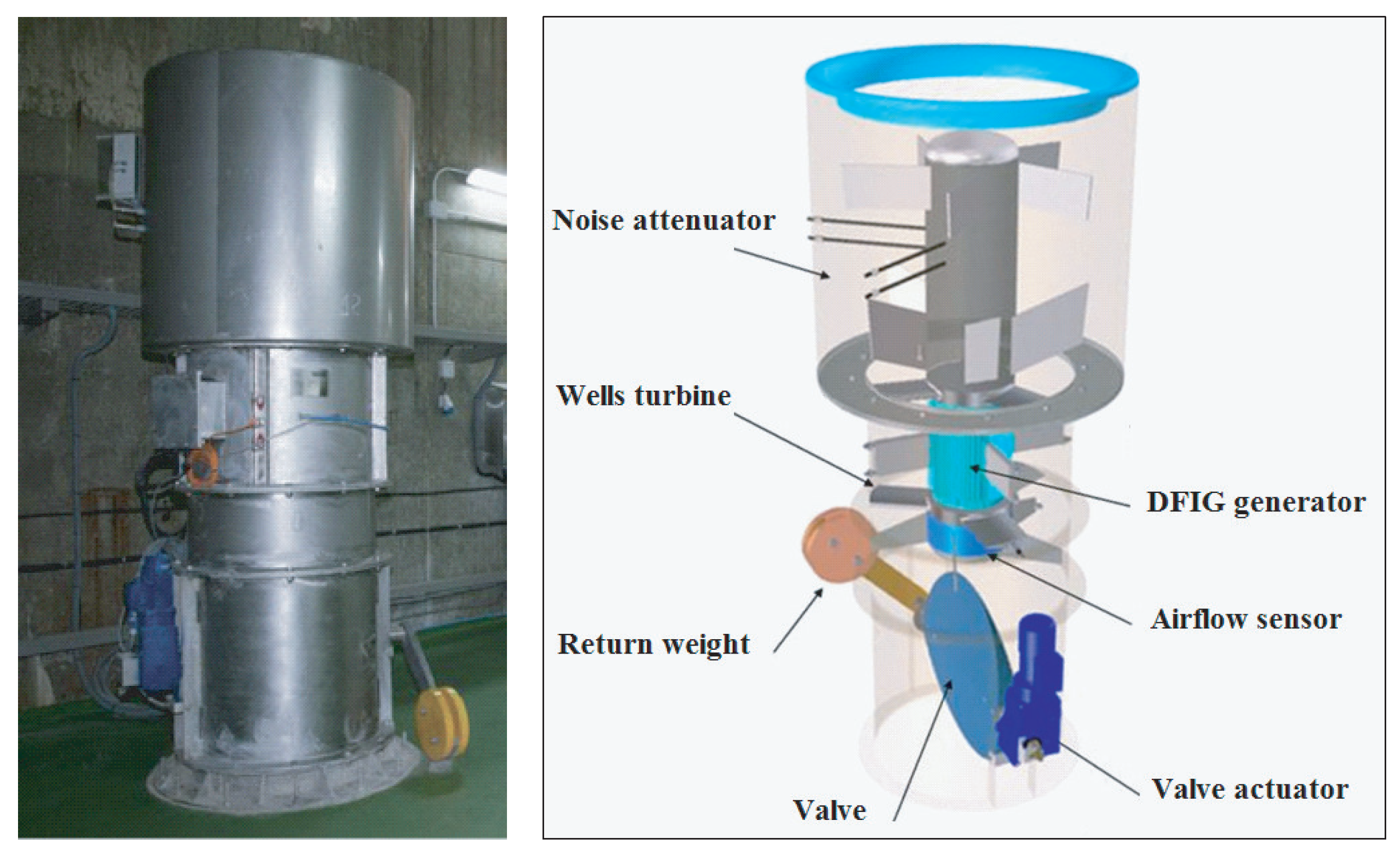
2.3. Wells Turbine Model
2.4. Doubly Fed Induction Generator Model
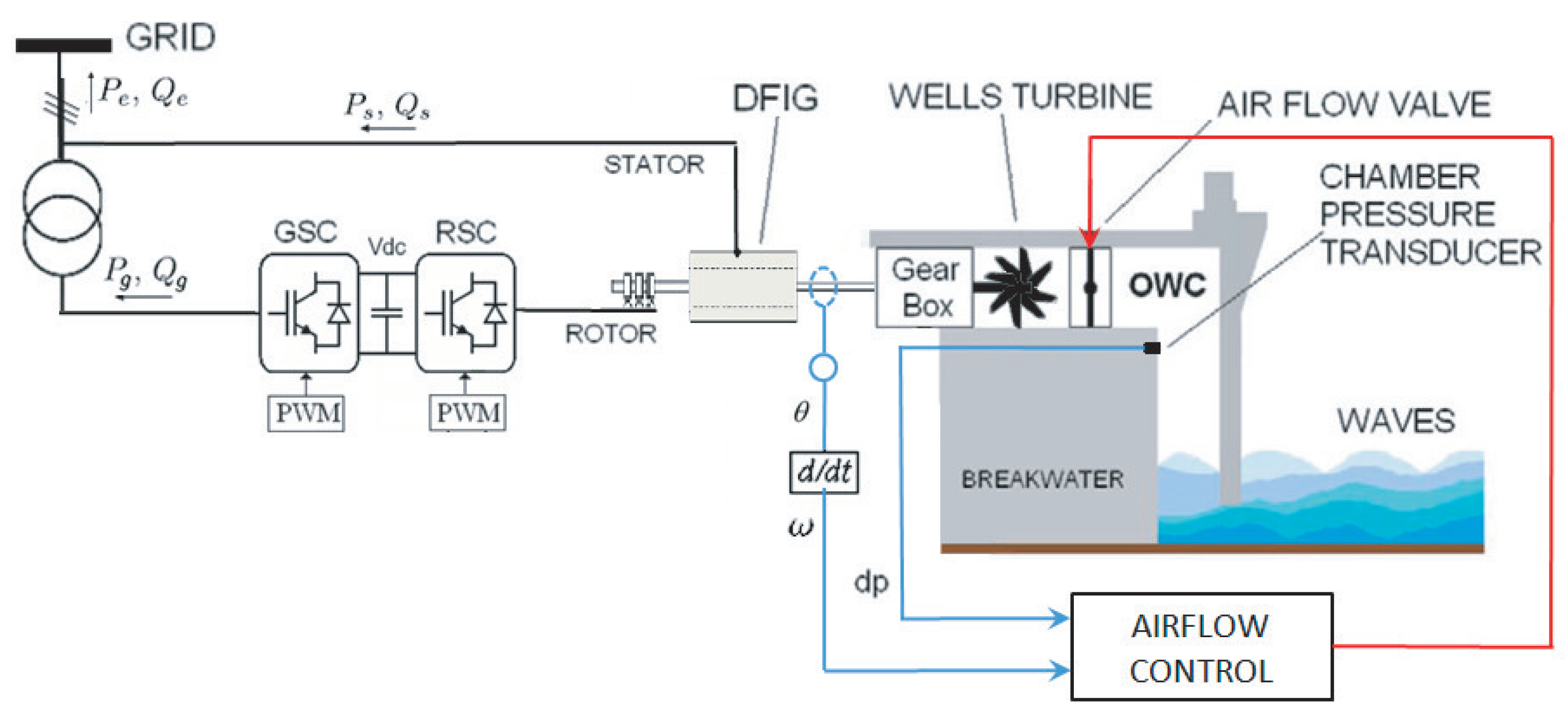
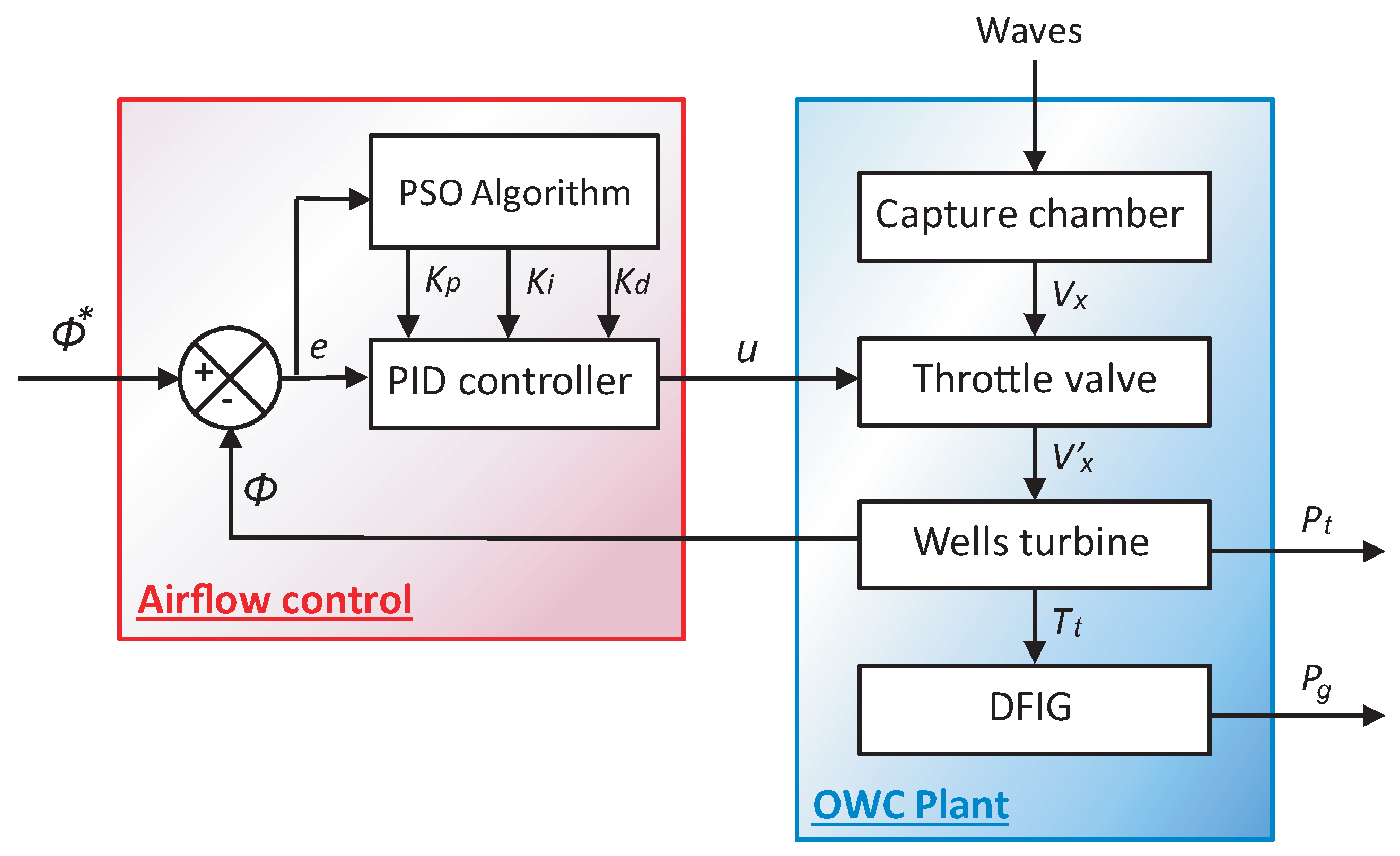
3. Airflow Control Strategy
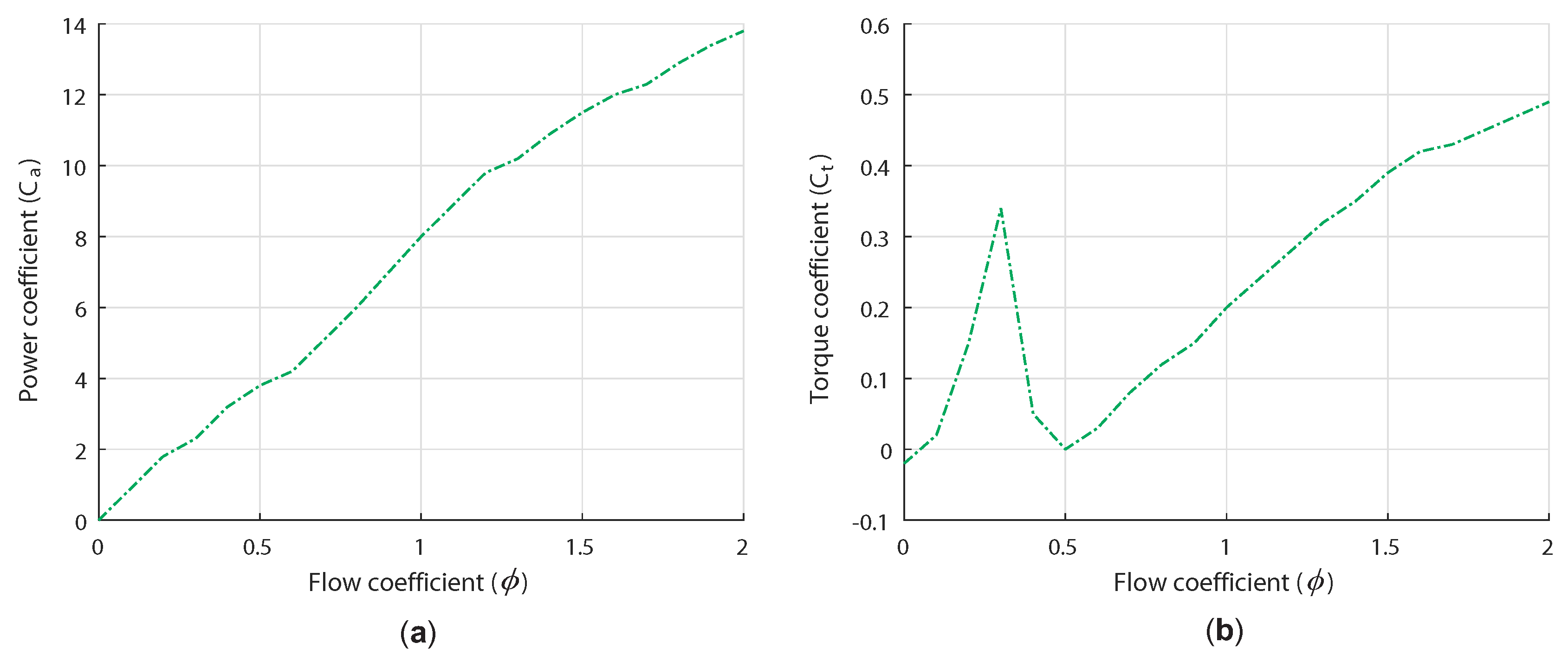
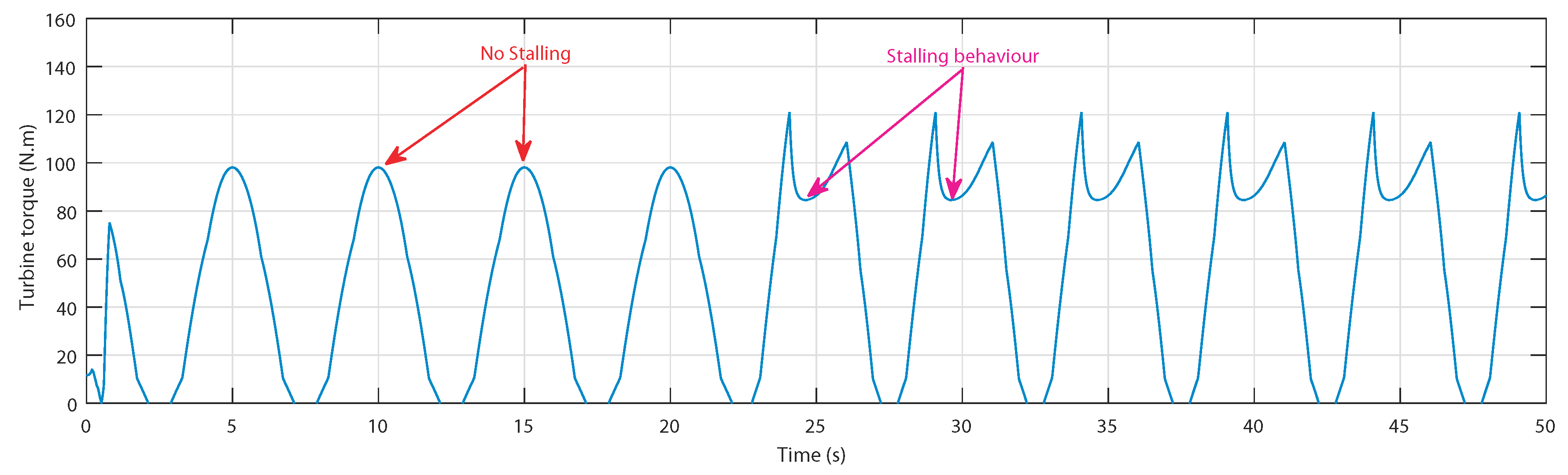
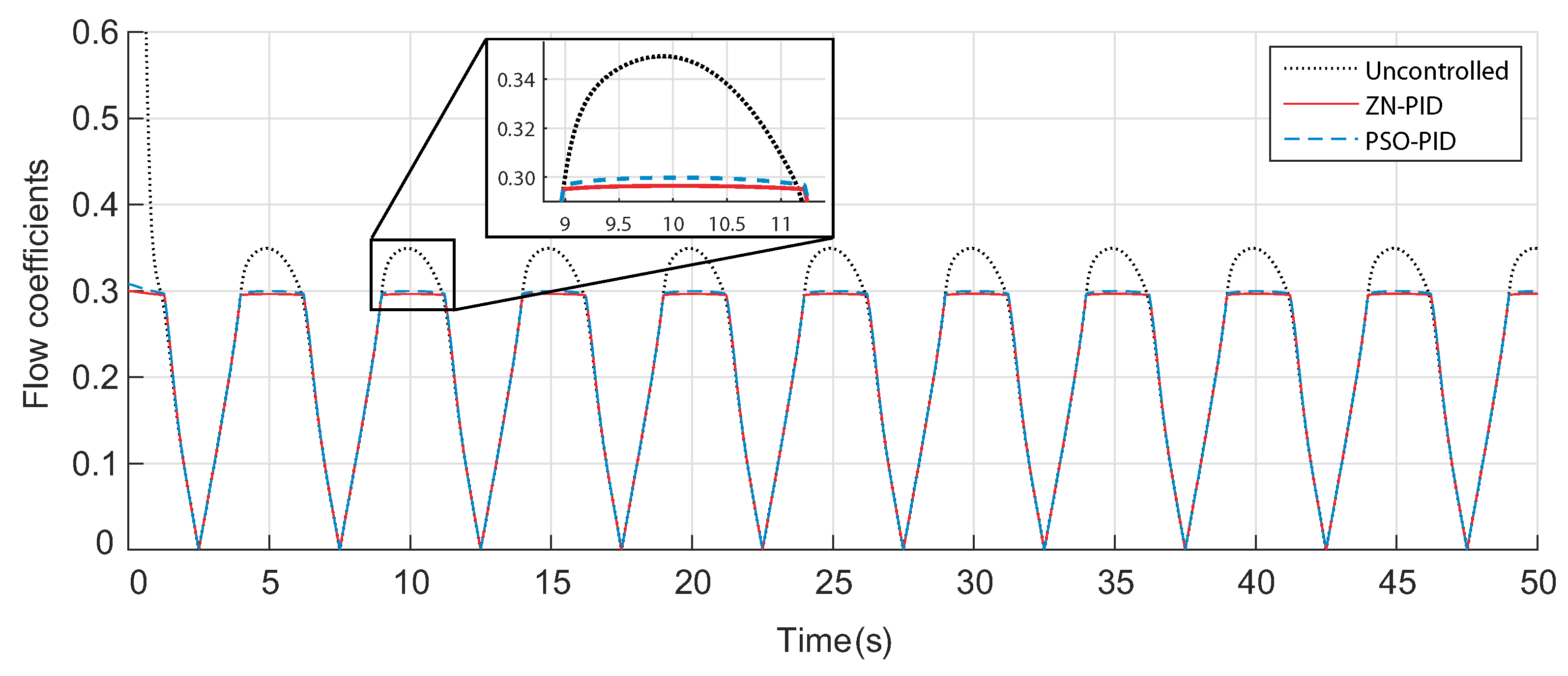
3.1. Stalling Behavior Problem
3.2. Control Problem Formulation
4. Symmetry-Breaking Constraints
- Variable symmetry where permuting variables are solution invariant defined as:
- Value symmetry where permuting solution values are solution invariant defined as:
- Variable/value symmetry where both variables and values permutation is solution invariant defined as:
5. Particle Swarm Optimization
| Algorithm 1 PSO algorithm |
| 1. Define parameters of PSO algorithm: , , , , , . |
| 2. Arbitrarily initialize the swarm particles’ positions and velocities . |
| 3. Assess this initial population and calculate and . |
| 4. Increment the iteration k and updated the position of every particle of the flock by means of the update Equations (24)–(26). |
| 5. Assess the associated fitness values |
| (i) if then and , |
| (ii) if then and . |
| where represents the best previous fitness of the particle and represents the best fitness in the whole swarm. |
| 6. If the stopping criterion is met, the program finishes and stops searching with the obtained solution . Otherwise, go back to step 4. |
6. Results and Discussion
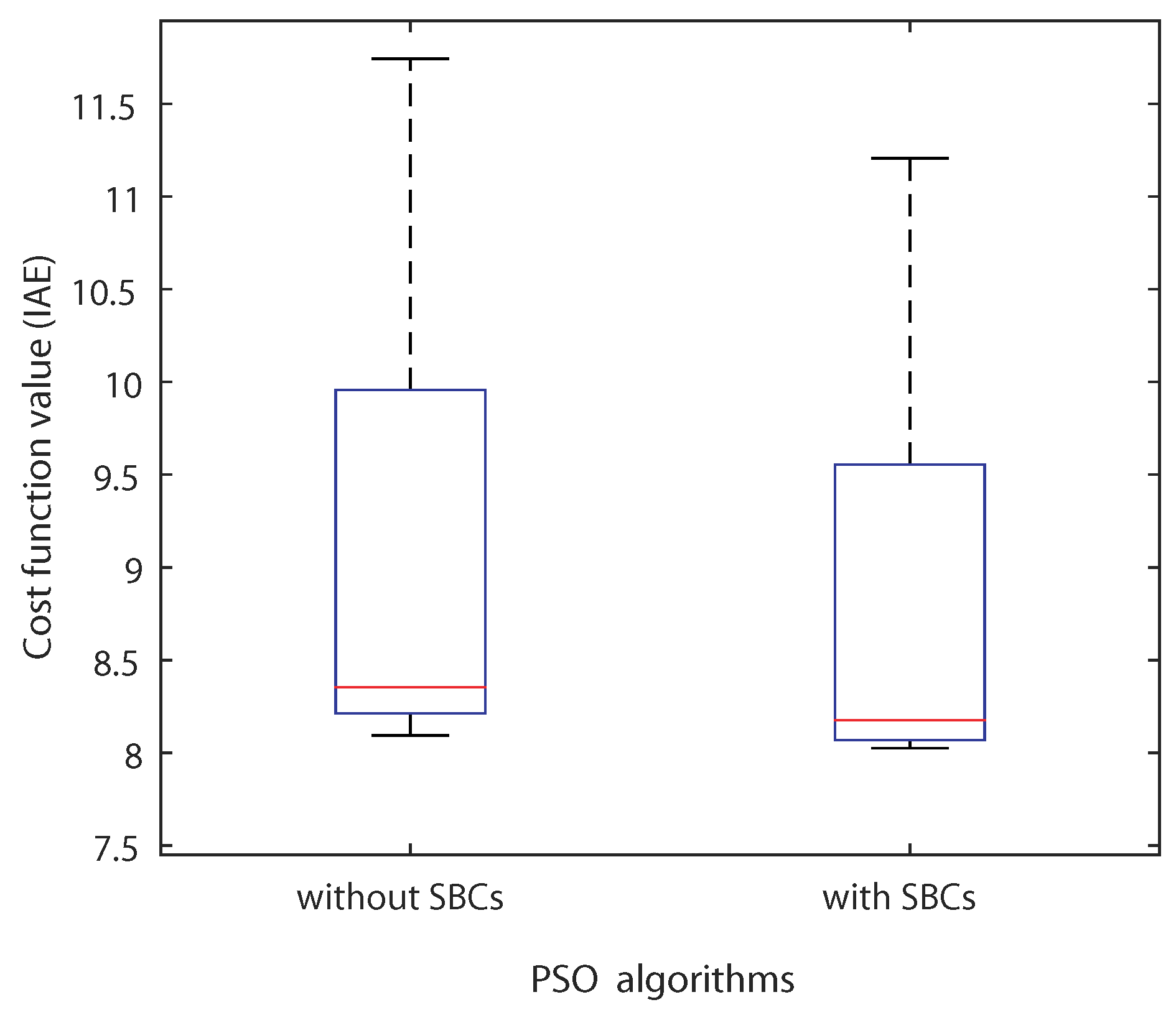
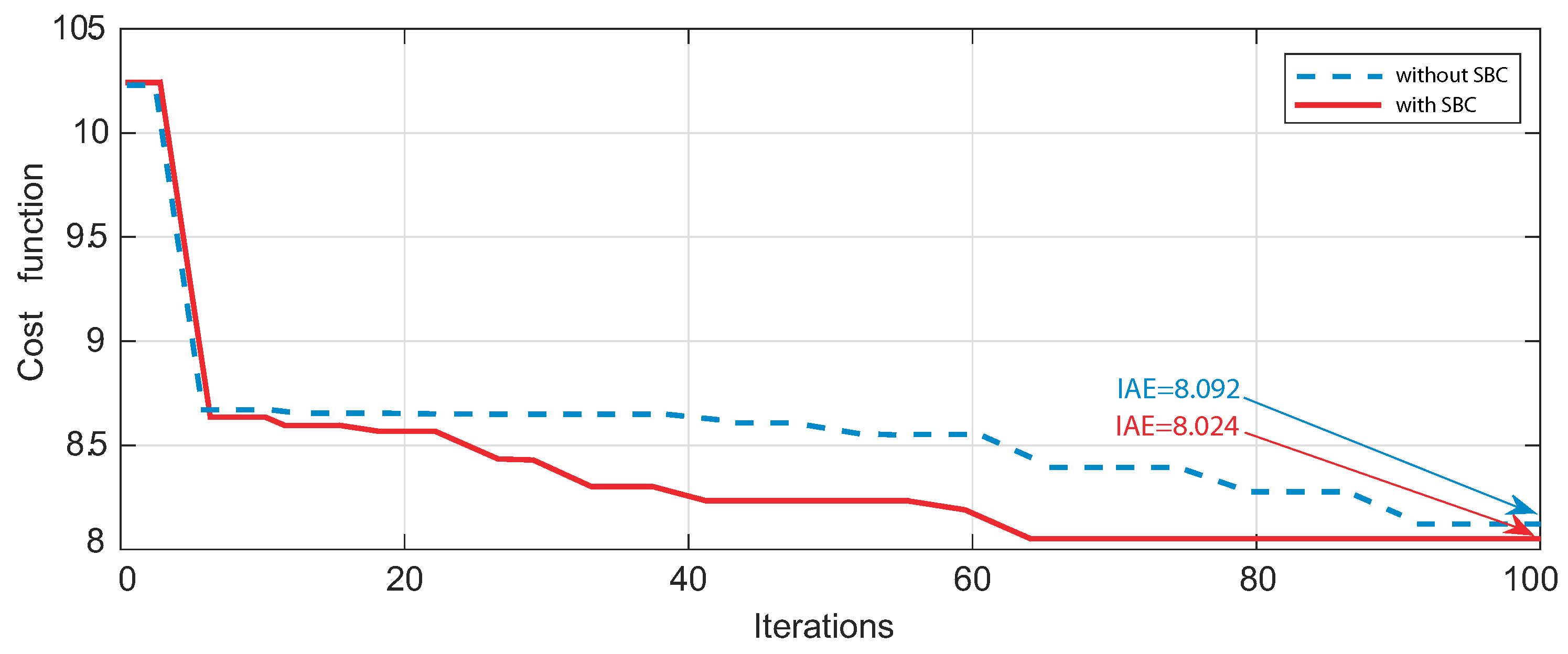
6.1. Optimization Results
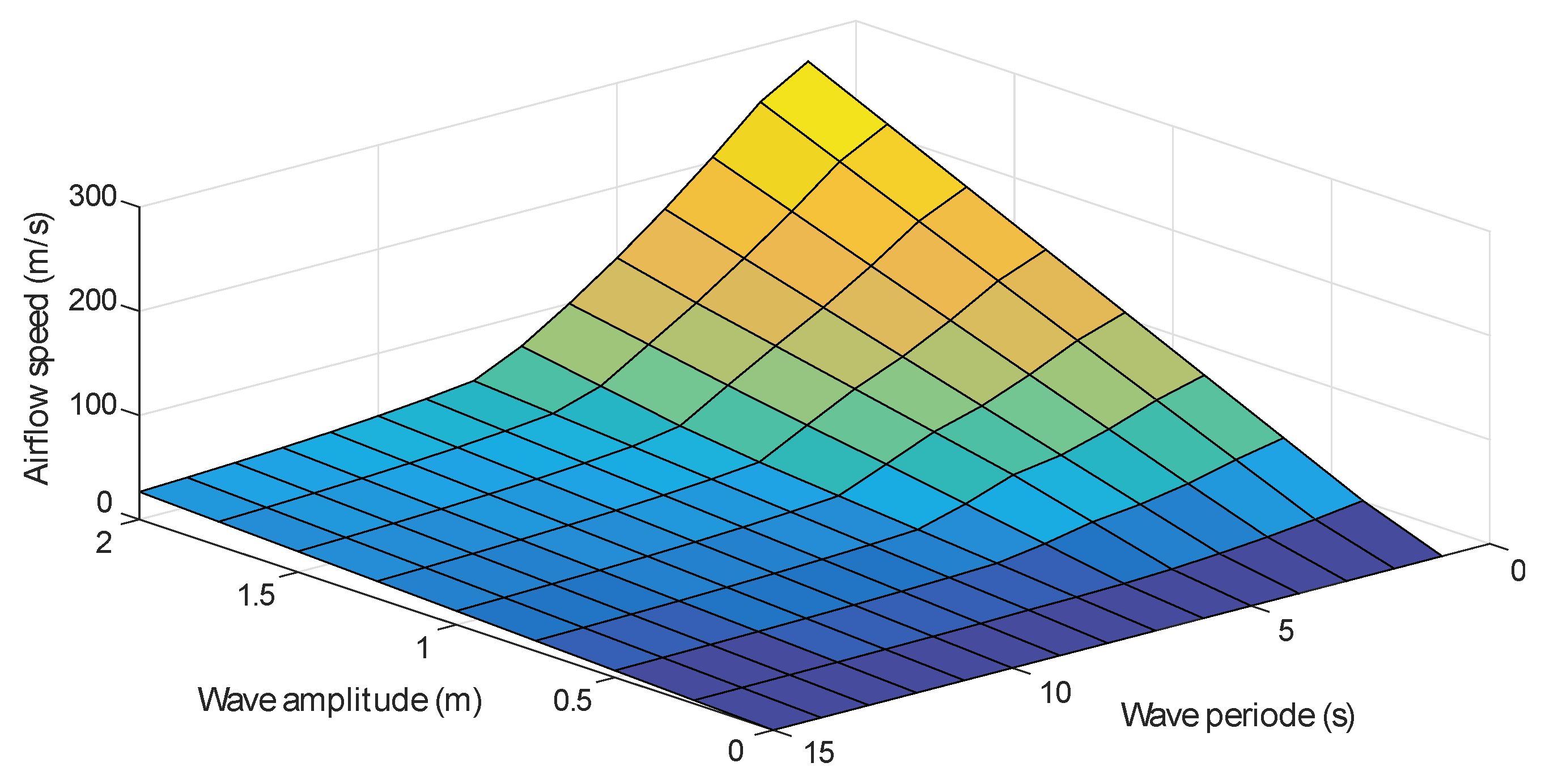
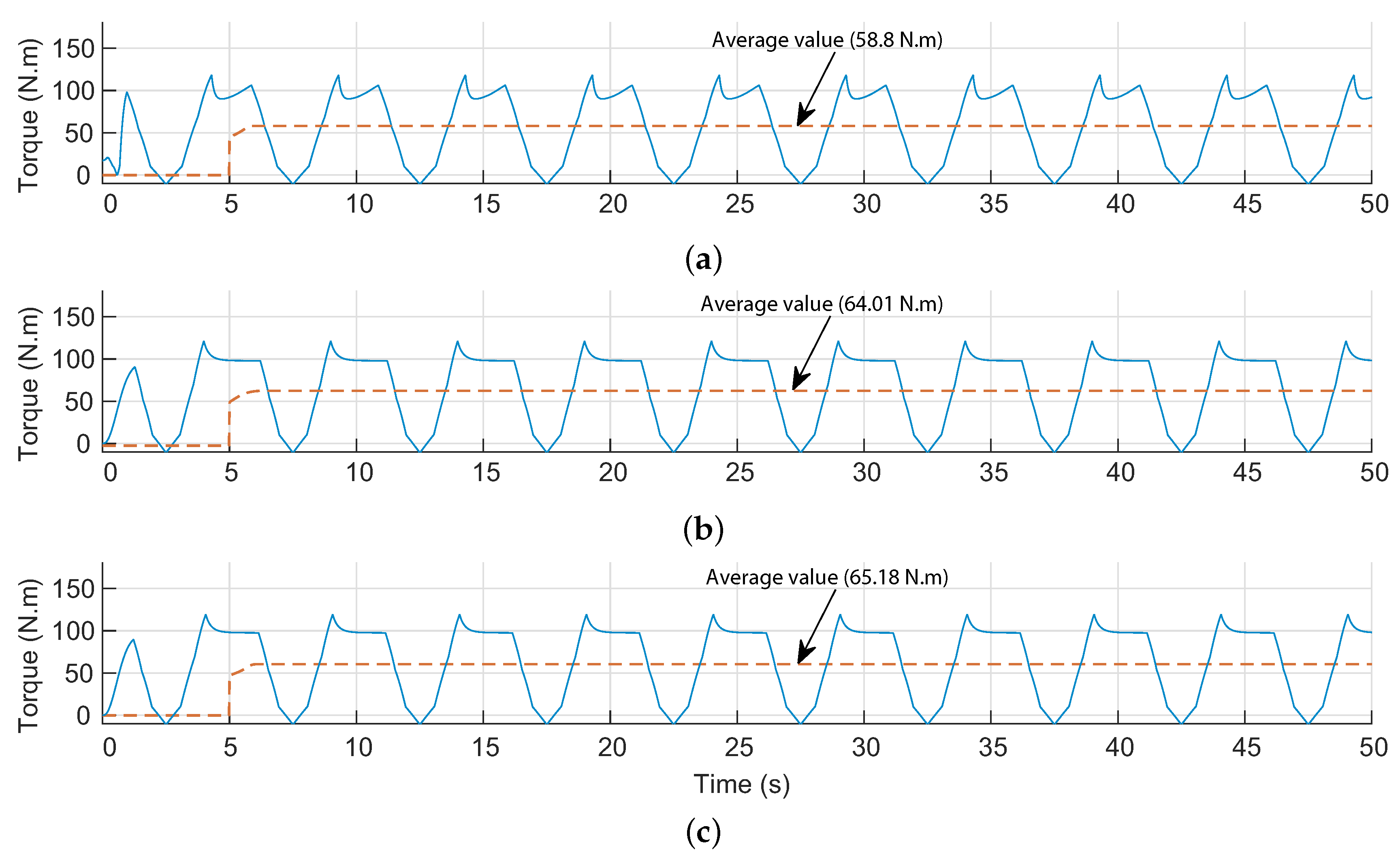
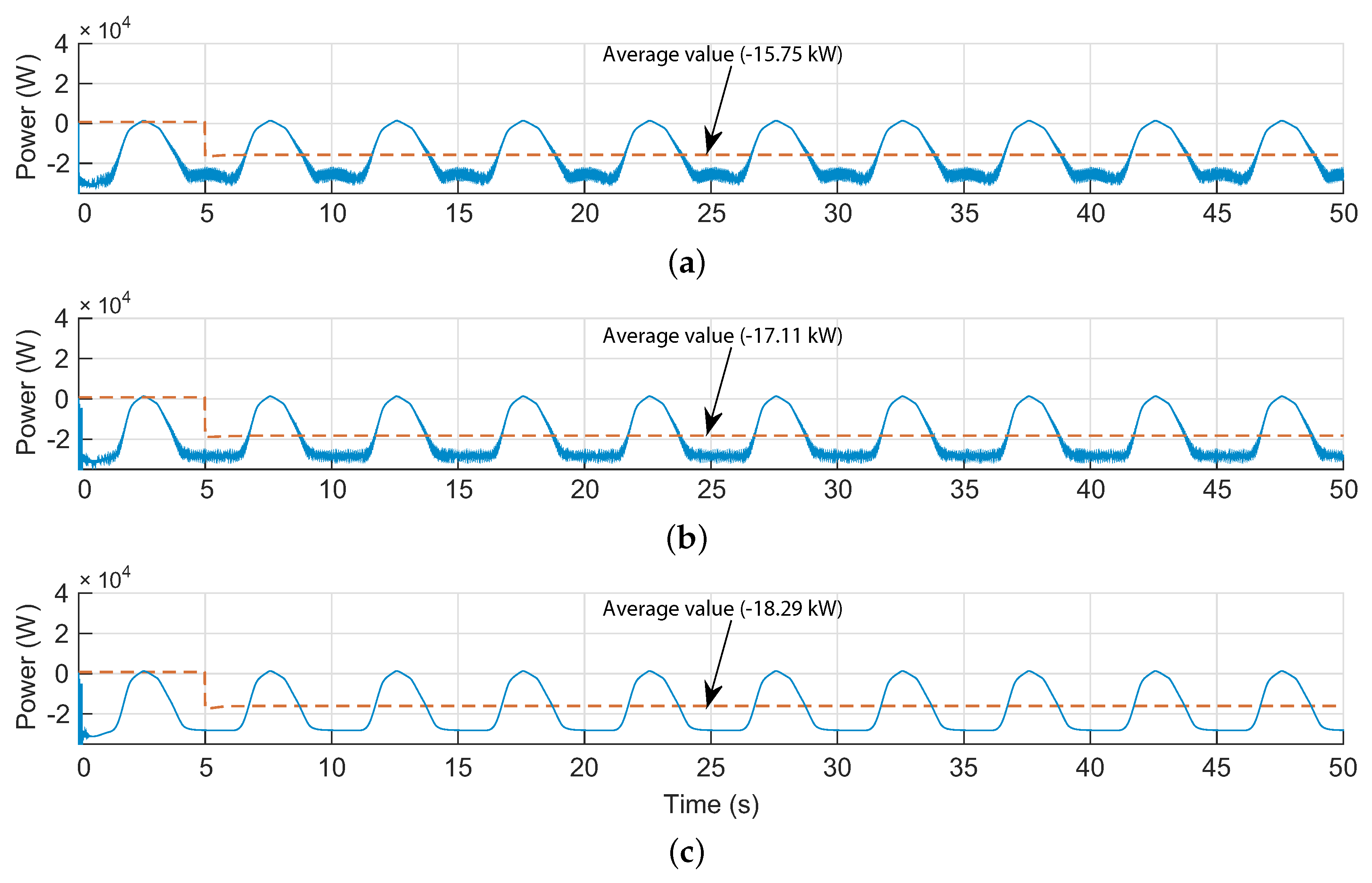
6.2. OWC Performance
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Wavelength, amplitude, and height (m) | |
| Sea depth and wave surface elevation (m) | |
| Wave period (s) and wave frequency (rad/s) | |
| g | Acceleration gravity (m/s) |
| Pressure drop (Pa) | |
| Capture chamber inner width and length (m) | |
| Capture chamber volume (m) and flow rate (m/s) | |
| Atmospheric density (kg/m) and airflow speed (m/s) | |
| Blade chord length, blade span and turbine diameter (m) | |
| Blade number, pole number, wave number, and turbine constant | |
| Electromagnetic and turbine torques (N·m) | |
| J | Turbo-generator inertia (kg·m) |
| Torque, power and flow coefficients | |
| Stator and rotor resistances () | |
| Stator and rotor inductances (H) | |
| Stator and rotor currents (A) | |
| Stator and rotor flux (Wb) | |
| Stator and rotor rotational speed (rad/s) | |
| e | Error between the reference variable and measured variable |
| u | Control signal obtained from the PID controller |
| Proportional, integral, and derivative gains of the PID controller | |
| P | Optimization problem |
| Optimal solution for the problem | |
| f | Cost function |
| Penalty function | |
| Scaling penalty parameter for the jth constraint | |
| Number of constraints | |
| Symmetry permutation | |
| ∑ | Set of symmetry permutations |
| Swarm particles positions and velocities | |
| Cognitive and social scaling factors | |
| w | Inertia factor |
| Best positions formerly found for the ith particle and the entire swarm at the kth iteration |
References
- Rusu, L.; Onea, F. Assessment of the performances of various wave energy converters along the European continental coasts. Energy 2015, 82, 889–904. [Google Scholar] [CrossRef]
- European Parliament. Directive 2009/28/EC of the European Parliament and of the Council of 23 April 2009 on the promotion of the use of energy from renewable sources and amending and subsequently repealing Directives 2001/77/EC and 2003/30/EC. Off. J. Eur. Union 2009, 140, 47. [Google Scholar]
- UNFCCC. Adoption of the Paris Agreement FCCC/CP/2015/L. 9/Rev. 1. 1. United Nations Framework Convention on Climate Change. Paris. December 2015. Available online: http://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf (accessed on 12 May 2020).
- Lavidas, G. Energy and socio-economic benefits from the development of wave energy in Greece. Renew. Energy 2019, 132, 1290–1300. [Google Scholar] [CrossRef]
- IRENA. Global Energy Transformation: A Roadmap to 2050, 2019th ed.; International Renewable Energy Agency: Abu Dhabi, UAE, 2019. [Google Scholar]
- Lehmann, M.; Karimpour, F.; Goudey, C.A.; Jacobson, P.T.; Alam, M.R. Ocean wave energy in the United States: Current status and future perspectives. Renew. Sustain. Energy Rev. 2017, 74, 1300–1313. [Google Scholar] [CrossRef]
- Maria-Arenas, A.; Garrido, A.J.; Rusu, E.; Garrido, I. Control Strategies Applied to Wave Energy Converters: State of the Art. Energies 2019, 12, 3115. [Google Scholar] [CrossRef]
- REN21. Renewables 2018 Global Status Report; REN21: Paris, France, 2018. [Google Scholar]
- Soukissian, T.H.; Denaxa, D.; Karathanasi, F.; Prospathopoulos, A.; Sarantakos, K.; Iona, A.; Georgantas, K.; Mavrakos, S. Marine Renewable Energy in the Mediterranean Sea: Status and Perspectives. Energies 2017, 10, 1512. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.K.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Hayward, J.; Behrens, S.; McGarry, S.; Osman, P. Economic modelling of the potential of wave energy. Renew. Energy 2012, 48, 238–250. [Google Scholar] [CrossRef]
- Neary, V.S.; Ahn, S.; Seng, B.E.; Allahdadi, M.N.; Wang, T.; Yang, Z.; He, R. Characterization of Extreme Wave Conditions for Wave Energy Converter Design and Project Risk Assessment. J. Mar. Sci. Eng. 2020, 8, 289. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Wave Power Absorption by Arrays of Wave Energy Converters in Front of a Vertical Breakwater: A Theoretical Study. Energies 2020, 13, 1985. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Conceptual Design and Simulation of a Self-Adjustable Heaving Point Absorber Based Wave Energy Converter. Energies 2020, 13, 1997. [Google Scholar] [CrossRef]
- Lee, H.H.; Chen, C.-H. Parametric Study for an Oscillating Water Column Wave Energy Conversion System Installed on a Breakwater. Energies 2020, 13, 1926. [Google Scholar] [CrossRef]
- Heath, T.V. A review of oscillating water columns. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Raghunathan, S. Performance of the Wells self-rectifying turbine. Aeronaut. J. 1985, 89, 369–379. [Google Scholar]
- Raghunathan, S. The Wells air turbine for wave energy conversion. Prog. Aerosp. Sci. 1995, 31, 335–386. [Google Scholar] [CrossRef]
- Avery, J. Symmetry-Adapted Basis Sets: Automatic Generation for Problems in Chemistry and Physics; World Scientific: Singapore, 2012. [Google Scholar]
- Carter, R.L. Molecular Symmetry and Group Theory; Wiley: New York, NY, USA, 1998; p. 201. [Google Scholar]
- Lockwood, E.H.; Macmillan, R.H. Geometric Symmetry; Cambridge University Press Archive: Cambridge, UK, 1978. [Google Scholar]
- Kosaka, I.; Swan, C.C. A symmetry reduction method for continuum structural topology optimization. Comput. Struct. 1999, 70, 47–61. [Google Scholar] [CrossRef][Green Version]
- Deü, J.F.; Larbi, W.; Ohayon, R. Piezoelectric structural acoustic problems: Symmetric variational formulations and finite element results. Comput. Methods Appl. Mech. Eng. 2008, 197, 1715–1724. [Google Scholar] [CrossRef]
- de León, M.; Cortés, J.; de Diego, D.M.; Martínez, S. General symmetries in optimal control. Rep. Math. Phys. 2004, 53, 55–78. [Google Scholar] [CrossRef]
- Kwakernaak, H. Symmetries in control system design. In Trends in Control; Springer: London, UK, 1995; pp. 17–51. [Google Scholar]
- Hasan, M.A. On Optimization Problems with Symmetric Constraints. In Proceedings of the 2005 5th International Conference on Information Communications & Signal Processing, Bangkok, Thailand, 6–9 December 2005; pp. 367–371. [Google Scholar]
- Walsh, T. Symmetry in constraint optimization. In Proceedings of the Seventh International Workshop on Symmetry in Constraint Satisfaction Problems (SymCon’07) in Conjunction with the International Conference on Principles and Practice of Constraint Programming (CP’2007), Providence, RI, USA, 23–27 September 2007; pp. 1–6. [Google Scholar]
- Ji, X.; Ma, F.; Zhang, J. Solving global unconstrained optimization problems by symmetry-breaking. In Proceedings of the 2009 Eighth IEEE/ACIS International Conference on Computer and Information Science, Shanghai, China, 1–3 June 2009; pp. 107–111. [Google Scholar]
- Puget, J.F. On the satisfiability of symmetrical constrained satisfaction problems. In Proceedings of the 7th International Symposium on Methodologies for Intelligent Systems (ISMIS’93), Trondheim, Norway, 15–18 June 1993; pp. 350–361. [Google Scholar]
- Crawford, J.; Ginsberg, M.; Luks, E.; Roy, A. Symmetry-breaking predicates for search problems. In Principles of Knowledge Representation and Reasoning: Proceedings of the Fifth International Conference (KR’96); Morgan Kaufmann Publishers: San Francisco, CA, USA, 1996; pp. 148–159. [Google Scholar]
- Puget, J.F. An efficient way of breaking value symmetries. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (AAAI-06), Boston, MA, USA, 16–20 July 2006; pp. 117–122. [Google Scholar]
- Gent, I.P.; Smith, B.M. Symmetry breaking in constraint programming. In Proceedings of ECAI-2000; IOS Press: Amsterdam, The Netherlands, 2000; pp. 599–603. [Google Scholar]
- Fahle, T.; Schamberger, S.; Sellmann, M. Symmetry breaking. In Proceedings of the 7th International Conference on Principles and Practice of Constraint Programming (CP2001), Paphos, Cyprus, 26 November–1 December 2001; Springer: Berlin, Germany, 2001; pp. 93–107. [Google Scholar]
- Roney-Dougal, C.M.; Gent, I.P.; Kelsey, T.; Linton, S. Tractable symmetry breaking using restricted search trees. In Proceedings of the 16th European Conference on Artificial Intelligence (ECAI 2004), Valencia, Spain, 22–27 August 2004; pp. 211–215. [Google Scholar]
- Legowski, A.; Niezabitowski, M. Robot path control based on PSO with fractional-order velocity. In Proceedings of the International Conference on Robotics and Automation Engineering (ICRAE), Jeju Island, Korea, 27–29 August 2016; pp. 21–25. [Google Scholar]
- M’zoughi, F.; Bouallègue, S.; Garrido, A.J.; Garrido, I.; Ayadi, M. Water Cycle Algorithm-based Airflow Control for an Oscillating Water Column-based Wave Generation Power Plant. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 118–133. [Google Scholar]
- M’zoughi, F.; Bouallègue, S.; Ayadi, M.; Garrido, A.J.; Garrido, I. Harmony Search Algorithm-based Airflow Control of an Oscillating Water Column-based Wave Generation Power Plants. In Proceedings of the 2018 International Conference on Advanced Systems and Electric Technologies (IC_ASET), Hammamet, Tunisia, 22–25 March 2018; pp. 249–254. [Google Scholar]
- M’zoughi, F.; Bouallègue, S.; Garrido, A.J.; Garrido, I.; Ayadi, M. Stalling-free Control Strategies for Oscillating-Water-Column-based Wave Power Generation Plants. IEEE Trans. Energy Convers. 2018, 33, 209–222. [Google Scholar] [CrossRef]
- M’zoughi, F.; Garrido, I.; Bouallègue, S.; Ayadi, M.; Garrido, A.J. Intelligent Airflow Controls for a Stalling-Free Operation of an Oscillating Water Column-Based Wave Power Generation Plant. Electronics 2019, 8, 70. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science MHS’95, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Clerc, M.; Kennedy, J. The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space. IEEE Trans. Evolut. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- AlRashidi, M.R.; El-Hawary, M.E. A survey of particle swarm optimization applications in electric power systems. IEEE Trans. Evol. Comput. 2008, 13, 913–918. [Google Scholar] [CrossRef]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Pandey, S.; Wu, L.; Guru, S.M.; Buyya, R. A particle swarm optimization-based heuristic for scheduling workflow applications in cloud computing environments. In Proceedings of the 2010 24th IEEE International Conference on Advanced Information Networking and Applications, Perth, Australia, 20–23 April 2010; pp. 400–407. [Google Scholar]
- M’zoughi, F.; Garrido, I.; Garrido, A.J.; De La Sen, M. ANN-Based Airflow Control for an Oscillating Water Column Using Surface Elevation Measurements. Sensors 2020, 20, 1352. [Google Scholar] [CrossRef]
- Sobey, R.; Goodwin, P.; Thieke, R.; Westberg, R.J., Jr. Application of Stokes, Cnoidal, and Fourier wave theories. Waterw. Port Coast. Ocean Eng. 1987, 113, 565–587. [Google Scholar] [CrossRef]
- Le Roux, J.P. An extension of the Airy theory for linear waves into shallow water. Coast. Eng. 2008, 55, 295–301. [Google Scholar] [CrossRef]
- Garrido, A.J.; Otaola, E.; Garrido, I.; Lekube, J.; Maseda, F.J.; Liria, P.; Mader, J. Mathematical Modeling of Oscillating Water Columns Wave-Structure Interaction in Ocean Energy Plants. Math. Probl. Eng. 2015, 2015, 727982. [Google Scholar] [CrossRef]
- Sarmento, A.J.N.A.; de O. Falcão, A.F. Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 1985, 150, 467–485. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Rodrigues, R.J.A. Stochastic modelling of OWC wave power plant performance. Appl. Ocean Res. 2002, 24, 59–71. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Gato, L.M.C. Air Turbines. In Comprehensive Renewable Energy; Sayigh, A., Ed.; Elsevier: Oxford, UK, 2012; Volume 8, pp. 111–149. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Setoguchi, T.; Takao, M. Current status of self rectifying air turbines for wave energy conversion. Energy Convers. Manag. 2006, 47, 2382–2396. [Google Scholar] [CrossRef]
- O’Sullivan, D.L.; Lewis, A. Generator selection and comparative performance in offshore oscillating water column. IEEE Trans. Energy Convers. 2011, 26, 603–614. [Google Scholar] [CrossRef]
- Alberdi, M.; Amundarain, M.; Garrido, A.J.; Garrido, I.; Casquero, O.; De la Sen, M. Complementary control of oscillating water column-based wave energy conversion plants to improve the instantaneous power output. IEEE Trans. Energy Convers. 2011, 26, 1021–1032. [Google Scholar] [CrossRef]
- Muller, S.; Diecke, M.; De Donker, R.W. Doubly fed induction generator systems for wind turbines. IEEE Ind. Appl. Mag.. 2002, 26–33. [Google Scholar] [CrossRef]
- Ledesma, P.; Usaola, J. Doubly fed induction generator model for transient stability analysis. IEEE Trans. Energy Convers. 2005, 20, 388–397. [Google Scholar] [CrossRef]
- Lima, R.M.; Novais, A.Q. Symmetry breaking in MILP formulations for unit commitment problems. Comput. Chem. Eng. 2016, 85, 162–176. [Google Scholar] [CrossRef]
- Law, Y.C.; Lee, J.H.M. Symmetry breaking constraints for value symmetries in constraint satisfaction. Constraints 2006, 11, 221–267. [Google Scholar] [CrossRef]
- Walsh, T. General symmetry breaking constraints. In Proceedings of the International Conference on Principles and Practice of Constraint Programming, Nantes, France, 25–29 September 2006; pp. 650–664. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Particle Swarm Optimization: Developments, Applications and Resources. In Proceedings of the IEEE Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; pp. 81–86. [Google Scholar]

| Capture Chamber | Wells Turbine | DFIG Generator | |
|---|---|---|---|
| = 4.5 m | n = 5 | = 0.5968 | = 18.45 kW |
| = 4.3 m | b = 0.21 m | = 0.6258 | = 400 V |
| =1.19 kg/m | l = 0.165 m | = 0.0003495 H | = 50 Hz |
| = 1029 kg/m | r = 0.375 m | = 0.324 H | |
| a = 0.4417 m | = 0.324 H | ||
| SBC | Cost Function | CPU Time (s) | |||||
|---|---|---|---|---|---|---|---|
| Worst | Mean | Best | S.D. | Worst | Mean | Best | |
| without | 11.7433 | 8.3576 | 8.0927 | 1.6928 | 7091 | 6745 | 6492 |
| with | 11.2061 | 8.3324 | 8.0243 | 1.4491 | 5876 | 5604 | 5328 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M’zoughi, F.; Garrido, I.; Garrido, A.J. Symmetry-Breaking for Airflow Control Optimization of an Oscillating-Water-Column System. Symmetry 2020, 12, 895. https://doi.org/10.3390/sym12060895
M’zoughi F, Garrido I, Garrido AJ. Symmetry-Breaking for Airflow Control Optimization of an Oscillating-Water-Column System. Symmetry. 2020; 12(6):895. https://doi.org/10.3390/sym12060895
Chicago/Turabian StyleM’zoughi, Fares, Izaskun Garrido, and Aitor J. Garrido. 2020. "Symmetry-Breaking for Airflow Control Optimization of an Oscillating-Water-Column System" Symmetry 12, no. 6: 895. https://doi.org/10.3390/sym12060895
APA StyleM’zoughi, F., Garrido, I., & Garrido, A. J. (2020). Symmetry-Breaking for Airflow Control Optimization of an Oscillating-Water-Column System. Symmetry, 12(6), 895. https://doi.org/10.3390/sym12060895







