Dynamical Approach to Decays of XYZ States

Abstract

We review the existing results on the exotic XYZ states and their decays obtained within the confined covariant quark model. This dynamical approach is based on a non-local Lagrangian of hadrons with quarks, has built-in quark confinement, and is suited well for the description of different multiquark states, including the four quark ones. We focus our analysis on the various decay modes of five exotic states, $X\left(3872\right)$, $Z_c\left(3900\right)$, $Y\left(4260\right)$, $Z_b\left(10610\right)$, and $Z_b^{\prime }\left(10650\right)$, aiming to clarify their internal quark structures. By considering mostly branching fractions and decay widths using the molecular-type or the tetraquark-type interpolating currents, conclusions about the nature of these particles are drawn: the molecular structure is favored for $Z_c\left(3900\right)$, $Z_b\left(10610\right)$, and $Z_b^{\prime }\left(10650\right)$ and the tetraquark for $X\left(3872\right)$ and $Y\left(4260\right)$.

1. Introduction

The concept of multiquark states composed of more then three quarks hypothesized decades ago [1] was for the first time confirmed in 2003 where multiquark state candidates were measured by the BES [2], BaBar [3], and Belle [4] experiments. The latter observation, seen in the ${\pi }^{+}{\pi }^{-}J/\psi$ invariant mass spectrum, was the first observation of a charmonium-like state $X\left(3872\right)$, which did not fit expectations of existing quark models for any conventional hadronic particle. The reason was mainly its measured mass 3872 MeV, not predicted by models, and also the difficulty in interpreting it as an excited charmonium ${\psi }^{\prime }$: its eventual decay into $\rho J/\psi$ is strongly suppressed because of isospin violation. In the following years, other heavy quarkonium-like states X, Y, Z were discovered, where Y usually denotes electrically neutral exotic (i.e., non-$c\overline{c}$) charmonia having quantum numbers $J^{PC}=1^{--}$, Z is used for charged states, and X labels any non-Y and non-Z cases. With the aim to report on the results and achievements of the confined covariant quark model, we narrow our review of experimental outcomes to a relevant subset of the whole exotic meson family.

The first observation of the $X\left(3872\right)$ mentioned in the previous paragraph was later confirmed in the $p\overline{p}$ collisions by the CDF [5] and D0 [6] experiments in 2004, by the LHCb experiment [7] in 2011, and also by the BESIIIcollaboration [8] in 2014. Further experimental investigations [9,10,11,12] increased the mass measurement precision, established the quantum numbers, and put limits on several decay related observables. As of now [13], $X\left(3872\right)$ is a particle with the mass $m_{X\left(3872\right)}=3871.69\pm 0.17$ MeV, width ${\mathsf{\Gamma }}_{X\left(3872\right)}<1.2$ MeV, and quantum numbers $I^G\left(J^{PC}\right)=0^{+}\left(1^{++}\right)$, mostly decaying to ${\overline{D}}^{*0}(\to {\overline{D}}^0{\pi }^0)D^0$.

Charmonium-like state $Y\left(4260\right)$ was for the first time observed by the BaBar experiment [14] in 2005 in the $J/\psi {\pi }^{+}{\pi }^{-}$ mass distribution. Its existence was further confirmed by the CLEO [15] (2006), Belle [16] (2007), and BESII [17] (2013) collaborations. Later investigations by BaBar [18] and BESIII [19] provided further updates on the mass and width parameters. With mass above the $D\overline{D}$ threshold, the $Y\left(4260\right)$ was also searched for in the open charm decay channels, however with negative results [20,21,22,23,24]. The $Y\left(4260\right)$ is [13] an $I^G\left(J^{PC}\right)=0^{-}\left(1^{--}\right)$ state with the mass and width $m_{Y\left(4260\right)}=4230\pm 8$ MeV, ${\mathsf{\Gamma }}_{Y\left(4260\right)}=55\pm 19$ MeV.

The study of the $Y\left(4260\right)$ decay channel $J/\psi {\pi }^{+}{\pi }^{-}$ by BESII [17] and Belle [25] in 2013 led to the discovery of the charged $Z_c\left(3900\right)$ resonance in the invariant mass distribution of $J/\psi {\pi }^{\pm }$. The $Z_c^{\pm }$ particle was in the same year observed also by the CLEO-c detector [26]. In addition, the latter experiment provided the first evidence of the neutral member of the $Z_c$ isotriplet, the $Z_c^0$ state, discovered in the ${\pi }^{0}J/\psi$ channel. A state $Z_c\left(3885\right)$ was seen in the $D{\overline{D}}^{*}$ spectrum of the $e^{+}{e}^{-}\to {\pi }^{\pm }{\left(D{\overline{D}}^{*}\right)}^{\mp }$ reaction at BESIII in 2014 [27]. Assuming it can be identified with the $Z_c\left(3900\right)$ particle, the measurement provided arguments in favor of $J^P=1^{+}$ quantum numbers. The same experiment reaffirmed in 2015 the existence of the neutral $Z_c$ state [28], in 2017 confirmed with high significance the $J^P=1^{+}$ assignment [29], and in 2019 provided the evidence for the ${\rho }^{\pm }{\eta }_c$ decay channel [30]. The D0 collaboration published the observation of the $Z_c\left(3900\right)$ state in $p\overline{p}$ collision data in 2018 [31] and studied its mass and width in [32] (2019). The current $Z_c$ parameters are [13] $m_{Z_c\left(3900\right)}=3887.2\pm 2.3$ MeV, ${\mathsf{\Gamma }}_{Z_c\left(3900\right)}=28.2\pm 2.6$ MeV and $I^G\left(J^{PC}\right)=1^{+}\left(1^{+-}\right)$. $Z_c\left(3900\right)$ as a charmonium-like state with an electric charge is a prominent candidate for an exotic multiquark state and is largely discussed in the existing literature.

Two narrow bottomonium-like four quark state candidates were detected in the Belle detector [33] in 2012. They were labeled $Z_b\left(10610\right)$ and $Z_b^{\prime }\left(10650\right)$ and were observed as peaks in the mass spectra of ${\pi }^{\pm }\mathsf{{\rm Y}}\left(ns\right),(n=1,2,3)$ and ${\pi }^{\pm }{h}_b\left(ms\right),(m=1,2)$. The same experiment published two other papers dedicated to these exotics. In [34], the evidence was given for the quantum number assignment $I^G\left(J^P\right)=1^{+}\left(1^{+}\right)$ for both of the states. In [35], they were observed in different decay channels $Z_b\left(10610\right)\to {[B{\overline{B}}^{*}+cc]}^{\pm }$ and $Z_b^{\prime }\left(10650\right)\to {[B^{*}{\overline{B}}^{*}+cc]}^{\pm }$, where one can notice the proximity of the two states to the corresponding $B^{(*)}{\overline{B}}^{*}$ thresholds. These decays dominated the studied final states, which besides two bottom mesons, included also a pion and for which the Born cross-section was given. The decay into $B\overline{B}$ was found to be suppressed with respect to the two previous final states, and an upper limit was given. The masses and widths are $m_{Z_b^{\pm }\left(10610\right)}$ = 10,607.2 ± 2.0 MeV, $m_{Z_b^{\prime }\left(10650\right)}$ = 10,652.2 ± 1.5 MeV, ${\mathsf{\Gamma }}_{Z_b^{\pm }\left(10610\right)}=18.4\pm 2.4\mathrm{MeV}$, and ${\mathsf{\Gamma }}_{Z_b^{\prime }\left(10650\right)}=11.5\pm 2.2\mathrm{MeV}$.

Growing evidence suggests that the mentioned and also other, unmentioned exotic heavy quarkonium-like states observed since 2003 cannot be described as simple hadrons in the usual quark model. The effort to understand their nature combined with the non-applicability of the perturbative approach in the low energy domain of quantum chromodynamics (QCD) resulted in a large number of more or less model dependent strategies. In existing reviews [36,37,38,39,40,41,42,43,44,45,46,47,48,49], different ideas are analyzed. The proximity of the $X,Y,Z$ masses to meson pair thresholds naturally leads to a popular concept of the hadronic molecule, more closely reviewed in different contexts. In [50], the authors studied the implications of the heavy quark flavor symmetry on molecular states. The authors of [51] argued in favor of a molecular picture using an isospin-exchange model, and a nice review of the molecular approach was given in [52]. A frequent treatment of four quark states is represented also by QCD sum rules [53,54,55] and different quark models. A dynamical approach based on a relativistic quark model with a diquark-antidiquark assumption was proposed in [56,57], where tetraquark masses were computed. A non-relativistic screened potential model, presented in [58], was used to compute the masses, electromagnetic decays, and E1 transitions of charmonium states. Treatment of tetraquarks as compact dynamical diquark-antidiquark systems in [59] had the ambition to explain why some of the exotic states preferred to decay into excited charmonia. Several hypotheses (molecular description, tetraquark description, hadro-charmonium picture) for different exotic states were investigated in [60] using tools based on the heavy quark spin symmetry: besides drawing conclusions for some XYZparticles, also possible discovery channels were given. The hybrid and tetraquark interpretation for several exotic states were discussed in paper [61] using the Born–Oppenheimer approximation. A very complete review of exotic states with some emphasis on the chromomagnetic interaction was provided in a recent publication [62]. The ideas of coupled channels ([63]) and heavy quark limit ([64]) are also often seen in the context of the exotic quarkonia. Finally, one has to mention the possibility of peaks in invariant mass distributions being explained by the kinematic effect. This was investigated in detail in a recent text [65]. The arguments for X, Y, and Z states not being purely kinematic effects were given in [66].

In the present paper, we want to review the description of the exotic heavy quarkonia-like states by the confined covariant quark model (CCQM). The model [67,68,69] was proposed and developed as a practical and reliable tool for the theoretical description of exclusive reactions involving the mesons, baryons, and other multiquark states. It was based on a non-local interaction Lagrangian, which introduces a coupling between a hadron and its constituent quarks. The Lagrangian guarantees a full frame independence and the computations relay on standard quantum field theory techniques where matrix elements are given by the set of quark-loop Feynman diagrams according to the $1/N_c$ expansion. Earlier, a confinement was not implemented in the model, and thus, it was not suited for heavy particles (with baryon mass exceeding those of the constituent quarks summed). This was changed in [69], where a smart cutoff was introduced for integration over the space of Schwinger parameters. Since then, arbitrary heavy hadrons could be treated by the CCQM. The CCQM represents a framework where the hadron and the quarks coexist, which raises questions about the proper description of bound states and the double counting. They are solved using a so-called compositeness condition. It guarantees, by setting the hadron renormalization constant $Z_H$ to zero, that the dressed state and the bare one have a vanishing overlap. In order to describe radiative decays, one also needs to introduce gauge fields properly in a non-local theory such as CCQM. This was done by the formalism developed in [70] where the path integral of gauge field appeared in the quark-field transformation exponential. One should also mention that the model had no gluons: their dynamics was effectively taken into account by the quark-hadron vertex functions, which depended on one hadron size related parameter. The model has a limited number of free parameters; besides the hadron related ones, it has six “global” parameters: five constituent quark masses and one universal cutoff. The model was applied to with success light and heavy mesons and baryons (e.g., [71,72,73,74,75,76]) and also to exotic four quark states [77,78,79,80,81,82,83]. The latter will be reviewed in the rest of this article.

All sketched features of the CCQM (interaction Lagrangian, confinement, compositeness condition, implementation of electromagnetic interaction) are addressed in more detail in Section 2. Section 3 is dedicated to the $X\left(3872\right)$ state and its decays to $J/\psi +\rho$ and $\overline{D}+D^{*}$. Its radiative decays are analyzed in Section 4. In Section 5, molecular and tetraquark hypotheses for the nature of $Z_c\left(3900\right)$ are put in place and the results compared with experimental data. The exotic to exotic reaction $Y\left(4260\right)\to Z_c{\left(3900\right)}^{\pm }+{\pi }^{\mp }$ and the decay of $Y\left(4260\right)$ to open charm are presented in Section 6. Decays of the bottomonium-like states $Z_b\left(10610\right)$ and $Z_b^{\prime }\left(10650\right)$ to several different final states are studied within the molecular picture in Section 7. We close the text by a summary and conclusion given in Section 8.

2. Confined Covariant Quark Model

2.1. Interaction Lagrangian

The dynamical description of hadrons in the CCQM follows from the interaction Lagrangian:

$${\mathcal{L}}_{\mathrm{int}}=g_H·H\left(x\right)·J_H\left(x\right),$$

(1)

where the hadronic field is coupled to a non-local quark current. The latter takes different forms for different hadrons:

$$J_M\left(x\right)=\int d{x}_1\int d{x}_2{F}_M(x;x_1,x_2)·{\overline{q}}_1^a\left(x_1\right){\mathsf{\Gamma }}_M{q}_2^a\left(x_2\right)$$

for the mesons,

$$J_B\left(x\right)=\int d{x}_1\int d{x}_2\int d{x}_3{F}_B(x;x_1,x_2,x_3)·{\mathsf{\Gamma }}_1{q}_1^{a_1}\left(x_1\right)\left(q_2^{a_2}\left(x_2\right)C{\mathsf{\Gamma }}_2{q}_3^{a_3}\left(x_3\right)\right)·{\epsilon }^{a_1{a}_2{a}_3}$$

for the baryons, and

$$J_T^{\mu }\left(x\right)=\int d{x}_1\dots \int d{x}_4{F}_T(x;x_1,\dots ,x_4)·\left(q_1^{a_1}\left(x_1\right)C{\mathsf{\Gamma }}_1{q}_2^{a_2}\left(x_2\right)\right)·\left({\overline{q}}_3^{a_3}\left(x_3\right){\mathsf{\Gamma }}_{2}C{\overline{q}}_4^{a_4}\left(x_4\right)\right)·{\epsilon }^{a_1{a}_{2}c}{\epsilon }^{a_3{a}_{4}c}$$

for the tetraquarks. Here, C stands for the charge conjugation matrix $C={\gamma }^0{\gamma }^2$ with $C=C^{†}=C^{-1}=-C^T$ and $\mathsf{\Gamma }$ is an appropriate Dirac matrix (or string of Dirac matrices) to describe the spin quantum numbers of the hadron. One has $C{\mathsf{\Gamma }}^T{C}^{-1}=\mathsf{\Gamma }$ for the (pseudo)scalar and axial-vector fields and $C{\mathsf{\Gamma }}^T{C}^{-1}=-\mathsf{\Gamma }$ for vectors and tensors. The color indices are denoted by superscripts $a_i$, and $F_H(x;x_1,\cdots ,x_n)$ represents a non-local vertex function, which characterizes the quark distribution inside the hadron. We assume it takes the form:

$$F_H(x;x_1,\cdots ,x_n)={\delta }^{\left(4\right)}\left(x-\sum _{i=1}^n{w}_i{x}_i\right){\mathsf{\Phi }}_H\left(\sum _{i<j}{(x_i-x_j)}^2\right),\mathrm{where}{w}_i=\frac{m_i}{{\sum }_{i=1}^n{m}_i}.$$

(2)

The first factor reflects the natural expectation that the barycenter of the quark system corresponds to the position of the hadron, and the second term has a general form dependent on the relative quark coordinates. Obviously, the vertex function is invariant under translations:

$$F_H(x+a;x_1+a,\cdots ,x_n+a)=F_H(x;x_1,\cdots ,x_n)$$

for any four-vector a. In principle, any form of the function ${\mathsf{\Phi }}_H$ is allowed as long as it has an appropriate fall-off behavior in the Euclidean momentum space to guarantee the ultraviolet convergence of the Feynman diagrams. Various alternatives of the vertex function for non-local quark currents were analyzed in [84], and it was found that the dependence of the observables on different choices was small. Because of convenience of performing calculations, the exponential form for the Fourier transform of the function ${\mathsf{\Phi }}_H$ was adopted:

$${\tilde{\mathsf{\Phi }}}_H(-K^2)=exp\left(\frac{K^2}{{\mathsf{\Lambda }}_H^2}\right)$$

(3)

where $K^2$ is the combination of the loop and external momenta. The minus sign indicates that we are working in the Minkowski space, and the wicked-rotated argument $K^2\to -K_E^2$ makes explicit the appropriate fall-off behavior in the Euclidean region. ${\mathsf{\Lambda }}_H$ is an adjustable parameter of the CCQM, which can be related to the hadron size. Additional free parameters are the constituent quark masses and a universal infrared cutoff (discussed in more detail later). Their values, summarized in Table 1, were determined by adjusting the model predictions to experimental data.

Table 1. Constituent quark masses and universal cutoff $\lambda$ in GeV.

${\mathit{m}}_{\mathit{u},\mathit{d}}$	${\mathit{m}}_{\mathit{s}}$	${\mathit{m}}_{\mathit{c}}$	${\mathit{m}}_{\mathit{b}}$	$\mathit{\lambda }$
$0.241$	$0.428$	$1.67$	$5.04$	$0.181$

2.2. Compositeness Condition

In the Lagrangian of the CCQM, quarks and hadrons are treated equally. However in nature, hadrons are made of quarks. Therefore, questions about an appropriate description of the bound states and double counting arise. The issue is resolved by imposing the so-called compositeness condition [85,86], which requires the renormalization constant of the hadron field to vanish. Since the renormalization constant $Z_H^{1/2}$ can be interpreted as the matrix element between the physical state and the corresponding bare state, $Z_H^{1/2}=0$ implies that the physical state has no overlap with the bare state and is therefore described as a bound state. For a spin-one particle, the compositeness condition reads:

$$\begin{array}{c}\hfill Z_H=1-g_H^2{\Pi }_H^{\prime }\left(m_H^2\right)=0,\end{array}$$

(4)

where ${\Pi }_H^{\prime }$ is the derivative of the scalar part of the vector-meson mass operator:

$$\begin{array}{ccc}\hfill {\Pi }_H^{\mu \nu }\left(p\right)& =& g^{\mu \nu }{\Pi }_H\left(p^2\right)+p^{\mu }{p}^{\nu }{\Pi }_H^{\left(1\right)}\left(p^2\right),\hfill \\ {\Pi }_H\left(p^2\right)& =& \frac{1}{3}\left(g_{\mu \nu }-\frac{p_{\mu }{p}_{\nu }}{p^2}\right){\Pi }_H^{\mu \nu }\left(p\right).\end{array}$$

The condition $Z_H^{1/2}=0$ also effectively removes the constituent degrees of freedom from the space of physical states and so eliminates the double counting. A general tetraquark self-energy diagram to be used for the compositeness condition is show in Figure 1.

Figure 1. General confined covariant quark model (CCQM) tetraquark self-energy diagram.

One should also notice that the application of the compositeness condition lowers the number of model parameters because its fulfillment is reached by tuning the coupling constant value. Equation (4) thus fixes the coupling and increases the predictive power of the CCQM over the wide range of hadronic data. The determination of $g_H$ for all participating hadrons by means of the compositeness condition is the first step in the application of the CCQM. It should be remarked that the compositeness condition can be interpreted also in terms of the normalization of the electric form factor at $q^2=0$, as shown in [69].

2.3. Infrared Confinement

If the mass of a hadron reaches the limit defined by the sum of the masses of constituent quarks, then in a model without a confinement, the hadron becomes unstable and decays into its constituents. In order to correct this unphysical behavior and enlarge the applicability of the model also to the (increasing) experimental data on heavy hadrons, the confinement of quarks was introduced in [69]. Its implementation assumes the Schwinger representation of quark propagators:

$$S\left(k\right)=\frac{(m+\cancel{k})}{m^2-k^2}=(m+\cancel{k})\underset{0}{\overset{\infty }{\int }}d\beta exp\{-\beta (m^2-k^2)\}$$

(5)

with the subsequent cutoff in the upper integration limit applied, in a clever way, to the whole structure of a Feynman diagram. The latter, containing l loops, m vertices, and n propagators, can be schematically written as:

$$\begin{array}{cc}\hfill \Pi (p_1,\cdots ,p_m)& =\int {\left(d^{4}k\right)}^l\prod _{i=1}^m{\mathsf{\Phi }}_{i+n}\left\{-\sum _j{({\kappa }_{i+n}^{\left(j\right)}+v_{i+n}^{\left(j\right)})}^2\right\}·\prod _{k=1}^n{S}_k({\kappa }_k+v_k)\hfill \\ & =\underset{0}{\overset{\infty }{\int }}{d}^n\beta F({\beta }_1,\cdots ,{\beta }_n),\hfill \end{array}$$

(6)

where $\mathsf{\Phi }$ symbolizes vertex functions, p denotes external momenta, v linear combinations of external momenta, k represents loop momenta, and $\kappa$ linear combinations of the latter. The expression in curly brackets is the argument of the vertex function in the momentum representation. The second line makes explicit the integration over the space of the Schwinger parameters with the whole structure of the first line catch in the F symbol. The next step is to go from the integration over the Schwinger parameters to the integration over the $n-1$ simplex of the dimensionless Feynman parameters combined with a one-dimensional integral over a dimension variable t by using the simple insertion of unity in the above expression:

$$1=\underset{0}{\overset{\infty }{\int }}dt\delta \left(t-\sum _{i=1}^n{\beta }_i\right).$$

One has:

$$\Pi =\underset{0}{\overset{\infty }{\int }}dt{t}^{n-1}\int d^n\alpha \delta \left(1-\sum _{i=1}^n{\alpha }_i\right)F(t{\alpha }_1,\cdots ,t{\alpha }_n).$$

(7)

Note that a dimension variable t is analogous of the Fock–Schwinger proper time. By performing an analytical continuation of the kinematical variables to the Minkowski space, one can encounter the branch points, which, in particular, correspond to the quark unitary thresholds. The appearance of the imaginary parts in Equation (7) is witnessed on the quark production in the physical spectrum, i.e., on the absence of the quark confinement. One possibility to resolve this problem is to cut the upper limit of the integration over the proper time t, i.e., $\infty \to 1/{\lambda }^2$ with $\lambda$ being the “infrared” cutoff parameter. This allows one to remove all singularities of the diagram related to the local quark propagators. The integral becomes smooth and always convergent. For clarity, one can demonstrate the approach on a scalar one-loop two-point function. One starts with the loop integral in the Euclidean space:

$$\Pi \left(p^2\right)=\int \frac{d^4{k}_E}{{\pi }^2}\frac{exp(-s{k}_E^2)}{[m^2+{(k_E+p_E/2)}^2][m^2+{(k_E-p_E/2)}^2]}.$$

(8)

By using the above transformations, one gets:

$$\Pi \left(p^2\right)=\underset{0}{\overset{\infty \to \frac{1}{{\lambda }^2}}{\int }}dt\frac{t}{{(s+t)}^2}{\int }_0^{1}d\alpha e^{-t[m^2-\alpha (1-\alpha )p^2]+\frac{st}{s+t}{(\alpha -1/2)}^2{p}^2},$$

(9)

where $p^2=-p_E^2$. The expression has a branch point at $p^2=4m^2$ as follows from the vanishing of the first term inside the exponential at $\alpha =1/2$. However, this singularity is removed by the cutoff.

We take the value of the cutoff parameter $\lambda$ presented in Table 1 as universal for all processes we describe.

2.4. Electromagnetic Interactions

Inclusion of the electromagnetic (EM) interaction into the non-local CCQM in a gauge invariant way requires a dedicated approach. Our main interest will be in the radiative decays of neutral particles (i.e., the X(3872) tetraquark; see [79]), and so, we will focus on the EM interactions of quarks. The free part of the quark Lagrangian is gauged using the standard minimal coupling prescription:

$${\partial }^{\mu }q\to ({\partial }^{\mu }-i{e}_q{A}^{\mu })q,{\partial }^{\mu }\overline{q}\to ({\partial }^{\mu }+i{e}_q{A}^{\mu })\overline{q},$$

(10)

with $e_u=2/3,e_d=-1/3$ in units of the proton charge. This defines the first part of the interaction Lagrangian of quarks with photons:

$${\mathcal{L}}_{int}^{EM\left(1\right)}=\sum _q{e}_q{A}_{\mu }\left(x\right)J_q^{\mu }\left(x\right),\mathrm{with}{J}_q^{\mu }\left(x\right)=\overline{q}\left(x\right){\gamma }^{\mu }q\left(x\right).$$

(11)

A second term comes from gauging the non-local quark-hadron interaction Lagrangian (1). First, one multiplies each quark field by an exponential expression, which depends on the gauge field:

$$q\left(x_i\right)\to exp\{-i{e}_{q}I(x_i,x,P)\}q\left(x_i\right),\overline{q}\left(x_i\right)\to exp\{i{e}_{q}I(x_i,x,P)\}\overline{q}\left(x_i\right),$$

(12)

with I being defined as the integral:

$$I(x_i,x,P)={\int }_x^{x_i}{A}^{\mu }\left(z\right)d{z}_{\mu }$$

over the path that connects the hadron and quark positions. It can be readily seen that the local gauge transformations:

$$\begin{array}{c}q\left(x_i\right)\to exp\{i{e}_{q}f\left(x_i\right)\}q\left(x_i\right),\overline{q}\left(x_i\right)\to exp\{-i{e}_{q}f\left(x_i\right)\}\overline{q}\left(x_i\right),\hfill \\ A^{\mu }\left(z\right)\to A^{\mu }\left(z\right)+{\partial }^{\mu }f\left(z\right),\hfill \end{array}$$

(13)

leave the Lagrangian unchanged for any arbitrary function f. Indeed, the gauge field induced modification of the path integral $I(x_i,x,P)\to I(x_i,x,P)+f\left(x_i\right)-f\left(x\right)$ is canceled by the contribution coming from the quark transformations. The exact form of the gauged non-local Lagrangian ${\mathcal{L}}^{EM\left(2\right)}$ depends on the quark current structure (i.e., hadron quantum numbers), and we will write down an explicit form of it in the dedicated section. To use the gauged Lagrangian in perturbative calculations, one expands the gauge exponentials into the powers of the coupling constant (and thus, powers of $A^{\mu }$) up to a desired order. The expansion contains only the derivatives of the path integral I, and using the approach proposed in [70,87], one can define them in a path independent manner:

$$\underset{d{x}^{\mu }\to 0}{lim}d{x}^{\mu }\frac{\partial }{\partial x^{\mu }}I(x,y,P)=\underset{d{x}^{\mu }\to 0}{lim}\left[I(x+dx,y,P^{\prime })-I(x,y,P)\right].$$

(14)

Here, $P^{\prime }$ denotes a path derived from P by extending P from its endpoint by $dx$. This definition gives:

$$\frac{\partial }{\partial x^{\mu }}I(x,y,P)=A_{\mu }\left(x\right),$$

(15)

where the independence of the derivative on the path P becomes explicit.

2.5. Selected Computational Aspects

To proceed with the calculations, it is convenient to use the following representation for the correlation function:

$${\mathsf{\Phi }}_X\left(\sum _{1\le i<j\le 4}{(x_i-x_j)}^2\right)=\left[\prod _{n=1}^3\int \frac{d{q}_n}{{\left(2\pi \right)}^4}\right]e^{-i{\displaystyle \sum _{i=1}^3}{q}_i(x_i-x_4)}{\tilde{\mathsf{\Phi }}}_X\left(-\frac{1}{2}\sum _{1\le i<j\le 3}{q}_i{q}_j\right).$$

(16)

It may be easily obtained by using the Jacobi coordinates. The Gaussian function form of the correlation function ${\tilde{\mathsf{\Phi }}}_X$ in Equation (3) can be joined with the exponents coming from the Schwinger representation of quark propagators given by Equation (5) into a single exponential function. Its argument takes a Gaussian form in loop momenta:

$$exp(kak+2kr+R),$$

(17)

where a is a $3\times 3$ matrix, $r=(r_1,r_2,r_3)$ is a vector constructed from external momenta, and the constant R behaves as a quadratic form of external momenta. As a result, one observes that, with respect to loop momenta, the general expression (6) is a product of a polynomial P (originating from evaluation of traces) with an exponential function. The tensorial loop momenta integration is then performed using the differential identity:

$$P\left(k_i^{\mu }\right)e^{2kr}=P\left(\frac{1}{2}\frac{\partial }{\partial r_{i\mu }}\right)e^{2kr},$$

(18)

which allows us the move the k independent differential operator in front of the integral. The action of the latter operator on the result of the integration is further simplified by applying a second operator identity:

$$P\left(\frac{1}{2}\frac{\partial }{\partial r_i}\right)e^{-r{a}^{-1}r}=e^{-r{a}^{-1}r}P\left(\frac{1}{2}\frac{\partial }{\partial r_i}-{[a^{-1}r]}_i\right),$$

(19)

which permits commuting the differential operator with the exponential. The next steps are automated using a FORM program [88]. It repeatedly performs the differentiation using the chain rule, thus effectively commuting the differential operator to the right (and eventually making it vanish by acting on a constant).

At last, one is left with an integral over the space of the Schwinger parameters (see Section 2.3). The latter is computed numerically with the help of a FORTRAN code. Most of the time, one is interested in the $q^2$ dependent hadronic form factors: for the purposes of this text, the CCQM should be seen as a smart and effective tool that provides these form factors from the assumed quark currents as inputs.

3. Strong Decays of $\mathbf{X}\left(\mathbf{3872}\right)$

3.1. Decays $X\to D^{*0}(\to D^0{\pi }^0){\overline{D}}^0$, $X\to {\rho }^0(\to {\pi }^{+}{\pi }^{-})\overline{J}/\psi$, and $X\to \omega (\to {\pi }^{+}{\pi }^{-}{\pi }^0)\overline{J}/\psi$

The controversy raised by the discovery of the $X\left(3872\right)$ state can be best seen in the large number of publications it provoked (with many different interpretations). The proximity of the $D^{*0}{D}^0$ threshold:

$$M_{X\left(3872\right)}-(M_{D^{*0}}+M_{D^0})=-0.30\pm 0.40\mathrm{MeV}$$

(20)

naturally suggests the idea of a loosely bound charm meson molecule. This idea was studied in several texts: implications of the molecular hypothesis for interference and binding effects were discussed in [89]; the authors of [90] found support for the molecular interpretation within a non-relativistic quark model; a published text [91] analyzed the molecular assumption in an effective field theory approach; and further works [92,93,94] based their analyses on an effective field theory with pion exchange, Monte Carlo simulations, and heavy quark spin symmetry. A rather strong support for the molecular picture was given in [95] (line shapes study) and [96] (potential model). The lattice study [97] found an explanation for $X\left(3872\right)$ in both the molecular and tetraquark scenario. An important group of analyses focused on charmonium [98,99,100] or mixed charmonium [101,102,103,104] explanations. Further arguments in favor of a charmonium structure followed from the Flatté analysis performed in [105], and both molecular and charmonium hypotheses were discussed in [106]. Several works [107,108,109,110] disfavored the molecular description. The authors of [107] based their conclusion on a non-relativistic quark model with the pion exchange, and the analysis presented in [108] favored the charmonium picture instead, while the conclusions in [109] were based on the pion and sigma exchange model. More rare were approaches based on the glueball picture [111] and chromomagnetic interaction [112]. The authors of [113] put in question the existence of a bound state at all. A hybrid hypothesis was considered in [114] and [115] (here, together with the molecular and charmonium one). Lattice computations in relation to $X\left(3872\right)$ were used in [116,117], QCD sum rules in [118,119], and the coupled channel approach in [120,121,122]. One should also mention the studies based on quark models [56,123,124] and other strategies [125,126,127].

The description of the $X\left(3872\right)$ state by the CCQM was presented in [78]. There, one assumed a tetraquark structure, and within this assumption, decays $X\to J/\psi +2\pi \left(3\pi \right)$ and $X\to {\overline{D}}^0+D^0+{\pi }^0$, proceeding through the off-shell $\rho$/$\omega$ and $D^{*}$ states respectively, were computed. In addition, possible implications of the $X\left(3872\right)$ dominance in the s-channel dissociation of $J/\psi$ were discussed.

When describing the $X\left(3872\right)$ state, one follows the suggestions of [123,128], where a symmetric spin distribution of this $J^{PC}=1^{++}$ state was proposed:

$${[cq]}_{S=0}{[\overline{c}\overline{q}]}_{S=1}+{[cq]}_{S=1}{[\overline{c}\overline{q}]}_{S=0}(q=u,d).$$

(21)

A non-local generalization of this diquark-antidiquark current is written as:

$$\begin{array}{ccc}{J}_{X_q}^{\mu }\left(x\right)& =& \int d{x}_1\dots \int d{x}_4\delta \left(x-\sum _{i=1}^4{w}_i{x}_i\right){\mathsf{\Phi }}_X\left(\sum _{i<j}{(x_i-x_j)}^2\right)J_{4q}^{\mu }(x_1\dots ,x_4),\\ J_{4q}^{\mu }& =& \frac{1}{\sqrt{2}}{\epsilon }_{abc}{\epsilon }_{dec}\left\{[q_a\left(x_4\right)C{\gamma }^5{c}_b\left(x_1\right)][{\overline{q}}_d\left(x_3\right){\gamma }^{\mu }C{\overline{c}}_e\left(x_2\right)]+({\gamma }^5\leftrightarrow {\gamma }^{\mu })\right\},\end{array}$$

(22)

with simplified weights resulting from only two quark flavors being present:

$$w_1=w_2=w_c=\frac{m_c}{2(m_q+m_c)},w_3=w_4=w_q=\frac{m_q}{2(m_q+m_c)}.$$

(23)

The strong isospin violation observed by comparing the $\rho$ and $\omega$ vector meson mediated decays:

$$\frac{\mathcal{B}(X\to J/\psi {\pi }^{+}{\pi }^{-}{\pi }^0)}{\mathcal{B}(X\to J/\psi {\pi }^{+}{\pi }^{-})}=1.0\pm 0.4\left(\mathrm{stat}\right)\pm 0.3\left(\mathrm{syst}\right)$$

(24)

experimentally established by Belle [129] suggested a mixed nature of the physical states $X_l$, $X_h$:

$$\begin{array}{ccc}{X}_l\equiv X_{\mathrm{low}}& =& X_{u}cos\theta +X_{d}sin\theta ,\\ X_h\equiv X_{\mathrm{high}}& =& -X_{u}sin\theta +X_{d}cos\theta ,\end{array}$$

where $\theta$ is the mixing angle. The state $X_u$ breaks the isospin symmetry maximally:

$$X_u=\frac{1}{\sqrt{2}}\{\underset{I=0}{\underbrace{\frac{X_u+X_d}{\sqrt{2}}}}+\underset{I=1}{\underbrace{\frac{X_u-X_d}{\sqrt{2}}}}\}.$$

The mixing angle is to be adjusted to fit the branching fraction ratio (24).

The first step in our calculation is to determine the coupling constant $g_X$ by using the so-called compositeness condition discussed before. The derivative of the tetraquark mass operator needed for this can be written as:

$$\begin{array}{cc}\hfill {\Pi }_X^{\prime }\left(p^2\right)& =\frac{1}{2p^2}{p}^{\alpha }\frac{\partial }{\partial p^{\alpha }}{\Pi }_X\left(p^2\right)\hfill \\ & =\frac{2g_X^2}{3p^2}\left(g_{\mu \nu }-\frac{p_{\mu }{p}_{\nu }}{p^2}\right)\prod _{i=1}^3\int \frac{d^4{k}_i}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_X^2\left(-K^2\right)\hfill \\ & \times \{-w_c\mathrm{tr}\left[S_c^{[12]}\cancel{p}{S}_c^{[12]}{\gamma }^5{S}_q^{[2]}{\gamma }^5\right]\mathrm{tr}\left[S_c^{[3]}{\gamma }^{\mu }{S}_q^{[13]}{\gamma }^{\nu }\right]+w_q\mathrm{tr}\left[S_c^{[12]}{\gamma }^5{S}_q^{[2]}\cancel{p}{S}_q^{[2]}{\gamma }^5\right]\mathrm{tr}\left[S_c^{[3]}{\gamma }^{\mu }{S}_q^{[13]}{\gamma }^{\nu }\right]\hfill \\ & \hspace{1em} -w_c\mathrm{tr}\left[S_c^{[12]}{\gamma }^5{S}_q^{[2]}{\gamma }^5\right]\mathrm{tr}\left[S_c^{[3]}\cancel{p}{S}_c^{[3]}{\gamma }^{\mu }{S}_q^{[13]}{\gamma }^{\nu }\right]+w_q\mathrm{tr}\left[S_c^{[12]}{\gamma }^5{S}_q^{[2]}{\gamma }^5\right]\mathrm{tr}\left[S_c^{[3]}{\gamma }^{\mu }{S}_q^{[13]}\cancel{p}{S}_q^{[13]}{\gamma }^{\nu }\right]\},\hfill \end{array}$$

(25)

where the short notations for the quark propagators and loop momenta are:

$$\begin{array}{ccc}\hfill S_c^{[12]}& =& S_c(k_1+k_2-w_{c}p),S_c^{[3]}=S_c(k_3-w_{c}p),\hfill \\ \hfill S_q^{[2]}& =& S_q(k_2+w_{q}p),S_q^{[13]}=S_q(k_1+k_3+w_{q}p),\\ \hfill K^2& =& \frac{1}{2}\sum _{i\le j}{k}_i{k}_j.\hfill \end{array}$$

The evaluation of this expression is related to the determination of the size parameter ${\mathsf{\Lambda }}_X$ value and allows us to study the ${\mathsf{\Lambda }}_X$ dependence of the results.

Because the $X\left(3872\right)$ mass lies close to the studied thresholds:

$$\begin{array}{c}\hfill m_X-(m_{J/\psi }+m_{\rho })=-0.90\pm 0.41\mathrm{MeV},\\ \hfill m_X-(m_{D^0}+m_{D^{*0}})=-0.30\pm 0.34\mathrm{MeV},\end{array}$$

the off-mass-shell character of the $\rho$, $\omega$, and $D^{*}$ vector mesons has to be taken into account when evaluating the transition amplitudes $X\to J/\psi +\rho \left(\omega \right)$ and $X\to D^{*0}{\overline{D}}^0$. The Feynman diagrams to be considered within the CCQM are depicted in Figure 2.

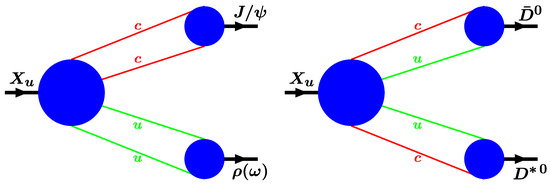
Figure 2. Feynman diagrams describing the decays $X\to J/\psi +\rho \left(\omega \right)$ and $X\to D+{\overline{D}}^{*}$.

In what follows, we use the notation for the light vector mesons $v^0=\rho ,\omega$. The amplitude of the decay $X_u\to \overline{D}+D^{*}$ is written as:

$$\begin{array}{cc}& M^{\mu \nu }\left(X_u(p,\mu )\to \overline{D}\left(q_1\right)+D^{*}(q_2,\nu )\right)=3\sqrt{2}{g}_X{g}_D{g}_{D^{*}}\int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_X\left(-K_2^2\right)\hfill \\ \times & {\tilde{\mathsf{\Phi }}}_D\left(-{(k_1+w_c{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{D^{*}}\left(-{(k_2+w_c{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[{\gamma }^5{S}_c\left(k_1\right){\gamma }^5{S}_u(k_1+q_1){\gamma }^{\mu }{S}_c\left(k_2\right){\gamma }^{\nu }{S}_u(k_2+q_2)\right]+(m_u\leftrightarrow m_c,w_u\leftrightarrow w_c)\hfill \\ =& g^{\mu \nu }{M}_{XD{D}^{*}}^{\left(1\right)}+q_1^{\mu }{q}_1^{\nu }{M}_{XD{D}^{*}}^{\left(2\right)}+q_1^{\mu }{q}_2^{\nu }{M}_{XD{D}^{*}}^{\left(3\right)}+q_2^{\mu }{q}_1^{\nu }{M}_{XD{D}^{*}}^{\left(4\right)}+q_2^{\mu }{q}_2^{\nu }{M}_{XD{D}^{*}}^{\left(5\right)}\hfill \end{array}$$

(26)

where the argument of the X-vertex function is equal to:

$$K_2^2=\frac{1}{8}{(k_1-k_2)}^2+\frac{1}{8}{(k_1-k_2+q_1-q_2)}^2+\frac{1}{4}{(k_1+k_2+w_{c}p)}^2.$$

The amplitude of the decay $X_u\to J/\psi +v^0$ is written as:

$$\begin{array}{cc}& M^{\mu \nu \rho }\left(X_u(p,\mu )\to J/\psi (q_1,\nu )+v^0(q_2,\rho )\right)=6g_X{g}_{J/\psi }{g}_{v^0}\int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_X\left(-K_1^2\right)\hfill \\ \times & {\tilde{\mathsf{\Phi }}}_{J/\psi }\left(-{(k_1+\frac{1}{2}{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{v^0}\left(-{(k_2+\frac{1}{2}{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[i{\gamma }^5{S}_c\left(k_1\right){\gamma }^{\nu }{S}_c(k_1+q_1){\gamma }^{\mu }{S}_u\left(k_2\right){\gamma }^{\rho }{S}_u(k_2+q_2)\right]\hfill \\ =& {\epsilon }^{q_1{q}_2\mu \nu }{q}_1^{\rho }{M}_{XJv}^{\left(1\right)}+{\epsilon }^{q_1{q}_2\mu \nu }{q}_2^{\rho }{M}_{XJv}^{\left(2\right)}+{\epsilon }^{q_1{q}_2\mu \rho }{q}_2^{\nu }{M}_{XJv}^{\left(3\right)}+{\epsilon }^{q_1{q}_2\nu \rho }{q}_1^{\mu }{M}_{XJv}^{\left(4\right)}\hfill \\ +& {\epsilon }^{q_1\mu \nu \rho }{M}_{XJv}^{\left(5\right)}+{\epsilon }^{q_2\mu \nu \rho }{M}_{XJv}^{\left(6\right)}+{\epsilon }^{q_1{q}_2\mu \rho }{q}_1^{\nu }{M}_{XJv}^{\left(7\right)}+{\epsilon }^{q_1{q}_2\nu \rho }{q}_2^{\mu }{M}_{XJv}^{\left(8\right)}\hfill \end{array}$$

(27)

where the argument of the X-vertex function is equal to:

$$K_1^2=\frac{1}{2}{(k_1+\frac{1}{2}{q}_1)}^2+\frac{1}{2}{(k_2+\frac{1}{2}{q}_2)}^2+\frac{1}{4}{(w_u{q}_1-w_c{q}_2)}^2.$$

In the latter expression, the number of Lorentz structures is reduced to six when X and $J/\psi$ are on the mass-shell because, in that case, one has ${ϵ}_{\mu }(q_1^{\mu }+q_2^{\mu })=0$ and ${ϵ}_{\nu }{q}_1^{\nu }=0$.

Obvious relations:

$$M(X_d\to J/\psi +\rho )=-M(X_u\to J/\psi +\rho ),M(X_d\to J/\psi +\omega )=M(X_u\to J/\psi +\omega )$$

allow expressing all amplitudes of physical states transitions in terms of the $X_u$ ones:

$$\begin{array}{ccc}\hfill M(X_{\ell /h}\to J/\psi +\omega )& =& (cos\theta \pm sin\theta )M(X_u\to J/\psi +\omega ),\hfill \\ M(X_{\ell /h}\to J/\psi +\rho )& =& (\pm cos\theta -sin\theta )M(X_u\to J/\psi +\rho ).\end{array}$$

The differential decay rate in the narrow-width approximation is written as [130]:

$$\begin{array}{ccc}\hfill \frac{d\mathsf{\Gamma }(X\to J/\psi +n\pi )}{d{q}^2}& =& \frac{1}{8m_X^2\pi }·\frac{1}{3}{|M_{XJv}|}^2\frac{{\mathsf{\Gamma }}_{v^0}{m}_{v^0}}{\pi }\frac{p^{*}\left(q^2\right)}{{(m_{v^0}^2-q^2)}^2+{\mathsf{\Gamma }}_{v^0}^2{m}_{v^0}^2}\mathcal{B}(v^0\to n\pi ),\hfill \\ \hfill \frac{1}{3}{|M_{XJv}|}^2& =& \frac{1}{3}\sum _{\mathrm{pol}}{|{\epsilon }_X^{\mu }{\epsilon }_{J/\psi }^{\nu }{\epsilon }_{v^0}^{\rho }{M}_{\mu \nu \rho }|}^2,\hfill \end{array}$$

(28)

where $p^{*}\left(q^2\right)={\lambda }^{1/2}(m_X^2,m_{J/\psi }^2,q^2)/2m_X$ is the momentum of the $v^0$ in the X rest frame. The allowed kinematic range is given by:

$${\left(n{m}_{\pi }\right)}^2\le q^2\le {(m_X-m_{J/\psi })}^2,$$

where $n=2$ for the $\rho$ meson and $n=3$ for the $\omega$ meson. The masses, decay widths, and branching fractions appearing in (28) were taken from PDG [13]. In addition to the model parameter values presented in Table 1, further model parameters are needed, namely the size parameters of the appearing mesons. Their values have been settled earlier and are presented in Table 2.

Table 2. Size parameters for selected mesons in GeV.

${\mathbf{\Lambda }}_{\mathit{\pi }}$	${\mathbf{\Lambda }}_{\mathit{\rho }/\mathit{\omega }}$	${\mathbf{\Lambda }}_{\mathit{D}}$	${\mathbf{\Lambda }}_{\mathit{D}*}$	${\mathbf{\Lambda }}_{\mathit{J}/\mathit{\psi }}$	${\mathbf{\Lambda }}_{{\mathit{\eta }}_{\mathit{c}}}$
$0.711$	$0.295$	$1.4$	$2.3$	$3.3$	$3.0$

Two adjustable parameters remain, the size parameter ${\mathsf{\Lambda }}_X$ and the mixing angle $\theta$. It was found out that the dependence of the branching fraction:

$$\frac{\mathsf{\Gamma }(X_u\to J/\psi +3\pi )}{\mathsf{\Gamma }(X_u\to J/\psi +2\pi )}\approx 0.25$$

(29)

on the size parameter ${\mathsf{\Lambda }}_x$ is in the CCQM small and close to $1/4$. Using this observation and the central value of the experimental ratio in Equation (24), one can deduce the mixing angle from:

$$\frac{\mathsf{\Gamma }(X_{l,h}\to J/\psi +3\pi )}{\mathsf{\Gamma }(X_{l,h}\to J/\psi +2\pi )}\approx 0.25·{\left(\frac{1\pm tan\theta }{1\mp tan\theta }\right)}^2\approx 1.$$

(30)

The latter equation yields $\theta \approx {18.4}^{\circ }$ for $X_l$ and $\theta \approx -{18.4}^{\circ }$ for $X_h$. When not considering the ratio, the sensitivity of the decay widths on the size parameter is more important. One may expect the size parameter value to be close to those of the charmonia ${\mathsf{\Lambda }}_{J/\psi }$ and ${\mathsf{\Lambda }}_{{\eta }_c}$, i.e., to be in the range $3\mathrm{GeV}<{\mathsf{\Lambda }}_X<4\mathrm{GeV}$. This range was scanned, and the behavior of the decay width is depicted in Figure 3.

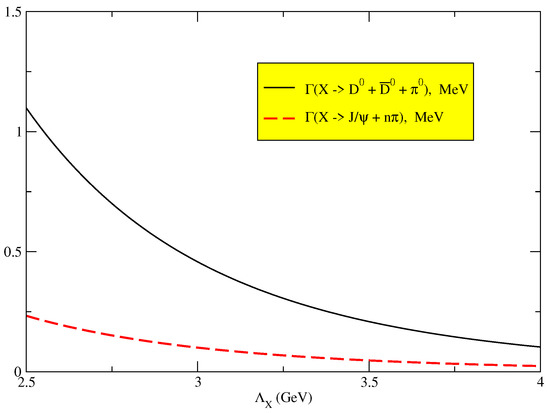
Figure 3. The dependence of the decay widths $\mathsf{\Gamma }(X_l\to {\overline{D}}^0{D}^0{\pi }^0)$ and $\mathsf{\Gamma }(X\to J/\psi +n\pi )$ on the size parameter ${\mathsf{\Lambda }}_X$.

One can conclude that the predicted values in the interval $2.5\le q^2\le 3.5$ GeV lie in the range $0.05\mathrm{MeV}<{\mathsf{\Gamma }}_{X\left(3872\right)}<0.23\mathrm{MeV}$, which is in agreement with the upper limit of $1.2\mathrm{MeV}$.

The differential rate of the decay $X\left(3872\right)\to {\overline{D}}^0{D}^0{\pi }^0$ in the narrow-width approximation is written as:

$$\begin{array}{ccc}\hfill \frac{d\mathsf{\Gamma }(X_u\to {\overline{D}}^0{D}^0{\pi }^0)}{d{q}^2}& =& \frac{1}{2m_X^2\pi }·\frac{1}{3}{|M_{XD{D}^{*}}|}^2·\frac{{\mathsf{\Gamma }}_{D^{*0}}{m}_{D^{*0}}}{\pi }\frac{p^{*}\left(q^2\right)\mathcal{B}(D^{*0}\to D^0{\pi }^0)}{{(m_{D^{*0}}^2-q^2)}^2+{\mathsf{\Gamma }}_{D^{*0}}^2{m}_{D^{*0}}^2},\hfill \\ \hfill \frac{1}{3}{|M_{XD{D}^{*}}|}^2& =& \frac{1}{3}\sum _{\mathrm{pol}}{|{\epsilon }_X^{\mu }{\epsilon }_{D^{*0}}^{\nu }{M}_{\mu \nu }|}^2,\hfill \end{array}$$

(31)

where $p^{*}\left(q^2\right)={\lambda }^{1/2}(m_X^2,m_{D^0}^2,q^2)/2m_X$ is the momentum of $D^{*0}$ in the X rest frame. The matrix element $M_{\mu \nu }$ was defined above by Equation (26). One has to note that the allowed kinematic range:

$$3.99928{\mathrm{GeV}}^2\approx {(m_{D^0}+m_{{\pi }^0})}^2\le q^2\le {(m_X-m_{D^0})}^2\approx 4.02672{\mathrm{GeV}}^2$$

is very narrow. Taking the masses, widths, and branching fractions of appearing $D^{*}$ mesons from [13,89,131,132,133,134], we can calculate the decay width:

$$\mathsf{\Gamma }(X_l\to {\overline{D}}^0{D}^0{\pi }^0)={cos}^2\theta \mathsf{\Gamma }(X_u\to {\overline{D}}^0{D}^0{\pi }^0)$$

and study its dependence on the size parameter ${\mathsf{\Lambda }}_X$. This is shown in Figure 3. By using the experimental data from PDG [13] for the ratio:

$$\begin{array}{ccc}\hfill {10}^5\mathcal{B}(B^{\pm }\to K^{\pm }X)·\mathcal{B}(X\to J/\psi {\pi }^{+}{\pi }^{-})& =& 0.95\pm 0.19,\hfill \\ {10}^5\mathcal{B}(B^{\pm }\to K^{\pm }X)·\mathcal{B}(X\to D^0{\overline{D}}^0{\pi }^0)\hfill & =& 10.0\pm 4.0,\end{array}$$

(32)

one finds:

$$\frac{\mathsf{\Gamma }(X\to D^0{\overline{D}}^0{\pi }^0)}{\mathsf{\Gamma }(X\to J/\psi {\pi }^{+}{\pi }^{-})}=10.5\pm 4.7.$$

(33)

The latter is to be compared to the CCQM prediction:

$$\frac{\mathsf{\Gamma }(X\to D^0{\overline{D}}^0{\pi }^0)}{\mathsf{\Gamma }(X\to J/\psi {\pi }^{+}{\pi }^{-})}{|}_{\mathrm{CCQM}}=6.0\pm 0.2,$$

(34)

where the uncertainty of the result reflects the uncertainty on ${\mathsf{\Lambda }}_X$. One can see that the two numbers agree within errors.

3.2. Implications of $X\left(3872\right)$ in the Charm Dissociation Process by Light Mesons

It is interesting to check the significance of $X\left(3872\right)$ in the reaction of the charm dissociation process $J/\psi +\rho \left(\omega \right)\to X\left(3872\right)\to \overline{D}{D}^{*}$, which plays an important role in heavy ion physics. This state will contribute to the s channel of the process. The X-addition to the full cross-section is written as:

$$\begin{array}{c}\sigma (J/\psi +v^0\to D\left(\overline{D}\right)+{\overline{D}}^{*}\left(D^{*}\right))=2{(cos\theta \mp sin\theta )}^2\sigma (J/\psi +v^0\to X_u\to \overline{D}+D^{*}),\hfill \\ \sigma (J/\psi +v^0\to X_u\to \overline{D}+D^{*})=\frac{1}{16\pi s}\frac{{\lambda }^{1/2}(s,m_D^2,m_{D^{*}}^2)}{{\lambda }^{1/2}(s,m_{J/\psi }^2,m_{v^0}^2)}·\frac{1}{9}\sum _{\mathrm{pol}}\frac{{|A|}^2}{{(s-m_X^2)}^2+{\mathsf{\Gamma }}_X^2{m}_X^2},\hfill \\ A={\epsilon }_{J/\psi }^{\nu }{\epsilon }_{v^0}^{\rho }{M}_{\mu \nu \rho }\left(-g^{\mu \alpha }+\frac{p^{\mu }{p}^{\alpha }}{m_X^2}\right){\epsilon }_{D^{*}}^{\beta }{M}_{\alpha \beta },\hfill \end{array}$$

(35)

where $p=p_1+p_2=q_1+q_2$. The ∓ sign in the first equation is negative for the $\rho$ meson and positive for $\omega$. A Breit–Wigner propagator is used with ${\mathsf{\Gamma }}_X=1\mathrm{MeV}$, and the size parameter value is fixed to ${\mathsf{\Lambda }}_X=3.5\mathrm{GeV}$. With this setting, the dependence of the cross-section on the energy $E=\sqrt{s}$ is shown in Figure 4.

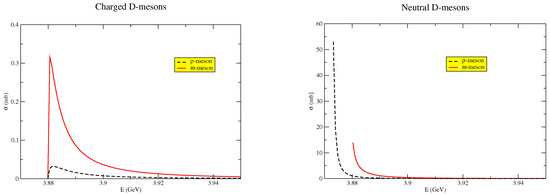
Figure 4. The cross-sections of the processes $J/\psi +v^0\to X\to D+D^{*}$. Charged D-mesons in left panel; neutral D-mesons in the right panel.

One can compare the predicted behavior to available results for the charged D-mesons: At $E=4.0\mathrm{GeV}$, a theoretical evaluation [135] predicts $\sigma (J/\psi +\pi \to D+{\overline{D}}^{*})=0.9\mathrm{mb}$, and the work in [136] predicted $\sigma (J/\psi +\rho \to D+{\overline{D}}^{*})=2.9\mathrm{mb}$ at $E=3.9\mathrm{GeV}$. In the case of $X\left(3872\right)$, the cross-section reaches the maximum of approximately $0.32\mathrm{mb}$ at $E=3.88\mathrm{GeV}$, and one can conclude that the expected contribution of $X\left(3872\right)$ in the charm dissociation is non-negligible.

4. Radiative Decays of $\mathit{X}\left(\mathbf{3872}\right)$

The first experimental evidence for the radiative decay of the $X\left(3872\right)$ particle was given in [129] by the Belle experiment. From the measured branching fraction product:

$$\mathcal{B}(B\to XK)·\mathcal{B}(X\to \gamma +J/\psi )=(1.8\pm 0.6\left(\mathrm{stat}\right)\pm 0.1\left(\mathrm{syst}\right))\times {10}^{-6}$$

(36)

the partial width ratio was deduced:

$$\frac{\mathsf{\Gamma }(X\to \gamma +J/\psi )}{\mathsf{\Gamma }(X\to {\pi }^{+}{\pi }^{-}J/\psi )}=0.14\pm 0.05.$$

(37)

This finding was supported by the BaBar observation [137]:

$$\mathcal{B}(B^{+}\to X{K}^{+})·\mathcal{B}(X\to \gamma +J/\psi )=(3.3\pm 1.0\left(\mathrm{stat}\right)\pm 0.3\left(\mathrm{syst}\right))\times {10}^{-6}$$

(38)

which had a limited significance of $3.4\sigma$. The same experiment reaffirmed the observation in 2009 [138] with smaller errors:

$$\mathcal{B}(B^{\pm }\to X{K}^{\pm })·\mathcal{B}(X\to \gamma +J/\psi )=(2.8\pm 0.8\left(\mathrm{stat}\right)\pm 0.1\left(\mathrm{syst}\right))\times {10}^{-6}$$

(39)

from which one can deduce [36]:

$$\frac{\mathsf{\Gamma }(X\to \gamma +J/\psi )}{\mathsf{\Gamma }(X\to {\pi }^{+}{\pi }^{-}J/\psi )}=0.22\pm 0.06.$$

(40)

BaBar also presented a result related to $\psi \left(2s\right)$:

$$\mathcal{B}(B^{\pm }\to X{K}^{\pm })·\mathcal{B}(X\to \gamma +\psi \left(2S\right))=(9.5\pm 2.7\left(\mathrm{stat}\right)\pm 0.6\left(\mathrm{syst}\right))\times {10}^{-6}.$$

(41)

In 2011, the Belle collaboration published measurements with $J/\psi$ and $\psi \left(2s\right)$ in the final state [139]:

$$\begin{array}{ccc}\hfill \mathcal{B}(B^{\pm }\to X{K}^{\pm })·\mathcal{B}(X\to \gamma +J/\psi )& =& ({1.78}_{-0.44}^{+0.48}\left(\mathrm{stat}\right)\pm 0.12\left(\mathrm{syst}\right))\times {10}^{-6},\hfill \\ \mathcal{B}(B^{\pm }\to X{K}^{\pm })·\mathcal{B}(X\to \gamma +\psi \left(2S\right))& <& 3.45\times {10}^{-6}.\hfill \end{array}$$

(42)

The first result was in good agreement with the previous one from the same experiment (36); however, the second number brought some tension when compared to BaBar and a later LHCb measurement [140]:

$$\begin{array}{c}\hfill \frac{\mathsf{\Gamma }(X\to \psi (2s)+\gamma )}{\mathsf{\Gamma }(X\to J/\psi +\gamma )}=\left\{\begin{array}{cc}3.4\pm 1.4\hfill & \mathrm{BaBar}\hfill \\ <2.0(90\%\mathrm{CL})\hfill & \mathrm{Belle}\hfill \\ 2.46\pm 0.64\left(\mathrm{stat}\right)\pm 0.29\left(\mathrm{sys}\right)\hfill & \mathrm{LHCb}\hfill \end{array}\right..\end{array}$$

(43)

The theoretical study of radiative $X\left(3872\right)$ decays includes several different approaches. Such decays were analyzed in [98] in the charmonium picture. The authors studied excited 1D and 2P states and their decays in relation with the electric dipole radiation and provided implications for quantum number assignments. The molecular hypothesis was considered in [106]. There, the authors argued that the validity of the molecular picture could be determined from the study of several $X\left(3872\right)$ decay channels (including some with the photon emission). The work in [141] was dedicated to radiative decays with two D mesons in the final state. It was claimed that the discrimination between the molecular and charmonium picture could be obtained via analysis of the photon spectrum. Several decay modes, which also included $J/\psi +\gamma$, were examined in [142] within a phenomenological Lagrangian approach. The predicted value of the radiative decay width depended on the model parameters and varied from 125 KeV to 250 KeV. In [143], $X\left(3872\right)$ was described as a mixture of charmonium and exotic molecular states and treated using QCD sum rules. The predicted radiative decay width ratio ${\mathsf{\Gamma }}_X(J/\psi \gamma )/{\mathsf{\Gamma }}_X(J/\psi {\pi }^{+}{\pi }^{-})=0.19\pm 0.13$ was in agreement with experimental measurements. The excited charmonium hypothesis and study of E1 decay widths within the relativistic Salpeter method was presented in [144]. A description based on a charmonium-like picture with high spin $2^{-+}$ using a light front quark model was proposed in [145]. Later works [146,147,148,149] were mostly interested in the puzzling ${\mathsf{\Gamma }}_X\left(\psi \left(2s\right)\gamma \right)/{\mathsf{\Gamma }}_X(J/\psi \gamma )$ ratio (43) and analyzed it with different approaches (quark potential model, single-channel approximation, coupled-channel approach, charmonium-molecule hybrid model, and an effective theory framework).

Here, we focus on the $J/\psi$ decay channel, which was studied using the CCQM in [79]. The non-local quark current for the $X\left(3872\right)$ hadron was given in the previous section; see Equation (22). The $J/\psi$ quark current is written as:

$$J_{J/\psi }^{\mu }\left(y\right)=\int d{y}_1\int d{y}_2\delta \left(y-\frac{1}{2}(y_1+y_2)\right)\times {\mathsf{\Phi }}_{J/\psi }\left({(y_1-y_2)}^2\right){\overline{c}}_a\left(y_1\right){\gamma }^{\mu }{c}_a\left(y_2\right).$$

(44)

The related size parameter was established in earlier works and has the value of ${\mathsf{\Lambda }}_{J/\psi }=1.738\mathrm{GeV}$. The knowledge of the quark currents enables us to give more details concerning the interaction with photons, addressed before in Section 2.4. The second part of the electromagnetic interaction Lagrangian stands:

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\mathrm{int}}^{\mathrm{EM}\left(2\right)}\left(x\right)& =& g_X{X}_{q\mu }\left(x\right)·J_{X_q-\mathrm{em}}^{\mu }\left(x\right)+g_{J/\psi }J/{\psi }_{\mu }\left(x\right)·J_{J/\psi -\mathrm{em}}^{\mu }\left(x\right),(q=u,d)\hfill \\ \hfill J_{X_q-\mathrm{em}}^{\mu }& =& \int d\overrightarrow{\rho }{\mathsf{\Phi }}_X\left({\overrightarrow{\rho }}^2\right)J_{4q}^{\mu }(x_1,\dots ,x_4)\left\{i{e}_q[I_x^{x_3}-I_x^{x_4}]+i{e}_c[I_x^{x_2}-I_x^{x_1}]\right\},\hfill \\ J_{J/\psi -\mathrm{em}}^{\mu }& =& \int d\rho {\mathsf{\Phi }}_{J/\psi }\left({\rho }^2\right)J_{2q}^{\mu }(x_1,x_2)i{e}_c[I_x^{x_1}-I_x^{x_2}],I_x^{x_i}\equiv I(x_i,x,P).\end{array}$$

where $J_{4q}^{\mu }$ and $J_{2q}^{\mu }$ correspond to the parts of usual currents (22), (44) not containing the vertex function. In order to make use of the definition (15), it is convenient to switch to the Fourier transforms of the vertex functions and quark fields:

$$\begin{array}{ccc}\hfill {\mathsf{\Phi }}_X\left({\overrightarrow{\rho }}^2\right)& =& \int \frac{d^4\overrightarrow{\omega }}{{\left(2\pi \right)}^4}{\tilde{\mathsf{\Phi }}}_X(-{\overrightarrow{\omega }}^2)e^{-i\overrightarrow{\rho }\overrightarrow{\omega }}={\tilde{\mathsf{\Phi }}}_X\left({\overrightarrow{\partial }}_{\rho }^2\right){\delta }^{\left(4\right)}\left(\overrightarrow{\rho }\right),\hfill \\ \hfill {\mathsf{\Phi }}_{J/\psi }\left({\rho }^2\right)& =& \int \frac{d^4\omega }{{\left(2\pi \right)}^4}{\tilde{\mathsf{\Phi }}}_{J/\psi }(-{\omega }^2)e^{-i\rho \omega }={\tilde{\mathsf{\Phi }}}_{J/\psi }\left({\partial }_{\rho }^2\right){\delta }^{\left(4\right)}\left(\rho \right),\hfill \\ \hfill q\left(x_i\right)& =& \int \frac{d^4{p}_i}{{\left(2\pi \right)}^4}{e}^{-i{p}_i{x}_i}\tilde{q}\left(p_i\right),\overline{q}\left(x_i\right)=\int \frac{d^4{p}_i}{{\left(2\pi \right)}^4}{e}^{i{p}_i{x}_i}\tilde{\overline{q}}\left(p_i\right),\hfill \end{array}$$

so that the differential operator can be placed in front of the path integrals:

$$\begin{array}{ccc}\hfill J_{X_q-\mathrm{em}}^{\mu }& =& \prod _{i=1}^4\int \frac{d^4{p}_i}{{\left(2\pi \right)}^4}{\tilde{J}}_{4q}^{\mu }(p_1,\dots ,p_4)\int d\overrightarrow{\rho }{\delta }^{\left(4\right)}\left(\overrightarrow{\rho }\right){\tilde{\mathsf{\Phi }}}_X\left({\overrightarrow{\partial }}_{\rho }^2\right)e^{-i(p_1{x}_1-p_2{x}_2-p_3{x}_3+p_4{x}_4)}·Q_X\hfill \\ & =& \prod _{i=1}^4\int \frac{d^4{p}_i}{{\left(2\pi \right)}^4}{\tilde{J}}_{4q}^{\mu }(p_1,\dots ,p_4)e^{-i(p_1-p_2-p_3+p_4)x}\int d\overrightarrow{\rho }{\delta }^{\left(4\right)}\left(\overrightarrow{\rho }\right)e^{-i\overrightarrow{\rho }\overrightarrow{\omega }}{\tilde{\mathsf{\Phi }}}_X\left({\overrightarrow{D}}_{\rho }^2\right)·Q_X\\ Q_X& =& i{e}_q[I_x^{x_3}-I_x^{x_4}]+i{e}_c[I_x^{x_2}-I_x^{x_1}],\hfill \end{array}$$

$$\begin{array}{ccc}\hfill J_{J/\psi -\mathrm{em}}^{\mu }& =& \prod _{i=1}^2\int \frac{d^4{p}_i}{{\left(2\pi \right)}^4}{\tilde{J}}_{2q}^{\mu }(p_1,p_2)\int d\rho {\delta }^{\left(4\right)}\left(\rho \right){\tilde{\mathsf{\Phi }}}_{J/\psi }\left({\partial }_{\rho }^2\right)e^{i(p_1{x}_1-p_2{x}_2)}·Q_{J/\psi }\hfill \\ & =& \prod _{i=1}^2\int \frac{d^4{p}_i}{{\left(2\pi \right)}^4}{\tilde{J}}_{2q}^{\mu }(p_1,p_2)e^{i(p_1-p_2)x}\int d\rho {\delta }^{\left(4\right)}\left(\rho \right)e^{ip\rho }{\tilde{\mathsf{\Phi }}}_{J/\psi }\left(D_{\rho }^2\right)·Q_{J/\psi }\hfill \\ Q_{J/\psi }& =& i{e}_c[I_x^{x_1}-I_x^{x_2}],\hfill \end{array}$$

where the long derivatives are defined as $D_{{\rho }_i}^{\mu }={\partial }_{{\rho }_i}^{\mu }-i{\omega }_i^{\mu }$ and $D_{\rho }^{\mu }={\partial }_{\rho }^{\mu }+i{p}^{\mu }$, $p=\frac{1}{2}(p_1+p_2)$ with ${\omega }_i$ being combinations of the integration four-vectors $p_i$ and mass parameters $w_q$ and $w_c$. Next, the identity involving the operator function action on the path integral [150] is applied:

$$F\left(D_{{\rho }_j}^2\right)I_x^{x_i}=\underset{0}{\overset{1}{\int }}d\tau F^{\prime }(\tau D_{{\rho }_j}^2-(1-\tau ){\omega }_j^2)w_{ij}·\left({\partial }_{{\rho }_j}^{\nu }{A}_{\nu }\left(x_i\right)-2i{\omega }_j^{\nu }{A}_{\nu }\left(x_i\right)\right)+F(-{\omega }_j^2)I_x^{x_i}.$$

(45)

Its validity extends to all functions F analytic at zero. The result for $X\left(3872\right)$ reads:

$$\begin{array}{ccc}\hfill J_{X_q-\mathrm{em}}^{\mu }\left(x\right)& =& \prod _{i=1}^4\int d^4{x}_i\int d^{4}y{J}_{4q}^{\mu }(x_1,\dots ,x_4)A_{\rho }\left(y\right)·E_X^{\rho }(x;x_1,\dots ,x_4,y),\hfill \\ \hfill E_X^{\rho }(x;x_1,\dots ,x_4,y)& =& \prod _{i=1}^4\int \frac{d^4{p}_i}{{\left(2\pi \right)}^4}\int \frac{d^{4}r}{{\left(2\pi \right)}^4}{e}^{-i{p}_1(x-x_1)+i{p}_2(x-x_2)+i{p}_3(x-x_3)-i{p}_4(x-x_4)-ir(x-y)}{\tilde{E}}_X^{\rho }(p_1,\dots ,p_4,r),\hfill \\ \hfill {\tilde{E}}_X^{\rho }(p_1,\dots ,p_4,r)& =& \underset{0}{\overset{1}{\int }}d\tau \sum _{j=1}^3\{e_c\left[-{\tilde{\mathsf{\Phi }}}_X^{\prime }(-z_{1j})l_{1j}^{\rho }+{\tilde{\mathsf{\Phi }}}_X^{\prime }(-z_{2j})l_{2j}^{\rho }\right]\hfill \\ & & +e_q\left[-{\tilde{\mathsf{\Phi }}}_X^{\prime }(-z_{4j})l_{4j}^{\rho }+{\tilde{\mathsf{\Phi }}}_X^{\prime }(-z_{3j})l_{3j}^{\rho }\right]\},\hfill \\ \hfill l_{ij}& =& w_{ij}(w_{ij}r+2{\omega }_j),(i=1,\dots ,4;j=1,\dots ,3),\hfill \\ \hfill z_{i1}& =& \tau {(w_{i1}r+{\omega }_1)}^2+(1-\tau ){\omega }_1^2+{\omega }_2^2+{\omega }_3^2,\hfill \\ \hfill z_{i2}& =& {(w_{i1}r+{\omega }_1)}^2+\tau {(w_{i2}r+{\omega }_2)}^2+(1-\tau ){\omega }_2^2+{\omega }_3^2,\hfill \\ \hfill z_{i3}& =& {(w_{i1}r+{\omega }_1)}^2+{(w_{i2}r+{\omega }_2)}^2+\tau {(w_{i3}r+{\omega }_3)}^2+(1-\tau ){\omega }_3^2.\hfill \end{array}$$

(46)

For $J/\psi$, one obtains:

$$\begin{array}{ccc}\hfill J_{J/\psi -\mathrm{em}}^{\nu }\left(y\right)& =& \int d^4{y}_1\int d^4{y}_2\int d^{4}z{J}_{2q}^{\nu }(y_1,y_2)A_{\rho }\left(z\right)E_{J/\psi }^{\rho }(y;y_1,y_2,z),\hfill \\ \hfill E_{J/\psi }^{\rho }(y;y_1,y_2,z)& =& \int \frac{d^4{p}_1}{{\left(2\pi \right)}^4}\int \frac{d^4{p}_2}{{\left(2\pi \right)}^4}\int \frac{d^{4}q}{{\left(2\pi \right)}^4}{e}^{-i{p}_1(y_1-y)+i{p}_2(y_2-y)+iq(z-y)}{\tilde{E}}_{J/\psi }^{\rho }(p_1,p_2,q),\hfill \\ \hfill {\tilde{E}}_{J/\psi }^{\rho }(p_1,p_2,q)& =& e_c\underset{0}{\overset{1}{\int }}d\tau \left\{-{\tilde{\mathsf{\Phi }}}_{J/\psi }^{\prime }(-z_{-})l_{-}^{\rho }-{\tilde{\mathsf{\Phi }}}_{J/\psi }^{\prime }(-z_{+})l_{+}^{\rho }\right\},\hfill \\ \hfill z_{\mp }& =& \tau (p\mp \frac{1}{2}q)-(1-\tau )p^2,l_{\mp }=p\mp \frac{1}{4}q,p=\frac{1}{2}(p_1+p_2).\hfill \end{array}$$

(47)

The amplitude evaluation requires evaluation of four Feynman diagrams displayed in Figure 5.

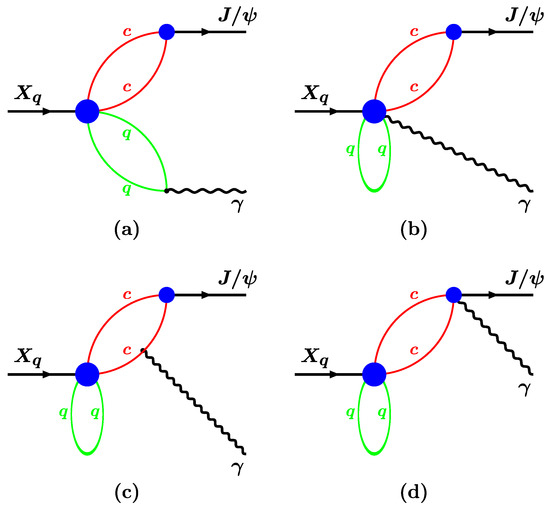
Figure 5. Four Feynman diagrams describing the decay $X\to \gamma +J/\psi$. One with the photon emission form the light quark line (a) and three bubble graphs (b–d).

The corresponding expression stands:

$$M(X_q\left(p\right)\to J/\psi \left(q_1\right)\gamma \left(q_2\right))=i{\left(2\pi \right)}^4{\delta }^{\left(4\right)}(p-q_1-q_2){\epsilon }_X^{\mu }{\epsilon }_{\gamma }^{\rho }{\epsilon }_{J/\psi }^{\nu }{T}_{\mu \rho \nu }(q_1,q_2),$$

(48)

where $T_{\mu \rho \nu }(q_1,q_2)$ can be expanded in terms of appropriate Lorentz structures. Using the on-mass shell condition, gauge invariance, and Schouten identities [151], one can show that only two independent structures remain:

$$T_{\mu \rho \nu }=W_A{\epsilon }_{q_1{q}_2\mu \rho }{q}_{2\nu }+W_B{\epsilon }_{q_1{q}_2\nu \rho }{q}_{1\mu }.$$

(49)

The functions $W_{A/B}$ are to be extracted from the expression following from the CCQM computation:

$$T_{\mu \rho \nu }(q_1,q_2)=\sum _{i=a,b,c,d}{T}_{\mu \rho \nu }^{\left(i\right)}(q_1,q_2),$$

(50)

where the separate contributions are written down:

$$\begin{array}{ccc}\hfill T_{\mu \rho \nu }^{\left(a\right)}& =& 6\sqrt{2}{g}_X{g}_{J/\psi }{e}_q\int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_X\left(-K_a^2\right){\tilde{\mathsf{\Phi }}}_{J/\psi }\left(-{(k_1+\frac{1}{2}{q}_1)}^2\right)\hfill \\ & \times & \frac{1}{2}\mathrm{tr}\left[{\gamma }_5{S}_c\left(k_1\right){\gamma }_{\nu }{S}_c(k_1+q_1){\gamma }_{\mu }{S}_q\left(k_2\right){\gamma }_{\rho }{S}_q(k_2+q_2)-({\gamma }_5\leftrightarrow {\gamma }_{\mu })\right],\hfill \\ \hfill K_a^2& =& \frac{1}{2}{(k_1+\frac{1}{2}{q}_1)}^2+\frac{1}{2}{(k_2+\frac{1}{2}{q}_2)}^2+\frac{1}{4}{(w_q{q}_1-w_c{q}_2)}^2,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_{\mu \rho \nu }^{\left(b\right)}& =& 6\sqrt{2}{g}_X{g}_{J/\psi }\int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{J/\psi }\left(-{(k_2+\frac{1}{2}{q}_1)}^2\right){\tilde{E}}_{X\rho }(p_1,\dots ,p_4,r)\hfill \\ & \times & \frac{1}{2}\mathrm{tr}\left[{\gamma }_5{S}_q\left(k_1\right){\gamma }_{\mu }{S}_c\left(k_2\right){\gamma }_{\nu }{S}_c(k_2+q_1)-({\gamma }_5\leftrightarrow {\gamma }_{\mu })\right],\hfill \\ \hfill p_1& =& k_2,p_2=k_2+q_1,p_3=p_4=-k_1,r=-q_2,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_{\mu \rho \nu }^{\left(c\right)}& =& 6\sqrt{2}{g}_X{g}_{J/\psi }{e}_c\int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_X\left(-K_c^2\right){\tilde{\mathsf{\Phi }}}_{J/\psi }\left(-{(k_2+q_2+\frac{1}{2}{q}_1)}^2\right)\hfill \\ & \times & \frac{1}{2}\mathrm{tr}\left[{\gamma }_5{S}_q\left(k_1\right){\gamma }_{\mu }{S}_c\left(k_2\right){\gamma }_{\rho }{S}_c(k_2+q_2){\gamma }_{\nu }{S}_c(k_2+p)-({\gamma }_5\leftrightarrow {\gamma }_{\mu })\right],\hfill \\ \hfill K_c^2& =& \frac{1}{2}{k}_1^2+\frac{1}{2}{(k_2+\frac{1}{2}p)}^2+\frac{1}{4}{w}_q^2{p}^2,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_{\mu \rho \nu }^{\left(d\right)}& =& 6\sqrt{2}{g}_X{g}_{J/\psi }{e}_c\int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_X\left(-K_c^2\right){\tilde{E}}_{J/\psi \rho }(p_1,p_2,q)\hfill \\ & \times & \frac{1}{2}\mathrm{tr}\left[{\gamma }_{\mu }{S}_q\left(k_1\right){\gamma }_5{S}_c\left(k_2\right){\gamma }_{\nu }{S}_c(k_2+p)-({\gamma }_5\leftrightarrow {\gamma }_{\mu })\right],\hfill \\ \hfill p_1& =& -k_2-p,p_2=-k_2,q=-q_2.\hfill \end{array}$$

One evaluates the traces and the loop momenta integrals, and the expression is re-arranged in two terms following the mentioned Lorentz structure. The behavior of coefficient functions $W_{A/B}$ is predicted using a numerical integration over the Schwinger parameters:

$$W_{A,B}=\underset{0}{\overset{\infty }{\int }}dt\underset{0}{\overset{1}{\int }}{d}^3\beta F_{A,B}(t,{\beta }_1,{\beta }_2,{\beta }_3).$$

(51)

The decay width is expressed as:

$$\mathsf{\Gamma }(X\to \gamma J/\psi )=\frac{1}{12\pi }\frac{|{\overrightarrow{q}}_2|}{m_X^2}\left(|H_L{|}^2+{|H_T|}^2\right),$$

(52)

where $H_i$ denote the helicity amplitudes:

$$H_L=i\frac{m_X^2}{m_{J/\psi }}|{\overrightarrow{q}}_2{|}^2{W}_A,H_T=-i{m}_X{|{\overrightarrow{q}}_2|}^2{W}_B$$

(53)

with $|{\overrightarrow{q}}_2|=\left(m_X^2-m_{J/\psi }^2\right)/\left(2m_X\right)$. The dependence of the predicted decay width on the size parameter ${\mathsf{\Lambda }}_X$ is shown in Figure 6.

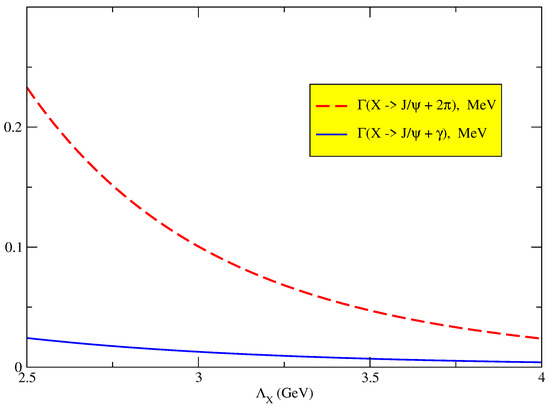
Figure 6. The dependence of the decay widths $\mathsf{\Gamma }(X_l\to \gamma +J/\psi )$ and $\mathsf{\Gamma }(X_l\to J/\psi 2\pi )$ on the size parameter ${\mathsf{\Lambda }}_X$.

If we follow the approach from the previous section and take ${\mathsf{\Lambda }}_X=3.0\pm 0.5\mathrm{GeV}$, then the model predicts:

$$\frac{\mathsf{\Gamma }(X_l\to \gamma +J/\psi )}{\mathsf{\Gamma }(X_l\to J/\psi +2\pi )}{|}_{\mathrm{CCQM}}=0.15\pm 0.03,$$

(54)

which is to be compared with the experimental results Equation (37) and Equation (40). One may conclude that the bound-tetraquark description of the $X\left(3872\right)$ state by the CCQM is in an agreement with the experimental observations.

5. Nature of ${\mathit{Z}}_{\mathit{c}}\left(\mathbf{3900}\right)$

As stated in the Introduction, the detected $Z_c\left(3900\right)$ decays include both the ${\pi }^{\pm }J/\psi$ and $D^{*}D$ final states (assuming $Z_c\left(3885\right)$ and $Z_c\left(3900\right)$ are the same particle). The ratio of the decay widths of these two channels was measured by BESIII [27]:

$$\frac{\mathsf{\Gamma }(Z_c\to D{\overline{D}}^{*})}{\mathsf{\Gamma }(Z_c\to \pi J/\psi )}=6.2\pm 1.1\left(\mathrm{stat}\right)\pm 2.7\left(\mathrm{syst}\right)$$

(55)

and represents a quantitative observation to be explained by the theorists. There are many different theoretical approaches that are trying to understand the nature of this state.

The tetraquark interpretation was intensively discussed within QCD sum rules [152,153,154] and also in the color flux-tube model [155]. The molecular scenario seems to be more abundant in the literature and is discussed or preferred in several theoretical frameworks. A light front theory description was presented in [156]; an effective field theory description was proposed in [157]; and QCD sum rules were used in [158,159]. The molecular interpretation was also supported by the quark model developed in [160]. The authors of [161] made a proposal for BESIII and forthcoming Belle II measurements by using also the molecular scenario. Further molecular picture oriented works can be found in [162] (constituent quark model, coupled channels) and in [163] (quark interchange model). It is interesting to note that most of the lattice QCD based studies obtained different results from previous ones: some did not see (within the approach they used) a bound state at all [164,165,166,167], invoked a threshold cusp explanation [168,169], or indicated that the understanding of $Z_c$ within the lattice QCD was only approaching [170]. For completeness, one can mention the charmonium hybrid interpretation studied in [171], the hadro charmonium picture presented in [172] with the tetraquark and molecular interpretation and the color magnetic interaction [173]. Further ideas can be found in [174,175,176,177,178,179,180,181,182,183,184].

The description of $Z_c\left(3900\right)$ in the framework of the CCQM was presented in [80]. Two options were tested: the molecular interpretation and the tetraquark hypothesis. For each option, the strong decays into $J/\psi {\pi }^{+}$, ${\eta }_c{\rho }^{+}$, ${\overline{D}}^0{D}^{*+}$, and ${\overline{D}}^{*0}{D}^{+}$ were computed and compared to available experimental data. First, we investigate the tetraquark hypothesis. In this scenario, the non-local $Z_c$ current is written as:

$$\begin{array}{ccc}\hfill J_{Z_c}^{\mu }\left(x\right)& =& \int d{x}_1\dots \int d{x}_4\delta \left(x-\sum _{i=1}^4{w}_i{x}_i\right)·{\mathsf{\Phi }}_{Z_c}\left(\sum _{i<j}{(x_i-x_j)}^2\right)J_{4q}^{\mu }(x_1,\dots ,x_4),\hfill \\ \hfill J_{4q}^{\mu }& =& \frac{i}{\sqrt{2}}{\epsilon }_{abc}{\epsilon }_{dec}\left\{[u_a\left(x_4\right)C{\gamma }_5{c}_b\left(x_1\right)][{\overline{d}}_d\left(x_3\right){\gamma }^{\mu }C{\overline{c}}_e\left(x_2\right)]-({\gamma }_5\leftrightarrow {\gamma }^{\mu })\right\}.\hfill \end{array}$$

(56)

The tetraquark mass operator looks like:

$$\begin{array}{ccc}\hfill {\Pi }_{Z_c}^{\mu \nu }\left(p\right)& =& 6\prod _{i=1}^3\int \frac{d^4{k}_i}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}^2\left(-{\overrightarrow{\omega }}^2\right)\hfill \\ & \times & \{\mathrm{tr}\left(S_4\left({\widehat{k}}_4\right){\gamma }_5{S}_1\left({\widehat{k}}_1\right){\gamma }_5\right)\mathrm{tr}\left(S_3\left({\widehat{k}}_3\right){\gamma }^{\mu }{S}_2\left({\widehat{k}}_2\right){\gamma }^{\nu }\right)\hfill \\ & & +\mathrm{tr}\left(S_4\left({\widehat{k}}_4\right){\gamma }^{\nu }{S}_2\left({\widehat{k}}_2\right){\gamma }^{\mu }\right)\mathrm{tr}\left(S_3\left({\widehat{k}}_3\right){\gamma }_5{S}_1^{(}{\widehat{k}}_1){\gamma }_5\right)\},\end{array}$$

(57)

where the momenta are defined by:

$$\begin{array}{ccc}\hfill {\widehat{k}}_1& =& k_1-w_{1}p,{\widehat{k}}_2=k_2-w_{2}p,{\widehat{k}}_3=k_3+w_{3}p,{\widehat{k}}_4=k_1+k_2-k_3+w_{4}p,\hfill \\ \hfill {\overrightarrow{\omega }}^2& =& 1/2(k_1^2+k_2^2+k_3^2+k_1{k}_2-k_1{k}_3-k_2{k}_3).\hfill \end{array}$$

The matrix elements of the decays $Z_c^{+}\to J/\psi +{\pi }^{+}$ and $Z_c^{+}\to {\eta }_c+{\rho }^{+}$ are written down:

$$\begin{array}{cc}& M^{\mu \nu }\left(Z_c(p,{ϵ}_p^{\mu })\to J/\psi (q_1,{ϵ}_{q_1}^{\nu })+{\pi }^{+}\left(q_2\right)\right)=\frac{6}{\sqrt{2}}{g}_{Z_c}{g}_{J/\psi }{g}_{\pi }\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{J/\psi }\left(-{(k_1+v_2{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left({\gamma }_5{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2){\gamma }^{\mu }{S}_2\left(k_1\right){\gamma }^{\nu }{S}_1(k_1+q_1)\right)+({\gamma }_5\leftrightarrow {\gamma }^{\mu })\right\}\hfill \\ =& A_{J/\psi \pi }{g}^{\mu \nu }+B_{J/\psi \pi }{q}_1^{\mu }{q}_2^{\nu },\hfill \end{array}$$

(58)

$$\begin{array}{cc}& M^{\mu \alpha }\left(Z_c(p,{ϵ}_p^{\mu })\to {\eta }_c\left(q_1\right)+\rho (q_2,{ϵ}_{q_2}^{\alpha })\right)=\frac{6}{\sqrt{2}}{g}_{Z_c}{g}_{{\eta }_c}{g}_{\rho }\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{{\eta }_c}\left(-{(k_1+v_2{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\rho }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left[{\gamma }_5{S}_4\left(k_2\right){\gamma }^{\alpha }{S}_3(k_2+q_2){\gamma }^{\mu }{S}_2\left(k_1\right){\gamma }_5{S}_1(k_1+q_1)\right]+({\gamma }_5\leftrightarrow {\gamma }^{\mu })\right\}\hfill \\ =& A_{{\eta }_c\rho }{g}^{\mu \alpha }-B_{{\eta }_c\rho }{q}_2^{\mu }{q}_1^{\alpha },\hfill \end{array}$$

(59)

where the argument of the $Z_c$-vertex function is given by:

$$\begin{array}{ccc}\hfill {\eta }_1& =& \frac{1}{2\sqrt{2}}\left(2k_1+(1-w_1+w_2)q_1-(w_1-w_2)q_2\right),\hfill \\ {\eta }_2& =& \frac{1}{2\sqrt{2}}\left(2k_2-(w_3-w_4)q_1+(1-w_3+w_4)q_2\right),\hfill \\ {\eta }_3& =& \frac{1}{2}\left((w_3+w_4)q_1-(w_1+w_2)q_2\right),{\overrightarrow{\eta }}^2={\eta }_1^2+{\eta }_2^2+{\eta }_3^2.\end{array}$$

The notations used are as follows: $m_1=m_2=m_c$, $m_3=m_4=m_d=m_u$, $v_1=m_1/(m_1+m_2)$, $v_2=m_2/(m_1+m_2)$, $u_3=m_3/(m_3+m_4)$, and $u_4=m_4/(m_3+m_4)$.

The amplitudes of the $Z_c^{+}\to {\overline{D}}^0+D^{*+}$ and $Z_c^{+}\to {\overline{D}}^{*0}+D^{+}$ decays are:

$$\begin{array}{cc}& M^{\mu \nu }\left(Z_c(p,{ϵ}_p^{\mu })\to {\overline{D}}^0\left(q_1\right)+D^{*+}(q_2,{ϵ}_{q_2}^{\nu })\right)=\frac{6}{\sqrt{2}}{g}_{Z_c}{g}_D{g}_{D^{*}}\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\delta }}^2\right){\tilde{\mathsf{\Phi }}}_D\left(-{(k_2+v_2{q}_2)}^2\right){\tilde{\mathsf{\Phi }}}_{D^{*}}\left(-{(k_1+u_1{q}_2)}^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left({\gamma }_5{S}_4(k_2+q_1){\gamma }_5{S}_1\left(k_1\right){\gamma }^{\nu }{S}_3(k_1+q_2){\gamma }^{\mu }{S}_2\left(k_2\right)\right)-({\gamma }_5\leftrightarrow {\gamma }^{\mu })\right\}\hfill \\ & =A_{\overline{D}{D}^{*}}{g}^{\mu \nu }-B_{\overline{D}{D}^{*}}{q}_2^{\mu }{q}_1^{\nu },\hfill \end{array}$$

(60)

$$\begin{array}{cc}& M^{\mu \alpha }\left(Z_c(p,{ϵ}_p^{\mu })\to {\overline{D}}^{*0}(q_1,{ϵ}_{q_1}^{\alpha })+D^{+}(q_2,)\right)=\frac{6}{\sqrt{2}}{g}_{Z_c}{g}_{D^{*}}{g}_D\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\delta }}^2\right){\tilde{\mathsf{\Phi }}}_{D^{*}}\left(-{(k_1+{\widehat{v}}_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_D\left(-{(k_2+{\widehat{u}}_4{q}_2)}^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left(S_4(k_2+q_1){\gamma }_5{S}_1\left(k_1\right){\gamma }_5{S}_3(k_1+q_2){\gamma }^{\mu }{S}_2\left(k_2\right){\gamma }^{\alpha }\right)-({\gamma }_5\leftrightarrow {\gamma }^{\mu })\right\}\hfill \\ =& A_{D^{*}D}{g}^{\mu \alpha }+B_{D^{*}D}{q}_1^{\mu }{q}_2^{\alpha },\hfill \end{array}$$

(61)

with the argument of the $Z_c$-vertex function being:

$$\begin{array}{ccc}\hfill {\delta }_1& =& -\frac{1}{2\sqrt{2}}\left(k_1-k_2+(w_1-w_2)(q_1+q_2)\right),\hfill \\ {\delta }_2& =& +\frac{1}{2\sqrt{2}}\left(k_1-k_2-(1+w_3-w_4)q_1+(1-w_3+w_4)q_2\right),\hfill \\ {\delta }_3& =& -\frac{1}{2}\left(k_1+k_2+(w_1+w_2)(q_1+q_2)\right),{\overrightarrow{\delta }}^2={\delta }_1^2+{\delta }_2^2+{\delta }_3^2.\end{array}$$

(62)

Now, the notation used is $m_1=m_2=m_c$, $m_3=m_4=m_d=m_u$, ${\widehat{v}}_2=m_2/(m_2+m_4)$, ${\widehat{v}}_4=m_4/(m_2+m_4)$, ${\widehat{u}}_1=m_1/(m_1+m_3)$, and ${\widehat{u}}_3=m_3/(m_1+m_3)$.

The decay width for the $1^{+}\left(p\right)\to 1^{-}\left(q_v\right)+0^{-}\left(q_s\right)$ transition is given by:

$$\mathsf{\Gamma }=\frac{1}{8\pi }\frac{1}{2s+1}\frac{|{\mathbf{q}}_{\mathbf{v}}|}{m^2}(|H_{+1+1}{|}^2+|H_{-1-1}{|}^2+|H_{00}{|}^2),$$

(63)

where H denotes the helicity amplitudes and ${\mathbf{q}}_{\mathbf{v}}$ is the three-momentum of the final state vector particle $q_v^{\mu }=(E_v,0,0,|{\mathbf{q}}_{\mathbf{v}}|)$. The helicity amplitudes can be related to the invariant amplitudes ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$, which parametrize the matrix element in terms of the Lorentz structures:

$$M={\mathcal{A}}_{1}m{g}^{\mu \rho }+{\mathcal{A}}_2\frac{1}{m}{q}_1^{\mu }{q}_2^{\rho }$$

(64)

by means of the relations:

$$H_{00}=-\frac{m}{m_1}{E}_v{\mathcal{A}}_1-\frac{1}{m_1}{|{\mathbf{q}}_{\mathbf{v}}|}^2{\mathcal{A}}_2,H_{+1+1}=H_{-1-1}=-m{\mathcal{A}}_1.$$

From the comparison of Equation (64) with Equations (58)–(61), one can express ${\mathcal{A}}_{1,2}$ as a function of $A_{xy},B_{xy}$. The results are importantly influenced by the fact that the amplitudes $A_{\overline{D}{D}^{*}}$ and $A_{D^{*}D}$ (Formulas (60) and (61)) vanish exactly within the CCQM description $A_{\overline{D}{D}^{*}}=A_{D^{*}D}=0$, and the contributions from the non-zero B amplitudes are strongly suppressed by the ${|{\mathbf{q}}_{\mathbf{v}}|}^5$ factor. Before arriving at the numerical predictions, the size parameters need to be specified, and a strategy with respect to the choice of ${\mathsf{\Lambda }}_{Z_c}$ value has to be settled. The numerical values of the size parameters were in [80] (i.e., the herein presented $Z_c$ analysis) re-adjusted with respect to those in [78] and are shown in Table 3.

Table 3. The size parameters for selected mesons in GeV used in the $Z_c\left(3900\right)$ analysis.

${\mathbf{\Lambda }}_{\mathbf{\pi }}$	${\mathbf{\Lambda }}_{\mathbf{\rho }/\mathbf{\omega }}$	${\mathbf{\Lambda }}_{\mathit{D}}$	${\mathbf{\Lambda }}_{\mathit{D}*}$	${\mathbf{\Lambda }}_{\mathit{J}/\mathbf{\psi }}$	${\mathbf{\Lambda }}_{{\mathbf{\eta }}_{\mathbf{c}}}$
$0.711$	$0.295$	$1.4$	$2.3$	$3.3$	$3.0$

As concerns the ${\mathsf{\Lambda }}_{Z_c}$ parameter, first, it is taken as ${\mathsf{\Lambda }}_{Z_c}=2.24\pm 0.10$ GeV to make the predicted value of the decay width $\mathsf{\Gamma }(Z_c^{+}\to J/\psi +{\pi }^{+})$ close to the one from [152,176]. One obtains:

$$\begin{array}{ccc}\hfill \mathsf{\Gamma }(Z_c^{+}\to J/\psi +{\pi }^{+})& =& \left({27.9}_{-5.0}^{+6.3}\right)\mathrm{MeV},\mathsf{\Gamma }(Z_c^{+}\to {\overline{D}}^0+D^{*+})\propto {10}^{-8}\mathrm{MeV},\hfill \\ \mathsf{\Gamma }(Z_c^{+}\to {\eta }_c+{\rho }^{+})& =& \left({35.7}_{-5.2}^{+6.3}\right)\mathrm{MeV},\mathsf{\Gamma }(Z_c^{+}\to {\overline{D}}^{*0}+D^{+})\propto {10}^{-8}\mathrm{MeV}.\end{array}$$

(65)

These outputs contradict the experimental number (see Equation (55)), which indicates a larger coupling to $D{D}^{*}$ than to the $J/\psi \pi$ mode. If trying to adjust the ${\mathsf{\Lambda }}_{Z_c}$ parameter to a more realistic value, the results do not become any better. Assuming ${\mathsf{\Lambda }}_{Z_c}=3.3\pm 1.1\mathrm{GeV}$, one gets:

$$\begin{array}{ccc}\hfill \mathsf{\Gamma }(Z_c^{+}\to J/\psi +{\pi }^{+})& =& \left({4.3}_{-0.6}^{+0.7}\right)\mathrm{MeV},\mathsf{\Gamma }(Z_c^{+}\to {\overline{D}}^0+D^{*+})\propto {10}^{-9}\mathrm{MeV},\hfill \\ \mathsf{\Gamma }(Z_c^{+}\to {\eta }_c+{\rho }^{+})& =& \left({8.0}_{-1.0}^{+1.2}\right)\mathrm{MeV},\mathsf{\Gamma }(Z_c^{+}\to {\overline{D}}^{*0}+D^{+})\propto {10}^{-9}\mathrm{MeV}.\end{array}$$

(66)

These predictions suggest that the tetraquark picture is not appropriate for the $Z_c\left(3900\right)$ state.

The molecular description of $Z_c\left(3900\right)$ appears as a natural alternative. In such a scenario, the non-local interpolation quark current is written as [53]:

$$J_{4q}^{\mu }=\frac{1}{\sqrt{2}}\left\{\left(\overline{d}\left(x_3\right){\gamma }_{5}c\left(x_1\right)\right)\left(\overline{c}\left(x_2\right){\gamma }^{\mu }u\left(x_4\right)\right)+\left(\overline{d}\left(x_3\right){\gamma }^{\mu }c\left(x_1\right)\right)\left(\overline{c}\left(x_2\right){\gamma }_{5}u\left(x_4\right)\right)\right\}.$$

(67)

By using similar steps as in the tetraquark analysis, one writes down the Fourier transformed $Z_c$ mass operator in the form:

$$\begin{array}{ccc}\hfill {\Pi }_{Z_c}^{\mu \nu }\left(p\right)& =& \frac{9}{2}\prod _{i=1}^3\int \frac{d^4{k}_i}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}^2\left(-{\overrightarrow{\omega }}^2\right)\hfill \\ & \times & \{\mathrm{tr}\left[{\gamma }_5{S}_1\left({\widehat{k}}_1\right){\gamma }_5{S}_3\left({\widehat{k}}_3\right)\right]·\mathrm{tr}\left[{\gamma }^{\mu }{S}_4\left({\widehat{k}}_4\right){\gamma }^{\nu }{S}_2\left({\widehat{k}}_2\right)\right]\hfill \\ & & +\mathrm{tr}\left[{\gamma }^{\mu }{S}_1\left({\widehat{k}}_1\right){\gamma }^{\nu }{S}_3\left({\widehat{k}}_3\right)\right]·\mathrm{tr}\left[{\gamma }_5{S}_4\left({\widehat{k}}_4\right){\gamma }_5{S}_2\left({\widehat{k}}_2\right)\right]\}\hfill \end{array}$$

(68)

in order to pin down the ${\mathsf{\Lambda }}_{Zc}$ dependence of the coupling $g_{Z_c}$. Next, the transition amplitudes are constructed:

$$\begin{array}{cc}& M^{\mu \nu }\left(Z_c(p,{ϵ}_p^{\mu })\to J/\psi (q_1,{ϵ}_{q_1}^{\nu })+{\pi }^{+}\left(q_2\right)\right)=\frac{3}{\sqrt{2}}{g}_{Z_c}{g}_{J/\psi }{g}_{\pi }\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{J/\psi }\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left({\gamma }_5{S}_1\left(k_1\right){\gamma }^{\nu }{S}_2(k_1+q_1){\gamma }^{\mu }{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2)\right)+({\gamma }_5\leftrightarrow {\gamma }^{\mu })\right\}\hfill \\ =& A_{J/\psi \pi }{g}^{\mu \nu }+B_{J/\psi \pi }{q}_1^{\mu }{q}_2^{\nu }.\hfill \end{array}$$

(69)

$$\begin{array}{cc}& M^{\mu \alpha }\left(Z_c(p,{ϵ}_p^{\mu })\to {\eta }_c\left(q_1\right)+\rho (q_2,{ϵ}_{q_2}^{\alpha })\right)=\frac{3}{\sqrt{2}}{g}_{Z_c}{g}_{{\eta }_c}{g}_{\rho }\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{{\eta }_c}\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\rho }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left({\gamma }_5{S}_1\left(k_1\right){\gamma }_5{S}_2(k_1+q_1){\gamma }^{\mu }{S}_4\left(k_2\right){\gamma }^{\alpha }{S}_3(k_2+q_2)\right)+({\gamma }_5\leftrightarrow {\gamma }^{\mu })\right\}\hfill \\ =& A_{{\eta }_c\rho }{g}^{\mu \alpha }-B_{{\eta }_c\rho }{q}_2^{\mu }{q}_1^{\alpha },\hfill \end{array}$$

(70)

$$\begin{array}{cc}& M^{\mu \nu }\left(Z_c(p,{ϵ}_p^{\mu })\to {\overline{D}}^0\left(q_1\right)+D^{*+}(q_2,{ϵ}_{q_2}^{\nu })\right)=\frac{9}{\sqrt{2}}{g}_{Z_c}{g}_D{g}_{D^{*}}\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\delta }}^2\right){\tilde{\mathsf{\Phi }}}_D\left(-{(k_2+v_4{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{D^{*}}\left(-{(k_1+u_1{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left({\gamma }^{\mu }{S}_1\left(k_1\right){\gamma }^{\nu }{S}_3(k_1+q_2)\right)·\mathrm{tr}\left({\gamma }_5{S}_4\left(k_2\right){\gamma }_5{S}_2(k_2+q_1)\right)\hfill \\ =& A_{\overline{D}{D}^{*}}{g}^{\mu \nu }-B_{\overline{D}{D}^{*}}{q}_2^{\mu }{q}_1^{\nu },\hfill \end{array}$$

(71)

$$\begin{array}{cc}& M^{\mu \alpha }\left(Z_c(p,{ϵ}_p^{\mu })\to {\overline{D}}^{*0}(q_1,{ϵ}_{q_1}^{\alpha })+D^{+}\left(q_2\right)\right)=\frac{9}{\sqrt{2}}{g}_{Z_c}{g}_{D^{*}}{g}_D\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\overrightarrow{\delta }}^2\right){\tilde{\mathsf{\Phi }}}_{D^{*}}\left(-{(k_1+{\widehat{v}}_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_D\left(-{(k_2+{\widehat{u}}_4{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left({\gamma }_5{S}_1\left(k_1\right){\gamma }_5{S}_3(k_1+q_2)\right)·\mathrm{tr}\left({\gamma }^{\mu }{S}_4\left(k_2\right){\gamma }^{\alpha }{S}_2(k_2+q_1)\right)\hfill \\ =& A_{D^{*}D}{g}^{\mu \alpha }+B_{D^{*}D}{q}_1^{\mu }{q}_2^{\alpha },\hfill \end{array}$$

(72)

where the argument of the function ${\tilde{\mathsf{\Phi }}}_{Z_c}$ is given by:

$$\begin{array}{ccc}\hfill {\delta }_1& =& -\frac{1}{2\sqrt{2}}\left(k_1+k_2+(1+w_1-w_2)q_1+(w_1-w_2)q_2)\right),\hfill \\ {\delta }_2& =& +\frac{1}{2\sqrt{2}}\left(k_1+k_2-(w_3-w_4)q_1+(1-w_3+w_4)q_2\right),\hfill \\ {\delta }_3& =& +\frac{1}{2}\left(-k_1+k_2+(1-w_1-w_2)q_1-(w_1+w_2)q_2)\right),{\overrightarrow{\delta }}^2={\delta }_1^2+{\delta }_2^2+{\delta }_3^2.\end{array}$$

(73)

The meaning of all other letters and symbols is the same as was in the previous paragraph dedicated to the tetraquark description. The decay widths are also evaluated in a fully analogous way. However, the parameter ${\mathsf{\Lambda }}_{Z_c}$ needs to be adjusted independently. Tuning its value in such a way so as to provide the best description of the BESIII measurement [27], one gets ${\mathsf{\Lambda }}_{Z_c}=3.3\pm 1.1$ GeV with the following values for the decay widths:

$$\begin{array}{ccc}\hfill \mathsf{\Gamma }(Z_c^{+}\to J/\psi +{\pi }^{+})& =& (1.8\pm 0.3)\mathrm{MeV},\mathsf{\Gamma }(Z_c^{+}\to {\overline{D}}^0+D^{*+})=\left({10.0}_{-1.4}^{+1.7}\right)\mathrm{MeV},\hfill \\ \mathsf{\Gamma }(Z_c^{+}\to {\eta }_c+{\rho }^{+})& =& \left({3.2}_{-0.4}^{+0.5}\right)\mathrm{MeV},\mathsf{\Gamma }(Z_c^{+}\to {\overline{D}}^{*0}+D^{+})=\left({9.0}_{-1.3}^{+1.6}\right)\mathrm{MeV}.\end{array}$$

(74)

One can see that the obtained results at this time are in agreement with the experimental observations by showing an enhancement of the $D{D}^{*}$ sector and are in agreement with the observed branching fraction ratio in Equation (55) within the errors. One can conclude that the CCQM supports the molecular picture of the $Z_c\left(3900\right)$ state.

6. The Nature of $\mathit{Y}\left(\mathbf{4260}\right)$

The distinctive characteristics of the $Y\left(4260\right)$ are its mass, which does not fit any charmonium in the same mass region, the suppression of open charm decays with respect to the $J/\psi {\pi }^{+}{\pi }^{-}$ final state, and the appearance of the exotic charmonium $Z_c\left(3900\right)$ among its decay products. This interesting mix of properties is addressed in quite a few theoretical works, and like in other cases, the molecular, tetraquark, and several other explanations are invoked.

A support for the molecular picture was provided by the QCD lattice computations in [185], by QCD sum rules in [186], by a meson exchange model in [187], and also by the authors of [188], which favored it over the hadro-charmonium interpretation. Further arguments for $Y\left(4260\right)$ being a molecule were based on the line shape study in [189], and the authors of [190] proposed an unconventional state with a large, but not completely dominant molecular component. An interesting paper [191] came up with a baryonic molecule concept, and the molecular hypothesis was also analyzed in [192,193,194,195].

On the contrary, the molecular scenario is strongly disfavored in [196] because of reasons related to the heavy quark spin symmetry and the molecular scenario was rejected in [197] in favor of a charmonium hybrid one. Here, the crux of the argument lies in an important separation between $Y\left(4260\right)$ mass and its decay threshold. Further arguments to support the charmonium or hybrid-charmonium picture were given in the publications [198,199,200].

One should also mention different quark models [201,202,203,204] with some of them favoring the tetraquark description of $Y\left(4260\right)$. The tetraquark hypothesis was also analyzed in the QCD sum rules study [205], and the coupled channels approach combined with the three-particle Faddeev equations was used to describe $Y\left(4260\right)$ in [206].

The analysis of $Y\left(4260\right)$ is within the CCQM [207] done in a similar way to the $Z_c$ case: its decay modes are analyzed in both the molecular and tetraquark scenario. With quantitative measurements related to $Y\left(4260\right)$ not being very numerous, one can analyze the partial decay widths to $J/\psi {\pi }^{+}{\pi }^{-}$ and open charm final states and see whether the latter ones are suppressed. The Feynman diagrams describing the studied transitions are drawn in Figure 7. The considered open charm final states include $D\overline{D}$, $D{\overline{D}}^{*}$, $D^{*}\overline{D}$, and $D^{*}{\overline{D}}^{*}$. As follows from the previous section, $Z_c\left(3900\right)$ is described as a molecular state (67).

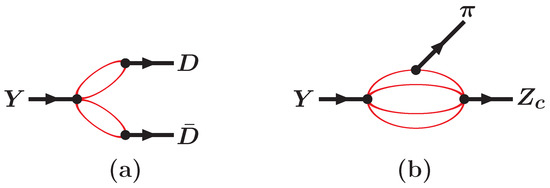
Figure 7. Feynman diagrams of the $Y\left(4260\right)$ decay to open charm (a) and $Z_c\pi$ (b).

The molecular-type non-local interpolating current for $Y\left(4260\right)$ is written as:

$$\begin{array}{ccc}\hfill J_{Y^{\mathrm{mol}}}^{\mu }\left(x\right)& =& \int d{x}_1\dots \int d{x}_4\delta \left(x-\sum _{i=1}^4{w}_i{x}_i\right){\mathsf{\Phi }}_Y\left(\sum _{i<j}{(x_i-x_j)}^2\right)J_{Y^{\mathrm{mol}};4q}^{\mu }(x_1,\dots ,x_4),\hfill \\ \hfill J_{Y^{\mathrm{mol}};4q}^{\mu }& =& \frac{1}{\sqrt{2}}\left\{\left(\overline{q}\left(x_3\right){\gamma }_{5}c\left(x_1\right)\right)·\left(\overline{c}\left(x_2\right){\gamma }^{\mu }{\gamma }_{5}q\left(x_4\right)\right)-({\gamma }_5\leftrightarrow {\gamma }^{\mu }{\gamma }_5)\right\},(q=u,d)\hfill \end{array}$$

(75)

with:

$$w_1=w_2=\frac{m_c}{2(m_q+m_c)},w_3=w_4=\frac{m_q}{2(m_q+m_c)}.$$

The matrix element corresponding to the open charm production is given by:

$$\begin{array}{cc}& M\left(Y_u(p,{ϵ}_p^{\mu })\to D_1^0\left(p_1\right)+{\overline{D}}_2^0\left(p_2\right)\right)=\frac{9}{\sqrt{2}}{g}_Y{g}_{D_1}{g}_{D_2}\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_Y\left(-{\mathsf{\Omega }}_q^2\right){\tilde{\mathsf{\Phi }}}_{D_1}\left(-{\ell }_1^2\right){\tilde{\mathsf{\Phi }}}_{D_2}\left(-{\ell }_2^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left({\gamma }_5{S}_c\left(k_1\right){\mathsf{\Gamma }}_2{S}_u\left(k_3\right)\right)\mathrm{tr}\left({\gamma }^{\mu }{\gamma }_5{S}_u\left(k_2\right){\mathsf{\Gamma }}_1{S}_c\left(k_4\right)\right)-({\gamma }_5\leftrightarrow {\gamma }^{\mu }{\gamma }_5)\right\},\hfill \end{array}$$

(76)

where:

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}_1\otimes {\mathsf{\Gamma }}_2=\left\{\begin{array}{cc}{\gamma }_5\otimes {\gamma }_5\hfill & \mathrm{for}D\overline{D}\hfill \\ {ϵ}_{{\nu }_1}^{*}{\gamma }^{{\nu }_1}\otimes {\gamma }_5\hfill & \mathrm{for}{D}^{*}\overline{D}\hfill \\ {ϵ}_{{\nu }_1}^{*}{\gamma }^{{\nu }_1}\otimes {ϵ}_{{\nu }_2}^{*}{\gamma }^{{\nu }_2}\hfill & \mathrm{for}{D}^{*}{\overline{D}}^{*}\hfill \end{array}\right.\end{array}$$

(77)

and the momenta are defined as:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_q^2& =& \frac{1}{2}\sum _{i\le j}{q}_i{q}_j,q_1=-k_1-w_1^{Y}p,q_2=k_4-w_2^{Y}p,q_3=k_3-w_3^{Y}p,\hfill \\ \hfill {\ell }_1& =& k_2+w_u^D{p}_1,{\ell }_2=-k_1-w_c^D{p}_2,k_3=k_1+p_2,k_4=k_2+p_1.\hfill \end{array}$$

The decay into $Z_c+\pi$ involves a three-loop diagram, and the corresponding matrix element is:

$$\begin{array}{cc}& M\left(Y_u(p,{ϵ}^{\mu })\to Z_c^{+}(p_1,{ϵ}^{\nu })+{\pi }^{-}\right)=\frac{9}{2}{g}_Y{g}_{Z_c}{g}_{\pi }\hfill \\ \times & \prod _{j=1}^3\left[\int \frac{d^4{k}_j}{{\left(2\pi \right)}^{4}i}\right]{\tilde{\mathsf{\Phi }}}_Y\left(-{\mathsf{\Omega }}_q^2\right){\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\mathsf{\Omega }}_r^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{\ell }^2\right){ϵ}_{\mu }\left(p\right){ϵ}_{\nu }^{*}\left(p_1\right)\hfill \\ \times & \sum _{\mathsf{\Gamma }}\mathrm{tr}\left({\mathsf{\Gamma }}_1{S}_c\left(k_1\right){\mathsf{\Gamma }}_2{S}_u\left(k_2\right)\right)\mathrm{tr}\left({\mathsf{\Gamma }}_3{S}_u\left(k_3\right){\mathsf{\Gamma }}_4{S}_d\left(k_4\right){\mathsf{\Gamma }}_5{S}_c\left(k_5\right)\right),\hfill \end{array}$$

(78)

where:

$$\begin{array}{cc}& \sum _{\mathsf{\Gamma }}\left[{\mathsf{\Gamma }}_1\otimes {\mathsf{\Gamma }}_2\right]·\left[{\mathsf{\Gamma }}_3\otimes {\mathsf{\Gamma }}_4\otimes {\mathsf{\Gamma }}_5\right]=\left[{\gamma }_5\otimes {\gamma }_5\right]·\left[{\gamma }^{\mu }{\gamma }_5\otimes {\gamma }_5\otimes {\gamma }^{\nu }\right]\hfill \\ -& \left[{\gamma }^{\mu }{\gamma }_5\otimes {\gamma }^{\nu }\right]·\left[{\gamma }_5\otimes {\gamma }_5\otimes {\gamma }_5\right]-\left[{\gamma }^{\mu }{\gamma }_5\otimes {\gamma }_5\right]·\left[{\gamma }_5\otimes {\gamma }_5\otimes {\gamma }^{\nu }\right]\hfill \end{array}$$

and the momenta are defined as:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_q^2& =& \frac{1}{2}\sum _{i\le j}{q}_i{q}_j;q_1=-k_1-w_1^{Y}p,q_2=k_5-w_2^{Y}p,q_3=k_2-w_3^{Y}p,\hfill \\ {\mathsf{\Omega }}_r^2& =& \frac{1}{2}\sum _{i\le j}{r}_i{r}_j;r_1=-k_5+w_1^Z{p}_1,r_2=k_1+w_2^Z{p}_1,r_3=k_4-w_3^Z{p}_1,\\ \ell & =& k_3+w_u^{\pi }{p}_2,k_4=k_3+p_2,k_5=k_1-k_2+k_3+p.\hfill \end{array}$$

In the tetraquark scenario, the non-local $Y\left(4260\right)$ current takes the form:

$$\begin{array}{ccc}\hfill J_{Y^{\mathrm{tet}}}^{\mu }\left(x\right)& =& \int d{x}_1\dots \int d{x}_4\delta \left(x-\sum _{i=1}^4{w}_i^Y{x}_i\right){\mathsf{\Phi }}_Y\left(\sum _{i<j}{(x_i-x_j)}^2\right)J_{Y^{\mathrm{tet}};4q}^{\mu }(x_1,\dots ,x_4),\hfill \end{array}$$

(79)

$$\begin{array}{ccc}\hfill J_{Y^{\mathrm{tet}};4q}^{\mu }& =& \frac{1}{\sqrt{2}}{ϵ}_{abc}{ϵ}_{dec}\left\{\left(q_a\left(x_4\right)C{\gamma }_5{c}_b\left(x_1\right)\right)\left({\overline{q}}_d\left(x_3\right){\gamma }^{\mu }{\gamma }_{5}C{\overline{c}}_e\left(x_2\right)\right)-({\gamma }_5\leftrightarrow {\gamma }^{\mu }{\gamma }_5)\right\}.\hfill \end{array}$$

(80)

The matrix element of the decay into $D\overline{D}$ is expressed as:

$$\begin{array}{cc}& M\left(Y_u^{\mathrm{tet}}(p,{ϵ}_p^{\mu })\to D_1^0\left(p_1\right)+{\overline{D}}_2^0\left(p_2\right)\right)=\frac{6}{\sqrt{2}}{g}_Y{g}_{D_1}{g}_{D_2}\hfill \\ \times & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_Y\left(-{\mathsf{\Omega }}_q^2\right){\tilde{\mathsf{\Phi }}}_{D_1}\left(-{\ell }_1^2\right){\tilde{\mathsf{\Phi }}}_{D_2}\left(-{\ell }_2^2\right)\hfill \\ \times & \left\{\mathrm{tr}\left({\gamma }_5{S}_c\left(k_1\right){\mathsf{\Gamma }}_2^D{S}_u\left(k_3\right){\gamma }^{\mu }{\gamma }_5{S}_c\left(k_2\right){\mathsf{\Gamma }}_1^D{S}_u\left(k_4\right)\right)-({\gamma }_5\leftrightarrow {\gamma }^{\mu }{\gamma }_5)\right\},\hfill \end{array}$$

(81)

with the momenta:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_q^2& =& \frac{1}{2}\sum _{i\le j}{q}_i{q}_j;q_1=-k_1-w_1^{Y}p,q_2=-k_2-w_2^{Y}p,q_3=k_3-w_3^{Y}p,\hfill \\ {\ell }_1& =& -k_2-w_c^D{p}_1,{\ell }_2=-k_1-w_c^D{p}_2,k_3=k_1+p_2,k_4=k_2+p_1.\hfill \end{array}$$

The matrix element of the decay into $Z_c\pi$ is given by:

$$\begin{array}{cc}& M\left(Y_u^{\mathrm{tet}}(p,{ϵ}^{\mu })\to Z_c^{+}(p_1,{ϵ}^{\nu })+{\pi }^{-}\left(p_2\right)\right)=3g_Y{g}_{Z_c}{g}_{\pi }\hfill \\ \times & \prod _{j=1}^3\left[\int \frac{d^4{k}_j}{{\left(2\pi \right)}^{4}i}\right]{\tilde{\mathsf{\Phi }}}_Y\left(-{\mathsf{\Omega }}_q^2\right){\tilde{\mathsf{\Phi }}}_{Z_c}\left(-{\mathsf{\Omega }}_r^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{\ell }^2\right)\hfill \\ \times & {ϵ}_{\mu }\left(p\right){ϵ}_{\nu }^{*}\left(p_1\right)\sum _{\mathsf{\Gamma }}\mathrm{tr}\left[{\mathsf{\Gamma }}_1^Y{S}_c\left(k_1\right){\mathsf{\Gamma }}_2^Z{S}_u\left(k_2\right){\mathsf{\Gamma }}_2^Y{S}_c\left(k_3\right){\overline{\mathsf{\Gamma }}}_1^Z{S}_d\left(k_4\right){\gamma }_5{S}_u\left(k_5\right)\right],\hfill \end{array}$$

(82)

with the momenta:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_q^2& =& \frac{1}{2}\sum _{i\le j}{q}_i{q}_j;q_1=-k_1-w_1^{Y}p,q_2=-k_3-w_2^{Y}p,q_3=k_2-w_3^{Y}p,\hfill \\ {\mathsf{\Omega }}_r^2& =& \frac{1}{2}\sum _{i\le j}{r}_i{r}_j;r_1=k_3+w_1^Z{p}_1,r_2=k_1+w_2^Z{p}_1,r_3=-k_4+w_3^Z{p}_1,\\ \ell & =& -k_4-w_d^{\pi }{p}_2,k_4=k_1-k_2+k_3+p_1,k_5=k_1-k_2+k_3+p.\hfill \end{array}$$

Here, the summation over $\mathsf{\Gamma }$ is defined by:

$$\sum _{\mathsf{\Gamma }}={\left[{\gamma }_5\otimes {\gamma }^{\mu }{\gamma }_5-{\gamma }^{\mu }{\gamma }_5\otimes {\gamma }_5\right]}^Y\otimes {\left[{\gamma }_5\otimes {\gamma }^{\nu }-{\gamma }^{\nu }\otimes {\gamma }_5\right]}^Z.$$

The considered decays comprise different combinations of pseudoscalar, vector, and axial-vector particles in the final state. The relevant expressions for the matrix elements and decay widths are written down:

$$\begin{array}{c}M(V\left(p\right)\to P\left(p_1\right)+P\left(p_2\right))={ϵ}_V^{\mu }{q}_{\mu }{G}_{VPP},q=p_1-p_2,\hfill \\ \mathsf{\Gamma }(V\to PP)=\frac{|{\mathbf{p}}_{\mathbf{1}}{|}^3}{6\pi m^2}{G}_{VPP}^2,\hfill \end{array}$$

$$\begin{array}{c}M(V\left(p\right)\to A\left(p_1\right)+P\left(p_2\right))={ϵ}_V^{\mu }{ϵ}_A^{*\nu }\left(g_{\mu \nu }A+p_{1\mu }{p}_{\nu }B\right),\hfill \\ \mathsf{\Gamma }(V\to AP)=\frac{|{\mathbf{p}}_{\mathbf{1}}|}{24\pi m^2}\{\left(3+\frac{|{\mathbf{p}}_{\mathbf{1}}{|}^2}{m_1^2}\right)A^2+\frac{m^2}{m_1^2}|{\mathbf{p}}_{\mathbf{1}}{|}^4{B}^2+\frac{m^2+m_1^2-m_2^2}{m_1^2}{|{\mathbf{p}}_{\mathbf{1}}|}^{2}AB,\hfill \end{array}$$

$$\begin{array}{c}M(V\left(p\right)\to V\left(p_1\right)+P\left(p_2\right))={ϵ}_V^{\mu }{ϵ}_V^{*{\nu }_1}{\epsilon }_{\mu {\nu }_1\alpha \beta }{p}^{\alpha }{p}_1^{\beta }{G}_{VVP},\hfill \\ \mathsf{\Gamma }(V\to VP)=\frac{|{\mathbf{p}}_{\mathbf{1}}{|}^3}{12\pi }{G}_{VVP}^2,\hfill \end{array}$$

$$\begin{array}{c}M(V\left(p\right)\to V\left(p_1\right)+V\left(p_2\right))={ϵ}_V^{\mu }{ϵ}_V^{*{\nu }_1}{ϵ}_V^{*{\nu }_2}\left\{p_{1\mu }{p}_{1{\nu }_2}{p}_{2{\nu }_1}A+g_{\mu {\nu }_1}{p}_{1{\nu }_2}B+g_{\mu {\nu }_2}{p}_{2{\nu }_1}C+g_{{\nu }_1{\nu }_2}{p}_{1\mu }D\right\},\hfill \end{array}$$

$$\begin{array}{c}\mathsf{\Gamma }(V\to V_1{V}_2)=\frac{|{\mathbf{p}}_{\mathbf{1}}{|}^3}{24\pi m_1^2{m}_2^2}\{m^2|{\mathbf{p}}_{\mathbf{1}}{|}^4{A}^2+[|{\mathbf{p}}_{\mathbf{1}}{|}^2-3m_1^2]B^2+[|{\mathbf{p}}_{\mathbf{1}}{|}^2+3m_2^2]C^2\hfill \\ +[|{\mathbf{p}}_{\mathbf{1}}{|}^2+3\frac{m_1^2{m}_2^2}{m^2}]D^2+|{\mathbf{p}}_{\mathbf{1}}{|}^2[m^2+m_1^2-m_2^2]AB+{|{\mathbf{p}}_{\mathbf{1}}|}^2[-m^2+m_1^2-m_2^2]AC\hfill \\ +|{\mathbf{p}}_{\mathbf{1}}{|}^2[m^2-m_1^2-m_2^2]AD+[2|{\mathbf{p}}_{\mathbf{1}}{|}^2-m^2+m_1^2+m_2^2]BC+[2|{\mathbf{p}}_{\mathbf{1}}{|}^2+m_1^2+\frac{m_1^2}{m^2}(m_2^2-m_1^2)]BD\hfill \\ +[-2|{\mathbf{p}}_{\mathbf{1}}{|}^2-m_2^2+\frac{m_2^2}{m^2}(m_2^2-m_1^2)]CD\}.\hfill \end{array}$$

The value of ${\mathsf{\Lambda }}_{Z_c}$ is set to $3.3$ GeV, and guided by our experience, we assume that ${\mathsf{\Lambda }}_{Y\left(4260\right)}=3.3\pm 0.1$ GeV. The numerical evaluation leads to the results presented in Table 4.

Table 4. Decay widths of the selected $Y\left(4260\right)$ transition in MeV.

Mode	Molecular-Type Current	Tetraquark Current
$Y\to Z_c^{+}+{\pi }^{-}$	$146\pm 13$	$5.77\pm 0.39$
$Y\to D^0+{\overline{D}}^0$	$11\pm 2$	$(0.42\pm 0.16)·{10}^{-3}$
$Y\to D^{*0}+{\overline{D}}^0$	$(0.39\pm 0.14)·{10}^{-2}$	$0.32\pm 0.09$
$Y\to D^{*0}+{\overline{D}}^{*0}$	0	$(0.19\pm 0.08)·{10}^{-3}$

In both scenarios, the open charm decays are suppressed with respect to the $J/\psi \pi$ decay channel. The discrimination between them is provided by the total decay width $\mathsf{\Gamma }[Y(4260)]=55\pm 19$ MeV, which is in contradiction with the molecular description. Thus, one can conclude that the CCQM approach favors the tetraquark structure of $Y\left(4260\right)$.

7. Bottomonium-Like States ${\mathit{Z}}_{\mathit{b}}\left(\mathbf{10610}\right)$ and ${\mathit{Z}}_{\mathit{b}}^{\prime }\left(\mathbf{10650}\right)$

Exotic quarkonia states appear also in the bottomonium sector: $Z_b\left(10610\right)$ and $Z_b^{\prime }\left(10650\right)$ are two examples. Even though the exotic bottomonia masses tend to be significantly higher than the charmonia ones, the underlying dynamics is similar, and one finds the molecular, tetraquark, and other hypotheses in theoretical approaches that describe them.

$Z_b\left(10610\right)$ and $Z_b^{\prime }\left(10650\right)$ were seen as molecules in the boson exchange model of [208], and the molecular picture was also favored in [209], where the spin structure of these two particles was analyzed. Further support of the molecular scenario came from the quark model based on a phenomenological Lagrangian used by the authors of [210] and also from other analyses preformed in [211] (QCD multipole expansion), [212] (effective field theory), [213] (pion exchange model), [214] (QCD sum rules, only $Z_b^{\prime }\left(10650\right)$ included), [215] (heavy quark spin symmetry and coupled channels analysis),and [216] (coupled channels approach with pion exchange model). A different set of works supports, with various intensity, the tetraquark structure of the two bottomonia states. In [217], the conclusion followed from an effective diquark-antidiquark Hamiltonian combined with meson-loop induced effects. The authors of [218] based their analysis on the QCD sum rules and interpreted $Z_b$ and $Z_b^{\prime }$ as axial-vector tetraquarks. The two works [219,220] also drew their conclusions from the QCD sum rules and allowed the tetraquark and molecular scenario. The former work suggested that $Z_b$ and $Z_b^{\prime }$ could have both the diquark-antidiquark and molecular components (following from a mixed interpolating current). The latter one excluded neither the tetraquark nor molecular the interpretation of $Z_b\left(10610\right)$, and the idea of a mixed current appeared also. The mentioned analyses could be supplemented by numerous other works [221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236,237,238,239,240,241] where further ideas and approaches were exploited.

The theoretical analysis of the $Z_b\left(10610\right)$ and $Z_b^{\prime }\left(10650\right)$ states by the CCQM was performed in [81]. The work assumed a molecular-type interpolating current, which is favored by most theoretical approaches when interpreting the experimental results. It is a natural choice reflecting the proximity of the particle masses to the corresponding thresholds:

$$\begin{array}{ccc}\hfill m\left(Z_b^{+}\right)& =& 10607.2\pm 2.0\mathrm{MeV},m\left(B^{*}\overline{B}\right)=10604\mathrm{MeV},\hfill \\ m\left({Z^{\prime }}_b^{+}\right)& =& 10652.2\pm 1.5\mathrm{MeV},m\left(B^{*}{\overline{B}}^{*}\right)=10649\mathrm{MeV}.\end{array}$$

The quantum numbers of the two states $I^G\left(J^{PC}\right)=1^{+}\left(1^{+-}\right)$ lead to the choice of (local) interpolating currents:

$$\begin{array}{ccc}\hfill J_{Z_b^{+}}^{\mu }& =& \frac{1}{\sqrt{2}}\left[\left(\overline{d}{\gamma }_{5}b\right)\left(\overline{b}{\gamma }^{\mu }u\right)+\left(\overline{d}{\gamma }^{\mu }b\right)\left(\overline{b}{\gamma }_{5}u\right)\right],\hfill \end{array}$$

(83)

$$\begin{array}{ccc}\hfill J_{Z_b^{\prime +}}^{\mu \nu }& =& {\epsilon }^{\mu \nu \alpha \beta }\left(\overline{d}{\gamma }_{\alpha }b\right)\left(\overline{b}{\gamma }_{\beta }u\right),\hfill \end{array}$$

(84)

which guarantees that, when considering the transitions into $B^{(*)}{\overline{B}}^{(*)}$, the $Z_b$ state can decay only to the $[{\overline{B}}^{*}B+c.c.]$ pair, while the $Z_b^{\prime }$ state can decay only to a ${\overline{B}}^{*}{B}^{*}$ pair. Decays into the $BB$ channels are not allowed.

Further decay channels include a bottomonium particle accompanied with a charged light meson. Taking into account the G parity, which is conserved in strong interactions and kinematic considerations, only three possible bottomonium-meson decay channels are available: $Z_b^{+}\to \mathsf{{\rm Y}}+{\pi }^{+}$, $Z_b^{+}\to h_b+{\pi }^{+}$ and $Z_b^{+}\to {\eta }_b+{\rho }^{+}$. All mentioned $Z_b^{+}$ transition can be arranged into three groups with respect to the spin kinematics:

$$\begin{array}{cc}{1}^{+}\to 1^{-}+0^{-}:\hfill & Z_b^{+}\to \mathsf{{\rm Y}}+{\pi }^{+},Z_b^{+}\to [{\overline{B}}^{*0}{B}^{+}+c.c.],Z_b^{+}\to {\eta }_b+{\rho }^{+},\hfill \\ 1^{+}\to 1^{+}+0^{-}:\hfill & Z_b^{+}\to h_b+{\pi }^{+},\hfill \\ 1^{+}\to 1^{-}+1^{-}:\hfill & Z_b^{+}\to {\overline{B}}^{*0}{B}^{*+}.\hfill \end{array}$$

The classification of the bottomonia particles based on their quantum numbers is shown in Table 5.

Table 5. The bottomonium states ${}^{2S+1}{L}_J$. We use the notation $\overleftrightarrow{\partial }=\overrightarrow{\partial }-\overleftarrow{\partial }$.

Quantum Number ${\mathit{I}}^{\mathit{G}}\left({\mathit{J}}^{\mathit{PC}}\right)$	Name	Quark Current	Mass (MeV)
$0^{+}\left(0^{-+}\right)$ ($S=0,L=0$)	${}^1{S}_0={\eta }_b\left(1S\right)$	$\overline{b}i{\gamma }^{5}b$	$9399.00\pm 2.30$
$0^{-}\left(1^{--}\right)$ ($S=1,L=0$)	${}^3{S}_1=\mathsf{{\rm Y}}$	$\overline{b}{\gamma }^{\mu }b$	$9460.30\pm 0.26$
$0^{+}\left(0^{++}\right)$ ($S=1,L=1$)	${}^3{P}_0={\chi }_{b0}$	$\overline{b}b$	$9859.44\pm 0.52$
$0^{+}\left(1^{++}\right)$ ($S=1,L=1$)	${}^3{P}_1={\chi }_{b1}$	$\overline{b}{\gamma }^{\mu }{\gamma }^{5}b$	$9892.72\pm 0.40$
$0^{-}\left(1^{+-}\right)$ ($S=0,L=1$)	${}^1{P}_1=h_b\left(1P\right)$	$\overline{b}{\overleftrightarrow{\partial }}^{\mu }{\gamma }^{5}b$	$9899.30\pm 0.80$

The expressions for matrix elements and decay widths depend on the spin structure and are for the three cases as follows.

• For $1^{+}\to 1^{-}+0^{-}$ transitions, the matrix element can be parameterized with two Lorentz structures:

  $$⟨1^{-}(q_1;\delta ),0^{-}\left(q_2\right)|T|1^{+}(p;\mu )⟩=(A{g}^{\mu \delta }+B{q}_1^{\mu }{q}_2^{\delta }){\epsilon }_{\mu }{\epsilon }_{1\delta }^{*}.$$

  (85)

  The invariant amplitudes A and B can be combined into the helicity amplitudes:

  $$\begin{array}{c}\hfill H_{00}=-\frac{E_1}{M_1}A-\frac{M}{M_1}|{\mathbf{q}}_{\mathbf{1}}{|}^{2}B,H_{+1+1}=H_{-1-1}=-A,\end{array}$$

  which are practical to express the decay width. For the derivation of the latter, it is useful to work in the rest frame of the initial particle, where $|{\mathbf{q}}_{\mathbf{1}}|={\lambda }^{1/2}(M^2,M_1^2,M_2^2)/2M$ is the three-momentum and $E_1=(M^2+M_1^2-M_2^2)/2M$ is the energy of the final state vector. Furthermore, the on-mass-shell character of the initial and final state particles is taken into account by $p^2=M^2$, $q_1^2=M_1^2$, $q_2^2=M_2^2$, and $p^{\mu }{\epsilon }_{\mu }=0$. One arrives at:

  $$\mathsf{\Gamma }=\frac{|{\mathbf{q}}_{\mathbf{1}}|}{24\pi M^2}\left\{|H_{+1+1}{|}^2+|H_{-1-1}{|}^2+{|H_{00}|}^2\right\}.$$

  (86)
• The matrix element for the $1^{+}\to 1^{+}+0^{-}$ transitions is expressed through one covariant term only:

  $$⟨1^{+}(q_1;\delta ),0^{-}\left(q_2\right)|T|1^{+}(p;\mu )⟩=C{q}_{1\alpha }{q}_{2_{\beta }}{\epsilon }^{\alpha \beta \mu \delta }{\epsilon }_{\mu }{\epsilon }_{1\delta }^{*}.$$

  (87)

  The decay with the formula can be written as:

  $$\mathsf{\Gamma }=\frac{|{\mathbf{q}}_{\mathbf{1}}{|}^{\mathbf{3}}}{12\pi M^2}{C}^2,$$

  (88)

  where one can note the p-wave suppression factor $|{\mathbf{q}}_{\mathbf{1}}{|}^{\mathbf{3}}$.
• As shown in [81], the matrix element for $1^{+}\to 1^{-}+1^{-}$ decay can be parameterized using three amplitudes:

  $$⟨1^{-}(q_1;\delta ),1^{-}(q_2;\rho )|T|1^{+}(p;\mu )⟩=\left(B_1{\epsilon }^{q_1{q}_2\rho \delta }{q}_1^{\mu }+B_2{\epsilon }^{q_1\mu \rho \delta }+B_3{\epsilon }^{q_2\mu \rho \delta }\right){\epsilon }_{\mu }{\epsilon }_{\delta }{\epsilon }_{\rho }.$$

  (89)

  The relation between the helicity amplitudes $H_{\lambda ;{\lambda }_1{\lambda }_2}$ ($\lambda ={\lambda }_1-{\lambda }_2$) and the invariant amplitudes can be shown to be:

  $$\begin{array}{ccc}\hfill H_{0;+1+1}& =& -H_{0;-1-1}=-E_1{A}_1-E_2{A}_2-M|{\mathbf{q}}_{\mathbf{1}}{|}^2{A}_5,\hfill \\ H_{+1;+10}& =& -H_{-1;-10}=\frac{(E_{1}M-M_1^2)}{M_2}{A}_1+M_2{A}_2-\frac{M^2}{M_2}|{\mathbf{q}}_{\mathbf{1}}{|}^2{A}_4,\\ H_{-1;0+1}& =& -H_{+1;0-1}=M_1{A}_1+\frac{(E_{1}M-M_1^2)}{M_1}{A}_2-\frac{M^2}{M_1}|{\mathbf{q}}_{\mathbf{1}}{|}^2{A}_3.\end{array}$$

  (90)
  The rate of the decay $1^{+}\left(p\right)\to 1^{-}\left(q_1\right)+1^{-}\left(q_2\right)$, finally, reads:

  $$\mathsf{\Gamma }=\frac{|{\mathbf{q}}_{\mathbf{1}}|}{24\pi M^2}·2\left\{|H_{0;+1+1}{|}^2+|H_{+1;+1}{|}^2+{|H_{-1;0+1}|}^2\right\}.$$

  (91)

Coming back to the CCQM description, one can write the non-local versions of Equations (83) and (84) as follows:

$$\begin{array}{ccc}\hfill J_{Z_b^{+}}^{\mu }\left(x\right)& =& \int d{x}_1\dots \int d{x}_4\delta \left(x-\sum _{i=1}^4{w}_i{x}_i\right){\mathsf{\Phi }}_{Z_b;Z_b;Z_b}\left(\sum _{i<j}{(x_i-x_j)}^2\right)J_{4q}^{\mu }(x_1,\dots ,x_4),\hfill \\ \hfill J_{Z_b;4q}^{\mu }& =& \frac{1}{\sqrt{2}}\left\{\left(\overline{d}\left(x_3\right){\gamma }_{5}b\left(x_1\right)\right)\left(\overline{b}\left(x_2\right){\gamma }^{\mu }u\left(x_4\right)\right)+\left(\overline{d}\left(x_3\right){\gamma }^{\mu }b\left(x_1\right)\right)\left(\overline{b}\left(x_2\right){\gamma }_{5}u\left(x_4\right)\right)\right\},\hfill \end{array}$$

(92)

$$\begin{array}{ccc}\hfill J_{Z_b^{\prime +}}^{\mu \nu }\left(x\right)& =& \int d{x}_1\dots \int d{x}_4\delta \left(x-\sum _{i=1}^4{w}_i{x}_i\right){\mathsf{\Phi }}_{Z_b}\left(\sum _{i<j}{(x_i-x_j)}^2\right)J_{Z_b^{\prime };4q}^{\mu \nu }(x_1,\dots ,x_4),\hfill \\ \hfill J_{Z_b^{\prime };4q}^{\mu \nu }& =& {\epsilon }^{\mu \nu \alpha \beta }\left(\overline{d}\left(x_3\right){\gamma }_{\alpha }b\left(x_1\right)\right)\left(\overline{b}\left(x_2\right){\gamma }_{\beta }u\left(x_4\right)\right),\hfill \end{array}$$

(93)

The interaction Lagrangian is constructed in the usual way for $Z_b$; in the case of $Z_b^{\prime }$, the stress tensor of the field is introduced $Z_{b,\mu \nu }^{\prime }={\partial }_{\mu }{Z}_{b,\nu }^{\prime }-{\partial }_{\nu }{Z}_{b,\mu }^{\prime }$:

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\mathrm{int},Z_b}& =& g_{Z_b}{Z}_{b,\mu }\left(x\right)·J_{Z_b}^{\mu }\left(x\right)+\mathrm{H}.\mathrm{c}.,\hfill \end{array}$$

(94)

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\mathrm{int},Z_b^{\prime }}& =& \frac{g_{Z_b^{\prime }}}{2M_{Z_b^{\prime }}}{Z}_{b,\mu \nu }^{\prime }\left(x\right)·J_{Z_b^{\prime }}^{\mu \nu }\left(x\right)+\mathrm{H}.\mathrm{c}..\hfill \end{array}$$

(95)

The factor $2M_{Z_b^{\prime }}$ is put into the denominator in order to preserve the same physical dimensions of the $g_{Z_b}$ and $g_{Z_b^{\prime }}$ couplings. The link between these couplings and the size parameters is done via the compositeness condition, which is based on the evaluation of hadronic mass operators. The latter are written in the momentum space as:

$$\begin{array}{ccc}\hfill {\tilde{\Pi }}_{Z_b}^{\mu \nu }\left(p\right)& =& \frac{9}{2}\prod _{i=1}^3\int \frac{d^4{k}_i}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b}^2\left(-{\overrightarrow{\omega }}^2\right)\hfill \\ & \times & \{\mathrm{tr}\left[{\gamma }_5{S}_1\left({\widehat{k}}_1\right){\gamma }_5{S}_3\left({\widehat{k}}_3\right)\right]\mathrm{tr}\left[{\gamma }^{\mu }{S}_4\left({\widehat{k}}_4\right){\gamma }^{\nu }{S}_2\left({\widehat{k}}_2\right)\right]\hfill \\ & & +\mathrm{tr}\left[{\gamma }^{\mu }{S}_1\left({\widehat{k}}_1\right){\gamma }^{\nu }{S}_3\left({\widehat{k}}_3\right)\right]\mathrm{tr}\left[{\gamma }_5{S}_4\left({\widehat{k}}_4\right){\gamma }_5{S}_2\left({\widehat{k}}_2\right)\right]\},\end{array}$$

(96)

$$\begin{array}{ccc}\hfill {\tilde{\Pi }}_{Z_b^{\prime }}^{\mu \nu }\left(p\right)& =& -9\frac{{\epsilon }^{\mu p\alpha \beta }{\epsilon }^{\nu p\rho \sigma }}{M_{Z_b^{\prime }}^2}\prod _{i=1}^3\int \frac{d^4{k}_i}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b^{\prime }}^2\left(-{\overrightarrow{\omega }}^2\right)\hfill \\ & \times & \mathrm{tr}\left[{\gamma }_{\rho }{S}_1\left({\widehat{k}}_1\right){\gamma }_{\alpha }{S}_3\left({\widehat{k}}_3\right)\right]\mathrm{tr}\left[{\gamma }_{\beta }{S}_4\left({\widehat{k}}_4\right){\gamma }_{\sigma }{S}_2\left({\widehat{k}}_2\right)\right],\hfill \end{array}$$

(97)

where ${\overrightarrow{\omega }}^2=1/2(k_1^2+k_2^2+k_3^2+k_1{k}_2-k_1{k}_3-k_2{k}_3)$ and:

$$\begin{array}{c}{\widehat{k}}_1=k_1-w_{1}p,{\widehat{k}}_2=k_2-w_{2}p,{\widehat{k}}_3=k_3+w_{3}p,\hfill \\ {\widehat{k}}_4=k_1+k_2-k_3+w_{4}p,{\epsilon }^{\mu p\alpha \beta }=p_{\nu }{\epsilon }^{\mu \nu \alpha \beta }.\hfill \end{array}$$

A list of matrix elements for different decay reactions as predicted by the CCQM is given in what follows. For each element, we provide, in the last line of the corresponding expression, the form factor parametrization of the matrix element to be compared with the appropriate expression from Equations (85), (87), and (89). Beforehand, let us also define the argument of ${\tilde{\mathsf{\Phi }}}_{Z_b}\left({\overrightarrow{\eta }}^2\right)$. One has:

$$\begin{array}{ccc}\hfill {\overrightarrow{\eta }}^2=\sum _{i=1}^3{\eta }_i^2{\eta }_1& =& +\frac{1}{2\sqrt{2}}\left(2k_1+(1+w_1-w_2)q_1+(w_1-w_2)q_2\right),\hfill \\ \hfill {\eta }_2& =& +\frac{1}{2\sqrt{2}}\left(2k_2-(w_3-w_4)q_1+(1-w_3+w_4)q_2\right),\\ \hfill {\eta }_3& =& +\frac{1}{2}\left((1-w_1-w_2)q_1-(w_1+w_2)q_2\right),\hfill \end{array}$$

where $w_i$ denotes four body reduced masses $w_i=m_i/{\displaystyle \sum _{j=1}^4}{m}_j$ and quarks are indexed as $q_1=q_2=b$, $q_3=q_4=d=u$.

• $1^{+}\to 1^{-}+0^{-}$ matrix elements parametrized as in Equation (85):

  $$\begin{array}{cc}& M^{\mu \delta }\left(Z_b(p,\mu )\to \mathsf{{\rm Y}}(q_1,\delta )+{\pi }^{+}\left(q_2\right)\right)=\frac{3}{\sqrt{2}}{g}_{Z_b}{g}_{\mathsf{{\rm Y}}}{g}_{\pi }\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{\mathsf{{\rm Y}}}\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \{\mathrm{tr}\left[{\gamma }_5{S}_1\left(k_1\right){\gamma }^{\delta }{S}_2(k_1+q_1){\gamma }^{\mu }{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2)\right]\hfill \\ & +\mathrm{tr}\left[{\gamma }^{\mu }{S}_1\left(k_1\right){\gamma }^{\delta }{S}_2(k_1+q_1){\gamma }_5{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2)\right]\}\hfill \\ =& A_{Z_b\mathsf{{\rm Y}}\pi }{g}^{\mu \delta }+B_{Z_b\mathsf{{\rm Y}}\pi }{q}_1^{\mu }{q}_2^{\delta },\hfill \end{array}$$

  (98)

  $$\begin{array}{cc}& M^{\mu \delta }\left(Z_b^{\prime }(p,\mu )\to \mathsf{{\rm Y}}(q_1,\delta )+{\pi }^{+}\left(q_2\right)\right)=3g_{Z_b^{\prime }}{g}_{\mathsf{{\rm Y}}}{g}_{\pi }\frac{i{\epsilon }^{\mu p\alpha \beta }}{M_{Z_b^{\prime }}}\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b^{\prime }}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{\mathsf{{\rm Y}}}\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[{\gamma }_{\alpha }{S}_1\left(k_1\right){\gamma }^{\delta }{S}_2(k_1+q_1){\gamma }_{\beta }{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2)\right]\hfill \\ =& A_{Z_b^{\prime }\mathsf{{\rm Y}}\pi }{g}^{\mu \delta }+B_{Z_b^{\prime }\mathsf{{\rm Y}}\pi }{q}_1^{\mu }{q}_2^{\delta },\hfill \end{array}$$

  (99)

  $$\begin{array}{cc}& M^{\mu \rho }\left(Z_b(p,\mu )\to {\eta }_b\left(q_1\right)+\rho (q_2,\rho )\right)=\frac{3}{\sqrt{2}}{g}_{Z_b}{g}_{{\eta }_b}{g}_{\rho }\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{{\eta }_b}\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\rho }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \{\mathrm{tr}\left[{\gamma }_5{S}_1\left(k_1\right){\gamma }_5{S}_2(k_1+q_1){\gamma }^{\mu }{S}_4\left(k_2\right){\gamma }^{\rho }{S}_3(k_2+q_2)\right]\hfill \\ & +\mathrm{tr}\left[{\gamma }^{\mu }{S}_1\left(k_1\right){\gamma }_5{S}_2(k_1+q_1){\gamma }_5{S}_4\left(k_2\right){\gamma }^{\rho }{S}_3(k_2+q_2)\right]\}\hfill \\ =& A_{Z_b{\eta }_b\rho }{g}^{\mu \rho }-B_{Z_b{\eta }_b\rho }{q}_2^{\mu }{q}_1^{\rho },\hfill \end{array}$$

  (100)

  $$\begin{array}{cc}& M^{\mu \rho }\left(Z_b^{\prime }(p,\mu )\to {\eta }_b\left(q_1\right)+\rho (q_2,\rho )\right)=3g_{Z_b^{\prime }}{g}_{{\eta }_b}{g}_{\rho }\frac{i{\epsilon }^{\mu p\alpha \beta }}{M_{Z_b^{\prime }}}\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b^{\prime }}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{{\eta }_b}\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\rho }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[{\gamma }_{\alpha }{S}_1\left(k_1\right){\gamma }_5{S}_2(k_1+q_1){\gamma }_{\beta }{S}_4\left(k_2\right){\gamma }^{\rho }{S}_3(k_2+q_2)\right]\hfill \\ =& A_{Z_b^{\prime }{\eta }_b\rho }{g}^{\mu \rho }-B_{Z_b^{\prime }{\eta }_b\rho }{q}_2^{\mu }{q}_1^{\rho }.\hfill \end{array}$$

  (101)
• $1^{+}\to 1^{+}+0^{-}$ matrix elements parametrized as in Equation (87):

  $$\begin{array}{cc}& M^{\mu \delta }\left(Z_b^{+}(p,\mu )\to h_b(q_1,\delta )+{\pi }^{+}\left(q_2\right)\right)=\frac{3}{\sqrt{2}}{g}_{Z_b}{g}_{h_b}{g}_{\pi }\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{h_b}\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \{\mathrm{tr}\left[{\gamma }_5{S}_1\left(k_1\right){\gamma }_5·\left(2k_1^{\delta }\right)S_2(k_1+q_1){\gamma }^{\mu }{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2)\right]\hfill \\ & +\mathrm{tr}\left[{\gamma }^{\mu }{S}_1\left(k_1\right){\gamma }_5·\left(2k_1^{\delta }\right)S_2(k_1+q_1){\gamma }_5{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2)\right]\}\hfill \\ =& {\epsilon }^{\mu \delta q_1{q}_2}{A}_{Z_b{h}_b\pi },\hfill \end{array}$$

  (102)

  $$\begin{array}{cc}& M^{\mu \delta }\left(Z_b^{\prime }(p,\mu )\to h_b(q_1,\delta )+{\pi }^{+}\left(q_2\right)\right)=3g_{Z_b^{\prime }}{g}_{h_b}{g}_{\pi }\frac{i{\epsilon }^{\mu p\alpha \beta }}{M_{Z_b^{\prime }}}\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b^{\prime }}\left(-{\overrightarrow{\eta }}^2\right){\tilde{\mathsf{\Phi }}}_{h_b}\left(-{(k_1+v_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{\pi }\left(-{(k_2+u_4{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[{\gamma }_{\alpha }{S}_1\left(k_1\right){\gamma }_5·\left(2k_1^{\delta }\right)S_2(k_1+q_1){\gamma }_{\beta }{S}_4\left(k_2\right){\gamma }_5{S}_3(k_2+q_2)\right]\hfill \\ & ={\epsilon }^{\mu \delta q_1{q}_2}{A}_{Z_b^{\prime }{h}_b\pi }.\hfill \end{array}$$

  (103)

The matrix elements describing decays to a pair of B mesons can be also listed within two groups depending on the quantum numbers. The argument of the $Z_b$-vertex function ${\overrightarrow{\delta }}^2$ is defined as:

$$\begin{array}{ccc}\hfill {\overrightarrow{\delta }}^2=\sum _{i=1}^3{\delta }_i^2;{\delta }_1& =& -\frac{1}{2\sqrt{2}}\left(k_1+k_2+(w_1-w_2)q_1+(1+w_1-w_2)q_2)\right),\hfill \\ \hfill {\delta }_2& =& +\frac{1}{2\sqrt{2}}\left(k_1+k_2+(1-w_3+w_4)q_1-(w_3-w_4)q_2\right),\hfill \\ \hfill {\delta }_3& =& +\frac{1}{2}\left(k_1-k_2+(w_1+w_2)q_1-(1-w_1-w_2)q_2)\right).\hfill \end{array}$$

(104)

The quark indices are similar to the previous case $q_1=q_2=b$, $q_3=q_4=d=u$, ${\widehat{v}}_2=m_2/(m_2+m_4)$, ${\widehat{v}}_4=m_4/(m_2+m_4)$, ${\widehat{u}}_1=m_1/(m_1+m_3)$, and ${\widehat{u}}_3=m_3/(m_1+m_3)$.

• $1^{+}\to 1^{-}+0^{-}$ matrix elements parametrized as in Equation (85):

  $$\begin{array}{cc}& M^{\mu \rho }\left(Z_b^{+}(p,\mu )\to {\overline{B}}^0\left(q_1\right)+B^{*+}(q_2,\rho )\right)=\frac{9}{\sqrt{2}}{g}_{Z_b}{g}_B{g}_{B^{*}}\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b}\left(-{\overrightarrow{\delta }}^2\right){\tilde{\mathsf{\Phi }}}_B\left(-{(k_2+v_4{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{B^{*}}\left(-{(k_1+u_1{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[{\gamma }^{\mu }{S}_1\left(k_1\right){\gamma }^{\rho }{S}_3(k_1+q_2)\right]\mathrm{tr}\left[{\gamma }_5{S}_4\left(k_2\right){\gamma }_5{S}_2(k_2+q_1)\right]\hfill \\ =& A_{Z_b\overline{B}{B}^{*}}{g}^{\mu \rho }-B_{Z_b\overline{B}{B}^{*}}{q}_2^{\mu }{q}_1^{\rho },\hfill \end{array}$$

  (105)

  $$\begin{array}{cc}& M^{\mu \alpha }\left(Z_b^{+}(p,\mu )\to {\overline{B}}^{*0}(q_1,\delta )+B^{+}\left(q_2\right)\right)=\frac{9}{\sqrt{2}}{g}_{Z_b}{g}_{B^{*}}{g}_B\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b}\left(-{\overrightarrow{\delta }}^2\right){\tilde{\mathsf{\Phi }}}_{B^{*}}\left(-{(k_1+{\widehat{v}}_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_B\left(-{(k_2+{\widehat{u}}_4{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[{\gamma }_5{S}_1\left(k_1\right){\gamma }_5{S}_3(k_1+q_2)\right]\mathrm{tr}\left[{\gamma }^{\mu }{S}_4\left(k_2\right){\gamma }^{\delta }{S}_2(k_2+q_1)\right]\hfill \\ =& A_{Z_b{B}^{*}B}{g}^{\mu \delta }+B_{Z_b{B}^{*}B}{q}_1^{\mu }{q}_2^{\delta }.\hfill \end{array}$$

  (106)
• $1^{+}\to 1^{-}+1^{-}$ matrix elements parametrized as in Equation (89):

  $$\begin{array}{cc}& M^{\mu \delta \rho }(Z_b^{\prime +}(p,\mu )\to B^{*0}(q_1,\delta )+{\overline{B}}^{*+}(q_2,\rho ))=9g_{Z_b^{\prime }}{g}_{B^{*}}{g}_{B^{*}}\frac{{\epsilon }^{\mu p\alpha \delta }}{M_{Z_b^{\prime }}}\hfill \\ & \int \frac{d^4{k}_1}{{\left(2\pi \right)}^{4}i}\int \frac{d^4{k}_2}{{\left(2\pi \right)}^{4}i}{\tilde{\mathsf{\Phi }}}_{Z_b^{\prime }}\left(-{\overrightarrow{\delta }}^2\right){\tilde{\mathsf{\Phi }}}_{B^{*}}\left(-{(k_1+{\widehat{v}}_1{q}_1)}^2\right){\tilde{\mathsf{\Phi }}}_{B^{*}}\left(-{(k_2+{\widehat{u}}_4{q}_2)}^2\right)\hfill \\ \times & \mathrm{tr}\left[{\gamma }_{\alpha }{S}_1\left(k_1\right){\gamma }^{\delta }{S}_3(k_1+q_1)\right]\mathrm{tr}\left[{\gamma }_{\beta }{S}_4\left(k_2\right){\gamma }^{\rho }{S}_2(k_2+q_2)\right]\hfill \\ =& B_1{q}_1^{\mu }{ϵ}^{q_1{q}_2\rho \delta }+B_2{ϵ}^{q_1\mu \rho \delta }+B_3{ϵ}^{q_2\mu \rho \delta }.\hfill \end{array}$$

  (107)

With all the above theoretical expressions, one can proceed to the numerical evaluation of the decay widths. The first step is the adjustment of the size parameters ${\mathsf{\Lambda }}_Z$ and ${\mathsf{\Lambda }}_Z^{\prime }$. They are tuned so as to respect the observables measured by the Belle collaboration [35]:

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{Z_b}\left(B{B}^{*}\pi \right)& =& (25\pm 7)\mathrm{MeV},\mathcal{B}(Z_b^{+}\to [B^{+}{\overline{B}}^{*0}+{\overline{B}}^0{B}^{*+}])={85.6}_{-2.0-2.1}^{+1.5+1.5}\%,\hfill \\ \hfill {\mathsf{\Gamma }}_{Z_b^{\prime }}\left(B^{*}{B}^{*}\pi \right)& =& (23\pm 8)\mathrm{MeV},\mathcal{B}(Z_b^{\prime +}\to {\overline{B}}^{*+}{B}^{*0})={73.7}_{-4.4-3.5}^{+3.4+2.7}\%,\hfill \end{array}$$

(108)

leading to:

$${\mathsf{\Lambda }}_{Z_b}=3.45\pm 0.05\mathrm{GeV}{\mathsf{\Lambda }}_{Z_b^{\prime }}=3.00\pm 0.05\mathrm{GeV}.$$

(109)

With the decays into B pairs dominating all other decay channels, we approximate the total decay width as the sum of all herein evaluated channels. The CCQM gives:

$${\mathsf{\Gamma }}_{Z_b}={30.9}_{-2.1}^{+2.3}\mathrm{MeV},{\mathsf{\Gamma }}_{Z_b^{\prime }}={34.1}_{-2.5}^{+2.8}\mathrm{MeV},$$

(110)

which is in fair agreement with (108). The predicted partial decay widths of $Z_b\left(10610\right)$ and $Z_b^{\prime }\left(10650\right)$ particles are summarized in Table 6.

Table 6. Particle decay widths for the $Z_b^{+}\left(10610\right)$ and $Z_b^{+}\left(10650\right)$.

Channel	Widths, MeV
	${\mathit{Z}}_{\mathit{b}}\left(\mathbf{10610}\right)$	${\mathit{Z}}_{\mathit{b}}\left(\mathbf{10650}\right)$
$\mathsf{{\rm Y}}\left(1S\right){\pi }^{+}$	$5.9\pm 0.4$	${9.5}_{-0.6}^{+0.7}$
$h_b\left(1P\right){\pi }^{+}$	$(0.14\pm 0.01)·{10}^{-1}$	${0.74}_{-0.04}^{+0.05}·{10}^{-3}$
${\eta }_b{\rho }^{+}$	$4.4\pm 0.3$	${7.5}_{-0.5}^{+0.6}$
$B^{+}{\overline{B}}^{*0}+{\overline{B}}^0{B}^{*+}$	${20.7}_{-1.5}^{+1.6}$
$B^{*+}{\overline{B}}^{*0}$		${17.1}_{-1.4}^{+1.5}$

The $Z_b$ and $Z_b^{\prime }$ decays are dominated [13] by ${\mathsf{\Gamma }}_{Z_b}({\mathit{B}}^{+}{\overline{\mathit{B}}}^{*0}+{\mathit{B}}^{*+}{\overline{\mathit{B}}}^0)=\left({85.6}_{-2.9}^{+2.1}\right)\%$ and ${\mathsf{\Gamma }}_{Z_b^{\prime }}\left({\mathit{B}}^{*+}{\overline{\mathit{B}}}^{*0}\right)=\left({74}_{-6}^{+4}\right)\%$, respectively, meaning that the bottomonia modes should not exceed 15 and 25 percent. This is observed for the $h_b\left(1P\right){\pi }^{+}$ final state; the other bottomonia channels are suppressed, but not so much as seen in the data:

$$\begin{array}{ccc}\hfill \frac{\mathsf{\Gamma }\left(Z_b\to \mathsf{{\rm Y}}\left(1S\right)\pi \right)}{\mathsf{\Gamma }\left(Z_b\to B{\overline{B}}^{*}+c.c.\right)}& \approx & 0.29,\frac{\mathsf{\Gamma }\left(Z_b\to {\eta }_b\rho \right)}{\mathsf{\Gamma }\left(Z_b\to B{\overline{B}}^{*}+c.c.\right)}\approx 0.21,\hfill \\ \frac{\mathsf{\Gamma }\left(Z_b^{\prime }\to \mathsf{{\rm Y}}\left(1S\right)\pi \right)}{\mathsf{\Gamma }\left(Z_b^{\prime }\to B^{*}{\overline{B}}^{*}\right)}& \approx & 0.56,\frac{\mathsf{\Gamma }\left(Z_b^{\prime }\to {\eta }_b\rho \right)}{\mathsf{\Gamma }\left(Z_b^{\prime }\to B^{*}{\overline{B}}^{*}\right)}\approx 0.44.\end{array}$$

The model also allows us to make predictions:

$$R_{\mathsf{{\rm Y}}\left(1S\right)\pi }=\frac{\mathsf{\Gamma }(Z_b\to \mathsf{{\rm Y}}\left(1S\right)\pi )}{\mathsf{\Gamma }(Z_b^{\prime }\to \mathsf{{\rm Y}}\left(1S\right)\pi )}=0.62\pm 0.06,R_{{\eta }_b\rho }=\frac{\mathsf{\Gamma }(Z_b\to {\eta }_b\rho )}{\mathsf{\Gamma }(Z_b^{\prime }\to {\eta }_b\rho )}=0.59\pm 0.06.$$

(111)

One can conclude that the CCQM provides, within a molecular picture, a fair description of $Z_b\left(10610\right)$/$Z_b^{\prime }\left(10650\right)$ states and related decay observables and catches the tendencies seen in experimental data. Some deviations are observed when the fraction of bottomonium in final states is considered.

8. Summary and Conclusions

The confined covariant quark model is an approach based on a non-local interaction Lagrangian of quarks and hadrons. It has many appealing features: a full Lorentz invariance, confinement, large applicability range (from mesons to exotic hadrons), inclusion of the electromagnetic interaction, and a limited number of free parameters. As a practical tool, it allows overcoming the difficulties related to the non-applicability of the perturbative approach for bound states in QCD. In this text, we used it to describe four quark exotic states $X\left(3872\right)$, $Z_c\left(3900\right)$, $Y\left(4260\right)$, $Z_b\left(10610\right)$, and $Z_b^{\prime }\left(10650\right)$. We demonstrated that the CCQM had enough predictive power to make the distinctions between various hypothesis, with respect to the exotic quarkonia mostly related to their structure (molecular versus tetraquark one). At the same time, the model provides a good description of experimental data without large deviations and predictions for future measurements. Concerning the structure of the studied particles, the molecular picture is favored for $Z_c\left(3900\right)$, $Z_b\left(10610\right)$, and $Z_b^{\prime }\left(10650\right)$ and the tetraquark one for $X\left(3872\right)$ and $Y\left(4260\right)$. These conclusions follow from the measured decay characteristics of the considered exotic states and the related model description: with the expected increase in the number and quality of experimental data, one may hope the quarkonia-structure puzzle will be solved in the years to come.