Abstract
In recent years, China’s government has encouraged the adoption of the TOT (Transfer-Operate-Transfer) model to realize the marketization of China’s public service stock projects. The TOT model is a cooperation mechanism through sharing investment, revenue and risks between the government and private partner. Therefore, a fair and reasonable revenue sharing method (RSM) is the key to the success of the TOT project. This paper aims to provide a fair and reasonable RSM based on a modified Shapley value with a triangular symmetric fuzzy structure element, which has better motivation, flexibility, forecasting function and dynamic precise distribution function. According to the factors that affect revenue sharing, the Shapley value is improved with initial correction coefficient composed of investment ratio, risk-sharing ratio, execution degree, and fuzzy payment to achieve fairness and reasonableness. The methodology is illustrated by a case study of a TOT project selected from Laohekou city of Hubei province, China. The results testify that the revenue-sharing ratios of participants is positively correlated with the initial correction coefficient, which make the RSM more motivating; and the Shapley value with fuzzy payment by using triangular symmetric fuzzy element function make the RSM more flexible, and it has both forecasting function and precise dynamic distribution function under project revenue uncertainty.
1. Introduction
The Chinese government encourages the transformation of China’s public service stock through TOT (transfer operation transfer) or ROT (reconstruction operation transfer) to reduce government debt and improve service quality. The financing platform companies participate in the transformation and operation of the cooperation projects between the government and private partners by introducing private partners, ROT is a project operation mode in which the government adds reconstruction and expansion contents on the basis of the TOT model. In this paper, the TOT model is mainly studied. The TOT project is a common model in stock PPP (public-private-partnership) projects [1]. A private partner usually pays a franchise fee to the government one-time at the beginning of a franchise. It can be seen that TOT project generally has a large investment and a long contract term, so flexible investment and revenue allocation are needed to reduce the risks of both parties. To encourage the active participation of private partner, the TOT project can achieve a win-win cooperation mechanism through sharing investment, revenue and risk between government and private partner. With this cooperation model, the benefits generated by cooperation were the focus of competition between the two parties in revenue allocation [2,3]. Therefore, the key to the success of TOT project is to realize fair and reasonable revenue sharing through a more flexible revenue allocation method [4,5,6].
At present, the research on the revenue allocation of PPP project has gained wide attention from scholars both at home and abroad. The revenue allocation methods of dynamic alliances in cooperative games mainly include the simplified Minimum Costs-Remaining Savings (MCRS) method, the Nash negotiation bargaining model, the core method, and the Shapley value method. Among them, the Nash negotiation bargaining model and the Shapley value method are the main way to study the revenue allocation between cooperative game alliances. The application of negotiation bargaining model in revenue allocation of PPP projects was mainly to achieve a revenue allocation scheme between the government and the private partner through bargaining about the franchise period or the franchise cost in the concession contract [7,8,9,10,11,12]. There were also scholars who determined the balance of interests between government and the private partner by means of agency mechanism and net cash flow financial model [1,13]. The above methods pay more attention to the static revenue allocation. The Shapley value method is one of the commonly used solution concepts in cooperative games. It takes the marginal contribution of alliance members as the basis of profit allocation, and gives a strict axiomatic description to subjective concepts such as “fairness” or “reasonableness”, providing a unique and fair solution [14,15].
However, the classic Shapley value method assumes that all parties in the game have equal capital investment and risk sharing in the project, what is inconsistent with the actual situation of the TOT project [16]. Therefore, it is necessary to improve the Shapley value in combination with the characteristics of the TOT project invested by the government and private partners in this paper. At present, the optimization and improvement of Shapley value method are mainly embodied in two aspects. First, in the theoretical research of the influence of uncertainty of the revenue function of the alliance on Shapley value, more literature used fuzzy geometry theory to extend the applicable conditions and scope of Shapley value in fuzzy payment, and proved its uniqueness [17,18]. On the other hand, it is mainly applied at the practical level. Many scholars have applied the theoretical research results of Shapley value and improved the specific characteristics of PPP projects [19,20]. From literature research, fewer scholars comprehensively modified the Shapley value from the fuzzy payment of the total revenue of the TOT project and the related factors affecting the revenue-sharing ratio (RSR), and systematically studied the problem of revenue sharing of the TOT project.
To sum up, this paper will use the modified Shapley value method for the TOT project revenue allocation, and modify the Shapley value from the perspectives of the uncertainty of the TOT project revenue and the factors affecting the RSR to build the TOT project RSM. The model will achieve fair and reasonable revenue allocation, make the interests of both parties balanced dynamically, and increase the flexibility of revenue allocation to reduce risks.
2. Shapley Value Approach and TOT Project Overview and Application Research
2.1. Shapley Value
Shapley value was a method proposed by Shapley L.S. in 1953 to solve the cost-sharing revenue allocation of alliance members in classical games. Because it had certain versatility and could guarantee a unique solution, it was a major way to study the fair revenue allocation within the alliance [10,21]. The fuzzy payment Shapley value was the revenue allocation problem among the alliance members of the cooperative game under the uncertainty of the payment function, which was one of the development directions of Shapley value in theoretical research. Chen et al. [17] used fuzzy set theory to extend the axioms of classical Shapley values to Shapley values with fuzzy payments. Chen et al. [17] made a fuzzy extension of Mares method in her doctoral dissertation, and proposed Shapley value with interval fuzzy payment and type-two fuzzy payment. In order to overcome the shortcomings, namely that Shapley values with interval value fuzzy payment cooperative game and fuzzy payment of type-two fuzzy value did not satisfy the validity axioms, the Shapley value of triangular fuzzy number fuzzy payment was proposed. Meng et al. [18] proposed that the participation rate of coalition members was real number [0~1], and the payment function was the general expression of Shapley value of fuzzy game with fuzzy numbers, and studied its characteristics and properties. Gao et al. [10] proposed two variables of Shapley value as the solution of fuzzy payment cooperative game, and proved the uniqueness of uncertain Shapley value. Basallote et al. [22] introduced an average-integral Shapley value for fuzzy games based on the crisp Shapley value. The above theoretical study of the fuzzy payment Shapley value provided a more mature method for the revenue sharing among the members of the cooperative game alliance under the uncertainty of the payment function. The research results in this aspect provided theoretical support for the analysis of the impact of TOT project revenue uncertainty on revenue sharing.
2.2. Research on TOT Project Revenue Allocation
TOT project revenue allocation refers to the revenue obtained by each participant in accordance with the method or mechanism stipulated in the contract under the established contract. At present, many scholars have studied the revenue allocation between government and private partner of PPP projects, while the research on revenue sharing of TOT projects is relatively rare. For the former, the bargaining model is mostly used to adjust the revenue allocation of both parties by using the franchise period or the franchise fee. For example, Li [23] reached a revenue sharing scheme between the government and the private sector through bargaining on concession contracts, but the subjectivity of learning efficiency in this method was determined to have a certain impact on its objectivity. Kumar et al. [24] used the bargaining model to simulate the bargaining problem between the private partner and the government on the operating period under the condition of information asymmetry. Battiston et al. [25] established a bargaining model for energy-saving profit allocation based on revenue sharing of energy performance contract (EPC), and determined the allocation time and proportion of energy-saving benefit. However, the bargaining results of both parties are in the form of intervals, failing to produce a precise allocation proportion. Wu [26] focused on the revenue allocation of PPP projects, and built a revenue allocation model with the help of NASH negotiation model based on the impact factors such as investment ratio, risk-sharing coefficient, contract execution degree, and contribution to the project. In the process of using the Nash negotiation model in the above literature, the non-uniqueness and uncertainty of the solution is a limitation of this method.
In addition, in other methodological studies, Wang [13] used agency mechanism to analyze the excess RSR in PPP projects, and considered that the excess RSR was related to investors’ fairness preference and effort cost coefficient. However, the method only carried out the revenue allocation on the excess revenue and did not extend to all revenues. Carbonara et al. [6] proposed a net revenue model for evaluating and measuring different EPC structures. The net present value difference was minimized to balance the profit demand of the private sector and the economic interests of the public sector. However, there were insufficient considerations about how much the participants contribute. Wang and Wang [27] constructed a revenue allocation model based on risk metrics according to the risk-benefit equilibrium principle, and determined the solution of benefit allocation quota and allocation time. It was obviously flawed to allocate energy saving benefits only according to the risk sharing ratio between energy service companies and customers. Cubukcu [28] used Shapley value for a fair division of surplus development rights in redevelopment of urban areas, the result showed that landowners can benefit from the highest possible development rights and share the surplus fairly. The above research shows that factors such as the proportion of investment, the proportion of risk sharing and the degree of effort have a great impact on revenue allocation. Risk allocation of demand between government and contractors was a key aspect of any PPP contract [29], and risk allocation was seen as a way to balance the benefits between partners in a PPP project [30,31]. Therefore, this paper will choose investment ratio and risk-sharing ratio to modify the Shapley value.
2.3. Application of Shapley Value Method in TOT Project
Improving Shapley value and applying it to revenue sharing among stakeholders in PPP projects are mainly reflected in two aspects: One hand, multi-weight improvements are made according to the influencing factors; on the other hand, the Shapley value is corrected by using fuzzy payment.
At present, more scholars use multi-weight to improve Shapley value. For example, Hu et al. [32] synthetically considered the proportion of investment, risk-sharing ratio, contract execution degree and contribution degree, and established a revenue allocation model of PPP project based on modified Shapely value, which made the model more objective, fair and reasonable. Li et al. [23] proposed a Shapley value model based on risk factors, investment contributions, and contribution factors of innovation capabilities in wastewater treatment projects and concluded that the Shapley value model can guarantee the fairness of revenue allocation of wastewater treatment PPP projects. In the above method of multi-weight correction Shapley value, most of the literature assumed that the total income of PPP projects remained unchanged. The revised value of this factor of the participants was subtracted from the original value of 1/n and the revenue sharing of the participants was adjusted according to the product of coefficient difference and total revenue of TOT project. The calculation method was relatively cumbersome. At the same time, the multi-weight correction Shapley value did not consider the effect of fuzzy payment on the Shapley value of the PPP project.
Yu and Li [33] introduced uncertainty into the interval revenue allocation model and proposed the interval Shapley value method based on the consideration of investment ratio, risk-sharing ratio, and execution degree on the improvement of Shapley value. The introduction of uncertainty in the literature only provided the fuzzy revenue sharing interval of the participants. However, this paper does not consider the impact of revenue uncertainty on the RSR and the precise matching between the total fuzzy revenue and the participants’ fuzzy revenue value. Xu and Liu [34] considered the indexes affecting the revenue distribution, such as the investment ratio, risk sharing ratio and contribution degree of the participants, and proposed the RSM for hydropower PPP projects based on the modified Shapley value method. This paper increased the fit of the model to the actual problems for a more comprehensive analysis of the influencing factors, and predicts the revenue sharing interval of the participants according to the project income interval, so as to make the income distribution more reasonable. However, it fails to realize the one-to-one correspondence between the project revenue interval and the revenue sharing interval of the participants.
From the literature study, it shows that many scholars have applied Shapley value modified by multiple weights, such as investment ratio, risk-sharing ratio, contract execution and contribution, to revenue allocation of PPP projects, or improved Shapley value from the perspective of fuzzy payment and applied it to revenue allocation of PPP projects. However, in the perspective of comprehensive correction of investment ratio, risk-sharing ratio and fuzzy payment Shapley value, the study of the revenue allocation of operational TOT projects was less, and it failed to achieve the exact correspondence between fuzzy payment, fuzzy RSR and fuzzy revenue sharing. Therefore, this paper constructed an RSM of a TOT project based on initial correction coefficient and fuzzy payment Shapley value and solved the above problems, and it is more motivating and fair to participants with initial correction coefficient. In addition, it can realize forecasting function and precise dynamic distribution function under project revenue uncertainty, and improve the flexibility of revenue allocation.
3. Basic Definition and Revenue Sharing Model Construction of TOT Project
3.1. Basic Definition
3.1.1. Definition 1
The characteristic function of the TOT project alliance
According to the Shapley value theory, the cooperation between the government department and private partner of the TOT project can be regarded as a cooperative game . All alliances in is . Alliance refers to the complete alliance of the government and private partner in the classic cooperative strategy. All alliances in are , and their cardinal numbers are .
The different subsets in N represent different cooperation modes, and also represent different eigenfunctions. The eigenfunction analysis of non-empty subsets in the TOT project cooperation alliance is as follows.
Subset represents that government completes public infrastructure projects alone, which is the traditional mode of infrastructure projects. The revenue of government in this mode is , which is simply written as .
Subset represents that private partner completes public infrastructure projects alone. At present, China’s infrastructure projects are not open to private partners, but this paper combines the experience of private partner in similar projects, assuming that private partner takes full responsibility for the public project, and its revenue is , simply recorded as .
Subset represents the cooperation of alliances between government department and private partner, namely the TOT model. The revenue of the TOT project is , simply recorded as .
Therefore, the Shapley value expression of the TOT project is as follows:
where, I represents the government department and the private partner.
represents the revenue of member i.
reflects the marginal contribution of government or private partner to alliance S.
indicates the probability of occurrence of each subset S.
3.1.2. Definition 2
Initial correction coefficient of investment ratio and risk-sharing ratio and execution degree of TOT project Shapley value
According to the literature review, this paper chooses investment ratio, risk-sharing ratioand execution degree to modify their impact on RSR at first [32,33,34,35]. It was also assumed that the investment ratio and risk-sharing ratio were linearly related to the RSR, and that the business model of the project did not change with the change of investment ratio, risk-sharing ratio andexecution degree.
Note the actual investment ratio and risk sharing ratio and execution degree of the government and private partner in the TOT project as , and and , respectively. On the basis of references [32,33,34], this paper put forward the initial correction coefficient of Shapley value, which is expressed as follows:
In the Formula, , and respectively represent the weights of the investment ratio and the risk-sharing ratio on the RSR, and satisfy . , and represent the investment ratio, risk-sharing ratio and execution degree of participant i respectively, and satisfy , .
revises the RSR according to the relative proportion, and changes the way in which the absolute value of the RSR of the participants is directly revised in the original literature. Therefore, can better reflect the rationality of the RSR.
For the cooperative game modified by , and , if the function is:
The function is called the Shapley value of the alliance cooperative game based on . However, this Shapley value is not the actual revenue sharing of the participants, but only reflects the RSR of the participants. The RSR and the revenue sharing of participants based on are:
3.1.3. Definition 3
TOT project fuzzy payment function and the Shapley value of participants
According to the references [16,33,36,37], is called the fuzzy cooperation game in the set . is a fuzzy payment function defined in the power set of defined and the interval number set of values, i.e. and . is called the cooperative game with fuzzy payment in , and its whole is recorded as G(N). The fuzzy function is:
This function is called Shapley value of TOT project based on fuzzy payment.
Combining with the meaning of RSR, this paper puts forward the participants’ RSR based on fuzzy payment, which is:
According to Equation (6) and Equation (7), varies with .
According to the relationship between RSR and revenue sharing, the revenue sharing of participants based on fuzzy payment is proposed. The expression is:
Similarly, will also change with .
3.1.4. Definition 4
Shapley value and RSR of TOT project based on and fuzzy payment function.
On the basis of Definitions 1, 2 and 3, for the fuzzy cooperative game and , is called the cooperative game with fuzzy payment in P(N), and its total is recorded as . If the fuzzy payment of TOT project fuzzy cooperative game based on the revision of investment ratio can be expressed as , then the fuzzy cooperative game is called fuzzy cooperative game based on and fuzzy payment.
The fuzzy function is:
This function is called Shapley value of TOT project based on and fuzzy payment.
The RSR of participants and the revenue sharing based on and fuzzy payment are:
According to Equations (9)−(11), it can be seen that and are functions of , which change with the value of the fuzzy payment function.
3.2. Construction of Revenue Sharing Model for TOT Projects
Fuzzy payment not only affects the revenue of TOT projects, but also affects the RSR. Therefore, it is necessary to first consider the improvement of the Shapley value by revenue uncertainty, which is the Shapley value of the TOT project based on fuzzy payment. Then it needs to consider the initial correction coefficient of factors such as the RSR, and the Shapley value and its membership function of the TOT project based on the initial correction coefficient and fuzzy payment according to the relevant definitions and formulas in 3.1 are constructed.
3.2.1. Fuzzy Payment Value and Shapley Value of TOT Project based on Triangular Fuzzy Structure Element
Let E be a triangular symmetric fuzzy structure element [16,38].
The fuzzy number generated linearly by the fuzzytriangular symmetric structure element is .
Let , we have:
The above formula satisfies , and .
3.2.2. Construction of TOT Project RSM Based on Initial Correction Coefficient and Fuzzy Payment
According to Definition 3 and Equation (12), TOT project fuzzy payment and its membership function based on the fuzzy structure element are:
According to Definition 4 and Equation (12), the RSR of participants and their membership functions under the modified Shapley value based on fuzzy structure elements are:
Similarly, the revenue sharing of participants and their membership functions based on the modified Shapley value are:
In summary, Equations (13)−(18) constitute the basic content of the TOT project RSM based on the modified Shapley value. Previous literature hypothesis implies that the participants’ RSR remains unchanged within the fuzzy revenue interval.
However, Equation (10) shows that there is a non-linear proportional relationship between the fuzzy RSR and the fuzzy payment function. The RSR varies according to fuzzy payment function. Therefore, the proposed in this paper clarifies the functional relationship between the RSR and the fuzzy payment function, and corrects the deficiencies of the previous literature, so it makes the RSM is more fair and reasonable.
3.3. Execution Degree
The execution degree refers to the degree of performance of the contract by all participants in the process of project implementation, as well as the positive actions taken to ensure the overall benefits of the project, such as active cooperation in the coordination work andactive response to emergencies [39,40]. Accordingly, the indicators of execution degreeare the degree of performance of the contract and the degree of coordination satisfaction and the degree of response to emergencies. As the influencing factors of revenue sharing, it can fully mobilize the enthusiasm of project participants and help to maximize the overall interest of the project. The indicators of coordination satisfaction and emergency response are obtained through the subjective evaluation of the assessors which are ambiguous. On the basis of the theory of intuitionistic fuzzy set, the index weight and expert evaluation information are expressed by intuitionistic fuzzy number, and the correction coefficient is determined by calculating the closeness between each participant and the ideal solution.
The first step is to construct the decision matrix of intuitionistic fuzzy set.
There are Z kinds of evaluation indexes for setting the degree of implementation. Intuitionistic fuzzy evaluation value of the expert for the index of the participant . . indicates the degree to which the participant meets the evaluation index [41,42]. Get the evaluation matrix of intuitionistic fuzzy set about the degree of execution.
In the second step, the positive and negative ideal solutions of intuitionistic fuzzy are determined. Intuitionistic fuzzy positive ideal solution is , it represents the best degree of implementation of the participants; The negative ideal solution is , it indicates the least satisfactory degree of implementation of the participant.
In the third step, we calculate the closeness between each participant and the ideal solution. Hausdorff distance is used to measure the distance between intuitionistic fuzzy sets [43]. The distance between participant and positive and negative ideal solutions are respectively
4. Case Analysis of TOT Project
4.1. Basic Situation of the Case
The Laohekou City Funeral Service Center in Hubei Province adopts a TOT approach to an existing project due to a decision of a city people’s government. A Cemetery Management Office in the city acted as a government authorized investment representative (hereinafter referred to as the government) jointly establishes a project company with private partner. The project company will purchase the existing project assets with 115.9 million yuan, invest 3 million yuan as the project liquidity, and finally invest 118.9 million yuan to start the project. The capital of the project company accounts for 30% of the total investment, about 35.7 million yuan; the government contributes about 7.1 million yuan, accounting for 20% of the capital; the private partner contributes about 28.6 million yuan, accounting for 80% of the capital; and the remaining about 83.2 million yuan is financed by bank loans. The TOT project has a franchise period of 15 years, and the investment return mechanism adopts a “user pays” approach.
Regardless of the time value of funds, if the project adopts the traditional method, the total net profit of the project during the franchise period is 28.3422 million yuan. If the project adopts TOT model, the total net profit of the project during the franchise period is 46.0585 million yuan. If the project is implemented by the private partner, the total net profit of the project during the franchise period is 45.5931 million yuan. The investment ratios of government and private partner are 0.8 and 0.2 respectively. The risk-sharing ratios are 0.24 and 0.76, respectively.
4.2. Revenue Sharing of TOT Projects Based on Modified Shapley Value
4.2.1. Revenue Sharing of TOT Projects Based on Classical Shapley Value
Without considering .
According to Definition 1, we have .
According to Formula (1), the revenue sharing of the government is:
Similarly, the revenue sharing of the private partner is:
Considering , Revenue sharing based on Shapley value improved by initial correction coefficient are as follow.
In this case, there are , , , , , , , and and . According to definition 2 and Equations (2)−(5), we have:
, , .
4.2.2. Revenue Sharing of Government and Private Partner Based on Fuzzy Payment
Suppose EMBED Equation. DSMT4 and . fluctuate by ±10%. According to definition 4 and Equations (12) and (14), it can be obtained that the fuzzy payment of the project undertaken by the government alone is . The fuzzy payment of the project undertaken by the private partner alone is . The fuzzy payment for the TOT project is .
According to Equation (6), the fuzzy Shapley value of government and private partner based on the fuzzy payment are:, and .
According to Equation (7), the fuzzy RSR of government and private partner based on the fuzzy payment are , and . Therefore, , and .
According to Equation (8), the fuzzy revenue sharing of government and private partner based on the fuzzy payment are , and . Therefore, , and .
4.2.3. Revenue Sharing and Membership Functions of Government and Private Partner Based on Modified Shapley Value
Fuzzy payment function and membership function of TOT project based on modified Shapley value with triangular symmetric fuzzy element E.
According to Equation (14), the fuzzy payment function of TOT project based on the modified Shapley value is .
The interval value of the TOT project payment function based on modified Shapley value is . According to Equation (15), its membership function is
Revenue sharing and membership functions of government and private partner of TOT project based on modified Shapley value with triangular symmetric fuzzy element E.
According to Equation (9), we have and .
According to Equations (10) and (15), we have , and .
Therefore, the interval value of is . According to Equation (16), its membership function is
Similarly, the interval value of is and its membership function is
According to Equations (11) and (17), the revenue sharing of the government and private partner based on the modified Shapley value is , and .
Therefore, the interval value of is . According to Equation (18), its membership function is
Similarly, the interval value of is and its membership function is:
5. Result Discussion
5.1. Project Overview and Parameter Determination
In this paper, 60 questionnaires were distributed to tot financing model research experts, practical workers, teachers and students studying tot in school, a total of 48 valid questionnaires were recovered. Among them, there are 8 tot financing mode experts, 9 enterprise management, 12 on-site management personnel, 8 university supervisors, 11 postgraduate students, all of whom have long-term experience in TOT related work or research. The questionnaire scores the weight of each factor and collates the data Table 1. The empirical evidence is consistent with the consistency test. By analyzing the case data and the objective conditions of each participant, we can get the scores of each participant on different influencing factors under different secondary indicators. See Table 2 for details.

Table 1.
Index weight value of risk-sharing influencing factors.

Table 2.
Scoring of force majeure risk.
5.2. The Effect of the Initial Correction Coefficient on the Revenue Sharing of Both Parties
5.2.1. Results Comparison of Classical Shapley Value and Shapley Value Improved by Initial Correction Coefficient
Based on classical Shapley value, there are , , , and .
Based on Shapley value of , there are , , , , and .
In Figure 1, (1) Because of , the contribution of government departments in the TOT project is relatively low; (2) Because both and are smaller than the hypothetical value of the classic Shapley value of 0.5, . That is, when the investment ratio and RSR of the government are reduced, the government’s revenue sharing and RSR will be greatly reduced, and vice versa. It suggests that the RSR and revenue sharing are positively correlated with the initial correction coefficient.
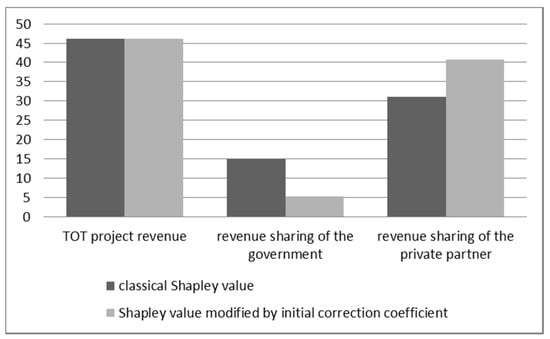
Figure 1.
Comparison of the revenue of the Transfer-Operate-Transfer (TOT) project and the revenue sharing of the government and private partner considering the initial correction coefficient and without considering the initial correction coefficient Unit: million yuan.
5.2.2. Results Comparison of Shapley Value with Fuzzy Payment and Modified Shapley Value
Based on the Shapley value of fuzzy payment, we have , , ; and .
Based on the improved Shapley value of and fuzzy payment, we have , , , , and .
Through comparative analysis, it is found that changes the fuzzy revenue sharing and RSR of the government and private partner. In this case, the government’s investment ratio and risk-sharing ratio are both less than the original assumption of the Shapley value which is 0.5. Therefore, the revenue sharing and RSR of the government are reduced with the decrease of the proportion of this factor, that is, when the investment of the participant and the risk-sharing ratio are small, the revenue sharing and the RSR are also small, and vice versa. That is to say, the value of is proportional to its RSR.
The analysis in this Section 5.2.1 and Section 5.2.2 shows that changes the RSRs and revenue sharing of the participants andthe RSR and revenue sharing of the private partner is positively correlated with . That is to say the higher , the more revenue sharing. Thus, the RSM based on modified Shapley value is fairer and more motivating to the participants.
5.3. The Effect of Fuzzy Payment on the Expected Revenue of TOT Projects and the Shapley Value of Both Parties
5.3.1. Results Comparison of Classical Shapley Value and Shapley Value with Fuzzy Payment
Based on classic Shapley value, we have , , , , and .
Based on fuzzy payment Shapley value, we have , , , , and .
The comparison shows that under the fuzzy payment function, the payment function changes from the exact value to the fuzzy interval value, and , , , respectively change from the exact value to the fuzzy interval value. The exact value is a special value in the fuzzy interval value.
5.3.2. Results Comparison of Shapley Value Improved by Initial Correction Coefficient and Modified Shapley Value
Under the condition of Shapley value based on , we have , , , , and .
Under the condition of Shapley value based on and fuzzy payment, we have , , , , and .
The comparison shows that the payment function changes from the exact value to the fuzzy interval value, and , , , respectively changes from the exact value to the fuzzy interval value. The exact value is a special value in the fuzzy interval value.
In this section of Section 5.3.1 and Section 5.3.2, the analysis shows that the RSR and revenue sharing of the participants change with the project revenue uncertainty. At the same time, the revenue sharing and RSR of the participants also form a corresponding fuzzy interval under project revenue uncertainty. Thus the RSM based on modified Shapley value can forecast the intervals of the RSR and revenue sharing of participants according to interval of the project revenue.
5.4. Potential Application of the RSM Based on Modified Shapley Value
According to the results of the case calculation, we have , , , , and . In the fuzzy payment function and the fuzzy revenue sharing interval of the participants, each specific value corresponds to its membership degree. For example, when the membership degree is 1, the TOT project’s payment function value is 46.06 million yuan, the government’s revenue sharing and RSR are 5.34 million yuan and 11.59%, respectively, and the private partner’s revenue sharing and RSR are 40.72 million yuan and 88.41%, respectively. They are shown in points , , , and in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, respectively.
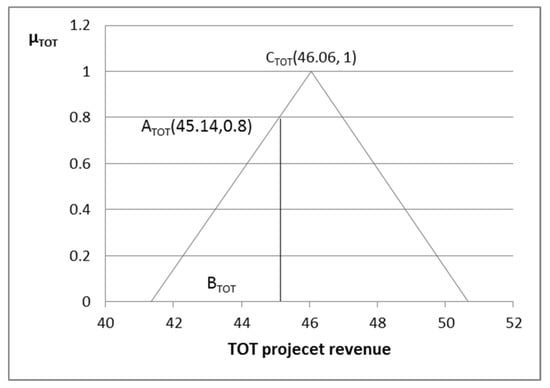
Figure 2.
Relation diagram between fuzzy revenue and membership function of TOT project.
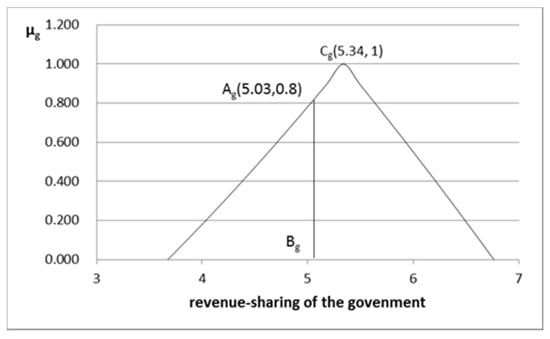
Figure 3.
Relation diagram between the government fuzzy revenue sharing and its membership function.
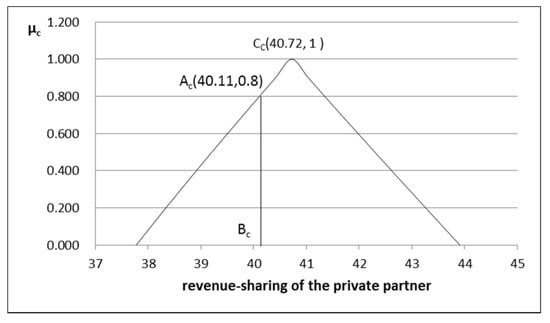
Figure 4.
Relation diagram between the fuzzy revenue sharing of the private partner and its membership function.
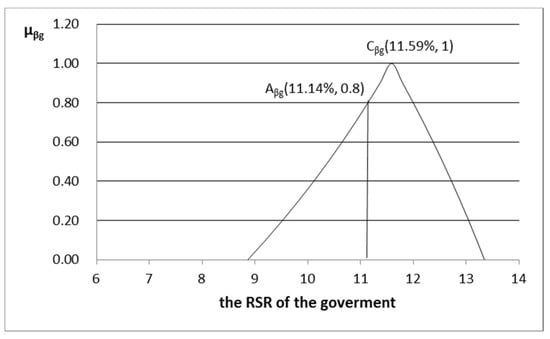
Figure 5.
Relation diagram between fuzzy revenue-sharing ratio (RSR) of the government and its membership function.
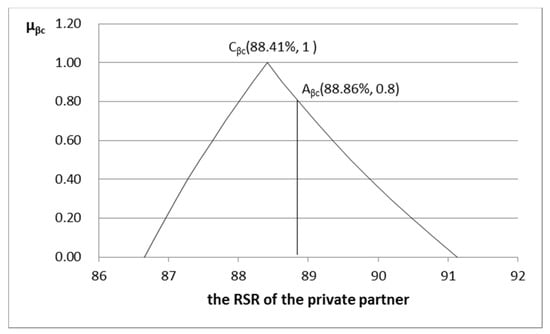
Figure 6.
Relation diagram between fuzzy RSR of the private partner and its membership function.
Therefore, according to the membership degree of the specific payment function value of TOT project based on triangular symmetric fuzzy structure element, the RSR and revenue sharing value of each participant corresponding to the same membership degree can be calculated. As shown in the BTOT point in Figure 2, the payment value of the corresponding TOT project is 45.14 million yuan, the corresponding fuzzy element is , and the membership degree is , which points ATOT. According to the corresponding relationship of the above membership degree, the fuzzy element value of each participant should be and the membership degree should be . The points corresponding to this membership degree are the points , , and in Figure 3, Figure 4, Figure 5 and Figure 6. That is to say, the payment value of TOT project is 45.14 million yuan, the corresponding government revenue sharing and its RSR are 5.03 million yuan and 11.14%, respectively, and the revenue sharing and its RSR of private partner are 40.11 million yuan and 88.86%, respectively.
In summary, the membership degree of the TOT project payment function, the participant’s RSR function and the participant’s revenue sharing function accurately determine the relationship of the three functions. Then, according to the actual value of the TOT project revenue and its corresponding membership degree during the contract execution period, the precise revenue sharing value of the participants can be determined. That is to say, the RSM based on the modified Shapley value can achieve theprecise dynamic distribution function under the project revenue uncertainty. Thus, it is more flexible under theproject revenue uncertainty.
5.5. Comparison of RSMs Based the Modified Shapley Value with Methods of References
(1) Comparison with the method of references [23,32]
In references [23,32], the revenue sharing of the government and private partneris respectively:
, indicates the comprehensive influence degree of each income distribution influencing factor on the interest distribution of two core stakeholders in the TOT project cooperation alliance.
The results of this method are:
In this paper, , .
The result reveals that the change ofrevenue sharing of participants based on Shapley value improved by in this paper is more moderate.
In this paper, the revenue sharing of participants varies with the relative value of contribution capacity and . It better reflects comprehensive contributions of the participants. However, the revenue sharing of participants just varies with the absolute value of in the references [23,32]. Hence the Shapley value improved by of this paper is fair in line with the contribution ratio of participant.
(2) Comparison of RSMs based the modified Shapley value with RSM of references [39,40]
The methods of references [33,34] and this paper are all improved with fuzzy payment and . Thus, they both have the forecasting function for giving the intervals of the revenue sharing.
In addition, the RSM in this paper is improved with fuzzy payment by using triangular fuzzy element function. It enables the method of this paper has precise dynamic distribution function rather than the methods of references [33,34].
(3) Comparison of the modifying forms and features of RSMs
In addition to the "fairness", the following features highlight the improved performance of the method. (1) Flexibility, where revenue sharing changes with income uncertainty. (2) Incentive, where RSR is positively correlated with investment ratio, risk-sharing ratio, and execution degree. (3) Forecasting, where the revenue sharing interval is forecast in line with the change of revenue. (4) Exactness, where the participant’s revenue sharing is an exact value rather than an interval value. The method of Reference
As shown in Table 3 each method has flexibility. Methods in references [23,32] are incentive and exact for the Shapley value is improved by are only improved by initial coefficient, but they cannot forecast the revenue-sharing interval and is lack of flexibility. References [33,34] are predictive and incentive and flexible, however they cannot achieve the precise dynamic distribution function. The RSM of this paper have all the features as shown in Table 3, particularly, it has the function of dynamic precise allocation because of using triangular symmetric fuzzy structural elements. Therefore, it is more flexible than the methods in references [33,34].

Table 3.
Comparison of modifying forms and features of revenue sharing methods(RSMs).
6. Conclusions
In this paper, an RSR of the TOT project based on modified Shapley value is proposed. Specific research results are as follows.
(1) The main research results of this paper are as follows: the initial correction coefficient based on investment rate and risk sharing rate and execution degree is established to simplify the calculation of relevant correction value; the results of case states clearly that the RSRs of participants is positively correlated with the initial correction coefficient. In addition, the RSR and revenue sharing of the participants change with the relative value rather than absolute value of each participant initial correction coefficient, so the RSM based on modified Shapley value can better reflect comprehensive contributions of the participants to TOT project revenue. Therefore, RSM based on the modified Shapley value is fair and motivating to the participants.
(2) The Shapley value of TOT project based on fuzzy payment and the RSM of TOT project based on modified Shapley value are constructed by using triangular symmetric fuzzy element function. The result of case demonstrates that the RSR and revenue sharing of participants become the interval values that correspond to the project revenue uncertainty. Therefore, the RSM either based on the modified Shapley value or based on the payment has forecasting function.
(3) The fuzzy payment function affects the total revenue, RSR and revenue sharing at the same time. The results of case suggest that there is a one-to-one correspondence among the intervals of RSR and revenue sharing and project revenue for the membership functions of RSR based on triangular symmetric fuzzy element. As a result, the RSM based on the modified Shapley value can achieve the precise dynamic distribution function under the project revenue uncertainty, what makes it more flexible under the project revenue uncertainty.
This paper modifies the Shapley value by considering the investment ratio, the risk-sharing ratio, execution degree and the uncertainty of the payment function, so that the modified Shapley value is more in line with the actual situation of the operational TOT project. In addition to the above main factors, there may be other influencing factors. Subsequent research will further identify other influencing factors through questionnaires, and further improve Shapley value in order to improve the consistency between the modified Shapley value and the actual situation of the operational TOT project, and improve the fairness, impartiality, accuracy and applicability of the RSM.
Author Contributions
Conceptualization, Y.D. and, J.F.; methodology, Y.D.; validation, Y.D., J.Z. and J.H.; formal analysis, Y.D. and J.F.; investigation, Y.D., J.Z. and J.H.; resources, J.F.; data curation, J.Z. and J.H.; writing—original draft preparation, Y.D.; writing—review and editing, J.F. and J.Z.; supervision, J.F.; project administration, Y.D.; funding acquisition, J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hubei Provincial Development and Reform Commission of China, grant number [20162s0013].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Almarri, K. Improving PPP contract design for procurement of public projects. In Proceedings of the 15th International Conference on Project Management, Valencia, Spain, 19–22 April 2016; pp. 19–27. [Google Scholar]
- Haake, C.-J.; Recker, S. The Generalized Nash Bargaining Solution for Transfer Price Negotiations Under Incomplete Information. Group Decis. Negot. 2018, 27, 905–932. [Google Scholar] [CrossRef]
- Borkotokey, S.; Mesiar, R. The Shapley value of cooperative games under fuzzy settings: A survey. Int. J. Gen. Syst. 2013, 43, 75–95. [Google Scholar] [CrossRef]
- Wicke, K.; Fischer, M. On the Shapley Value of Unrooted Phylogenetic Trees. Bull. Math. Boil. 2018, 81, 618–638. [Google Scholar] [CrossRef]
- Zwalf, S.; Hodge, G.; Alam, Q. Choose Your Own Adventure: Finding a Suitable Discount Rate for Evaluating Value for Money in Public-Private Partnership Proposals *. Aust. J. Public Adm. 2017, 76, 301–315. [Google Scholar] [CrossRef]
- Carbonara, N.; Pellegrino, R. Public-private partnerships for energy efficiency projects: A win-win model to choose the energy performance contracting structure. J. Clean. Prod. 2018, 170, 1064–1075. [Google Scholar] [CrossRef]
- Sequeira, L.; De La Cruz, J.L.; Ruiz-Mas, J.; Saldana, J.; Fernandez-Navajas, J.; Almodovar, J. Building an SDN Enterprise WLAN Based on Virtual APs. IEEE Commun. Lett. 2016, 21, 374–377. [Google Scholar] [CrossRef]
- Auriol, E.; Picard, P.M. A theory of BOT concession contracts. J. Econ. Behav. Organ. 2013, 89, 187–209. [Google Scholar] [CrossRef]
- Hanaoka, S.; Palapus, H.P. Reasonable concession period for build-operate-transfer road projects in the Philippines. Int. J. Proj. Manag. 2012, 30, 938–949. [Google Scholar] [CrossRef]
- Gao, J.; Yang, X.; Liu, D. Uncertain Shapley value of coalitional game with application to supply chain alliance. Appl. Soft Comput. 2017, 56, 551–556. [Google Scholar] [CrossRef]
- Zhou, Z.; Ota, K.; Dong, M.; Xu, C. Energy-Efficient Matching for Resource Allocation in D2D Enabled Cellular Networks. IEEE Trans. Veh. Technol. 2017, 66, 5256–5268. [Google Scholar] [CrossRef]
- Fan, S.; Ai, Q.; Piao, L. Bargaining-based cooperative energy trading for distribution company and demand response. Appl. Energy 2018, 226, 469–482. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J. Evaluation of the excess revenue sharing ratio in PPP projects using principal–agent models. Int. J. Proj. Manag. 2015, 33, 1317–1324. [Google Scholar] [CrossRef]
- Ettori, S.; Fabian, A.C.; White, D.A. On the mass distribution in the Shapley Supercluster inferred from X-ray observations. Mon. Not. R. Astron. Soc. 1997, 289, 787–800. [Google Scholar] [CrossRef]
- Sharma, S.; Abhyankar, A. Loss allocation of radial distribution system using Shapley value: A sequential approach. Int. J. Electr. Power Energy Syst. 2017, 88, 33–41. [Google Scholar] [CrossRef]
- Hu, B.; Meng, C.; Xu, N.; Son, Y.-J. Three-echelon supply chain coordination with a loss-averse retailer and revenue sharing contracts. Int. J. Prod. Econ. 2016, 179, 192–202. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Q.; Wang, M. Profit allocation scheme among partners in virtual enterprises based on Fuzzy Shapley values. J. Beijing Inst. Technol. 2007, 1, 122–126. [Google Scholar] [CrossRef]
- Meng, F.; Zhao, J.; Zhang, Q. The Shapley function for fuzzy games with fuzzy characteristic functions. J. Intell. Fuzzy Syst. 2013, 25, 23–35. [Google Scholar] [CrossRef]
- Chen, S.; Meng, J.; Yao, H. Profit distribution of water diversion project of PPP model based on the Shapley. South-to-North Water Transf. Water Sci. Technol. 2018, 16, 202–208. [Google Scholar]
- Zhang, B. The income distribution of the energy performance contracting projects under uncertain conditions—On the analysis of fuzzy cooperative game. J. Beijing Inst. Econ. Manag. 2016, 31, 22–27. [Google Scholar]
- Song, B.; Seol, H.; Park, Y. A patent portfolio-based approach for assessing potential R&D partners: An application of the Shapley value. Technol. Forecast. Soc. Chang. 2016, 103, 156–165. [Google Scholar] [CrossRef]
- Basallote, M.; Hernández-Mancera, C.; Jiménez-Losada, A. A new Shapley value for games with fuzzy coalitions. Fuzzy Sets Syst. 2020, 383, 51–67. [Google Scholar] [CrossRef]
- Li, Y.; Huang, T.; Li, N.; Bao, Z.; Feng, W.; Bai, M. Equitable Distribution of Wastewater Treatment PPP project on shapley value method with ANP risk correction. J. Residuals Sci. Technol. 2016, 13, 810–817. [Google Scholar]
- Kumar, N.S.; Thangamani, M. Multi-Ontology Based Points of Interests (MO-POIS) and Parallel Fuzzy Clustering (PFC) Algorithm for Travel Sequence Recommendation with Mobile Communication on Big Social Media. Wirel. Pers. Commun. 2018, 103, 991–1010. [Google Scholar] [CrossRef]
- Battiston, F.; Perc, M.; Latora, V. Determinants of public cooperation in multiplex networks. New J. Phys. 2017, 19, 073017. [Google Scholar] [CrossRef]
- Wu, M. Research on the benefit distribution of PPP project based on NASH negotiation model. Eng. Econ. 2016, 26, 78–80. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L. Research of income sharing model in contract energy management mechanism. Energy Technol. Manag. 2007, 4, 92–93. [Google Scholar] [CrossRef]
- Cubukcu, K.M. The problem of fair division of surplus development rights in redevelopment of urban areas: Can the Shapley value help? Land Use Policy 2020, 91, 104320. [Google Scholar] [CrossRef]
- Zhou, H.; Ma, X.; Chen, H.; Ding, W. A Novel Approach to Group Decision-Making with Interval-Valued Intuitionistic Fuzzy Preference Relations via Shapley Value. Int. J. Fuzzy Syst. 2017, 20, 1172–1187. [Google Scholar] [CrossRef]
- Xie, J. Information, Risk Sharing, and Incentives in Agency Problems. Int. Econ. Rev. 2017, 58, 157–182. [Google Scholar] [CrossRef]
- Burke, R.; Demirag, I. Risk transfer and stakeholder relationships in Public Private Partnerships. Account. Forum 2017, 41, 28–43. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, W.; Ye, X. Profit allocation of PPP model based on the revised Shapley. J. Ind Eng. Eng. Manag. 2011, 25, 149–154. [Google Scholar] [CrossRef]
- Yu, T.; Li, H. Research on profit distribution of PPP project based on Shapley value. China Real Estate 2017, 15, 33–41. [Google Scholar] [CrossRef]
- Xu, S.; Liu, L. Research on Income Distribution of Hydropower PPP Project Based on Modified Interval Shapley Value Method. Water Resour. Power 2018, 36, 122–126. [Google Scholar]
- Medda, F. A game theory approach for the allocation of risks in transport public private partnerships. Int. J. Proj. Manag. 2007, 25, 213–218. [Google Scholar] [CrossRef]
- Li, S.; Ma, X.; Yang, C. A combined thermal power plant investment decision-making model based on intelligent fuzzy grey model and ito stochastic process and its application. Energy 2018, 159, 1102–1117. [Google Scholar] [CrossRef]
- Wen, F.; Zhao, Y.; Zhang, M.; Hu, C. Forecasting realized volatility of crude oil futures with equity market uncertainty. Appl. Econ. 2019, 51, 6411–6427. [Google Scholar] [CrossRef]
- Shen, Y. Platform retailing with slotting allowance and revenue sharing. J. Oper. Res. Soc. 2018, 69, 1033–1045. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, H.; Liu, J. Incentive game of investor speculation in PPP highway projects based on the government minimum revenue guarantee. Transp. Res. Part A Policy Pract. 2019, 125, 20–34. [Google Scholar] [CrossRef]
- Liu, J.; Gao, R.; Cheah, C.Y.J.; Luo, J. Incentive mechanism for inhibiting investors’ opportunistic behavior in PPP projects. Int. J. Proj. Manag. 2016, 34, 1102–1111. [Google Scholar] [CrossRef]
- Planas, M.I.G.; Klymchuk, T. Perturbation analysis of a matrix differential equation = ABx. Appl. Math. Nonlinear Sci. 2018, 3, 97–104. [Google Scholar] [CrossRef]
- Ghaemi, N.F.; Rostamy, M.M. Extension of TOPSIS for Group Decision-Making Based on the Type-2 Fuzzy Positive and Negative Ideal Solutions. Int. J. Ind. Math. 2010, 2, 199–213. [Google Scholar]
- Bogoya, J.M.; Vargas, A.; Cuate, O.; Schütze, O. A (p,q)-Averaged Hausdorff Distance for Arbitrary Measurable Sets. Math. Comput. Appl. 2018, 23, 51. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).