Superfields, Nilpotent Superfields and Superschemes †
Abstract
1. Introduction
2. Superspaces and Scalar Superfields
2.1. Some Mathematical Definitions
2.2. Superfields
3. The Even Rules Principle
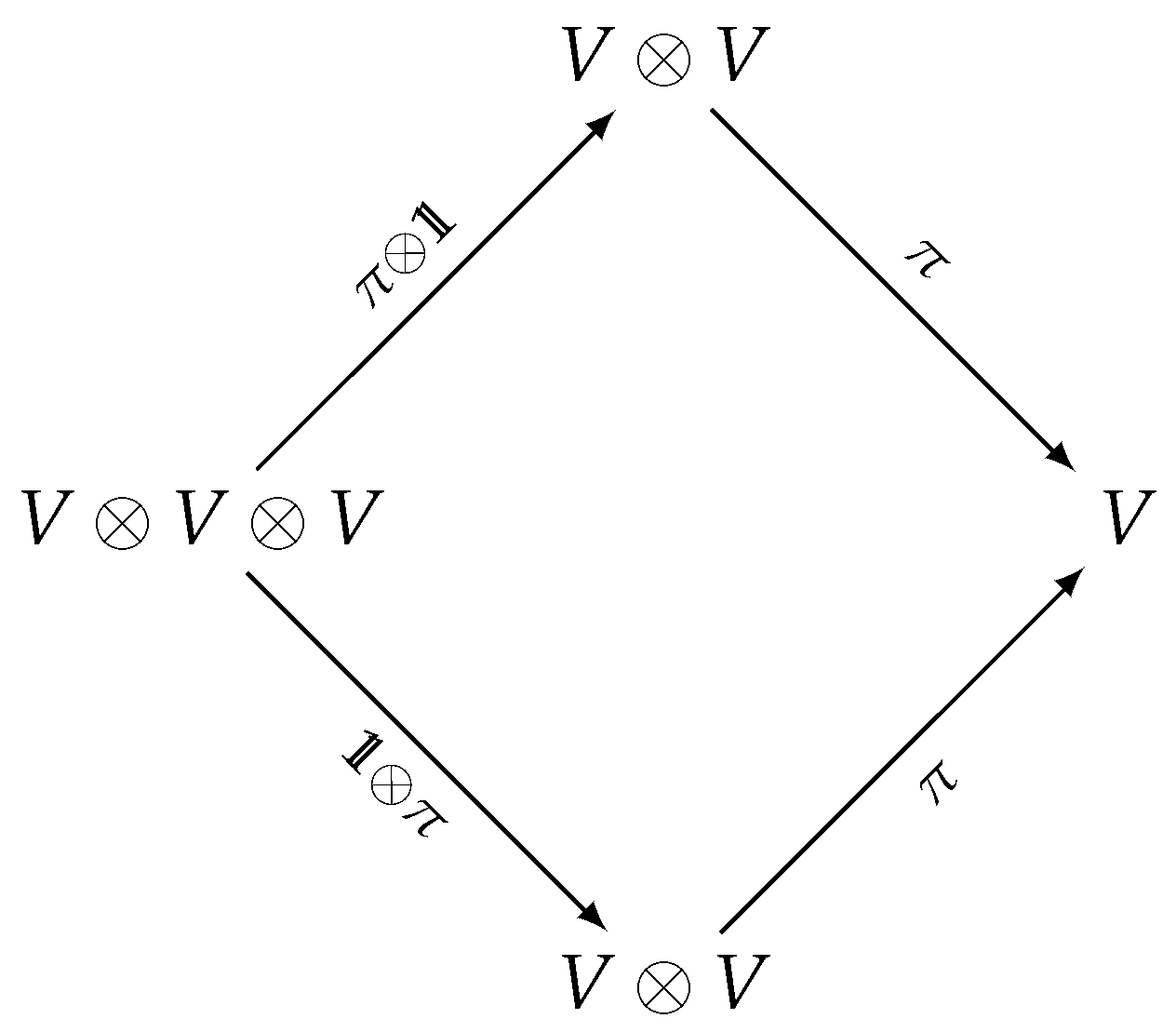 is commutative. On the other hand, we say that the superalgebra is commutative if, given the flip map,
is commutative. On the other hand, we say that the superalgebra is commutative if, given the flip map,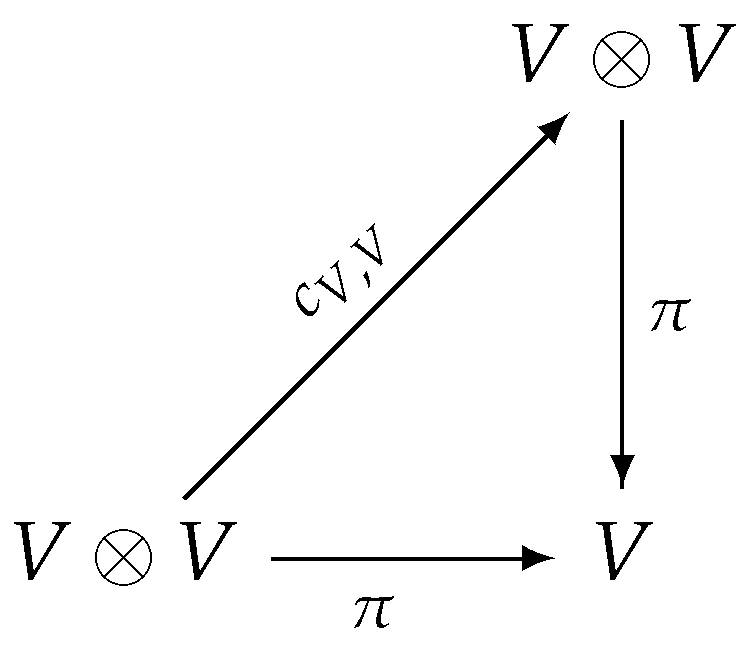 commutes.
commutes.- even. Then, we may take (in an arbitrary algebra ) and:
- even, odd. Then, we take for example , , and . The equality:determines .
- odd, odd. It is enough to consider , and the equality:determines .
4. How to Deal with Algebraic Constraints
4.1. Schemes and Superschemes
4.2. Constraint
4.3. General Constraint
4.4. Cubic Constraint with Two Superfields
4.5. Cubic Constraint with an Arbitrary Number of Superfields
5. A Non-Algebraic Constraint
6. Observables and Nilpotent Variables
- 1.
- We consider the ring of polynomials in one variable . The prime ideals of F are of the form , or the ideal . It is not difficult to see that the residue field at is and is the field of rational functions.
- 2.
- If the ground field is , we have that every irreducible polynomial in generates a prime ideal. We still have the maximal ideals as that give all the points of . At them, the residue field is . However, for example, the irreducible polynomial also generates a prime ideal. It is not difficult to realize that the elements of the residue field are of the form , with and x such that , so .
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Some Basic Definitions
- 1.
- .
- 2.
- for all .
- 1.
- Continuous, differentiable, real analytic, or complex analytic functions on a topological space are all sheaves of algebras.
- 2.
- Sections of a vector bundle over a topological space are a sheaf of modules over some algebra of functions.
- 3.
- Constant functions over a topological space are, generically, only a presheaf. If the space is connected, then the sheaf condition is satisfied. Furthermore, on a not necessarily connected space, one can define the sheaf of locally constant functions, that is functions that are constant on an open neighborhood of each point.
Appendix B. Notation for Spinors
Appendix C. Supersymmetry Transformations
References
- Berezin, F.A.; Leites, D.A. Supermanifolds. Dokl. Akad. Nauk. SSSR 1975, 224, 505–508. [Google Scholar]
- Kostant, B. Graded manifolds, graded Lie theory and prequantisation. In Lecture Notes in Mathematics 570; Reetz, B.K.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1977; pp. 177–306. [Google Scholar]
- Leites, D.A. Introduction to the theory of supermanifolds. Uspekhi Mat. Nauk. 1975, 35, 1–64. [Google Scholar] [CrossRef]
- Manin, Y.I. Gauge Field Theory and Complex Geometry; Springer: Berlin, Germany, 1988; pp. 45–98. [Google Scholar]
- Deligne, P.; Morgan, J.W. Notes on Supersymmetry (following J. Bernstein). In Quantum Fields and Strings: A Course for Mathematicians, Vol 1; Deligne, P., Etingof, P., Freed, D.S., Jeffrey, L., Kazhdan, D., Morgan, J., Morrison, D.R., Witten, E., Eds.; AMS: Providence, RI, USA, 1999; pp. 32–58. [Google Scholar]
- Varadarajan, V.S. Supersymmetry for Mathematicians: An Introduction. Courant Lecture Notes, 11; AMS: Providence, RI, USA, 2004. [Google Scholar]
- Carmeli, C.; Caston, L.; Fioresi, R.; Dimitrov, I. Mathematical Foundations of Supersymmetry. EMS Serie Lectures in Mathematics; EMS: Zurich, Switzerland, 2011. [Google Scholar]
- Fioresi, R.; Lledó, M.A. The Minkowski and Conformal Superspaces: The Classical and the Quantum Pictures; World Scientific Publishing: Singapore, 2015. [Google Scholar]
- Schwarz, A.S. On the definition of superspace. Theor. Math. Phys. 1984, 60, 657–660, (Translated from Russian Teor. Mat. Fiz. 1984, 60, 37–42). [Google Scholar]
- For a Beautiful Exposition of the Meaning of the Functor of Points, See the First Lecture by P. Deligne in the Supermoduli Workshop at the Simons Center (May 2015). Available online: http://scgp.stonybrook.edu/video_portal/results.php?event_id=87 (accessed on 15 January 2017).
- Voronov, A. Mappings of supermanifolds. Theor. Math. Phys. 1984, 60, 660–664. [Google Scholar] [CrossRef]
- DeWitt, B. Supermanifolds; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Rogers, A. Graded manifolds, supermanifolds and infinite dimensional Grassmann algebras. Comm. Math. Phys. 1986, 105, 375–384. [Google Scholar] [CrossRef]
- Sachse, C. A categorical formulation of superalgebra and supergeometry. arXiv 2008, arXiv:0802.4067. [Google Scholar]
- Freed, D. Five Lectures on Supersymmetry; AMS: Providence, RI, USA, 1999. [Google Scholar]
- Eisenbud, D.; Harris, J. The Geometry of Schemes; Springer: New York, NY, USA, 2000. [Google Scholar]
- Bonavolontà, G.; Kotov, A. On the space of supermaps between smooth supermanifolds. arXiv 2013, arXiv:1304.0394. [Google Scholar]
- Fioresi, R.; Lledó, M.A.; Varadarajan, V.S. The Minkowski and conformal superspaces. J. Math. Phys. 2007, 48, 113505. [Google Scholar] [CrossRef]
- Volkov, D.V.; Akulov, V.P. Is the neutrino a Goldstone particle? Phys. Lett. B 1973, 46, 109–110. [Google Scholar] [CrossRef]
- Rocek, M. Linearizing the Volkov-Akulov Model. Phys. Rev. Lett. 1978, 41, 451–453. [Google Scholar] [CrossRef]
- Casalbuoni, R.; De Curtis, D.; Dominici, D.; Feruglio, F.; Gatto, R. Non-Linear realization of supersymmetry algebra from supersymmetric constraint. Phys. Lett. B 1989, 220, 569–575. [Google Scholar] [CrossRef]
- Komargodski, Z.; Seiberg, N. From linear SUSY to constrained superfields. JHEP 2009, 0909, 066. [Google Scholar] [CrossRef]
- Ghilencea, D.M. Comments on the nilpotent constraint on the goldstino superfield. Mod. Phys. Lett. A 2016, 31, 1630011. [Google Scholar] [CrossRef]
- Brignole, A.; Feruglio, F.; Zwirner, F. On the effective interactions of a light gravitino with matter fermions. JHEP 1997, 1811, 1. [Google Scholar] [CrossRef]
- Dall’Agata, G.; Ferrara, S.; Zwirner, F. Minimal scalar-less matter-coupled supergravity. Phys. Lett. B 2016, 752, 263–266. [Google Scholar] [CrossRef]
- Vercnocke, B.; Wrase, T. Constrained superfields from an anti-D3-brane in KKLT. JHEP 2016, 1608, 132. [Google Scholar] [CrossRef]
- Kallosh, R.; Vercnocke, B.; Wrase, T. String theory origin of constrained multiplets. JHEP 2016, 1609, 063. [Google Scholar] [CrossRef]
- Castellani, L.; Catenacci, R.; Grassi, P.A. Super quantum mechanics in the integral form formalism. Ann. Inst. Heri Poincaré 2018, 19, 1385–17417. [Google Scholar] [CrossRef]
- Berezin, F.A. The Method of Second Quantization; Academic Press: New York, NY, USA, 1996. [Google Scholar]
- Berezin, F.A.; Marinov, M.S. Particle spin dynamics as the Grassmann variant of classical mechanics. Ann. Phys. 1997, 104, 336–362. [Google Scholar] [CrossRef]
- Ferrara, S.; Lledó, M.A. Some aspects of deformations of supersymmetric field theories. JHEP 2000, 5, 8. [Google Scholar] [CrossRef]
- Lledó, M.A. Deformed supersymmetric field theories. Mod. Phys. Lett. A 2001, 16, 305–310. [Google Scholar] [CrossRef]
- Kontsevich, M. Deformation quantization of Poisson manifolds, I. Lett. Math. Phys. 2003, 66, 157–216. [Google Scholar] [CrossRef]
- Fioresi, R.; Lledó, M.A.; Varadarajan, V.S. On the deformation quantization of algebraic varieties. Int. J. Math. 2005, 4, 419–435. [Google Scholar] [CrossRef]
- Kontsevich, M. Deformation quantization of algebraic varieties. Lett. Math. Phys. 2006, 56, 271–294. [Google Scholar] [CrossRef]
- Ferrara, S.; Wess, J.; Zumino, B. Supergauge multiplets and superfields. Phys. Lett. B 1974, 51, 239–241. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lledó, M.A. Superfields, Nilpotent Superfields and Superschemes. Symmetry 2020, 12, 1024. https://doi.org/10.3390/sym12061024
Lledó MA. Superfields, Nilpotent Superfields and Superschemes. Symmetry. 2020; 12(6):1024. https://doi.org/10.3390/sym12061024
Chicago/Turabian StyleLledó, María Antonia. 2020. "Superfields, Nilpotent Superfields and Superschemes" Symmetry 12, no. 6: 1024. https://doi.org/10.3390/sym12061024
APA StyleLledó, M. A. (2020). Superfields, Nilpotent Superfields and Superschemes. Symmetry, 12(6), 1024. https://doi.org/10.3390/sym12061024




