Analysis of Key Elements of Truss Structures Based on the Tangent Stiffness Method
Abstract
1. Introduction
2. Stiffness-Based Evaluation Method for Element Importance
- (a)
- According to the symmetry of the truss structures, the simulated model is obtained.
- (b)
- The stiffness matrix of the undamaged structures is calculated based on the topology and geometry of the truss, the cross-sections and the material behavior of the elements, and the boundary of the structures.
- (c)
- The Newton–Raphson method is used to get the determinant of the tangent stiffness of the undamaged structures under external loads.
- (d)
- Delete the ith element, and obtain the determinant of the tangent stiffness of the structure after the failure of the element i.
- (e)
- Calculate the element importance index of element i based on Equation (1).
- (f)
- Repeat (d) and (e) to obtain element importance indices of all elements.
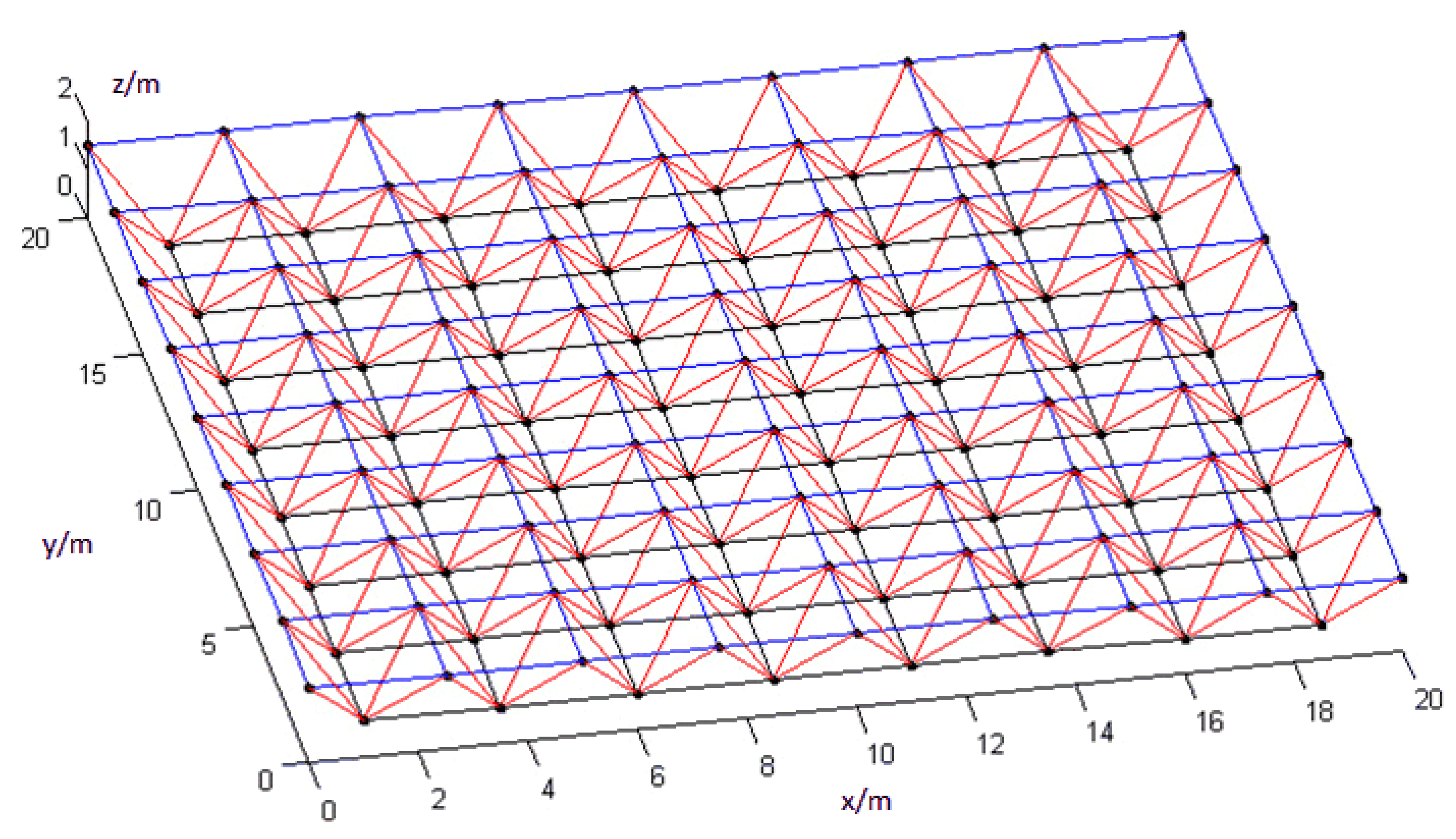
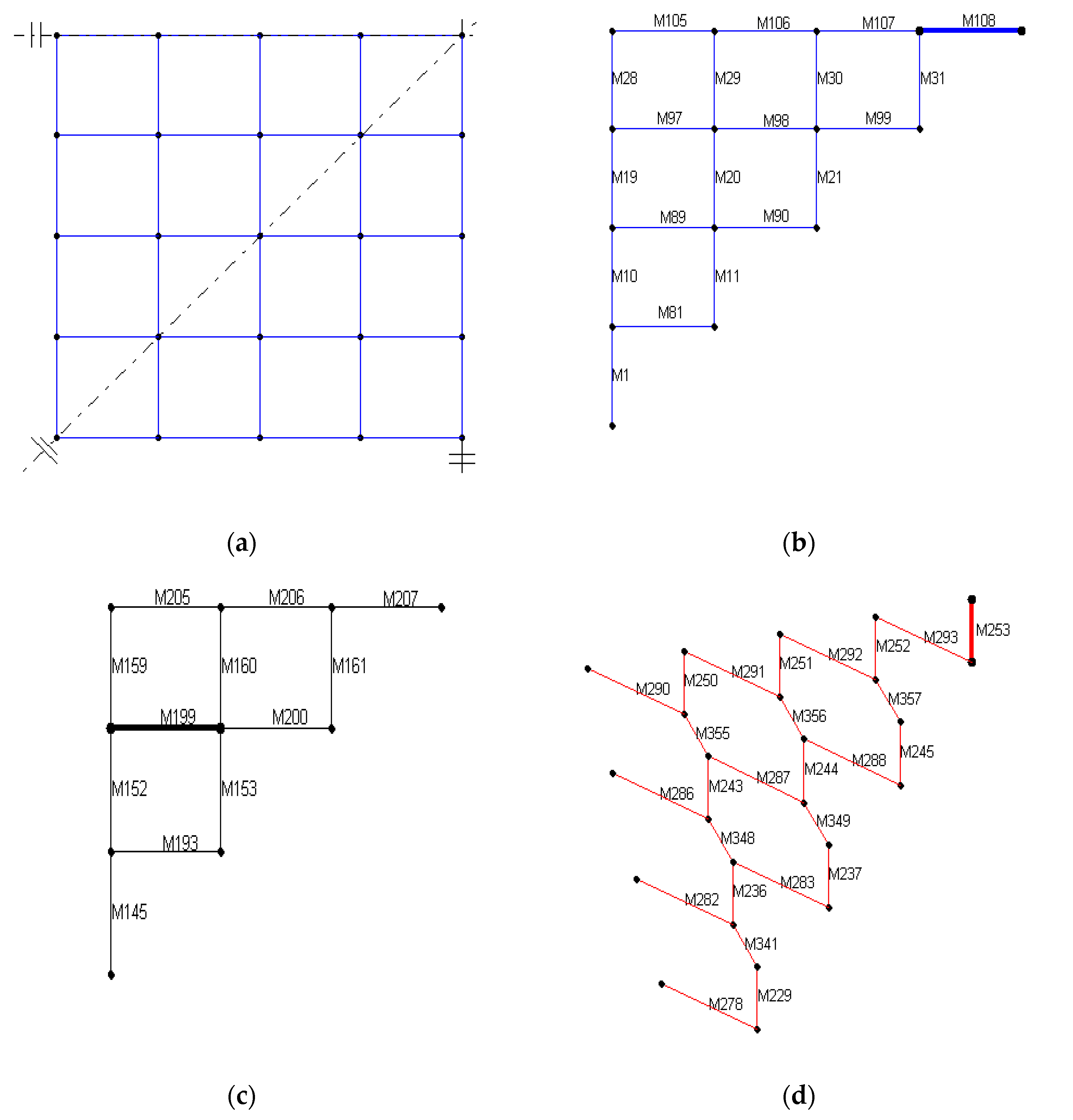
3. Analysis of a Square Pyramid Grid
3.1. Effect of the Support Condition
3.2. Effect of the Element Stiffness
4. Effect of the Geometric Parameters
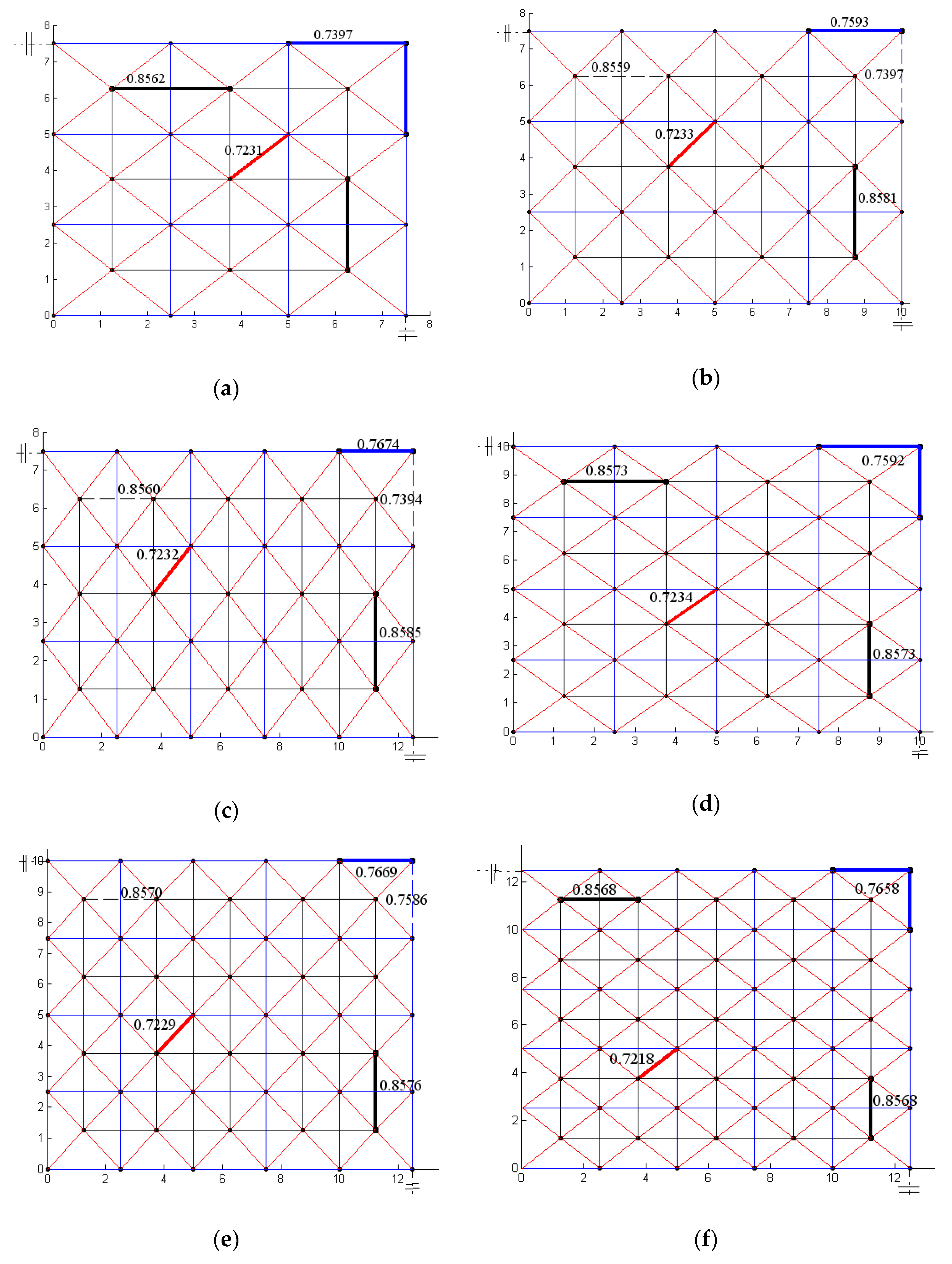
4.1. Number of the Grids
4.2. Sizes of the Grids
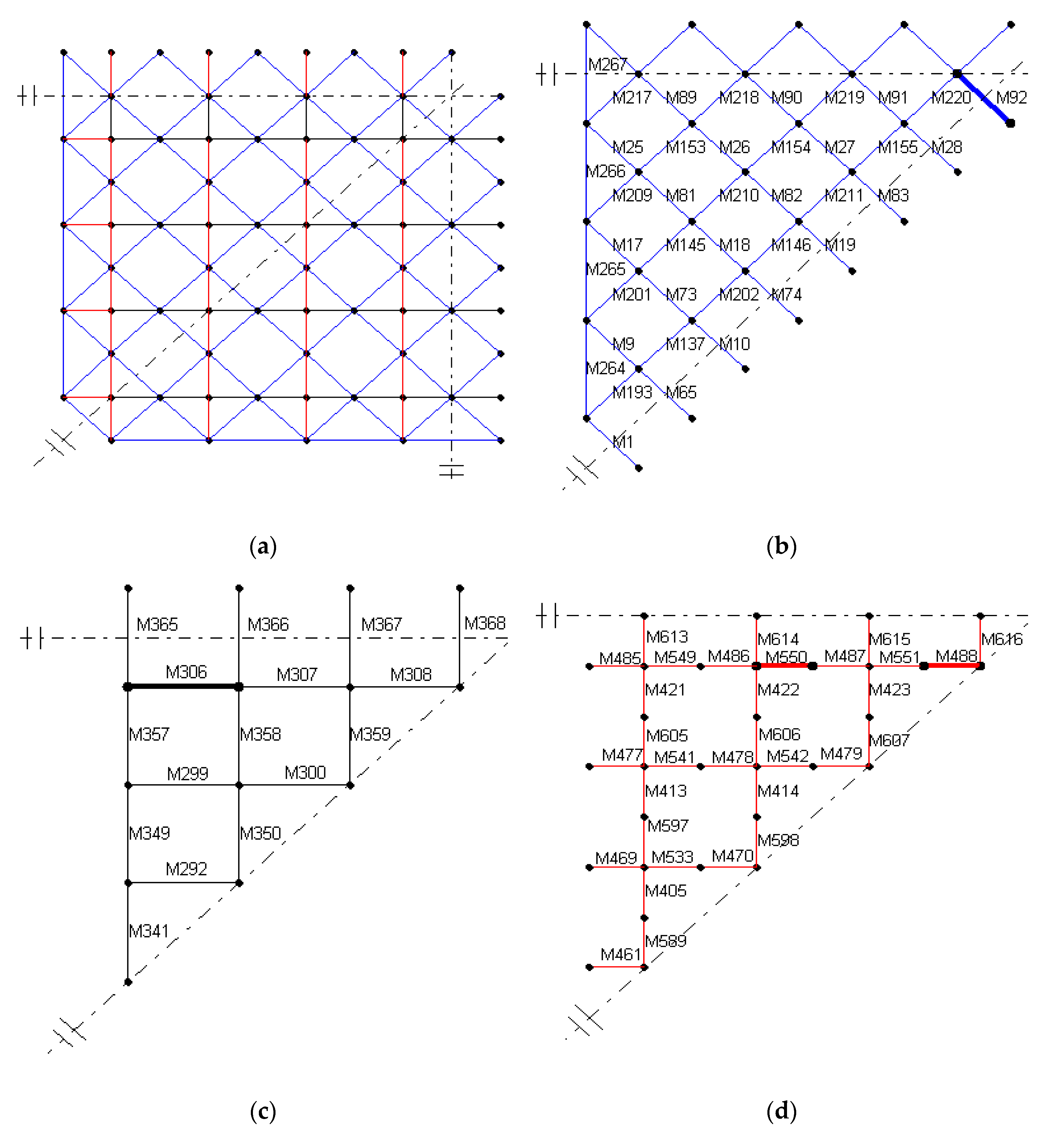
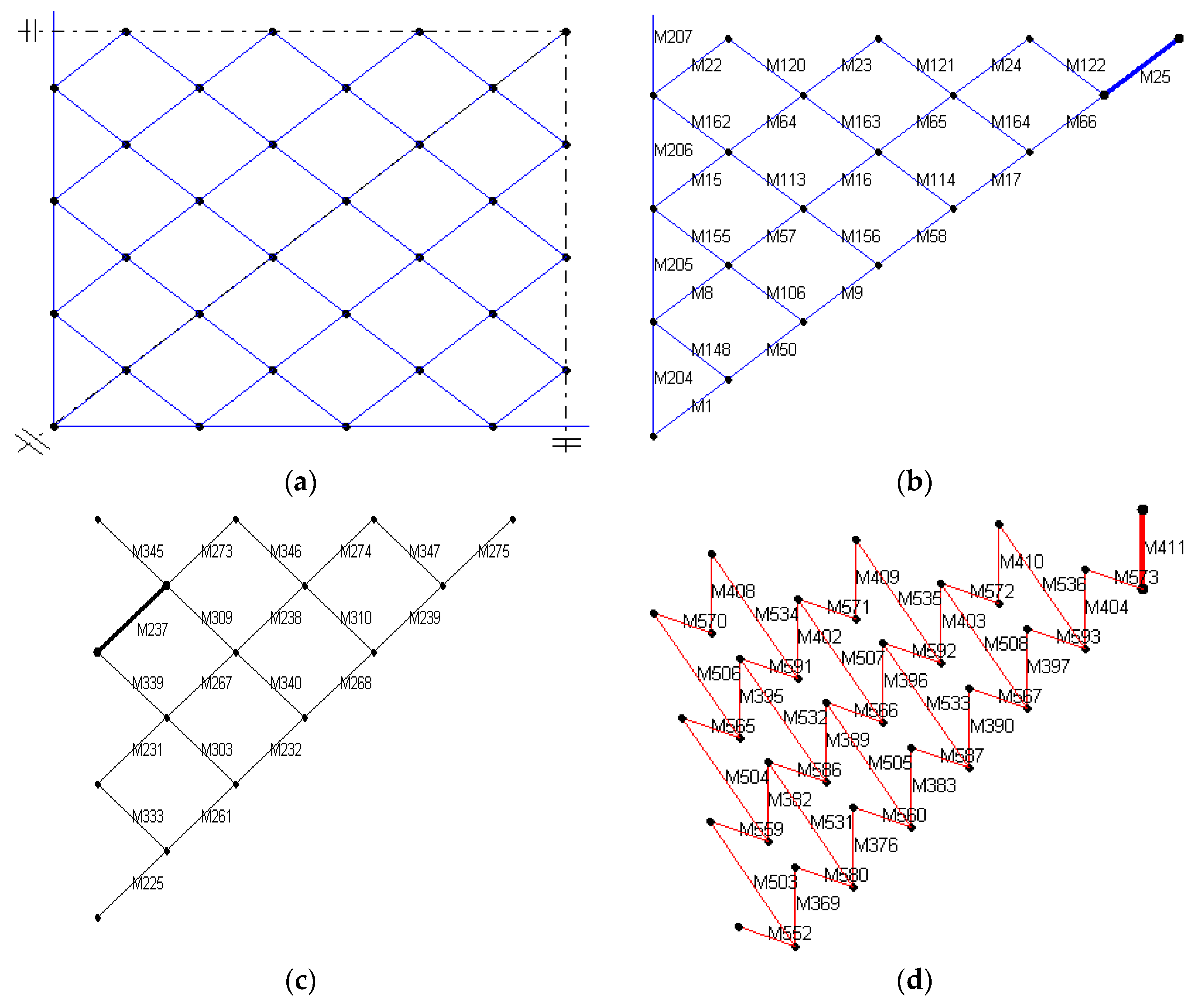
5. Effects of the Topology of the Grid Structures
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mashhadiali, N.; Kheyroddin, A. Progressive collapse assessment of new hexagrid structural system for tall buildings. Struct. Des. Tall Spec. Build. 2013, 23, 947–961. [Google Scholar] [CrossRef]
- Kang, S.-B.; Tan, K.H. Behaviour of precast concrete beam–column sub-assemblages subject to column removal. Eng. Struct. 2015, 93, 85–96. [Google Scholar] [CrossRef]
- Kang, S.-B.; Tan, K.H. Robustness Assessment of Exterior Precast Concrete Frames under Column Removal Scenarios. J. Struct. Eng. 2016, 142, 04016131. [Google Scholar] [CrossRef]
- Weng, J.; Lee, C.; Tan, K.H.; Lim, N.S. Damage assessment for reinforced concrete frames subject to progressive collapse. Eng. Struct. 2017, 149, 147–160. [Google Scholar] [CrossRef]
- Le, J.-L.; Xue, B. Probabilistic analysis of reinforced concrete frame structures against progressive collapse. Eng. Struct. 2014, 76, 313–323. [Google Scholar] [CrossRef]
- Pirmoz, A.; Liu, M. Finite element modeling and capacity analysis of post-tensioned steel frames against progressive collapse. Eng. Struct. 2016, 126, 446–456. [Google Scholar] [CrossRef]
- Shayanfar, M.; Javidan, M.M. Progressive Collapse-Resisting Mechanisms and Robustness of RC Frame–Shear Wall Structures. J. Perform. Constr. Facil. 2017, 31, 04017045. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Khattab, R. Assessment of Progressive Collapse Resistance of Steel Structures with Moment Resisting Frames. Buildings 2019, 9, 19. [Google Scholar] [CrossRef]
- Kim, J.; Park, J. Design of special truss moment frames considering progressive collapse. Int. J. Steel Struct. 2014, 14, 331–343. [Google Scholar] [CrossRef]
- De Biagi, V. Structural behavior of a metallic truss under progressive damage. Int. J. Solids Struct. 2016, 82, 56–64. [Google Scholar] [CrossRef]
- Zhao, X.; Yan, S.; Chen, Y.; Xu, Z.; Lu, Y. Experimental study on progressive collapse-resistant behavior of planar trusses. Eng. Struct. 2017, 135, 104–116. [Google Scholar] [CrossRef]
- Fu, F.; Parke, G.A.R. Assessment of the Progressive Collapse Resistance of Double-Layer Grid Space Structures Using Implicit and Explicit Methods. Int. J. Steel Struct. 2018, 18, 831–842. [Google Scholar] [CrossRef]
- Ye, L.P.; Lin, X.C.; Qu, Z.; Lu, X.Z.; Pan, P. Evaluating method of element importance of structural system based on generalized structural stiffness. J. Archit. Civ. Eng. 2010, 27, 1–6. [Google Scholar]
- Jiang, X.; Chen, Y. Progressive Collapse Analysis and Safety Assessment Method for Steel Truss Roof. J. Perform. Constr. Facil. 2012, 26, 230–240. [Google Scholar] [CrossRef]
- Zhu, N.; Ye, J. Structural vulnerability of a single-layer dome based on its form. J. Eng. Mech. 2014, 140, 112–127. [Google Scholar]
- Chen, C.H.; Zhu, Y.F.; Yao, Y.; Huang, Y. Progressive collapse analysis of steel frame structure based on the energy principle. Steel Compos. Struct. 2016, 21, 553–571. [Google Scholar] [CrossRef]
- Chen, C.H.; Zhu, Y.F.; Yao, Y.; Huang, Y.; Long, X. An evaluation method to predict progressive collapse resistance of steel frame structures. J. Constr. Steel Res. 2016, 122, 238–250. [Google Scholar] [CrossRef]
- Gordini, M.; Habibi, M.R.; Tavana, M.; TahamouliRoudsari, M.; Amiri, M. Reliability Analysis of Space Structures Using Monte-Carlo Simulation Method. Structures 2018, 14, 209–219. [Google Scholar] [CrossRef]
- Cai, J.; Jia, W.; Feng, J.; Wang, F.; Xu, Y. Applications of stiffness-based evaluation method to element importance of truss systems. J. Civ. Eng. Manag. 2017, 23, 562–572. [Google Scholar] [CrossRef]
- Li, L.-L.; Li, G.-Q.; Jiang, B.; Lü, Y. Analysis of robustness of steel frames against progressive collapse. J. Constr. Steel Res. 2018, 143, 264–278. [Google Scholar] [CrossRef]
- Tian, L.M.; Wei, J.P.; Hao, J.P. Method for evaluating the progressive collapse resistance of long-span single-layer spatial grid structures. Adv. Steel Constr. 2019, 15, 109–115. [Google Scholar]
- Yan, S.; Zhao, X.; Rasmussen, K.J.; Zhang, H. Identification of critical members for progressive collapse analysis of single-layer latticed domes. Eng. Struct. 2019, 188, 111–120. [Google Scholar] [CrossRef]
- Zhang, J.; Guest, S.D.; Ohsaki, M. Symmetric prismatic tensegrity structures: Part I. Configuration and stability. Int. J. Solids Struct. 2009, 46, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Guest, S.D.; Ohsaki, M. Symmetric prismatic tensegrity structures. Part II: Symmetry-adapted formulations. Int. J. Solids Struct. 2009, 46, 15–30. [Google Scholar] [CrossRef]
- Chen, Y.; Sareh, P.; Yan, J.; Fallah, A.S.; Feng, J. An Integrated Geometric-Graph-Theoretic Approach to Representing Origami Structures and Their Corresponding Truss Frameworks. J. Mech. Des. 2019, 141, 091402. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, Q.; Feng, J.; Xu, Y. Modeling and Kinematic Path Selection of Retractable Kirigami Roof Structures. Comput. Civ. Infrastruct. Eng. 2018, 34, 352–363. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, J.; Sareh, P.; Feng, J. Feasible Prestress Modes for Cable-Strut Structures with Multiple Self-Stress States Using Particle Swarm Optimization. J. Comput. Civ. Eng. 2020, 34, 04020003. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.; Cai, J.; Zhang, J.; Feng, J. Closed-Form Solutions for the Form-Finding of Regular Tensegrity Structures by Group Elements. Symmetry 2020, 12, 374. [Google Scholar] [CrossRef]
- Pandey, P.; Barai, S.V. Structural Sensitivity as a Measure of Redundancy. J. Struct. Eng. 1997, 123, 360–364. [Google Scholar] [CrossRef]

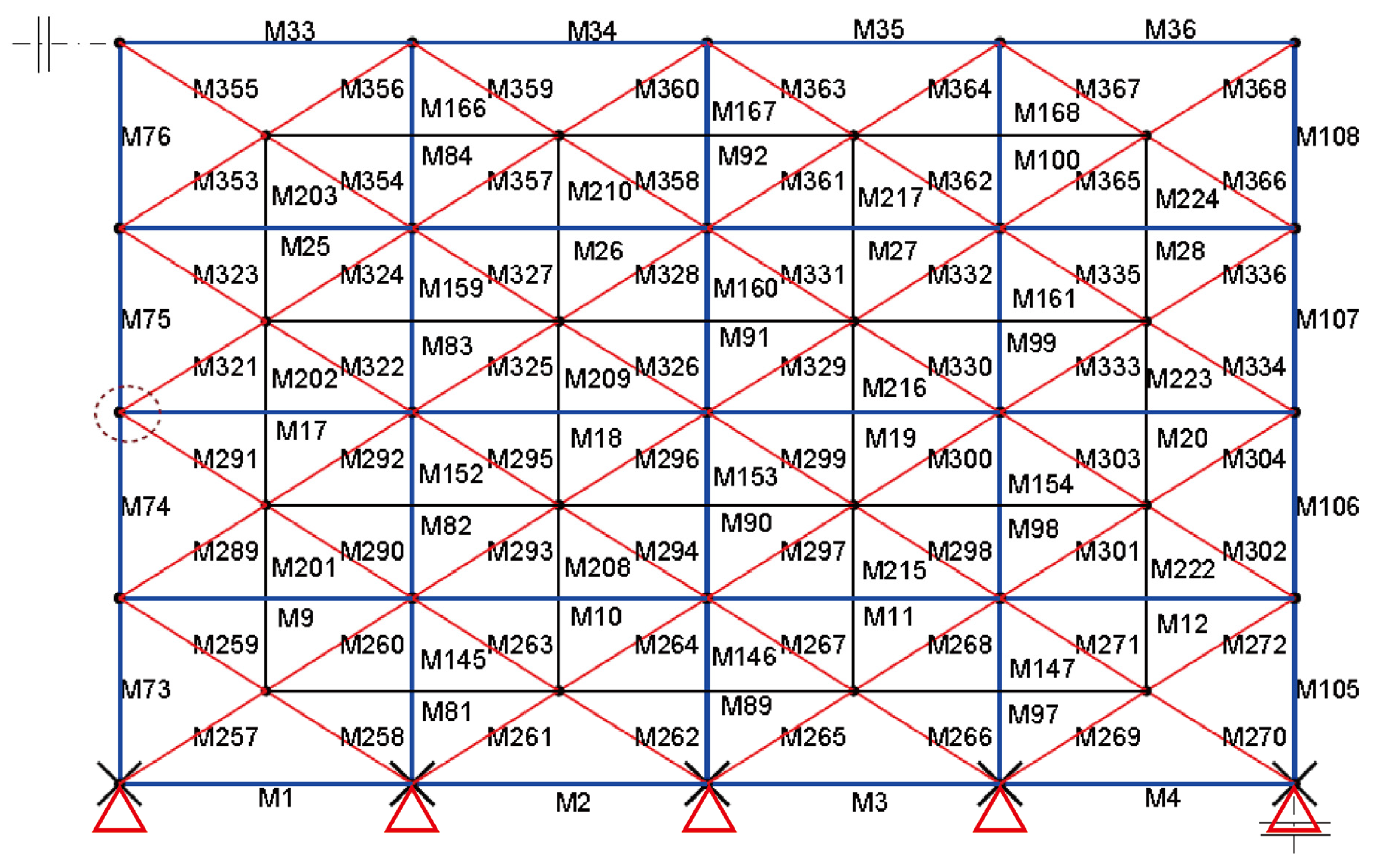
| Element Number | Opposite Boundary Fixed Support | All Boundary Fixed Support | Percent Change (%) | Element Number | Opposite Boundary Fixed Support | All Boundary Fixed Support | Percent Change (%) |
|---|---|---|---|---|---|---|---|
| 9 | 0.999 | 0.6308 | 36.86 | 167 | 0.82 | 0.8004 | 2.39 |
| 10 | 0.8649 | 0.7127 | 17.60 | 168 | 0.8 | 0.7816 | 2.30 |
| 12 | 0.781 | 0.7506 | 3.89 | 201 | 0.9381 | 0.8009 | 14.63 |
| 17 | 0.999 | 0.6478 | 35.16 | 202 | 0.901 | 0.7377 | 18.12 |
| 18 | 0.8737 | 0.7258 | 16.93 | 203 | 0.8864 | 0.7215 | 18.60 |
| 20 | 0.7986 | 0.7591 | 4.95 | 208 | 0.8648 | 0.8517 | 1.51 |
| 33 | 0.999 | 0.6506 | 34.87 | 210 | 0.8052 | 0.7695 | 4.43 |
| 36 | 0.8035 | 0.7601 | 5.40 | 215 | 0.8609 | 0.8569 | 0.46 |
| 76 | 0.8279 | ---- | ---- | 222 | 0.86 | 0.8579 | 0.24 |
| 89 | 0.6542 | 0.6478 | 0.98 | 224 | 0.7888 | 0.7816 | 0.91 |
| 92 | 0.762 | 0.7591 | 0.38 | 257 | 0.6498 | 0.5041 | 22.42 |
| 105 | 0.6517 | 0.6506 | 0.17 | 291 | 0.862 | 0.5347 | 37.97 |
| 108 | 0.7608 | 0.7601 | 0.09 | 296 | 0.7448 | 0.7244 | 2.74 |
| 145 | 0.8156 | 0.8009 | 1.80 | 325 | 0.7445 | 0.6958 | 6.54 |
| 146 | 0.7479 | 0.7377 | 1.36 | 329 | 0.7291 | 0.7061 | 3.15 |
| 147 | 0.7286 | 0.7215 | 0.97 | 334 | 0.7197 | 0.7103 | 1.31 |
| 152 | 0.8738 | 0.8517 | 2.53 | 355 | 0.8676 | 0.5185 | 40.24 |
| 153 | 0.8118 | 0.7889 | 2.82 | 360 | 0.7405 | 0.7191 | 2.89 |
| 154 | 0.7888 | 0.7695 | 2.45 | 368 | 0.7249 | 0.7158 | 1.26 |
| 166 | 0.8767 | 0.8579 | 2.14 |
| Element Number | φ60 × 3 | φ60 × 4 | φ63 × 5 |
|---|---|---|---|
| 9 | 0.6333 | 0.6294 | 0.6262 |
| 18 | 0.7281 | 0.7248 | 0.7222 |
| 36 | 0.7627 | 0.7592 | 0.7563 |
| 100 | 0.7627 | 0.7591 | 0.7562 |
| 160 | 0.7666 | 0.7971 | 0.8244 |
| 166 | 0.8295 | 0.8573 | 0.8808 |
| 201 | 0.7611 | 0.8002 | 0.8332 |
| 257 | 0.5245 | 0.5023 | 0.4829 |
| 296 | 0.7334 | 0.7234 | 0.7148 |
| 360 | 0.7287 | 0.7181 | 0.7092 |
| Element Number | 2.5 m × 1.5 m | 2.5 m × 2.0 m | 2.5 m × 2.5 m | 2.5 m × 3.0 m |
|---|---|---|---|---|
| 9 | 0.6021 | 0.6144 | 0.6294 | 0.6460 |
| 36 | 0.7362 | 0.7470 | 0.7592 | 0.7716 |
| 100 | 0.8355 | 0.7996 | 0.7591 | 0.7187 |
| 108 | 0.8356 | 0.7996 | 0.7592 | 0.7188 |
| 160 | 0.7636 | 0.7794 | 0.7971 | 0.8154 |
| 166 | 0.8274 | 0.8417 | 0.8573 | 0.8731 |
| 222 | 0.9506 | 0.9068 | 0.8573 | 0.8074 |
| 224 | 0.9012 | 0.8384 | 0.7808 | 0.7301 |
| 296 | 0.6870 | 0.7060 | 0.7234 | 0.7385 |
| 360 | 0.6850 | 0.7016 | 0.7181 | 0.7333 |
| Element Number | Load (kN) | Element Number | Load (kN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 0 | 5 | 10 | 15 | ||
| 9 | 0.5947 | 0.5962 | 0.5976 | 0.5991 | 365 | 0.7884 | 0.7892 | 0.7899 | 0.7907 |
| 65 | 0.6516 | 0.6529 | 0.6541 | 0.6554 | 413 | 0.8824 | 0.8829 | 0.8834 | 0.8839 |
| 92 | 0.8543 | 0.8548 | 0.8552 | 0.8556 | 461 | 0.6472 | 0.6484 | 0.6496 | 0.6509 |
| 155 | 0.8536 | 0.8541 | 0.8546 | 0.8550 | 485 | 0.7884 | 0.7892 | 0.7900 | 0.7907 |
| 220 | 0.8538 | 0.8543 | 0.8547 | 0.8552 | 488 | 0.9612 | 0.9613 | 0.9614 | 0.9615 |
| 292 | 0.9072 | 0.9076 | 0.9079 | 0.9083 | 542 | 0.9603 | 0.9606 | 0.9608 | 0.9611 |
| 306 | 0.9136 | 0.9140 | 0.9145 | 0.9149 | 550 | 0.9611 | 0.9614 | 0.9617 | 0.9619 |
| 308 | 0.8566 | 0.8573 | 0.8581 | 0.8589 | 616 | 0.9604 | 0.9606 | 0.9608 | 0.9609 |
| Element Number | Load (kN) | Element Number | Load (kN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 0 | 5 | 10 | 15 | ||
| 11 | 0.7939 | 0.7953 | 0.7968 | 0.7982 | 229 | 0.9473 | 0.9479 | 0.9485 | 0.9490 |
| 31 | 0.8311 | 0.8323 | 0.8335 | 0.8346 | 237 | 0.9501 | 0.9506 | 0.9512 | 0.9517 |
| 81 | 0.7816 | 0.7831 | 0.7846 | 0.7861 | 243 | 0.9446 | 0.9452 | 0.9458 | 0.9464 |
| 90 | 0.8033 | 0.8047 | 0.8060 | 0.8074 | 244 | 0.9487 | 0.9492 | 0.9498 | 0.9503 |
| 107 | 0.8195 | 0.8207 | 0.8220 | 0.8232 | 250 | 0.9448 | 0.9453 | 0.9458 | 0.9463 |
| 108 | 0.8313 | 0.8325 | 0.8337 | 0.8348 | 253 | 1.0000 | 0.9983 | 0.9984 | 0.9985 |
| 145 | 0.8919 | 0.8927 | 0.8934 | 0.8942 | 278 | 0.7160 | 0.7180 | 0.7199 | 0.7219 |
| 159 | 0.7973 | 0.7987 | 0.8001 | 0.8014 | 283 | 0.7836 | 0.7852 | 0.7868 | 0.7883 |
| 193 | 0.9034 | 0.9040 | 0.9047 | 0.9053 | 287 | 0.7839 | 0.7855 | 0.7871 | 0.7887 |
| 199 | 0.9043 | 0.9050 | 0.9056 | 0.9062 | 291 | 0.7894 | 0.7910 | 0.7925 | 0.7940 |
| 205 | 0.9031 | 0.9038 | 0.9045 | 0.9052 | 341 | 0.7619 | 0.7636 | 0.7653 | 0.7670 |
| 207 | 0.8192 | 0.8205 | 0.8218 | 0.8230 | 357 | 0.7768 | 0.7784 | 0.7800 | 0.7815 |
| Element Number | Load (kN) | Element Number | Load (kN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 0 | 5 | 10 | 15 | ||
| 1 | 0.8176 | 0.8207 | 0.8238 | 0.8267 | 382 | 0.9561 | 0.9572 | 0.9583 | 0.9593 |
| 22 | 0.7881 | 0.7917 | 0.7952 | 0.7985 | 390 | 0.9417 | 0.9428 | 0.9439 | 0.9449 |
| 25 | 0.8550 | 0.8574 | 0.8597 | 0.8620 | 408 | 0.9545 | 0.9559 | 0.9571 | 0.9585 |
| 113 | 0.7853 | 0.7889 | 0.7924 | 0.7958 | 411 | 1.0000 | 0.9984 | 0.9986 | 0.9989 |
| 122 | 0.8505 | 0.8529 | 0.8554 | 0.8577 | 503 | 0.8268 | 0.8296 | 0.8324 | 0.8351 |
| 225 | 0.8816 | 0.8836 | 0.8855 | 0.8874 | 534 | 0.7843 | 0.7880 | 0.7917 | 0.7952 |
| 237 | 0.8974 | 0.8991 | 0.9008 | 0.9024 | 536 | 0.7746 | 0.7784 | 0.7822 | 0.7858 |
| 275 | 0.8264 | 0.8293 | 0.8322 | 0.8350 | 552 | 0.6889 | 0.6941 | 0.6992 | 0.7042 |
| 345 | 0.8953 | 0.8970 | 0.8987 | 0.9003 | 559 | 0.7275 | 0.7321 | 0.7366 | 0.7409 |
| 369 | 0.9390 | 0.9400 | 0.9411 | 0.9421 | 573 | 0.7821 | 0.7858 | 0.7894 | 0.7929 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Li, C.; Xu, Y.; Zhang, Q.; Wang, F.; Cai, J. Analysis of Key Elements of Truss Structures Based on the Tangent Stiffness Method. Symmetry 2020, 12, 1008. https://doi.org/10.3390/sym12061008
Feng J, Li C, Xu Y, Zhang Q, Wang F, Cai J. Analysis of Key Elements of Truss Structures Based on the Tangent Stiffness Method. Symmetry. 2020; 12(6):1008. https://doi.org/10.3390/sym12061008
Chicago/Turabian StyleFeng, Jian, Changtong Li, Yixiang Xu, Qian Zhang, Fang Wang, and Jianguo Cai. 2020. "Analysis of Key Elements of Truss Structures Based on the Tangent Stiffness Method" Symmetry 12, no. 6: 1008. https://doi.org/10.3390/sym12061008
APA StyleFeng, J., Li, C., Xu, Y., Zhang, Q., Wang, F., & Cai, J. (2020). Analysis of Key Elements of Truss Structures Based on the Tangent Stiffness Method. Symmetry, 12(6), 1008. https://doi.org/10.3390/sym12061008






