New Soliton Solutions of Fractional Jaulent-Miodek System with Symmetry Analysis

Abstract

New soliton solutions of fractional Jaulent-Miodek (JM) system are presented via symmetry analysis and fractional logistic function methods. Fractional Lie symmetry analysis is unified with symmetry analysis method. Conservation laws of the system are used to obtain new conserved vectors. Numerical simulations of the JM equations and efficiency of the methods are presented. These solutions might be imperative and significant for the explanation of some practical physical phenomena. The results show that present methods are powerful, competitive, reliable, and easy to implement for the nonlinear fractional differential equations.

1. Introduction

Integral and derivative operators of any arbitrary order are the basis of fractional calculus, which has been of great interest for researchers due to its dynamic behavior and exact description of nonlinear complex phenomena in numerous fields in science and engineering [1,2,3,4,5,6]. Analytical methods have played an essential role for Fractional partial differential equations (FPDEs) [1,2,3,4]. Lie symmetry analysis also gives a powerful and effectual implement for generating invariant solutions. The theory of symmetry analysis is based on the invariance of variables [7,8,9,10,11,12,13,14]. Hence, the study of symmetry analysis has been made a huge interest for researchers during past decades.

Time-fractional coupled Jaulent-Miodek (JM) type equations [15,16,17] is considered as:

$$D_t^{\alpha }u+u_{xxx}+\frac{3}{2}v{v}_{xxx}+\frac{9}{2}{v}_x{v}_{xx}-6u{u}_x-6uv{v}_x-\frac{3}{2}{u}_x{v}^2=0$$

(1)

and

$$D_t^{\alpha }v+v_{xxx}-6u_{x}v-6u{v}_x-\frac{15}{2}{v}_x{v}^2=0$$

(2)

where $0<\alpha \le 1$ denotes the fractional-order derivative.

The coupled JM equations were first introduced by Jaulent and Miodek [18] by using inverse scattering transform with the help of energy dependent Schrödinger potentials. The Equations (1) and (2) also have a relation with Euler-Darboux equation, which has been presented by Matsuno [19]. The Darboux transformation of the JM spectral problem has been studied by Xu [20]. By using hereditary symmetries, Ruan and Lou [21] have presented the symmetries of Jaulent-Miodek hierarchy. The sech and tanh–coth methods have been used by Wazwaz [22] and some more methods like homotopy analysis [23], exp-function [24], extended tanh [25], hyperbolic tangent [26] were presented in the literature for approximate and exact solutions of classical coupled Jaulent-Miodek equation.

A large interest has been focused for the improvement of past methods dealing with solutions of FPDEs. The fractional coupled JM equations play an important role in several areas of science such as fluid mechanics, plasma physics, condense matter physics, optics and associates with energy dependent Schrödinger potential [27,28,29,30,31,32]. As the practical application of fractional Jaulent–Miodek (JM) system, the Wang and Xia has studied its super-Hamiltonian structure using fractional supertrace identity [33].

Some of these methods for solving fractional coupled JM equation are: method of homotopy perturbation natural transform [34], Sumudu transform [15], residual power series method (RSPM) and q-homotopy analysis method (q-HAM) [17], Hermite wavelet [35], (G’/G)-expansion and hyperbolic tangent [16].

This article deals with fractional coupled JM system by utilizing an original fractional logistic function method [36], which has been presented in Section 3. Moreover, in the corresponding section, the numerical simulation has been done for analyzing the physical properties of the solutions. In Section 4, the symmetry analysis with conservation laws [37,38] for time-fractional coupled JM, equations have been presented. In Section 4, the fractional Lie group analysis method for symmetry properties [39,40] of fractional JM system are applied more precisely. Furthermore, conservation laws [37,41] also have been presented in order to get a new conserved vector by utilizing theorems of conservation law.

2. Theory of Fractional Operators

2.1. Riemann–Liouville (RL) Fractional Derivative

The fractional order Riemann–Liouville (RL) derivative of order $\alpha$(>0) is defined as [1,3]

$$D_t^{\alpha }f(t)=\{\begin{array}{l}\frac{1}{\mathsf{\Gamma }\left(m-\alpha \right)}\frac{d^m}{d{t}^m}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-\tau \right)}^{\left(m-\alpha -1\right)}f\left(\tau \right)}d\tau if m -1<\alpha <m, m\in \mathrm{N}, \\ \frac{d^{m}f\left(t\right)}{d{t}^m} if \alpha =m, m\in \mathrm{N},\end{array}$$

(3)

Riemann–Liouville (RL) derivative of order $\alpha$(>0) has subsequent property [1,2,3] is given as:

$$D^{\alpha }{t}^{\beta }=\frac{\mathsf{\Gamma }\left(\beta +1\right) t^{\beta -\alpha }}{\mathsf{\Gamma }\left(\beta -\alpha +1\right)} , \beta >\alpha -1.$$

(4)

2.2. Local Fractional-Order Derivative

Assume $h(\stackrel{\leftharpoonup }{x})\in C_{\alpha }(m,n)$, where $C_{\alpha }(m,n)$ denotes $\alpha$ times differentiable with each derivative continuous in $(m,n)$. Then, the derivative with fractional order $\alpha$ at $\stackrel{\leftharpoonup }{x}={\stackrel{\leftharpoonup }{x}}_0$ is defined as [42,43]

$$h^{(\alpha )}({\stackrel{\leftharpoonup }{x}}_0)={\frac{d^{\alpha }h(\stackrel{\leftharpoonup }{x})}{d{\stackrel{\leftharpoonup }{x}}^{\alpha }}|}_{\stackrel{\leftharpoonup }{x}={\stackrel{\leftharpoonup }{x}}_0}={\displaystyle \underset{\stackrel{\leftharpoonup }{x}\to {\stackrel{\leftharpoonup }{x}}_0}{\lim }}\frac{{\Delta }^{\alpha }(h(\stackrel{\leftharpoonup }{x})-h({\stackrel{\leftharpoonup }{x}}_0))}{{(\stackrel{\leftharpoonup }{x}-{\stackrel{\leftharpoonup }{x}}_0)}^{\alpha }}$$

(5)

where ${\Delta }^{\alpha }(h(\stackrel{\leftharpoonup }{x})-h({\stackrel{\leftharpoonup }{x}}_0))\cong \mathsf{\Gamma }(1+\alpha )(h(\stackrel{\leftharpoonup }{x})-h({\stackrel{\leftharpoonup }{x}}_0))$ and $0<\alpha \le 1$.

And has following property [42,43]:

If $z(\stackrel{\leftharpoonup }{x})=(h\circ u)(\stackrel{\leftharpoonup }{x})$, where $u(\stackrel{\leftharpoonup }{x})=f(\stackrel{\leftharpoonup }{x})$, then

$$\frac{d^{\alpha }z(\stackrel{\leftharpoonup }{x})}{d{\stackrel{\leftharpoonup }{x}}^{\alpha }}=h^{(1)}\left(f(\stackrel{\leftharpoonup }{x})\right)f^{(\alpha )}(\stackrel{\leftharpoonup }{x})$$

(6)

when $h^{(1)}\left(f(\stackrel{\leftharpoonup }{x})\right)$ and $f^{(\alpha )}(\stackrel{\leftharpoonup }{x})$ exist.

3. The Brief Descriptions of the Fractional Logistic Function Method and Implementations

3.1. Brief Description of the Proposed Method

The section emphasizes describing a comparatively new analytic method for getting solutions for the FPDEs. The procedure for the proposed method has been described in the following manner:

Step 1:

The FPDE is given as:

$$Q(u,D_t^{\alpha }u,\dots , u_x, u_{xx}, u_{xxx},\dots )=0, 0<\alpha \le 1,$$

(7)

where $u(x,t)$ is a function.

Step 2:

Solution of Equation (7) is presented as

$$u(x,t)=U(\xi ), \xi =kx-\frac{\gamma t^{\alpha }}{\mathsf{\Gamma }(\alpha +1)},$$

(8)

where $\gamma$ and $k$ are parameters.

Then, (6) [44,45] can reduce the fractional derivative into the following form

$$D_t^{\alpha }u={\sigma }_t{U}_{\xi }{D}_t^{\alpha }\xi$$

Then, the Equation (7) can be reduced by using Equation (7), by the following form:

$$Q(U,\gamma U^{\prime },\dots , k{U}^{\prime },k^2{U}^{″},k^3{U}^{‴},\dots )=0$$

(9)

Step 3:

Here, the exact solution of Equation (7) is mentioned in terms of the polynomial in $\varphi (\xi )$ as follows:

$$U(\xi )=a_0+{\displaystyle \sum _{i=1}^n{a}_i{\varphi }^i(\xi )},$$

(10)

where $\varphi (\xi )$ is considered as the sigmoid function or logistic function [46,47], is defined as follows:

$\varphi (\xi )=\frac{e^{\xi }}{1+e^{\xi }}$ and satisfies the following Riccati equation:

$${\varphi }_{\xi }=\varphi -{\varphi }^2,$$

(11)

and the value of $n$ can be evaluated by using the homogenous balancing principle [48,49]. Moreover, the derivatives of different order for the function $U(\xi )$ can be determined by using Equation (11).

Step 4:

Now, the coefficients $a_i$ are determined by putting Equation (11) into Equation (9) and solving the acquired algebraic equations obtained by equating coefficients of ${\phi }^i$ to 0.

Step 5:

Unknowns obtained in step 4 are written into Equation (10) to get the solutions for Equation (7).

3.2. Soliton Solutions for JM System

The logistic function method is employed for solving Equation (1). By using Equation (8) in Equation (1), we have:

$$\begin{array}{ll}-\gamma U^{\prime }(\xi )+k^3{U}^{‴}(\xi )+& \frac{3k^3}{2}V(\xi )V^{‴}(\xi )+\frac{9k^3}{2}{V}^{\prime }(\xi )V^{″}(\xi )\\ & -6kU(\xi )U^{\prime }(\xi )-6kU(\xi )V(\xi )V^{\prime }(\xi )-\frac{3}{2}k{U}^{\prime }(\xi )V^2(\xi )=0,\end{array}$$

(12)

and

$$-\gamma V^{\prime }(\xi )+k^3{V}^{‴}(\xi )-6k{U}^{\prime }(\xi )V(\xi )-6kU(\xi )V^{\prime }(\xi )-\frac{15k}{2}V(\xi )V^2(\xi )=0,$$

(13)

Similar to Equation (10), let us consider the solutions of the governing system are presented by following mathematical equations as

$$U(\xi )=a_0+{\displaystyle \sum _{i=1}^n{a}_i{\phi }^i} \mathrm{and} V(\xi )=b_0+{\displaystyle \sum _{i=1}^m{b}_i{\phi }^i}$$

(14)

By means of homogenous balance principle [48,49], we get $n=2$ and $m=1$. Thus, the solutions are:

$$U(\xi )=a_0+a_1\phi +a_2{\varphi }^2 \mathrm{and} V(\xi )=b_0+b_1\phi ,$$

(15)

where $\phi$ follows satisfies Equation (11).

Putting Equation (15) with Equation (11) into Equations (12) and (13), equating the obtained coefficient of ${\phi }^i$ to 0, we get:

Set 1:

$$\gamma =\frac{k^3}{4}, a_0=-\frac{k^2}{32}, a_1=-\frac{3k^2}{8}, a_2=\frac{3k^2}{8}, b_0=\frac{ik}{2\sqrt{2}}, b_1=-\frac{ik}{\sqrt{2}}.$$

For set 1, the following hyperbolic solutions can be obtained as

$$\begin{array}{c}{U}_{11}=-\frac{k^2(\cosh (\xi )+7)}{32(1+\cosh (\xi ))}\\ V_{12}=-\frac{ik\tanh \left(\frac{\xi }{2}\right)}{2\sqrt{2}}\end{array}$$

(16)

where $\xi =kx-\frac{k^3{t}^{\alpha }}{4\mathsf{\Gamma }(\alpha +1)}$.

Set 2:

$$\gamma =\frac{k^3}{4}, a_0=-\frac{k^2}{32}, a_1=-\frac{3k^2}{8}, a_2=\frac{3k^2}{8}, b_0=-\frac{ik}{\sqrt{2}}, b_1=\frac{ik}{\sqrt{2}}$$

For set 2, the following hyperbolic solutions can be obtained as

$$\begin{array}{c}{U}_{21}=-\frac{k^2(\cosh (\xi )+7)}{32(1+\cosh (\xi ))}\\ V_{22}=-\frac{ik(1+3\cosh (\xi )+3\sinh (\xi ))}{2\sqrt{2}(1+\cosh (\xi )+\sinh (\xi ))}\end{array}$$

(17)

where $\xi =kx-\frac{k^3{t}^{\alpha }}{4\mathsf{\Gamma }(\alpha +1)}$.

Set 3:

$$\gamma =\frac{11k^3}{5}, a_0=\frac{k^2}{20}, a_1=-2k^2, a_2=2k^2, b_0=i\sqrt{5}k, b_1=-2i\sqrt{5}k$$

For set 3, the following hyperbolic solutions can be obtained as

$$\begin{array}{c}{U}_{31}=\frac{k^2(\cosh (\xi )-19)}{20(1+\cosh (\xi ))}\\ V_{32}=-i\sqrt{5}k\tanh \left(\frac{\xi }{2}\right)\end{array}$$

(18)

where $\xi =kx-\frac{11k^3{t}^{\alpha }}{5\mathsf{\Gamma }(\alpha +1)}$.

Set 4:

$$\gamma =\frac{11k^3}{5}, a_0=\frac{k^2}{20}, a_1=-2k^2, a_2=2k^2, b_0=-i\sqrt{5}k, b_1=2i\sqrt{5}k$$

For set 4, the following hyperbolic solutions can be obtained as

$$\begin{array}{c}{U}_{41}=\frac{k^2(\cosh (\xi )-19)}{20(1+\cosh (\xi ))}\\ V_{42}=i\sqrt{5}k\tanh \left(\frac{\xi }{2}\right)\end{array}$$

(19)

where $\xi =kx-\frac{11k^3{t}^{\alpha }}{5\mathsf{\Gamma }(\alpha +1)}$.

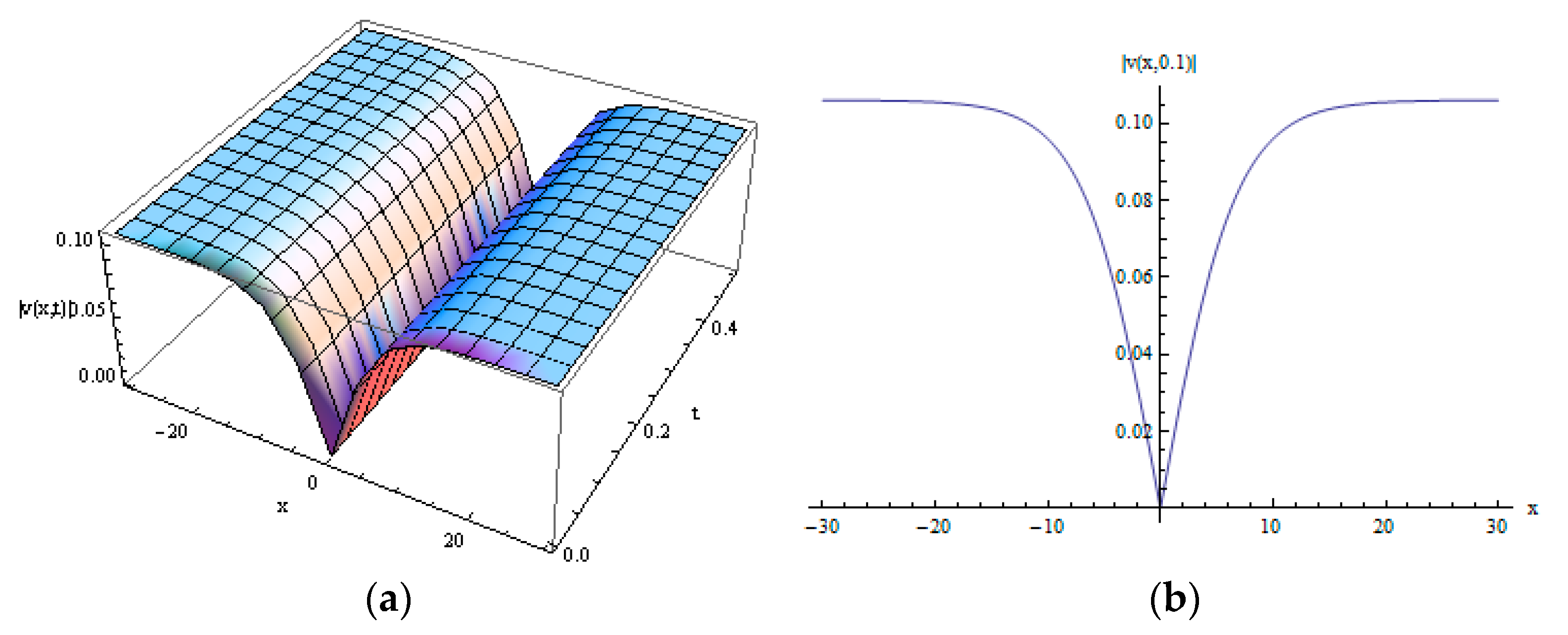
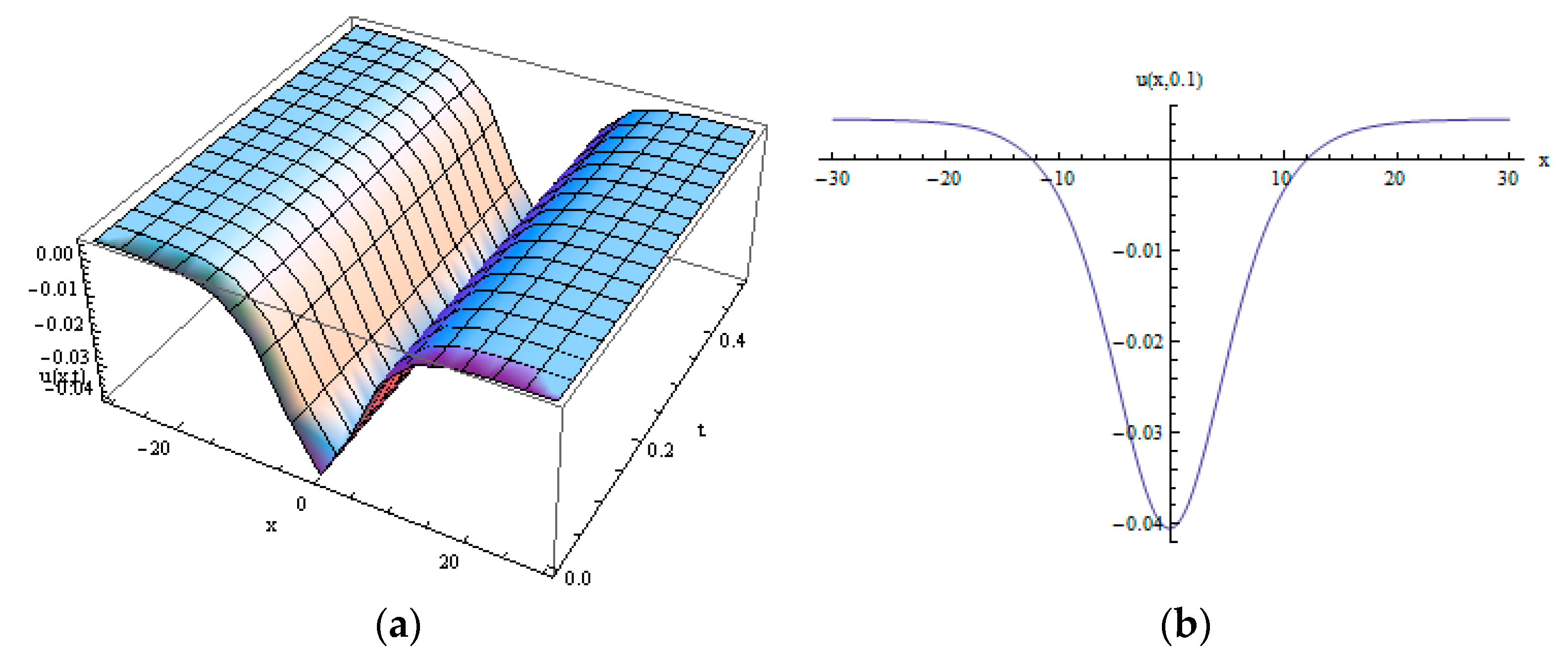
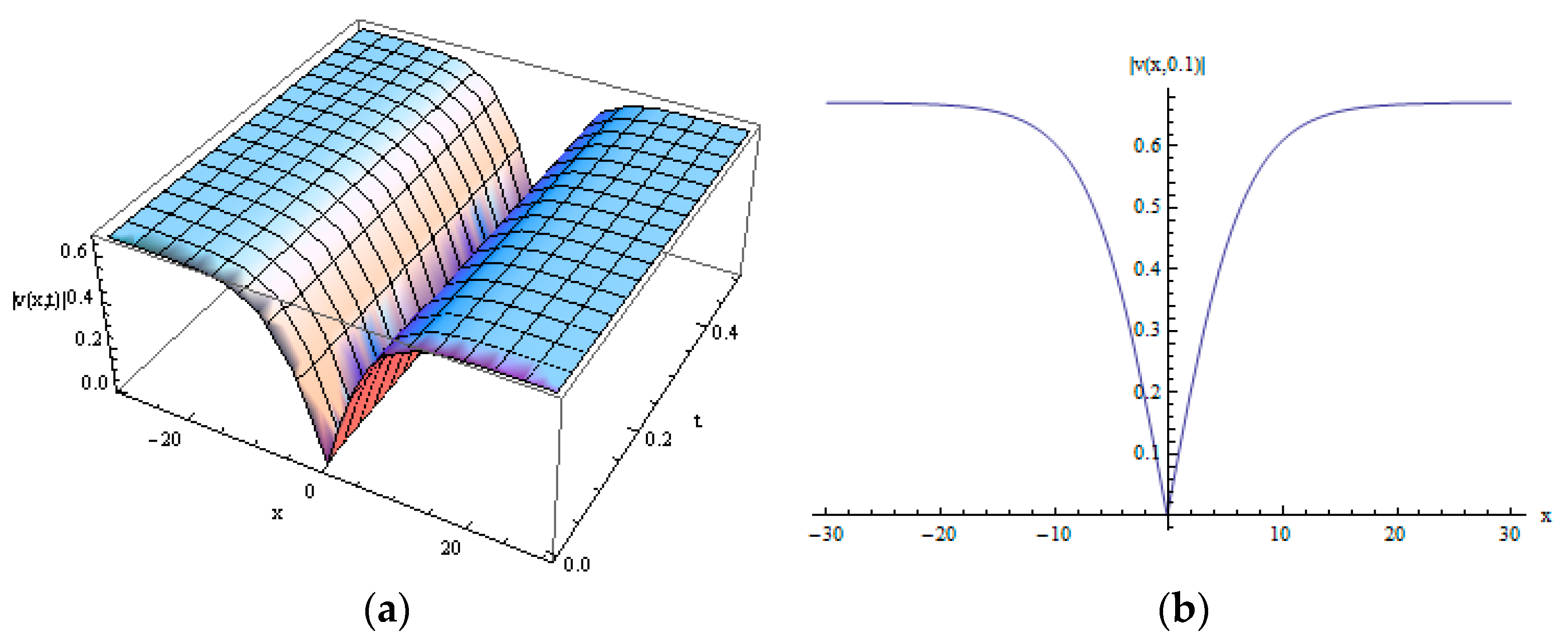
3.3. Numerical Simulations

This part emphasizes on numerical simulation for the Equations (1) and (2) by the fractional logistic equation method. Furthermore, the Equations (16) and (18) have been used here for generating solutions graphs.

The Figure 1, Figure 2, Figure 3 and Figure 4 illustrates obtained solutions of governing equations.

Case 1: For $\alpha =0.1$ (Fractional order)

Case 2: For $\alpha =0.1$ (Fractional order)

4. Lie Symmetry Analysis Method

4.1. Theory of Symmetry Analysis Method

In this part, the general method for generating the symmetries of FPDEs is discussed by means of fractional Lie symmetry analysis.

Consider

$$D_t^{\alpha }u=F(t,x,u,u_x,u_{xx},u_{xxx},v,v_x,v_{xx},v_{xxx}, \dots )$$

(20)

$$D_t^{\alpha }v=G(t,x,u,u_x,u_{xx},u_{xxx},v,v_x,v_{xx},v_{xxx}, \dots )$$

(21)

Let us now consider that the Equations (20) and (21) are invariant in one-parameter Lie group transformation:

$$\begin{array}{c}\overleftrightarrow{x}\to x+\epsilon \xi (t,x,u,v)+O({\epsilon }^2),\\ \overleftrightarrow{t}\to t+\epsilon \tau (t,x,u,v)+O({\epsilon }^2),\\ \overleftrightarrow{u}\to u+\epsilon \eta (t,x,u,v)+O({\epsilon }^2),\\ \overleftrightarrow{v}\to v+\epsilon \vartheta (t,x,u,v)+O({\epsilon }^2),\\ D_t^{\alpha }\overleftrightarrow{u}\to D_t^{\alpha }u+\epsilon {\eta }_{\alpha }^0(t,x,u,v)+O({\epsilon }^2),\\ D_t^{\alpha }\overleftrightarrow{v}\to D_t^{\alpha }v+\epsilon {\vartheta }_{\alpha }^0(t,x,u,v)+O({\epsilon }^2),\\ \frac{\partial \overleftrightarrow{u}}{\partial \overleftrightarrow{x}}\to \frac{\partial u}{\partial x}+\epsilon {\eta }^x(t,x,u,v)+O({\epsilon }^2),\\ \frac{\partial \overleftrightarrow{v}}{\partial \overleftrightarrow{x}}\to \frac{\partial v}{\partial x}+\epsilon {\vartheta }^x(t,x,u,v)+O({\epsilon }^2),\\ \frac{{\partial }^2\overleftrightarrow{u}}{\partial {\overleftrightarrow{x}}^2}\to \frac{{\partial }^{3}u}{\partial x^3}+\epsilon {\eta }^{xx}(t,x,u,v)+O({\epsilon }^2),\\ \frac{{\partial }^2\overleftrightarrow{v}}{\partial {\overleftrightarrow{x}}^2}\to \frac{{\partial }^{2}v}{\partial x^2}+\epsilon {\vartheta }^{xx}(t,x,u,v)+O({\epsilon }^2),\\ \frac{{\partial }^3\overleftrightarrow{u}}{\partial {\overleftrightarrow{x}}^3}\to \frac{{\partial }^{3}u}{\partial x^3}+\epsilon {\eta }^{xxx}(t,x,u,v)+O({\epsilon }^2),\\ \frac{{\partial }^3\overleftrightarrow{v}}{\partial {\overleftrightarrow{x}}^3}\to \frac{{\partial }^{3}v}{\partial x^3}+\epsilon {\vartheta }^{xxx}(t,x,u,v)+O({\epsilon }^2),.\\ \dots \end{array}$$

(22)

where $\epsilon <<1$ is considered as a group parameter, $\tau$, $\eta$, $\vartheta$, $\xi$ are infinitesimals. Total expression for ${\eta }^x$, ${\eta }^{xx}$, ${\eta }^{xxx}$, ${\vartheta }^x$, ${\vartheta }^{xx}$ and ${\vartheta }^{xxx}$ are:

$$\begin{array}{l}{\eta }^x=D_x(\eta )-u_x{D}_x(\xi )-u_t{D}_x(\tau ),\\ {\eta }^{xx}=D_x({\eta }^x)-u_{xx}{D}_x(\xi )-u_{xt}{D}_x(\tau ),\\ {\eta }^{xxx}=D_x({\eta }^{xx})-u_{xxx}{D}_x(\xi )-u_{xxt}{D}_x(\tau ),\\ {\vartheta }^x= D_x(\vartheta )-v_x D_x(\xi )-v_t D_x(\tau ),\\ {\vartheta }^{xx}=D_x({\vartheta }^x)-v_{xx}{D}_x(\xi )-v_{xt}{D}_x(\tau ),\\ {\vartheta }^{xxx}=D_x({\vartheta }^{xx})-v_{xxx}{D}_x(\xi )-v_{xxt}{D}_x(\tau )\end{array}$$

(23)

where $D_{x^j}= \frac{\partial }{\partial x^j}+u_j\frac{\partial }{\partial u}+v_j\frac{\partial }{\partial v}+u_{jk}\frac{\partial }{\partial u_k}+v_{jk}\frac{\partial }{\partial u_k}+\dots$, $j, k=1, 2, 3, \dots$ and $u_j=\frac{\partial u}{\partial x^j}$,$v_j=\frac{\partial v}{\partial x^j}$, $u_{jk}=\frac{{\partial }^{2}u}{\partial x^j\partial x^k}$, $v_{jk}=\frac{{\partial }^{2}v}{\partial x^j\partial x^k}$ and so on.

$$V=\xi (t,x,u,v)\frac{\partial }{\partial x}+\tau (t,x,u,v)\frac{\partial }{\partial t}+\eta (t,x,u,v)\frac{\partial }{\partial u}+\vartheta (t,x,u,v)\frac{\partial }{\partial v}$$

(24)

$V$ satisfies:

$${\mathrm{P}{\mathrm{r}}^{(n)}\mathrm{V}({\Delta }_1)|}_{{\Delta }_1=0}=0 \mathrm{and} {\mathrm{P}\mathrm{r}{ }^{(n)}V({\Delta }_2)|}_{{\Delta }_2=0}=0, n =1, 2, \dots ,$$

(25)

here, $\mathrm{Pr}$ denotes the prolongation for the given vector and

$${\Delta }_1:=D_t^{\alpha }u-F(t,x,u,u_x,u_{xx},u_{xxx},v,v_x,v_{xx},v_{xxx}, \dots )$$

and

$${\Delta }_2:=D_t^{\alpha }v-G(t,x,u,u_x,u_{xx},u_{xxx},v,v_x,v_{xx},v_{xxx}, \dots )$$

Now, by considering the usual structure of RL fractional operator, the transformations of system (22) has been formed. We have

$${\tau (x,t,u,v)|}_{t=0}=0$$

(26)

By RL derivative, the $\alpha$-th infinitesimal [50,51,52] with Equation (26) can be presented as follows:

$${\eta }_{\alpha }^0=D_t^{\alpha }(\eta )+\xi D_t^{\alpha }(u_x)-D_t^{\alpha }(\xi u_x)+D_t^{\alpha }(D_t(\tau )u)-D_t^{\alpha +1}(\tau u)+\tau D_t^{\alpha +1}(u)$$

and

$${\vartheta }_{\alpha }^0=D_t^{\alpha }(\vartheta )+\xi D_t^{\alpha }(v_x)-D_t^{\alpha }(\xi v_x)+D_t^{\alpha }(D_t(\tau )v)-D_t^{\alpha +1}(\tau v)+\tau D_t^{\alpha +1}(v)$$

(27)

where the $D_t^{\alpha }$ denotes the total fractional differential operator.

We have:

$$D_t^{\alpha }(f(t)g(t))={\displaystyle \sum _{m=0}^{\infty }\left(\begin{array}{l}\alpha \\ m\end{array}\right)}{D}_t^{\alpha -m}f(t)D_t^{m}g(t), \alpha >0$$

(28)

where

$$\left(\begin{array}{l}\alpha \\ m\end{array}\right)=\frac{{(-1)}^{m-1}\alpha \mathsf{\Gamma }(m-\alpha )}{\mathsf{\Gamma }(1-\alpha )\mathsf{\Gamma }(m+1)}$$

We also have

$${\eta }_{\alpha }^0=D_t^{\alpha }(\eta )-\alpha D_t^{\alpha }(\tau )\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}-{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n\end{array}\right)}{D}_t^n(\xi )D_t^{\alpha -n}{u}_x-{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n+1\end{array}\right)}{D}_t^{n+1}(\tau )D_t^{\alpha -n}(u)$$

and

$${\vartheta }_{\alpha }^0=D_t^{\alpha }(\vartheta )-\alpha D_t^{\alpha }(\tau )\frac{{\partial }^{\alpha }v}{\partial t^{\alpha }}-{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n\end{array}\right)}{D}_t^n(\xi )D_t^{\alpha -n}{v}_x-{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n+1\end{array}\right)}{D}_t^{n+1}(\tau )D_t^{\alpha -n}(v)$$

(29)

We have:

$$\frac{d^{m}g(h(t))}{d{t}^m}={\displaystyle \sum _{k=0}^m{\displaystyle \sum _{r=0}^k\left(\begin{array}{l}k\\ r\end{array}\right)}}\frac{1}{k!}{[-h(t)]}^r\frac{d^m}{d{t}^m}[h{(t)}^{k-r}]\frac{d^{k}g(h)}{d{h}^k}$$

(30)

Now by using Equations (28) and (30) with $f(t)=1$, we have

$$D_t^{\alpha }(\eta )=\frac{{\partial }^{\alpha }\eta }{\partial t^{\alpha }}+{\eta }_u\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}-u\frac{{\partial }^{\alpha }{\eta }_u}{\partial t^{\alpha }}+{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n\end{array}\right)}\frac{{\partial }^n{\eta }_u}{\partial t^n}{D}_t^{\alpha -n}(u)+\mu$$

and

$$D_t^{\alpha }(\vartheta )=\frac{{\partial }^{\alpha }\vartheta }{\partial t^{\alpha }}+{\vartheta }_v\frac{{\partial }^{\alpha }v}{\partial t^{\alpha }}-v\frac{{\partial }^{\alpha }{\eta }_v}{\partial t^{\alpha }}+{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n\end{array}\right)}\frac{{\partial }^n{\vartheta }_v}{\partial t^n}{D}_t^{\alpha -n}(v)+\lambda$$

(31)

where

$$\mu ={\displaystyle \sum _{n=2}^{\infty }{\displaystyle \sum _{m=2}^n{\displaystyle \sum _{k=2}^m{\displaystyle \sum _{r=0}^{k-1}\left(\begin{array}{l}\alpha \\ n\end{array}\right)}}}}\left(\begin{array}{l}n\\ m\end{array}\right)\left(\begin{array}{l}k\\ r\end{array}\right)\frac{1}{k!}\frac{t^{n-\alpha }}{\mathsf{\Gamma }(n+1-\alpha )}{(-u)}^r\frac{{\partial }^m}{\partial t^m}(u^{k-r})\frac{{\partial }^{n-m+k}\eta }{\partial t^{n-m}\partial u^k}$$

and

$$\lambda ={\displaystyle \sum _{n=2}^{\infty }{\displaystyle \sum _{m=2}^n{\displaystyle \sum _{k=2}^m{\displaystyle \sum _{r=0}^{k-1}\left(\begin{array}{l}\alpha \\ n\end{array}\right)}}}}\left(\begin{array}{l}n\\ m\end{array}\right)\left(\begin{array}{l}k\\ r\end{array}\right)\frac{1}{k!}\frac{t^{n-\alpha }}{\mathsf{\Gamma }(n+1-\alpha )}{(-v)}^r\frac{{\partial }^m}{\partial t^m}(v^{k-r})\frac{{\partial }^{n-m+k}\vartheta }{\partial t^{n-m}\partial v^k}$$

Thus, Equation (29) yields

$$\begin{array}{c}{\eta }_{\alpha }^0=\frac{{\partial }^{\alpha }\eta }{\partial t^{\alpha }}+({\eta }_u-\alpha D_t(\tau ))\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}-u\frac{{\partial }^{\alpha }{\eta }_u}{\partial t^{\alpha }}+\mu \\ +{\displaystyle \sum _{n=1}^{\infty }\left[\left(\begin{array}{l}\alpha \\ n\end{array}\right)\frac{{\partial }^{\alpha }{\eta }_u}{\partial t^{\alpha }}-\left(\begin{array}{l}\alpha \\ n+1\end{array}\right)D_t^{n+1}(\tau )\right]}{D}_t^{\alpha -n}(u)-{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n\end{array}\right)}{D}_t^n(\xi )D_t^{\alpha -n}{u}_x,\end{array}$$

and

$$\begin{array}{c}{\vartheta }_{\alpha }^0=\frac{{\partial }^{\alpha }\vartheta }{\partial t^{\alpha }}+({\vartheta }_v-\alpha D_t(\tau ))\frac{{\partial }^{\alpha }v}{\partial t^{\alpha }}-u\frac{{\partial }^{\alpha }{\vartheta }_v}{\partial t^{\alpha }}+\lambda \\ +{\displaystyle \sum _{n=1}^{\infty }\left[\left(\begin{array}{l}\alpha \\ n\end{array}\right)\frac{{\partial }^{\alpha }{\vartheta }_v}{\partial t^{\alpha }}-\left(\begin{array}{l}\alpha \\ n+1\end{array}\right)D_t^{n+1}(\tau )\right]}{D}_t^{\alpha -n}(v)-{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\alpha \\ n\end{array}\right)}{D}_t^n(\xi )D_t^{\alpha -n}{v}_x\end{array}$$

(32)

4.2. Lie Symmetry

By third prolongation in Equations (1) and (2), we can obtain infinitesimals:

$$\begin{array}{c}\xi =\alpha x{c}_2+c_1,\\ \tau =3t{c}_2,\\ \eta =-2u\alpha c_2,\\ \vartheta =-v\alpha c_2.\end{array}$$

(33)

Lie algebra corresponding to infinitesimal symmetry of governing system is spanned by

$$V_1=\frac{\partial }{\partial x}$$

(34)

$$V_2=x\alpha \frac{\partial }{\partial x}+3t\frac{\partial }{\partial t}-2u\alpha \frac{\partial }{\partial u}-v\alpha \frac{\partial }{\partial v}$$

(35)

Now, corresponding to Equations (1) and (2), we have following infinitesimal generators given as [7,8]

$$V=c_1{V}_1+c_2{V}_2$$

4.3. Similarity Reduction

Case 2: The following characteristic equation can be obtained by using the infinitesimal generator in Equation (35), given as

$$\frac{dx}{x\alpha }=\frac{dt}{3t}=-\frac{du}{2u\alpha }=-\frac{dv}{v\alpha }$$

(36)

After solving Equation (36), the following similarity variable can be obtained, given as

$$X=x{t}^{\frac{-\alpha }{3}}$$

(37)

$$u=F(X)t^{\frac{-2\alpha }{3}}$$

(38)

$$v=G(X)t^{\frac{-\alpha }{3}}$$

(39)

Theorem 1.

The transformation (38) and (39) reduces Equations (1) and (2) to the following form of Ordinary differential equations (ODEs) given as:

$$\left(P_{\frac{3}{\alpha }}^{1-\frac{5\alpha }{3}, \alpha }F\right)(X)+F_{XXX}+\frac{3}{2}G{G}_{XXX}+\frac{9}{2}{G}_X{G}_{XX}-6 F{F}_X-6FG{G}_X-\frac{3}{2} F_X{G}^2=0$$

(40)

$$\left(P_{\frac{3}{\alpha }}^{1-\frac{4\alpha }{3}, \alpha }G\right)(X)+G_{XXX}-6 G{F}_X-6F{G}_X-\frac{15}{2} G_X{G}^2=0$$

(41)

with the Erdélyi-Kober operator$P_{\beta }^{\tau ,\alpha }$:

$$\left(P_{\beta }^{\tau ,\alpha }F\right):=\underset{j=0}{\prod ^{n-1}}\left(\tau +j-\frac{1}{\beta }X\frac{d}{dX}\right)\left(K_{\beta }^{\tau +\alpha ,n-\alpha }F\right)(X)$$

(42)

and

$$\left(P_{\beta }^{\tau ,\alpha }G\right):=\underset{j=0}{\prod ^{n-1}}\left(\tau +j-\frac{1}{\beta }X\frac{d}{dX}\right)\left(K_{\beta }^{\tau +\alpha ,n-\alpha }G\right)(X)$$

(43)

where, the Erdélyi-Kober fractional integral operator can be expressed as:

$$\left(K_{\beta }^{\tau +\alpha ,n-\alpha }F\right)(X):=\{\begin{array}{l}\frac{1}{\mathsf{\Gamma }(\alpha )}{\displaystyle \underset{1}{\overset{\infty }{\int }}{\left(u-1\right)}^{\alpha -1}{u}^{-(\tau +\alpha )}F\left(X{u}^{\frac{1}{\beta }}\right)du, \alpha >0,}\\ F(X), \alpha =0.\end{array}$$

(44)

and

$$\left(K_{\beta }^{\tau +\alpha ,n-\alpha }G\right)(X):=\{\begin{array}{l}\frac{1}{\mathsf{\Gamma }(\alpha )}{\displaystyle \underset{1}{\overset{\infty }{\int }}{\left(u-1\right)}^{\alpha -1}{u}^{-(\tau +\alpha )}G\left(X{u}^{\frac{1}{\beta }}\right)du, \alpha >0,}\\ G(X), \alpha =0.\end{array}$$

(45)

and

$$n=\{\begin{array}{l}[\alpha ]+1, \alpha \in \mathcal{N},\\ \alpha , \alpha \notin \mathcal{N}.\end{array}$$

(46)

4.4. Conservation Laws of Time-Fractional Coupled JM Equations

Let us consider the following conservation vectors viz. $C^1$ and $C^2$ for the Equations (1) and (2), which satisfies the conservation equations expressed as:

$${[D_t(C^1)+D_x(C^2)]}_{(1.1), (1.2)}=0$$

(47)

A Lagrangian of Equations (1) and (2) is:

$$\begin{array}{c}\mathrm{L}=\omega (x,t)(D_t^{\alpha }u+u_{xxx}+\frac{3}{2}v{v}_{xxx}+\frac{9}{2}{v}_x{v}_{xx}-6u{u}_x-6uv{v}_x-\frac{3}{2}{u}_x{v}^2)\\ +\gamma (x,t)(D_t^{\alpha }v+v_{xxx}-6u_{x}v-6u{v}_x-\frac{15}{2}{v}_x{v}^2)\end{array}$$

(48)

where, $\gamma$ and $\omega$ are dependent variables.

By considering Equation (48), the action integral can be defined as:

$${\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{\Omega }{\overset{}{\int }} \mathrm{L}(x, t, u, v, \omega , \gamma , D_t^{\alpha }u, u_x, u_{xxx}, D_t^{\alpha }v, v_x,v_{xxx})dx dt}}$$

(49)

The Euler-Lagrangian operator is given by

$$\frac{\delta }{\delta u}=\frac{\partial }{\partial u}+{(D_t^{\alpha })}^{*}\frac{\partial }{\partial D_t^{\alpha }u}-D_x\frac{\partial }{\partial u_x}-D_x^3\frac{\partial }{\partial u_{xxx}}$$

(50)

and

$$\frac{\delta }{\delta v}=\frac{\partial }{\partial v}+{(D_t^{\alpha })}^{*}\frac{\partial }{\partial D_t^{\alpha }v}-D_x\frac{\partial }{\partial v_x}-D_x^2\frac{\partial }{\partial v_{xx}}-D_x^3\frac{\partial }{\partial v_{xxx}}$$

(51)

where ${(D_t^{\alpha })}^{*}={(-1)}^n{}_{t}I_T^{n-\alpha }{D}_t^n$ is the adjoint operator of $D_t^{\alpha }$.

Euler Lagrange equations:

$$\frac{\delta \mathrm{L}}{\delta u}=0, \mathrm{and} \frac{\delta \mathrm{L}}{\delta v}=0$$

(52)

Considering the case of the independent variables $t,$ $x$ and the dependent variables $v(x,t)$, $u(x,t),$ we have

$$\overline{X}+D_t(\tau )I+D_x(\xi )I=W_1\frac{\delta }{\delta u}+W_2\frac{\delta }{\delta v}+D_t{C}^1+D_x{C}^2$$

(53)

where $\frac{\delta }{\delta u}$, $\frac{\delta }{\delta v}$ are the Euler-Lagrange operators and $I$ is the identity operator, $C^1$ and $C^2$ are the conserved vectors, and

So $\overline{X}$ is given as

$$\begin{array}{c}\overline{X}=\xi \frac{\partial }{\partial x}+\tau \frac{\partial }{\partial t}+\eta \frac{\partial }{\partial u}+\vartheta \frac{\partial }{\partial v}+{\eta }_{\alpha }^0\frac{\partial }{\partial D_t^{\alpha }u}+{\vartheta }_{\alpha }^0\frac{\partial }{\partial D_t^{\alpha }v}\\ +{\eta }^x\frac{\partial }{\partial u_x}+{\eta }^{xxx}\frac{\partial }{\partial u_{xxx}}+{\vartheta }^x\frac{\partial }{\partial v_x}+{\vartheta }^{xx}\frac{\partial }{\partial v_{xx}}+{\vartheta }^{xxx}\frac{\partial }{\partial v_{xxx}}\end{array}$$

(54)

Lie characteristic function $W_1$ and $W_2$ are:

$$\begin{array}{c}{W}_1=\eta -\tau u_t-\xi u_x\\ W_2=\gamma -\tau v_t-\xi v_x\end{array}$$

Here, for $V_1$, we have following conserved vectors

$$\begin{array}{c}{W}_1=-u_x\\ W_2=-v_x\end{array}$$

(55)

Here, for $V_2$, we have following conserved vectors

$$\begin{array}{c}{W}_1=-2u\alpha -x\alpha u_x-3t{u}_t\\ W_2=-v\alpha -x\alpha v_x-3t{v}_t\end{array}$$

(56)

In case of RL fractional differentiation in Equations (1) and (2), the components of the conserved vector can be written as follows:

For $W_1=-2u\alpha -x\alpha u_x-3t{u}_t$ and $W_2=-v\alpha -x\alpha v_x-3t{v}_t$, we have

$$\begin{array}{c}{C}^1=\tau \mathrm{L}+{}_{0}D_t^{\alpha -1}(W_1)\frac{\partial \mathrm{L}}{\partial {}_{0}D_t^{\alpha }u}+J\left(W_1,D_t\frac{\partial \mathrm{L}}{\partial {}_{0}D_t^{\alpha }u}\right)+{}_{0}D_t^{\alpha -1}(W_2)\frac{\partial \mathrm{L}}{\partial {}_{0}D_t^{\alpha }v}+J\left(W_2,D_t\frac{\partial \mathrm{L}}{\partial {}_{0}D_t^{\alpha }v}\right),\\ =\omega {}_{0}D_t^{\alpha -1}(-2u\alpha -x\alpha u_x-3t{u}_t)+J((-2u\alpha -x\alpha u_x-3t{u}_t),{\omega }_t)\\ +\gamma {}_{0}D_t^{\alpha -1}(-v\alpha -x\alpha v_x-3t{v}_t)+J((-v\alpha -x\alpha v_x-3t{v}_t),{\gamma }_t).\end{array}$$

(57)

$$\begin{array}{l}{C}^2=\xi \mathrm{L}+W_1\left[\frac{\partial \mathrm{L}}{\partial u_x}+D_x{D}_x\left(\frac{\partial \mathrm{L}}{\partial u_{xxx}}\right)\right]+W_2\left[\frac{\partial \mathrm{L}}{\partial v_x}-D_x\left(\frac{\partial \mathrm{L}}{\partial v_{xx}}\right)+D_x{D}_x\left(\frac{\partial \mathrm{L}}{\partial v_{xxx}}\right)\right]\\ +D_x(W_1)\left[-D_x\left(\frac{\partial \mathrm{L}}{\partial u_{xxx}}\right)\right]+D_x(W_2)\left[\frac{\partial \mathrm{L}}{\partial v_{xx}}-D_x\left(\frac{\partial \mathrm{L}}{\partial v_{xxx}}\right)\right]+D_x{D}_x(W_1)\left(\frac{\partial \mathrm{L}}{\partial u_{xxx}}\right)+D_x{D}_x(W_2)\left(\frac{\partial \mathrm{L}}{\partial v_{xxx}}\right)\\ \hspace{1em}=\frac{1}{2}((4\alpha v_x{\gamma }_x+6\alpha u_x{\omega }_x+9t{v}_t{v}_x{\omega }_x+3x\alpha v_x^2{\omega }_x+6t{\omega }_x{u}_{xt}+6t{\gamma }_x{v}_{xt}+9tv{\omega }_x{v}_{xt}\\ \hspace{1em}\hspace{1em}+2x\alpha ({\omega }_x{u}_{xx}+{\gamma }_x{v}_{xx})+3x\alpha v{\omega }_x{v}_{xx}-2\alpha v{\gamma }_{xx}-6t{v}_t{\gamma }_{xx}-2x\alpha v_x{\gamma }_{xx}-4\alpha u{\omega }_{xx}\\ \hspace{1em}\hspace{1em}-3\alpha v^2{\omega }_{xx}-6t{u}_t{\omega }_{xx}-9t{v}_x{\omega }_{xx}-2x\alpha u_x{\omega }_{xx}+v{v}_x(9\alpha {\omega }_x-3x\alpha {\omega }_{xx}))\\ \hspace{1em}\hspace{1em}+\gamma (36\alpha uv+15\alpha v^3+12v(3t{u}_t+x\alpha u_x)+12u(3t{v}_t+x\alpha v_x)+15v^2(3t{v}_t+x\alpha v_x)\\ \hspace{1em}\hspace{1em}-6\alpha v_{xx}-6t{v}_{xxt}-2x\alpha v_{xxx})+\omega (24\alpha u^2+18\alpha u{v}^2+12u(3t{u}_t+x\alpha u_x)\\ \hspace{1em}\hspace{1em}+3v^2(3t{u}_t+x\alpha u_x)-12\alpha v_x^2+12uv(3t{v}_t+x\alpha v_x)-18t{v}_x{v}_{xt}-8\alpha u_{xx}-12\alpha v{v}_{xx}\\ \hspace{1em}\hspace{1em}-9t{v}_t{v}_{xx}-9x\alpha v_x{v}_{xx}-6t{u}_{xxt}-9tv{v}_{xxt}-2x\alpha u_{xxx}-3x\alpha v{v}_{xxx}))\end{array}$$

(58)

5. Conclusions

Fractional logistic function technique is proposed for soliton solutions of fractional JM system. Numerical simulation for solutions has been shown for analyzing the physical nature of obtained solutions. Moreover, Lie group analysis technique is proposed for investigation of symmetry properties and conservation laws for fractional Jaulent-Miodek system. Conservation laws for the system are acquired by new theorem and formal Lagrangian. These analyses are relatively new and reliable for finding exact solutions and constructing conservation laws with generating similarity solutions for the FPDEs. Furthermore, this method enriches the solution of the equations, which is of great significance for study of the FPDEs.