1. Introduction
In the standard model of elementary particles and according to current experiments, there exist three generations of matters but we do not know why. Matter particles are fermions of spin
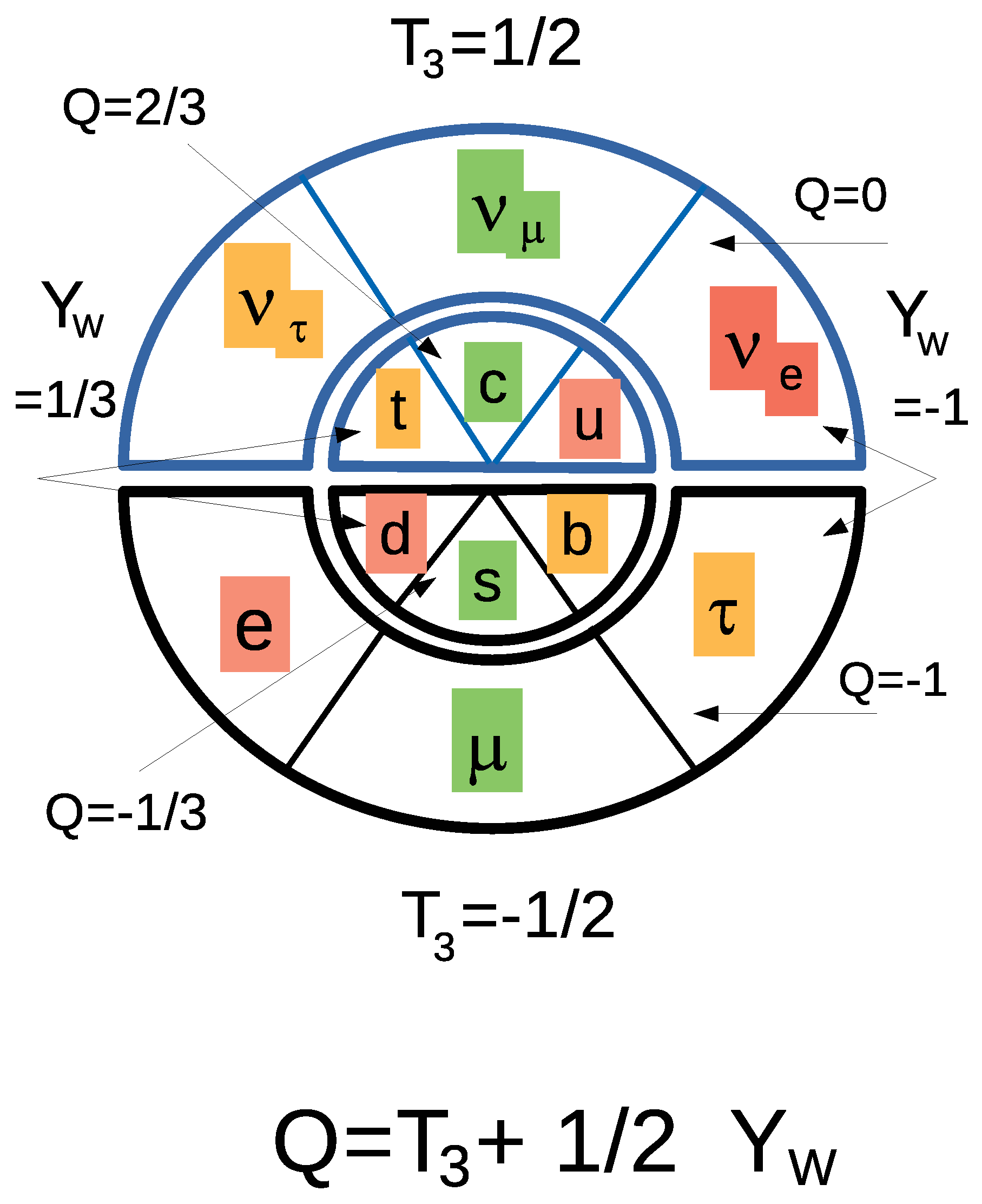
and comprise the quarks (responsible for the strong interactions) and leptons (responsible for the electroweak interactions as shown in
Table 1 and
Figure 1).
In order to explain the CP-violation (the non-invariance of interactions under the combined action of charged-conjugation (C) and parity (P) transformations) in quarks, Kobayashi and Maskawa introduced the so-called Cabibbo-Kobayashi-Maskawa unitary matrix (or CKM matrix) that describes the probability of transition from one quark
i to another
j. These transitions are proportional to
, where the
’s are entries in the CKM matrix [
1,
2]
There is a standard parametrization of the CKM matrix with three Euler angles
(the Cabbibo angle),
,
, and the CP-violating phase
. Taking
and
, the CKM matrix reads
Similarly, the charged leptons
e,
and
are related to three generations of flavors of neutrinos
,
and
in the charged-current weak interaction. Neutrino mass
can be deduced with probability
, where the
’s are the amplitudes of mass eigenstates
i in flavor
. The so-called Pontecorvo–Maki–Nakagawa–Sakata unitary matrix (or PMNS matrix) is as follows [
3]
where the entries in the matrix mean the range of values allowed by present day experiments.
As for the CKM matrix, the three mixing angles are denoted , , , and the CP-violating phase is called .
The current experimental values of angles for reproducing entries in the CKM and PMNS matrices are in
Table 2.
Over the last twenty years, a paradigm has emerged wherein there may exist an underlying discrete symmetry jointly explaining the mixing patterns of quarks and leptons [
4,
5]. This assumption follows from the fact that the CKM matrix is found to be closed to the identity matrix and the entries in the PMNS matrix are found to be of order 1 except for the almost vanishing
. A puzzling difference between quark and lepton mixing lies in the fact that there is much more neutrino mixing than mixing between the quark flavors. Up and down quark matrices are only slightly misaligned, while there exists a strong misalignment of charged leptons with respect to neutrino mass matrices. A valid model should account for these features.
The standard model essentially consists of two continuous symmetries, the electroweak symmetry
(that unifies the electromagnetic and weak interactions) and the quantum chromodynamics symmetry
(that corresponds to strong interactions). There are several puzzles not explained within the standard model, including the flavor mixing patterns, the fermion masses, and the CP violations in the quark and lepton sectors. There are astonishing numerical coincidences such as the Koide formula for fermion masses [
6,
7], the quark-lepton complementarity relations
,
[
8] and efficient first order models such as the tribimaximal model [
9,
10,
11,
12] and the “Golden ratio” model [
13,
14]. For instance, tribimaximal mixing gives values of angles as
≈ 35.3°,
= 45°,
= 0 and
= 0, compatible with earlier data. Such a model could be made more realistic by taking two CP-phases instead of one [
12]. In Reference [
14], the conjecture is that reality is information-theoretic as its core and the Golden Ratio is the fundamental dimensionless constant of Nature.
Currently, many discrete models of quark-lepton mixing patterns are based on the representations of finite groups that are both subgroups of
and
[
15,
16,
17,
18,
19,
20,
21,
22]. In the same spirit, we add to this body of knowledge by selecting valid subgroups of unitary groups with a criterion borrowed from the theory of generalized quantum measurements.
One needs a quantum state (called a fiducial state) and one also requires that such a state be informationally complete under the action of a
d-dimensional Pauli group
. If such a state is not an eigenstate of a
d-dimensional Pauli group, it allows one to perform universal quantum computation [
23,
24,
25]. In the above papers, valid states belong to the eigenstates of mutually commuting permutation matrices in a permutation group derived from the coset classes of a free group with relations. From here, the fiducial state will have to be selected from the characters
of a finite group
G with the number of conjugacy classes
defining the Hilbert space dimension. Groups under consideration should obey two rules (a) the character table of
G contains both 2- and 3-dimensional representations with at least one of them faithful and (b) there are minimal informationally complete measurements under the action of a
d-dimensional Pauli group over the characters of these representations. The first criterion is inspired by the current understanding of quark and lepton mixings (and the standard model) and the second one by the theory of magic states in quantum computing [
23]. Since matter particles are spin
fermions, it is entirely consistent to see them under the prism of quantum measurements.
In the rest of this introduction we recall what we mean by a minimal informationally complete quantum measurement (or MIC). In
Section 2, we apply criteria (a) and (b) to groups with small
, where we can perform the calculations. Then we extrapolate to some other groups with
. Most groups found from this procedure fit the current literature as being viable for reproducing lepton and quark mixing patterns. In
Section 3, we examine the distinction between generalized CP symmetry and CP violation and apply it to our list of viable groups.
2. Informationally Complete Characters for Quark/Lepton Mixing Matrices
The standard classification of small groups is from their cardinality. Finite groups relevant to quark and lepton mixings are listed accordingly [
9,
15,
18]. We depart from this habit by classifying the small groups
G of interest versus the number
of their conjugacy classes. This motivation is due to the application of criterion (b), where we need to check whether the action of a Pauli group in the
d-dimensional Hilbert space
results in a minimal informationally complete POVM (or MIC).
A list of finite groups
G according to the number of their conjugacy classes (complete only up to
) is in Ref. [
29]. It can also be easily recovered with a simple code in MAGMA [
30]. For our application to quark and lepton mixings, we need much higher
d. In practice, we use existing tables of subgroups of
(of cardinality up to 2000 in [
9,
15,
18] and up to 1025 in [
21] to select our group candidates.
Table 3 gives the list of
small groups with
found to satisfy the two following rules: (a) the character table of
G contains both 2- and 3-dimensional representations with at least one of them faithful and (b) the quantum measurement is informationally complete under a
d-dimensional Pauli group.
According to the quoted references in column 5 of
Table 3, the 16 groups lead to good models for the absolute values of entries in the CKM and PMNS matrices except for the ones that have the factor
in their signature. The two extra groups
and
arise when one takes into account the generalized CP symmetry, as in
Section 3.
Table 5 gives an extrapolation to groups with higher
where criterion (a) is satisfied but where (b) could not be checked. Most groups in the two tables have been found to be viable models, and several of them belong to known sequences.
In
Table 3 and
Table 5, the first column is the standard small group identifier in which the first entry is the order of the group (as in [
15]). In the second column, one finds the signature in terms of a direct product (with the symbol ×), a semidirect product (with the symbol ⋊), a dot product (with the symbol .) or a member of a sequence of groups such as the
sequence found to contain many viable groups for quark and lepton mixings. The third column gives the number of irreducible characters/conjugacy classes. Other information is about the geometry of the group. To obtain this geometry, one first selects the smallest permutation representation on
letters of
G. Then one looks at the two-point stabilizer subgroup
of smallest cardinality in the selected group
G. The incidence matrix of such a subgroup turns out to be the
l-partite graph
that one can identify from the graph spectrum. Such a method is already used in our previous papers about magic state type quantum computing [
23,
24,
25], where other types of geometries have been found. Finally, column 5 refers to papers where the group under study leads to a viable model both for quark and lepton mixing patterns. The recent reference [
21] is taken separately from the other references singled out with the index † in the tables. It is based on the alternative concept of a two-Higgs-doublet model.
2.1. Groups in the Series and More Groups
An important paper dealing with the series
as a good model for lepton mixing is [
16]. A group in this series has to be spontaneously broken into two subgroups, one abelian subgroup
in the charged lepton sector and a Klein subgroup
in the neutrino sector (with neutrinos seen as Majorana particles). The superscripts
S,
T and
U refer to the generators of their corresponding
group in the diagonal charged lepton basis. In this particular model, there is trimaximal lepton mixing with (so called reactor angle)
fixed up to a discrete choice, an oscillation phase zero or
and the (so-called atmospheric angle)
= 45° ±
.
It is shown in [
2] (Table I) that two groups in this series with
and
provide leading order leptonic mixing patterns within 3-sigma of current best fit with acceptable entries in the CKM matrix. The small group
also satisfies this requirement. Additionally, if one accepts that neutrinos are Dirac particles, the residual symmetry group of neutrino masses is no longer restricted to the Klein group but may be any abelian group. In such a case, four small groups which are
and the small groups
,
and
predict acceptable entries for the quark and lepton mixing matrices [
2] (Table II). It is noticeable that our small selection of groups (from requirements (a) and (b)) include all of them except for the group
whose two-dimensional representations are not MICs.
Still assuming that neutrinos are Dirac particles and with loose enough constraints on
, paper [
18] includes
-groups with
(it does not lie in our
Table 3) and
in their selection, as well as groups
,
and
, the latter groups are in our
Table 5. Additional material [
18] provides very useful information about the ability of a group to be a good candidate for modeling the mixing patterns. According to this reference, the groups
with
, 11, 14 and 18, and small groups
and
, that are in our tables, also match Dirac neutrinos with a 3-sigma fit and quark mixing patterns for triplet assignment.
Three extra groups (the binary icosahedral group ), and in our tables, whose signature has a factor equal to the binary icosahedral group , can be assigned with a doublet and a singlet for quarks but cannot be generated by the residual symmetries in the lepton sector.
2.2. Exceptional Subgroups of
The viability of so-called exceptional groups of
for lepton mixings have been studied in [
22] by assuming neutrinos to be either Dirac or Majorana particles. These subgroups are listed according to the number of their conjugacy classes in
Table 6. They are
(a subgroup of
),
,
,
,
and
. Only group
has Klein subgroups and thus supports a model with neutrinos as Majorana particles. Group
is already in our
Table 3 and potentially provides a valid model for quark/lepton mixings by assuming neutrinos are Dirac particles.
According to our
Table 6, all these exceptional groups have informationally complete characters in regard to most of their faithful three-dimensional representations. Another useful piece of information is about groups
and
that are informationally complete in regard to their 5-dimensional representations. Models based on the
family symmetry are in [
31,
32].
3. Generalized CP Symmetry, CP Violation
Currently, many models focus on the introduction of a generalized CP symmetry in the lepton mixing matrix [
12,
31,
33]. The Dirac CP phase
for leptons is believed to be around
[
33]. A set of viable models with discrete symmetries including generalized CP symmetry has been derived in [
34], where full details about the so-called semidirect approach and its variant are provided. Most finite groups used for quark/lepton mixings without taking into account the CP symmetry survive as carrying generalized CP symmetries in the model described in [
34]. It is found that two extra groups
and
, that have triplet assignments for the quarks, can be added. This confirms the relevance of
models in this context. Group
was added to our short
Table 4, where we see that all of its 2- and 3-dimensional characters are informationally complete.
We follow Reference [
35] in distinguishing generalized CP symmetry from a “physical” CP violation. A “physical” CP violation is a prerequisite for baryogenesis that is the matter-antimatter asymmetry of elementary matter particles. The generalized CP symmetry was introduced as a way of reproducing the absolute values of the entries in the lepton and quark mixing matrices and, at the same time, explaining or predicting the phase angles. A physical CP violation, on the other hand, exchanges particles and antiparticles and its finite group picture had to be clarified.
It is known that the exchange between distinct conjugacy classes of a finite group
G is controlled by the outer automorphisms
u of the group. Such (non trivial) outer automorphisms have to be class-inverting to correspond to a physical CP violation [
35]. This is equivalent to a relation obeyed by the automorphism
that maps every irreducible representation
to its conjugate
with
a unitary symmetric matrix.
A criterion that ensures that this relation is satisfied is given in terms of the so-called twisted Frobenius-Schur indicator over the character
where
if
is even and
otherwise.
Following this criterion, there are three types of groups
1. the groups of type I: there is at least one representation for which , these groups correspond to a physical CP violation,
2. groups of type II: for (at least) one automorphism the ’s for all representations are non zero. The automorphism u can be used to define a proper CP transformation in any basis. There are two sub-cases:
Case II A, all ’s are for one of those u’s,
Case II B, some ’s are for all candidates u’s.
A simple program written in the Gap software allows one to distinguish these cases [
35] (Appendix B).
Applying this code to our groups in
Table 3,
Table 5 and
Table 6, we find that all groups are of type II A or type I. Type I groups corresponding to a physical CP violation are
where we could check that our criteria (a) and (b) apply, the exceptional group
in
Table 6 and groups
,
,
of
Table 5.