Bias Reduction for the Marshall-Olkin Extended Family of Distributions with Application to an Airplane’s Air Conditioning System and Precipitation Data
Abstract
1. Introduction
2. Bias Correction of MLE
- Step 0: choose an initial value for , say . A possible value can be , where is the MLE for considering that are iid from .
- Step 1: For choose as the vector that maximizes the profile log-likelihood function in relation to .
- Step 2: For do as the solution for in (6) considering .
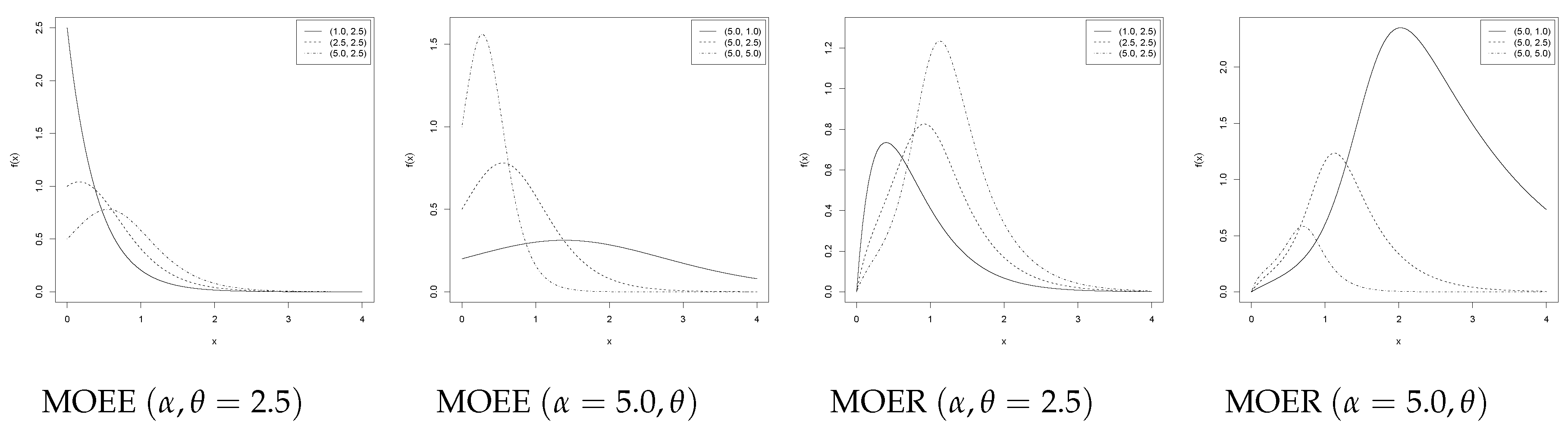
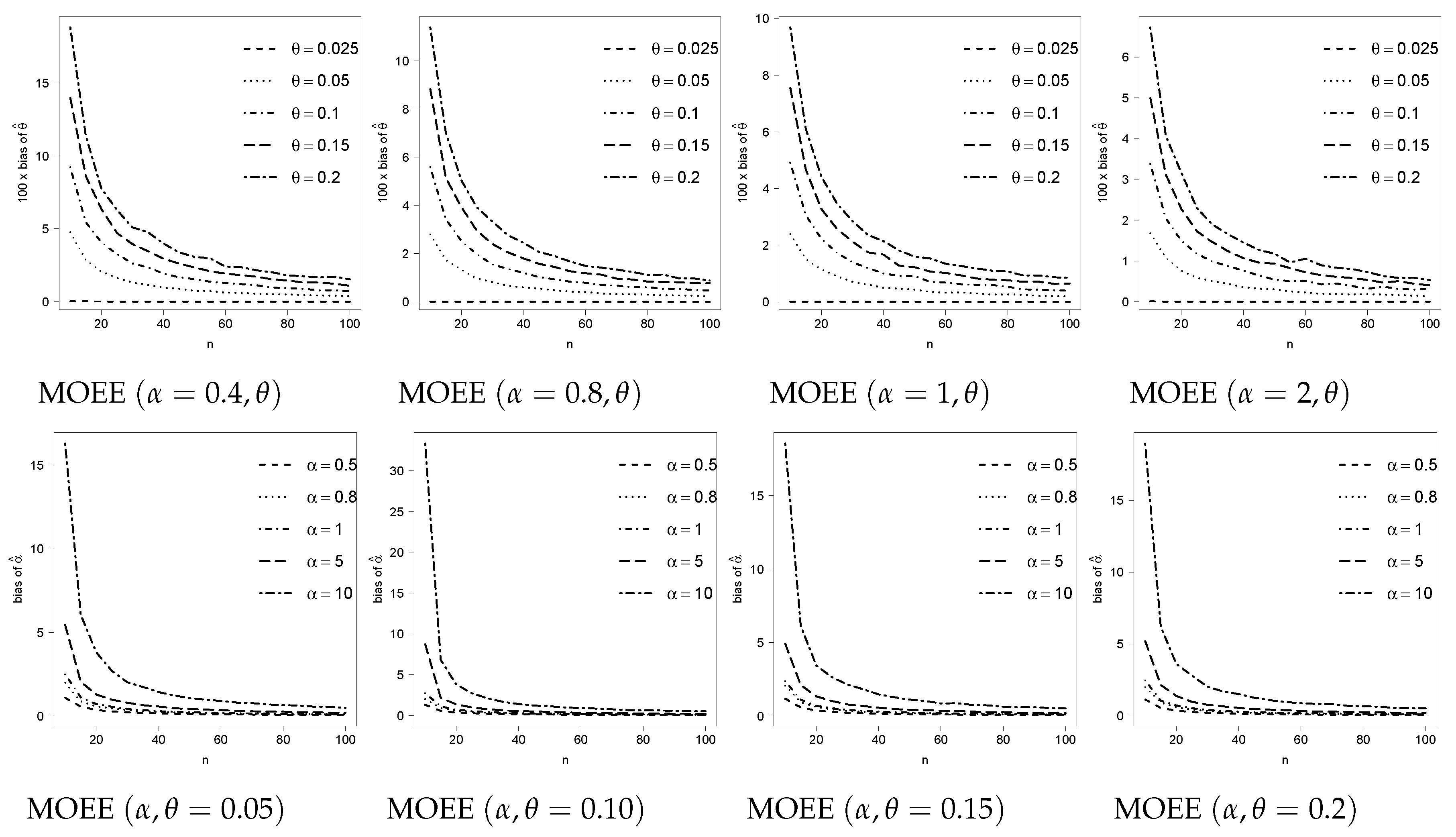
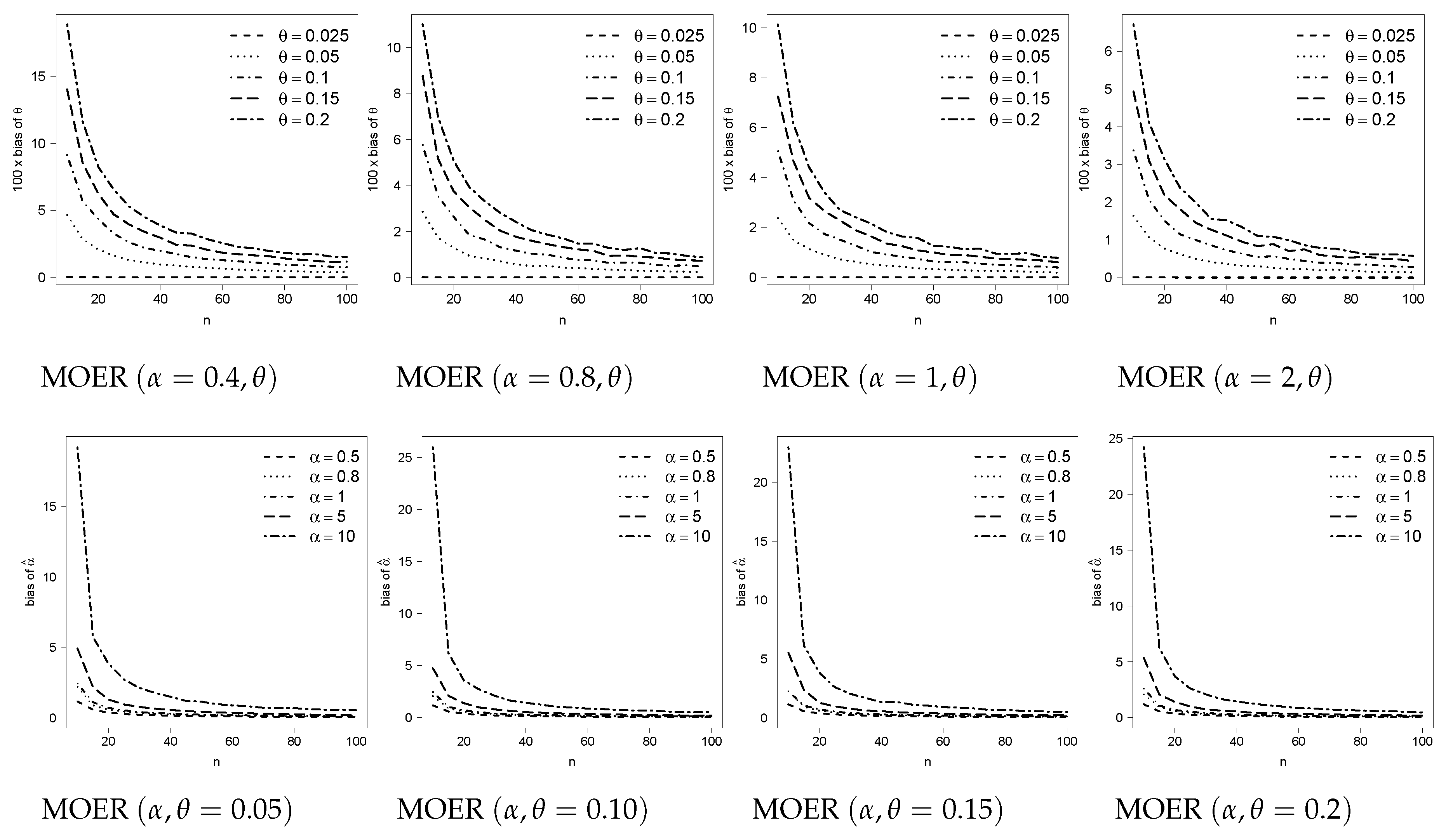
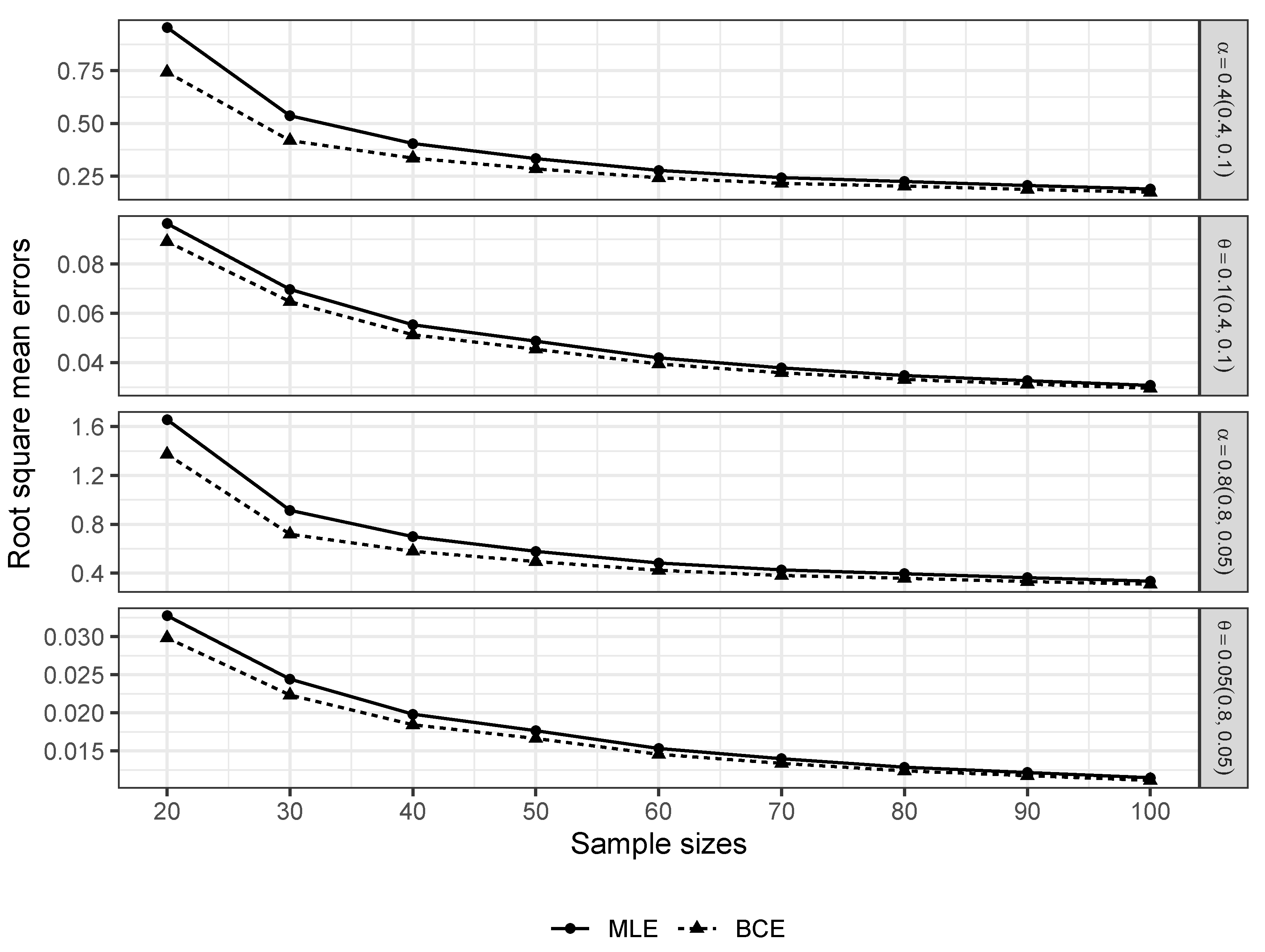
3. Numerical Results
3.1. Reducing the Bias in the MOEE and MOER Models
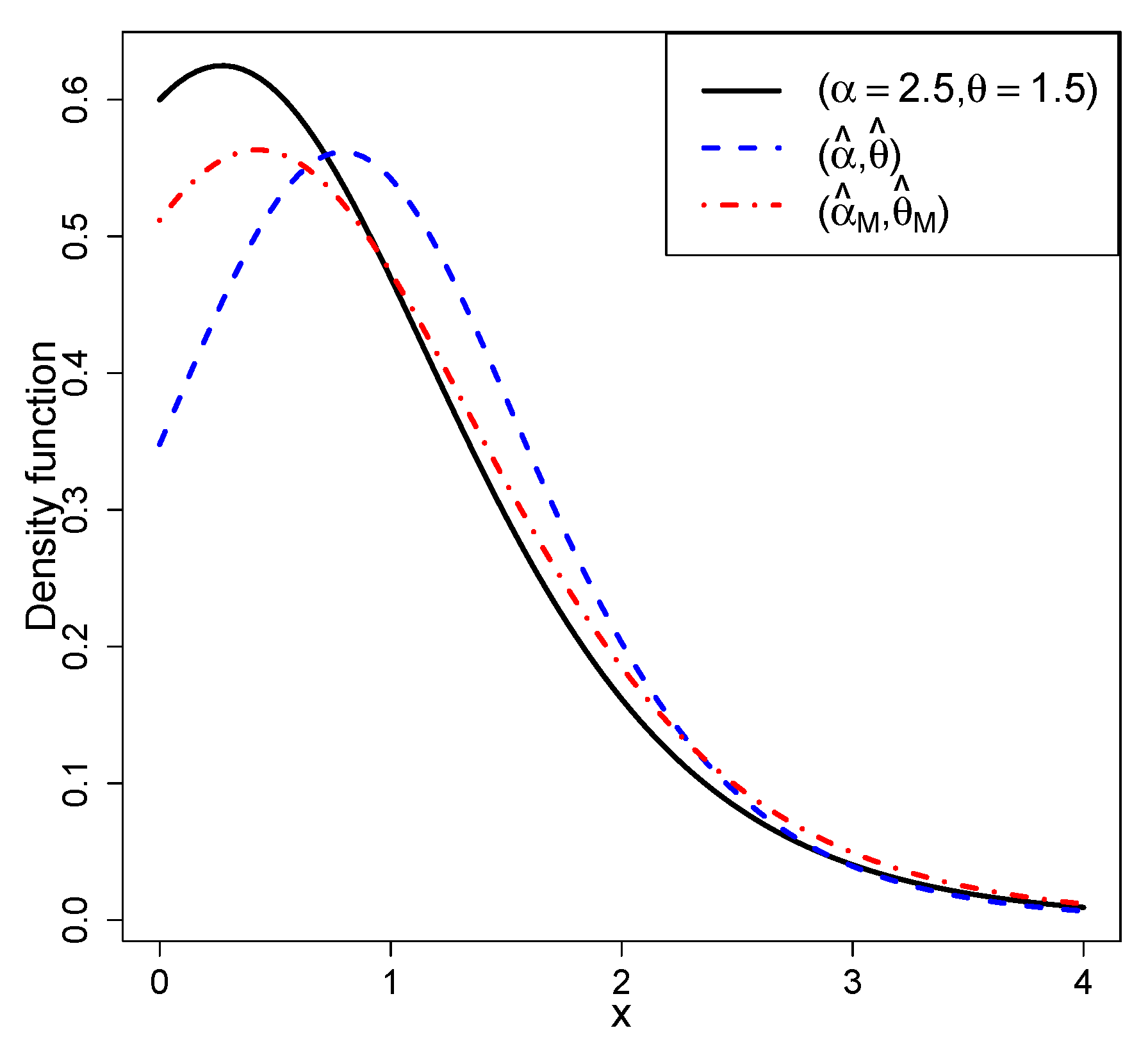
3.2. A Simulated Example with Outliers
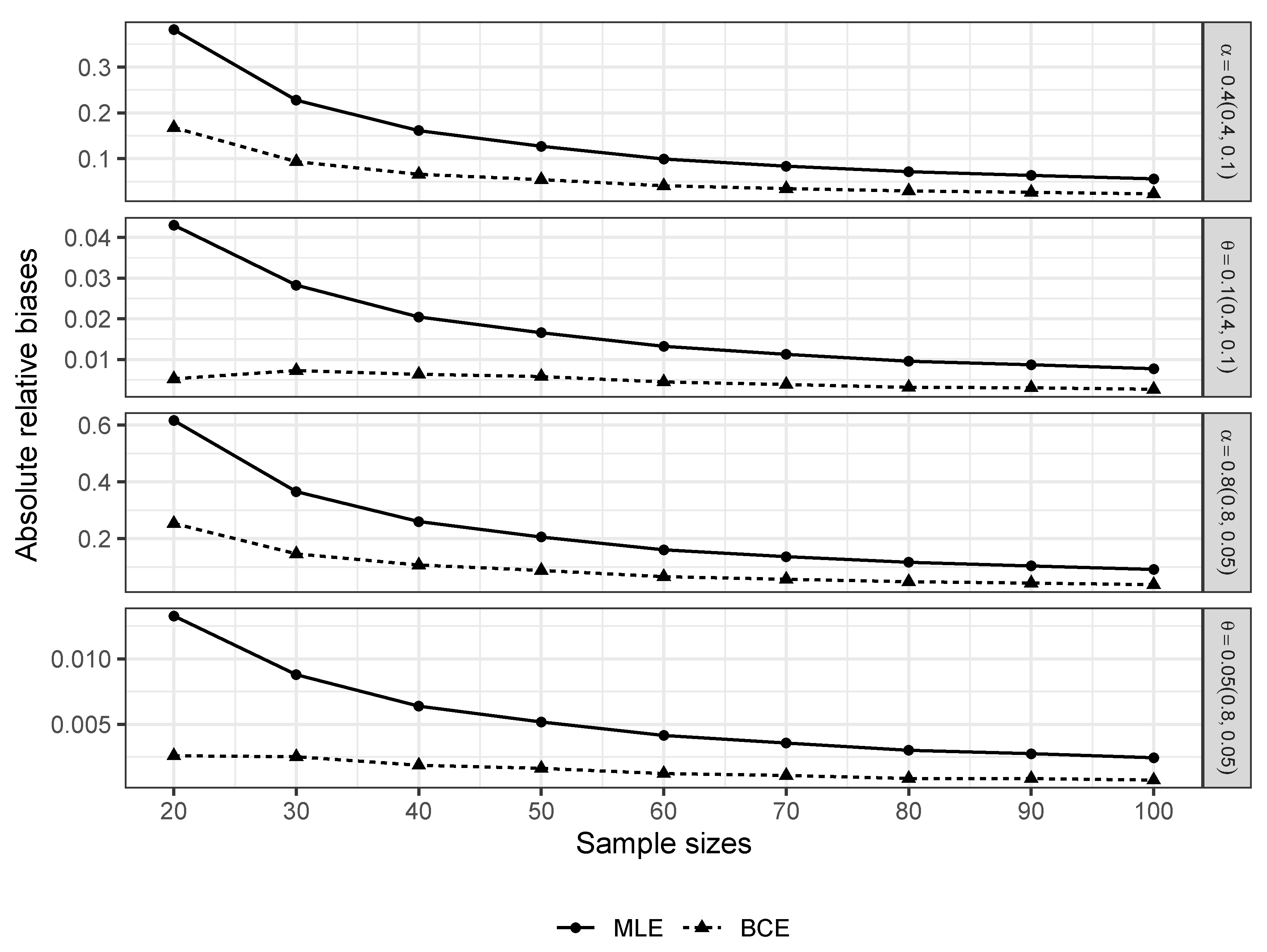
4. Two Applications
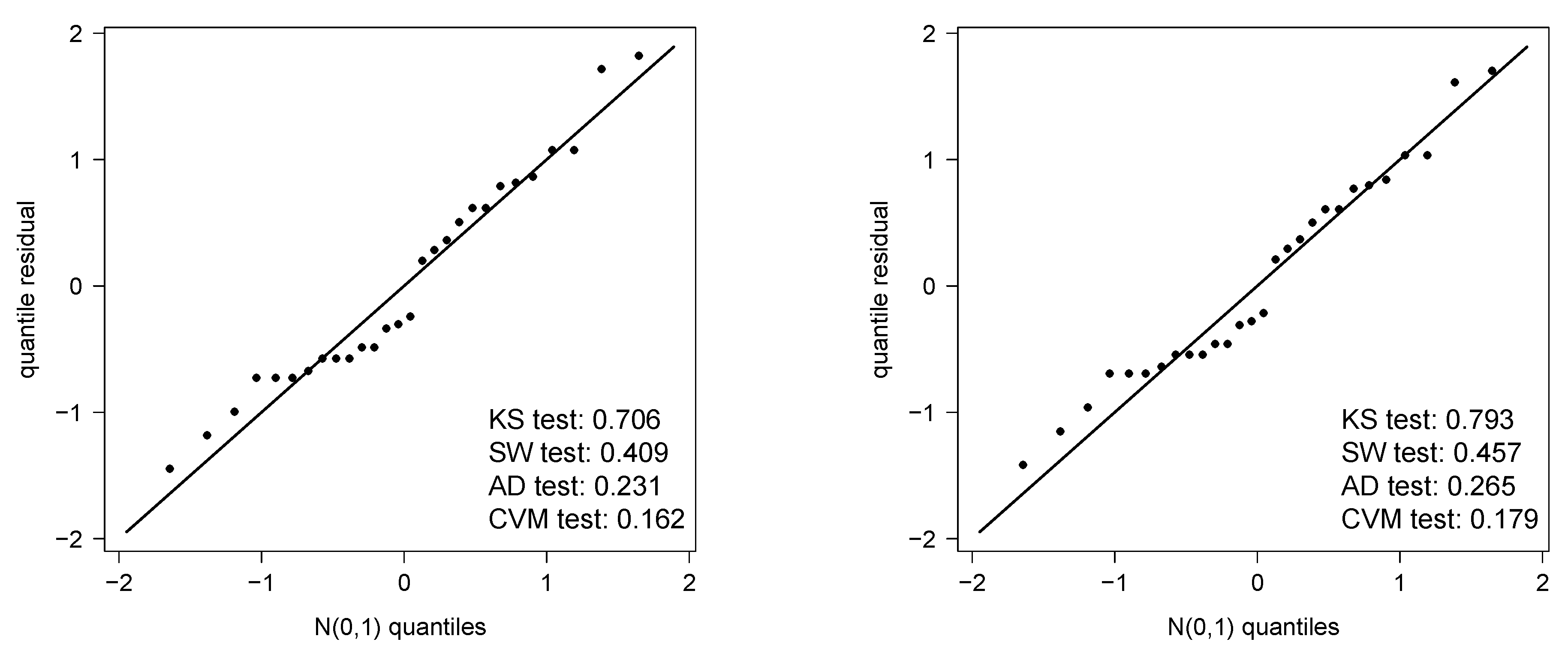
4.1. Air Conditioning System of an Airplane Data Set
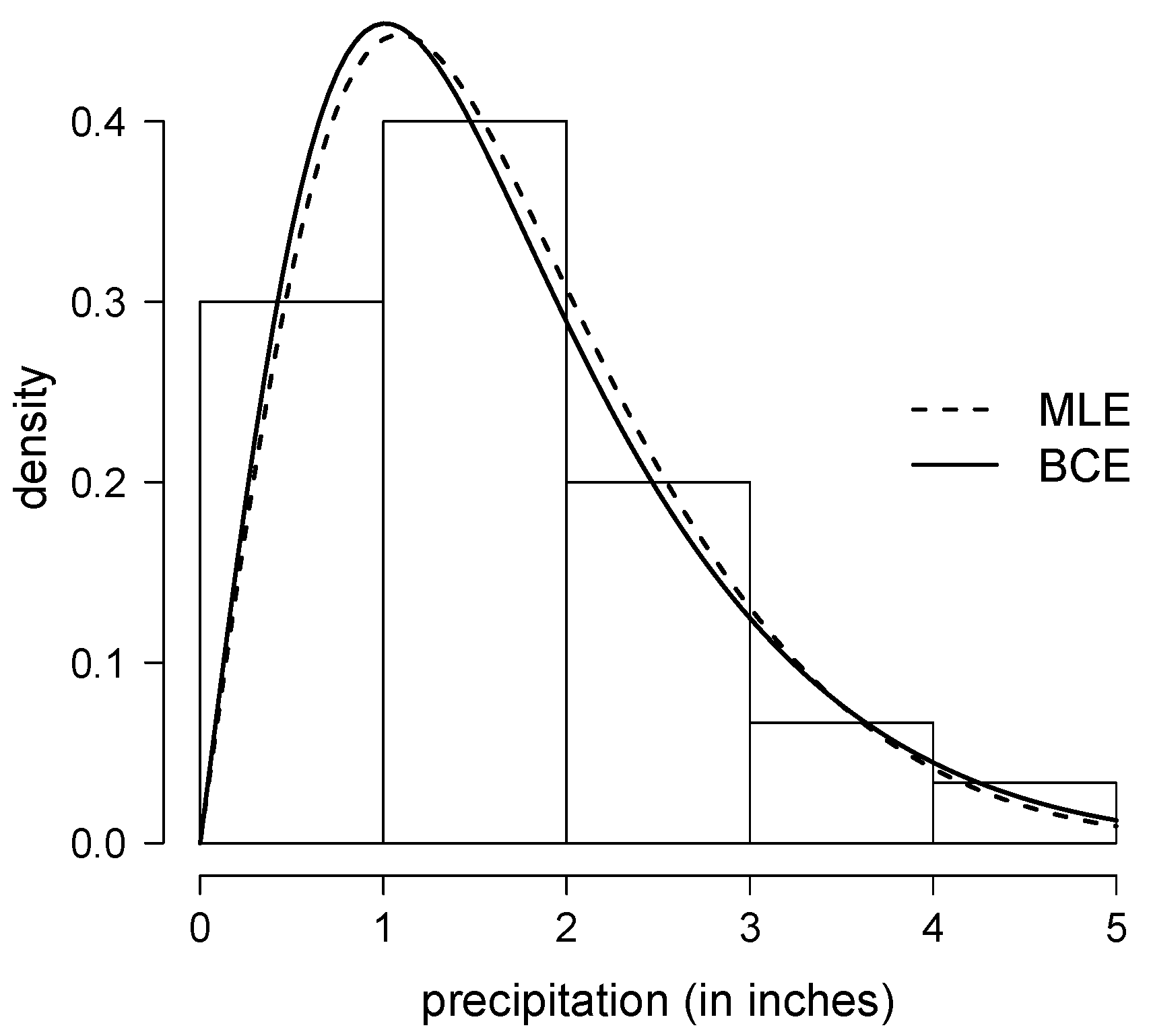
4.2. Precipitation Data Set
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Details of the Computation of M(α)
Details of the Asymptotic CI Used in Application 2
References
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. Life Distributions. Structure of Nonparametric, Semipara- Metric and Parametric Families; Springer: New York, NY, USA, 2007. [Google Scholar]
- Castellares, F.; Lemonte, A.J. On the Marshall-Olkin extended distributions. Commun. Stat. Theory Methods 2016, 45, 4537–4555. [Google Scholar] [CrossRef]
- Ghitany, M.E. Marshall-Olkin extended pareto distribution and its application. Int. J. Appl. Math. 2005, 18, 17–32. [Google Scholar]
- Ghitany, M.E.; Al-Hussaini, E.K.; Jarallah, R.A. Marshall-Olkin extended Weibull distribution and its application to censored data. J. Appl. Stat. 2005, 32, 1025–1034. [Google Scholar] [CrossRef]
- Ristic, M.M.; Kanichukattu, J.; Joseph, A. A marshall-olkin gamma distribution and minification process. STARS Int. J. Sci. 2007, 1, 107–117. [Google Scholar]
- Ghitany, M.E.; Al-Awadhi, F.A.; Alkhalfan, L.A. Marshall-olkin extended lomax distribution and its application to censored data. Commun. Stat. Theory Methods 2007, 36, 1855–1866. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Kotz, S. Reliability properties of extended linear failure-rate distributions. Probab. Eng. Inf. Sci. 2007, 21, 441–450. [Google Scholar] [CrossRef]
- Jayakumar, K.; Mathew, T. On a generalization to Marshall–Olkin scheme and its application to Burr type XII distribution. Stat. Pap. 2008, 49, 421–439. [Google Scholar] [CrossRef]
- García, V.; Gómez, E.; Vásquez-Polo, F. A new skew generalization of the normal distribution: Properties and applications. Comput. Stat. Data Anal. 2010, 54, 2021–2034. [Google Scholar] [CrossRef]
- Gómez-Déniz, E. Another generalization of the geometric distribution. Test 2010, 19, 399–415. [Google Scholar] [CrossRef]
- Lemonte, A. A new extension of the Birnbaum-Saunders distribution. Braz. J. Probab. Stat. 2013, 27, 133–149. [Google Scholar] [CrossRef]
- Cordeiro, G.; Lemonte, A. On the Marshall-Olkin extended Weibull distribution. Stat. Pap. 2013, 54, 333–353. [Google Scholar] [CrossRef]
- Cordeiro, G.; Lemonte, A.; Ortega, E. The Marshall-Olkin family of distributions: Mathematical properties and new models. J. Stat. Theory Pract. 2013, 8, 343–366. [Google Scholar] [CrossRef]
- Alshangiti, A.M.; Kayid, M.; Alarfaj, B. A new family of Marshall-Olkin extended distributions. J. Comput. Appl. Math. 2014, 271, 369–379. [Google Scholar] [CrossRef]
- Alizadeh, M.; Cordeiro, G.M.; De Brito, E.; Demétrio, C.G.B. The beta Marshall-Olkin family of distributions. J. Stat. Distrib. Appl. 2015, 2, 1–18. [Google Scholar] [CrossRef]
- Ristić, M.; Kundu, D. Marshall-Olkin generalized exponential distribution. Metron 2015, 73, 317–333. [Google Scholar] [CrossRef]
- Benkhelifa, L. The Marshall-Olkin extended generalized Lindley distribution: Properties and applications. Commun. Stat. Simul. Computation. 2017, 46, 8306–8330. [Google Scholar] [CrossRef]
- Afify, A.Z.; Cordeiro, G.M.; Yousof, H.M.; Saboor, A.; Ortega, E.M.M. The Marshall-Olkin additive Weibull distribution with variable shapes for the hazard rate. Hacet. J. Math. Stat. 2018, 47, 365–381. [Google Scholar] [CrossRef]
- Javed, M.; Nawaz, T.; Irfan, M. The Marshall-Olkin Kappa distribution: Properties and applications. J. King Saud Univ. Sci. 2019, 31, 684–691. [Google Scholar] [CrossRef]
- Mansoor, M.; Tahir, M.H.; Cordeiro, G.M.; Provost, S.B.; Alzaatreh, A. The Marshall-Olkin logistic-exponential distribution. Commun. Stat. Theory Methods 2019, 48, 220–234. [Google Scholar] [CrossRef]
- Yousof, H.M.; Afify, A.Z.; Alizadeh, M.; Nadarajah, S.; Aryal, G.; Hamedani, G. The Marshall-Olkin generalized-G family of distributions with applications. Statistica 2018, 78, 273–295. [Google Scholar]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resour. Res. 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Guney, Y.; Tuac, Y.; Arslan, O. Marshall-Olkin distribution: Parameter estimation and application to cancer data. J. Appl. Stat. 2017, 44, 2238–2250. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Cordeiro, G.M.; Yousof, H.M.; Pescim, R.R.; Afify, A.Z.; Nadarajah, S. The Weibull Marshall-Olkin family: Regression model and application to censored data. Commun. Stat. Theory Methods 2019, 48, 4171–4194. [Google Scholar] [CrossRef]
- Nassar, M.; Kumar, D.; Dey, S.; Cordeiro, G.M.; Afify, A.Z. The Marshall-Olkin alpha power family of distributions with applications. J. Comput. Appl. Math. 2019, 1, 41–53. [Google Scholar] [CrossRef]
- Cox, D.R.; Snell, E.J. A general definition of residuals. J. R. Society. Ser. B Methodol. 1968, 30, 248–275. [Google Scholar] [CrossRef]
- Firth, D. Bias reduction of maximum likelihood estimates. Biometrika 1993, 80, 27–38. [Google Scholar] [CrossRef]
- Sartori, N. Bias prevention of maximum likelihood estimates for scalar skew normal and skew t distributions. J. Stat. Plan. Inference 2006, 136, 4259–4275. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Cribari-Neto, F. An introduction to Bartlett Corrections and Bias Reduction; Springer: Berlin/Heidelberg, Geramny, 2014. [Google Scholar]
- Arrué, J.; Arellano-Valle, R.B.; Gómez, H.W. Bias reduction of maximum likelihood estimates for a modified skew normal distribution. J. Stat. Comput. Simul. 2016, 86, 2967–2984. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Linhart, H.; Zucchini, W. Model Selection; John Wiley and Sons: New York, NY, USA, 1986. [Google Scholar]
- Dunn, P.; Smyth, G. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
- Hinkley, D. On quick choice of power transformation. Am. Stat. 1977, 26, 67–69. [Google Scholar] [CrossRef]
- Magalhães, T.M.; Botter, D.A.; Sandoval, M.C.; Pereira, G.H.A.; Cordeiro, G.M. Skewness of maximum likelihood estimators in the varying dispersion beta regression model. Commun. Stat. Theory Methods 2019, 48, 4250–4260. [Google Scholar] [CrossRef]
- Magalhães, T.M.; Gallardo, D.I.; Gómez, H.W. Skewness of maximum likelihood estimators in the weibull censored data. Symmetry 2019, 11, 1351. [Google Scholar] [CrossRef]

| , | , | |||||||
|---|---|---|---|---|---|---|---|---|
| n | Estimator of | Estimator of | Estimator of | Estimator of | ||||
| MLE | BCE | MLE | BCE | MLE | BCE | MLE | BCE | |
| 10 | 2.329 | 1.374 | 0.385 | 0.062 | 2.481 | 1.588 | 0.297 | 0.116 |
| (0.855) | (0.656) | (1.283) | (1.104) | (0.851) | (0.642) | (1.036) | (0.924) | |
| 20 | 0.711 | 0.311 | 0.184 | 0.033 | 0.715 | 0.385 | 0.144 | 0.011 |
| (0.780) | (0.693) | (0.743) | (0.670) | (0.780) | (0.664) | (0.619) | (0.578) | |
| 30 | 0.414 | 0.170 | 0.122 | 0.030 | 0.408 | 0.193 | 0.096 | 0.017 |
| (0.749) | (0.699) | (0.564) | (0.520) | (0.749) | (0.700) | (0.474) | (0.447) | |
| 40 | 0.295 | 0.120 | 0.089 | 0.021 | 0.290 | 0.130 | 0.070 | 0.014 |
| (0.732) | (0.692) | (0.465) | (0.435) | (0.736) | (0.700) | (0.394) | (0.376) | |
| 50 | 0.233 | 0.098 | 0.072 | 0.019 | 0.228 | 0.099 | 0.057 | 0.012 |
| (0.713) | (0.686) | (0.417) | (0.395) | (0.717) | (0.690) | (0.354) | (0.339) | |
| Parameter | True | Original | with Outlier | ||
|---|---|---|---|---|---|
| Value | MLE | BCE | MLE | BCE | |
| 2.5 | 3.873 | 2.174 | 5.223 | 2.866 | |
| 1.5 | 1.839 | 1.464 | 1.817 | 1.467 | |
| Parameter | MLE | BCE |
|---|---|---|
| 0.380 (0.272) | 0.285 (0.225) | |
| 0.010 (0.005) | 0.008 (0.005) |
| Parameter | MLE | BCE | ||||
|---|---|---|---|---|---|---|
| Estimate | SE | Bias | Estimate | SE | Bias | |
| 0.514 | 0.351 | 0.255 | 0.394 | 0.270 | 0.213 | |
| 0.185 | 0.087 | 0.041 | 0.157 | 0.080 | 0.039 | |
| q | MLE | BCE | ||
|---|---|---|---|---|
| 95% IC | Width | 95% IC | Width | |
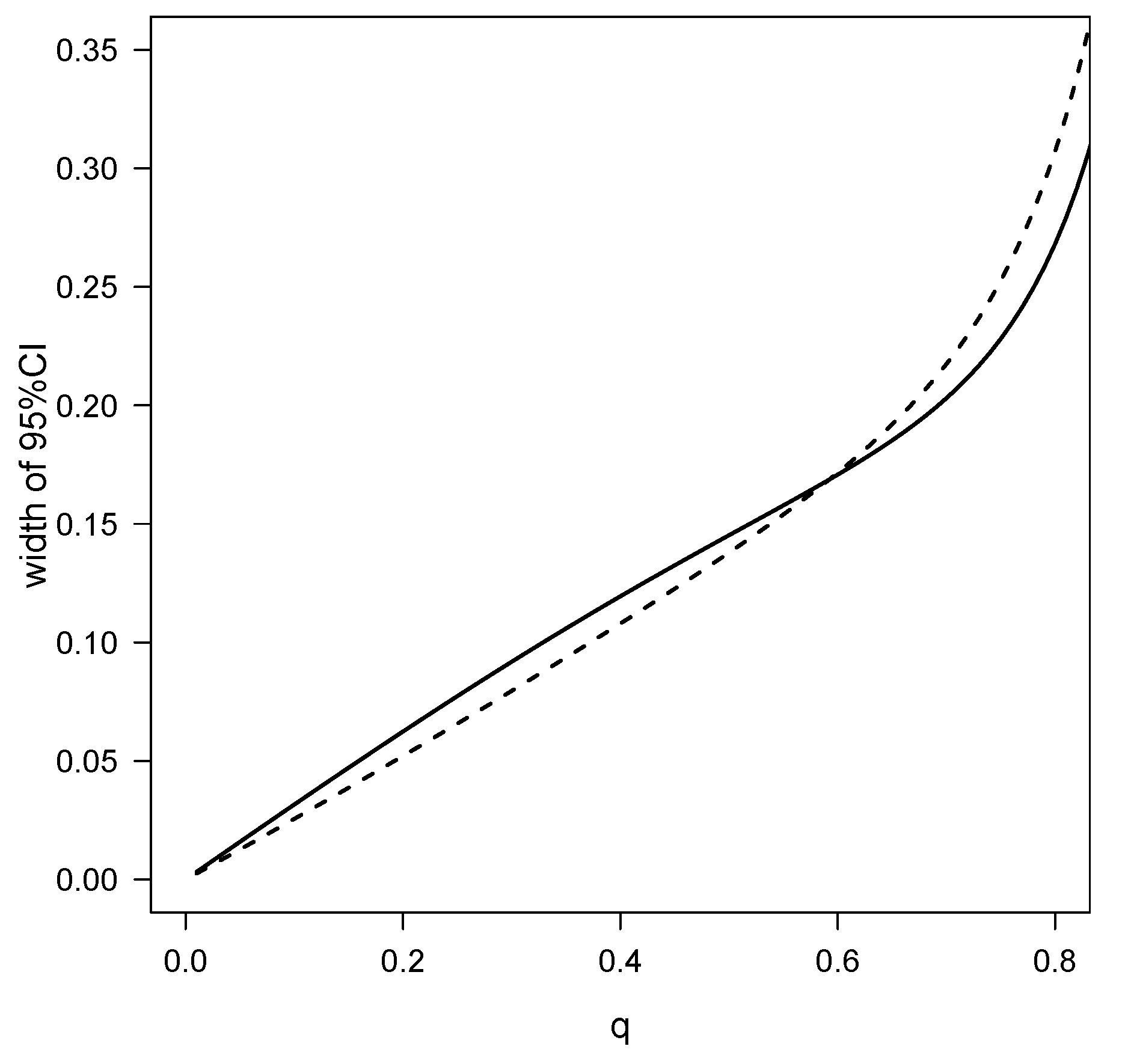
| 0.10 | (0.5313–0.5629) | 0.0316 | (0.5106–0.5361) | 0.0256 |
| 0.25 | (0.8845–0.9619) | 0.0773 | (0.8553–0.9210) | 0.0657 |
| 0.50 | (1.4225–1.5678) | 0.1452 | (1.3882–1.5261) | 0.1379 |
| 0.75 | (2.1286–2.3566) | 0.2281 | (2.1067–2.3593) | 0.2526 |
| 0.90 | (2.8078–3.2958) | 0.4880 | (2.8108–3.4102) | 0.5994 |
| 0.99 | (3.5118–5.7177) | 2.2059 | (3.3545–6.3541) | 2.9996 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magalhães, T.M.; Gómez, Y.M.; Gallardo, D.I.; Venegas, O. Bias Reduction for the Marshall-Olkin Extended Family of Distributions with Application to an Airplane’s Air Conditioning System and Precipitation Data. Symmetry 2020, 12, 851. https://doi.org/10.3390/sym12050851
Magalhães TM, Gómez YM, Gallardo DI, Venegas O. Bias Reduction for the Marshall-Olkin Extended Family of Distributions with Application to an Airplane’s Air Conditioning System and Precipitation Data. Symmetry. 2020; 12(5):851. https://doi.org/10.3390/sym12050851
Chicago/Turabian StyleMagalhães, Tiago M., Yolanda M. Gómez, Diego I. Gallardo, and Osvaldo Venegas. 2020. "Bias Reduction for the Marshall-Olkin Extended Family of Distributions with Application to an Airplane’s Air Conditioning System and Precipitation Data" Symmetry 12, no. 5: 851. https://doi.org/10.3390/sym12050851
APA StyleMagalhães, T. M., Gómez, Y. M., Gallardo, D. I., & Venegas, O. (2020). Bias Reduction for the Marshall-Olkin Extended Family of Distributions with Application to an Airplane’s Air Conditioning System and Precipitation Data. Symmetry, 12(5), 851. https://doi.org/10.3390/sym12050851








