EDSQ Operator on 2DS and Limit Behavior
Abstract
1. Introduction
2. Methods
- a.
- b.
3. Theoretical Result
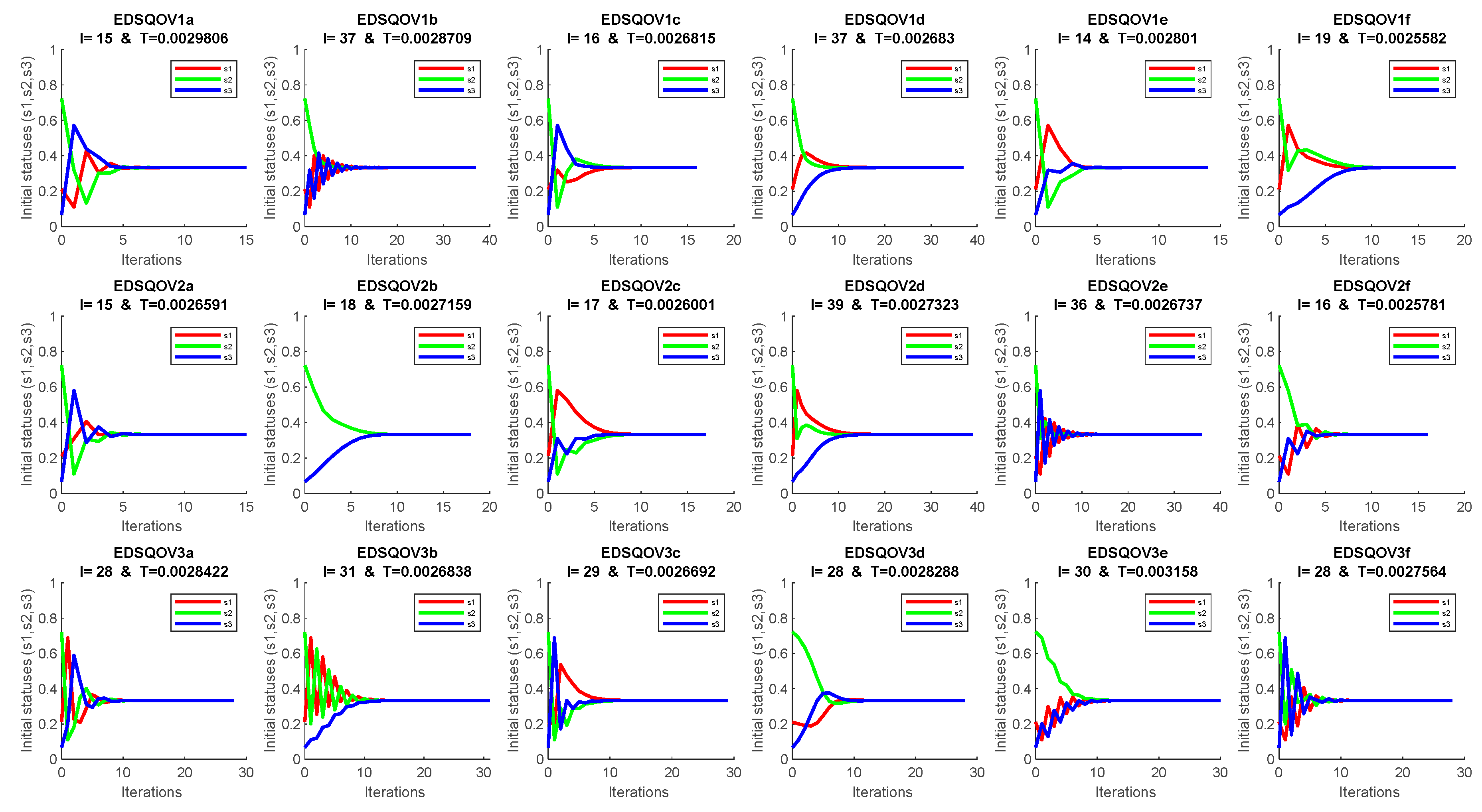
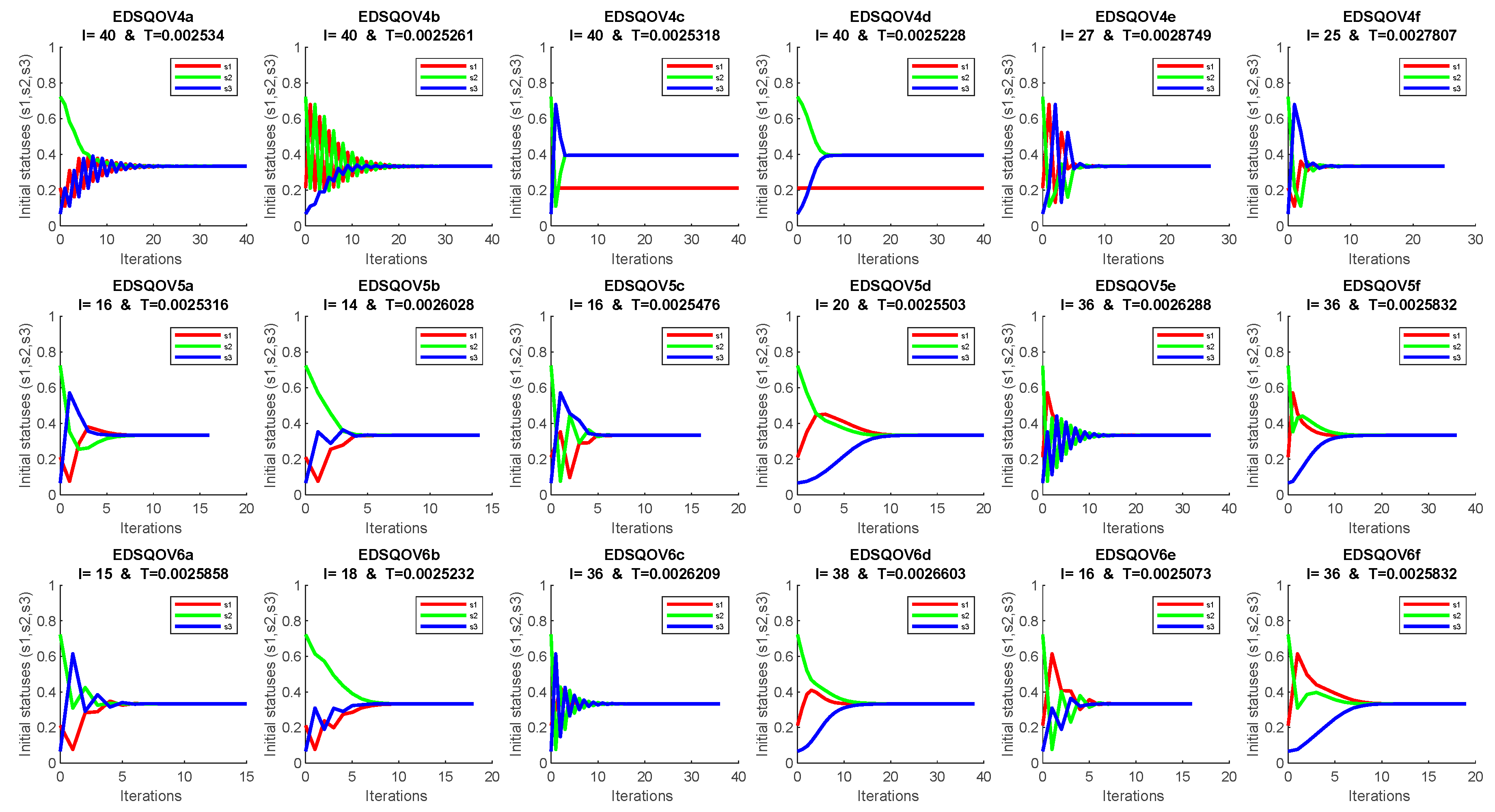
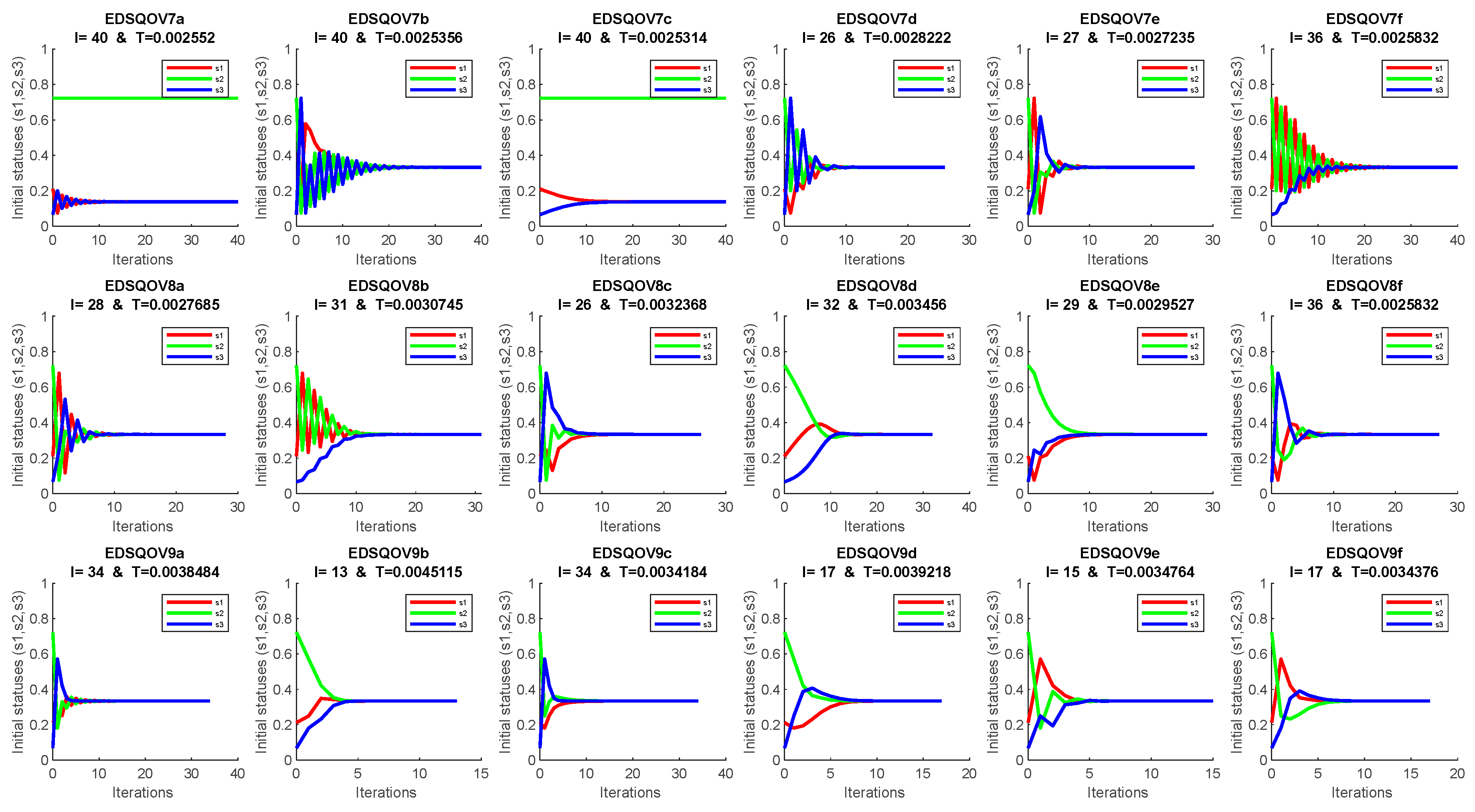
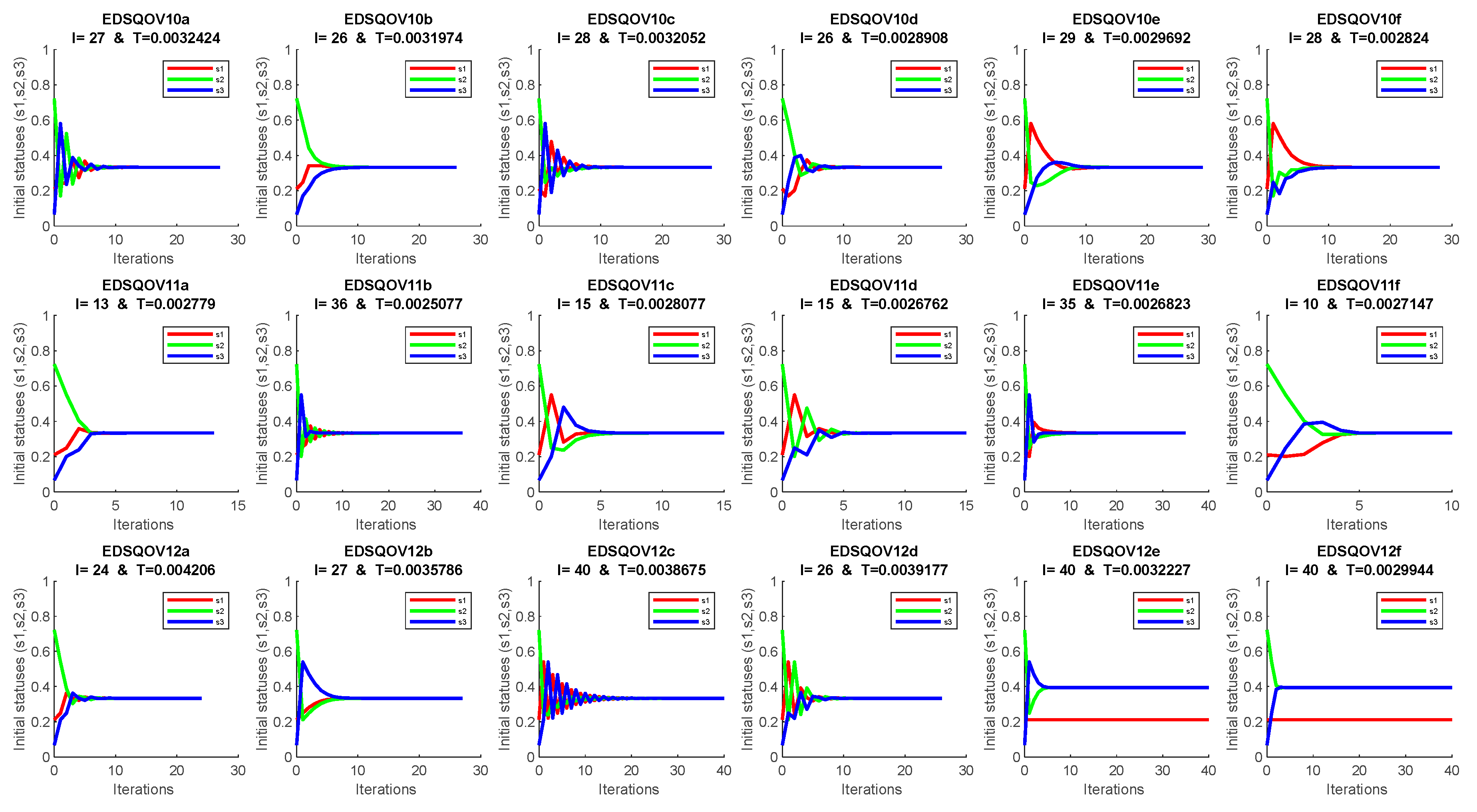
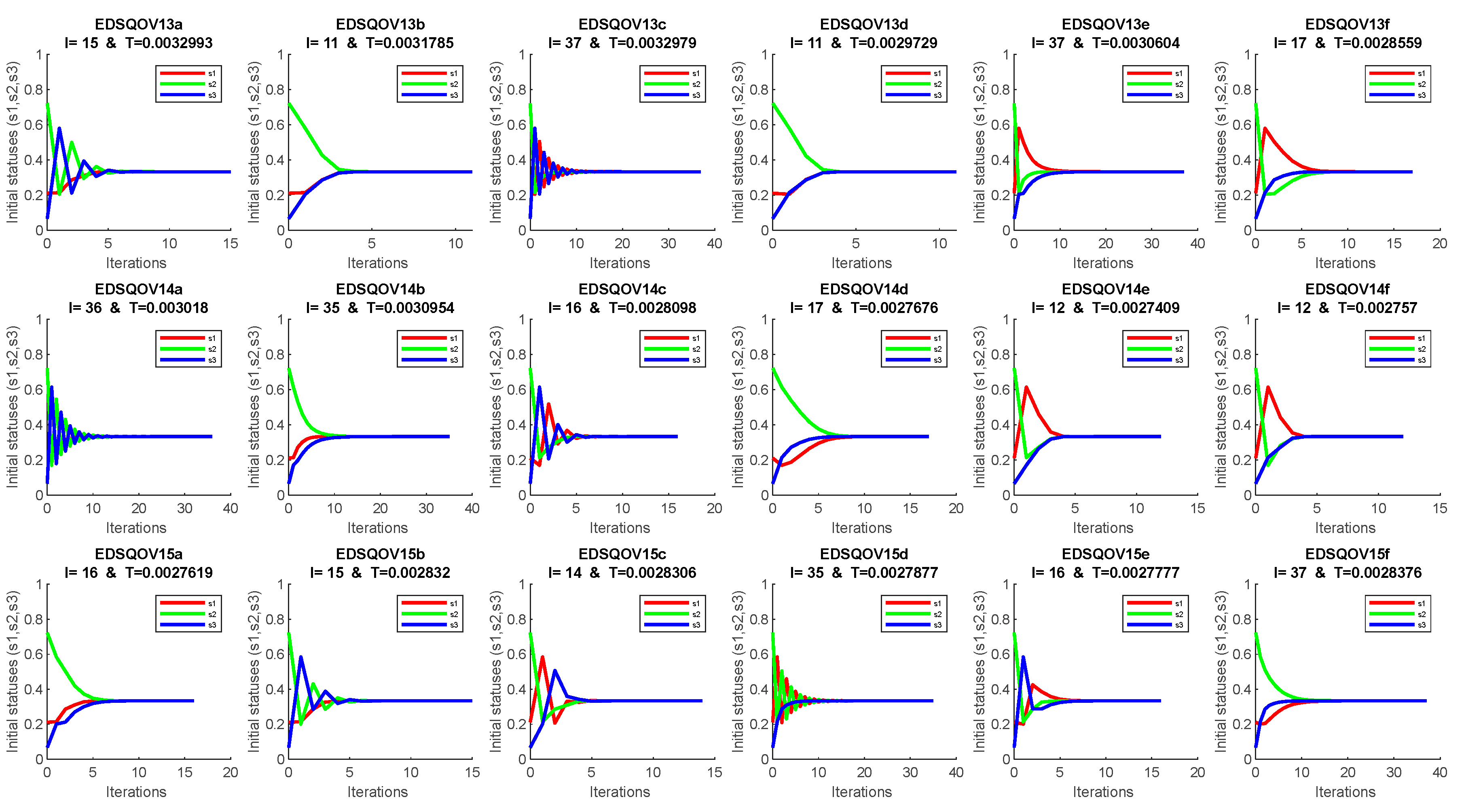
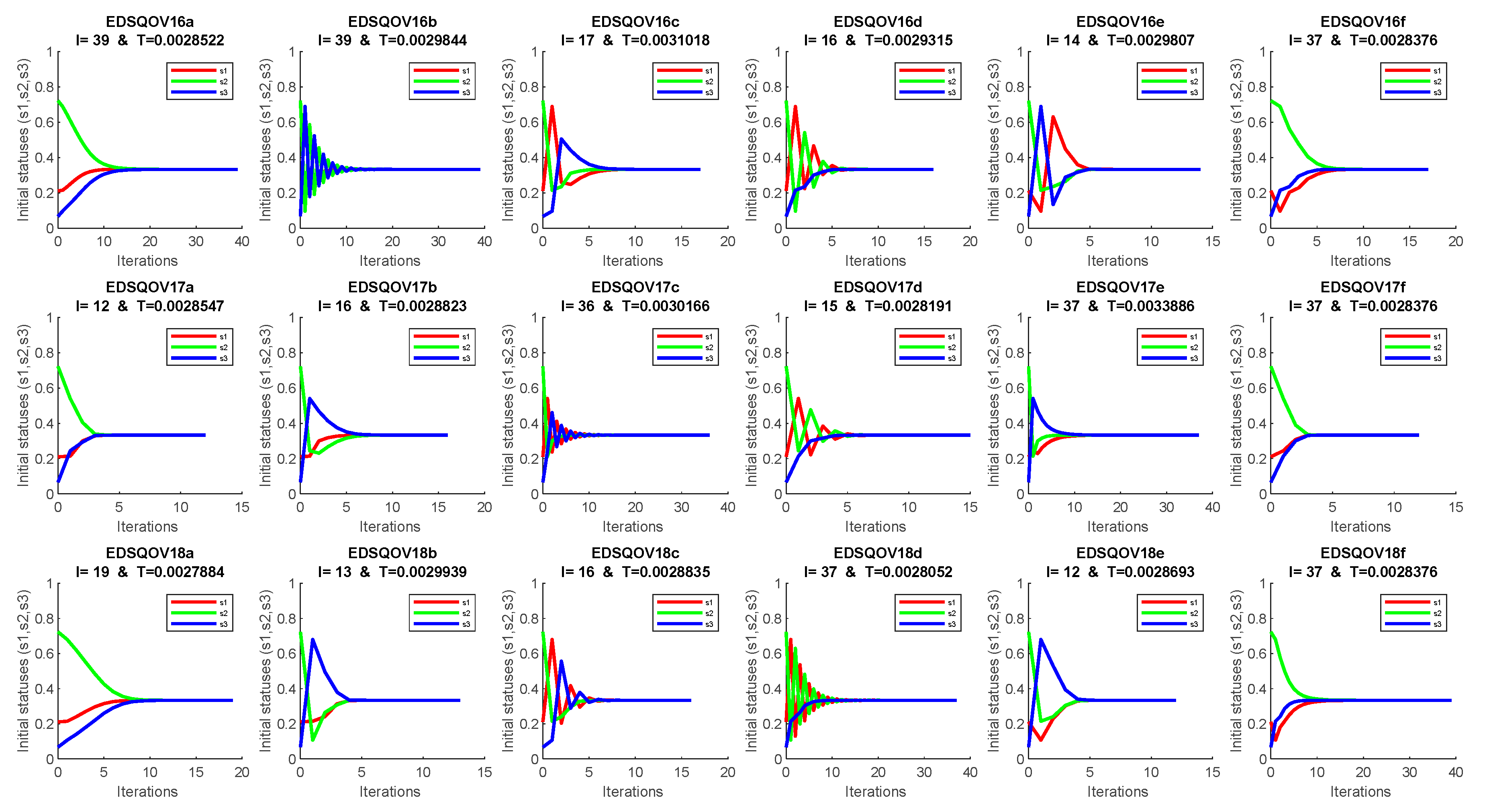
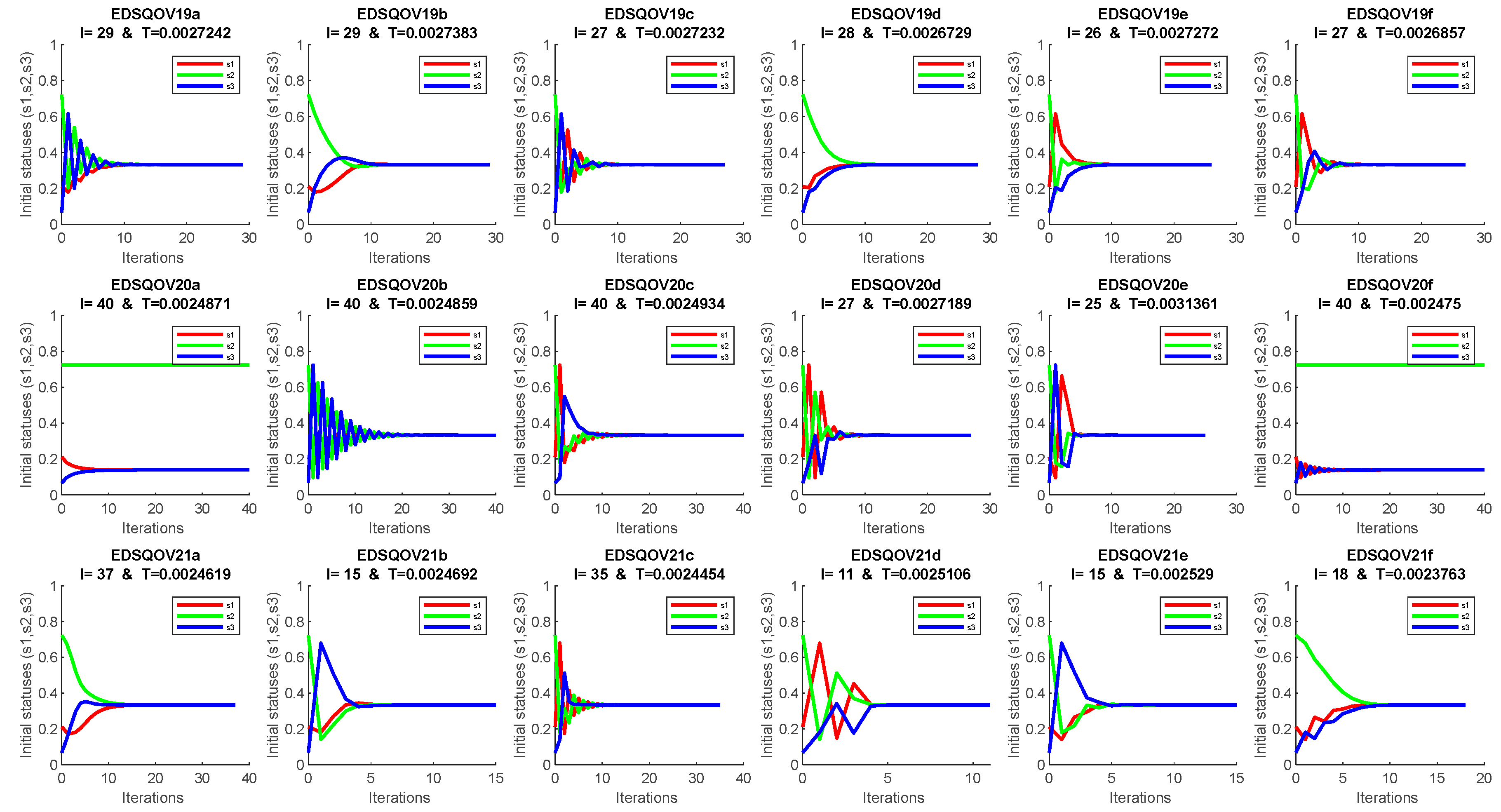
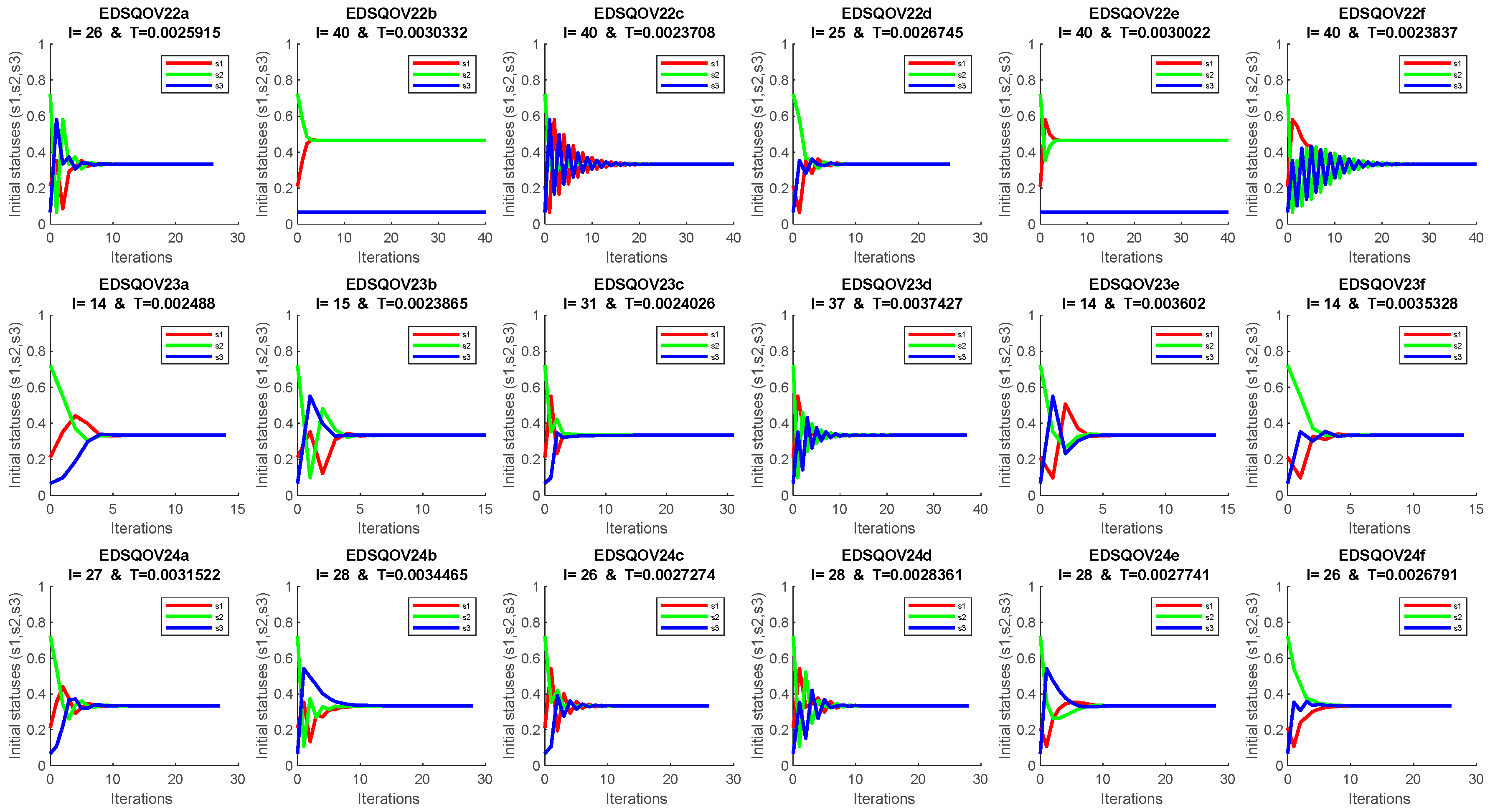
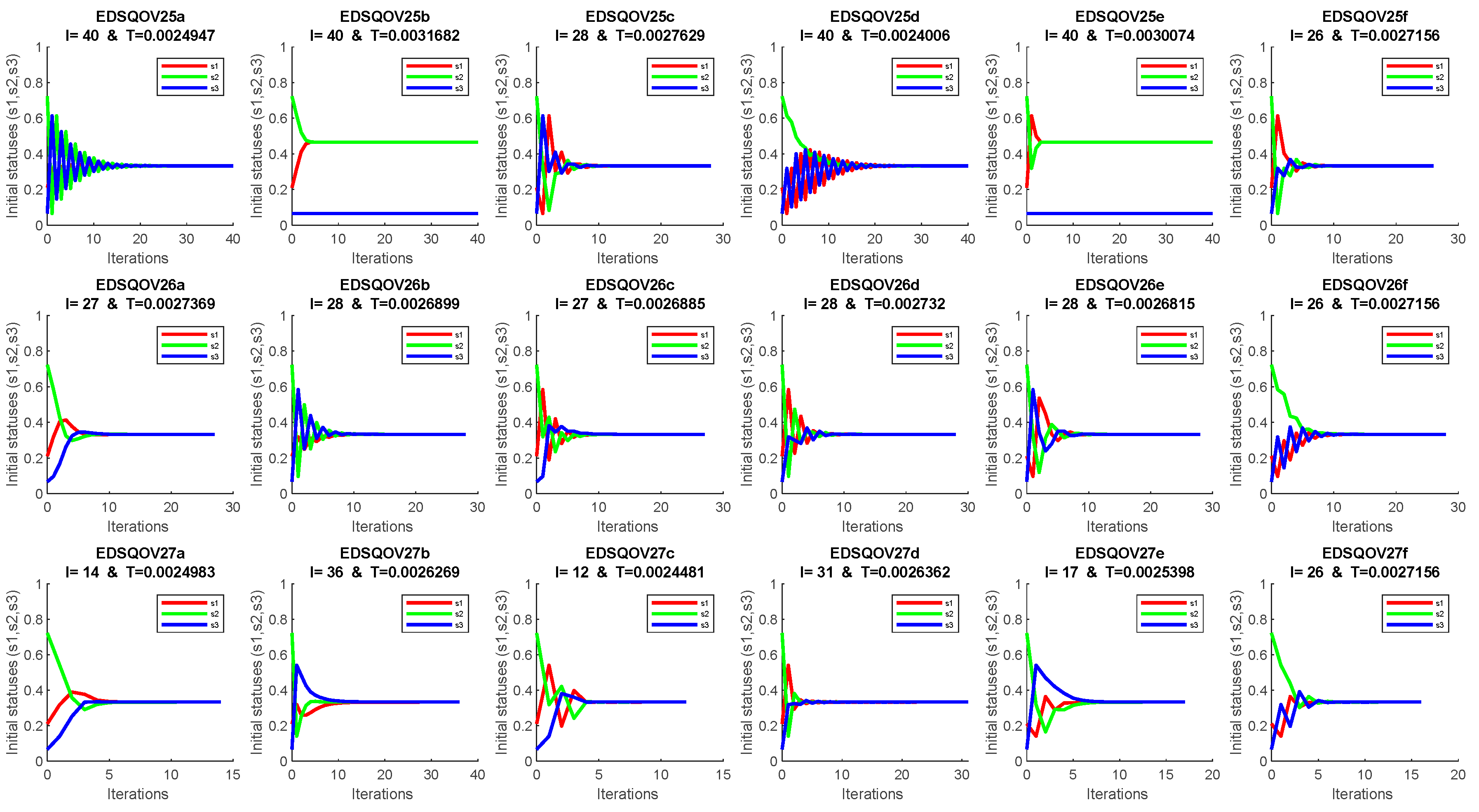
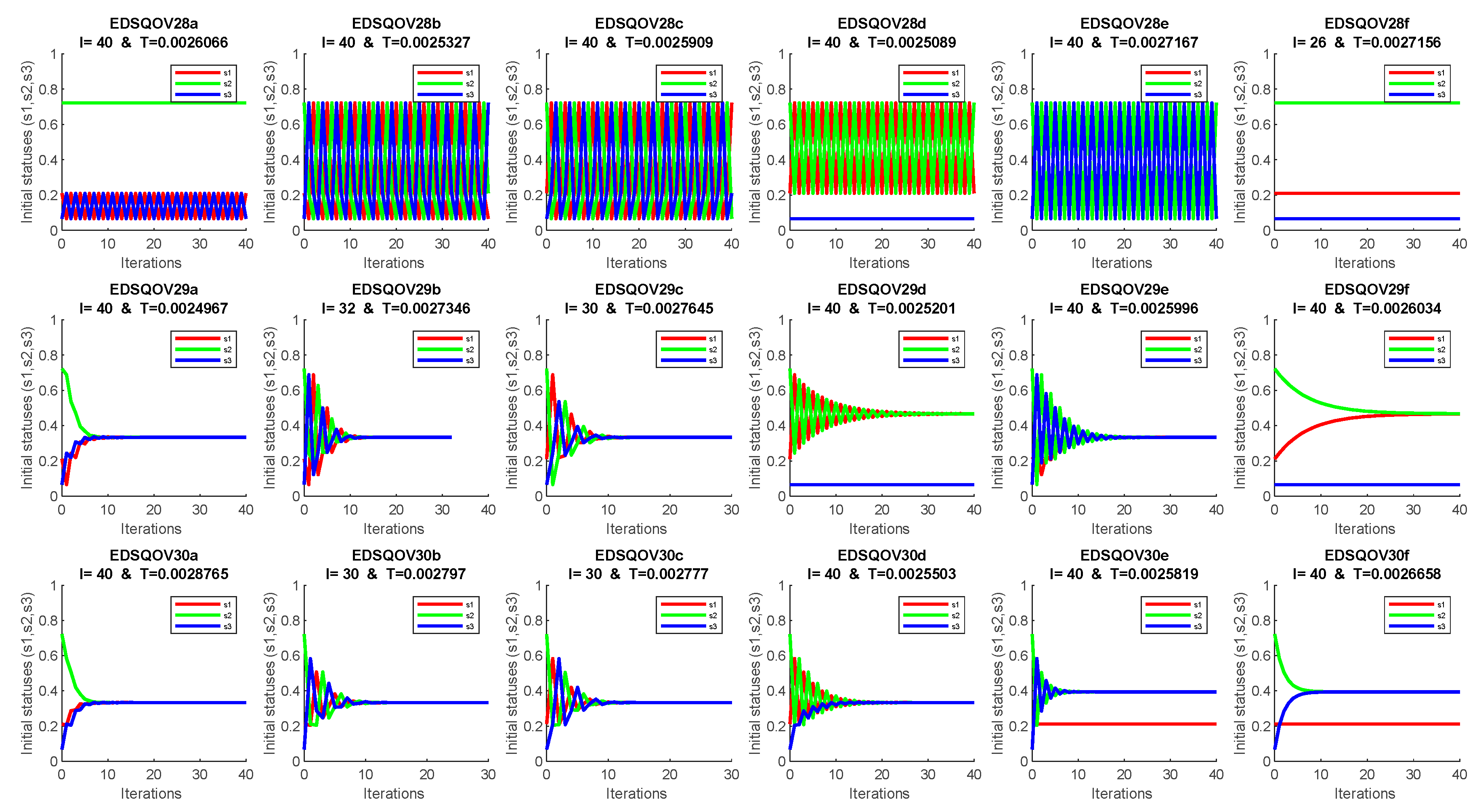
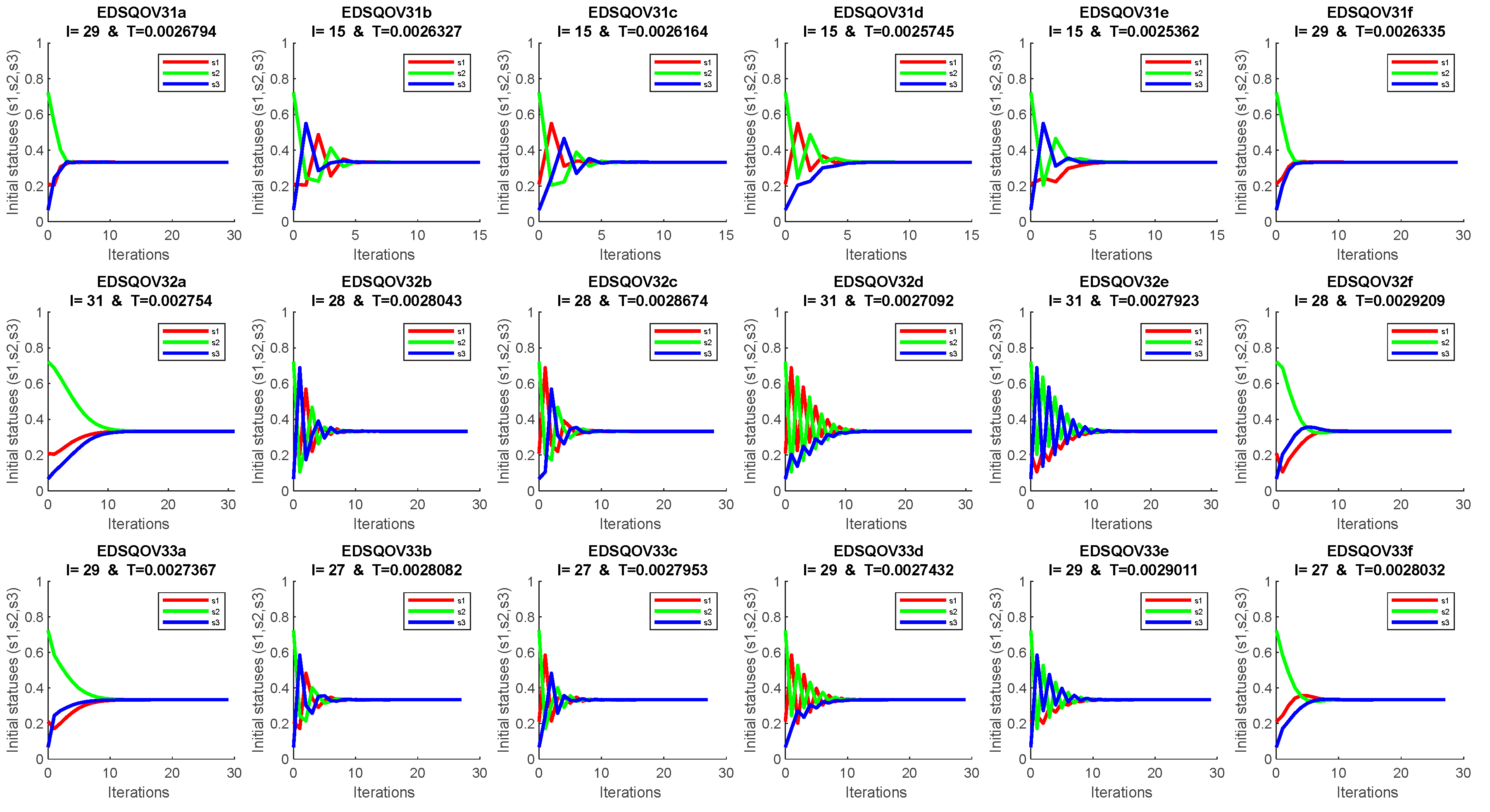
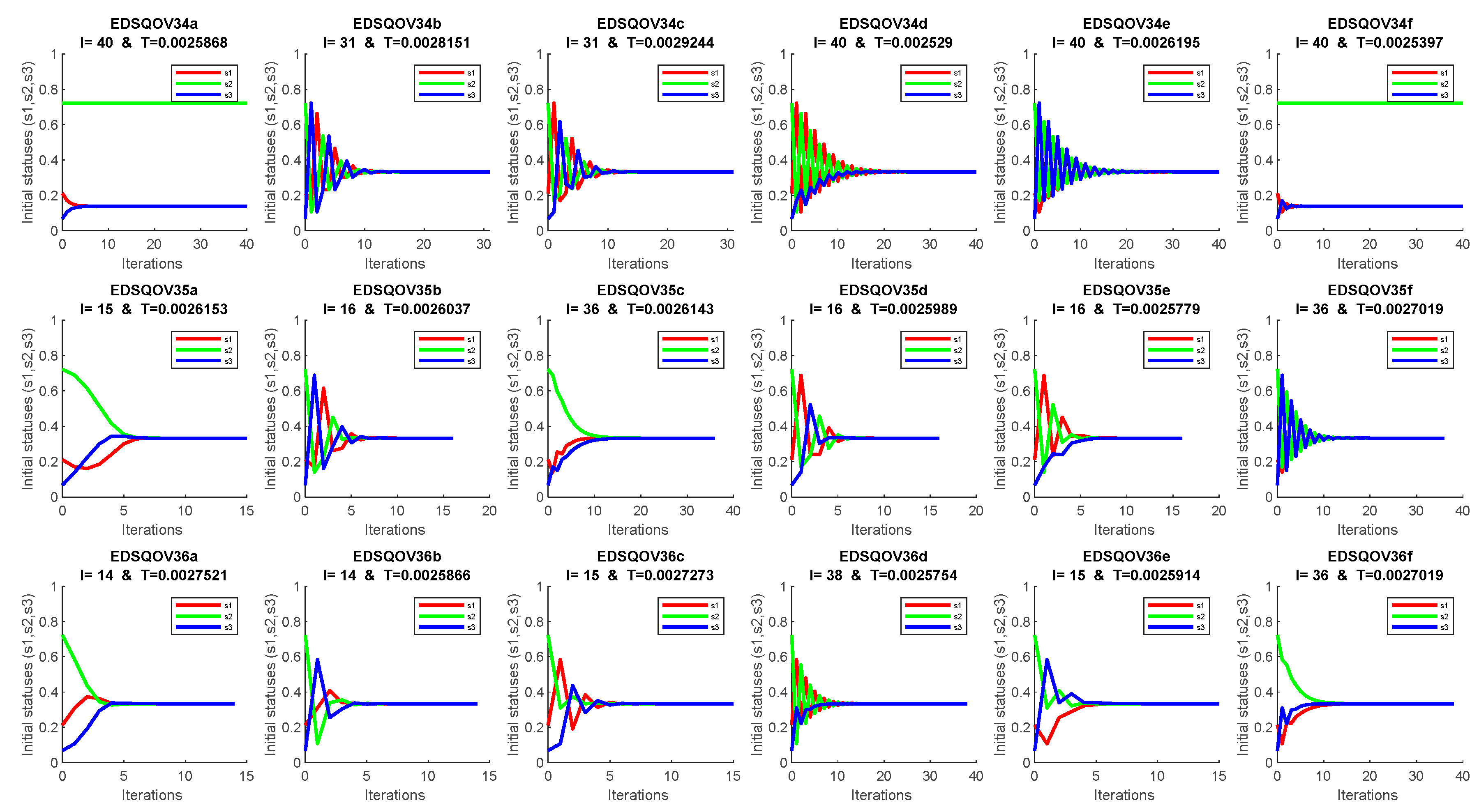
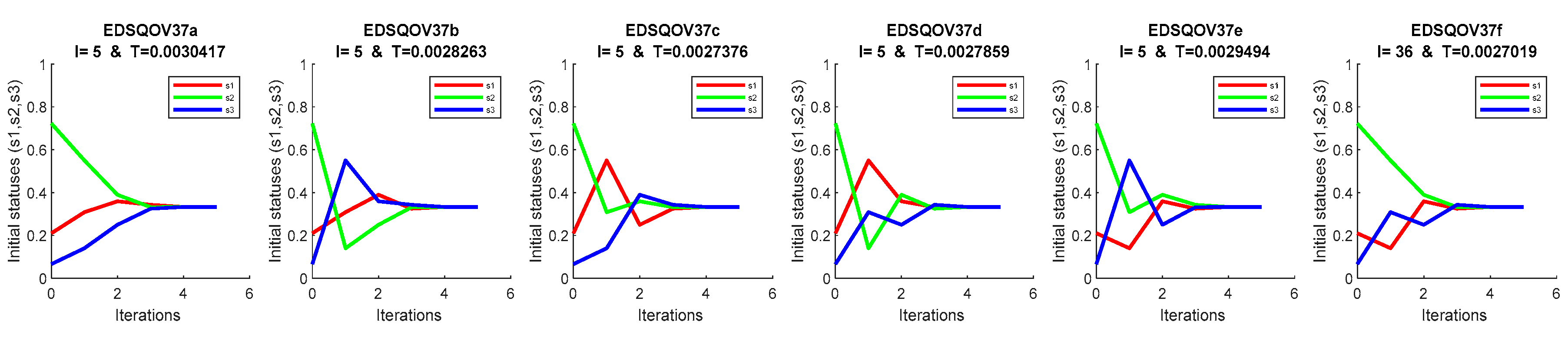
4. Discussion and Numerical Solution
5. Conclusion and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The EDSQOs on 2DS
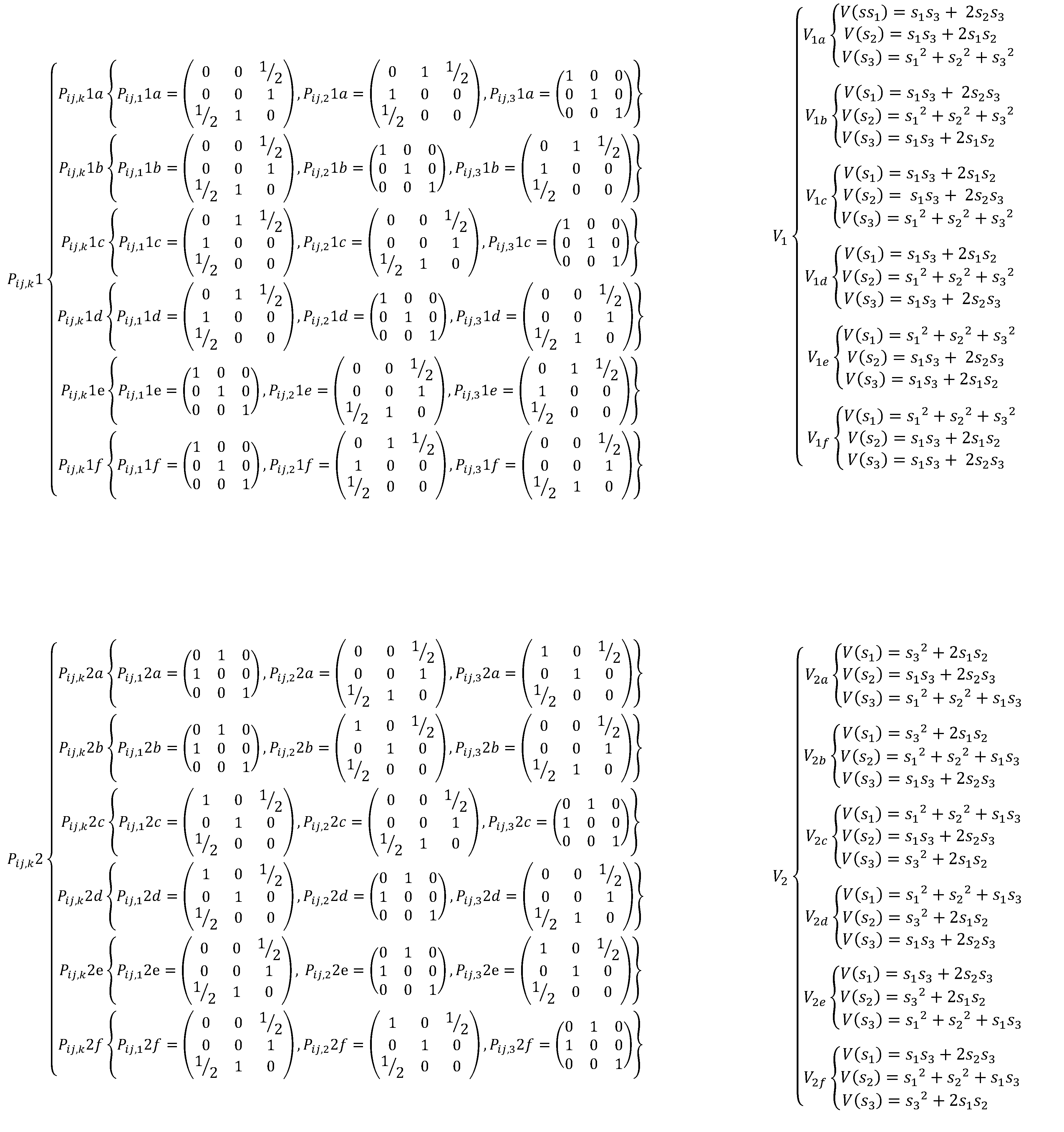
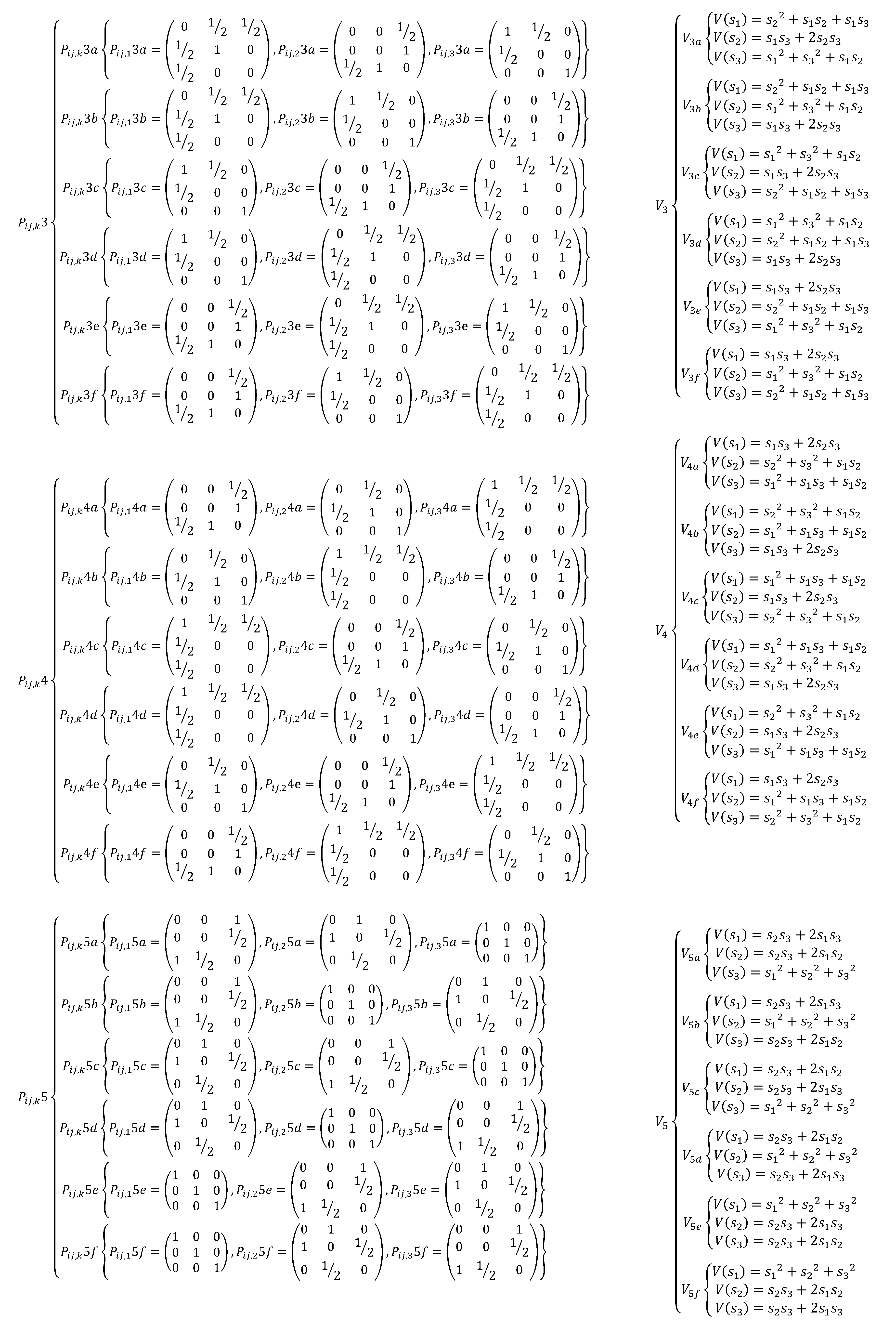

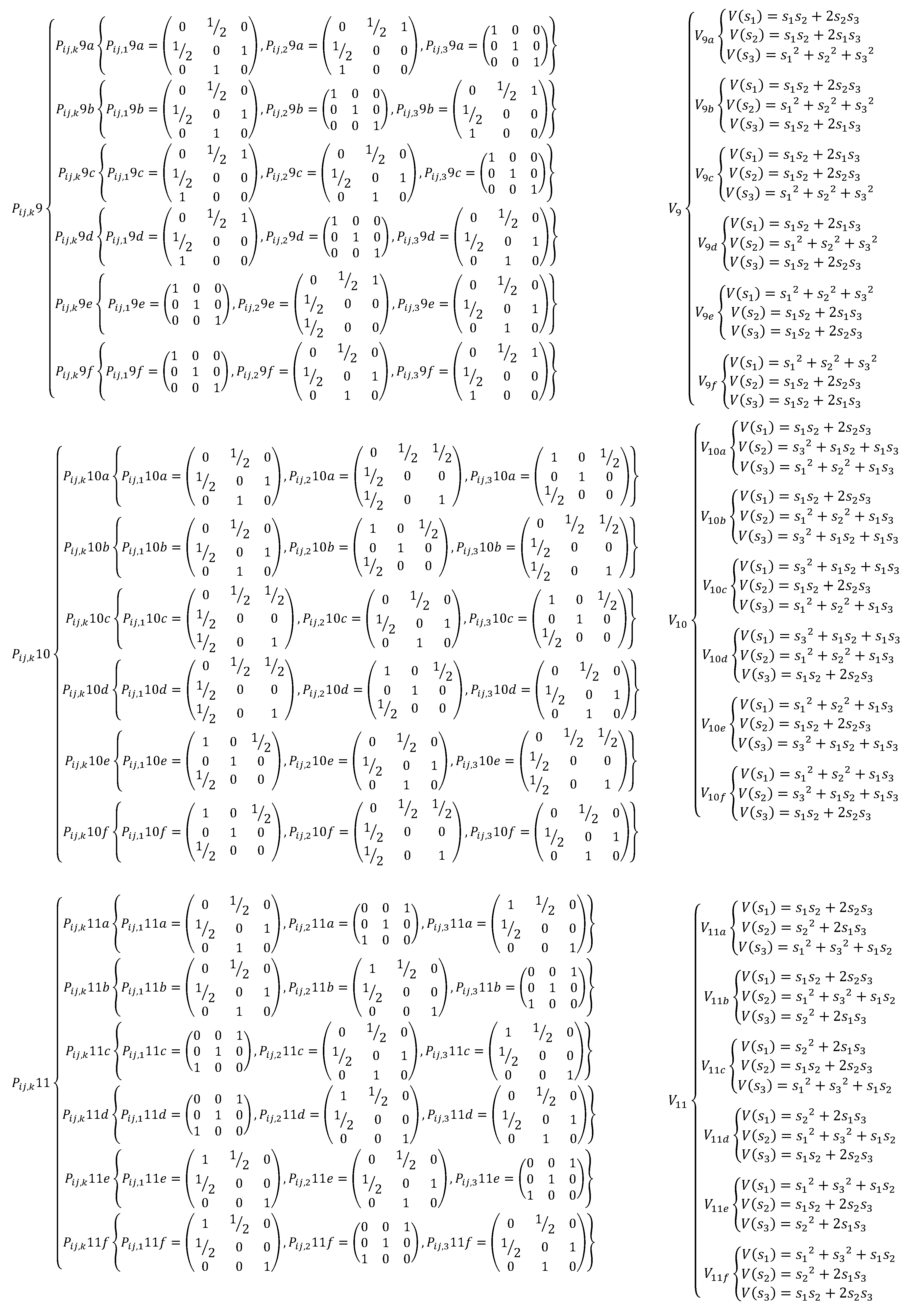



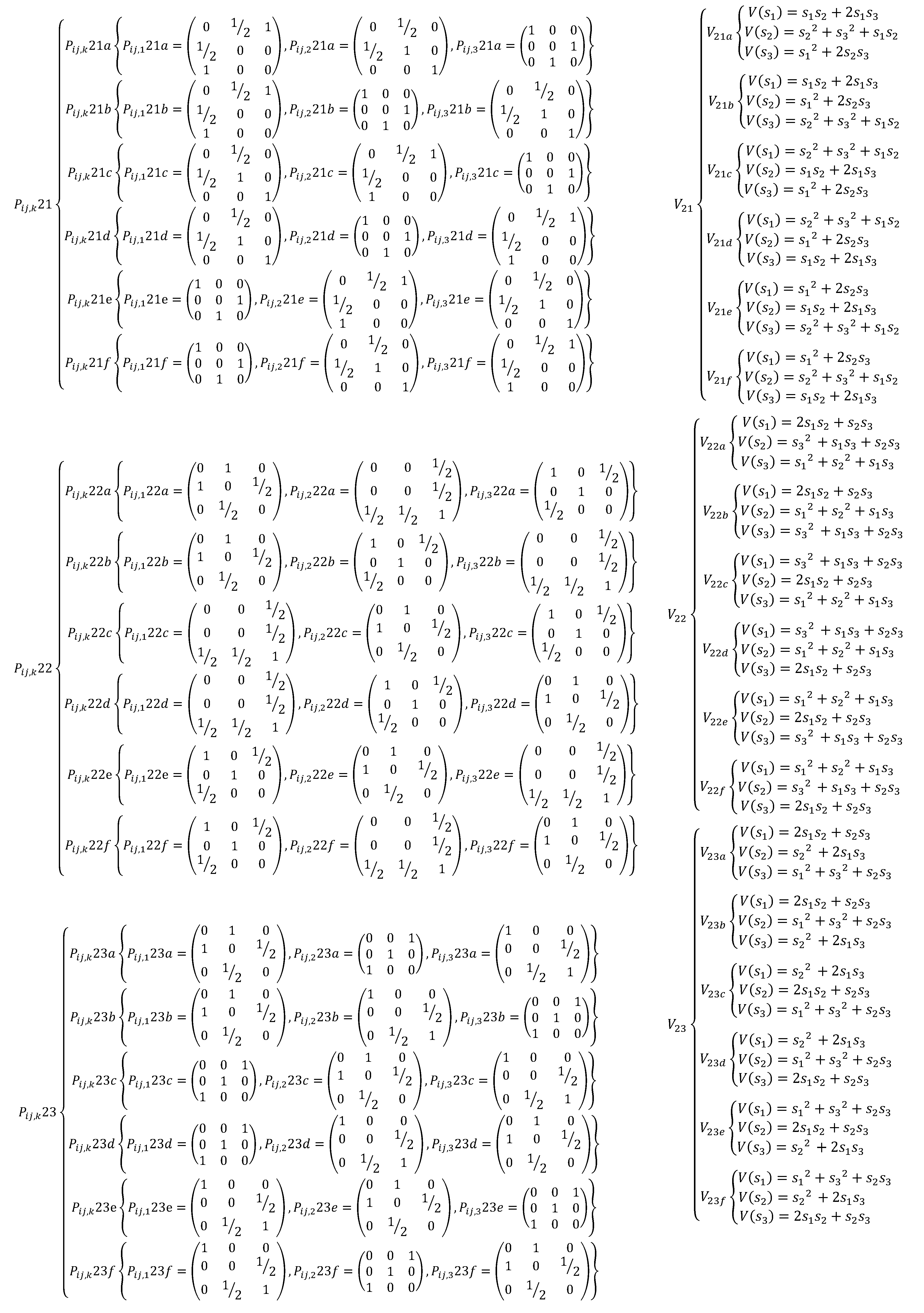
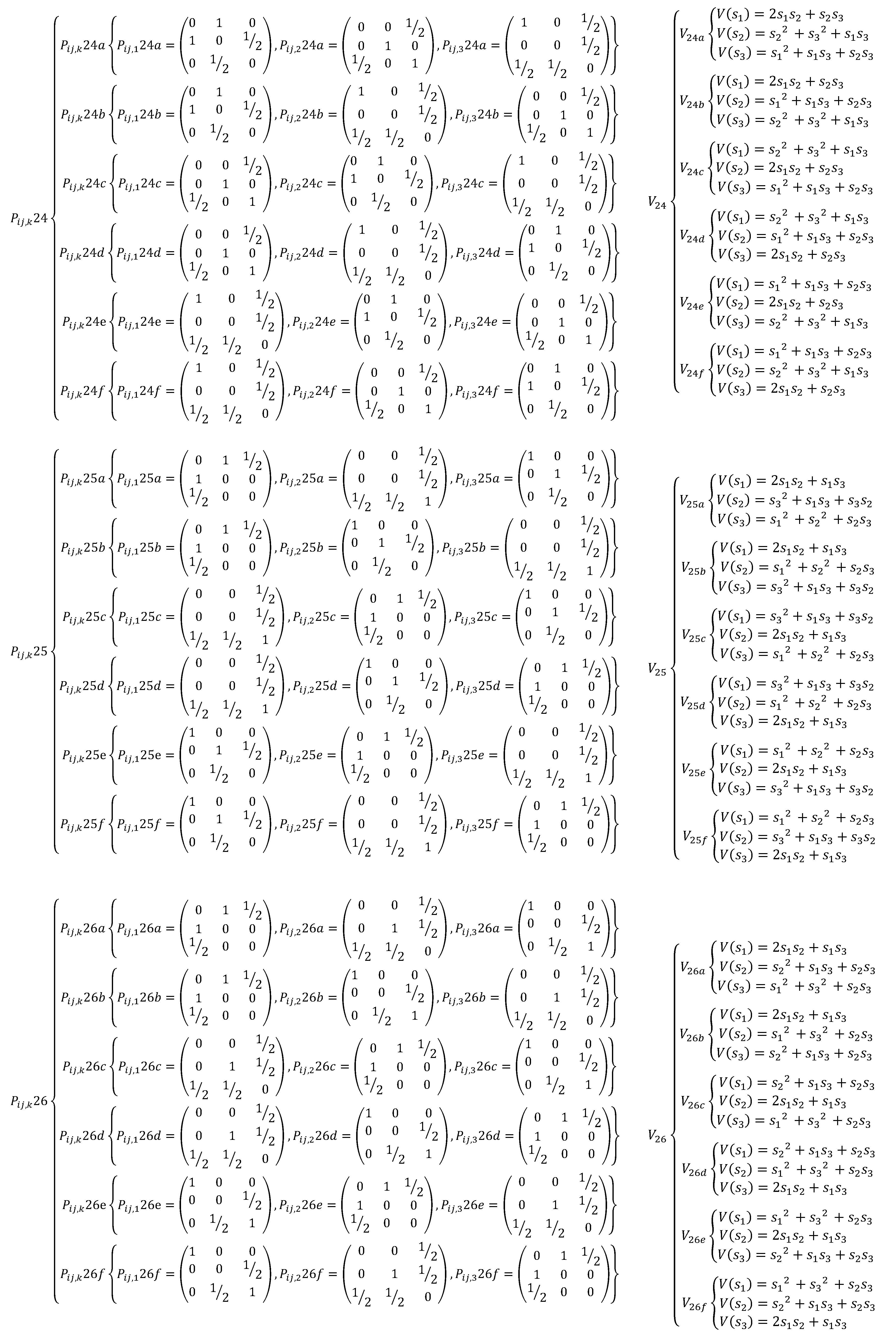
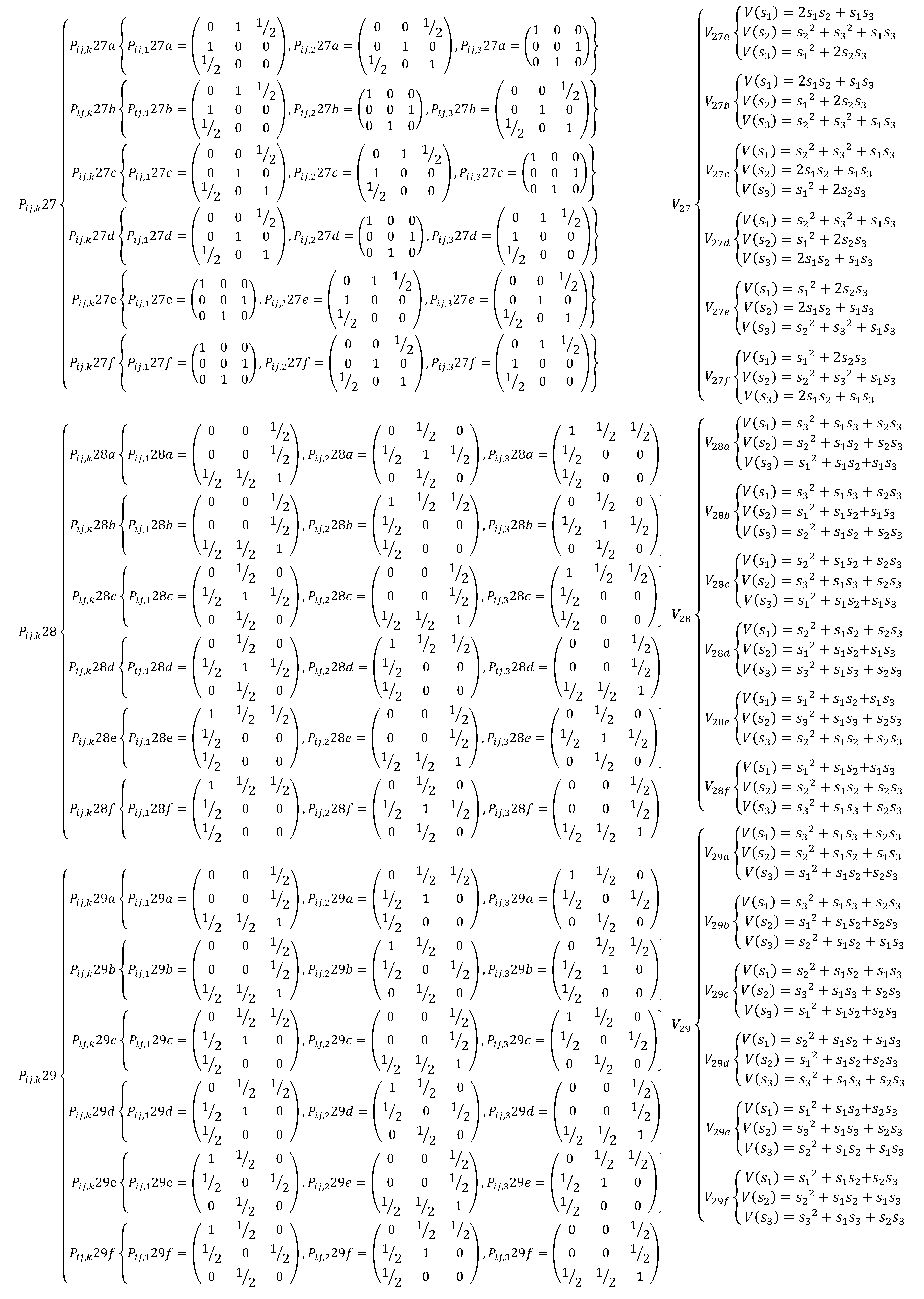
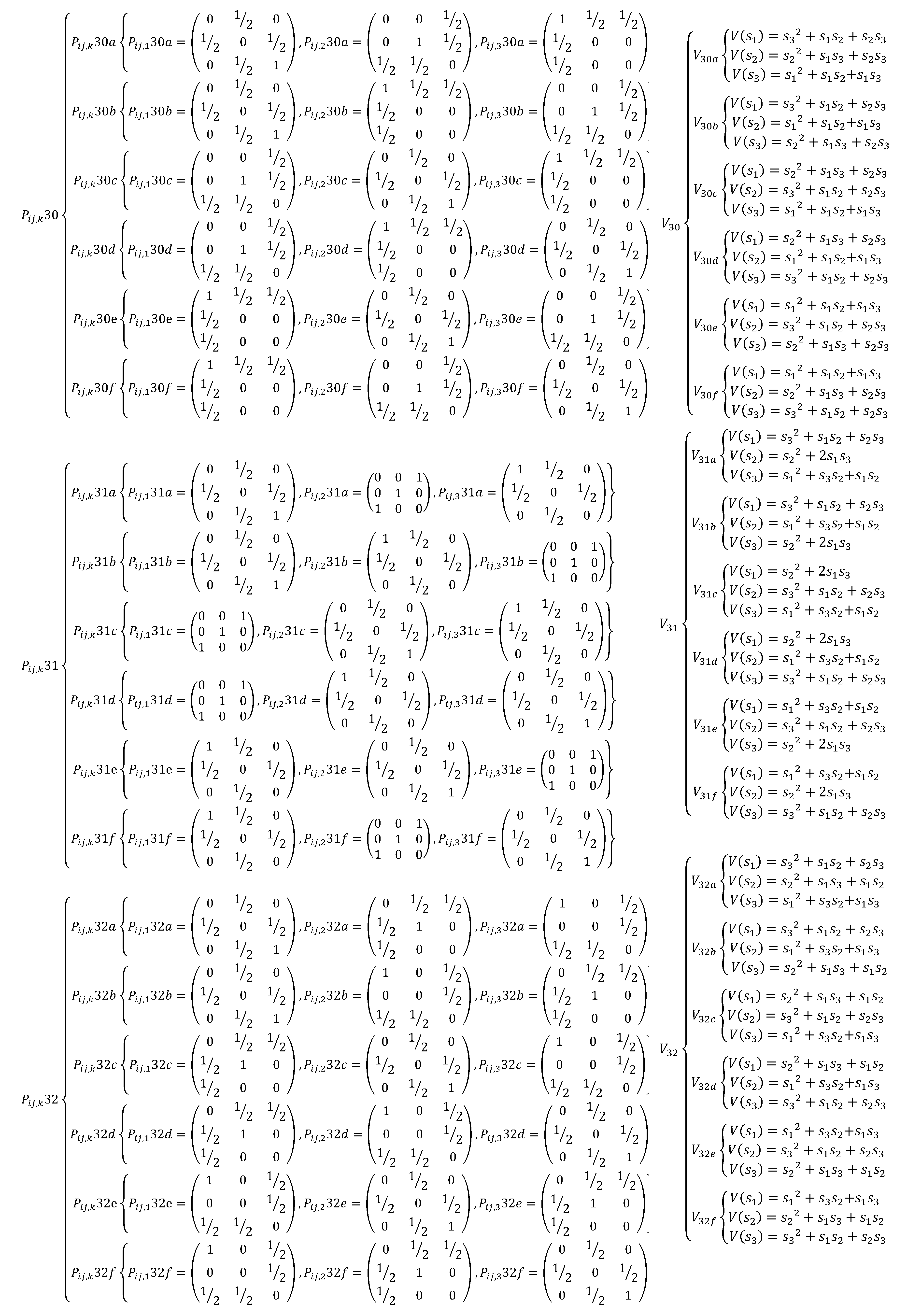

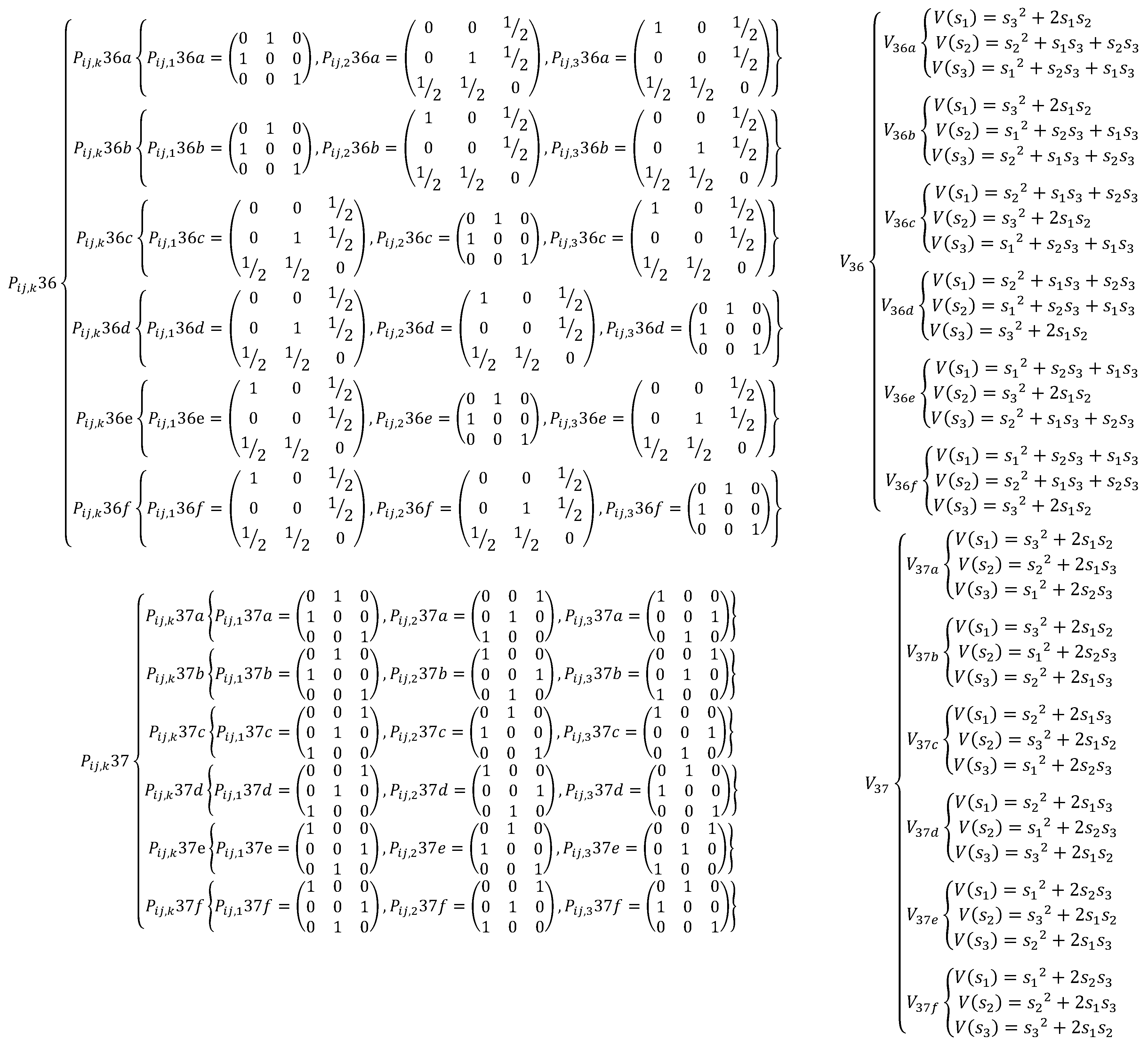
References
- Lyubich, Y.I.; Vulis, D.; Karpov, A.; Akin, E. Mathematical structures in population genetics. Biomathematics 1992, 22, 373. [Google Scholar]
- Abdulghafor, R.; Shahidi, F.; Zeki, A.; Turaev, S. Dynamics classifications of extreme doubly stochastic quadratic operators on 2d simplex. In Advanced Computer and Communication Engineering Technology; Springer: Berlin/Heidelberg, Germany, 2016; pp. 323–335. [Google Scholar]
- Abdulghafor, R.; Shahidi, F.; Zeki, A.; Turaev, S. Dynamics of doubly stochastic quadratic operators on a finite-dimensional simplex. Open Math. 2016, 14, 509–519. [Google Scholar] [CrossRef]
- Shahidi, F.; Ganikhodzhaev, R.; Abdulghafor, R. The dynamics of some extreme doubly stochastic quadratic operators. Middle East J. Sci. Res. 2013, 13, 59–63. [Google Scholar]
- Abdulghafor, R.; Turaev, S.; Abubakar, A.; Zeki, A. The extreme doubly stochastic quadratic operators on two dimensional simplex. In Proceedings of the 2015 4th International Conference on Advanced Computer Science Applications and Technologies (ACSAT), Kuala Lumpur, Malaysia, 8–10 December 2015; pp. 192–197. [Google Scholar]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Hassan, R. The nonlinear limit control of EDSQOs on finite dimensional simplex. Automatika 2019, 60, 404–412. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A. Necessary and Sufficient Conditions for Complementary Stochastic Quadratic Operators of Finite-Dimensional Simplex. Sukkur IBA J. Comput. Math. Sci. 2017, 1, 22–27. [Google Scholar] [CrossRef]
- Ganikhodzhaev, R.N. On the definition of bistochastic quadratic operators. Russ. Math. Surv. 1993, 48, 244–246. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Shahidi, F. The convergence consensus of multi-agent systems controlled via doubly stochastic quadratic operators. In Proceedings of the 2015 International symposium on agents, multi-agent systems and robotics (ISAMSR), Putrajaya, Malaysia, 18–19 August 2015; pp. 59–64. [Google Scholar]
- Abdulghafor, R.; Turaev, S.; Tamrin, I. Nonlinear consensus for multi-agent systems using positive intractions of doubly stochastic quadratic operators. Int. J. Perceptive Cogn. Comput. 2016, 2, 19–22. [Google Scholar] [CrossRef]
- Bernstein, S. Solution of a mathematical problem connected with the theory of heredity. Ann. Math. Stat. 1942, 13, 53–61. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Almotairi, S.; Almohamedh, H.; Turaev, S.; Almutairi, B. Nonlinear Consensus Protocol Modified from Doubly Stochastic Quadratic Operators in Networks of Dynamic Agents. Symmetry 2019, 11, 1519. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Zeki, A.; Al-Shaikhli, I. Linear and nonlinear stochastic distribution for consensus problem in multi-agent systems. Neural Comput. Appl. 2018, 32, 261–277. [Google Scholar]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Othman, M. An overview of the consensus problem in the control of multi-agent systems. Automatika 2018, 59, 143–157. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Almotairi, S.; Almohamedh, H.; Almutairi, B.; Bajahzar, A.; Almutairi, S.S. A Nonlinear Convergence Consensus: Extreme Doubly Stochastic Quadratic Operators for Multi-Agent Systems. Symmetry 2020, 12, 1519. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S. Consensus of fractional nonlinear dynamics stochastic operators for multi-agent systems. Inf. Fusion 2018, 44, 1–21. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Izzuddin, M. Nonlinear Models for Distributed Consensus Modified from DSQO in Networks of Dynamic Agents. In Proceedings of the 4th International Conference on Mathematical Sciences, Putrajaya, Malaysia, 15–17 November 2016. [Google Scholar]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Al-Shaikhli, I. Reach a nonlinear consensus for MAS via doubly stochastic quadratic operators. Int. J. Control 2018, 91, 1431–1459. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Abubaker, A. Nonlinear convergence algorithm: Structural properties with doubly stochastic quadratic operators for multi-agent systems. J. Artif. Intell. Soft Comput. Res. 2018, 8, 49–61. [Google Scholar] [CrossRef]
- Ganikhodzhaev, R.N. Quadratic stochastic operators, Lyapunov functions, and tournaments. Russ. Acad. Sci. Sb. Math. 1993, 76, 489. [Google Scholar] [CrossRef]
- Ganikhodzhaev, R.; Shahidi, F. Doubly stochastic quadratic operators and Birkhoff’s problem. Linear Algebra Appl. 2010, 432, 24–35. [Google Scholar] [CrossRef][Green Version]
- Shahidi, F.A.; Osman, M.T.A. The Limit behavior of the trajectories of dissipative quadratic stochastic operators on finite-dimensional simplex. J. Differ. Equations Appl. 2013, 19, 357–371. [Google Scholar] [CrossRef]
- Shahidi, F. On dissipative quadratic stochastic operators. Appl. Math. Inf. Sci. 2008, 2, 211–223. [Google Scholar]
- Shahidi, F. Necessary and sufficient conditions for doubly stochasticity of infinite-dimensional quadratic operators. Linear Algebra Appl. 2013, 438, 96–110. [Google Scholar] [CrossRef]
- Mirsky, L. Even doubly-stochastic matrices. Math. Ann. 1961, 144, 418–421. [Google Scholar] [CrossRef]
- Mirsky, L. Results and Problems in the Theory of Doubly-Stochastic Matrices. Group 1963, 334, 319–334. [Google Scholar] [CrossRef]
- Ryff, J.V. On the representation of doubly stochastic operators. Pacific J. Math 1963, 13, 1379–1389. [Google Scholar] [CrossRef]
- Ryff, J.V. Orbits of L1 Functions under Doubly Stochastic Transformations. Trans. Am. Math. Soc. JSTOR 1965, 117, 92–100. [Google Scholar]
- Wang, Z.; Duan, Z.; Cao, J. Impulsive synchronization of coupled dynamical networks with nonidentical Duffing oscillators and coupling delays. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 13140. [Google Scholar] [CrossRef]
- Olkin, I.; Marshall, A.W. Inequalities: Theory of Majorization and Its Applications; Academic Press: Cambridge, MA, USA, 2016; Volume 143. [Google Scholar]
- Ganikhodzhaev, R.N.; Rozikov, U.A. Quadratic stochastic operators: Results and open problems. arXiv 2009, arXiv:0902.4207. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulghafor, R.; Almohamedh, H.; Almutairi, B.; Wani, S.; Alharbi, A.; Almutairi, S.S.; Almotairi, S. EDSQ Operator on 2DS and Limit Behavior. Symmetry 2020, 12, 820. https://doi.org/10.3390/sym12050820
Abdulghafor R, Almohamedh H, Almutairi B, Wani S, Alharbi A, Almutairi SS, Almotairi S. EDSQ Operator on 2DS and Limit Behavior. Symmetry. 2020; 12(5):820. https://doi.org/10.3390/sym12050820
Chicago/Turabian StyleAbdulghafor, Rawad, Hamad Almohamedh, Badr Almutairi, Sharyar Wani, Abdullah Alharbi, Sulaiman Sulmi Almutairi, and Sultan Almotairi. 2020. "EDSQ Operator on 2DS and Limit Behavior" Symmetry 12, no. 5: 820. https://doi.org/10.3390/sym12050820
APA StyleAbdulghafor, R., Almohamedh, H., Almutairi, B., Wani, S., Alharbi, A., Almutairi, S. S., & Almotairi, S. (2020). EDSQ Operator on 2DS and Limit Behavior. Symmetry, 12(5), 820. https://doi.org/10.3390/sym12050820




