Thermoelectric Relations in the Conformal Limit in Dirac and Weyl Semimetals
Abstract
1. Introduction
2. Thermoelectric Relations
3. Thermoelectric Coefficient in the Conformal Invariant Point in Dirac Semimetals
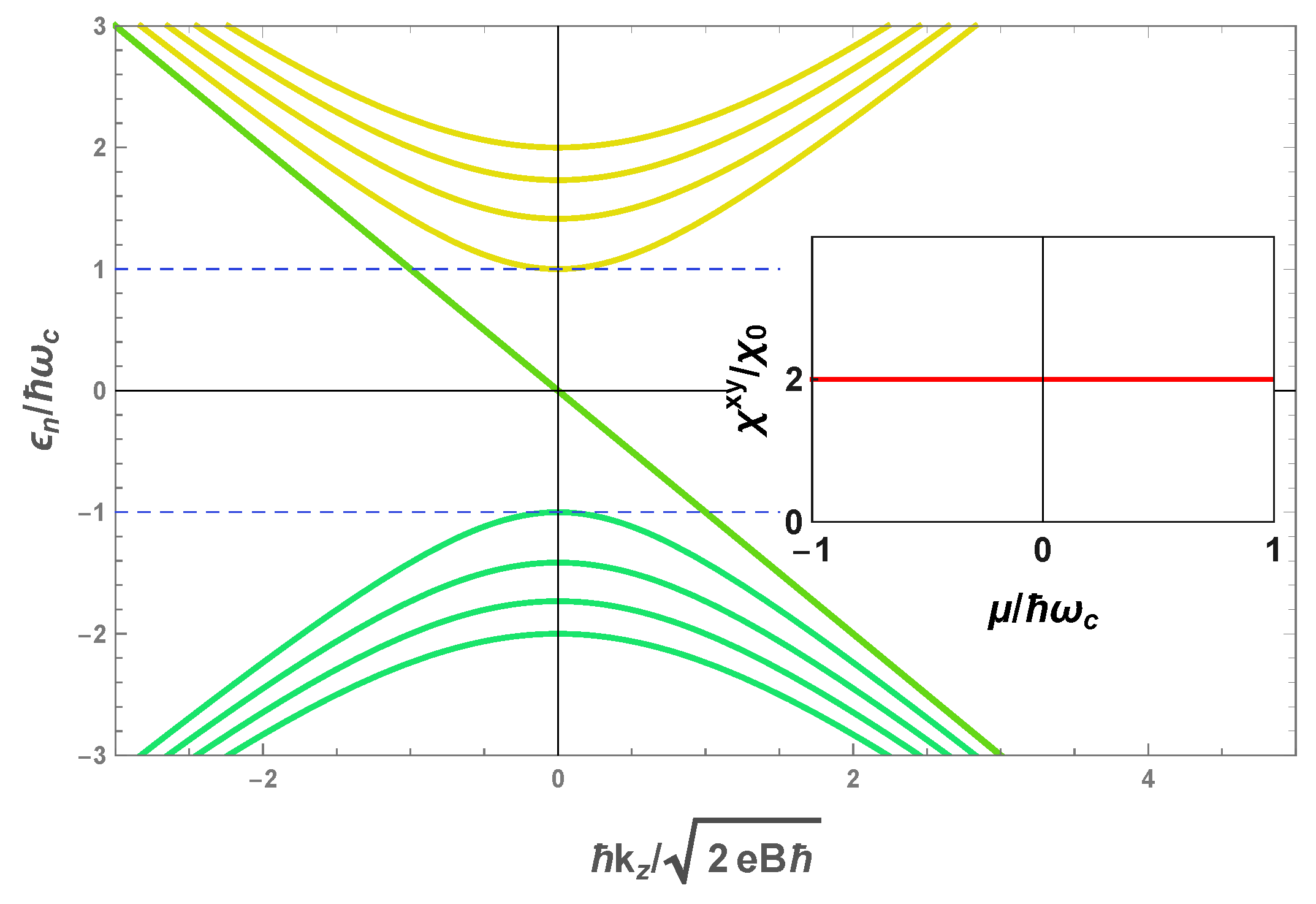
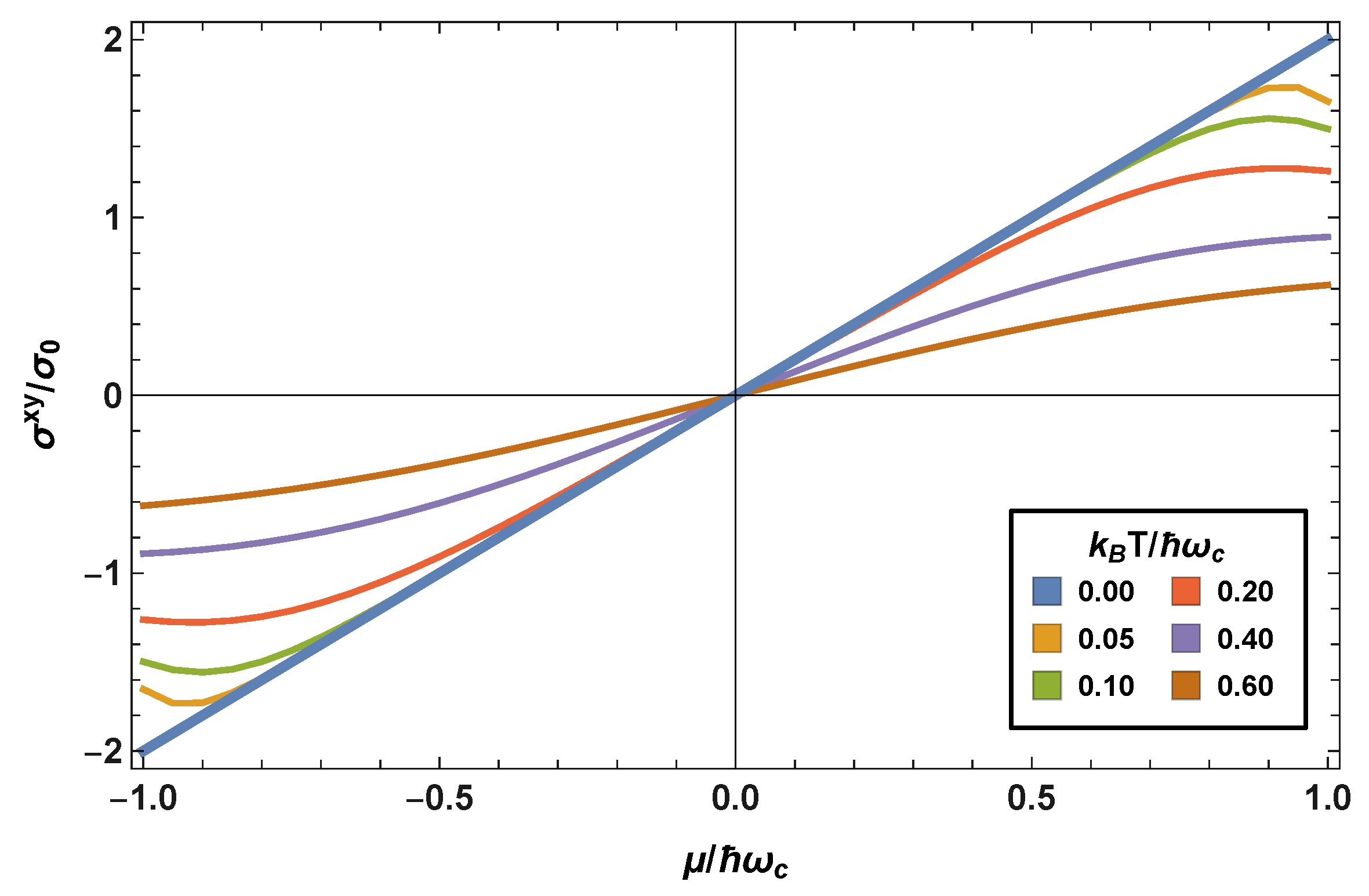
4. The Hall Conductivity
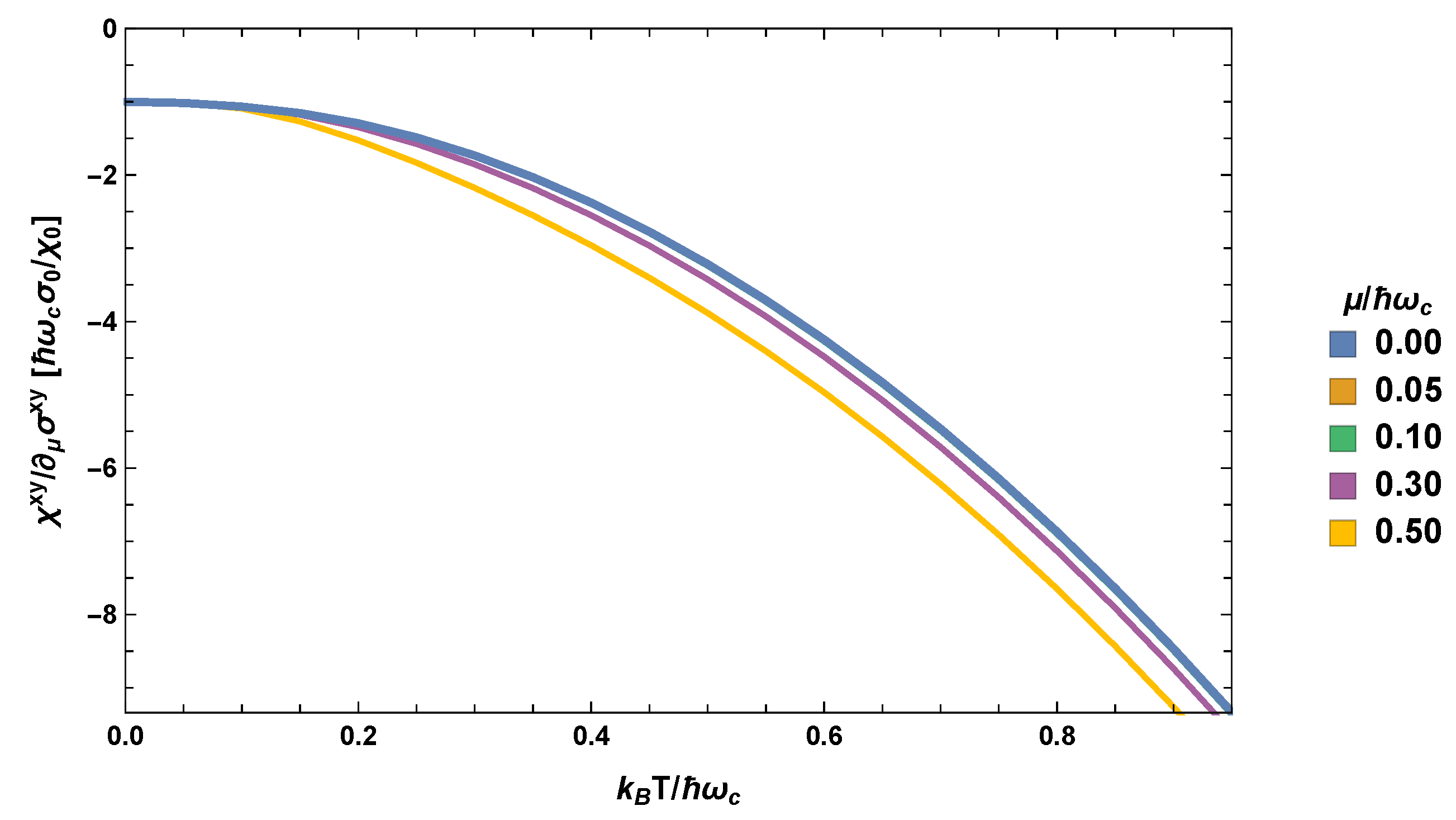
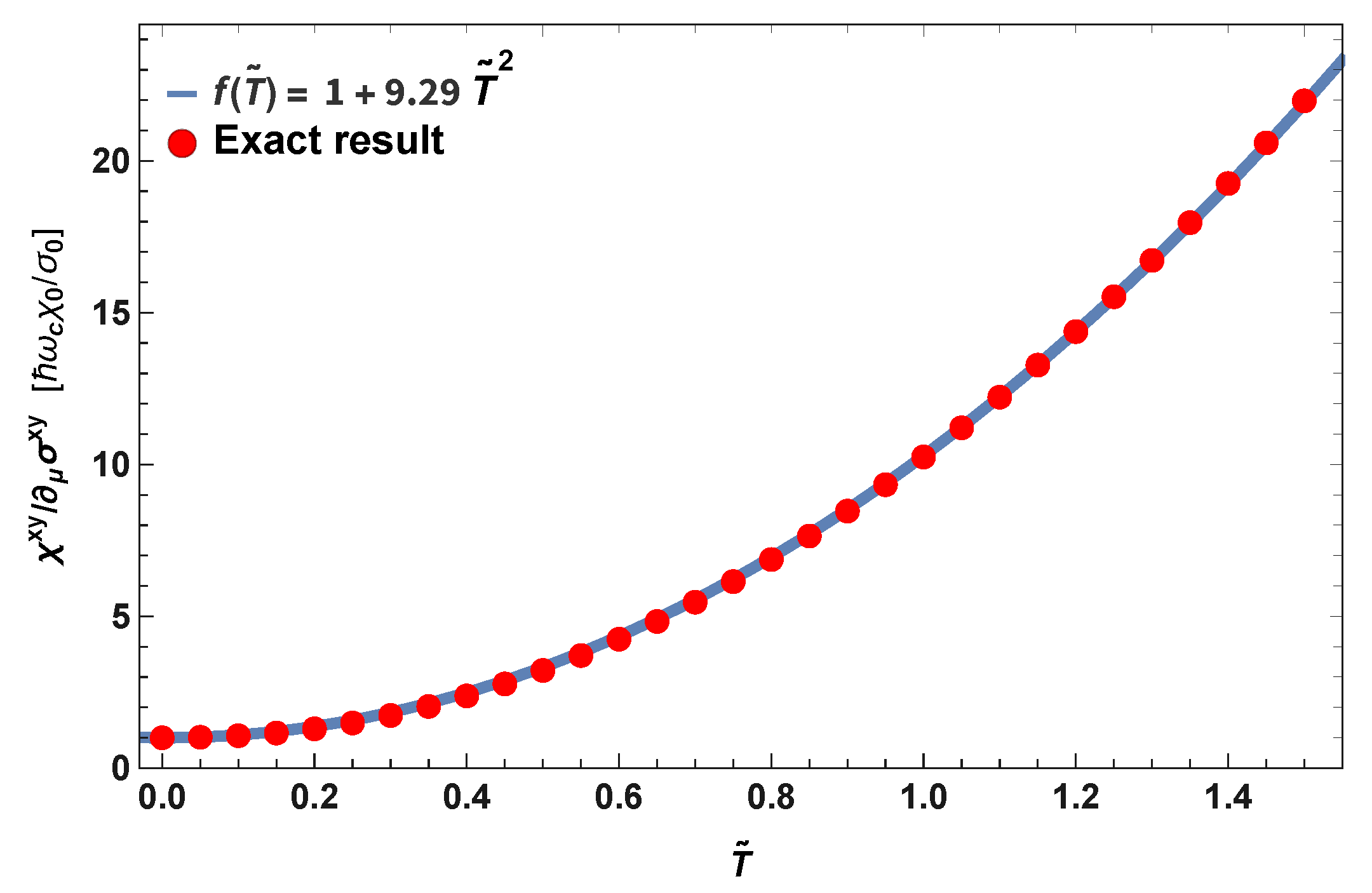
5. The Mott Relation
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiong, J.; Kushwaha, S.K.; Liang, T.; Krizan, J.W.; Hirschberger, M.; Wang, W.; Cava, R.J.; Ong, N.P. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 2015, 350, 413. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.X.; Liu, H.; Wang, J.; Liao, Z.M.; Yu, D.P. Giant negative magnetoresistance induced by the chiral anomaly in individual Cd3As2 nanowires. Nat. Commun. 2015, 6, 10137. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, S.-Y.; Belopolski, I.; Yuan, Z.; Lin, Z.; Tong, B.; Bian, G.; Alidoust, N.; Lee, C.-C.; Huang, S.-M.; et al. Signatures of the Adler Bell Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Commun. 2016, 7, 10735. [Google Scholar] [CrossRef]
- Landsteiner, K. Anomalous transport of Weyl fermions in Weyl semimetals. Phys. Rev. B 2014, 89, 075124. [Google Scholar] [CrossRef]
- Gooth, J.; Schierning, G.; Felser, C.; Nielsch, K. Quantum materials for thermoelectricity. MRS Bull. 2018, 43, 187. [Google Scholar] [CrossRef]
- Behnia, K.; Aubin, H. Nernst effect in metals and superconductors: A review of concepts and experiments. Rep. Prog. Phys. 2016, 79, 046502. [Google Scholar] [CrossRef]
- Sondheimer, E.H. The theory of the galvanomagnetic and thermomagnetic effects in metals. Proc. R. Soc. Lon. Ser. A Math. Phys. Sci. 1948, 193, 484. [Google Scholar]
- Cutler, M.; Mott, N.F. Observation of Anderson Localization in an Electron Gas. Phys. Rev. 1969, 181, 1336–1340. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Xiao, D.; Yao, Y.; Fang, Z.; Niu, Q. Berry-Phase Effect in Anomalous Thermoelectric Transport. Phys. Rev. Lett. 2006, 97, 026603. [Google Scholar] [CrossRef] [PubMed]
- Checkelsky, J.G.; Ong, N.P. Thermopower and Nernst effect in graphene in a magnetic field. Phys. Rev. B 2009, 80, 081413. [Google Scholar] [CrossRef]
- Wei, P.; Bao, W.; Pu, Y.; Lau, C.N.; Shi, J. Anomalous Thermoelectric Transport of Dirac Particles in Graphene. Phys. Rev. Lett. 2009, 102, 166808. [Google Scholar] [CrossRef] [PubMed]
- Proskurin, I.; Ogata, M. Thermoelectric Transport Coefficients for Massless Dirac Electrons in Quantum Limit. J. Phys. Soc. Jpn. 2013, 82, 063712. [Google Scholar] [CrossRef]
- Ghahari, F.; Xie, H.Y.; Taniguchi, T.; Watanabe, K.; Foster, M.S.; Kim, P. Enhanced Thermoelectric Power in Graphene: Violation of the Mott Relation by Inelastic Scattering. Phys. Rev. Lett. 2016, 116, 136802. [Google Scholar] [CrossRef]
- Liang, T.; Gibson, Q.; Xiong, J.; Hirschberger, M.; Koduvayur, S.P.; Cava, R.J.; Ong, N.P. Evidence for massive bulk Dirac fermions in Pb1−xSnxSe from Nernst and thermopower experiments. Nat. Commun. 2013, 4, 2696. [Google Scholar] [CrossRef] [PubMed]
- Lundgren, R.; Laurell, P.; Fiete, G.A. Thermoelectric properties of Weyl and Dirac semimetals. Phys. Rev. B 2014, 90, 165115. [Google Scholar] [CrossRef]
- Lucas, A.; Davison, R.A.; Sachdev, S. Hydrodynamic theory of thermoelectric transport and negative magnetoresistance in Weyl semimetals. Proc. Natl. Acad. Sci. USA 2016, 113, 9463–9468. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Miransky, V.A.; Shovkovy, I.A.; Sukhachov, P.O. Anomalous thermoelectric phenomena in lattice models of multi-Weyl semimetals. Phys. Rev. B 2017, 96, 155138. [Google Scholar] [CrossRef]
- Manna, K.; Muechler, L.; Muechler, L.; Kao, T.-H.; Stinshoff, R.; Zhang, Y.; Gooth, J.; Kumar, N.; Kreiner, G.; Koepernik, K.; et al. From colossal to zero: Controlling the Anomalous Hall Effect in Magnetic Heusler Compounds via Berry Curvature Design. Phys. Rev. X 2018, 8, 041045. [Google Scholar] [CrossRef]
- Nakai, R.; Nagaosa, N. Nonreciprocal thermal and thermoelectric transport of electrons in noncentrosymmetric crystals. arXiv 2018, arXiv:1812.02372. [Google Scholar] [CrossRef]
- Skinner, B.; Fu, L. Large, nonsaturating thermopower in a quantizing magnetic field. Sci. Adv. 2018, 4, 2621. [Google Scholar] [CrossRef]
- Muñoz, E.; Soto-Garrido, R. Thermoelectric transport in torsional strained Weyl semimetals. J. Appl. Phys. 2019, 125, 082507. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Torre, I.; Kumar, R.K.; Ben Shalom, M.; Tomadin, A.; Principi, A.; Auton, G.H.; Khestanova, E.; Novoselov, K.S.; Grigorieva, I.V.; et al. Negative local resistance caused by viscous electron backflow in graphene. Science 2016, 351, 1055–1058. [Google Scholar] [CrossRef] [PubMed]
- Crossno, J.; Shi, J.K.; Wang, K.; Liu, X.; Harzheim, A.; Lucas, A.; Sachdev, S.; Kim, P.; Taniguchi, T.; Watanabe, K.; et al. Observation of the Dirac fluid and the breakdown of the Wiedemann-Franz law in graphene. Science 2016, 351, 1058–1061. [Google Scholar] [CrossRef] [PubMed]
- Moll, P.J.W.; Kushwaha, P.; Nandi, N.; Schmidt, B.; Mackenzie, A.P. Evidence for hydrodynamic electron flow in PdCoO2. Science 2016, 351, 1061–1064. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Shytov, A.V.; Levitov, L.S.; Kumar, R.K.; Berdyugin, A.I.; Ben Shalom, M.; Grigorieva, I.V.; Geim, A.K.; Falkovich, G. Fluidity onset in graphene. Nat. Commun. 2018, 9, 4533. [Google Scholar] [CrossRef]
- Gooth, J.; Menges, F.; Kumar, N.; Süß, V.; Shekhar, C.; Sun, Y.; Drechsler, U.; Zierold, R.; Felser, C.; Gotsmann, B. Thermal and electrical signatures of a hydrodynamic electron fluid in tungsten diphosphide. Nat. Commun. 2018, 9, 4093. [Google Scholar] [CrossRef]
- Jaoui, A.; Fauqué, B.; Rischau, C.W.; Subedi, A.; Fu, C.; Gooth, J.; Kumar, N.; Süß, V.; Maslov, D.L.; Felser, C.; et al. Departure from the Wiedemann–Franz law in WP2 driven by mismatch in T-square resistivity prefactors. NJP Quantum Mater. 2018, 3, 64. [Google Scholar] [CrossRef]
- Chernodub, M.N.; Cortijo, A.; Vozmediano, M.A.H. Generation of a Nernst Current from the Conformal Anomaly in Dirac and Weyl Semimetals. Phys. Rev. Lett. 2018, 120, 206601. [Google Scholar] [CrossRef]
- Chernodub, M.N. Anomalous Transport Due to the Conformal Anomaly. Phys. Rev. Lett. 2016, 117, 141601. [Google Scholar] [CrossRef]
- Arjona, V.; Chernodub, M.N.; Vozmediano, M.A.H. Fingerprints of the conformal anomaly in the thermoelectric transport in Dirac and Weyl semimetals: Result from a Kubo formula. Phys. Rev. B 2019, 99, 235123. [Google Scholar] [CrossRef]
- Ziman, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1960. [Google Scholar]
- Jonson, M.; Mahan, G.D. Mott’s formula for the thermopower and the Wiedemann-Franz law. Phys. Rev. B 1980, 21, 4223–4229. [Google Scholar] [CrossRef]
- Smrcka, L.; Streda, P. Transport coefficients in strong magnetic fields. J. Phys. C Solid State Phys. 1977, 10, 2153–2161. [Google Scholar] [CrossRef]
- Jonson, M.; Girvin, S.M. Thermoelectric effect in a weakly disordered inversion layer subject to a quantizing magnetic field. Phys. Rev. B 1984, 29, 1939–1946. [Google Scholar] [CrossRef]
- Cooper, N.R.; Halperin, B.I.; Ruzin, I.M. Thermoelectric response of an interacting two-dimensional electron gas in a quantizing magnetic field. Phys. Rev. B 1997, 55, 2344–2359. [Google Scholar] [CrossRef]
- Qin, T.; Niu, Q.; Shi, J. Energy Magnetization and the Thermal Hall Effect. Phys. Rev. Lett. 2011, 107, 236601. [Google Scholar] [CrossRef]
- Andreev, A.V.; Kivelson, S.A.; Spivak, B. Hydrodynamic Description of Transport in Strongly Correlated Electron Systems. Phys. Rev. Lett. 2011, 106, 256804. [Google Scholar] [CrossRef]
- Pu, Y.; Chiba, D.; Matsukura, F.; Ohno, H.; Shi, J. Mott Relation for Anomalous Hall and Nernst Effects in Ga1−xMnxAs Ferromagnetic Semiconductors. Phys. Rev. Lett. 2008, 101, 117208. [Google Scholar] [CrossRef]
- Ryu, S.; Moore, J.E.; Ludwig, A.W.W. Electromagnetic and gravitational responses and anomalies in topological insulators and superconductors. Phys. Rev. B 2012, 85, 045104. [Google Scholar] [CrossRef]
- Kim, K.S. Role of axion electrodynamics in a Weyl metal: Violation of Wiedemann-Franz law. Phys. Rev. B 2014, 90, 121108. [Google Scholar] [CrossRef]
- Liang, T.; Gibson, Q.; Ali, M.N.; Liu, M.; Cava, R.J.; Ong, N.P. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 2015, 14, 280–284. [Google Scholar] [CrossRef]
- Liang, T.; Lin, J.; Gibson, Q.; Gao, T.; Hirschberger, M.; Liu, M.; Cava, R.J.; Ong, N.P. Anomalous Nernst Effect in the Dirac Semimetal Cd3As2. Phys. Rev. Lett. 2017, 118, 136601. [Google Scholar] [CrossRef] [PubMed]
- Watzman, S.J.; McCormick, T.M.; Shekhar, C.; Wu, S.C.; Sun, Y.; Prakash, A.; Felser, C.; Trivedi, N.; Heremans, J.P. Dirac dispersion generates unusually large Nernst effect in Weyl semimetals. Phys. Rev. B 2018, 97, 161404. [Google Scholar] [CrossRef]
- Sakai, A.; Mizuta, Y.P.; Nugroho, A.A.; Sihombing, R.; Koretsune, T.; Suzuki, M.-T.; Takemori, N.; Ishii, R.; Nishio-Hamane, D.; Arita, R.; et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 2018, 14, 1119. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Collins, J.C.; Duncan, A.; Joglekar, S.D. Trace and dilatation anomalies in gauge theories. Phys. Rev. D 1977, 16, 438–449. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Ninomiya, M. The Adler-Bell-Jackiw anomaly and Weyl fermions in a crystal. Phys. Lett. B 1983, 130, 389. [Google Scholar] [CrossRef]
- Kumar, G.S.; Prasad, G.; Pohl, R.O. Experimental determinations of the Lorenz number. J. Mater. Sci. 1993, 28, 4261–4272. [Google Scholar] [CrossRef]
- Gooth, J.; Niemann, A.C.; Meng, T.; Grushin, A.G.; Landsteiner, K.; Gotsmann, B.; Menges, F.; Schmidt, M.; Shekhar, C.; Süß, V.; et al. Experimental signatures of the mixed axial gravitational anomaly in the Weyl semimetal NbP. Nature 2017, 547, 23005. [Google Scholar] [CrossRef]
- Schindler, C.; Galeski, S.; Schnelle, W.; Wawrzyńczak, R.; Abdel-Haq, W.; Guin, S.N.; Kroder, J.; Kumar, N.; Fu, C.; Borrmann, H.; et al. Anisotropic electrical and thermal magnetotransport in the magnetic semimetal GdPtBi. Phys. Rev. B 2020, 101, 125119. [Google Scholar] [CrossRef]
- Vu, D.; Zhang, W.; Şahin, C.; Flatté, M.; Trivedi, N.; Heremans, J.P. Thermal chiral anomaly in the magnetic-field induced ideal Weyl phase of Bi89Sb11. arXiv 2019, arXiv:1906.02248. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arjona, V.; Borge, J.; Vozmediano, M.A.H. Thermoelectric Relations in the Conformal Limit in Dirac and Weyl Semimetals. Symmetry 2020, 12, 814. https://doi.org/10.3390/sym12050814
Arjona V, Borge J, Vozmediano MAH. Thermoelectric Relations in the Conformal Limit in Dirac and Weyl Semimetals. Symmetry. 2020; 12(5):814. https://doi.org/10.3390/sym12050814
Chicago/Turabian StyleArjona, Vicente, Juan Borge, and María A. H. Vozmediano. 2020. "Thermoelectric Relations in the Conformal Limit in Dirac and Weyl Semimetals" Symmetry 12, no. 5: 814. https://doi.org/10.3390/sym12050814
APA StyleArjona, V., Borge, J., & Vozmediano, M. A. H. (2020). Thermoelectric Relations in the Conformal Limit in Dirac and Weyl Semimetals. Symmetry, 12(5), 814. https://doi.org/10.3390/sym12050814



