1. Introduction
All graphs considered in this paper are simple, finite, connected and undirected. The distance between two vertices u and v is the length of the shortest path between them, it is denoted as . If two vertices are adjacent, we write . The maximum distance from to any other vertex in G is called the eccentricity, , of v. For a vertex , is a subgraph obtained by removing the vertex v and all the edges adjacent to v. Similarly for any edge , is a subgraph obtained by removing the edge e from G. For a subset , is a subgraph achieved by removing all the vertices in U and all the edges adjacent to any vertex of U.
A graph is said to be an
apex graph if it contains a vertex whose removal yields a planar graph. In topological graph theory, apex graphs play a vital role [
1]. Alkanes play in an important role in chemistry, pharmaceutics and related fields. The apex graph produces trees (alkanes) after removing certain vertices. A graph
G is called an
ℓ-apex tree if there exists a vertex subset
with cardinality
l such that
is a tree and there is no other subset of smaller cardinality with this property. Elements of the set
A are called
apex vertices, and
A is called an
ℓ-apex vertex set. We denote the set of all
ℓ-apex trees of order
n by
. The elements of the set
are called just
apex trees. Note that a tree is always an
0-apex tree.
When vertices represent the atoms and the edge between them are the bonds, then the graph
G is called a
molecular graph. In 1947, Wiener [
2] proposed the first topological index,
, nowdays called
Wiener index,
In [
2,
3,
4], Wiener showed that there exists correlations between the Wiener index of the molecular graph of an organic compound and different physical and chemical properties of the molecular compound. Later were introduced many variatoins, like
hyper-Wiener index
and the
generalized Wiener index
Notice that for
and 1, we obtain the Wiener index and the Harary index, respectively. For further studies on the Wiener index and its variations, we refer [
5,
6,
7,
8,
9,
10,
11,
12,
13] and references there in. In the paper we consider also some other newer indices as eccentric connectivity index, generalized degree distance, and others. We define them in the sequel.
In recent years, many papers on
ℓ-apex trees have published. Here we mention only few of them. In [
14], authors found the extremal
ℓ-apex trees with respect to matching energy. Xu et al. [
15] obtained the sharp bounds on weighted Harary indices for apex trees and
ℓ-apex trees. Extremal first and second Zagreb indices of apex trees have investigated in [
16] and they also characterized the extremal
ℓ-apex trees.
2. One Extremum
Let I be a graph invariant which is strictly monotonic with respect to adding edges. That is, either for every graph G and every we have , in which case we say that I is decreasing; or for every graph G and every , we have , in which case we say that I is increasing.
Let
G be an
ℓ-apex tree. Denote by
A an
ℓ-apex set of vertices of
G, add an edge connecting two vertices of
A and denote by
the resulting graph. Obviously,
is a tree. However, it can happpen that
is a
-apex tree for
. For example, take the graph
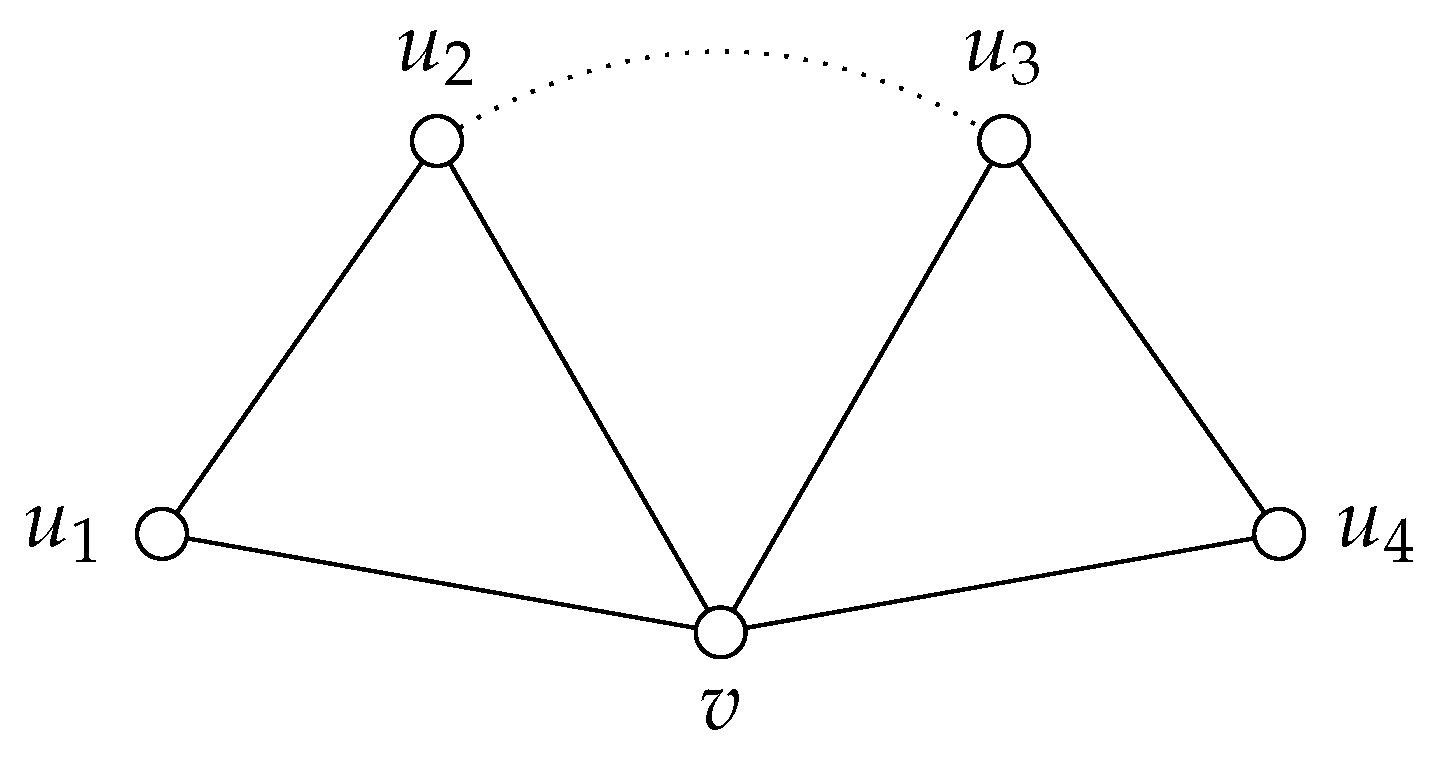
G from
Figure 1 consisting of two triangles sharing a vertex. Notice that
G has five vertices and it is a 2-apex tree. Then,
is a 2-apex set of
G, but
is just a 1-apex tree. Hence to obtain extremal graphs, one cannot apply the monotonicity of
I in a random way. Nevertheless, the following holds.
Theorem 1. Let I be a strictly monotonic invariant and let G be an ℓ-apex tree on n vertices, where and , such that
Then, G is the join , where T is a tree on vertices.
Proof. We present proof for the case when I is decreasing, the proof for the case when I is increasing is generally the same.
So let G be an ℓ-apex tree of order n with the minimum value of I, and let A be an ℓ apex set of vertices of G. Then is a tree with vertices. Denote this tree by T.
Consider all pairs of vertices such that and . Some such pairs are edges of G, but some are not. Denote by a graph obtained from G after adding all such pairs , where . Since I is decreasing, we have with equality if and only if . It remains to prove that is ℓ-apex tree.
Since is T, the graph is a k-apex tree for . Let B be a set of vertices of which has less than ℓ vertices. Then has at least 3 vertices. If then by the construction of we have is the join , and since T is a tree on at least 2 vertices, is not a tree. On the other hand if then there are at least two vertices in . Let . Then both x and y are connected to all vertices of , and so is not a tree. Thus, is ℓ-apex tree. □
In what follows, we will apply the above result to several topological indices. We start with generalized Wiener index and several derived indices, afterwards we consider connective eccentricity index, and finally we deal with generalized degree distance.
2.1. Generalized Wiener Index
Observe that in all pairs of vertices are at distance 1 with the exception of pairs of non-adjacent vertices of T, which are at distance 2. Since there are such pairs of vertices regardless of the shape of T, for invariants depending only on the tree T can be arbitrary. Hence, for the generalized Wiener index we have the following corollary.
Corollary 1. Let G be an ℓ-apex tree on n vertices, where and , and let . Then, the following two claims hold:
If then has the minimum value if and only if , where T is any tree on vertices;
If then has the maximum value if and only if , where T is any tree on vertices.
Moreover, in the extremal case Proof. Since is decreasing if and increasing if , the structural part is a direct consequence of Theorem 1. Since there are pairs of vertices of G which distance is 2 while all other pairs are adjacent, we get the value of . □
The above corollary has consequences on some derived indices.
2.1.1. Wiener Index
Observe that for
the invariant
is the Wiener index, and by Corollary 1 the extremal value is
2.1.2. Harary Index
On the other hand for
the invariant
is the Harary index, and by Corollary 1 the extremal value is
2.1.3. Hyper-Wiener Index
Summing up
and
gives us the hyper-Wiener index
, and again by Corollary 1 regarding the minimum value, the extremal graph is
and the extremal value can be again similarly derived as in the previous two indicies
2.2. Connective Eccentricity Index
Regarding Theorem 1, there are strictly monotonic invariants for which
T cannot be arbitrary. One such is
connective eccentricity index, defined as
Mathematical properties and applications of the connective eccentricity index can be found in [
17,
18,
19,
20,
21], while the authors in [
22] discussed the extramal total eccentricity of
l-apex trees. For this index, we have the following.
Corollary 2. Let G be an ℓ-apex tree on n vertices, where and . Then has the maximum value if and only if , where T is the star on vertices. Moreover, in the extremal case Proof. Since
is increasing, the extremal graph is
by Theorem 1. Thus,
Now the contribution of every
is
since
and
in this case. If
then its contribution is
if
v is connected to all vertices of
, and
otherwise. Notice that the former case happens only if
T is a star and
v is its center. Since
which is a constant not depending on
T, for any tree
T on
vertices
is a constant with a unique exception when
T is the star, for which
is bigger. Hence, the maximum value of
is attained when
when
T is the star.
The extremal value of could be easily calculated using the fact that endvertices of T contribute by , while the other vertices of G contribute by . □
2.3. Generalized Degree Distance Index
Analogous situation occures for generalized degree distance
if
. We have the following result.
Corollary 3. Let G be an ℓ-apex tree on n vertices, where and , and let . Then has the maximum value if and only if , where T is the star on vertices. Moreover, in the extremal case Proof. Since
is increasing if
, the extremal graph is
by Theorem 1. Denote
. Then
If
then
, so the third sum of (
1) is
which is a constant depending on
n and
ℓ, but not on the structure of
T. If
and
then
. For fixed
v, the sum of
in the second sum sums to
. Hence, also the second sum in (
1) is a constant depending on
n and
ℓ, but not on the structure of
T.
Now consider
. Then
For
exactly
distances are 1 while the others are 2. Hence, for
the sum
is a constant, and so it suffices to consider
Observe that running through all distinct
also
is a constant since it equals
. So, we can rewrite (
2) in the following way:
The second sum in the above expression turns to be a constant depending only of
n and
ℓ, so the maximum value of
is achived when we maximize
and it is obtained when for all adjacent pairs the sum of degrees
is maximum possible. Since
u and
v are adjacent vertices in a tree on
vertices,
. Moreover, every pair of adjacent vertices in
T satisfies
if and only if every endvertex of
T has eccentricity at most 2 in
T. Therefore the extremal graph is
where
T is the star on
vertices.
For calculating the extremal value of
observe that
vertices of
G have degree
while the other have degree
. Thus,
□
We state here one consequences of the above corollary.
Additively Weighted Harary Index
Observe that for
the invariant
is
additively weighted Harary index (also known as
reciprocal degree distance), and by Corollary 3 the extremal value is
3. Other Extremum
Now we consider the opposite extremum. Since this case is more complicated, we concentrate on 1-apex trees, i.e. apex trees. Though, it will be interesting to be conisdered the case itself.
We have:
Theorem 2. Let I be a strictly monotonic invariant and let G be an apex tree on vertices such that
Then G is a unicyclic graph and its unique cycle has a vertex of degree 2.
Proof. We present proof for the case when I is decreasing, the proof for the case when I is increasing is generally the same.
So let G be a 1-apex tree of order n with the maximum value of I, and let a be the apex vertex of G. Then is a tree with vertices. Denote this tree by T.
Suppose first then G is a tree, and hence G is not a 1-apex tree. Therefore .
Now suppose that . Then, remove one edge incident with a and denote the resulting graph by . Observe that consists of a tree T and a vertex a incident to at least two vertices of T, so has a cycle. Since is a tree, is an 1-apex tree, and , a contradiction.
By the above two paragraphs, we conclude that and a lies in a unique cycle of G. Thus, the claim follows. □
Generalized Wiener Index
For the generalized Wiener index
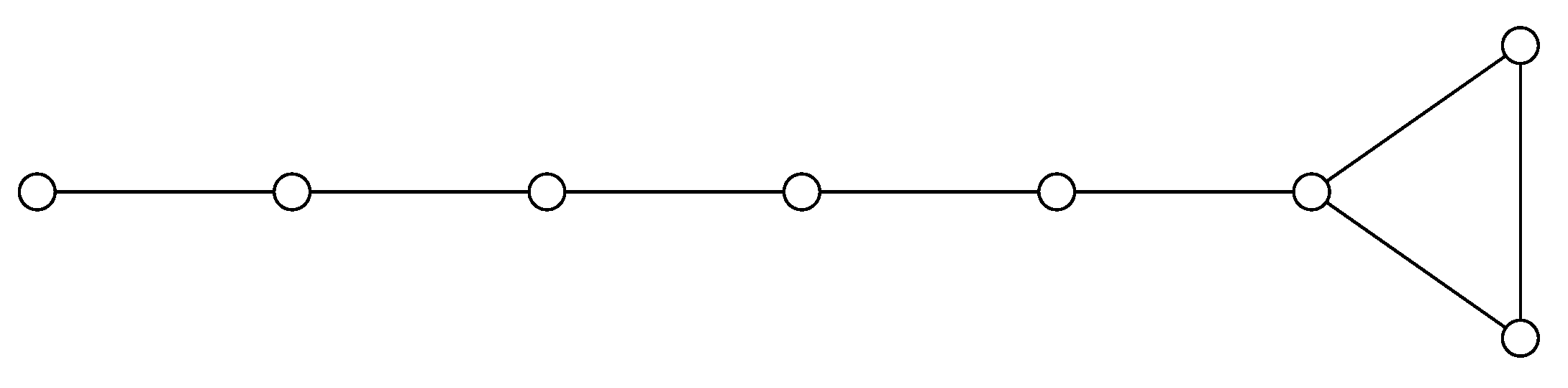
we have the following result. But before we state it, we give one definition. The
dumbbell graph
is obtained from a path
and disjoint
and
by connecting
to a vertex of
and connecting
to a vertex of
. Thus the order of so constructed graph is
. Note that without loss of generality, we can always assume that
. For an illustration, see the graph shown in
Figure 2. If
then it is an
-apex graph, if
and
, then it is a
-apex graph, and finally if
, it is a 0-apex graph.
Corollary 4. Let G be an apex tree on vertices, and let . Then the following two claims hold:
If then has the maximum value if and only if ;
If then has the minimum value if and only if .
Moreover, in the extremal case Proof. We present proof for the case when is decreasing. The proof for the case when is increasing is generally the same.
By Theorem 2,
G consists of a tree
T and a vertex
a of degree two attached to two vertices of
T. We have
Denote the vertices of
T by
so that for every
i,
, the vertex set
induces a connected graph. This connected graph is a tree and we denote it by
. Then
. For
, we have
Since is connected, is maximum if . Since and the maximum for is achieved for all i, , only if T is a path, is maximum if T is a path on vertices.
Since
a is connected to two vertices of
T, we have
and equality is attained only if
T is a path on
vertices and
a is adjacent to one endvertex of
T and to its neighbour. Hence,
G is
.
From (
3) we get
which gives the formula. □
For
the invariant
is Wiener index, and by Corollary 4 the extremal value is
On the other hand for
the invariant
is Harary index, and by Corollary 1 the extremal value is
It seems to be that is the extremal graph also for if . Analogously, seem to be extremal graph also for and if .
4. Further Work
We considered in the paper the extremal values of monotonic distance-based topological indices for the class of ℓ-apex trees. In particular we have done this for Wiener index, and henceforth for the Wiener index and the Harary index, and also for some newer indices as connective eccentricity index, generalized degree distance, and others. For the one extreme value we obtain that the extremal graph is a join of a tree and a clique. Regarding the other extreme value, which turn to be a harder problem, we obtain results here only for . Furthermore, it will be a challenge for the readers to consider higher ℓ.
It seems that the study of topological indices on apex graphs is wide open, and one can take many directions. Just to mention few of them:
Modified generalized degree distance. This index is defined as
is increasing if
. However, it seems to be that if
is big enough then
is maximum if
where
T is the balanced double star.
Maximum of Wiener index for bigger ℓ. Let G be an ℓ-apex tree on n vertices, where and , such that G has maximum Wiener index. It seems that G is the balanced dumbbell graph. i.e. , where , , and .
Minimum of connective eccentricity index for bigger ℓ. For
, let
be the graph obtained from a path
by connecting
and
to every vertex of a stable set of size
. See
Figure 3. It is easy to see that
is an
ℓ-apex graph under assumption that
. It seems graphs
and
are good candidates for the smallest possible value for the connective eccentricity index.
Author Contributions
All the authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partially supported by Slovenian research agency ARRS, program no. P1-0383, Slovak research grants APVV-15-0220, APVV-17-0428, VEGA 1/0142/17 and VEGA 1/0238/19. The research was also supported by the UPAR Grants of United Arab Emirates University, Al Ain, UAE via Grant No. G00002590 and G00003271.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mohar, B. Apex graphs with embeddings of face-width three. Discret. Math. 1997, 176, 203–210. [Google Scholar] [CrossRef][Green Version]
- Wiener, H. Structural determination of paraffin boiling point. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Wiener, H. Vapor pressure-temperature relationships among the branched paraffin hydroarbons. J. Phys. Chem. 1948, 52, 425–430. [Google Scholar] [CrossRef]
- Wiener, H. Correlation of heats of isomerization, and differences in heats of vaporization of isomers, among the paraffin hydroarbons. J. Am. Chem. Soc. 1944, 69, 2636–2638. [Google Scholar] [CrossRef]
- Diudea, M.V. Wiener and hyper—Wiener numbers in a single matrix. J. Chem. Inf. Comput. Sci. 1996, 36, 833–836. [Google Scholar] [CrossRef]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Knor, M.; Škrekovski, R. Wiener index of line graphs. In Quantitative Graph Theory: Mathematical Foundations and Applications; Dehmer, M., Emmert–Streib, F., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 279–301. [Google Scholar]
- Knor, M.; Skrekovski, R.; Tepeh, A. Mathematical aspects of Wiener index. ARS Math. Contemp. 2016, 11, 327–352. [Google Scholar] [CrossRef]
- Randic, M.; Gou, X.; Oxley, T.; Krishnapriyan, H.; Naylor, L. Wiener matrix invariants. J. Chem. Inf. Comput. Sci. 1994, 34, 361–367. [Google Scholar] [CrossRef]
- Shang, Y. Bounds of distance Estrada index of graphs. Ars Comb.-Waterloo 2016, 128, 287–294. [Google Scholar]
- Shang, Y. Further Results on Distance Estrada Index of Random Graphs. Bull. Malays. Math. Soc. Ser. 2018, 41, 537–544. [Google Scholar] [CrossRef]
- Zhou, B.; Gutman, I. Relations between Wiener, hyper-Wiener and Zagreb indices. Chem. Phys. Lett. 2004, 394, 93–95. [Google Scholar]
- Xu, K.; Liu, M.; Das, K.C.; Gutman, I.; Furtula, B. A Survey on Graphs Extremal with Respect to Distance–Based Topological Indices. MATCH Commun. Math. Comput. Chem. 2014, 17, 461–508. [Google Scholar]
- Xu, K.; Zheng, Z.; Das, K.C. Extremal t-apex trees with respect to matching energy. Complexity 2015, 21, 238–247. [Google Scholar] [CrossRef]
- Xu, K.; Wang, J.; Das, K.C.; Klavžar, S. Weighted Harary indices of apex trees and k-apex trees. Discret. Appl. Math. 2015, 189, 30–40. [Google Scholar] [CrossRef]
- Akhter, N.; Jamil, M.K.; Tomescu, I. Extremal first and second Zagreb indices of apex trees. UPB Sci. Bull. Ser. A 2016, 78, 221–230. [Google Scholar]
- De, N.; Nayeem, S.A.; Pal, A. Connective eccentricity index of some thorny graphs. Ann. Pure Appl. Math. 2014, 7, 59–64. [Google Scholar]
- Gupta, S.; Singh, M.; Madan, A.K. Connective eccentricity Index: A novel topological descriptor for predicting biological activity. J. Mol. Graph. Model. 2000, 18, 18–25. [Google Scholar] [CrossRef]
- Yu, G.; Qu, H.; Tang, L.; Feng, L. On the connective eccentricity index of trees and unicyclic graphs with given diameter. J. Math. Anal. Appl. 2014, 420, 1776–1786. [Google Scholar] [CrossRef]
- Xu, K.; Das, K.C.; Liu, H. Some extremal results on the connective eccentricity index of graphs. J. Math. Anal. App. 2016, 433, 803–817. [Google Scholar] [CrossRef]
- Yu, G.; Feng, L. On Connective Eccentricity Index of Graphs. MATCH Commun. Math. Comput. Chem. 2013, 69, 611–628. [Google Scholar]
- Akhter, N.; Yasin, H.I. Extremal total eccentricity of k-apex trees. Open J. Discret. Appl. Math. 2020, 3, 8–10. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).