Micromachined Rate-Integrating Gyroscopes: Concept, Asymmetry Error Sources and Phenomena
Abstract
1. Introduction
- (1)
- We applied a separation principle method to deeply characterize the error sources of RIG operation. A real MEMS gyro has a variety of non-ideal factors, and it is difficult to quantify their influences. Separated error study can simplify the analysis and better characterize the consequences.
- (2)
- We abridged the ZRO drift phenomena and scientific principles. The error factors of frequency split, damping and quality factor mismatch are added to the ideal gyro model and analyzed. Their errors, as time domain phenomena, are also explained to help engineers locate the major drifting source in practice.
- (3)
- We verified the theoretical study through a case to case comparison. A series of tests were utilized to demonstrate the influences of the major error sources with visualized trajectories.
2. Theoretical Analysis of RIG Errors and Phenomena
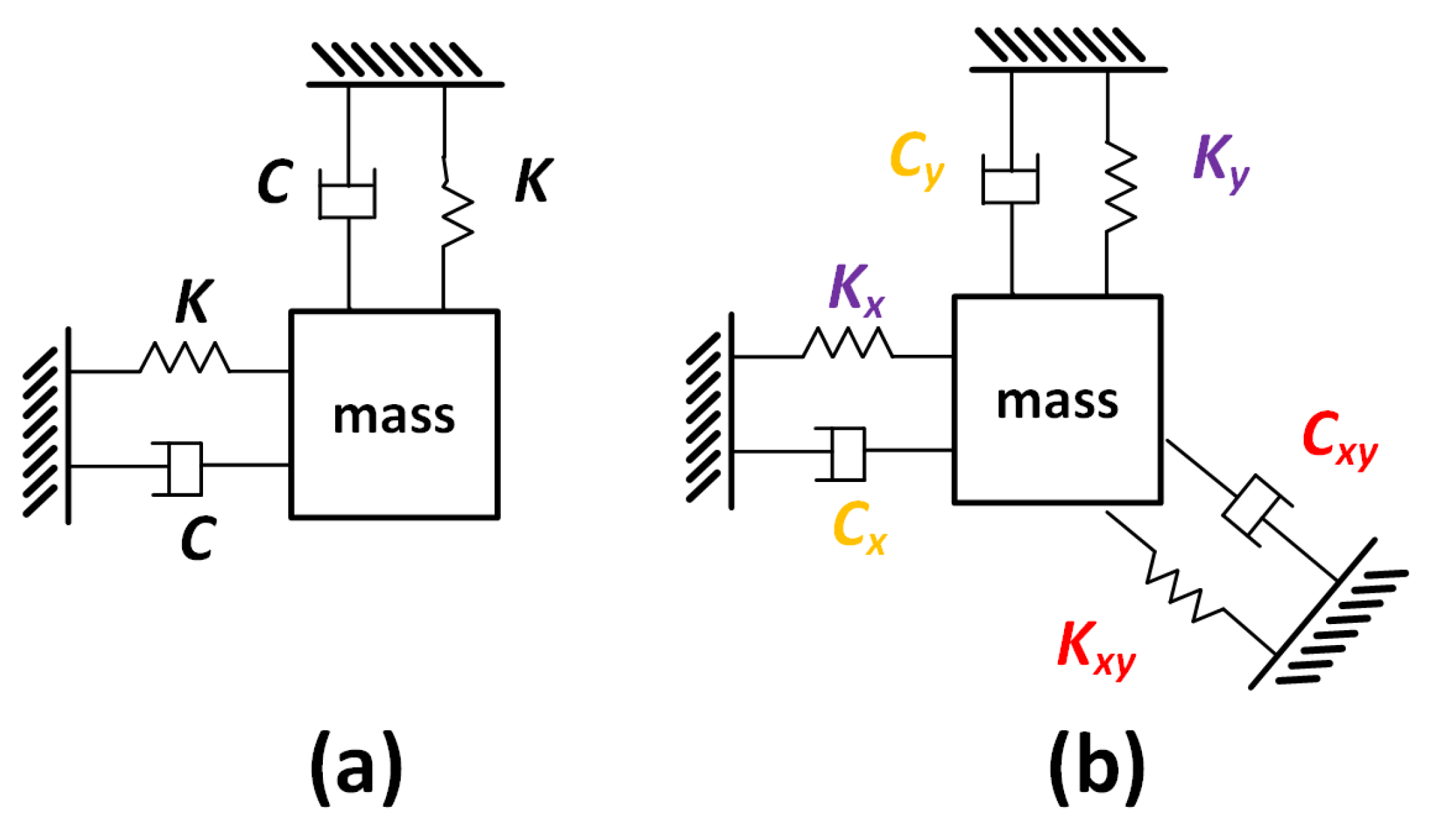
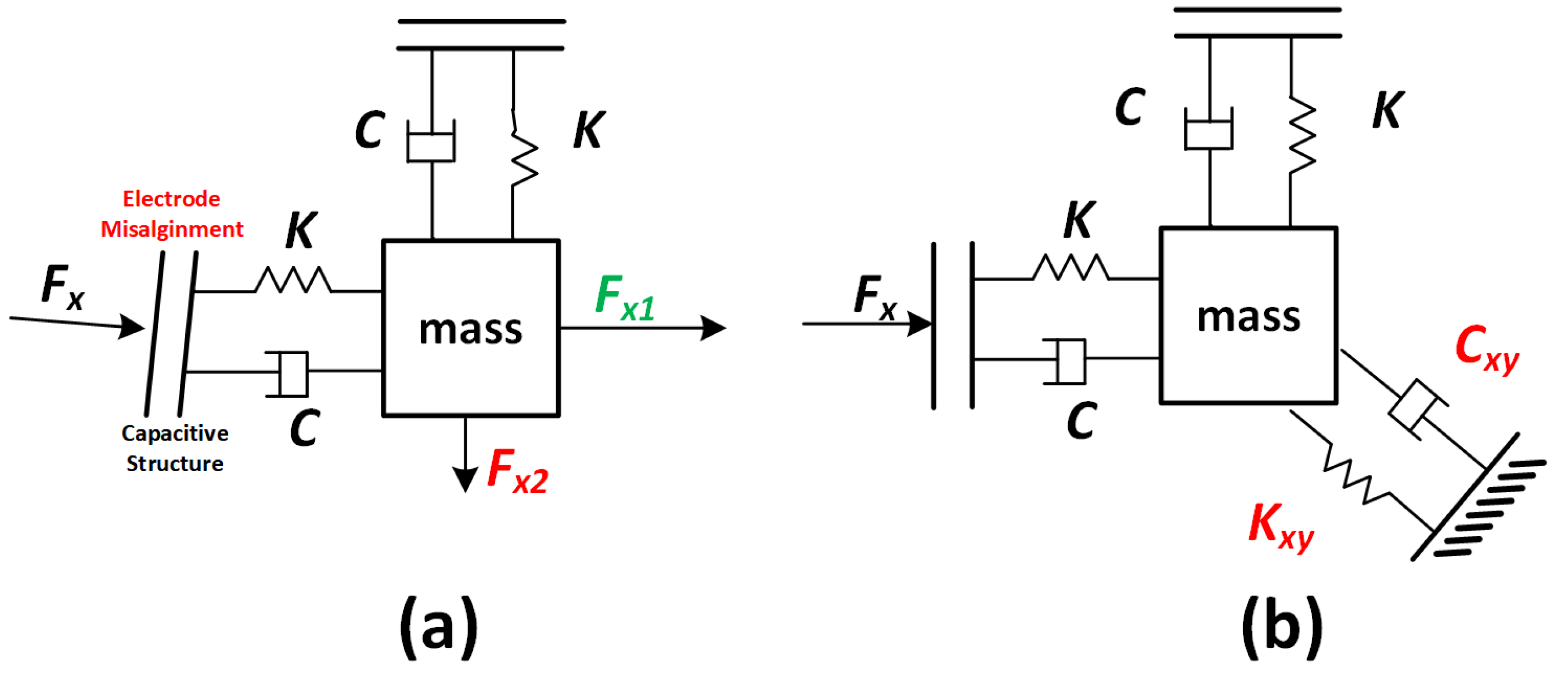
2.1. Ideal Symmetric RIG Principle
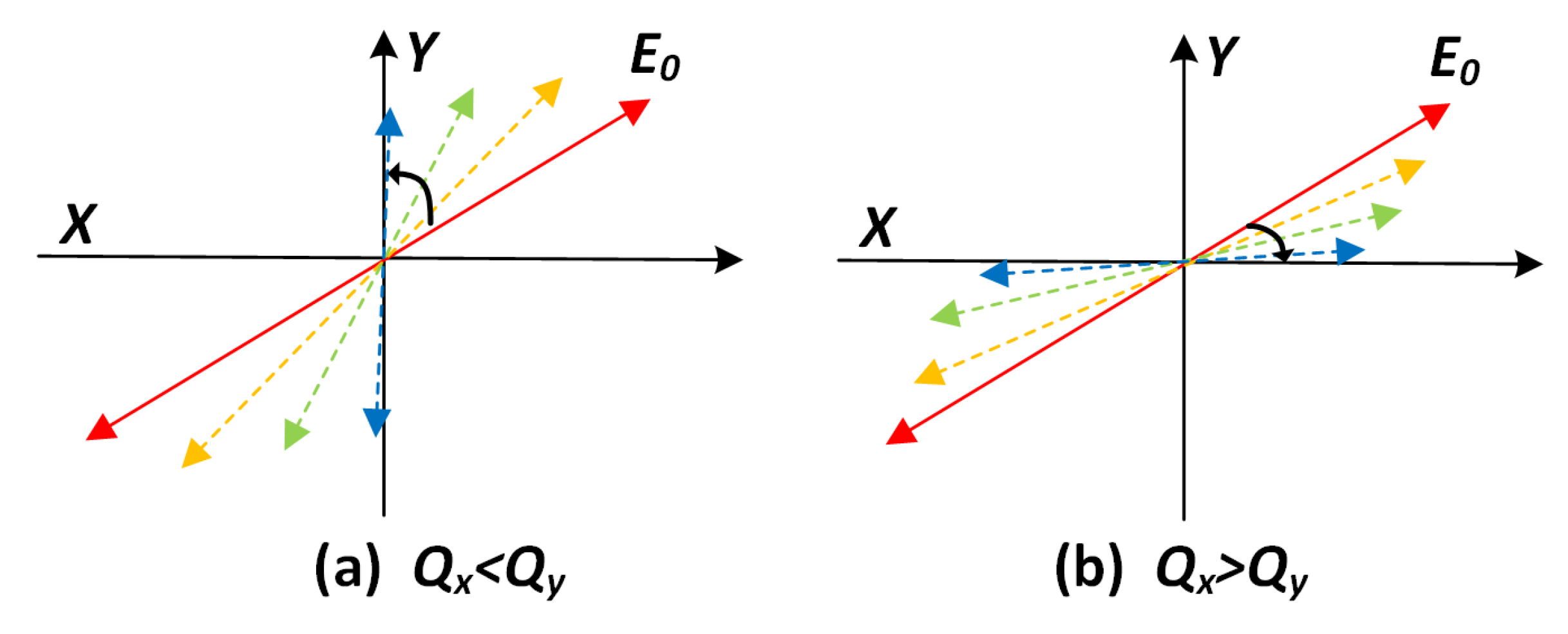
2.2. RIG with Anisoelasticity
- (1)
- The anisotropic properties of the material. MEMS gyros are typically made by single crystal silicon, whose mechanical properties are different along different orientations because of its crystal structures. Even assuming that the mechanical structures of each vibration mode are fabricated as perfectly symmetric, the equivalent stiffness would be different.
- (2)
- Fabrication imperfection. The micro gyros are fabricated through a series of processes, including photolithography, etching and deposition. Though these processes are considered mature enough to withhold the mechanical tolerance, it is very common to yield a stiffness difference level of 5% between the two modes.
- (3)
- Thermal mechanical deformations. As the temperature changes, the dimensions of the MEMS gyro also expand/shrink to result in equivalent stiffness variation. The variations of the two modes will not be uniform which will lead to further splitting.
2.3. RIG with Damping Error Factors
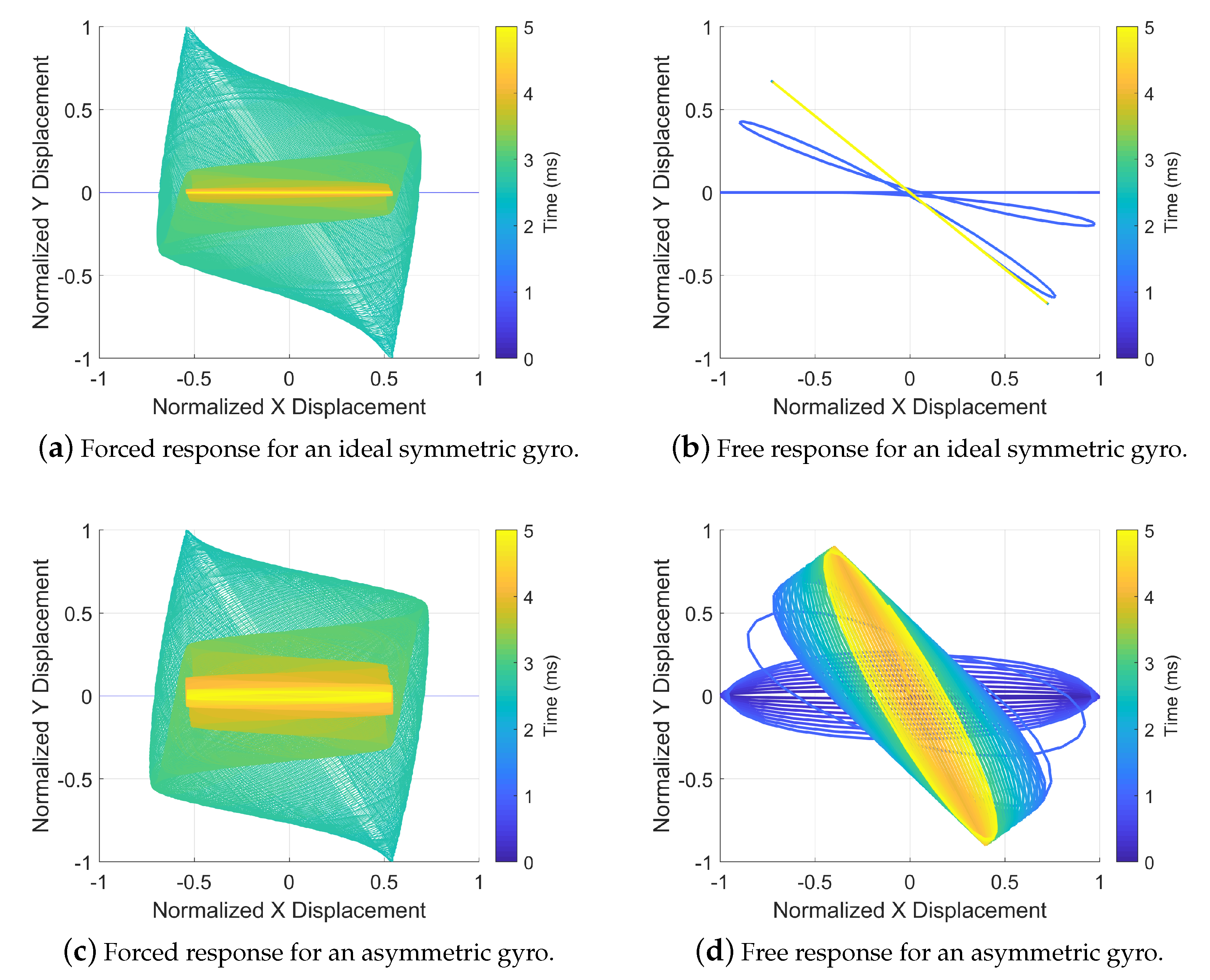
3. Validation and Discussions
3.1. Simulation Configuration
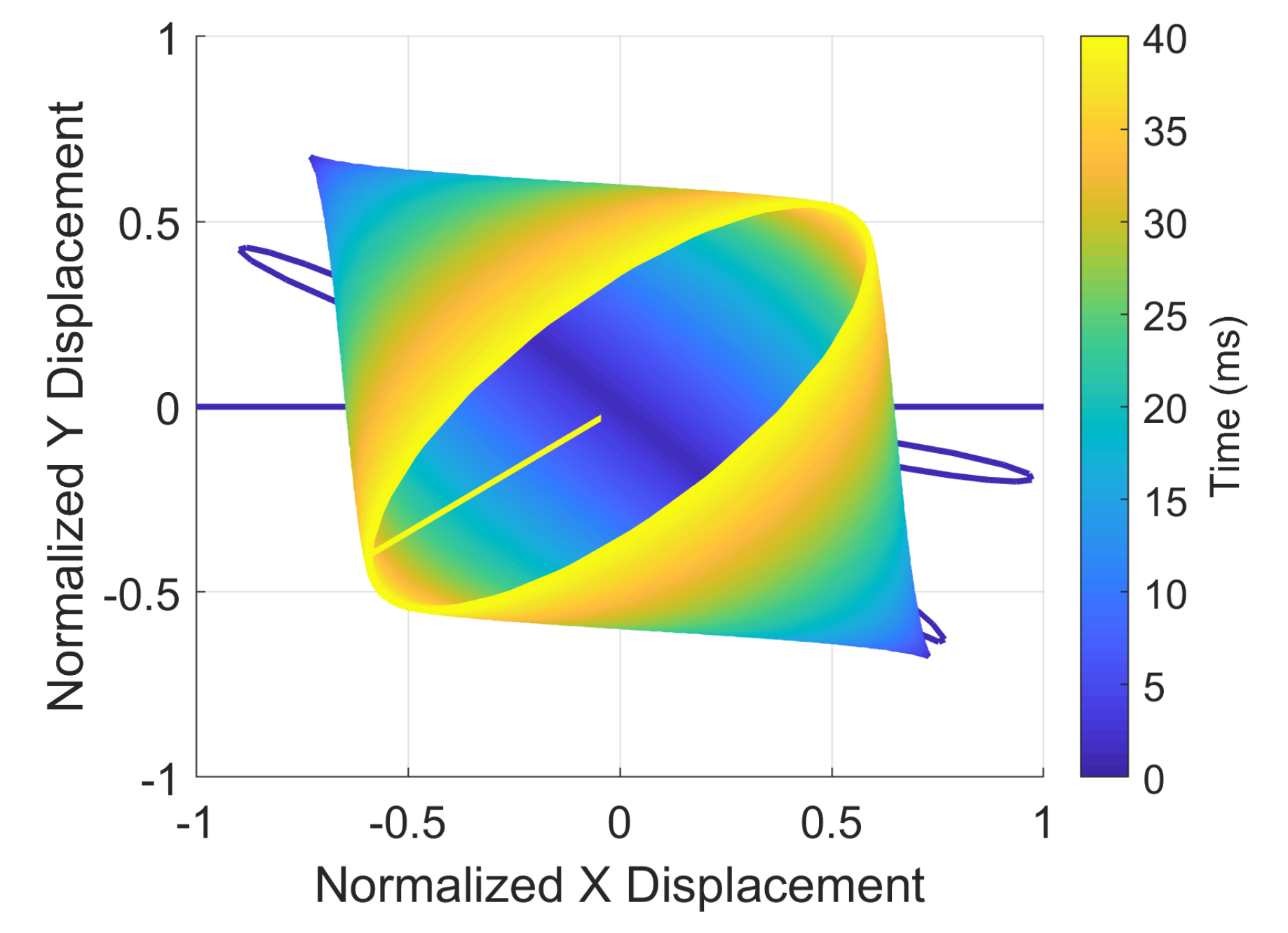
3.2. Stiffness Mismatch and Coupling Results
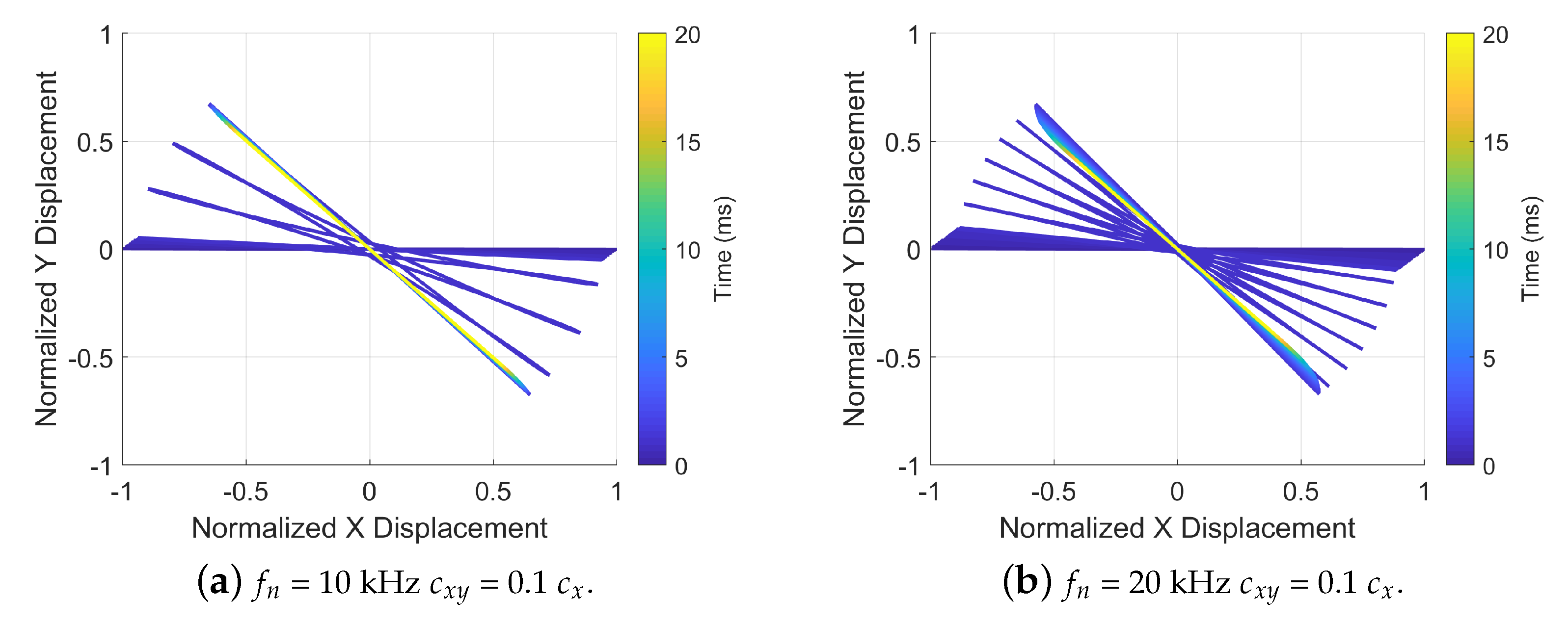
3.3. Damping Coupling and Quality Factor Mismatch Results
3.4. Discussions and Suggestions
- (1)
- The periodic oscillation motions at the angle output are caused by the frequency split or stiffness coupling.
- (2)
- The exponential drift toward one major axis/mode is induced by the quality factor mismatch and damping coupling term.
- (1)
- When giving the symmetry the highest priority, e.g., designing a gyro in a converse way to reduce the frequency split/damping mismatch/mode coupling, even conducting a lower quality factor is acceptable. Developing a gyro using isotropic materials (e.g., poly silicon) is another solution.
- (2)
- Evaluating the RIG behavior, locating the major error source and modifying the design according to the analysis in this work. If the symmetry is already reaching the limits, it can be further optimized. If the ZRO pattern is dominated by drifting behavior, a higher Q and lower resonant frequency can improve the ZRO stability; if the ZRO behaves in an oscillation manner, higher resonant frequencies will reduce this error.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ZRO | Zero rate output |
| MEMS | Micro-electro-mechanical systems |
| Q | Quality factor |
| RIG | Rate-integrating gyroscopes |
| WA | Whole-angle |
Appendix A. Detailed Derivation of Conventional Rate Gyro System
References
- Hiller, T.; Kuhlmann, B.; Buhmann, A.; Roth, H. Noise contributions in a closed-loop MEMS gyroscope for automotive applications. In Proceedings of the 2017 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27–30 March 2017. [Google Scholar]
- Marek, J. MEMS for automotive and consumer electronics. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 7–11 February 2010. [Google Scholar]
- Kranz, M.S.; Hudson, T.D.; Ashley, P.R.; Ruffin, P.B.; Tuck, J. Single-layer silicon-on-insulator MEMS gyroscope for wide dynamic range and harsh environment applications. In MEMS Components and Applications for Industry, Automobiles, Aerospace, and Communication; International Society for Optical Engineering: San Francisco, CA, USA, 2001. [Google Scholar]
- Jia, Y.; Li, S.; Qin, Y.; Cheng, R. Error analysis and compensation of MEMS rotation modulation inertial navigation system. IEEE Sens. J. 2018, 18, 2023–2030. [Google Scholar] [CrossRef]
- Shen, X.; Yuan, D.; Chang, R.; Jin, W. A Nonlinear Observer for Attitude Estimation of Vehicle-Mounted Satcom-on-the-Move. IEEE Sens. J. 2019, 19, 8057–8066. [Google Scholar] [CrossRef]
- Ayazi, F.; Najafi, K. A HARPSS polysilicon vibrating ring gyroscope. J. Microelectromech. Syst. 2001, 10, 169–179. [Google Scholar] [CrossRef]
- Trusov, A.A.; Atikyan, G.; Rozelle, D.; Meyer, A.; Zotov, S.; Simon, B.; Shkel, A. Flat is not dead: Current and future performance of Si-MEMS quad mass gyro (QMG) system. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium-PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 252–258. [Google Scholar]
- Li, Q.; Xiao, D.; Zhou, X.; Xu, Y.; Zhuo, M.; Hou, Z.; He, K.; Zhang, Y.; Wu, X. 0.04 degree-per-hour MEMS disk resonator gyroscope with high-quality factor (510 k) and long decaying time constant (74.9 s). Microsyst. Nanoeng. 2018, 4, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kline, M.; Yeh, Y.C.; Eminoglu, B.; Izyumin, I.; Daneman, M.; Horsley, D.; Boser, B. MEMS gyroscope bias drift cancellation using continuous-time mode reversal. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers & Eurosensors XXVII), Barcelona, Spain, 6–20 June 2013; pp. 1855–1858. [Google Scholar]
- Gu, H.; Zhao, B.; Zhou, H.; Liu, X.; Su, W. MEMS Gyroscope Bias Drift Self-Calibration Based on Noise-Suppressed Mode Reversal. Micromachines 2019, 10, 823. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Xie, Z.; Bai, X.; Kwan, T. Design of a 1-Bit MEMS Gyroscope Using the Model Predictive Control Approach. Sensors 2019, 19, 730. [Google Scholar] [CrossRef] [PubMed]
- Cui, M.; Huang, Y.; Wang, W.; Cao, H. MEMS Gyroscope Temperature Compensation Based on Drive Mode Vibration Characteristic Control. Micromachines 2019, 10, 248. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wen, H.; Wisher, S.; Norouzpour-Shirazi, A.; Lei, J.; Chen, H.; Ayazi, F. An FPGA-Based Interface System for High-Frequency Bulk-Acoustic-Wave Microgyroscopes With In-Run Automatic Mode-Matching. IEEE Trans. Instrum. Meas. 2020, 69, 1783–1793. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, S.; Bo, Y.; Li, W.; Tian, W.; Guo, J. A Mixed Deep Recurrent Neural Network for MEMS Gyroscope Noise Suppressing. Electronics 2019, 8, 181. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, S.; Chen, Y.; Bo, Y.; Han, L.; Guo, J.; Feng, Z.; Zhou, H. Performance Analysis of a Deep Simple Recurrent Unit Recurrent Neural Network (SRU-RNN) in MEMS Gyroscope De-Noising. Sensors 2018, 18, 4471. [Google Scholar] [CrossRef] [PubMed]
- Tsukamoto, T.; Tanaka, S. FM/rate integrating MEMS gyroscope using independently controlled CW/CCW mode oscillations on a single resonator. In Proceedings of the 2017 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27–30 March 2017; pp. 1–4. [Google Scholar]
- Prikhodko, I.P.; Zotov, S.A.; Trusov, A.A.; Shkel, A.M. Foucault pendulum on a chip: Rate integrating silicon MEMS gyroscope. Sens. Actuators Phys. 2012, 177, 67–78. [Google Scholar] [CrossRef]
- Gregory, J.A.; Cho, J.; Najafi, K. Novel mismatch compensation methods for rate-integrating gyroscopes. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 252–258. [Google Scholar]
- Gregory, J.A. Characterization, Control and Compensation of MEMS Rate and Rate-Integrating Gyroscopes. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 2012. [Google Scholar]
- Askari, S.; Asadian, M.H.; Shkel, A.M. High quality factor MEMS gyroscope with whole angle mode of operation. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Moltrasio, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar]
- Gando, R.; Maeda, S.; Masunishi, K.; Tomizawa, Y.; Ogawa, E.; Hatakeyama, Y.; Itakura, T.; Ikehashi, T. A MEMS rate integrating gyroscope based on catch-and-release mechanism for low-noise continuous angle measurement. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 944–947. [Google Scholar]
- Hu, Z.; Gallacher, B.J. Precision mode tuning towards a low angle drift MEMS rate integrating gyroscope. Mechatronics 2018, 56, 306–317. [Google Scholar] [CrossRef]
- Friedland, B.; Hutton, M. Theory and error analysis of vibrating-member gyroscope. IEEE Trans. Autom. Control. 1978, 23, 545–556. [Google Scholar] [CrossRef]
- Leoncini, M.; Bestetti, M.; Bonfanti, A.G.; Facchinetti, S.; Langfelder, G. Fully integrated, 406 uA, 5 degree/hr, full digital output Lissajous frequency-modulated gyroscope. IEEE Trans. Ind. Electron. 2018, PP, 1. [Google Scholar]
- Lynch, D.D.; Lynch, D. Vibratory gyro analysis by the method of averaging. In Proceedings of the 2nd St. Petersburg Conference on Gyroscopic Technology and Navigation, St. Petersburg, Russia, 24–25 May 1995. [Google Scholar]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Z.; Wu, J.; Li, C.; Zhao, W.; Cheng, Y. Micromachined Rate-Integrating Gyroscopes: Concept, Asymmetry Error Sources and Phenomena. Symmetry 2020, 12, 801. https://doi.org/10.3390/sym12050801
Qi Z, Wu J, Li C, Zhao W, Cheng Y. Micromachined Rate-Integrating Gyroscopes: Concept, Asymmetry Error Sources and Phenomena. Symmetry. 2020; 12(5):801. https://doi.org/10.3390/sym12050801
Chicago/Turabian StyleQi, Zhenxiang, Jin Wu, Chong Li, Wanliang Zhao, and Yuxiang Cheng. 2020. "Micromachined Rate-Integrating Gyroscopes: Concept, Asymmetry Error Sources and Phenomena" Symmetry 12, no. 5: 801. https://doi.org/10.3390/sym12050801
APA StyleQi, Z., Wu, J., Li, C., Zhao, W., & Cheng, Y. (2020). Micromachined Rate-Integrating Gyroscopes: Concept, Asymmetry Error Sources and Phenomena. Symmetry, 12(5), 801. https://doi.org/10.3390/sym12050801





