Abstract
A clonogenic assay is a biological technique for calculating the Surviving Fraction (SF) that quantifies the anti-proliferative effect of treatments on cell cultures: this evaluation is often performed via manual counting of cell colony-forming units. Unfortunately, this procedure is error-prone and strongly affected by operator dependence. Besides, conventional assessment does not deal with the colony size, which is generally correlated with the delivered radiation dose or administered cytotoxic agent. Relying upon the direct proportional relationship between the Area Covered by Colony (ACC) and the colony count and size, along with the growth rate, we propose MF2C3, a novel computational method leveraging spatial Fuzzy C-Means clustering on multiple local features (i.e., entropy and standard deviation extracted from the input color images acquired by a general-purpose flat-bed scanner) for ACC-based SF quantification, by considering only the covering percentage. To evaluate the accuracy of the proposed fully automatic approach, we compared the SFs obtained by MF2C3 against the conventional counting procedure on four different cell lines. The achieved results revealed a high correlation with the ground-truth measurements based on colony counting, by outperforming our previously validated method using local thresholding on L*u*v* color well images. In conclusion, the proposed multi-feature approach, which inherently leverages the concept of symmetry in the pixel local distributions, might be reliably used in biological studies.
1. Introduction
Clonogenic assays represent a well-established technique commonly used in biological laboratories for estimating the ability of a single cell, which underwent a specific treatment (e.g., irradiation, chemotherapy or monoclonal antibody administration), to self-duplicate and create a colony. Therefore, the colonies originate from cells that retain the capacity to produce progeny after treatment and their number reflects the efficacy of the cytotoxic agent itself [1]. The protocol essentially consists of four steps: (i) cells are plated before (to create a control) and after treatment; (ii) cells are incubated to allow for the formation and growth of colonies; (iii) fixation and staining of colonies; (iv) plates are manually analyzed by human operators to quantify the Colony-Forming Units (CFUs). Traditionally, only cell clusters with more than 50 cells are considered in the count. This arbitrary threshold is a practical assumption for detecting colonies to the naked eye [1].
The aim of the assay is to obtain two fundamental measurements to quantitatively assess the effectiveness and validity of the treatment, namely: (i) the Plating Efficiency (PE) of untreated cells (used as a control), described as the ratio between the colony numbers counted and the plated cells number; (ii) the Surviving Fraction (SF), which estimates cells’ vitality after treatment [2].
Although the first two steps follow a well-defined procedure, the subjectivity of the manual counting process introduces an intra-/inter-operator variability of the results. Moreover, with regard to the analyzed cell line, the grown colonies have very different characteristics in terms of size, shape, and homogeneity: some cell lines make up small and well-defined/high-contrast colonies compared to the background, whereas others might give rise to large and evanescent colonies, which are very difficult to detect and quantify to the naked eye. An additional difficulty of the quantification process concerns the colonies that remarkably grow and tend to merge together. Moreover, these manual CFU quantification procedures are extremely time-consuming and also error-prone. Typically, in order to reduce the inter-reader error, the average of several manual counts is considered. The main issue regarding clonogenic survival assays is represented by inter- and intra-operator variability, nevertheless, clonogenic assay is still considered as a well-established technique to identify clonogenic cells after a specific cell treatment [3]. This concern affects each technique based on manual counting and thus also the colony formation assay [4]. However, an extensive analysis of several clonogenic assay results has been recently carried out and it demonstrated that, despite inter-operator differences, clonogenic assays can be still considered as a robust method to study the ability of cells to form colonies [5].
These motivations have led various research groups to tackle this important quantification task, developing automatic approaches for clonogenic assay evaluation. Relying upon our previous work in [6], we propose here a multi-feature automatic approach based on the spatial Fuzzy C-Means (sFCM) clustering [7,8,9] for cell colony detection. This novel approach exploits entropy and standard deviation (SD) as local image features aiming at discriminating the colonies with respect to the background, as well as to enhance clonogenic assay quantification.
In the experiments, the proposed multi-feature solution outperformed similar solutions based on native—i.e., Red Green Blue (RGB)—or converted—e.g., International Commission on Illumination (CIE) L*u*v*—color spaces, especially with cell lines difficult to analyze and quantify even for expert human operators. Unlike many literature works that used hardware devices for the acquisition and positioning of the well/plate, we exploited the Circle Hough Transform (CHT) [10,11] to dynamically detect the wells (regardless of position changes and without any need for specific hardware) by leveraging our fully automated strategy proposed in [6]. As a matter of fact, the detection of the wells/plates employed for the clonogenic could affect the SF quantification.
This manuscript is organized as follows: Section 2 analyzes the literature work addressing the clonogenic evaluation issue; Section 3 describes the analyzed cell lines, as well as the cell colony local descriptors and theoretical concepts about CHT and sFCM algorithms; Section 4 describes the proposed multi-feature automatic approach; Section 5 illustrates the performed experiments and the obtained results; Section 6 compares the proposed method with existing approaches; finally, Section 7 draws the conclusions and provides future developments about this contribution.
2. Background
The current manual clonogenic assay procedures, still commonly used, suffer from quantification errors related to subjectivity of CFU count, as well as to the difficulties to detect colonies. With more details, inter- but also the intra-operator variability represents a weakness of the typical manual counting technique. Accordingly, several automatic tools to segment images of cell colonies have been realized in the latest years to overcome this issue. Early automated approaches for clonogenic quantification have already appeared in the literature since the ’80s [12,13,14,15,16,17]. In recent years, many other computational solutions were developed.
Some solutions require specific hardware, sometimes ad-hoc designed and implemented—also using 3D printing technologies—mostly to acquire the cell colony images [18,19,20,21]. These devices are intended to ensure correct positioning (because Regions of Interest (ROIs) detection approaches used fixed positioning masks) and uniform lighting. Barber et al. [18] developed an automated colony counter, tested on four cell types, relying on a specific hardware apparatus coupled with a Charge-Coupled Device (CCD) camera enabling high-quality image acquisition of the culture flasks. For image processing, two different methods were available and the user was required to manually select the appropriate method according to the cell type for correctly identifying the cell colonies. Bernard et al. [19] introduced an image segmentation method based on a model relying on prior colony knowledge. The approach, tested on Chinese hamster lung fibroblast cell lines, used a specific hardware apparatus to hold the Petri dish in the correct and fixed position, as well as to provide an adequate lighting. The image acquisition was performed by a CCD camera connected to a personal computer. Dahle et al. [20] designed a cost-effective and efficient device employing a flat-bed scanner to acquire 12 Petri dishes at the same time, for automated counting of mammalian cell colonies. Colony detection was performed by placing ROIs automatically onto a fixed location of the Petri dishes. User interaction was necessary to select the correct global threshold on the histogram of each ROI. Siragusa et al. [21] developed a semi-automated image-based cell colony counter, called ‘CoCoNut’, as an ImageJ plugin, exploiting a 3D-printed photographic light-box to achieve optimal lighting conditions during image acquisition phase. The method was tested on two cell lines. User interaction was required for the adjustment of a parameter concerning the smallest colony area to be counted.
Approaches proposed in [22,23,24,25,26] were tested on small bacterial colonies or microorganisms. Typically, bacteria produce colonies with a well-defined circular shape and adjacent colonies rarely merging together. Conversely, human cell colonies can present a wide variety of scenarios, with irregular shape and a size variability, leading to large joined and overlapped colonies. Clarke et al. [22] described a colony counting tool, called ‘NICE’, which can exploit for image acquisition an ordinary camera as well as flat-bed scanner. The developed software combines extended minima and thresholding approaches for colonies segmentation. The tool was tested on Escherichia coli and Streptococcus pneumonia bacteria. NICE represents a helpful tool in bacteria colony enumeration, but no test on human cells was performed. Geissmann et al. [23] proposed a method for circular object detection, called ‘OpenCFU’. This approach used a high-definition camera or a webcam for image acquisition, along with a white trans-illuminator to optimize image contrast. The experiments were performed on Staphylococcus aureus and Escherichia coli. The colonies were detected using a recursive thresholding procedure with different threshold values and, in order to eliminate elements that are not colonies (e.g., the edge of the well), a subsequent selection of the identified circular components was performed [27]. Finally, the distance transform was applied to separate merged colonies. Similarly, Chiang et al. [24] proposed an automated counting system, using an ad-hoc built hardware apparatus for Petri dish image acquisition. The processing pipeline exploits Principal Component Analysis (PCA) and Otsu’s thresholding to extract Escherichia coli K-12 bacterial colonies [28]. In [25], Khan et al. proposed an approach exploiting adaptive thresholding for colony detection and the watershed algorithm to separate merged colonies. The approach was tested on four different bacterial species including Escherichia coli, Klebsiella pneumoniae, Pseudomonas aeruginosa, and Staphylococcus aureus. Boukouvalas et al. [26] proposed an approach that automatically separates each dilution in images of Petri dishes, prepared using the Single Plate Serial Dilution Spotting (SP-SDS) technique, and counts the total CFUs. This approach exploited region-based shape descriptors for quantification of colonies isolated and cross-correlation granulometry for the quantification of CFU in agglomerates. In the experimental trials, publicly available images, as well as proprietary images acquired at their laboratory, were used. The obtained results were evaluated in terms of accuracy, precision, and sensitivity. A comparison was performed against the approaches in [23] and [29] on images of bacterial colonies (namely, Streptococcus mutans, Candida albicans, Staphylococcus aureus). Bewes et al. [30] developed an approach that identifies the number of colonies using the Hough transform. Three cell lines were analyzed: malignant melanoma (MM576), non-small cell lung cancer (NCI-H460), and neuroblastoma (IMR-32). This approach assumed that colonies are circular in shape and that they are not attached each other. However, this condition does not always hold. Regardless of the specific computational methods/algorithms used, also in the approaches proposed by Marotz et al. [31], Niyazi et al. [32], Wouters et al. [33], Choudhry [34], and Cai et al. [35], the colonies were approximated to a circular shape and loosely merged together. This represents a very simple operating scenario, more often valid with bacterial colonies, rather than case studies that consider human cell lines. Indeed, human cell colonies generally have variable shapes with very jagged and not well-defined contours; thus, these approaches mostly designed for bacterial colonies cannot properly separate the human colonies from the background.
All the aforementioned approaches refer to the quantification of the number of colonies. Some research groups changed their point of view, passing from the CFU number to the area occupied by the colonies. In fact, these ‘alternative’ approaches calculate the Area Covered by Colony (ACC) for clonogenic quantification [6,36]. Area-based approaches represent a good alternative able to reduce the errors mentioned above and make it possible to provide an equivalent measure to the numerical manual colony count. In fact, experimental evidence obtained has shown how this measure is correlated with the colonies number. In particular, Guzmán et al. [36] developed an ImageJ plugin—named ‘ColonyArea’—for the analysis of focus formation assays, by processing 6- or 24-well images. Multi-well detection and separation was performed by means of a static mask obtained considering dimensions of the 6- or 24-well plate used. The approach was tested on T98G cells. To overcome possible problems due to the use of a fixed mask and incorrect positioning during acquisition, in [6] we proposed a fully automatic approach exploiting CHT [10,11] to automatically detect all wells on the processed multi-well plates, and local adaptive thresholding to quantify the ACC. Experimental tests were performed on MCF7 and MCF10A human cells. By using the CHT, no mask was needed for well detection, making it possible to have a fully automatic clonogenic quantification procedure.
The presence of overlapping groups represents a further complication in the SF evaluation procedure. Colony overlaps might occur when nearby colonies, due to the growth, merge together forming a single agglomeration that is typically difficult to quantify. Szénási et al. [37] presented an evaluation and comparison of algorithms finalized to detect overlapping cell nuclei. Even with cell cultures, during growth it may happen that nearby colonies merge together and then continue to grow upon each other. It should be noted that biologists, in the manual quantification process, generally neglect such overlaps. The approach in [37] would not be directly applied to the context of the clonogenic assay, for at least two reasons: (i) greater variability of the shapes to identify; (ii) overlaps are not easily identifiable especially with low-contrast colonies. In the case of the cell nucleus, the overlap is limited to two nuclei, thus the detection of the superimposed nuclei is relatively less challenging than the identification of colonies with a non-convex shape.
Detection approaches relying upon visual characteristics alone—for instance, based on color spaces—work only on well-defined colonies. On the contrary, with ‘difficult’ cell lines that acquire low coloration and colony morphology is not compact, they do not allow for accurate and reliable colony identification and, consequently, clonogenic quantification. Starting from all these practical and methodological considerations, we decided to develop a fully automatic approach—called MF2C3—exploiting a multi-feature fuzzy clustering algorithm, which does not require any dedicated hardware and allows for clonogenic assay evaluation even with not well-defined colonies.
3. Materials and Methods
This section describes the cell lines analyzed in the experiments, as well as provides the theoretical knowledge about the entropy and the SD features, used as colony local descriptors. Furthermore, the CHT and sFCM algorithms, used to automatically detect wells and to separate the colony and background classes, respectively, are formalized. Finally, the metric used to assess the SF in this ACC-based method is provided.
3.1. Cell Lines
In our experiments, four types of human cells were considered, namely: MCF7, MCF10A, T98G, and U251MG (Figure 1). MCF7 and MCF10A are two breast epithelial cell lines used often in the field of biomedical research, whereas T98G and U251MG cells are two human glioblastoma cell lines used in brain cancer research and drug development [38,39,40]. In order to show the improvement obtained by the new multi-feature MF2C3 approach, with respect to results obtained in [6], we repeated the tests on the same MCF7 and MCF10A datasets. Moreover, with the goal of extending the tests on other and more challenging cell lines, we considered also T98G and U251MG cells, which are slightly more difficult to quantify (for their lower tendency of absorbing the dye for cell-coloring) with respect to MCF7 and MCF10A.
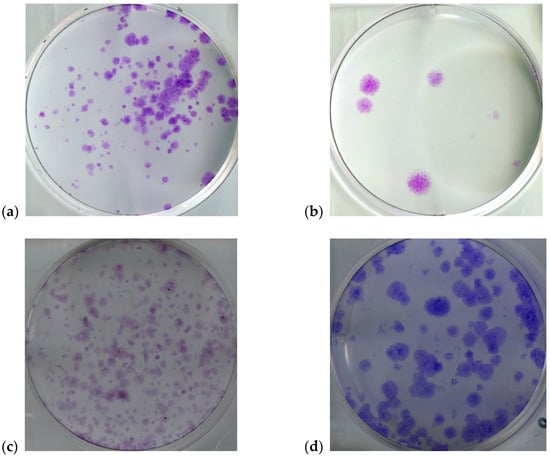
Figure 1.
Examples of the analyzed cell types: (a) MCF7; (b) MCF10A; (c) T98G; (d) U251MG. It is possible to notice how the characteristics (e.g., size, shape, contrast, coloration) vary across the various cell lines. As described by [3], the images were taken after 2 weeks of cell incubation post-treatments.
Clonogenic assays aim to study the efficacy of a specific treatment by indirectly associating it to the number of clones arising from tumor cells that have a stem phenotype. It is shown that each cell line can possess a different stemness potential that can easily be found also among clonogenic cells belonging to the same cell line [41]. Such a biological heterogeneity can be also linked to the differential capability of cells to retain their staining and thus the difficulty in their identification. Moreover, the biological heterogeneity has been extensively analyzed to perform all the histochemical analyses that are currently used in diagnostic practice. Differential staining reactions represent, in fact, a strong tool used by pathologists to identify cancer cells with different biological properties within the same cell population [42] and the same heterogeneous staining pattern can be therefore found in a clonogenic assay.
Following the standard protocol [3], the cells, after an incubation period of 15 days, were fixed and stained with a crystal-violet dye. Two weeks of cell incubation post-treatments represent the average time span during which a clonogenic assay is usually performed as described by [3], which is considered the key reference protocol regarding the clonogenic survival assays. For the quantification procedure, the plates were manually analyzed: the obtained SF values, averaged over three independent counting (from three different expert biologists L.M., F.P.C. and M.C. with 20, 14 and 12 years of experience in biomedicine and radiobiology research, respectively) measurements for each well, represent the ground-truth for the proposed multi-feature automatic clustering approach.
As illustrated in Table 1, for each cell line a specific number of plates was considered, treated with different doses of particles (i.e., protons, photons) and/or cytotoxic agent (i.e., curcumin, Cur-SNLB). The images of the plates were acquired by a general-purpose desktop flat-bed scanner.

Table 1.
Type of cell lines considered and number of wells processed in the experimental tests.
3.2. Cell Colony Feature Extraction
In addition to the conventional space color encoding of the input images, the entropy and SD were extracted as descriptive features. Entropy represents a statistical measure of randomness characterizing the input image texture, while SD represents a statistical term used to measure the amount of variability/dispersion around the average. In order to quantify these properties locally for each pixel of the well image , a square sliding window , centered on the pixel with , was considered. Unlike the RGB and L*u*v* encodings, with entropy and SD, even by means of a visual inspection, it is possible to note that colonies are more easily detectable. Entropy and SD, defined by Equations (1) and (2), were computed by using the built-in MatLab functions entropyfilt and stdfilt, respectively:
where:
- is the normalized gray level histogram counts for the current sliding window (obtained from the native RGB color space using the rgb2gray MatLab built-in function);
- and are the dimensions of the pixel matrix (, considering that the well, automatically detected, is circular);
- is the number of gray levels considered after the quantization (in our case, );
- is the local mean considering a sliding window of size .
For border pixels, symmetric padding was used: the values of padding pixels are a mirror reflection of the border pixels in the input image. Figure 2 and Figure 3 depict the entropy and the SD, respectively, obtained from each of the processed cells line. These texture features inherently rely upon the concept of symmetry in the pixel local distributions by extracting statistical measures, such as in the case of the Haralick’s features based on either a symmetric or non-symmetric Gray-Level Co-occurrence Matrix [43].
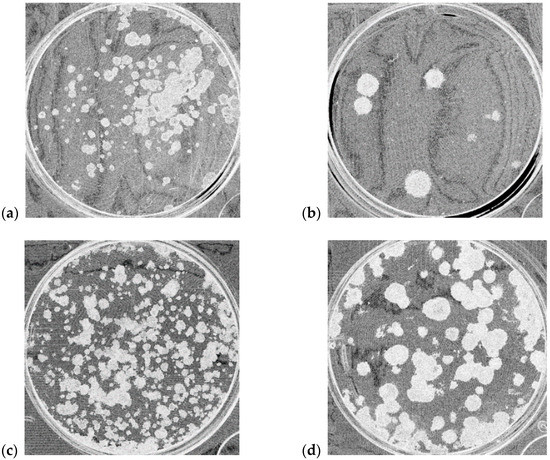
Figure 2.
The entropy feature extracted from the four-well image examples shown in Figure 1: (a) MCF7; (b) MCF10A; (c) T98G; (d) U251MG.
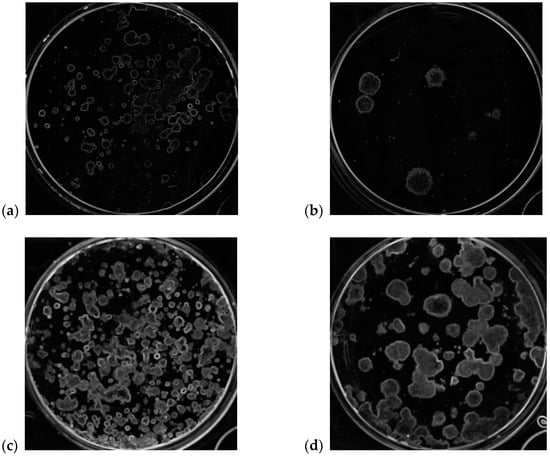
Figure 3.
The SD feature extracted from the four-well image examples shown in Figure 1: (a) MCF7; (b) MCF10A; (c) T98G; (d) U251MG.
3.3. Circle Hough Transform
The detection of the ROIs containing the cells is a fundamental step for accurate and reliable ACC quantification. In fact, if this step is based on manual procedures or relies on masks with a fixed position [18,19,20,21,22,23,24,25,30,35,36] it can easily produce misalignments, and the identification of the ROI (e.g., plate/well) is not perfect, causing colony quantification errors.
As in our previous work [6], we leverage a CHT-based strategy that automatically detects all the wells within the acquired cell images: in all the tests—carried out on 6-well plates—the detection of the regions to be processed has always been performed without errors and with a perfect alignment between the yielded circular ROIs and the corresponding wells.
Essentially, the CHT [10,11] converts a searching problem for circular curves in a simpler surface intersection search by means of a so-called accumulator matrix [44]. Since the radius of the well is known, the parameter space is generated, considering each pixel , by the center coordinates , according to Equation (3). In our application, the radius of each well is known according to the plate specifications. Considering that the CHT can find circles of a known radius, as well as circles having any radius, we parameterized the data relating to the various types of plates, so we just selected the plate to be processed and the tool automatically set the value of the well radius properly. In [6], we showed that the CHT-based method correctly detected the wells in 6-, 12-, 24-, and 48-well plates (produced by Corning® Inc., Corning, NY, USA). In this specific study, the experiments were performed only on 6-well plates, where each well has a diameter of 34.80 mm. Regardless of the number of wells, the image acquisitions on the scanner are always performed in the same way, in terms of both focal distance and resolution, so that the zoom factor does not change. The circle candidates are produced by voting in the parameter space center points , and then the local maxima are selected in the accumulator matrix. Formally, each point in the parameter space, representing a circle center, must meet conditions in Equation (4), where is the angular coordinate with respect to the positive x-axis, by using a polar coordinate system [45]:
3.4. Spatial FCM Clustering
To segment cell colonies within wells, instead of the traditional FCM algorithm [46,47], we used sFCM clustering, which integrates spatial information to enhance segmentation results [7]. The sFCM clustering approach takes a feature vector as input, composed of the entropy and SD local features for each pixel, and performs a separation between the two classes (i.e., cell colonies and background) by explicitly taking into account local properties.
The traditional unsupervised FCM algorithm aims at finding the intrinsic partitioning of an unlabeled dataset, , with N rows containing the input D-dimensional feature vectors (), into clusters (i.e., non-empty partitions of the input dataset), as introduced in [46,48]. An input dataset is sub-divided into groups (i.e., regions in image segmentation tasks), which are identified by a centroid. The number of clusters is assumed to be known a priori [9] and the output partition is a set family .
Differently from the crisp K-means algorithm [49], the FCM scheme allows for partial membership to multiple classes [50] with varying degrees by means of fuzzy logic [51]. Thus, the matrix denotes a fuzzy -partition of the set using the membership functions , with values representing the similarity membership of each element to the i-th fuzzy set (i.e., the cluster ) and must meet the following conditions:
Let be a set of D-dimensional prototype vectors, called centroids, which are associated with the C clusters. The membership function values are assigned to each feature vector in the data matrix according to the relative distance of each feature vector from the centroids in . Thus, this clustering algorithm aims to optimize the objective function in Equation (6), representing a generalized least-squares error problem:
where:
- is the fuzzification constant (weighting exponent: ) that determines the fuzziness degree of the classification process. If , the FCM algorithm approximates hard K-means. In general, the higher the value, the greater the fuzziness degree will be (the most common choice is );
- is the fuzzy -partition of the data matrix ;
- is the squared distance between and , computed through an induced norm on (usually the Euclidean norm).
Therefore, the data matrix is partitioned by iteratively searching for the optimal fuzzy partition , denoted by the pair , which locally minimizes the objective function . During the -th iteration, the prototype set , storing the centroid values , as well as the elements of the matrix are estimated and updated according to Equations (7) and (8), respectively:
Afterwards, each object is compared with the elements of the centroid set and is then mapped onto the nearest cluster. The iterative procedure ends when the convergence condition (i.e., the improvement of objective function between two consecutive iterations is lower than a fixed tolerance value ) or the maximum number of allowed iterations is reached. The initial partitions in are randomly generated by imposing that the sum of the elements of each column is equal to one. We set and in the criterion that compares the value of the objective function between two consecutive iterations.
However, the classic FCM clustering algorithm does not take into account any spatial relationship among pixels since all the samples are used as disperse and independent points, making it sensitive to noise and other imaging artefacts [52]. Accordingly, the integration of spatial information might be beneficial. The initial version of the sFCM algorithm was formulated as a regularization term to penalize the FCM objective function in Equation (6)—which relies upon pixel values alone regardless of their location—by conveying spatial information and constraining the behavior of the membership functions, similarly to methods used in the regularization and Markov Random Field (MRF) theory [53]. Thus, a fuzzy local similarity measure is integrated into its objective function, aimed at decreasing the sensitivity to noise, as well as preserving image details [54]. Accordingly, the objective function of the robust Fuzzy Local Information C-Means (FLICM) algorithm estimates spatially smooth membership functions by introducing a fuzzy factor as a regularizer via the -th pixel as the center of the local window defined by the neighborhood , i.e., a squared window of pixels.
The alternative sFCM version proposed by Chuang et al. [7], elegantly maintains the same formulation and objective function as the classic FCM algorithm described above, just by modifying the update rules with the local spatial content in the image. With the goal of exploiting the contextual information—denoted by the neighborhood , i.e., a squared window of pixels—a spatial function is defined as in [8,9]:
Basically, just like the membership function, the spatial function represents the membership degree of pixel belonging to the j-th cluster: the higher its values, the larger the number of neighbors that will belong to the same clusters. The spatial function modifies the membership function of a pixel according to the membership statistics of its neighbors as follows:
where is computed according to Equation (8). Finally, as in the case of the classic FCM algorithm, the centroid vector is updated according to Equation (7) by just using in place of . In particular, the parameters and control the contribution relative to the original membership (considering pixel intensity alone) and spatial components, respectively. As a special case, the pair denotes the traditional FCM algorithm.
The incorporation of the spatial component considerably improves the performance: (i) in a homogeneous region, the spatial functions emphasize the original membership, so the clustering results are not affected; (ii) in noisy regions, spurious blobs or misclassified pixels may be corrected.
3.5. Surviving Fraction Quantification
Conventional manual counting of cell colonies is performed by following the guidelines defined in [3]:
- The Plating Efficiency (η) represents the fraction of colonies formed from cells that were not exposed to the treatment, considering the number of grown colonies and the number of plated cells, and must be determined for each experiment;
- The Survival Fraction (SF) represents the surviving fraction of cells after any treatment (i.e., irradiation or cytotoxic agent), calculated taking into account the PE of untreated cells, the number of colonies grown after treatment and the number of plated cells.
The and SF are defined as in Equations (11) and (12), respectively. Similar to the conventional manual procedure, in our trials the SF is measured considering that the ACC of untreated cells is the reference (100%), and then it is used to normalize the treated SF, as in Equation (13):
3.6. MF2C3 Parameter Settings
To determine the best settings for MF2C3, we relied upon the relevant literature work, as well as on experimental evidence. With reference to the sFCM algorithm, the neighborhood, which incorporates the spatial information, was defined via a squared window of size pixels, where was used in all the tests according to [7]. Regarding the parameters and (i.e., the pixel intensity and spatial information weights in Equation (10)), Chuang et al. compared the pairs (i.e., the traditional FCM), , and on multiple brain Magnetic Resonance Imaging (MRI) sequences [55]; overall, the configuration yielded the best clustering performance even on noisy images. These findings were confirmed in [9]. Therefore, for a balance between the intensity and spatial components, as well as being supported by [7,9], both the functioning parameters and were set to 1 in our implementation.
Since this is the first approach based on local descriptors for clonogenic assay evaluation, we investigated the size of the sliding window , composed of pixels, since it might affect the extracted textural information [56]. With this goal, we considered a calibration set consisting of 20 randomly selected images (5 for each cell line described in Section 3.1) and the values were tested in terms of the clonogenic assay evaluation performance, measured as the absolute error between the automatic area-based SF against the manual gold-standard measurement (i.e., ). More specifically, the extracted feature vectors were fed into the sFCM clustering (with the configuration ) and the area-based SF was calculated. The line plot (with the dots and error bars denoting the average absolute error and standard deviation for each setting, respectively) in Figure 4 depicts the trend of the results obtained by varying the parameter . The setting with achieved the best performance, obtaining both the lowest mean absolute error and standard deviation. As a final design choice, we consistently maintained the same size for both the sliding window (with pixels) and the squared neighborhood (with size pixels) employed in the spatial FCM clustering algorithm. Therefore, also supported by the literature about local feature extraction [56], we set pixels for all the experiments.
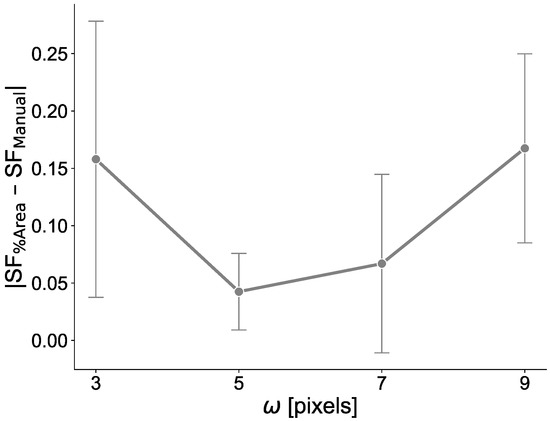
Figure 4.
Parameter setting of the sliding window used for the local feature extraction (with size ω × ω pixels), in terms of the absolute error by considering ω ∈ {3, 5, 7, 9}. The calibration set was composed of 20 randomly selected images (5 for each cell line). The dots and the error bars denote the mean and standard deviation for each setting, respectively.
4. The Proposed Multi-Feature Automatic Clustering Approach
This section describes the proposed approach that, exploiting a multi-feature fuzzy clustering, enhances the automatic clonogenic assay quantification. Figure 5 shows the flow diagram with the main steps composing the processing pipeline. Starting from the acquired plate image, the wells are automatically detected and, successively, the cell colonies detected. The SF is quantified by considering the ACC, according to Equation (13). It should be noted that the SF value obtained by our approach could represent an equivalent measure of the traditional SF obtained by counting the number of colonies. However, as previously confirmed in [6], these SF values are highly correlated with traditional SFs (in terms of Pearson’s correlation coefficient r). To some extent, ACC-based SF might be readily integrated into the biological practice, even though radiobiological models (such as the linear-quadratic model) are based on the number of colonies according to curve fitting over multiple time-points. The biological heterogeneity between the different cell lines is directly correlated not just to capacity with the ability to form colonies, but results also in a greater or lesser tendency to take dye. As the experimental results have shown, this phenotypic heterogeneity means that this measure is more correct as the colonies are easier to detect.
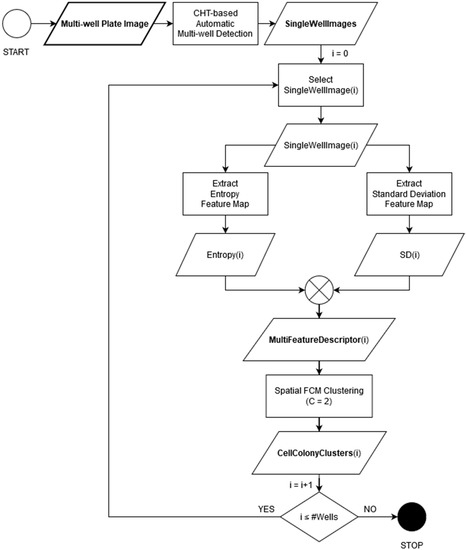
Figure 5.
Overall flow diagram of MF2C3, the proposed multi-feature spatial Fuzzy C-Means (sFCM) clustering approach for automatic clonogenic assay evaluation. The data block with thick-line borders represents the input multi-well plate image. The bold variable names denote vectors composed of single-well images, feature maps or cell colony clusters.
Considering that the proposed approach represents an evolution of our previous work already validated in [6], some of the processing pipeline steps are maintained. Indeed, the proposed approach exploits the CHT [10,11] to automatically detect the wells in the input multi-well plate image: this represents a significant facilitation for the operator, who does not have to identify each well manually or by means of fixed/pre-computed masks. Subsequently, in order to enhance the contrast between the colonies and the background, each well undergoes gamma correction with unitary constant factor and exponent to slightly increase the pixel intensity values [57].
Focusing on the main processing phase, i.e., the colony detection and segmentation, this approach proposed two novelties with respect to the method in [6]: (i) entropy and SD local descriptors are used instead of the L*u*v* color space, and (ii) the sFCM clustering is used for colony detection instead of adaptive thresholding. These choices, which leverage the local image features, improve the discriminating power of the approach on the previously processed cell lines (i.e., MCF7 and MCF10A), as well as on cell lines slightly more difficult to quantify (e.g., T98G and U251MG). Entropy and SD are concatenated together to make a multi-feature descriptor [58], which is the input of the sFCM clustering.
The proposed method was implemented by using the MatLab® development environment (The MathWorks, Natick, MA, USA) version 2016b. The Graphical User Interface (GUI) exploited the built-in MatLab GUI Development Environment (GUIDE).
Figure 6 illustrates the GUI of the tool implemented by exploiting the proposed multi-feature automatic approach, while Figure 7 shows one segmentation example achieved using the sFCM clustering algorithm with two classes () for each cell line by also displaying a detail of the analyzed well with over-imposed segmentation results.
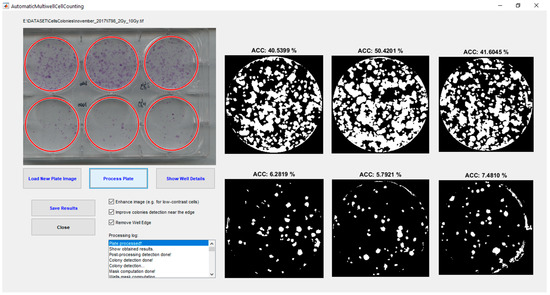
Figure 6.
Graphical User Interface (GUI) of the proposed automatic approach for clonogenic evaluation.


Figure 7.
Colony segmentation results obtained by using MF2C3, via sFCM clustering with C = 2 using the entropy and SD descriptors extracted from the input images in Figure 1: (a) MCF7; (b) MCF10A; (c) T98G; (d) U251MG. For each sub-image, a portion of the well is enlarged by over-imposing the corresponding segmentation result via a red contour.
5. Experimental Results
The SF values automatically obtained by considering the percentage of ACC were compared against the conventional measurement based on colony counting alone. In order to quantify the performance of the proposed multi-feature approach, the correlation between the manual numerical quantification of the clonogenic and the well ACC was evaluated. More specifically, the automated results were compared and correlated against SFs obtained by the manual counting procedure. Figure 8 depicts the scatter plots concerning the proposed automatic multi-feature SF (SF%Area) versus the manual colony counts (SFManual). Each diagram shows the correlation coefficients obtained on MCF7, MCF10, T98G, and U251MG cell cultures (by exploiting 79, 40, 40, and 40 samples, respectively) treated with different doses of radiation or cytotoxic agent. The experimental findings, in terms of coefficient values, showed a high level of correlation between multi-feature automatic approach and manual cell colony quantification for all the analyzed cell lines. More specifically: Figure 8a shows excellent results; in Figure 8b, the equality straight-line reveals a positive offset in the SF%Area measurements, by slightly over-estimating the manual colony counts SFManual (in approximately 52% of the cases for SF%Area > 0.40); on the contrary, Figure 8c is characterized by a moderate negative offset in the SF%Area measurements for 60% of the samples; considering SF%Area < 0.45, the results automatically obtained by MF2C3 on the U251MG cell line (Figure 8d) slightly over-estimate the manual measurements in about 62% of the samples. We can conclude that, considering the four different experimental data, no systematic error is found in terms of under-/over-estimation.
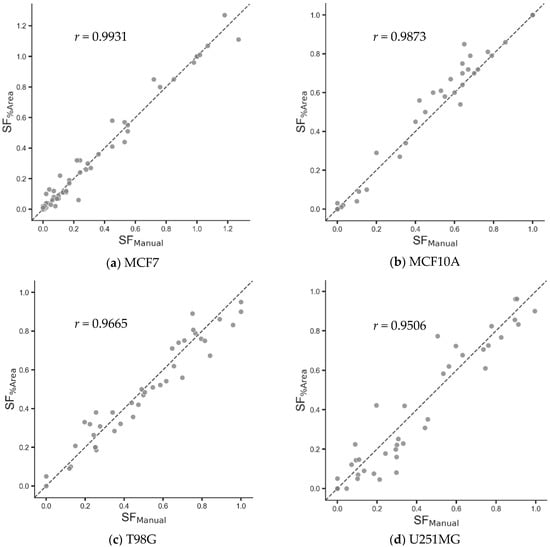
Figure 8.
Scatter plots of the automated MF2C3 Area Covered by Colony (ACC)-based Surviving Fraction (SF) evaluation (SF%Area) versus the mean manual colony counting measurements (SFManual) from three distinct biologists, for: (a) MCF7, (b) MCF10A, (c) T98G, and (d) U251MG cell lines. Each diagram reports data related to the proposed detection approach exploiting multi-feature spatial FCM, using entropy and standard deviation as descriptive features of the colonies. The equality line through the origin is drawn as a dashed line and each diagram also displays the corresponding Pearson’s correlation coefficient.
More details about the Pearson’s linear correlation coefficient calculation are depicted in Table 2. The correlation coefficients obtained by MF2C3 were compared against the approach proposed in [6], which makes use of an adaptive thresholding on the image in the L*u*v* color space. We used the Fisher’s z-transformation to assess the significance of the difference between two Pearson’s correlation coefficients [59], by using a significance level of 0.05. In all the tested cell lines, MF2C3 achieved the highest Pearson’s correlation coefficients, by significantly outperforming the thresholding-based approach in [6] in the case of MCF7. MCF10A, and U251MG cell lines. In particular, the clonogenic assays with U251MG cells were found to be the most challenging to evaluate.

Table 2.
Pearson’s correlation coefficient between the automatic ACC-based SF values (SF%Area) and the conventional colony counting measurements (SFManual) on the analyzed MCF7, MCF10A, T98G, and U251MG cell lines. The results achieved by MF2C3 are compared against the approach proposed in [6]. The corresponding significance level (p value) and the statistical significance between the correlation coefficients was assessed by the Fisher’s z-transformation. Boldface values indicate statistical significance.
The agreement between the developed automatic area-based approaches and the manual colony counting measurement can be graphically represented by the Bland–Altman plot in Figure 9 for all the four analyzed cell types [60]. As a matter of fact, along with correlation coefficients, the Bland–Altman analysis better displays the data by plotting the pairwise difference between the measurements by the two methods against their mean. This representation allows us to investigate any possible relationship between the discrepancies and the ground-truth value. With more details, the 95% limits of agreement, estimated by mean difference 1.96 standard deviation of the differences, clearly help to detect any outliers (i.e., extreme observations). Figure 9 reveals that both MF2C3 and the previous work in [6] (denoted as red and blue circles, respectively) achieved reproducible results also considering the whole range of the SF measurements concerning the analyzed cell lines. In particular, MF2C3 consistently presents lower difference values (i.e., samples mostly concentrated along the mean line), as well as a smaller number of outliers (especially, in the case of the T98G and U251MG cell lines), compared to the thresholding-based approach in [6]. Confirming the findings from Figure 8, neither systematic discrepancy between the measurements nor bias can be observed.
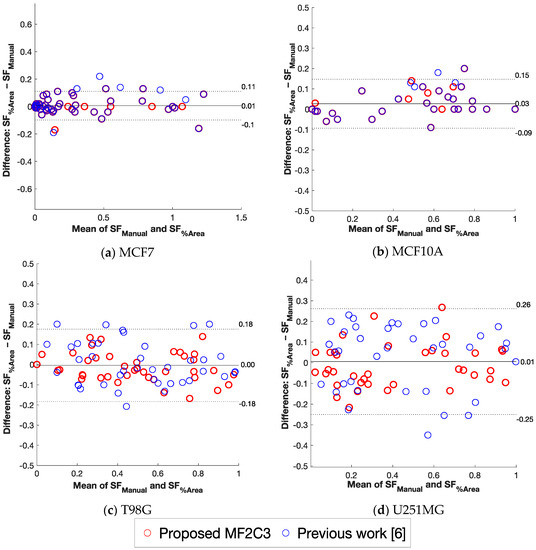
Figure 9.
Bland–Altman plots of the automated ACC-based SF evaluation (SF%Area) versus the manual colony counting measurements (SFManual), for: (a) MCF7, (b) MCF10A, (c) T98G, and (d) U251MG cell lines. The results yielded by the proposed MF2C3 approach and the previous work [6] are displayed as red and blue circles, respectively. Solid horizontal and dashed lines denote the mean and ±1.96 standard deviation values, respectively.
6. Discussion and Comparisons
In the literature, there are several approaches that cope with clonogenic assay quantification (Table 3). The main reason that leads to the use of automatic or semi-automatic methodologies lies in the possibility that computer-aided approaches can reduce or eliminate the subjectivity of the manual procedure, currently still widely used. Although some solutions are really interesting and valid, none of these methods fully solves all the problems. As a matter of fact, numerous approaches require specific hardware in order to acquire the cell colony images [18,19,20,21]. These solutions—specifically designed and implemented—implement systems for the correct illumination and positioning of the plates containing the cell cultures. The aim is to have a ‘controlled environment’ to avoid misalignments and be capable of reducing the variability of ambient lighting during the acquisition phase and improving/facilitating subsequent processing. Other literature approaches have been developed and tested taking bacteria or microorganism colonies (e.g., Staphylococcus aureus, Streptococcus pneumonia, Escherichia coli) as a reference [22,23,24,25,26]. This means that, in the processing pipeline, these methodologies often deal with the identification of circular-shaped objects. The approach in [26] developed to be used also with the SP-SDS technique differs from the others. This is certainly valid, but it should be noted that also in this case the experimental results were obtained on images of bacterial colonies, which produce colonies practically punctiform, with an almost perfectly circular shape and rarely give rise to agglomerations. Moreover, in [30,31,32,33,34,35], the colonies produced by cell cultures are circular and almost always separate from each other. This alleviates the issues in distinguishing and quantifying colonies. This represents a very simple operating scenario, which does not always correspond to real case studies in human cells. Indeed, human cell colonies can have very jagged contours and variable shapes. Finally, fully automatic systems reduce operator dependency and the consequent variability of results which can affect test repeatability. For this reason, in addition to having automatic systems for the segmentation of the colonies, it is appropriate that the detection phase of the ROI containing the colonies is also automatic (e.g., Petri plates, circular wells in a multi-well plate, rectangular flasks).

Table 3.
Comparison among the related literature approaches.
Most literature approaches [18,19,20,21,22,24,25,30,35,36] used fixed positioning masks or manual procedures for the identification of the ROI containing the colonies. For this reason, we used the CHT for automatic well detection. It is not the first time in the literature that the Hough transform has been applied to the problem by the clonogenic assay [23,30]. However, in [30], the CHT was not used for the well detection, but for colonies detection, which were approximated to circular objects. Instead, our automatic well detection procedure leverages the CHT, thus eliminating the misalignment errors of the plate during the acquisition phase.
Summarizing, the main characteristics of MF2C3 are the following:
- Fully automatic approach that does not require any human intervention, allowing for eliminating the subjectivity of the quantification;
- No need for specific hardware during the images acquisition phase. Since just a general-purpose flat-bed scanner is required, every laboratory can use our approach, without having to acquire any additional hardware;
- Using a multi-feature local descriptor as input of the sFCM clustering algorithm for cell colony detection. This novel approach, exploiting entropy and SD, was tested on four human cell lines and obtained excellent results.
Many experimental trials were carried out in order to test the validity of the proposed approach. In particular, Table 2 shows that, in the case of the MCF7 and MCF10A cell lines, the multi-feature approach achieves a higher correlation coefficient than in [6] (exploiting L*u*v* coding and adaptive thresholding). With slightly more difficult cell lines to detect (i.e., T98G and U251MG), the MF2C3 obtains higher correlation results. For completeness, we performed again segmentations and reported the results on these last cell lines, obtaining much lower correlation values, due to the fact that with the difficult lines the approach in [6] does not properly work. Overall, the experimental results obtained demonstrate how this new multi-feature approach, which combines entropy and SD, improves the performance of validated single-feature approaches.
7. Conclusions
Clonogenic assay evaluation represents a technique widely used in biological research, aimed at quantifying the effect of a specific treatment (e.g., radiation, cytotoxin agent) with antitumoral/antiproliferative effects. Unfortunately, the current identification of colonies (i.e., CFUs) is not a straightforward procedure to be performed manually under a stereomicroscope, because some cell lines are particularly ‘difficult’, requiring special and careful procedures to be quantified, through microscopic analysis. Furthermore, this time-consuming methodology, which still today relies upon human quantification, is affected by intra- and inter-operator variability. There are several approaches in the literature, proposing computer-aided methods, but none of these completely solves the problem.
Starting from our previous validated approach in [6], developed and tested on the MCF7 and MCF10A human cell lines, here we aimed to address the quantification of cell lines that are slightly more difficult to quantify, such as T98G and U251MG, since they produce low-contrast colonies. The proposed multi-feature approach MF2C3, jointly exploiting entropy and standard deviation, aims to enhance the colonies detection with respect to the background. The use of these two local features and an unsupervised Machine Learning approach, namely the sFCM clustering algorithm [7], allowed us to implement—leveraging also the CHT [10,44]—a fully automatic approach for accurate clonogenic quantification based on ACC. In order to quantify the effectiveness of the proposed approach, the automated ACC-based SF evaluation (SF%Area) showed high correlation values against the manual colony counting measurements (SFManual) on the MCF7, MCF10A, T98G, and U251MG human cells lines. Overall, MF2C3, which relies upon the concept of symmetry in the pixel local distributions, significantly outperformed our previous thresholding-based approach presented in [6].
In the near future, we plan to increase the number of samples per experimental setting, as well as test MF2C3 on other cell lines according to the next biological in vivo studies [61]. Moreover, we aim at improving colony counting also by splitting the merged colonies by means of watershed-based approaches [62]. Our ultimate goal is to integrate the reliable results achieved by MF2C3 into quantitative biology analyses involving the evaluation of antiproliferative drug effects [63], by also being beneficial to Systems Biology models [64].
Author Contributions
Conceptualization, C.M., L.R., L.M., F.P.C. and G.R.; methodology, C.M., L.R. and V.C.; software, M.C.; validation, C.M., L.R., L.M., F.P.C. and M.C.; formal analysis, C.M. and L.R.; investigation, C.M., L.R., L.M., F.P.C., M.C. and V.C.; resources, C.M., L.M., F.P.C., V.C. and G.R.; data curation, C.M., L.M., F.P.C. and M.C.; writing—original draft preparation, C.M. and L.R.; writing—review and editing, C.M., L.R., L.M., F.P.C., M.C., V.C. and G.R.; visualization, C.M. and L.R.; supervision, G.R.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Puck, T.T.; Marcus, P.I. Action of x-rays on mammalian cells. J. Exp. Med. 1956, 103, 653–666. [Google Scholar] [CrossRef] [PubMed]
- Chapman, J.D. Can the two mechanisms of tumor cell killing by radiation be exploited for therapeutic gain? J. Radiat. Res. 2014, 55, 2–9. [Google Scholar] [CrossRef] [PubMed]
- Franken, N.A.; Rodermond, H.M.; Stap, J.; Haveman, J.; van Bree, C. Clonogenic assay of cells in vitro. Nat. Protoc. 2006, 1, 2315–2319. [Google Scholar] [CrossRef] [PubMed]
- Lumley, M.A.; Burgess, R.; Billingham, L.J.; McDonald, D.F.; Milligan, D.W. Colony counting is a major source of variation in CFU-GM results between centres. Br. J. Haematol. 1997, 97, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Nuryadi, E.; Komatsu, S.; Hirota, Y.; Shibata, A.; Oike, T.; Nakano, T. Robustness of clonogenic assays as a biomarker for cancer cell radiosensitivity. Int. J. Mol. Sci. 2019, 20, 4148. [Google Scholar] [CrossRef]
- Militello, C.; Rundo, L.; Conti, V.; Minafra, L.; Cammarata, F.P.; Mauri, G.; Gilardi, M.C.; Porcino, N. Area-based cell colony surviving fraction evaluation: A novel fully automatic approach using general-purpose acquisition hardware. Comput. Biol. Med. 2017, 89, 454–465. [Google Scholar] [CrossRef]
- Chuang, K.S.; Tzeng, H.L.; Chen, S.; Wu, J.; Chen, T.J. Fuzzy c-means clustering with spatial information for image segmentation. Comput. Med. Imaging Graph. 2006, 30, 9–15. [Google Scholar] [CrossRef]
- Li, Y.l.; Shen, Y. An automatic fuzzy c-means algorithm for image segmentation. Soft Comput. 2010, 14, 123–128. [Google Scholar] [CrossRef]
- Li, B.N.; Chui, C.K.; Chang, S.; Ong, S.H. Integrating spatial fuzzy clustering with level set methods for automated medical image segmentation. Comput. Biol. Med. 2011, 41, 1–10. [Google Scholar] [CrossRef]
- Hough, P.V.C. Method and Means for Recognizing Complex Pattern. U.S. Patent 3,069,654, 18 December 1962. [Google Scholar]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Thielmann, H.W.; Hagedorn, R.; Freber, W. Evaluation of colony-forming ability experiments using normal and DNA repair-deficient human fibroblast strains and an automatic colony counter. Cytometry 1985, 6, 130–136. [Google Scholar] [CrossRef] [PubMed]
- Parry, R.L.; Chin, T.W.; Donahoe, P.K. Computer-aided cell colony counting. Biotechniques 1991, 10, 772–774. [Google Scholar] [PubMed]
- Wilson, I.G. Use of the IUL Countermat automatic colony counter for spiral plated total viable counts. Appl. Environ. Microbiol. 1995, 61, 3158–3160. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, D.P.; Pal, A.; Sarma, S.E.; Majumder, D.D. Bacterial colony counting using distance transform. Int. J. Biomed. Comput. 1995, 38, 131–140. [Google Scholar] [CrossRef]
- Hoekstra, S.J.; Tarka, D.K.; Kringle, R.O.; Hincks, J.R. Development of an automated bone marrow colony counting system. In Vitro Toxicol. 1998, 11, 207–213. [Google Scholar]
- Dobson, K.; Reading, L.; Scutt, A. A cost-effective method for the automatic quantitative analysis of fibroblastic colony-forming units. Calcif. Tissue Int. 1999, 65, 166–172. [Google Scholar] [CrossRef]
- Barber, P.R.; Vojnovic, B.; Kelly, J.; Mayes, C.R.; Boulton, P.; Woodcock, M.; Joiner, M.C. Automated counting of mammalian cell colonies. Phys. Med. Biol. 2001, 46, 63–76. [Google Scholar] [CrossRef]
- Bernard, R.; Kanduser, M.; Pernus, F. Model-based automated detection of mammalian cell colonies. Phys. Med. Biol. 2001, 46, 3061–3072. [Google Scholar] [CrossRef]
- Dahle, J.; Kakar, M.; Steen, H.B.; Kaalhus, O. Automated counting of mammalian cell colonies by means of a flat bed scanner and image processing. Cytom. Part A 2004, 60, 182–188. [Google Scholar] [CrossRef]
- Siragusa, M.; Dall’Olio, S.; Fredericia, P.M.; Jensen, M.; Groesser, T. Cell colony counter called CoCoNut. PLoS ONE 2018, 13, e0205823. [Google Scholar] [CrossRef]
- Clarke, M.L.; Burton, R.L.; Hill, A.N.; Litorja, M.; Nahm, M.H.; Hwang, J. Low-cost, high-throughput, automated counting of bacterial colonies. Cytom. Part A 2010, 77, 790–797. [Google Scholar] [CrossRef] [PubMed]
- Geissmann, Q. OpenCFU, a new free and open-source software to count cell colonies and other circular objects. PLoS ONE 2013, 8, e54072. [Google Scholar] [CrossRef] [PubMed]
- Chiang, P.J.; Tseng, M.J.; He, Z.S.; Li, C.H. Automated counting of bacterial colonies by image analysis. J. Microbiol. Methods 2015, 108, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.U.M.; Torelli, A.; Wolf, I.; Gretz, N. AutoCellSeg: Robust automatic colony forming unit (CFU)/cell analysis using adaptive image segmentation and easy-to-use post-editing techniques. Sci. Rep. 2018, 8, 7302. [Google Scholar] [CrossRef] [PubMed]
- Boukouvalas, D.T.; Prates, R.A.; Leal, C.R.L.; de Araújo, S.A. Automatic segmentation method for CFU counting in single plate-serial dilution. Chemometr. Intell. Lab. Syst. 2019, 195, 103889. [Google Scholar] [CrossRef]
- Najman, L.; Couprie, M.; Bertrand, G. Watersheds, mosaics, and the emergence paradigm. Discret. Appl. Math. 2005, 147, 301–324. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Boukouvalas, D.T.; Belan, P.; Leal, C.R.L.; Prates, R.A.; de Araújo, S.A. Automated colony counter for single plate serial dilution spotting. In Proceedings of the Iberoamerican Congress on Pattern Recognition (CIARP), Madrid, Spain, 19–22 November 2018; Springer International Publishing: Cham, Switzerland, 2018; Volume 11401, pp. 410–418. [Google Scholar]
- Bewes, J.M.; Suchowerska, N.; McKenzie, D.R. Automated cell colony counting and analysis using the circular Hough image transform algorithm (CHiTA). Phys. Med. Biol. 2008, 53, 5991–6008. [Google Scholar] [CrossRef]
- Marotz, J.; Lubbert, C.; Eisenbeiss, W. Effective object recognition for automated counting of colonies in Petri dishes (automated colony counting). Comput. Methods Programs Biomed. 2001, 66, 183–198. [Google Scholar] [CrossRef]
- Niyazi, M.; Niyazi, I.; Belka, C. Counting colonies of clonogenic assays by using densitometric software. Radiat. Oncol. 2007, 2, 4. [Google Scholar] [CrossRef]
- Wouters, A.; Pauwels, B.; Lambrechts, H.A.J.; Pattyn, G.G.O.; Ides, J.; Baay, M.; Meijnders, P.; Lardon, F.; Vermorken, J.B. Counting clonogenic assays from normoxic and anoxic irradiation experiments manually or by using densitometric software. Phys. Med. Biol. 2010, 55, N167–N178. [Google Scholar] [CrossRef] [PubMed]
- Choudhry, P. High-throughput method for automated colony and cell counting by digital image analysis based on edge detection. PLoS ONE 2016, 11, e0148469. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Chattopadhyay, N.; Liu, W.J.; Chan, C.; Pignol, J.P.; Reilly, R.M. Optimized digital counting colonies of clonogenic assays using ImageJ software and customized macros: Comparison with manual counting. Int. J. Radiat. Biol. 2011, 87, 1135–1146. [Google Scholar] [CrossRef] [PubMed]
- Guzman, C.; Bagga, M.; Kaur, A.; Westermarck, J.; Abankwa, D. ColonyArea: An ImageJ plugin to automatically quantify colony formation in clonogenic assays. PLoS ONE 2014, 9, e92444. [Google Scholar] [CrossRef]
- Szénási, S.; Vámossy, Z.; Kozlovszky, M. Evaluation and comparison of cell nuclei detection algorithms. In Proceedings of the 16th IEEE International Conference on Intelligent Engineering Systems (INES), Lisbon, Portugal, 13–15 June 2012; pp. 469–475. [Google Scholar] [CrossRef]
- Neve, R.M.; Chin, F.; Fridlyand, J.; Yeh, J.; Baehner, F.L.; Fevr, T.; Clark, L.; Bayani, N.; Coppe, J.P.; Tong, F.; et al. A collection of breast cancer cell lines for the study of functionally distinct cancer subtypes. Cancer Cell 2006, 10, 515–527. [Google Scholar] [CrossRef]
- Bravatà, V.; Minafra, L.; Russo, G.; Forte, G.I.; Cammarata, F.P.; Ripamonti, M.; Casarino, C.; Augello, G.; Costantini, F.; Barbieri, G.; et al. High dose ionizing radiation regulates gene expression changes in MCF7 breast cancer cell line. Anticancer Res. 2015, 35, 2577–2591. [Google Scholar]
- Minafra, L.; Bravatà, V.; Russo, G.; Forte, G.I.; Cammarata, F.P.; Ripamonti, M.; Candiano, G.; Cervello, M.; Giallongo, A.; Perconti, G.; et al. Gene expression profiling of MCF10A breast epithelial cells exposed to IOERT. Anticancer Res. 2015, 35, 3223–3234. [Google Scholar]
- Rennerfeldt, D.A.; Van Vliet, K.J. Concise review: When colonies are not clones: Evidence and implications of intracolony heterogeneity in mesenchymal stem cells. Stem Cells 2016, 34, 1135–1141. [Google Scholar] [CrossRef]
- Amsterdam, A.; Shezen, E.; Raanan, C.; Schreiber, L.; Slilat, Y.; Fabrikant, Y.; Melzer, E. Differential staining of γ synuclein in poorly differentiated compared to highly differentiated colon cancer cells. Oncol. Rep. 2012, 27, 1451–1454. [Google Scholar] [CrossRef][Green Version]
- Rundo, L.; Tangherloni, A.; Galimberti, S.; Cazzaniga, P.; Woitek, R.; Sala, E.; Nobile, M.S.; Mauri, G. HaraliCU: GPU-powered Haralick feature extraction on medical images exploiting the full dynamics of gray-scale levels. In Proceedings of the 14th International Conference on Parallel Computing Technologies (PaCT), Almaty, Kazakhstan, 19–23 August 2019; Springer International Publishing: Cham, Switzerland, 2019; Volume 11657, pp. 304–318. [Google Scholar] [CrossRef]
- Illingworth, J.; Kittler, J. The adaptive Hough transform. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 690–698. [Google Scholar] [CrossRef]
- Atherton, T.J.; Kerbyson, D.J. Size invariant circle detection. Image Vis. Comput. 1999, 17, 795–803. [Google Scholar] [CrossRef]
- Bezdek, J.C. Objective function clustering. In Pattern Recognition with Fuzzy Objective Function Algorithms, 1st ed.; Springer-Verlag New York, Inc.: Secaucus, NJ, USA, 1981; pp. 43–93. ISBN 978-1-4757-0452-5. [Google Scholar] [CrossRef]
- Rundo, L.; Militello, C.; Russo, G.; Garufi, A.; Vitabile, S.; Gilardi, M.C.; Mauri, G. Automated prostate gland segmentation based on an unsupervised fuzzy C-means clustering technique using multispectral T1w and T2w MR imaging. Information 2017, 8, 49. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inform. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Udupa, J.K.; Samarasekera, S. Fuzzy connectedness and object definition: Theory, algorithms, and applications in image segmentation. Graph. Models Image Process. 1996, 58, 246–261. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Chen, S.C. A novel kernelized fuzzy c-means algorithm with application in medical image segmentation. Artif. Intell. Med. 2004, 32, 37–50. [Google Scholar] [CrossRef]
- Caponetti, L.; Castellano, G.; Corsini, V. MR brain image segmentation: A framework to compare different clustering techniques. Information 2017, 8, 138. [Google Scholar] [CrossRef]
- Pham, D.L. Spatial models for fuzzy clustering. Comput. Vis. Image Underst. 2001, 84, 285–297. [Google Scholar] [CrossRef]
- Gong, M.; Liang, Y.; Shi, J.; Ma, W.; Ma, J. Fuzzy c-means clustering with local information and kernel metric for image segmentation. IEEE Trans. Image Process. 2012, 22, 573–584. [Google Scholar] [CrossRef]
- Rundo, L.; Militello, C.; Russo, G.; Vitabile, S.; Gilardi, M.C.; Mauri, G. GTVcut for neuro-radiosurgery treatment planning: An MRI brain cancer seeded image segmentation method based on a cellular automata model. Nat. Comput. 2017, 17, 521–536. [Google Scholar] [CrossRef]
- Bouteldja, S.; Kourgli, A. An efficient CBIR system for high resolution remote sensing images. In Proceedings of the Iberoamerican Congress on Pattern Recognition (CIARP), Madrid, Spain, 19–22 November 2018; Springer International Publishing: Cham, Switzerland, 2018; Volume 11401, pp. 392–400. [Google Scholar] [CrossRef]
- Rundo, L.; Tangherloni, A.; Nobile, M.S.; Militello, C.; Besozzi, D.; Mauri, G.; Cazzaniga, P. MedGA: A novel evolutionary method for image enhancement in medical imaging systems. Expert Syst. Appl. 2019, 119, 387–399. [Google Scholar] [CrossRef]
- Nanni, L.; Brahnam, S.; Salvatore, C.; Castiglioni, I. Texture descriptors and voxels for the early diagnosis of Alzheimer’s disease. Artif. Intell. Med. 2019, 97, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.L.; Rosenthal, R.; Rubin, D.B. Comparing correlated correlation coefficients. Psychol. Bull. 1992, 111, 172. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Minafra, L.; Porcino, N.; Bravatà, V.; Gaglio, D.; Bonanomi, M.; Amore, E.; Cammarata, F.P.; Russo, G.; Militello, C.; Savoca, G.; et al. Radiosensitizing effect of curcumin-loaded lipid nanoparticles in breast cancer cells. Sci. Rep. 2019, 9, 11134. [Google Scholar] [CrossRef]
- Gamarra, M.; Zurek, E.; Escalante, H.J.; Hurtado, L.; San-Juan-Vergara, H. Split and merge watershed: A two-step method for cell segmentation in fluorescence microscopy images. Biomed. Signal Process. Control 2019, 53, 101575. [Google Scholar] [CrossRef]
- Harris, L.A.; Frick, P.L.; Garbett, S.P.; Hardeman, K.N.; Paudel, B.B.; Lopez, C.F.; Quaranta, V.; Tyson, D.R. An unbiased metric of antiproliferative drug effect in vitro. Nat. Methods 2016, 13, 497–500. [Google Scholar] [CrossRef]
- Ortega, O.O.; Lopez, C.F. Interactive multiresolution visualization of cellular network processes. iScience 2020, 23, 100748. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).