Similar Seismic Activities Analysis by Using Complex Networks Approach
Abstract
1. Introduction
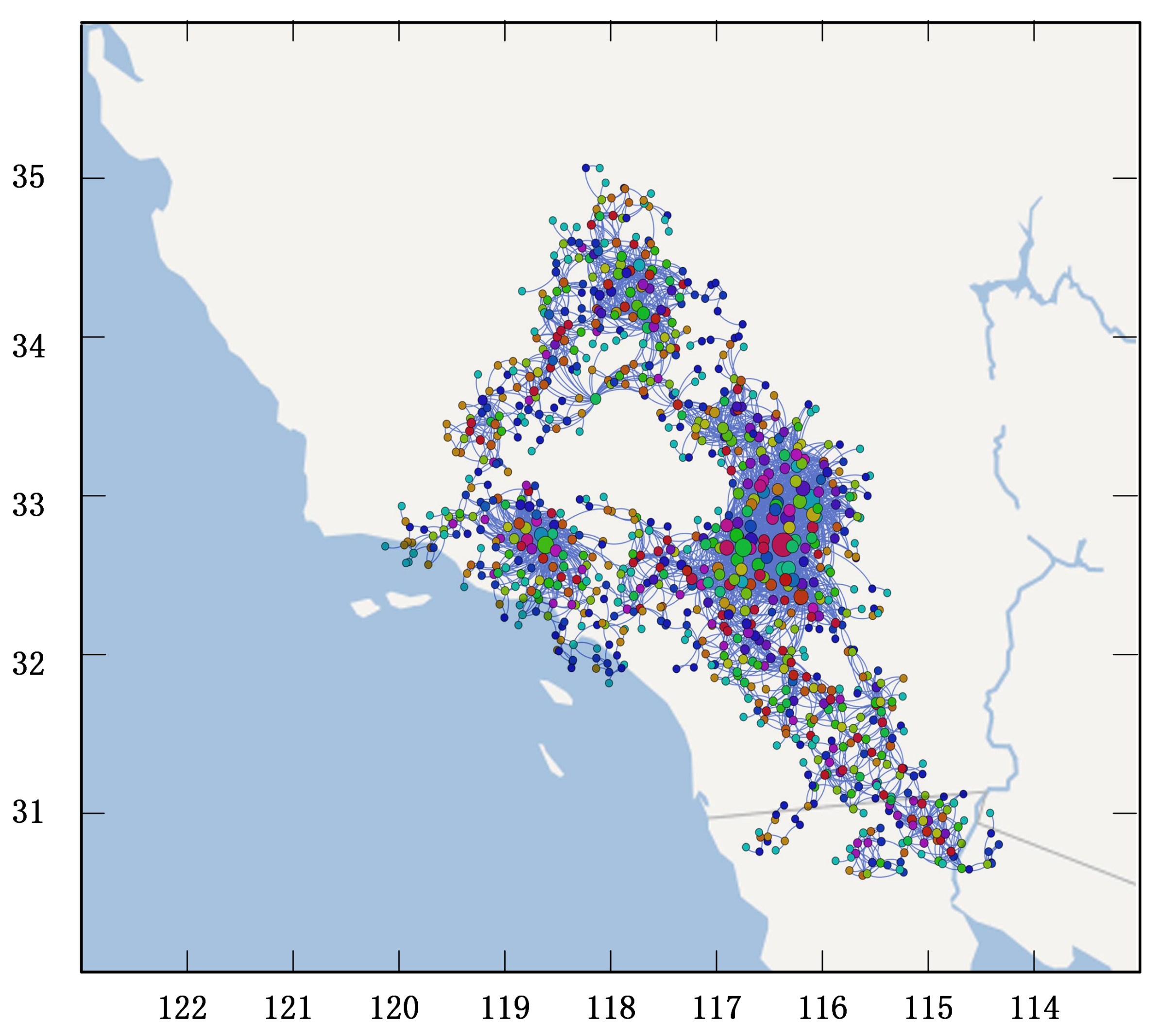
2. Data and Network Construction
- a
- Southern California Seismic Network (SCSN). California belongs to the Pacific Rim seismic zone, where earthquakes occur frequently. The center provides seismic data for the California region for more than 80 years from 1932 to the present, with more than 500,000 public seismic records. With the continuous improvement of data acquisition and measurement methods, SCSN has more than 400 detection stations in different places.
- b
- Japan University Network Earthquake Catalog (JUNEC). Japan is located at the junction of the Asia–Europe plate and the Pacific plate, belongs to the Pacific Rim seismic zone. The crustal movement is active, so Japan is a country with frequent earthquakes. JUNEC provides seismic data for the geographical region of Japan from 1985 to 1998.
- c
- Advanced National Seismic System (ANSS). ANSS includes a national Backbone network, the National Earthquake Information Center (NEIC), the National Strong Motion Project, and 15 regional seismic networks operated by USGS and its cooperative organizations. This system provides a huge amount of worldwide seismic data, close to 3 million records.
3. Method
3.1. Basic Network Properties
- a
- Degree distribution is the probability distribution of the degrees k over the whole network. Scale-free property of earthquake networks with has been studied by many studies [9,14,16]. The exponent is proved to approach a fixed value, remaining invariant, as the cell size becomes larger than a certain value [35].
- b
- Strength of the node is defined as , where is the weight of a connection between two different nodes as mentioned before. Here we use average strength to describe the average influencing degree among nodes in the network. It has been observed that the probability distributions of nodal strengths follow power law decay forms. Chakraborty et al. used strengths to analyze the rich-club feature in the weighted earthquake network. However, this feature is not found in unweighted network [36].
- c
- Clustering coefficient is the ratio of existing edges connecting a node’s neighbors to each other to the maximum possible number of such edges. The weighted clustering coefficient [37] is defined as where (s) are the elements of the adjacency matrix. The average clustering coefficient is defined by . The clustering coefficient has been investigated in many studies of earthquake network [10,14,19]. It implies the degree of clustering of the network. Abe et al. found that before main shocks, the values of the clustering coefficient is stable but suddenly jump up when the main shocks occur, and then slowly decay following a power law to become stable again [19].
- d
- Average path length l is defined as the average number of steps along the shortest paths for all possible pairs of network nodes. Let , where , denotes the shortest distance between and . Then, the average path length L is . Many researchers have found that earthquake networks have a very short average path length leading to the concept of a small world where one node is connected to another through a very short path [10,14]. Short average path length in earthquake network may implies quick transfer of energy [10].
- e
- Coreness. K-core decomposition analysis is used to define the location of the node. This process assigns an integer index or coreness to each node, representing its position according to successive layers (k shells) in the network. The coreness index is a very robust metric, and in the case of incomplete information, the node is not significantly influenced. The max value of coreness K represents the number of layers of the network. He et al. [33] found different values of K in different regions. They also found that the highest core (or layer) is generally related to a deep hierarchy of the earthquake network structure.
- f
- Entropy is a metric of uncertainty for a network. The weighted entropy is defined as , where is the probability distribution of . The network entropy is an important indicator describing the heterogeneity of network. Lin et al. [21] focused on the dynamic evolution of the structure entropy of the earthquake network and captured the changes of network structure entropy before and after the main shocks.
3.2. Network Similarity
4. Results
4.1. Hierarchical Clustering Result
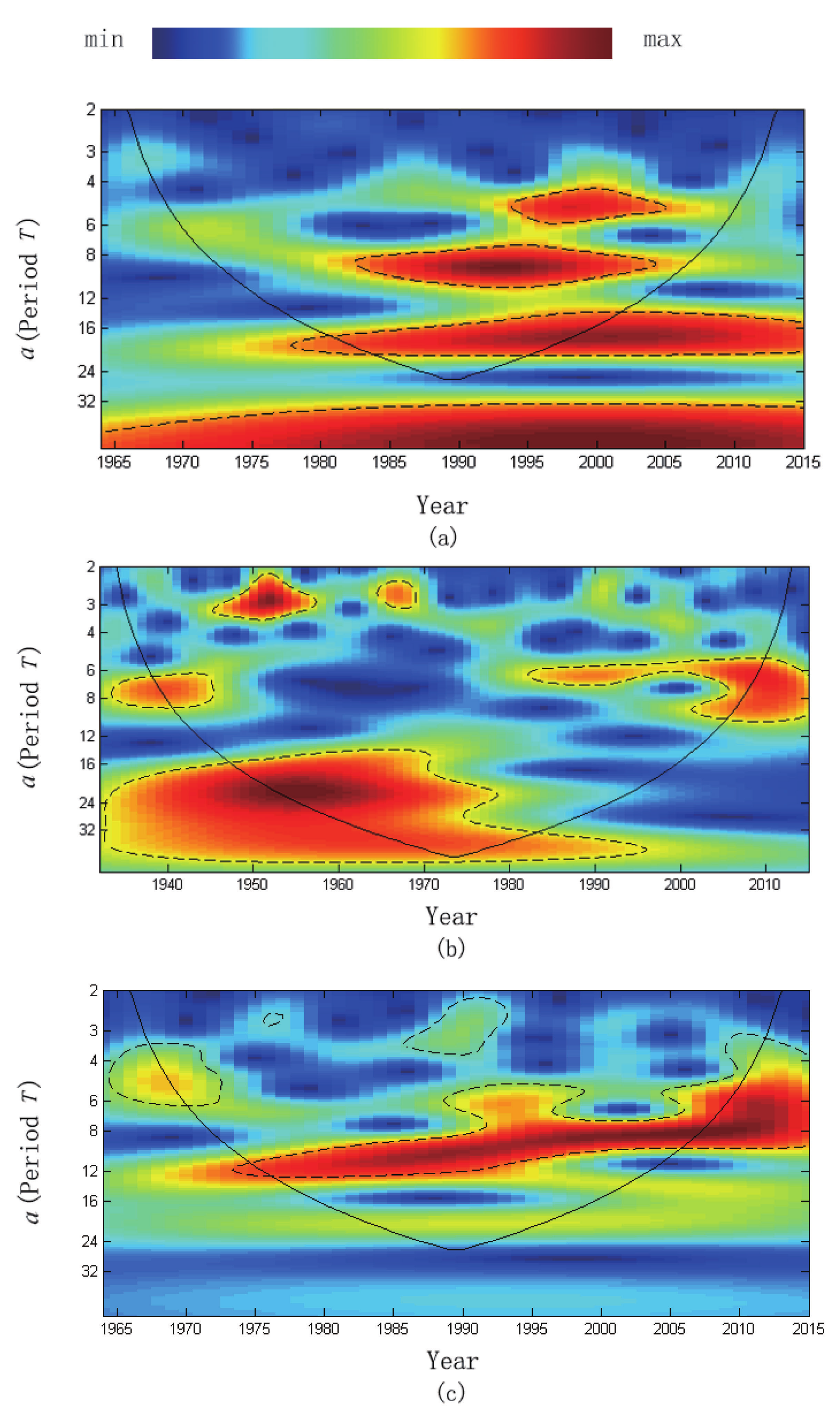
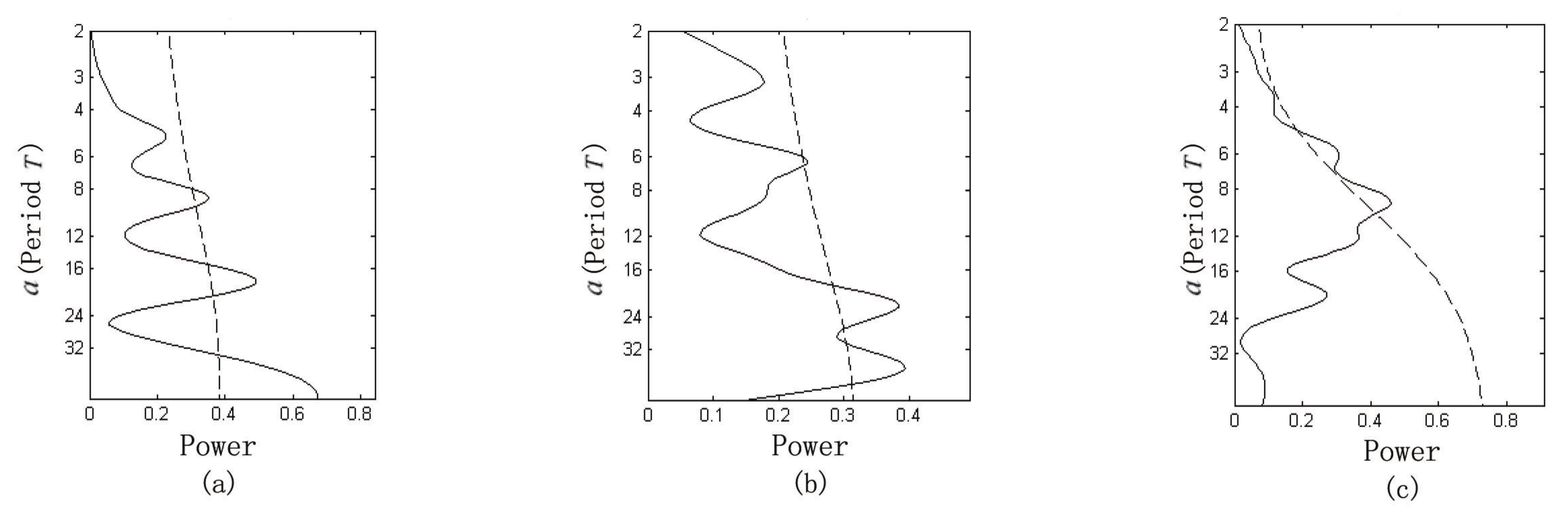
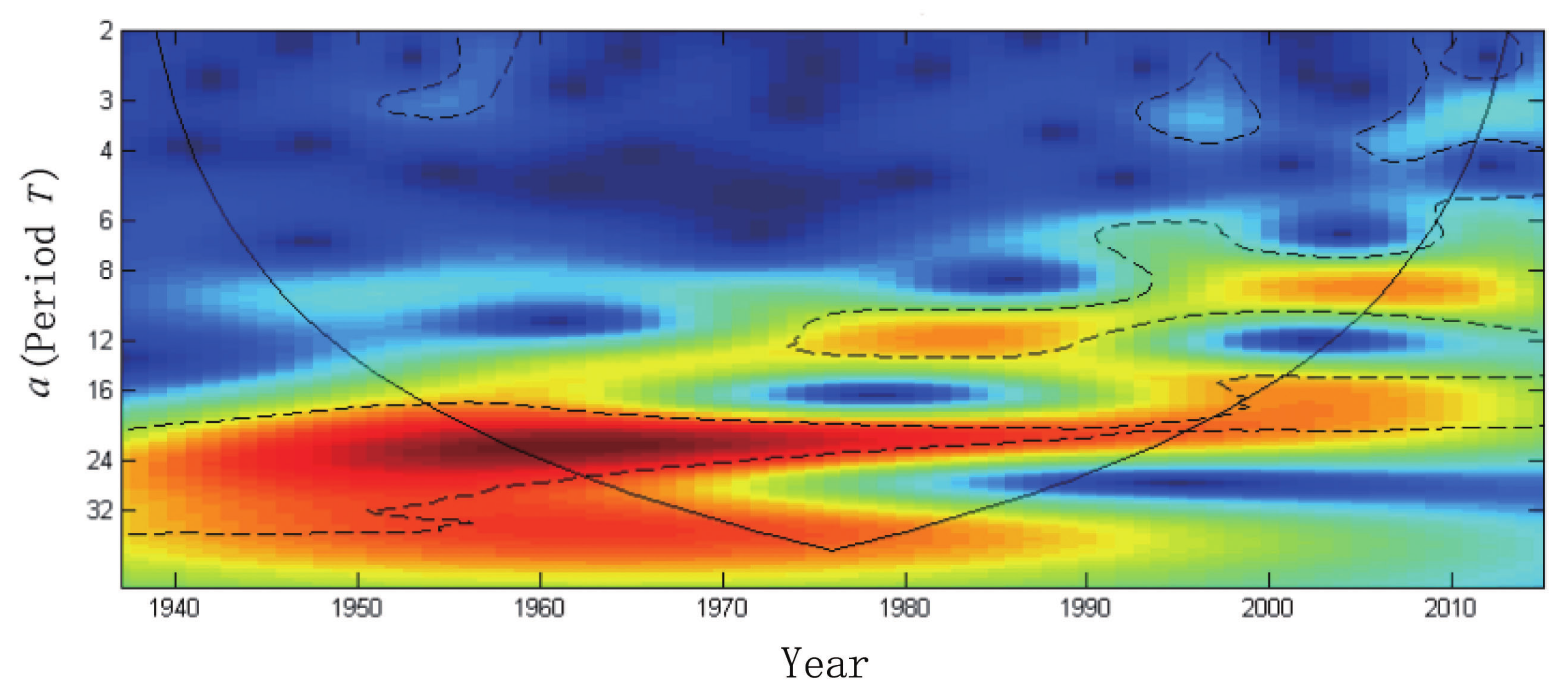
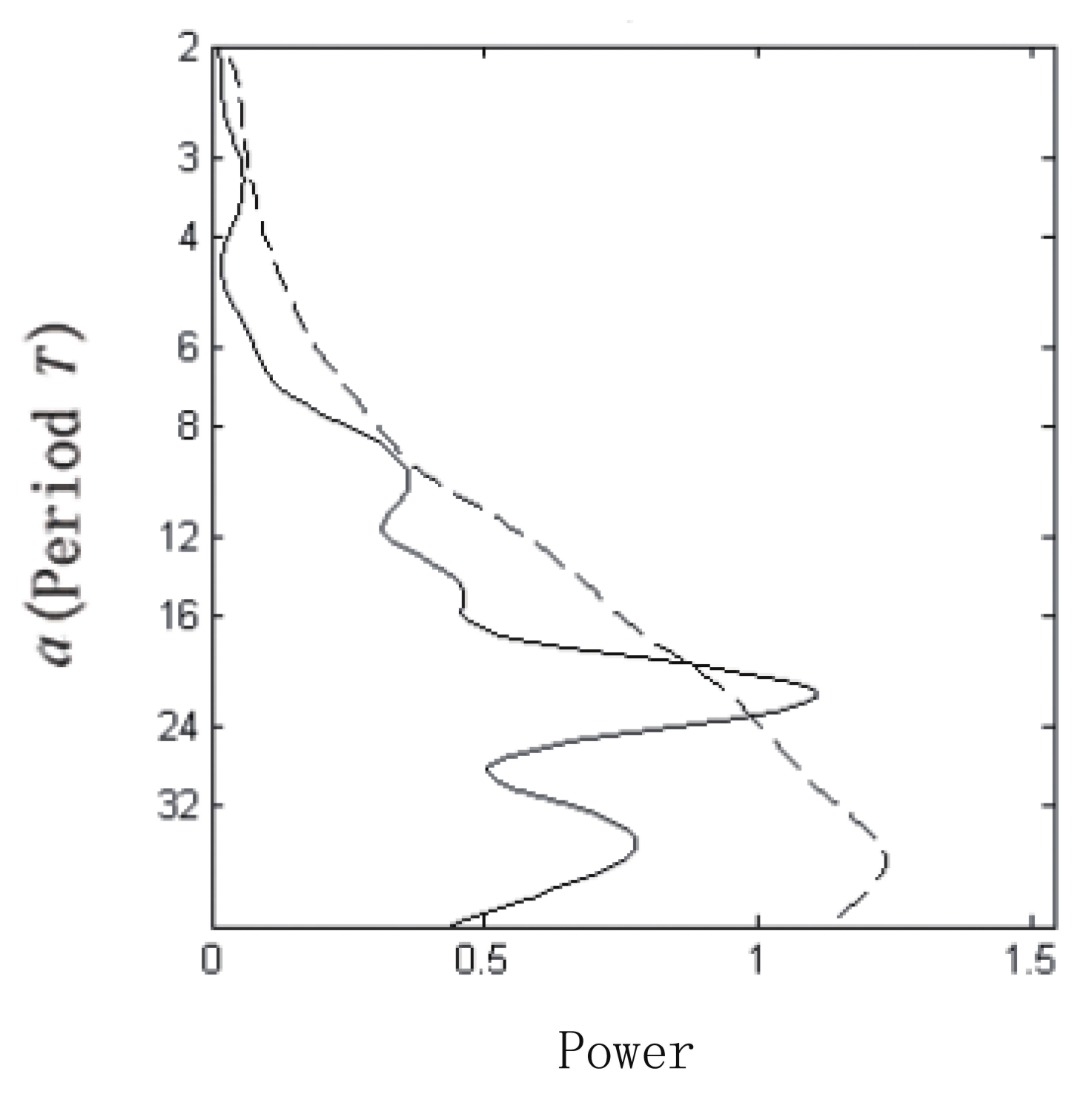
4.2. Wavelet Analysis
4.3. Period Analysis of Seismicity
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hohmann, S. Unicellsys—Understanding the cell’s functional organization. J. Biotechnol. 2010, 150, 545. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Battiston, S.; Castri, M.; Servedio, V.D.P.; Caldarelli, G. The scale-free topology of market investments. Phys. A Stat. Mech. Appl. 2005, 350, 491–499. [Google Scholar] [CrossRef]
- Kitsak, M.; Riccaboni, M.; Havlin, S.; Pammolli, F.; Stanley, H.E. Scale-free models for the structure of business firm networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 81, 036117. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Borgatti, S.; Mehra, A.; Brass, D.J.; Labianca, G. Network Analysis in the Social Sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhao, H.; Cai, W.; Xu, J.-Q.; Ai, J. A modular attachment mechanism for software network evolution. Phys. A Stat. Mech. Its Appl. 2013, 392, 2025–2037. [Google Scholar] [CrossRef]
- Roth, C.; Kang, S.M.; Batty, M.; Barthelemy, M. Structure of Urban Movements: Polycentric Activity and Entangled Hierarchical Flows. PLoS ONE 2011, 6, e15923. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Scale-free network of earthquakes. EPL 2004, 65, 581. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Small-world structure of earthquake network. Phys. A Stat. Mech. Appl. 2004, 337, 357–362. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Complex earthquake networks: Hierarchical organization and assortative mixing. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 026113. [Google Scholar] [CrossRef] [PubMed]
- Tenenbaum, J.N.; Havlin, S.; Stanley, H.E. Earthquake networks based on similar activity patterns. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 046107. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, A. A complex network model for seismicity based on mutual information. Phys. A Stat. Mech. Appl. 2013, 392, 2498–2506. [Google Scholar] [CrossRef]
- He, X.; Zhao, H.; Cai, W.; Liu, Z.; Si, S.-Z. Earthquake networks based on space–time influence domain. Phys. A Stat. Mech. Appl. 2014, 407, 175–184. [Google Scholar] [CrossRef]
- Rezaei, S.; Darooneh, A.H.; Lotfi, N.; Asaadi, N. The earthquakes network: Retrieving the empirical seismological laws. Phys. A Stat. Mech. Appl. 2017, 471, 80–87. [Google Scholar] [CrossRef]
- Min, S.; Chang, K.-H.; Kim, K.; Lee, Y.-S. Feature of topological properties in an earthquake network. Phys. A Stat. Mech. Appl. 2016, 442, 268–275. [Google Scholar] [CrossRef]
- Pasten, D.; Czechowski, Z.; Toledo, B. Time series analysis in earthquake complex networks. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 083128. [Google Scholar] [CrossRef]
- Lotfi, N.; Darooneh, A.H.; Rodrigues, F.A. Centrality in earthquake multiplex networks. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 063113. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Dynamical evolution of clustering in complex network of earthquakes. Eur. Phys. J. B 2007, 59, 93–97. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Dynamical evolution of the community structure of complex earthquake network. EPL 2012, 99, 313–316. [Google Scholar] [CrossRef]
- Lin, M.; Fan, X.X.; Wang, G.; Zhao, G. Network structure entropy and its dynamical evolution for recurrence networks from earthquake magnitude time series. Eur. Phys. J. B 2016, 89, 131. [Google Scholar] [CrossRef]
- Deyasi, K.; Chakraborty, A.; Banerjee, A. Network similarity and statistical analysis of earthquake seismic data. Phys. A Stat. Mech. Appl. 2017, 481, 224. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M. Seismic Electric Signals: An additional fact showing their physical interconnection with seismicity. Tectonophysics 2013, 589, 116–125. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S. Study of the temporal correlations in the magnitude time series before major earthquakes in Japan. J. Geophys. Res. Phys. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- Mintzelas, A.; Sarlis, N.V. Minima of the fluctuations of the order parameter of seismicity and earthquake networks based on similar activity patterns. Phys. A Stat. Mech. Appl. 2019, 527, 121293. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S. Scale-specific order parameter fluctuations of seismicity in natural time before mainshocks. Europhys. Lett. 2011, 96, 59002. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Identifying sudden cardiac death risk and specifying its occurrence time by analyzing electrocardiograms in natural time. Appl. Phys. Lett. 2007, 91, 064106. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Complex-network description of seismicity. Nonlinear Process. Geophys. 2006, 13, 145–150. [Google Scholar] [CrossRef]
- Ferreira, D.; Papa, A.R.; Menezes, R. Small world picture of worldwide seismic events. Phys. A Stat. Mech. Appl. 2014, 408, 170–180. [Google Scholar] [CrossRef]
- Sarlis, N.V. Magnitude correlations in global seismicity. Phys. Rev. E 2011, 84, 022101. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Christopoulos, S.-R. Natural time analysis of the Centennial Earthquake Catalog. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 023123. [Google Scholar] [CrossRef] [PubMed]
- Gardner, J.; Knopoff, L. Is the sequence of earthquakes in southern california, with aftershocks removed, poissonian? Bull. Seismol. Soc. Am. 1974, 64, 1363–1367. [Google Scholar]
- He, X.; Zhao, H.; Cai, W.; Li, G.-G.; Pei, F.-D. Analyzing the structure of earthquake network by k-core decomposition. Phys. A Stat. Mech. Appl. 2015, 421, 34–43. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; He, X.; Pei, F.-D.; Li, G.-G. Bayesian prediction of earthquake network based on space–time influence domain. Phys. A Stat. Mech. Appl. 2016, 445, 138–149. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Determination of the scale of coarse graining in earthquake networks. EPL 2012, 87, 48008–48012. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mukherjee, G.; Manna, S.S. Weighted network analysis of earthquake seismic data. Phys. A Stat. Mech. Appl. 2015, 433, 336–343. [Google Scholar] [CrossRef]
- Alain, B.; Marc, B.; Alessandro, V. The Architecture of Complex Weighted Networks: Measurements and Models; World Scientific: Singapore, 2007; pp. 67–92. [Google Scholar]
- Soundarajan, S.; Eliassi-Rad, T.; Gallagher, B. A Guide to Selecting a Network Similarity Method. In Proceedings of the 2014 SIAM International Conference on Data Mining, Philadelphia, PA, USA, 24–26 April 2014. [Google Scholar]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P.J. Interdecadal changes in the enso–monsoon system. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Du, P. The 18.6 year seismic cycle in global major seismic regions. J. Seismol. Res. 1993, 3, 03. [Google Scholar]
- Pin-Ren, D.U. 18.6 years seismic cycle and the preliminary exploration for its cause. Chin. J. Geophys. 1994, 37, 362–369. [Google Scholar]
- Barbot, S.; Lapusta, N.; Avouac, J.-P. Under the Hood of the Earthquake Machine: Toward Predictive Modeling of the Seismic Cycle. Science 2012, 336, 707–710. [Google Scholar] [CrossRef] [PubMed]
- Uchida, N.; Matsuzawa, T.; Ellsworth, W.L.; Imanishi, K.; Okada, T.; Hasegawa, A. Source parameters of a m4.8 and its accompanying repeating earthquakes off kamaishi, ne japan:implications for the hierarchical structure of asperities and earthquake cycle. Geophys. Res. Lett. 2007, 34, 153–175. [Google Scholar] [CrossRef]
- Matsuzawa, T.; Igarashi, T.; Hasegawa, A. Characteristic small-earthquake sequence off Sanriku, northeastern Honshu, Japan. Geophys. Res. Lett. 2002, 29, 381–384. [Google Scholar] [CrossRef]
- Zhang, C. Periodic analysis of global seismic activity. Earthq. Res. China 1985, 1, 24–31. [Google Scholar]
- Kilston, S.; Knopoff, L. Lunar–solar periodicities of large earthquakes in southern California. Nature 1983, 304, 21–25. [Google Scholar] [CrossRef]

| Name | Period | Site URL |
|---|---|---|
| SCSN | 1932 to the present | scedc.caltech.edu/ |
| JUNEC | 1985–1998 | kea.eri.u-tokyo.ac.jp |
| ANSS | 1863 to the present | www.quake.geo.berkeley.edu/anss/ |
| Name | Symbol | Implication |
|---|---|---|
| Exponent of power law | The heterogeneity of degree distribution | |
| Strength | S | Influencing degree among nodes |
| Clustering coefficient | C | The degree of clustering of earthquake network |
| Average path length | L | Efficiency of transfering energy |
| Max coreness | K | Hierachy of earthquake network |
| Entropy | H | The heterogeneity of nodal strength |
| Time | Magnitude | Latitude | Longitude |
|---|---|---|---|
| 1992/06/28 | 7.3 | 34.200 | −116.437 |
| 1999/10/16 | 7.1 | 34.603 | −116.265 |
| 2010/04/04 | 7.2 | 32.286 | −115.295 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Wang, L.; Liu, Z.; Liu, Y. Similar Seismic Activities Analysis by Using Complex Networks Approach. Symmetry 2020, 12, 778. https://doi.org/10.3390/sym12050778
He X, Wang L, Liu Z, Liu Y. Similar Seismic Activities Analysis by Using Complex Networks Approach. Symmetry. 2020; 12(5):778. https://doi.org/10.3390/sym12050778
Chicago/Turabian StyleHe, Xuan, Luyang Wang, Zheng Liu, and Yiwen Liu. 2020. "Similar Seismic Activities Analysis by Using Complex Networks Approach" Symmetry 12, no. 5: 778. https://doi.org/10.3390/sym12050778
APA StyleHe, X., Wang, L., Liu, Z., & Liu, Y. (2020). Similar Seismic Activities Analysis by Using Complex Networks Approach. Symmetry, 12(5), 778. https://doi.org/10.3390/sym12050778




