Abstract
When solving a Multi-Criteria Decision-Making problem of any degree of complexity, many researchers rely on the analytic hierarchy process (AHP). To consider mutual connections between criteria and clusters at the same level and not only the hierarchical structure between criteria and subcriteria, researchers often upgrade from AHP to the Analytic Network Process (ANP), which also examines the interdependency of criteria. However, the ANP method requires a large number of pairwise comparisons. In the case of a complex decision-making problem, the authors of this paper suggest upgrading the AHP method with the graph theory and matrix approach (GTMA) for several reasons: (1) The new method is based on digraphs and permanent value computation, which does not require a hypothesis about interdependency; (2) in case of similar alternatives, the distinguishable coefficient of the new method is higher than those computed for AHP and ANP; (3) the new method allows decision makers to rank comparable alternatives and to combine structurally similar methods without increasing the number of comparisons and the understanding of the results. The developed method (AH-GTMA) is validated by a numerical example of a complex decision-making problem based on a symmetrical set of similar alternatives, a third party logistic provider (3PLP) selection problem.
1. Introduction
Decision making based on qualitative and quantitative criteria is a significant challenge in all sectors. Generally algebraic and topological conditions that allow one to find the optimal solution are partially considered in decision-making, as it is not easy to verify the optimality of the solution in the case of a large number of attributes. The result obtained is usually considered optimal only if it meets the local expectations of the decision makers [1].
Decision makers often attempt to make the right decision using one or more Multi-Criteria Decision-Making (MCDM) method. There is a large number of MCDM methods that vary greatly in terms of methodology, difficulty, and format of results. Decision makers frequently use the method that is most popular, most user friendly, not too time consuming and meets their expectations. To reduce the weaknesses of one MCDM method, the selected method is frequently integrated with one or even more methods.
The most frequently used MCDM method is the analytic hierarchy process (AHP) as defined by Saaty [2]. The method has a clear mathematical formulation and results are illustrated by a simple and clear hierarchical structure. Generally, results are acceptable for the decision makers (leadership). In practice, however, the number of attributes used is too high and the interactive nature of these attributes is seldom checked, so the results obtained cannot be valid [3].
Some researchers add the Analytic Network Process (ANP), defined by Saaty and Vargas, to the AHP to examine or confirm the results obtained. The ANP method is also based on pairwise comparisons but allows for interdependency between attributes [4]. The graphic structure of the results is a complicated digraph that allows for feedback, at times causing decision makers to be sceptical about the results obtained. The complexity of the ANP method (number of pairwise comparisons and consistency checks) increases with the number of criteria involved and the number of alternatives analysed. In the case of large decision-making problems, it cannot be easy to compute and understand the results.
Like AHP and ANP, the Graph Theory and Matrix Approach (GTMA) method is based on a graph structure and on pairwise comparisons, but decision makers do not need to evaluate whether attributes are dependent, as in the case of AHP. Using GTMA, the total number of pairwise comparisons is of the same order as in the AHP method and therefore much lower than in the case of ANP. Like the ANP, the GTMA method considers alternatives as part of the decision-making problem, but the value of each alternative is considered in less detail than in the AHP and the ANP [1].
The logistics provider (LP) selection process is a complex decision-making process with many alternatives and no independent criteria. It seems that AHP and ANP to the fullest extent meet researchers’ and decision makers’ expectations, since they are those most frequently used. AHP has been applied as an individual method in 9 published papers, and combined with other methods, most frequently with the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), in 23 cases. ANP has been used less frequently, only in 12 cases. It was used 4 times individually and in the rest of the cases integrated with other methods. However, AHP and ANP have never been integrated with the GTMA method. As far as we are aware, the GTMA method has so far been used for a second party logistics provider (2PLP) selection problem, which is a less complex decision-making process in respect to the selection of other logistics services providers (3PLP, 4PLP) [5].
Integration of AHP and ANP with one or even more methods, on the one hand, generates more accurate results. But, on the other hand, integration neglects the point of view and abilities of users. Integrated methods, obtained by aggregation of two or more methods, are more complex, require more knowledge, and some of them are more time-consuming. In past studies, a significant contribution to science has been made in this field, which is, of course, indispensable. However, the aspect of the user of these methods was very obviously overlooked in practice, which is a matter of concern, as an e-survey [6] has shown that many companies are addressing LP selection decisions on their own.
Thus, decision makers, managers, and practitioners face a great dilemma about which method to choose in decision-making problems since they do not have a deep knowledge of the methods, lack experience regarding the use of methods, and do not know all the methods available. They still need a relatively simple, but reliable, method, or integrated methods, which would enable greater accuracy of the selected alternative and would even simplify and speed up the selection process, especially in case of complex problems.
Proposing such a method is the aim of this paper. To meet this aim, this paper (1) defines an integration of the AHP and the GTMA method which avoids the need for the more complex ANP method but at the same time defines a graph structure between criteria (and alternatives) that takes into account feedback relations, as ANP does; (2) presents a numerical example of a LP selection problem, to compare the two most frequently used MCDM methods (AHP and ANP) with the proposed AH-GTMA method; (3) highlights the AH-GTMA property to be a simple method but which allows the definition (evaluation) of the relationships between the elements involved in the complex decision-making process, including feedback; and (4) helps decision makers to make a proper decision in cases of very similar alternatives, respect the criteria set since the AH-GTMA method has a higher distinguishability coefficient with regard to the AHP and the ANP method.
Among the surfeit of different methods available to facilitate the work of decision-makers, the integration of AHP and GTMA is an appropriate selection tool, as it saves time and, most important, enables the choice of appropriate alternative aggregating methods that are based on the same algebraic requirements and method of computation. The risk of selecting the inappropriate partner is therefore lower.
The remainder of this article is structured as follows: the next (second) section provides a review of the selection of logistics providers (LPs) using AHP, ANP, and GTMA methods and a review of the application of the integrated AHP and GTMA method in general. The third section presents a hybrid AHP and GTMA approach for solving a complex decision-making problem. The computational results of applying the proposed approach on one complex decision-making numerical example are provided in Section 4. Finally, the discussion and conclusion are presented in the last section.
2. Literature Review
An extensive literature review on the selection of LPs (used as a numerical example for the validation of the results), using AHP, ANP, and GTMA methods, was undertaken for this paper. From 1999 (when the first articles in this field began to appear) to 2019, 45 papers on this topic were found to have been published.
2.1. Literature Review on the Selection of LPs Using AHP
The AHP method was applied as a stand-alone method or in combination with other methods in 32 papers. Xiu and Chen evaluated [7] Chinese third-party logistics providers using the combination method of AHP and entropy. An integrated AHP and mixed integer linear programming model (MIP) was used to select the appropriate carrier by Mohammaditabar and Teimoury [8]. Lehmusvaara, Tuominen, and Korpela presented a framework for the selection of a trucking company based on AHP and MIP [9]. The AHP and entropy approaches were applied to calculate the objective weights in the selection of a reverse LP [10]. An integrated intuitional fuzzy AHP and SWOT method was utilised by Tavana [11] for outsourcing reverse logistics. The integration of the fuzzy analytic hierarchy process (FAHP) and Evaluation based on Distance from Average Solution (EDAS) was employed by Ecer [12] to select a proper 3PL provider. “An integrated approach, combining quality function deployment (QFD), fuzzy set theory, and an AHP approach” was used by Ho et al. [13] to evaluate and select the optimal third-party logistics service providers (3PLs).
Papers [14,15] presented a combined model based on “FAHP for the evaluation and ranking of selection criteria and Vlsekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) for the final selection of a reverse logistics partner”. An integrated AHP and VIKOR approach was also used to examine Chinese third party logistics providers [16].
An AHP model was applied by the Turkish automotive industry to select the best 3PL provider among four candidates [17]. An evaluation framework and AHP methodology was also employed by Soh [18] and Gürcan et al. [19] for selecting a suitable 3PL provider. The purpose of some papers [20,21] was to present an AHP decision model for selecting a third party logistics (3PL) provider. 3PL providers were also “selected by evaluating weights on the basis of a company’s selected criteria through the AHP” [22]. A global LP was also selected using an AHP by Göl and Çatay [23]. A paper [24] “in the form of a case study provided a structured decision-making model for the selection of the most suitable logistics provider using the analytic hierarchy process (AHP)”. The article [25] offered information on the conformity assessment of 3PL by using the AHP method.
Ziping, Chiang, and Tzeng [26] deployed the modified FAHP to find a 3PL “for the supplier selection problem in fuzzy dynamic decision environments”. A support system for logistics service provider selection was also based on the FAHP method in three studies [27,28,29], and a paper [29], in which a Colombian manufacturing company selected a 3PLP. The study [30] aimed “to efficiently assist decision makers in determining the most appropriate third-party reverse logistics provider” using an artificial neural network and FAHP.
Papers [31,32,33] proposed the use of the “FAHP approach based on a technique for order preference by similarity to the ideal solution (TOPSIS) for evaluating and selecting an appropriate logistics service provider, where the ratings of each alternative and importance weight of each criterion are expressed in triangular fuzzy numbers”. An improved AHP and TOPSIS method was also used for the selection of 3PL service providers [34,35,36,37,38,39]. An FAHP and TOPSIS approach was also applied in evaluating the performance of third party logistics service providers for effective supply chain management [40].
Other papers [41,42] “proposed a hybrid model of AHP and preference ranking organization method for enrichment evaluation (PROMETHEE) in 3PLP selection” and [29,43] aimed to identify the selection criteria used by logistics service providers in Turkey’s cement sector by using FAHP.
2.2. Literature Review on the Selection of LPs Using ANP
The ANP method was adopted in 12 cases, mostly integrated with other methods. Yilmaz et al. [44] employed ANP to determine the best LP to work with. Fadavi, Khanghah, and Asli [45] used “fuzzy preference programming and ANP to form a model for the selection of partners for outsourcing providers”. In the view of Cooper, Tadikamalla, and Shang [46] the ANP model presents a framework for selecting the 3PLP that can significantly improve the supply chain. Jharkharia and Shankar [47] also applied ANP in the selection of a LP.
Liou and Chuang [48] proposed a new “Decision-Making Trial and Evaluation Laboratory (DEMATEL)–ANP-VIKOR methodology” for selecting a LP. Hsu, Liou, and Chuang [49] presented a novel hybrid model, combining a “Decision Making Trial and Evaluation Laboratory (DEMATEL) and an ANP method called DANP”, which considers the dependent relationships between the criteria in order to select an outsourcing provider.
To provide selections of logistics outsourcing providers in a global supply chain, Wong [50] applied “a fuzzy analytic network process (FANP) and pre-emptive fuzzy integer goal programming (PFIGP)”. Thakkar et al. [51] applied an interpretive structural model (ISM) and ANP for the selection of third-party logistics (3PL) service providers. “An integrated ANP—intuitionistic fuzzy set (IFS)—grey relation analysis (GRA)” was used by Zareinejad and Javanmard [52] to investigate relationships among criteria and to identify the most important criteria in the selection of LPs.
3PL selection problems were also analysed using an interval type-2 fuzzy ANP method [53]. An integrated ANP and the “intuitionistic fuzzy-grey superiority and inferiority ranking (IFG-SIR)” was also developed by Tavana et al. [54] to help an industrial production group select a LP. In a study written by Esra Aytaç, Ay [55] a model based on DEMATEL, ANP and Data Envelopment Analysis (DEA) is presented for the selection of 3PL providers. Raut et al. [56] help decision makers in evaluating and selecting the most environmental LP provider using a two-phase model based on DEA and ANP.
2.3. Literature Review on the Use of GTMA in General
Unlike the AHP and ANP methods, GTMA has been very rarely used in the field of logistics or supply chains and even more rarely in the selection of a LP. The authors managed to find only one example using this method. Kabir and Sumi [5] designed a simple but systematic approach to evaluate a transportation firm by an automotive battery manufacturing company in Bangladesh by integrating the fuzzy Delphi method (FDM) with GTMA.
A few more articles, that applied individual or integrated GTMA can be found in the field of the entire supply chain. A graph theory and matrix approach (GTMA) has been used by Muduli et al. [57] to evaluate factors that prevent green supply chain implementation. Agrawal et al. [58] applied the graph theory and matrix approach to select the best alternative among four alternatives: Returned products for repair, reuse, and resell as new, repair or refurbish and resell. In the paper of Mohaghar et al. [59] a novel technique by combination of “decision-making trial and evaluation laboratory and graph theory and matrix approach techniques” was proposed to select a supplier. An individual GTMA method was also used to select a supplier by Athawale et al. [60]. In the paper of Malik et al. [61] the GTMA method was discussed to find the location of a collection centre for reverse logistics.
3. The Integration of AHP and GTMA Method (AH-GTMA) to Solve Complex Decision-Making Problems
A decision-making problem is considered complex if the number of alternatives is more than 9 or the criteria involved in the decision are not independent. Thus, the network structure of the decision-making process is branched and allows feedback.
On the basis of the proposed literature review, it is possible to note that authors attempt to use the AHP method, since the results obtained can easily be explained using a tree graph structure and are well accepted by the experts involved in the decision-making process. It is also possible to note that the number of criteria that can be correctly evaluated by the AHP method is limited to 5–9, since Saaty bases the AHP method on findings from cognitive science that evaluated a person’s working memory capacity on the order of 7 ± 2 [62,63,64,65,66,67,68].
In the case of a large number of criteria, those must be grouped to form a tree structure of two or more levels. In addition, the number of levels should be between 5 and 9, for the same reason. A reduction in the number of levels is possible by decomposing them into a set of smaller tree structures, but this can complicate the formulation and understanding of the whole problem [66].
Authors seldom study the relations between the criteria and their independency, since in practice it is very difficult to define the interrelations between criteria, especially if they are of a different nature: Tangible or intangible.
For these reasons, in a case of complex decision-making problems, in this section the leadership techniques AHP and GTMA methods are integrated to define a decision-making tool that aggregates the analytic properties and the easy consistency check of relative importance judgments of the AHP method with the visual appraisal of the attributes and their interrelations proposed by the GTMA method.
The GTMA method and the permanent value computation is also used as a totally objective measure that can include the structural characteristics of the decision-making problem in the final rank [69].
The steps of the proposed AH-GTMA method are described below.
3.1. Definition of the Alternatives, Attributes/Criteria, Clusters, and the Network Structure
In complex decision-making problems identification of proper criteria is a very important step, but, even more important is to aggregate the criteria into an effective decision-making model with a simple structure. Another consideration is that the number of pairwise comparisons that have to be made by decision makers can reduce the effectiveness of the decision. Integration of the AHP and GTMA methods allows decision makers to skip the structure definition step that is crucial in the ANP method while still detecting the relationships and feedback between elements in the decision-making problem. In addition, the number of pairwise comparisons is fewer than when the ANP method is used.
Criteria are permutated and grouped to define a bilevel structure: Inside of each group, criteria are independent and related to the same aspect of decision. The procedure is repeated until all the criteria have been divided into groups consisting of fewer than 9 independent criteria.
Thus are defined the primary criteria level and a subcriteria level , where .
3.2. Normalization of Positive and Negative Alternatives’ Attributes
Attributes that are used to evaluate alternatives can be expressed in different units (cost, efficiency, etc.). Some attributes can define negative characteristics of alternatives, others positive characteristics. To define a uniform measure of the alternatives it is necessary to normalize attribute values. Let are the attributes of alternative , , in respect to the criteria .
In case of positive attributes, normalization is accomplished by dividing the attribute value by the maximum value of the examined attribute category:
In case of negative attributes, normalization is accomplished by dividing the minimum value of the examined attribute category by the attribute value:
3.3. Definition of the Relative Importance of Alternatives within the Clusters, Using the AHP Method
Relative importance of the alternative within each cluster from the cluster set is computed using the AHP method and criteria from the subcriteria level that is part of this cluster.
Pairwise comparison matrices are reciprocal, with a unit diagonal, rational square matrix. Elements are defined by pairwise comparison of criteria, from the subcriteria level that is part of the considered cluster, using a numerical “(verbal) scale from 1 (equivalency of importance between the factors) to 9 (extreme favour of one factor with respect to the other)” as defined by Saaty [70,71].
All the reciprocal matrices , defined on the basis of consistency judgments, have a rank of 1 and only one eigenvalue that is different from zero, so it is possible to write , where are the associated right eigenvectors that define the weights in each cluster, from the cluster set . Using Saaty’s method, it is possible to compute the weights by normalizing the components of each eigenvector by the arithmetic mean [72]:
where . The approximation of each eigenvalue is computed as:
On the basis of the characteristics of the comparison matrices, the consistency of the method can be checked, in all clusters, using the maximum eigenvalue technique [73]. The consistency index is defined as:
In all clusters the consistency ratio is then computed—the consistency must be less or equal to 0.1. RI is the Random Index computed by Saaty [74].
3.4. Digraph Definition, Permanent Computation, and Final Rank of the Alternatives
The graph theory and matrix approach (GTMA) method is based on digraphs and permanent value. A digraph (directed graph) D is a pair , where is the set of vertices and is a set of oriented arcs (edges), , [75]. Nodes were used to represent the attributes/criteria that must be considered in a decision-making problem and edges are used to represent the degree of relationship between nodes (criteria) and the direction (mutuality) of the relations. If node is more important than node , a directed edge is drawn from node to node . If node is more important than node , then the edge is narrowed in the opposite direction [3,75].
In the proposed method the number of vertices is equal to the number of clusters .
The Performance Attributes Matrix (PAM) is a square matrix, the elements on the main diagonal are the attributes and the other entries express the relative importance between them:
The values of are defined using Equation (3):
The permanent of each square matrix , is a polynomial function in the entry of the matrix similar to the determinant, [75,76]:
where and is a symmetric group of all the permutations of the elements of the set .
Based on the algebraic characteristics of the permanent and on the application to graph theory, it is possible to use the Permanent of the matrix to characterise the configuration and the performance of the system expressed by the digraph [1,77].
The Performance Attribute Index (PAI) is defined as the Permanent of the matrix where the values of are obtained from real numerical evaluations (that are then normalised) or are evaluated using a numerical scale from 0 (exceptionally low) to 10 (exceptionally high) [1,3,75].
The relative importance between two attributes is evaluated using a scale from 0 to 1 and satisfies the following property [75]:
A verbal definition of the relative importance evaluation is presented in Table 1.

Table 1.
Relative importance of performance attributes [75].
For each alternative , using the defined digraph the Performance Attribute Index can be computed, then alternative performances are ranked from the highest value of PAI (best alternative) to the lowest value of PAI (worst alternative).
The entries of the PAG matrix are computed based on pairwise comparisons, Equation (9) and Table 1.
The PAG matrix and are computed for each examined alternative . Then using Equation (8) the PAI index is computed and alternatives can be ranked.
The criteria define the nodes of the digraph; edges are defined considering the degree of relationship between the nodes. The obtained structure is a digraph called the Performance Attributes Graph (PAG).
3.5. Evaluation of the Pairwise Comparisons Number among the AHP, ANP, and the AH-GTMA Method
The AH-GTMA method reduces, with respect to the ANP method, the total number of necessary pairwise comparisons but at the same time defines a complex network structure similar to the ANP that is well accepted and easy to understand for practitioners. The number of pairwise comparisons is kept in the same order as in the AHP method.
In the AH-GTMA method the total number of pairwise comparisons () is comparable to the total number () of pairwise comparisons of the AHP method. The computation of the values on the main diagonal of the square PAM matrix requires the same number of comparisons within each cluster in the AHP method. The values of the other elements of the PAM matrix, based on Equation (9), requires the same number of comparisons as the comparisons between clusters in the AHP method, [78]:
The structure of the ANP method, compared to the AHP method, results in a large increase in the number of pairwise comparisons (), required to explain all the connections between the elements of the network [79]:
where is the number of clusters, is the number of alternatives, is the number of criteria, is the number of elements in the cluster and is the number of dependencies of the element from cluster with respect to the element .
4. Numerical Example
In this section, the proposed method is applied to a numerical example of one of the largest pharmaceutical manufacturers in Slovenia. The numerical example is based on real data, parameters, and comparisons. The results obtained and methods used are also compared.
To focus on core business and decrease infrastructure and management costs, the manufacturer decided to outsource warehousing services to 3PLPs. The manufacturer had already collaborated with two largest 3PLPs located in Slovenia in the past. Nevertheless, it agreed to invite also other of the largest and experienced 3PLPs, located in Slovenia, to tender. Only small 3PLPs or 3PLPs who have no experience in storing pharmaceutical products were not invited.
The manufacturer prepared a list of criteria (attributes) on their own: Cost of warehousing, costs of inventory management, additional service costs, opening hours, order size, and configuration flexibility, possibility to change order details, shipment errors (quality, quantity and place), product variety, ability to provide added value services, response time, possibility for temperature control and humidity, delivery accuracy, real time data transfer, use of technology (Radio Frequency Identification (RFID)/barcode), separation of storage areas, type of handling equipment depending on the drive, number of docks, characteristics of docks, distance to highway connection, worker satisfaction, types and quality of communication, personal relationships with key customers, willingness to assume risk, and data security. Due to a large number of criteria and uncertainty whether criteria are independent or not, the pharmaceutical manufacturer was faced with a dilemma regarding which method to use: (1) The AHP, with a well-accepted hierarchical structure that however neglects the interdependency of criteria and feedback, (2) the more complex ANP, that takes into account relationships between criteria and alternatives, but has a complex structure difficult to explain in practice, or (3) two or more methods to obtain a proper decision. The pharmaceutical manufacturer solved a simple decision-making problem in the past, nothing complex as warehousing service. To avoid this problem, they requested the authors of this paper to suggest the appropriate method or several methods able to address the complexity of the problem and to perform all calculations. The authors, therefore, proposed to use less-known methods, based on different computation techniques, the AH-GTMA method. The method defines a graph structure and evaluations that are well accepted and is also easy to understand for practitioners.
The authors first suggested grouping the criteria into six clusters in order to form groups of criteria that evaluate the same aspect of decision-making and at the same time are independent of each other, see Table 2.

Table 2.
Criteria clustering.
Then a request for proposals was sent, by the manufacturer, to large and experienced 3PLPs in Slovenia. Seven 3PLPs submitted bids. One bid was incomplete, and one 3PLP did not meet all the criteria. In the end, five of the largest Slovenian and international 3PLPs were selected for evaluation. In Table 3 (left half of the Table 3, 1–7 columns), the 3PLP evaluations, performed by the manufacturer, are presented according to defined criteria, using a five-step scale from 1 (poor) to 5 (excellent). Their assessments were found to be high and very similar, which makes a proper choice very difficult. Therefore, a decision-making method capable of discriminating between the alternatives is required.

Table 3.
Third party logistic provider (3PLP) evaluation.
Thus, authors of this paper normalized attributes according to Equations (1) and (2), since some criteria are negative attributes and others are positive.
Then, we suppose that the clusters and criteria are independent of one another and feedback between the criteria and alternatives is not taken into consideration. On the basis of these assumptions, it is possible to define a three-level tree graph structure and to use the AHP method.
According to Saaty’s comparison scale and the steps of the AHP method, the defined criteria are pairwise compared, by the manufacturer. Then, the weights vectors at the criteria levels and the cluster level are computed, by the authors, using Equation (3). Also, consistency check is performed according to Equation (5) and CR values are computed, which are all less than 0.1.
According to the defined AHP hierarchical network, using data from Table 4 the alternatives are ranked accordingly: 3PLP2(0.9837) ≻ 3PLP3(0.9741) ≻ 3PLP4(0.9483) ≻ 3PLP1(0.8713) ≻ 3PLP5 (0.7834) ≻ 3PLP6(0.7524).

Table 4.
The analytic hierarchy process (AHP) weights vectors at the cluster level and at the criteria level.
Generally, it is difficult to evaluate the independence of criteria and the influence of alternatives to criteria and vice versa. In this case, the AHP method cannot be used. It is necessary to define a more complicated network structure in which feedback is allowed. The ANP method must be used in such cases. The presented numerical example is of this type, as there are relationships between the clusters and also the alternatives cause feedback relationships.
The ANP network is composed of seven clusters (—costs, —services, —information technology (IT), —infrastructure and suprastructure, —human resources, —risk management, Alternatives).
The weight computation and alternative ranking is done by computing the limit supermatrix where the diagonal blocks are all the same. The final priorities of all the elements in the matrix are obtained by normalizing the blocks. The results are presented in Table 5.

Table 5.
Final priorities of the analytic network process (ANP) method.
According to the defined ANP network structure, the alternatives are ranked accordingly: 3PLP3, 3PLP2, 3PLP1, 3PLP4, 3PLP5 and 3PLP6. 3PLP2(1) = 3PLP3(1) ≻ 3PLP4(0.9403) ≻ 3PLP1 (0.9321) ≻ 3PLP5(0.8085) ≻ 3PLP6(0.77259). The ANP method ordered alternatives in the same way as the AHP method, but is not able to differentiates between the first and second alternatives.
The AH-GTMA method is based on a digraph, so no hypothesis of independence between the attributes is necessary, the number of vertices is equal to 6 and is the cardinality of the clusters set used in the AHP method. Using Equation (6) and Table 1, the Performance Attributes Matrix (PAM) is defined (see Table 6). The elements on the main diagonal are computed using normalized values from Table 3 and Equation (7).

Table 6.
Performance Attributes Matrix (PAM) matrix values.
For each alternative (3PLP) the Performance Attribute Index (PAI) was computed. According to the digraph structure of the AH-GTMA method, results and ranks are presented in Table 7.

Table 7.
Performance Attribute Index (PAI) rank values.
Comparing rankings obtained using the AHP method, the ANP method and the AH-GTMA method it is possible to note that all methods propose the same ranking order except for the ANP method, which is not capable of differentiating between the best alternative and the second best. To show the differences between the ranking results of proposed methods, obtained LPs evaluations are normalized, to define the normalised relative closeness coefficient , [80]:
where is the 3PLPi final evaluation.
In Figure 1 normalised relative closeness coefficients are presented for the AHP, ANP, and AH-GTMA methods. It is possible to see that the yellow line representing the AH-GTMA method is steeper than those (blue and orange) related to the AHP and ANP methods, that also are very close. This indicates that the degree of difference is more relevant in the AH-GTMA methods than in the other two, which allows you to define a ranking even when the alternatives have very similar evaluations with respect to the used criteria.
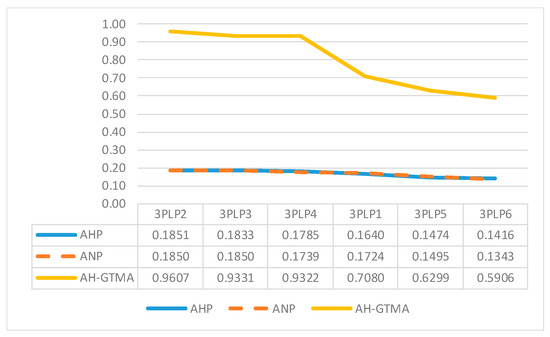
Figure 1.
Normalised relative closeness coefficient for AHP, ANP, and AH-GTMA (graph theory and matrix approach).
The differences between any two neighbouring alternatives could be computed via the distinguishable coefficient , defined as [80]:
The larger the values and the average value of the distinguishable coefficients better is the evaluation and the effectiveness of the decision-making [80].
Figure 2 presents the values of the distinguishable coefficients for the AHP, ANP, and AH-GTMA methods. The yellow line, corresponding to the AH-GTMA method, is higher than the other two and also the mean distinguishable coefficient value is higher, so the AH-GTMA method has better distinguishability and allows decision makers to make a proper decision in case of alternatives that are very similar, with respect to the criteria set.
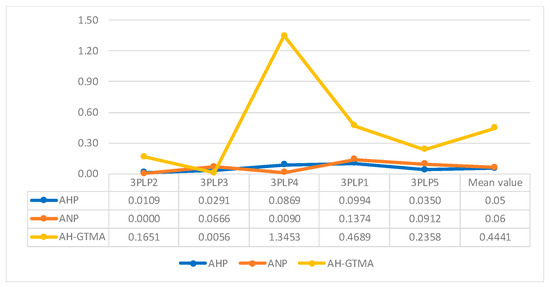
Figure 2.
Distinguishable coefficient Ki for AHP, ANP, and AH-GTMA.
In order to validate the proposed method, a sensitivity analysis of the most significant criteria is also carried out. From Table 4 it is possible to note that, in the AHP evaluation, the most important criteria are two: Cost of warehousing () and costs of inventory management ().
Thus, the sensitivity analysis is performed separately for each method and for each criterion by changing the value of the criterion weight from 0.0001 to 0.95 by a step of 0.05 (the values of the other criteria are not changed) to evaluate the impact of performed change to the alternatives ranking. The results are presented in Figure 3.
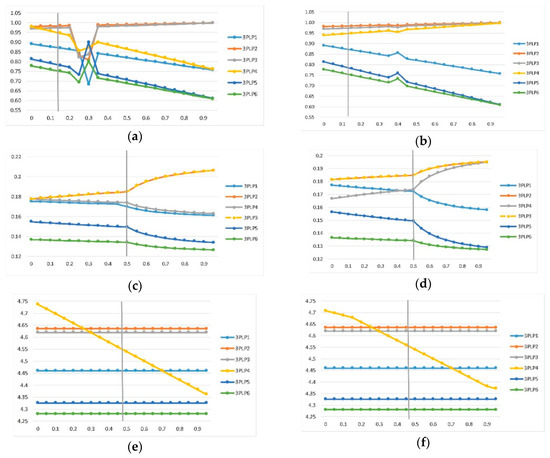
Figure 3.
Sensitivity analysis: (a) criteria C11 and AHP method; (b) criteria C12 and AHP method; (c) criteria C11 and ANP method; (d) criteria C12 and ANP method; (e) criteria C11 and AH-GTMA method; (f) criteria C12 and AH-GTMA method.
In Figure 3, the vertical grey line represents the optimal solution for each method. In the case of the AHP method it is possible to note that if the weight is between 0.2 and 0.35 the ranking of the alternatives is not stable (Figure 3a). A variation of the weight (Figure 3b) does not change the final ranking of the alternatives by the AHP method, but if the weight is increased above 0.5 then the distinctiveness between the alternatives (3PLP2, 3PLP3, and 3PLP4) decreases significantly. In the case of the ANP method (Figure 3d) the solution is not stable. If the weight is increased above 0.5 the rank of the alternatives changes to 3PLP2 = 3PLP3 3PLP4 > 3PLP1 > 3PLP5 > 3PLP6, so that the alternative 3PLP4 has a better rank than 3PLP1.
In the case of the AH-GTMA method (Figure 3e,f) the variation in the weight of the two main criteria, between 0.3 and 0.7, does not change the final ranking of the alternatives. Before the lower limit of the range the rank of the alternatives changes to 3PLP4 > 3PLP2 > 3PLP3 > 3PLP1 > 3PLP5 > 3PLP6; and after the upper limit of the range the rank of the alternatives changes to 3PLP2 > 3PLP3 > 3PLP1 > 3PLP4 > 3PLP5 > 3PLP6. At the same time, as in the original solution, the distinctiveness between the alternatives is maintained.
The AH -GTMA method thus enables decision makers to make the right decision in the case of very similar alternatives with a stable ranking and a more stable distinguishability, with respect to the AHP and ANP methods.
In case of large (complex) decision-making problems it is also important to minimize the number of required pairwise comparisons. An excessive number of comparisons, with respect to the well accepted AHP method, can induce DMs to make errors caused by inattention. Thus decision makers, managers, and practitioners, since they do not have a deep knowledge of the methods, often neglect time-consuming methods at the expense of the accuracy of results. In the proposed numerical example, using Equations (10) and (11) and analysing the decision matrix (supermatrix), the required pairwise comparisons in the AHP and the AH-GTMA methods total 65, while ANP requires 812.
5. Discussion and Conclusions
From the literature review it is possible to note that the GTMA method was used in the LP selection problem in one only article (while the integration of the AHP and the GTMA method has never been used), although it is much simpler than the most frequently used ANP method.
When using the ANP method, the decision maker needs to define a complex cluster network structure with feedback connections, so the number of required pairwise comparisons is very high and rapidly increases when increasing the number of criteria (see Equation (11)). Moreover, in all clusters a consistency check is mandatory. The decision maker needs to make pairwise comparisons between clusters, criteria, and alternatives, keeping consistency in mind. One positive characteristic of the ANP method is the possibility to structure a decision problem process in detail and to include all the elements: Criteria, alternatives, relations, implications, and feedback.
The AH-GTMA method also includes the interdependency of the attributes and impact of the attributes in the decision-making process expressed through the use of the AHP evaluation in all the clusters. The relative importance of criteria (attributes) and the alternative values are given as the input of the permanent function and the performance attribute index is obtained as output. Thus, in this case the number of attributes does not complicate the computation of the output index and also the consistency check is made within the cluster, when the AHP method is used. Moreover, decision makers do not need to evaluate any correlations and influences between the various elements of the decision-making graph.
Comparing the AH-GTMA, AHP, and ANP methods in order to detect the most user friendly and effective in a case of complex decision-making problems, all of which are based on a digraph structure, the authors have found that the AH-GTMA produces equivalent results to the other two methods, is much easier to use than the ANP and, most importantly, the method is easier in the case of complex decision-making problems (a large number of criteria and alternatives and interdependency between the elements), such as the LP selection problem. Moreover, in case of very similar alternatives, the distinguishable coefficient of the AH-GTMA method is higher than those computed for the AHP and ANP. Therefore, the AH-GTMA method allows decision makers to rank comparable (very close) alternatives. The AH-GTMA method, moreover, allows decision makers to combine structurally similar methods without increasing the number of comparisons and the understanding of the results. The method is therefore very useful in every decision-making problem where a decision maker requires a ranking of alternatives (also very close) and in every field/sector where many numbers of criteria and alternatives exist.
There are only a few articles [58,59,60,61] that deal with the supplier selection problem and use the GTMA method, and only one article [5] that designed a systematic approach to evaluate a transportation firm by integrating FDM with GTMA. In regard to those articles the authors propose an integration of the AHP and the GTMA method, allowing for interdependency between attributes, and can be efficiently used instead of the more complicated ANP method (large number of comparisons). Moreover, the authors also computed the distinguishable index between the alternative ranks and made a sensitivity analysis to highlight that the efficiency of the defined AH-GTMA method in cases of complex decision-making problems with very similar alternatives.
Paramasivan, Senthil, and Rajam Ramasamy [3] are the only authors who compare the AHP, the ANP and the GTMA methods and use it on the equipment selection problem. In their article there are no sensitivity and distinguishability analyses on obtained results. The authors only conclude that the GTMA can be applied to any type of optimization problem, especially on those involving a large number of attributes. The authors of this paper confirmed all the already known facts of the past studies. Even more, by performing sensitivity analyses and computing the distinguishable index between the alternative ranks, the authors illustrate that the AH-GTMA method enables decision makers to make a proper decision in case of alternatives that are very similar, with a stable ranking and high distinguishability with respect to the AHP and the ANP methods.
The present analysis answers the decision makers’ dilemma regarding which method or combinations of methods to apply in complex decision-making. Decision makers need a relatively simple, reliable method which is not terribly time consuming. They do not have a deep knowledge of the methods and lack experience regarding the use of methods. AH-GTMA increases the efficiency of the complex decision-making problem, reduces the risk of the improper selection of an alternative and encourages decision makers to use MCDM methods. The method is not as time consuming as the ANP and meets decision makers’ expectations.
The results developed in this paper call for further analysis in other sectors in addition to the logistics sector. The authors are sure that this research will stimulate additional theory-building in this field and that the proposed comparison will be further improved using qualitative and quantitative methods. One option would be a multiple case study methodology for evaluating the proposed method.
The authors are sure that the assertions put forward in this paper will lead to the greater use of the proposed method, but also to the growing recognition that an effective solution to the decision-making problem requires an uncomplicated, robust and reliable method which is easy to use.
Author Contributions
Authors’ Conceptualization, D.T.-S.; data curation, D.T.-S. and P.B.; formal analysis, P.B. and D.T.-S.; investigation, P.B. and D.T.-S.; methodology, D.T.-S.; validation; D.T.-S. and P.B.; writing—original draft D.T.-S.; writing—review and editing, P.B. and D.T.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rao, R.V. Decision Making in the Manufacturing Environment: Using Graph Theory and Fuzzy Multiple Attribute Decision Making Methods; Springer: London, UK, 2007. [Google Scholar]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Paramasivam, V.; Senthil, V.; Rajam Ramasamy, N. Decision making in equipment selection: An integrated approach with digraph and matrix approach, AHP and ANP. Int. J. Adv. Manuf. Technol. 2011, 54, 1233–1244. [Google Scholar] [CrossRef]
- Saaty, T.; Vargas, L. The Analytic Network Process; Springer US: Boston, MA, USA, 2006; pp. 1–26. [Google Scholar] [CrossRef]
- Kabir, G.; Sumi, R.S. Integrating fuzzy Delphi with graph theory and matrix methods for evaluation of hazardous industrial waste transportation firm. Int. J. Logist. Econ. Glob. 2012, 4, 221–237. [Google Scholar] [CrossRef]
- Bajec, P.; Tuljak-Suban, D. A Framework for Detecting the Proper Multi-Criteria Decision-Making Method Taking into Account the Characteristics of Third-Party Logistics, the Requirements of Managers, and the Type of Input Data. In Application of Decision Science in Business and Management; Márquez, F.P.G., Ed.; IntechOpen: Rijeka, Croatia, 2019. [Google Scholar] [CrossRef][Green Version]
- Xiu, G.; Chen, X. The third party logistics supplier selection and evaluation. J. Softw. 2012, 7, 1783–1790. [Google Scholar] [CrossRef]
- Mohammaditabar, D.; Teimoury, E. Integrated freight Transportation carrier selection and network flow assignment: Methodology and case study. J. Appl. Sci. 2008, 8, 2928–2938. [Google Scholar] [CrossRef]
- Lehmusvaara, A.; Tuominen, M.; KORPELA, J. An integrated approach for truck carrier selection. Int. J. Logist. Res. Appl. 1999, 2, 5–20. [Google Scholar] [CrossRef]
- Ji, G. Market-motivated value systems, reverse logistics and the evaluation model for the third party reverse logistics providers. Int. Logist. Trade 2006, 4, 53–92. [Google Scholar] [CrossRef]
- Tavana, M.; Zareinejad, M.; Di Caprio, D.; Kaviani, M.A. An integrated intuitionistic fuzzy AHP and SWOT method for outsourcing reverse logistics. Appl. Soft Comput. 2016, 40, 544–557. [Google Scholar] [CrossRef]
- Ecer, F. Third-party logistics (3PLs) provider selection via Fuzzy AHP and EDAS integrated model. Technol. Econ. Dev. Econ. 2018, 24, 615–634. [Google Scholar] [CrossRef]
- Ho, W.; He, T.; Lee, C.K.M.; Emrouznejad, A. Strategic logistics outsourcing: An integrated QFD and fuzzy AHP approach. Expert Syst. Appl. 2012, 39, 10841–10850. [Google Scholar] [CrossRef]
- Prakash, C.; Barua, M. A combined MCDM approach for evaluation and selection of third-party reverse logistics partner for Indian electronics industry. Sustain. Prod. Consum. 2016, 7, 66–78. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Göçer, F.; Karabulut, Y. A new group decision making approach with IF AHP and IF VIKOR for selecting hazardous waste carriers. Measurement 2019, 134, 66–82. [Google Scholar] [CrossRef]
- Shan, L. Research on logistics service providers selection based on AHP and VIKOR. In Intelligent Computing and Information Science; Springer: New York, NY, USA, 2011; pp. 93–98. [Google Scholar]
- Hasan, K.; Albayrakoglu, M.M. Selecting a third-party logistics provider for an autmomtive company: An analytic hierarchy process model. In Proceedings of the International Symposium on the Analytic Hierarchy Process, Viña Del Mar, Chile, 3–6 August 2007. [Google Scholar]
- Soh, S. A decision model for evaluating third-party logistics providers using fuzzy analytic hierarchy process. Afr. J. Bus. Manag. 2010, 4, 339–349. [Google Scholar]
- Gürcan, Ö.F.; Yazıcı, İ.; Beyca, Ö.F.; Arslan, Ç.Y.; Eldemir, F. Third Party Logistics (3PL) Provider Selection with AHP Application. Procedia Soc. Behav. Sci. 2016, 235, 226–234. [Google Scholar] [CrossRef]
- Daim, T.U.; Udbye, A.; Balasubramanian, A. Use of analytic hierarchy process (AHP) for selection of 3PL providers. J. Manuf. Technol. Manag. 2012, 24, 28–51. [Google Scholar] [CrossRef]
- Teker, S.Ç. The Implementation of Analytic Hierarchy Process In Pharmaceutical Industry For Selection Process Of 3rd Party Logistics Service Provider. Öneri Dergisi 2017, 12, 107–124. [Google Scholar]
- Garg, K.; Agarwal, V.; Jha, P. Transportation Decision Making Through Logistics Outsourcing and 3PL Selection in an Integrated Closed-Loop Supply Chain. In Proceedings of the Fourth International Conference on Soft Computing for Problem Solving, Silchar, Assam, India, 27–29 December 2014; pp. 473–485. [Google Scholar]
- Göl, H.; Çatay, B. Third-party logistics provider selection: Insights from a Turkish automotive company. Supply Chain Manag. Int. J. 2007, 12, 379–384. [Google Scholar] [CrossRef]
- Sardana, G.; Thatchenkery, T.; Vijayvargiya, A.; Dey, A. An analytical approach for selection of a logistics provider. Manag. Decis. 2010, 48, 403–418. [Google Scholar]
- Niestrój, K. The Conformity Assessment of Lead Logistics Provider and Third Party Logistics Preferences Using Analytic Hierarchy Process Method (AHP). J. Econ. Manag. Univ. Econ. Katow. 2013, 2013, 61–74. [Google Scholar]
- Chiang, Z.; Tzeng, G.-H. A Third Party Logistics Provider for the Best Selection in Fuzzy Dynamic Decision Environments. Int. J. Fuzzy Syst. 2009, 11, 9. [Google Scholar]
- Çakir, E.; Tozan, H.; Vayvay, O. A method for selecting third party logistic service provider using fuzzy AHP. J. Naval Sci. Eng. 2009, 5, 38–54. [Google Scholar]
- Nitin Kumar, S.; Atul Kumar, S.; Anoop Kumar, S. Fuzzy-AHP: A Boon in 3PL Decision Making Process. In Theoretical and Practical Advancements for Fuzzy System Integration; Li, D.-F., Ed.; IGI Global: Hershey, PA, USA, 2017; pp. 97–125. [Google Scholar] [CrossRef]
- Ramírez-Flórez, G.; Tabares-Urrea, N.; Osorio-Gómez, J.C. Fuzzy AHP for 3PL supplier’s performance evaluation considering risk. Facultad de Ingeniería 2017, 26, 165–172. [Google Scholar]
- Efendigil, T.; Önüt, S.; Kongar, E. A holistic approach for selecting a third-party reverse logistics provider in the presence of vagueness. Comput. Ind. Eng. 2008, 54, 269–287. [Google Scholar] [CrossRef]
- Kabir, G. Third party logistic service provider selection using fuzzy AHP and TOPSIS method. Int. J. Qual. Res. 2012, 6, 71–79. [Google Scholar]
- Rajesh, R.; Pugazhendhi, S.; Muralidharan, C.; Ganesh, K. Development of a composite model for selection of third party logistics service provider. Int. J. Electron. Cust. Relatsh. Manag. 2009, 3, 375–401. [Google Scholar] [CrossRef]
- Singh, R.K.; Gunasekaran, A.; Kumar, P. Third party logistics (3PL) selection for cold chain management: A fuzzy AHP and fuzzy TOPSIS approach. Ann. Oper. Res. 2018, 267, 531–553. [Google Scholar] [CrossRef]
- Xiuqing, Y.; Lina, Z. Study on Selection of 3pl service providers based on improved AHP and TOPSIS method. J. Henan Univ. Sci. Technol. 2013, 3, 127–129. [Google Scholar]
- Perçin, S. Evaluation of third-party logistics (3PL) providers by using a two-phase AHP and TOPSIS methodology. Benchmarking Int. J. 2009, 16, 588–604. [Google Scholar] [CrossRef]
- Kumar, P. An integrated model of AHP and TOPSIS for 3PL evaluation. Asia Pac. Bus. Rev. 2008, 4, 14–21. [Google Scholar] [CrossRef]
- Akman, G.; Baynal, K. Logistics Service Provider Selection through an Integrated Fuzzy Multicriteria Decision Making Approach. J. Ind. Eng. 2014, 2014, 794918. [Google Scholar] [CrossRef]
- Kishore, P.; Padmanabhan, G. An Integrated Approach of Fuzzy AHP and Fuzzy TOPSIS to Select Logistics Service Provider. J. Manuf. Sci. Prod. 2016, 6, 51–59. [Google Scholar] [CrossRef]
- Bianchini, A. 3PL provider selection by AHP and TOPSIS methodology. Benchmarking Int. J. 2018, 25, 235–252. [Google Scholar] [CrossRef]
- Singh, R.; Shankar, R.; Kumar, P.; Singh, R.K. A fuzzy AHP and TOPSIS methodology to evaluate 3PL in a supply chain. J. Model. Manag. 2012, 7, 287–303. [Google Scholar]
- Bansal, A.; Kumar, P. 3PL selection using hybrid model of AHP-PROMETHEE. Int. J. Serv. Oper. Manag. 2013, 14, 373–397. [Google Scholar] [CrossRef]
- Gupta, R.; Sachdeva, A.; Bhardwaj, A. Selection of logistic service provider using fuzzy PROMETHEE for a cement industry. J. Manuf. Technol. Manag. 2012, 23, 899–921. [Google Scholar] [CrossRef]
- Jung, H. Evaluation of Third Party Logistics Providers Considering Social Sustainability. Sustainability 2017, 9, 777. [Google Scholar] [CrossRef]
- Yilmaz, O.; Endüstri, B.Y.; Güneri, A.F.; Gülsün, B.; Özgürler, Ş. A solution to customer selection problem in logistics using the Analytic Network Process (ANP). In Proceedings of the Trends in the Development of Machinery and Associated Technology, TMT Mediteranean Cruise, Venice, Italy, 11–18 September 2010. [Google Scholar]
- Fadavi, A.; Khanghah, A.S.; Asli, M.N. A Hybrid Model for Supplier Selection in Outsourcing: Evidence from Shima Film Company in Iran. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 3298–3305. [Google Scholar] [CrossRef]
- Cooper, O.; Tadikamalla, P.; Shang, J. Selection of a Third-Party Logistics Provider: Capturing the Interaction and Influence of Performance Metrics with the Analytical Network Process. J. Multi Criteria Decis. Anal. 2012, 19, 115–128. [Google Scholar] [CrossRef]
- Janssen, L.; Claus, T.; Sauer, J. Literature review of deteriorating inventory models by key topics from 2012 to 2015. Int. J. Prod. Econ. 2016, 182, 86–112. [Google Scholar] [CrossRef]
- Liou, J.J.H.; Chuang, Y.-T. Developing a hybrid multi-criteria model for selection of outsourcing providers. Expert Syst. Appl. 2010, 37, 3755–3761. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Liou, J.J.H.; Chuang, Y.-C. Integrating DANP and modified grey relation theory for the selection of an outsourcing provider. Expert Syst. Appl. 2013, 40, 2297–2304. [Google Scholar] [CrossRef]
- Wong, J.-T. DSS for 3PL provider selection in global supply chain: Combining the multi-objective optimization model with experts’ opinions. J. Intell. Manuf. 2012, 23, 599–614. [Google Scholar] [CrossRef]
- Thakkar, J.; Deshmukh, S.; Gupta, A.; Shankar, R. Selection of third-party logistics (3PL): A hybrid approach using interpretive structural modeling (ISM) and analytic network process (ANP). Supply Chain Forum Int. J. 2005, 6, 32–46. [Google Scholar] [CrossRef]
- Zareinejad, M.; Javanmard, H. Evaluation and selection of a third-party reverse logistics provider using ANP and IFG-MCDM methodology. Life Sci. J. 2013, 10, 350–355. [Google Scholar]
- Senturk, S.; Erginel, N.; Binici, Y. Interval Type-2 Fuzzy Analytic Network Process for Modelling a Third-party Logistics (3PL) Company. J. Mult. Valued Logic Soft Comput. 2017, 28, 311–333. [Google Scholar]
- Tavana, M.; Zareinejad, M.; Santos-Arteaga, F.J.; Kaviani, M.A. A conceptual analytic network model for evaluating and selecting third-party reverse logistics providers. Int. J. Adv. Manuf. Technol. 2016, 86, 1705–1721. [Google Scholar] [CrossRef]
- Esra Aytaç, A.; Egül, A.T. Integration of DEMATEL, ANP and DEA methods for third party logistics providers’ selection. Manag. Sci. Lett. 2016, 6, 325–340. [Google Scholar] [CrossRef]
- Raut, R.; Kharat, M.; Kamble, S.; Kumar, C.S. Sustainable evaluation and selection of potential third-party logistics (3PL) providers: An integrated MCDM approach. Benchmarking Int. J. 2018, 25, 76–97. [Google Scholar] [CrossRef]
- Muduli, K.; Govindan, K.; Barve, A.; Geng, Y. Barriers to green supply chain management in Indian mining industries: A graph theoretic approach. J. Clean. Prod. 2013, 47, 335–344. [Google Scholar] [CrossRef]
- Agrawal, S.; Singh, R.K.; Murtaza, Q. Disposition decisions in reverse logistics: Graph theory and matrix approach. J. Clean. Prod. 2016, 137, 93–104. [Google Scholar] [CrossRef]
- Mohaghar, A.; Kashef, M.; Khanmohammadi, E. A novel technique to solve the supplier selection problems: Combination of decision making trial & evaluation laboratory, graph theory and matrix approach methods. Int. J. Ind. Eng. 2014, 25, 103–113. [Google Scholar]
- Athawale, V.M.; Mukherjee, P.; Chakraborty, S. Supplier Selection Using Multi-Criteria Decision-Making Methods. IUP J. Oper. Manag. 2009, 8, 831–851. [Google Scholar]
- Malik, S.; Kumari, A.; Agrawal, S. Selection of Locations of Collection Centers for Reverse Logistics Using GTMA. Mater. Today Proc. 2015, 2, 2538–2547. [Google Scholar] [CrossRef]
- Zhuang, Z.-Y.; Lin, C.-C.; Chen, C.-Y.; Su, C.-R. Rank-Based Comparative Research Flow Benchmarking the Effectiveness of AHP–GTMA on Aiding Decisions of Shredder Selection by Reference to AHP–TOPSIS. Appl. Sci. 2018, 8, 1974. [Google Scholar] [CrossRef]
- Safari, H.; Faghih, A.; Fathi, M.R. Integration of graph theory and matrix approach with fuzzy AHP for equipment selection. J. Ind. Eng. Manag. (JIEM) 2013, 6, 477–494. [Google Scholar]
- Chaghooshi, A.J.; Safari, H.; Fathi, M.R. Integration of fuzzy AHP and fuzzy GTMA for location selection of gas pressure reducing stations: A case study. J. Manag. Res 2012, 4, 152–169. [Google Scholar]
- Singh, D.; Rao, R. A hybrid multiple attribute decision making method for solving problems of industrial environment. Int. J. Ind. Eng. Comput. 2011, 2, 631–644. [Google Scholar] [CrossRef]
- Mu, E.; Pereyra-Rojas, M. Practical Decision Making: An Introduction to the Analytic Hierarchy Process (AHP) Using Super Decisions V2; Springer: Pittsburg, PA, USA, 2017. [Google Scholar]
- Brunelli, M. Introduction to the Analytic Hierarchy Process; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Saaty, T.L. Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World; RWS Publications: Pittsburgh, PA, USA, 1990. [Google Scholar]
- Lanjewar, P.B.; Rao, R.V.; Kale, A.V. Assessment of alternative fuels for transportation using a hybrid graph theory and analytic hierarchy process method. Fuel 2015, 154, 9–16. [Google Scholar] [CrossRef]
- Saaty, T.L. Axiomatic Foundation of the Analytic Hierarchy Process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Tuljak-Suban, D.; Bajec, P. The Influence of Defuzzification Methods to Decision Support Systems Based on Fuzzy AHP with Scattered Comparison Matrix: Application to 3PLP Selection as a Case Study. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2018, 26, 475–491. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process: The Organization and Prioritization of Complexity; Rws Publications: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Kordi, M. Comparison of Fuzzy and Crisp Analytic Hierarchy Process (AHP) Methods for Spatial Multicriteria Decision Analysis in GIS; University of Gävle: Gävle, Sweden, 2008. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Geetha, N.K.; Sekar, P. Graph Theory Matrix Approach–A Qualitative Decision Making Tool. Mater. Today Proc. 2017, 4, 7741–7749. [Google Scholar] [CrossRef]
- Beineke, L.W.; Wilson, R.J.; Cameron, P.J. Topics in Algebraic Graph Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Jurkat, W.B.; Ryser, H.J. Matrix factorizations of determinants and permanents. J. Algebra 1966, 3, 1–27. [Google Scholar] [CrossRef]
- Tung, Y.A. Time complexity and consistency issues in using the AHP for making group decisions. J. Multi Criteria Decis. Anal. 1998, 7, 144–154. [Google Scholar] [CrossRef]
- Kadoić, N.; Divjak, B.; Begičević Ređep, N. Integrating the DEMATEL with the analytic network process for effective decision-making. Cent. Eur. J. Oper. Res. 2018. [Google Scholar] [CrossRef]
- Han, Q.; Li, W.; Song, Y.; Zhang, T.; Wang, R. A New Method for MAGDM Based on Improved TOPSIS and a Novel Pythagorean Fuzzy Soft Entropy. Symmetry 2019, 11, 905. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).