Abstract
This letter extends my recent paper on antiferromagnetic NiO [Structural Distortion Stabilizing the Antiferromagnetic and Insulating Ground State of NiO, Symmetry 2020, 12(1), 56] by including also the paramagnetic phase of this compound. I report evidence that paramagnetic NiO possesses a narrow, roughly half-filled energy band that produces a nonadiabatic atomic-like motion providing the basis for a Mott insulator in the paramagnetic phase. While the atomic-like motion operating in the antiferromagnetic phase is adapted to the symmetry of the antiferromagnetic state, in the paramagnetic phase, the related localized states are represented by optimally localized Wannier functions possessing the full fcc symmetry of paramagnetic NiO. The nonadiabatic Wannier states are twofold degenerate, have d-like symmetry, and are situated at the Ni atoms.
1. Introduction
In my previous paper [1] on NiO, I reported evidence that the structural distortion of antiferromagnetic NiO stabilizes the antiferromagnetic and insulating ground state of this compound. This state is enabled by the nonadiabatic atomic-like motion of the electrons in the “magnetic super band” defined within the nonadiabatic Heisenberg model (NHM) [1]. Because this atomic-like motion only exists in the space group of the antiferromagnetic phase, paramagnetic NiO should be metallic.
However, paramagnetic NiO is also found to be an insulator [2]. As is generally accepted [3], Mott insulation is in any case a manifestation of atomic-like electrons [4] occupying localized orbitals as long as possible and performing their band motion by hopping from one atom to another. In view of my observation that the nonadiabatic atomic-like motion defined within the NHM is evidently responsible for the insulating ground states of antiferromagnetic BaMnAs and antiferromagnetic NiO [1], I ask in this letter whether also in the conventional band structure of the fcc paramagnetic phase of NiO there exists a narrow half-filled energy band producing a nonadiabatic atomic-like motion at the Fermi level. In the following Section 2, I show that this is actually the case.
2. Nonadiabatic Atomic-Like Motion in Paramagnetic NiO
Any atomic-like motion as defined within the NHM is represented by optimally localized symmetry-adapted Wannier function being an exact unitary transformation of the Bloch functions of a narrow, roughly half-filled energy band [1]. For the construction of such Wannier functions, we need a closed energy band in the conventional band structure [1] not connected by symmetry with other bands. Just as in my former papers, a closed complex of individual energy bands is referred to a closed (single) band consisting of branches [5]. However, such narrow closed bands generally cannot be found in the band structures of the metals unless we consider superconducting or magnetic bands [5] possessing a reduced symmetry.
An exception (but presumably not the only exception) is paramagnetic NiO, as demonstrated by Figure 1 and Table 1. Figure 1 shows the conventional band structure of paramagnetic NiO as determined in [1]. Each row in Table 1 defines a band with Bloch functions that can be unitarily transformed into Wannier functions being
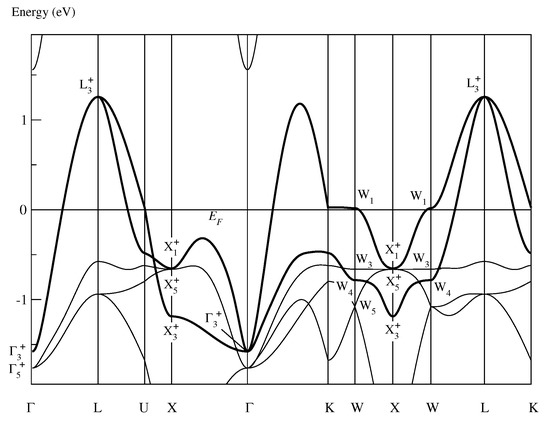
Figure 1.
Conventional band structure of paramagnetic fcc NiO as given in Figure 1 of [1]. The notations of the points of symmetry in the Brillouin zone for follow Figure 3.14 of [7], and the symmetry labels are defined in Table A1 of [1]. The “insulating band” is highlighted by the bold line.

Table 1.
Symmetry labels of the Bloch functions at the points of symmetry in the Brillouin zone for (225) of all the energy bands with symmetry-adapted and optimally localized Wannier functions centered at the Ni (Table a) and O (Table b) atoms, respectively.
- as well localized as possible (according to Definition 5 of [5]);
- centered at the Ni (Table a) or O (Table b) atoms; and
- symmetry-adapted to (according to Equation (10) of [5]).
Thus, the Wannier functions of each listed band may define a nonadiabatic atomic-like motion in paramagnetic NiO when the band is roughly half-filled [6].
The bands in Table 1 are determined following Theorem 5 of Ref. [5]. However, the group theory of Wannier functions presented in [5] is consistently restricted to Wannier functions belonging to a one-dimensional representation of the point group of their position, as it is suggested by superconducting and magnetic bands (Section 2.2 of [5]). Nevertheless, the formalism can be extended to degenerate Wannier functions. This shows that Theorem 5 is applicable to degenerate Wannier functions when the complex numbers in Equation (39) of [5] are interpreted as the characters of the ith representation of . Clearly, the and are identical for one-dimensional representations.
By inspection of Figure 1 and Table 1, we recognize that, first, the “active band” highlighted by the bold lines in the band structure of paramagnetic NiO has the symmetry of band 5 in Table 1a and that, secondly, no partly filled band in the band structure of paramagnetic NiO possesses the symmetry of any band in Table 1b. Thus, the active band provides localized states in the paramagnetic phase of NiO allowing the electrons to perform a strongly correlated nonadiabatic atomic-like motion stabilized by the nonadiabatic condensation energy [6]. The nonadiabatic localized states are situated at the Ni atoms and possess symmetry ensuring that the nonadiabatic Hamiltonian of the atomic-like electrons commutes with the symmetry operators of the cubic space group [6].
The active band is neither a magnetic nor a superconducting band because the localized states have the full symmetry of the paramagnetic space group . I call it “insulating band” because it comprises all the branches crossing the Fermi level meaning that all the electrons at the Fermi level take part in the nonadiabatic atomic-like motion.
Definition 1.
The Bloch functions of an “insulating band” can be unitarily transformed into optimally localized Wannier functions symmetry adapted to the full paramagnetic space group of the material in such a way that each Bloch function at the Fermi level belongs to the insulating band.
Thus, the insulating band may produce an Mott insulator in the paramagnetic phase of NiO in the same way as the magnetic super band may produce an insulating ground state in the antiferromagnetic phase [1].
3. Discussion
Since both antiferromagnetic and paramagnetic NiO are insulators, the magnetic super band of antiferromagnetic NiO [1] as well as the insulating band of paramagnetic NiO (Section 2) are (nearly) half-filled and produce a nonadiabatic atomic-like motion evidently stabilizing the Mott insulator. The localized states defining the respective nonadiabatic atomic-like motion are, however, quite different:
3.1. Antiferromagnetic NiO
The nonadiabatic localized states are situated at both the Ni and O atoms and are adapted to the low symmetry of the monoclinic magnetic group (defined in Equation (12) of [1]) of the magnetic structure. The related nonadiabatic atomic-like motion stabilizes both the antiferromagnetic state and the Mott insulator and breaks down in the paramagnetic phase.
3.2. Paramagnetic NiO
The nonadiabatic localized states are situated only at the Ni atoms and are adapted to the full symmetry of the fcc paramagnetic phase. They are twofold degenerate and belong to the representation of the point group of their position. A localized state may be called a “d-like” state because it is a part of an atomic d state splitting into a and a state in the fcc crystal field; see Table 2.7 of [7]. The related nonadiabatic atomic-like motion evidently stabilizes the Mott insulation because it is in accordance with the general consent that the insulating phase occurs in crystals with partially occupied d shells [3,8] being “somehow localized” [2]. Notably, the nonadiabatic atomic-like motion within the NHM allows a polymorphous description of atomic-like electrons [3] because the electronic orbitals within the nonadiabatic localized states possess the symmetry of the lattice on the average of time, but not at any moment (while in the adiabatic system the electrons move on rigid orbitals being symmetric with respect to the lattice at any moment); see Section II of [6].
4. Conclusions
The NHM provides an atomic-like motion in both antiferromagnetic and paramagnetic NiO being evidently the basis of the Mott insulation in this compound. This letter demonstrates again that the nonadiabatic atomic-like motion defined within the NHM has physical reality and may qualify a material to be a Mott insulator. Of course, the other antiferromagnetic and insulating metal monoxides MnO, FeO, and CoO should also be examined in terms of magnetic super bands and insulating bands.
Funding
This publication was supported by the Open Access Publishing Fund of the University of Stuttgart.
Acknowledgments
I am very indebted to Guido Schmitz for his support of my work.
Conflicts of Interest
The author declares no conflict of interest.
References
- Krüger, E. Structural Distortion Stabilizing the Antiferromagnetic and Insulating Ground State of NiO. Symmetry 2019, 12, 56. [Google Scholar] [CrossRef]
- Brandow, B. Electronic structure of Mott insulators. Adv. Phys. 1977, 26, 651–808. [Google Scholar] [CrossRef]
- Trimarchi, G.; Wang, Z.; Zunger, A. Polymorphous band structure model of gapping in the antiferromagnetic and paramagnetic phases of the Mott insulators MnO, FeO, CoO, and NiO. Phys. Rev. B 2018, 97, 035107. [Google Scholar] [CrossRef]
- Hubbard, J. Elelectron correlations in narrow energy bands. Proc. R. Soc. Lond. Ser. A 1963, 276, 238–257. [Google Scholar]
- Krüger, E.; Strunk, H.P. Group Theory of Wannier Functions Providing the Basis for a Deeper Understanding of Magnetism and Superconductivity. Symmetry 2015, 7, 561–598. [Google Scholar] [CrossRef]
- Krüger, E. Nonadiabatic extension of the Heisenberg model. Phys. Rev. B 2001, 63, 144403-1-13. [Google Scholar] [CrossRef]
- Bradley, C.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids; Claredon: Oxford, UK, 1972. [Google Scholar]
- Austin, I.G.; Mott, N.F. Metallic and Nonmetallic Behavior in Transition Metal Oxides. Science 1970, 168, 71–77. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).